Probing the effects of gating on the ion occupancy of the K⁺ channel selectivity filter using 2D IR spectroscopy

Abstract

The interplay between the intracellular gate and the selectivity filter underlies the structural basis for gating in potassium ion channels. Using a combination of protein semisynthesis, two-dimensional infrared (2D IR) spectroscopy, and molecular dynamics (MD) simulations, we probe the ion occupancy at the S1 binding site in the constricted state of the selectivity filter of the KcsA channel when the intracellular gate is open and closed. The 2D IR spectra resolve two features, whose relative intensities depend on the state of the intracellular gate. By matching the experiment to calculated 2D IR spectra of structures predicted by MD simulations, we identify the two features as corresponding to states with S1 occupied or unoccupied by K⁺. We learn that S1 is >70% occupied when the intracellular gate is closed and <15% occupied when the gate is open. Comparison of MD trajectories show that opening of the intracellular gate causes a structural change in the selectivity filter, which leads to a change in the ion occupancy. This work reveals the complexity of the conformational landscape of the K⁺ channel selectivity filter and its dependence on the state of the intracellular gate.

Graphical Abstract

Introduction

Potassium ion channels are essential to the process of electrical signaling in excitable cells, carrying out their function through the seamless switching between conductive and non-conductive conformations¹. The ion pathway through a K⁺ channel is controlled (gated) at two distinct points: the selectivity filter and the bundle crossing² (Fig. 1A). The selectivity filter consists of four K⁺ binding sites that are formed mainly by the backbone carbonyl oxygens (labeled S1–S4, extracellular to intracellular) (Fig. 1B). Structural studies on the KcsA K⁺ channel have identified two distinct conformations of the selectivity filter that are referred to as the conductive and the constricted states³. In the conductive conformation, the carbonyl oxygens point inwards to facilitate the coordination of K⁺ ions, thereby creating a low energy barrier to the passage of K⁺ ions. The conductive conformation has an average ion occupancy of 0.5 in each of the four binding sites at equilibrium^3–4. In the constricted state, the selectivity filter pinches in at Gly77, splaying the carbonyls outwards, thereby destabilizing the S2 and S3 ion binding sites and preventing ion conduction^{1d, 2a, 3b}. The other locus at which K⁺ permeation is controlled is the inner bundle gate which is formed by crossing of the pore lining transmembrane helices, one from each subunit. At neutral pH in the KcsA channel, the bundle gate is in the closed state wherein the separation between the helices is too narrow for the permeation of a K⁺ ion (Fig. 1C). At low pH, the bundle gate is in the open conformation with a large separation between the helices that allow the permeation of K⁺.

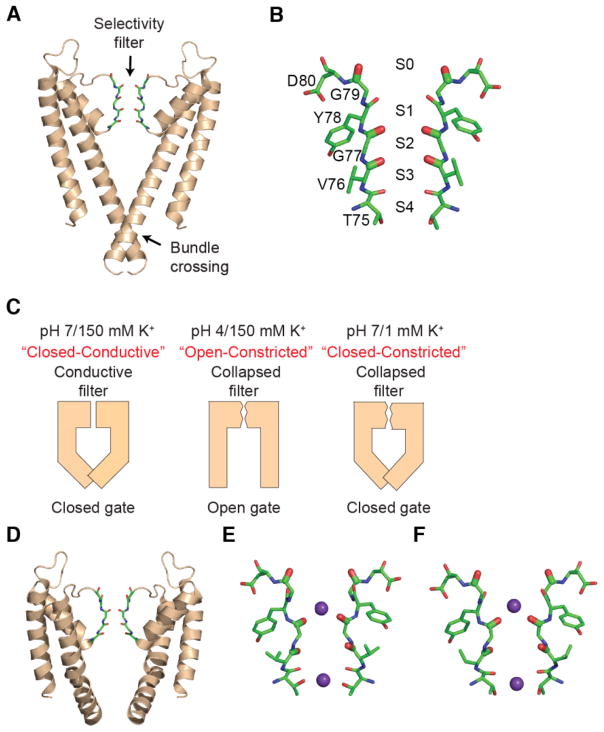
Fig. 1. Structures of KcsA with constricted selectivity filter and open or closed intracellular gates.

(A) Structure of the wild-type KcsA channel (pdb: 1K4C). Two opposite subunits of the tetrameric channel are shown. The selectivity filter (sticks) and the intracellular bundle crossing of the channel are indicated. (B) The backbone carbonyls of residues Thr75 to Gly79 line the selectivity filter and comprise the four ion binding sites (denoted S1 to S4). (C) Different experimental conditions modulate the conformations of the selectivity filter and intracellular gate. At pH 7 and 150 mM K⁺, the selectivity filter is in a conductive conformation and the bundle crossing gate is closed. At pH 4 and 150 mM K⁺, the selectivity filter is constricted and the gate open. Similarly, at pH 7 and 1 mM K⁺, the selectivity filter is constricted and the gate closed. (D) Structure of KcsA in the open-constricted state (pdb: 3F5W). (E) Selectivity filter of KcsA in the open-constricted state (pdb: 3F5W). (F) Selectivity filter of KcsA in the closed-constricted state (pdb: 1K4D).

The bundle crossing gate and the selectivity filter are allosterically coupled. The opening of the bundle crossing gate promotes the transition of the selectivity filter from the conductive to the constricted conformation ^{2a, 5}. Furthermore, depleting the selectivity filter of conductive ions promotes the selectivity filter into the constricted conformation ^{3b, 4}. Thus, the conformation of the two gates in the KcsA channel can be experimentally controlled by sample conditions: high K⁺ and neutral pH favor a channel where the selectivity filter is conductive and the gate is closed (Fig. 1C) ^{3a, 6}. At low pH the inner gate is open, triggering the collapse of the selectivity filter at steady state (Fig 1C)^2a. Finally, low K⁺ promotes the collapse of the selectivity filter even if the inner gate closed (Fig. 1C). Therefore, at neutral pH and low K⁺ (i.e. pH 7, 1 mM K⁺), KcsA is in the “closed-constricted” state, whereas at low pH and high K⁺ (i.e. pH 4, 150 mM K⁺), the channel is in the “open-constricted” conformation. These manipulations and the high degree of coupling between the inner gate and the selectivity filter provide a unique opportunity to study the effects of the large amplitude conformational changes at the inner gate on the structure and ion occupancy of the selectivity filter.

The structure, dynamics and ion occupancy of the selectivity filter has been investigated by X-ray crystallography^3–4, nuclear magnetic resonance (NMR)⁷, and computational approaches⁸. X-ray crystallography elegantly provides the structure of the selectivity filter but does not inform us on the dynamics or the absolute ion occupancies at the selectivity filter sites. Absolute occupancies for heavy ions like Tl⁺ in the KcsA selectivity filter have been determined from anomalous scattering experiments⁴. Similar experiments for K⁺ ions are challenging as the anomalous scattering power of K⁺ is very weak compared to Tl⁺ and have not been reported for the KcsA channel. Likewise, NMR spectroscopy, which has given us insight into conformational dynamics of the selectivity filter^7b and allosteric coupling of the two gates⁹, cannot provide information on the absolute ion occupancies within the filter. Computational approaches such a MD simulations inform us on the dynamics of the selectivity filter, but the predictions of MD simulations are critically dependent on the force field used¹⁰. It is very difficult for MD simulations to correctly predict the correct populations of ion occupancies in the selectivity filter whose energy differences are close to k_BT and within the accuracy of current force fields. To provide a new perspective, we use a combination of 2D IR spectroscopy and molecular dynamics (MD) simulations to investigate the selectivity filter.

Molecular vibrations are reporters of their local electrostatic environment, giving insight into protein structure and dynamics, solvation, and ion binding ^{6, 11}. The time resolution of 2D IR spectroscopy is on the order of picoseconds, which not only provides an instantaneous snapshot of the ensemble of structures and ion binding configurations present under specific experimental conditions, but also allows for 2D IR spectra to be calculated from short MD simulations⁶. As a result, a trajectory that is nanosecond or microseconds in duration can be broken into picosecond segments, each of which can be classified by their structures to create sub-ensembles of structures. Improvements in semi-classical theories in the past few years have made simulated 2D IR spectra of proteins very accurate¹². Thus, the simulated 2D IR spectra calculated for each sub-ensemble can be compared to experiment to provide a test for its prevalence and estimate its contribution to the complete ensemble ^{6, 13}. In essence, the comparison provides an experimental means for ascertaining the relative weights of the populations of each structural state predicted by MD simulations.

We have recently used 2D IR spectroscopy in conjunction with semisynthesis and MD simulations to probe the ion binding configurations of a potassium ion channel selectivity filter in the conductive conformation ⁶. Here, we apply this combined approach to probe the effect of the intracellular gate on the selectivity filter. We determine the ion occupancy and overall conformational distributions of the selectivity filter of the KcsA channel in the open-constricted and closed-constricted conformations. Our results indicate that changes in the intracellular gate are linked to changes in the selectivity filter conformational heterogeneity that are distinct to those triggered by K⁺ depletion. The existence of previously undetected conformational subensembles appear to underlie changes ion affinity at the S1 site in the selectivity filter and point to additional complexities in the conformational dynamics of K⁺ selectivity filter.

Materials and Methods

Semisynthesis of Isotope-Labeled and Control KcsA Channels

The modular semisynthesis of the ¹³C¹⁸O labeled KcsA channel has been described previously ^{6, 14}. Briefly, ¹³C¹⁸O glycine and valine were prepared using an established method ¹⁵ in which Gly-1-¹³C and L-Val-1-¹³C (Cambridge Isotope Laboratories) were ¹⁸O exchanged using ¹⁸O water (Isotec) in acidic conditions. The amino groups of the exchanged ¹³C¹⁸O L-Val and Gly were then protected by tert-butyloxycarbonyl (Boc) using protocols described ^{6, 16}. These protected amino acids were used for the solid phase peptide synthesis (SPPS) of the pore peptide (KcsA_70–81 with the sequence Thz-ETATTVGYGDL-COSR, in which Thz refers to the 1,3-thiazolidine-4-carboxo group). The pore peptide was purified using reverse-phase HPLC and the identity and purity were confirmed using ES-MS.

The recombinant expression and purification of the N-peptide (KcsA_1–69) and C-peptide (KcsA_82–160) have been described previously and were used without modification ^{14, 17}. The KcsA polypeptide was assembled from the recombinant N- and C-peptides and the isotopically labeled pore peptide by two sequential native chemical ligation (NCL) reactions as described previously⁶. Following the semisynthesis, KcsA polypeptide was folded into the native tetrameric state using in vitro folding previously described protocols¹⁷. Following in vitro folding, the KcsA channel was initially purified using immobilized metal affinity chromatography¹⁷. Then, the N-terminal His₆ tag and the 35 C-terminal residues (KcsA_125–160) were removed using previously described methods⁶ and the semisynthetic isotope-labeled channel was purified using size exclusion chromatography (SEC) on a Superdex S-200 column using 50 mM Tris-HCl (pH 7.5), 150 mM KCl and 0.25% (w/v) decyl-β-D- maltoside (DM) as the column buffer. For the 1 mM K⁺ sample, the purified KcsA channel was dialyzed against 50 mM Tris-HCl (pH 7.5), 1 mM KCl and 0.25% DM. Transfer of the KcsA channel to pH 4.0 was carried out by dialysis against 50 mM 1, 4 Diethylpiperazine (pH 4.0), 150 mM KCl and 0.25% DM followed by SEC using the same buffer. The semisynthetic channel has been shown to be functionally similar to the native protein^{14, 18}. The control (unlabeled) KcsA sample was recombinantly expressed and purified as described in previous work ^{6, 19}. Both the labeled and unlabeled KcsA samples at the end of these protocols were in 0.25% (w/v) DM in the buffers described above. Under these conditions, the protein is stable for months at room temperature.

Sample preparation for 2D IR Spectroscopic Measurements

The methods for preparing both the labeled and unlabeled KcsA samples for 2D IR spectroscopic measurements have been described previously⁶. Briefly, samples of KcsA were dried onto a CaF₂ window and subsequently exchanged with 99.9% atom% D deuterium oxide (Sigma-Aldrich) until there is was a marked decrease in the observed water background and absorption at 6 μm. The sample was dried a final time and rehydrated with deuterium oxide to yield a final concentration of 11–14 mg/mL (0.82–1.04 mM) of monomeric KcsA. The samples were then sandwiched between two CaF₂ windows separated by a 56 μm spacer.

2D IR Spectroscopy

The methods for data collection and processing have been described in detail ^6,15. In summary, ~100 fs pulses centered at 800 nm were generated with a commercial oscillator and regenerative amplifier (Spectra-Physics Solstice). The 800 nm light was used to pump a commercial optical parametric amplifier (Topas, Light Conversion) to generate signal and idler. The resultant wavelengths were then mixed in Type II AgGaS₂ crystal of a home-built difference frequency generation setup to produce 6 μm mid-IR light. The mid-IR light was then split into pump and probe lines using a CaF₂ beamsplitter. The pump pulse was sent through a Ge acousto-optic modulator based pulse shaper described²⁰ to generate our pump pulse pair. The pump and probe pulses were then spatially and temporally overlapped at the sample²¹, and the generated 2D IR signal (which follows the probe beampath) was dispersed by a commercial monochromator (Princeton Instruments) onto a 2×64-element mercury cadmium telluride (MCT) array. All spectra were taken with a 0 fs waiting time between the pump and probe pulses.

Difference Spectra

Difference spectra were generated from the labeled and unlabeled spectra as described previously⁶. Briefly, we subtracted the 2D IR spectra collected for labeled and unlabeled KcsA to remove the background from the acid side chains in the frequency range of the ¹³C¹⁸O isotope labels after the spectra were normalized to the ¹²C¹⁶O main band at (ω_pump, ω_probe) = (1652 cm⁻¹, 1656 cm⁻¹) for the low pH spectra, and the ¹²C¹⁶O main band at (ω_pump, ω_probe) = (1648 cm⁻¹, 1656 cm⁻¹) for the low K⁺ spectra. The intensity of the residual amide I feature from the subtraction was minimized by shifting the frequency of the unlabeled spectrum by less than half a pixel along each axis, eliminating background without altering the spectral features.

Molecular Dynamics Simulations of Closed-constricted and Open-constricted KcsA

The methods for the MD simulations of the closed-constricted and open-constricted states of KcsA have been previously described in detail²². Briefly, a 532 ns MD simulation of the closed-constricted state of KcsA in 1-palmitoyl-2-oleoyl-glycero-3-phosphatidylcholine (POPC) was generated using initial coordinates from the crystal structure 1K4D. The simulation was run in an NVT ensemble at 310 K with a Berendsen thermostat (τ = 0.2 ps) using a CHARMM PARAM27 force field and a modified TIP3P water model. The concentration of potassium for these simulations is 1 M. For the open-constricted state, a 532 ns MD simulation of KcsA in a 3:1 mixture of POPC:POPG lipids (where POPG is 1-palmitoyl-2-oleoylglycero-3-phosphatidylglycerol) in 150 to 200 mM potassium chloride was generated and run using CHARMM36 force fields. To maintain the open state of the channel, care was taken to protonate Glu71 as well as all other residues along the activation gate. As quality control, we compared the structures from the MD simulations to the structures obtained by X-ray crystallography, and the results showed that the channel structure was largely conserved between lipids and micelles (data not shown).

Calculation of 2D IR Spectra

Initial configurations for the closed- and open- constricted states, were extracted from the trajectories generated from the MD simulations²². From the 532 ns trajectory, we extracted snapshots every 250 ps, breaking the trajectories into 2128 snapshots which were successively used for response function and 2D IR spectra simulations. All the simulations were carried out using GROMOS53a6 force field²³ and SPC water model²⁴ as implemented in GROMACS 4.5.1 suite of packages ²⁵. Each snapshot, following 3000 steps of steepest-descent minimization, provided a starting point for shorter 25 ps simulations from which the coordinates were extracted every 20 fs and used for 2D IR simulations. Thus, each snapshot, out of 2128 used, corresponded to a single 2D IR spectrum and the final spectra were obtained by averaging over a set of frames.

The amide I vibrational Hamiltonians were calculated using methodologies described previously²⁶. In brief, the diagonal frequencies were calculated using the frequency map developed by Skinner et al ^26b. The frequency map relates the vibrational frequency with the electric field components projected onto the C and N atoms of each amide group in a chromophore as well as takes into account the so-called nearest-neighbor effects²⁷ on frequencies and vibrational couplings. The formula used to calculate the vibrational frequencies of the isotope-labeled amide groups is given as follows

$${\omega }_{01}=1647+7729E_C-3576E_N$$ (1)

To account for vibrational coupling between different amide units, we applied the transition dipole couplings (TDC) approach developed by Torii and Tasumi²⁸ as well as the previously mentioned nearest-neighbor coupling scheme which was derived as a function of the Ramachandran angles to include the effects of relative orientation of the neighboring amino acids ²⁷.

2D IR spectra were simulated using the same theoretical concepts as described elsewhere ²⁹. The vibrational frequency of the overtone (1–2) transition was taken into account by applying a constant offset of −14 cm⁻¹ with respect to the fundamental (0–1) frequency. The vibrational lifetime contribution to the 2D IR lineshape was included ad hoc in the response function formulae with the time constant for vibrational relaxation T₁ = 600fs. All response function calculations and 2DFFT were done using the NISE2A code developed by Jansen and co-workers ³⁰. All calculated 2D IR spectrum reported in this manuscript have a 12 cm⁻¹ shift applied to both the pump and probe axes, which was calibrated using closed-conductive full trajectory simulations and the experimental data.

Hamiltonian Clustering Analysis

To understand how structural features of the selectivity filter can be related to frequencies and lineshapes in the 2D IR spectra, a Hamiltonian clustering analysis was performed. In this study, the clustering algorithm was based on analyzing the vibrational Hamiltonians, obtained from the frequency map, and grouping them through the k-means clustering algorithm³¹. This approach is advantageous because it groups structures from distinct spectra based on the observables, which removes the need to predefine parameters such as bond distances and angles. Following the clustering, various structural analyses can be carried out on each group separately. We employed two different clustering criteria – one based on the eigenvalues of the vibrational Hamiltonians (data not shown) and another one based on vibrational couplings between different isotope-labeled amide groups. Both methods yielded similar results, however, the coupling-based algorithm produced slightly more distinctive spectra and is, in general, more flexible since different coupling pairs can be considered. All the analyses presented in the manuscript were carried out on structures grouped using the coupling-based approach.

The coupling pairs were chosen based on our isotopic labeling scheme. The criteria included both the coupling between Val76 and Gly77 on the same monomer ( ${\delta }_{ij}^{V76-G77}$) as well as the intersite couplings between Gly77 residues on different monomers ( ${\delta }_{ij}^{G77-G77}$) according to the following formula:

$${\mathit{\Delta }}_{ij}={\delta }_{ij}^{V76-G77}+0.5{\delta }_{ij}^{G77-G77}$$ (2)

The parameter Δ_ij is used as a metric to determine how similar individual Hamiltonian pairs are. The values of ${\delta }_{ij}^{V76-G77}$ and ${\delta }_{ij}^{G77-G77}$ were calculated by extracting the couplings from Hamiltonians i and j, and is expressed as a sum of squared differences (SSD) for each Hamiltonian pairs. The first cluster is seeded with both Hamiltonians i and j from the smallest calculated Δ_ij. Once the first cluster is formed, the parameter Δ_ij is then calculated between the ungrouped Hamiltonians i and each Hamiltonian j already assigned to a group. While minimizing, the next Hamiltonian i is added to the group if Δ_ij is smaller than the cutoff value of 20 (cm⁻¹)² for each Hamiltonian j in the group. This process is iterated until no more Hamiltonians i fit the criteria. If there are still ungrouped Hamiltonians, a new cluster is created with the ungrouped Hamiltonians i and j of the smallest parameter Δ_ij. This is performed iteratively until all vibrational Hamiltonians are assigned to a cluster. All structural analyses were done on trajectories of individual clusters using tools commonly available in GROMACS 4.5.1 and VMD 1.9.2 packages ³².

Results and Discussion

2D IR spectra can be measured for entire proteins, but spectral congestion leads to intrinsic difficulties in interpretation. This can be overcome through semisynthetic approaches where isotope labels can be incorporated at specific sites of interest. We have focused on the amide I vibrational mode region of the IR spectrum, which is mainly comprised by the carbonyl stretch in the protein backbone. Thus, we selectively ¹³C¹⁸O isotope label the Val76, Gly77, and Gly79 backbone carbonyls (Fig. 1B), shifting the frequency of these residues by 65 cm⁻¹ to a region of the spectrum free of the 122 other backbone carbonyls. By labeling these positions, 2D IR signals become particularly sensitive to the S1, S2, and S3 binding sites in the selectivity filter (Fig. 1B) ^{6, 33}. However, acidic side-chains still absorb in the region of the isotope labels and therefore a background spectrum was obtained from unlabeled KcsA prepared from otherwise identical conditions. Subtracting this background from all experimental spectra generates a difference spectrum that better resolves the isotope labeled features ⁶. In principle, the isotope labels could also be resolved in a similar manner using FTIR spectroscopy^33–34. In 2D IR spectroscopy, the ¹³C¹⁸O labels are better resolved because the signals scale as the absorptivity squared whereas in FTIR spectroscopy they scale linearly³⁵. Since the ¹³C¹⁸O labels are strong absorbers, they become more pronounced over background signals that are weaker absorbers even if those weak absorbers have higher concentrations³⁶.

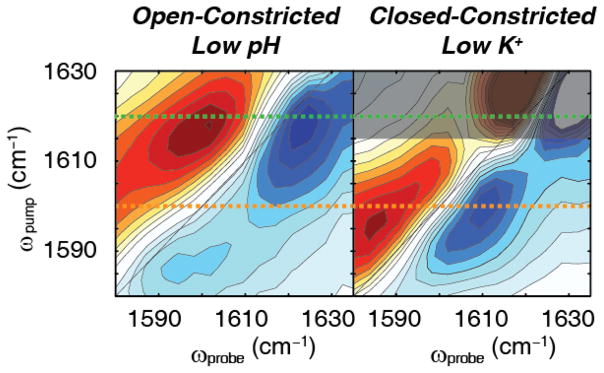
Shown in Fig. 2 are the experimental 2D IR difference spectra for KcsA under conditions that stabilize the open-constricted (low pH and high K⁺ concentrations) and closed-constricted states (neutral pH and low K⁺ concentrations). Under conditions for the open-constricted state, the difference 2D IR spectrum reveals a single pair of peaks, with the blue negative peak corresponding to the ν=0→1 transition and the red positive peak corresponding to the 1→2 transition. The peak pair absorbs around ω_pump = 1618 cm⁻¹ along the pump axis (Fig. 2A). This spectrum is distinct from the previously published spectrum for the selectivity filter in the conductive state in which we see two distinct pairs of peaks, which we later show to correspond to structural conformations of the filter ⁶. The single pair of peaks observed in the difference 2D IR spectrum for the open-constricted state indicates that there does not appear to be structural differences in the channel that are resolved by the experiments here. In the previous study⁶, a flipped state was observed in which the Val76 carbonyl pointed away from the selectivity filter, but that conformation is not observed under the conditions studied here. Under conditions set for the closed-constricted state, a single peak pair of similar intensity is also resolved in the 2D IR difference spectrum, but at a much lower frequency ω_pump = 1599 cm⁻¹ (Fig. 2B). We note that the background signal in the low K⁺ spectra are twice that of the low pH spectra, and could not be reliably subtracted above 1615 cm⁻¹, which we indicate by the darkened region of Fig. 2B. The observed set of peaks are 19 cm⁻¹ below the peak pair observed for low pH, which indicates a significant change in the system. This is a surprising result because we would expect that the selectivity filter would be energetically and conformationally equivalent whether it was driven toward the constricted state by allosteric means (opening the inner gate) or by chemical manipulation (depleting K⁺). Thus, observing two different sets of peaks with a frequency difference of 19 cm⁻¹, indicates that the two constricted conformations of the filter are not equivalent when the inner gate is either open or closed, revealing previously unknown complexities in the conformational landscape of the selectivity filter. The changes in the vibrational frequency observed for the two constricted conformations of the selectivity filter could be either due to a change in the protein structure, the ion occupancy, or the solvation environment in the selectivity filter. As will be shown below, further analysis reveals that the observed shift in the vibrational frequency reflects an unexpected change in K⁺ ion occupancy at the outer binding site S1 of the constricted selectivity filter when the inner gate is either closed or open.

Fig. 2. 2D IR difference spectra of KcsA in low pH and low KCl conditions.

(A) Difference spectrum of KcsA in 150 mM KCl, pH 4 buffer. In this buffer condition, the intracellular gate opens, but the selectivity filter is constricted, creating the open-constricted state. We use the maximum of the 0→1 transition to mark the absorption frequency. The difference spectrum shows a set a pair of high frequency peaks with the (blue) fundamental peak at (ω_pump, ω_probe) = (1618 cm⁻¹, 1624 cm⁻¹). (B) Difference spectrum of KcsA in 1 mM KCl, pH 7 buffer. At pH 7, the intracellular gate remains closed. At low potassium concentration the selectivity filter collapses. Thus, these conditions create the closed-constricted state. In this spectrum, we observe a single pair of peaks with the (blue) fundamental peak at the peak maximum of (ω_pump, ω_probe) = (1599 cm⁻¹, 1609 cm⁻¹). The darkened region indicates background signals that could not be reliably subtracted. Dashed lines at ω_pump = 1620 cm⁻¹ (green) and ω_pump = 1600 cm⁻¹ (orange) are shown as guides.

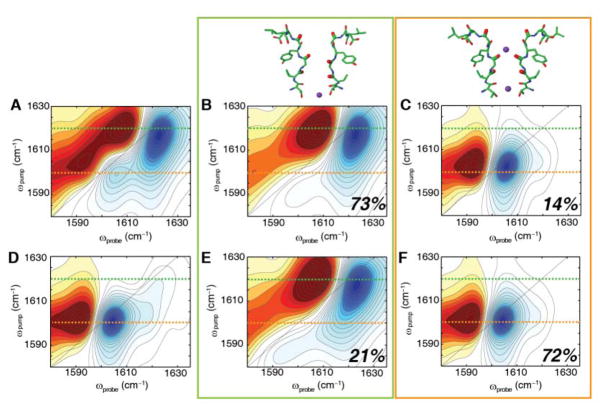
To ascertain the origin of the two distinct infrared signals, we turned to MD simulations. Trajectories of 532 ns in duration were generated for KcsA in the open-constricted and closed-constricted conformations²². For each, a 2D IR spectrum was calculated every 250 ps, and the resulting 2128 snapshots summed to generate a 2D IR spectrum that represents that state. The resulting 2D IR spectra are shown in Fig. 3A and 3D for the open-constricted and closed-constricted states, respectively. The spectrum of the open-constricted state (Fig. 3A) has two pairs of peaks, one at ω_pump = 1617 cm⁻¹ and a weaker set of peaks at ω_pump = 1602 cm⁻¹. The calculated spectrum for the closed-constricted state also has two sets of peaks, centered at ω_pump = 1617 and 1601 cm⁻¹, with the lower frequency peak dominating the spectrum.

Fig. 3. Two major conformations of KcsA selectivity filter from 2D IR simulations for the (top) open-constricted state and (bottom) closed-constricted state.

(A) Calculated 2D IR spectrum of the entire MD trajectory of the open-constricted state reveals a major peak at ω_pump = 1617 cm⁻¹ and a minor peak at ω_pump = 1602 cm⁻¹. Similar to the closed-constricted state analysis (top), two major ion binding configurations are revealed. (B) Spectrum for structural confomation with no K⁺ ion at the S1 binding site, exhibiting a high frequency peak at ω_pump = 1617 cm⁻¹ and constituting 73% of the states observed in the MD trajectory of the open-constricted state. (C) Spectrum for states in which the S1 site is occupied, which accounts for 14% of all the structures in the MD trajectory. The calculated spectrum of this conformation reveals a single low frequency peak at ω_pump = 1602 cm⁻¹. (D) Calculated 2D IR spectrum of the entire MD trajectory of the closed-constricted state reveals a major peak at ω_pump = 1601 cm⁻¹. (E) Simulated spectrum of the structural configuration without a K⁺ ion in S1 shows a high frequency peak at ω_pump = 1617 cm⁻¹. This configuration in 21% of the structural snapshots. (F) The simulated spectrum for the structural sub-ensemble with a K⁺ ion bound at S1, which accounts for 72% of the structural snapshots in the MD trajectory. The major peak has a peak frequency of ω_pump = 1601 cm⁻¹. Dashed lines at ω_pump = 1620 cm⁻¹ (green) and ω_pump = 1600 cm⁻¹ (orange) are shown as guides. All spectra are normalized to the most intense peak.

To determine the origins of these peaks, we looked for variations in KcsA structure at the Val76 and Gly77 residues, since those are the two residues that we monitor in our experiments. Previously⁶, we show that these residues are sensitive to the S1–S3 binding sites in the filter and that the Gly79 does not contribute significantly to the intensities of the peaks that we observe in our experiments since it is on the outside of the filter. To look for structural variations, we examined the vibrational Hamiltonian, rather than the structure itself, because it is the element that dictates the 2D IR spectrum and thus provides the most direct mean to identify structural differences. To do so, we defined a quantity Δ_ij from non-diagonal components in the vibrational Hamiltonian as a sum of the intra-monomer couplings between Val76 and Gly77 and the inter-monomer couplings of Gly77 (see in Eq. 2 in Materials and Methods). As described in the Materials and Methods section, Δ_ij was calculated for each of the 2128 snapshots, giving a measure of the local Val76-Gly77 conformation every 250 ps for the 532 ns trajectory. For each snapshot, the variation in Δ_ij was calculated and the corresponding structure binned into one of 11 groups accordingly. The 2D IR spectrum was then computed for each group. This is analogous to a clustering of structures based on conformational similarity ³⁷, but the quantity Δ_ij is more directly tied to the 2D IR experiment because it is the vibrational couplings that dictate the spectrum.

Based on this analysis, we found that >90% of the Hamiltonians for the open-constricted state of KcsA fell into one of two distinct structural groups. One group contains 73% of the structural population. Its 2D IR spectrum is shown in Fig. 3B and is dominated by a pair of peaks at ω_pump = 1617 cm⁻¹. The other group comprises 14% of the instantaneous snapshots in the MD trajectory. Its 2D IR spectrum is shown in Fig. 3C, which exhibits a pair of peaks at ω_pump = 1602 cm⁻¹. The remaining 13% of the picosecond structures are distributed throughout the other groups (shown in Fig. S1), although we note that 1% of the structures are binned into groups with ≤ 2 structures in each. Having sub-divided the MD trajectory by structure, we then analyzed the ion occupancies at the S1 binding site for each grouping. The grouping with the 1617 cm⁻¹ frequency that contained 73% of the population, has no ion at S1. In contrast, the grouping with the 1602 cm⁻¹ frequency that contained 14% of the population, almost always has an ion at S1. Thus, these two groupings represent structures without and with K⁺ ions at S1, respectively. Their differences in frequency are a result of the ion itself, because binding of a K⁺ ion lowers the vibrational frequency by 26–31 cm⁻¹ due to electrostatic interactions between the ion and the carbonyls. The dihedral angles between Val76 and Gly77 with and without bound K⁺ ion are the nearly same within 1–2°, indicating that they have nearly identical backbone structures (ψ = −35.70±0.27° and −32.79±0.35°, and φ = 84.46±0.29° and 81.93±0.27° for the 1617 and 1602 cm⁻¹ groupings, respectively). A more direct marker is associated with distance between the Gly77 residues of different monomers. The distances are 5.9 Å and 4.6 Å for the 1617 and 1602 cm⁻¹ groupings, respectively (Fig. S3). Thus, the open-constricted states with and without bound K⁺ yield two different sub-ensembles of structures in the vicinity of the Gly77 carbonyl of the selectivity filter, each of which has a distinct 2D IR spectrum. The accompanying structural change that alters the distance between the backbone carbonyls of the Gly77 residues raises the frequency by 5–7 cm⁻¹ because of vibrational coupling. The sum of these effects creates the 19 cm⁻¹ difference in 2D IR frequency between the two states.

Following a similar procedure, we also analyzed the closed-constricted state. Analysis of this state also reveals two major groupings that together account for >87% of the trajectory (see Fig. S2 for all groupings). The simulated spectra of the two groups are shown in Fig. 3E and F, which contain 21% and 72% of the population, respectively. The spectra are very similar to the spectra found for the open-constricted states, with one spectrum exhibiting a peak pair at ω_pump = 1617 cm⁻¹ and the other spectrum a peak pair at 1601 cm⁻¹. Indeed, from a structural point of view the selectivity filter, configurations of the closed-constricted state are nearly identical to that of the open-constricted state: the dihedral angles are nearly invariant (ψ = −37.15±0.34° and −34.59±0.20°, and φ = 83.55±0.48° and 82.63±0.24° for the 1617 and 1602 cm⁻¹ groupings, respectively) and the distances between the Gly77 residues are 5.4 Å and 4.6 Å for the 1617 and 1601 cm⁻¹ spectra, respectively. Further analysis of ion occupancies shows that there is no K⁺ ion at the S1 binding site for the 1617 cm⁻¹ grouping, but there is an ion at S1 for the 1601 cm⁻¹ grouping. Thus, the open-constricted and closed-constricted states contain the same two structural sub-ensembles at the Val76-Gly77 residues and these two structural sub-ensembles each correlate with the same ion configuration. Our analysis of the spectra of the sub-ensembles reveals two parameters that define the relative occupancy of the S1 binding site: the peak position and intensity. The peak position correlates with the ion occupancy of the S1 binding site, with the lower frequency of 1602 cm⁻¹ indicating the presence of an ion and the higher frequency of 1617 cm⁻¹ denoting the absence of an ion at the site. Similarly, the peak intensity reflects the population of these two situations. If we take into account all of the simulations of the open-constricted state, 85% of the peak intensity lies in the higher frequency peak, which suggests that 85% of the structures in the ensemble lack an ion in the S1 binding site.

The frequencies of the two structural sub-ensembles predicted from simulations are in very good agreement with the observed experimental frequencies. In the experimental spectrum of the open-constricted state, we measured features at 1618 cm⁻¹, while in the experimental spectrum of the closed-constricted state we see a peak pair at 1599 cm⁻¹. Thus, the observed experimental frequencies are bi-modal, like the simulations, and match the simulated frequencies to within 1 or 2 cm⁻¹. The simulations also reproduce the 2D lineshapes, recapitulating the homogeneous and inhomogeneous linewidths of the residues, which is another assurance for the validity of the simulations. Therefore, we assign the two experimentally observed features to the two structures predicted by simulation. It then follows that the intensities of the 2D IR features at 1618 and 1599 cm⁻¹ give the populations of the states without and with K⁺ bound at S1, respectively. However, the intensities of the experimental and simulated features at these two frequencies are not in perfect agreement, indicating that the populations predicted by simulation are not correct, at least for the open-constricted state. In the experiment of the open-constricted state, the ion occupied feature at 1599 cm−1 is <10% the intensity of the 1617 cm⁻¹ feature whereas the simulations predict that it should be 40%. Because the transition dipole strength of the carbonyls is larger in the ion-bound state than it is in the ion-free state, 40% actually corresponds to 14% of the population (e.g. the ion-bound state has a disproportionate contribution to the spectrum). Thus, taking the transition dipole strengths into account in the experiment, <10% intensity means that K⁺ in the open-constricted state is bound <3.5% of the time. We note that we are unable to resolve the high frequency peak in the closed-constricted state because the background subtraction is more difficult for low K⁺ samples.

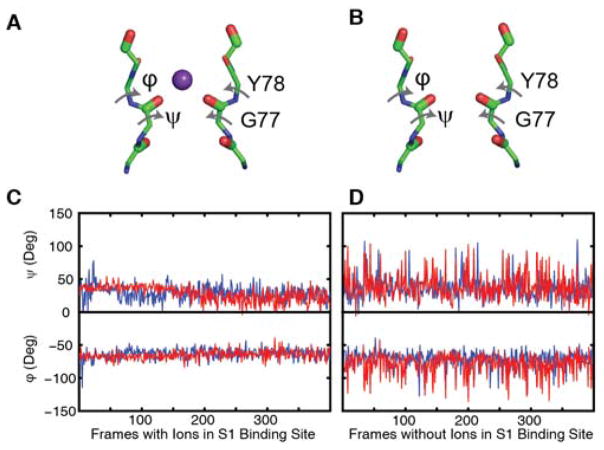
MD simulations are not expected to properly predict populations created by free energy differences close to k_BT, because that energy difference is below the accuracy of the force fields¹⁰. Nonetheless, experimental validation of simulated frequencies and 2D lineshapes provides confidence that the MD simulations do correctly predict the backbone structure of the selectivity filter and corresponding ion binding configurations. Thus, it makes sense to use the simulations to glean structural details that are not available from the experiments themselves. As noted above, the Val76/Gly77 dihedral angles differ by no more than a couple of degrees between the states with and without an ion while the distance between the Gly77 residues varies by 1 Å or less. Another notable difference is that the selectivity filter is much more dynamic with no ion bound at S1. Shown in Fig. 4 are plots for the dihedral angles of the residues that span the S1 binding site taken from a representative subset of the 2128 snapshots sampled from the 532 ns trajectory. When an ion is bound, the angles deviate 7–10°, but the deviations are 14–18° without an ion at S1. The averages and deviations are nearly the same between the open-constricted and closed-constricted states, and so while binding of an ion at S1 correlates with a difference in G77 distances and dynamics of the S1 site, there must be changes elsewhere (other than Val76/Gly77 backbone geometry) that are responsible for the differences in ion occupancy caused by gating.

Fig. 4. Structural differences between the filters with and without ions in the closed and open states.

Illustration defining φ and ψ angles for the states in which a K⁺ ion is (A) bound and (B) not bound at the S1 site taken from representative snapshots of the 2128 frames sampled from the 532 ns trajectory. Plot of the φ and ψ angles when (C) an ion is bound and when (D) an ion is not bound at the S1 binding site, showing that the filter fluctuates less when an ion is present. Dihedral angles are shown for the two major conformations of the (red) open-constricted and (blue) closed-constricted states. The φ angle is defined by the Gly77 carbonyl carbon, Tyr78 amide nitrogen, Tyr78 C_α, and the Tyr78 carbonyl carbon. The ψ angle is defined by the Gly77 amide nitrogen, Gly77 C_α, Gly77 carbonyl carbon and Tyr78 amide nitrogen.

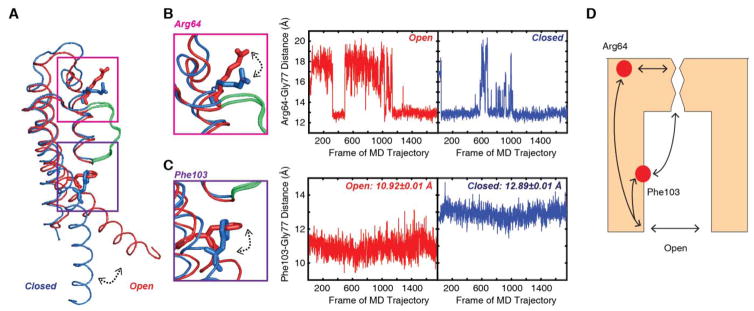
To identify differences in structure, we examined each of the two sub-ensembles of states with the intracellular gate open and closed. When the intracellular gate is open, the selectivity filter is only 0.5 Å wider than for the state without a K⁺ ion (5.9 Å versus 5.4 Å between Gly77 residues) and there is no difference in width for the state with a bound K⁺ when the intracellular gate is open or closed. Thus, neither the backbone nor the width of the selectivity filter (as measured by Gly77 distances) appears to explain the difference in S1 occupancy between the open- and closed-constricted states. However, outside of the selectivity filter, the simulations show substantial changes in nearby residues Phe103 and Arg64 when the intracellular gate is closed versus open (Fig. 5). Phe103 is in the inner helix and rotates upward and closer to the selectivity filter on channel opening (Fig. 5C). This movement of Phe103 has been previously reported and has been postulated to be critical for constriction of the selectivity filter with the opening of the intracellular gate^{5, 8b}. The other residue identified, Arg64, is in the turret region and opening of the intracellular gate causes the Arg side chain to swing closer to the S1 site (Fig. 5B). This change in the position of the Arg64 side chain could have an electrostatic effect on the S1 site thereby influencing the K⁺ affinity at this site. Amino acid substitutions at Phe103 and Arg64 have been previously shown to affect C-type inactivation in the KcsA channel^{5, 38}. C-type inactivation is a conformational change at the selectivity filter triggered by the opening of the intracellular gate that renders the channel non-conductive³⁹. It has been proposed that the constricted state of the selectivity filter corresponds to the C-type inactivated state but other studies have indicated that the constricted state corresponds to a deep-inactivated state, which is outside the range of conformations adopted by the selectivity filter of the KcsA channel under normal functional conditions^{5, 40}. Given that filter constriction and C-type inactivation are coupled to the opening of the intracellular gate, it is not surprising that the KcsA channel residues identified in this study are a part of the communication pathway also effect C-type inactivation.

Fig. 5. Coupling of the intracellular gate involves residues Arg64 and Phe103 near the selectivity filter.

(A) Overlay of the open (red) and closed (blue) monomer of KcsA. The selectivity filter is shown in green. (B) When the intracellular gate is closed, the Arg64 residue is closer to the selectivity filter, as shown by the blue trace of the Arg64-Gly77 distance which measures the distance between the Arg C_ζ and the Gly77 carbonyl oxygen. When the gate opens, the distance between the Arg64 and the Gly77 residues increases. (C) Likewise, the distance between the Phe103 C_β and the Gly77 carbonyl oxygen varies between closed and open states. In the closed state, the Phe103 and Gly77 is further apart, with a distance of 12.89 ± 0.01 Å. When the transmembrane helix rotates as the intracellular gate opens, the distance between these two residues decreases to values of 10.92 ± 0.01 Å. (D) Illustration of proposed mechanism for conformational changes in the selectivity filter upon gate opening. The communication pathway between the gate and the selectivity filter is facilitated by residues along the gating and pore helices, including Phe103 and Arg64.

We do anticipate that the communication pathway between the intracellular gate and the selectivity filter involves other residues in addition to Phe103 and Arg64. We expect that if we do a similar study with mutants of Arg64 and Phe103 that prefer one conformation over another, we can modulate the populations of these states with these mutations or combination of mutations. It is beyond the scope of this study, but one could imagine that a mutant such as F103A, which has been shown to severely impair inactivation and increase open probability of the KcsA channel^{5, 8b}, would give rise to a spectrum that indicates that the S1 binding site for a majority of states is largely unoccupied. Similarly, for a mutant that favors the closed-constricted state, we would expect a distribution of states that reflects a higher population of states with an ion bound in the S1 binding site.

Conclusion

We show, based on experimental 2D IR spectra and a comparison to simulated 2D IR spectra from MD trajectories, that the constricted (non-conductive) conformation of the KcsA channel selectivity filter established by allosteric means (opening of the intracellular gate) or by chemical manipulation (depleting K⁺) are not energetically or conformationally equivalent. Indeed, an important insight derived from these observations is the demonstration of conformational subensembles with explicit energetic influence on the ion occupancy of the selectivity filter. The ability of 2D IR spectroscopy to sample ps snapshot ensembles has allowed an unprecedented look at an enhanced conformational landscape for the K⁺ channel selectivity filter where the ion occupancy (at S1) depends on the state of the intracellular gate. An analogous approach using FTIR spectroscopy would be more difficult because of larger background and no ability to measure homogeneous and inhomogeneous lineshapes. In the closed-constricted conformation (low K⁺ and pH 7), we show that S1 binding site is occupied >70% of the time whereas in the open-constricted conformation, the S1 site is only occupied 14% of the time based on the simulated data. Based on the population of the bound and the free states when the gate is open versus closed and the K⁺ concentration, we can calculate the K_d, which gives a measure of the change in K⁺ affinity. The change in occupancy at the S1 site indicates a roughly 500–1000 fold decrease in K⁺ affinity upon opening the intracellular gate. Based on the simulations of the channels with the open and closed inner gate, we speculate that Phe103 and Arg64 play important roles in coupling the intracellular gate to the collapse of the filter and for altering the ion binding affinity at the S1 site. This study highlights the combination of protein semisynthesis, 2D IR spectroscopy and MD simulations as a particularly powerful approach for investigating ion binding sites in membrane channel proteins.