Confounding, Causality and Confusion: The Role of Intermediate Variables in Interpreting Observational Studies in Obstetrics

Abstract

Both prospective and retrospective cohort, and case-control studies are some of the most important study designs in epidemiology because, under certain assumptions, they can mimic a randomized trial when done well. These assumptions include but not limited to properly accounting for two important sources of bias: confounding and selection bias. While not adjusting the causal association for an intermediate variable will yield an unbiased estimate of the exposure-outcome’s total causal effect, it is often that obstetricians will want to adjust for an intermediate variable to assess if the intermediate is the underlying driver of the association. Such a practice must be weighed in light of the underlying research question, and whether such an adjustment is necessary should be carefully considered. Gestational age is, by far, the most commonly encountered variable in obstetrics that is often mislabeled as a confounder when, in fact, it may be an intermediate. If, indeed, gestational age is an intermediate but if mistakenly labeled as a confounding variable and consequently adjusted in an analysis, the conclusions can be unexpected. The implications of this over adjustment of an intermediate as though it were a confounder can render an otherwise persuasive study downright meaningless. This commentary provides an exposition of confounding bias, collider stratification and selection biases, with applications in obstetrics and perinatal epidemiology.

Introduction

Randomized controlled trials (RCT), by design, are the least affected by biases that otherwise remain entrenched in observational studies. Despite biases, prospective and retrospective cohort, and case-control studies are one of the most important study designs in epidemiology because, under certain assumptions, they can mimic a randomized trial. These assumptions include properly accounting for the numerous possible sources of biases (see recent text books^{1, 2} for a comprehensive review of biases), notably confounding and selection biases. Failure to address these biases can render the findings from an otherwise persuasive observational study from difficult to interpret at best to downright meaningless at worst.

Inferring causal associations was once thought feasible only in RCT designs. However, with the advent of modern statistical and epidemiologic methods, drawing causal inferences from observational studies has become tenable, but only under certain assumptions (see Cole and Hernan³ for a review). This commentary deals with the following questions: What are the some of the criteria to infer causal associations in observational studies? Where does confounding fit in to the big picture for drawing causal inferences? What are the connections and caveats between these two concepts? Can sound research go astray when variables thought to be confounders are actually intermediates and are adjusted in an exposure-disease paradigm? What are these intermediates, how does one recognize them, and what price does one pay when models are “over-adjusted” for these intermediaries? The impetus and motivation for this commentary is the confusion in the myriad of manuscripts in obstetrics and gynecology journals where there appears to be a general confusion regarding the right answers to questions such as “which variables to adjust” and “which ones to steer clear of”. Many a time, such intermediates go unrecognized. These are the topics of rest of this commentary.

An Illustrative Example with Implications in Obstetrics

Before we delve into a discussion of biases in observational epidemiology, we highlight an important illustration in perinatal epidemiology and obstetrics to motivate the problem. The example relates to a study designed to estimate the association of preeclampsia and the risk of cerebral palsy.⁴ Preeclampsia is a strong predictor of gestational age at delivery.^{5, 6} Even in the absence of preeclampsia, the early delivery itself confers increased risk of cerebral palsy;⁷ in the setting of preeclampsia and early delivery, this risk is appears compounded.⁸ It is, therefore, tempting to adjust the total effect of the preeclampsia-cerebral palsy causal association for gestational age. Because of this adjustment, studies evaluating the association between preeclampsia and cerebral palsy have uncovered a puzzling paradox. At preterm gestations (implying implicit stratification or restriction for gestational age), preeclampsia remains protective for cerebral palsy, with a reversal in risk at term gestations.

Using a population-based cohort study from Norway with 849 cerebral palsy cases and 615,668 normal infants, Strand and colleagues⁴ report a 2.5-fold increased odds of cerebral palsy among infants born to preeclamptic mothers (odds ratio [OR] 2.5, 95% confidence interval [CI] 2.0, 3.2). This OR was slightly attenuated (OR 2.1, 95% CI 1.7, 2.7) when the association was adjusted for infants that were small for gestational age (SGA). Further adjustments for both SGA and preterm delivery reversed the association in favor of preeclampsia being protective of cerebral palsy (OR 0.7, 95% CI 0.6, 1.0) (this paradoxical observation of reduced risk of cerebral palsy at preterm gestations in the setting of preeclampsia has been reported in several other studies).⁹ Someone unfamiliar with the concepts of confounding and intermediates might quickly (and incorrectly, of course!) interpret the association as “it is better for women diagnosed with preeclampsia be delivered at preterm gestations, so cerebral palsy can be prevented or its risk reduced”. Is an adjustment for SGA and preterm delivery appropriate? Will such an adjustment yield an unbiased estimate of the purported association? Should one even conclude that at preterm gestations, preeclampsia is protective of cerebral palsy?

Indeed, based on the strength of evidence, and given that preeclampsia is associated with gestational age at delivery,^10–13 and gestational age, in turn, is a powerful predictor of cerebral palsy,⁸ one might infer that the preeclampsia-preterm delivery-cerebral palsy association might be causal. This argument has led epidemiologists to investigate if unmeasured confounding may be a reason for this paradox.^{14, 15} In other words, women diagnosed with preterm preeclampsia are so inherently different from those that deliver at term, and adjustment for all measured risk factors (for preterm delivery) may still not resolve the paradox. The potential for unmeasured confounding (and failure to correct for this bias), coupled with inappropriate adjustment for an intermediate variable, is the underlying culprit of the paradox.¹⁶ When statistical methods to account for unmeasured confounders are incorporated, the paradox resolves and selection bias can be eliminated! If the intermediate variable is not considered in an analysis, the paradox does not arise, as seen in the preeclampsia-cerebral palsy example with a total effect odds ratio of 2.5 (95% CI 2.0, 3.2) discussed earlier.

Such paradoxes are not uncommon in epidemiology. For example, perinatal mortality being lower at preterm than at term gestations involving comparisons between babies born at high versus low altitudes,¹⁷ African-American versus Caucasian¹⁸ and Hispanic babies,¹⁹ twins versus singletons,²⁰ US births compared with Norwegian²¹ and Belgian births,²² and the protective effect of smoking on preeclampsia,²³ to name a few.

Unfortunately, such solutions often come with drawbacks – by not adjusting for an intermediary variable one cannot separate the effects of preeclampsia on cerebral palsy that operates through preterm delivery (called the indirect or “mediated effect”) versus the risk of cerebral palsy in relation to preeclampsia that is independent of preterm delivery (called the direct effect). In doing so, we are left addressing a question that is fundamentally different from the one that was originally intended: what is the total effect of the preeclampsia-cerebral palsy association, regardless of gestational age? While this solution is sound from an epidemiologists’ perspective, it does leave the astute obstetrician with the lingering question… “Yes, of course, but what about gestational age?” This issue is addressed later in the commentary.

Directed Acyclic Graph (DAG)

Before delving in to an understanding confounding bias, or broadly how a relationship between an exposure and an outcome can be depicted, it is important to figure out a way to represent them graphically. The DAG is a tool whose utility lies in developing a “blue print” of how the exposure-outcome relationship can be depicted with confounding, exposures of interest, and mediating variables.²⁴ A DAG also provides an indication of which variables are confounders that need to be adjusted for in an analysis, and which ones do not qualify as confounders. DAGs can also help to identify the presence of selection bias.²⁵ Pearl²⁶ formalized the concept of DAGs, also referred to as causal diagrams. Good introductions to DAGs, their conceptualization, construction, and applicability to study designs are available,^{15, 27, 28} and we urge readers to familiarize themselves with this important method.²⁹

As the name suggests, the construction of a DAG involves three essential functions: (i) directed; (ii) acyclic; and (iii) graph; each function is briefly described here. The relationship amongst variables is depicted in unidirectional arrows or “paths” (never bidirectional). This is referred to as “directed”. The second is “acyclic”, which denotes that the paths cannot be depicted as a circle. Lastly, the “graph” indicates that the whole conceptualization of the causal pathways connecting all the variables can be graphically visualized.

Each variable in a DAG is called a node, with the causal paths connecting two or more nodes. In figure 1a, for example, X is considered as a cause or an ancestor of Y; stated backwards, Y is a descendant of (or caused by) X. One excellent and free resource to depict and develop complicated DAG³⁰ can be found at http://dagitty.com/ where the minimal set of adjustment variables is the resulting output.

Figure 1.

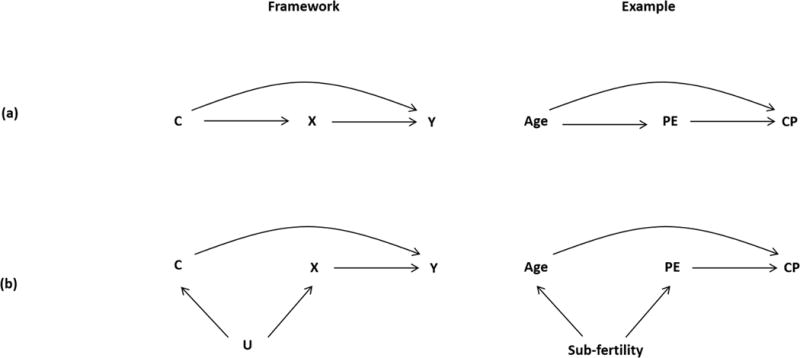
DAGs representing two scenarios for confounding. The left panels show the framework for confounding, and the right panels provide illustrations of confounding of the preeclampsia (PE) and cerebral palsy (CP) association with maternal age (Age) as a potential confounder, and sub-fertility as an unmeasured confounder

We denote sub-fertility as an unmeasured confounder in the broadest sense when, in fact, sub-fertility may serve as a marker for an underlying condition that results in both conception delay and preeclampsia, should a conception occur

Confounding Bias

Confounding bias occurs when there is a failure to adjust for common causes of both the exposure and the outcome. The criteria for confounding are that the third variable (the confounder, C) should be casually associated with both the exposure (X) and the outcome (Y), and C is not on the causal pathway between X and Y (Figure 1a).^{31, 32} An extension of this definition is depicted in Figure 1b, which demonstrates that unmeasured common causes (U) can also be a source of confounding of the X→Y relationship. For example, sub-fertility (as a marker for an underlying condition that results in both conception delay and preeclampsia, should a conception occur) serves as a common cause of both maternal age at conception and preeclampsia, and its effect on cerebral palsy only operates through age and preeclampsia. In this scenario, not considering sub-fertility status would lead to a confounding bias on the estimate of the impact of preeclampsia on cerebral palsy.

Role of Intermediate Variables and Overadjustment

To place terminology into context, we refer to overadjustment as the undesirable consequence of adjusting for an intermediate variable that lies on a causal pathway from exposure to outcome.^{15, 23} Simply put, these are variables that do not qualify as confounders. Figure 2a shows a causal DAG representing the simplest case of overadjustment bias. In this scenario, one can estimate the total effect of X on Y by not adjusting for the intermediate variable I. However, if control is made for the intermediate variable I, then the total causal effect of the X→Y association cannot be consistently estimated. Heretofore, we broadly define “control” to imply regression-based adjustment, stratification, or matching on the intermediary variable. Importantly, “restriction” also falls in this broad category that we refer to as “control”. An example of restriction is one where an investigator restricts the study of preeclampsia on cerebral palsy to babies delivered preterm.

Figure 2.

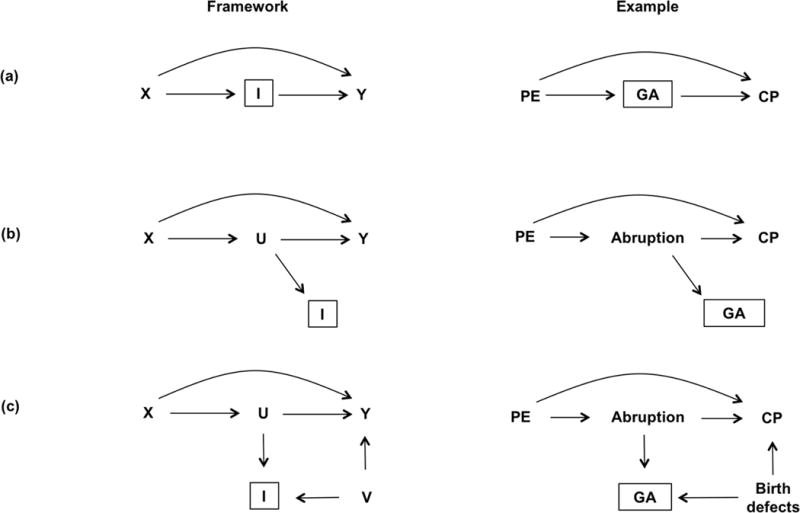
DAGs representing three scenarios for variables acting as intermediates. The left panels show the framework for an intermediate variable, and the right panels show illustrations of how an intermediate variable, gestational age (GA), may affect the preeclampsia (PE) and cerebral palsy (CP) association, with placental abruption as an unmeasured intermediate (U). V is another unmeasured confounder, for example, birth defects

Referring back to the example, if the model includes an adjustment for preterm delivery (I), a variable in the causal pathway between preeclampsia and cerebral palsy,³⁴ the association will be biased. Since gestational age appears in the causal pathway between preeclampsia and cerebral palsy, one can separate the direct and indirect preeclampsia effects by simply adjusting for gestational age, or its proxy such as preterm delivery. However, it will be under the premise that there are no other unmeasured confounders amongst these three variables (Fig 2a), or adjustment for a consequence of an intermediate (Figure 2b). Note that in Figure 2b, the intermediate variable I is the consequence (or a proxy of the consequence) of the intermediate variable U, which itself is typically unmeasured.

An example of this scenario is adjustment for preterm delivery status on the relationship between preeclampsia and cerebral palsy because preterm status is a direct consequence of gestational age (or descendent of an intermediate variable). One can again consistently estimate the total causal effect of exposure on outcome by ignoring I, the imperfect proxy for the unmeasured intermediate variable U. However, if one controls for the variable I in Figure 2b, which is a proxy for variable U (on a causal pathway between exposure and outcome) the total causal effect of the X→Y association again cannot be consistently estimated. To clarify, if an intermediate such as gestational age is adjusted on the preeclampsia-cerebral palsy association, the total effect will be underestimated. Such adjustments will undoubtedly result in biased (and therefore incorrect) estimates of associations.

If one does adjust for gestational age or preterm delivery in the presence of an unmeasured confounder between gestational age and cerebral palsy, the preeclampsia-cerebral palsy will be rendered biased — a bias called “collider stratification bias”^{35, 36} (Figure 2c). A collider stratification bias occurs when no attempt is made to distinguish a variable that is a confounder versus the variable that is in the causal pathway (the intermediate variable), and when the intermediate variable is adjusted in an analysis.

Collider Stratification Bias or Selection Bias? Same Thing, Different Name

Collider stratification bias is a phenomenon that occurs when the exposure-outcome association is induced by control (or matching, restriction, stratification, or multivariable adjustment) on an intermediate variable I that is affected by the exposure and a sharing common causes of the intermediate with the outcome (Figure 2c). In the preeclampsia-cerebral palsy example, a collider bias will rear its ugly head when the preeclampsia-cerebral palsy association is adjusted for gestational age (or preterm delivery) combined with the presence of an unmeasured confounder of the gestational age →cerebral palsy relationship, even in the absence of an association of gestational age and cerebral palsy. A potential unmeasured intermediate may be placental abruption, and a potential unmeasured confounder may include birth defects or race. In such a scenario, the total causal effect of the preeclampsia-cerebral palsy association will be biased due to the adjustment of an intermediate variable coupled with one or more unmeasured confounders. However, not adjusting for gestational age avoids the collider and will yield an unbiased estimate of the total effect.

Selection bias is defined as the distortion of an association between two variables that occurs by “controlling” on a common effect creating a collider. The result in this setting is a selection bias that is different from bias due to confounding. The vagueness in the previous definitions of confounding may cause confusion between confounding and selection bias. Confounding is a bias due to the existence of a common cause of exposure and outcome, which, by definition, occurs temporally prior to both exposure and outcome.³⁷ In contrast, a common effect, such as gestational age in the preeclampsia-cerebral palsy scenario, must occur temporally after the exposure (preeclampsia → gestational age). Adjusting on such a common effect (i.e., a collider) can result in selection bias. In the preeclampsia-cerebral palsy example, “gestational age” is a collider.

Collider Stratification Bias and Overadjustment

The combined presence of unmeasured confounding between the intermediate variable and the outcome, and inappropriate adjustment for an intermediate variable is what leads to selection bias. Specifically, we introduce DAGs in Figure 3 that represent collider stratification bias with three illustrations for each scenario. The left panels show the theoretical framework for an intermediate variable, the middle panels show illustrations of how adjusting for an intermediate variable, I, depicted in a box and labeled a “collider” with gestational age as the intermediate, will induce bias of the preeclampsia-cerebral palsy association. The right panels show the risks of cerebral palsy on the y-axis, by gestational age on the x-axis, among women with and without preeclampsia. Placental abruption is assumed to be an unmeasured variable.

Figure 3.

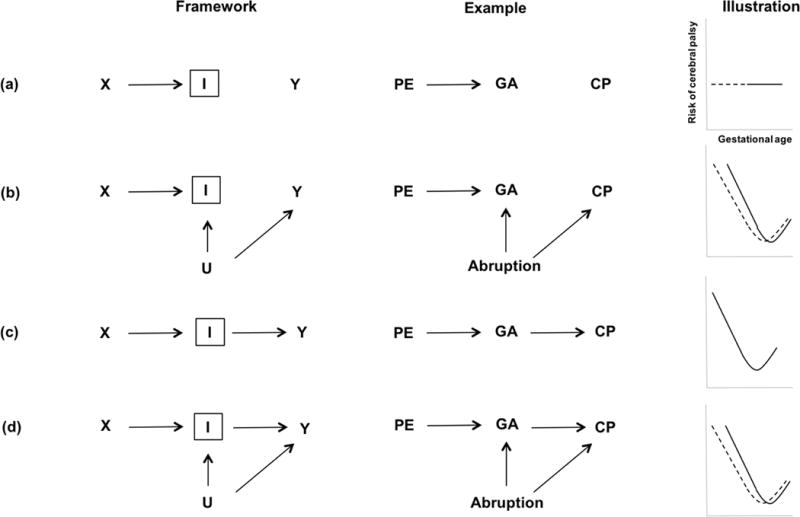
DAGs representing collider stratification bias with three illustrations for each scenario. The left panels show the theoretical framework for an intermediate variable, the middle panels show illustrations of how adjusting for an intermediate variable, I, depicted in a box and labeled a “collider” with gestational age (GA) as the intermediate, will induce bias of the preeclampsia (PE) and cerebral palsy (CP) association. The right panels show the risks of cerebral palsy on the y-axis by gestational age on the x-axis, among women with (solid line) and without preeclampsia (dashed line). Placental abruption is assumed to be an unmeasured variable.

To highlight the general problem, we illustrate a sequence of causal scenarios where we control variables affected by exposure, such as U or I in the DAG that could depict gestational age. Alternatively, adjusting for a consequence or descending proxy I of an unmeasured intermediate variable U (or U itself, if it were measured), is also susceptible to selection bias or collider-stratification bias. In this scenario, the unmeasured common cause V of the proxy variable M and the outcome Y causes additional bias in the association between exposure X and outcome Y within levels of M. Figure 3a–f are 6 possible scenarios extending the DAG’s in Figure 2 to allow unmeasured common causes of any set of variables.

The Relationship Between DAGs and Their Functional Forms

As an extension of the preeclampsia-cerebral palsy example, one can also see how different causal scenarios can render different functional forms or shapes on the relationship between preeclampsia and cerebral palsy as a function of gestational age stratification or adjustment, inspired by the work of Hernandez-Diaz and colleagues.¹⁵ The simplest causal DAG to describe this scenario is depicted in Figure 3a. The DAG implies no association between gestational age, preeclampsia and cerebral palsy, which would make the incidence rate of cerebral palsy curve flat, meaning no association of preeclampsia with cerebral palsy at all levels of gestational age. The shape of this association could, in principle still under the setting of no association between preeclampsia and cerebral palsy, be modified depending on the presence of an unmeasured or measured common cause between cerebral palsy and gestational age, such as placental abruption (Figure 3b). The variable U (or abruption) guarantees that the incidence of cerebral palsy will not be flat (as seen in Figure 3a), creating a spurious association between preeclampsia and cerebral palsy when adjusted for gestational age. If one were to change the assumptions and assume that gestational age, but not preeclampsia, has a direct effect on cerebral palsy, we can see the simplest structure depicted in Figure 3c. In this scenario, gestational age causes cerebral palsy, and thus the cerebral palsy curve is not flat. However, when an adjustment is made for gestational age, there is no association between preeclampsia and cerebral palsy. The cerebral palsy curve is the same for women experiencing preeclampsia as normotensive women. In other words, the (unconditional) association between preeclampsia and cerebral palsy is mediated entirely through the preeclampsia effect on gestational age. Again, as in Figure 3b, the presence of another unmeasured variable U such a placental abruption, will induce an association between preeclampsia and cerebral palsy conditional on gestational age (Figure 3d). This will lead to a biased relationship induced by improper adjustment for the intermediate variable gestational age, and sometimes creating paradoxical results due to selection bias.

Now as depicted in Figure 3e–h, we assume the additional existence of a direct effect of preeclampsia on cerebral palsy to all of the previously described situations. By adding a direct effect of preeclampsia on cerebral palsy, the cerebral palsy curve for preeclampsia is also shifted upwards across all gestational age levels and we assume the effect of preeclampsia is not modified by gestational age depicted in Figure 3e. A common unmeasured cause, such as abruption, induces a new source of association between preeclampsia and cerebral palsy conditional on gestational age, which may result in intersecting the incidence of cerebral palsy curves, even under the assumption that preeclampsia increases cerebral palsy at all gestational ages (Figure 3f).

Let’s now assume that there is no causal relationship between gestational age and cerebral palsy as depicted in Figure 3g; cerebral palsy curves are therefore flat across gestational age. Because of the direct effect of preeclampsia on cerebral palsy, the curve for women with preeclampsia is shifted upwards. Again, by adding the unmeasured common causes (abruption, for example) of gestational age and cerebral palsy (Figure 3h) in the causal model, we induce a spurious association and selection bias.

Why the Confusion?

Some confusion between confounding and selection bias may have resulted from definitions of confounding, which were not explicit about confounding being a bias due to the existence of a common cause of exposure and outcome. By definition, a common cause must occur “temporally prior” to both the exposure and the outcome. However, a way to control for confounding includes adjusting for a measured confounder that may occur temporally after (posterior) the exposure if it is on a causal pathway from the common cause to the outcome, or temporally after both the exposure and outcome if it is a consequence (descendant) of the common cause. Getting back to the preeclampsia-cerebral palsy example, a confounder that would meet this criterion is gestational age at delivery. In contrast, by definition, a common effect must temporally occur after both the exposure and outcome. Selection bias results when one adjusts an exposure-outcome association on such a common effect. This type of adjustment will render the estimates of association measures biased. Some commonly encountered scenarios in obstetrics and gynecology of confounding and overadjustment are presented in Table 1.

Table 1.

Some commonly encountered scenarios in obstetrics where adjustment for confounding factors are judged appropriate or inappropriate

Research question	Main exposure (X)	Outcome (Y)	Confounding/intermediate	Estimation of the total effect
Is preterm birth associated with increased perinatal mortality?	Preterm birth	Perinatal mortality	Smoking during pregnancy	Smoking is a confounder; should be adjusted
Does preterm birth confer increased risk of neurological deficits?	Preterm birth	Neurological outcome at two years	Chorioamnionitis	Chorioamnionitis is a confounder; should be adjusted
Is low first trimester PAPP-A associated with increased risk of placental abruption?	PAPP-A	Placental abruption	Smoking	Pre-pregnancy smoking preceding PAPP-A can be a confounder
Does preeclampsia confer protection for cerebral palsy at preterm gestations?	Preeclampsia	Cerebral palsy	Gestational age	Gestational age is an intermediate variable; should not be adjusted
Is prepregnancy maternal obesity associated with increased risk of stillbirth?	Prepregnancy obesity (BMI)	Stillbirth	Weight gain during pregnancy	Weight gain is an intermediate variable; should not be adjusted44
Is small for gestational age (a proxy for IUGR) associated with increased stillbirth risk?	Small for gestational age	Stillbirth	Prepregnancy BMI	Prepregnancy BMI is a confounder, and requires adjusting for it
Is weight gain in the first pregnancy associated with the risk of small for gestational age infants in the second pregnancy?	Weight gain in the first pregnancy	Small for gestational age in the second pregnancy	Prepregnancy BMI in the second pregnancy	Prepregnancy BMI in the second pregnancy is an intermediate; should not be adjusted
Does maternal calcium supplementation during pregnancy reduce childhood blood pressure?	Maternal calcium supplementation	Childhood blood pressure	Infant weight	Infant weight is an intermediate variable; should not be adjusted
Does maternal nutrition supplement during pregnancy reduce infant mortality?	Maternal nutrition	Infant mortality	Maternal weight gain	Maternal weight gain is an intermediate variable; should not be adjusted
Will intrapartum MgSO4 administration in women in preterm labor reduce the risk of cerebral palsy?	Magnesium sulfate (MgSO4)	Cerebral palsy	Gestational age	Since gestational age is both a cause of the exposure and the outcome, it should be adjusted

So how do we resolve this confusion? The definitions of what constitutes a confounder versus an intermediate are highly nuanced, yet can profoundly affect inferences in wrong hands. A variable labeled as a confounder for one causal scenario may actually be an intermediate in a different causal question. This alone is sufficient to indicate that there are no methods to distinguish one from another, a phenomenon that arguably equates to a “black box” epidemiology approach^{38, 39} (as a word of caution, the authors of this manuscript are not agnostic toward black-box epidemiology). Approaching the variable as a confounder versus an intermediate is best determined keeping the causal question in mind, and allowing biology to guide the investigator to arrive at the correct labeling of which is which, with DAG’s as a statistical tool to arrive at the distinction.

Where Do We Go from Here?

Recognizing the distinctions between a confounder versus an intermediate variable is the absolute first step in sound epidemiologic practice. Recognizing an impending collider stratification or selection bias when a collider variable is mistakenly (or knowingly) labeled as a confounder is perhaps the second step to sound analysis and reporting. Laying down the blue print of the various pathways linking the exposure to the outcome (DAG) is paramount for all studies. While not adjusting the causal association for an intermediate variable (overadjustment) will yield an unbiased estimate of the exposure-outcome’s total causal effect, it is often that obstetricians will want to adjust for an intermediate variable – gestational age, in particular – to assess if the intermediate is the underlying driver of the association. This phenomenon is an unfortunate occurrence in several noteworthy manuscripts in obstetrics and gynecology, and all science goes astray! Such adjustments may seem trivial, important, and downright essential for meaningful clinical interpretations, but additional steps must be taken to ensure that adjustment for an intermediate doesn’t leave the association biased.

Three approaches can be taken to estimate the effect of an exposure on the outcome while controlling for an intermediate: conditioning on the predicted risk of the intermediate, conditioning on the intermediate itself with sensitivity analysis, and conditioning on the principal stratum.^{40, 41} Each approach carries with it a different interpretation, a different set of assumptions and, when relevant, different methods for sensitivity analysis. As the existing literature has made clear, conditioning on an intermediate in perinatal epidemiology can be problematic and can give rise to severe biases, such as overadjustment and collider stratification biases.

Depending on the scientific question, conditioning on an intermediate is not necessary and is best avoided. Nevertheless, there are situations in which such conditional effects are of scientific or policy interest.⁴² We have shown that several alternative approaches⁴⁰ can be used to draw inferences in such settings. These methodological tools are imperfect, rely on strong assumptions, and call for cautious interpretation of the causal associations. In a cleverly titled manuscript entitled “Wizard of Odds”, MacLehose and Kauffman⁴³ argue that the approaches suggested (conditioning on predicted risk of the intermediate, sensitivity analysis and principal stratum) will, in the real word, probably not be that helpful to us, even though they are all reasonable and grounded in theory. Nonetheless, we believe that these methods do have a place in causal inference, and they are all useful to provide reasoning regarding the direct and conditional effects of an exposure on an outcome with intermediates.

Some Caveats

For estimation of total causal effects, not only is it unnecessary, but it can also harmful, to adjust for a variable on a causal pathway from exposure to disease, or for a consequence (descending proxy) of a variable on a causal pathway from exposure to outcome. Estimation of direct effects of exposures (such as the effect of preeclampsia not mediated through gestational age) on outcomes (such as cerebral palsy) by controlling for an intermediate variable (such as gestational age) are not valid when there are unmeasured shared causes of gestational age and cerebral palsy. Such estimates are vulnerable to collider-stratification bias. Concluding an absence of a collider bias based on the RRs with and without adjustment for the collider being “similar” is no justification to retain the adjustment for a collider – such arguments should be avoided. The approaches we have described in this commentary are applicable to perinatal epidemiology more generally. Conditioning (or matching, restriction, stratification or multivariable adjustment) on an intermediate in perinatal epidemiology (or even beyond!) can be problematic and will give rise to biased associations leading to incorrect biological inferences.

Key Messages.

• An understanding of the intricacies of, and distinctions between, a confounder and an intermediate variable, remains essential for drawing robust inferences

• A confounder is a variable that should be casually associated with both the exposure and the outcome, and is not on the causal pathway between X and Y. An unmeasured common cause can also be a source of confounding of the X→Y relationship

• We refer to overadjustment as the undesirable consequence of adjusting for an intermediate variable that lies on a causal pathway from exposure to outcome

• Avoiding an impending collider stratification or selection bias when a collider variable is mistakenly (or knowingly) adjusted (or stratified or matched) in a model as a confounder is paramount

• Laying down the blue print of the various pathways linking an exposure to the outcome through a Directed Acyclic Graph (DAG) will help in understanding the connections amongst the variables, and will provide indications of which confounders need to be adjusted and which ones should not be adjusted

• While not adjusting the causal association for an intermediate variable (over-adjustment) will yield an unbiased estimate of the exposure-outcome’s total causal effect, it is often that obstetricians will want to adjust for an intermediate variable to assess if the intermediate is the underlying driver of the association.

• Gestational age is, by far, the most common variable that is often mislabeled as a confounder when, in fact, it may be an intermediate. Control for such intermediates must be weighed in light of the underlying research question, and whether such an adjustment is necessary should be carefully considered