Abstract
We introduce a fast information matching (FIM) method for transforming time domain data into spatial images through handshaking between fast and slow degrees of freedom. The analytics takes advantage of the detailed time series available from biomolecular computer simulations, and it yields spatial heat maps that can be visualized on 3D molecular structures or in the form of interaction networks. The speed of our efficient mutual information solver is on the order of a basic Pearson cross-correlation calculation. We demonstrate that the FIM method is superior to linear cross-correlation for the detection of nonlinear dependence in challenging situations where measures for the global dynamics (the “activity”) diverge. The analytics is applied to the detection of hinge-bending hot spots and to the prediction of pairwise contacts between residues that are relevant for the global activity exhibited by the molecular dynamics (MD) trajectories. Application examples from various MD laboratories include the millisecond bovine pancreatic trypsin inhibitor (BPTI) trajectory using canonical MD, a Gaussian accelerated MD folding trajectory of chignolin, and the heat-induced unfolding of engrailed homeodomain (EnHD). The FIM implementation will be freely disseminated with our open-source package, TimeScapes.
Graphical abstract
Introduction
Molecular dynamics (MD) simulation of biomolecular structures has been termed a “computational microscope”1,2 the detailed imaging of the spatial domain, whereas the complexity of MD data mostly lies in the temporal domain, as detailed trajectories of each atom are recorded. What has been missing was a direct link between the detailed time domain data of MD and a static, spatial image that can visualize the functionally relevant time-dependent information contained in long trajectories. Here, we provide such a link by presenting a fast information matching (FIM) method that transforms time-domain information into spatial heat maps.
The newly developed FIM computes the mutual information between the fast, local rates of change of user-selected, functionally relevant variables with the slow, global rate of change (the “activity”) of the simulated system. The idea of fast variables enabling slow conformational changes has been prominently proposed for the dynamics of adenylate kinase by Kern et al.3 The novelty of our approach is in using the bridging between fast and slow modes to enable spatial imaging, where the user is free to choose a modality of interest for the heat-map analysis.
In this work, we have explored two heat-map modalities that were introduced with the Python-based TimeScapes package:4 Hinge bending of proteins and pairwise residue distance geometry.
The turning.py tool performs a mapping of functionally important residues whose fast, local backbone-turning motion (hinge bending) exhibits a statistical dependence on the slow, global dynamics. The modality is based on “pivot residue” pseudodihedral angles defined by four consecutive α carbons,5 whose absolute time differentials are compared against a global activity function that tracks the slow time scale change in the structure (such as returned by agility.py or terrain.py in TimeScapes,4 see Methods).
The tagging.py tool also performs a mapping of functionally important residues. However, the analysis is based on pairwise residue distances whose absolute time differentials exhibit a statistical dependence on the slow, global activity (or with a user-specified external order parameter). This approach originated in the analysis of the millisecond BPTI simulation, where the heat maps (Figure S9 in Shaw et al.6) were based on a correlation of the fast variables with the membership of specific conformational clusters (Table S2 in Shaw et al.6). In the current paper we generalize the idea to report on the importance of specific pairs of amino acid contacts for the global dynamics exhibited by the MD trajectory.
Our analytics of fast and slow time series can be performed either with the Pearson cross-correlation or with the new FIM approach introduced in this paper. The statistical ranking of degrees of freedom is necessary because the raw time series in an MD trajectory exhibits significant noise from trajectory striding and thermal fluctuations. For example, the rate of change of “pivot residue” dihedral angles used in Figure 1(a,c) is on the order of π/2 (Figure S1). It is therefore necessary to characterize the desired modalities with a statistical approach. The new FIM approach introduced here has the advantage of detecting nonlinear relationships due to the use of mutual information, whereas the Pearson correlation is restricted to linear dependence. (One of our test cases, EnHD, provides a striking example of the differences between the CC and MI approaches.) The statistical heat maps can then be projected back to residue space, yielding a localization of functional hot spots on a 3D atomic structure.
Figure 1.
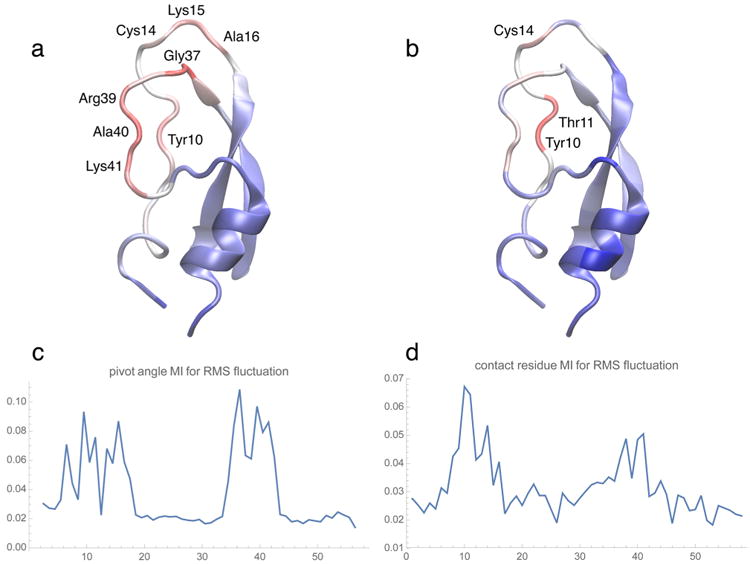
BPTI heat maps (backbone “new cartoon” representation of the initial structure used in the simulation) and the corresponding MI residue profiles. Molecular graphics figures of heat maps and 3D conformations in the present paper were created with the program VMD,25 using a linear red-white-blue color scale (from high to low values). (a,c) MI between the RMS fluctuation and pivot angle absolute rate of change as a function of the BPTI residue number. (Pivot dihedral angles were attributed to the half-points between the residue indices of the center atoms.) (b,d) MI values for all contacts, after projection onto the residue chain (see text). The RMS fluctuation was computed with the TimeScapes agility.py program using a sliding window of length δ = 5 μs.4 Default parameters were used for the turning.py and tagging.py programs to compute the MI profiles. The complete results of the BPTI analysis are provided in supplementary Figure S2.
We demonstrate our computational methods on three trajectories from diverse simulation approaches: (1) The millisecond-length bovine pancreatic trypsin inhibitor (BPTI) trajectory by Shaw et al.6 This groundbreaking canonical MD trajectory remains relatively stable, with only five essential conformations that are visited repeatedly. The limited conformational variability and long simulation time provide a gold standard of sampling for both hinge bending and pairwise-distance geometry. (2) The chignolin folding trajectory simulated by the McCammon group with Gaussian accelerated molecular dynamics (GaMD).7 This 300 ns trajectory of a small peptide (10 residues) exhibits rapid folding dynamics on a modified energy landscape that accelerates the folding dynamics by 4–5 orders of magnitude. The trajectory illustrates the use of the “pivot residue” dihedral angles for detecting a key residue involved in the folding process. (3) A 60 ns engrailed homeodomain (EnHD) unfolding trajectory from the Dynameomics project of the Dagget group.8 Our pairwise-distance-geometry analytics highlights specific contacts that are lost during the heat-induced unfolding of the protein.
The paper is organized as follows: In Methods, we first describe the statistical approach for the analysis and the existing art of using TimeScapes, in particular with respect to detection of the necessary slow activity functions. This introduction is followed by the development of the FIM methodology. In Results, we describe applications of our methods to the three trajectories of interest. We provide some general guidelines for the choice of parameters. In Conclusions, we discuss advantages and limitations of our FIM approach and topics for future research.
Methods
Statistical Characterization of Time Series by Handshaking between Fast and Slow Degrees of Freedom
Let {Xi(t)} be a family of “local” user-selected, real-valued variables that can be indexed by primary or tertiary location in the protein structure (e.g., the Xi(t) can be attributed to a residue or residue pair denoted by a suitably chosen indexing scheme i). In addition, we assume that the Xi(t) are “fast” variables, that is, they exhibit fluctuations on time scales on the order of the frame length of the discrete MD trajectory. Furthermore, let a(t) denote a “slow” non-negative activity function that describes the “global” rate of change of the simulated system over long time scales (as introduced by Wriggers et al.4 and described in the following). Finally, let I(f,g) denote a statistical measure of dependence of two discrete random variables f and g (such as Pearson cross-correlation or MI). The coefficient
| (1) |
then provides an estimate of the spatial importance of local changes in the protein structure for global activity. The RXi,a values can be used to rank all members of the family {Xi(t)}, which, after appropriate mapping to spatial features i, yields a heat map of the importance of the fast, local variables for the slow, global activity. Our transformation of time series data to spatial images is generalizable to any type of user-selected imaging modality X(t). In this paper, however, we restrict our discussion to the pivot angles and pairwise residue distances mentioned above.
Existing Art: TimeScapes
TimeScapes is a Python-based program package that can be used to efficiently detect and characterize significant conformational changes in simulated biomolecular systems.4 TimeScapes was originally developed by Willy Wriggers et al. while at D. E. Shaw Research, and following its release into the public domain, it is now disseminated on our academic Web site, http://timescapes.biomachina.org. The earlier paper4 provides the best reference for the originally intended event detection and activity monitoring applications.
We have pointed out above that the programs tagging.py and turning.py make use of slow, global activity rate functions to perform a mapping of residues relevant to the global activity. There are two types of activity functions supported, one of which is further subdivided into two variants: (1) The RMS fluctuation of Cartesian coordinates in a Gaussian-weighed sliding window are computed with agility.py. (2) The package also makes use of a coarse-grained model to reduce the level of detail in the spatial representations of long MD trajectories. TimeScapes decomposes structural changes into side chain contact-forming and -breaking activity using the terrain.py tool. The activity may be computed from changes in a cutoff-based nearest-neighbor graph or from a so-called Generalized Masked Delaunay graph.4 A total of three activity functions were thus available for comparison.
The major innovation introduced in this paper is the development of the FIM method and its porting to the existing TimeScapes tools. Detailed usage examples will be described in the Results.
Mutual Information
Let f, g be discrete, real-valued random variables defined on a probability space Ω. In our context, these variables will have finite sets of values, say Vf and Vg, respectively, and Ω itself will be a finite set, each of whose points has equal probability. The entropy of f is defined as
| (2) |
where pf is the probability density function of f. The joint entropy of the pair (f,g) is defined similarly as
| (3) |
where pf,g is the joint probability density function. The mutual information of the variables f, g is defined as
| (4) |
which can easily be written as
| (5) |
and also as an expectation:
| (6) |
where M = |Ω| and Ω = {x1,…,xM}. Further details regarding these concepts can be found in the book by Cover and Thomas.9
If the random variables are not discrete, the above equations give approximations in terms of samples, in which case a problem arises as to the accurate estimation of the probability density functions involved. A second problem is how to reduce the computational complexity.
Several approaches have been proposed to address these issues. Bernhard and Kubin10 improved an earlier algorithm by Fraser,11 which is based on recursively partitioning the value space of the random variables as a way to obtain a histogram for the estimation of the joint probability density functions. This approach has the attractive feature of having a complexity that is linear in the dimension of the random variables (as opposed to Fraser's algorithm, which is exponential), but like Fraser's, its complexity in M is O(M log M). Moreover, since these algorithms are based on binning of the samples for density estimation, their accuracy is questionable.
Another approach was proposed by Pham,12 who uses a kernel density estimation method (as we do) and a compactly supported kernel to simplify computations. He uses a coarse grid to evaluate the densities—coarse enough so that, at most, three points of the grid fall into the supports of the shifted kernel. This yields a complexity that is linear in M. However, the coarseness of the grid makes the accuracy questionable. In addition, there is no proposed method for selecting the bandwidth.
Heldmann13 proposed a method that is also based on kernel density estimation as well as expanding the kernel in Fourier series. This method achieves a linear complexity in M but does not provide a way to determine the appropriate bandwidth. We build on this approach by (1) providing a method for optimal bandwidth selection; (2) developing alternate formulas for cases of very small bandwidths; and (3) improving the accuracy by means of a modified Fourier expansion of the kernel.
Computing the Mutual Information
In order to efficiently compute the three probability density functions involved in eq 6, we first estimate them using the Parzen window approach, whereby each sample is replaced by a Gaussian function centered at the sample's value:
| (7) |
(and similarly for pg(t)), where Wσ is a scaled Gaussian kernel:
| (8) |
For the joint probability density function, a 2D Gaussian kernel is used:
| (9) |
where Σ is the bandwidth matrix However, empirical evidence15 suggests that using a diagonal matrix usually provides sufficiently accurate density estimates, and that using the full bandwidth matrix does not significantly or necessarily improve the accuracy. Thus, we shall use the following:
| (10) |
hence
| (11) |
Substituting eqs 7 and 11 into eq 6, we obtain the following:
| (12) |
The accurate estimation of the bandwidths σ1 and σ2 is crucial, as the density estimators (eqs 7 and 11) are critically dependent on them. The existing methods for bandwidth determination are fairly unreliable and not very practical (see Wand and Jones16). Hence, we have developed a new method, based on fitting the integral of eq 7 to the cumulative distribution function of f. Details are given in Appendix A.
Next, we normalize signals f and g, such that their values lie in the interval . The reason for this will become clear soon. The bandwidths σ1 and σ2 are scaled accordingly, so that the mutual information, eq 12, remains unaltered. Now the differences f(xj) − f(xm) and g(xj) − g(xm) lie between −1 and 1. This allows us to expand Wσ1 and Wσ2 in Fourier series on the interval [−1,1]:
| (13) |
where Na is chosen in such a way that is less than a prescribed accuracy ε. The are given by the following:
| (14) |
Since this integral cannot be evaluated in terms of elementary functions, we approximate it by integrating over the whole real line:
| (15) |
This approximation is good, provided that the exponential function is already small at ±1. We found that this condition is amply satisfied in all our application cases. (Should this condition not be satisfied, it would just be a matter of numerically integrating eq 14.) This yields the following:
| (16) |
We note that Heldmann et al.13 use a similar expansion, although theirs is valid only on the interval , which might introduce significant errors if the signals are concentrated toward the end points of their ranges (e.g., square waves, black-and-white images, etc.).
If either or both bandwidths σ1,σ2 are very small, the corresponding cutoff frequencies N1 or N2 need to be made very large in order for the Fourier expansion of the kernel (eq 13) to be accurate, with a consequent increase in computing time and storage requirements. In this case, we use an alternative approach, described in Appendix B. Otherwise, we proceed as follows. Using eq 13, we can now compute the sums occurring in eq 12:
| (17) |
where
| (18) |
The sums can be computed efficiently by means of the nonequispaced fast Fourier transform, or NFFT.17 This approach allows the fast computation of two types of sums:
| (19) |
| (20) |
where IN denotes a d-dimensional interval of integer numbers, from −N/2 to N/2 − 1 in each dimension. The NFFT method generalizes the standard FFT by allowing the nodes zj ∈ ℝd to be any vectors, without the restriction of belonging to a regular grid, as is the case with the standard FFT. A technical requirement in this method is that the nodes have their components between −1/2 and 1/2. This is the reason for scaling the signals f and g, as mentioned above.
Thus, the can be evaluated using eq 20 as
| (21) |
i.e., the adjoint NFFT computed with Hj = 1 and zj = −f(xj)/2. Then, can be evaluated likewise, using eq 19, as
| (22) |
i.e., the direct NFFT computed with and zj = −f(xj)/2. We also have the corresponding formulas for the second sum in the denominator in eq 12:
| (23) |
and
| (24) |
The numerator in eq 12 is computed along the same lines:
| (25) |
Where
| (26) |
which can be evaluated by means of a 2D adjoint NFFT, using eq 20 with :
| (27) |
and then J2 can be computed as a 2D direct NFFT (eq 19):
| (28) |
Complexity
The naive calculation of eq 12 is quite costly: O(M2) evaluations of exponential functions. Instead, the complexity of the NFFT-based approach is linear in M. In fact, each NFFT calculation costs18 O(Nd log N + M), where d is the dimension of the problem. In the present context, d is either 1 (in eqs 21, 22, 23, and 24) or 2 (in eqs 27, and 28). In our application cases, the value of Na is fairly small, roughly between 100 and 500, while M is much larger, typically between 103 and 107. Figure 2 compares the actual timings for a test case using three methods: the naive calculation, the NFFT-based method, and the “split” method, which consists of directly computing the quantities , , γkl, , , and J2(xj) by their defining formulas instead of by means of the NFFT. This approach has a complexity of O(Nd M), which is intermediate between the NFFT-based approach and the naive approach. For comparison, we note that the complexity of the Pearson cross-correlation calculation is O(M) as well, but with a smaller constant.
Figure 2.
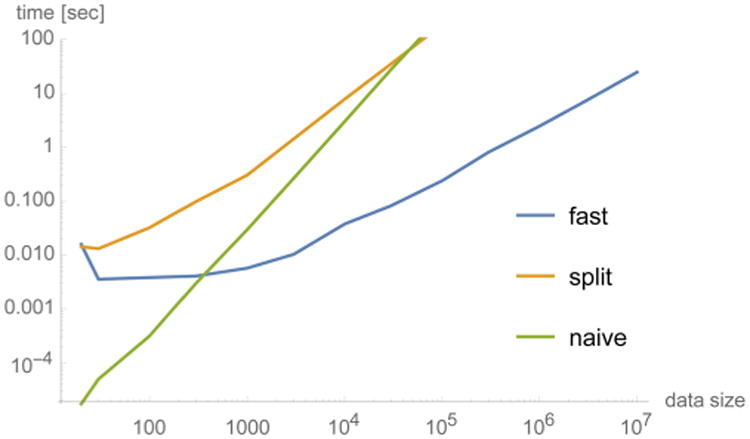
Performance comparison between various mutual information methods (eq 12). The test data set consisted of two identical cosine signals sampled at M points. The “fast” method, based on the NFFT, has a complexity that is asymptotically linear in the data size M, which is the same order as the classical Pearson cross-correlation, but with a larger constant.
Summary of Formulas
Here we collect the main equations for mutual information calculation used in the Results section. We have two cases: (1) normal bandwidths and (2) small bandwidths. (The meaning of “small” is defined in Appendix B, under “Threshold to Switch Between the Two Formulas”.)
Formulas for Normal Bandwidths
The formula in this case comes from eq 12:
| (29) |
where the J terms are computed using the following formulas:
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
| (35) |
Formulas for Small Bandwidths
First, we define the matrices:
| (36) |
| (37) |
for all 1 ≤ j,m ≤ M. Also, denote
| (38) |
and
| (39) |
| (40) |
| (41) |
We have three cases:
-
σ1 is small and σ2 is normal:
(42) -
σ2 is small and σ1 is normal:
(43) -
Both σ1 and σ2 are small:
(44)
The derivations of the above formulas are given in Appendix B.
Results
We demonstrate the above methods on three trajectories from diverse simulation approaches. The goal is to identify functionally important residues by finding relations between their fast, local dynamics and a slow, global “activity function.” As briefly justified in Methods, we considered three types of activity functions:
RMS fluctuation of Cartesian atomic coordinates (after least-squares fitting of the trajectory to the initial structure) in a Gaussian-weighed sliding window. This is the most conservative approach, and it works even for small peptides comprised of only a few amino acids.
- The combined rate of contact-forming and -breaking events observed in a time-dependent coarse-grained graph that consists of one representative atom per protein side chain. This rate can be computed using two different types of graphs:
- “Cutoff”: defines contacts by means of two cutoff distances, with an in-between buffer that suppresses trivial recrossings. This approach was shown to be sensitive to protein unfolding and yields a differentiated view of forming and breaking events.4
- “GMD”: defines contacts by means of the “Generalized Masked Delaunay” tetrahedralization of the coarse-grained model. This approach yields global monitoring of the structural variability of the molecule similar to RMS fluctuation, as opposed to the cutoff method, which is more sensitive to local changes. Anecdotal evidence from earlier work suggests that the GMD graph activity provides the best option for monitoring protein unfolding activity.4
The coefficients RX,a (eq 1) between the fast dynamics and the slow activity functions were then computed in two ways: with the Pearson correlation and with the newly developed FIM. The results were visualized in the 2D pairwise residue space or on the 1D sequence/3D structure in the form of heat maps.
BPTI
The first test was based on a 1 ms simulation of the folded 58-residue protein BPTI6 using standard MD. The native-state BPTI trajectory was represented by 10 300 frames in 100 ns steps. The BPTI trajectory is very stable, and due to its length, spanning nearly 12 orders of magnitude in time scales relative to the integration time step, provides an excellent gold standard for our validation. The reliable application of both the tagging.py and turning.py tools is evidenced by the results shown in Figures 1 and S2. The three activity measures shown in the latter are very similar to one another, resulting in comparable cross-correlation (CC) and MI profiles. This similarity demonstrates that the analysis is robust and that the new FIM method performs as expected (Figure S2). We have therefore selected only the MI results for RMS fluctuation activity for illustration purposes in Figure 1.
We can observe in Figure 1 that the most important residues for pivot angle and contact distance analysis are both located in a relatively unstructured loop region, which was described earlier to be very flexible, allowing four internal water molecules to exchange with the bulk.6 This flexibility is graphically depicted by the heat maps in Figure 1a,b. The pivot angle analysis in Figure 1a provides an illustration of the most active backbone-twisting and turning residues. These residues had earlier been shown to have the most dynamic content (as measured by the P2 internal correlation functions6). The found amino acids are among the most discriminative residues identified in Table S2 of the paper by Shaw et al.:6 Cys14, Ala16, Gly37, Arg39, and Lys41 stabilized three of five essential conformations representing the trajectory. Tyr10 featured an unusually mobile aromatic ring.6 The forming and breaking of contacts of this residue and of its neighbor Tyr11 are also identified in Figure 1b,d to be most important for the global dynamics.
It is important to note that the data in Figure 1b,d is a projection. The original data in pairwise residue space is plotted in Figure 3. Let Xi,j(t) denote the time series of the distance between residue i and residue j (we use the distance between the representative side-chain atom of each residue, as defined by Wriggers et al.4). In Figure 3 we construct the positive symmetric matrix RX,a(i,j) of ranking coefficients between the time series Xi,j(t) and a(t). This matrix describes the statistical relationship of every residue pair (i,j) with the activity function a(t). We found empirically that the matrices RX,a(i,j) display a banded structure, with certain columns (or rows) having large values for most of the rows (or columns). These bands of uniformly large values in the matrix RX,a(i,j), which are prominent in Figure 3, are due to the global nature of the statistical relationship between the activity and “the concomitant change of distances from a particular residue to multiple parts of the BPTI structure”.6 The particular structure of this matrix implies that we can compress the columns of RX,a(i,j) to their average RX,a(i), as shown in Figure 1b,d. In the following, we will also perform such compression of the contact matrices in the chignolin and EnHD cases.
Figure 3.
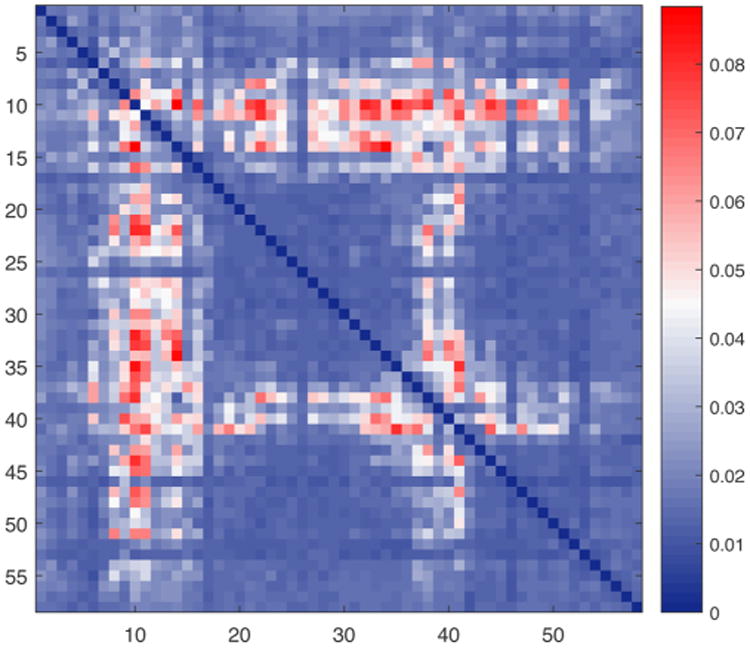
BPTI. Two-dimensional pairwise interaction heat map between residues. The banded structure of the symmetric matrix is clearly visible. Averaging along rows (or columns) yields the heat map shown in Figure 1b,d. For coloring and parameter information, see the caption of Figure 1.
In addition, we performed analyses on two abridged trajectories: one comprising the initial 0.1 ms and one comprising the initial 0.32 ms. A comparison with results from the full trajectory showed that the heat maps are robust under changes in simulation length, at least for the well-sampled BPTI trajectory (see Figures S3 and S4 for more details).
Chignolin
The second case study was the folding of the 10-residue chignolin peptide, which was recently simulated by Miao, Feher, and McCammon using GaMD to 300 ns.7 (The particular trajectory we analyzed is the one labeled “sim1” in Figures S1 and S2 of their paper, exhibiting 3000 frames in 100 ps steps.) GaMD performs MD on a flattened energy landscape that accelerates barrier crossing. The chignolin trajectory was chosen for two reasons. First, we wanted to explore whether our analysis, involving temporal smoothing parameters,4 could be applied to accelerated MD simulations with noncanonical chemical time. Second, we were interested in a suitable test system for our pivot angle analysis. In the above case of BPTI, the ends of the flexible loops were restrained by the stable structure, and the observed pivot regions were spread out over multiple residues. We hoped that the unrestrained termini of a short peptide in a folding simulation would provide a clearer example of localized hinge bending or pivoting.
Since chignolin is a very small molecule, the activity measures based on the coarse-grained cutoff or GMD graphs were poorly sampled: There was no noticeable (graph) activity present for the majority of the simulation time after about 20 ns, when the peptide settled in the native conformation (data not shown). The RMS fluctuation, however, gave a more nuanced representation of the folded state after convergence, so we chose it as the sole activity measure for our analysis. Figure 4 illustrates the detection of key residues involved in the folding trajectory.
Figure 4.
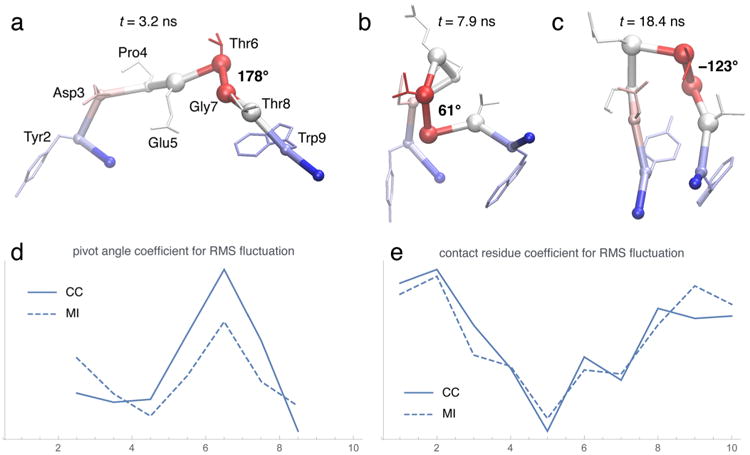
Chignolin heat maps and residue profiles. (a,b,c) Snapshots of folding events along the trajectory with the heat map from (d) superimposed. The backbone is shown as an α-carbon trace with α carbons highlighted as small spheres (except numbers 5, 6, 7, and 8, which are shown as large spheres). The dominant pivot angle (dihedral formed by α carbons 5, 6, 7, and 8) is labeled in degrees. Side chains are indicated in “licorice” representation. (d,e) Comparison between CC and MI, as functions of residue number, when using the RMS fluctuation curve as the activity measure. The sliding window length in the agility.py program was δ = 1 ns.4 Default parameters were used for the turning.py and tagging.py programs for the pivot angle analysis (d) and for the contact analysis (e). Pivot dihedral angles in (d) were attributed to the half-points between the residue indices of the center atoms. The full pairwise contact matrix for the MI data in (e) is shown in the “TOC” figure of the abstract (where diameter or color of circles encode the projected MI, and height or color of arcs encode the pairwise MI) and also (in matrix form) in supplementary Figure S5.
The pivot angle analysis in Figure 4d reports a single dominant pivot point in the structure, defined by the (pseudo-) dihedral centered on α carbons 6 and 7. Figure 4a,b,c shows three folding events that are associated with large changes in this pivot angle, with the profile of Figure 4d superimposed on them as heat maps. The folding process is complete when the important residues in the C and N-termini make contact, as shown in Figure 4e. The residues at the ends of the chain are significantly more active than those in the central region in regard to contact forming, due to their importance in stabilizing the folded state (more details are shown in Figure S5). In both the contact and pivot angle analysis, we see a high degree of similarity between the results obtained by the CC approach and those from MI.
EnHD
The third and final application of our method was to a single unfolding trajectory of the Engrailed homeodomain (EnHD), which was originally simulated to 42 ns as a single molecule,19 and later extended to the full 60 ns length that we analyze here,8 with a trajectory frame rate of 10 ps. (It is interesting to note that McCully et al.20 simulated a multi-molecular system consisting of 32 copies of this protein. They compared this with 10 single-molecule simulations, the one we are using here being the #2 among those 10.) Following the well-known Dynameomics approach of the Daggett lab,21 the unfolding was induced here by heating the system to 225 °C, which was selected because the heat-induced unfolding reproduces data from experiments and lower-temperature simulations.8
The EnHD trajectory was chosen because we wanted to test the behavior of our new FIM approach under elevated temperature conditions, where the Pearson cross-correlation failed to give consistent results when used with diverse activity functions. Figure 5a shows that, in this case, the activity measures are quite different from one another. The reason is that the heat-induced swelling and unfolding of the initial structure leads to a downward trend in the graph activities as the structure unfolds. In contrast, the RMS fluctuation exhibits an upward trend because the unfolded protein is less constrained by packing interactions. Thus, the RMS curve emphasizes pivot angles that are important in the later part of the trajectory, while the other two activity measures are sensitive to pivot angles that are relevant at earlier stages. Hence the complementarity of the CC curves in Figure 5b, whereas the MI will detect anticorrelated patterns as well, resulting in highly consistent curves, as shown in Figure 5d. Likewise, there is a dramatic difference between the CC and MI in the contact analysis. In Figure 5c, the CC essentially fails to detect any significant contacts based on the graph-based activities. The CC plots for the graph-based activities are also very dissimilar from those for the RMS fluctuation (CC coefficient −0.44 and −0.12 for cutoff and GMD, respectively), while for the MI plots in Figure 5e, there is good agreement with the RMS fluctuation-based plot (CC coefficient 0.80 and 0.60 for cutoff and GMD, respectively). Clearly, the use of MI rescues the performance of the challenging graph activities. This is presumably due to the fact that MI captures any type of functional dependency between two signals while the CC only detects linear relations.
Figure 5.
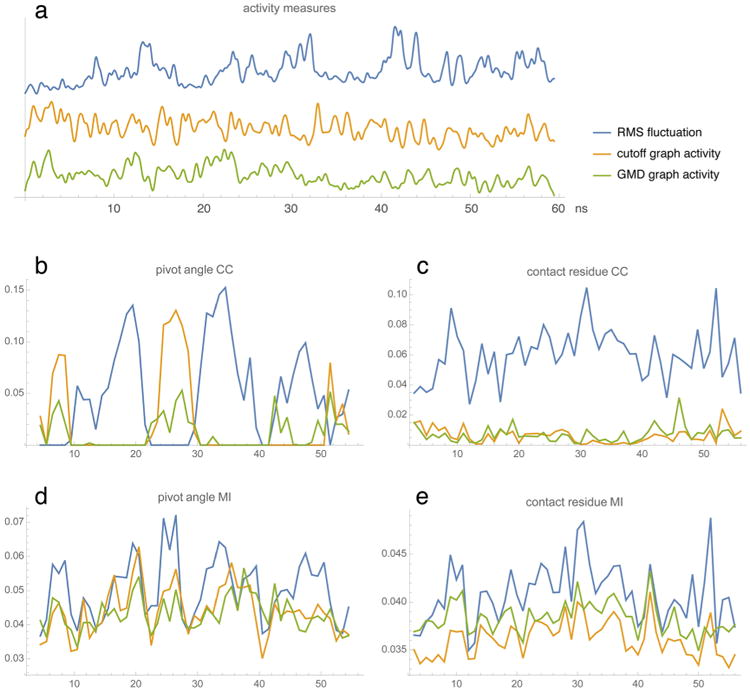
EnHD activity and residue profiles. (a) Three activity measures (see main text; arbitrary amplitudes and offsets) as functions of the simulation time in ns. The RMS fluctuation was computed with the TimeScapes agility.py program using a sliding window of length δ = 500 ps.4 The parameters used by terrain.py were cut1 = 6 Å, cut2 = 7 Å, δ = 500 ps for the cutoff graph activity and cut1 = 2, cut2 = 3, δ = 500 ps for the GMD graph activity.4 (b,d) Pivot angle CC and MI profiles as functions of residue number. (Pivot dihedral angles were attributed to the half-points between the residue indices of the center atoms.) (c,e) Contact residue CC and MI values projected on the residue chain. The three curves in each plot (b, c, d, and e) correspond to the activity measures in (a). Default parameters were used for the tagging.py and turning.py programs.
Figure 6 shows again in (a,b,c) the three EnHD contact residue heat-map projections computed with MI to demonstrate their similarity. The analysis in (d,e,f) highlights dominant residues that are responsible for contacts between helices I, II, and III.20 After 0.31 ns, there is some initial contact loss between helices I and II, and helix II starts to melt. After 2.38 ns, the contact between helix I and III at Lys52 is lost, and helix II melts further. After 6.84 ns, the helices are separated, and the tertiary structure starts to unravel. Incidentally, the Lys52 residue detected by our analysis can be mutated to Ala to increase the folding rate of the protein by about double.8
Figure 6.
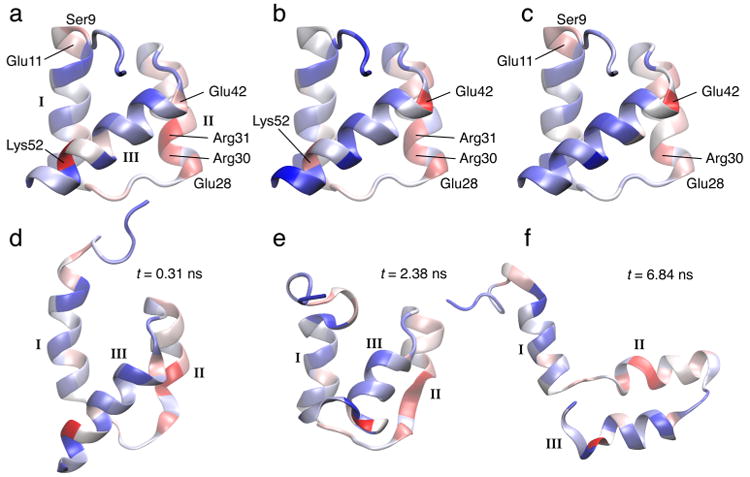
EnHD heat maps computed from activities in Figure 5(a) (color and rendering scheme as in Figure 1; Roman numerals label the three helices HI, HII, and HIII). (a) Contact residue MI heat map for RMS fluctuation activity (superimposed on the initial crystal structure). (b) Contact residue MI heat map for cutoff graph activity. (c) Contact residue MI heat map for GMD graph activity. The heat maps in (a), (b), and (c) correspond to the residue profiles in Figure 5e. (d,e,f) Snapshots of unfolding events along the trajectory with the heat map from (a) superimposed.
Conclusions
We have developed a novel FIM method for transforming time domain data into spatial images through handshaking between fast and slow degrees of freedom. The method was applied to three distinct MD trajectories to demonstrate its usefulness. The BPTI observations were robust under changes of activity function or statistical characterization, and thus provide confidence in the new FIM analysis. The BPTI results also agree well with earlier analysis results6 while providing a new way to attribute functional relevance to specific amino acids. The chignolin analysis confirms that the pivot residue and contact residue modalities can be complementary tools in the study of folding simulations. The results suggest that our theory is agnostic of chemical time scales and that long-time scale simulations are not required, as long as conformational changes are adequately sampled. The EnHD case not only provides an example of mapping the contact loss during the unfolding; it also demonstrates the higher robustness of the MI approach over the earlier cross-correlation.
In our tests, FIM was only about a factor of 5 slower than the earlier Pearson correlation approach. Since FIM provides superior results, we recommend using it in conjunction with the RMS fluctuation activity. The only potential weakness of our FIM approach is due to the uniform Parzen window approach, which at present does not adapt well to activities that are zero-valued. This problem requires an adaptive bandwidth allocation in future work. Meanwhile, the RMS fluctuation activity (or a large system size) avoids the issue. For the heat-map analysis, the RMS fluctuation appears to be the more robust choice among the activity measures, so we recommend it in general, unless a user has a specific reason to pick one of the graph-based activities.
This paper is the first to describe the FIM approach in detail, but more work could be done. Ideas for future work include:
The advantages and limitations of the tools should be tested further in an exhaustive exploration of the parameter space. We have provided examples of parameters that worked for us in this paper.
Our design of eq 1 was optimized for non-negative activities, but alternative functional forms could also be implemented. We have already proposed a variant of the tagging.py tool in earlier work, where instead of an activity an external time series was used, and instead of the rate of change, the direct correlation with pairwise distances was computed.6 The use of filters and different types of activity functions could also be explored. The absolute value for the (discrete) time differentials in eq 1 is required for linear measures I, as a(t) is non-negative. This absolute could be dropped when using the nonlinear FIM method (at a slight loss in sampling precision), but clearly this idea is most promising when signed activity functions are used.
The theory of eq 1 could be easily generalized to alternative modalities X(t). At present, this would require a user to write a new Python routine for every desired variable, similar to tagging.py and turning.py. It would be desirable in future work to develop a selection language on top of Python that enables the exploration of additional relevant degrees of freedom.
All software described in this paper will be freely disseminated with version 1.4 of our open-source package TimeScapes at http://timescapes.biomachina.org.
Supplementary Material
Acknowledgments
We thank John Heumann for his comments on mutual information. We thank Yinglong Miao and J. Andrew McCammon for providing the chignolin trajectory and for discussions. We also thank Michelle McCully and Valerie Daggett for providing the EnHD trajectory and for their biological interpretation. This work was supported by National Institutes of Health Grant R01GM62968.
Appendix A: Optimal Bandwidth Determination
As pointed out earlier, since the existing methods for bandwidth selection have unsatisfactory performance,14 we developed our own approach to solve this problem. We are after the value of σ that makes the Parzen approximation (eq 7)
| (45) |
as close as possible to the actual probability density function pf(s) of f.
The method we propose is as follows. Let F: ℝ → [0, 1] be the cumulative distribution function of f:
| (46) |
The first step is to obtain a continuous, piecewise-linear version of this step function. Basically, this is done by connecting the midpoints of adjacent “steps” (horizontal segments) of F. This initial polygonal is modified at points where the resulting slope would exceed a prescribed threshold (1000 by default) by replacing those points with the midpoint between the previous point and the first succeeding point of the polygonal that makes the slope less than the threshold. A second refinement is to smooth the resulting polygonal by convolving it with a Gaussian kernel whose standard deviation is 10% of that of f. These steps virtually eliminate the spurious oscillation in the slope of the polygonal that results from the unevenness of the sampling. Let us call the final piecewise-linear approximation FPL.
The next step is to fit the integral of eq 45 to FPL, the best fit yielding the desired σ. For this, we need an approximation of the normal cumulative distribution function. A very good tradeoff between simplicity and accuracy is given by the 1-parameter logistic approximation:22,23
| (47) |
Then, the integral of eq 45 can be approximated by the following:
| (48) |
The sought-after bandwidth is the value of σ that minimizes the L2 norm of the difference:
| (49) |
This minimization is efficiently carried out by the golden subdivision method, using as a starting point the “quick and simple” bandwidth selector:24
| (50) |
where σf is the standard deviation of f, as estimated from the sample.
To test this approach, we used some common density functions and visually verified the quality of the fitting. A shortcoming of this approach is that the bandwidths are constant rather than dependent on the sample point. This is noticeable in cases in which the probability density function has peaks of greatly different widths. However, this limitation exists in all methods that assume constant bandwidth.
Appendix B: Special Formulas for Small Bandwidths
When either or both bandwidths σ1, σ2 are very small, the cutoff frequency N needs to be made very large in order for the Fourier expansion of the kernel (eq 13) to be accurate. In this case, the efficiency of the method degrades, and the storage requirements increase. Hence, it is necessary to use an alternative approach to handle these cases.
The main MI equation (eq 12) can be written in a more compact form:
| (51) |
Where
| (52) |
| (53) |
with
| (54) |
| (55) |
Let us consider first the case in which σ1 is small but σ2 is not. Then, the problematic quantities to be computed are Σmajm and Σmajmbjm. The former can be estimated as the following:
| (56) |
where . This yields the estimate
| (57) |
where
| (58) |
As described below, the “small” threshold that we use is σmin = 0.002. Since the fjm range between 0 and 1, the exponential function acts effectively as a step function, which justifies the validity of the estimate in eq 57.
The numerator Σmajmbjm can be estimated along the same lines:
| (59) |
Hence, the MI equation becomes
| (60) |
In this equation, the sum in the denominator can be computed efficiently as before, using the NFFT. The sum in the numerator, however, is not amenable to such an approach, but since the number of terms is usually very small, its computation is also efficient.
The case in which σ2 is small but σ1 is not follows in the same way:
| (61) |
where and
| (62) |
Finally, if both σ1 and σ2 are small, we can further the calculation from eq 60:
| (63) |
and
| (64) |
where
| (65) |
Hence, the final formula for this case is
| (66) |
Threshold to Switch Between the Two Formulas
As mentioned after eq 13, the value of Na is derived so the coefficients (eq 16) become less than a prescribed accuracy . This inverse relation between N and σ provides us with a value σmin corresponding to the maximum value of N that is practical. In our computations, we took ε = 10−9 and Nmax = 1000, which yield σmin = 0.002. Values of σ lower than this are considered small, and the formulas above are used in this case.
Footnotes
Supporting Information: The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.6b02136. Additional figures showing time series, residue profiles, and pairwise interaction matrix (PDF)
The authors declare no competing financial interest.
References
- 1.Lee EH, Hsin J, Sotomayor M, Comellas G, Schulten K. Discovery Through the Computational Microscope. Structure. 2009;17:1295–1306. doi: 10.1016/j.str.2009.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dror RO, Dirks RM, Grossman JP, Xu H, Shaw DE. Biomolecular Simulation: A Computational Microscope for Molecular Biology. Annu Rev Biophys. 2012;41:429–452. doi: 10.1146/annurev-biophys-042910-155245. [DOI] [PubMed] [Google Scholar]
- 3.Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D. A Hierarchy of Timescales in Protein Dynamics is Linked to Enzyme Catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 4.Wriggers W, Stafford KA, Shan Y, Piana S, Maragakis P, Lindorff-Larsen K, Miller PJ, Gullingsrud J, Rendleman CA, Eastwood MP, et al. Automated Event Detection and Activity Monitoring in Long Molecular Dynamics Simulations. J Chem Theory Comput. 2009;5:2595–2605. doi: 10.1021/ct900229u. [DOI] [PubMed] [Google Scholar]
- 5.Yan B, Zhang W, Ding J, Arnold E. Pivot Residue: An Analysis of Domain Motion in Proteins. J Protein Chem. 1999;18:807–811. doi: 10.1023/a:1020641904152. [DOI] [PubMed] [Google Scholar]
- 6.Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, et al. Atomic-Level Characterization of the Structural Dynamics of Proteins. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- 7.Miao Y, Feher VA, McCammon JA. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J Chem Theory Comput. 2015;11:3584–3595. doi: 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gianni S, Guydosh NR, Khan F, Caldas TD, Mayor U, White GWN, DeMarco ML, Daggett V, Fersht AR. Unifying features in protein-folding mechanisms. Proc Natl Acad Sci U S A. 2003;100:13286–13291. doi: 10.1073/pnas.1835776100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cover TM, Thomas JA. Elements of Information Theory. 2nd. Wiley; Hoboken, NJ: 2006. [Google Scholar]
- 10.Bernhard HP, Kubin G. Signal Processing VII: Theories and Applications. Elsevier; Edinburgh, Scotland, U.K: 1994. A Fast Mutual Information Calculation Algorithm; pp. 50–53. [Google Scholar]
- 11.Fraser AM, Swinney HL. Independent Coordinates for Strange Attractors from Mutual Information. Phys Rev A: At, Mol, Opt Phys. 1986;33:1134–1140. doi: 10.1103/physreva.33.1134. [DOI] [PubMed] [Google Scholar]
- 12.Pham DT. 4th International Symposium on Independent Component Analysis and Blind Signal Separation (ICA 2003) Nara, Japan: 2003. Fast Algorithm for Estimating Mutual Information, Entropies and Score Functions; pp. 17–22. [Google Scholar]
- 13.Heldmann S, Mahnke O, Potts D, Modersitzki J, Fischer B. Bildverarbeitung fur die Medizin 2004. In: Tolxdorff T, Braun J, Handels H, Horsch A, Meinzer HP, editors. Informatik aktuell. Springer; Berlin Heidelberg: 2004. pp. 448–452. [Google Scholar]
- 14.Wand MP, Jones MC. Kernel Smoothing. 1st. Chapman and Hall; London: 1995. [Google Scholar]
- 15.Reference 14, section 4.6.
- 16.Reference 14, chapter 3.
- 17.Potts D, Steidl G, Tasche M. Modern Sampling Theory: Mathematics and Applications. In: Benedetto JJ, Ferreira PJSG, editors. Applied and Numerical Harmonic Analysis. Birkhäuser; Boston: 2001. pp. 247–270. [Google Scholar]
- 18.Kunis S. Inauguraldissertation. Universität zu Lübeck; Lübeck: 2006. Nonequispaced FFT—Generalisation and Inversion. [Google Scholar]
- 19.Mayor U, Johnson CM, Daggett V, Fersht A. R Protein folding and unfolding in microseconds to nanoseconds by experiment and simulation. Proc Natl Acad Sci U S A. 2000;97:13518–13522. doi: 10.1073/pnas.250473497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCully ME, Beck DAC, Daggett V. Multimolecule Test-tube Simulations of Protein Unfolding and Aggregation. Proc Natl Acad Sci U S A. 2012;109:17851–17856. doi: 10.1073/pnas.1201809109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.van der Kamp MW, Schaeffer RD, Jonsson AL, Scouras AD, Simms AM, Toofanny RD, Benson NC, Anderson PC, Merkley ED, Rysavy S, et al. Dynameomics: A Comprehensive Database of Protein Dynamics. Structure. 2010;18:423–435. doi: 10.1016/j.str.2010.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Savalei V. Logistic Approximation to the Normal: the KL Rationale. Psychometrika. 2006;71:763–767. [Google Scholar]
- 23.Johnson NL, Kotz S, Balakrishnan N. Continuous Univariate Distributions. 2nd. Chapter 23 Vol. 2. Wiley; New York: 1995. [Google Scholar]
- 24.Reference 14, section 3.2.
- 25.Humphrey WF, Dalke A, Schulten K. VMD: Visual Molecular Dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


