Applications of NMR and computational methodologies to study protein dynamics

Abstract

Overwhelming evidence now illustrates the defining role of atomic-scale protein flexibility in biological events such as allostery, cell signaling, and enzyme catalysis. Over the years, spin relaxation nuclear magnetic resonance (NMR) has provided significant insights on the structural motions occurring on multiple time frames over the course of a protein life span. The present review article aims to illustrate to the broader community how this technique continues to shape many areas of protein science and engineering, in addition to being an indispensable tool for studying atomic-scale motions and functional characterization. Continuing developments in underlying NMR technology alongside software and hardware developments for complementary computational approaches now enable methodologies to routinely provide spatial directionality and structural representations traditionally harder to achieve solely using NMR spectroscopy. In addition to its well-established role in structural elucidation, we present recent examples that illustrate the combined power of selective isotope labeling, relaxation dispersion experiments, chemical shift analyses, and computational approaches for the characterization of conformational sub-states in proteins and enzymes.

Graphical Abstract

1. Introduction

Proteins are not rigid entities but flexible assemblies. Despite the broad range of growth and living conditions inside eukaryotic and prokaryotic cells, a number of studies have efficiently demonstrated that changes in molecular flexibility of proteins and enzymes on various time scales results in significant loss of biological function and/or phenotypic defects ^1–4. Each protein exists as an ensemble of conformations that undergo continuous exchange within several spatial and temporal scales, relying on these motions to achieve their biological function. To fully grasp, predict, and eventually engineer efficient protein behavior at the molecular level, it is therefore crucial to understand the effects of conformational exchange and atomic-scale protein flexibility on biological function. To this day, nuclear magnetic resonance (NMR) spectroscopy represents one of the most powerful techniques available to unravel and investigate such dynamic protein behaviors on several time frames (Table 1). Technological developments and continuous improvements in processing power have recently allowed computational approaches to significantly complement NMR methodologies, providing spatial directionality and structural representations not easily or rapidly achievable by NMR. The present review article showcases several recent studies and methodologies characterizing protein and enzyme dynamics, primarily illustrating advances in NMR relaxation and computational approaches, coupled to other biophysical approaches. Recent examples demonstrating the combined power of selective isotope labeling, relaxation dispersion experiments, chemical shift analyses, and computational approaches are presented.

Table 1.

General outline of different NMR methodologies employed to quantify protein dynamics on a broad range of time frames. Partly adapted from ref. ¹⁰.

Method	Description	Information provided	Time Scale of Protein Motions Investigated	Exchange Ratea (kex) Characterized	Selected References
H/D Exchange	Detection of hydrogen exchange with a fully deuterated solvent: disappearance of amide proton signals over time	Solvent accessibility, hydrogen bond strength, slow conformational exchange	Seconds-minutes		91,92
Real-Time NMR (RT NMR)	Direct detection of dynamic processes by quantifying the time-dependence of NMR signal intensity after a perturbation of the system	Protein folding, solvent hydrogen-exchange, slow conformational exchange	Seconds	kex < 1 s−1 kex ≪ Δω	93,94
ZZ-exchange (Exchange Spectroscopy; EXSY)	Simultaneous determination of 15N longitudinal relaxation and chemical exchange during a mixing delay	Slow conformational exchange such as domain movement, ligand binding and release, topological interconversion of secondary structure, cis-trans isomerization	Milliseconds-seconds	kex ≈ 0.2–100 s−1 kex ≪ Δω	95,96
Chemical-and Dark-state Exchange Saturation Transfer (CEST/DEST)	Saturation transfer by chemical exchange between invisible (minor, excited) state and visible (major, ground) state	Information on invisible states, populations of the states, exchange rates and slow-intermediate conformational exchange such as small domain movements	Milliseconds	kex ≈ 10–100 s−1 kex ≤ Δω	6,28
Carr-Purcell Meiboom-Gill Relaxation Dispersion (CPMG RD)	Attenuation of chemical exchange broadening by applying refocusing pulses: reduce transverse relaxation R2 sensitive to motions	Kinetic, thermodynami c, and structural information for intermediate-fast exchange processes such as side chain reorientation, loop motions, secondary structure changes and hinged domain movements	Microseconds-milliseconds	kex ≈ 200–6,000 s−1 kex ≈ Δω	37,82,97
R1ρ rotating frame relaxation dispersion (RF RD)	Attenuation of chemical exchange broadening by applying refocusing pulses: reduce relaxation R1ρ sensitive to motions	Fast-intermediate conformational exchange such as motions of loops, side chains and secondary structure elements	Microseconds -milliseconds	kex ≈ 10,000–50,000 s−1 kex ≥ Δω	5
Paramagnetic Relaxation Enhancement (PRE)	Increased rate of relaxation due to magnetic dipolar interaction between a nucleus and an unpaired electron of a spin label	Lowly populated states of macromolecules and their complexes, non-specific interactions, ligand binding sites, fast dynamic processes	Microseconds	kex ≈ 100,000 s−1 kex ≫ Δ ω	15
R1, R2 and heteronuclear NOE relaxation (nuclear spin relaxation)	Analysis of longitudinal and transverse relaxation rates and the associated heteronuclear NOEs, sensitive to protein motions	Fast conformational exchange such as bond vibration and libration, side chain rotamer interconversion, random coil, loop motions, and backbone torsion angle rotation	Picoseconds - nanoseconds		16,98
Residual Dipolar Coupling (RDC)	Combined analysis of dipolar coupling constants measured in an array of experimental conditions	Structural states of a protein in solution, orientation of bond vectors, fast conformational exchange	Picoseconds-milliseconds		17,99
Chemical Shift Covariance (CHESCA) or Projection (CHESPA) Analysis	Analysis of residue networks that show correlated changes in chemical shifts due to perturbations in the system (mutations, ligand binding, etc.)	Allosteric networks, ligand binding sites			43,44,49–51

^aThe exchange rate (k_ex) is proportional to the chemical shift difference (in Hertz) between two exchanging states (Δω).

Excellent compendia have recently covered the theoretical aspects of NMR methodologies available for quantifying protein dynamics on a broad range of time frames, i.e. from picoseconds to hours ^5–17. To prevent undue repetition of the same theoretical concepts, the present report neither aims to offer a comprehensive overview of these NMR methodologies, nor to fully cover the wide array of protein systems exemplifying the importance of conformational flexibility in protein function. Rather, the goal is to illustrate to a general audience how the combination of newer developments with now established methods such as the NMR nuclear spin and relaxation dispersion experiments have become indispensable tools for providing a uniquely thorough understanding of the historically elusive protein dynamics and allosteric processes occurring in many biological systems. Non-technical readers should nevertheless be informed that most recent advancements have seen rigorous targeting of distinct atomic probes in protein backbone and residue side chains (HN, Hα, NH₂, Cα, C′, CH₃, etc.), in addition to effectively overcoming the classical size limitation of protein complexes amenable to NMR investigation ^18,19. Protein relaxation still requires dedicated access to high-field NMR spectrometers (typically between 500 MHz and 1GHz ¹H frequencies) and for extended periods of time (hours/days). This is due to the relatively low signal sensitivity of the method, especially in light of long three-dimensional heteronuclear experiments. However, significant advances over the past 10–15 years have lifted many classical limitations of the NMR technique, effectively providing a more complete understanding of the time-dependent properties of exchange processes occurring during protein function and allosteric communication.

2. Selective isotope labeling: overcoming protein size limitation in relaxation

For a long time, protein NMR applications were limited by the size of the molecular complexes under investigation. This was primarily attributed to a number of experimental factors pertaining to physical limitations of the technique and isotope labeling methodologies ²⁰. One of the most important limitations in protein NMR is the fact that higher molecular weight protein monomers or multimeric complexes tumble (or rotate) more slowly in solution than their smaller counterparts. This affects relaxation parameters and results in spectral broadening (or dampening) of NMR signals. Effectively, if a high molecular weight protein is uniformly labeled with ¹³C/¹⁵N isotopes throughout its primary structure, the relevant spectral NMR resonances are likely to be overlapped with other resonances, and therefore masked (or completely invisible) to the experimentalist. The uniform isotope labeling methodology required to achieve NMR signal presents another limitation for NMR of large proteins. Signal resolution for any multidimensional NMR experiment on a uniformly labeled large protein or protein complex results in a significant percentage of resonance overlaps, preventing detailed atomic-scale analyses for many of the overlapping residues.

Recent years have seen significant improvements in selective isotope protein labeling methodologies, effectively eliminating some of the disadvantages of uniform labeling ²⁰. A convincing example of selective labeling coupled to recent protein dynamics developments was illustrated by the Kay group on high molecular weight systems, particularly the 20S core particle (CP) proteasome ^21,22. Focusing on ‘metabolic tricks’ limiting isotope labeling to the methyl groups of Ile, Leu, Met, and Val residues, the authors have efficiently characterized functionally relevant motions in this megadalton complex. The 20S core particle (CP) proteasome is a 670-kDa complex formed by a combination of 2 alpha and 2 beta ring barrel structures that build a molecular machine involved in degrading cellular proteins that have become damaged over time. Due to massive size limitations, standard uniform isotope labeling prevents clear atomic-scale investigation. Using unlabeled (therefore invisible to NMR) beta protomers and highly deuterated, selectively labeled ¹³CH₃-Methionine residues in the alpha protomers (5 of which are found in the N-terminal pore entrance), the authors elegantly characterized the functional gating mechanism of this macromolecular complex by combining mutagenesis with paramagnetic resonance enhancement (PRE). The authors combined their NMR analyses with spin labels inside and outside the proteasome lumen, taking advantage of the PRE effect to study the conformational changes in the molecular gating mechanism ^21,22.

This example illustrates the power of combining selective protonation with mutagenesis, NMR relaxation, and PRE effects to investigate the dynamical behavior of high molecular weight protein complexes. Originally elusive, well-defined selective labeling protocols are now readily available to any skilled protein expression experimentalist ^8,19, allowing one to significantly improve the investigation of conformational exchange for large protein complexes using NMR relaxation dispersion (see below).

3. Investigating the microsecond to millisecond time frame to probe biologically relevant protein sub-states involved in allostery and enzyme function

Arguably one of the most influential and now routinely employed methodologies of the past 15 years in solution-state NMR is the investigation of free and ligand-bound protein complexes using relaxation dispersion. Relaxation dispersion NMR allows the characterization of low populated, ‘invisible’ sub-states sampled by proteins in solution, either in their free states or as they perform their catalytic function in the presence of binding partners. For instance, the Carr-Purcell-Meiboom-Gill (CPMG) and R_1ρ rotating frame experiments have been collectively employed to investigate conformational exchange rates (k_ex) occurring in proteins over time frames that roughly span ~100 to ~50,000 events per second (s⁻¹) ^9,23 (Figure 1). In addition to their relatively simple usage and implementation on multiple atomic probes (most of which are now available in standard and TROSY versions) ^19,24, relaxation dispersion experiments are especially popular in light of the overlapping time scale of the characterized rates of motion with the slower microsecond-millisecond (μs-ms) time frame of relevant biological processes such as protein folding, enzyme catalysis, ligand binding, etc. Recent advances have emerged to improve the breadth of ¹⁵N-labeled protein investigation by complementing the fast time scale (fast picosecond-nanosecond [ps-ns]) R₁, R₂, and heteronuclear NOE (hNOE) nuclear spin relaxation with CPMG and/or R_1ρ. This was done by selectively targeting ¹³C, ¹H and/or ²H dynamic spin probes and by improving spectral sensitivity ^25–27.

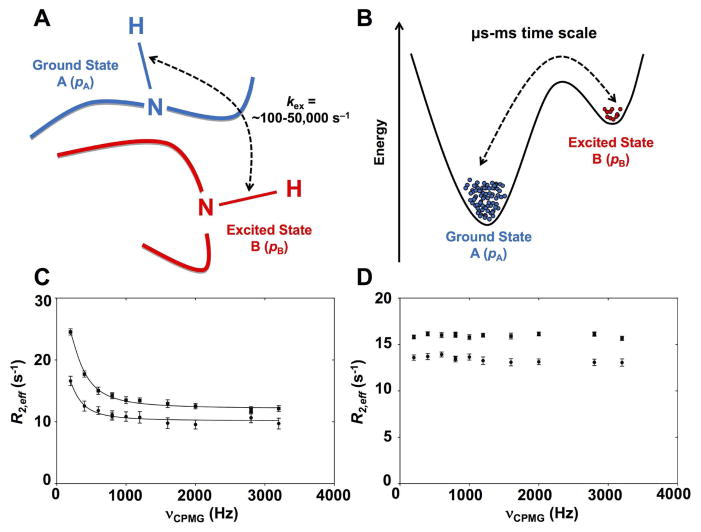
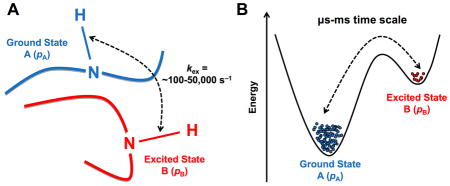
Figure 1. Schematic depiction of exchange between two protein conformational substates on the μs-ms time scale.

A) Schematic representation of a backbone residue HN vector experiencing conformational exchange between ground state A and excited state B on the μs-ms time scale. The popular Carr-Purcell-Meiboom-Gill (CPMG) and R_1ρ rotating frame relaxation dispersion experiments have been collectively employed to investigate conformational exchange rates (k_ex) for residues experiencing conformational exchange in proteins over time frames that roughly span ~100 to ~50,000 events per second (s⁻¹), overlapping the time scale of relevant biological events. B) Energetic representation of the two-site exchange between ground state A (higher population, p_A), and excited state B (lower population p_B, often invisible on fast and intermediate NMR time scales) ^23,53,100. NMR relaxation dispersion experiments can provide rates of exchange (k_ex), populations (p_Ap_B), and chemical shifts between interconverting species (Δω). C) Representative experimental ¹⁵N-CPMG NMR curves at 500 MHz (circles) and 800 MHz (squares) for a backbone HN vector experiencing conformational exchange on the μs-ms time scale in a protein. D) Flat experimental ¹⁵N-CPMG NMR profiles at 500 MHz (circles) and 800 MHz (squares) for a backbone HN vector that does not experience conformational exchange on the μs-ms time scale. The somewhat limited atomistic details on directionality and length-scales provided by NMR for these movements can readily be complemented by MD simulations, which offer full atomistic details of the conformational populations.

More recent methodologies, such as the NMR chemical exchange saturation transfer (CEST) experiment ^6,28,29, probe the same ms time frame and have provided improved sensitivity, in addition to allowing subtler conformational changes and better characterization of slower exchange processes (e.g. k_ex = 50–150 s⁻¹). The CEST experiment can also simultaneously take advantage of the CEST-derived R₁ and R₂ data to extract S² order parameters reporting on the ps-ns time scale ³⁰. In spin-relaxation NMR, the order parameter S² is typically extracted from the model-free approach using experimental R₁, R₂, and hNOE NMR data ^31–33. This parameter is used to characterize the amplitude of the internal motions of a ¹H-¹⁵N bond vector on the ps-ns time scale. S² measures the degree of spatial restriction of each backbone ¹H-¹⁵N vector, describing an array of atomic-site motions ranging from fully unrestricted (S² = 0) to completely restricted (S² = 1) on this particular time frame. The CEST approach showed remarkably good agreement with standard R₁, R₂, and hNOE nuclear spin relaxation data, in addition to considerably improving NMR acquisition time (hours instead of days). The CPMG method can further be extended at the other end of the time spectrum, allowing the investigation of systems with exchange rates as high as 6,000 s^{−1 34}. The combined analysis of both amide ¹⁵N and ¹H^N CPMG profiles and major state exchange-induced ¹⁵N chemical shifts measured in ¹H^N-¹⁵N heteronuclear multiple-quantum coherence (HMQC) and heteronuclear single-quantum coherence (HSQC) data sets allows the accurate extraction of exchange parameters and chemical shift difference between the interconversion states of systems exchanging with rates of ~6,000 s⁻¹.

In addition to the biological importance of the μs-ms time frame, and relative ease of technical implementation, recent examples of relaxation dispersion NMR have been employed with selective labeling and other biophysical methodologies to yield a complete portrait of protein allostery in various systems. A comprehensive enzymatic characterization also typically takes advantage of other biophysical techniques such as circular dichroism spectroscopy (CD) and/or isothermal titration calorimetry (ITC) ^35,36. A study on the allosteric mechanism of the heterodimeric 51-kDa glutamine amidotransferase imidazole glycerol phosphate synthase (IGPS) recently exemplified a subtle yet functionally relevant behavior observed through long-range allosteric motional transmission upon small-molecule effector binding to this enzyme involved in purine and histidine biosynthetic pathways in bacteria ^37,38. In this work, the authors combined ITC with ¹H,¹³C-TROSY-HMQC and methyl-TROSY multiple-quantum CPMG dispersion — all solely permitted because of selective isotope labeling of Ile, Leu, and Val methyl groups — to illustrate that the IGPS complexes with allosteric effectors distinctively respond to long-range (>15 Å) millisecond dynamics. Binding of allosteric effectors, monitored using ITC, revealed favorable enthalpic and entropic contributions to the free energy change, suggesting a shallow binding pocket for the effectors, consistent with docking and MD simulations. Interestingly, the authors demonstrate a direct linear correlation between the number of flexible residues on the μs-ms time scale and the catalytic efficiency (k_cat/K_m) of the glutaminase activity, further confirming the dynamic behavior of amino acid residues that were previously shown to be critical for relaying allosteric information from independent biochemical studies ^37,38.

These results highlight how protein-ligand complexes between IGPS and allosteric effectors with varying modulating efficiencies result in significantly distinct dynamic residue networks on the catalytic time frame of the enzyme. Further strengthening these observations, the authors observe that only the catalytically productive ternary complex between IGPS (the proper allosteric effector) and the PRFAR substrate yields a dynamic pathway with a shared, global exchange-rate constant (k_ex) for nearly all residues undergoing millisecond exchange in the enzyme. Although other IGPS allosteric activators also trigger millisecond motions, the exchange rates of individual dynamic residues are not concerted nor localized at selective residue positions essential for optimal allosteric communication. In addition to perturbing the unique profile of IGPS conformation, these suboptimal effectors also show concomitant gaps in their abilities to enhance glutamine hydrolysis ^37,38.

This work further illustrates the power of combining biophysical, computational, and new NMR methodologies to improve our understanding of allostery, offering the means to observe ‘invisible’ conformational sub-states that would have remained experimentally elusive just a few years ago. Performing these experiments using classical non-TROSY ¹H,¹⁵N-HSQC titrations, coupled with standard backbone ¹H,¹⁵N-CPMG relaxation would have yielded overly crowded spectra without significant resolution to observe the subtle molecular and motional effects described in these studies. Also, reports have illustrated the lack of significant structural changes caused by effector binding to IGPS (root-mean-square deviation of 0.41 Å between the apo and holo forms) ³⁷. As a result, previous crystal structures ³⁹ and fluorescence quenching experiments examining solvent accessibility ⁴⁰ were unable to provide definitive information on the intricate atomic-scale details underlying allosteric transmission in this enzyme system, further illustrating the power of the NMR methodology combination described here.

4. Uncovering potential allosteric sites using the NMR chemical shift covariance (CHESCA) and projection (CHESPA) analyses

Recent years have also seen the development of a variety of approaches that investigate NMR chemical shift perturbations to identify potential allosteric networks and structural dynamics in proteins ^41–46. The Melacini group introduced the chemical shift covariance analysis (CHESCA) approach ⁴⁴ to identify dynamically driven intramolecular amino acid networks. CHESCA uses a combination of agglomerative clustering and singular value decomposition to identify amino acid networks that show correlated changes in chemical shifts due to perturbations arising from ligand binding or mutations.

The CHESCA approach involves the following steps: first, a matrix M of combined ¹H and ¹⁵N chemical shifts of a protein in the apo and multiple perturbed states is used to calculate inter-residue Pearson’s correlation coefficients. The resulting symmetric matrix R of pairwise correlation coefficients is analyzed using the agglomerative clustering (AC) method ⁴⁷ to identify cluster(s) of coupled amino acid residues. AC assigns the first intracluster link for a residue pair with the highest correlation coefficient (r_ij). Subsequent intracluster links are assigned between the first pair and nearest neighbor based on the highest value of correlation coefficient to either of the residues in the original pair. These intracluster links, which can be visualized using dendrograms, identify cluster(s) of residues that show concerted response to perturbations. Clusters with more than three residues are grouped into ‘networks’. At this point, however, it is unclear whether these networks play a role in allostery.

To assign a function to the identified network(s), a correlation coefficient matrix R_I is computed using combined ¹H and ¹⁵N chemical shifts for a subset of amino acid residues (M_I) of the network(s) identified using AC, as described above. R_I is analyzed again using AC to cluster functional states (such as active vs. inactive states) based on residues rather than grouping residues based on functional states. Selvaratnam et al. applied this approach to the cAMP binding domain of EPAC using chemical shifts of the apo and activator (analog) bound states.

The authors identified two networks of amino acids, one separating active and inactive states of the protein, and another separating the bound and apo states. These observations indicate the role of these two networks in allostery. They further used singular value decomposition (SVD) ^44,48 to validate the functional networks identified through hierarchical clustering of AC. By using combined chemical shift differences relative to an antagonist-bound form of EPAC as reference, the authors identified residue networks involved in ligand binding and allostery, respectively.

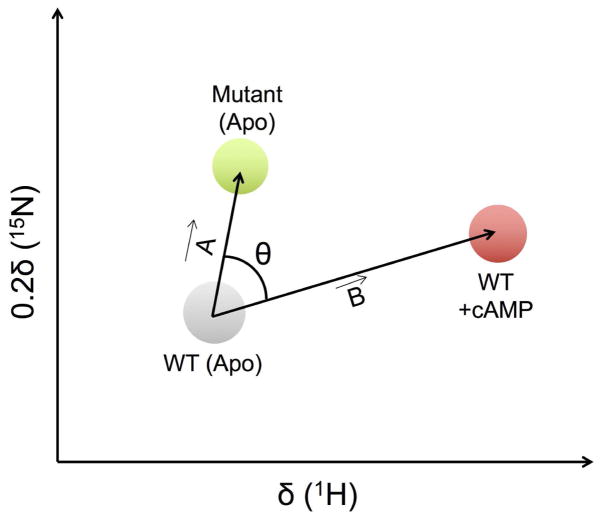
The Melacini group also introduced the chemical shift projection analysis (CHESPA) to quantify the size and direction of perturbations induced by ligand binding or point mutations (Figure 2) ⁴³. In CHESPA, two residue-specific descriptors of this perturbation, i.e. the direction (cosθ) and magnitude (fractional shift X), are calculated based on the chemical shift changes observed in the perturbed system. The fractional shift X is calculated as the ratio of vector A along vector B and the magnitude of vector B:

$$X=\frac{\overrightarrow{A}·\overrightarrow{B}}{{\left|\overrightarrow{B}\right|}^2}$$

Figure 2. Illustration of the CHESPA approach.

¹H-¹⁵N resonance assignments for apo, mutant and cAMP-bound forms of EPAC are represented as grey, green, and red circles, respectively. The compounded chemical shift upon mutation and ligand binding is calculated as the magnitude of vectors A and B, respectively (see text for details). θ represents the angle between vector A and B. Figure adapted from ref. ⁴³.

The fractional shift X is a scalar quantity and is complemented by cosθ, which reports on the relative orientation of vectors A and B, θ being the angle between vectors A and B:

$$\text{cos}\theta =\frac{\overrightarrow{A}·\overrightarrow{B}}{\left|\overrightarrow{A}\right|\left|\overrightarrow{B}\right|}$$

Of note is the fact that this approach is valid when the exchange in the free and ligand-bound conformations is fast on the NMR time scale. The presence of two or more states in the fast exchange regime could compromise the linear chemical shift pattern exploited by the CHESPA method, resulting in cosθ values below unity. Thus, cosθ values approaching unity suitably report on two-state equilibrium through the fractional shift X.

Much like CHESCA, the CHESPA approach was first applied on the EPAC model system by comparing the chemical shift changes arising from mutations and ligand binding to identify amino acid residues that (de)stabilize protein conformations associated with ligand binding ⁴³. In this study, the fractional shift X is positive if the mutation shifts the equilibrium towards the active state, and negative if the displacement is in the opposite direction. The value of X approaches 0 if variations caused by the mutation are negligible relative to those caused by ligand binding and/or if vectors A and B are orthogonal. Finally, X ≈ 1 indicates that the magnitude of the chemical shift is identical for mutation and ligand binding events. The direction of movement is quantified using cosθ (Figure 2). Residues with cosθ ≈ 1 show displacements in the same direction for both apo-mutant and ligand-bound states, whereas residues significantly affected by mutation display cosθ < 1. In this example, the L237W mutant of EPAC was shown to stabilize the inactive state, while cAMP binding activated wild type (WT) EPAC. The chemical shift difference between apo-WT and apo-mutant induced by amino acid substitution was calculated as the magnitude of vector A connecting apo-WT and apo-mutant peaks in the plane of ¹H and scaled ¹⁵N spectra (Figure 2). Similarly, the chemical shift difference induced upon ligand binding was computed as the magnitude of vector B connecting apo-WT and cAMP-bound WT peaks. The projection of vector A onto vector B is a measure of the shift of the conformational equilibrium between protein conformations found in free and bound states. In a recent study, Selvaratnam et al. combined the CHESPA and CHESCA approaches to characterize the effects of mutations on the inactive vs. active conformational equilibria of apo EPAC ⁴⁹. The CHESPA analysis was used to remove the false positives in the allosteric clusters obtained through the hierarchical clustering of residue pairs in CHESCA.

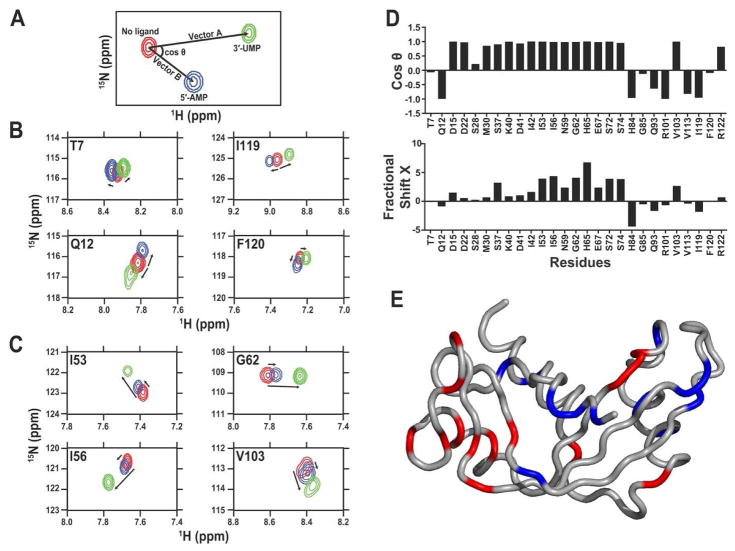
The CHESPA approach can also be used to investigate the effect of long-range residue network behavior occurring upon distinct ligands binding to an enzyme, as recently illustrated by the binding of 3′-UMP and 5′-AMP to human angiogenin (Figure 3) ⁵⁰. In this study, the authors highlighted the existence of two distinct, long-range clusters of residue networks either displaying correlated or uncorrelated chemical shift trajectories upon binding of each ligand to the purine- or pyrimidine-specific subsites of the angiogenin catalytic cleft, suggesting a structural rearrangement or allosteric response linked to ligand binding in this enzyme. Finally, using alanine to glycine substitutions, Axe et al. probed structural and dynamical changes in the α-subunit of tryptophan synthase ⁵¹. By combining the projection (CHESPA) and covariance (CHESCA) analyses for the free and ligand-bound forms of the wild-type and mutant enzymes, they identified point mutations that stabilized three conformational states, corresponding to the free form, glyceraldehyde-3-phosphate (product) bound and active (indole-bound) states. The authors further illustrated that the dynamical properties of the allosteric networks of amino acid residues identified from the covariance analysis differed in each of these states.

Figure 3. Application of CHESPA to human angiogenin.

Projection analysis describing independent and coordinated residue variations upon 5′-AMP and 3′-UMP binding to human angiogenin subsites. (A) Graphical representation of the CHESPA approach described in ref. ⁴³. The ¹H-¹⁵N position of the peak is represented for the free (red) and bound forms (5′-AMP in blue and 3′-UMP in green) of the enzyme. Arrows indicate the movement of the ¹H-¹⁵N chemical shift (length and direction) for each peak from its origin (in red) to its saturated position (blue and green). Projection analysis of eight selected residues responding in (B) independent or (C) coordinated manner in human angiogenin. (D) Direction cosθ and magnitude (fractional shift X) of the chemical shift perturbation of a subset of residues of angiogenin upon binding to saturation of the 5′-AMP and 3′-UMP. The cosθ quantifies the angle between vectors A (3′-UMP) and B (5′-AMP) from its initial position in the free form of the enzyme. The fractional shift X represents the fractional composite of vectors A and B induced by the ligand-induced chemical shift change. Collectiveness was observed for residues with a cosθ ~ 1, as previously described ⁴³. (E) Residues showing coordinated displacements (cosθ ~ 1) are represented in red on the three-dimensional structure of human angiogenin, while residues showing uncoordinated displacements (cosθ ≠ 1) are shown in blue. Reprinted with permission from ref. ⁵⁰. Copyright 2015 Wiley.

5. Enhancing the structural and time-evolution throughput of NMR spectroscopy using computational and theoretical approaches

5.1. Combining NMR observables and MD simulations to characterize protein motion

Molecular dynamics (MD) simulations provide a time-evolution ‘movie’ of atomic-level motions based on Newton’s laws of motions. Classical molecular mechanics describe the potential energy of a molecule, such as a protein, as a function of its atomic coordinates and dictate the interactions between atoms over the course of an MD simulation ⁵². The various force-constants associated with inter-atomic interactions are collectively referred to as a force-field. MD trajectories, which correspond to a collection of conformational snapshots sampled during the simulation, are analyzed using a variety of approaches to identify conformational states that are potentially important for function ⁵³. While conformational motions in proteins are observed over a wide range of time scales — from the fast femtosecond-picosecond (fs-ps) to the slower millisecond-second (ms-s) — the range of time scales accessible by MD is currently limited due to the speed of central/graphical processing units and related computer hardware. Until recently, sampling from MD simulations was typically on the order of hundreds of nanoseconds. Enhanced sampling techniques, alongside advances in computational resources, now enable routine conformational sampling on the μs time scale, with specialized supercomputing facilities reporting longer ms time scale simulations ^54,55. MD simulations have been used in combination with NMR to identify allosteric networks of conformational motions that play an important role in enzyme function ^10,56,57.

A diverse array of other sequence and structure based computational approaches have also been used to identify and characterize protein flexibility on the fast time scale ^58,59, in addition to characterizing allosteric networks that display motions on the slower μs-ms time frame via dynamical coupling of distal residues in proteins ^60–62. For example, DynaMine is a sequence-based approach that provides a statistical and quantitative analysis of protein backbone flexibility on the fast time scale (ps-ns) for each amino acid of the protein ⁵⁹. Statistical coupling analysis is another approach that uses sequence datasets of protein families to identify co-evolving amino acid networks important for distinct biochemical functions ^63,64. Using this approach, Reynolds et al. identified a co-evolving amino acid network in the dihydrofolate reductase family undergoing millisecond conformational dynamics that was strongly correlated with enzyme catalysis ⁶¹.

Accurate prediction of NMR observables such as chemical shifts, residual dipolar couplings (RDCs), and order parameters (S²) from protein coordinates has facilitated the characterization of protein dynamics through the comparison between NMR and molecular simulation ensembles ⁶⁵. Algorithms such as SHIFTX2, SHIFTS, CamShift, SPARTA+, and others have been used to predict chemical shifts from structural coordinates obtained from MD simulations ^66–69. Chemical shifts have also been used to compute order parameters (S²) for MD ensemble coordinates. Comparison of the predicted S² with experimental observations facilitates the quantitative characterization of fast time scale dynamics of the protein backbone, providing a range of conformations associated with the observed order parameters ^65,70,71. Further, MD can complement structural observations that are missing from NMR relaxation ^72,73.

In recent years, a number of studies have combined MD and NMR chemical shift analyses to probe conformational dynamics in proteins. For example, Robustelli et al. compared dynamically averaged chemical shifts predicted from MD simulation ensembles with experimental NMR shifts to characterize the effect of conformational dynamics on the observed chemical shift pattern in proteins. Using 100 ns and 1 μs simulations of two homologs of ribonuclease H (RNase H), they showed that ensemble averaged chemical shifts calculated from MD are in better agreement with NMR observables than those predicted from static X-ray structures ⁴². By probing the dynamical properties of regions displaying improved chemical shift agreement with experiment, the authors showed that these improvements result from: 1) a population weighted sampling of multiple conformational states, and 2) sampling within individual conformational basins. Further, analysis of averaged chemical shifts from MD simulations also identified erroneous conformations resulting from inadequacies of the force-field. These observations highlight the use of dynamically averaged chemical shifts to probe conformational dynamics in proteins.

NMR chemical shifts have also been used as replica-averaged structural restraints for MD simulations to characterize the dynamics of ribonuclease A (RNase A) ^31–33. Camilloni et al. showed that agreement between calculated and experimental chemical shifts was improved in the chemical shift restrained ensembles relative to unrestrained MD ensembles. Comparison of the free energy landscape of RNase A for the unrestrained and restrained MD ensembles showed that the restrained MD simulations sample the major and minor conformational states reported for RNase A, with the calculated population of the minor state consistent with previous experimental reports. These observations highlight the importance of using chemical shifts to bias the conformational landscape to reproduce dynamical properties of a protein in molecular dynamics simulations.

A number of NMR observables other than chemical shifts have also been used as restraints for MD simulations, either alone or by combining several observables ^11,75. Several studies have compared NMR residual dipolar couplings (RDCs) with predicted RDCs from MD ensembles to characterize backbone and side-chain dynamics over a range of time scales ^{12,13,76–79}. Markwick et al. combined plain and accelerated MD (AMD) simulations with experimental RDCs to characterize conformational dynamics of the GB3 protein over the faster ns and slower ms time scales ⁷⁸. In a subsequent study, the authors combined a novel AMD/SVD approach with extensive NMR observables to determine the time-resolved structural dynamics of ubiquitin over a broad time scale (ps-ms) ⁸⁰. SVD allowed the determination of optimal scalar J-coupling and RDC alignment tensor parameters. The population weighted average scalar couplings were shown to be in good agreement with experimental observations.

Computational MD simulations and experimentally extracted NMR relaxation parameters are now being routinely used as complementary approaches to characterize protein dynamics on multiple time scales. Among recent examples, this combined method was used to uncover amino acid residues associated with allosteric communication in Pin1 and IGPS (as reviewed above and in ref. ¹⁴). Cross-correlation analyses of protein motions from MD trajectories have highlighted changes in correlated motions upon binding of effector molecules to IGPS ^38,81. NMR and MD were also recently integrated to characterize the dynamical properties of the Streptomyces lividans xylanase B2 (XlnB2) in the free and ligand-bound states ⁸². Ligand binding was shown to induce enhanced conformational dynamics of residues that interact with the ligand in the thumb loop and finger regions of the enzyme. Finally, by comparing order parameters from MD simulations with NMR observables, Fisette et al. showed that better agreement is observed with structured elements (α-helices and β-sheets) while sampling of loop regions by MD were insufficient to reproduce the experimental observations for these regions ⁸³. In a subsequent study, the authors characterized the dynamical properties of two β-lactamases upon substrate binding ⁸⁴ (also reviewed in ref. ⁶⁵). By comparing order parameters obtained from MD and NMR for the free form, they showed excellent agreement for ordered regions while differences were observed for the less ordered loop regions. For the substrate-bound state, back-calculated order parameters from MD showed localized differences upon binding near catalytic residues.

5.2. Conformational fluctuations and sub-states characterization using the Quasi Anharmonic Analysis (QAA)

NMR techniques such as CPMG can provide the rate of exchange between distinct conformations constituting discrete conformational sub-states, enabled by concerted motions of residue networks that occur on the μs-ms time scale. For instance, many residues in a loop can experience similar individual exchange rates (k_ex), suggesting a concerted group (or global) motion on this particular time frame. Rates of conformational exchange of surface loop regions have been shown to coincide with the catalytic turnover in several enzyme systems ^85–87. This has led to a significant interest in linking events associated with these dynamic exchange rates with particular molecular mechanisms involved in protein function. Unfortunately, while possible, NMR is somewhat limited in its ability to provide rapid atomistic details on directionality and length-scales for these movements. Therefore, integration of computational and NMR techniques is becoming increasingly popular for the characterization of conformational substates and their populations. In combination with experimental NMR relaxation data, MD simulation techniques can be used to build a hierarchy of conformational states. With statistical sampling, MD can provide information on populations associated with each state and can also be extended to calculate the kinetic information about the interconversion between the states (Figure 1B). The rates and magnitudes of interconversion are correlated with the CPMG-based relaxation parameters. Once validated, the computationally obtained conformational sub-states can provide detailed information about the orientation and other structural (and dynamical) properties of individual atoms, residues, and whole proteins.

A novel computational approach, the Quasi Anharmonic Analysis (QAA), was developed to identify sub-states in the conformational landscape of proteins ^88,89. QAA uses higher order statistics of positional variations associated with sampling of conformational states from MD simulations and provides insights into the role of conformational fluctuations on longer time scales. It permits the identification of conformational sub-states along a reaction pathway that exhibit structural and dynamical properties important for function. Although a number of alternate approaches exist, the advantage of QAA lies in its ability to correctly identify energetically homogeneous conformational sub-states that correlate well with experimental information. Using T4 lysozyme and ubiquitin as model systems, Ramanathan et al. applied QAA to identify and characterize the hierarchical organization of conformational sub-states in these proteins ⁸⁸. The authors also characterized conformational sub-states associated with the cis/trans isomerization of proline peptide bonds catalyzed by the enzyme cyclophilin A (CypA)⁸⁸. They identified a separate conformational sub-state corresponding to the transition state of the reaction pathway in CypA, where motions of clusters of residues were shown to adopt conformations that promote the transition state.

In combination with NMR relaxation dispersion experiments, QAA was recently used to identify the conformational sub-states associated with the substrate and product bound states of wild-type (WT) and a single point mutant form of RNase A ⁹⁰. MD simulation trajectories of the apo, reactant, and product-bound states were used for QAA. Analysis of the top QAA modes revealed reduced global conformational motions in the mutant, corresponding to the interconversion between the reactant to product states, relative to the WT enzyme. Further, enhanced conformational dynamics of the surface loop 4 was observed in the apo and ligand-bound states of the mutant form. These enhanced loop motions were shown to be consistent with significant changes observed in the ligand binding and catalytic properties of the enzyme. Further analysis revealed a lack of correlated motions of two surface loop regions (loops 1 and 4) in the mutant, suggesting a role of this correlated motion for optimal catalysis in the WT enzyme ⁹⁰.

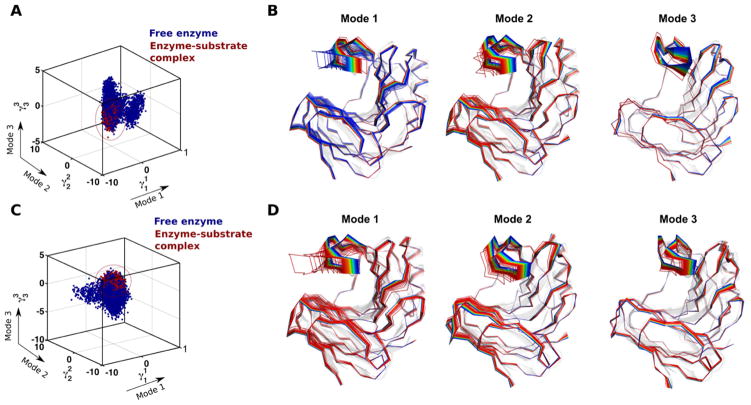
Further illustrating the power of this combined experimental-theoretical method, Gagné et al. used ¹⁵N-CPMG, microsecond time-scale MD simulations, and QAA to investigate the conformational fluctuations associated with the binding of substrates in xylanase B2 from Streptomyces lividans (XlnB2) ⁸². Using simulations of the apo enzyme and 6- and 9-unit xylan substrates bound to the enzyme as input for QAA, they characterized the dynamic modes and structural interactions of the enzyme that facilitate substrate binding (Figure 4). Details of the role of structural interactions of protein residues with ligand during the binding process and the range of motions (amplitude) that each residue undergoes were identified. It was discovered that the apo protein also samples the subset of conformations required for ligand binding. Quantitative characterization of these states would help in identifying the relationship between the rate of conformational exchange and the rate of ligand binding.

Figure 4. Conformational sub-states of xylanase B2 (XlnB2) from Streptomyces lividans determined using computational simulations and QAA.

Representative conformations along the top three modes for the interconversion between free and (A–B) X6-bound and (C–D) X9-bound XlnB2 binary complexes. A total of 200,000 conformational snapshots obtained from the MD simulations were used as input for QAA to identify the top QAA-independent component vectors for characterizing the primary dynamics associated with the substrate binding process in XlnB2. Reprinted with permission from ref. ⁸². Copyright 2016 American Chemical Society.

6. Conclusion

Technological advancements remain critical for improving NMR resolution and spectroscopic data acquisition when studying atomic-scale protein flexibility. The present review nevertheless illustrates that recent developments stem from the combination of clever isotope labeling schemes and carefully selected relaxation methods that either selectively target specific spin probes and/or improve spectral sensitivity, in addition to taking advantage of other biophysical techniques such as circular dichroism spectroscopy and/or isothermal titration calorimetry to characterize protein motions on multiple time frames. Finally, the combination of experimental NMR with computational methods aimed at predicting NMR chemical shifts, order parameters, and/or conformational sub-state populations (e.g. the quasi-anharmonic analysis, or QAA approach) now pave the way to an ever-increasing understanding of functionally relevant time-dependent motional events essential to biological function at the atomic level.

Highlights.

• Atomic flexibility on multiple time scales plays a defining role in protein function

• NMR relaxation allows the characterization of protein conformational sub-states

• Computational and biophysical applications further expand the range of NMR methods

• This review presents recent application progress to a general biochemical audience