Bias in image analysis and its solution: unbiased stereology

Abstract

Although the human eye is excellent for pattern recognition, it often lacks the sensitivity to detect subtle changes in particle density. Because of this, quantitative evaluation may be required in some studies. A common type of quantitative assessment used for routine toxicology studies is two-dimensional histomorphometry. Although this technique can provide additional information about the tissue section being examined, it does not give information about the tissue as a whole. Furthermore, it produces biased (inaccurate) data that does not take into account the size, shape, or orientation of particles. In contrast, stereology is a technique that utilizes stringent sampling methods to obtain three-dimensional information about the entire tissue that is unbiased. The purpose of this review is to illuminate the sources of bias with two-dimensional morphometry, how it can affect the data, and how that bias is minimized with stereology.

Introduction

Qualitative histopathology of tissue sections remains the gold standard for routine safety assessment studies, and pathologists play a unique and important role in identifying potential safety concerns. However, the human eye lacks the sensitivity to detect subtle changes in cell or object quantity. For example, a previous study found that a 33% reduction in total hippocampal neuron number could not be appreciated by pathologists, even when viewing side-by-side photomicrographs¹. For that reason, more sensitive techniques have been employed for these quantitative endpoints.

A commonly utilized technique to obtain quantitative information from histologic tissue sections is two-dimensional (2D) morphometry. With this technique, manual or automated analysis is performed on single or multiple tissue sections to obtain quantitative information, such as number of cells or other objects, linear measurements, or total area of positive staining (after the application of a cellular marker such as an immunohistochemical stain). Although these methods can supply the pathologist with quantitative information, the resulting data only pertain to the histologic section being examined. Counts or measurements performed on single thin 2D sections really have no correlation with what is present in a 3D structure. Furthermore, histomorphometry makes several assumptions about the tissue sections, all of which are sources of bias. Because of this, the data are inaccurate, often overestimating the object number or even showing trends that are in the opposite direction of the truth. In turn, professional and regulatory societies are increasingly becoming wary of 2D data.

Unlike histomorphometry, stereology does not make assumptions about the tissue and can supply accurate three-dimensional (3D) estimates of number, volume, surface area, or length. Stereology utilizes stringent sampling methods and calculations based on statistical theory and stochastic geometry that can be applied to virtually any tissue type from any species. The results are absolute estimates rather than densities or ratios. Furthermore, recent advances in technology have made stereology more approachable and efficient, allowing it to be used more readily in both investigational and safety assessment studies.

Limitations of 2-Dimensional Morphometry

Although 2D morphometry can provide additional quantitative information about the tissue sections being examined, it also makes several assumptions about the tissue, all of which are sources of bias. Bias leads to a difference between the mean of the estimator and the true population mean. This can include both type I error, in which an effect is detected that is not really present (a “false positive”) or type II error, in which an effect that is present is undetected (a “false negative”). In toxicology studies, the true population mean is most often unknown, and this stresses the importance of having unbiased data.

With 2D methods, the most optimum tissue sections are often analyzed. These sections are nonrandom tissue samples and they introduce sampling bias. With sampling bias, some of the cells or objects of interest are less likely to be included in the sample than others. One assumption made when tissues are sampled in such a way is that the entire organ or area of interest is homogeneous and that the section being analyzed is truly representative of the tissue as a whole. This is often not the case, particularly for certain tissues such as the brain. For example, the appearance of a small anatomical area such as the arcuate nucleus can change dramatically even in a single Bregma level². It can be extremely difficult to section the brain at exactly the same location in every animal, which may impact the ability to compare between animals and across treatment groups. Furthermore, if the entire cerebral cortex is the region of interest, a single section through the brain will not be representative of that area as a whole. Additional sampling bias comes into play when the microscopic fields of view are chosen. Often these fields are chosen “randomly” by the scientist, introducing substantial inherent user bias, and the chosen fields may not be representative of the tissue as a whole. Because the tissue sections and fields of view are non-random, statistical analysis of intergroup differences is not completely valid, as all statistical methods for hypothesis testing presume random sampling^{3, 4}.

Another assumption is that there is no change in organ size or volume. It is known that this is not the case during tissue processing, particularly with paraffin processing. For example, one study found that glomerular volume estimates were 40% lower for kidneys embedded in paraffin when compared with those embedded in glycol methacrylate, a soft plastic⁵. Another study found a similar degree of shrinkage when lung tissues were embedded in paraffin, and also observed some shrinkage with simple glycol methacrylate embedding⁶.

Two-dimensional morphometry also assumes that test article-treated tissue will experience the same amount of shrinkage during processing as control animal tissue. This is also often not the case. For example, treatment of rats and hamsters with testosterone and 17β-estradiol implants leads to testicular atrophy, and these animals had lower testes volumes when compared with untreated control animals^{7, 8}. In addition, the testes of the treated animals experienced a higher degree of fixation and processing-related tissue shrinkage when compared with controls^{7, 8}. It is known that density estimates, such as those obtained through 2D profile counting, are very sensitive to the effects of tissue shrinkage, and that a higher degree of shrinkage leads to overestimation of cell number and underestimation of tissue volume. In this study, this over-estimation of cell number led to a lack of statistical significance between the number of Leydig cells in the control group and the group treated with testosterone and 17β-estradiol, even when a correction factor was applied⁷. This was in contrast to estimates derived from unbiased stereological methods, in which significantly lower Leydig cell number estimates were noted in the treated animals when compared with the control group. It is important in any study utilizing quantitative microscopic methods to measure the degree of tissue shrinkage in each animal and to choose an appropriate embedding medium to minimize tissue shrinkage. Furthermore, certain stereological methods, such as the fractionator for number estimation, are insensitive to shrinkage⁹.

When a thin 2D section is taken through a 3D structure, little information about that 3D structure is maintained. If the cross-sectional profile of an object, such as an alveolus in the lung, is small, it may simply mean that the object was sectioned at its periphery; thus, the size of the profile does not correlate to the size of the 3D object. This is particularly a problem when cell or object number is the desired estimate, as profile counts are not an accurate estimate of cell or object number¹⁰. All information about particle size and shape is lost when a 2D histologic section is taken through a 3D tissue, and there is no known direct mathematical relationship between the number of 2D profiles and the number of 3D particles within a histological section. The presence of these “profiles” is highly influenced by their size, shape, orientation, and distribution within the tissue, and 2D morphometry makes many assumptions about these attributes. Instead of being counted according to their number, cells become counted according to their size or orientation, with larger cells or those oriented perpendicular to the sectioning plane having a higher chance of being counted. In addition, the thickness of the tissue section will influence the number of profiles present. Therefore, profile counting is a highly biased method of counting objects. This bias was illustrated in a study examining the number of CD68-positive and CD3-positive cells in lung biopsies using 2D and 3D methods¹¹. In that study, there was an overall overestimation of cells when counted by 2D methods and there was a statistically significant difference in mean CD68+/CD3+ ratios between 2D and 3D counting methods. Several other studies have also illustrated the disagreement between 2D profile counting and actual cell number (Table 1). Pakkenberg et al. determined that estimation of total neuron number in the substantia nigra through 2D profile counting led to an overestimate at an order of 30–40% when compared to unbiased 3D methods¹². In addition, a review of several studies examining the difference in substantia nigra neuron number between normal patients and those with Parkinson’s disease by 2D profile counting found differences that ranged from as little as 31% to as much as 80%, a very wide range¹².

Table 1. Studies Illustrating Disagreement in Results Using 2D and 3D Methods.

In some cases, differences in 2D estimates between treated and control groups can actually be in the opposite direction of the truth! For example, a study found that mean vertebral trabecular connectivity (an estimate of trabecular bone number) in calcium-restricted ovariectomized minipigs was found to be less than that of control pigs when 2D methods were used, whereas 3D stereological methods found the mean to be 69% higher in the calcium-restricted ovariectomized group¹³.

One additional limitation of 2D morphometric methods is that the results are often expressed as ratios or densities, such as the number of profiles per unit area of tissue. In contrast, results with stereology are expressed as absolute estimates of the tissue or structure in 3D using geometrical principles. Results expressed as ratios rely on the size and packing density of the structure of interest and are irrespective of the reference space, which can be affected by treatment. One cannot extrapolate densities to absolute values without knowing how this reference space (total tissue) was affected; therefore, it is imperative in any study to measure the reference space and avoid what is referred to as “the reference trap”. Furthermore, the cells or objects themselves can change in size and/or shape with treatment, which will affect density estimates. As is the issue with nonrandom sampling, statistical methods also cannot be validly applied to ratios⁴.

Some methods have been introduced that claim to correct for the size, shape, and/or orientation issues with 2D morphometry, and believe to be able to convert profile counts into absolute numbers. These include the Floderus method and the Abercrombie method (among others) in which counts are corrected for section thickness and/or particle diameter and other issues claim to be taken into account, such as fragments of objects that are lost due to sectioning or distortion of objects on histological sections^{14, 15}. With the Abercrombie method, profile counts are corrected by multiplying the count by the mean nuclear diameter and then dividing by mean nuclear diameter plus section thickness¹⁵. However, this method assumes that all nuclei are spherical, that one can recognize all nuclear fragments, and that the section is perfectly smooth, all of which are not the case with most tissue sections¹⁶. The issue with these techniques is that they are all still based on assumptions about particle size and/or shape, such as the assumption that nuclei are round or that the largest diameter profiles represent the largest cells, and are therefore biased in and of themselves^{8, 17}. They also make the assumption that all particles are oriented similarly in the tissue section. Furthermore, the results are still expressed as densities or ratios, and not absolute numbers. Several studies have shown the inaccuracies of these corrections factors. For example, the above mentioned studies by Mendis-Handagama showed that the lack of difference between control and treated animals when counting Leydig cells by 2D morphometry was in part due to the assumption that Leydig cell nuclei are spherical according to the Floderus method^{7, 8}. The above study by Pakkenberg et al. found that applying the Floderus correction formula to the 2D estimates of neuron number reversed the direction of error in the results, leading to an underestimation of approximately 20–40%¹².

In conclusion, regardless of the sophistication level of the image analysis platform used, bias introduced by the sectioning and sampling process, as well as bias due to assumptions about the tissue and objects of interest, cannot be eliminated.

Positions Taken by Professional Societies and Journal Editorial Boards

Because of the known bias with 2D quantitative methods, several professional societies and journal editorial boards have published guidelines on what quantitative methods should be used when evaluating for certain parameters or certain tissue types.

In 2010, an official joint statement on the standards of quantitative assessment of lung structure was published by the American Thoracic Society and European Respiratory Society¹⁸. This statement concluded that alveolar number and size could only be accurately measured using stereological probes (the disector) and not from simple 2D counts or measurements. Additional manuscripts have been published that call attention to the sampling and sectioning bias introduced by 2D morphometric methods, and recommend that stereology be used for quantification of lung structures^{19, 20}. An additional concern with the lung is consistent and adequate inflation of the tissue during fixation, as the majority of the tissue consists of air and the amount of air present fluctuates widely in vivo¹⁸. Several guidance documents on fixation and preparation of lung tissue for stereology have been published^{18, 21}.

In 1996, the editors of the journal Neurobiology of Aging published a short editorial stating that previously published 2D methods for counting the number of neurons or other objects were biased and based on assumptions about the size, shape, and orientation of the objects²². They went on to say that these methods do not ensure representative samples and can lead to counts that deviate from the truth by varying degrees. From that point forward, any article published in that journal that contained results on neuron or other object number had to employ unbiased stereological techniques. In the same year, a position paper and an editorial were published in the Journal of Comparative Neurology stating that if manuscripts submitted to the journal from that point forward used profile counting to obtain neuron or synapse number, including when assumption-based correction factors were used, investigators needed to clearly discuss their reasoning for using these methods, which would stand up to critical review^{16, 23}.

In 1999, a review article was published in the Journal of the American Society of Nephrology that described the applications of stereology in kidney research²⁴. This article stated that a 2D section through a 3D kidney tissue results in an irreversible change in both qualitative and quantitative information, and that the only way to solve this problem is by using stereologic methods. Therefore, stereology is the technique of choice whenever 3D quantitative information needs to be extracted from 2D tissue sections of kidney. In the same issue of the journal, an editorial was published stating that from that point forward, the journal editors would only accept manuscripts that utilized appropriate stereologic methods for quantifying structures in the kidney²⁵.

Position papers have even been published on the use of stereological methods to sample and quantify changes in the placenta^{26, 27}_.

How Stereology Avoids Bias

In contrast with 2D morphometry, stereology is design-based rather than assumption-based and is therefore unbiased (accurate), yielding results that are close to the true population mean. No assumptions are made about the size, shape, orientation, or distribution of the objects being counted or measured²⁸.

The first way in which bias is avoided in stereology is through the principle of systematic uniform random sampling (SURS). This is a method in which every structure of interest within the tissue has an equal probability of being sampled. The first section through the tissue is taken at a random start (hence the word “random” within the name) and remaining sections are taken at regular sampling intervals (“systematic”) throughout the tissue, until it has been exhaustively sectioned. This eliminates the sampling bias that is so prevalent with 2D methods. For small tissues, this can be completely accomplished at the microtomy stage, whereas several sub-sampling steps may be required for larger tissues. At each sampling step, the fraction of the tissue (or region of interest) being sampled can be kept track of and applied when the final estimates are calculated, a process known as fractionator sampling⁹. If all structures do not have an equal probability of being sampled, the estimate will always be biased, regardless of the technique used²⁹.

For some estimates, such as surface area or length, the orientation of the tissue sections is also important if the objects of interest are anisotropic, or dependent on orientation. For example, the orientation of capillaries within the heart is dependent on the orientation of the cardiomyocytes³⁰. In these cases, tissues may need to be randomly oriented in all directions (isotropic sections) or randomly rotated around an axis (vertical sections). This eliminates the bias of selecting non-randomly oriented structures based on their orientation within the tissue section. Generation of isotropic sections is generally performed by either the orientator or the isector technique, both of which have been outlined in detail previously^31,32,33.

SURS can also be applied when selecting fields of view within the tissue section for analysis. The user can dictate the percentage of the tissue that should be sampled and the computer will randomly choose the first field of view, then sample the remaining fields of view at regularly spaced intervals across the tissue (or region of interest), with the spacing between fields of view dependent on the user-inputted percentage of sampling. This avoids sampling bias within the chosen tissue sections.

Stereology avoids the bias of “the reference trap” through obtaining an unbiased estimate of the reference volume before any other parameters are measured. Alternatively, for cell number estimates, Fractionator sampling can be used (as described above), which is insensitive to shrinkage^{9, 34}. Several methods can be used to estimate the reference volume. An easy method is by Archimedes’ principle, in which the change in buoyancy of the organ is measured³⁵. Alternatively, a point grid can be randomly placed over SURS sampled slabs of the tissue (grossly) or tissue sections (under low magnification) and volume can be estimated using Cavalieri’s principle, in which the volume equals the sum of all cross-sectional areas multiplied by the distance between the sections^{31, 36}. The cross-sectional area can be calculated by multiplying the number of points intersecting the tissue by the area per point. If the volume is measured after any tissue processing occurs, it is important to keep track of the tissue shrinkage. This can be done through weighing the tissue prior to and after processing, and estimating the percentage of shrinkage³⁷. The total tissue volume for each animal can then be corrected for the amount of shrinkage that occurred. This eliminates the bias that results from assuming that control and test article-treated tissue respond equally to tissue shrinkage.

Within each field of view, appropriate stereological probes are applied, which minimizes geometrical bias. The probes are designed and applied in such a way that the cells or objects are sampled unbiasedly, regardless of their size, shape, or orientation. The correct probe is chosen based on the desired endpoint (volume, surface area, or length), with the dimension of the probe and dimension of the endpoint of interest adding up to 3, and strict rules are utilized as to when the intersections between the probe and the object of interest are counted (Fig. 1). For example, a line probe (1D) is applied for the estimation of surface area (2D), and the number of intersections between the line and the object of interest are counted. The number of intersections and length of the line are then utilized in the final estimation of surface area density, which is eventually transformed into absolute surface area by multiplying by the reference volume. These rules can be applied to any tissue from any species, and are thus universally standardized. For specific examples illustrating the use of these probes in toxicology studies, the reader is referred to Brown and Gundersen et al^{37, 38}.

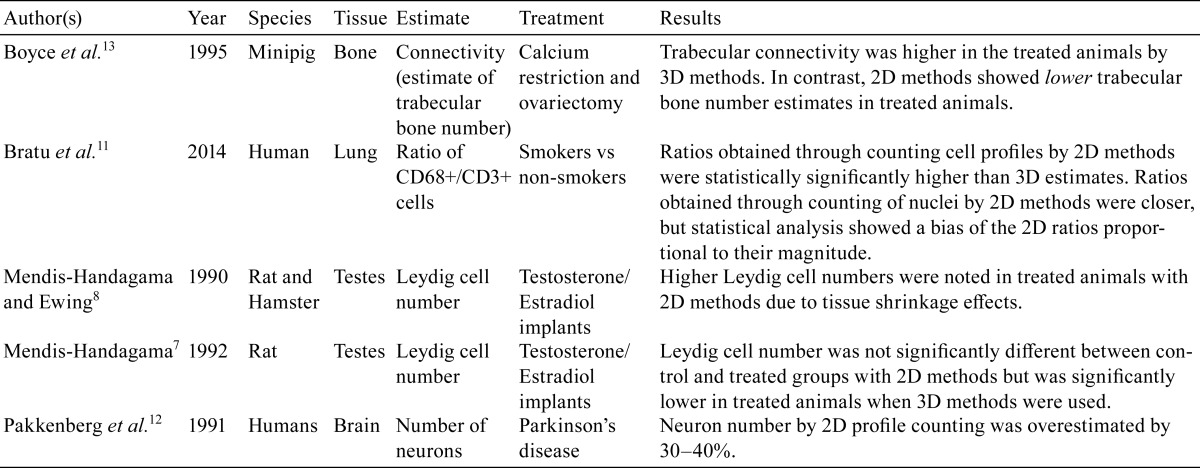
Fig. 1.

Application of stereological test systems (probes) to sampled microscopic fields of view. (a) For estimation of volume (3D), a dimensionless point probe (green crosses) is laid over the sampled microscopic fields of view. Intersections between the tissue or region of interest and the upper right-hand corner of the points are tagged. In this example, intersections between the granular layer of the cerebellum and the point probes are tagged (A). Rat brain, Hematoxylin and eosin (H&E) stain, 20× magnification. (b) For estimation of surface area (2D), a 1-dimensional (1D) line probe (blue line) is laid over the sampled microscopic fields of view. Intersections between the object of interest and the upper edge of the line between the endpoints (encircled blue crosses) are tagged. In this example, intersections between the alveolar septal tissue and the line are tagged (A). Rat lung, H&E stain, 40× magnification. (c) For length (1D), or number (dimensionless) estimates, an unbiased counting frame is applied to the sampled microscopic fields of view. The unbiased counting frame has 2 inclusion lines (green lines) and 2 exclusion lines (red lines), and objects are counted if they are within the counting frame (A) or touching the inclusion lines (B), but not if they are touching the exclusion lines (X). For number estimates, the 3D disector also has to be utilized (see Fig. 2). Rat brain, immunohistochemically stained for choline acetyltransferase (ChAT), 20× magnification.

For cell number estimates, a 3D probe known as the disector is utilized, which samples cells according to the number rather than according to their size, shape, or orientation^{28, 34}. It eliminates the potential biases associated with 2D morphometry in that it involves direct counting of objects in a defined volume of space. Like SURS, the disector ensures that all objects have an equal probability of being counted or sampled^{28, 34}. It does this by reducing the object to a “unique counting feature”, such as the nucleus, nucleolus, or top of the cell. Objects are only counted within the volumetric probe when this unique counting feature is present. Two types of disectors exist, the physical disector and the optical disector. In the physical disector, serial thin sections are collected and matching microscopic fields are captured. The fields are placed side by side and an unbiased counting frame is applied (Fig. 2), which has 2 inclusion lines and 2 exclusion lines. Cells are counted if the unique counting feature is present within one field but not within the other. If the tissue were sectioned exhaustively and every serial section was examined, 2D methods would result in drastic over-estimation of cell number, particularly for those cells that are large or oriented perpendicular to the sectioning plane, because the cell would be counted in more than one section (Fig. 3). In contrast, if the disector principle were applied as a serial reconstruction of the tissue, and cells were only counted if they were present in one section but not in the next, the absolute correct number of cells would be counted (Fig. 3). The principles of SURS are applied to sample a portion of the tissue and increase efficiency, yet still achieve an unbiased 3D absolute estimate of cell number. With the optical disector, single thick (at least 30 micrometers) sections are taken at each sampling interval and cells are counted in chosen sampling fields by focusing through the section slowly under a high magnification oil objective. This type of disector is, in and of itself, 3D, and it is intuitive that if the tissue were exhaustively sectioned into optical disectors and they were all stacked upon one another (such as with a 3D reconstruction), an accurate total number of cells would be obtained (Fig. 4).

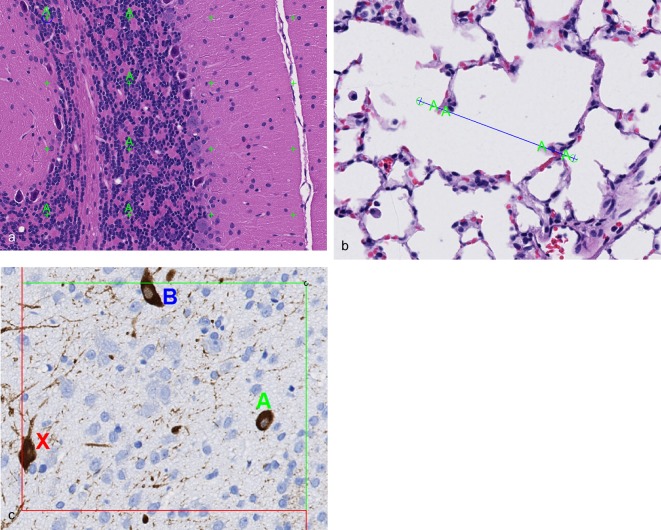
Fig. 2.

Application of the physical disector for estimation of cell or object number. Matching microscopic fields of view from serial sections are captured and placed side by side. A unique counting feature is chosen (in this case, the nucleus), and cells are counted if they are within the unbiased counting frame and the unique counting feature is present in one field but not the other. In this example, one cell is counted (green circumflex) because the nucleus is present in the field on the left but not in the field on the right. Other cells (red X) are not counted because the nucleus is not present on either side or the cell is outside of the counting frame. Rat brain, immunohistochemically stained for ChAT, 20× magnification.

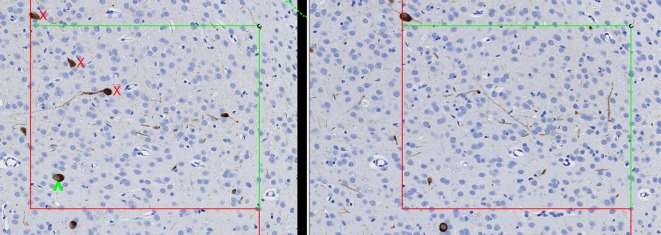
Fig. 3.

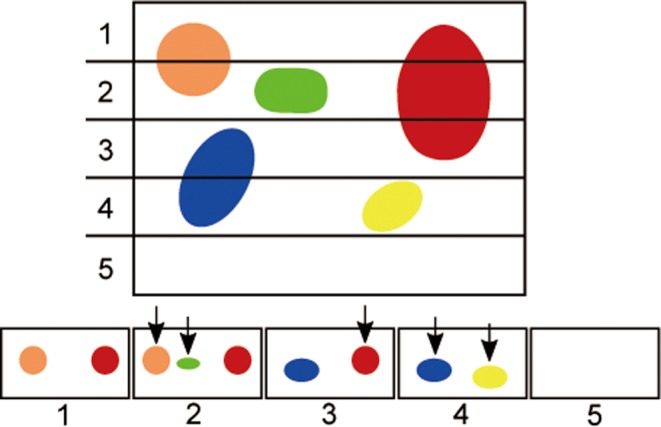
Illustration of what occurs when a 3D tissue is exhaustively sectioned into 2D sectioning planes. If all of the sectioning planes (1 through 5 in this example) are laid out side by side and objects are only counted if they are present within one section but not within the next section, as occurs with the physical disector, each object would only be counted once (arrows). This would result in the correct number of objects being counted; 5 in this example. In contrast, if the tissue is exhaustively sectioned and objects are counted on every sectioning plane without the application of the disector, the number of objects would be over-estimated. In this case, the total number of objects counted would be 9. Notice that objects that are larger and perpendicularly oriented to the sectioning plane (i.e. the red object) would have a higher tendency to be over-counted.

Fig. 4.

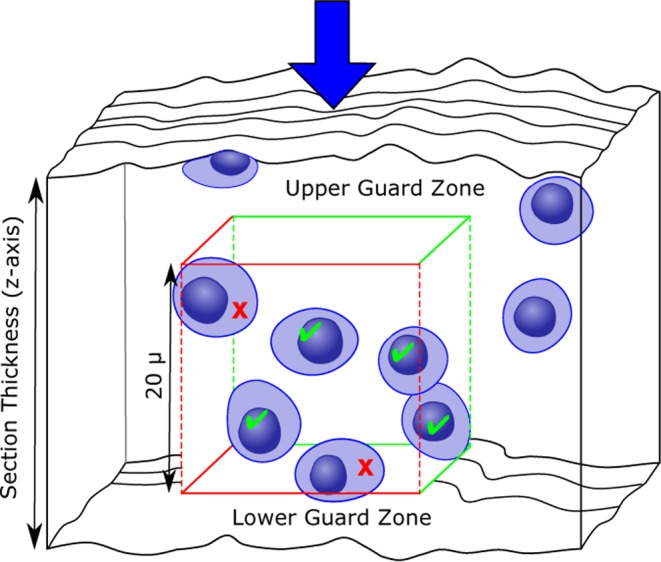
Illustration of counting objects using the optical disector, as viewed from the side. The optical disector is, in and of itself, a 3D probe. Objects are counted by focusing through thick sections on high magnification starting at the section surface (arrow) and counting cells as the unique counting feature (such as the nucleus) comes into focus. If this were applied to the entire tissue, the correct number of objects would be counted. As with physical disectors, an unbiased counting frame is applied to each selected microscopic field of view and cells are only counted when they are within the counting frame or touching the green inclusion lines (green checkmarks), but not when they are touching the red exclusion lines (red X). An additional aspect of the optical disector is the guard zone. These are areas at the top and bottom of the section where cells are not counted due to uneven section thickness, artifacts, or loss of cell nuclei. It is important to have a thickness of at least 15–20 micrometers within which to count cells once the guard zones are excluded.

When optical disectors are utilized, additional steps need to be put into place in order to minimize bias. The first is the use of guard zones. These are areas at the top and bottom of the section in which loss of cell nuclei, irregular tissue shrinkage, or artifacts from tissue sectioning (such as knife cuts) can occur (Fig. 4)^{39, 40}. The size of the guard zones can be determined during a pilot study by plotting the Z-distribution of the counts; that is, where in the depth of the tissue section (Z-axis) the cells are being counted. The location where the number of counts taper off at the top and bottom of the tissue section are then used as the guard zones for the study (Fig. 5). It is important to note that a thickness of at least 15–20 micrometers should remain in which to count cells once the guard zones are excluded. The next area in which additional bias can occur with the use of optical disectors is in estimating tissue thickness. It has been determined that section thickness can vary even within the same tissue section when thick sections are used^{39, 40}. Because of this, the section thickness has to be measured at each sampled microscopic field of view. This is done through the use of an microcator, or length gauge, that is attached to the microscope and can accurately measure the focal position of the microscope stage along the z-axis⁴¹. The section thickness at each field of view (weighted for the number of counts present) is then averaged and used when calculating the final absolute number estimate.

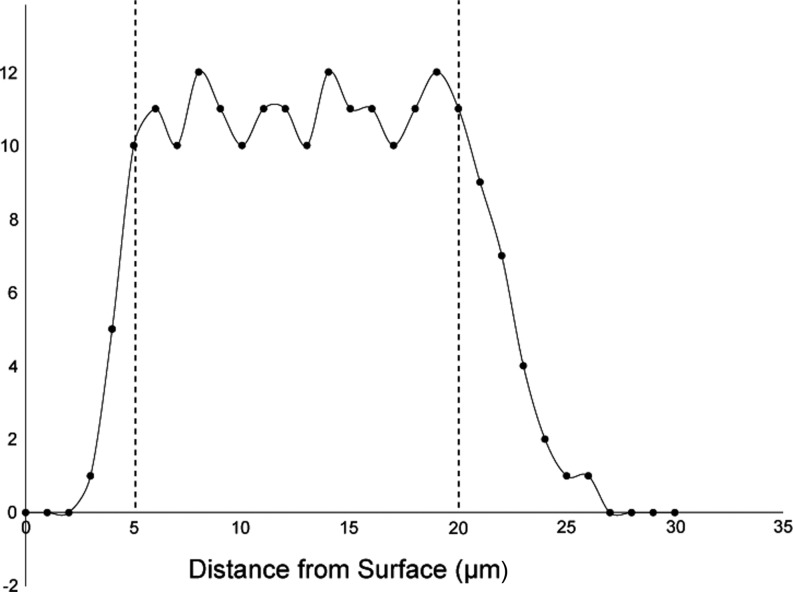
Fig. 5.

Illustration of a Z-distribution graph. In a pilot study, the number of cells counted at each location in the Z-axis (the section thickness) can be plotted. This can be used to determine where in the section thickness the number of cell counts drops off, which can then be applied as guard zones. In this example, the number of counts tapers dramatically less than 5 micrometers from the surface, and again approximately 20 micrometers into the section. For the study, guard zones would be applied so that no cells are counted from 0–5 micrometers and from 20–30 micrometers within the section thickness.

Bias versus Precision

It is important to remember that precision is not the same thing as bias. Precision is the reproducibility of the estimate (its variance), which is directly related to the amount of sampling. When the sampling strategy is more rigorous, the estimate will be more precise with lower variability. By contrast, bias is the level of accuracy of the estimate. An unbiased estimate has a mean that is close to the true population mean, and the data can either be precise or imprecise. The nice thing about stereology is that the precision can be estimated by calculating the coefficient of error (CE). The sampling strategy can then be made more stringent if needed in order to increase the precision of the estimator⁴². With 2D morphometry, there is no way to measure the precision of the estimate. Any estimates of variability obtained with 2D methods give information about the measurement process only, not about the estimate itself or the tissue as a whole. It is also important to note that just because an estimate is highly precise and therefore reproducible, it does not mean that it is accurate (that the mean is close to the true population mean). In order for the estimate to be accurate, it must be unbiased.

In general, the CE and biological variability (coefficient of error, or CV) are measured in a small pilot study (i.e. 3–5 animals) and an equation is applied to determine whether the estimator is precise enough³⁷. This equation is termed PROBE (precision range of an optimally balanced estimator), and is calculated as CV² / CE². If the result of the equation is more than 2, the estimator is considered to be of adequate precision. If the result is less than 2, the order then taken to increase precision is typically as follows: 1) increase the density of the stereologic probe on the sampled fields of view (i.e. apply more points/lines or a larger counting frame); 2) increase the percentage of the tissue sections sampled (i.e. capture more fields of view for analysis); 3) increase the number of sections analyzed per animal (i.e. capture 12 or more sections rather than 8–10); 4) include more animals in the study. For specific examples of CE calculations in toxicology studies, the reader is referred to Brown and Gundersen et al^{37, 38}.

Unlike precision, bias cannot be improved upon by increased sampling stringency. Furthermore, it is often impossible to determine whether the data are biased or not, particularly when bias is introduced due to inappropriate assumptions about geometry (i.e. size, shape, and/or orientation of the objects). The data points may be closely clustered together and appear precise (i.e. have low variability), but the mean may be very far from the true population mean due to inherent bias! That is why it is so important to avoid bias when sampling tissue sections and objects within those sections.

Lowering Sampling Bias in 2D Morphometry

Although some bias with 2D methods simply cannot be avoided (i.e. geometrical bias when counting objects), there are ways in which other types of bias can be minimized to the extent possible. The most prominent bias with 2D methods aside from geometrical bias is sampling bias. To minimize the sampling bias at the time of organ sampling, stereological methods of SURS can be applied. This will ensure that all cells or objects of interest have an equal chance of being represented. It will also increase the number of tissue sections available for analysis, which will increase the likelihood that the results are more representative of the tissue as a whole. It is important to remember that if not all objects have an equal probability of being sampled at the organ sampling stage, then the final estimate will always be biased, regardless of the counting technique that is used.

A second instance in which sampling bias occurs with 2D methods is in the selection of microscopic fields of view for analysis. Often, the scientist selects a certain number of “random” fields and then manual or automated analysis is applied. With some computer software systems, scanned slides can be imported for whole-slide image analysis and stereological sampling methods (SURS) can also be applied at this stage. The user can select a percentage of the tissue to sample and the computer can select the first field of view randomly and then sample the tissue at regular intervals thereafter. This eliminates the inherent user bias that occurs when a scientist chooses fields of view himself or herself.

The issue of the “reference trap” can be minimized by taking into account any changes in the reference space that occur due to tissue processing or treatment. Minimizing the effects due to tissue processing can be accomplished by estimating total global shrinkage for each tissue, as explained previously. Detecting changes due to treatment may require estimation of total tissue volume by Archimedes’ principle or Cavalieri’s principle, also described previously. This should be accomplished prior to organ sampling in order to obtain the total reference space volume. Measuring the effects on the reference space will give more meaning to the ratio or density values obtained with 2D morphometric methods.

As previously stated, the presence of profiles within a 2D histological section is highly influenced by their size, shape, orientation, and distribution within the tissue, and cells become counted according to their size or orientation rather than according to their number. Unfortunately, this geometrical bias cannot be eliminated; therefore, cell number estimates must utilize the disector in order to be accurate.

Caveats of Stereology

One important caveat of stereology is that it cannot usually be performed retrospectively. One of the main principles of sampling for stereology (using SURS) is that every object has an equal chance of being represented. This cannot be fulfilled if tissues have already been sampled at the necropsy stage. Therefore, if it is known that stereology may be needed for a study, it is best to involve a stereologist from the beginning so that the tissues can be collected, sampled, and fixed appropriately, should stereological analysis need to be conducted at a later date.

Another important caveat of stereology is that a pilot study is imperative in order to ensure the correct sectioning, sampling, and staining principles are utilized. These animals can be used to determine the optimal organ sampling protocol, histochemical or immunohistochemical staining procedures, and the best way to sample microscopic fields of view and apply stereological test systems. The CE and CV can also be calculated to ensure adequate precision of the estimator, and the sampling stringency can be increased if needed. Additionally, pilot studies can be beneficial for optical disector studies in determining the appropriate guard zones.

In addition, stereology studies require trained, skilled histotechnologists in order to produce samples that are as pristine as possible, and often require computer software and other specialized equipment. These advanced software systems, however, have made stereology increasingly practical and efficient.