Abstract
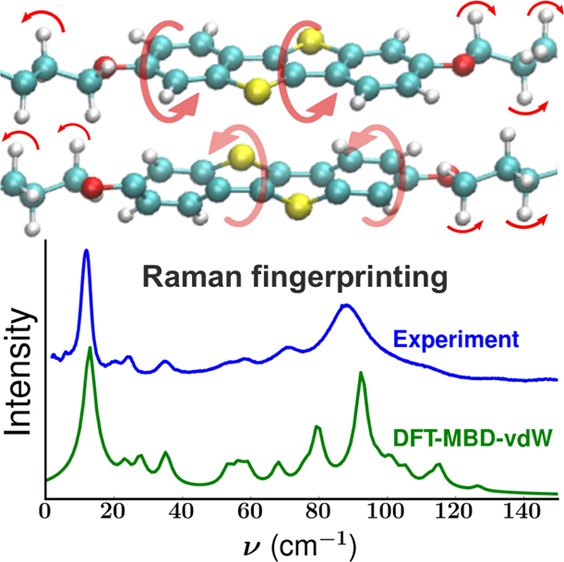
A combined experimental and theoretical approach, consisting of lattice phonon Raman spectroscopy and density functional theory (DFT) calculations, is proposed as a tool for lattice dynamics characterization and polymorph phase identification. To illustrate the reliability of the method, the lattice phonon Raman spectra of two polymorphs of the molecule 2,7-dioctyloxy[1]benzothieno[3,2-b]benzothiophene are investigated. We show that DFT calculations of the lattice vibrations based on the known crystal structures, including many-body dispersion van der Waals (MBD-vdW) corrections, predict experimental data within an accuracy of ≪5 cm–1 (≪0.6 meV). Due to the high accuracy of the simulations, they can be used to unambiguously identify different polymorphs and to characterize the nature of the lattice vibrations and their relationship to the structural properties. More generally, this work implies that DFT-MBD-vdW is a promising method to describe also other physical properties that depend on lattice dynamics like charge transport.
Understanding and controlling polymorphism is important in materials science due to the significant impact a change in the solid state packing can have on physical properties.1 Therefore, identifying different polymorphs of a material is key for a full understanding and characterization of its properties. Lattice phonon Raman spectroscopy is one method that has found utility for polymorph discrimination. By measuring Raman spectra in the low-wavenumber region (<150 cm–1), the technique probes intermolecular interactions and is therefore sensitive to the differences in molecular packing between different polymorphs.2,3 Advantages of this technique are that it is nondestructive and spatially resolved in the micrometer range, meaning that in mixed-phase systems domains of different polymorphs can be rapidly identified. This has potential applications in many fields, for example, when characterizing thin films of organic semiconductors.4 Here, it is known that new polymorphs, so-called surface-mediated phases,5 can appear, which have different properties than the bulk polymorphs. The location and identification of different phases is thus crucial in order to understand the properties of organic optoelectronic devices produced from such thin films.6,7
While differences in the Raman spectra in the low-wavenumber region mean that one can conclude whether more than one polymorph is present, linking the different spectra to specific polymorphs remains a significant challenge. The natural approach would be to compare against Raman measurements of a sample containing only one polymorph. However, to be able to link a Raman spectrum to a specific phase, X-ray diffraction measurements of the reference samples are necessary. Moreover, other issues such as crystal orientation, crystal quality, or experimental resolution can make phase identification difficult. Therefore, the precise location and identification of specific polymorphic phases is not currently possible using Raman spectroscopy without the application of additional characterization methods. A potential solution to this issue would be the calculation of lattice phonon Raman spectra of a known crystal structure, which could then be compared with the experimental Raman data to unambiguously assign the phases present. This, nonetheless, poses a substantial challenge with regards to the accuracy of calculations of vibrational properties. Although Raman spectra can be accurately calculated in the intramolecular region (wavenumbers > 150 cm–1),8−11 good agreement between theory and experiment in the low-wavenumber region has so far proved elusive. Quasi-harmonic lattice dynamics calculations based on force field potentials (FFPs) have been shown to be in qualitative agreement with experimental data (to within 20 cm–1).12 However, as Raman spectra of different polymorphs will typically have peaks very close to one another in the low-wavenumber region of the spectra (within <5 cm–1), this degree of accuracy is not sufficient to clearly identify different polymorphs. This calls for an accurate description of intermolecular vibrations, which requires a model that correctly describes van der Waals (vdW) interactions. The majority of models rely on a long-range pairwise interatomic term that is added to the total energy. In the framework of density functional theory, a wide spectrum of approaches, with different levels of accuracy, are currently available.13−23 In this work, we show that highly accurate results can be obtained from DFT calculations including many-body dispersion (MBD)-vdW corrections.19 To demonstrate that, calculated Raman spectra in the region of intermolecular vibrations (i.e., up to 150 cm–1) are compared to experimental measurements. The method is applied to two polymorphs of the organic semiconductor 2,7-dioctyloxy[1]benzothieno[3,2-b]benzothiophene (C8O-BTBT-OC8). C8O-BTBT-OC8 (Figure 1a) is known to form two polymorphs with different packing motifs; the most thermodynamically stable parallel stacked (PS) phase (Figure 1b) is readily grown as a single crystal, while the metastable herringbone (HB) phase (Figure 1c) is a surface-mediated phase where the molecular packing conforms to a flat substrate surface and can be kinetically trapped during crystal growth.24,25 The crystal structure of the PS phase has previously been determined, while only the unit cell of the HB phase was so far identified;24 its precise crystal structure is determined here for the first time.
Figure 1.
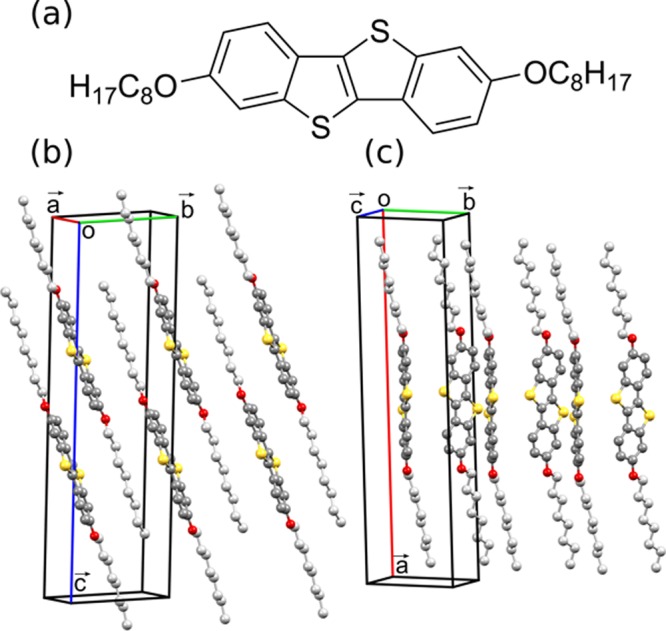
(a) Chemical structure of C8O-BTBT-OC8 and (b) molecular packing in the PS phase24 and the (c) HB phase. The HB phase structure has been solved in this work from single-crystal X-ray diffraction data. Carbon atoms are colored gray (dark gray in the aromatic core and light gray in the alkyl chains), sulfur atoms yellow, and oxygen atoms red; hydrogen atoms have been removed for clarity.
Figure 2a,b,d shows the measured lattice phonon Raman spectra, in the energy region below 150 cm–1, of the polycrystalline powder and crystals grown from hexane solution at different evaporation rates (see the Experimental and Computational Methods section). The modes in this wavenumber region are mainly determined by intermolecular interactions and in a first approximation can be thought of as the librations and translations of the molecules as a whole. As a consequence, they are very sensitive to the details of the molecular packing. In Raman spectroscopy measurements, only modes with wavenumber k = 0 (i.e., those in which the molecules of all cells vibrate in phase) are detected, and the resulting spectra represent the fingerprint of a specific crystal structure.26 Two different Raman patterns are obtained depending on the crystal growth conditions. The polycrystalline powder obtained after material synthesis (Figure 2a), as well as crystals grown from hexane solution in a partially covered vial [C] (Figure 2b), show characteristic peaks at 12 and 88 cm–1. Crystals grown from a hexane solution in an uncovered vial [UC] (Figure 2d) show a different pattern, with intense bands at 7, 18, 89, and 103 cm–1, suggesting the presence of a different polymorph compared to the powder and covered hexane [C] sample.
Figure 2.
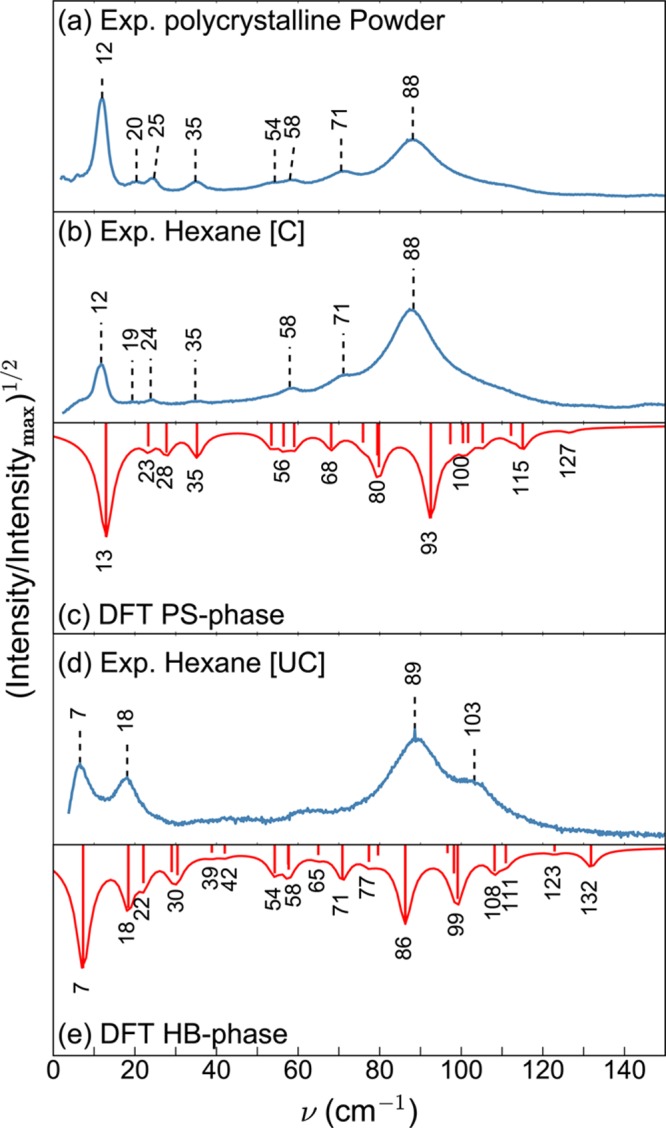
Experimental Raman spectra of C8O-BTBT-OC8 in the lattice phonon regime of (a) polycrystalline powder and of crystals grown from a hexane solution (b) in partially covered vials [C] and (d) in uncovered vials [UC]. Experiments are compared to DFT calculations of the Raman spectra of (c) the PS phase and (e) the HB phase. For the sake of comparison, the square root of the intensities, normalized to the maximum intensity, is plotted instead of linear intensities. The Lorentzian functions around the calculated peak positions are drawn as a guide for the eye.
On the basis of the known crystal structures of the two polymorphs (see below), DFT calculations of the Raman spectra of both the PS and HB phases were performed (Figure 2c,e). The experimentally observed peaks can be identified in the calculated spectra to within an accuracy of ≪5 cm–1 (≪0.6 meV). On the basis of the calculated spectra, the lattice phonon Raman spectrum of the polycrystalline powder (Figure 2a) and also the spectrum of the crystal grown from hexane [C] (Figure 2b) can be assigned to that of the PS phase (Figure 2c). Conversely, the Raman spectrum of the crystal grown from hexane [UC] (Figure 2d) can be associated with the HB phase (Figure 2e).
Polymorph identification from Raman spectra is validated by X-ray measurements. X-ray powder diffraction measurements show that the polycrystalline powder packs in the PS phase,25 while the crystal grown from hexane [UC] packs in the HB phase. Bearing in mind that the polycrystalline powder and the crystal from hexane [C] show the same characteristic Raman spectra; this means that the hexane [C] sample also packs in the PS phase. As the HB phase crystal structure has been solved in this work from synchrotron single-crystal X-ray diffraction measurements, a general description can be given here (detailed crystallographic data is provided in Table 1s of the Supporting Information(27,28)). It was found that the structure of the HB phase has a monoclinic unit cell containing a half crystallographically independent molecule in the asymmetric unit. The unit cell dimensions of a = 31.056(6) Å, b = 7.663(2) Å, c = 5.996(1) Å, α = γ = 90°, and β = 94.18(3)° are in excellent agreement with the previously determined values (with the a and c axis directions switched) of the metastable surface-mediated phase.24 In contrast to the PS phase, where the molecules arrange with an interdigitated layered structure in a triclinic crystal system,24,25 a herringbone packing motif without interdigitation of molecules is found (cf. Figure 1c); this packing motif is also observed for other dialkylated BTBT derivatives (Cn-BTBT-Cn, with n = 8, 10, 12).29
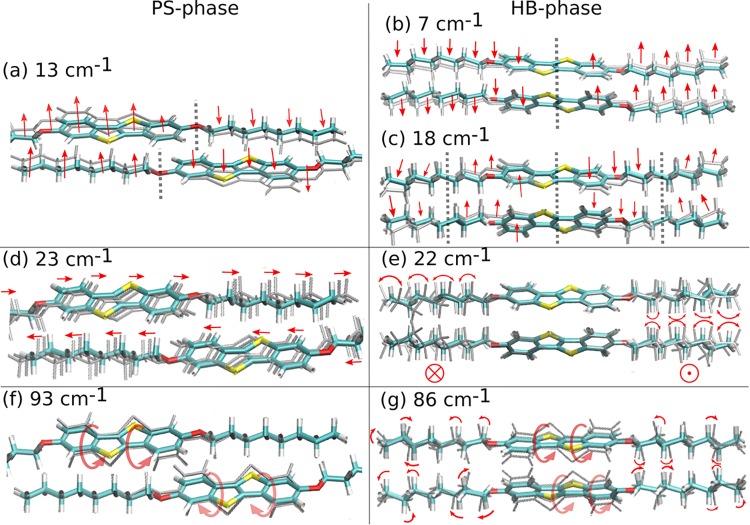
Aside from allowing unambiguous phase identification, accurate phonon calculations also provide detailed information on the nature of the vibrational modes. In particular, they provide insight into their relationship to the structural packing of the system. To illustrate this point, prototypical Raman-active modes of both polymorphs are compared. A schematic representation of these modes is provided in Figure 3; direct visualization of all active modes reported in Figure 2c,e is available through animations supplied with the Supporting Information. The high-intensity peak measured at 12 cm–1 (calculated at 13 cm–1) for the PS phase is found to result from a symmetrical wagging of the molecule perpendicular to the plane of the aromatic units (Figure 3a). For the HB phase, two Raman-active peaks are calculated in that wavenumber region at 7 and 18 cm–1. The former arises from a mode with the same wagging character as the mode calculated at 13 cm–1 for the PS phase (Figure 3b). For the mode at 18 cm–1, the number of nodes in the displacement pattern increases (see vertical dashed lines in Figure 3c), and the central segments of the molecules tilt in directions opposite to the outer parts of the alkyl chains. An equivalent vibration can also be found in the PS phase at 35 cm–1 (see animation in the Supporting Information). The energy shift is attributed to the fact that in the PS phase aromatic units neighbor alkyl chains, while in the HB phase aromatic and aliphatic segments are next to each other. This changes the interaction potentials and, consequently, the energies of the vibrational modes. Raman-active modes appearing in both polymorphs at very similar wavenumbers can in fact correspond to fundamentally different vibrations. This is very difficult to determine solely based on experiments and is illustrated for the Raman-active modes calculated at 23 cm–1 (PS) and 22 cm–1 (HB). The former originates from out-of-phase translations of neighboring molecules in the direction of the long molecular axis (Figure 3d), while the latter corresponds to wagging of the molecules perpendicular to the plane of visualization in Figure 3e, combined with torsions of the alkyl chains. Interestingly, both sets of vibrations occur in both polymorphs, but only one of them is Raman-active in each polymorph. This is associated with the fact that different packing motifs yield different structural symmetries and hence distinct responses of the polarizability to the vibrations of the system.
Figure 3.
Visualization of different Raman-active lattice modes of the HB and PS phases given with the calculated peak positions. Arrows indicate the direction of the displacement, while gray shadows depict the moving part of the system. Dashed gray lines indicate nodes.
Another interesting consequence of the packing differences is observed for the Raman-active modes at 93 cm–1 (PS) and 86 cm–1 (HB). They are dominated by torsional motions of the aromatic sections (Figures 3f,g), but the movement of the alkyl chains in the two polymorphs (modes) is fundamentally different. For the vibration at 93 cm–1 in the PS phase, atoms of the alkyl chains stay immobile (Figure 3f). Conversely, the packing of the HB phase favors librations of the alkyl chains for the mode at 86 cm–1 (Figure 3g). This mode combines a wagging of the aromatic core with torsions of the alkyl side chains. Again, the different movements can be associated with the different nearest-neighbor motifs with respect to the different parts of the molecules in the PS (aromatic–aliphatic) and HB (aromatic–aromatic, aliphatic–aliphatic) phases. A further aspect relating the structure to vibrational properties is associated with the change in volume between the two structures. The increase in volume of the unit cell in the HB phase (VPS = 1324.76 Å3, VHB = 1423.15 Å3) releases constraints on the molecular vibrations due to a less dense packing, which is consistent with the generally observed shift of the lattice modes of this polymorph toward lower wavenumbers (see the phonon density of states, Figure 1s, in the Supporting Information).
Beyond the above considerations, the relationships between the packing motif and intermolecular vibrations have direct implications on all properties that depend on lattice vibrations, such as charge and heat transport. For example, dynamic disorder originating from thermal vibrations limits charge transport properties in molecular semiconductors.30 Tightening the intermolecular interactions, that is, the vdW forces, is thus currently explored as a strategy to improve transport across these systems.31 In this context, the present work shows that DFT-MBD-vdW simulations are able to provide highly accurate predictions of the vibrational properties of molecular crystals. To show the portability of the DFT-MBD-vdW approach to describe intermolecular vibrations, we also tested systems other than C8O-BTBT-OC8. Also in those cases we found a similarly good agreement between calculated and measured Raman spectra. This is shown for two polymorphs of the molecule dibenzo-tetrathiafulvalene (DB-TTF) in the Supporting Information. The overall results presented here thus indicate that DFT-MBD-vdW simulations could reliably assist in the design of novel materials.
In summary, the two previously reported polymorphs24 of the molecule C8O-BTBT-OC8 have been obtained by control of the evaporation rate of hexane solutions. The crystal structure of the HB phase has been determined from single-crystal X-ray diffraction data. The two polymorphs show very different lattice phonon Raman spectra in the intermolecular region below 150 cm–1. Experimental and DFT calculated Raman spectra show excellent agreement, typically within an accuracy of ≪5 cm–1 (0.6 meV). As a consequence, provided that the crystal structures of different polymorphs are known, DFT-MBD-vdW calculations can be used to calculate lattice phonon Raman patterns at a level of accuracy that allows identification of the phases present in samples characterized by Raman scattering measurements. This offers the possibility to unambiguously identify and locate different polymorph domains within mixed-phase systems. The advantage of the simulations is that they provide direct access to the molecular motions associated with the relevant eigenmodes. This in turn provides insight into how intermolecular vibrations are affected by changes in the packing motif. Moreover, from a knowledge-driven materials design point of view, this work opens new routes toward reliable prediction of vibrational-dependent properties of materials, such as charge transport and thermal transport in organic semiconductors.
Experimental and Computational Methods
Different batches of crystals of C8O-BTBT-OC8 were grown by evaporation from hexane solutions in which the polycrystalline C8O-BTBT-OC8 was dissolved. The rate of evaporation of the solution was controlled by partially covering the vial during evaporation (slower crystallization) or leaving it uncovered (faster crystallization). For the crystal structure solutions of the HB phase, data were collected at the XRD1 beamline of the Elettra Synchrotron,32 Trieste (Italy).
Simulations were performed using the Python program vasp_Raman.py,3300 which uses the vasp package33−36 as backend. The Perdew–Burke–Ernzerhof (PBE) functional for the exchange and correlation37 and projector-augmented wave potentials for all of the elements were used.38,39
Acknowledgments
This work was funded by the Austrian Climate and Energy Fund (KLIEN) and the Austrian Research Promotion Agency (FFG) through the project “ThermOLED” [FFG No. 848905], and by the Austrian Science Fund [FWF No. 25887]. This work has been financially supported by a concerted research action of the French Community of Belgium (ARC Project No. 20061), by the Walloon Region (WCS Project No. 1117306), and by the Belgian National Fund for Scientific Research (FNRS, Project No. 2.4565.11). The computational results presented have been achieved using the Vienna Scientific Cluster (VSC). The authors thank the Elettra synchrotron for the allocation of beamtime on the XRD1 beamline.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b01634.
Detailed information about the experimental procedures and simulations, phonon density of states of the PS and HB phases, and calculated Raman spectra of two polymorphs of the molecule dibenzo-tetrathiafulvalene,4,40 compared to experimental data (PDF)
Crystallographic data of the HB phase crystal structure (CIF)
Crystallographic data of the HB phase crystal structure (PDF)
Animations of all Raman active modes reported in Figure 2c,e (ZIP)
The authors declare no competing financial interest.
Notes
CCDC-1557531 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44 1223 336033.
Supplementary Material
References
- Bernstein J.Polymorphism in Molecular Crystals; Oxford University Press, 2007. [Google Scholar]
- Roy S.; Chamberlin B.; Matzger A. J. Polymorph Discrimination Using Low Wavenumber Raman Spectroscopy. Org. Process Res. Dev. 2013, 17, 976–980. 10.1021/op400102e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C.-F.; Okajima H.; Hamaguchi H.-o.; Shigeto S. Imaging Molecular Crystal Polymorphs and their Polycrystalline Microstructures in Situ by Ultralow-frequency Raman Spectroscopy. Chem. Commun. 2014, 50, 12973–12976. 10.1039/C4CC05955G. [DOI] [PubMed] [Google Scholar]
- Brillante A.; Bilotti I.; Della Valle R. G.; Venuti E.; Girlando A. Probing Polymorphs of Organic Semiconductors by Lattice Phonon Raman Microscopy. CrystEngComm 2008, 10, 937–946. 10.1039/b804317e. [DOI] [Google Scholar]
- Jones A. O. F.; Chattopadhyay B.; Geerts Y. H.; Resel R. Substrate-Induced and Thin-Film Phases: Polymorphism of Organic Materials on Surfaces. Adv. Funct. Mater. 2016, 26, 2233–2255. 10.1002/adfm.201503169. [DOI] [Google Scholar]
- Mas-Torrent M.; Rovira C. Role of Molecular Order and Solid-State Structure in Organic Field-Effect Transistors. Chem. Rev. 2011, 111, 4833–4856. 10.1021/cr100142w. [DOI] [PubMed] [Google Scholar]
- Chung H.; Diao Y. Polymorphism as an Emerging Design Strategy for High Performance Organic Electronics. J. Mater. Chem. C 2016, 4, 3915–3933. 10.1039/C5TC04390E. [DOI] [Google Scholar]
- Roma G. Linear Response Calculation of First order Raman Spectra of Point Defects in Silicon Carbide. Phys. Status Solidi A 2016, 213, 2995–2999. 10.1002/pssa.201600036. [DOI] [Google Scholar]
- Costa S. N.; Freire V. N.; Caetano E. W. S.; Maia F. F.; Barboza C. A.; Fulco U. L.; Albuquerque E. L. DFT Calculations with van der Waals Interactions of Hydrated Calcium Carbonate Crystals CaCO3·(H2O, 6H2O): Structural, Electronic, Optical, and Vibrational Properties. J. Phys. Chem. A 2016, 120, 5752–5765. 10.1021/acs.jpca.6b05436. [DOI] [PubMed] [Google Scholar]
- Demichelis R.; Civalleri B.; Ferrabone M.; Dovesi R. On the Performance of Eleven DFT Functionals in the Description of the Vibrational Properties of Aluminosilicates. Int. J. Quantum Chem. 2010, 110, 406–415. 10.1002/qua.22301. [DOI] [Google Scholar]
- Többens D. M.; Kahlenberg V. Improved DFT Calculation of Raman spectra of Silicates. Vib. Spectrosc. 2011, 56, 265–272. 10.1016/j.vibspec.2011.04.002. [DOI] [Google Scholar]
- Brillante A.; Bilotti I.; Biscarini F.; Della Valle R. G.; Venuti E. Polymorphs of α-Sexithiophene Probed by Lattice Phonon Raman Microscopy. Chem. Phys. 2006, 328, 125–131. 10.1016/j.chemphys.2006.06.018. [DOI] [Google Scholar]
- Dion M.; Rydberg H.; Schröder E.; Langreth D. C.; Lundqvist B. I. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. 10.1103/PhysRevLett.92.246401. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; Scheffler M. Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Steinmann S. N.; Corminboeuf C. A Generalized-Gradient Approximation Exchange Hole Model for Dispersion Coefficients. J. Chem. Phys. 2011, 134, 044117. 10.1063/1.3545985. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; DiStasio R. A.; Car R.; Scheffler M. Accurate and Efficient Method for Many-Body van der Waals Interactions. Phys. Rev. Lett. 2012, 108, 236402. 10.1103/PhysRevLett.108.236402. [DOI] [PubMed] [Google Scholar]
- Bučko T.; Lebègue S.; Hafner J.; Ángyán J. G. Improved Density Dependent Correction for the Description of London Dispersion Forces. J. Chem. Theory Comput. 2013, 9, 4293–4299. 10.1021/ct400694h. [DOI] [PubMed] [Google Scholar]; PMID: 26589148.
- Bučko T.; Lebégue S.; Ángyán J. G.; Hafner J. Extending the Applicability of the Tkatchenko-Scheffler Dispersion Correction via Iterative Hirshfeld Partitioning. J. Chem. Phys. 2014, 141, 034114. 10.1063/1.4890003. [DOI] [PubMed] [Google Scholar]
- Ambrosetti A.; Reilly A. M.; DiStasio R. A. Jr.; Tkatchenko A. Long-range Correlation Energy Calculated from Coupled Atomic Response Functions. J. Chem. Phys. 2014, 140, 18A508. 10.1063/1.4865104. [DOI] [PubMed] [Google Scholar]
- Bučko T.; Lebégue S.; Gould T.; Ángyán J. G. Many-body Dispersion Corrections for Periodic Systems: an Efficient Reciprocal Space Implementation. J. Phys.: Condens. Matter 2016, 28, 045201. 10.1088/0953-8984/28/4/045201. [DOI] [PubMed] [Google Scholar]
- Jones A. O. F.; Geerts Y. H.; Karpinska J.; Kennedy A. R.; Resel R.; Röthel C.; Ruzié C.; Werzer O.; Sferrazza M. Substrate-Induced Phase of a [1]Benzothieno[3,2-b]benzothiophene Derivative and Phase Evolution by Aging and Solvent Vapor Annealing. ACS Appl. Mater. Interfaces 2015, 7, 1868–1873. 10.1021/am5075908. [DOI] [PubMed] [Google Scholar]
- Ruzié C.; Karpinska J.; Laurent A.; Sanguinet L.; Hunter S.; Anthopoulos T. D.; Lemaur V.; Cornil J.; Kennedy A. R.; Fenwick O.; et al. Design, Aynthesis, Chemical Stability, Packing, Cyclic Voltammetry, Ionisation Potential, and Charge Transport of [1]Benzothieno[3,2-b][1]benzothiophene Derivatives. J. Mater. Chem. C 2016, 4, 4863–4879. 10.1039/C6TC01409G. [DOI] [Google Scholar]
- Brillante A.; Bilotti I.; Albonetti C.; Moulin J.-F.; Stoliar P.; Biscarini F.; de Leeuw D. Confocal Raman Spectroscopy of α-Sexithiophene: From Bulk Crystals to Field-Effect Transistors. Adv. Funct. Mater. 2007, 17, 3119–3127. 10.1002/adfm.200700004. [DOI] [Google Scholar]
- Demitri N.CCDC-1557531. Cambridge Structural Database, 2017
- Groom C. R.; Bruno I. J.; Lightfoot M. P.; Ward S. C. The Cambridge Structural Database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72, 171–179. 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izawa T.; Miyazaki E.; Takimiya K. Molecular Ordering of High-Performance Soluble Molecular Semiconductors and Re-evaluation of Their Field-Effect Transistor Characteristics. Adv. Mater. 2008, 20, 3388–3392. 10.1002/adma.200800799. [DOI] [Google Scholar]
- Illig S.; Eggeman A. S.; Troisi A.; Jiang L.; Warwick C.; Nikolka M.; Schweicher G.; Yeates S. G.; Henri Geerts Y.; Anthony J. E.; et al. Reducing Dynamic Disorder in Small-Molecule Organic Semiconductors by Suppressing Large-Amplitude Thermal Motions. Nat. Commun. 2016, 7, 10736. 10.1038/ncomms10736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fratini S.; Mayou D.; Ciuchi S. The Transient Localization Scenario for Charge Transport in Crystalline Organic Materials. Adv. Funct. Mater. 2016, 26, 2292–2315. 10.1002/adfm.201502386. [DOI] [Google Scholar]
- Lausi A.; Polentarutti M.; Onesti S.; Plaisier J. R.; Busetto E.; Bais G.; Barba L.; Cassetta A.; Campi G.; Lamba D.; et al. Status of the Crystallography Beamlines at Elettra. Eur. Phys. J. Plus 2015, 130, 43. 10.1140/epjp/i2015-15043-3. [DOI] [Google Scholar]
- Fonari A.; Stauer S.. vasp raman.py; https://github.com/raman-sc/VASP/, 2013.
- Kresse G.; Hafner J. Ab initio Molecular Dynamics for Liquid Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Brillante A.; Bilotti I.; Della Valle R. G.; Venuti E.; Mas-Torrent M.; Rovira C.; Yamashita Y. Phase Recognition by Lattice Phonon Raman Spectra: The Triclinic Structure of the Organic Semiconductor Dibenzo-Tetrathiafulvalene. Chem. Phys. Lett. 2012, 523, 74–77. 10.1016/j.cplett.2011.12.026. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.