Abstract
CpXRh(III)-catalyzed C-H functionalization reactions are a proven method for the efficient assembly of small molecules. However, rationalization of the effects of cyclopentadienyl (CpX) ligand structure on reaction rate and selectivity has been viewed as a black box, and a truly systematic study is lacking. Consequently, predicting the outcomes of these reactions is challenging because subtle variations in ligand structure can cause notable changes in reaction behavior. A predictive tool is, nonetheless, of considerable value to the community as it would greatly accelerate reaction development. Designing a data set in which the steric and electronic properties of the CpXRh(III) catalysts were systematically varied allowed us to apply multivariate linear regression algorithms to establish correlations between these catalyst-based descriptors and the regio-, diastereoselectivity, and rate of model reactions. This, in turn, led to the development of quantitative predictive models that describe catalyst performance. Our newly-described cone angles and Sterimol parameters for CpX ligands served as highly correlative steric descriptors in the regression models. Through rational design of training and validation sets, key diastereoselectivity outliers were identified. Computations reveal the origins of the outstanding stereoinduction displayed by these outliers. The results are consistent with partial η5−η3 ligand slippage that occurs in the transition state of the selectivity-determining step. In addition to the instructive value of our study, we believe that the insights gained are transposable to other Group 9 transition metals and pave the way toward rational design of C-H functionalization catalysts.
Graphical abstract
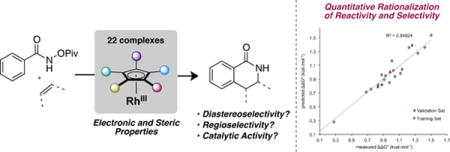
INTRODUCTION
Physical and chemical properties of metal complexes can be modulated by changing the ligands on the metal center or by modifying the substituents on the ligand framework.1 Consequently, much effort has been directed toward the design, synthesis, and use of new ligands that contain substituents with varying steric and electronic properties.2
Rh(III)-catalyzed C-H activation is an attractive mode of catalysis for the synthesis of small molecules.3 This approach has the advantage of low catalyst loading, with reactions often performed under mild conditions allowing broad functional group tolerance. Following the seminal work of Miura/Satoh4 and Fagnou,5 our group6 and others7 have developed a plethora of reactions to access a variety of heterocycles.8 Among these transformations, [Cp*RhCl2]2 and its cationic forms are nearly universally employed as the rhodium source and are considered privileged catalysts for such reactions.
The prominence of cyclopentadienyl (Cp) ligands in contemporary transition metal chemistry can be traced to several key features including the large M-Cp dissociation bond energy. The pentamethylcyclopentadienyl ligand (Cp*) is certainly the best known Cp derivative. Compared to the parent Cp ligand, Cp* is sterically more demanding and the methyl groups on Cp* increase the electron density on the metal center. The increased donation from the Cp* results in a greater π-backbonding to other ligands. Likewise, Cp* complexes are more easily oxidized than their Cp analogues. In comparison with CpRh(III) complexes, Cp*Rh(III) analogues are soluble in most organic solvents. For these reasons, Cp*Rh(III) is considered to be the catalyst of choice for C-H activation reactions.
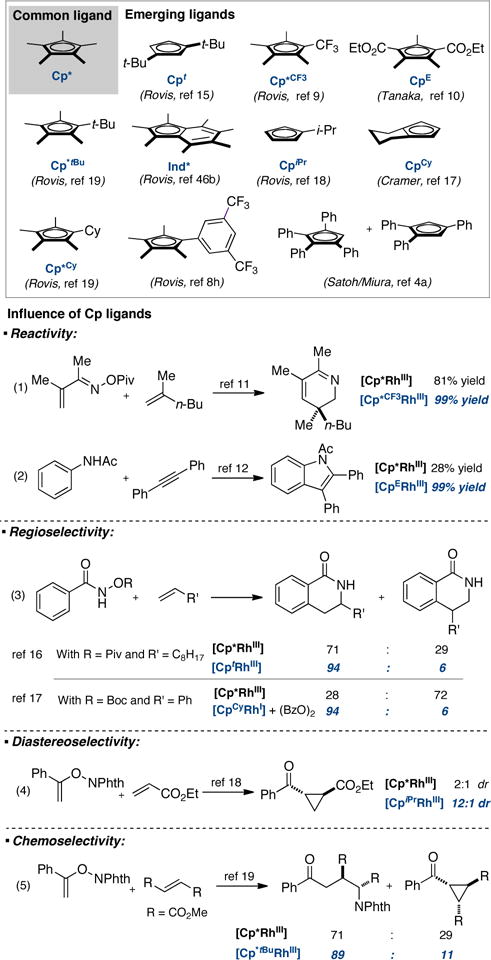
Recently, we and others changed this paradigm by identifying several cyclopentadienyl ligands as alternatives for Cp* (Figure 1). Steric and electronic manipulation of the Cp ligand, sometimes quite subtle, leads to significant changes in reactivity as well as regio-, diastereo-, and chemoselectivity:
The use of electron-deficient Cp ligands such as Cp*CF3 9 and CpE 10 in place of Cp*Rh(III) complexes increases reactivity for the synthesis of dihydropyridines11 and indoles (eqs. 1 and 2).12
Initial reports by Fagnou13 and Glorius14 showed the isotropic [Cp*Rh(III)] catalyst results in a mixture of regioisomers (generally a 2:1 ratio) for the insertion of aliphatic alkenes into benzohydroxamate. However, we have recently shown that a more sterically demanding di-tert-butyl-cyclopentadienyl ligand (Cpt)15 on rhodium delivers the dihydroisoquinolinones with synthetically useful regioselectivities (typically >10:1 regioisomer ratio, eq. 3).16 Simultaneously, Cramer and co-workers reported that a tetrahydroindenyl ligand (CpCy) also affords exquisite regioselectivities for a similar transformation.17
We have recently described a cyclopropanation reaction involving the coupling between N-enoxyphthalimides and electron-deficient alkenes (eq. 4).18 Crucial to the success of this reaction was the use of a monoisopropylcyclopentadienyl ligand (CpiPr) for Rh(III) which allows the formation of trans-disubstituted cyclopropanes in excellent diastereoselectivities. We later identified a sterically bulky tert-butyl-tetramethylcyclopentadienyl ligand (Cp*tBu) capable of driving the reaction toward an alternative carboamination path delivering the corresponding adducts instead of the competitive cyclopropanation products with excellent chemoselectivities (eq. 5).19
Figure 1. Cyclopentadienyl-based ligands in Rh(III)-catalyzed C-H activation reactions.
Although the development of new cyclopentadienyl ligands (CpX) for Rh(III)-catalysis undeniably has the potential to impact the field, several questions remain. One can appreciate the diversity of ligand substitution patterns ranging from mono-, di- to pentasubstituted cyclopentadienyls with distinct electronic and steric properties. Subtle variations in CpX ligand derivatives often have a sizable impact on reactivity and selectivity for which the steric and electronic origins remain unclear. Often, the attempts to establish a relationship between the structure of a catalyst and its reactivity lead to a speculative analysis.
Recently, Sigman and co-workers elegantly displayed multivariate linear regression analysis to quantitatively describe the interplay between the structure of a catalyst and selectivity.20 Importantly, this approach possesses predictive power to assist further catalyst design. Inspired by Sigman’s work, we undertook a comprehensive study to shed light on cyclopentadienyl ligand effects in Rh(III) catalysis. We began by synthesizing a large collection of systematically-perturbed CpXRh(III) complexes. Molecular descriptors that quantify these structural changes were then identified and measured. We investigated the performance of these catalysts in model reactions to probe the interplay between the structure and reactivity of CpXRh(III) complexes in C-H activation reactions. Subsequently, multivariate regression was utilized to establish correlations between structural properties and reactivity/selectivity in order to determine the requirements for optimal catalyst performance. In addition to the comprehensive and instructive value of this study, we expect that this work could serve the community as a starting point for the design of new cyclopentadienyl-type ligands in order to uncover the full potential of Rh(III) chemistry. Moreover, this approach is transposable to other metals with the emergence of new promising methodologies employing Cp*Co(III)21 and Cp*Ir(III)22 catalysts in C-H activation.
RESULTS AND DISCUSSION
Ligand library
At the outset of our study, we synthesized a library of 22 dimeric Rh(III) catalysts bearing various cyclopentadienyl-type ligands (Rh1–22, Figure 2). Among this set of ligands, several had been described previously by us (Rh2–3,19 Rh7,8h Rh10–11,9,19 and Rh20–2215,18,46b) and others (Rh1310 and Rh19,17 Figure 1). Nevertheless, we became restricted by the narrow number of CpXRh(III) derivatives available in the literature. To overcome this limitation, we undertook the synthesis of a new collection of CpXRh(III) complexes (Rh4–6, Rh8–9, and Rh14–18).
Figure 2. Structures of dimeric [CpXRhCl2]2 complexes used in this study.
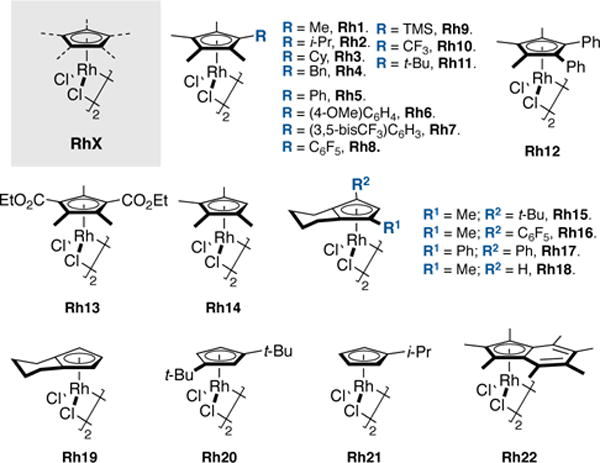
We prepared cyclopentadienyl derivatives with different substitution patterns ranging from mono-, di-, tri, tetra- to pentasubstituted with the goal to cover the widest spectrum of steric and electronic properties accessible for these Rh(III) complexes. X-ray crystal structures were obtained for most of these [CpXRhCl2]2 complexes (see Supporting Information).23 Similarly to the Cp*Rh(III) complex (Rh1), the plane of the various CpX rings is perpendicular to the Rh-Cp(centroid) axis, with negligible tilting. With a set of Rh(III) catalysts in hand, we initiated a systematic experimental and computational study of their steric and electronic properties. Such analysis will serve as a foundation for understanding ligand effects in Rh(III)-catalyzed reactions.
Evaluating electronic effects
As a starting point, we sought to define a set of quantitative electronic descriptors for our library of CpXRh(III) complexes, bearing in mind that a rigorous delineation between the steric and electronic properties of a ligand is challenging, since both are inherently related (vide infra). For our purposes, six approaches were chosen to quantify ligand electronic properties. The data is summarized in Table 1.
Table 1.
Electronic parameters for CpXRh(III) complexes

| ||||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| CpXRh Complex | δ31P(ppm)a | JRh-P(Hz)a | ν(CO)(cm−1)b
|
E1/2(V)c
|
Natural charge at Rh (qRh)d | σ(103Rh) (ppm)e | ||
| anti-sym νA | sym νS |
|
|
|||||
| Rh1
|
114.2 | 215.9 | 2016 | 1948 | −1.34 | −2.22 | 0.556 | −681.3 |
| Rh2
|
112.9 | 216.2 | 2016 | 1948 | −1.33 | −2.25 | 0.558 | −685.5 |
| Rh3
|
113.0 | 216.5 | 2016 | 1948 | −1.34 | −2.22 | 0.559 | −683.3 |
| Rh4
|
112.7 | 214.1 | 2017 | 1950 | −1.30 | −2.16 | 0.557 | −676.7 |
| Rh5
|
111.1 | 214.3 | 2019 | 1952 | −1.24 | −2.07 | 0.559 | −696.6 |
| Rh6
|
111.7 | 214.9 | 2017 | 1949 | −1.25 | −2.12 | 0.559 | −687.5 |
| Rh7
|
108.6 | 211.3 | 2026 | 1961 | −1.18 | −1.88 | 0.556 | −682.9 |
| Rh8
|
105.9 | 209.4 | 2016 | 1952 | −1.09 | −1.92 | 0.561 | −708.0 |
| Rh9
|
110.3 | 211.8 | 2019 | 1953 | −1.27 | −2.13 | 0.562 | −699.1 |
| Rh10
|
104.5 | 205.8 | 2040 | 1977 | −1.04 | −1.79 | 0.552 | −697.4 |
| Rh11
|
110.8 | 214.6 | 2017 | 1950 | −1.33 | −2.23 | 0.560 | −677.9 |
| Rh12
|
108.8 | 211.6 | 2022 | 1956 | −1.15 | −1.94 | 0.560 | −706.7 |
| Rh13
|
99.1 | 197.1 | 2044 | 1984 | −0.84 | −1.93 | 0.566 | −756.8 |
| Rh14
|
114.5 | 212.3 | 2025 | 1960 | −1.25 | −2.14 | 0.554 | −687.2 |
| Rh15
|
112.9 | 214.7 | 2018 | 1950 | −1.25 | −2.09 | 0.562 | −681.4 |
| Rh16
|
110.4 | 209.4 | 2033 | 1967 | −1.04 | −1.77 | 0.562 | −722.1 |
| Rh17
|
112.5 | 209.4 | 2016 | 1962 | −1.06 | −1.81 | 0.564 | −726.4 |
| Rh18
|
116.4 | 210.0 | 2024 | 1960 | −1.18 | −2.01 | 0.558 | −702.1 |
| Rh19
|
115.6 | 207.0 | 2032 | 1967 | −1.10 | −1.90 | 0.555 | −712.8 |
| Rh20
|
108.4 | 206.3 | 2025 | 1957 | −1.08 | −2.04 | 0.563 | −719.9 |
| Rh21
|
110.5 | 201.6 | 2036 | 1968 | −1.01 | −1.89 | 0.557 | −742.7 |
| Rh22
|
107.4 | 226.7 | 2021 | 1963 | −1.07 | −1.74 | 0.574 | −817.4 |
31P NMR of [CpXRhP(OEt)3Cl2] complexes (Rh”) in CD2Cl2.
IR spectroscopy on [CpXRh(CO)2] complexes in C6D6 (Rh’).
Measured by square wave voltammetry on [CpXRhCl2]2 complexes (Rh) relative to Cp2Fe+/Cp2Fe. Reported E1/2 values represent the average of two experiments.
Calculated from atomic Natural Population Analysis (NPA).
Gauge-Including Atomic Orbital (GIAO) calculated isotropic 103Rh nuclear shielding tensors.
IR stretching frequencies
Classically, the Tolman electronic parameter (TEP) is used to probe the electron-donating or -withdrawing ability of phosphine ligands coordinated to a metal center.24 This concept was later extended to characterize CpX ligands on various transition metals.25 Thus, we sought to measure TEP values for [CpXRh(CO)2] complexes (Rh’) as an indicator of electronic density at the metal center, with the assumption that the trends observed for low-valent Rh(I) would be transposable to high-valent Rh(III) complexes.26 To do so, Rh(I)-carbonyl complexes (Rh’) were synthesized from their corresponding [CpXRhCl2]2 congeners (Rh). The frequencies of symmetric (νS) and antisymmetric (νA) stretching bands of the CO ligands on Rh(I) were then acquired by IR spectroscopy (Table 1). For each Rh’ complex, one can observe two strong bands in the 2016–2044 and 1948–1984 cm−1 regions that are assigned as the anti-symmetric and symmetric stretching modes, respectively. We anticipated that more electron-donating CpX ligands increase the electron density at the metal center and consequently increase the intensity of back-donation into the CO π* orbital, which in turn weakens and lengthens the CO bond. This lowers the CO stretching frequency. Conversely, more electron-withdrawing CpX ligands give Rh’ complexes with higher CO stretching frequencies.
Anti-symmetric CO stretching frequencies (νA) are depicted in Figure 3, A. A closer analysis shows that penta-alkylated complexes Rh’1–4 and Rh’11 possess similar electronic properties (νA in the range 2016–2017 cm−1) and are among the most electron-rich complexes in the collection of Rh(III) catalysts. In accordance with the electronic nature of substituents on the aryl ring of ligands of the type C5Me4Ar in complexes Rh’5–7, the electron density at the metal center increases in the order of Rh’6 < Rh’5 < Rh’7 (2017 < 2019 < 2026 cm−1). However, for the perfluorinated complex Rh’8, this trend is no longer valid. Indeed, according to the scale, its electron density is closer to that of Rh’6 (2016 vs. 2017 cm−1), which is counterintuitive considering the high electronegativity of fluorine atoms. The presence of a strongly electron-withdrawing substituent such as CF3 on the Cp ring decreases the electron density substantially (Rh’10, 2040 cm−1). When a TMS group is attached to the Cp ring (Rh’9, 2019 cm−1) the Rh(I) complex is surprisingly more electron-deficient than the parent Rh’1 (2016 cm−1). Notably, the heptamethylindenyl Rh(I) complex (Rh’22, 2021 cm−1) is markedly more electron-deficient than the parent Cp*Rh(I) complex (Rh’1, 2016 cm−1).
Figure 3. A selection of ground-state molecular descriptors used for electronic parameterization.

(A) Anti-symmetric CO stretching frequencies (νA). (B) Experimental 31P chemical shifts (δP). (C) Redox half-potentials for the Rh(III/II) couple . (D) Computed 103Rh isotropic shielding tensors (σRh).
31P NMR data
The phosphorus atom of a coordinated phosphine ligand is directly influenced by the electronic environment in the vicinity of the metal center.27 As an alternative approach for electronic parameterization of CpX ligands, we converted the dimeric [CpXRhCl2]2 complexes (Rh) into their corresponding monomeric triethylphosphite adducts ([CpXRhP(OEt)3Cl2], Rh”). We then used 31P NMR to measure the chemical shift of the phosphorus nucleus (δP) and the coupling constant between phosphorus and rhodium (JRh-P). The collected data for 31P chemical shifts (δP) was compiled to construct an empirical scale of electronic properties of CpX ligands (Figure 3, B). As can be seen, in the case of penta-alkylated complexes Rh”1–4 and Rh”11, the 31P chemical shift decreases as the electron-donating ability of the CpX ligand increases. This observation is consistent with stronger shielding of the phosphorus nucleus in more electron-rich Rh(III) complexes. On the other hand, complexes Rh”5–7 that bear a phenyl substituent no longer follow this trend. In the case of mono- (Rh”21) and disubstituted (Rh”20) complexes, the small differences in δP values do not account for the expected decrease in electron density. Complexes such as Rh”10 and Rh”13 that are among the most electron-deficient according to the νA scale, are found to be the most deshielded on the δP scale.
Redox potentials
Next, we measured the redox potentials of Rh complexes reasoning that they would be influenced by the electronic properties of the CpX ligands. This parameter also benefits by avoiding a derivatization of the parent complexes (introduction of ancillary ligand). To perform the study, half-potentials of reduction (E1/2)28 of Rh1–22 were measured by square-wave voltammetry. The results are summarized in Table 1. Two irreversible one-electron reductions are observed, corresponding to Rh(III/II) and Rh(II/I) redox couples. The results for the Rh(III/II) couple are ordered and presented in Figure 3, C. The redox scale displays a more pronounced intuitive character when compared to the νS and δP scales. Accordingly, penta-alkylated complexes Rh1–4 and Rh11 display the lowest reduction potentials (−1.34 – −1.30 V), which places them among the most electron-rich ones. The presence of electron-withdrawing substituents on the CpX ring affects the redox potentials in a predictable manner, increasing in the order of Rh1 < Rh6 < Rh5 < Rh7 < Rh8 < Rh10 < Rh13 (−1.34 – −0.84 V). Decreasing the degree of alkylation of the CpX ring leads to more easily reducible complexes (Rh1 < Rh14 < Rh18 < Rh19 < Rh20 < Rh21, −1.34 – −1.01 V), consistent with a decrease in electron density. Finally, the heptamethylindenyl complex Rh22 (−1.07 V) is significantly more electron-deficient than the parent Cp* complex (Rh1, −1.34 V).
Computed electronic parameters
Density functional theory (DFT) calculations were carried out to investigate the electronic characteristics of the CpXRh(III) complexes. Geometries of all 22 rhodium dimers (Rh) were optimized at the wB97XD/def2-SVPP level of theory which was found to be the most accurate of several functionals surveyed.29 The electron density at the metal center in each complex was evaluated in terms of the Natural Population Analysis (NPA) atomic charges at Rh (qRh) and the isotropic 103Rh nuclear shielding tensor (σRh). These properties are computed directly for each Rh center and are therefore complimentary to our experimental parameters, which capture changes in electron density at the metal center indirectly.30 A scale of σRh for complexes Rh1–22 is shown in Figure 3, D. In this case, the most deshielded (i.e. more negative σRh) Rh centers are found in Rh8, Rh13, and Rh21, which are also the most electron-deficient complexes according to the νA and scales. The 103Rh shielding tensors of mono- (Rh21), di-(Rh19 and Rh20), tri- (Rh18), tetra- (Rh14) and penta-alkylated (Rh1–4 and Rh11) complexes are less negative, showing increased shielding with more substituted CpX rings. Increasing the number of phenyl groups on the ligand leads to greater deshielding of the 103Rh nucleus (Rh5–7 vs. Rh17 and Rh12), suggesting a through-space π-effects in ligands of the type C5Me4Ar. According to the computed σRh scale, the heptamethylindenyl complex Rh22 contains the most electron-deficient Rh center.
Evaluating steric effects
Steric parameterization employing experimentally- and computationally-determined molecular descriptors has been studied for over 60 years.31,32,33,34,35 The evaluation of steric properties of CpX ligands in rhodium complexes was accomplished by using two approaches (Table 2).
Table 2.
Steric parameters for CpXRh(III) complexes

| |||||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| CpXRh Complex | Cone Angle ΘBa
|
Cone Angle ΘSb (°) | Sterimol Parametersc
|
||||
| ΘB (°) | ΘB,min (°) | ΘB,max (°) | L (Å) | B1 (Å) | B5 (Å) | ||
| Rh1
|
178.7 | 176.2 | 179.5 | 175.0 | 3.74 | 3.98 | 4.28 |
| Rh2
|
189.5 | 177.1 | 229.8 | 186.2 | 6.31 | 3.98 | 5.58 |
| Rh3
|
190.2 | 177.1 | 230.8 | 186.9 | 6.50 | 3.96 | 7.63 |
| Rh4
|
179.9 | 178.2 | 181.5 | 176.2 | 7.73 | 3.98 | 6.70 |
| Rh5
|
189.2 | 177.9 | 226.8 | 185.9 | 5.96 | 3.98 | 7.60 |
| Rh6
|
189.3 | 179.0 | 226.3 | 186.0 | 5.88 | 3.98 | 9.71 |
| Rh7
|
193.2 | 177.5 | 244.8 | 190.0 | 9.38 | 3.97 | 8.32 |
| Rh8
|
191.8 | 178.3 | 235.4 | 188.3 | 7.06 | 3.95 | 8.14 |
| Rh9
|
179.4 | 174.9 | 184.4 | 174.6 | 3.90 | 2.71 | 4.30 |
| Rh10
|
183.1 | 177.3 | 191.2 | 179.5 | 4.65 | 3.98 | 4.79 |
| Rh11
|
190.8 | 176.4 | 231.4 | 187.5 | 6.32 | 3.96 | 5.69 |
| Rh12
|
194.1 | 178.6 | 221.0 | 190.9 | 5.99 | 3.98 | 7.59 |
| Rh13
|
194.5 | 178.5 | 245.9 | 190.5 | 8.00 | 4.02 | 7.33 |
| Rh14
|
176.4 | 174.0 | 178.9 | 171.4 | 3.73 | 3.27 | 4.27 |
| Rh15
|
195.6 | 173.7 | 227.8 | 191.3 | 6.18 | 3.38 | 5.61 |
| Rh16
|
193.3 | 173.8 | 227.1 | 188.3 | 6.17 | 3.48 | 8.18 |
| Rh17
|
197.3 | 173.9 | 218.0 | 193.0 | 5.53 | 4.12 | 7.60 |
| Rh18
|
185.2 | 174.3 | 208.6 | 179.8 | 4.95 | 2.86 | 5.55 |
| Rh19
|
184.6 | 173.7 | 210.6 | 178.2 | 4.94 | 2.86 | 5.56 |
| Rh20
|
194.2 | 172.5 | 227.6 | 187.8 | 6.31 | 2.88 | 5.63 |
| Rh21
|
178.3 | 170.9 | 194.7 | 171.0 | 5.45 | 2.86 | 5.63 |
| Rh22
|
183.4 | 178.6 | 187.1 | 180.6 | 4.05 | 4.03 | 6.56 |
All parameters computed from wB97XD/def2-SVPP optimized structures:
Using Bondi atomic van der Waals radii, cone angles as defined in Figure 8, A.
Using CPK atomic radii as used in Verloop’s original Sterimol program, lengths as defined in Figure 4, B.
See Supporting Information for details.
Tolman cone angles (TCA)
Steric bulk has been quantified extensively for phosphine ligands using the approach initially developed by Tolman.36 Inspired by the TCA definition for dissymetrically-substituted phosphines, we adapted the formalism to substituted CpX ligands (Figure 4, A).37 Accordingly, angles αi between the vector defined by the Rh-Cp(centroid) axis and the vectors tangential to the outer most atomic sphere of each substituent Ri are measured in DFT-optimized structures (see Supporting Information). Assuming that free rotation of the CpX ring around the Rh-Cp(centroid) axis takes place in solution, each substituent Ri occupies one of the five ring positions only 20% of the time. Thus, for a Cp ring with two possible substituent types RS (small) and RL (large) the average cone angle is given by eq. 6 where n is the number of RL substituents. Considering Corey-Pauling-Koltun (CPK) models,38 angles αS and αL have to be corrected to account for atomic van der Waals (VdW) radii using eq. 7 to give half-vertex angles θi for each substituent type. With VdW radii taken from Bondi’s compilation,39 the cone angles are indexed as “Bondi” ΘB. When atomic radii are taken from Verloop’s original parameters (vide infra), the cone angles are indexed as “Sterimol” (ΘS). While Bondi defined a single radius for each element, those used in Sterimol take into account formal hybridization and functional group. For example, nine different atom types are used to describe carbon.
Figure 4. Steric descriptors of CpX ligands.
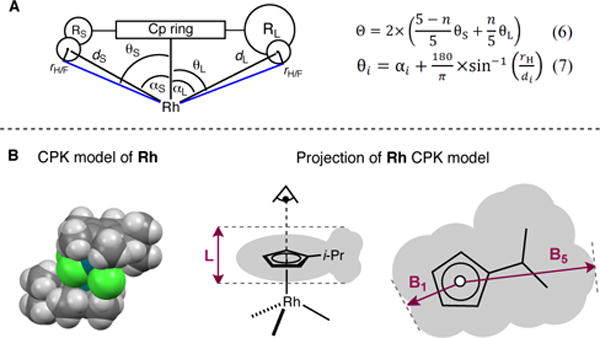
(A) Definition of the Tolman cone angle for a CpX ligand with two substituent types (RS and RL). αi = angle between the vector defined by the Rh-Cp(centroid) axis and the vector tangential to the outermost atomic sphere (Hmax) of each substituent Ri; di = distance between the Rh atom and the center of Hmax; θi = half-vertex angle to Hmax corrected for atomic VdW radius; rH = VdW radius of Hmax; Θ = averaged cone angle for the entire ligand. (B) Definition of Sterimol parameters. All angles and distances are measured on CPK models. B1 = minimum width of the CpX ligand perpendicular to the Rh-Cp(centroid) axis; B5 = maximum width; L = Rh-Cp(centroid) distance.
Elaborating on the above definitions, cone angles for all 22 Rh complexes were determined from DFT-optimized geometries (Table 2). The results for averaged Bondi cone angles (ΘB) are collated in Figure 5, A.
Figure 5. A selection of geometrical descriptors used for steric parameterization.

(A) Averaged Bondi cone angles (ΘB). (B) Difference of cone angles Θmax−Θmin. (C) Sterimol B5−B1 values.
According to the ΘB scale, catalysts Rh12, Rh13, Rh15, Rh17, and Rh20 give rise to the largest cones, ranging from 194.2° to 197.3°. In the case of complexes Rh12 and Rh20, this large value can be explained by the presence of two large tert-butyl or phenyl groups tethered to the Cp ring. For Rh15 and Rh17, one large tert-butyl or phenyl group in conjunction with a fused cyclohexyl ring40 increase the overall bulkiness of the catalyst. The very large cone angle calculated for complex Rh13 (194.5°) is at first sight counterintuitive. It can be rationalized by considering the lowest-energy conformation of Rh13, where the carbonyl groups are slightly twisted and point the ethyl chains down towards the metal. The presence of outliers such as Rh13 reveals the limitations of the convention used to calculate Tolman cone angles. On the other hand, the size of the cone decreases when the degree of substitution of the Cp ring diminishes, in the order of Rh1 > Rh21 > Rh14 (178.7−176.4°) for cyclopentadienyl ligands, and Rh18 > Rh19 (185.2° vs. 184.6°) for cyclohexyl-fused ring systems. In contrast, the heptamethylindenyl complex Rh22 has a relatively small ΘB cone angle (183.4°). While averaged cone angles seem to adequately describe the total isotropic volume of CpX ligands, the subtleties of their shape are not accounted for by the ΘB value alone. We reasoned that a refined picture would be achieved by disassembling this value into subparameters. In an attempt to do so, the minimum (ΘB,min) and maximum (ΘB,max) Bondi cone angles, defined as the half-vertex angles to the smallest and largest substituents on the CpX ring, respectively, were extracted. The value Θmax−Θmin was then calculated to underline molecular anisotropy. A relative scale is presented in Figure 5, B. Accordingly, complexes Rh7, Rh9, and Rh13 have the largest cone angle anisotropy, while Rh1, Rh4 and Rh14 are more uniformly-shaped. Interestingly, complex Rh20, which gives the highest regioselectivity in the 1-decene insertion reaction (vide infra), displays a pronounced anisotropic character. On the other hand, complex Rh22 that leads to one of the highest diastereoselectivities for cyclopropene insertion (vide infra), shows very small cone angle anisotropy. Further elaborating on the idea of operating with steric subparameters, a different set of multi-dimensional steric descriptors was investigated.
Sterimol parameters
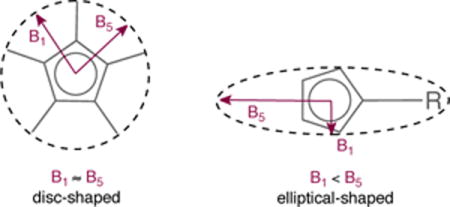
Sterimol parameters are molecular steric descriptors developed for use in quantitative structure-activity relationships (QSAR).41 They have recently found application in asymmetric catalysis, correlating more strongly than empirically-determined (isotropic) Charton or Taft parameters in several linear and non-linear structure-selectivity relationships.42 Verloop developed the Sterimol program43 to describe the anisotropic nature of a substituent’s steric demands through a combination of subparameters, three of which remain in current use: two width parameters (B1 and B5) and a length parameter (L). In the original (Fortran) implementation, Sterimol parameters are generated from a list of atom types (based on element, hybridization and functional group) and dihedral angles from which the atomic coordinates are generated using tabulated bond lengths and angles, while the molecule surface is defined by CPK atomic radii. However, in principle it is also possible to define molecular coordinates using e.g. DFT-optimization along with a set of atomic radii. We first established that for a set of given structures we generated identical Sterimol parameters using either the original Fortran77 code, MMP+, or an in-house Python implementation. To define the steric profile of CpX ligands, a simple modification of Verloop’s original approach was required. DFT-optimized geometries were used where the width subparameters (B1 and B5) are calculated according to the CPK surface of the CpX ring when viewed along the Rh-Cp(centroid) axis (Figure 4, B). The L subparameter is calculated by measuring the length of the system along the Rh-Cp(centroid) axis. The B1 and B5 subparameters are calculated in the standard way by taking the perpendicular distance from the axis to the tangential, peripheral plane nearest to, and furthest from, the L axis. The value B5−B1 constitutes a simplified representation of anisotropy of the CpX ligand in the plane of the ring (Figure 5, C). As can be seen, disc-shaped CpX ligands like those found in complexes Rh1, Rh10, and Rh14 give rise to small B5−B1 values, and thus little anisotropy. Ligands with a more elliptical shape, like those in complexes Rh6–8 and Rh16 lead to larger B5−B1 values, and thus more pronounced anisotropic character.44 However, the Sterimol approach does not account for the high anisotropy of Rh20 that was observed with Θmax−Θmin values. This inconsistency stems from the definition of the B5 subparameter. If a second substituent that is at least as large as the one giving rise to B5 is present on the Cp ring, its influence on the shape of the ligand will be ignored. This issue also occurs in complexes Rh12, Rh13, and Rh17 bearing two identically large substituents attached to the Cp ring. Additionally, one should recognize that the Sterimol approach only considers dimensions inside the plane of the Cp ring. Arguably, more interesting for studying our model reactions is the out-of-plane steric bulk in the vicinity of the metal since substrate binding occurs at this site. Cone angle anisotropy (Θmax−Θmin, vide supra) might be more suited for this purpose. Nevertheless, we believe that when associated together, cone angles and Sterimol parameters might complement each other and provide a more complete description of the steric environment around the CpX ligand.
Overall, the above analysis reveals that small changes in the structure of the CpX ligand can readily affect the steric and electronic properties of the CpXRh(III) catalyst. We were then interested to study the impact of these catalyst perturbations on reactivity and selectivity in model reactions.
Choice of model reactions
Rh(III)-catalyzed insertion of alkenes into benzohydroxamic acid derivatives to produce dihydroisoquinolinones has been investigated extensively (Figure 6, A).16b,19,45 A unified mechanism can be drawn (Figure 6, B). It has been shown by kinetic isotope effect experiments that C-H insertion is often the turnover-limiting step in these reactions. With the assumption that the equilibrium constant for active catalyst generation is large enough (k1/k−1 > k2), the overall rate of reaction can be approximated by the rate of the C-H insertion step alone (k2 ≈ kobs). Moreover, depending on the nature of the π-component, the migratory insertion step becomes selectivity-determining. Regio- and diastereoselectivity values represent relative rate measurements . Therefore, selectivity and rate data sets can provide key insights regarding specific molecular interactions responsible for selectivity as well as catalytic activity. In this regard, two CpXRh(III)-catalyzed reactions previously developed in our group were selected as models (vide infra). We then systematically measured the regio- and diastereoselectivities as well as the catalytic activity obtainable with various Rh(III) catalysts (Rh1–22). Subsequently, the obtained data sets were correlated to experimental and computational ground-state catalyst properties, with the goal of gaining insight into the molecular features responsible for optimal catalyst performance.
Figure 6. Model reactions.
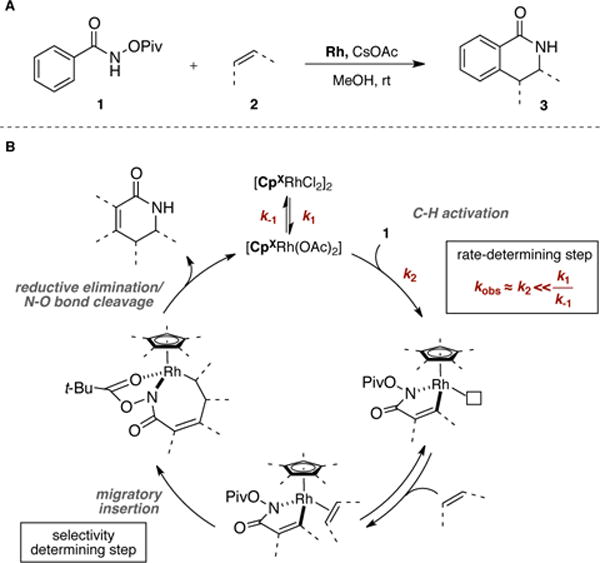
(A) Rh(III)-catalyzed annulation reaction between hydroxamic acid derivatives and alkenes for the synthesis of 3,4-dihydroisoquinolones. (B) General mechanism.
1-Decene insertion
As previously discussed, the regioselectivity of Rh(III)-catalyzed insertion of 1-decene 2a into the C-H bond of O-pivaloyl benzhydroxamic acid 1 is strongly dependent on the nature of the CpX ligand on rhodium leading to a mixture of regioisomers 3a and 3a’ (Figure 7, A).19 On the basis of catalyst performance in the title reaction, several trends emerge (Figure 7, B). For ligands of the type C5Me4R, increasing the steric bulk of the R substituent (see the ΘB scale, R = t-Bu > Ph > Cy > i-Pr > Me) leads to a higher regioisomer ratio (Rh11 > Rh5 > Rh3 > Rh2 > Rh1, 8.7−2.4:1 rr). Considering ligands of the type C5Me4Ar, more electron-rich aromatic rings according to values (Ar = H > 4-OMe > 3,5-bis-CF3 > C6F5, Figure 4, C) lead to better regioselectivity accordingly (Rh5 > Rh6 > Rh7 > Rh8, 5.3−3.0:1 rr). For structurally related ligands of the type C5Me4R, more electron-withdrawing substituents according to the scale (R = CF3 > Bn > Me) increase the regioselectivity of the reaction (Rh10 > Rh4 > Rh1, 3.7−2.4:1 rr). The results are conveniently visualized on a free energy scale (Figure 7, C).
Figure 7. Influence of CpX ligand structure on the regioselectivity of 1-decene insertion.
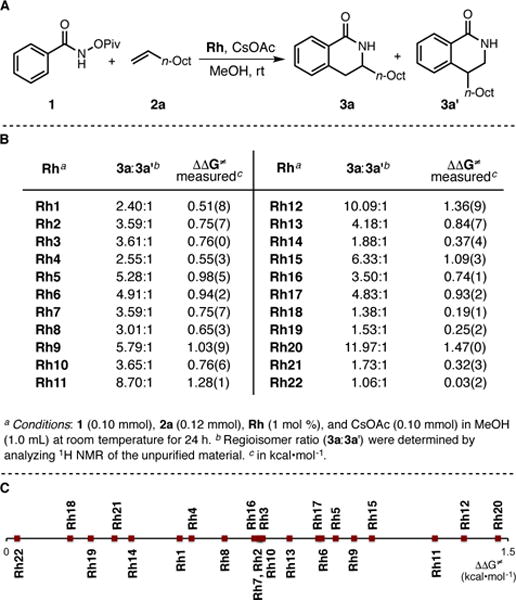
(A) Coupling of O-pivaloyl benzhydroxamate 1 and 1-decene 2a. (B) Regioisomer ratios obtained with different CpXRh(III) complexes. (C) Scale of regioisomer ratios in the form of activation energy differences (ΔΔG‡).
Cyclopropene insertion
The diastereoselectivity of cyclopropene insertion into the C-H bond of O-pivaloyl benzhydroxamate 1 is strongly dependent on the nature of the CpX ligand on the Rh(III) catalyst (Figure 8).46 Indeed, when a cyclopropene bearing a prostereogenic center such as 2b is used, two diastereomeric products arise (3b and 3b’). In the major diastereomer 3b, the bulkier phenyl substituent is placed on the convex face of the molecule (Figure 8, A). When analyzing the diastereomeric ratios obtained with different CpXRh(III) complexes, few similarities can be drawn with the trends observed for the regioselectivity of 1-decene insertion (Figure 7, B). Notably, with ligands of the type C5Me4R, increasing the steric bulk of the R substituent (see ΘB values for R = t-Bu > Ph > Cy > i-Pr > Me) leads to higher diastereomeric induction (Rh11 > Rh5 > Rh3 > Rh2 > Rh1, 9.6−5.8:1 dr). Additionally, increasing the degree of substitution of the Cp ring yields a more selective reaction (Rh1 > Rh14 > Rh18 > Rh19, 5.8−0.9:1 dr), but complex Rh21 falls out of the general trend (Rh21 > Rh19, 1.1:1 vs. 0.9:1 dr). Interestingly, while performing well in the previous reaction, Rh20 (12:1 rr, Figure 7, B) fails to produce high diastereoselectivity in the present reaction (5.0:1 dr, Figure 8, B). The opposite holds true for the heptamethylindenyl ligand (Rh22) that gives 15.2:1 dr for cyclopropene insertion, in contrast to 1.1:1 rr for 1-decene insertion. On the other hand, complex Rh12 displays equally good performances in both transformations (10.1:1 rr and 19.5:1 dr).47 A scale for diastereoselectivity is depicted below (Figure 8, C).
Figure 8. Influence of CpX ligand structure on the diastereoselectivity of cyclopropene insertion.
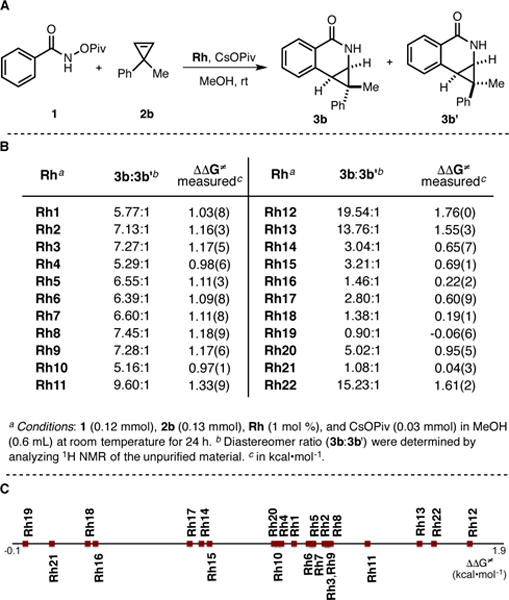
(A) Coupling of benzhydroxamic acid derivative 1 and cyclopropene 2b.
(B) Diastereomer ratios obtained with different CpXRh(III) complexes. (C) Scale of diastereomer ratios in the form of activation energy differences (ΔΔG‡).
Kinetic measurements
To gain further insight into the influence of ligand structure on the outcome of Rh(III)-catalyzed reactions, the rate of 1-decene (2a) insertion into O-pivaloyl benzhydroxamate (1) was monitored for catalysts Rh1–22 by 1H-NMR spectroscopy (Figure 9). The recorded concentration of products (3a+3a’) vs. time profiles were readily fitted to single-exponential curves, suggesting first-order behavior in all cases (Figure 9, A). This implies that CH activation is turnover limiting regardless of the nature of the catalyst. The extracted rate constants are presented in Figure 9, C.
Figure 9.
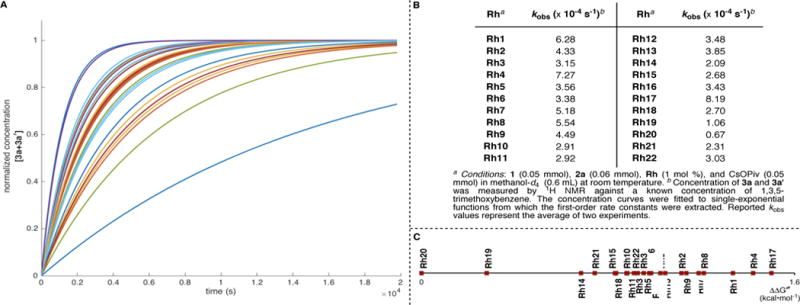
Catalytic activity of CpXRh(III) complexes for 1-decene (2a) insertion. (A) Normalized concentration of 3a + 3a’ vs. time. (B) Extracted first-order rate constants (kobs). (C) Scale of rate constants in the form of activation energy differences (ΔΔG‡).
For CpX ligands of the type C5Me4R, the reaction is faster when a weakly electron-withdrawing substituent is present. Accordingly, Rh4 (R = Bn, , kobs = 7.28×10−4s−1) is faster than Rh1 (R = Me, , kobs = 6.28×10−4 s−1). Whereas Rh6–8 are all three faster than Rh5 ( ,−1.25, −1.18, −1.09 vs. −1.25 V; kobs = 5.09−4.38 vs. 3.30×10−4 s−1). Substituents with large ΘB values slow down the reaction, for example, the rate decreases in the order of Rh1 > Rh2 > Rh5 >> Rh11 (6.28−2.92 ×10−4 s−1). Very bulky CpX ligands, such as those found in complexes Rh11, Rh12, and Rh20 lead to the slowest reaction rates (2.92, 3.48, 0.66 ×10−4 s−1, respectively). When CpX ligands contain strongly electron-withdrawing groups such as CF3 and CO2Et (Rh10 and Rh13, respectively) the rate decreases significantly. Decreasing the number of substituents on the Cp ring tends to slow down the reaction considerably (Rh1 >> Rh14, Rh21, 6.28 vs. 2.09, 2.31 ×10−4 s−1). An exception are cyclohexyl-fused ligands like those in complexes Rh15–19 for which the rate is somewhat restored, especially when additional substituents on the Cp ring are present. Indeed, complex Rh17 gives rise to the fastest catalytic activity in the series (8.19×10−4 s−1). The kinetic data is arranged according to their respective free energies in Figure 9, C.
Having defined the model reactions and the parameter space accordingly, we performed multivariate linear regression to correlate the relevant catalyst parameters to regioselectivity, diastereoselectivity, and rate.
Correlating catalyst-based parameters to selectivity and rate of model reactions
Ideally, a single electronic and/or a single steric parameter will capture the covariance of catalyst structure with reaction outcome, as in a Hammett or Taft analysis. But often, the molecular diversity of a large catalyst library cannot be distilled to one or two dimensions. Instead, an ensemble of quantitative molecular descriptors is usually required to account for all the subtleties of chemical structure. Moreover, the steric and electronic components of these parameters cannot be completely decoupled from one another, except in rare cases.34,35,48 Recently, stepwise linear regression algorithms found widespread utility in handling the typically large number of parameters involved in multivariate free energy relationships.21,36,37
With the appropriate library of CpXRh(III) complexes in hand (Figure 2), the selectivity and reactivity data sets of model reactions were used to produce correlations between the experimental values and catalyst-based molecular descriptors. The parameter set consisted of 15 elements, including 31P (δP) chemical shifts, computed 103Rh shielding tensors (σRh), Rh-P coupling constants (JRh-P), IR stretching frequencies (νS and νA), redox potentials ( and ), natural charge on Rh atom (qRh), Sterimol parameters(L, B1, B5), and cone angles (ΘS, ΘB, ΘB,max, and ΘB,min). We first constructed global regression models (GMs) for regioselectivity, diastereoselectivity, and rate, each composed of all 22 catalysts and employing only linear combinations of parameters from the set. In cases where a large number of parameters had to be used to obtain a good fit, interaction terms were included to reduce the number of elements of the correlation equations. GMs were parameterized with either a principal (training set 1, or T1) or two secondary (T2 and T3) training sets (grey circles, Figures 10, 11, 13). T1 is comprised of 18 structures, namely Rh1–7, Rh9, Rh10, Rh13, Rh14, Rh16–22. In T2, complex Rh22 is replaced by Rh8, while in T3, complex Rh13 is replaced by Rh8 and Rh15 is replaced by Rh4. The CpXRh(III) complexes selected for the training sets cover the spectrum of regio- and diastereoselectivities representative of the different substitution patterns of CpX ligands. The remaining structures were left out for the validation sets (red triangles, Figures 10, 11, 13). To evaluate the statistical accuracy of all regression models, we graphically represented predicted vs. measured ΔΔG‡, which is the free energy difference, in kcal•mol−1, between the regio- or diastereomeric transition states leading to isomeric products.
Figure 10. Mathematical correlations of normalized catalyst parameters to regioselectivity (ΔΔG‡) for the 1-decene insertion reaction.
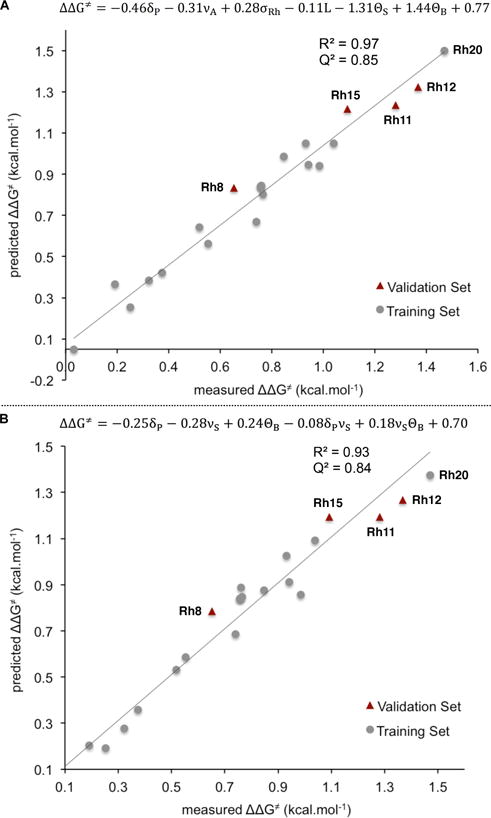
(A) Global model for Rh1–22 with training set I. (B) Global model for Rh1–22, including two interaction terms (δP·νS and νS·ΘB).
Figure 11. Mathematical correlations of normalized catalyst parameters to diastereoselectivity (ΔΔG‡) for the cyclopropene insertion reaction.

(A) Global model for Rh1–22 with training set I. (B) Global model for Rh1–22 with training set II. (C) Global model for Rh1–22 with training set III.
Figure 13. Mathematical correlation of normalized catalyst parameters to catalytic activity (ΔΔG‡) for the 1-decene insertion reaction.
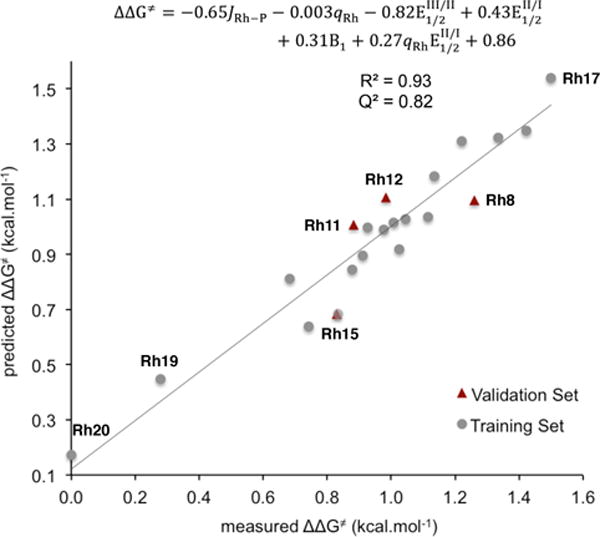
Global model for Rh1-22 including an interaction term .
Correlating regioselectivity
Our purpose was to produce multivariate correlations to describe the origins of regioselectivity in the 1-decene insertion reaction (Figure 10). When employing T1 as the training set, a statistically robust regression model was obtained (R2 = 0.97, Figure, 10, A), composed of three “electronic” terms, namely 31P chemical shifts (δP), antisymmetric CO stretching frequencies (νA), and 103Rh shielding tensor (σRh), as well as three “steric” components, namely L parameters, and Sterimol and Bondi cone angles (ΘS and ΘB). The regioselectivity model demonstrates an overall good agreement between predicted ΔΔG‡ values and experimental data. The predictive capability of this regression model was confirmed through external validation with complexes Rh8, Rh11, Rh12, and Rh15, as well as a Q2 value test.49 As the relationships in Figure 10 are normalized equations, the magnitude of the coefficients gives insight on the relative influence of each parameter on selectivity. Hence, the “electronic” parameters δP, νA, and σRh have the largest coefficients (0.46, 0.31, and 0.28, respectively) and, consequently, an important influence on regioselectivity. On the other hand, the Sterimol parameter L gives a small steric contribution (0.11). It is interesting to note that the relative weights of ΘS and ΘB are similar in magnitude but opposite in sign (−1.31 vs. +1.44), and overweight all other parameters in the equation. Such behavior is commonly observed when alike parameter couples are used in the correlation (e.g., νS and νA, and , or ΘS and ΘB). Additionally, pronounced co-variance between these couples is observed (see Supporting Information). We propose that the regression algorithm couples ΘS and ΘB together in form of a weighted difference, which gives rise to a crossed parameter (aΘS-bΘB) with increased correlative power. This purely mathematical adjustment compensates for the deficiency of averaged cone angles to account for the caveats of steric structure when taken separately.
In an oversimplified analysis, assuming perfect separation of electronic and steric components for each parameter, the percent contribution of electronic character is estimated at 81% by using eq. 8,
| (8) |
where ci are the relative weights of “electronic” parameters, and cj are the contributions from “steric” parameters. For coupled parameters like ΘS and ΘB, the difference between coefficients is taken to measure the relative weight of the entire term. Such a high electronic component for the regioselectivity model seems at first glance counterintuitive. In our opinion, this is possible because some of the employed “electronic” parameters like δP and JRh-P already have a significant steric component embedded into them.
While our linear GM has the advantage of incorporating the entire set of catalysts into the correlation, the complexity of the resultant equation (six linear terms) renders its interpretation challenging. To reduce the number of parameters needed to accurately describe regioselectivity, interaction terms were included into the regression process (Figure 10, B). While keeping the statistical quality at the same level (R2 = 0.96), the number of required parameters for the interaction model is reduced twofold, leaving three linear terms (δP, νS, and ΘB) and two interaction terms, namely δP·νS and νS·ΘB. Interestingly, both interaction terms contain the electronic νS parameter but, while in the first term the frequency interacts with another electronic term (δP), in the second one an interaction with a steric parameter (ΘB) is observed. The larger coefficient for the latter (0.08 vs. 0.18) supports the empirical observation of an interplay between steric and electronic properties of the catalyst when describing regioselectivity.
Correlating diastereoselectivity
We also searched for correlations between the diastereoselectivity of cyclopropene insertion (represented as ΔΔG‡) and the molecular descriptors of CpX ligands (Figure 11). When using T1 as the training set, a regression model was found where the predicted selectivities closely match those measured (R2 = 0.97, Figure 11, A). Three electronic parameters [31P chemical shifts (δP), NBO charges at rhodium (qRh), and Rh(III/II) redox potentials ] and one steric parameter [the minimum Bondi cone angle (ΘB,min)] are used in the correlation. A relatively large coefficient (0.10) for ΘB,min is consistent with substrate approach on the less hindered side of the CpX ligand in the diastereoselectivity-imparting step.50 Further substantiation of the model was provided through external validation with an additional set of four CpXRh(III) complexes. As depicted in Figure 11, A, the model displays accurate predictive capability for estimating the performance of complexes Rh8, Rh11 and Rh15, and a Q2 value of 0.91. However, complex Rh12 is obviously an outlier and its high diastereoselectivity (19.5:1 dr, ΔΔG‡ = 1.76 kcal.mol−1, Figure 8, B) is not well predicted (vide infra). Classically, kinks or breaks in univariate correlations (e.g., Hammett plots) are indicative of a change in mechanism for certain data set members. In cases where multivariate correlations are applied, this change could be identified through the presence of obvious outliers.23j Building on these observations, we sought to explore the possibility that a similar scenario took place with catalyst Rh12 during the selectivity-determining step, and if a change in mechanism is a requirement for high diastereomeric induction. Furthermore, we questioned whether Rh12 is an isolated case or such behavior could be extended to other members of the catalyst library. We were particularly interested in the performances of complexes Rh13 and Rh22 that give rise to high diastereomer ratios (ΔΔG‡ = 1.55 kcal•mol−1, and ΔΔG‡ = 1.61 kcal•mol−1, respectively, Figure 8, B). First, in order to check whether Rh22 is an outlier, an additional regression model was constructed with training set T2 that leaves both Rh12 and Rh22 out of the parameterization process (Figure 11, B). A suitable model was indeed found (R2 = 0.98), making use of 31P chemical shifts (δP), 103Rh shielding tensors (σRh), Rh(II/I) redox potentials , Sterimol B1 parameters and cone angles (ΘS). Inclusion of the Sterimol B1 parameter is consistent with substrate approach on the less hindered side of the CpX ligand. When validating the model with an external set of four members, Rh12 and Rh22 are both outliers this time. This result suggests that the high diastereoselectivities exhibited by catalysts Rh12 and Rh22 might arise from a change in structure of the transition state.
In contrast, this was not the case for complex Rh13. A linear diastereoselectivity model was constructed with training set T3 that now includes Rh22, while Rh12 and Rh13 are left out of the parameterization process (Figure 11, C). This time, the relevant parameters are 31P chemical shifts (δP), 103Rh-31P coupling constants (JRh-P), Rh(II/I) redox potentials , and Sterimol B1 parameters. Interestingly, while Rh12 is once again an obvious outlier with this training set, the high diastereomeric induction observed experimentally for Rh13 is well described by the regression model (R2 = 0.96). This result implies that, contrary to Rh12 and Rh22: (i) the performance of catalyst Rh13 in the cyclopropene insertion reaction can be predicted accurately on the basis of ground-state steric and electronic properties of the catalyst, and (ii) that a mechanism change is not a prerequisite for high diastereomeric induction. It is important to note that the involvement of an alternate mechanistic regime for complexes Rh12 and Rh22 is a unique asset of the cyclopropene insertion reaction. Indeed, Rh12 and Rh22 are no longer outliers in regioselectivity models.51
In order to shed light on the origins of the high levels of diastereomeric induction displayed by catalysts Rh12 and Rh22 in the cyclopropene insertion reaction, competing transition structures (TSs) for the selectivity-determining migratory insertion step48b were investigated computationally (Figure 12).52 We found structural differences in the metal π–coordination for these ligands, with Rh12 and Rh22 showing larger variation than Rh1 in the five Rh-C distances associated with the Rh-Cp interaction. These coordination modes thus have greater (η3 + η2) character than (η5) Rh1. This effect, which may be quantified in terms of a slippage parameter, which reflects the average difference between longest and shortest M-C distances (see SI), is further magnified in the insertion TSs. The anomalously high diastereoselectivity obtained with the Ind* ligand (Rh22) results from greater slippage in the favored insertion TS. The better slippage capability of the indenyl ligand towards a η3 + η2 bonding mode increases the diastereoselectivity by accommodating the methyl group in the exo-trans TS leading to the major diastereomer. The stereoselectivity is enhanced due to differences in ligand bonding mode and geometry. This effect is most pronounced for complexes Rh12 and Rh22, which are more prone to hapticity change. Because the ground-state parameters that we use to construct our regression models cannot describe this phenomenon adequately, it might explain why the prediction fails for complexes Rh12 and Rh22. It is interesting to see that although the reactions involving 1-decene or cyclopropene insertion are in essence very close, they differ in terms of catalyst features to achieve high performances.
Figure 12.
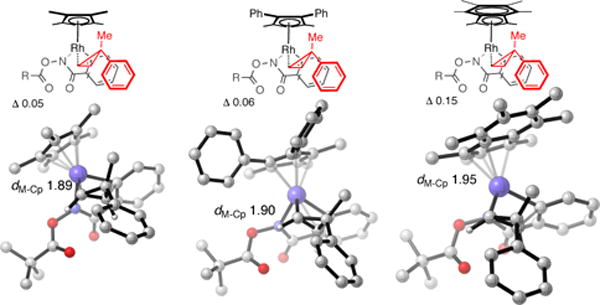
Optimized exo-trans transition structures for cyclopropene insertion leading to the major diastereomer (from left to right, Rh1, Rh12, Rh22).
After studying the selectivity-imparting step of the model reactions in detail, we investigated the catalytic activity of complexes Rh1–22 next, by establishing multivariate correlations between reaction rate and the set of catalyst-based descriptors.
Correlating reaction rate
The C-H bond cleavage event constitutes the rate-determining step in both model reactions. We anticipated that a thorough analysis of this particular step would shed light on the catalyst requirements for high catalytic activity.
To initiate our study, the rate constants (kobs) shown in Figure 9, B were converted to their corresponding Gibbs free energies of activation according to the Eyring equation . The regression model was then parameterized with training set T1, leaving Rh8, Rh11, Rh12 and Rh15 out for the validation set. While being strongly correlative (R2 = 0.95) and possessing accurate predictive capability (Q2 = 0.82), the linear rate model is complicated by the large number of parameters it requires (8 terms) and reveals little regarding the interactions at the origin of high catalytic activity (see Supporting Information). As depicted in Figure 13, a statistically reliable interaction model (R2 = 0.94) was constructed by employing 103Rh-31P coupling constants (JRh-P), natural charges at rhodium (qRh), Rh(III/II) and Rh(II/I) redox potentials ( and ), Sterimol B1 parameters, and an interaction term . Similarly to the behavior observed for cone angles ΘS and ΘB in the regioselectivity model, the relative weights of redox potentials and are similar in magnitude but opposite in sign (−0.82 vs. +0.43). This implies that mixing of these parameters occurs during the regression process. Sterimol B1 parameter is the only steric term in the equation and is consistent with preferred substrate approach from the least hindered dimension of the CpX ligand in the transition state of the C-H bond cleavage step.53 Besides natural charges (qRh), the interaction term makes use of redox potentials , both being descriptors of electron density at the metal center of Rh complexes. Two of the highest reaction rates were observed for catalysts Rh4 and Rh17 that have one of the most positive qRh and most negative values. While qRh numbers become more positive for more electron-rich Rh(III) centers, redox potentials become more negative for more electron-rich complexes. Thus, the interplay between qRh and that display opposite tendencies might account for the experimentally-observed optimum of catalyst electronegativity required to tune the reaction rate.
CONCLUSIONS
In conclusion, we have developed a series of quantitative linear regression models that correlate reaction outcome such as selectivity and reactivity to catalyst-based parameters. Our parameterization process consisted of collecting experimental and computational data for a large library of CpXRh(III) complexes. Two model reactions were chosen to study correlations, one involving the insertion of 1-decene and the other that of cyclopropene. The influence of ligand structure on the first step (C-H activation) was probed by measuring reaction rate and the influence on the second step (alkene insertion) was investigated by measuring reaction regio- and diastereoselectivities. While good correlations are seen for regioselectivity and rate, two obvious outliers occurred between predicted and measured ΔΔG‡ for the diastereo-selectivity model. DFT calculations have shown that the uncommonly high selectivity displayed by the outliers can be explained by partial η5−η3 ligand slippage occurring in the transition state of the selectivity-determining step. It is interesting to note that this does not seem to take place during 1-decene insertion. Our regression models show predictive capability, allowing for determination of reaction selectivity and rate given a set of descriptive parameters for a chosen ligand. We hope that this study could serve as a starting point for the design of new cyclopentadienyl-type ligands and uncover the full potential of Rh(III) chemistry.
Supplementary Material
Acknowledgments
We thank NIGMS (GM80442 to T.R.) for support, and acknowledge the use of the EPSRC UK National Service for Computational Chemistry Software (CHEM870 to R.S.P.) in carrying out this work and the dirac cluster at the University of Oxford (EP/L015722/1).
Funding Sources
NIGMS (GM80442)
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website.
Experimental procedures, analytical data, NMR spectra and computational methods (PDF)
X-Ray data (PDF)
Experimental and computational data (XLSX)
Author Contributions
References
- 1.Wilkinson G, Gillard RD, McCleverty JA. Comprehensive Coordination Chemistry. Vol. 2 Pergamon; New York: 1987. [Google Scholar]
- 2.Collman JP, Hegedus LS, Norton JR, Finke RG. Principles and Applications of Organotransition Metal Chemistry. University Science Books; Mill Valley, CA: 1987. p. 57. [Google Scholar]
- 3.For recent reviews, see:; (a) Colby DA, Bergman RG, Ellman JA. Chem Rev. 2010;110:624. doi: 10.1021/cr900005n. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Satoh T, Miura M. Chem Eur J. 2010;16:11212. doi: 10.1002/chem.201001363. [DOI] [PubMed] [Google Scholar]; (c) Patureau FW, Glorius F. Angew Chem Int Ed. 2011;50:1977. doi: 10.1002/anie.201007241. [DOI] [PubMed] [Google Scholar]; (d) Patureau FW, Wencel-Delord J, Glorius F. Aldrichimica Acta. 2012;45:31. [Google Scholar]; (e) Song G, Wang F, Li X. Chem Soc Rev. 2012;41:3651. doi: 10.1039/c2cs15281a. [DOI] [PubMed] [Google Scholar]; (e) Chiba S. Chem Lett. 2012;41:1554. [Google Scholar]
- 4.(a) Ueura K, Satoh T, Miura M. Org Lett. 2007;9:1407. doi: 10.1021/ol070406h. [DOI] [PubMed] [Google Scholar]; (b) Umeda N, Tsurugo H, Satoh T, Miura M. Angew Chem Int Ed. 2008;47:4019. doi: 10.1002/anie.200800924. [DOI] [PubMed] [Google Scholar]; (c) Fukutani T, Umeda N, Hirano K, Satoh T, Miura M. Chem Commun. 2009:5141. doi: 10.1039/b910198e. [DOI] [PubMed] [Google Scholar]; (d) Morimoto K, Hirano K, Satoh T, Miura M. Org Lett. 2010;12:2068. doi: 10.1021/ol100560k. [DOI] [PubMed] [Google Scholar]; (d) Mochida S, Umeda N, Hirano K, Satoh T, Miura M. Chem Lett. 2010;39:744. [Google Scholar]
- 5.Stuart DR, Bertrand-Laperle M, Burgess KMN, Fagnou K. J Am Chem Soc. 2008;130:16474. doi: 10.1021/ja806955s. [DOI] [PubMed] [Google Scholar]
- 6.Hyster TK, Rovis T. J Am Chem Soc. 2010;132:10565. doi: 10.1021/ja103776u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.(a) Song G, Chen D, Pan CL, Crabtree RH, Li X. J Org Chem. 2010;75:7487. doi: 10.1021/jo101596d. [DOI] [PubMed] [Google Scholar]; (b) Rakshit S, Patureau FW, Glorius F. J Am Chem Soc. 2010;132:9585. doi: 10.1021/ja104305s. [DOI] [PubMed] [Google Scholar]
- 8.For selected examples, see:; (a) Uto T, Shimizu M, Ueura K, Tsurugi H, Satoh T, Miura M. J Org Chem. 2008;73:298. doi: 10.1021/jo7022087. [DOI] [PubMed] [Google Scholar]; (b) Rakshit S, Patureau FW, Glorius F. J Am Chem Soc. 2010;132:9585. doi: 10.1021/ja104305s. [DOI] [PubMed] [Google Scholar]; (c) Du Y, Hyster TK, Rovis T. Chem Comm. 2011;47:12074. doi: 10.1039/c1cc15843k. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Pham MV, Ye B, Cramer N. Angew Chem Int Ed. 2012;51:197. doi: 10.1002/anie.201206191. [DOI] [PubMed] [Google Scholar]; (e) Neely JM, Rovis T. J Am Chem Soc. 2013;135:66. doi: 10.1021/ja3104389. [DOI] [PMC free article] [PubMed] [Google Scholar]; (f) Hyster TK, Ruhl KE, Rovis T. J Am Chem Soc. 2013;135:5364. doi: 10.1021/ja402274g. [DOI] [PMC free article] [PubMed] [Google Scholar]; (g) Liu G, Shen Y, Zhou Z, Lu X. Angew Chem Int Ed. 2013;52:6033. doi: 10.1002/anie.201300881. [DOI] [PubMed] [Google Scholar]; (h) Davis TA, Wang C, Rovis T. Synlett. 2015:1520. doi: 10.1055/s-0034-1381006. [DOI] [PMC free article] [PubMed] [Google Scholar]; (i) Archambeau A, Rovis T. Angew Chem Int Ed. 2015;54:13337. doi: 10.1002/anie.201504150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Neely JM, Rovis T. J Am Chem Soc. 2014;136:2735. doi: 10.1021/ja412444d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shibata Y, Tanaka K. Angew Chem Int Ed. 2011;50:11109. doi: 10.1002/anie.201105517. [DOI] [PubMed] [Google Scholar]
- 11.Romanov-Michailidis F, Sedillo KS, Neely JM, Rovis T. J Am Chem Soc. 2015;137:8892. doi: 10.1021/jacs.5b04946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.(a) Hoshino Y, Shibata Y, Tanaka K. Adv Synth Catal. 2014;356:1577. [Google Scholar]; (c) Fukui M, Hoshino Y, Satoh T, Miura M, Tanaka K. Adv Synth Catal. 2014;356:1638. [Google Scholar]
- 13.(a) Guimond N, Gouliaras C, Fagnou K. J Am Chem Soc. 2010;132:6908. doi: 10.1021/ja102571b. [DOI] [PubMed] [Google Scholar]; (b) Guimond N, Gorelsky SI, Fagnou K. J Am Chem Soc. 2011;133:6449. doi: 10.1021/ja201143v. [DOI] [PubMed] [Google Scholar]
- 14.Rakshit S, Grohmann C, Besset T, Glorius F. J Am Chem Soc. 2011;133:2350. doi: 10.1021/ja109676d. [DOI] [PubMed] [Google Scholar]
- 15.(a) Hyster TK, Rovis T. Chem Comm. 2011;47:11846. doi: 10.1039/c1cc15248c. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Hyster TK, Rovis T. Chem Sci. 2011;2:1606. doi: 10.1039/C1SC00235J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hyster TK, Dalton DM, Rovis T. Chem Sci. 2015;6:254. doi: 10.1039/c4sc02590c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wodrich MD, Ye B, Gonthier JF, Corminboeuf C, Cramer N. Chem Eur J. 2015;20:15409. doi: 10.1002/chem.201404515. [DOI] [PubMed] [Google Scholar]
- 18.Piou T, Rovis T. J Am Chem Soc. 2014;136:11292. doi: 10.1021/ja506579t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Piou T, Rovis T. Nature. 2015;527:86. doi: 10.1038/nature15691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.For selected examples, see; (a) Harper KC, Sigman MS. Science. 2011;333:1875. doi: 10.1126/science.1206997. [DOI] [PubMed] [Google Scholar]; (b) Harper KC, Vilardi SC, Sigman MS. J Am Chem Soc. 2013;135:2482. doi: 10.1021/ja4001807. [DOI] [PubMed] [Google Scholar]; (c) Milo A, Bess EN, Sigman MS. Nature. 2014;507:210. doi: 10.1038/nature13019. [DOI] [PubMed] [Google Scholar]; (d) Bess EN, DeLuca RJ, Tindall DJ, Oderinde MS, Roizen JL, Du Bois J, Sigman MS. J Am Chem Soc. 2014;136:5783. doi: 10.1021/ja5015508. [DOI] [PMC free article] [PubMed] [Google Scholar]; (e) Bess EN, Bischoff AJ, Sigman MS. Proc Nat Acad, Sci. 2014;111:14698. doi: 10.1073/pnas.1409522111. [DOI] [PMC free article] [PubMed] [Google Scholar]; (f) Milo A, Neel AJ, Toste FD, Sigman MS. Science. 2015;347:737. doi: 10.1126/science.1261043. [DOI] [PMC free article] [PubMed] [Google Scholar]; (g) Bess EN, Guptill DM, Davies HML, Sigman MS. Chem Sci. 2015;6:3057. doi: 10.1039/c5sc00357a. [DOI] [PMC free article] [PubMed] [Google Scholar]; (h) Hickey DP, Schiedler DA, Matanovic I, Doan PV, Atanassov P, Minteer SD, Sigman MS. J Am Chem Soc. 2015;137:16179. doi: 10.1021/jacs.5b11252. [DOI] [PubMed] [Google Scholar]; (i) Mougel V, Santiago CB, Zhizhko PA, Bess EN, Varga J, Frater G, Sigman MS, Copéret C. J Am Chem Soc. 2015;137:6699, 6699. doi: 10.1021/jacs.5b03344. [DOI] [PubMed] [Google Scholar]; (j) Neel AJ, Milo A, Sigman MS, Toste FD. J Am Chem Soc. 2016;138:3863. doi: 10.1021/jacs.6b00356. [DOI] [PMC free article] [PubMed] [Google Scholar]; For a recent review, see; (k) Sigman MS, Harper KC, Bess EN, Milo A. Acc Chem Res. 2016;49:1292. doi: 10.1021/acs.accounts.6b00194. [DOI] [PubMed] [Google Scholar]
- 21.For pioneering work, see; (a) Yoshino T, Ikemoto H, Matsunaga S, Kanai M. Angew Chem Int Ed. 2013;52:2207. doi: 10.1002/anie.201209226. [DOI] [PubMed] [Google Scholar]; For recent examples, see; (b) Suzuki Y, Sun B, Sakata K, Yoshino T, Matsunaga S, Kanai M. Angew Chem Int Ed. 2015;54:9944. doi: 10.1002/anie.201503704. [DOI] [PubMed] [Google Scholar]; (c) Li J, Ackermann L. Angew Chem Int Ed. 2015;54:3635. doi: 10.1002/anie.201409247. [DOI] [PubMed] [Google Scholar]; (d) Hummel JR, Ellman JA. J Am Chem Soc. 2015;137:490. doi: 10.1021/ja5116452. [DOI] [PMC free article] [PubMed] [Google Scholar]; (e) Yu DG, Gensch T, de Azambuja T, Vasquez-Cespedes S, Glorius F. J Am Chem Soc. 2014;136:17722. doi: 10.1021/ja511011m. [DOI] [PubMed] [Google Scholar]
- 22.For a review, see:; Shin K, Kim H, Chang S. Acc Chem Res. 2015;48:1040. doi: 10.1021/acs.accounts.5b00020. [DOI] [PubMed] [Google Scholar]
- 23.Single crystals for complexes Rh13 and Rh16 of adequate quality were not obtained.
- 24.Tolman CA. Chem Rev. 1977;77:313. [Google Scholar]
- 25.(a) Shen J, Basolo F, Nombel P, Lugan N, Lavigne G. Inorg Chem. 1996;35:755. [Google Scholar]; (b) du Plooy KE, du Toit J, Levendis DC, Coville NJ. J Organomet Chem. 1996;508:231. [Google Scholar]; (c) du Plooy KE, Ford TA, Coville NJ. J Organomet Chem. 1999;579:348. [Google Scholar]
- 26.(a) Rerek ME, Basolo F. J Am Chem Soc. 1984;106:5908. [Google Scholar]; (b) Cheong M, Basolo F. Organometallics. 1988;2041 [Google Scholar]
- 27.(a) Lyatifov IR, Gulieva GI, Babin VN, Materikova RB, Petrovskii PV, Fedin EI. J Organomet Chem. 1996;15:2469. [Google Scholar]; (b) Meir EJM, Kozminski W, Linden A, Lusenberger P, von Philipsborn W. Organometallics. 1996;15:2469. [Google Scholar]; (c) Fabrello A, Dinoi C, Perrin L, Kalck P, Maron L, Urrutigoity M, Dechy-Cabaret O. Magn Reson Chem. 2010;48:848. doi: 10.1002/mrc.2677. [DOI] [PubMed] [Google Scholar]
- 28.(a) Mason JG, Rosenblum M. J Am Chem Soc. 1960;82:4206. [Google Scholar]; (b) Kuwana R, Bublitz DE, Hoh GLK. J Am Chem Soc. 1960;82:5811. [Google Scholar]; (c) Langmaier J, Samec Z, Varga V, Horacek M, Mach K. J Organomet Chem. 1999;579:348. [Google Scholar]; (d) Langmaier J, Samec Z, Varga V, Horacek M, Choukroun R, Mach K. J Organomet Chem. 1999;326:93. [Google Scholar]
- 29.This DFT methodology has been previously applied to the study of Rh-catalysis and metal-ligand dissociation to give quantitative agreement with experimental results; (a) Sperger T, Sanhueza IA, Kalvet I, Schoenebeck F. Chem Rev. 2015;115:9532. doi: 10.1021/acs.chemrev.5b00163. [DOI] [PubMed] [Google Scholar]; (b) Straker R, Peng Q, Mekareeya A, Paton RS, Anderson EA. Nat Commun. 2016;7:10109. doi: 10.1038/ncomms10109. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Peng Q, Paton RS. Acc Chem Res. 2016;49:1042. doi: 10.1021/acs.accounts.6b00084. [DOI] [PubMed] [Google Scholar]; (d) Raju RK, Bengali AA, Brothers EN. Dalton Trans. 2016;45:13766. doi: 10.1039/c6dt02763f. [DOI] [PubMed] [Google Scholar]
- 30.Santiago CB, Milo A, Sigman MS. J Am Chem Soc. 2016;138:13424. doi: 10.1021/jacs.6b08799. [DOI] [PubMed] [Google Scholar]
- 31.Winstein S, Holness NJ. J Am Chem Soc. 1955;77:5562. [Google Scholar]
- 32.(a) Adams R, Yuan HC. Chem Rev. 1933;12:261. [Google Scholar]; (b) Bott G, Field LD, Sternhell S. J Am Chem Soc. 1980;102:5618. [Google Scholar]
- 33.Niksch T, Görls H, Weigand W. Eur J Inorg Chem. 2010;95 [Google Scholar]
- 34.Taft RW. J Am Chem Soc. 1953;75:4538. [Google Scholar]
- 35.Charton M. J Org Chem. 1976;41:2217. [Google Scholar]
- 36.(a) Müller TE, Mingos DM. Transition Met Chem. 1995;20:533. [Google Scholar]; (b) Fey N, Harvey JN, Lloyd-Jones GC, Murray P, Orpen AG, Osborne R, Purdle M. Organometallics. 2008;27:1372. doi: 10.1021/om300312t. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Jover JS, Fey N, Harvey JN, Lloyd-Jones GC, Orpen AG, Owen-Smith GJJ, Murray P, Hose DRJ, Osborne R, Purdle M. Organometallics. 2010;29:6245. doi: 10.1021/om300312t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.(a) Maitlis PM. Chem Soc Rev. 1981:1. [Google Scholar]; (b) Grimmer NE, Coville NJ. S Afr J Chem. 2001;54:118. [Google Scholar]; (c) Coville NJ, Loonat MS, White D, Carlton L. Organometallics. 1992;11:1082. [Google Scholar]; (d) Bauer H, Glöckner A, Tagne Kuate AC, Schäfer S, Sun Y, Freytag M, Tamm M, Walter MD, Sitzmann H. Dalton Trans. 2014;43:15818. doi: 10.1039/c4dt01581a. [DOI] [PubMed] [Google Scholar]
- 38.(a) Corey RB, Pauling L. The Review of Scientific Instruments. 1953;24:621. [Google Scholar]; (b) Pauling L. The Nature of the Chemical Bond. 1931;53:1367. [Google Scholar]
- 39.Bondi A. J Phys Chem. 1964;68:441. [Google Scholar]
-
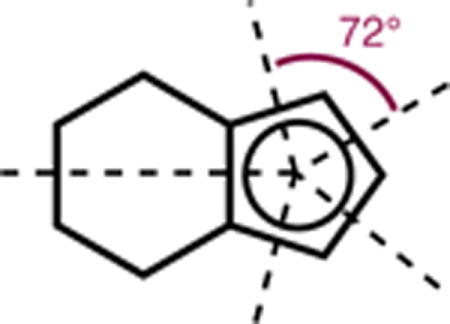
40.Since some of the ligands contain fused ring systems (e.g., indenyl, tetrahydroindenyl), the ligand was partitioned into 5 equal parts (72° segments for a CpX ligand), from each of which a single contributing angle was generated that contributed to the final cone angle.;
- 41.(a) Verloop A, Tipker J. In: Biological Activity and Chemical Structure. Buisman JA, editor. Elsevier; 1977. p. 63. [Google Scholar]; (b) Verloop A. In: IUPAC Pesticide Chemistry. Miyamoto J, editor. Vol. 1. Vol. 339. Pergamon; 1983. [Google Scholar]; (c) Verloop A, Tipker J. In: QSAR in Drug Dosing and Toxicology. Hadzi B, Jerman-Blazic B, editors. Vol. 97. Elsevier; 1987. [Google Scholar]
- 42.Harper KC, Bess EN, Sigman MS. Nat Chem. 2012;4:366. doi: 10.1038/nchem.1297. [DOI] [PubMed] [Google Scholar]
- 43.Verloop A. In: Drug Design. Ariens EJ, editor. Vol. 3. Vol. 133. Academic Press; 1976. [Google Scholar]
-
44.Vectors B1 and B5 describe an ellipse in the plane of the CpX ring.;
- 45.(a) Presset M, Oehlrich D, Rombouts F, Molander GA. Org Lett. 2013;15:1528. doi: 10.1021/ol400307d. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Webb NJ, Marsden SP, Raw SA. Org Lett. 2014;16:4718. doi: 10.1021/ol502095z. [DOI] [PubMed] [Google Scholar]; For asymmetric reactions, see:; (c) Hyster TK, Knorr L, Ward TR, Rovis T. Science. 2012;338:500. doi: 10.1126/science.1226132. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Ye B, Cramer N. Science. 2012;338:504. doi: 10.1126/science.1226938. [DOI] [PubMed] [Google Scholar]
- 46.(a) Hyster TK, Rovis T. Synlett. 2013:1842. doi: 10.1055/s-0033-1339510. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Semakul N, Jackson KE, Paton RS, Rovis T. Chem Sci. 2017 doi: 10.1039/C6SC02587K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rh12 is a superior catalyst to the previously reported Rh22 (ref 46b)
- 48.Hammett LP. Chem Rev. 1935;17:125. [Google Scholar]
- 49.A Q2 value that is close to R2 value indicates a good predictive capability of a model.
- 50.By using eq. 8 and with the same caveats discussed above, the electronic contribution to diastereoselectivity is estimated at 91%.
- 51.Regression models built to describe the regioselectivity of 1-decene insertion display no outliers with all three training sets (T1, T2, and T3) employed, see Supporting Information for more details.
- 52.Peng Q, Duarte F, Paton RS. Chem Soc Rev. 2016;45:6093. doi: 10.1039/c6cs00573j. [DOI] [PubMed] [Google Scholar]
- 53.By using the normalized coefficients and eq. 8 and considering the caveats discussed above, the electronic contribution to rate is estimated at 81%.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


