Abstract
Robotic needle steering systems have the potential to greatly improve medical interventions, but they require new methods for medical image guidance. Three-dimensional (3-D) ultrasound is a widely available, low-cost imaging modality that may be used to provide real-time feedback to needle steering robots. Unfortunately, the poor visibility of steerable needles in standard grayscale ultrasound makes automatic segmentation of the needles impractical. A new imaging approach is proposed, in which high-frequency vibration of a steerable needle makes it visible in ultrasound Doppler images. Experiments demonstrate that segmentation from this Doppler data is accurate to within 1–2 mm. An image-guided control algorithm that incorporates the segmentation data as feedback is also described. In experimental tests in ex vivo bovine liver tissue, a robotic needle steering system implementing this control scheme was able to consistently steer a needle tip to a simulated target with an average error of 1.57 mm. Implementation of 3-D ultrasound-guided needle steering in biological tissue represents a significant step toward the clinical application of robotic needle steering.
Index Terms: Image-guided intervention, robotic needle steering, ultrasound doppler, ultrasound imaging
I. Introduction
PERCUTANEOUS interventions involving the insertion of needles to anatomic targets within the body are applied in the diagnosis and treatment of many diseases. We will describe the treatment of liver cancer, our intended application. Percutaneous radiofrequency ablation (RFA) is a common treatment option for liver cancer patients who are not eligible for resection or transplantation. In this procedure, long electrodes are inserted through the skin into the liver, and used to ablate cancerous tissue. Current percutaneous RFA of liver cancer suffers from significant limitations [1]. Straight electrodes are unable to reach tumors in some portions of the liver because they are blocked by vasculature, lung, or other sensitive structures. Large tumors require multiple electrode insertions, with each puncture through the liver capsule increasing the risk of hemorrhage. This increased risk can make patients with advanced liver disease or severe comorbidities ineligible for the RFA procedure. Successful treatment requires a margin of cancer-free tissue to be ablated around the tumor, in order to reduce the likelihood of recurrence [2]. For medium to large tumors, developing a sufficient ablative margin is highly dependent on the clinician’s ability to locate the electrode tip over multiple passes using medical imaging for guidance [3]. Similar limitations also affect other percutaneous procedures, such as biopsy and brachytherapy, and treatment of diseases other than liver cancer.
Robotic needle steering enables the insertion of flexible needles along controlled, curved, three-dimensional (3-D) paths through tissue [4], [5]. Robotic needle steering offers the potential to improve percutaneous interventions with both long and short needle steering paths. Long needle steering paths can allow RFA electrodes to reach around sensitive structures to previously unattainable targets, and to reach multiple tumors across the liver with a single capsule wound. Short needle steering paths can allow percutaneous RFA to be safely applied to larger tumors than previously possible, by creating precise ablations of arbitrary shape. In this paper, our methods are inspired by the second, ablation-shaping application. Steering through a larger workspace within the liver will require further development and integration of path planning and control algorithms.
Multiple methods for achieving needle steering have been developed, including manipulation of the needle base [4], [6], external manipulation of the surrounding tissue [7], and control of precurved, overlapping cannula sections [8]. In this study, we focus on bent-tip needle steering. As depicted in Fig. 1, a flexible needle with a bent tip will naturally curve when inserted into tissue, as a result of the lateral force acting on the needle tip. By axially rotating the needle shaft, a robotic system can select the direction of curvature, and thus steer a flexible needle through a 3-D workspace. These flexible steerable needles can also be inserted along approximately straight paths by rotating the needle at a relatively high rate during insertion. A duty-cycle approach [9], which combines intervals of pure insertion with intervals of rotation, can generate a range of curvatures.
Fig. 1.
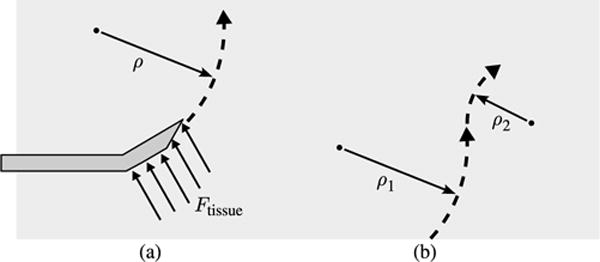
Bent-tip needle steering: (a) As a flexible needle with a bent tip is inserted into solid tissue, the lateral forces acting at the tip cause it to follow a curved path through the tissue. (b) Through a duty-cycle approach that combines rotation and insertion, the radius of curvature of needle insertion paths can be varied during steering.
While robotic needle steering systems and algorithms have been discussed extensively in the literature, progression toward in vivo tests and patient studies has been limited [10]. One major obstacle, and the focus of this paper, is the integration of medical imaging systems that can provide real-time feedback of needle pose to robotic systems when steering in biological tissues.
II. Prior Work
A. Control of Steerable Needles
There is significant prior art relevant to image-guided control of needle steering, both for bent-tip steerable needles and other approaches. DiMaio and Salcudean formulated rigid needle insertion as a trajectory planning and control problem, defining a needle manipulation Jacobian for base control [4]. Glozman and Shoham [6] and Neubach and Shoham [11] used inverse kinematics to control base-manipulation needle steering, with X-ray and ultrasound image feedback, respectively. Ko and Rodriguez y Baena used a model predictive control algorithm for trajectoryfollowing control of a bioinspired actuated flexible needle [12]. For bent-tip steering, a number of control approaches have been described based on a nonholonomic model of steerable needle motion in tissue [5]. Reed et al. demonstrated image-guided needle steering in a planar workspace [13], by combining a planar motion planner [14], an image-guided controller [15], and a torsion compensator [16]. Wood et al. formulated trajectory tracking controllers based on duty cycling for 2-D [9] and 3-D [17] trajectories. Bernardes et al. combined closed-loop image feedback with intraoperative replanning to deal with obstacles and dynamic workspaces [18]. Rucker et al. [19] used a sliding mode controller with feedback from an electromagnetic tracking system. This control scheme has the advantage that it does not require any prior knowledge of needle curvature. Recently, Abayazid et al. demonstrated bent-tip needle control in gelatin and chicken breast using a robotically controlled ultrasound transducer to track the tip [20].
Without methods for imaging needles in biological tissues, experimental validation of many of these methods has been limited to 2-D workspaces in transparent artificial tissues such as agar or polyvinyl chloride rubber, with optical cameras used to simulate medical imaging. These artificial tissues provide only limited validation, as their mechanical properties are significantly different from biological tissues [21]. Although some studies have applied more realistic medical imaging methods [6], [11], [20], ultrasound imaging has only been applied in tightly controlled experimental conditions, yielding best-case needle visibility.
B. Segmentation of Needles From Ultrasound Images
Computed tomography (CT) imaging, magnetic resonance (MR) imaging, and X-ray imaging could all potentially be applied to intraoperative guidance of steerable needles, but each of these modalities has significant drawbacks. Our work uses 3-D ultrasound because of its many advantages. Ultrasound systems image in real time, do not produce ionizing radiation, and are not strongly affected by the presence of metal objects such as needles. Perhaps most importantly, ultrasound systems are inexpensive and portable, and are already standard equipment in existing operating rooms and treatment suites.
Ultrasound does have disadvantages, such as low signal-to-noise ratio and poor image resolution compared to MR or CT. When imaging needles, ultrasound image quality is highly dependent on the angle between the ultrasound imaging plane and the needle. At some angles, significant reverberation artifacts generated by the highly reflective needle surfaces may appear. At other angles, the needle may not be visible at all, as the reflected waves may be dispersed away from the transducer [22]. Even when the needle can be identified, various imaging artifacts can make it difficult to locate the tip of the needle along its axis.
A large amount of prior art exists on the automatic segmentation of needles from B-mode (grayscale) ultrasound data, with much of it focused on segmenting straight needles using a variant of the Hough transform. Although the Hough transform is computationally intensive, real-time segmentation of straight needles has been demonstrated using variations on the algorithm, including dual-plane projections [23], coarse-fine sampling [24], [25], and parallel implementation on a graphics processing unit [26]. Other similar algorithms, such as the parallel integral projection transform, have also been applied [27]. Similar methods have been described for segmenting curved needles. Slightly curved needles can be segmented using a standard Hough transform method [28], [29], while more strongly curved needles can be segmented by including a parametrization of needle bending [28], [30], [31].
The underlying issue that makes automatic needle segmentation a difficult problem is the poor visibility of needles in standard B-mode ultrasound data. Several of the described methods have shown promising results in favorable conditions. However, image-guided robotic needle steering requires segmentation algorithms that can process large 3-D datasets containing highly curved, extremely thin (e.g., 0.5-mm diameter) needles at undesirable orientations relative to the transducer. Rather than contribute a new algorithm that attempts to overcome these challenges, our aim in this study was to reduce the complexity of the segmentation task, by leveraging the needle steering robot to produce ultrasound image data that more clearly reveal the needle.
C. Doppler-Based Segmentation
Ultrasound Doppler is a diagnostic technique that measures frequency shifts in reflected ultrasonic waves that result from motion. Color and power Doppler imaging, which are available on most modern ultrasound systems, are commonly applied to overlay blood flow data on B-mode ultrasound. Vibrating solid objects have also been shown to produce recognizable Doppler signals [32]. This concept has been applied to localize straight needles [33]–[35] and needle tips [36] in 2-D ultrasound, as well as instruments in cardiac interventions [37], [38] and other applications [39], [40]. This technique has not previously been applied to segment highly curved needles.
In our segmentation method, low-amplitude high-frequency vibration is applied to a steerable needle using an actuator located outside the tissue, and the resulting motion along the length of the needle is detected using power Doppler ultrasound imaging as depicted in Fig. 2. In an initial feasibility study [41], we found that our segmentation method was within 1–2 mm of manual segmentation from B-mode data. In that early work, piezoelectric diaphragms were spot welded to stainless steel wires, and used to generate vibration as a proof of concept. In this paper, we describe the design and validation of a new needle steering robot, with an integrated voice coil actuator that clips to the steerable needle and vibrates it during insertion. We also describe a needle control algorithm that incorporates this new segmentation method to allow closed-loop control of steerable needles in simulated tasks. Since our imaging and control methods are not constrained to translucent tissue simulants or 2-D needle paths, we are able to perform validation tests for 3-D needle steering in ex vivo animal tissues.
Fig. 2.
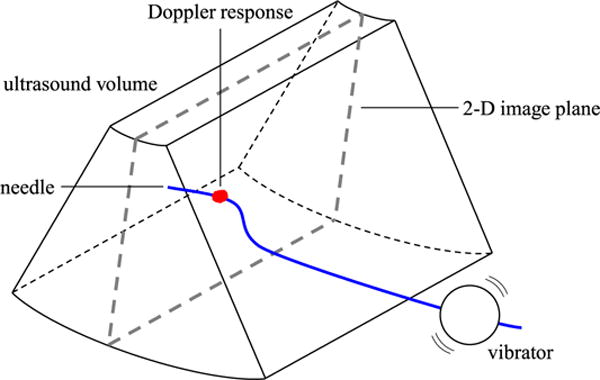
Needle segmentation concept. A voice coil actuator (vibrator) vibrates the needle, resulting in a Doppler response around the needle cross section in a 2-D ultrasound image. The needle is segmented by localizing the Doppler response across the sweep of a mechanical 3-D ultrasound transducer, and fitting a curve through the resulting points.
III. 3-D Ultrasound-Guided Needle Steering
Fig. 3 shows a block diagram of our closed-loop control algorithm for ultrasound guidance of needle steering. The goal of the closed-loop system is to steer the needle tip toward a target point t defined in the ultrasound coordinate system. In the following sections, our segmentation algorithm, steering planner, and robot controller will be described in detail.
Fig. 3.
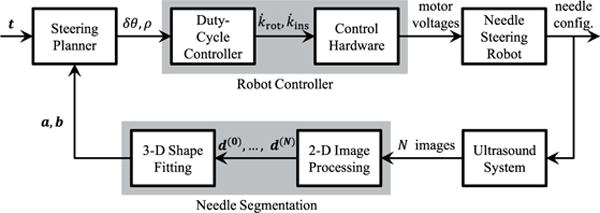
Block diagram of closed-loop control in ultrasound-guided needle steering. Automatic segmentation of the needle from 3-D ultrasound data provides feedback of needle configuration to a steering planner, which identifies the needle rotation and curvature necessary to reach a target point. A duty-cycle controller generates the velocity commands that allow motor control hardware to move the needle tip along the desired path to the target.
A. Needle Segmentation
Throughout the description of our algorithm, we will assume that the needle is oriented roughly orthogonal to the imaging plane of a mechanical 3-D ultrasound transducer, as depicted in Fig. 2. An actuator is used to vibrate the needle, and the resulting motion of the needle and surrounding tissue produces a Doppler signal across the series of N Doppler images generated by the ultrasound system. Segmentation proceeds in two stages, as depicted in Fig. 4. First, the cross section of the needle is localized in each image through 2-D image processing. Second, the 3-D shape of the needle is reconstructed by fitting a curve to the series of points.
Fig. 4.
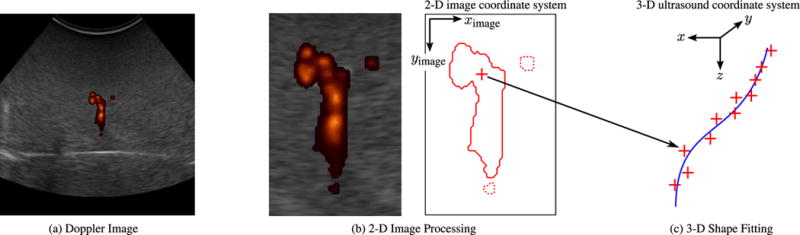
Segmentation algorithm: (a) Doppler image. A 2-D ultrasound Doppler image from a series of N captured over a sweep of the imaging plane. (b) 2-D image processing. Doppler patches with fewer than 300 connected pixels are assumed to be noise and discarded (dotted lines). The remaining Doppler data (solid line) are used to estimate the position of the needle cross section (cross). In the lateral (ximage) direction, the position is estimated as the centroid of the Doppler response. In the axial (yimage) direction, the position is estimated as the lower bound of the region that contains one quarter of the integrated Doppler intensity. (c) 3-D shape fitting. The 2-D-localized points are combined in 3-D based on position information from the 3-D ultrasound transducer. Third-order polynomial curves are fit to the identified points in order to define the needle’s 3-D shape over the series of N images.
1) 2-D Image Processing
To remove Doppler noise, patches with less than 300 connected pixels are removed. (For comparison, the Doppler patch centered around the needle typically has a connected area of 1000–2000 pixels.) After this preprocessing step, the image coordinates of the needle cross section are estimated based on the remaining Doppler response. As seen in the example image in Fig. 4, the Doppler response from the vibration generally appears as an irregular, roughly circular patch centered on the needle, with a color comet tail artifact in the axial (yimage) direction [42]. The lateral (ximage) coordinate of the needle is, thus, estimated as the centroid of the Doppler response. To account for the color comet tail, the axial image coordinate of the needle is estimated as the point that separates one-quarter of the integral of the Doppler response above, and three-quarters below. These fractions were selected empirically based on the results of our feasibility study [41].
We define the x, y, and z directions of the 3-D ultrasound coordinate system to be in the lateral, axial, and elevational directions, respectively. Based on the geometry of the ultrasound transducer, the needle points are mapped from the 2D image coordinate system to the 3-D ultrasound coordinate system, yielding the set of N needle points d(0), …, d(N). Each holds the x-y-z coordinates of detected needle point i.
2) 3-D Shape Fitting
Based on the Doppler points identified in the previous step, we resolve the shape of the needle by defining the x and y coordinates as functions of the z coordinate over the range of d(0), …, d(N). In this study, we use third-order polynomial functions
| (1) |
and solve for the vectors of polynomial coefficients that minimize the sum of the squared error over the measured Doppler points. We selected this curve type because a third-order polynomial was sufficient to represent the range of curved needle paths we considered in this study. Additionally, low-order polynomials have the advantage that they average out noise in the 2-D Doppler points, which is important in our method. Longer, more tortuous paths would require more sophisticated curves, possibly segmented polynomials constrained to be tangent at transition points.
B. Steering Planner
The steering planner interprets the segmentation results in order to estimate the pose of the needle tip, described by a needle tip frame. The steering planner then identifies a path from the tip position to the target point. The radius of the path ρ and the incremental needle rotation δθ needed to follow the path are output to the robot controller, which drives the motors of the needle steering robot.
1) Estimating Tip Frame
We define the needle tip frame as shown in Fig. 5. The origin of the tip frame is located at point p, which is the distal end of the needle. For simplicity, we ignore the local geometry of the bent tip. The tip frame is oriented with the ztip-axis tangent to the needle at p, and the ytip-axis pointing in the direction of curvature. The center of curvature for the circular needle path c lies on the ytip-axis, at a distance ρ from p. In our model, rotating the base of the needle by δθ causes the needle tip frame to rotate by δθ about the ztip-axis, while inserting the needle causes the tip point p to move along a circular path of radius ρ.
Fig. 5.
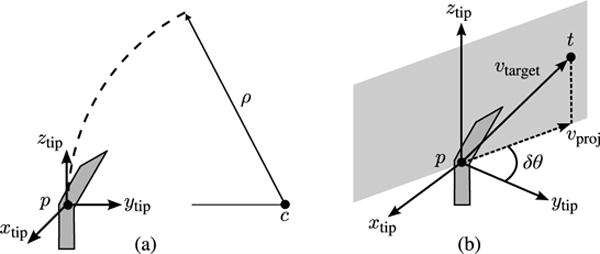
Steering planner: (a) The needle tip frame is located at the distal end of the needle. The frame is oriented with the ztip-axis tangent to the needle, and the ytip -axis pointing toward the center of curvature. The needle follows a circular path of radius ρ. (b) The steering planner determines the incremental rotation δθ and the path radius ρ that will cause the needle tip p to reach the target point t.
Based on the segmentation result, the tip point p is identified using the z-coordinate of the most distal Doppler point and the polynomial curve functions
| (2) |
While it should also be possible to estimate the tip frame orientation based on the needle segmentation result, for example, by fitting a circular arc to a curved section of the 3-D segmentation result to define the steering direction, we have found that in the current implementation the Doppler segmentation results are too noisy to allow reliable estimation of the tip frame orientation. Instead, we apply a small angle approximation, and assume that the ztip-axis remains close to the z-axis of the 3-D ultrasound coordinate system throughout steering. The orientation of the tip frame can, thus, be specified completely by a rotation of θ about the z-axis. We make rotation angle θ a system variable, and update it after each iteration of the steering planner
| (3) |
This approach ignores torsional deflection of the steerable needle as result of friction between the needle and tissue. While substantial torsional deflection has been demonstrated in artificial tissues, in biological tissues the needle tip rotation has been shown to follow the base rotation to within a few degrees [16].
2) Path Planning
At each iteration, the steering planner identifies the simplest possible path to the target point t based on the estimated tip pose. As shown in Fig. 5, this path is the circular arc that is tangent to the estimated ztip-axis, and passes through t. Unlike other needle control approaches described in Section II [19], [20], our replanning approach does not attempt to minimize total needle rotation, and requires an estimate of maximum needle curvature. However, it is sufficient to demonstrate accurate closed-loop steering for small paths.
C. Robot Controller
The robot controller consists of two components. A duty-cycle controller generates motor velocity commands based on the desired needle rotation and curvature as output by the steering planner. Motor control hardware drives the motors of the needle steering robot based on the velocity commands.
1) Duty-Cycle Controller
The goal of the duty-cycle controller is to determine the desired velocities for the rotation and insertion stages, and . It is first necessary to calculate the duty-cycle fraction, DC, based on the desired radius of curvature. Assuming a known minimum radius of curvature for the specific needle-tissue pair, DC can be calculated as
| (4) |
The insertion velocity is set to a constant value during steering. To achieve the duty-cycle effect, the rotation stage alternates between constant velocity and zero velocity with the needle held at angle θ. The ratio of time spent rotating (Trot) to time holding at angle θ (Thold) is determined from the duty-cycle ratio DC
| (5) |
Rotation time Trot is constant and equal to the time required to complete a full rotation. Hold time Thold is, thus, varied to achieve the desired ratio DC.
2) Control Hardware
There are many possible hardware implementations that could be used to drive the motors of the needle steering robot. In the system we use for experimental validation in Section IV, the rotation and insertion motors are each driven by integrated motion control systems. These systems accept velocity commands (i.e., , ) and drive the motors using proportional-integral (PI) control. In our system, PI control constants were tuned using manufacturer supplied software.
IV. Experimental Validation
In this section, we describe experimental validation of our algorithms for closed-loop 3-D ultrasound-guided needle steering.
A. Apparatus
1) Ultrasound Imaging
A SonixMDP ultrasound console (Ultrasonix Medical Corp., Richmond, BC, Canada) with a convex mechanical 3-D transducer (4DC7-3/40) was used for imaging. Custom software incorporating the Ultrasonix research SDK package was used to control imaging parameters and capture images. Power Doppler imaging mode was selected over color Doppler imaging because of the lack of aliasing and reduced sensitivity to imaging angle. Pulse repetition frequency (PRF) was set to 1428 Hz, as this setting yielded the best results in our initial feasibility study [41]. Wall motion filter was set to maximum in order to minimize Doppler artifacts resulting from the motion of the imaging plane. Each sweep consisted of 61 scan-converted 2-D images, captured at angular increments of approximately 0.7°.
2) Needle Steering Robot
Fig. 6 shows the needle steering robot used to validate our control method. Similar to previously described needle steering robots [43], our system has two active degrees of freedom (DOF) that control needle insertion and needle rotation. Unlike previous needle steering robots, our system incorporates a vibration module that generates the high-frequency motion necessary to visualize the needle using ultrasound Doppler.
Fig. 6.
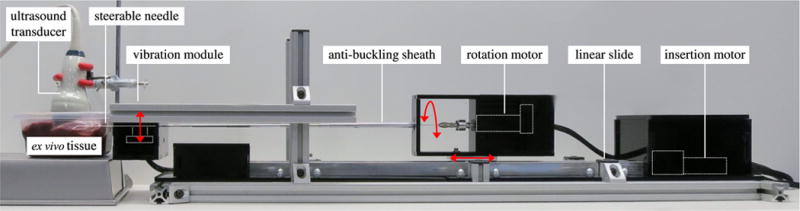
Experimental setup. Needle steering robot consisting of actuated linear slide, rotation stage, and vibration module (red arrows indicate actuation); ex vivo bovine liver tissue; 3-D ultrasound transducer.
The rotational DOF is actuated by a geared DC motor (A-max 22-110160; Maxon Motor, Sachseln, Switzerland) that is connected directly to the needle through a pin-vise clamp. The insertion DOF is actuated by a DC motor (GM9234S016; Ametek, Berwyn, PA, USA) that drives a linear slide (SPMA2524W4; VelMex, Bloomfield, NY, USA). Both the rotation DOF and insertion DOF are driven by integrated motion controllers (MCDC3006S; Faulhaber, Schnaich, Germany). The vibration module, shown in Fig. 7, consists of a voice coil actuator (HIAX19C01-8; HiWave, Little Gransden, U.K.) that is driven by a transistor circuit at a user-variable frequency of 400, 600 or 800 Hz. These frequencies are roughly centered around the peak output point of the voice coil actuator and, thus, produce the strongest responses in the power Doppler image data. To produce the maximum vibration along the needle, the vibration module was designed to be as close as possible to the target tissue, and is attached to the distal end of the needle steering robot. The needle is mated to the actuator using a 3-D-printed plastic clip.
Fig. 7.

Vibration module. A voice coil actuator is attached to the steerable needle using a 3-D-printed clip, and used to vibrate the needle vertically (in and out of the page).
3) Needles
Solid Nitinol wires 0.38 mm (0.015 inches), 0.48 mm (0.019 inches) and 0.58 mm (0.023 inches) in diameter were used as needles. The needles had 45° beveled tips and 4.5-mm distal sections bent 35° off axis.
4) Tissue Simulant
Ex vivo bovine liver tissue obtained fresh from a local butcher was used as the tissue simulant in all testing.
B. Segmentation Accuracy
As mentioned in Section II, we previously described a feasibility study in which we measured the accuracy of our Doppler segmentation method using piezoelectric elements welded to stainless steel wires [41]. In that study, we examined the sensitivity of the method to tissue composition, vibration frequency, and Doppler PRF, and found that only PRF greatly affected the accuracy of segmentation. Based on comparison with manual segmentation, we found the average error to be 1–2 mm acrossmost conditions.
In this study, we evaluated the accuracy of segmentation when using a needle steering robot with an integrated actuator to vibrate flexible Nitinol needles. We again considered the impact of vibration frequency, although at a lower range than our previous experiment because of the lower center frequency of the voice coil actuator compared to the previous piezoelectric actuator. We also considered the impact of needle curvature, needle diameter, and position of the needle in the lateral image direction. Two needle curvatures (straight and maximum curvature), two lateral positions (image center and lateral edge), three needle diameters (0.38, 0.48, and 0.58 mm), and three vibration frequencies (400, 600, and 800 Hz) were tested. Each parameter was varied individually around the base case of a straight, 0.48-mm needle centered in the image and vibrated at 600 Hz.
Three separate insertions and scans were performed for each test condition. Segmentation accuracy was evaluated by comparison with a reference manual segmentation of the needle from B-mode data, within the native image planes of the 3-D ultrasound transducer. To create the reference data, the center of the needle was manually selected in each 2-D B-mode image in which it was visible. The needle was visible in approximately 50% of the B-mode images captured over most sweeps.
Given K manually selected needle points m(0),…, m(K), we defined the segmentation error for the ith point
| (6) |
For this segmentation accuracy testing, the Doppler segmentation method and the reference manual segmentation were both implemented in MATLAB.
The precision of the reference data was quantified by measuring variability between repeated manual segmentations of the same B-mode volumes. Although this does not measure the absolute accuracy of the reference data, it provides an indication of manual segmentation error. Across four repeated segmentations each for eight needle scans (four of straight needles and four of curved needles), the standard distance deviation
| (7) |
was calculated, where is the distance in the image plane between the ith manually selected needle point and the corresponding mean center, and M is the total number of comparison points. With M = 684 data points, we found the standard distance deviation for the manual segmentation to be Sxy = 0.23 mm.
C. Closed-Loop Steering
We validated the needle segmentation algorithm and steering controller in a series of needle steering tests. The algorithms described above were implemented in C++ using the ITK and VTK libraries [44] for image analysis. Six insertion tests were performed, using 0.48-mm needles with bent tips as described above. In each test, a brachytherapy sheath was used to insert a cylindrical stainless steel bead into a liver tissue specimen, in order to generate a target. The beads were 3 mm in diameter and 5 mm long, and were oriented for maximum visibility in the 3-D B-mode images (i.e., with the long axis of the beads approximately perpendicular to the axial direction of the ultrasound) to enable the manual reference segmentation. The 3-D ultrasound transducer was applied to the tissue and oriented so that the target was near the boundary of the ultrasound volume in the z (elevational) direction. The steerable needle was then inserted until it was just visible at the opposite end of the ultrasound volume. The initial position of the steerable needle tip p relative to the target t was varied within a rectangular workspace with approximate dimensions of 20 × 20 × 30 mm. This workspace is representative of ablation shaping for medium-sized liver tumors (between 30 and 50 mm in diameter) using a single RF electrode, assuming a rigid needle or other introducer was used to initially place the steerable needle near the target. The dimensions of the needle steering path for each closed-loop steering test are listed in Section V. The initial orientation of the steerable needle tip was such that the tip frame was aligned with the ultrasound coordinate system (i.e., θ = 0°). After these initial insertion steps, a 3-D ultrasound volume was captured, and the bead was manually segmented to yield the position of the target in the 3-D ultrasound frame. Point t was placed on the surface of the bead closest to the starting position of the needle tip. The needle was then automatically steered toward the target until the system detected that the needle tip had reached the target depth in the z direction, at which point insertion was stopped. Targeting error was measured as the 3-D distance between the target point t and the needle tip p at the end of the test.
In this study, the control algorithm depicted in Fig. 3 was implemented in discrete increments. The control inputs of rotation and duty cycle were held constant over increments of insertion. At the end of each increment, insertion was stopped, and the needle was vibrated, scanned, and segmented automatically. The steering controller was then applied to determine the rotation and duty-cycle inputs for the following increment. Relatively large 5-mm insertion increments were selected for testing to reduce deformation of the tissue due to needle stiction. Insertion velocity was set to yield a linear needle insertion rate of 100 mm/min. Maximum rotation velocity was set to yield a rotary needle velocity of 60 RPM.
Minimum radius of curvature ρmin for the 0.48-mm needle in ex vivo bovine liver tissue was measured in a separate initial experiment. The steerable needle was inserted into the liver without rotation, scanned and segmented, and a circular arc was fit to the segmentation results. Over four repetitions, the average radius of curvature was found to be 51.4 mm, which is within the range of curvature values previously reported in ex vivo tissue [10]. This was the value of ρmin used by the steering planner to calculate the duty cycle ratio DC based on the desired radius of curvature.
V. Results and Discussion
Fig. 8 shows example 2-D ultrasound images taken from volumetric sweeps of steerable needles in ex vivo liver. Both B-mode and power Doppler images are shown. The needle cross section was visible in approximately 50% of the B-mode images captured over most sweeps. As shown in the figure, the high-frequency vibration of the needle causes a power Doppler response centered around the needle cross section.
Fig. 8.
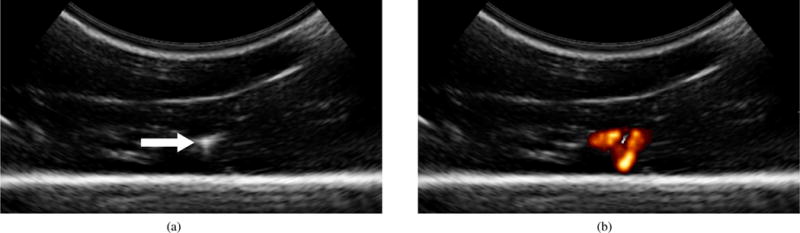
Two-dimensional ultrasound images taken from volumetric sweeps of steerable needles inserted into ex vivo liver: (a) B-mode ultrasound image used for manual segmentation. The needle cross section is indicated. (b) Corresponding power Doppler ultrasound image captured during needle vibration. The Doppler response surrounds the needle cross section.
Fig. 9 shows the 3-D Doppler data generated by a vibrating needle, along with the corresponding Doppler centroids and the best-fit polynomial curve. Volumetric frame rate using the SonixMDP system was 0.2 Hz for power Doppler data at an imaging depth of 50 mm. Software run-times were approximately 60 ms per image for the 2-D image processing algorithm and 15 ms per sweep for the steering planner, when implemented on the SonixMDP’s integrated processor.
Fig. 9.
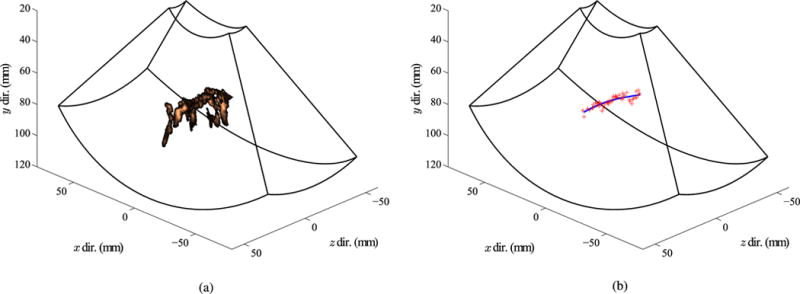
Example segmentation of needle using Doppler method: (a) Power Doppler response around the needle in each image. (b) Reconstructed needle shape (blue curve), fit through the centroids of the Doppler data in each image (red crosses).
A. Segmentation Accuracy
Fig. 10 summarizes the results of the segmentation accuracy tests. Across all tests, the maximum segmentation error was 3.18 mm, the minimum segmentation error was 0.13 mm, the mean segmentation error was 1.24 mm, and the standard deviation of the segmentation error was 0.57 mm. In the base case tests (straight, 0.48-mm needle centered in the image and vibrated at 600 Hz), the mean segmentation error was 0.92 mm and the standard deviation of the segmentation error was 0.93 mm.
Fig. 10.
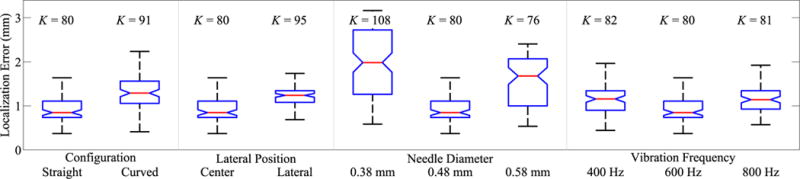
Segmentation accuracy results. Two needle configurations (straight, curved), two image positions (center, lateral), three needle diameters (0.38, 0.48, 0.58 mm), and three vibration frequencies (400, 600, 800 Hz) were tested. For each group, red line indicates median error, blue box indicates 25th and 75th percentile, and whiskers indicate minimum and maximum error. Number of data points for each group is also indicated.
In the needle curvature test, curved and straight needles had similar segmentation errors, with somewhat higher errors in the curved configuration. The mean error was 0.85 mm for straight needles, and 1.36 mm for curved needles. We conclude that for transducers initially oriented as shown in Fig. 2, our segmentation method is suitable for the range of needle geometries that can be achieved by bent-tip steering in biological tissue (with ρmin ≈ 50 mm). The current implementation does fail if the steerable needle is exactly parallel to the imaging plane, thus presenting a linear rather than circular cross section. However, this can be avoided by placing the 3-D transducer so the needle is initially approximately perpendicular to the imaging plane. Applying the Doppler segmentation technique without constraint on the transducer orientation, or with other 3-D ultrasound implementations—such as freehand tracked 3-D ultrasound—might require modification of the image analysis method.
Needle diameter had a significant effect on segmentation accuracy. Mean error was 0.85 mm for 0.48-mm needles, versus 1.98 mm for 0.38-mm needles, and 1.68 mm for 0.58-mm needles. The significant change in mean error for the 0.48-mm needles is surprising given the relatively small change in needle diameter. The complexity of the wave mechanics that govern the transmission of vibrations along a flexible needle in viscous tissue makes it difficult to theorize why needle diameter appears to be an important factor. This issue is worthy of future study for two reasons. First, because improved understanding of the motion around the vibrating needle might allow for new Doppler processing algorithms that specifically target the generated motion. Second, because specific needle geometries may be required for other clinical applications (for example, brachytherapy systems would likely require hollow needles).
Lateral image position and vibration frequency did not have significant impacts on segmentation accuracy. In the lateral position test, the mean error was 0.85 mm for needles centered in the image, and 1.24 mm for needles on the lateral edge. In the vibration frequency test, the mean error was 1.16 mm for 400-Hz vibration, 0.85 mm for 600-Hz vibration, and 1.14 mm for 800-Hz vibration. In the case of vibration frequency, the insensitivity is in agreement with our previous study [41], where varying vibration frequency over a much larger range did not significantly affect segmentation accuracy.
B. Closed-Loop Steering
Table I lists results from six successful closed-loop needle steering tests. For each test, the number of insertion increments (Ninc), the x-y-z dimensions of the complete needle steering path (δx, δy, and δz), and the final error in tip placement relative to the target (efinal) are listed. Mean tip placement error was 1.57 mm over the six tests, which is close to the mean error in Fig. 10 for that configuration.
TABLE I.
Closed-Loop Needle Steering Results
| Test | Ninc | δx (mm) | δy (mm) | δz (mm) | efinal (mm) |
|---|---|---|---|---|---|
| 1 | 6 | 1.99 | 10.74 | 29.09 | 1.57 |
| 2 | 7 | 8.42 | 7.15 | 29.16 | 1.73 |
| 3 | 6 | 7.81 | 2.63 | 31.44 | 1.27 |
| 4 | 6 | 8.04 | 6.81 | 31.78 | 2.08 |
| 5 | 6 | 1.75 | 5.06 | 26.46 | 1.89 |
| 6 | 6 | 6.13 | 3.83 | 32.26 | 0.86 |
Fig. 11 shows the needle shapes reconstructed during incremental closed-loop steering in Test 6. The ytip-axis was initially aligned with the y-axis of the ultrasound coordinate system. After Scan 1, the steering planner compensated by rotating the ytip-axis toward the target (δθ = −58.7°). The steering planner gave smaller corrections based on Scans 2 to 5, as a result of deviation from the steering model and noise in the measurement of point p. After Scan 6, when the needle tip was within several millimeters of the target, the steering planner output a large unnecessary rotation correction (δθ = −97.7°), but over such a small distance it had little effect. Final tip placement error efinal was 0.86 mm for this test.
Fig. 11.
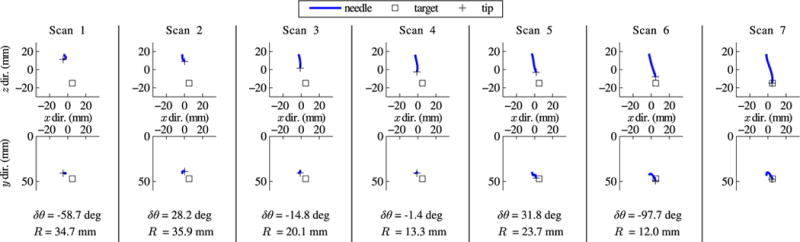
Closed-loop needle steering results. Orthogonal views of successive incremental scans during needle steering in ex vivo tissue, with the output from the steering planner after each scan below. The needle base was inserted 5 mm between each scan, with rotation and duty cycle determined by the steering planner. Error in placing the tip at the target bead was 0.86 mm after the final insertion.
In addition to the six tests listed in Table I, there were several tests that failed as a result of poor needle steering behavior. Bent-tip needle steering requires a homogeneous solid medium. If the steerable needle tip impacts an obstacle which it does not pierce through, such as a bone or blood vessel, the path of the needle may deviate greatly from what is expected. Fig. 12(a) shows the reconstructed needle shapes from one such failed test. In this test, the needle appeared to impact one of several small vessels that could be visualized in ultrasound before the final scan. Fig. 12(b) shows examples of these small vessels in a section of liver specimen.
Fig. 12.
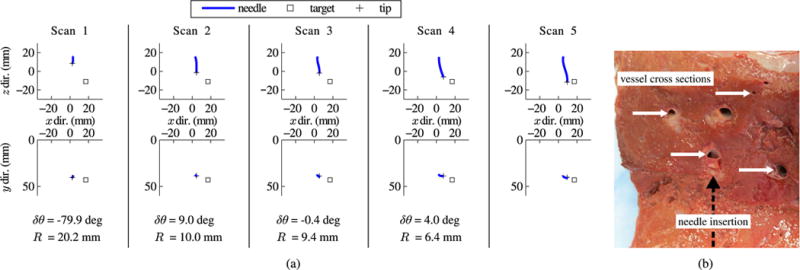
Closed-loop needle steering results. Example of failed needle steering: (a) Orthogonal views of successive incremental scans during needle steering in ex vivo tissue, with the output from the steering planner after each scan below. The needle base was inserted 5 mm between each scan, with rotational orientation and duty-cycle setting determined by the steering planner outputs. Error in placing the tip at the target bead was 8.14 mm after the final insertion. The needle failed to reach the target due to interference from internal vessels that could be visualized in the ultrasound images. (b) Section of tissue sample with example vessels and approximate direction of needle insertion indicated.
C. Discussion
The implementations we have described are capable of segmenting a curved needle with average error of 1–2 mm, and steering a needle to a target with an average error of 1.57 mm. This is roughly equivalent to manual targeting error with medical image guidance, which has been shown to be 2 mm or higher on average [45]–[47]. Studies on percutaneous RFA of liver cancer generally suggest that an ablative margin of 5–10 mm around a tumor is necessary to prevent recurrence of cancer [1]–[3]. However, recent work has reported that ablative margins as small as 3 mm are associated with a lower rate of local tumor progression [48]. This suggests that a targeting error of 2 mm may be tolerable. Overall, the experimental results described in this paper show that our segmentation and control algorithms approach the accuracy and consistency necessary for a practical clinical application such as RFA of liver cancer. Still, there are several areas for improvement.
So far, we have applied our segmentation and control algorithms to sequences of incremental insertions, rather than to constant velocity insertions. A delay of several seconds after each incremental insertion would be undesirable in a clinical setting, although perhaps not prohibitive. In our current experimental setting, we were limited by the capture rate of our 3-D Doppler system. (Doppler imaging frame rates are generally slower than B-mode imaging frame rates.) There are promising options for improving the speed of both the image capture and image processing. For example, since our segmentation algorithm can be applied to the raw 2-D images, each individual frame of data could be processed immediately upon capture by the sweeping ultrasound array, rather than after capturing a complete volume. This would allow image capture and segmentation to take place concurrently, greatly reducing overall imaging time.
Continuous 3-D ultrasound-guided steering using our method would also require continuous vibration of the needle for the Doppler segmentation. This raises the issue of the effect of vibration on steering. While we expect the impact to be small based on the magnitude of the vibration (the estimated amplitude of vibration was less than 0.5 mm), the mechanical interaction between the needle and deformable biological tissue is complex and may be sensitive to this perturbation. Although initial anecdotal testing has not revealed any impact, these issues require further study.
Apart from increasing the speed of image capture and segmentation, there are several other directions for improving the Doppler segmentation method. Information on mechanical properties of the needle, such as minimum bending radius, could be used to improve the initial 2-D segmentation, for example by limiting the search region for the needle cross section based on the maximum possible needle curvature. Combining data from multiple ultrasound scan modes (e.g., Doppler data, B-mode data, RF scanline data, and elastography data) could also potentially improve the accuracy and consistency of segmentation.
In our current implementation, the orientation of the tip frame is derived from segmentation results using a small angle approximation. While this approximation is reasonable for the range of needle steering paths described in Section V.B, which are representative of ablation shaping around a tumor, the approximation would fail for longer paths steering through a large workspace in the liver. For this application, we plan to implement an unscented Kalman filter or other similar estimation scheme. This will allow position feedback to be combined with a kinematic model of needle tip motion, in order to estimate the complete tip pose.
Needle vibration is currently achieved by an actuator connected to the proximal end of the steerable needle. In this implementation, the Doppler response decreases moving along the needle toward the tip, as the vibrations are damped out by the surrounding tissue. For very long insertion paths, or more viscous tissues, the amplitude of vibration at the tip might be too small to allow a reliable Doppler segmentation. We are currently exploring other actuation schemes that vibrate the needle tip directly, as in [36] or [39], although integrating these actuators into submillimeter steerable needles is a difficult practical problem.
With vibration of the needle, the added potential for tissue damage is an issue that must be considered carefully. Unfortunately, both the tissue strain around the vibrating shaft and the displacement of the sharp needle tip are difficult to measure experimentally, and it was not possible to quantify these factors in the current work. Histological analysis after steering in an in vivo model, as in [10], would likely be required to evaluate tissue damage. As stated earlier, the displacement of the needle shaft is in the submillimeter range at the needle base, and decreases along the needle shaft due to tissue damping. While we thus expect the resulting tissue damage to be minimal, this issue is again worthy of further study.
It should be noted that the duty-cycling approach we apply to control steerable needle curvature has largely been validated in homogeneous artificial tissues, although several examples of duty cycling in biological tissues have been reported [49]–[51]. Recent work [50] suggests that the linear relationship between duty cycle and curvature described in (4) may oversimplify steerable needle behavior in heterogeneous biological tissue. Fortunately, the closed-loop structure of our steering algorithm compensates for deviation from the expected relationship, and for variation in ρmin. Alternatively, a control scheme that does not rely on duty cycling, such as the sliding mode control described in [19], could be employed.
Design of a practical needle steering robot that is appropriate for in vivo testing is another important direction for future research directed toward clinical needle steering. Since the vast majority of prior needle steering methods have been evaluated in artificial or ex vivo tissues, needle steering robots described to date have not generally been appropriate for actual clinical environments. We will modify our robot design to delineate disposable components, sterilizable components, and components that must be draped or otherwise isolated. While our segmentation approach introduces the voice coil actuator and connecting clip, these components should not greatly complicate sterilization since they are both internal to the robot and can easily be made disposable.
VI. Conclusion
We have demonstrated a method for 3-D ultrasound guidance of robotic needle steering in biological tissue. The use of ultrasound Doppler imaging, in combination with high-frequency low-amplitude vibration of the steerable needle, greatly simplifies a challenging segmentation problem. using the Doppler method, unsophisticated image processing methods can localize the needle with run-times of approximately 60 ms per image, and error on the order of 1–2 mm for relevant needle configurations. This segmentation algorithm is robust to curvature, image orientation, and vibration frequency. Experiments in ex vivo bovine liver tissue demonstrate that our method allows a needle steering robot to reach a simulated target with an average error below 2 mm.
In our future work, we will continue to refine our methods for ultrasound-image guidance, with the goal being implementation of a clinical needle steering system for RFA of liver cancer. This serves as a first step toward deploying needle steering systems in a variety of organ systems and clinical applications.
Acknowledgments
The authors wish to acknowledge the contribution of T. Jiang to the construction of the needle steering robot.
Biographies

Troy K. Adebar received the B.A.Sc. degree in mechanical engineering in 2009 and the M.A.Sc. degree in electrical and computer engineering in 2011, both from The University of British Columbia, Vancouver, BC, Canada. He is currently working toward the Ph.D. degree in mechanical engineering at Stanford University, Stanford, CA, USA.
His research interests include robotics, image-guided intervention, and medical devices.

Ashley E. Fletcher received the B.A.Sc. degree in mechanical engineering in 2012 from Massachusetts Institute of Technology, Cambridge, MA, USA. She is currently working toward the M.S. degree in mechanical engineering at Stanford University, Stanford, CA, USA.

Allison M. Okamura (F’11) received the B.S. degree from the University of California, Berkeley, CA, USA, in 1994, and the M.S. and Ph.D. degrees from Stanford University, Stanford, CA, in 1996 and 2000, respectively, all in mechanical engineering.
She is currently an Associate Professor of mechanical engineering at Stanford University, Stanford, CA, USA, where she is also the Robert Bosch Faculty Scholar. Her research interests include haptics, teleoperation, medical robotics, virtual environments and simulation, neuromechanics and rehabilitation, prosthetics, and engineering education.
Dr. Okamura received the 2004 National Science Foundation CAREER Award, the 2005 IEEE Robotics and Automation Society Early Academic Career Award, and the 2009 IEEE Technical Committee on Haptics Early Career Award. She is an Associate Editor of the IEEE TRANSACTIONS ON HAPTICS.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Troy K. Adebar, Department of Mechanical Engineering, Stanford University, Stanford, CA 94035 USA
Ashley E. Fletcher, Department of Mechanical Engineering, Stanford University, Stanford, CA 94035 USA
Allison M. Okamura, Department of Mechanical Engineering, Stanford University, Stanford, CA 94035 USA.
References
- 1.Gervais DA, Goldberg N, Brown DB, Soulen MC, Millward SF, Rajan DK. Society of interventional radiology position statement on percutaneous radio frequency ablation for the treatment oflivertumors. J Vasc Interv Radiol. 2009;20(1):3–8. doi: 10.1016/j.jvir.2008.09.007. [DOI] [PubMed] [Google Scholar]
- 2.Kim YS, Rhim H, Cho OK, Koh BH, Kim Y. Intrahepatic recurrence after percutaneous radiofrequency ablation of hepatocellular carcinoma: Analysis of the pattern and risk factors. Eur J Radiol. 2006;59(3):432–441. doi: 10.1016/j.ejrad.2006.03.007. [DOI] [PubMed] [Google Scholar]
- 3.Dodd GD, Frank MS, Chopra S, Chintapalli KN. Radiofrequency thermal ablation: Computer analysis of the size of the thermal injury created by overlapping ablations. Amer J Roentgenol. 2001;177(4):777–782. doi: 10.2214/ajr.177.4.1770777. [DOI] [PubMed] [Google Scholar]
- 4.Di Maio SP, Salcudean SE. Needle steering and motion planning in soft tissues. IEEE Trans Biomed Eng. 2005 Jun.52(6):965–974. doi: 10.1109/TBME.2005.846734. [DOI] [PubMed] [Google Scholar]
- 5.Webster RJ, III, Kim JS, Cowan NJ, Okamura AM, Chirikjian GS. Nonholonomic modeling of needle steering. Int J Robot Res. 2006;25(5):509–526. [Google Scholar]
- 6.Glozman D, Shoham M. Image-guided robotic flexible needle steering. IEEE Trans Robot. 2007 Jun.23(3):459–67. [Google Scholar]
- 7.Mallapragada VG, Sarkar N, Podder TK. Robot-assisted realtime tumor manipulation for breast biopsy. IEEE Trans Robot. 2009 Apr.25(2):316–324. [Google Scholar]
- 8.Webster RJ, III, Romano JM, Cowan NJ. Mechanics of precurved-tube continuum robots. IEEE Trans Robot. 2009 Feb.25(1):67–78. [Google Scholar]
- 9.Wood NA, Shahrour K, Ost MC, Riviere CN. Needle steering system using duty-cycled rotation for percutaneous kidney access. Proc Int Conf IEEE Eng Med Biol Soc. 2010:5432–5435. doi: 10.1109/IEMBS.2010.5626514. [DOI] [PubMed] [Google Scholar]
- 10.Majewicz A, Marra SP, van Vledder MG, Lin M, Choti MA, Song DY, Okamura AM. Behavior of tip-steerable needles in ex vivo and in vivo tissue. IEEE Trans Biomed Eng. 2012 Oct.59(10):2705–2715. doi: 10.1109/TBME.2012.2204749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Neubach Z, Shoham M. Ultrasound-guided robot for flexible needle steering. IEEE Trans Biomed Eng. 2010 Apr.57(4):799–805. doi: 10.1109/TBME.2009.2030169. [DOI] [PubMed] [Google Scholar]
- 12.Ko SY, Rodriguez y Baena F. Trajectory following for a flexible probe with state/input constraints: An approach based on model predictive control. Robot Auton Syst. 2012;60:509–521. [Google Scholar]
- 13.Reed KB, Majewicz A, Kallem V, Alterovitz R, Goldberg K, Cowan NJ, Okamura AM. Robot-assisted needle steering. IEEE Robot Autom Mag. 2011 Dec.18(4):33–46. doi: 10.1109/MRA.2011.942997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Alterovitz R, Branicky M, Goldberg K. Motion planning under uncertainty for image-guided medical needle steering. Int J Robot Res. 2008;27(11–12):1361–1374. doi: 10.1177/0278364908097661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kallem V, Cowan NJ. Image guidance of flexible tip-steerable needles. IEEE Trans Robot. 2009 Feb.25(1):191–196. doi: 10.1109/TRO.2008.2010357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Reed KB, Okamura AM, Cowan NJ. Modeling and control of needles with torsional friction. IEEE Trans Biomed Eng. 2009 Dec.56(12):2905–2916. doi: 10.1109/TBME.2009.2029240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wood NA, Lehocky CA, Riviere CN. Algorithm for three-dimensional control of needle steering via duty-cycled rotation. Proc IEEE Int Conf Mechatronics. 2013:237–241. [Google Scholar]
- 18.Bernardes MC, Adorno BV, Poignet P, Borges GA. Robot-assisted automatic insertion of steerable needles with closed-loop imaging feedback and intraoperative trajectory replanning. Mechatronics. 2013;23:630–645. [Google Scholar]
- 19.Rucker DC, Das J, Gilbert HB, Swaney PJ, Miga MI, Sarkar N, Webster RJ. Sliding mode control of steerable seedles. IEEE Trans Robot. 2013 Oct.29(5):1289–1299. doi: 10.1109/TRO.2013.2271098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Abayazid M, Vrooijink GJ, Patil S, Alterovitz R, Misra S. Experimental evaluation of ultrasound-guided 3D needle steering in biological tissue. Int J Comput Assist Radiol Surg. doi: 10.1007/s11548-014-0987-y. to be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wedlick TR, Okamura AM. Characterization of robotic needle insertion and rotation in artificial and ex vivo tissues. Proc IEEE RAS EMBS Int Conf Biomed Robot Biomechatronics. 2012:62–68. [Google Scholar]
- 22.Cheung S, Rohling R. Enhancement of needle visibility in ultrasound-guided percutaneous procedures. Ultrasound Med Biol. 2004;30(5):617–624. doi: 10.1016/j.ultrasmedbio.2004.02.001. [DOI] [PubMed] [Google Scholar]
- 23.Ding M, Cardinal HN, Fenster A. Automatic needle segmentation in 3D ultrasound images using two orthogonal 2D image projections. Med Phys. 2003;30(2):222–234. doi: 10.1118/1.1538231. [DOI] [PubMed] [Google Scholar]
- 24.Ding M, Fenster A. A real-time biopsy needle segmentation technique using Hough transform. Med Phys. 2003;30(8):2222–2233. doi: 10.1118/1.1591192. [DOI] [PubMed] [Google Scholar]
- 25.Zhou H, Qiu W, Ding M, Songgen Z. Automatic needle segmentation in 3D ultrasound images using 3D improved Hough transform. Proc SPIE Med Imag.: Image-Guided Procedures Modeling. 2008;6918:691 821-1–691 821-9. [Google Scholar]
- 26.Novotny PM, Stoll JA, Vasilyev NV, del Nido PJ, Dupont PE, Zickler TE, Howe RD. GPU based real-time instrument tracking with three-dimensional ultrasound. Med Im Anal. 2007;11(5):458–464. doi: 10.1016/j.media.2007.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Barva M, Uhercik M, Mari JM, Kybic J, Duhamel JR, Liebgott H, Hlavac V, Cachard C. Parallel integral projection transform for straight electrode localization in 3-D ultrasound images. IEEE Trans Ultrason Ferroelectr Freq Control. 2008 Jul.55(7):1559–1569. doi: 10.1109/TUFFC.2008.833. [DOI] [PubMed] [Google Scholar]
- 28.Okazawa SH, Ebrahimi R, Chuang J, Rohling RN, Salcudean SE. Methods for segmenting curved needles in ultrasound images. Med Im Anal. 2006;10(3):330–342. doi: 10.1016/j.media.2006.01.002. [DOI] [PubMed] [Google Scholar]
- 29.Aboofazeli M, Abolmaesumi P, Mousavi P, Fichtinger G. A new scheme for curved needle segmentation in three-dimensional ultrasound images. Proc IEEE Int Symp Biomed Imag.: Nano Macro. 2009:1067–1070. doi: 10.1109/ISBI.2009.5193240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Neshat HRS, Patel RV. Real-time parametric curved needle segmentation in 3D ultrasound images. Proc IEEE RAS EMBS Int Conf Biomed Robot Biomechatronics. 2008:670–675. [Google Scholar]
- 31.Uhercík M, Kybic J, Liebgott H, Cachard C. Model fitting using RANSAC for surgical tool localization in 3D ultrasound images. IEEE Trans Biomed Eng. 2010 Aug.57(8):1907–1916. doi: 10.1109/TBME.2010.2046416. [DOI] [PubMed] [Google Scholar]
- 32.Holen J, Waag RC, Gramiak R. Representations of rapidly oscillating structures on the Doppler display. Ultrasound Med Biol. 1985;11(2):267–272. doi: 10.1016/0301-5629(85)90125-5. [DOI] [PubMed] [Google Scholar]
- 33.Armstrong G, Cardon L, Vlkomerson D, Lipson D, Wong J, Rodriguez LL, Thomas JD, Griffin BP. Localization of needle tip with color Doppler during pericardiocentesis: In vitro validation and initial clinical application. J Amer Soc Echocardiography. 2001;14:29–37. doi: 10.1067/mje.2001.106680. [DOI] [PubMed] [Google Scholar]
- 34.Feld R, Needleman L, Goldberg B. Use of a needle-vibrating device and color Doppler imaging for sonographically guided invasive procedures. Amer J Roentgenol. 1997;168:255–256. doi: 10.2214/ajr.168.1.8976955. [DOI] [PubMed] [Google Scholar]
- 35.Hamper UM, Savader BL, Sheth S. Improved needle-tip visualization by color Doppler sonography. Amer J Roentgenol. 1991;156(2):401–402. doi: 10.2214/ajr.156.2.1898823. [DOI] [PubMed] [Google Scholar]
- 36.Harmat A, Rohling RN, Salcudean SE. Needle tip localization using stylet vibration. Ultrasound Med Biol. 2006;32(9):1339–1348. doi: 10.1016/j.ultrasmedbio.2006.05.019. [DOI] [PubMed] [Google Scholar]
- 37.Fronheiser MP, Idriss SF, Wolf PD, Smith SW. Vibrating interventional device detection using real-time 3-D color Doppler. IEEE Trans Ultrason Ferroelectr Freq Control. 2008 Jun.55(6):1355–1362. doi: 10.1109/TUFFC.2008.798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Reddy KE, Light ED, Rivera DJ, Kisslo JA, Smith SW. Color Doppler imaging of cardiac catheters using vibrating motors. Ultrasonic Imag. 2008;30:247–250. doi: 10.1177/016173460803000408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.McAleavey SA, Rubens DJ, Parker KJ. Doppler ultrasound imaging of magnetically vibrated brachytherapy seeds. IEEE Trans Biomed Eng. 2003 Feb.50(2):252–255. doi: 10.1109/TBME.2002.807644. [DOI] [PubMed] [Google Scholar]
- 40.Rogers AJ, Light ED, Smith SW. 3-D ultrasound guidance of autonomous robot for location of ferrous shrapnel. IEEE Trans Ultrason Ferroelectr Freq Control. 2009 Jul.56(7):1301–1303. doi: 10.1109/TUFFC.2009.1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Adebar TK, Okamura AM. 3D segmentation of curved needles using Doppler ultrasound and vibration. Proc Int Conf Inf Process Comput.-Assisted Interventions. 2013;7915:61–70. [Google Scholar]
- 42.Tchelepi H, Ralls PW. Color comet-tail artifact: Clinical applications. Amer J Roentgenol. 2009;192(1):11–18. doi: 10.2214/AJR.07.3893. [DOI] [PubMed] [Google Scholar]
- 43.Webster RJ, III, Memisevic J, Okamura AM. Design considerations for robotic needle steering. Proc Int Conf Robot Autom. 2005:3588–3594. [Google Scholar]
- 44.Yoo T, Ackerman MJ, Lorensen WE, Schroeder W, Chalana V, Aylward S, Metaxas D, Whitaker R. Engineering and algorithm design for an image processing API: A technical report on—The insight toolkit. Proc Med Meets Virtual Reality. 2002:586–592. [PubMed] [Google Scholar]
- 45.Crocetti L, Lencioni R, De Beni S, See TC, Pina CD, Bartolozzi C. Targeting liver lesions for radiofrequency ablation: An experimental feasibility study using a CT-US fusion imaging system. Invest Radiol. 2008;43(1):33–39. doi: 10.1097/RLI.0b013e31815597dc. [DOI] [PubMed] [Google Scholar]
- 46.Maier-Hein L, Tekbas A, Seitel A, Pianka F, Müller SA, Satzl S, Schawo S, Radeleff B, Tetzlaff R, Franz AM, Müller-Stich BP, Wolf I, Kauczor HU, Schmied BM, Meinzer HP. In vivo accuracy assessment of a needle-based navigation system for CT-guided radiofrequency ablation of the liver. Med Phys. 2008;35(12):5385–5396. doi: 10.1118/1.3002315. [DOI] [PubMed] [Google Scholar]
- 47.Schubert T, Jabob AL, Pansini M, Liu D, Gutzeit A, Kos S. CT-guided interventions using a free-hand, optical tracking system: Initial clinical experience. Cardiovasc Inter Rad. 2013;36:1055–1062. doi: 10.1007/s00270-012-0527-5. [DOI] [PubMed] [Google Scholar]
- 48.Kim YS, Lee WJ, Rhim H, Lim HK, Choi D, Lee JY. The minimal ablative margin of radiofrequency ablation of hepatocellular carcinoma (> 2 and < 5 cm) needed to prevent local tumor progression: 3D quantitative assessment using CT image fusion. Amer J Roentgenol. 2010;195(3):758–765. doi: 10.2214/AJR.09.2954. [DOI] [PubMed] [Google Scholar]
- 49.Engh JA, Minhas DS, Kondziolka D, Riviere CN. Percutaneous intracerebral navigation by duty-cycled spinning of flexible bevel-tipped needles. Neurosurgery. 2010;67(4):1117–1123. doi: 10.1227/NEU.0b013e3181ec1551. [DOI] [PubMed] [Google Scholar]
- 50.Patil S, Burgner J, Webster RJ, III, Alterovitz R. Needle steering in 3-D via rapid replanning. IEEE Trans Robot. doi: 10.1109/TRO.2014.2307633. to be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Swaney PJ, Burgner J, Gilbert HB, Webster RJ., III A flexture-based steerable needle: High curvature with reduced tissue damage. IEEE Trans Biomed Eng. 2013 Apr.60(4):906–909. doi: 10.1109/TBME.2012.2230001. [DOI] [PMC free article] [PubMed] [Google Scholar]


