Non-parametric regression in clustered multistate current status data with informative cluster size

Abstract

Datasets examining periodontal disease records current (disease) status information of tooth-sites, whose stochastic behavior can be attributed to a multistate system with state occupation determined at a single inspection time. In addition, the tooth-sites remain clustered within a subject, and the number of available tooth-sites may be representative of the true PD status of that subject, leading to an ‘informative cluster size’ scenario. To provide insulation against incorrect model assumptions, we propose a nonparametric regression framework to estimate state occupation probabilities at a given time and state exit/entry distributions, utilizing weighted monotonic regression and smoothing techniques. We demonstrate the superior performance of our proposed weighted estimators over the un-weighted counterparts via. a simulation study, and illustrate the methodology using a dataset on periodontal disease.

1 Introduction

Multistate models (Hougaard, 1999; Kneib & Hennerfeind, 2008) are popularly used in biomedical research to model complex time-continuous disease evolution based on multivariate time-to-event data, allowing the study units to move reversibly or irreversibly through a succession of discrete states before entering an absorbing state (Lan & Datta, 2010b). Each state corresponds to a health condition of a study unit over the course of the disease, such as alive and disease free, alive with disease, dead, etc. Multistate models are often quantified by state occupation probabilities as functions of time (similar to the survival function in traditional survival analysis), and these are often related to the distributions function of state entry and exit times in any event history settings. However, the actual transition times can be subjected to current status censoring, when the study unit is observed only once at a random inspection time. Thus, we observe only the state occupied at inspection (not failed or censored as in usual survival analysis), and the time of inspection in a multistate current status framework, which represents a more severe form of censoring.

The evolution of periodontal disease (PD), like any other complex disease, can be characterised via. a multistate model, where the outcome of interest is the disease status measured per tooth site at an inspection time, clustered within a subject. In addition, the cluster sizes are informative (Williamson et al., 2003), i.e., the number of available tooth-sites within a cluster (subject) is inversely correlated to the (overall) PD status of the subject, and overlooking this would lead to study units contributing equally to the data likelihood leading to overweighing the larger clusters, and bias in parameter estimates. For analyzing traditional clustered (correlated) survival data, various marginal approaches have been proposed under the proportional hazards framework (Wei et al., 1989; Spiekerman & Lin, 1998; Clegg et al., 1999), or considering the accelerated failure type model, additive hazards model and linear transformations model (Lin & Wei, 1992; Cai et al., 2000; Yin & Cai, 2004). Extensions to incorporate the informative cluster size (ICS) scenario (Cong et al., 2007; Hoffman et al., 2001) include adapting the ICS methodology developed for clustered binary data via within-cluster resampling (Hoffman et al., 2001), weighted generalized estimating equations (Williamson et al., 2003), etc. However, such a framework for multistate current status data (as in our case) has not yet been explored.

The current literature is inundated with various parametric and semi-parametric approaches to direct estimation of state occupation probabilities (Gray, 1992,9) and cumulative incidence curves (Scheike et al., 2008), modeling transition hazards (Satten et al., 1998), and multistate models (Andersen & Keiding, 2002; Kneib & Hennerfeind, 2008; Andersen & Perme, 2008) Inarguably, these methods produce relatively precise inference for estimation of covariate effects under the correct model; however, in reality, a practitioner is often confronted with the difficulty to determine the most suitable model for a particular dataset. Hence, to insulate against incorrect model assumptions, a fully nonparametric approach might be viable, although one would necessarily require a larger sample size to enjoy the full benefits of going nonparametric. Although our current clustered multistate framework poses more challenges than the traditional survival analysis setup, only the nonparametric estimators can serve as the benchmark (Doksum & Yandell, 1983) to the shape of the regression functions on the various marginal quantities discussed above, and can be the starting block for further parametric and semi-parametric analysis.

The literature on nonparametric estimation in multistate models is rather limited, and mostly tackles the usual survival setup (Aalen, 1980; Dabrowska, 1987,9; McKeague & Utikal, 1990; Li & Datta, 2001). An interesting hybrid approach (Andersen et al., 2003; Andersen & Klein, 2007) is to study the effect of covariates in a multistate model by starting from a nonparametric marginal estimator followed by a semi-parametric modeling of the corresponding jackknife based pseudo-values. Nonparametric estimation for multistate current status (Datta & Sundaram, 2006; Lan & Datta, 2010b) considers product-limit estimators of state occupation probabilities and state entry/exit time distributions; the special case of competing risk models was investigated by Jewell et al. (2003) and Groeneboom et al. (2008). Lan & Datta (2010a) develop nonparametric bootstrap tests comparing the occupation probabilities, entry, exit and waiting times in the current status multistate setup. Nonparametric regression for multistate current status data remains vastly absent in the literature, except for an unpublished manuscript by Burr & Gomatam (2002). Motivated by a real dataset on PD (Reich & Bandyopadhyay, 2010), we propose a nonparametric multistate regression model to evaluate dental disease progression, incorporating informative cluster sizes and clinical risk factors. Our estimators are obtained conditional given a single (continuous or discrete) covariate, and are based on similar re-weighting principles (Datta & Satten, 2001,0) and kernel-smoothed estimates of the component counting and number-at-risk process. The underlying premise is free of the usual structural assumptions (Markov, or semi-Markov) of a multistate model, but have a directed tracking structure such as: State 1 → State 2 → State 3. The main contribution of this paper is to provide a non-parametric regression estimator given the value of a continuous covariate, based on multistate current status data and to extend it to clustered data in an informative cluster size (ICS) setting.

The rest of the paper is organized as follows. Section 2 introduces notation, and develops the methodology for the nonparametric regression estimators with adjustments for the informative cluster size. The global performance of the estimators is evaluated via. a finite sample simulation study, and presented in Section 3. Section 4 applies the methodology developed to the motivating dataset on PD. Finally, Section 5 presents some concluding remarks. Additional results and a theoretical justification are placed in an appendix.

2 Nonparametric Regression Estimators for Multistate Model

2.1 Notation and Convention

We assume ℜ = {0, …, M} is the finite state space for our underlying multistate model with a directed tracking topology, where each state j ∈ ℜ can be reached from an initial state 0 following a unique path π(j): 0 = s₁ → s₂ ··· → s_j+1 = j. We still allow the possibility that not all individuals need to be at the root state 0 at time 0. The current status data for each individual l can be represented as {C_l, S_l(C_l), X_l}, where the inspection time C_l is independent of the multistate process {S_l(t), t ≥ 0} given the continuous X_l. We further assume that all transition times and censoring variables are continuous, and the data for the individuals l = 1, …, n are independent, and identically distributed. Additional notations and assumptions will be needed when the data are clustered.

2.2 Regression estimators for unclustered data

2.2.1 State occupation probabilities

We begin by reviewing the non-parametric estimation for the state occupation probabilities for unclustered (i.e., independent) current status data (Datta & Sundaram, 2006). We note that in Datta & Sundaram (2006), only marginal (i.e., not conditional on a covariate) estimators were obtained. The two key ingredients were (i) estimated transition counts and (ii) estimated number at risk. In this paper, we extend these ideas to conditional processes given a continuous covariate by introducing appropriate kernel based weights at various stages of this construction.

Consider two states j and j′ in ℜ, and let U_jj′ denote the (latent) transition time of an individual from state j to j′ (define it to be ∞, if this transition is not made by the individual). Henceforth, in our model development, we suppress the subscript l corresponding to an individual, wherever possible, for notational convenience. However, we imply that the pertinent stochastic quantities varies with l. Let $N_{j{j}^{\prime }}^{\ast }(t)$ denote the usual counting process counting the number of j to j′ transitions in [0, t] with the complete data, defined as $N_{j{j}^{\prime }}^{\ast }(t)={\sum }_{l=1}^{n}I(U_{l,j{j}^{\prime }}\le t)$. By the laws of large numbers, for any t ≥ 0, we have

$$n^{-1}{N}_{j{j}^{\prime }}^{\ast }(t)\stackrel{P}{\to }{n}^{-1}E{N}_{j{j}^{\prime }}^{\ast }(t)=P\{U_{j{j}^{\prime }}\le t\}=n_{j{j}^{\prime }}(t).$$ (2.1)

Given the independence between the inspection time C and the multistate process, the right hand side of the equality can be expressed as the regression function E(I (U_jj′ ≤ C)|C = t). Note that we assume all past transitions (j to j′) before time t are known, and the counting process $N_{j{j}^{\prime }}^{\ast }(t)$ can be computed at the inspection time C. Thus, $n^{-1}{N}_{j{j}^{\prime }}^{\ast }(·)$ can be obtained by a nonparametric regression estimator of I (U_jj′ ≤ C) given C.

Next, let $Y_j^{\ast }(t)$ is the number of individuals ‘at risk’ of transition out of state j at time t, defined as $Y_j^{\ast }(t)={\sum }_{l=1}^{n}I\left(S_l(t-)=j\right)$, with S(t−) representing the state occupied just before time t. Thus, the limit of $n^{-1}{Y}_j^{\ast }(t)$ in probability is P_r{S(t−) = j} = P_j(t−). However, unlike the counting process of transition counts, the $Y_j^{\ast }$ process does not have to be monotonic for a transient state j. Therefore, Datta & Sundaram (2006) used kernel smoothing rather than weighted isotonic regression to estimate this process.

In order to compute the regression functions given a continuous covariate X, we need to compute weighted versions of this estimated process where the weight corresponding to the lth observation is ϕ_h(x−X_l). Here, ϕ_h can be any scaled log concave kernel (normal kernel for this study) with bandwidth h (Wand & Jones, 1995). As before, since Pr{U_jj′ ≤ t|X = x} is monotonic in t, $n^{-1}{N}_{j{j}^{\prime }}^{\ast }(·\mid x)$ can be constructed by a weighted isotonic regression of I (U_jj′ ≤ C) on C, based on the pairs (C_l, I (U_l,jj′ ≤ C_l)) with weights ϕ_h(x−X_l), such that $n^{-1}{N}_{j{j}^{\prime }}^{\ast }(·\mid x)$ is a step function for each x taking values $n^{-1}{N}_{j{j}^{\prime }}^{\ast }(·\mid x)=R_l(x)$ say, that minimizes the weighted sum of squares ${\sum }_{l=1}^n{\varphi }_h(x-X_{[l]}){\{R_l(x)-I(U_{[l],j{j}^{\prime }}\le C_{(l)})\}}^2$, subject to R₁(x) ≤ ··· ≤ R_n(x), where [l] denotes the index in the original data such that C_[l] equals the lth order statistic C_(l). The weighted sum of squares can be written as a quadratic form with a diagonal weight matrix which can be solved by a direct application of R package isotone, using (generalized) pooled adjacent violators algorithm (GPAVA) (de Leeuw et al., 2009). The long flat parts in $N_{j{j}^{\prime }}^{\ast }(·\mid x)$ resulting from the application of the GPAVA are removed using kernel-smoothing techniques (Mukerjee, 1988; Nadaraya, 1964; Watson, 1964) while maintaining monotonicity. This yields the final estimator

$${\widehat{N}}_{j{j}^{\prime }}(t\mid x)=\frac{{\sum }_{l=1}^n{N}_{j{j}^{\prime }}^{\ast }(C_l\mid x)K_{\stackrel{\sim }{h}}(C_l-t)}{n^{-1}{\sum }_{l=1}^n{K}_{\stackrel{\sim }{h}}(C_l-t)},$$ (2.2)

where K_h̃ = h̃⁻¹K(./h̃) > 0 is a (differentiable) log-concave density (e.g., the standard normal), and 0 < h̃ = h̃ (n) ↓ 0 is the associated data dependent bandwidth sequence determined by Wand and Jones criteria (using R function dpik).

The kernel estimated number at risk process, given X = x, is a locally weighted version of the corresponding estimated process in Datta & Sundaram (2006) given by

$${\widehat{Y}}_j(t\mid x)\doteqdot \frac{{\sum }_{l=1}^n{\varphi }_h(x-X_l)I(s_l(C_l)=j)K_{\stackrel{\sim }{h}}(C_l-t)}{n^{-1}{\sum }_{l=1}^n{\varphi }_h(x-X_l)K_{\stackrel{\sim }{h}}(C_l-t)}.$$ (2.3)

Finally, the class of regression estimators for state occupation probabilities will be computed using the identity: ${\widehat{P}}_j(t\mid x)=n^{-1}{\sum }_{k=0}^M\left({\widehat{Y}}_k(0+\mid x)\right){\left(\widehat{P}(0,t\mid x)\right)}_{kj}$, where (P̂ (0, t|x)_kj is the kjth element the matrix P̂ (0, t|x) = Π_(0,t] (I + dÂ(u|x)), and Ŷ_k(0 + |x)/n are the relative proportions of individuals at time 0 in various states. Here Â(u|x) is a conditional estimated Aalen-Johansen estimator based on current status data:

$${\widehat{A}}_{j{j}^{\prime }}(t\mid x)=\{\begin{array}{ll}{\int }_0^t{J}_j(u,x){\widehat{Y}}_j{(u\mid x)}^{-1}d{\widehat{N}}_{j{j}^{\prime }}(u\mid x)\hfill & j\ne j^{\prime },\hfill \\ -{\sum }_{j^{\prime }\ne j}{\widehat{A}}_{j{j}^{\prime }}(t\mid x)\hfill & j=j^{\prime },\hfill \end{array}$$ (2.4)

where J_j(u, x) = I(Ŷ_j(u|x) > 0).

Consistency of the above Aalen-Johansen type estimator to the corresponding population integrated hazard rates can be established using the same line of arguments as in Datta & Sundaram (2006), combined with the non-parametric regression arguments in Mostajabi & Datta (2013). Consistency of estimated state occupation probabilities follows from that of the Aalen-Johansen type estimator by the continuous mapping theorem and the basic arguments laid out in Datta & Satten (2001).

2.2.2 State entry/exit time distributions

Let δ_j be the (unobserved) indicator of the event that an individual would ever enter state j. For any two states j and j′ in ℜ, let U_j and V_j be the entry and exit times for state j respectively. The corresponding distribution function of U_j is F_j(t) = P(U_j ≤ t|δ_j = 1), where F₀(t) = 1 for all t ≥ 0. Let S^j be the set of states of ℓ such that state j is on the path from 0 to ℓ. Therefore, the entry time distribution to state j is estimated as:

$${\widehat{F}}_j(t\mid x)=\frac{{\sum }_{\ell \in S^j}{\widehat{P}}_{\ell }(t\mid x)}{{\sum }_{\ell \in S^j}{\widehat{P}}_{\ell }(\infty \mid x)},$$

where P̂_ℓ(∞|x) = lim_t→∞ P̂_ℓ(t|x). In other words, F̂_j(t|x) is the normalized sum of estimated state occupation probabilities of state j and all other states that come after j in the progressive system, given x.

Analogously, the distribution function of the state exit time V_j is given by G_j(t|x) = P(V_j ≤ t|δ_j = 1), where G_j(t|x) = 0 if j is a terminal state, for all t ≥ 0. For a transient state j, Ĝ_j(t|x) is computed as the normalized sum of estimated state occupation probabilities of all other states that come after j in the progressive system, as

$${\widehat{G}}_j(t\mid x)=\frac{{\sum }_{\ell \in S^j\backslash j}{\widehat{P}}_{\ell }(t\mid x)}{{\sum }_{\ell \in S^j}{\widehat{P}}_{\ell }(\infty \mid x)}.$$

Consistency of the estimators of state entry and exit time distributions follow from that of the state occupation probability estimators.

2.3 Estimation for clustered data with informative cluster size

We now consider a setting where individuals undergoing their multistate systems are clustered so that the multistate processes of individuals belonging to the same cluster may be dependent; however these processes for individuals belonging to different clusters are independent. We use i to index cluster and l to index individuals within cluster. Thus, the multistate process of an individual will be denoted by S_il = {S_il(t): t ≥ 0}. We let m denote the total number of clusters and for 1 ≤ i ≤ m, n_i denotes the size of the ith cluster. Note that $Q={\sum }_{i=1}^m{n}_i$ denotes the total sample size.

We consider the situation where the cluster sizes are potentially informative. As indicated in the introduction, the ICS phenemonon has received some attention in recent years. This means the cluster size n_i is random, and influenced by some measured or unmeasured (e.g., latent factors) cluster level covariates that also correlate with multistate processes in the cluster. See the Simulation section for a data generation scheme leading to ICS.

Assuming that the multistate processes S_il and the covariates X_il within a given cluster i are exchangeable, we are interested in the marginal state occupation probabilities P_j(t) = Pr{S_il(t) = j}, or in the marginal conditional (e.g., regression) state occupation probabilities P_j(t|x) = Pr{S_il(t) = j |X_il = x}. More generally, let I have a discrete uniform distribution on {1, ···, m} and given I = i, let J = J(i) be a uniformly distributed index on {1, ···, n_i}. Then S_IJ can be interpreted as the multistate process corresponding to a randomly chosen individual from a randomly chosen cluster. Define the marginal state occupation probability by

$$P_j(t)=E(I\{S_{IJ}(t)=j\})=E\left(m^{-1}\sum _{i=1}^m\sum _{l=1}^{n_i}{n}_i^{-1}I\{S_{il}(t)=j\}\right),t\ge 0,$$ (2.5)

where E denotes a joint expectation over all random variables/processes invloved in defining the indicator event. The case of a marginal regression function can also be treated more generally.

We note the use of inverse cluster size weighting in the above definition and in various formulas in the rest of this subsection. In the appendix, we show that under some conditions, this general definition coincides with the interpretation given earlier. In case of ICS, the corresponding formulas without the inverse cluster size weightings may lead to biased answers. This is reflected in the simulation results presented in the next section.

Let the ordered inspection times C′s in the pooled sample be C₍₁₎ ≤ ··· ≤ C_(Q), and r(i, l) be the rank of C_il in the pooled sample. Then in this case, $n^{-1}{N}_{j{j}^{\prime }}^{\ast }(·\mid x)$ will be a step function for each x taking values $n^{-1}{N}_{j{j}^{\prime }}^{\ast }(C_{(il)}\mid x)=R_{il}(x)$ say, that minimizes the weighted sum of squares

$$\sum _{i=1}^m\frac{1}{n_i}\sum _{l=1}^{n_i}{\varphi }_h(x-X_{[il]}){\{R_{r(i,l)}(x)-I(U_{[il],j{j}^{\prime }}\le C_{(il)})\}}^2$$ (2.6)

subject to R₁(x) ≤ ··· ≤ R_Q(x). As mentioned above, we use additional weight that is the inverse cluster size $\frac{1}{n_i}$ so that we can downweight the contribution of individual members of larger clusters to equally balance the total contributions of all clusters (Lee et al., 1992). A formal interpretation of a marginal distribution to justify this can be given as before. The smoothed estimate for the counting process (in Subsection 2.2) is given by:

$${\widehat{N}}_{j{j}^{\prime }}(t\mid x)=\frac{{\sum }_{i=1}^m\frac{1}{n_i}{\sum }_{l=1}^{n_i}{N}_{j{j}^{\prime }}^{\ast }(C_{il}\mid x)K_{\stackrel{\sim }{h}}(C_{il}-t)}{Q^{-1}{\sum }_{i=1}^m\frac{1}{n_i}{\sum }_{l=1}^{n_i}{K}_{\stackrel{\sim }{h}}(C_{il}-t)},$$ (2.7)

and the corresponding at-risk set estimator (given X) with ICS is defined as:

$${\widehat{Y}}_j(t\mid x)\doteqdot \frac{{\sum }_{i=1}^m\frac{1}{n_i}{\sum }_{l=1}^{n_i}{\varphi }_h(x-X_{il})I(S_{il}(C_{il})=j)K_{\stackrel{\sim }{h}}(C_{il}-t)}{Q^{-1}{\sum }_{i=1}^m\frac{1}{n_i}{\sum }_{l=1}^{n_i}{\varphi }_h(x-X_l)K_{\stackrel{\sim }{h}}(C_{il}-t)}.$$ (2.8)

Note that the ICS adjustment enters the estimation framework through equations (2.7) and (2.8). Other formulas described in Sections 2.1 and 2.2 can be extended in a similar way by using the present versions of the adjusted transition counts and number at riak processes. Estimators for state entry and exit times are functions of state occupation probabilities as described in Section 2.2. Once the state occupation probabilities are extended to clustered data with ICS, both state entry and exit time distributions can be naturally extended as well. Finally, it may be worth pointing out that if we suppress the ϕ_h factors from (2.6) and (2.8), we would obtain the marginal state occupation probability estimators.

2.4 Extensions to clustered data with informative sub-cluster size

The inverse cluster size methodology of Williamson et al. (2003) as adapted in the previous section will be inadequate in situations where a discrete subject (i.e., unit) level covariate influences the multistate process and the size of the sub-clusters formed by different values of the covariate within a cluster. Although, our PD data set does not have this issue, we still wanted to extend our methodology in this paper to cover this type of situation so that our readers are more fully equipped in case they encounter such a data set. Here, one needs to use a more complex weighting to account for such imbalances in the data (Huang & Leroux, 2011; Pavlou, 2012).

As before, suppose X be the univariate covariate whose regression effect we are studying. In addition, we also have a unit/individual level discrete covariate Z_il taking values in the set {z₁, …, z_K} that defines the sub-cluster size. For each cluster i, let subcluster k denote the set of indices l with Z_il = z_k. Also, let $n_{ik}={\sum }_{l=1}^{n_i}I(Z_{il}=z_k)$ denote the size of the kth cluster. Assuming all sub-cluster sizes are positive (with probability one), we could use the following weighted least squares objective function

$$\sum _{k=1}^K\frac{1}{n_{ik}}\sum _{l:Z_{il}=z_k}{\varphi }_h(x-X_{[il]}){\{R_{r(i,l)}(x)-I(U_{[il],j{j}^{\prime }}\le C_{(il)})\}}^2$$

to obtain the monotonized estimator of the counting processes $N_{j{j}^{\prime }}^{\ast }(·\mid x)$, which will lead to the smoothed estimator

$${\widehat{N}}_{j{j}^{\prime }}(t\mid x)=\frac{{\sum }_{k=1}^K\frac{1}{n_{ik}}{\sum }_{l:Z_{il}=z_k}{N}_{j{j}^{\prime }}^{\ast }(C_{il}\mid x)K_{\stackrel{\sim }{h}}(C_{il}-t)}{Q^{-1}{\sum }_{k=1}^K\frac{1}{n_{ik}}{\sum }_{l:Z_{il}=z_k}{K}_{\stackrel{\sim }{h}}(C_{il}-t)}.$$ (2.9)

Similarly, the number at risk process can be estimated as

$${\widehat{Y}}_j(t\mid x)=\frac{{\sum }_{k=1}^K\frac{1}{n_{ik}}{\sum }_{l:Z_{il}=z_k}{\varphi }_h(x-X_{il})I(S_{il}(C_{il})=j)K_{\stackrel{\sim }{h}}(C_{il}-t)}{Q^{-1}{\sum }_{k=1}^K\frac{1}{n_{ik}}{\sum }_{l:Z_{il}=z_k}{\varphi }_h(x-X_{il})K_{\stackrel{\sim }{h}}(C_{il}-t)}.$$ (2.10)

Note that the weighting scheme has a marginalization interpretation as before. In this case, we are interested in the distribution of a typical individual unit of a typical sub-cluster of a typical cluster.

3 Simulation study

3.1 The setup

To compare finite sample performances of the nonparametric estimators of state occupation probabilities for multistate models with and without the ICS adjustments using the inverse cluster size reweighting, we perform a detailed simulation study using a three stage tracking model (State 1 → State 2 → State 3) which includes the initial, transient and absorbing stages (Fan & Datta, 2011). In this setting, state occupation probabilities take the following form:

$$\begin{array}{c}{\widehat{P}}_1(t\mid x)=exp\left\{-{\int }_0^t\frac{d{\widehat{N}}_{12}(u\mid x)}{{\widehat{Y}}_1(u\mid x)}\right\},\\ {\widehat{P}}_2(t\mid x)={\int }_0^{t}exp\left\{-{\int }_u^t\frac{d{\widehat{N}}_{23}(v\mid x)}{{\widehat{Y}}_2(v\mid x)}\right\}\frac{{\widehat{P}}_1(u\mid x)d{\widehat{N}}_{12}(u\mid x)}{{\widehat{Y}}_1(u\mid x)},\text{and}\\ {\widehat{P}}_3(t\mid x)=exp\left\{-{\int }_0^t\frac{{\widehat{P}}_2(u\mid x)d{\widehat{N}}_{23}(u\mid x)}{{\widehat{Y}}_2(u\mid x)}\right\}.\end{array}$$ (3.1)

Also, the state entry time distributions equal the state exit time distribution of the previous state since there is only one path for this progressive system. Therefore,

$$\begin{array}{c}{\widehat{G}}_1(t\mid x)={\widehat{F}}_2(t\mid x)=\frac{{\widehat{P}}_2(t\mid x)+{\widehat{P}}_3(t\mid x)}{{\widehat{P}}_1(\infty \mid x)+{\widehat{P}}_2(\infty \mid x)+{\widehat{P}}_3(\infty \mid x)},\text{and}\\ {\widehat{G}}_2(t\mid x)={\widehat{F}}_3(t\mid x)=\frac{{\widehat{P}}_3(t\mid x)}{{\widehat{P}}_2(\infty \mid x)+{\widehat{P}}_3(\infty \mid x)}.\end{array}$$

The current status data for each cluster unit l in a cluster i consists of {C_il, S(C_il), X_il} for l = 1 ··· n_i and i = 1 ··· m. The total survival time (equivalent to the entry time of the absorbing state 3) is generated as follows:

$$log(T_{2,il})={\beta }_1{Z}_1+{\beta }_2{Z}_{2,i}+{\beta }_3{Z}_{3,i}+{\beta }_4{Z}_{4,il}+{\beta }_5{Z}_{5i}+{\alpha }_i+{\epsilon }_{il},$$ (3.2)

where Z_il1 ≡ 1, Z_2,i is a cluster level discrete (binary) covariate, Z_3,i is a cluster level continuous covariate, Z_4,il is a unit level continuous covariate, and Z_5,i is the interaction term between Z_2,i, Z_3,i, and α_i is a cluster-specific random effect. Specifically, Z_2,i = I(1 ≤ i ≤ m/2) where I represents the indicator function, $Z_{3,i}~N(1,{\sigma }_3^2),Z_{4,il}~N(1,{\sigma }_4^2)$, Z_5,il = Z_2,iZ_3,i, ${\alpha }_i~N(0,{\sigma }_{\alpha }^2)$ and ${\epsilon }_{il}~N(0,{\sigma }_{\epsilon }^2)$. State 1 exit time T_1,il is generated as a proportion of T_2,il, where the proportions are uniformly distributed. We use uniform distribution to generate the current status censoring time with range (0, max(T_2,il)]. Our simulation designs cover a wide range of data generation mechanisms, varying with the number of clusters, the regression coefficients, the error densities, cluster-specific random effects density, the informative cluster size mechanism, and the covariate distributions. These are listed as follows:

• Number of clusters: m = 30 (moderate), and m = 200 (large).

• Two sets of parameter values: (i) β₁ = 0.3, β₂ = 0.4, β₃ = β₄ = −0.2, β₅ = −0.3, and (ii) β₁ = 0.8, β₂ = 1, β₃ = β₄ = −0.75, β₅ = −1.5. (Note, we let β₃ equal to β₄ to reduce the number of simulation setups)

• Continuous covariates generated as stated before with variances: ${\sigma }_3^2={\sigma }_4^2=0.15$, or ${\sigma }_3^2={\sigma }_4^2=0.15$.

• Cluster-specific random effects variance: ${\sigma }_{\alpha }^2=0.15$, or 0.25.

• Error variance: ${\sigma }_{\epsilon }^2=0.05$, or 0.20.

• Covariate for the regression function: X = Z₄.

• ICS scenarios: For the first scenario, let g(α_i) = γ₁ + γ₂α_i. The cluster sizes were randomly generated as $n_i=1+n_i^{\ast }$, where $n_i^{\ast }~\text{Poisson}(\mathit{exp}(g({\alpha }_i)))$, i.e., the cluster size depends only on the cluster random-effect α_i. We consider two sets of parameters: γ₁ = 1.5, γ₂ = 3 and γ₁ = −1, γ₂ = 4.

  For the second scenario, the cluster size is a function of both α_i and the cluster level covariate Z_2,i. Here, g(α_i) = γ₁ + γ₂α_i + γ₃Z_5,iα_i. The cluster sizes were randomly generated as $n_i=1+n_i^{\ast }$, where $n_i^{\ast }~\text{Poisson}(exp(g({\alpha }_i)))$. Once again, we consider two sets of parameters: γ₁ = 1.5, γ₂ = 3, γ₃ = 1 and γ₁ = −1, γ₂ = 4, γ₃ = −4.

3.2 Estimation accuracy measured by the L₁ risk

The global performance of the regression estimators of state occupation probabilities was assessed via the expected L₁ distance Δ, defined as Δ:= E ∫ |θ̂(t)−θ̂_T (t)| dF_Q(t), where θ̂ and θ̂_T denote respectively, the estimates of the state occupation probability θ from the current status data and its targeted counterpart based on data generated with 1000 clusters. The integrating measure is the empirical distribution function of the transition times, given as F_Q(t) = Q⁻¹ Σ I{C_il ≤ t}. Δ = 0 implies complete agreement on the support of the observed C. We calculate Δ via Monte Carlo averaging with a replication size of 5000.

For the two scenarios on ICS generation, the targeted state occupation probabilities at any given time t are computed as follows. Generate a single large sample of M = 1000 clusters, and the corresponding transition times T_1,il, T_2,il. For the first scenario, we consider estimating the marginal (i.e., not conditional on X) state occupation probabilities. In this case, the targeted state occupation probabilities are taken as:

$$\begin{array}{c}{\widehat{P}}_1(t)=\frac{1}{M}\sum _{i=1}^M\frac{1}{n_i}\sum _{l=1}^{n_i}I(T_{1,il}>t),\\ {\widehat{P}}_2(t)=\frac{1}{M}\sum _{i=1}^M\frac{1}{n_i}\sum _{l=1}^{n_i}I(T_{1,il}\le t<T_{2,il}),\\ {\widehat{P}}_3(t)=\frac{1}{M}\sum _{i=1}^M\frac{1}{n_i}\sum _{l=1}^{n_i}I(T_{2,il}\le t).\end{array}$$

For the second scenario, the target probabilities are computed as:

$$\begin{array}{c}{\widehat{P}}_1(t\mid x)=\frac{\frac{1}{M}{\sum }_{i=1}^M\frac{1}{n_i}{\sum }_{l=1}^{n_i}I(T_{1,il}>t)\varphi (\frac{Z_{4,il}-x}{h})}{\frac{1}{M}{\sum }_{i=1}^M\frac{1}{n_i}{\sum }_{l=1}^{n_i}\varphi (\frac{Z_{4,il}-x}{h})}\\ {\widehat{P}}_2(t\mid x)=\frac{\frac{1}{M}{\sum }_{i=1}^M\frac{1}{n_i}{\sum }_{l=1}^{n_i}I(T_{1,il}<t<T_{2,il})\varphi (\frac{Z_{4,il}-x}{h})}{\frac{1}{M}{\sum }_{i=1}^M\frac{1}{n_i}{\sum }_{l=1}^{n_i}\varphi (\frac{Z_{4,il}-x}{h})}\\ {\widehat{P}}_3(t\mid x)=\frac{\frac{1}{M}{\sum }_{i=1}^M\frac{1}{n_i}{\sum }_{l=1}^{n_i}I(T_{2,il}\le t)\varphi (\frac{Z_{4,il}-x}{h})}{\frac{1}{M}{\sum }_{i=1}^M\frac{1}{n_i}{\sum }_{l=1}^{n_i}\varphi (\frac{Z_{4,il}-x}{h})}\end{array}$$

where ϕ is standard normal and h is a data-dependent bandwidth sequence (Wand & Jones, 1995). For the second scenario, the L₁ distance was calculated at the first and third quartile of Z_4,il from the target cluster. Table 1 presents the L₁ risks of weighted (by inverse cluster size) and unweighted estimators, represented by superscript w and uw respectively, for cluster sizes m = 30 and 200 for the following parameter setting, that was arbitrarily selected from all combinations: β₁ = 0.3, β₂ = 0.4, β₃ = β₄ = −0.2, β₅ = −0.3, ${\sigma }_3^2=0.15,{\sigma }_{\alpha }^2=0.25,{\sigma }_{\epsilon }^2=0.05$, γ₁ = 1.5, γ₂ = 3, γ₃ = 1. Results for a number of additional settings are reported in Tables 4–14 in the Appendix. The overall conclusions from all the tables are similar.

Table 1.

Simulation results showing the L₁ risk of state occupation probability estimators based on 5000 Monte Carlo runs in presence of ICS. The row P̂_j represents the values corresponding to the marginal state occupation probability of state j (the Monte Carlo standard errors were ≤ 0.0007); the rows ${\widehat{P}}_j^{Q1}$ and ${\widehat{P}}_j^{Q3}$ correspond to the values for the conditional state occupation probabilities given X for the first and third quartiles, respectively, of the unit-level covariate Z_4,il (the Monte Carlo standard errors were ≤ 0.0004).

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	200w	200uw		30w	30uw	200w	200uw
P̂1	0.021	0.048	0.018	0.052	${\widehat{P}}_1^{Q1}$	0.019	0.048	0.015	0.057
P̂2	0.018	0.048	0.014	0.054	${\widehat{P}}_2^{Q1}$	0.019	0.052	0.013	0.063
P̂3	0.051	0.091	0.046	0.100	${\widehat{P}}_3^{Q1}$	0.044	0.094	0.037	0.112
					${\widehat{P}}_1^{Q3}$	0.018	0.042	0.014	0.047
					${\widehat{P}}_2^{Q3}$	0.017	0.044	0.012	0.051
					${\widehat{P}}_3^{Q3}$	0.047	0.082	0.040	0.094

Table 4.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.15), ε_il ~ N(0, 0.2), γ₁ =−1, γ₂ = 4, γ₃ =−4. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.005.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.048	0.076	0.025	0.071	${\widehat{P}}_1^{Q1}$	0.048	0.089	0.027	0.086
P̂2	0.066	0.092	0.037	0.081	${\widehat{P}}_2^{Q1}$	0.065	0.115	0.039	0.111
P̂3	0.082	0.133	0.045	0.126	${\widehat{P}}_3^{Q1}$	0.062	0.133	0.037	0.141
					${\widehat{P}}_1^{Q3}$	0.042	0.070	0.021	0.067
					${\widehat{P}}_2^{Q3}$	0.054	0.083	0.028	0.079
					${\widehat{P}}_3^{Q3}$	0.081	0.130	0.037	0.122

Table 14.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.15), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.05), γ₁ = 1.5, γ₂ = 3, γ₃ = 1. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.076	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.049	0.086	0.027	0.086
P̂2	0.068	0.092	0.038	0.081	${\widehat{P}}_2^{Q1}$	0.065	0.108	0.038	0.111
P̂3	0.083	0.131	0.047	0.127	${\widehat{P}}_3^{Q1}$	0.065	0.126	0.036	0.141
					${\widehat{P}}_1^{Q3}$	0.042	0.067	0.022	0.067
					${\widehat{P}}_2^{Q3}$	0.052	0.077	0.027	0.079
					${\widehat{P}}_3^{Q3}$	0.080	0.121	0.036	0.123

As revealed from Table 1, our ICS adjusted regression estimators outperformed the ‘without ICS adjusted’ counterparts for both scenarios. For the weighted estimators, the L₁ risks decrease as the number of clusters increases. The results are indicative of their large sample consistency although the rate of convergence might be slow, which is to be expected. The biases for the unweighted estimators do not go away with increasing number of clusters indicating that such estimators are not valid in presence of ICS.

3.3 Coverage of smoothed bootstrap based confidence intervals

Nonparametric regression (conditional state occupation probabilities) induces difficulty in the asymptotic analysis of our estimators. In addition, operations such as GPAVA will add to the complication, and the final asymptotic distribution may not be tractable in a usable form, say for construction of confidence intervals (CI). A practical/working alternative may be a bootstrap-based CI. Guided by existing results (Li & Datta, 2001) for bootstrapping nonparametric regression estimators, we proposed a smoothed bootstrap where a larger bandwidth is used for centering the resampled statistic.

The current problem is an example of non-standard asymptotics for which the naive bootstrap will not work. In addition to the issue of clustered data, the estimators we are trying to bootstrap involves smoothing. It has been demonstrated that with a naive centering, bootstrap cannot capture the bias term in the smoothed estimator (Faraway & Jhun, 1990). One way of circumventing the problem is to resample from an oversmoothed estimator, followed by centering based on the oversmoothed estimator. Theoretical validity of these type of smoothed bootstrap has been established in Li & Datta (2001). Hence, we used the following resampling scheme in order to tackle the issues of bootstrapping smoothed estimators based on clustered data. First, a bootstrap sample { $n_i^{\ast },C_{il}^{\ast },S_{il}^{\ast }(C_{il}^{\ast }),X_{il}^{\ast },1\le l\le n_i^{\ast }$, 1 ≤ i ≤ m} was obtained via simple random sampling with replacement of the entire clusters of observations {n_i, C_il, S_il(C_il), X_il, 1 ≤ l ≤ n_i, 1 ≤ i ≤ m}, where m is the total number of clusters and n_i is the size of the ith cluster, as defined before. Note, here we do not resample individual records, but the entire clusters of data values, following Field & Welsh (2007). This preserves the dependence structure within the clusters, and also the informativeness. Let g = max(h^0.8, h̃^0.8), where h and h̃ were the bandwidths described in Section 2.2. Since typically both h and h̃ are less than 1, g is going to be larger than these bandwidths, which is needed for the over-smoothing mentioned before. We then smooth the inspection times by $C_{il}^{\ast }\leftarrow C_{il}^{\ast }+g{\epsilon }_{il}$, where ε_il follows a truncated standard normal distribution with lower boundary equals to negative of minimum of $C_{il}^{\ast }$.

For 0 < α < 1, let Δ̂_1−α(t) be the (1 − α)-th bootstrap percentile of the distribution of $\mid {sin}^{-1}\sqrt{{\widehat{P}}_j^{\ast }(t;\stackrel{\sim }{h}\mid x)}-{sin}^{-1}\sqrt{{\widehat{P}}_j(t;g\mid x)}\mid$, where P̂^* uses the same bandwidth as in the original but is based on the bootstrap sample; however, P̂_j(t; g|x) for centering is recomputed from the original sample but using the new bandwidth g. Then, our (1 − α) × 100% pointwise CI for the state j occupation probability at time t is given by

$$\left|{sin}^2\left\{max\left(0,\sqrt{{\widehat{P}}_j(t;\stackrel{\sim }{h}\mid x)}-{\widehat{\mathrm{\Delta }}}_{1-\alpha /2}\right)\right\},{sin}^2\left\{min\left(\frac{\pi }{2},\sqrt{{\widehat{P}}_j(t;\stackrel{\sim }{h}\mid x)}+{\widehat{\mathrm{\Delta }}}_{1-\alpha /2}\right)\right\}\right|,$$ (3.3)

where P̂_j(t|x). Note that the PD data application (Section 4) also uses the same rule to obtain g.

We evaluate the performance of the smoothed bootstrap based confidence intervals in the ICS scenario 2. A set of 1000 bootstrap replicates was used to calculate the bootstrap percentiles for each original sample in 1000 Monte Carlo trials. From Table 2, we note that the empirical coverage probabilities of bootstrap-based 95% CIs are reasonable. The overall coverage improved for more extreme time values with the number of clusters.

Table 2.

Coverage probabilities for the weighted estimator of state occupation probabilities based on 1000 Monte Carlo runs and 1000 bootstrap samples per run at nominal level 0.05. This is evaluated at ten fixed time points when the unit level covariate X = Z_4,il equals its third quartile.

Time	n = 50	n = 100	n = 200
0.75	0.94	0.94	0.95
1	0.96	0.96	0.97
1.25	0.96	0.96	0.97
1.5	0.98	0.98	0.98
1.75	0.98	0.98	0.99
2	0.97	0.99	1.00
2.25	0.97	0.99	1.00
2.5	0.95	0.98	0.99
2.75	0.92	0.96	0.96
3	0.88	0.92	0.93

4 Application

The motivating PD data was collected as part of a clinical study to explore the relationship between PD and diabetes (determined by the popular marker HbA1c, or ‘glycosylated hemoglobin’) in the Type-2 diabetic adult Gullah-speaking African-Americans residing in the coastal sea-islands of South Carolina by the Center for Oral Health Research (COHR) at the Medical University of South Carolina (MUSC) (Fernandes et al., 2009). The relationship between periodontal disease and diabetes level has been previously studied in the dental literature (Faria-Almeida et al., 2006; Taylor & Borgnakke, 2008). We selected 288 patients with complete covariate information and with at least one tooth present at inspection.

Dental hygienists often use a periodontal probe to measure clinical attachment level (or CAL) at six sites per tooth throughout the mouth (excluding the third molars). The CAL is defined as the distance down a tooths root detached from the surrounding bone. Additionally, several patient-level covariates were obtained, including age (in years), gender (1 = Female, 0 = Male), body mass index or BMI (in kg/m2), smoking status (1 = a smoker, 0 = never) and HbA1c (1 = High, 0 = controlled). Of the 288 subjects, 76% were female, 31% were current or past smokers, and 41% had a high HbA1c level (≥ 7). BMI is classified as Overweight (with 25 ≤ BMI < 30), Obese I (with 30 ≤ BMI < 40), Obese III (with BMI ≥ 40). The (clustered) multistate current status data consists of the PD states determined by CAL values at each of the 6 sites per tooth, with the current status times calculated as the difference between the patient’s age and dentition time for each tooth. Note that the dentition/eruption time varies by tooth and subject, and is unknown for this population. Hence, we fix the eruption times at a common value representing the population averaged eruption time of US adults, available at the American Dental Association weblink (http://www.ada.org/2930.aspx). The various states of our multistate model are: CAL = 0 representing State 0 (healthy); CAL in [1, 2] representing State 1 (slight PD); CAL in [3, 4] representing State 2 (moderate PD); and CAL >= 5 or missing, representing State 3 (severe PD), following the American Association of Periodontology (AAP) 1999 classification (Armitage, 1999). The prevalence of the states of PD by various covariates are presented in Table 3. Each patient is treated as a cluster, with the maximum cluster size be 168 when all teeth are present.

Table 3.

Prevalence in terms of frequencies (column percentages) of the PD states in the Gullah dataset grouped by gender, smoking status and Hba1c status.

State	Male	Female	Non-Smoker	Smoker	HbA1c High	HbA1c Controlled
Healthy	928(12)	3084(12)	2991(13)	1021(10)	1792(13)	2220(12)
Early	5086(63)	15487(63)	14446(63)	6127(63)	8426(62)	12147(63)
Moderate	1458(18)	4383(18)	3967(17)	1874(19)	2356(17)	3485(18)
Severe	577(7)	1732(7)	1588(7)	721(7)	926(7)	1383(7)

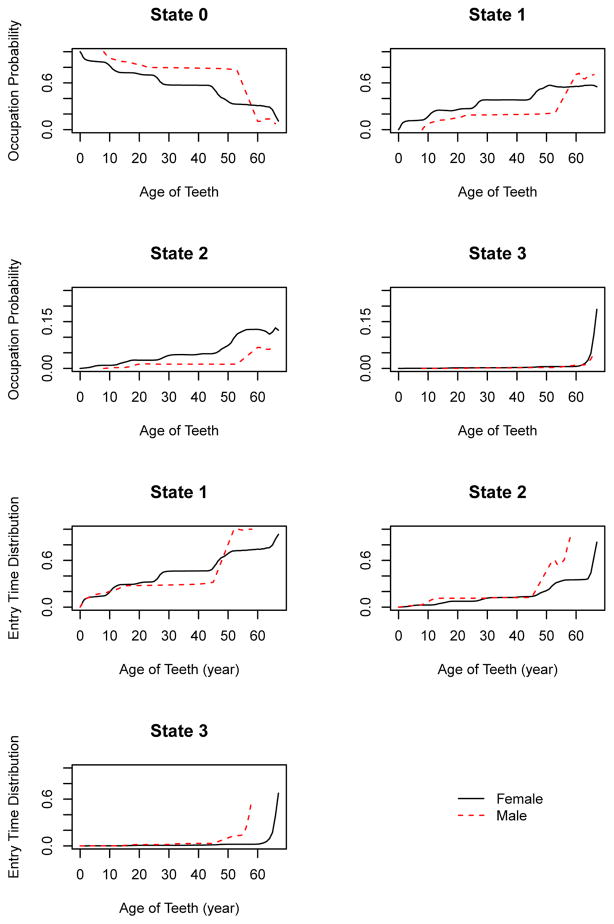
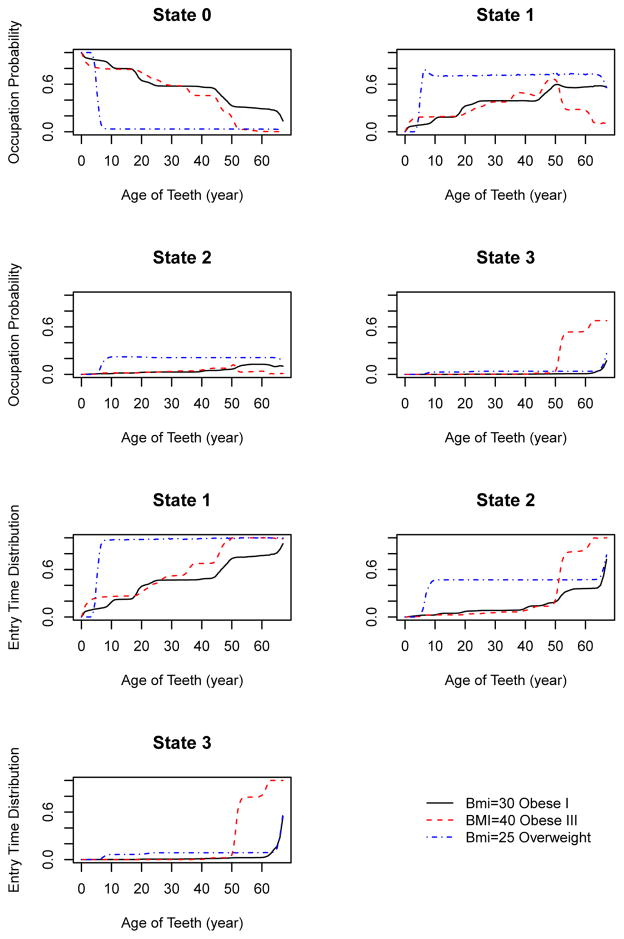
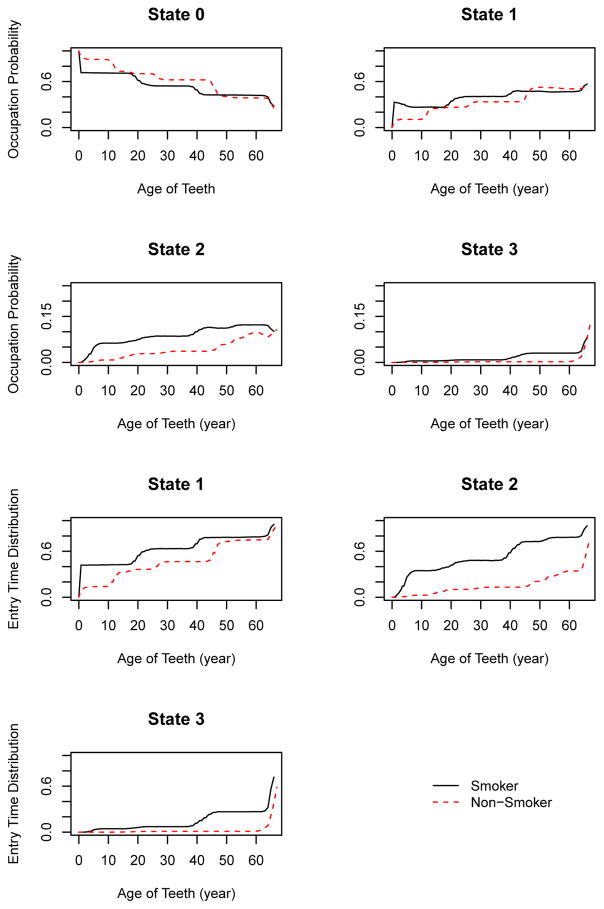
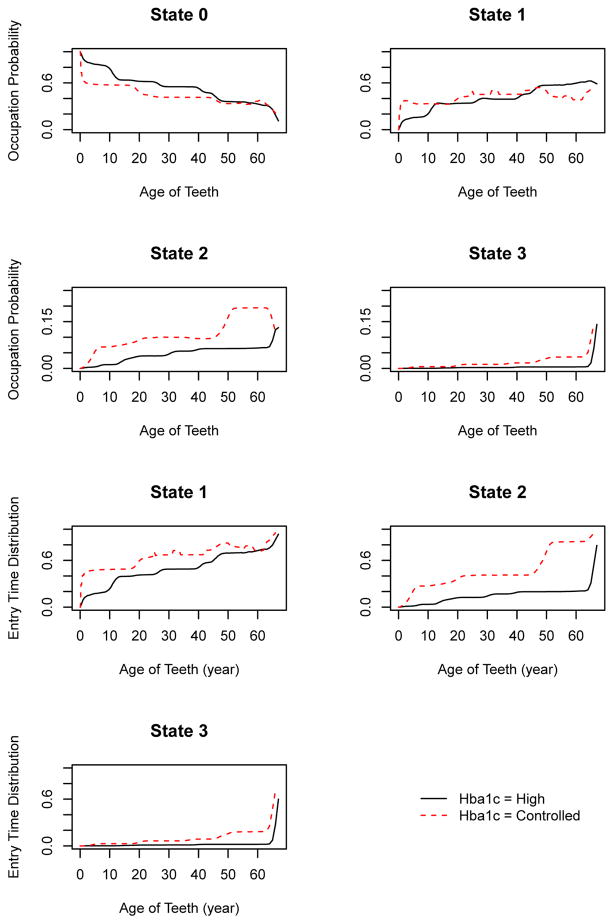
Note that BMI is the only quantitative covariate in our case study. The other covariates are naturally categorical and the corresponding conditional estimators are just the marginal estimators obtained using the sub-samples that correspond to each level of the covariate. The state occupation probabilities and state entry/exit time distributions for the PD data are estimated and plotted by gender, smoking status, HbA1c category and the BMI level (only 3 arbitrarily selected levels are used for the display) in Figures 1–4. Females are more frequently detected than males across all disease states before 73.5 years of age (Figure 1). From Figure 2, current or former smokers tend to be diagnosed more often at all stages of PD than non-smokers at all ages, except for slight PD until age 60.5 years old and beyond. In addition, smokers enter the various disease states at a higher rate than non-smokers across all states and ages. Patients with controlled HbA1c were detected more often with moderate PD across all ages (see Figure 3), compared to the high HbA1c group. However, both HbA1c groups had similar performances when PD is severe. From Figure 4, we observe that the effect of obesity (BMI) on PD varies with age. For the overweight patients (BMI between 25 and 29.9), the periodontal health deteriorated quickly from 20 years of age, is the most observed group for slight and moderate PD states, and also for the severe PD state till 63.5 years of age. However, the impact of the Class III obesity group (BMI ≥ 40) was predominant at higher ages (> 65 years), as compared to the overweight and Class I-II obese (BMI between 30 and 39.9) groups, for severe PD.

Figure 1.

Estimates of state occupation probabilities and entry/exit time distributions for healthy (State 0), early (State 1), moderate (State 2) and severe (State 3) PD categories by gender from the dataset.

Figure 4.

Estimates of state occupation probabilities and entry/exit time distributions for healthy (State 0), early (State 1), moderate (State 2) and severe (State 3) PD categories by BMI levels from the dataset.

Figure 2.

Estimates of state occupation probabilities and entry/exit time distributions for healthy (State 0), early (State 1), moderate (State 2) and severe (State 3) PD categories by smoking status from the dataset.

Figure 3.

Estimates of state occupation probabilities and entry/exit time distributions for healthy (State 0), early (State 1), moderate (State 2) and severe (State 3) PD categories by HbA1c status from the dataset.

Note that we can test the overall effect of a cluster level covariate X on the state occupation probability P_j by comparing the marginal and the conditional state occupation probabilities using the L₁ distance test statistic

$$T:=m^{-1}\sum _{i=1}^m\int \mid {\widehat{P}}_j(t)-{\widehat{P}}_j(t\mid X_i)\mid d{F}_Q(t),$$ (4.1)

where F_Q is as before (see the Simulation section). Its p-value can be computed using a null boot-strap that resamples { $n_i^{\ast },C_{il}^{\ast },S_{il}^{\ast }(C_{il}^{\ast }):1\le l\le n_i^{\ast }$}, 1 ≤ i ≤ m, and { $X_i^{\ast }$}, 1 ≤ i ≤ m, separately from the respective collections of original data values and then concatenates them together to form { $X_i^{\ast },n_i^{\ast },C_{il}^{\ast },S_{il}^{\ast }(C_{il}^{\ast }),1\le l\le n_i^{\ast }$}, 1 ≤ i ≤ m. For computational savings, we approximated this test statistic by comparing at five percentiles of the covariate distribution and a grid of fifty time points (representing age of teeth). Using this nonparametric and omnibus test, statistical significance at 5% was reached only for the effect of BMI on the severe PD state occupation probabilities (bootstrap based p-value = 0.006).

5 Conclusion

We present a nonparametric regression framework for clustered current status data observed at multiple disease states under the ICS scenario. Although each of these issues (current status multi-state data, non-parametric regression of state occupation probabilities, clustered data with ICS) has been separately studied in the literature, the combination of the three is new. As demonstrated by the application to the PD data, such a combination could arise in practice. This work extends the previous nonparametric estimation strategies presented in Lan & Datta (2010b) for the estimation of marginal state occupation probabilities using current status data and the work by Mostajabi & Datta (2013) for non-parametric regression under right censored data. Both simulation studies and application to a real dataset on PD reveal the superior performance of the ICS-adjusted estimators over the non-ICS ones.

Although our data application is on PD, there are other contexts where a unified framework combining multi-state models, current status data, and informative cluster size is justified. For example, in an epidemiological study on dental caries, subjects around a specific age (say, 19 years) may be inspected to determine the age distribution of dental caries development in young adults (as defined by a specific age range). Here, the event whether caries has developed or not at the exact age of inspection is a current status information. The teeth within a mouth are clustered, the number of teeth is potentially informative of the carries development (due to its connection to the overall oral health), and the caries development occurs through a sequential progression of states. Another example could be on determining the distribution of an ongoing staphylococcus infection in hospitals in a given locality. Here, patients within a hospital are inspected for presence/absence of infection, and the corresponding event times for each patient (given by the number of days since hospitalization determined from their admission record) would represent clustered current status event times. Once again, the number of patients within a hospital (cluster size) can be informative of the underlying infection, related through quality of care, management, greater individual-individual contact, etc, and the associated infection can exhibit a multistate progression.

ICS is a topic of considerable interest in recent times (Huang & Leroux, 2011; Nevalainen et al., 2014). In particular, the recent article by Seaman et al. (2014) compares and contrasts various proposed schemes that uses weighted (Williamson et al., 2003) and doubly-weighted (Huang & Leroux, 2011) generalized estimating equations (GEE), and shared random-effects (Li et al., 2011). Our current framework is nonparametric. How our method compares with the GEE-type or random-effects based propositions for multistate current status data is of interest. In addition, PD clinical trials generate more complex clustered-longitudinal data where tooth-site level longitudinal profiles are generated, along with covariates that can be time varying. This leads to more complex interval-censoring issues, with possible ICS scenario reflective of the periodontal health at a specific time point. The methods developed in this paper can certainly be adapted to this scenario, and remains a viable area for future research.

Our present demonstration handles one covariate at a time. Multiple covariates are common in most applications, and use of a fully non-parametric approach will suffer from the ‘curse of dimensionality’. However, a semi-parametric approach, such as a single index model for the counting and number at risk processes for each time point may be viable. Very recently, Siriwardena et al. (2016) developed the details for right-censored survival data. Extending it to the multi-state current status framework will be explored elsewhere.

Table 5.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.15), ε_il ~ N(0, 0.2), γ₁ = 1.5, γ₂ = 3, γ₃ = 1. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.004.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.049	0.078	0.026	0.069	${\widehat{P}}_1^{Q1}$	0.049	0.087	0.027	0.087
P̂2	0.068	0.093	0.038	0.078	${\widehat{P}}_2^{Q1}$	0.066	0.111	0.038	0.114
P̂	0.085	0.135	0.047	0.122	${\widehat{P}}_3^{Q1}$	0.067	0.128	0.035	0.147
					${\widehat{P}}_1^{Q3}$	0.042	0.068	0.022	0.069
					${\widehat{P}}_2^{Q3}$	0.054	0.080	0.028	0.081
					${\widehat{P}}_3^{Q3}$	0.078	0.122	0.036	0.126

Table 6.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.15), ε_il ~ N(0, 0.05), γ₁ = −1, γ₂ = 4, γ₃ = −4. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.004.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.048	0.076	0.025	0.071	${\widehat{P}}_1^{Q1}$	0.048	0.089	0.027	0.086
P̂2	0.066	0.092	0.037	0.081	${\widehat{P}}_2^{Q1}$	0.065	0.115	0.039	0.111
P̂3	0.082	0.133	0.045	0.126	${\widehat{P}}_3^{Q1}$	0.062	0.133	0.037	0.141
					${\widehat{P}}_1^{Q3}$	0.042	0.070	0.021	0.067
					${\widehat{P}}_2^{Q3}$	0.054	0.083	0.028	0.079
					${\widehat{P}}_3^{Q3}$	0.081	0.130	0.037	0.122

Table 7.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.15), ε_il ~ N(0, 0.05), γ₁ = 1.5, γ₂ = 3, γ₃ = 1. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.004.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.049	0.078	0.026	0.069	${\widehat{P}}_1^{Q1}$	0.049	0.087	0.027	0.087
P̂2	0.068	0.093	0.038	0.078	${\widehat{P}}_2^{Q1}$	0.066	0.111	0.038	0.114
P̂3	0.085	0.135	0.047	0.122	${\widehat{P}}_3^{Q1}$	0.067	0.128	0.035	0.147
					${\widehat{P}}_1^{Q3}$	0.042	0.068	0.022	0.069
					${\widehat{P}}_2^{Q3}$	0.054	0.080	0.028	0.081
					${\widehat{P}}_3^{Q3}$	0.078	0.122	0.036	0.126

Table 8.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.2), γ₁ = −1, γ₂ = 4, γ₃ = −4. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.078	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.049	0.088	0.027	0.087
P̂2	0.07	0.092	0.037	0.08	${\widehat{P}}_2^{Q1}$	0.067	0.112	0.037	0.114
P̂3	0.082	0.13	0.046	0.126	${\widehat{P}}_3^{Q1}$	0.070	0.132	0.035	0.145
					${\widehat{P}}_1^{Q3}$	0.043	0.068	0.022	0.068
					${\widehat{P}}_2^{Q3}$	0.053	0.081	0.028	0.081
					${\widehat{P}}_3^{Q3}$	0.076	0.123	0.037	0.125

Table 9.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.2), γ₁ = 1.5, γ₂ = 3, γ₃ = 1 The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.076	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.049	0.087	0.027	0.085
P̂2	0.068	0.092	0.038	0.081	${\widehat{P}}_2^{Q1}$	0.067	0.112	0.039	0.110
P̂3	0.083	0.131	0.047	0.127	${\widehat{P}}_3^{Q1}$	0.063	0.128	0.037	0.140
					${\widehat{P}}_1^{Q3}$	0.042	0.068	0.022	0.067
					${\widehat{P}}_2^{Q3}$	0.053	0.082	0.029	0.080
					${\widehat{P}}_3^{Q3}$	0.074	0.124	0.038	0.123

Table 10.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.3), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.05), γ₁ = −1, γ₂ = 4, γ₃ = −4. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.078	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.049	0.088	0.027	0.087
P̂2	0.07	0.092	0.037	0.08	${\widehat{P}}_2^{Q1}$	0.067	0.112	0.037	0.114
P̂3	0.082	0.13	0.046	0.126	${\widehat{P}}_3^{Q1}$	0.070	0.132	0.035	0.145
					${\widehat{P}}_1^{Q3}$	0.043	0.068	0.022	0.068
					${\widehat{P}}_2^{Q3}$	0.053	0.081	0.028	0.081
					${\widehat{P}}_3^{Q3}$	0.076	0.123	0.037	0.125

Table 11.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.15), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.2), γ₁ = −1, γ₂ = 4, γ₃ = −4. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.078	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.047	0.088	0.027	0.087
P̂2	0.07	0.092	0.037	0.08	${\widehat{P}}_2^{Q1}$	0.067	0.116	0.038	0.113
P̂3	0.082	0.13	0.046	0.126	${\widehat{P}}_3^{Q1}$	0.069	0.136	0.037	0.144
					${\widehat{P}}_1^{Q3}$	0.042	0.070	0.021	0.068
					${\widehat{P}}_2^{Q3}$	0.052	0.082	0.028	0.081
					${\widehat{P}}_3^{Q3}$	0.074	0.124	0.037	0.126

Table 12.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.15), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.2), γ₁ = 1.5, γ₂ = 3, γ₃ = 1. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.076	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.049	0.086	0.027	0.086
P̂2	0.068	0.092	0.038	0.081	${\widehat{P}}_2^{Q1}$	0.065	0.108	0.038	0.111
P̂3	0.083	0.131	0.047	0.127	${\widehat{P}}_3^{Q1}$	0.065	0.126	0.036	0.141
					${\widehat{P}}_1^{Q3}$	0.042	0.067	0.022	0.067
					${\widehat{P}}_2^{Q3}$	0.052	0.077	0.027	0.079
					${\widehat{P}}_3^{Q3}$	0.080	0.121	0.036	0.123

Table 13.

Simulation results of mean L₁ distances for estimators of state occupation probabilities based on 5000 Monte Carlo trials. Parameters used for data generation are Z_3,i ~ N (1, 0.15), α_i ~ N (0, 0.25), ε_il ~ N(0, 0.05), γ₁ = −1, γ₂ = 4, γ₃ = −4. The superscripts w and uw represent, respectively, the weighted and unweighted estimates. The standard errors are ≤ 0.003.

m	First scenario: Marginal					Second scenario: Conditional
	30w	30uw	100w	100uw		30w	30uw	100w	100uw
P̂1	0.05	0.078	0.026	0.072	${\widehat{P}}_1^{Q1}$	0.047	0.088	0.027	0.087
P̂2	0.07	0.092	0.037	0.08	${\widehat{P}}_2^{Q1}$	0.067	0.116	0.038	0.113
P̂3	0.082	0.13	0.046	0.126	${\widehat{P}}_3^{Q1}$	0.069	0.136	0.037	0.144
					${\widehat{P}}_1^{Q3}$	0.042	0.070	0.021	0.068
					${\widehat{P}}_2^{Q3}$	0.052	0.082	0.028	0.081
					${\widehat{P}}_3^{Q3}$	0.074	0.124	0.037	0.126

Appendix

Theoretical justification of the inverse cluster size marginalization

Proposition

Assume that V_i:= {n_i, S_i1, ···, S_ini}, 1 ≤ i ≤ m, are independent and identically distributed random elements. Suppose the S_il within a given cluster i are exchangeable given the cluster size n_i Then P_j(t) given by (2.5) equals

$$P_j(t)=Pr\{S_{il}(t)=j\},$$

for any i and l.

Proof

By definition

$$\begin{array}{c}{P}_j(t)=E(I\{S_{IJ}(t)=j\})=E\left(m^{-1}\sum _{i=1}^m\sum _{l=1}^{n_i}{n}_i^{-1}I\{S_{il}(t)=j\}\right)\\ =E\left(\sum _{l=1}^{n_i}{n}_i^{-1}I\{S_{il}(t)=j\}\right),\text{by}\text{the}\text{i.i.d.}\text{assumption},\\ =E\left\{E\left(n_i^{-1}\sum _{l=1}^{n_i}I\{S_{il}(t)=j\}|n_i\right)\right\}\\ =E\left\{n_i^{-1}\sum _{l=1}^{n_i}E\left(I\{S_{il}(t)=j\}|n_i\right)\right\}\\ =E\left\{n_i^{-1}\sum _{l=1}^{n_i}E\left(I\{S_{i1}(t)=j\}|n_i\right)\right\},\text{by}\text{conditional}\text{exchangeability},\\ =E\left\{E\left(I\{S_{i1}(t)=j\}|n_i\right)\right\}\\ =E\left\{E\left(I\{S_{il}(t)=j\}|n_i\right)\right\},\text{by}\text{conditional}\text{exchangeability},\\ =EI\{S_{il}(t)=j\}=Pr\{S_{il}(t)=j\}.\end{array}$$

Note: As can be seen from the proof, the conditional exchangeability assumption can be weakened to that of conditional identical distribution of the S_il.

Additional L₁ risk results

The L₁ risk values for other combinations of the simulation parameters are presented in Tables 4–14. The weighted and the unweighted estimates are listed side-by-side, represented by superscript w and uw, respectively, for cluster sizes m = 30 and 100. Data were generated based on the following scenarios: (a) for ICS scenario 1, the parameters used for state 2 exit times are β₁ = 0.8, β₂ = −0.75, β₃ = β₄ = 1, β₅ = −1.5, $Z_{3,i}\sim N(1,{\sigma }_3^2),{\alpha }_i\sim N(0,{\sigma }_{\alpha }^2),{\epsilon }_{il}\sim N(0,{\sigma }_{\epsilon }^2)$ and we estimate the marginal state occupation probabilities; (b) for ICS scenario 2, an additional parameter γ₃ is needed to generate ICS associated with X and we calculate the conditional state occupation probabilities where the given value of the covariate X was set at each of the first and the third quartiles of the covariate distribution.