The human mitochondrial single-stranded DNA-binding protein displays distinct kinetics and thermodynamics of DNA binding and exchange

Abstract

The human mitochondrial ssDNA-binding protein (mtSSB) is a homotetrameric protein, involved in mtDNA replication and maintenance. Although mtSSB is structurally similar to SSB from Escherichia coli (EcoSSB), it lacks the C-terminal disordered domain, and little is known about the biophysics of mtSSB–ssDNA interactions. Here, we characterized the kinetics and thermodynamics of mtSSB binding to ssDNA by equilibrium titrations and stopped-flow kinetic measurements. We show that the mtSSB tetramer can bind to ssDNA in two distinct binding modes: (SSB)₃₀ and (SSB)₆₀, defined by DNA binding site sizes of 30 and 60 nucleotides, respectively. We found that the binding mode is modulated by magnesium ion and NaCl concentration, but unlike EcoSSB, the mtSSB does not show negative intersubunit cooperativity. Global fitting of both the equilibrium and kinetic data afforded estimates for the rate and equilibrium constants governing the formation of (SSB)₆₀ and (SSB)₃₀ complexes and for the transitions between the two binding modes. We found that the mtSSB tetramer binds to ssDNA with a rate constant near the diffusion limit (2 × 10⁹ m⁻¹ s⁻¹) and that longer DNA (≥60 nucleotides) rapidly wraps around all four monomers, as revealed by FRET assays. We also show that the mtSSB tetramer can directly transfer from one ssDNA molecule to another via an intermediate with two DNA molecules bound to the mtSSB. In conclusion, our results indicate that human mtSSB shares many physicochemical properties with EcoSSB and that the differences may be explained by the lack of an acidic, disordered C-terminal tail in human mtSSB protein.

Introduction

Single-stranded DNA-binding protein (SSB)³ is essential in all kingdoms of life and functions by binding to single-stranded DNA (ssDNA) intermediates that form transiently during genome maintenance (1). The mtSSBs are found in all eukaryotes, are evolutionarily conserved, and are essential for mitochondrial DNA replication (2–4). The human mtSSB exists as a stable tetramer (5, 6) and is thought to function in the regulation and/or protection of mtDNA D-loops (4, 7) and in other aspects of mtDNA genome maintenance and repair (8). The mtSSB appears to function with the mitochondrial DNA polymerase (Pol-γ) and the mitochondrial DNA helicase (mtDNA helicase, also known as Twinkle) to form a replisome. It has been reported that mtSSB stimulates mtDNA replication (9, 10); however, subsequent studies showed that stimulation of Pol-γ activity by mtSSB is only achieved at low salt concentration (20 mm NaCl), whereas inhibitory effects are observed at moderate to higher salt concentrations ([NaCl] > 50 mm) (11). The salt-dependent behavior may arise from the switch in binding modes, as observed previously in studies on SSB from Escherichia coli (EcoSSB) (1, 12). However, no reliable kinetic or thermodynamic analyses of mtSSB binding to ssDNA have been reported. These biophysical properties need to be established as a foundation for studies of the role of mtSSB in mtDNA replication.

EcoSSB is a well-characterized bacterial ssDNA-binding protein that serves as the prototype for many biochemical, structural, and mechanistic studies of DNA binding proteins (1, 13, 14). The EcoSSB tetramer is able to bind ssDNA in at least two different binding modes (15), (SSB)₆₅ and (SSB)₃₅, where the number denotes the number of nucleotides (nt) occluded by a single tetramer. In the (SSB)₆₅ binding mode, the ssDNA fully wraps around the tetramer, interacting with all four subunits, and is favored at high salt concentrations (15) and low protein/DNA ratios (16). In the (SSB)₃₅ binding mode, the ssDNA only interacts with two subunits of the tetramer and is favored in low salt concentrations (15) and in high protein/DNA ratios (12, 17, 18). It is well established (17, 19) that the EcoSSB tetramers bind short ssDNA fragments (≤35 nt) with negative cooperativity, with the first two subunits binding DNA with much higher affinity than the remaining two subunits, so the structure should be considered as a dimer of dimers. This negative cooperativity increases at lower salt concentrations and promotes the (SSB)₃₅ binding mode on longer ssDNA (15, 19). In other words, at low salt concentrations, even longer DNA binds only 35 nucleotides per SSB tetramer, thus defining the “(SSB)₃₅ binding mode” as opposed to the “(SSB)₆₅ binding mode” in which the DNA wraps around SSB contacting all four subunits. In both binding modes, the EcoSSB tetramer is able to diffuse along ssDNA without dissociating (20), which is thought to be critical for its function in promoting recombination via the formation of RecA filaments on ssDNA (13), presumably by transiently melting DNA secondary structure, such as hairpins, ahead of the RecA filament and by facilitating strand exchange.

The mtSSB shares a high degree of sequence and structural homology with the oligonucleotide-binding domain of the EcoSSB (5, 6) except at the C terminus. The EcoSSB contains a nine-amino acid sequence (C-terminal tail) that binds to more than a dozen different proteins that it recruits to their sites of function in DNA replication, repair, and recombination (1, 21), and it regulates the ssDNA binding affinity and cooperativity between binding sites (22). In human mtSSB, this C-terminal tail is completely missing (5), which raises the questions of whether mtSSB may show distinct ssDNA binding modes and whether the kinetic and thermodynamic basis for formation of protein–DNA complexes is different from that for EcoSSB. In the case of Plasmodium falciparum SSB (PfSSB) (23, 24), which has a C terminus different from that of EcoSSB, the PfSSB tetramers bind ssDNA only in the fully wrapped modes with occluded site size between 55 and 62 nt, with no evidence for formation of highly cooperative ssDNA binding modes. The mtSSB tetramer has been shown to bind ssDNA with a site size of about 50–70 nt at moderate to high [NaCl] (25); however, whether it can form a cooperative (SSB)₃₅ mode at lower [NaCl] has not been examined. Moreover, very little is known about the kinetics and thermodynamics involved in the formation of mtSSB–ssDNA complex, which is critical to understand the physiological role of mtSSB involved in mtDNA replication. In the only quantitative study published to date, binding was fit to a Hill equation, suggesting positive cooperativity and relatively weak binding (26).

Here, we have undertaken the first comprehensive thermodynamic and kinetic study on the ssDNA binding properties of human mtSSB by reproducing most of the key studies performed on EcoSSB over the past 30 years, but we have globally fit the equilibrium and kinetic data to derive a comprehensive, unifying model. Similar to EcoSSB, the mtSSB binds to ssDNA in two different modes, but with slightly shorter occluded sizes, forming (SSB)₆₀ and (SSB)₃₀ complexes, which are modulated by the salt and Mg²⁺ concentrations. Results obtained from stopped-flow fluorescence and equilibrium binding data were globally fit to the models shown in Schemes 1 and 2. For the (SSB)₃₀ binding mode, two molecules of ssDNA₃₀ (dT₃₀) are able to bind sequentially to one mtSSB tetramer (Scheme 1). For the (SSB)₆₀ binding mode, ssDNA₆₀ (dT₆₀) binds and wraps around the mtSSB tetramer (Scheme 2). We also show that DNA exchange occurs via an intermediate with two ssDNA molecules bound per mtSSB tetramer without the requisite formation of free protein as described in Scheme 2. The data are well represented by the models, allowing us to accurately determine the rate constants governing each step. Interestingly, unlike the EcoSSB, the mtSSB does not display the dramatic negative intratetramer cooperativity for binding short ssDNA molecules, which may be a consequence of the lack of a C-terminal tail in the mtSSB.

Scheme 1.

Model for mtSSB binding to ssDNA dT₃₀ (D₃₀). The minimal model was shown for the mtSSB tetramer (SSB) binding to D₃₀ to form SSB–D₃₀, and a second D₃₀ can bind to the tetramer when DNA is in excess. This model was used to globally fit kinetic and equilibrium binding data shown in Fig. 4. The rate constants are for the reaction in buffer A with 20 mm NaCl and 10 mm Mg²⁺ and are summarized with confidence intervals in Table 3. As described under “Results,” the ratios of rate constants were maintained during data fitting: k₊₁ = 2 × k₊₂, and k₋₂ = 2 × k₋₁, to account for stoichiometry of binding and lack of intersubunit cooperativity.

Scheme 2.

Model for mtSSB binding to ssDNA dT₆₀ (D₆₀) and for DNA exchange. The minimal model is shown for the mtSSB tetramer (SSB) binding to D₆₀ to form SSB–D₆₀. Isomerization of SSB–D₆₀ to the fully wrapped form, SSB–D_60,wrapped, leads to tighter binding. A second DNA (D₆₀) can bind to the SSB–D₆₀ to form a ternary intermediate SSB–D₆₀–D₆₀ to achieve the direct transfer of mtSSB between two ssDNA molecules. The model was used to globally fit kinetic and equilibrium binding data shown in Figs. 5 and 6. The rate constants describe the reaction in buffer A with 100 mm NaCl and 10 mm Mg²⁺, with confidence intervals summarized in Table 4. In fitting the data, the rate constants in brackets were held fixed at the values shown, as described under “Results.”

Results

Occluded site size of mtSSB on poly(dT)

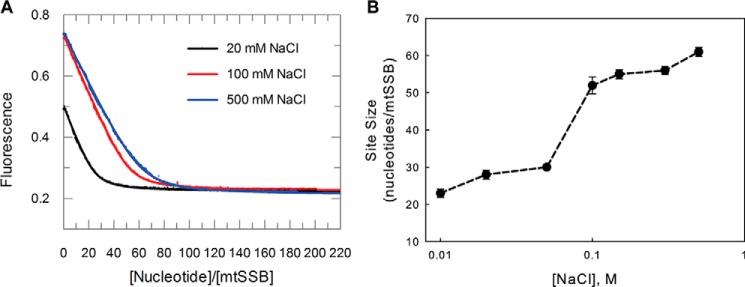
One of the primary parameters describing protein–DNA interactions is its occluded site size (footprint). Because the site size depends upon the salt concentration for EcoSSB (15), we first determined whether the NaCl concentration also affects the ssDNA occluded site size for mtSSB. As shown in Fig. 1A, the tryptophan fluorescence quenching of mtSSB upon binding poly(dT) was monitored at three different NaCl concentrations (20, 100, and 500 mm) in buffer A (20 mm Tris–Cl, pH 7.5, 5% glycerol, 0.1 mm Na₃EDTA) containing 10 mm MgCl₂. Instead of using the conventional method of estimating the site size from the interception of two straight lines (23, 27), the data were fit more rigorously to a modified quadratic equation (see “Experimental procedures” and Equation 5) to derive the site size (Fig. 1, A and B) and K_d. On poly(dT), titrations of the mtSSB tetramer show well-defined endpoints with site sizes of 60 ± 4 nt/tetramer at salt concentrations > 200 mm NaCl and 28 ± 3 nt/tetramer at low salt concentrations (<50 mm NaCl). The site sizes are slightly smaller than those of the EcoSSB tetramer, which are ∼65 and ∼35 nt/tetramer, at high and low [NaCl], respectively. This may be due to smaller size of mtSSB tetramer and, in particular, the lack of the C-terminal tail in mtSSB.

Figure 1.

Determination of site size of mtSSB tetramer on poly(dT) DNA. A, titrations of the mtSSB tetramer (40 nm) with increasing concentrations of poly(dT) were performed by monitoring protein tryptophan fluorescence quenching in buffer A with 20 mm NaCl (black), 100 mm NaCl (red), or 500 mm NaCl (blue), in the presence of 10 mm MgCl₂. The site sizes were determined by fitting the data to Equation 5. Fitted curves are superimposed on the data. B, the derived site size is plotted against the [NaCl]. Error bars, S.D.

The occluded site size does not necessarily reflect the minimal ssDNA length to which the mtSSB can bind. To assess this, we performed a series of equilibrium titration experiments to measure the binding affinity of mtSSB with varying lengths of ssDNA (15–70 nt) at different [NaCl] (20, 100, and 500 mm) using the protein fluorescence signal. As summarized in Table 1, the ssDNA binding affinity decreases as a function of increasing salt concentration. In 20 mm NaCl, the binding of dT₆₀ to the mtSSB tetramer was too tight to be measured accurately. For ssDNA shorter than 20 nucleotides, the DNA binding affinity dramatically decreased as a function of DNA length. For example, the apparent binding with dT₁₅ was too weak to be accurately measured in 500 mm NaCl, but it was 2.6 ± 0.02 μm at 100 mm NaCl and 1.1 ± 0.01 μm in 20 mm NaCl. These results suggest that ∼20 nucleotides are the minimal lengths for the mtSSB tetramer to form a reasonably stable complex at physiological salt concentrations. It is also interesting to note the anomalously lower apparent affinity of mtSSB in binding DNA 45 or 75 nt in length at 20 mm NaCl, which may be due to less optimal binding of a second mtSSB so that the observed binding affinity is an unresolved composite of the two binding events. Moreover, as described in detail below, the equation-based fitting of two sequential binding events is unreliable.

Table 1.

Dissociation constants for mtSSB binding to different lengths of ssDNA

The dissociation constant was measured for various lengths of DNA by fitting protein fluorescence titration data to a quadratic equation. All K_d values are given in nm. Experiments were performed using 50 nm mtSSB in the presence of 10 mm MgCl₂. NA, not available.

ssDNA	Kd at different NaCl concentrations
	20 mm	100 mm	500 mm
nt	nm
75	4 ± 0.5	3 ± 0.3	14.3 ± 0.2
60	<0.1	0.06 ± 0.01	14.1 ± 0.5
45	29 ± 1.1	27 ± 1.2	30.1 ± 1.5
30	1 ± 0.5	33 ± 1.1	87 ± 1.1
20	21 ± 1.2	60 ± 5.5	122 ± 2.7
15	1100 ± 11	2600 ± 1.3	NA

The mtSSB tetramer displays two binding modes dependent on [NaCl] and [Mg²⁺]

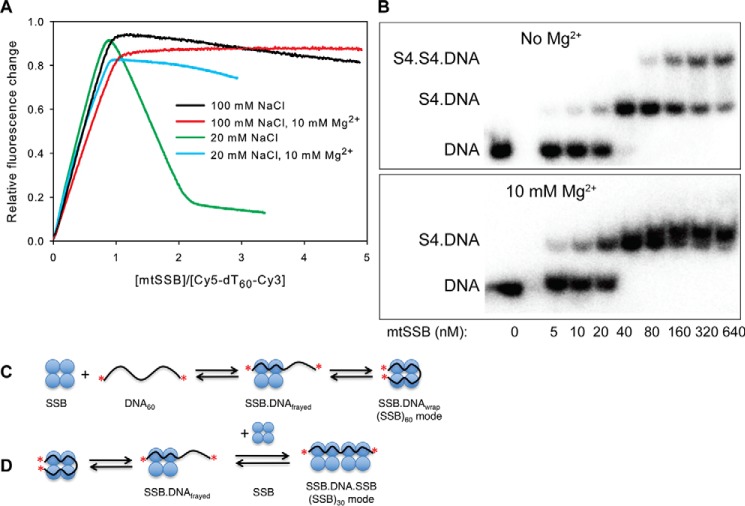
To further explore the salt concentration dependence of binding, we performed equilibration titration experiments using the dT₆₀ ssDNA with the two ends labeled with Cy3 and Cy5 fluorophores (Fig. 2). Note that we are titrating increasing concentrations of mtSSB with a fixed concentration of dT₆₀. As suggested from studies on the EcoSSB, the dT₆₀ should fully wrap around the protein to form the (SSB)₆₀ complex, bringing the Cy3 and Cy5 fluorophores close together to give a high FRET signal (model in Fig. 2C). In buffer A with 100 mm NaCl, a high-FRET complex is formed with 1:1 stoichiometry, consistent with formation of a fully wrapped (SSB)₆₀ complex (Fig. 2A, black). Upon further titration with increasing mtSSB concentration, a decrease in Cy5-FRET fluorescence was observed, which was most notable at 20 mm NaCl in the absence of Mg²⁺ (Fig. 2A, green). With 20 mm NaCl, the amplitude of the Cy5-FRET signal reached a maximum point at a stoichiometry of 1:1 and then dropped to a minimum at a stoichiometry of 2:1 (mtSSB/DNA). The decrease in FRET signal reflects the binding of a second mtSSB tetramer to the DNA, leading to separation of the Cy3 and Cy5 fluorophores in transitioning from the SSB₆₀ to the SSB₃₀ mode with two mtSSBs per DNA.

Figure 2.

mtSSB binds to ssDNA in two different binding modes, modulated by concentrations of NaCl and Mg²⁺. A, a fixed concentration of Cy5-dT₆₀-Cy3 (40 nm) was titrated with increasing concentrations of mtSSB tetramer while monitoring the FRET fluorescence (emission from Cy5 when exciting Cy3) in buffer A with 100 mm NaCl (black), with 100 mm NaCl and 10 mm Mg²⁺ (red), with 20 mm NaCl (green), or with 20 mm NaCl and 10 mm Mg²⁺ (blue). The data (except for the red line) showed a biphasic nature, suggesting the formation of two types of complexes, (SSB)₆₀ and (SSB)₃₀, which were characterized by high and low FRET values, respectively. B, effect of Mg²⁺ on the binding modes of mtSSB protein to dT₆₀ measured by gel shift. The reaction solutions contained 30 nm ³²P-labeled dT₆₀ and the indicated concentrations of mtSSB (0–640 nm) in buffer A with 100 mm NaCl (−Mg²⁺) or with 100 mm NaCl and 10 mm MgCl₂ (+Mg²⁺). The products were separated by polyacrylamide gel electrophoresis with the running buffer containing the same concentration of Mg²⁺ as in the reaction solutions and were then visualized by autoradiography. C, schematic showing the binding and wrapping of DNA around mtSSB. The red asterisks illustrate the Cy5 and Cy3 labels. D, schematic showing binding of a second mtSSB to the SSB–DNA complex to transition from the (SSB)₆₀ mode to the (SSB)₃₀ mode. For reasons described under “Results,” we illustrate this reaction involving the binding of SSB to a partially frayed intermediate in equilibrium with the fully wrapped complex.

In contrast, very little decrease in Cy5-FRET fluorescence was observed upon the further addition of mtSSB in the presence of 10 mm Mg²⁺ at 100 mm NaCl after the initial formation of a 1:1 mtSSB–dT₆₀ complex (Fig. 2A, red), suggesting that the mtSSB predominantly forms the (SSB)₆₀ binding mode under these conditions. These data show that higher salt concentrations and especially the presence of Mg²⁺ dramatically inhibit the formation of the (SSB)₃₀ complex.

To directly visualize different binding modes, we resolved the protein–DNA complexes on native polyacrylamide gels. As shown in Fig. 2B, when increasing concentrations of mtSSB tetramer were added to dT₆₀ at 100 mm NaCl in the absence of Mg²⁺, an initial complex with gel mobility lower than that of unbound DNA was formed at the substoichiometric protein concentrations. A further increase in the concentration of mtSSB tetramer (up to 21-fold excess) resulted in the decrease of this initial complex and the appearance of a second complex of even lower gel mobility (Fig. 2B). These results indicated that two tetramers of mtSSB protein were able to bind to one dT₆₀ at a high [mtSSB]/[DNA] ratio in the absence of Mg²⁺. A different result was obtained in the presence of 10 mm Mg²⁺ (Fig. 2B, bottom). In this case, an initial complex was again formed up to stoichiometric [mtSSB]/[DNA] protein concentrations. However, in contrast to the results obtained in the absence of Mg²⁺, there was no indication of the formation of the second complex at the highest concentration of mtSSB examined in the presence of Mg²⁺ (Fig. 2B). The gel results support our interpretation of the fluorescence signals and indicate that only a single tetramer of mtSSB was able to bind to one dT₆₀ molecule in the presence of 10 mm Mg²⁺ and 100 mm NaCl.

Calorimetric determination of the ΔH for mtSSB–dT₆₀ binding

We next used isothermal titration calorimetry (ITC) to obtain estimates for the enthalpy and affinity for DNA binding. It should be noted that compared with the fluorescence methods, the lower sensitivity of ITC requires higher protein concentrations, making estimates of binding affinity far less accurate at the lower NaCl and MgCl₂ concentrations due to the low K_d values relative to the protein concentration. The results of ITC measurements for the binding of dT₆₀ to mtSSB tetramers in buffer A with 10 mm Mg²⁺ and varying salt concentrations are shown in Fig. 3A. Note that we are titrating dT₆₀ into a fixed concentration of mtSSB. Consistent with the fluorescence titration experiments (Table 1), the binding is very tight at NaCl concentrations from 20 to 400 mm but is weakened at 1 m NaCl, allowing us to determine K_d = 33 ± 3.3 nm in 1 m NaCl. In 20 mm NaCl and 10 mm Mg²⁺, an initial weaker binding was detected when the mtSSB was in excess of dT₆₀, due to the binding of two mtSSB tetramers to dT₆₀, leading to a baseline shift at low dT₆₀/mtSSB ratios. As the dT₆₀/mtSSB ratio approached unity, the equilibrium shifted to the tight-binding 1:1 complex. This is consistent with the fluorescence equilibrium titration data (Fig. 2A). As summarized in Table 2, the ΔH values are all negative with a maximum magnitude of −88 ± 1.2 kcal/mol in 20 mm NaCl and 10 mm Mg²⁺, which is a smaller magnitude than that of EcoSSB binding to dT₆₀ (−146 ± 1 kcal/mol) (28). The overall enthalpy changes exhibit a decrease in magnitude as a function of [NaCl], demonstrating the large effect of salt concentration on ΔH (Table 2). A plot of ΔH versus log[NaCl] was linear with a slope of 23 kcal/mol, which is about half of the value reported for EcoSSB (29). In either case, the salt concentration dependence reflects the release of Cl⁻ from mtSSB upon binding ssDNA.

Figure 3.

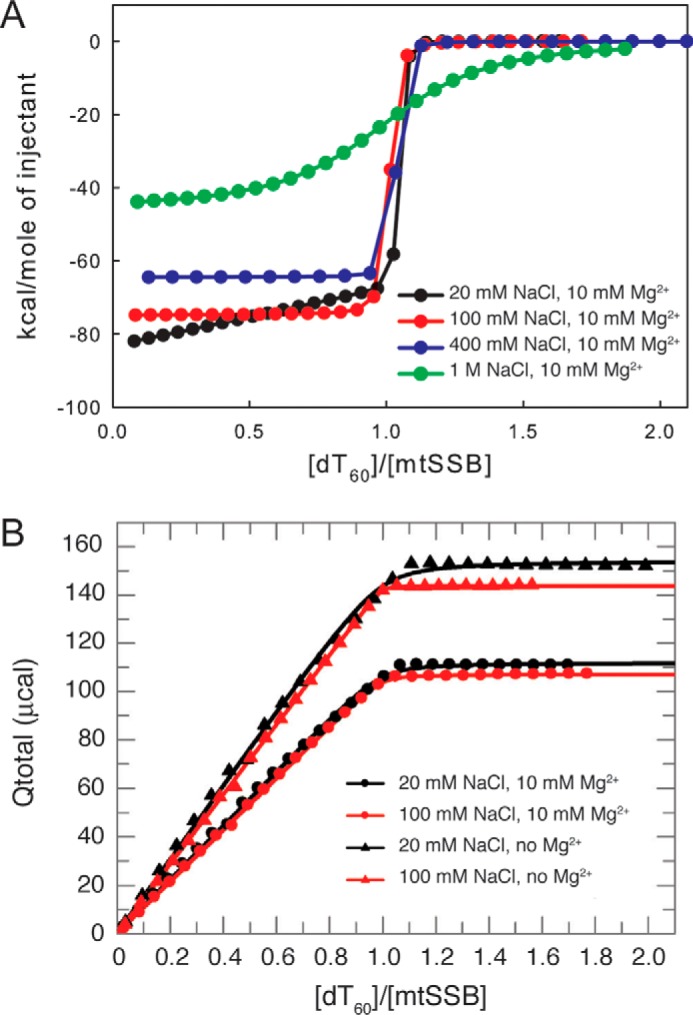
Determination of ΔH and K_d of mtSSB tetramer binding to dT₆₀ ssDNA by isothermal titration calorimetry. A, effects of salt concentration on the ΔH and K_d for mtSSB binding to dT₆₀. Shown are ITC titrations of mtSSB (1 μm) with dT₆₀ ssDNA (0–2 μm) in buffer A containing 10 mm Mg²⁺ with 20 (black), 100 (red), 400 (blue), and 1 m NaCl (green). With the exception of the data at 1 m NaCl, the binding is very tight, as demonstrated by the abrupt transition between the linear binding regime and complete reaction. B, plot of total heat release (Q_total) (μcal) as a function of the molar ratio between dT₆₀ and mtSSB tetramer, obtained by integration of the differential heat release profiles as illustrated in A. Solid lines represent the best fits of data to the quadratic equation to obtain ΔH and K_d values listed in Table 2. The net ΔH values were computed from the Q_total values by dividing by the moles of mtSSB present in the reaction cell (∼1.38 nmol).

Table 2.

Thermodynamic parameters derived by ITC for binding dT₆₀

Observed enthalpies and K_d values were derived by fitting integrated ITC data to a quadratic equation as described under “Experimental procedures.” In the absence of Mg²⁺ at 20 and 100 mm NaCl, the binding was too tight to measure reliably, with a concentration of 1 μm mtSSB during the measurement, so that the K_d values in parentheses should be considered as upper limits. ND, not determined.

[NaCl]	10 mm MgCl2		No MgCl2
	ΔH	Kd	ΔH	Kd
mm	kcal/mol	nm	kcal/mol	nm
20	−88 ± 1.2	(1.1 ± 0.3)	−110 ± 1.2	<1
100	−75 ± 0.5	(1.0 ± 0.6)	−95 ± 0.5	<1
400	−64 ± 0.9	3.1 ± 1.7	ND	ND
1000	−46 ± 0.5	33 ± 3.3	ND	ND

It should be noted that “integrated” ITC data (Fig. 3A) are usually presented as the first derivative of a typical titration curve. Therefore, as illustrated in Fig. 3B, we have integrated the ITC data to provide titration curves that can be fitted more rigorously by using conventional quadratic equations and by computer simulation to afford simultaneous fitting of kinetic and equilibrium binding data as described below. Using this approach, we examined whether magnesium affects the apparent binding affinity or the binding enthalpies for mtSSB–dT₆₀ interaction. As shown in Fig. 3B, the heat released increases linearly with [dT₆₀] until saturation is reached at a 1:1 stoichiometry with a net ΔH of −110 ± 1.2 kcal/mol at 20 mm NaCl and −95 ± 0.9 kcal/mol at 100 mm NaCl in the absence of Mg²⁺ (summarized in Table 2). The presence of magnesium decreased the magnitude of the binding enthalpies to −88 ± 1.2 kcal/mol in 20 mm NaCl and to −75 ± 0.5 kcal/mol in 100 mm NaCl, and the apparent binding affinity was weakened with an apparent K_d of 1.1 ± 0.3 nm in 20 mm NaCl and 1.2 ± 0.5 nm in 100 mm NaCl, determined by fitting the data to the quadratic equation (Fig. 3B). It should be noted, however, that these binding affinities are significantly underestimated, as shown by subsequent analysis using fluorescence methods (see Fig. 5). Our results show that divalent magnesium is much more efficient than monovalent sodium in shielding the negative charged phosphate groups of the ssDNA (30) and thus can more effectively attenuate the interaction of charged residues in mtSSB with the phosphate groups of ssDNA.

Figure 5.

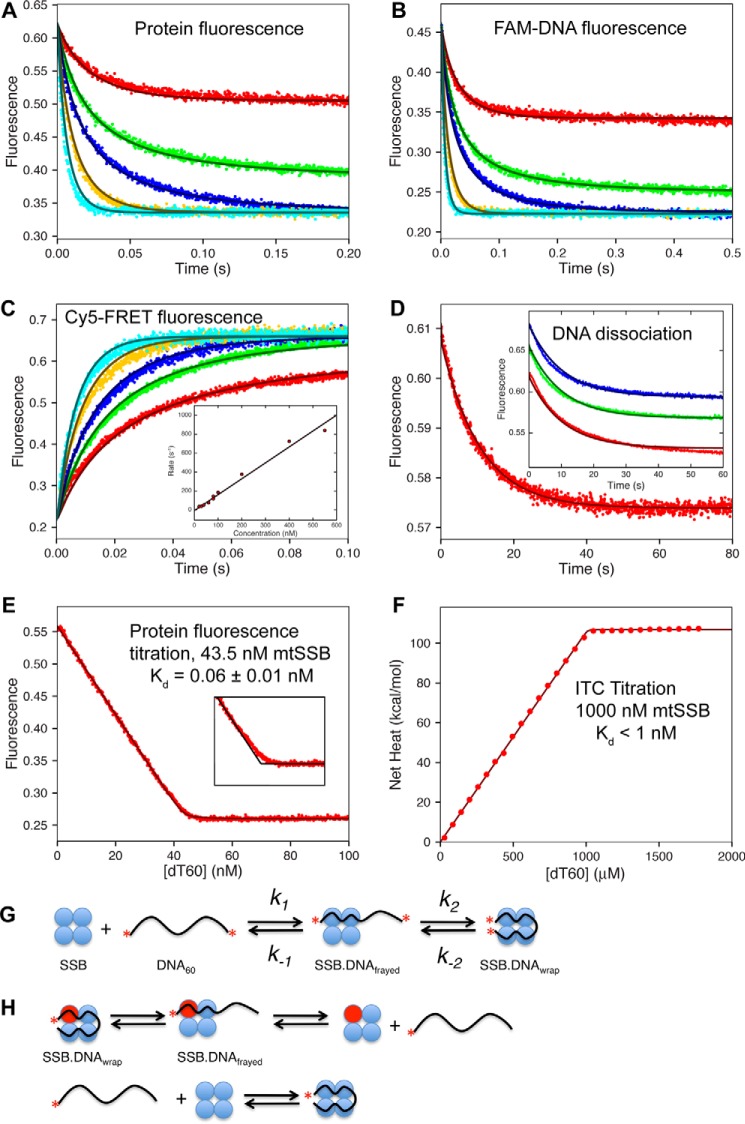
Global fitting of kinetic and equilibrium titration data for mtSSB binding to dT₆₀ in 100 mm NaCl and 10 mm Mg²⁺. A, the kinetics of mtSSB binding to dT₆₀ ssDNA were monitored by protein fluorescence. [DNA] = 10, 20, 30, 50, and 80 nm; [mtSSB] = 25 nm. B, the kinetics of mtSSB binding to FAM-labeled dT₆₀. [FAM-dT₆₀] = 20 nm; [mtSSB] = 10, 18, 24, 45, and 80 nm. C, the kinetics of mtSSB binding to Cy5-dT₆₀-Cy3 ssDNA. [DNA] = 20 nm; [mtSSB] = 20, 30, 40, 60, and 80 nm. Inset, rate versus concentration up to 550 nm mtSSB; slope = 1.7 ± 0.3 nm⁻¹ s⁻¹. D, the release of Cy5-dT₆₀ from the AF555-labeled mtSSB. The Cy5 fluorescence was monitored after mixing a preformed 1:1 complex of Cy5-dT₆₀–AF555-labeled mtSSB (30 and 31 nm, respectively) with excess unlabeled mtSSB (5 μm). Fitting the data to a single exponential revealed an observed rate of 0.1 ± 0.01 s⁻¹. Inset, repeating the experiment at 7 (red), 10 (green), or 12 μm (blue) unlabeled mtSSB gave the same rate. E, fluorescence titration of mtSSB (45 nm) with increasing concentrations of dT₆₀ (x axis). Fitting the data with a quadratic equation gives K_d = 0.06 ± 0.01 nm, consistent with the global data fitting and confidence contour analysis. The inset shows a close-up of the data near the point of 1:1 stoichiometry compared with the line for infinitely tight binding, in black. Global fitting defined an active mtSSB concentration of 43.5 nm. F, ITC titration of mtSSB (1 μm) with dT₆₀ ssDNA (0–2 μm) in buffer A containing 10 mm Mg²⁺ with 100 mm NaCl. Fitting the data to a quadratic equation reveals a K_d = 1 ± 0.6 nm, but we more accurately interpret the results to show only that K_d < 1 μm. G, schematic showing the two-step binding of dT₆₀ to SSB, where the two red asterisks represent the Cy5 and Cy3 labels, giving a high FRET signal in the fully wrapped state. H, schematic showing the exchange between labeled (red sphere) and unlabeled protein. As described under “Results,” the exchange monitored with excess protein requires the dissociation of DNA prior to binding the unlabeled protein. All data were fit globally to the model shown in Scheme 2 to give the smooth lines based upon numerical integration of the rate equations. The smooth lines drawn in all of the figures shown here were derived from the global fit to the full data set according to the model and rate constants shown in Scheme 2.

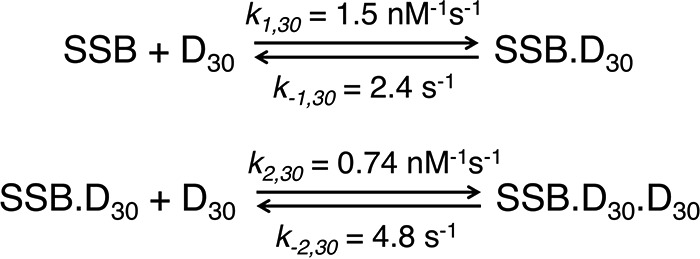
The mtSSB tetramer binds two molecules of dT₃₀ with high affinity but little intramolecular cooperativity

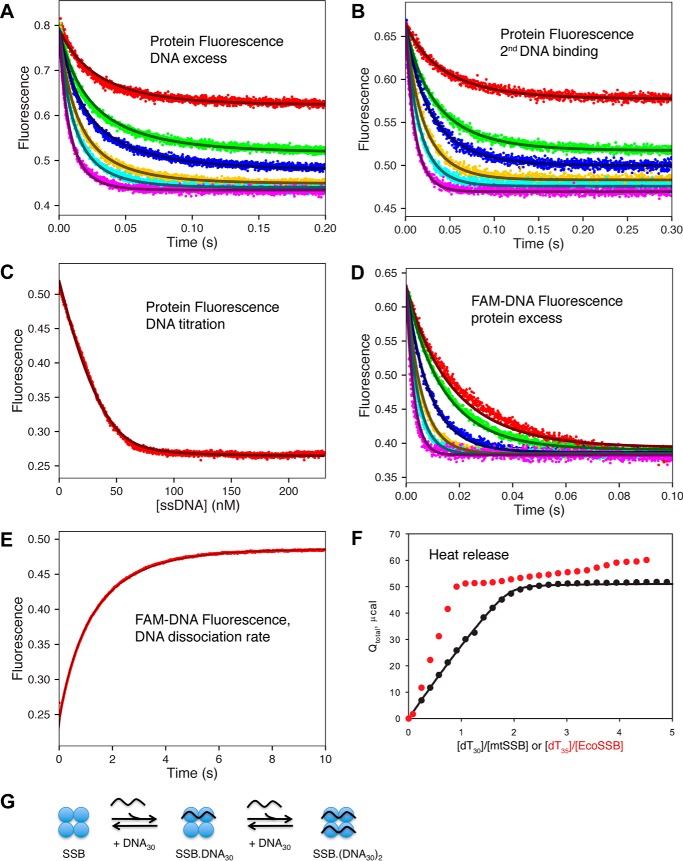
We begin our analysis of the kinetics and equilibria for DNA binding to mtSSB with studies on the binding of dT₃₀, in part to determine whether a negative cooperativity might exist for ssDNA binding to mtSSB tetramer, but also to provide a baseline for comparison with the binding of longer DNA. We performed stopped-flow experiments to measure the DNA (dT₃₀) binding and dissociation rates in 20 mm NaCl with 10 mm Mg²⁺. Fig. 4A shows the time course of protein fluorescence quenching upon mixing the mtSSB tetramer with various concentrations of dT₃₀ DNA. The traces can be fit to a double-exponential equation with the two observed rates governed by second-order rate constants: ∼1 and 0.5 nm⁻¹ s⁻¹ for the fast and slow phases, respectively. In other words, each phase depended on a DNA concentration consistent with a second-order DNA binding event. Because fitting data to double exponentials can be unreliable, we show only the global fit to the entire data set as described below (Scheme 1). The rate constant for binding the second dT₃₀ molecule was also estimated by mixing a preformed 1:1 mtSSB–dT₃₀ complex with an excess of dT₃₀ (Fig. 4B). Here the data could be fit a to a single exponential, and the mtSSB concentration dependence of the observed rate gave an apparent second-order rate constant of 0.5 nm⁻¹ s⁻¹. These data reinforce our interpretation of the biphasic kinetics as due to the binding to the first and second DNA molecules with a fluorescence signal attributed to each binding event.

Figure 4.

Kinetics, equilibria, and thermodynamics of mtSSB binding to dT₃₀ ssDNA. A, the kinetics of mtSSB binding to dT₃₀ ssDNA were monitored by protein fluorescence with DNA in excess (except for the lowest concentration). [DNA] = 15, 30, 40, 60, 80, and 120 nm; [mtSSB] = 20 nm. B, kinetics of binding a second ssDNA to mtSSB–DNA₃₀. Equimolar concentrations of mtSSB and dT30 (42 nm each) were allowed to equilibrate and then were diluted 1:1 with various concentrations of dT30 (15, 30, 40, 60, 80, and 120 nm, final concentrations), and the protein fluorescence was recorded. C, equilibrium titration of mtSSB (30 nm) with increasing concentrations of dT₃₀ monitored by following protein fluorescence. D, the kinetics of mtSSB binding to FAM-dT₃₀ were monitored by fluorescein fluorescence with protein in excess. [FAM-dT₃₀] = 20 nm; [mtSSB] = 40, 50, 80, 120, 160, and 240 nm. E, measurement of the dissociation rate of FAM-dT₃₀ from mtSSB. The fluorescein-labeled DNA fluorescence was monitored upon mixing a preformed 1:1 mtSSB–dT₃₀ complex (20 and 22 nm, respectively) with an excess of unlabeled dT₆₀ (600 nm). F, measurement of heat release (μcal) upon titration of mtSSB (490 nm) with increasing concentrations of dT₃₀ (0–2,500 nm), as measured by ITC. Data for ITC titration of EcoSSB with dT₃₅ (red dots) are shown as a comparison, with an x axis of dT₃₅/EcoSSB. All data for mtSSB kinetics and equilibria were fit globally to the model shown in Scheme 1 to give the smooth lines based upon numerical integration of the rate equations with no simplifying assumptions. Fluorescence is given in arbitrary units, and in global data fitting, individual experimental outputs were modeled with different scaling factors to reflect the setup of the instrument on different days. G, schematic showing the sequential binding of two dT₃₀ strands of ssDNA to the mtSSB tetramer (SSB). Note that for EcoSSB, the binding of the second DNA is much weaker (negative cooperativity), which is not apparent with mtSSB.

We also measured the DNA association rate determined by monitoring the fluorescein quenching of 6-fluorescein amidite (FAM)-dT₃₀ upon binding to varying concentrations of mtSSB, with mtSSB in excess (Fig. 4D). The concentration dependence of the observed rate gave a second-order rate constant of 2 nm⁻¹ s⁻¹, which is twice that for the DNA association rate as measured by monitoring the protein fluorescence. We suggest that the 2-fold increase in the apparent second-order rate constant for DNA binding observed when mtSSB is in excess over the DNA arises because the observed pseudo-first-order rate constant is determined by the concentrations of binding sites of the species in excess, and mtSSB has two sites per tetramer for binding dT₃₀. In contrast, in experiments with DNA in excess, the pseudo-first-order rate constant is defined by the concentration of DNA sites (one per DNA molecule). This difference in the pseudo-first-order rate constant, depending on whether DNA or mtSSB is in excess, is not seen with dT₆₀ (described below), because there are two binding sites on both the dT₆₀ DNA and the mtSSB. It should also be noted that in fitting the data by computer simulation, as described below, these complications in interpreting the observed rates (pseudo-first-order rate constants) are avoided because the data are fit to derive intrinsic rate constants, not eigenvalues.

The EcoSSB tetramer displays negative cooperativity for binding two molecules of dT₃₅, and this negative cooperativity is most evident at low salt concentrations, where the binding affinity of the second dT₃₅ molecule is ∼200-fold weaker than the binding of the first dT₃₅ molecule (23). To investigate whether the mtSSB displays negative cooperativity similar to EcoSSB, we performed the equilibrium titrations of the mtSSB tetramer with increasing concentrations of dT_30, monitored by protein fluorescence (Fig. 4C) and ITC (Fig. 4F). For comparison, we also performed parallel experiments with EcoSSB tetramer titrated with dT₃₅ (red points). As shown in Fig. 4F, the heat released in forming the mtSSB–dT₃₀ complex follows a single binding isotherm, reaching saturation at a ratio of 2:1 dT30/mtSSB tetramer. In contrast, the heat released in titrating EcoSSB with dT₃₅ is markedly biphasic, with the first, tight-binding event reaching saturation at a ratio of 1:1 EcoSSB/dT₃₅ DNA, followed by a much weaker binding that does not reach saturation in the concentration range explored. Rather, after binding the first dT₃₅, the signal only increases slowly, requiring a 200-fold higher concentration of dT₃₅ to reach saturation of the second binding site. In comparison, the ITC signal reaches saturation at a stoichiometry of two dT₃₀ molecules per mtSSB, implying that both binding events have K_d values less than the concentration of mtSSB in the experiment.

Equilibrium titrations based upon protein fluorescence show the same trends. Although the fluorescence data for mtSSB clearly show two sequential binding events with a weaker K_d for the second, it is only weaker by a factor of ∼4 (Scheme 1), compared with the 200-fold effect seen with EcoSSB. It should be noted here that fitting based upon numerical integration of the rate equations (computer simulation) affords a reliable, good fit to the data (Fig. 4C, smooth lines), something that is problematic in fitting based upon an equation for two sequential binding events with similar K_d values that are less than the concentration of mtSSB, because the quadratic equation is invalid in this situation.

The rate of dissociation of FAM-dT₃₀ ssDNA from (SSB)₃₀ complex was measured directly in a competition experiment using a large excess (10-fold) of unlabeled dT₆₀ (Fig. 4E). We first formed a stoichiometric mtSSB–dT₃₀ complex (20 and 22 nm, respectively) using FAM-labeled DNA and then mixed with an excess of unlabeled dT₆₀ (600 nm). The fluorescein fluorescence followed a single exponential rise with the observed rate of 1.2 s⁻¹, which defines the rate of dissociation of dT₃₀ from the mtSSB tetramer. We observed the same rate at higher concentrations of excess unlabeled dT₆₀ (data not shown), supporting our assignment of the rate of 1.2 s⁻¹ to the rate constant for DNA dissociation. Moreover, in globally fitting the data, we modeled the exact reaction with the known rate constant for binding dT₆₀, so that we do not need make any assumptions regarding the rate of binding the competing DNA relative to the rate of rebinding dT₃₀. Thus, in modeling the reactions explicitly, the rate constant derived for the dissociation of dT₃₀ does not depend on the relative excess of dT₆₀ used in the experiment. This is another advantage in global data fitting.

Fitting of stopped-flow kinetic data to double exponential functions and fitting of equilibrium binding data to multiple K_d values can be quite error-prone. Therefore, we elected to only show the results of global data fitting, which overcomes the many limitations of fitting data to equations. Moreover, in fitting based on numerical integration of the rate equations, we account for both the rates and amplitudes of observed reactions. The rate constants estimated from the conventional fitting were used as starting values to globally fit all data using the model shown in Scheme 1. The smooth curves in Fig. 4 were all derived in fitting the data to a single unifying model with rate constants shown in Scheme 1 as described in detail in supplemental Figs. S1 and S2, where we also show the results of confidence contour analysis (supplemental Fig. S3 and supplemental Table S1) to demonstrate that the data accurately define on and off rate constants and the K_d values for the binding of the first and second ssDNA dT₃₀ molecules.

This analysis shows that mtSSB binds to the second dT₃₀ with only a 4-fold decrease of the affinity relative to the first dT₃₀ ssDNA. The 4-fold lower binding affinity is due to a 2-fold slower on rate and a 2-fold faster off rate constant for the second dT₃₀. In binding the first dT₃₀, there are two binding sites on the mtSSB, but only one available site in binding the second dT₃₀. Accordingly the apparent second-order rate constant, expressed relative to the concentration of mtSSB tetramers, is 2-fold faster for the first compared with the second binding event. Similarly, there is a 2-fold higher probability of dissociation of one of the two dT₃₀ molecules from the SSB–D₃₀–D₃₀ complex compared with the SSB–D₃₀ complex. Thus, based on the number of sites, k₊₁ = 2 × k₊₂ and k₋₂ = 2 × k₋₁.

$$\begin{array}{c}\text{SSB}+{\text{D}}_{30}\underset{k_{\text{off}}}{\overset{2\hspace{0.17em}\times \hspace{0.17em}{k}_{\text{on}}}{\rightleftarrows }}\hspace{0.17em}\text{SSB}-{\text{D}}_{30}\\ \text{SSB}-{\text{D}}_{30}+{\text{D}}_{30}\underset{2\hspace{0.17em}\times \hspace{0.17em}{k}_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftarrows }}\hspace{0.17em}\text{SSB}-{\text{D}}_{30}-{\text{D}}_{30}\\ \text{Reactions}\hspace{0.17em}1\hspace{0.17em}\text{and}\hspace{0.17em}2\end{array}$$

$$K_d=\frac{k_{\text{off}}}{k_{\text{on}}}=\frac{2.4{\text{s}}^{-1}}{0.74\hspace{0.17em}{\text{nM}}^{-1}{\text{s}}^{-1}}=3.2\text{nM}$$ (Eq. 1)

If we use the normalized on and off rates per site, the true K_d for each site is 3.2 nm. Of course, the effective K_d values are still 1.6 and 6.5 nm for the first and second sites, respectively. This quantitative analysis demonstrates that the two binding sites are independent and identical with no signs of intramolecular cooperativity.

Based on preliminary data fitting that suggested the 2:1 relationship between pairs of rate constants, we constrained the parameters to maintain these relationships in the refinement of the data fitting to obtain the results shown in Fig. 4 and Scheme 1. We also allowed the four rate constants to be independent parameters in fitting and obtained comparable rate constants. The results of each method of data fitting, along with S.E. estimates derived from confidence contour analysis, are summarized in Table 3.

Table 3.

Rate constants for mtSSB binding to dT₃₀

Rate constants were derived in globally fitting data shown in Fig. 4. Data were fit with the rate constants linked in a 2:1 ratio as described under “Results,” where k₊₁ = 2 × k₊₂ and k₋₂ = 2 × k₋₁. Alternatively, the rate constants were unlinked, allowing the four rate constants to be independent variables during data fitting. In each case the S.E. values, shown in parentheses, were estimated from confidence contour analysis providing upper and lower limits with a χ² threshold of 0.98 (minimum/observed χ²).

	k+1,30	k−1,30	k2,30	k−2,30
	nm−1 s−1	s−1	nm−1 s−1	s−1
Linked	1.47 (1.42–1.53)	2.39 (2.32–2.47)	0.737 (0.71–0.765)	4.78 (4.64–4.94)
Unlinked	1.48 (1.40–1.57)	2.59 (2.33–2.85)	0.75 (0.673–0.871)	4.39 (3.74–5.21)

Kinetics of the binding of the mtSSB tetramer to dT₆₀

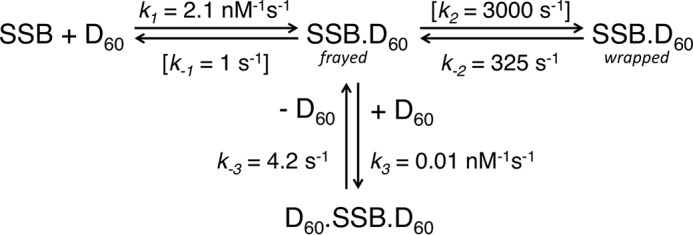
The kinetics of the mtSSB protein binding to dT₆₀ ssDNA were monitored by stopped-flow methods using the quenching of the intrinsic protein fluorescence of the mtSSB upon ssDNA binding, as well as using extrinsic fluorescence probes on the ssDNA (Fig. 5). We performed experiments in buffer A with 100 mm NaCl and 10 mm Mg²⁺, which approximates physiological ionic conditions. The progress of the concentration-dependent reaction was monitored using either protein fluorescence quenching (Fig. 5A) or quenching of the FAM-labeled DNA fluorescence (Fig. 5B) upon forming the protein–DNA complex. We initially fit the data at the higher concentrations (pseudo-first-order conditions) shown in Fig. 5 (A and B) to a single-exponential equation to derive an estimate of the second-order rate constant (k₁) for DNA binding, which was used subsequently for the refined global fitting of all data in Fig. 5 to derive the model and rate constants shown in Scheme 2. The second-order rate constant for substrate binding obtained from the global fit to all of the data was 2.1 ± 0.1 nm⁻¹ s⁻¹. Globally fitting only the concentration series data for protein fluorescence or only the FAM-labeled DNA gave values of 2.26 or 2.14 ± 0.1 nm⁻¹ s⁻¹, respectively.

In Scheme 2, we explicitly include the two-step sequence with DNA wrapping following the formation of the initial complex. Changes in the mtSSB protein fluorescence are expected to be a linear function of site occupancy, because the crystal structure shows that each tryptophan residue stacks on bases in the DNA (31), so the signals for initial binding and wrapping should be similar in magnitude. However, the step leading to quenching of a single fluorophore-labeled ssDNA will depend on when the fluorophore comes in proximity to the protein, which may be first or last during the binding/wrapping sequence. As such, the FAM fluorescence may be a mixture of contributions from the two steps. However, if the second step (wrapping) was fast, the kinetics would still follow a single exponential for either measurement, rate-limited by the initial binding.

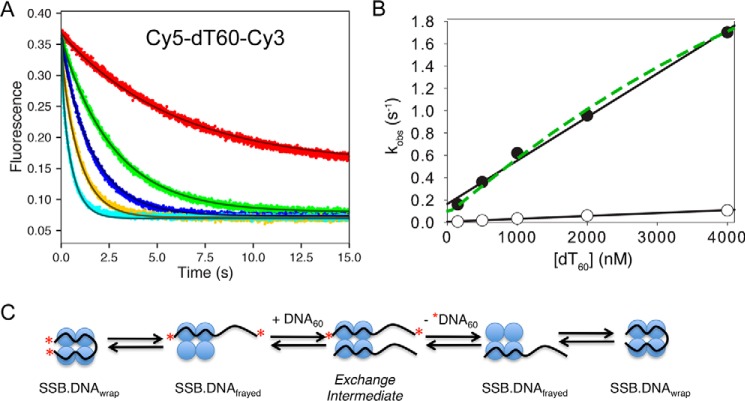
Kinetics of mtSSB binding to Cy5-dT₆₀-Cy3 demonstrates that wrapping of DNA is very fast

The formation of a fully wrapped structure must occur in multiple steps (Scheme 2 and Fig. 5G), although the second step could be sufficiently fast so that the reaction appears to occur in a single step. To measure the kinetics of the ssDNA wrapping around the protein after the initial binding, we used a Cy5-dT₆₀-Cy3 ssDNA molecule so that the signal would mainly be due to the formation of the fully wrapped mtSSB–ssDNA complex (32). Stopped-flow experiments were performed by mixing Cy5-dT₆₀-Cy3 with various concentrations of mtSSB (Fig. 5C). The fluorescence time courses from both the Cy5-FRET and the quenching of protein fluorescence signals are described adequately by single-exponential functions. Globally fitting the FRET data alone gave a second-order rate constant for DNA binding of 1.8 ± 0.1 nm⁻¹ s⁻¹. This value was sufficiently close to the values measured for the protein fluorescence and FAM-labeled DNA signals to support global fitting of the full data set shown in Fig. 5 with a rate constant of 2.1 ± 0.1 nm⁻¹ s⁻¹. Therefore, these experiments indicate that complete wrapping of the ssDNA around the mtSSB tetramer must occur much faster than the binding event (Scheme 2), which explains the observation that ssDNA binding and wrapping appear to occur simultaneously on the stopped-flow time scale.

Measurements of the rate of binding/wrapping using the Cy3-Cy5 FRET signal showed a linear increase in rate up to ∼800 s⁻¹ at a concentration of mtSSB of 550 nm (Fig. 5C, inset). Therefore, the DNA wrapping rate constant (k₂) must be ≫800 s⁻¹. As part of our global data fitting described below, confidence contour analysis established a lower limit of k₂ = 1,750 s⁻¹. At this threshold and below, the rate constant led to a statistically significant deviation of the calculated curves relative to the data, as measured by increases in χ². Therefore, during global data fitting, we used a nominal value of k₂ = 3,000 s⁻¹ (Scheme 2). This value was chosen as an arbitrary number sufficiently large so that its value did not impact the results in fitting data; accordingly, we are modeling the data to derive the equilibrium constant, K₂, not individual rate constants.

Kinetics of dissociation

To measure the kinetics of DNA dissociation, we used the Alexa Fluor 555-labeled mtSSB^T125C (AF555-mtSSB^T125C). Thr-125 is at the extreme end of the C terminus of the mtSSB protein (5) and does not appear to be involved directly in DNA binding. Control experiments showed that the AF555-mtSSB^T125C binds to dT₆₀ DNA with rate and equilibrium constants identical with the wild-type enzyme when measured using intrinsic protein fluorescence (data not shown). Moreover, we labeled under conditions to achieve approximately one fluorophore per mtSSB tetramer. The wrapping of Cy5-dT₆₀ DNA around AF555-mtSSB^T125C tetramer yields a high FRET state due to the close proximity between Cy5 and AF555 fluorophore in a fraction of the complexes. To measure the kinetics of dissociation, we performed a competition experiment by mixing preformed Cy5-dT₆₀–AF555-mtSSB^T125C (25 nm) complex with excess unlabeled mtSSB (5 μm). As shown in Fig. 5D, the Cy5-FRET fluorescence followed a single exponential decay with the observed rate of 0.1 s⁻¹. In Scheme 2, we model the dissociation as a two-step reaction; given that K₂ = 9, only 10% of the species exist in a state to dissociate with a rate constant of 1 s⁻¹ (see Equation 2 below) to give a net dissociation rate of 0.1 s⁻¹.

Two pieces of evidence support our conclusion that this rate constant represents the dissociation of the DNA from the mtSSB–DNA complex and not via an exchange intermediate with two mtSSBs bound. First, the binding of a second mtSSB to the complex ((SSB)₃₀ binding mode) was not observed under these experimental conditions (100 mm NaCl and 10 mm Mg²⁺), even at very large protein/DNA ratios (Fig. 2). Second, experiments performed at higher mtSSB concentrations gave the same rate (Fig. 5D, inset). Thus, the observed rate under large excess of unlabeled protein (∼200-fold) should only reflect the dissociation of Cy5-dT₆₀ DNA from the labeled protein (Fig. 5 and Scheme 2). The ratio of the net rate constants for dissociation and binding defines a K_d = 0.1 s⁻¹/2.1 nm⁻¹ s⁻¹ = 0.05 nm. It should be noted that we designed our experiment based upon competition with mtSSB rather than DNA because, as shown below, DNA exchange occurs at a rate faster than dissociation of the DNA.

Equilibrium titrations

An equilibrium titration was performed by monitoring the protein fluorescence change as a function of increasing concentrations of dT₆₀ (Fig. 5E). Fitting the data to a quadratic equation (not shown) gave a K_d = 0.06 ± 0.01 nm and an active site concentration of 43.5 nm in this experiment (the nominal concentration in the experiment was 45 nm). With 2,000 data points and a high signal/noise ratio, the data are sufficient to define both the stoichiometry and the K_d, the latter of which is based upon the significant deviation of the data from the two limiting asymptotes for infinitely tight binding, as shown in the inset to Fig. 5E. Thus, we can accurately determine the K_d although the mtSSB concentration was 700-fold greater than the K_d. Moreover, the K_d agrees with the value calculated from the ratio of the rate constants for binding and dissociation. In fact, the smooth lines shown in Fig. 5 were all drawn based upon the rate constants shown in Scheme 2.

For comparison, we show the results obtained with ITC, performed at a concentration of 1 μm mtSSB in Fig. 5F. Fitting the data to a quadratic equation gave a K_d = 1 ± 0.6 nm. However, with only 30 data points and the relatively high concentration of enzyme required (16,667-fold higher than the 0.06 nm K_d value), the data are clearly not sufficient to define the K_d value, but rather only set an upper limit. Of course, the ITC data do define the enthalpy change, which can be combined with the more accurate K_d value obtained from the fluorescence titration and the kinetic measurements to yield the following:ΔG⁰ = −14.6 kcal/mol; ΔH = −75 kcal/mol; −TΔS⁰ = 60.4 kcal/mol at 37° C.

Thus, the binding is driven by the large negative enthalpy change overcoming an unfavorable entropy change. These results are consistent with the ionic interactions seen in the crystal structure of EcoSSB wrapped with ssDNA (33).

Global data fitting with two-step binding

Note that in Scheme 2, we have modeled the two-step binding reaction as an initial association of DNA with the mtSSB tetramer followed by fast wrapping, although data only define the net on and off rates. The postulated intermediate state is based upon the observations documenting the existence of the (SSB)₃₀ binding mode and measurements of the DNA dissociation rate for this species (Scheme 1). In other words, the stable formation of the (SSB)₃₀ at lower salt concentrations supports the possible transient existence of a similar state at physiological salt concentrations. In modeling our data collected with dT₆₀ at 100 mm NaCl and 10 mm MgCl₂, we propose that the rate of dissociation of DNA from the intermediate, frayed DNA state (Scheme 2) may be similar to the rate of dissociation of the dT₃₀. By analogy to the data derived using the dT₃₀ DNA, we make the simplifying approximation that when the dT₆₀ is frayed, it will dissociate with a rate constant comparable with the rate of dissociation of the dT₃₀ DNA at ∼1 s⁻¹. To construct the full scheme, we hold a nominal value of k₋₁ = 1 s⁻¹ and set k₂ at a rate of 3,000 s⁻¹, which represents a minimum value that does not affect the data fitting; any value > 3,000 s⁻¹ gives an identical fit. In this manner, we fit data to derive only the equilibrium constant, K₂, not the individual rate constants, and the binding rate constant, k₁.

The data in Fig. 5 were fit globally to provide estimates for k₁ = 2.1 ± 0.1 nm⁻¹ s⁻¹ and k₋₂ = 325 ± 20 s⁻¹ (to define K₂ = 9.23 ± 0.57); these are the only kinetic parameters derived, in addition to the 13 fluorescence scaling factors and ΔH (see supplemental Figs. S4–S6). The S.E. values reported in Table 4 were derived by confidence contour analysis, allowing all of the scaling factors to vary during the data fitting, as described in supplemental Fig. S7 and supplemental Table S2. The smooth lines shown in Fig. 5 represent the best global fit to all experiments with the rate constants shown in Scheme 2.

Table 4.

Rate constants for mtSSB binding to dT₆₀

Rate constants were derived from globally fitting data shown in Figs. 5 and 6. Values in brackets were held fixed during the data fitting, as described under “Results.” Values in parentheses show the lower and upper limits derived by confidence contour analysis with a χ² threshold of 0.98 (minimum/observed χ²) (41, 48). Net K_d = 1/(K₁ × (1 + K₂)) = 0.05 nm.

Rate constant	Value	Equilibrium constant
k1 (nm−1 s−1)	2.1 (2.0–2.2)	1/K1 = 0.5 nm
k−1 (1 s−1)	[1]
k2 (1 s−1)	[3,000]	K2 = 9.2
k−2 (1 s−1)	325 (302–349)
k3 (nm−1 s−1)	0.01 (0.010–0.012)	1/K3 = 420 nm
k−3 (1 s−1)	4.2 (3.4–7.7)

This analysis suggests that the equilibrium constant for wrapping of the DNA around mtSSB is not large: K₂ = 9.2 ± 0.6. According to this model, the net DNA dissociation rate is given by the following,

$$k_{-1,\text{app}}=\frac{k_{-1}}{1+K_2}=\frac{1}{1+9.2}=0.1\hspace{0.17em}{\text{s}}^{-1}$$ (Eq. 2)

consistent with the fitting of the data in Fig. 5D to a single exponential. Of course, this represents a circular argument, so it should only be taken as an illustration of the math behind the data fitting.

This analysis suggests that the wrapping reaction is only slightly favorable, which may play an important role in the biology of mtSSB by increasing the population of the partially frayed state to facilitate strand exchange, which we measure in the following set of experiments.

The mtSSB tetramer can directly transfer between two ssDNA molecules

The EcoSSB tetramer can rapidly diffuse along DNA or switch between DNA molecules while remaining tightly bound (14, 20), and the rate of transfer appears to be determined by the availability of free DNA binding sites within the SSB–DNA complex. To understand whether the strand exchange mechanism is a universal phenomenon that also applies to mtSSB, the kinetics of DNA exchange from the (SSB)₆₀ complex was measured by a competition experiment between labeled and unlabeled DNA. As shown in Fig. 6A, a preformed 1:1 mtSSB–Cy5-dT₆₀-Cy3 complex was mixed with varying concentrations of a large excess of unlabeled dT₆₀ (25–500-fold excess). A decrease in Cy5-FRET fluorescence provides a signal for the unwrapping and the dissociation of Cy5-dT₆₀-Cy3 from mtSSB to coincide with the binding of unlabeled DNA. Each time course in Fig. 6A is described adequately by a single exponential decay. Values of k_obs increase linearly with increasing concentrations of unlabeled dT₆₀ (Fig. 6B, filled circles).

Figure 6.

Kinetics of DNA exchange of dT₆₀ bound to mtSSB. A, the Cy3-Cy5 FRET fluorescence time courses were monitored after mixing a preformed mtSSB–Cy3-Cy5-dT₆₀ complex (20 and 25 nm, respectively) with varying concentrations of unlabeled dT₆₀ (50, 500, 1,000, 2,000, and 4,000 nm) in buffer A with 100 mm NaCl and 10 mm Mg²⁺. B, observed rates of DNA exchange (k_obs) obtained by fitting data in A to a single-exponential (+Mg²⁺; filled circles) and from the same experiments but without Mg²⁺ (open circles) plotted as a function of [dT₆₀] (raw data in the absence of Mg²⁺ not shown). The estimated apparent second-order rate constants from the linear fits of the data were 0.4 and 0.03 μm⁻¹ s⁻¹ in the presence and absence of Mg²⁺, respectively. Data in Figs. 5 and 6A were fit globally to the model shown in Scheme 2 with the rate constants governing the DNA dissociation steps to give the smooth lines. The dashed green line shows the curve predicted from the rate constants derived by global data fitting. C, schematic showing the process of exchange between labeled and unlabeled DNA. As described under “Results,” the exchange monitored with excess protein requires the dissociation of DNA prior to binding the unlabeled protein, whereas the exchange in the presence of excess DNA proceeds via a ternary exchange intermediate.

If the strand exchange occurred via a mechanism in which the DNA dissociated and then the free mtSSB was trapped by the excess unlabeled DNA, the observed rate would be independent of dT₆₀ concentration when the ratio of unlabeled to labeled DNA exceeded ∼10-fold. A linear increase in exchange rate (above the baseline rate of 0.1 s⁻¹) provides evidence for the active participation of the excess dT₆₀ in the exchange reaction. These data demonstrate that during exchange, free mtSSB protein is almost never formed. Rather, the data imply a model (Scheme 2) in which a ternary intermediate (D₆₀–SSB–D₆₀) is formed by binding of the competitor DNA (D₆₀) to the partially frayed (SSB)₆₀ complex (SSB–D₆₀). The slope determined from the linear analysis of data (filled circles) in Fig. 6B (0.0004 nm⁻¹ s⁻¹), defines the observed second-order rate constant (k_obs) for the exchange reaction.

In globally fitting the data in Fig. 6A in concert with the data in Fig. 5, the rate constants for the exchange reactions, shown in Scheme 2, were derived. The second-order rate constant for the binding of DNA to the frayed mtSSB–DNA complex was estimated to be k₃ = 0.01 nm⁻¹ s⁻¹. To relate this rate constant to the observed rate versus total DNA concentration, we have to correct for the fraction of the mtSSB–DNA complex in the frayed state (1/(1 + K₂)). In addition, a factor of 2 is required because there will be an equal probability of releasing either the labeled or unlabeled DNA from the DNA–SSB–DNA exchange intermediate. According, we can calculate the apparent second-order rate constant for DNA exchange, k_3,app, as follows,

$$k_{\text{obs}}=\frac{k_{-1}+k_3\times \left[\text{D}\right]/2}{1+K_2}$$ (Eq. 3)

$$k_{3,\text{app}}=\frac{k_3/2}{1+K_2}=\frac{0.01/2}{10.2}=0.0005\hspace{0.17em}{\text{nM}}^{-1}{\text{s}}^{-1}$$ (Eq. 4)

where 1/(1 + K₂) represents the fraction of (SSB)₆₀ complexes that are frayed, and k₃ is the second-order rate constant for binding of the competitor DNA to the frayed mtSSB–DNA complex. The predicted apparent second-order rate constant is comparable with that measured in Fig. 6B by fitting to a single exponential function.

The full solution to the two-step reaction involves the roots of a quadratic equation, with the concentration dependence of the slow phase approximating a hyperbola (34). The dashed line in Fig. 6B was calculated from the model shown in Scheme 2, suggesting a slight curvature in the concentration dependence. The intercept in Fig. 6B defines the DNA dissociation rate in the absence of DNA. This rate constant (0.1 s⁻¹) is identical to that derived in experiments to measure the dissociation rate with excess unlabeled mtSSB (k_−1,app). The slope defines the active participation of the excess DNA in stimulating the exchange.

Effect of Mg²⁺ concentration on the kinetics of DNA binding and exchange

We performed similar competition experiments in the absence of Mg²⁺ and monitored the fluorescence change upon unwrapping or release of Cy5-dT₆₀-Cy3 from a preformed (SSB)₆₀ complex. The observed second-order rate constant in the absence of Mg²⁺ was 0.03 μm⁻¹ s⁻¹ (Fig. 6B, open circles), which is ∼10-fold less than that obtained in the presence of 10 mm Mg²⁺. The decrease in the observed rate of the DNA transfer can be attributed to a 10-fold drop of the DNA unwrapping rate constant (k₋₂), suggesting a more stable fully wrapped (SSB)₆₀ complex in the absence of Mg²⁺. In the absence of Mg²⁺, mtSSB binds more tightly to dT₆₀ in both 20 and 100 mm NaCl (shown in Fig. 3A). The DNA association rate constant (k₁) is not significantly affected by Mg²⁺ concentration (supplemental Fig. S8). Thus, the major effect of Mg²⁺ is to increase the DNA dissociation rate and to disfavor formation of the SSB₃₀ DNA binding mode.

Discussion

The human mtSSB has been implicated in regulating the mitochondrial D-loops together with transcription factor A (4, 7) and in coordinating with Pol-γ and the mtDNA helicase to replicate the mtDNA genome (9, 10). Before this work, no kinetic studies had been done to understand how the mtSSB–ssDNA complex might form and be recycled especially during lagging strand synthesis. This kinetic information is essential for understanding the role of mtSSB in studies of other enzymes in vitro, such as Pol-γ and mtDNA helicases, because the mtSSB is used frequently in kinetic studies of these enzymes (9, 11, 35).

In this report, we describe a comprehensive model for the binding of mtSSB to DNA derived by globally fitting multiple experiments with both short and long ssDNA (dT₃₀ and dT₆₀). In fitting data to a single unifying model for each DNA, we take advantage of the complementary information content of different experiments. For example, the kinetics of binding are generally a function of the sum of the forward and reverse rates, whereas the equilibrium constant defines their ratio. Simultaneously fitting both kinetic and equilibrium data affords resolution of both forward and reverse rate constants. Direct measurement of the dissociation rate provides an additional check for consistency. This is clearly exemplified in the binding of dT₃₀ DNA (Fig. 4 and Scheme 1) and the binding of dT₆₀ DNA (Fig. 5 and Scheme 2). The rigorous methods used to fit the equilibrium titration and kinetic data globally to a single unifying model afforded more accurate kinetic constants governing each step, thereby increasing confidence in our models because of the increased stringency in data fitting. In addition to the kinetics of ssDNA binding and dissociation, we also defined the kinetics and mechanism of DNA exchange.

Modeling sequential binding of two dT₃₀ molecules

Unlike EcoSSB, the human mtSSB shows no signs of negative cooperativity in binding the second dT₃₀. Rather, the data indicate that the two ssDNA molecules bind with equal affinity per site. However, because there are two sites on each mtSSB tetramer, the second dT₃₀ molecule appears to bind with a 4-fold weaker affinity than the first. Taking into account the number of sites available for binding and dissociating DNA, the model can be reduced to a simple two-step sequential reaction with equal binding and dissociation rates normalized per site, as summarized in Scheme 1. This model and the rate constants account for the kinetics of binding measured using either protein tryptophan fluorescence or FAM-DNA fluorescence and including equilibrium titrations using either fluorescence or ITC (Fig. 4).

This model leads to an unusual titration curve, as seen in Fig. 4C, performed with 30 nm mtSSB. The underlying mechanism leads to two sequential binding events with apparent K_d values of 1.6 and 6.5 nm. However, fitting the data to a quadratic equation gives an apparent K_d = 1.7 nm and a total mtSSB concentration of 48 nm. This demonstrates that fitting to a quadratic equation is inappropriate for two sequential tight binding steps, which is understandable because the equation was derived for only a single binding event. Fitting based upon simulation fully accounts for the shape of the concentration dependence, overcoming limitations of conventional data fitting for two sequential tight binding steps.

Modeling the binding and wrapping of dT₆₀ and DNA strand exchange

When ssDNA is long enough to bind to all four subunits in SSB, it wraps around the tetramer. Here we employed three different fluorescence signals to monitor the kinetics of binding and dissociation: protein tryptophan fluorescence, FAM-DNA fluorescence, and FRET from a Cy3-Cy5 pair at the ends of the ssDNA to measure wrapping, as first described by Kozlov and Lohman (32). Because the data could be interpreted as if the signal were arising from a single binding step, we conclude that the wrapping is much faster than the initial binding at concentrations of SSB and ssDNA employed in measurements of the kinetics. However, we chose to fit the data to a full model, including a transient intermediate with the ssDNA frayed. Although the data do not define the rate of wrapping (k₂; Scheme 2), globally fitting the data in Fig. 5C along with the rest of the data in Fig. 5 affords a lower limit on k₂ > 1,750 s⁻¹ based on confidence contour analysis. We chose a value of k₂ = 3,000 s⁻¹ to represent a nominal minimal value sufficiently large so that the data fitting allowed calculation of K₂ = k₂/k₋₂, independent of the actual rate constants.

We also suggested that the rate of dissociation (k₋₁; Scheme 2) may be comparable to the rate of dissociation of the short ssDNA (k_−1,30; Scheme 1). The net dissociation rate of 0.1 s⁻¹, relative to k₋₁ = 1 s⁻¹, led to the conclusion that K₂ = 9, meaning that 10% of the bound ssDNA was in the frayed state (Equation 2). It is important to consider the implications of this approximation. If k₋₁ were >1 s⁻¹, then the fraction frayed DNA would be smaller; however, it is unlikely that a frayed dT₆₀ ssDNA would dissociate at a rate faster than that of a much shorter dT₃₀ ssDNA molecule. A value of k₋₁ <1 s⁻¹ would require a larger fraction of frayed DNA, which seems unlikely, given the magnitude of the Cy3-Cy5 FRET signal and the binding site size measurements. For these reasons, we believe that our approximation is reasonable and certainly correct within an order of magnitude.

Global data fitting

Global analysis of the DNA binding and dissociation kinetics together with equilibrium titrations constrained the rate constants governing each step to give the values shown in Scheme 2 and Table 4. We have fixed the forward rate constant forming the wrapped (SSB)₆₀ state (k₂ = 3,000 s⁻¹) so that data fitting provided the corresponding reverse rate constant (k₋₂) of 325 ± 20 s⁻¹, thus defining the equilibrium constant for DNA wrapping, K₂ = 9.2. The direct transfer of the SSB between DNA molecules proceeds through a DNA exchange intermediate involving the association of the competitor DNA with the frayed (SSB)₆₀ complex (k₃ = 0.01 nm⁻¹ s⁻¹). The 400-fold decrease of the DNA association rate (compared with k₁) may be due to the limited binding site exposed on the partially frayed (SSB)₆₀ complex for the competitor DNA, and this is consistent with the results of equilibrium titration experiments (Table 1) that show that the mtSSB tetramer binds to 15–20-nt ssDNA with a K_d of ∼1 μm. The K_d for binding the second DNA in the exchange intermediate is 420 μm (Table 4).

Kinetics of DNA exchange

We interpret the kinetics of DNA exchange based on the postulate that the DNA must be partially frayed to allow the binding of a second molecule (20). The DNA concentration dependence of the strand exchange (Fig. 6) demonstrates that the second DNA molecule binds to the mtSSB–DNA complex and stimulates exchange. Moreover, the DNA concentration dependence of the exchange rate defines the apparent second-order rate constant for the DNA binding to the frayed mtSSB–DNA species. Here again, we model the kinetics based on the approximation that 10% of the mtSSB–DNA complex is in the frayed state that can directly bind the second DNA molecule. We estimate a second-order rate constant (k₃; Scheme 2) to be 0.01 nm⁻¹ s⁻¹ = 10 μm⁻¹ s⁻¹). Correcting for the fact that only 10% of the mtSSB–DNA complex can bind the second DNA, and including the postulate that there is an equal probability of dissociation of either of the two bound DNA molecules in the exchange intermediate, we calculate an apparent second-order rate constant k_3,app = 0.5 μm⁻¹ s⁻¹ (Equations 3 and 4). This is essentially the result obtained by conventional fitting of the concentration dependence (Fig. 6B).

In the presence of Mg²⁺, the observed rate of the strand transfer is comparable in both 20 mm NaCl and 100 mm NaCl with the rate limited by the kinetic partitioning between the displacements of one of the two strands. In the absence of Mg²⁺, the observed strand transfer slows down by 10-fold (Fig. 6B), and this is due to a 10-fold decrease of the unwrapping rate. We suggest that the effect of Mg²⁺ on the rate of direct transfer by mtSSB might be physiologically important, because the presence of Mg²⁺ can significantly increase the rate of mtSSB moving on the ssDNA and thus not slow down the Pol-γ replication rate during the lagging strand synthesis.

Comparisons between mtSSB and EcoSSB

Table 5 shows a comparison of rate constants derived here for the human mtSSB and those derived for EcoSSB (20, 32). Although the solution conditions differ, the rate constants for binding the first ssDNA are similar. The second-order rate constants for mtSSB binding dT₃₀ are slightly faster than those observed for binding dT₃₅ to EcoSSB. However, the rate of dissociation of the first ssDNA is 24-fold faster for mtSSB, and the apparent K_d,1 is correspondingly weaker. This difference could be due to the absence of Mg²⁺ in the studies on EcoSSB. The largest difference between the two proteins is in the negative cooperativity, leading to much weaker binding of the second ssDNA by the EcoSSB. This negative cooperativity is thought to be important in facilitating DNA strand exchange. However, the binding of the second ssDNA is only 3-fold weaker for EcoSSB relative to that for mtSSB. It is mainly that the first binding is tighter for the EcoSSB.

Table 5.

Comparison of rate constants for mtSSB and EcoSSB

Rate constants are listed for DNA binding and release for short ssDNA (dT₃₀ for mtSSB and dT₃₅ for EcoSSB) and for full-length ssDNA (dT₆₀ for mtSSB and dT₇₀ for EcoSSB) and for the DNA concentration dependence of the DNA exchange reaction. Rate constants are numbered as in Schemes 1 and 2. The net DNA dissociation rate, k_−1,app, is calculated from Equation 2. The apparent second order rate constant for DNA exchange, k_3,app, is calculated from Equations 3 and 4. Rate constants for EcoSSB are from Refs. 20 and 32, measured in 0.2 m NaCl, pH 8.1, at 25°C. Rate constants for mtSSB from this report were determined in 0.1 m NaCl, 10 mm Mg²⁺, pH 7.5, at 37°C.

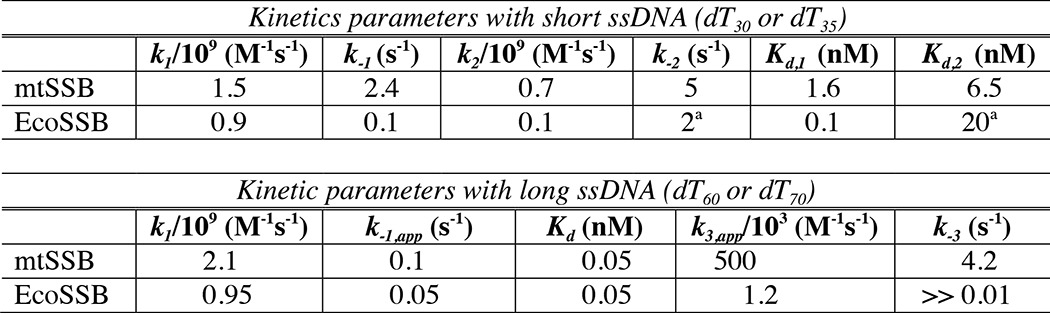
^a Estimated from the 200-fold reduction in binding affinity for the second binding.

In comparing these results for dT₆₀ binding with EcoSSB (Table 5), we see that the kinetics of ssDNA binding and dissociation are comparable, although the second-order rate constant for ssDNA binding is 2-fold faster for mtSSB than for EcoSSB, stretching even further the theoretical limit for a diffusion-controlled reaction (32). However, a faster dissociation rate for mtSSB leads to an identical K_d value. The very real difference is in the kinetics of strand exchange. The apparent second-order rate constant for strand exchange (k_3,app) is 400-fold faster for the mtSSB compared with EcoSSB. This difference could be due to the absence of Mg²⁺ in the EcoSSB assays (as shown here in Fig. 6B for mtSSB) and/or the effect of the C-terminal disordered tail that is present only on the EcoSSB. Other proteins that associate with EcoSSB may modulate this exchange rate as part of the many important functions in recombination and replication.

Salt concentration dependence and site size

Similar to E. coli SSB, as well as other SSBs, such as yeast RPA (36), Streptococcus pneumoniae SSB (37), Deinococcus radiodurans SSB (38), and Thermus aquaticus SSB (39), the human mtSSB is able to bind ssDNA in multiple modes, namely (SSB)₆₀ and (SSB)₃₀ (Figs. 1 and 2). The amplitude of the tryptophan quenching upon poly(dT) binding reflects the extent of wrapping of ssDNA around the mtSSB tetramer (15). The (SSB)₃₀ binding mode is observed at <20 mm NaCl and shows a fluorescence quenching that is 50–60% relative to that of (SSB)₆₀ (>100 mm NaCl) binding mode (Fig. 1A), reflecting the fact that only two subunits on average interact with poly(dT) in (SSB)₃₀ mode, whereas all four subunits interact with poly(dT) in (SSB)₆₀ mode. The different binding modes make different amounts of DNA accessible to other proteins. It has been proposed that the (SSB)₃₅ binding mode observed for E. coli SSB is involved in DNA replication, although this has not been demonstrated (40). It is possible that fluctuating ionic conditions or cofactors in the mitochondrion could modulate the transition between two binding modes of mtSSB and Pol-γ in vivo, or the observed salt concentration dependence could echo the effects of other factors that regulate mtSSB binding to DNA.

We have examined the kinetics of mtSSB tetramer binding to dT₆₀ and dT₃₀ in two different [NaCl] (20 and 100 mm) and in the presence or absence of Mg²⁺ (10 mm). Under low-salt conditions, a high degree of negative intrasubunit cooperativity in the (SSB)₃₅ binding mode has been reported for EcoSSB, S. pneumoniae SSB (37), D. radiodurans SSB (38), and T. aquaticus SSB (39). Although the molecular basis for this negative cooperativity is not well understood, it has been suggested that it is due at least in part to electrostatic repulsions between the phosphoryl groups of the segments of ssDNA that bound in the first dimer and the segments of ssDNA bound in the second dimer of the SSB tetramer and that the relief of negative intrasubunit cooperativity that is observed at higher-salt conditions may be due to a reduction in this electrostatic repulsion that results from the binding of cations to the ssDNA. The mtSSB did not show negative cooperativity in the dT₃₀ binding modes at low salt concentration (20 mm), as compared with EcoSSB. This could be a consequence of the lack of the C-terminal tail in mtSSB. The importance of the C-terminal tail in modulating the binding mode change was reported for PfSSB, which does not show negative cooperativity in dT₃₅ binding mode (23, 24), and the amino acid composition of the C-terminal tail in PfSSB (23) is different from the EcoSSB.

Calorimetry

Calorimetric measurements of mtSSB binding to dT₆₀ show that the binding enthalpy change (ΔH⁶⁰_obs) is slightly less than the values measured for E. coli SSB binding to dT₆₅ under similar conditions, possibly due to the smaller size of the protein. Note that apparent binding affinity (binding free energy) for mtSSB–dT₆₀ is comparable with that measured for E. coli SSB–dT₆₅ binding in high-salt conditions (>0.5 m NaCl), suggesting that the mtSSB–ssDNA interaction is driven by a more favorable entropy change. This is consistent with the observation for the ssDNA binding of the C-terminal tail-truncated E. coli SSB (22), which shows an increase in ssDNA binding affinity due to more favorable entropy change. Similar to the E. coli SSB (28, 29), the [NaCl] and [MgCl₂] have large effects on ΔH⁶⁰_obs, with an increase of ΔH⁶⁰_obs as the [NaCl] or [MgCl₂] increases, which is probably caused by the release of bound Cl⁻ from SSB occurring with ΔH > 0 (28). As for the (SSB)₃₀ binding mode, the total ΔH³⁰_obs (−90 ± 5.5 kcal/mol) for saturating the mtSSB tetramer with two molecules of dT₃₀ is equal to the ΔH⁶⁰_obs (−88 ± 1.2 kcal/mol) within experimental uncertainty, under identical solutions (Figs. 3 and 6), consistent with the fact that one dT₆₀ molecule interacts with all four mtSSB subunits, whereas two molecules of dT₃₀ are required to interact with all four mtSSB subunits.

Summary

We have established the kinetics and thermodynamics of binding ssDNA to the human mtSSB. By globally fitting data from a variety of signals, including both kinetic and equilibrium titration experiments, we have defined a single unifying model each for the binding of either short (dT₃₀) or long (dT₆₀) spanning either half or all of the DNA binding sites. The data reveal some similarities but also surprising differences in comparison with EcoSSB, which has been studied extensively for the past 30 years. One common feature that is important biologically is that the rate of dissociation of SSB from ssDNA is relatively slow, with a half-life of 6–12 s, which is too slow to account for rates of DNA replication. The human mitochondrial DNA polymerase replicates DNA at a rate of 50–100 s⁻¹ (42–45), so the mtSSB would impede replication if dissociation were required. DNA strand exchange is much faster than dissociation but may be limited to rates of ∼4 s⁻¹, which may accommodate recombination but not replication. Accordingly, it is reasonable to suggest that the mtSSB is able to roll or slide along ssDNA ahead of the replication fork. Our current studies lay the foundation for more analysis of the mechanism of sliding/rolling and for reconstitution of the human mtDNA replisome to more rigorously pursue the role of the human mtSSB in DNA replication.

Experimental procedures

Reagents and buffers

[γ-³²P]ATP (3,000 Ci/mmol) was purchased from PerkinElmer Life Sciences. Unlabeled deoxynucleotides were from Promega (Madison, WI). All oligonucleotides were from Integrated DNA Technology and purified on a 10–15% polyacrylamide denaturing gel containing 6 m urea. The poly(dT) was purchased from Midland Certified Reagent Co. (Midland, TX). The average size is between 300 and 800 nucleotides. The concentrations of NaCl and MgCl₂ used in the experiments are specified throughout.

Proteins and DNA

The human cDNA for mtSSB was obtained from OriGene (Rockville, MD). The coding sequence for the gene was examined using MitoProt, which indicated that the first 20 amino acids had the highest probability for constituting the mitochondrial targeting sequence (46). Accordingly, the presumed mtSSB mature protein coding sequence (codons 21–148) was amplified by PCR and subcloned into expression vector pcIts ind+ (47) and then transformed into E. coli C2984 competent cells to overexpress the protein following chemical and temperature induction as described (47). The cell pellets (20 g) were thawed on ice in 5 volumes of lysis buffer (HEPES, pH 7.6, 0.25 mm EDTA, and 1 mm DTT) plus 1 tablet of protease inhibitor mixture (Roche Applied Science). The resuspended cells were lysed by sonication, and cell debris was removed by centrifugation at 15,000 × g for 30 min at 4 °C. The supernatant was loaded onto an Affi-Gel blue affinity column (1.6 × 10 cm) equilibrated with lysis buffer + 50 mm NaCl at a flow rate of 1 ml/min at 4 °C. The column was washed with 5 column volumes (CV) of lysis buffer + 50 mm KCl followed by 5 CV of lysis buffer plus 800 mm NaCl. The mtSSB was eluted with 5 CV of lysis buffer plus 0.5 m KSCN. The eluent was collected, and protein was precipitated by adding ammonium sulfate to 35% (w/v) saturation and stirring on ice for 1 h. The protein precipitate was collected by centrifugation at 17,000 × g for 15 min at 4 °C. The protein pellet was dissolved in 10 ml of dialysis buffer (25 mm HEPES, pH 7.6, 50 mm NaCl, 0.1 mm EDTA, 2 mm DTT, 10% glycerol) and dialyzed against the same buffer for 4 h at 4 °C. The dialysate was loaded onto a Hi-TRAP SP column (5 ml) equilibrated with dialysis buffer, and mtSSB was eluted with a linear 0.05–0.5 m salt gradient. We also prepared a mutant form of mtSSB (A125C), which was then labeled using Alexa Fluor 555 maleimide to achieve 20% labeling per tetramer as described previously (13). The fractions containing mtSSB were identified by 12% SDS-PAGE and pooled, yielding protein with an estimated purity of >95%. The final concentration of mtSSB was determined using the extinction coefficient ϵ₂₈₀ = 19,060 m⁻¹ cm⁻¹ per monomer. All concentrations of mtSSB cited here are for the concentration of tetramers. EcoSSB was generously provided by Dr. Timothy M. Lohman (Washington University, St. Louis, MO).

For experiments using radioactively labeled DNA, a kinase reaction was performed to phosphorylate the 5′-end of ssDNA with [γ-³²P]ATP. All ssDNA concentrations were determined using the extinction coefficient provided by the manufacturer.

Fluorescence equilibrium titrations

For experiments determining the occluded size of mtSSB on ssDNA, binding of protein to poly(dT) was examined by monitoring the quenching of tryptophan protein fluorescence upon titration with DNA using the TMX-1000 equilibrium titration module for the SF-300x stopped-flow (KinTek Corp., Austin, TX). The poly(dT) was purchased from Midland Certified Reagent Co. The average size is between 300 and 800 nt. Protein fluorescence was observed with excitation at 296 nm (4 nm bandpass) and observing emission at 340 nm (25-nm bandwidth filter from Semrock, Rochester, NY). The reaction was carried out at 37 °C in buffer A containing 10 mm Mg²⁺ and different [NaCl], as indicated in Fig. 1A. The data were analyzed with a modified quadratic fitting method according to Equation 5.

$$F=F_0+\Delta F\times \frac{E_0+D_0/N+K_d-\sqrt{{\left(E_0+D_0/N+K_d\right)}^2-4\times E_0+D_0/N}}{2\times E_0}$$ (Eq. 5)

where F is the observed fluorescence, F₀ is the initial fluorescence of mtSSB protein alone, ΔF is the amplitude of the signal, and E₀ and D₀ are the total concentrations of mtSSB and DNA (expressed as nucleotide concentration) after mixing. Estimates of the site size (N) and K_d (along with the fluorescence scaling factors F₀ and ΔF) were derived by fitting the data to Equation 5 by nonlinear regression.

For experiments measuring the binding affinity of mtSSB to dT₃₀ or dT₆₀, the fluorescence change from either tryptophan quenching of mtSSB protein or from fluorophore quenching of FAM-labeled ssDNA was monitored upon mtSSB binding to the ssDNA. For experiments monitoring FRET using Cy5-(dT)₆₀-Cy3 ssDNA, changes in Cy5 fluorescence upon binding of mtSSB to DNA were examined by exciting the Cy3 donor at 530 nm and monitoring the emission from the Cy5 fluorophore at 650 nm using bandpass filters from Semrock.

Isothermal titration calorimetry

ITC experiments were performed at 37 °C using a VP-ITC calorimeter (GE Healthcare) by titrating mtSSB or EcoSSB solutions in the cell (0.5–1 μm) with dT₆₀ or dT₃₀ (5–10 μm concentrations in the syringe) in buffer A with NaCl and MgCl₂ concentrations indicated in each experiment. Prior to analysis, both protein and DNA were dialyzed extensively against the buffer. The control titration, which consisted of the same titration solution, but with buffer in the sample cell, was subtracted from each experiment, accounting for the heat of dilution. The raw ITC data were analyzed using a one-step binding model in the Origin software provided by MicroCal. ITC data are usually presented as the first derivative of a titration curve, which confounds more rigorous analysis. For global data fitting, heat release was integrated to obtain the cumulative sum of the heat change, which was then plotted against the concentration of protein (e.g. Fig. 3B) so that the data could be fit using the model indicated.

Fluorescence stopped-flow kinetics

Stopped-flow experiments were performed at 37 °C using a KinTek AutoSF-120 stopped-flow instrument. The reactant solutions were prepared on ice and then equilibrated at 37 °C for at least 5 min prior to mixing. In experiments for monitoring mtSSB tryptophan fluorescence, an excitation wavelength of 296 nm was used, and the emission fluorescence was monitored at 340 nm (25-nm bandwidth filter from Semrock). In experiments for monitoring FAM fluorescence using 5′-FAM-(dT)₆₀ ssDNA, an excitation of wavelength of 485 nm was used, and the emission fluorescence was monitored at 520 nm using bandpass filters from Semrock. In experiments using 5′-Cy5-(dT)₆₀-Cy3-dT ssDNA, Cy3 was excited at 530 nm, and fluorescence from Cy5 was monitored at 650 nm using bandpass filters from Semrock. The mixing dead time was <1 ms. Each shot contained 20 μl from each chamber, and 10 shots were averaged.

Global data fitting

Data were first analyzed for one- or two-exponential components by conventional fitting. Ultimately, all of the data were globally fit using KinTek Explorer, using the models in Schemes 1 and 2 for dT₃₀ and dT₆₀ ssDNA, respectively. Methods for globally fitting the data and the results of confidence contour analysis are described in detail in the supplemental material.

Gel shift assay

The ssDNA binding reaction solution contained buffer A plus 100 mm NaCl and the concentrations of MgCl₂, [³²P]-5′-(dT)₆₀, and mtSSB protein indicated in the legend to Fig. 2B. The solutions were incubated at 37 °C for 15 min. Aliquots were removed and analyzed by electrophoresis on 6% native polyacrylamide gel with a running buffer consisting of 25 mm Tris acetate (pH 7.5) and the same concentration of magnesium as in the reaction solutions. Gels were dried and exposed to phosphor screens. Radioactive bands were detected with a Typhoon 9400 scanner (GE Healthcare) and quantified with ImageQuant software (GE Healthcare).

Author contributions

Y. Q. performed the experiments and assisted with the data fitting and writing of the paper. K. A. J. conceived of the study and worked with Y. Q. in the data fitting and writing of the paper.