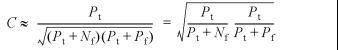Discovering common stem–loop motifs in unaligned RNA sequences

Abstract

Post-transcriptional regulation of gene expression is often accomplished by proteins binding to specific sequence motifs in mRNA molecules, to affect their translation or stability. The motifs are often composed of a combination of sequence and structural constraints such that the overall structure is preserved even though much of the primary sequence is variable. While several methods exist to discover transcriptional regulatory sites in the DNA sequences of coregulated genes, the RNA motif discovery problem is much more difficult because of covariation in the positions. We describe the combined use of two approaches for RNA structure prediction, FOLDALIGN and COVE, that together can discover and model stem–loop RNA motifs in unaligned sequences, such as UTRs from post-transcriptionally coregulated genes. We evaluate the method on two datasets, one a section of rRNA genes with randomly truncated ends so that a global alignment is not possible, and the other a hyper-variable collection of IRE-like elements that were inserted into randomized UTR sequences. In both cases the combined method identified the motifs correctly, and in the rRNA example we show that it is capable of determining the structure, which includes bulge and internal loops as well as a variable length hairpin loop. Those automated results are quantitatively evaluated and found to agree closely with structures contained in curated databases, with correlation coefficients up to 0.9. A basic server, Stem–Loop Align SearcH (SLASH), which will perform stem–loop searches in unaligned RNA sequences, is available at http://www.bioinf.au.dk/slash/.

INTRODUCTION

Transcriptional regulation is well studied in many experimental systems and many examples have been analyzed in detail. It is usually accomplished by transcription factors that bind to DNA near the start of transcription to affect the rate of initiation. Numerous examples of binding sites for specific factors are known, including many DNA–protein complexes with structures determined by crystallography (1). While much less studied, it is clear that post-transcriptional regulation of gene expression is also common. A recent study showed that for many yeast genes the levels of mRNA are not highly correlated with the protein levels (2). One mechanism of post-transcriptional regulation is for a regulatory protein to bind to a motif in the mRNA and affect its translation or stability. However, unlike the DNA binding proteins, the RNA binding proteins often recognize motifs that are composed of both sequence and structure constraints (3,4). The combination of sequence and structure motifs is not compatible with standard sequence motif search approaches, which partly explains why there are so few known examples of structure-based regulatory binding sites.

When a set of transcriptionally coregulated genes are discovered, several pattern recognition approaches are available to predict binding sites for the regulatory proteins (5–9). But these methods depend on the binding sites having a semi-conserved sequence pattern and do not work if the regulatory sites depend on a conserved structure. The goal of this paper is to describe an approach that is capable of discovering a common stem–loop motif in post-transcriptionally coregulated genes, which may represent the binding site for the regulatory protein. The method not only identifies the putative motif in each sequence, but also provides a representation of its sequence and structure pattern that can be used to search for other occurrences of the same regulatory site.

Currently, the most reliable method of inferring RNA secondary structure is by comparing multiple sequences expected to have the same structure (10–13). The difficulty with determining RNA secondary structure by such a comparative analysis is in obtaining a good alignment of those sequences. Once a good alignment is available most of the secondary structure can be determined by fairly simple measures of covariation (14). Further refinement of the secondary structure, and even elucidation of elements of the tertiary structure, can be obtained by more complex analyses (15–18). However, each of these methods requires the alignment of the sequences to be known. Methods for multiple alignment of sequences, such as CLUSTALW (19), do not perform well on aligning structural RNAs because they are not able to consider structure. Recently developed methods work toward automating comparative sequence analysis by using genetic algorithms and likelihood measures of covariance (20,21); these approaches find motifs that subsequently might be aligned. This is in contrast to our approach, which optimizes structure and alignment simultaneously. For many RNAs the sequences are only partially conserved, and equally (or more) important is the conservation of structure. Indeed, the success of comparative methods requires that the sequence be variable while the structure is conserved. Therefore, obtaining a good alignment of the sequences requires taking the secondary structure of the RNAs into account.

Stochastic context-free grammars (SCFGs) (22,23) are a very good method for representing RNA structures. They are related to hidden Markov models, which are now commonly used to represent protein families (24,25), except that they also capture the constraints of the base pairs in the RNA structure. Given an alignment of related RNA sequences, an SCFG program such as COVE (22) can build a model representing the sequences and structure of that RNA family. The model can be used to align new sequences to the family and to search databases for new members of the family (26). Furthermore, SCFG methods can take unaligned sequences and simultaneously produce an alignment and the model of the family, using an expectation-maximization algorithm (22,23). While not guaranteed to find the correct, or even mathematically optimal, alignment, the method usually performs well on sequences that can be aligned from end to end, that is on the ‘global alignment’ problem (27). However, current SCFG programs were not designed to solve the ‘local alignment’ problem, where only a portion of each sequence contains a common motif that is sought. In theory, SCFGs can be designed to identify motifs in longer sequences, but we are sceptical that they will work effectively because the search space is much larger for local alignments than global alignments and the method is much more likely to converge to a local optimum rather than the globally optimum alignment.

FOLDALIGN was developed specifically for the identification of local motifs in RNA sequences, where the motif is composed of both sequence and structure constraints (28,29). FOLDALIGN uses a dynamic programming algorithm that is guaranteed to find the highest scoring local alignment between two sequences, or between a sequence and an alignment of other sequences. Of course, the highest scoring alignment may not be correct; even thermodynamically-based folding algorithms such as Zuker’s MFOLD (30,31) that are guaranteed to find the predicted lowest energy structure often do not find the biologically correct structure. FOLDALIGN compares each sequence to every other sequence and saves some number of the highest scoring alignments. If even one of these pair-wise alignments is correct it is likely to be reinforced as the other sequences are added to the alignment, thereby identifying the true local motif in the set of sequences. However, FOLDALIGN is computationally more expensive than COVE, so its advantage is primarily for the determination of local structures. Once those local structures are identified, they can be used by COVE to develop models suitable for aligning new sequences and doing database searches.

In this paper we evaluate a strategy of combining FOLDALIGN and COVE to automatically determine the common structure in a set of related RNAs. We first ran FOLDALIGN to obtain predictions of the structural alignment, then trained COVE’s SCFG model on that alignment. The SCFG model can then be used to align the remaining sequences not included in the FOLDALIGN alignment, and it could also be used to refine the alignment provided by FOLDALIGN. We tested the combined approach on a stem–loop region of archaeal SSU rRNAs, and compared it to using COVE alone. This dataset was used because the well curated database of structural alignments allows us to make a quantitative evaluation of the performance of the method (32). But to make the dataset representative of examples where the common motif occurs within regions of otherwise unrelated sequences, we truncated the sequences at random positions surrounding the core motif so that only a local alignment was possible between all of the sequences. We also tested the method on a set of ferritin iron responsive elements (IREs) and their untranslated regions (UTRs) that had been made more variable. This tested whether the method could identify common regulatory motifs that occurred at variable positions within UTRs that are even more variable, and therefore more difficult to identify, than are IRE elements.

MATERIALS AND METHODS

Data extraction and processing

A set of 311 archaea 16S ribosomal sequences was extracted via the Internet from the SSU rRNA database (http://www-rna.uia.ac.be/ssu/) (32). The corresponding sequences can be found in other rRNA databases (http://www.cme.msu.edu/RDP/html and http://www.rna.icmb.utexas.edu) (33,34), but structural alignments do not seem to be available. From the archaeal sequences, we excised alignment positions 5703–6027 (corresponding to 1400–1501 in Escherichia coli).

The archaeal set of 311 subsequences was further filtered for the absence of any indeterminant or missing base assignments within the considered region, resulting in 117 sequences. We further reduced the set to eliminate sequences that are >90% identical (35). This process left 34 sequences. Finally, these sequences were further randomly truncated at both ends by up to 20 nt to ensure that the sequences only aligned locally. Sequence lengths varied from 61 to 105. A few examples of these sequences are shown in Figure 1A.

Figure 1.

(A) Sequences from the archaeal SSU rRNA that only align locally, and (B) IRE/UTR sequences generated with higher degree of degeneracy. Upper case letters indicate base pair regions (the two outermost uppercase letters base pair, and so on).

The selection process has the advantage of increasing the reliability of the resulting alignment as well as decreasing the dataset to a computationally tractable size for FOLDALIGN. The sequences in the final dataset are as follows, where the numbers in parentheses are GenBank accession numbers: Acidianus brierleyi (D26489), Caldococcus noboribetus (D85038), Cenarchaeum symbiosum (U51469), Desulfurococcus mobilis (M36474), Metallosphaera sp. (D85508_D38776), Pyrobaculum aerophilum (L07510), Pyrodictium occultum (M21087), Stygiolobus azoricus 2 (D85520), Sulfolobus metallicus 2 (D85519), Sulfolobus solfataricus 2 (D26490), Sulfurisphaera ohwakuensis (D85507_D38775), Thermofilum pendens (X14835), Thermoproteus tenax (M35966), Archaeoglobus fulgidus (X05567_Y00275), Bacterial sp. 34 (X92171), Bacterial sp. 36 (X92172), Haloarcula vallismortis (U17593), Halobacteriaceae gen. sp. 2 (AJ002946), Halorubrum sodomense (D13379), Natronobacterium magadii (X72495), Methanobacterium sp. (AF028690), Methanobacterium thermoautotrophicum 5 (AE000940_AE000666), Methanothermus fervidus (M32222), Methanococcus jannaschii 3 (U67517_L77117), Methanococcus vannielii (M36507), Methanoculleus marisnigri (AF028693), Methanosarcina frisius (X69874), Methanospirillum hungatei (M60880), Methanothrix soehngenii (X16932_X51423), Pyrococcus sp. 2 (Z70247), Thermococcus mexicalis (Z75218), Thermococcus stetteri (Z75240), Ferromonas metallovorans (AJ224936) and Thermoplasma acidophilum (M38637_M20822).

The ferritin IRE-like data were constructed as follows. We searched in the UTR database (36) for entries with keywords ‘ferritin’ and ‘5′UTR’ from which we obtained 59 sequences. Of these, 16 had ‘IRE’ in their entry, but only 14 were used: one sequence was discarded as it was very long (630 nt) for FOLDALIGN, another because it was a pseudogene. The length of the remaining UTRs varied from ∼100–330 nt.

The selected IRE regions were highly conserved in sequence as well as structure, such that sequence motif finders, such as CONSENSUS (37) can find them within the UTRs. To make the search more challenging, and representative of motifs that are highly variable in sequence but with conserved structure, we modified the IREs and the UTRs that contain them by the following procedure. For each of the 14 sequences the structure element was removed and the remaining UTR was shuffled in sequence such that the dinucleotide distribution was conserved (38). A new structure element was generated and put back into the shuffled UTR at a random location. The general IRE consensus structure motif (39) in the ferritin UTRs (across the 14 extracted sequences) is listed as:

NNNNNCNNNNNCAGWGHNNNNNNNNNN

(((((.(((((......))))))))))

where the parentheses indicate base pairing, N ε {A, C, G, U}, W ε {A, U}, H ε {A, C, U}. This was changed minimally to:

NNNNNCNNNNNCAXGWGHNNNNNNNNNN

(((((.(((((.......))))))))))

where X is chosen randomly among the four nucleotides and no symbol (i.e., leaving the loop region as it is). The base pairs in the stem region were randomized by choosing each of the base pairs AU, CG, GU and their counterparts, in the proportions 3/16, 3/16 and 2/16, which lowers the bias of U-G content in the stem region, compared to having the base pairs with equally probable frequencies. This procedure was repeated four times and we obtained a set of 56 sequences, where the first 14 sequences were used by FOLDALIGN to see if it could generate a core alignment for COVE, which searched for the motif among the remaining 42 sequences. Some examples of the resulting sequences are shown in Figure 1B.

Computational approaches

The primary tools applied in this work are FOLDALIGN (28,29) and COVE (22). COVE is based on the use of a SCFG model and uses a dynamic programming algorithm to optimize pairwise mutual information values from a tree representation of the secondary structure.

FOLDALIGN is based on the algorithm presented by Sankoff (40) to simultaneously align and predict the common structure in a set of RNA sequences. For structural alignment of two sequences, FOLDALIGN works locally and can be interpreted as a mixture of the local alignment and maximum number of base pairs algorithms (41,42). For details on how the algorithm works we refer to Gorodkin et al. (29).

The greedy part of the FOLDALIGN algorithm has similarities to CLUSTAL (19) and CONSENSUS (37) in comparing two entities of sequences to each other (here one of the entities is always just one sequence). As the first step is always to compute all pairwise alignments, the final alignment is independent of the order the sequences are presented to the program. In the following steps the s best alignments are saved.

The constraint to stem–loop type structures ensures a time complexity of O(L⁴NM³s), which otherwise would be O(L⁶NM³s), for aligning up to M ≤ N sequences of length L. However, constraints built into FOLDALIGN, such as limiting the size of the motif searched for as well as the number of gaps between the entities compared, might in some cases provide a time complexity close to O(L³NM³s). The memory requirements in general scale as O(L⁴N). Thus, two crucial factors that control time complexity are s and M. To allow for in-depth analysis and comparison between FOLDALIGN alignments and database alignment, we used M = N, and s ∼ N for the rRNA stem–loop region. This was very slow, and in general was not a feasible approach. However, we could use this to estimate small values of s and M, which could be applied to the IRE-like case where core motifs can be found in reasonable time.

FOLDALIGN does perform reasonably on sequences of length up to ∼300, with appropriate restrictions. It should be noted that this time complexity is still a huge reduction compared to the Sankoff version and other variants (29). In contrast, the time complexity of COVE is O(L³N), clearly making it suitable for larger scale search and refinement of a given dataset. Importantly, when comparing the two algorithms for local motif search in large sequences, FOLDALIGN has already reduced the input sequence length by several factors, making COVE even faster. Thus, in such cases times are not directly comparable. However, our general experience is that FOLDALIGN is of the order of hours/days, whereas COVE is of the order of seconds/minutes, which is also clear from comparing the two time complexities.

The FOLDALIGN score for multiple alignments is computed as the sum of the scores taken over all pairs of sequences in the alignment. Therefore, the score of round r (the multiple alignment of r sequences) can be written as:

1

where s_lk is the pairwise score between sequence l and k, when they are included in and constrained by the alignment of the r sequences. Assuming that all the sequences in the alignment are reasonably similar, and the pairwise score s_lk is approximately constant c, we readily see that the score should grow as:

2

Thus, if this assumption holds, S_r/r as a function of r should be a straight line. The coefficient c can be interpreted as the average (round normalized) score of the all the pairwise alignments of the newly added sequence and each of the (r – 1) sequences in the already existing alignment. The recursion of course applies when a sequence with the same properties as the round r – 1 sequence enters the alignment at round r. Thus, two different competing motifs could behave in this way, but have different constants. Likewise, when a motif shortens it can result in the change of slope (c). Thus, the break points tell us when the FOLDALIGN motif is likely to change, and when a primary core motif has been obtained.

Performance evaluation

To evaluate the alignments relative to the database, we applied Matthews correlation coefficient (43), a measure that is commonly used in bioinformatics, for example in protein structure and gene finding evaluations (44,45). This measure can be applied to RNA secondary structure prediction as well to quantify the agreement between the predicted structural alignment and the SSU rRNA database assignment. For each sequence in a structural alignment the two secondary structure assignments can be compared by counting the number of pairs for which both assignments have base pairs between the same positions (true positives P_t), the prediction has base pairs and the database does not (false positives P_f), the number of pairs for which both assignments do not have base pairs (true negatives N_t), and the number of pairs for which the prediction does not have base pair assignment but the database does (false negatives N_f). The numbers can be added for each sequence in the alignment, and the Matthews correlation coefficient can be computed:

3

Note that this measure also applies to base pair predictions of a single sequence for any method, including energy prediction (46).

A frequently applied method of comparing a structure to a database is to report the number of predicted base pairs that are also base pairs in the database assignment, that is, to report P_t/(P_t + N_f), which is the fraction of correctly predicted base pairs of all true base pairs. This measure is also called the sensitivity. Another frequently applied measure is the specificity P_t/(P_t + P_f), which here is the rate of true predicted base pairs of all predicted base pairs.

RNA secondary structure imposes constraints on the correlation coefficient: as there are no more than N/2 base pairs for a sequence of length N, P_t + N_f ≤ N/2. Likewise, if the methods for predicting secondary structure alone predict no more than N/2 base pairs, P_t + P_f ≤ N/2. As the total number of possible pairs is N(N – 1)/2, the constraints imply that N_t ≥ N(N – 3)/2 + P_t, which is at least a factor N larger than P_t, P_f and N_f. Equation 3 can easily be written as:

4

where N_f/N_t → 0 and P_f/N_t → 0 for N → ∞. For any reasonable prediction method (P_t > 0), with at least P_t ∼ P_f or P_t ∼ N_f, we can write:

5

which is recognized as the geometric mean of the sensitivity and specificity. Thus, such an average provides a better evaluation than just reporting the fraction P_t/(P_t + N_f), because both types of false base pair predictions are taken into account. This approximates the expression in equation 3 very well (see below). Note the reduction in the expression if N_f = P_f, which is the case if the number of predicted base pairs is the same as the true number of base pairs. In a similar way, it can be shown that the lower bound to C scales as –1/2(N – 3), which goes towards zero for N going to infinity. Thus, the constraints governed by RNA secondary structure have some interesting effects on the correlation coefficient, and its range becomes reduced to the interval between zero and one. It should, however, be mentioned that ‘random’ predictions still lead to a correlation coefficient of zero. RNA secondary structure induces an anti-symmetry to the correlation coefficient, as it is not possible to exactly predict the opposite of the number of base pairs, as any prediction always allows for many true negatives. Notice also that Matthews correlation coefficient can be written as the difference between the products of two geometric means, that is C = C_PtC_Nt – C_PfC_Nf, where:

The interpretation of C_Pt and C_Nt is clear. C_Pf is the geometric mean of the sensitivity and specificity for wrong predictions of positives. Likewise, C_Nf is such a mean for negatives.

We can also evaluate the improvement of COVE scores when FOLDALIGN provides a seed alignment, compared to COVE used alone. COVE scores measure the log probability (in bits) of the aligned sequences compared to a null model (22). The objective of COVE is to find the SCFG model and alignment of sequences that maximizes the score. So, if using FOLDALIGN seeds improves the score of the COVE alignment, this indicates that COVE did not attain the globally optimum alignment and provides a measure of how much improvement is obtained.

RESULTS

Here we present the automated structural alignments performed by FOLDALIGN and COVE. The archaeal small SSU rRNA dataset shows controlled studies of FOLDALIGN score growth, FOLDALIGN impact on COVE and performance evaluation of the strategy when quantitatively compared to the database alignment. The IRE-like dataset demonstrates the ability of FOLDALIGN to identify a motif with highly variable sequence but conserved structure, located at various positions in long UTR sequences, and then to build a COVE model that can be used to identify additional occurrences of the motif in other sequences.

Automated structural alignments and FOLDALIGN score analysis

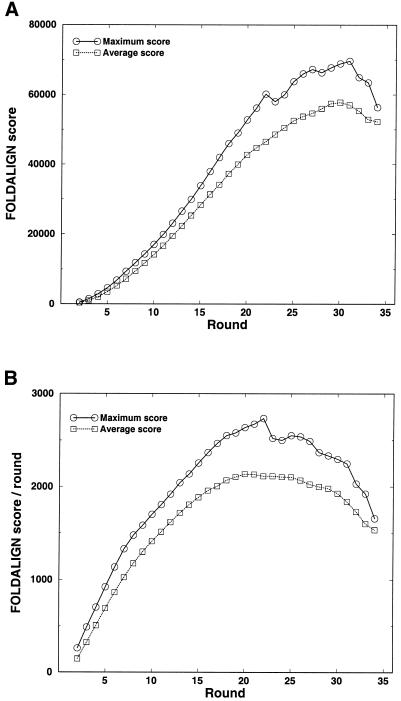
We considered the set of the 34 archaeal small SSU rRNA sequences. We focussed on analyzing the score growth of FOLDALIGN, which was helpful in pointing out useful COVE seed alignments consisting of a small number of sequences only. We referred to an alignment of a given number of sequences as the corresponding round in the FOLDALIGN algorithm. An example of score growth is given in Figure 2. FOLDALIGN captured the alignment very well up to round 31, where the greedy algorithm broke down (see below). The empirical inflection point was at round 22. At round 23 a mismatch occurred which made the consensus structure consist of a bulge, which, summed across all sequences in the alignment, caused a drop in score (alignments not shown). At round 32 a more serious misalignment occurred that decreased the absolute score. Note that a decrease in the score does not necessarily imply a misalignment; it may also mean that the newly added sequence contains a shorter version of the core motif, which misses some elements that the previously aligned sequences contained.

Figure 2.

Score growth for the locally alignable sequences. For comparison, the average scores of all alignments have been included: (A) raw FOLDALIGN score and (B) round–normalized FOLDALIGN score. At round two, the best score was a factor of 1.5 higher than the average score.

As described by Gorodkin et al. (29), the highest-scoring alignment does not necessarily describe a consensus motif best. This is in part due to the progressive construction of the multiple alignment and the dependence of the score on the number of sequences aligned (if the pairwise score between any two sequences is approximately constant). As argued in the Materials and Methods, such behavior should be detectable by considering the score normalized by the round, and core motifs are thereby obtained.

In fact, a more refined picture of events is seen in Figure 2B. There are several linear regions with different slopes: round 2–7, 8–18 and 25–31 with different (decreasing) slopes. These regions can be well fit by linear regression (and linear correlation coefficients at 0.99 or better), with the two former regions having slopes at 214 and 109. This shows a drop in score growth, which is due to reduced alignment length. Importantly, this provides us with a subset of the most significant alignments, and indicates a class of just a few sequences that contains the motif.

Both structure logo (47) and mutual information plots (48) of FOLDALIGN round 31 and database alignment shows that the automated alignment is in good agreement with the database alignment (data not shown).

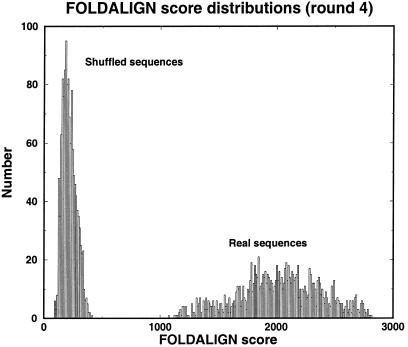
In addition, we also studied a large number of FOLDALIGN runs on shuffled sequences that did not contain any significant motif. See Figure 3 for an example. This was clear in two ways, by considering the score growth, but also through comparison of the distributions of scores (real versus shuffled) for each round. Already at round 2 the scores differed significantly. The score distribution of shuffled sequences appears to consist of a single peak only, whereas the score distribution appears multi-modal for real sequences.

Figure 3.

The score distribution for round 4. For comparison, the distribution of a set where the nucleotides were shuffled while preserving the di-nucleotide distribution in the sequences (38). The same distribution was also obtained from a mono-nucleotide shuffling.

The difference between the score distribution of a particular motif and shuffled sequences, which each represent different (pseudo) structures, represents two extremes in distinguishing varying structural motifs. Clearly if the dataset is not dominated by a single motif, but by multiple motifs, one would expect such score distributions to fall in between these two. Dealing with multiple motifs, one can take out the most significant one, and in a subsequent run identify secondary motifs.

As the probability of finding the motifs is a combination of the sequence information content and the mutual information (47), structural variability lowers the information content of a common motif, and that will make it difficult, or impossible, to find a single representative motif. FOLDALIGN score statistics and related issues have been discussed elsewhere (9,49).

Completing the alignments by combining FOLDALIGN and COVE

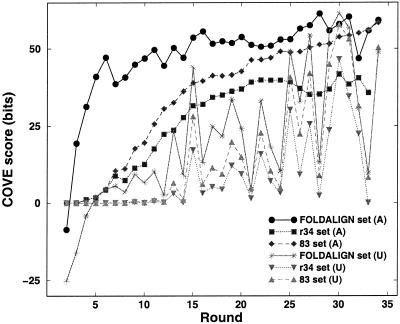
Here we systematically investigated the performance of COVE using the best FOLDALIGN alignment at each round. First we analyzed the results using the raw COVE score (measured in bits), as plotted for increasing rounds in Figure 4. For each round r, COVE was applied on three types of data: the sequences completing the best FOLDALIGN alignment (FOLDALIGN set), the remaining 34 – r sequences from the similarity reduced set (r34 set) and all the remaining 83 sequences from the total of 117 sequences we started out with (83 set). The r34 set acts as an ‘independent’ test set, since the sequences used to train the covariance model are removed, and no very highly similar sequences remain. For each of these three sets, two types of covariance models were made: those making use of the alignment made by FOLDALIGN (A), and those for which the model is built on the same sequences, but unaligned (U). The local motif was searched for by a COVE scanning module.

Figure 4.

COVE performance on the best FOLDALIGN alignment for increasing rounds. Covariance models were made using the FOLDALIGN alignment, or the corresponding sequences without the alignment. For each such case we report the average performance on the sequences themselves, the average performance on the remaining sequences in the r34 set, and on the remaining 83 of the total 117 sequences in the dataset.

It is evident from the curves that using FOLDALIGN alignments to train COVE does in general significantly enhance COVE’s performance. The performance of COVE on the unaligned sequences varied dramatically on the training sets from different rounds, whereas when trained using the FOLDALIGN alignments the scores were nearly always higher and much less variable. As expected, the performance on the test set (r34 set) was consistently lower than that on sequences used to build the model. The performance on the 83 set converges to that of the FOLDALIGN set (for both A and U models), which is also not surprising, as there are many sequences that are similar to those used to train the COVE models. Once again using the FOLDALIGN alignment significantly enhanced performance for both the r34 and 83 sets. One striking result is that when run on the training set, COVE managed to obtain almost maximum performance when trained with only six FOLDALIGN sequences. The other sets, r34(A) and 83(A), required more training examples (about 20) to achieve near maximum performance. These rounds agree very well with the piecewise linearity found from the FOLDALIGN score growth in Figure 2B, as they correspond to the inflections in the curve, and represent changes in the (core) motifs that appear in the FOLDALIGNed sequences. It is clear that the combination of FOLDALIGN and COVE can improve on both of them, especially because FOLDALIGN only assigns the consensus structure to any sequence, whereas COVE assigns an individual structure, but also because COVE is an order of magnitude faster than FOLDALIGN. The resulting combined alignment does indeed resemble the database alignment, which again is evident from studying structure logos and mutual information plots (47,48).

As mentioned in the Materials and Methods, this analysis covered a large parameter space resulting in high time complexity. The running time for FOLDALIGN on a DELL PowerEdge 6300 with four 500 MHz PIII processors was ∼3 weeks. However, as we shall see later, the full run is not needed, nor is the large parameter space coverage (saving the 40 best sequences at each round). Also, we allowed for very large differences in gaps when computing the score (29). This inclusive coverage was used to ensure a trustworthy analysis could be made.

However, for most application-specific problems, such as the IRE-like element search shown later, the effective running time is ∼10–12 h using a single processor only. This is still admittedly quite slow, but nonetheless useful. The COVE runs were of the order of seconds in training models and scan for the local motifs. But, as mentioned, COVE also works on a much smaller sequence length than FOLDALIGN.

We also made a quick test of whether the trained COVE models would be suitable for scanning genomes. Using the model trained on FOLDALIGN round 31, we scanned M.janaschii and Pyrococcus abyssi for the characteristic hairpin (using a window size of 125 nt). The size of these genomes is in the range 1.75–1.80 million bases, and the scan took ∼14 h for each. In both cases the real hairpins were found with scores of 84–87, while the next highest scores anywhere in the genome were <3.

Performance evaluation of the database alignment and the automated structural alignments

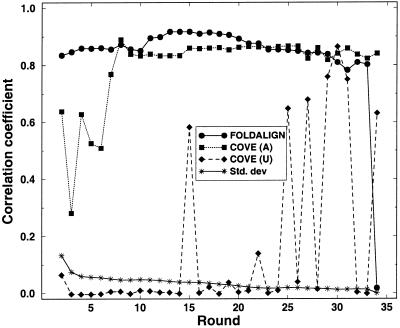
Here we made the comparison of database and predicted alignments more rigorous by computing Matthews correlation coefficient (3), and thereby obtained a quantitative measure that simultaneously includes both assignments. We also calculated the correlation coefficient for COVE alignments. The correlation coefficients were computed as follows: for each sequence region in a structural alignment, the structure from the prediction was compared to the corresponding structure assigned in the database. (Thus, gaps in the two structure assignments were ignored.) For each sequence P_t, P_f, N_t and N_f were counted and added to the numbers found for the previous sequence. After counting all sequences the correlation coefficient was computed from the final four numbers. The results are shown in Figure 5.

Figure 5.

The correlation coefficients for each round comparing the database alignment to FOLDALIGN, COVE (A) and COVE (U). The standard deviations of FOLDALIGN scores have been included to indicate the descent of low score alignment that have high correlation coefficient, for increasing rounds.

The correlation coefficients were only computed on the final region of the sequences entering the alignments. As FOLDALIGN reduced the length of the sequences to the common motif, and COVE aligned the full-length sequences, the comparison between FOLDALIGN and COVE is slightly biased. However, differences can still be found. As above, COVE without FOLDALIGN seeds [COVE (U)] did not perform well (as expected). When applying the FOLDALIGN alignment to COVE [COVE (A)] the performance increased, and was comparable to that of FOLDALIGN.

As mentioned above, FOLDALIGN misaligned sequences after round 31, but COVE (A) aligned the sequences correctly. This appeared as a small growth in the difference between the correlation coefficient of FOLDALIGN and COVE (A). The drastic drop in the FOLDALIGN correlation coefficient at round 34 was due to a misalignment of two sequences.

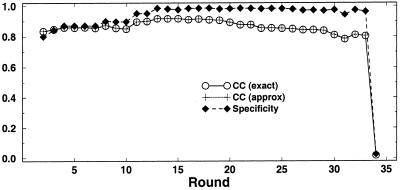
To test whether Matthews correlation coefficient for RNA secondary structure prediction can be well approximated by the geometric mean of the sensitivity and specificity, we compared the approximation to the accurately calculated correlation coefficients. An example is shown in Figure 6. We see that the geometric mean approximation was very accurate, and this goes for all the correlation curves shown in Figure 5.

Figure 6.

The accurate calculation of Matthews correlation coefficient, compared to the geometric mean approximation. For comparison, the specificity is shown. An example for FOLDALIGN on locally alignable sequences is shown. As FOLDALIGN requires all sequences to base pair to assign common base pair, and the structure for each sequence in general can have more base pairs than consensus, the false negative rate should be expected to be higher than the false positive rate. Thus, the specificity is higher than the sensitivity (data not shown).

Selecting an alignment generated by an alignment method is a fundamental problem: there exist many almost equally good alignments. The more general question of asking about the probability of an alignment can lead to alignment methods that do not produce any alignments (50). FOLDALIGN, however, indicates the round from which to select an alignment where many (suboptimal) alignments look much the same, and also indicates the alignment having the highest score at that round. The application of COVE to the alignment produced by FOLDALIGN allows for it to be improved upon by the iterative refinement method of COVE.

Searching for stem–loops in UTR-like sequences

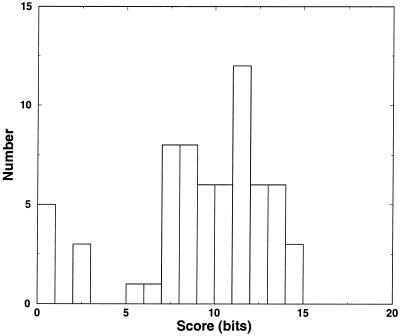
As a completely independent test of the results obtained on the archaeal SSU rRNA dataset above, we used 14 of the 56 sequences from the ferritin IRE-like dataset. FOLDALIGN found the stem–loop motif as shown in Figure 7. For the original set without degeneracy the motif is conserved enough in sequence that it could even be found by the local sequence alignment method CONSENSUS (37). But by making it more variable, including a variable length loop, it could not be identified using CONSENSUS, nor by any global alignment method (data not shown). Using the results obtained above it is clear that a motif discovered by FOLDALIGN from just a small number of sequences is sufficient to provide a good seed alignment to COVE. Even though the motif starts to appear at round 3–4, and the previous results indicated the seed alignment of just six sequences might be useful for COVE, we provided the 14 sequence seed alignment to COVE. Not surprisingly, the normalized score formed a linear function of round number (data not shown). Training COVE on this seed alignment and searching the remaining 42 sequences picked up all the motifs. However, a few additional hits were also picked up by COVE, but by considering the score distribution, a threshold of 5 bits was found (Fig. 8). At that threshold there were no false negatives and only one false positive, which could be identified by an unusual structure (data not shown).

Figure 7.

The local alignment found by FOLDALIGN. The motifs were distributed randomly in UTR-like sequences of length 100–330 nt, as shown in Figure 1. FOLDALIGN located the motifs and aligned them by their structure. The last line indicates the structure assignment, using parentheses to indicate individual base pairs.

Figure 8.

Distribution of COVE scores on all 56 sequences when the alignment shown in Figure 7 was used as a core alignment. The distribution suggest a natural score cut-off to discard false hits.

In this example we show that FOLDALIGN was able to discover a stem–loop motif, sharing only a few conserved bases of sequence but a common structure, within otherwise unrelated sequences. Finding a few examples of the motif was sufficient to train a COVE model which could then be used to identify additional occurrences of the motif in other sequences. Once the motif pattern is identified, other approaches might also be used to identify additional occurrences in a large database search (26,51,52).

DISCUSSION

We have addressed the problem of finding structural RNA motifs (stem–loop) within a set of sequences that have nothing else in common. We developed an approach that is a combination of two other methods, FOLDALIGN and the SCFG-based COVE. Methods designed to identify sequence motifs, but which ignore structure, cannot solve this problem, nor can COVE alone because it does not identify local alignments. FOLDALIGN can solve the problem but is too slow for large collections of data or long sequences. By combining both approaches we had a fairly efficient and reliable method that was capable of finding an IRE-like stem–loop motif in a set of randomized UTR sequences.

The approach was first studied carefully on a set of archaeal rRNA stem–loop regions that were excised so they only aligned locally. Using the curated database alignment it was possible to evaluate the methodology quantitatively through Matthews correlation coefficient. We obtained correlation coefficients from 0.8 to 0.9 between predicted structural alignments and database, indicating the usefulness of the combined approach.

By studying the FOLDALIGN score growth more carefully we could detect changes in the existing motif as new sequences were added to the alignment. In that way early core motifs were detected and could be given to COVE and near optimal performance could be obtained. In this way the approaches could be optimally combined.

There are two main reasons why a correlation coefficient of 1.0 (perfect agreement) is not obtainable here. From a probabilistic point of view a statistical alignment approach (50,53) would compute the probability of any alignment of the N sequences, P(x₁,…,x_N), and we would have to consider the distribution of structural alignments rather than any particular instance. As there will be many alignments with almost the same probability, it is in the end somewhat arbitrary which one is selected from the method (leaving aside the question of which one is true). Further, it is important to point out that different alignment methods in general would lead to different probability density distributions. Nonetheless, the same conclusions about the relationships among the sequences can most likely be drawn from a large number of alignments for any given method.

As this is the case, there will always be a small variation between a database alignment and a prediction method when they both include only secondary structure information. Including three-dimensional information (assuming it is available) would be a clear improvement. Other contributions to false predictions are that FOLDALIGN only assigns the consensus structure to any sequence in its alignment and individual sequences may have more structure than the common elements. COVE can correct that limitation, but often does not. Improvements to the COVE program may even further increase the agreement between the fully automated alignment and that in the databases, which have been refined through expert intervention.

Incorporating evolutionary information of an estimated phylogenetic tree (54,18) would undoubtedly lead to improved performance, and a more consistent assignment of base pairs to the individual sequences.

The idea of applying an evolutionary model that assumes simultaneous compensatory substitutions, that is substituting base pairs in one sequence with base pairs in another (54–56), is in agreement with the basic construction of the FOLDALIGN score. In particular, Tillier and Collins (55) derived parameters which measured the degree of sequence conservation versus covariation in a set of phylogenetically related sequences, and such information can be incorporated into the FOLDALIGN scoring scheme by weighing the sequence similarity component against the base pair component of the scoring matrix.

The speed and efficiency of FOLDALIGN can be improved, which allows us to analyze longer sequences and consider more varied structures. In particular, the greedy algorithm can identify sets of aligned sequences that are mutually consistent and merge them directly, saving a large number of intermediate comparisons. Including more varied structure allows searches for more complicated regulatory motifs, for example internal ribosomal entry sites. It is also possible to align regions that are mutually consistent, while re-evaluating the non-consistent regions, perhaps through the application of COVE over the region in doubt only. Such interspersed use of FOLDALIGN and COVE (or a similar method), along with phylogenetic information, should improve its prediction accuracy even more.

As the large scale sequencing projects are being followed up by genome-wide projects to uncover regulatory networks, the ability to identify functional sites in RNA sequences will become increasingly important. The combination of the two RNA motif identification programs FOLDALIGN and COVE improves upon the capabilities of either alone, and promises an effective means of identifying such RNA motifs.

We have constructed a server that can perform basic stem–loop searches by combining FOLDALIGN and COVE, as described here. The SLASH server (Stem–Loop Align SearcH) is available at http://www.bioinf.au.dk/slash/.