Abstract
The hypothesis that brain pathways form 2D sheet-like structures layered in 3D as “pages of a book” has been a topic of debate in the recent literature. This hypothesis was mainly supported by a qualitative evaluation of “path neighborhoods” reconstructed with diffusion MRI (dMRI) tractography. Notwithstanding the potentially important implications of the sheet structure hypothesis for our understanding of brain structure and development, it is still considered controversial by many for lack of quantitative analysis. A means to quantify sheet structure is therefore necessary to reliably investigate its occurrence in the brain. Previous work has proposed the Lie bracket as a quantitative indicator of sheet structure, which could be computed by reconstructing path neighborhoods from the peak orientations of dMRI orientation density functions. Robust estimation of the Lie bracket, however, is challenging due to high noise levels and missing peak orientations. We propose a novel method to estimate the Lie bracket that does not involve the reconstruction of path neighborhoods with tractography. This method requires the computation of derivatives of the fiber peak orientations, for which we adopt an approach called normalized convolution. With simulations and experimental data we show that the new approach is more robust with respect to missing peaks and noise. We also demonstrate that the method is able to quantify to what extent sheet structure is supported for dMRI data of different species, acquired with different scanners, diffusion weightings, dMRI sampling schemes, and spatial resolutions. The proposed method can also be used with directional data derived from other techniques than dMRI, which will facilitate further validation of the existence of sheet structure.
Graphical Abstract

1. Introduction
A recent debate on the existence of ‘sheet structures’ in the brain has gained much attention from the neuroscience and diffusion MRI (dMRI) communities (Catani et al., 2012; Wedeen et al., 2012a; Wedeen et al., 2012b). While the term sheets had already been suggested in several contexts before (Kindlmann et al., 2007; Schultz et al., 2010; Smith et al., 2006; Vilanova et al., 2004; Yushkevich et al., 2008; Zhang et al., 2003), Wedeen et al. (2012b) proposed a different and specific definition of brain sheet structure: a composition of two sets of tracts that locally cross each other on the same surface. Such crossing-fiber sheets should not be confused with white matter tracts that approximate thin single-fiber sheets by themselves (e.g. parts of the corpus callosum and the corona radiata). According to Wedeen et al. this geometric structure was, although “mathematically specific and highly atypical”, deemed to be “characteristic of the brain pathways”, “not unfathomable but unlimited”, and “consistent with embryogenesis” (Wedeen et al., 2012a; Wedeen et al., 2012b).
To support the sheet structure hypothesis, Wedeen et al. (2012b) reconstructed so-called path neighborhoods with dMRI tractography: pathways were tracked from a seed point, and paths incident on these pathways were subsequently computed. With this method, sheet structures were observed pervasively in white matter and found consistently across species and scales. In a response to this finding, Catani et al. (2012) suggested that the observed “grid pattern is most likely an artifact attributable to the limitations of their method”. These limitations included the lower angular resolution of the dMRI method used in Wedeen et al. (2012b), which has a negative impact on the tractography reconstructions of path neighborhoods. In addition, Catani et al. (2012) emphasized that dMRI reconstructions of pathways cannot be equated to true axons. Finally, they stated that comprehensive quantitative analysis is necessary to reliably assess the occurrence of sheet structure in the brain and in different individuals. This would allow the investigation of sheet structure extent, location, and orientation as novel quantitative features of brain structure.
Quantitative analysis of sheet structure requires a measure that is specific to the existence of this geometry. Previous work has shown that the Lie bracket, a mathematical concept from differential geometry, captures information on the existence of sheet structure (Tax et al., 2015; Tax et al., 2014a; Tax et al., 2016b; Wedeen et al., 2012b; Wedeen et al., 2014). Specifically, the Lie bracket can be computed from two vector fields, and is a vector field itself. If the two constituent vector fields are tangent to the orientations of two associated tracts, then the Lie bracket is an indicator of sheet structure between these tracts. In dMRI, such vector fields can be derived, for example, from the peak directions of diffusion or fiber orientation density functions (dODFs or fODFs).
Estimating a Lie bracket from dMRI peak directions is greatly challenged by the sensitivity of dMRI to noise and the inherent spatial discretization. In addition, dMRI peaks are not clustered into distinct vector fields a priori. In previous work we have proposed to compute the Lie bracket by reconstructing an extensive amount of path neighborhoods (Tax et al., 2015; Tax et al., 2014a; Tax et al., 2016b), inspired by the qualitative reconstructions in (Wedeen et al., 2012b). More specifically, by taking small ‘loops’ along the tractography pathways of two vector fields, we could obtain an estimate of the Lie bracket. In this so-called flows-and-limits approach, dMRI peaks were clustered into distinct vector fields during tractography. By computing the Lie bracket for repeated dMRI measurements or for different bootstraps of a single measurement, we were able to derive a sheet probability index (SPI) (Tax et al., 2016a; Tax et al., 2016b). SPI values close to 1 indicate that the underlying vector fields are highly supportive of sheet structure.
The previously proposed flows-and-limits approach for estimating the Lie bracket suffers from several limitations. First, it relies on tractography and storage of a large amount of loops, and is thus computationally very expensive. Second, computing the Lie bracket with this method suffers from the same intrinsic limitations as tractography, notably its sensitivity to parameter settings (e.g., step size). Finally, because the algorithm has to keep track of the assignment of peaks to vector fields during tractography, it is unclear how to proceed when peaks are missing. This happens frequently due to for example noise, modeling imperfections, or at the boundaries of fiber bundles. The unwanted termination of loops in such cases may severely impact the accuracy and precision of the Lie bracket and SPI estimates.
In this work we use the pipeline to compute the SPI developed in previous work (Tax et al., 2016b), but propose a new approach to compute the Lie bracket based on a conceptually different but equivalent definition. Instead of using the flows-and-limits approach, we here use the fact that the vector fields are defined on subsets of the 3D Euclidean space. The Lie bracket can thus be expressed in terms of derivatives of the vector fields with respect to the three spatial variables (which we will henceforth denote by ‘the coordinate approach’). Taking derivatives of vector fields is, however, complicated: a straightforward finite difference implementation is far from stable for our purpose. Therefore, we adopt a method called normalized convolution (Knutsson and Westin, 1993) to calculate vector field derivatives and subsequently the Lie bracket. This approach was designed to cope with noise and uncertainty in data, and is thus more robust with respect to missing peaks and inaccuracies in for example the clustering of peaks into distinct vector fields.
This paper is organized as follows. In Section 2 we will first briefly recapitulate the mathematical condition for the existence of sheet structure, involving the Lie bracket of vector fields (Tax et al., 2015; Tax et al., 2014a; Tax et al., 2016b; Wedeen et al., 2012b; Wedeen et al., 2014). In addition, we will present the flows-and-limits and coordinate definitions in more detail, and discuss their implementations. For the coordinate approach, this involves the implementation of normalized convolution and the clustering of vector fields in a spatial neighborhood. Finally, we will present the experiments on vector field simulations, dMRI simulations, and real data. In Sections 3 and 4, we will describe and discuss the corresponding results. Preliminary results of this work have been presented at the ISMRM (Tax et al., 2016c).
2. Methods
Section 2.1 explains which condition two vector fields have to fulfill in order to form sheet structures. Section 2.2 describes the two definitions of the Lie bracket and their corresponding algorithms (i.e., the flows-and-limits and coordinate approaches). The computation of vector field derivatives with normalized convolution is outlined in Section 2.2.2.1 and the approach for clustering of vector fields in a spatial neighborhood is presented in Section 2.2.2.2.
2.1 The Lie Bracket as an indicator of sheet structure
Consider the set of directions (or vectors) at each position of the brain M ⊂ ℝ3, which we assume to be representative of the underlying local fiber architecture. Tractography processes then assume that in a specific part of the brain NV ⊂ M there exists a smooth 3D vector field V that can be integrated into integral curves (or streamlines) ΦV (s, p). Here, p denotes the starting position, s the arc length, and the vector at location p. Similarly, two smooth vector fields V and W in a brain region NV ∩ NW can potentially be integrated into integral surfaces or sheet structures.
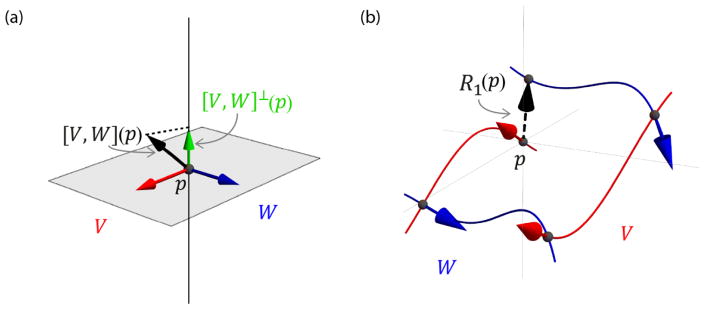
The Lie bracket of two vector fields V and W defines a third vector field [V, W] that holds information on the presence of sheet structure. More specifically, to investigate whether two vector fields locally form a sheet structure we compute the normal component of the Lie bracket at a point which p is then perpendicular to both V(p) and W(p) (Fig 1a):
| [1] |
Fig. 1.
(a) To investigate the existence of sheet structure, we consider the relation of the Lie bracket [V, W](p) (black arrow) to the plane spanned by vectors V(p) (red arrow) W(p) and (blue arrow). More specifically, we evaluate the normal component of the Lie bracket [V, W]⊥(p) (green arrow). When it is zero, sheet structure exists. (b) Definition of the Lie bracket as the closure R(p) when trying to move around in an infinitesimal loop along the integral curves of V and W. Here, the loop corresponding to the closure R1is displayed (Eq. [2]).
According to the Frobenius theorem (Lang, 1995; Spivak, 1979), the condition for sheet structure is then fulfilled at all points p ∈ NV ∩ NW where [V, W]⊥(p) = 0 (Tax et al., 2015; Tax et al., 2014a; Tax et al., 2016b; Wedeen et al., 2012b). In other words, the Lie bracket [V, W](p) must lie in the plane spanned by V(p) and W(p). Note that we will use shorthand notations [·, ·]p = [·, ·](p) and .
2.2 Computation of the Lie bracket
In this Section, we explain the two definitions of the Lie bracket and their corresponding implementations.
2.2.1 Flows-and-limits definition
In previous work, we have used the definition of the Lie bracket as the deviation from p, or closure R(p) = (r1, r2, r3)(p) (with ri the components) when trying to move around in an infinitesimal loop along the integral curves of V and W (Fig. 1b) (Tax et al., 2015; Tax et al., 2014a; Tax et al., 2016b; Wedeen et al., 2012b; Wedeen et al., 2014).
With streamline tractography, loop configurations can be reconstructed to estimate their corresponding closures:
| [2] |
Here, denotes the flow along V for some fixed time or distance h (with arc length parameterization), the estimate of the flow as approximated by tractography, ∘ indicates function composition, and h1 and h2 are the walking distances along the integral curves of V and W, respectively. We choose h1, h2 ∈ {−hmax, −hmax + Δh, −hmax + 2Δh, …, −Δh, Δh, …, hmax}with hmax the maximum walking distance and Δh a step size, resulting in K difference vectors (1200 for hmax = 5 voxel size and Δh = 0.5 voxel size, where we hereafter shorten voxel size to voxels).
If h1 and h2 are sufficiently small, there exists an approximately linear relationship between the product h1 h2and a difference vector component ri (i ∈ [1,2,3]), with the corresponding component of the Lie bracket [V, W]i being the steepness of the line:
| [3] |
We can compute an estimate of the Lie bracket with a simple linear least squares fit
| [4] |
Here, R is a K × 3 matrix with the estimated closures R̂(p), H is a K × 1 matrix with the products of the used h1 and h2 for the corresponding difference vector, β is a 1 × 3 matrix with the Lie bracket components , and ε is a K × 3 matrix with normally distributed errors.
2.2.2 Coordinate definition
The Lie bracket can also be computed with respect to a coordinate system. In our case, V and W are vector fields on a subset of the 3D Euclidean space (i.e., M ⊂ ℝ3) and can therefore each be represented by a vector-valued function in standard Cartesian coordinates (x1, x2, x3). The Lie bracket is then given by
| [5] |
where JV is the Jacobian matrix of the vector-valued function V = (v1, v2, v3)T:
| [6] |
JW · V can be interpreted as the directional derivative or ‘rate of change’ of W in the direction of V. The Lie bracket indicates the difference of the rate of change of W in the direction of V and the rate of change of V in the direction of W, hence its definition as the commutator of vector fields.
To compute the Lie bracket we thus need an approximation of the Jacobians JV and JW of the vector fields. Differentiation of discretized and noisy vector fields is, however, a notoriously unreliable operation. A straightforward finite differences implementation amplifies high frequency noise, and does not provide a stable solution in our case. More importantly, for our application it is not guaranteed that a vector field has a vector at every location within a neighborhood of the point of operation, because of noise or modeling imperfections. Interpreting such a missing vector as a vector with zero magnitude will introduce severe errors. We therefore adopt the normalized convolution approach (Knutsson and Westin, 1993) which is able to cope with noisy, discretized, and missing data and automatically takes care of normalization during convolution. In the next subsections, we will explain this approach in detail and outline the implementation for our application.
2.2.2.1 Normalized convolution
The problem of ill-posed differentiation can be addressed by convolution (Florack, 2013; Koenderink and Van Doorn, 1990). General convolution can be defined as
| [7] |
where B denotes a real linear filter basis, ⊗ is the tensor product, a tilde ˜ above the operator (e.g. ⊗̃) denotes convolution with that operator, and ξ = x − p is the local spatial coordinate.
Normalization and connection to linear least squares
One problem with directly applying Eq. [7] is that the result is scaled when the basis is not orthonormal. For example, applying a Gaussian derivative basis function, the value resulting from the operation will depend on the standard deviation of the Gaussian unless the basis function is normalized appropriately. In our application, the actual value of the normal component of the Lie bracket is important, and we thus have to take into account a normalization factor. A normalized version of Eq. [7] is
| [8] |
where−1 denotes the inverse.
Intuitively, convolution obtains a new description of the original representation of a neighborhood in terms of a new set of basis functions. Here, the original representation is a vector for each voxel accompanied by a basis of impulse functions at each voxel location. Ideally, the new set of basis functions is chosen in such a way that the neighborhood can be better understood. In fact, Eq. [8] obtains such a representation that is optimal in the least square sense: it produces the linear least squares (LLS) estimates for the coefficients corresponding to the new basis B. To clarify this, we will explicitly write out Eq. [8] for our application.
To estimate the first order derivatives in the Jacobian of a vector field V we choose
| [9] |
This holds a close connection to calculating derivatives of a ‘smoothed’ signal by fitting low-degree polynomials to every component vi of V in a neighborhood of p (Savitzky and Golay, 1964). In this case, each polynomial includes only terms up to first order, i.e. . We now write this problem as a regression equation
| [10] |
where, V is an N3 × 3 matrix with the vectors V in a neighborhood of p with size N × N × N, B is a N3 × 4 matrix with the basis B evaluated in each point of the neighborhood of p, α is a 4 × 3 matrix with the coefficients for every polynomial ϒi, and ε is an N3 × 3 matrix with normally distributed errors. The least squares solution for the coefficients α can then be obtained by solving the normal equations, yielding
| [11] |
which corresponds to Eq. [8]. We can now see that the result of convolution with the basis in Eq. [9] is a regularized vector and an estimate of the Jacobian at the point p(ξ = 0), calculated from the fitted polynomials (v̂i(p) = ϒi(0), ):
| [12] |
Normalized convolution and connection to weighted linear least squares
Knutsson and Westin (1993) considered a more general case of Eq. [8], and proposed to assign a scalar component to both the data and the operator that represents their certainty. More specifically, the vector field V is accompanied by a non-negative scalar function c representing its certainty, and the operator filter basis B is accompanied by a non-negative scalar function a representing its applicability (the operator equivalent to certainty). If we view a and c as additional independent variables, a generalized version of Normalized convolution can be expressed (by abuse of notation) as
| [13] |
Here · denotes the scalar product and ·̃ convolution with the scalar product (Knutsson and Westin, 1993). Explicitly writing out the terms for our application gives:
For the certainty and applicability functions we choose
| [14] |
| [15] |
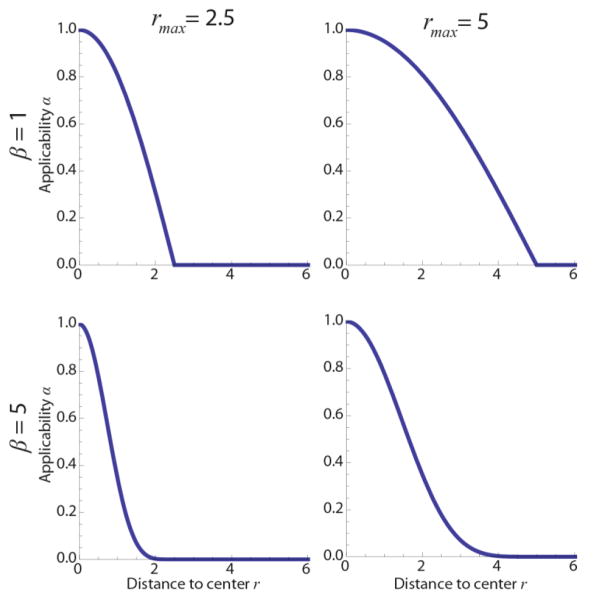
Here, q ∈ ℝ3, and the certainty c is thus set to zero when a vector is missing. Furthermore, r is the distance to the neighborhood center, and a(r) is shown in Fig. 2 for different β and rmax, which determine the ‘weight’ of data points in the neighborhood. Here, β determines the power or the ‘sharpness’ of the function. To reduce the number of parameters in the algorithm, we choose rmax = 0.5 Nδ, with N and δ the kernel and voxel sizes, respectively. Since the voxel size is fixed, parameter N thus directly tunes rmax. This ensures that the applicability function has a value of zero beyond the kernel size and no zeros along the axes of the kernel, since this would only increase computation time.
Fig. 2.
Applicability function a(r) for different rmax and β (Eq. [15]).
Normalized convolution obtains a new description of the original representation, but now the original basis is accompanied by a strength or certainty c. A missing vector can then be interpreted as a missing basis impulse function (i.e. by setting the certainty to zero), rather than a vector with zero magnitude. Normalized convolution obtains a description in the new basis such that the local weighted mean square error is minimal, corresponding to a weighted linear least squares approach (WLLS):
| [16] |
The weights in the diagonal matrix W are then given by
| [17] |
where the subscript i refers to the ith local spatial coordinate in the N × N × N neighborhood. To summarize, the result of normalized convolution (Eq. [12]) in an N × N × N spatial neighborhood of a point p is a WLLS estimate of the vector and Jacobian at point p. These estimates can be directly substituted into Eq. [5] to obtain an estimate of the Lie bracket.
2.2.2.2 Clustering of peaks in a spatial neighborhood
In the computation of the Lie bracket we have thus far assumed that two vector fields exist in a neighborhood of the point of operation that can be derived from dMRI data. However, dMRI data typically allow the extraction of a variable number of peaks per voxel without a notion to which local vector field (or fiber population) they belong. We will call the set of peaks at a spatial location a frame, and the frames in a spatial neighborhood thus have to be clustered. We match each vector of a frame at a point in the spatial neighborhood to the frame of the center voxel (the reference frame). In this work, we cluster the frames in an N × N × N spatial neighborhood using a front-propagation approach that starts from the center of the neighborhood (Jbabdi et al., 2010). As the similarity measure we use the total cosine similarity, i.e. we find the configuration for which the total angle difference with a previously clustered frame at a nearby location is minimal. We set an angle threshold to constrain the maximum angle between corresponding vectors of frames. The clustering algorithm is detailed in Appendix A.
2.3 Evaluation of sheet structure
Once the Lie bracket of a pair of vector fields has been computed with the flows-and-limits method or the coordinate method, we can examine the existence of sheet structure by extracting the normal component of the estimated Lie bracket (Eq. [1]) and determine whether it is ‘sufficiently close’ to zero. This condition is hard to evaluate, however, since a single noisy estimate of the Lie bracket normal component does not provide information on its variability. If we assume repeated MRI measurements that yield multiple Lie bracket estimates, a sheet probability index (SPI) can be calculated (Tax et al., 2016a; Tax et al., 2016b). This index was introduced to address the issue of noise and to provide an intuitive sheet indicator. In short, the estimates are checked for normality using a Shapiro-Wilks test and the mean μ and standard deviation σ are estimated. Subsequently, the integral probability Pλ inside the region [−λ, λ] can be calculated for the estimated distribution N(μ, σ2). We can tune the parameter λ where a higher value for λ will allow larger deviations from zero. An SPI value close to 1 corresponds to a high likelihood of sheet structure, whereas an SPI close to 0 indicates that there are significant deviations from sheet structure. In practice, if only one dataset is acquired, we generate residual bootstraps to calculate the SPI (see Section 2.4.2.3).
The SPI can be visualized for pairs of vector fields throughout the brain by means of a sheet tensor (Tax et al., 2016b). Given a pair of vector fields V and W, the sheet tensor at location p is defined as
| [18] |
Here β1 denotes the largest eigenvalue of the tensor (V(p)⊗V(p) + W(p)⊗ W(p)). The sheet tensor can then be represented by an ellipsoid, of which the third eigenvector is normal to the span of V and W. The ellipsoid is colored according to the third eigenvector by using the well-known diffusion tensor imaging (DTI) coloring scheme of (Zhang et al., 2006). The SPI divided by β1 determines the size of the ellipsoid (a larger SPI results in a tensor with a larger semi-axis) and the angle between V and W determines its shape (a lower angle results in a more anisotropic sheet tensor).
2.4 Data
We evaluated the two proposed methods on different types of data: analytical vector fields, dMRI simulations, and real dMRI data.
2.4.1 Analytical vector field simulations
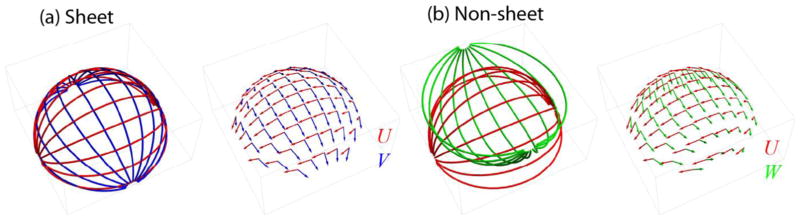
We defined three vector fields that are tangent to a sphere with radius ρ(U and V are tangent to the upper hemisphere, W is tangent to the lower hemisphere, see (Tax et al., 2016b) and Appendix B). Vector fields U and V form sheets (i.e. ), whereas U and W do not form a sheet except at x1 = 0, x2 = 0. The normal component of the Lie bracket is dependent on the radius ρ and the spatial coordinates. These simulations allowed us to evaluate the methods for Lie bracket calculation as a function of curvature κ = 1/ρ and non-commutativity of the pair U and W. The vector fields were discretized on a Cartesian grid with voxel size δ and noise was added by drawing random samples of a Watson distribution (Chen et al., 2015; Mardia and Jupp, 2009) with concentration parameter k > 0 (‘SNR level’, higher k results in smaller perturbations). We generated 50 noise iterations in the experiments.
2.4.2 Diffusion MRI data
2.4.2.1 Simulations
dMRI signals were simulated using a ZeppelinStickDot model (Ferizi et al., 2014) with the fiber direction defined by the noise-free vector fields described in the previous section. We simulate single-shell datasets with 90 directions and b = 3000 s/mm2. Noise was added according to a Rician distribution.
2.4.2.2 Real data
We used the following dMRI data sets: 1) the b = 3000 s/mm2 shell with diffusion directions of a subject of the WU-Minn Human Connectome Project (HCP) with an isotropic voxel size of 1.25 mm (Sotiropoulos et al., 2013; Van Essen et al., 2013); and 2) two ex-vivo monkey brain datasets of the same brain with b = 4000 s/mm2, one dataset had an isotropic voxel size of 0.3 mm and 60 diffusion directions, while the other dataset had an isotropic voxel size of 0.4 mm and 120 diffusion directions (Calabrese et al., 2015). The SNR of both datasets was measured in the cortex on the b = 0 image, and was 131 for the 0.4 mm and 96 for the 0.3 mm datasets, respectively.
2.4.2.3 Processing
The monkey brain datasets were corrected for motion and eddy current distortions using ExploreDTI (Leemans et al., 2009; Leemans and Jones, 2009). All datasets were processed using constrained spherical deconvolution (CSD, lmax = 8) (Tournier et al., 2007). The response function for the simulated data was generated from the ZeppelinStickDot model, and the response function for real data was computed using recursive calibration (Tax et al., 2014b). Peaks were extracted using a Newton optimization algorithm (Jeurissen et al., 2011) with a maximum number of 3 peaks and an fODF peak threshold of 0.1. To compute the SPI, we generated 50 noise iterations for simulated data, and 20 residual bootstrap realizations for real dMRI data from a single set of noisy measurements (Jeurissen et al., 2013). The peaks extracted from the different bootstrap realizations were clustered using the method described in Section 2.2.2.2, with the peaks extracted from the original data representing the reference frames. The SPI was calculated within a white matter mask dilated by one voxel. For the HCP data the mask was derived from the T1-weighted image using FSL-Fast (Zhang et al., 2001), and for the monkey brain datasets it was derived from the FA and MD images since no T1-weighted image was available (FA > 0.4 or FA > 0.15 with MD < 2.5 · 10−4 mm2/s adapted for ex-vivo data (Sherbondy et al., 2008)).
3. Results
Section 3.1 presents the results for analytical vector field simulations, Section 3.2 for dMRI simulations, and Section 3.3 for real data. We have systematically evaluated different aspects of both algorithms. Table 1 gives an overview of all the experiments, highlighting which settings were varied in each experiment.
Table 1.
Overview of the experiments, varied parameters are highlighted.
| Dataset properties | Coordinate parameters | Flows and limits parameter | SPI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sec./Fig. | Voxel size δ[mm] | k/SNR | Curvature κ[mm−1] | Lie bracket normal component [−1] | Angle threshold [°] | Dropout fraction | Kernel size N [voxels] | Sharpness β | rmax | hmax [voxels] | λ | |
| Analytical vector field simulations | 3.1.1/3 | Varied {.5,1,2} |
Fixed 250 |
Fixed 1/26 |
Fixed .031 |
NA | NA | Varied {3,7,9,11} |
Varied {1, …, 10} |
Varied | NA | NA |
| 3.1.2/4 | Varied {.5,1,2} |
Varied {50, … 450, ∞} |
Fixed 1/26 |
Fixed .031 & 0 |
NA | NA | Fixed 11 |
Fixed 1 |
Varied | Fixed 5 |
NA | |
| 3.1.3/5 | Fixed 1 |
Fixed 250 |
Fixed 1/26 |
Fixed .031 & 0 |
NA | Varied {.01, …,.2} |
Varied {3,7,9,11} |
Fixed 1 |
Varied | Varied (Polders et al.,) |
NA | |
| 3.1.4/S1 | Fixed 1 |
Varied {50, … 450, ∞} |
Varied 1/{5, 15, 25} |
NA | Varied {15, …, 55} |
Varied {.01, …,.2} |
NA | NA | NA | NA | NA | |
| dMRI simulations | 3.2.1/6a | Fixed 1 |
Varied {10, …, 50} |
Fixed 1/26 |
Fixed .031 & 0 |
Fixed 35 |
NA | Fixed 11 |
Fixed 1 |
Fixed | Fixed 5 |
NA |
| 3.2.2/6b | Fixed 1 |
Fixed 20 |
Varied 1/{8, …, 33} |
Fixed .031 & 0 |
Fixed 35 |
NA | Fixed 11 |
Fixed 1 |
Fixed | Fixed 5 voxels |
NA | |
| 3.2.3/6c | Fixed 1 |
Fixed 20 |
Fixed 1/26 |
Varied {0, …, 0.04} |
Fixed 35 |
NA | Fixed 11 |
Fixed 1 |
Fixed | Fixed 5 voxels |
NA | |
| Diffusion MRI real date | 3.3.1/S2 | Fixed 1.25 |
Fixed | NA | NA | Fixed 35 |
NA | NA | NA | Fixed | NA | NA |
| 3.3.1/7 | Fixed 1.25 |
Fixed | NA | NA | Fixed 35 |
NA | Fixed 11 |
Fixed 1 |
Fixed | Fixed 5 voxels |
.008 | |
| 3.3.1/S3a | Fixed 1.25 |
Fixed | NA | NA | Varied {15, 35, 45} |
NA | Fixed 11 |
Fixed 1 |
Fixed | NA | .008 | |
| 3.3.1/S4 | Fixed 1.25 |
Fixed | NA | NA | Fixed 35 |
NA | Varied {7, 11} |
Varied (Sporns, 200) |
Varied | NA | .008 | |
| 3.3.2/8 | Fixed .3 & .4 |
Fixed | NA | NA | Fixed 35 |
NA | Fixed 11 |
Fixed 1 |
Fixed 1.65 |
NA | Fixed .015 & .02 |
|
3.1 Analytical vector field simulations
With the analytical vector fields we will first investigate the influence of the parameters in the coordinate implementation (kernel size N and β) on the accuracy and precision of the Lie bracket normal component estimates. Subsequently, we will compare the coordinate and flows-and-limits implementations for varying voxel sizes, SNR levels, and peak dropout fractions. These experiments all use the predefined clustering of vector fields, i.e. the vector fields as they were simulated. We will also investigate the performance of the clustering method, which is described in Section 2.2.2.2 and Appendix A.
3.1.1 Coordinate implementation: Influence of spatial resolution and parameter settings
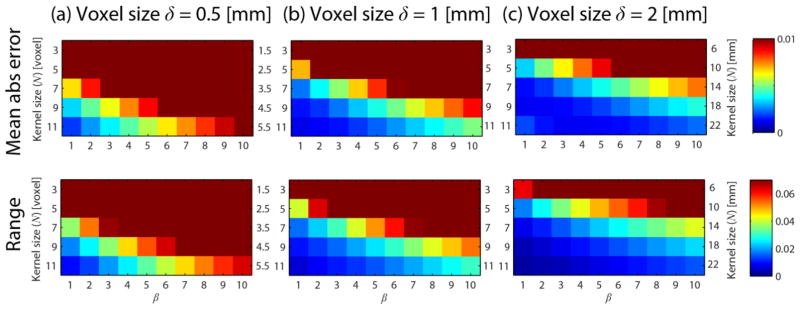
Fig. 3 shows the mean absolute error (upper row) and the range (maximum value minus minimum value, bottom row) of the Lie bracket normal component estimated values for the non-sheet vector field pair U and W (see Section 2.4.1 and Appendix B). The columns a-c show the results for different voxel sizes δ = {0.5, 1,2} mm. Each color plot shows the results for different settings of kernel size N and β. The following settings were used: curvature κ = 1/ρ = 1/26 mm−1, ‘SNR level’ k = 250, and p = (10, −10,0) yielding a non-zero Lie bracket normal component .
Fig. 3.
Mean absolute error (first row) and range (second row) of estimates for different voxel sizes δ = {0.5, 1,2} mm (a–c, columns). Each color plot shows the results for different choices for the kernel size N (indicated in voxel on the left side of each graph and in mm on the right side of each graph) and different settings for β. We used κ = 1/ρ = 1/26 mm−1, k = 250, and p = (10, −10,0).
The mean absolute error and range of the estimates generally decrease for 1) increasing voxel size at a given parameter setting, 2) increasing kernel size N, and 3) decreasing β. This means that incorporating neighborhood information over a larger scale in mm is generally beneficial for the accuracy and precision of the Lie bracket normal component estimate. There is a limit to this, however: at δ = 2, N = 11, β = 1 the mean absolute error of the estimates starts to increase again. In the remainder of the simulation experiments, where we simulate δ = 1, we will use β = 1.
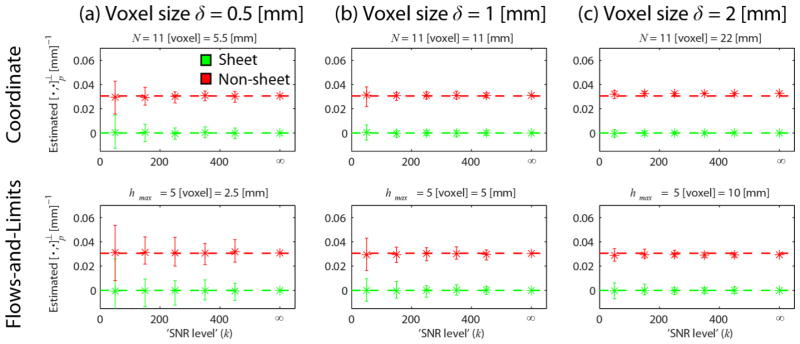
3.1.2 Coordinate vs. flows-and-limits implementation: Influence of spatial resolution and noise
Fig. 4 shows results for different voxel sizes δ = {0.5, 1,2} mm (a–c), for the coordinate implementation (top row, N = 11 voxels and β = 1) and the flows-and-limits implementation (bottom row, hmax = 5 voxel and Δh = 0.5 voxel). Each plot shows the range and mean for different SNR levels k for the sheet pair (U and V, green) and the non-sheet pair (U and W, red) defined in Section 2.4.1 and Appendix B. The ground truth value is indicated by the dashed line. We set the curvature κ = 1/ρ = 1/26 mm−1 and evaluate at point p = (10, −10,0).
Fig. 4.
Mean (asterisks) and range (error bars) of for different voxel sizes δ = {0.5, 1,2} mm (a–c, columns) and the two different implementations (rows). We used N = 11 voxel and β = 1, and hmax = 5 voxel and Δh = 0.5 voxel (the corresponding values in mm are given above each plot). Each plot shows the estimates in the case of sheet (green, indicated by the dashed line) and non-sheet (red, ) for different SNR levels k. We set κ = 1/ρ = 1/26 mm−1, and p = (10, −10,0).
The range of the estimates becomes smaller with 1) increasing SNR level k and 2) increasing voxel size for both implementations. In all cases, the coordinate implementation has a higher precision (lower variability) than the flows-and-limits implementation. This indicates that it potentially has a higher power to distinguish sheet configurations from non-sheet configurations. At a voxel size of δ = 2 mm, the estimates start to be slightly biased (i.e. start deviating from their true value) for both implementations and the used parameter settings.
3.1.3 Coordinate vs. flows-and-limits implementation: Influence of dropouts and parameter settings
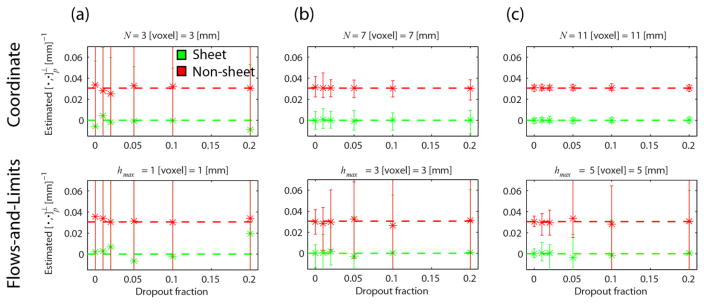
Fig. 5 shows the mean and range of the estimates as a function of the dropout fraction: For every noise iteration we randomly remove a certain fraction of peaks of each vector field. The rows show the results for the coordinate implementation (top, β = 1) and the flows-and-limits implementation (bottom) for different parameter settings of each method (columns). We used κ = 1/ρ = 1/26 mm−1, p = (10, −10,0), δ = 1 mm, and k = 250.
Fig. 5.
Mean (asterisks) and range (error bars) of for different ‘spatial neighborhood settings’ (a–c, columns): N = {3,7,11} voxel with β = 1 with for the coordinate implementation (top row) and hmax = {1,3,5} with voxel with Δh = 0.5 voxel for the flows-and-limits implementation (the corresponding values in are noted above each plot). Each plot shows the estimates in the case of sheet (green) and non-sheet (red) for different dropout fractions. We set κ = 1/ρ = 1/26 mm−1, k = 250, and p = (10, −10,0).
It becomes immediately apparent that the flows-and-limits implementation is much more sensitive to dropouts than the coordinate implementation: the range of the estimates is much larger for the former method. While for a limited use of spatial neighborhood information (N = 3 or hmax = 1 voxel) neither method is able to distinguish sheets from non-sheets, the coordinate implementation performs markedly better at higher N even for high dropout fractions. In fact, in this case the dropout fraction does not affect the precision and mean of the estimates (up to the tested fraction). For the flows-and-limits implementation the precision of the estimates decreases with dropout fraction, while the mean remains close to the true value.
3.1.4 Coordinate implementation: Evaluation of clustering of frames in a spatial neighborhood
The results presented so far use the predefined clustering of the vector fields and are thus not affected by clustering errors. Here, we evaluate the clustering algorithm presented in Section 2.2.2.2 and Appendix A on non-sheet vector field pairs U and W with different radii (ρ = {5,15,25}mm) and a third constant vector field in the z-direction. For each radius we generated 50 noise instances with k = {50,150,250,350,450,∞} and different dropout fractions {0,0.01,0.02,0.05,0.1,0.2}). We count the number of peaks that were not clustered correctly, where we distinguish between peaks that did not get a label at all and peaks that got an incorrect label.
Supplementary Fig. S1 shows the peak clustering error as a fraction of the total number of peaks simulated and for different angle threshold settings. In all erroneous cases the algorithm failed to assign the peaks to a vector field; a wrong assignment to a vector field did not occur in the evaluated cases. The number of non-clustered peaks generally increased with dropout fraction. In fact, this led to a larger fraction of dropouts than initially simulated, but did not have a significant effect on the Lie bracket estimates in analogy with Fig. 5 upper row (results not shown).
3.2 Diffusion MRI simulations
In this Section we present a comparison of the two methods for dMRI simulated data. Sections 3.2.1 to 3.2.3 outline the influence of SNR, curvature, and commutativity of the non-sheet vector field on the Lie bracket normal component estimates.
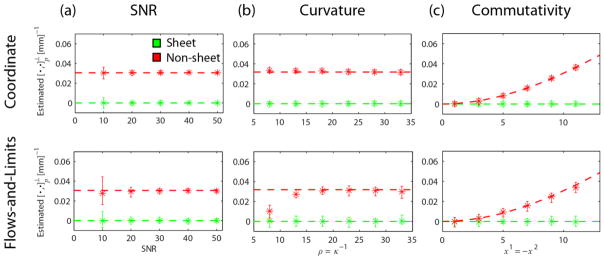
3.2.1 Coordinate vs. flows-and-limits implementation: Influence of SNR
Fig. 6a shows the results for different SNR levels for the coordinate (top, β = 1 and N = 11 voxels) and flows-and-limits (bottom, hmax = 5 voxels) implementations. We used κ = 1/ρ = 1/26 mm−1, p = (10, −10,0) and voxel size δ = 1 mm.
Fig. 6.
Mean (asterisks) and range (error bars) of for the coordinate implementation (top row N = 11 voxels, β = 1) and the flows-and-limits implementation (bottom row hmax = 5 voxels, Δh = 0.5 voxels) in the case of sheet (green) and non-sheet (red). In every experiment, we vary one factor while keeping others constant: (a) varying SNR, constant κ = 1/ρ = 1/26 mm−1, p = (10, −10,0), δ = 1 mm; (b) varying curvature and p, constant , SNR = 20, δ = 1 mm; (c) varying p and (non-sheet case), constant SNR = 20, κ = 1/ρ = 1/26 mm−1, δ = 1 mm.
Higher SNR increases the precision of the estimates for both methods. For an SNR of 10–20 the estimates were more precise for the coordinate implementation, while for higher SNR this effect is less pronounced. The mean of the estimates was close to the true value in all cases.
3.2.2 Coordinate vs. flows-and-limits implementation: The influence of curvature
Fig. 6b presents the mean and precision of the Lie bracket normal component estimates as a function of curvature κ of the integral curves (ρ = κ−1 = {8,13,18,23,28,33}mm). Results are shown for the coordinate (top, β = 1 and N = 11 voxels) and flows-and-limits (bottom, hmax = 5 voxels) implementations. We simulated an SNR of 20 and a voxel size δ = 1 mm. We evaluated the Lie bracket normal component at different points for the different curvatures to keep the magnitude of the Lie bracket constant (i.e. 0 and 0.031 for the sheet and non-sheet vector field pairs, respectively). Note that for each curvature the point of evaluation was the same for the sheet and non-sheet vector field pairs.
The precision of the estimates was higher for the coordinate implementation in all cases. For a radius larger than 23 mm, the mean of the estimates is in line with the true value. For a radius smaller than 23 mm in the non-sheet case, the mean of the estimates is only slightly off for the coordinate implementation, while it significantly deviates from the true value for the flows-and-limits implementation.
3.2.3 Coordinate vs. flows-and-limits implementation: The influence of commutativity
Fig. 6c shows the results for different points p = (x−1, −x−1,0), where the Lie bracket normal component magnitude of the non-sheet vector field pair (i.e. its ‘non-commutativity’) varies while the curvature remains constant at κ = 1/26 mm−1. Here, x1 = {1,3,5,7,9,11}mm. The Lie bracket was evaluated at the same points for the sheet vector field pair as a reference. Results are shown for the coordinate (top, β = 1 and N = 11 voxels) and flows-and-limits (bottom, hmax = 5 voxels) implementations. We used an SNR of 20 and voxel size δ = 1 mm.
In all cases, the estimates have a higher precision for the coordinate implementation than for the flows-and-limits implementation. The mean of the estimates corresponds well to the true value in all cases. For x1 > 11 edge effects will start to play a role in the flows-and-limits implementation (results not shown).
3.3 Diffusion MRI real data
3.3.1 In vivo HCP data
We first evaluated the performance of the clustering algorithm with real dMRI data. Supplementary Fig. S2 shows the peak clustering of an 11 × 11 × 11 neighborhood at three different anatomical locations, where we used an angle threshold of 35°. Overall the clustering looks plausible, and the integral curves corresponding to these vector fields would exhibit significant curvature at this scale (integral curves are not shown, with some abuse of terminology we will say that the vector fields exhibit curvature). However, at some locations the clustering appeared to be challenging: near the edges of the neighborhood, discontinuities occurred in a few occasions. Since the operator applicability reduces towards the edges, the effect of such wrongly clustered peaks generally stays limited.
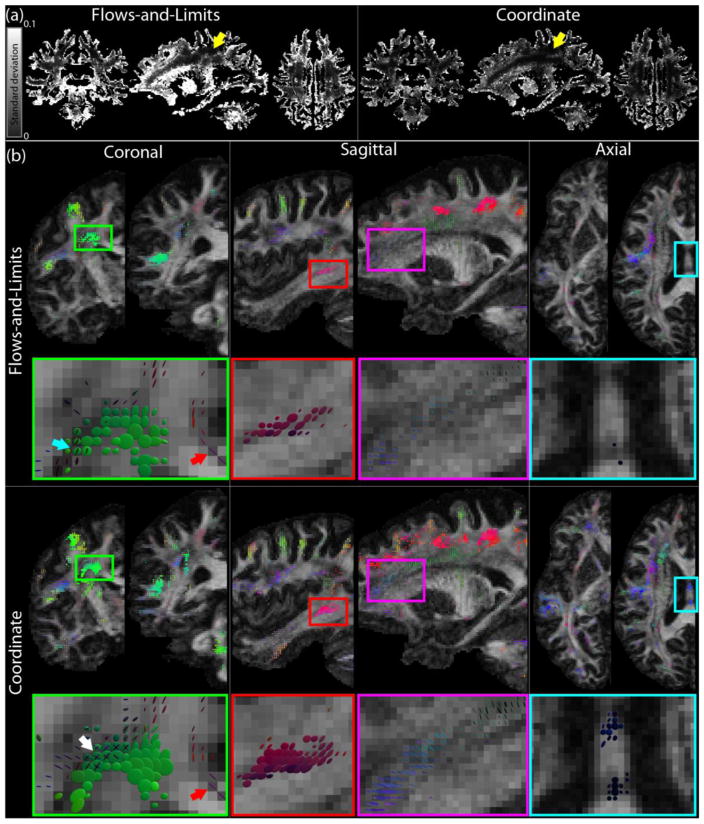
Fig. 7 displays results of the Lie bracket normal component and SPI estimation for the HCP data, where we compare the flows-and-limits (hmax = 5 voxels) and coordinate (β = 1, N = 11 voxels) implementations. Fig. 7a shows maps of the standard deviation of over the 20 bootstraps for both methods (two largest peaks in the WM). Overall, the flows-and-limits approach maps look brighter, which indicates that the standard deviation of the estimates is higher. We used these standard deviation maps to find an appropriate value for λ in the SPI calculation (see section 2.3). To this end, we identified spatially continuous regions with a Lie bracket normal component close to zero and a low standard deviation (an example area is indicated with yellow arrows in Fig. 7a). We chose λ to be approximately two times the standard deviation in such areas, i.e. λ = 0.008. We observed that in these areas, the standard deviation is relatively similar between the flows-and-limits and coordinate approaches. Note that areas in which only a single fiber population can be identified, have a standard deviation of zero since no Lie bracket calculation was possible.
Fig. 7.
Lie bracket and SPI computation on real in vivo HCP data: a comparison between the flows-and-limits and coordinate methods. (a) Standard deviation of the Lie bracket normal component estimates. Yellow arrows indicate areas where the mean is close to zero and the standard deviation is spatially uniform and low. The values in these areas were used to find an appropriate value for λ. (b) Sheet tensors on coronal, sagittal, and axial slices, for the flows-and-limits and coordinate implementations (λ = 0.008, sheet tensors with SPI < 0.2 are not shown for clarity). White arrow: crossing sheets found with the coordinate implementation, but not with the flows-and-limits method; blue arrow: crossing sheets found with the flows-and-limits method; red arrow: high SPI between the cingulum and the corpus callosum.
Fig. 7b shows sheet tensors on different coronal, sagittal, and axial slices. We compare the flows-and-limits method (two top rows) with the coordinate implementation (two bottom rows). In most cases, high SPI areas that could be found with the flows-and-limits method were also identified with the coordinate method. An example is the high SPI area highlighted with a green rectangle on a coronal slice and the enlarged image below. The green sheet tensors indicate a high SPI between pathways of the corpus callosum and the corticospinal tract. On a coarse scale these regions look similar, but the enlarged image shows some subtle differences. The white arrow indicates a location where all three crossing fiber populations have a high SPI with the coordinate method: they form crossing sheets. These regions did not have a high SPI for each pair of fiber populations when using the flows-and-limits implementation. In turn, the crossing sheets that were identified with the flows-and-limits method (more inferior, indicated with the blue arrow) were not identified with the coordinate method: the SPI was significantly lower or the Lie bracket normal component estimates for the corresponding fiber populations were not always normally distributed and therefore no SPI was calculated. Finally, the red arrow indicates a high SPI in a region where the cingulum and corpus callosum cross. This high SPI region is consistently found with both methods.
Several high SPI areas that are found with both methods are more ‘extensive’ when using the coordinate implementation. Examples are the areas indicated with the red and purple rectangles in the sagittal slices of Fig. 7b. The area highlighted in the red box shows a high SPI which likely occurs between pathways of the arcuate fasciculus and association pathways. The purple box in the coordinate case highlights a high SPI area in which the sheet tensors seem to be layered. While this layering appears fairly continuous for the coordinate implementation, it is not obviously present for the flows-and-limits implementation.
Some high SPI areas are exclusively found with the coordinate method. Examples are the region in the brainstem on the coronal slice and the area highlighted by the blue box in the axial slice (see Fig. 7b). A zoom of this area is also depicted below the axial slices, and shows a region where parts of the corpus callosum and the fornix pathways cross. The coordinate implementation finds a high SPI coherently over a number of voxels, whereas the flows-and-limits implementation hardly finds any high SPI voxels.
Fig. S3a shows results where we varied the angle threshold ([15° 35° 45°]) of the clustering algorithm, several major high-SPI areas can consistently be recognized for all angle thresholds. However, a too low ‘conservative’ angle threshold can cause an inability to detect very curved sheets, whereas a too high threshold can lead to wrong clustering results and a decrease of accuracy and precision of the algorithm. These findings are in agreement with results for the flows-and-limits implementation (Tax et al., 2016b). Fig. S4 displays the SPI estimation where we varied parameters of the coordinate implementation (β = {1,4}, N = {7,11}voxels). Even though there are subtle differences, only changing either β or N does not seem to affect the major high-SPI areas based on visual inspection. However, when both β is increased and decreased (thereby reducing the amount and weight of the neighborhood information), the accuracy and precision of the Lie bracket estimates decreases accordingly. This is in agreement with the simulation results in Fig. 3. As a result, the normality condition for SPI calculation is often not satisfied or the SPI decreases, hence the reduced amount of visible sheet tensors for β = 4, N = 7.
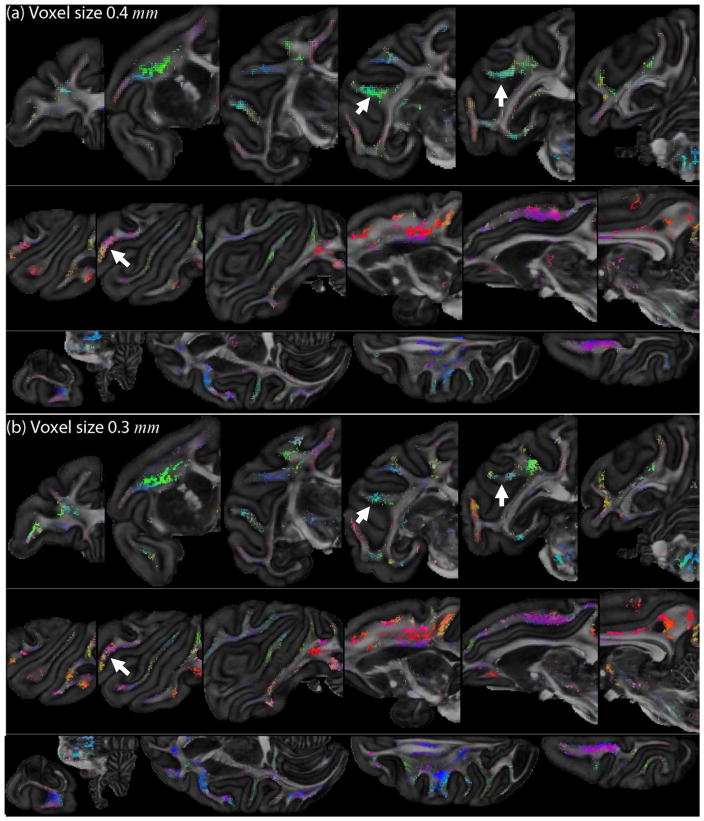
3.3.2 Ex vivo animal data
Fig. 8 shows SPI maps for the ex vivo monkey datasets: the 0.4 mm voxel size data in Fig. 8a and the 0.3 mm voxel size data in Fig. 8b. Here, we used the coordinate approach to estimate the Lie bracket. For each dataset, sheet tensors on coronal (top), sagittal (middle) and axial (bottom) slices are displayed. Here, we set rmax in mm the same for both datasets, i.e. rmax = 0.5 · 11 · 0.3 mm based on N = 11 for the 0.3 mm dataset. The standard deviation of the estimated Lie bracket normal components was generally larger for the 0.3 mm than for the 0.4 mm dataset (results not shown). An appropriate value for λ was obtained in a similar manner as described in Section 3.3.1 (λ = 0.015 for the 0.3 mm dataset and λ = 0.020 for the 0.4 mm dataset). Many high-SPI areas can consistently be recognized in both datasets. The 0.3 mm dataset shows more discontinuous high-SPI areas, likely because the normality condition is not fulfilled locally. Examples of such areas are highlighted with white arrows.
Fig. 8.
SPI maps for the ex vivo monkey brain. (a) Dataset with a voxel size of 0.4 mm isotropic and 120 directions (λ = 0.015). (b) Dataset with a voxel size of 0.3 mm isotropic and 60 directions (λ = 0.020). Sheet tensors with Pλ < 0.2 are not shown for clarity. White arrows highlight examples of high-SPI regions that are more discontinuous in the 0.3 mm dataset.
4. Discussion
The existence of sheet structure at multiple scales throughout the brain is an ongoing topic of debate (Catani et al., 2012; Galinsky and Frank, 2016; Tax et al., 2016b; Wedeen et al., 2012a; Wedeen et al., 2012b), mainly because obtaining proof with reliable quantification is challenging. Previous work has proposed the SPI as a novel quantitative measure to investigate the extent at which directional data support sheet structure (Tax et al., 2015; Tax et al., 2014a). The SPI is based on the calculation of the Lie bracket of two vector fields. In previous work, we have proposed a pipeline to compute the SPI with the Lie bracket estimated by the flows-and-limits method (Tax et al., 2016b). In addition, we have investigated several important statements in the sheet structure debate, i.e. the role of orthogonal angles and the influence of diffusion acquisition scheme and modeling (i.e. DSI vs spherical deconvolution). In this work, we proposed the coordinate method to calculate the Lie bracket, which can be applied to directional data such as peaks resulting from dMRI. We compared this method to the previously proposed flows-and-limits approach on the basis of vector field simulations, dMRI simulations, and real dMRI data. We have shown results of SPI calculations on various datasets of different species, scanners, spatial resolutions, and acquisition settings. In the following sections, we will discuss the different choices we made for the clustering of peaks and the calculation of derivatives with normalized convolution. We will also compare the flows-and-limits and coordinate approaches in terms of performance and implementation/computation considerations. Finally, we will discuss several remaining challenges and outline potential avenues for future work.
4.1 Clustering of vector fields
Calculation of the Lie bracket requires the frames in voxels to be clustered into distinct vector fields, which poses a challenging sorting problem in dMRI. The clustering of peaks is also an issue in most tractography algorithms: a tract is propagated along a direction that has the smallest angle with the incoming direction. However, tractography algorithms generally do not take into account the entire frame at the current and previous locations. In the flows-and-limits implementation this is taken into account, that is, the vectors of a frame are clustered into vector fields during the tractography process. The angle threshold on the peaks that are followed can be interpreted directly as a constraint on the curvature of the tract. Sorting peaks along a tract seems a more natural way of clustering than directly comparing peaks in nearby voxels, which mostly do not lie along the same pathway. This comparison of nearby voxels is done in the front-propagation approach for the coordinate implementation. We have observed that the approach of clustering peaks along tracts has fewer problems to recognize the edge (i.e., the domain of definition) of a vector field than the front-propagation approach. For example, at the white-gray matter boundary, we found that the flows-and-limits reconstruction of loops terminated more often naturally because, for instance, peaks were missing or the angle between the peaks was too large. The peaks in gray matter are less reliable because we used a single white matter response function for CSD throughout the brain. A solution to this would be the use of a tissue-specific response function (Jeurissen et al., 2014; Roine et al., 2015). Instead, we used a mask here to take into account only the peaks within the white matter. On the other hand, the front-propagation approach has the advantage that it suffers less from missing peaks resulting from modeling imperfections or noise. Where the loop reconstruction in the flows-and-limits approach terminates in this case, the front-propagation approach can use the information from more than one six-connected voxel to cluster the peaks in a given voxel.
We opted for a front-propagation clustering approach for the coordinate implementation because a direct comparison of all voxels in the N × N × N neighborhood with the center voxel could give errors in the case of strong curvature of the vector fields. An angle threshold of 35 degrees seemed to be a good trade-off between including incorrect peaks into a vector field and excluding correct peaks from the vector field in the configurations investigated (e.g. see Fig. S1 for excluding peaks). However, we still observed some discontinuities of clustered vectors towards the edges of the spatial neighborhood in real data (Fig. S2). In future work this angle threshold could be made dependent on the voxel size and the expected curvature of the vector fields, and it could be investigated in a wider range of configurations. The influence of incorrectly clustered peaks towards the edges is minimized by the decreasing applicability of the filter basis as the distance from the center voxel increases. Overall, the sorting of peaks is an interesting and challenging problem by itself. Future work could be directed to improve this process, for example by exploiting the use of tractography clustering in this context (e.g. (O’Donnell and Westin, 2007)), or by taking into account microstructural information for each population and assuming that this is continuous along trajectories (e.g. (Girard et al., 2015)).
4.2 Coordinate implementation: Parameter choices
The normalized convolution approach requires a choice of applicability function (including parameter settings for rmax or N and β), certainty function, and filter basis. For the applicability function we chose a power of the cosine function with a period of 4rmax. We chose the cosine function because it is zero rmax at and thus has no truncation jumps, but other choices could be explored in future work. Fig. 3 shows that a lower value for β decreases the mean absolute error and improves the precision of the estimates up to a certain point. We generally scaled according to the kernel size N and the voxel size δ(i.e. rmax = 0.5Nδ) to reduce the number of parameters, but the drawback is that rmax can only be tuned in ‘discrete steps’. rmax and N can also be set as two independent parameters to increase the flexibility at the cost of simplicity. Increasing N for a given voxel size leads to a higher precision (simulation experiments in Figs. 3 and 4), but comes at the cost of a lower accuracy beyond a given point (Fig. 3). A possible explanation for this is that computing the derivatives from the fitted first-order polynomials is not sufficient anymore and higher-order polynomials have to be taken into account to accurately describe the neighborhood further away from the center. Also, increasing beyond the domain of definition of one of the vector fields might increase the risk of clustering errors (see also Section 4.1). In the monkey brain datasets, we chose the same rmax in mm for the two spatial resolutions. This means that the effective kernel size N in voxels used for the 0.4 mm dataset is smaller, which is expected to come with a decrease in precision (Fig. 3) of the estimates for a given SNR. However, the SNR of the 0.4 mm dataset is larger than that of the 0.3 mm dataset (131 vs 96 on the b = 0 images), and the number of acquired directions was higher (120 vs 60), which in fact increased the precision of the estimates for the 0.4 mm dataset (see Section 3.3.2). This motivates the data-driven way to defining the λ parameter for SPI calculation.
We currently set the certainty of a vector either to zero or to one depending on whether it is absent or present. However, theoretically it can take any value between zero and one, and could, for example, be based on the angle with its six-connected neighbors. So instead of setting a hard threshold on the angle that two vectors in neighboring voxels are allowed to make in order to belong to the same vector field, the certainty could be defined as a function of this angle. An example result is shown in Fig. S3b: the SPI is calculated with the certainty of a vector linearly increasing with the inner product between two vectors during clustering. Other factors such as peak magnitude and SNR could also be used to tune the certainty of vectors.
In practice, the filter basis in Eq. [9] is sufficient to calculate the first order derivatives of the vector fields and can be extended to calculate higher-order derivatives. Future work could explore the effect of fitting higher-order polynomials on the accuracy and precision of the estimated Jacobians and vectors at the center of the neighborhood.
4.3 Flows-and-limits vs. coordinate implementation: Performance
We have investigated the effect of different factors on the performance of the flows-and-limits and coordinate methods, viz. spatial neighborhood, spatial resolution, missing peaks, SNR, curvature, and commutativity.
Our results show that the precision of the Lie bracket normal component estimates (Figs. 3 to 7) is consistently higher for the coordinate implementation than for the flows-and-limits implementation, which can be attributed mainly to the higher degree of neighborhood information used in the former. In our experiments we aim to allow both methods to probe neighborhood information at a similar distance from the center voxel: an hmax of 5 voxels would result in a total walking distance of 11 voxels along one vector field if it was perfectly parallel to the discretization grid (hence, we compare to a kernel size of N = 11 voxels). However, the vector fields are generally curved and the flows-and-limits approach only probes vectors that are on the same pathway, whereas the coordinate approach can utilize information of the whole N × N × N neighborhood. The results with a given hmax and N = 2hmax + 1 for the respective methods can thus not strictly be compared one-to-one. Further increasing hmax might lead to a higher precision, but it comes at the cost of increased computational demands (since more pathways have to be stored), a lower accuracy beyond a given point (similar to e.g. Fig. 3 for the coordinate implementation), and the increased risk of clustering errors when hmax extends beyond the domain of definition of one of the vector fields (see Section 4.1). Another explanation for the better performance of the coordinate implementation is that it gives regularized versions of the vectors at location p where the Lie bracket is to be computed. This is expected to reduce the influence of noise on the computation of the Lie bracket normal component, as seen e.g. in Fig. 4. In contrast, the flows-and-limits implementation uses the original (noisy) vectors at point p to compute the Lie bracket normal component. We note that for the real data in Fig. 7 the estimated standard deviation was approximately the same between the two methods in the spatially continuous region indicated with yellow arrows. Hence, we used the same λ for the SPI computation.
Figs. 3 and 4 indicate that the precision of the Lie bracket normal component estimates decreases for smaller voxel size while keeping SNR and spatial neighborhood in voxels constant. Because the extent of the spatial neighborhood in millimeters then decreases, the perturbation of the vectors becomes more significant relative to the quantity that we aim to measure, the rate of change of one vector field along the other vector field. This perturbation is more or less independent of the voxel size. This effect is more prominent for the flows-and-limits approach than for the coordinate implementation.
Curvature and commutativity did not affect the precision of the estimates (Fig. 6). A higher curvature, however, did influence the accuracy of the flows-and-limits non-sheet estimates. We observed that this was a combined effect of 1) the design of the vector field, 2) the ability of the used dMRI technique (CSD in this case) to resolve crossing fibers at small angles, and 3) the sensitivity of the flows-and-limits implementation to what we call edge effects. At a radius as small as 8 mm, the edge of the spatial neighborhood for the Lie bracket estimation starts to come in the vicinity of the edge of the simulated vector fields (see Appendix B). At this edge, the vectors of the non-sheet pair have a crossing angle beyond the angular resolution of CSD. As such, only one peak can be found and many paths are terminated. This effect is larger in one side of the neighborhood, to wit the side near the edge of the vector field, where becomes larger. As each path is weighted equally in the LLS fit in Eq. [10], the result is more determined by the paths in the direction away from the edge (where becomes smaller). This effect does not occur in the same simulations with analytical vector fields (results not shown), and is thus not caused by the flows-and-limits method alone: the method is just more sensitive to these missing peaks at the edge. While it remains the question whether the edges of our simulated vector fields are representative of a scenario that truly occurs in the brain, it shows that the coordinate implementation is more robust to these effects. Missing peaks also affect the accuracy and precision of the flows-and-limits estimates significantly. We note that missing peaks do not only have an effect on the quantification of sheet structure with the flows-and-limits method, but they also make visual examination challenging because pathways will terminate prematurely.
4.4 Flows-and-limits vs. coordinate implementation: Computational issues
The flows-and-limits and coordinate methods are two conceptually different but equivalent approaches to defining the Lie bracket. They do differ greatly in implementation: whereas the flows-and-limits approach is based on tractography, the coordinate implementation works directly on the vector fields. The flows-and-limits approach requires the reconstruction and storage of points and clustered directions of many loops, and it is therefore demanding in terms of memory if many voxels are processed simultaneously. The coordinate approach based on normalized convolution is easier to implement, but has to be performed voxel-by-voxel because the vector fields have to be clustered in each neighborhood. In this work, the computation speed of the coordinate approach was increased tremendously by making use of multi-core processing capabilities. On a parallel system with 72 Intel(R) Xeon(R) E7-8870 v3 @2.10Ghz dual cores with equal access to 1TB of RAM, the computation time of the Lie bracket of the two largest peaks of a HCP dataset (344371 white matter voxels) was approximately 25 minutes for the flows-and-limits method and 6 minutes for the normalized convolution method. Further optimization of the code is possible to decrease the computation time.
4.5 Further improvements and future work
The computation and visualization of the SPI involves multiple steps, and this manuscript specifically focused on the estimation of the Lie bracket. We already discussed potential improvements for the clustering of vector fields, but other steps in the pipeline could also be improved. Future work could focus on finding alternatives for the normality condition, which might be relaxed, and on automatic tuning of the value of λ. In addition, within a voxel, all peaks from the different bootstraps are currently clustered towards the peaks of the original (non-bootstrapped) data. This clustering procedure could be potentially improved by an iterative scheme that tries to update the mean of the clusters, such as with a k-means clustering principle with k the number of peaks within a voxel. Furthermore, visualization of the sheet tensors is currently based on the original (noisy) vectors, whereas instead the regularized vectors obtained with the coordinate implementation could be used. This could potentially circumvent the presence of unexpected shapes of sheet tensors with high SPI such as those originating from the crossing between the fornix and corpus callosum pathways (see Fig. 7). Whereas nearly orthogonal crossings in this region were expected to result in circular flat sheet tensors, some sheet tensors had a more ellipsoidal profile. This was likely caused by spurious peaks resulting from partial volume effects with CSF. Furthermore, future work could be directed towards trying to avoid the peak extraction altogether, and calculate a sheetness indicator more directly from the ODFs. Finally, whereas reproducibility of high SPI areas can already be qualitatively appreciated from Fig. 8, a future study could quantify the consistency of sheet structures in a larger cohort.
4.6 Sheet or no sheet?
The quantitative detection of sheet structures relies on the accurate and precise estimation of the Lie bracket. Optimizing this step in the pipeline is therefore important to obtain a reliable SPI. Both analytical vector field simulations and dMRI simulations show that the coordinate approach (combining the front-propagation clustering with normalized convolution) can achieve a higher accuracy and precision at the scale investigated than the flows-and-limits approach (combining the frame clustering during tractography with estimation of the closures).
To be able to interpret our findings in the brain, however, several strong assumptions have to be made. First, in dMRI it is generally assumed that the peak directions directly represent the directions of underlying fiber pathways. Although this assumption is often considered to be valid (e.g. in connectivity studies), it is well-known that various limitations of dMRI (e.g. imperfect modeling and noise) challenge its validity. Second, the clustering approaches in both the coordinate and flows-and-limits approaches assume some kind of smoothness of the vector fields and the underlying tracts by means of the angle thresholds. Even though this is likely a valid assumption at a sufficiently fine scale in the brain (i.e. when you zoom in far enough tracts likely exhibit a continuity to transport information), it remains to be investigated whether this is valid throughout the whole brain at the scale of the voxel. Third, when we resolve dMRI crossings we assume that the underlying fibers indeed cross each other, or at least run in a sufficiently-near vicinity of each other. The finite voxel size of dMRI might give rise to ‘partial volume sheets’ where, given the scale of the voxel, two tracts seem to locally form a sheet according to the definition (e.g. the fornix and the corpus callosum, which ‘touch’ rather than cross each other at the scale of the voxel). We note, however, that these challenges in detecting the brain’s sheet structures are mostly related to the ability of dMRI to reflect the true underlying fiber architecture (i.e. modeling and resolution), rather than to the method proposed here to compute the Lie bracket. We therefore expect that future advances in dMRI and other techniques that give directional information combined with quantitative approaches to estimate the Lie bracket will provide a deeper insight in the extensiveness of these structures in the brain. At this stage, we merely state that the data supports the existence of sheet structures at several locations in the brain at the investigated scales, and that the coordinate approach can detect these structures more reliably than the flows-and-limits approach given that the assumptions are valid.
Even though some structures like ‘partial volume sheets’ might seem questionable in that they only resemble sheet structures ‘through the glasses of dMRI’ at the given scale, such sheets are still a “mathematically specific and highly atypical” feature of the data (Wedeen et al., 2012a). One configuration in which two bundles trivially form sheets is when they both have a curvature of zero. To see if this structure is truly ‘special’ or only occurs at regions where the tracts exhibit no curvature, future work will quantitatively relate the SPI to the curvature of tracts. However, visual inspection already reveals that tracts also form sheets while being significantly curved at this scale (e.g. CST, corpus callosum). If these sheet structures indeed represent a real feature of brain organization, they could be a ‘fingerprint’ left behind by the chemotactic gradients during embryogenesis (Wedeen et al., 2012b). The idea here is that the sheet structures naturally arise from the interaction of equipotential surfaces of these gradients in an early stage of development. Future work is needed to further validate this interesting hypothesis.
5. Conclusion
Reliable quantification of the brain’s sheet structure is needed to assess its presence and configurational properties such as extent and location across individuals (Catani et al., 2012). In this work, we have proposed the coordinate implementation to estimate the normal component of the Lie bracket, which is an indicator of sheet structure between two vector fields. We have compared this method to the previously proposed flows-and-limits approach by performing simulations and experiments with real data. We show that the coordinate approach can achieve a higher precision of the Lie bracket normal component estimates. It is more robust against missing peaks resulting from noise or modeling imperfections, increasing the accuracy. Our results demonstrate that the SPI can be quantified with the proposed approach for datasets from different species, scanners, voxel sizes, and diffusion gradient sampling schemes, and in both in vivo and ex vivo datasets.
Highlights.
A new method is proposed to quantify the extent of sheet structure in the brain
Clustering and computing derivatives of diffusion MRI fiber directions is required
Normalized convolution is adopted to calculate these derivatives
The reliability of the method is demonstrated with simulations and experimental data
The method is more robust than a recent method that is based on tractography
Acknowledgments
The authors thank many colleagues in the field for useful discussions. C.T. is supported by a grant (No. 612.001.104) from the Physical Sciences division of the Netherlands Organization for Scientific Research (NWO), and is grateful to dr. ir. Marina van Damme and University Fund Eindhoven for financial support. The research of A.L. is supported by VIDI Grant 639.072.411 from NWO. T.D. gratefully acknowledges NWO (No 617.001.202) for financial support. The authors acknowledge the NIH grants R01MH074794, P41EB015902, P41EB015898. The work of A.F. is part of the research programme of the Foundation for Fundamental Research on Matter (FOM), which is financially supported by the Netherlands Organisation for Scientific Research (NWO). Data were provided by the Duke Center of In Vivo Microscopy, and NIH/NIBIB national Biomedical Technology Resource Center (P41 EB015897) with additional funding from NIH/1S10 ODOD010683-01. Data were provided in part by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. Data collection and sharing for this project was provided in part by the MGH-USC Human Connectome Project (HCP; Principal Investigators: Bruce Rosen, M.D., Ph.D., Arthur W. Toga, Ph.D., Van J. Wedeen, MD). HCP funding was provided by the National Institute of Dental and Craniofacial Research (NIDCR), the National Institute of Mental Health (NIMH), and the National Institute of Neurological Disorders and Stroke (NINDS). HCP data are disseminated by the Laboratory of Neuro Imaging at the University of California, Los Angeles.
Appendices
Appendix A: Clustering of frames in an N × N × N spatial neighborhood
We will first describe the algorithm to cluster two frames based on their total cosine similarity, and subsequently the front-propagation approach to cluster frames in a spatial neighborhood. We consider an ordered set of n vectors [Y1, …,Yn] at a position q, and m vectors1 in {Z1, …,Zm} some point r close to q. The ordered set [Y1, …,Yn] defines the reference frame, i.e., it is assumed that n vector U,V, … fields are present in the spatial neighborhood of q satisfying U(q) = Y1,V(q) = Y2, …. The clustering algorithm aims to find a permutation of the frame (an ordered set [ZP1, …,ZPn]) that corresponds to the reference frame, so that we can set U(r) = ZP1, V(r) = ZP2, … for some permutation P of [1, …,n]. Here, Pi denotes the index given by the ith element of P, and ZPi = 0 implies that no matching vector was found.
Algorithm for the clustering of frames {Z1, …,Zm} given an ordered frame [Y1, …,Yn]
- Compute the cosine similarity Sij between Yi and Zj for all i ∈ {1, …,n}, j ∈ {1, …,m} (recall that Yi and Zj are unit or zero vectors):
[19] - For every n-permutation P of [1, …,m], compute the similarity energy of the permutation by:
[20] Determine the permutation for which is maximum, and define the reordered set of vectors [ZP1, …,ZPn].
If Yi · ZPi has a negative sign, set ZPi to −ZPi.
Apply an angle threshold on ZPi. If |Yi · ZPi| < t for some threshold t ∈ ℝ, set ZPi to 0.
Return [ZP1, …,ZPn].
Algorithm for the clustering of frames in an N × N × N spatial neighborhood of point p
Start from point with ordered frame [Y1, …,Yn] satisfying U(p) = Y1,V(p) = Y2, ….
-
While there are still non-clustered frames in the neighborhood, do the following for each of the K voxels clustered in the previous iteration (denoted by its location qk, k ∈ {1, …,K}, for the first iteration q1 = p):
Identify the 6-connected voxels denoted by their locations {r1, …,r6}.
Keep the L voxels that have not been visited before and that fall within the N × N × N spatial neighborhood of point p, i.e. voxels {r1, …,rL}.
For every voxel rl, l ∈ {1, …,L},, calculate the cosine similarities for each pair of vectors of the frames [U(qk),V(qk), …] and {Z1(rl), … Zm(rl)} with Eq. [20].
If voxel rl is a 6-connected neighbor of more than one previously clustered voxel (we take as an example here two voxels qk1 and qk2 with k1 ≠ k2), take the mean of the cosine similarities with the frames [U(qk1),V(qk1), …] and [U(qk2),V(qk2), …]. This corresponds to taking the cosine similarity with the ‘mean frame’ ([U(qk1),V(qk1), …] + [U(qk2),V(qk2), …])/2.
Cluster the frame {Z1(rl), …, Zm(rl)} to this ‘mean frame’ using the algorithm for clustering of two frames described previously.
Return U,V, …
Appendix B: Analytical vector field simulations
We define three vector fields U,V, and W, where U and V are tangent to the upper hemisphere with radius ρ and W is tangent to the lower hemisphere with radius ρ (see Fig. A1 (Tax et al., 2016a; Tax et al., 2016c)):
| [21] |
Here and (with i = 1,2). The integral curves of these vector fields have constant curvature κ = 1/ρ.
Vector fields U and V form a sheet, so that . U and W generally do not form a sheet, and the normal component of the Lie bracket [U,W]p at p ∈ {x ∈ ℝ3(x1)2 + (x2)2 < ρ2,x1 ≠ 0, x2 ≠ 0} is given by
| [22] |
Fig. A1.
Integral curves and sampled vectors of pair U and V that form a sheet (a), and pair U and W and that do not form a sheet (b).
Footnotes
If m < n, we append n − m zero-vectors to the list {Z1, …,Zm}, so in the following we can take m ≥ n.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Reference List
- Calabrese E, Badea A, Cofer G, Qi Y, Johnson GA. A Diffusion MRI Tractography Connectome of the Mouse Brain and Comparison with Neuronal Tracer Data. Cereb Cortex. 2015;25:4628–4637. doi: 10.1093/cercor/bhv121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catani M, Bodi I, Dell’acqua F. Comment on “The geometric structure of the brain fiber pathways”. Science. 2012;337:1605. doi: 10.1126/science.1223425. [DOI] [PubMed] [Google Scholar]
- Chen YH, Wei D, Newstadt G, DeGraef M, Simmons J, Hero A. Parameter estimation in spherical symmetry groups. Signal Processing Letters, IEEE. 2015;22:1152–1155. [Google Scholar]
- Ferizi U, Schneider T, Panagiotaki E, Nedjati-Gilani G, Zhang H, Wheeler-Kingshott CA, Alexander DC. A ranking of diffusion MRI compartment models with in vivo human brain data. Magn Reson Med. 2014;72:1785–1792. doi: 10.1002/mrm.25080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Florack L. Image structure. 10. Springer Science & Business Media; 2013. [Google Scholar]
- Galinsky VL, Frank LR. The Lamellar Structure of the Brain Fiber Pathways. Neural Comput. 2016:1–24. doi: 10.1162/NECO_a_00896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard G, Rutger F, Descoteaux M, Deriche R, Wassermann D. AxTract: Microstructure-Driven Tractography Based on the Ensemble Average Propagator. Inf Process Med Imaging. 2015;24:675–686. doi: 10.1007/978-3-319-19992-4_53. [DOI] [PubMed] [Google Scholar]
- Jbabdi S, Behrens TE, Smith SM. Crossing fibres in tract-based spatial statistics. Neuroimage. 2010;49:249–256. doi: 10.1016/j.neuroimage.2009.08.039. [DOI] [PubMed] [Google Scholar]
- Jeurissen B, Leemans A, Jones DK, Tournier JD, Sijbers J. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution. Hum Brain Mapp. 2011;32:461–479. doi: 10.1002/hbm.21032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeurissen B, Leemans A, Tournier JD, Jones DK, Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp. 2013;34:2747–2766. doi: 10.1002/hbm.22099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeurissen B, Tournier JD, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. Neuroimage. 2014;103:411–426. doi: 10.1016/j.neuroimage.2014.07.061. [DOI] [PubMed] [Google Scholar]
- Kindlmann G, Tricoche X, Westin CF. Delineating white matter structure in diffusion tensor MRI with anisotropy creases. Medical Image Analysis. 2007;11:492–502. doi: 10.1016/j.media.2007.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutsson H, Westin CF. Normalized and differential convolution. IEEE CVPR. 1993:515–523. [Google Scholar]
- Koenderink JJ, Van Doorn AJ. Receptive field families. Biological cybernetics. 1990;63:291–297. [Google Scholar]
- Lang S. Differential and Riemannian Manifolds, Graduate Texts in Mathematics ed. Springer-Verlag; New York: 1995. [Google Scholar]
- Leemans A, Jeurissen B, Sijbers J, Jones DK. ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data. In Proceedings of the 17nd Annual Meeting of the ISMRM; 2009. p. 3537. [Google Scholar]
- Leemans A, Jones DK. The B-matrix must be rotated when correcting for subject motion in DTI data. Magn Reson Med. 2009;61:1336–1349. doi: 10.1002/mrm.21890. [DOI] [PubMed] [Google Scholar]
- Mardia KV, Jupp PE. Directional statistics. 494. Wiley. com; 2009. [Google Scholar]
- O’Donnell LJ, Westin CF. Automatic tractography segmentation using a high-dimensional white matter atlas. IEEE Trans Med Imaging. 2007;26:1562–1575. doi: 10.1109/TMI.2007.906785. [DOI] [PubMed] [Google Scholar]
- Polders DL, Leemans A, Hendrikse J, Donahue MJ, Luijten PR, Hoogduin JM. Signal to noise ratio and uncertainty in diffusion tensor imaging at 1.5, 3.0, and 7.0 Tesla. J Magn Reson Imaging. 2011;33:1456–1463. doi: 10.1002/jmri.22554. [DOI] [PubMed] [Google Scholar]
- Roine T, Jeurissen B, Perrone D, Aelterman J, Philips W, Leemans A, Sijbers J. Informed constrained spherical deconvolution (iCSD) Med Image Anal. 2015;24:269–281. doi: 10.1016/j.media.2015.01.001. [DOI] [PubMed] [Google Scholar]
- Savitzky A, Golay MJE. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Analytical Chemistry. 1964;36:1627–1639. [Google Scholar]
- Schultz T, Theisel H, Seidel HP. Crease surfaces: from theory to extraction and application to diffusion tensor MRI. IEEE Trans Vis Comput Graph. 2010;16:109–119. doi: 10.1109/TVCG.2009.44. [DOI] [PubMed] [Google Scholar]
- Sherbondy AJ, Dougherty RF, Ben-Shachar M, Napel S, Wandell BA. ConTrack: finding the most likely pathways between brain regions using diffusion tractography. J Vis. 2008;8:15–16. doi: 10.1167/8.9.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, Behrens TE. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31:1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, Feinberg DA, Yacoub E, Lenglet C, Van Essen DC, Ugurbil K, Behrens TE. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage. 2013;80:125–143. doi: 10.1016/j.neuroimage.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spivak M. A comprehensive introduction to differential geometry. Publish or Perish, inc; 1979. [Google Scholar]
- Sporns O. Chapter 14 - The Human Connectome: Linking Structure and Function in the Human Brain. In: Behrens HJ-B, editor. Diffusion MRI. Academic Press; San Diego: 2009. pp. 309–332. [Google Scholar]
- Tax CMW, Dela Haije T, Fuster A, Duits R, Viergever MA, Calabrese E, Johnson GA, Florack LMJ, Leemans A. Towards quantification of the brain’s sheet structure in diffusion MRI data. International BASP Frontiers Workshop; 2015. p. 74. [Google Scholar]
- Tax CMW, Dela Haije T, Fuster A, Duits R, Viergever MA, Florack LMJ, Leemans A. Towards quantification of the brain’s sheet structure: Evaluation of the discrete Lie bracket. Proceedings of the 22nd Annual Meeting of the ISMRM; 2014a. p. 0975. [Google Scholar]
- Tax CMW, Dela Haije T, Fuster A, Westin CF, Viergever MA, Florack LMJ, Leemans A. Mapping the brain’s “Sheet Probability Index” (SPI) with diffusion MRI: Sheet happens?!. Proceedings of the 24th Annual Meeting of the ISMRM; 2016a. p. 0791. [Google Scholar]
- Tax CMW, Dela HT, Fuster A, Westin CF, Viergever MA, Florack L, Leemans A. Sheet Probability Index (SPI): Characterizing the geometrical organization of the white matter with diffusion MRI. Neuroimage. 2016b;142:260–279. doi: 10.1016/j.neuroimage.2016.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tax CMW, Jeurissen B, Vos SB, Viergever MA, Leemans A. Recursive calibration of the fiber response function for spherical deconvolution of diffusion MRI data. NeuroImage. 2014b;86:67–80. doi: 10.1016/j.neuroimage.2013.07.067. [DOI] [PubMed] [Google Scholar]
- Tax CMW, Westin CF, Dela Haije T, Fuster A, Viergever MA, Florack LMJ, Leemans A. Robust assessment of the brain’s sheet structure using normalized convolution. Proceedings of the 24th Annual Meeting of the ISMRM; 2016c. p. 2073. [Google Scholar]
- Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage. 2007;35:1459–1472. doi: 10.1016/j.neuroimage.2007.02.016. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K. The WU-Minn Human Connectome Project: an overview. NeuroImage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilanova A, Berenschot G, Van Pul C. DTI visualization with streamsurfaces and evenly-spaced volume seeding. Eurographics Association; 2004. pp. 173–182. [Google Scholar]
- Wedeen VJ, Mortazavi F, Wang R, Isaac Tseng W, Witzel T, Nummenmaa A, orrison W, tanley HE, ald L, osene D. Grid structure of brain pathways - Validation and the character of turns. Proceedings of the 22nd Annual Meeting of the ISMRM; 2014. p. 0803. [Google Scholar]
- Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng WY. Response to comment on “the geometric structure of the brain fiber pathways”. Science. 2012a;337:1605. doi: 10.1126/science.1223493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng WY. The geometric structure of the brain fiber pathways. Science. 2012b;335:1628–1634. doi: 10.1126/science.1215280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich PA, Zhang H, Simon TJ, Gee JC. Structure-specific statistical mapping of white matter tracts. Neuroimage. 2008;41:448–461. doi: 10.1016/j.neuroimage.2008.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, van Zijl PC, Mori S. Image contrast using the secondary and tertiary eigenvectors in diffusion tensor imaging. Magn Reson Med. 2006;55:439–449. doi: 10.1002/mrm.20767. [DOI] [PubMed] [Google Scholar]
- Zhang S, Demiralp C, Laidlaw DH. Visualizing diffusion tensor MR images using streamtubes and streamsurfaces. Visualization and Computer Graphics, IEEE Transactions on. 2003;9:454–462. [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]