Cohort- and age-related decline in elder’s life satisfaction: is there really a paradox?

Abstract

Absence of age-related decline in elder’s life satisfaction (LS), found in several studies from the last quarter of the twentieth century, has been labelled a “paradox”, as it contrasts with increasing psycho-social and health risks in old age. To explain these findings, the present study was based on the hypothesis of a cohort effect on the LS of those born in the first half of the twentieth century, which might have overlayed and thus obscured the age-related decline in cross-sectional studies. In addition, it was hypothesized that the age-related decline in LS accelerates over the old age period such that the “paradox” would not hold for old–old subjects. Longitudinal analysis was conducted by means of multilevel mixed models, using data from the German Socio-Economic Panel. Analyzing single-item measures of LS from 16 panel waves (1984–1999), the findings confirm both hypotheses. For the young–old, cohort- and age-related decline was found with about equal decrements in LS per year of birth or age, neutralizing age-group differences in cross-sectional comparisons. For the old–old, the age-related decline appeared accelerated, outnumbering the cohort effect.

Introduction

Throughout the past decade of gerontological research, reasoning about subjective well-being (SWB) in old age has dealt with what has been labelled a “stability despite loss paradox” (Kunzmann et al. 2000). Several empirical studies reported absence of age-related decline in SWB (e.g. Smith et al. 1999; Diener and Suh 1997; Horley and Lavery 1995; Herzog and Rodgers 1981; Larson 1978), which contrasts with multiple psycho-social losses (e.g. Baltes and Mayer 1999) and increased health risks (e.g. Kolberg 1999; Coni et al. 1992), qualifying late adulthood as a period of decline with respect to objective quality of life. To explain the paradox, theoretical discussion has focussed on older people’s ability to adapt to worsening conditions and maintain stable SWB under severe losses (Staudinger 2000; Baltes and Carstensen 1996; Brandtstädter and Greve 1994). However, apart from this highly important topic of gerontological reasoning, the present study aims at an alternative explanation of the findings mentioned previously, which does not at all regard these as paradoxical: age-related decline may exist, but might have been overlaid and covered by a cohort effect in the samples of elders surveyed in these studies.

To explicate this assumption, first some differentiations have to be made regarding the published empirical evidence for the paradox: (1) non-existence of a negative age effect has been consistently found for measures of life satisfaction (LS), the so-called cognitive component of SWB (Diener et al. 1999; Veenhoven 1996), whereas findings concerning affective well-being are less clear (Kunzmann et al. 2000). Thus, the paradox should be considered more as a paradox of LS in particular, than as of SWB in total. (2) Evidence presented so far has been largely derived from cross-sectional studies (Diener and Suh 1997), which cannot clearly indicate the absence of age-related decline. In particular, examination of age-related change in cross-sectional designs is hampered by the possibility of cohort effects overlaying the effects of chronological age. However, few longitudinal studies concerning age-related change in LS have been published (for an overview see Schilling 2003, 2005). In sum, these studies evidence high “monotonic” stability of LS judgements in general (i.e. high autocorrelation across repeated measures of LS), which should not be mistaken as stability in a strict sense, meaning there is an absence of any intraindividual changes. Concerning mean level changes of LS over old age, evidence based on longitudinal data seems rare and inexplicit. Most recently, Mroczek and Spiro (2005) evidenced a curvilinear pattern of change in LS over the 40–85 age range, with LS declining beyond age 65. (3) Absence of cross-sectional age-related decline has been found repeatedly in samples surveyed in the past quarter of the twentieth century, whereas studies based on data from the 1960s or early 1970s do report age-related decline (Wilson 1967; Doyle and Forehand 1984). Thus, it seems that age-related decline in LS vanished towards the end of the century.

Considerations on cohort-related decline in LS

Regarding the older adults surveyed in the studies cited earlier, consideration of a cohort effect may make sense: the subjects mostly have been persons living in western industrialized countries, born in the early decades of the twentieth century. Compared with the situation when these individuals were young, their old age circumstances could be characterized in terms of increased prosperity and political stability, technical innovation and improvement of medical treatments, which took part mainly in the decades after the Second World War. Disastrous historical events shocked western societies in the first half of the twentieth century, compromising the young lives of most of the people, who have experienced old age in the past decades under relatively peaceful and stable historical circumstances. Apart from thinking about the impacts of the World Wars and the economic depression in between, the more ordinary benefits which came as a result of economic and scientific progress deserve attention in this regard as well. For example, consider the time-consuming and laborious handling of such an everyday task as washing clothes, before washing machines and tumble-dryers became common household equipment. Moreover, people born in the early twentieth century saw the rapid development of medical treatment options for diseases which were major health threats during their youth, but now are nearly eliminated as causes of death (Fries 1980). Altogether, for the developed western countries it seems reasonable to assume that living conditions in the 1980s or 1990s appeared desirable to most of the older people compared with the living conditions they experienced in younger age. If so, it could also be assumed that these perceptions establish a positive effect on the elders’ subjective evaluations of current life, as provided in satisfaction judgements.

This assumption is in line with theoretical reasoning about satisfaction, which has been vitally nurtured by the idea that these judgements imply some kind of comparison of actual with target states of living conditions (Veenhoven 1996). According to this idea, people build up subjective standards defining how life should be, and the closer their reality comes to this ideal, the more satisfied they are. Probably the most prominent theoretical implementation of this approach is Michalos’ (1985) multiple discrepancies theory, which proposes several standards for comparison in generating satisfaction judgements, including conditions experienced in the past. With respect to this theoretical framework, having spent some substantial part of the early life under more adverse societal circumstances may reduce subjective standards, producing some kind of “frugality” in LS.

Thus, a cohort effect on LS such that early years spent under adverse conditions promote lower standards and therefore less discrepancy and higher satisfaction, could be hypothesized to exist. The present work was based on the assumption of such a cohort effect in terms of a quantitative relation, expecting the multitude of adverse historical experience to impact on LS. That is, this impact may increase with the portion of lifetime spent in this epoch, and the bigger the share of years of life in the war and pre-war era, the better the evaluation of current life under welfare conditions.

Considerations on simultaneous age- and cohort-related decline in LS

Overlay of age and cohort effects

If some decline in LS comes along with old age, and if a cohort effect works as explained previously, these effects would be at work in between-group differences in cross-sectional age group comparisons carried out for samples of older adults in the last quarter of the twentieth century. However, they would work in opposite directions, to some extent neutralizing each other: the older the subjects are, the bigger the losses in objective quality of life reducing LS, and the longer the life period spent under adverse societal conditions, increasing LS under end-of-century conditions. A schematic illustration of the resulting pattern is sketched in Fig. 1: bold printed arrows symbolize the mean-level trajectories of elder cohorts, with the starting point at some age marking the beginning of the old age phase. Scheme a figures age-related decline in all three cohorts without any cohort effect. A cross-sectional comparison at time t would reveal mean-level differences which might be interpreted correctly as age-related, or incorrectly as cohort-related. In scheme b, there is no decline within each cohort, but the older the cohort, the higher its average satisfaction. Cross-sectional comparison at t would reveal differences which might be interpreted correctly as cohort-related, or incorrectly as age-related. Scheme c depicts the overlay of age- and cohort-related decline: with older cohorts starting from a higher level (cohort effect), declining with the same rate of change across time (age effect), the lines overlap and cross-sectional comparison at time t would reveal no between-group differences.

Fig. 1.

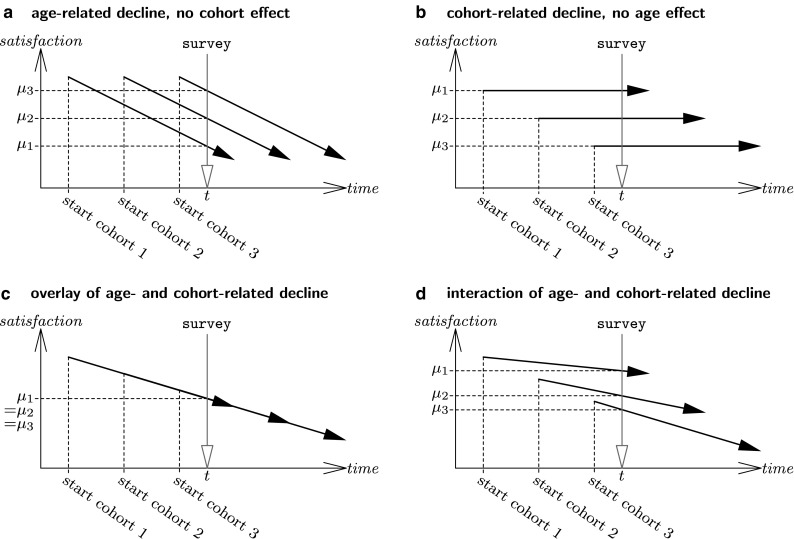
Schematic illustrations of age- and cohort-related decline

It should also be understood from the schematic illustration, that the assumption of an overlay of age-related with cohort-related decline, capable of producing cross-sectional stability of mean levels of LS, needs the specification that cohort and age effects must be of similar size regarding rates of change per time unit. If the time unit would be years, the decline per year of age (i.e. the slopes of the trajectories) should be the same as the average decrease per year of birth across cohorts.

Interaction of age and cohort effects

In Fig. 1, a fourth pattern has been depicted, figuring interaction of age-related with cohort-related decline (scheme d). Such interaction could be considered if the argument about the cohort effect as explicated earlier is driven one step further: perhaps past experience of adverse societal conditions impacts on age-related decline in LS. From the viewpoint of discrepancies theory, having had lower subjective standards in the past may facilitate discrepancy reduction by downward readjustment of the standards if losses in objective living conditions happen. Thus, having spent early years in the first half of the century may promote adaptation to worsening conditions in old age, weakening age-related decline in LS, as sketched in scheme d.

However, it should be understood that in the presence of an interaction, cross-sectional mean-level stability would be a rare and specific event (e.g. constructing scheme d such that all trajectories meet at some point would imply inequality of means at all other points in time). Therefore, the finding of mean-level stability in a great many of studies could be understood as at least tentative evidence against such interaction.

Non-linearities of age or cohort effects

With respect to age-related decline, linearity of the trajectories depicted in Fig. 1 could be called into question. As age-related decline should come along with societal and health risks accelerating across the old age period (Baltes and Smith 1999; Coni et al. 1992), age-related decline in LS might also accelerate, that is, only slight age-related decline in mean-level LS may be observed across a period of transition into old age, speeding up through the “young–old” period (e.g. from age 60 to 75, see Neugarten 1974), toward steeper declines in the “old–old” ages (e.g. 75+). However, with rapid increases of risks towards the end of the age range, presumably boosting the age effect on LS over the old–old period, acceleration of age-related decline over the young–old period might be minor, and hence a linear age effect model may still hold as acceptable approximation across this period.

Furthermore, the cohort-related decline cannot be assumed to work linearly across the whole range of birth dates observed in large population-based samples at the end of the twentieth century. For younger cohorts born after the Second World War, there should be no more effects of past experience of adverse societal conditions. For those born in the first half of the twentieth century, cohort-related decline in LS may be sufficiently approximated by a linear model. This corresponds to the cohort hypothesis as explained previously, which comprehends a quantitative relation of time spent under adverse historical conditions with LS, and no further differentiation regarding the LS of specific cohorts born in this historical period.

Aims of the study and hypotheses

The present work aimed to examine the effects of age and cohort in a longitudinal sample of elders surveyed within the past two decades of the twentieth century in Germany. In particular, analysis was based on two hypotheses:

• First, for those in transition into and in the young–old age, an overlay of cohort-related and age-related decline as explained previously and depicted schematically in Fig. 1, scheme c, is at work.

• Second, for subjects in the old–old age range, age-related decline is accelerated and outnumbers cohort-related decline.

Methods

Sample

Statistical analyses have been conducted on data from the West German subsample of the German Socio-Economic Panel (SOEP). Designed as a representative sample of private households in former West Germany, this longitudinal database started in 1984 with 4,528 households, including 9,076 respondents (for close database description see SOEP Group 2001, or SOEP homepage at http://www.diw.de/english/sop/). Follow-up with annually repeated interviews is ongoing. For the analyses presented below, data of the 16 subsequent panel waves from 1984 to 1999 were used. SOEP covers a broad range of social science topics, such as employment, earnings, health and satisfaction indicators. Person-level data are collected from all persons belonging to the sample households aged 16 years and older. Respondents are also followed up if they leave the original sample households, in which case their new households with all new household members are added to the database in subsequent surveys. The initial sampling did not include institutionalized persons, but respondents who moved into institutions were followed up, such that the database comprises persons institutionalized since 1984.

The initial West German SOEP sample has been found highly representative of the overall population, with older adults being slightly underrepresented (Haisken-DeNew and Frick 2003). Net panel attrition is quite low, the 1999 survey comprises 6,045 respondents, which is 67% of the 1984 sample size. Regarding selectivity of attrition, overall statements cannot be made easily, as predictors for unsuccessful follow-up or refusal changed across the panel waves (Kroh and Spieß 2005). For example, refusal to report income appeared as a significant predictor of refusal to participate in 10 of 15 subsequent follow-ups up to 1999, and older age was related to higher refusal rates in four waves. Notably, health state never predicted subsequent refusal, whereas male gender and low income did so only twice. Unsuccessful follow-up (i.e. inability to reach the household) was increased for single households in four panel waves.

The analyses presented below were run on subgroups of elder respondents defined as follows: sample A consists of all subjects born within the years 1924–1939, that is, respondents who reached the age of 60 within the measurement period 1984–1999, comprising an age range from 45 (born 1939, measured 1984) to 75 (born 1924, measured 1999). Thus, sample A covers the transition into old age and the young–old ages, for which the overlay of age- and cohort-related decline has been particularly hypothesized. For reasons of comparison, sample B was generated by shifting the cohort range 15 years backwards, comprising all respondents born 1909–1924, that is, those who reached the age of 75 within the measurement period (age range 60–90). According to the second hypothesis, sample B was expected to reveal increasing importance of age-related decline, as it covers the young–old and old–old ages. Finally, analyses were conducted on the total group of elder respondents included in samples A and B, that is, sample C consists of respondents born within the years 1909–1939.

Measures

The SOEP covers annually repeated single-item measures of LS. The item asks for present satisfaction with life to be rated on a 0–10 numerical scale (0=“absolutely dissatisfied”, 10=“absolutely satisfied”). Regarding the psychometric properties of single-item LS measures, Veenhoven (1996) reviews findings on validity and reliability, concluding that single-item measures on satisfaction work about equally well as multi-item inventories, providing sufficiently valid and reliable LS measurement. Reliability estimates for the SOEP satisfaction items provided by Landua (1993), Schräpler (1995) and Schilling (2003) seem overall acceptable.

In the analyses subsequently presented, the variable cohort denotes 1-year birth cohorts, that is, cohort is measured simply as respondent’s year of birth. Respondent’s age was computed as year of survey minus year of birth.

Statistical modelling

Longitudinal data analysis was conducted by means of multilevel mixed models (e.g. Verbeke and Molenberghs 2000; Maas and Snijders 2003). The key concept of longitudinal multilevel models, often referred to as growth curve models, is to treat longitudinal data as hierarchically structured: the measurements at different points in time (first level) are nested within individuals (second level). This constitutes a hierarchical regression model that decomposes the dependent variable’s overall variance into a within-subject component (intraindividual variation over each person’s repeated measurements) and a between-subject component (interindividual variation over the persons). Doing so, effects of within-subject predictors (varying within persons) are modelled such that these are further decomposed into a fixed effect, which can be understood as the mean effect over all individuals, and a random variance component due to interindividual variation of this effect. Effects of between-subject predictors (varying between, but not within persons) must be modelled as fixed only.

Growth curve models were specified with age as within-subject predictor and cohort as between-subject predictor of LS. Basically, linear effects of age and cohort were modelled. Regarding the age effect, this implies estimation of the constant average rate of change across the age range included in the analysis, which due to the first hypothesis stated above can be regarded as crucial quantity to be compared with the average rate of change per year of birth. However, to deal with possible acceleration of age-related change across the old age period, as stated in the second hypothesis, models combining higher degree polynomial (quadratic, cubic) age effects with a linear cohort effect were tested as well. Age–cohort interactions were included in all models.

Samples A and B were chosen particularly for computation of the basic model comprising only linear effects of age and cohort. As explained previously, linearity of the age effect over a larger age range was not expected, but might hold approximately across such a restricted range of age as included in sample A. Moreover, samples A and B allow for transformations of the age scale such that the zero-point is set to age 60 and 75, respectively, which is within the age range passed through the observation period by each birth cohort from the respective sample. This property seems desirable, as the estimation of the cohort effect fits the average between-cohort differences at age zero. If some cohorts have not been observed at this age, this can be understood as prolonging these cohorts’ age-related trajectories to the zero-point of age, which would not yield their correct average LS at age zero if trajectories have been modelled linearly, but in fact do not follow the linear curvature over the whole age range. Therefore, acceleration of age-related decline as assumed in the second hypothesis might unduly inflate estimates of the cohort effect when a larger range of birth cohorts is included in the analysis. Moreover, estimates of the cohort–age interaction would be biased as well: the early cohorts would be measured only in their late age years with steeper declines in LS, whereas the later cohorts would be measured younger with slower decline, producing an erroneous impression of cohort-related acceleration of the decline.

Acceleration of LS decline across the whole old age period may be fitted by use of a higher degree polynomial function of age, which could also mitigate the problem of biased cohort estimation when a broader range of older cohorts is included into analysis. Thus, sample C was chosen to check for acceleration of age-related decline by the use of higher degree polynomials. To check which polynomial function adequately describes age-related change, some preliminary analyses were conducted, following suggestions by Verbeke and Molenberghs (2000, pp. 35–40): starting with the linear polynomial and successively increasing the degree of the polynomial age function by one (leaving out cohort), the overall coefficients R ²_meta of multiple determination were computed, and significance was tested by use of the F _meta-test (i.e. testing linear vs quadratic, quadratic vs cubic, etc.). However, as Verbeke and Molenberghs emphasize, this procedure should not be taken as a formal test for model adequacy, but rather as a tool to explore the adequate growth function. Therefore, choice of the order of the polynomials on age might also be guided by considerations, such as parsimony and interpretability of the growth function.

The multilevel mixed models were computed by use of procedure MIXED implemented in SAS 8.2 software package (SAS Institute Inc. 1999), executing the restricted maximum likelihood estimation method. Computations of R ²_meta and F _meta-tests were made by use of a SAS macro provided by Verbeke and Molenberghs (2000).

It should be noted with respect to panel dropout that this type of analysis implies unbiased estimation for data “missing at random”. To put it simply, the likelihood is maximized with respect to all the data available from each respondent. That is, neither listwise deletion of cases with missing data, nor single imputation of missing values is applied, which would provide unbiased estimation only under the restrictive “missing completely at random” condition. Reviewing the “state of art” in missing data treatment, Schafer and Graham (2002) recommended the use of maximum-likelihood-based procedures to deal with longitudinal dropout, including dropout caused by death of respondents.

Results

Sample description

Table 1 provides statistics for a general description of the analysis samples. The total sample C comprised 3,913 subjects that reported LS at least at one of the 16 measurement occasions analysed. Sample sizes and dropout rates were not equally distributed across birth cohorts; however, for the first measurement occasion each cohort contained more than 50 subjects, but few subjects from the earliest cohorts stayed up to the last measurement, with two cohorts comprised of less than ten subjects at the 1999 measurement (i.e. eight and nine respondents born within the years 1909 and 1911, respectively).

Table 1.

Means, standard deviations and numbers of non-missing values of life satisfaction in analysis samples

	M			S			N
	A	B	C	A	B	C	A	B	C
1984	7.46	7.50	7.47	2.10	2.21	2.14	2,380	1,483	3,738
1985	7.26	7.37	7.30	2.04	2.20	2.10	2,142	1,287	3,317
1986	7.25	7.50	7.34	1.96	2.07	2.00	1,989	1,159	3,045
1987	7.13	7.29	7.18	1.91	2.08	1.97	1,927	1,093	2,922
1988	7.06	7.08	7.06	1.98	2.18	2.05	1,826	996	2,733
1989	7.07	7.10	7.08	1.99	2.11	2.04	1,699	914	2,531
1990	7.26	7.16	7.22	1.83	2.12	1.94	1,628	880	2,425
1991	7.46	7.36	7.42	1.67	2.03	1.80	1,576	820	2,316
1992	7.32	7.11	7.24	1.74	2.04	1.85	1,527	769	2,218
1993	7.31	7.13	7.23	1.83	2.10	1.92	1,478	721	2,124
1994	7.11	7.02	7.06	1.85	2.05	1.92	1,418	662	2,008
1995	7.10	6.82	7.00	1.85	2.19	1.97	1,382	603	1,914
1996	7.15	6.96	7.08	1.81	2.10	1.90	1,344	549	1,822
1997	6.99	6.82	6.93	1.81	2.13	1.90	1,288	514	1,735
1998	6.97	6.83	6.93	1.90	2.11	1.95	1,215	466	1,617
1999	7.05	6.78	6.97	1.83	2.21	1.92	1,155	410	1,509

M Sample mean, S standard deviation, N number of non-missing values. A = respondents born in 1924–1939, B = respondents born in 1924–1939, C = respondents born within the years 1909–1939

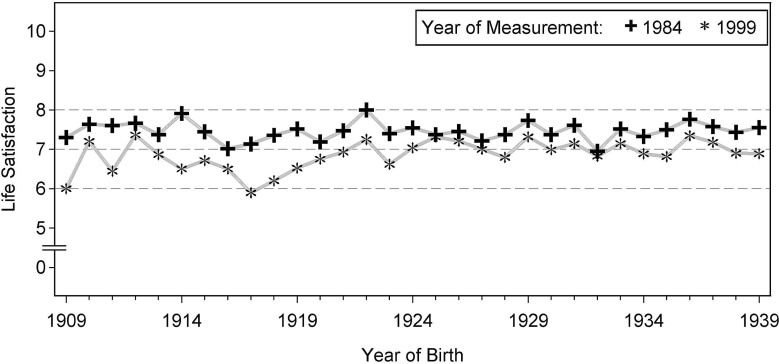
As can be seen in Table 1, a slight downward tendency appeared in the mean LS values across the whole measurement period. For a closer description with respect to age- or cohort-related trends in LS, the mean LS values per age/cohort and measurement occasion would provide insight. However, to avoid excessive printout of numbers, only the birth cohorts’ mean values for the first and last measurement occasion are shown in Fig. 2. In view of the values depicted, three aspects seem notable: first, despite some fluctuation, no general tendency to increase or decrease appears in the 1984 mean values, covering the age range from 45 to 75. That is, in a 1984 cross-sectional age-group comparison, no age-related decline would appear and “paradox” mean-level stability across young–old age would be found once again. Second, mean- level stability also appears for the 1999 means, except some tentative downward tendency visible for the earliest cohorts. Thus, in the 1999 cross-sectional comparison, mean-level stability would be found again up to about ages 75–80, but some age-related decline appears in the very old ages. Third, it deserves mentioning that all 1999 mean values lie below their 1984 counterparts, that is, “longitudinally” some decline of mean-level LS is visible for all cohorts.

Fig. 2.

Mean values of LS per birth cohort at measurement occasions 1984 and 1999

Mixed model results

Linear growth models

Table 2 presents the results from the computation of the mixed models with linear age and cohort effects. To interpret the estimates, the zero-point transformations of the age and cohort scales should be noted: for samples A and C, the zero-points of age and cohort were shifted to 60 and 1924, respectively, and to 75 and 1909 for sample B. Also, it should be mentioned that in samples A, B and C the overall variances of the LS values were 3.627, 4.517 and 3.921, respectively, such that the residual variances shown in Table 2 come up to 49.2, 49.1 and 49.9% of unexplained variance in samples A, B and C, respectively.

Table 2.

Fixed and random effect estimates from linear mixed models

	Sample A	Sample B	Sample C
Fixed regression coefficients
Intercept	7.401**	7.234**	7.604**
Age	−0.033**	−0.132**	−0.054**
Cohort	−0.038**	−0.035**	−0.059**
Age×cohort	0.001	0.006**	0.003**
Random variances and covariances
Variance intercept	1.812**	2.474**	1.820**
Variance age	0.010**	0.011**	0.008**
Covariance intercept–age	0.022**	0.057**	−0.007*
Residual variance	1.783**	2.216**	1.957**
Δa−2LL	1,061.2**	316.7**	975.8**

Sample A = respondents born within the years 1924–1939, sample B = respondents born within the years 1909–1924, sample C = respondents born within the years 1909–1939. Asterisks refer to statistical significance (t test for fixed effects, Wald-test for random covariances, χ²-test for Δ_−2LL) with *P < 0.05, **P<0.001

^aDeviance tests, i.e. reduction in −2LL compared with random intercept (compound symmetry) model

With respect to the hypotheses stated earlier, the fixed age and cohort effects estimates are of primary concern. To produce an overlay of age- and cohort-related decline as depicted in Fig. 1, scheme c, these effects should be negative and of about the same size, and no age–cohort interaction should exist. As can be seen in Table 2, this was found for sample A, with nearly equal decrements in LS per additional years of age and birth. As the overlay was particularly hypothesized for the age range covered by sample A, these results confirm the first hypothesis. For sample B the linear age effect and the age–cohort interaction appear substantially increased compared with the sample A results, while in both samples the cohort effect was estimated as about the same size. In sample B, the significant interaction indicates that the earlier the year of birth, the steeper the slopes. This means that from the youngest cohort, measured at ages 60–75, to the oldest cohort, measured at ages 75–90, the decrement per year of age increases. Thus, the estimates for sample B reflect an acceleration of age-related decline as assumed with the second hypothesis. Finally, results for sample C are in line with the expectations, with all fixed effects significant, indicating some overall age- and cohort-related decline. Notably, sample C reveals an increase in the cohort effect, compared with samples A and B, which can be explained by the considerations made in the Methods section, regarding the inadequacy of a linear age function across the sample C age range in case of an acceleration of age-related decline.

All random effects presented in Table 2 appear statistically significant in single-parameter Wald tests. Furthermore, the deviance tests indicate significance of between-subject variance in the rates of change per year of age (for test procedures, see Maas and Snijders 2003). Although the hypotheses presented earlier refer to the existence rather than the variability of age-related change in LS, significance of this variability should be noted as a reminder that the fixed age effects as estimated in the present analyses do not tell the whole story. Of course, the changes in the older adults’ LS vary substantially, due to varying conditions affecting LS in old age. However, the significant fixed effects estimates must be understood as evidence that on average LS declines across the old age period.

Non-linear growth models

To check for acceleration of LS decline across the whole old age period covered in sample C, higher degree polynomial functions of age were fitted. As explained in the Methods section, preliminary computations of the overall coefficient R ²_meta of multiple determination and the F _meta-test were carried out for stepwise increases of the degree of the polynomials (Verbeke and Molenberghs 2000). In sum, the results strongly indicated substantial improvements of fit gained with an expansion of the linear growth function up to the fifth degree polynomial, but they do not show a drop in the stepwise R ²_meta improvement, which would qualify one of these polynomial functions to be chosen for further analysis. However, with respect to the detection of acceleration of age-related decline towards the end of the age range, fourth or higher degree polynomials might not provide too much additional information. Therefore, to keep the models parsimonious, only the quadratic and cubic growth functions were used for the final analyses.

Table 3 shows sample C results of the mixed models with quadratic and cubic age effects, combined with the linear effect of cohort. To keep presentation brief, only the fixed effects estimates are shown. Regarding the random variances and covariances, all these were significant in both models’ of Wald tests, except the covariance between linear and quadratic age component in the cubic age effect model.

Table 3.

Fixed effects estimates from mixed models involving quadratic and cubic growth functions

	Quadratic	Cubic
Intercept	7.426**	7.456**
Age	−0.016*	−0.020*
Age2	−0.002**	−0.001
Age3		−0.000*
Cohort	−0.042**	−0.043**
Age×cohort	−0.001	0.001
Age2×cohort	0.000**	0.000
Age3×cohort		−0.000**

Results computed for sample C (respondents born within the years 1909–1939), asterisks refer to statistical significance (t tests) with *P<0.01, **P<0.001

For both models a significant negative cohort effect evidences some general trend of cohort-related decline again in LS. Regarding the age effect components, the quadratic model estimates indicate a significant rate of age-related change at age 60 (linear component) and a highly significant acceleration of age-related decline across the 60+ ages (quadratic component). Also, the results show some significant interaction of the acceleration with cohort, such that the later the subjects have been born, the slower the acceleration of age-related decline. Regarding the cubic model’s results, significance of the cubic age component and of this component’s interaction with cohort indicates a negative cubic trend in age-related change for the “reference cohort” born 1924, getting stronger the later the subjects have been born. Interpreting these results, it should be noted that shifting the zero-point of the age scale might change size and significance of the linear components, as well as the cubic age function’s quadratic component (see e.g. Biesanz et al. 2004).

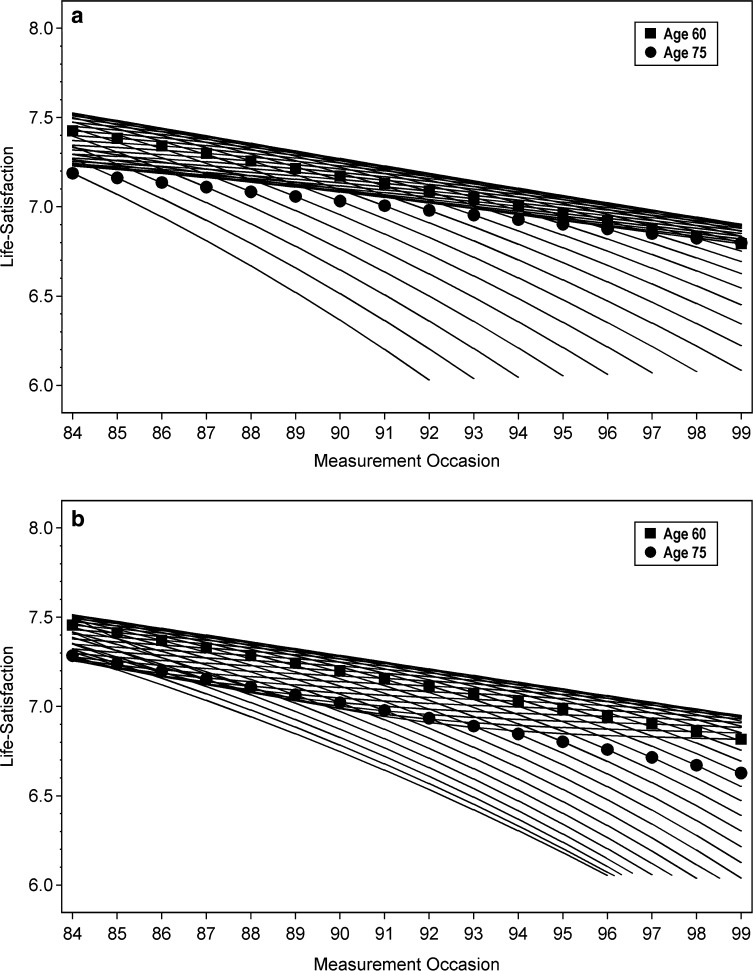
To provide better insight into the meaning of these results, Fig. 3 shows the trajectories predicted from the estimates of the quadratic and cubic mixed models. That is, for each cohort included in sample C, the mean LS curve over the 1984–1999 time period was computed from the fixed effect estimates presented in Table 3, and the curves for all 31 cohorts have been depicted. In each trajectory the ages 60 and 75 have been marked by squares and dots, respectively (i.e. the curve for the 1909 cohort starts with a dot on the left side, as this cohort is aged 75 in the year 1984, whereas the curve for the 1939 cohort ends with a square on the right side, as it reaches age 60 in the year 1999). The trajectories predicted from the quadratic model, shown in Fig. 3a, show a pattern which matches the hypotheses quite well: first, the negative cohort effect is visible in the declining trend of the “age-60-squares” across the measurement period, whereas all curves appear with negative slopes, indicating age-related decline in general. Second, for the most part the trajectories run very close to each other, cumulating within a narrow range of 0.3–0.1 points on the LS scale, such that in cross-sectional comparisons at any of the measurement occasions, most of the predicted cohort means would not differ much from each other. Thus, some approximate overlay of age- and cohort-related decline is visible. Third, crossing the “age-75-dots”, all trajectories depart from that densely cumulated area, declining steeply and thereby evidencing acceleration of age-related decline in the old–old age period.

Fig. 3.

Mean LS trajectories of birth cohorts as predicted from mixed models estimates

The picture does not change substantially when the trajectories predicted from the cubic model are displayed. In Fig. 3b, again the declining trend of the “age-60-squares”, as well as some overall decline in all curves appears. Also, the trajectories largely run close to each other, and show steeper decline across the old–old age period. Therefore, an approximate overlay of age- and cohort-related decline over the young–old ages and the acceleration of age-related decline in the old–old period are evidenced again in the cubic model results. However, with respect to the younger ages covered by sample C, inclusion of the third degree polynomial produces some divergence of the curvatures as predicted from the quadratic model. A close look at the curves for those cohorts, measured in their younger ages below 50 (i.e. the five curves with the “age-60-squares” on the rightmost side of the panel), shows steeper decline in the beginning, which decelerates to a period of stability from about age 55 to 60. After about age 60, age-related decline accelerates again.

Discussion

In general, the results presented in this paper confirm the hypothesis of an overlay of age- and cohort-related decline in the trajectories of mean LS for subjects in their young–old ages over the past two decades of the twentieth century. Moreover, acceleration of age-related decline, indicating substantial losses in LS over the old–old age period, was evidenced. Therefore, the basic implication derivable from these analyses is contradictory to the notion of “stability despite loss” in old age. It seems that there is age-related decline in LS over the old age period, and findings of paradox stability might be highly specific for cross-sectional age-group comparisons comprising the young–old only and conducted in the past decades of the twentieth century. Under these particular conditions, cohort-related decline in LS may obscure the negative age effect.

Of course, these findings come with limitations, calling for caution in interpretation. In particular, three points should be stressed in this regard: first, it may be called into question if single-item measures of LS as used in the SOEP survey are sufficient to study change in LS. Studies involving multi-item LS measurement may enable more reliable analysis of intraindividual change, for example, modelling true-score change freed from measurement error with longitudinal structural equation models. However, as aforementioned in the Methods section, the psychometric quality of the single-item measures has been found at least acceptable. Second, it may be called into question to what extent the results found for a German sample may generalize to other societies. The present paper’s fundamental assumption of a cohort effect at work for those born in the first half of the twentieth century bears on social and historical developments, such as the economic depression in the 1920s and the Second World War, which affected German society with particular intensity. Therefore, a less pronounced cohort effect may be at work in countries where these adverse conditions took place less intensely (as, e.g. the USA, which was unaffected territorially by acts of war).

Third, it should be noted that differences due to age and cohort appearing in longitudinal, but not in cross-sectional comparisons, might statistically also be attributable to the time of measurement. Initiated by Schaie’s (1965) general developmental model, the disentangling of age, cohort and time of measurement effects has become a major methodological issue for the study of developmental processes. As any of the three can be calculated from the others, age, cohort and time are perfectly confounded, thus constituting a “developmental muddle” (Donaldson and Horn 1992) for any statistical modelling approach aiming at the simultaneous estimation of the unique effects of these three predictors. In a strict sense, this muddle cannot be solved, but several proposals have been made to overcome it in practical terms (e.g. Donaldson and Horn 1992; Masche and van Dulmen 2004). However, any such approach has to bear on theoretical assumptions or, in statistical terms, on a priori constraints on some of the effects emerging from an age×cohort×time design. In the present study, effects of time of measurement on LS were not modelled at all. It comes to mind, indeed, that the German reunification took place in 1990 and might have caused some common upswing of positive mood, which might have also impacted people’s LS (in fact, Table 1 shows such temporary increase in mean LS, with local maxima in 1991). However, an alternative explanation for the results presented earlier would have to rest on time-related declines in LS over the whole 1984–1999 period.

Apart from these limitations, the importance of the age and cohort effects reported earlier deserves some consideration. The estimated age- and cohort-related decrements in LS might seem quite small in face of the standard deviations shown in Table 1. However, LS is susceptible to different sources of impact varying between the aged persons (objective living conditions, personality, affect, etc.), among those conditions under increased risk in old age. With conditions of LS—and changes in these conditions—varying between old-aged persons, substantial variation in the LS trajectories in old age must be expected and was evidenced in the present analyses by the highly significant random between-subject variances of the models’ age effects. Therefore, an overall negative age effect, bearing on age as proxy for losses frequent in old age, cannot be expected to be particularly strong in terms of variance explanation. However, it might be stronger (or weaker, or even reversed) in subgroups more homogenous in terms of living conditions, such as institutionalized elders. Furthermore with respect to the cohort effect, a similar argument must be made, as belonging to the same birth cohort neither guarantees the same amount of exposure to adverse living conditions in the early twentieth century, nor the same benefit from positive welfare conditions in recent times. Thus, the old-aged people may differ substantially in how much their current LS judgements are influenced by negative past experiences, and the effect of cohort, indicating the average of all such influences across all persons, again should not be expected to be too strong.

In view of these considerations, only weak but significant effects of cohort and age may be regarded as a strong result, evidencing substantial tendencies of age- and cohort-related decline despite this diversity of impacts on LS, varying between subjects. Particularly, the negative effects of age presented earlier, coming along with substantial between-subject variances, evidence a large share of worsening LS among the elder individuals, with lots of intraindividual declines steeper than the mean-level decline indicated through the fixed effects estimates. Thus, from the present study’s results, it can be concluded that people in their old ages do not keep their LS stable despite loss, but tend to become more and more dissatisfied throughout the old age period.