Estimation of distal arm joint angles from EMG and shoulder orientation for transhumeral prostheses

Abstract

In this paper, we quantify the extent to which shoulder orientation, upper-arm electromyography (EMG), and forearm EMG are predictors of distal arm joint angles during reaching in eight subjects without disability as well as three subjects with a unilateral transhumeral amputation and targeted reinnervation. Prior studies have shown that shoulder orientation and upper-arm EMG, taken separately, are predictors of both elbow flexion/extension and forearm pronation/supination. We show that, for eight subjects without disability, shoulder orientation and upper-arm EMG together are a significantly better predictor of both elbow flexion/extension during unilateral (R² = 0.72) and mirrored bilateral (R² = 0.72) reaches and of forearm pronation/supination during unilateral (R² = 0.77) and mirrored bilateral (R² = 0.70) reaches. We also show that adding forearm EMG further improves the prediction of forearm pronation/supination during unilateral (R² = 0.82) and mirrored bilateral (R² = 0.75) reaches. In principle, these results provide the basis for choosing inputs for control of transhumeral prostheses, both by subjects with targeted motor reinnervation (when forearm EMG is available) and by subjects without target motor reinnervation (when forearm EMG is not available). In particular, we confirm that shoulder orientation and upper-arm EMG together best predict elbow flexion/extension (R² = 0.72) for three subjects with unilateral transhumeral amputations and targeted motor reinnervation. However, shoulder orientation alone best predicts forearm pronation/supination (R² = 0.88) for these subjects, a contradictory result that merits further study.

1. Introduction

In this paper, we quantify the extent to which different combinations of shoulder orientation, upper arm electromyography (EMG), and forearm EMG are predictors of distal arm joint angles during arm movements. Prediction of these joint angles is useful for enabling position-based control of upper-limb prostheses [1, 2, 3, 4, 5]. In particular, the results of this study are important to improving simultaneous control of elbow flexion/extension and forearm pronation/supination in prostheses used by people with transhumeral amputations.

1.1. Prediction of Distal Arm Joint Angles Using EMG or Shoulder Orientation

Two prior studies have shown that shoulder orientation and upper arm EMG, taken separately, are predictors of both elbow flexion/extension and forearm pronation/supination. Pulliam et al. [6] used EMG recordings from the upper arm and chest to predict the angles of the elbow and forearm simultaneously. Specifically, they implemented a time-delayed adaptive neural network (TDANN) to predict the angles of elbow flexion/extension (E_FE) and forearm pronation/ supination (F_PS) [7, 8]. Their results showed that across multiple types of reaching movements (single-joint movements, single-joint movements with a load, simultaneous degree-of-freedom movements, and activities of daily living), the network could on average predict elbow flexion/extension within 10–15° and forearm pronation/supination within 20–25° of their actual values. A separate study by Kaliki et al. [9] suggests that when reaching, distal arm kinematics can be predicted by using shoulder orientation as the input to a cascade correlation neural network. In this study, subjects were seated and asked to reach to a vertical handle that moved to uniformly distributed positions in the subjects reaching workspace. Motion capture was used to determine the joint angles at the shoulder. Their network resulted in R² values above 0.7, denoting a strong correlation.

1.2. Combining EMG and Shoulder Orientation for Prediction

Preliminary results from a single subject without disability have suggested that the combination of shoulder orientation and EMG can improve the accuracy of estimating distal arm joint angles [10]. Blana et al. [1] showed that subjects without disability could control a virtual arm using EMG and arm kinematics, suggesting that this combination of inputs could be feasible for prosthesis control. However, they did not quantify the extent to which this combination outperforms EMG and kinematic inputs individually, nor did they test their control strategy on subjects with amputations. In this paper, we compare the performance of our predictors for eight subjects without disability and three subjects with unilateral transhumeral amputations and targeted reinnervation when using shoulder orientation, upper arm EMG, forearm EMG, and combinations of these as inputs. In principle, these results provide the basis for choosing inputs for control of transhumeral prostheses, both by people with targeted motor reinnervation (when forearm EMG is available) and without reinnervation (when forearm EMG is not available).

1.3. Simultaneous Control of Multiple Degrees of Freedom

The results of this study are important in enabling simultaneous control of distal arm joint angles in upper limb prosthetic devices. Simultaneous control of multiple degrees of freedom in the arm are required to easily complete activities of daily living, such as pouring water from a bottle or reaching for objects [2]. Muceli and Farina [2] and Jiang et al. [3] have shown that wrist kinematics during mirrored movements of multiple degrees of freedom simultaneously could be predicted using neural networks from forearm EMG, which would be useful for people with transradial amputations to control a prosthetic hand. Ameri et al. [4, 5] used support vector regression and artificial neural networks to estimate multiple wrist joint angles and forces in subjects without impairment. Young et al. [11] classified simultaneous hand movements using EMG-based pattern recognition. Our work looks at predictors for elbow and forearm joint angles from EMG and shoulder orientation in order to enable simultaneous control of prostheses for people with transhumeral amputations.

It should be noted that the prediction of the distal arm joint angles was done in an offline context—data collected from subjects were not used in real-time for myoelectric control. Jiang et al. [12] have shown that when simultaneous control of hand kinematics is performed online in real-time, predictors that performed significantly differently in offline studies gave similar performances in online tasks, with respect to R². We discuss this limitation of our study in Section 4.4.

1.4. Outline of Paper

The paper is organized as follows. In Section 2, we explain the methods used for acquiring upper arm EMG and arm joint angles during reaching, as well as the predictors we use for estimation. In Section 3, we present the results of the predictors in estimating the distal arm joint angles using different inputs consisting of EMG, shoulder orientation, and their combinations. We give recommendations on choosing inputs for transhumeral prosthetic controllers as well as discussing the rationale for these recommendations in Section 4, followed by our overall conclusions in Section 5.

2. Methods

Eight adult subjects (ages 20–25, four male, four female) without disability and three adult subjects (ages 28–48, three male) with unilateral right transhumeral amputations and targeted motor reinnervation (TMR) surgery volunteered for the experiments. Subjects were asked to perform a standard center-out reaching task [1, 13], simultaneously actuating elbow and forearm joint angles to achieve various target arm configurations (Fig. 1). Subjects without disability were used as controls and performed two experiments on separate days. In the first experiment, the control subjects were asked to make unilateral reaches with their right arms, while in the second experiment they were asked to make mirrored bilateral reaches. Finally, the TMR subjects participated in an experiment in which they were asked to perform mirrored bilateral reaches as though both of their arms were unimpaired. Further details for the three experiments are given below. All subjects gave informed consent to participate in this research study and to have their data published. The study was approved by the Institutional Review Board at the University of Illinois at Urbana-Champaign (IRB #12823).

Figure 1.

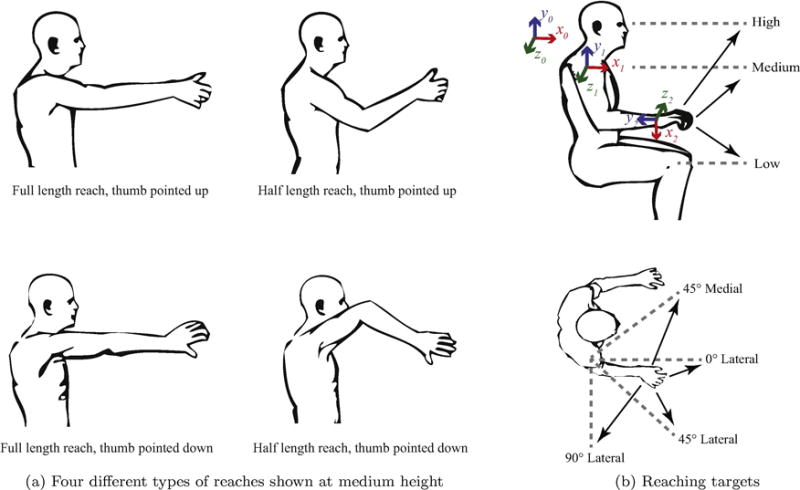
Reaching locations and types. The four different types of reaches are shown in (a). The starting position of the arms and targets are shown in (b) with three heights (top) an four mediolateral locations (bottom). A total of 48 reaches are made for the training set and repeated again for the testing set.

2.1. Experimental Setup

2.1.1. Control: Unilateral Reaches with Ipsilateral EMG Placement

The control subjects were seated in a chair, placing their right forearms on their laps, palms down, elbows bent at 90° with respect to the humerus. Subjects were asked to make four types of center-out reaches, as shown in Fig. 1a. The reaching types can be described as 1) full length, forearm supinated (open hand with thumbs pointing up), 2) half length, forearm supinated, 3) full length, forearm pronated (open hand with thumbs pointing down), and 4) half length, forearm pronated). The subjects were asked to perform each type of reach to four mediolateral locations at three heights for a total of 12 reaches per type (Fig. 1b). The four mediolateral locations were across the body, directly in front, 45° lateral to the front, and directly out to the side. The heights were at waist, shoulder, and eye levels. Subjects were asked to hold the reach for a count of three seconds before returning to the start position. As soon as the subject completed the 12 reaches for a particular type, recording stopped. All 48 of these reaches were repeated twice. The first set of 48 reaches was used as the training dataset, and the repeated second set of 48 reaches was used as the testing dataset so that each dataset had the same representative reaches for evaluation. Like in [9], a single testing set was used to test the generalizability of our estimation techniques. Finally, a validation reaching set was taken in which the subjects randomly selected and performed as many of the reaches from the prior sets as they could within 30 seconds.

Thirteen bipolar surface EMG electrodes (Delsys, Inc. 16-channel Bagnoli system) were positioned on the right arm of each subject: three on the anterior, middle, and posterior deltoid, two on the long and short heads of the biceps, two on the long and lateral heads of the triceps, and six equidistant around the circumference of the forearm. The subjects wore a wrist brace to restrict wrist movement during reaching tasks.

An OptiTrack motion capture system (NaturalPoint, Inc., Corvallis, OR) was used to determine the location of bony landmarks. Specifically, reflective markers were placed over the radial styloid, ulnar styloid, lateral epicondyle, olecranon, and acromion. From the locations of these markers, the angles for the shoulder, elbow, and forearm were calculated according to ISB standards [14]. Rotation about the global x, y, and z axes corresponded to shoulder abduction/adduction, internal/external rotation, and flexion/extension, respectively. Rotation about the forearm’s y-axis (the vector formed from the lateral epicondyle to ulnar styloid) corresponded to forearm pronation/supination, and rotation about the z-axis of the humerus (the cross product of the forearm’s y-axis and the vector formed from the lateral epicondyle to acromion) corresponded to elbow flexion/extension. The coordinate frames are shown in Fig. 1b. Clinically meaningful Euler angles were extracted to determine the orientation for the shoulder (YXY) and the forearm (ZXY) according to ISB standards. A hardware trigger was used to sync the recording of motion capture and EMG data.

2.1.2. Control: Mirrored Bilateral Reaches with Contralateral EMG Placement

To more closely match the experimental conditions used with the TMR subject, control subjects were asked to participate in a second experiment in which they performed bilateral mirrored reaching movements. The reaches performed were the same as the unilateral reaches, but they were mirrored with the left arm so that the shoulder, elbow, and forearm joint angles would match. Training using mirrored bilateral movements has been successfully implemented in previous studies to estimate arm forces [15] and hand kinematics [2, 16, 17] using EMG from the contralateral arm.

Motion capture markers were placed on the left arm, while EMG was recorded on the contralateral arm in order to match experimental conditions to be used with the TMR subjects. However, because standard practice is to use bony landmarks to compute joint angles, and in the case of the TMR subjects all the bony landmarks used to compute shoulder angles were only present in their umimpaired left arms, shoulder markers were placed on the left arm for both the control subjects and TMR subjects rather than the contralateral arm. For control subjects, when performing reaches where each arm crossed the midline of the body, the right arm crossed under the left arm in order to prevent occlusion of the markers on the left.

2.1.3. TMR Subject: Mirrored Bilateral Reaches with Contralateral EMG Placement

For the TMR subject, the arm movements performed were the same as the mirrored bilateral reaches with contralateral EMG placement for the control subjects. Eleven EMG sensors were placed on the impaired right arm: three on the anterior, middle, and posterior deltoid, one on the long head of the biceps, one on the reinnervated short head of the biceps used for closing the hand, one on the long head of the triceps, one on the reinnervated lateral head of the triceps used for opening the hand, and four placed near the reinnervated sites used for pattern recognition to control forearm pronation/supination, wrist flexion/extension, as well as various hand grips. Electrodes were not placed on the unimpaired ipsilateral side since we had a limited number of electrodes and would expect those results to be similar to those of the control subjects performing unilateral reaches with ipsilateral EMG placement. Due to the absence of the distal portion of the right arm, the TMR subjects did not need to place their impaired right arms underneath their left arms when performing mirrored reaches across the body—instead, they were kept at the same height.

2.2. Data Processing

All data were processed using MATLAB (MathWorks, Inc., Natick, MA). EMG data were recorded at 1000 Hz. After acquisition, the data were filtered with a 5th-order Butterworth high-pass filter with a cutoff frequency of 10 Hz to remove movement artifacts. The EMG data were windowed at 200 ms with an overlap of 75 ms to make an effective timestep of 125 ms. Four time-domain features were extracted from each channel: mean absolute value, waveform length, number of zero crossings, and number of slope sign changes [6, 18].

Motion capture data were recorded at 100 Hz. After the motion capture data were cleaned, the data were filtered using a 4th-order Butterworth high-pass filter with a cutoff frequency of 15 Hz to remove movement artifacts. To reduce data size, the data were then downsampled to 8 Hz to match the effective timestep of the post-processed EMG data. To allow a full window width for the EMG data, the first sample was offset to 200 ms before sampling every 125 ms afterwards. The three Euler angles for the shoulder and two for the elbow and forearm were then extracted.

The data were arranged into sets of predictors and targets for the estimation techniques. The predictors consisted of the shoulder orientation angles, upper arm EMG, EMG from TMR sites (or their anatomical analogues in control subjects), and their combinations. The targets were the two forearm Euler angles described previously, corresponding to E_FE and F_PS.

2.3. Estimation Techniques

Two nonparametric estimation methods were separately used to predict E_FE and F_PS: locally weighted projection regression (LWPR) and a time-delayed adaptive neural network (TDANN).

2.3.1. Locally Weighted Projection Regression (LWPR)

LWPR [19] is a form of nonlinear regression suited especially for data with a high number of input dimensions that include redundant or uninformative dimensions. Consequently, a separate dimensionality reduction step is not necessary. Since our input dimensions range from 3 (shoulder angles only) to 55 (shoulder angles, upper arm EMG, and forearm EMG), LWPR is particularly useful for our data. The input space is divided into a number of local receptive fields over which linear regression is performed. LWPR has been used in previous studies to estimate the grasping force of a prosthetic hand using EMG [20]. We used the version 1.2.4 of the LWPR library written in C with MATLAB bindings from the University of Edinburgh [21]. Because of the differences in input dimension sizes, the initial distance metrics were tuned for each set of inputs. A grid optimization search between 10 to 300 in steps of 10 was used to find the optimal size of the initial distance metric. The initial distance metric that worked best for shoulder orientation only was a diagonal matrix of ones, size 250 × 250. For all the other inputs, a diagonal matrix of ones, size 20 × 20, generally gave the best performance. A Gaussian kernel was used for the activation function of each receptive field. A grid optimization search for the weight activation threshold and pruning weight was performed with values ranging from 0.1 to 1.0 in steps of 0.1. A weight activation threshold of 0.2 and a pruning weight of 0.7 generally gave the best performance.

2.3.2. Time-Delayed Adaptive Neural Network (TDANN)

A two-layer TDANN was created using MATLAB’s neural network toolbox. This type of network was used to effectively capture the sequential nature of motion capture and EMG time-series data. The network used a hidden layer size of 20 and had an input delay of 7, found to be optimal to predict distal arm joint angles in [6], making a separate dimensionality reduction step unnecessary. Initial weights and biases were randomly assigned. Data were split into training, testing and validation sets, as previously described in Section 2.1.1. To prevent overfitting, the network would stop after 1000 weight updates or earlier if the performance of the validation set failed to improve after five weight updates.

2.4. Analysis

Root mean square error (RMSE) and the coefficient of determination (R²) are standard metrics used to assess the performance of joint angle estimation [6, 9, 10]. RMSE is reported in degrees and the lower the value, the better the fit to the data. We calculate RMSE as follows:

$$\mathit{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \sum _{t=0}^N{\left({\widehat{x}}_t-x_t\right)}^2}},$$

where x_t is the actual joint angle at data point t, ${\widehat{x}}_t$ is the estimated joint angle at data point t, and N is the total number of data points. R² indicates the amount of variance explained by the estimation model, and ranges from 0 to 1. Values higher than 0.7 indicate a strong fit to the data. We calculate R² as follows:

$$R^2=1-\frac{{\displaystyle {\sum }_{t=0}^N{\left({\widehat{x}}_t-x_t\right)}^2}}{{\displaystyle {\sum }_{t=0}^N{\left(x_t-\overline{x}\right)}^2}},$$

where x_t is the actual joint angle at data point t, ${\widehat{x}}_t$ is the estimated joint angle at data point t, $\overline{x}$ is the average of x_t over all N data points, and N is the total number of data points.

3. Results

Results for control subjects with ipsilateral EMG placement are shown in Table 2. The following abbreviations will be used in describing the input feature sets: SO=shoulder orientation, U=upper arm, F=forearm. Combinations of inputs are denoted with a + symbol. Across all estimation techniques, the best performance in estimating E_FE was given by the combination of shoulder orientation and upper arm EMG, SO+EMG_U, when using LWPR (RMSE=10.65, R²=0.72). The combination of all inputs—shoulder orientation, upper arm EMG, and forearm EMG (SO+EMG_U+F)—also performed well with an RMSE=10.87 and R²=0.7. For F_PS, the best performance was given by SO+EMG_U+F using LWPR (RMSE=21.35°, R²=0.82). EMG_U+F and SO+EMG_U also showed strong performances with mean R² values of 0.74 and 0.77, respectively. An example of the LWPR estimation of E_FE and F_PS for a single reach is shown in Fig. 2.

Table 2.

RMSE and R² performance of LWPR and TDANN for 5 different sets of inputs in estimating (a) elbow flexion/extension, E_FE, and (b) forearm pronation/supination, F_PS, of control subjects performing unilateral reaches. Averages over 8 subjects are shown. The best performing input set among the estimators is highlighted in gray. SO = shoulder orientation, U = upper arm, F = forearm.

(a) Control (Unilateral) EFE
	SO		EMGU		EMGU+F		SO+EMGU		SO+EMGU+F
	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2
LWPR mean	13.59	0.56	12.38	0.61	12.08	0.63	10.65	0.72	10.87	0.70
LWPR std	3.49	0.12	3.00	0.16	3.08	0.15	2.83	0.08	3.06	0.09
TDANN mean	13.36	0.57	12.79	0.58	12.60	0.60	12.66	0.62	11.69	0.66
TDANN std	3.05	0.13	2.63	0.13	2.35	0.15	2.72	0.10	2.00	0.08

(b) Control (Unilateral) FPS
	SO		EMGU		EMGU+F		SO+EMGU		SO+EMGU+F
	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2
LWPR mean	34.63	0.58	31.00	0.64	25.78	0.74	23.69	0.77	21.35	0.82
LWPR std	12.30	0.21	9.83	0.16	10.73	0.15	7.14	0.13	1.99	0.09
TDANN mean	35.70	0.54	33.92	0.57	29.54	0.68	31.53	0.62	25.03	0.76
TDANN std	9.72	0.18	6.97	0.14	8.14	0.12	9.81	0.18	6.28	0.09

Figure 2.

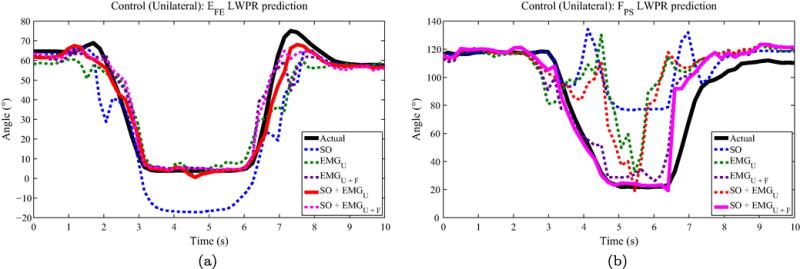
Control (unilateral) single-reach joint angle prediction. Example reach showing the performance of LWPR with different input feature sets for (a) E_FE and (a) F_PS. The actual joint angle trajectory is shown in a solid black line, while the best performing input feature set is shown with a solid colored line. The other feature sets are dashed.

Similar results were achieved for control subjects performing mirrored bilateral reaches, as shown in Table 3. Specifically, using SO+EMG_U as inputs in LWPR again gave the best performance in estimating E_FE (RMSE=11.09, R²=0.72), followed closely by SO+EMG_U+F (RMSE=11.38, R²=0.71). In estimating F_PS, SO+EMG_U+F again gave the best performance (RMSE=25.42, R²=0.75).

Table 3.

RMSE and R² performance of LWPR and TDANN for 5 different sets of inputs in estimating (a) elbow flexion/extension, E_FE, and (b) forearm pronation/supination, F_PS, of control subjects performing bilateral reaches. Averages over 8 subjects are shown. The best performing input set among the estimators is highlighted in gray. SO = shoulder orientation, U = upper arm, F = forearm.

(a) Control (Bilateral) EFE
	SO		EMGU		EMGU+F		SO+EMGU		SO+EMGU+F
	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2
LWPR mean	14.13	0.57	13.19	0.60	12.48	0.64	11.09	0.72	11.38	0.71
LWPR std	3.35	0.14	2.20	0.14	2.10	0.12	1.28	0.07	1.60	0.08
TDANN mean	14.01	0.56	15.12	0.47	15.47	0.53	12.24	0.66	12.21	0.64
TDANN std	2.21	0.13	2.60	0.18	4.22	0.17	1.82	0.10	1.58	0.11

(b) Control (Bilateral) FPS
	SO		EMGU		EMGU+F		SO+EMGU		SO+EMGU+F
	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2
LWPR mean	34.41	0.62	39.85	0.42	31.29	0.63	29.06	0.70	25.42	0.75
LWPR std	15.41	0.20	16.44	0.17	15.87	0.20	13.49	0.15	14.76	0.19
TDANN mean	33.39	0.61	44.53	0.37	36.37	0.54	34.94	0.56	33.53	0.62
TDANN std	14.31	0.21	18.70	0.18	16.46	0.20	15.46	0.18	17.70	0.21

Table 4 shows the results for the TMR subjects when performing mirrored bilateral reaches. Similar to the control subjects, SO+EMG_U using LWPR performed the best for estimating E_FE (RMSE=12.12, R²=0.72). All the inputs combined performed almost as well (RMSE=12.61, R²=0.71). For estimating F_PS, the best performance was achieved by SO alone (RMSE=12.07, R²=0.88) and the subsequent addition of EMG inputs to shoulder orientation had degraded performance. This result is in contrast to the performance of the estimators for control subjects, in which the combination of all inputs performed best. Figure 3 shows the performance of LWPR using SO+EMG_U as the input feature set for E_FE, and SO as the feature set for F_PS.

Table 4.

RMSE and R² performance of TDANN and LWPR for 5 different sets of inputs in estimating (a) elbow flexion/extension, E_FE, and (b) forearm pronation/supination, F_PS, of 3 TMR subjects with EMG placement on the reinnervated arm. The best performing input set among the estimators is highlighted in gray. SO = shoulder orientation, U = upper arm, RS = reinnervated sites including pattern recognition sites.

(a) TMR EFE
	SO		EMGU		EMGU+F		SO+EMGU		SO+EMGU+F
	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2
LWPR mean	15.32	0.64	17.58	0.45	17.00	0.51	12.12	0.72	12.61	0.71
LWPR std	3.24	0.07	5.07	0.06	4.73	0.07	2.74	0.09	3.00	0.10
TDANN mean	15.54	0.63	17.63	0.46	18.44	0.45	14.67	0.62	15.29	0.61
TDANN std	3.82	0.05	4.94	0.15	4.00	0.17	2.95	0.16	5.01	0.09

(b) TMR FPS
	SO		EMGU		EMGU+F		SO+EMGU		SO+EMGU+F
	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2	RMSE	R2
LWPR mean	12.07	0.88	24.73	0.37	22.62	0.47	14.16	0.81	14.18	0.81
LWPR std	3.59	0.05	2.90	0.09	2.85	0.14	4.16	0.08	4.20	0.09
TDANN mean	12.64	0.85	24.38	0.43	26.42	0.43	17.01	0.71	20.00	0.65
TDANN std	4.61	0.08	3.20	0.15	8.21	0.12	6.27	0.12	2.13	0.08

Figure 3.

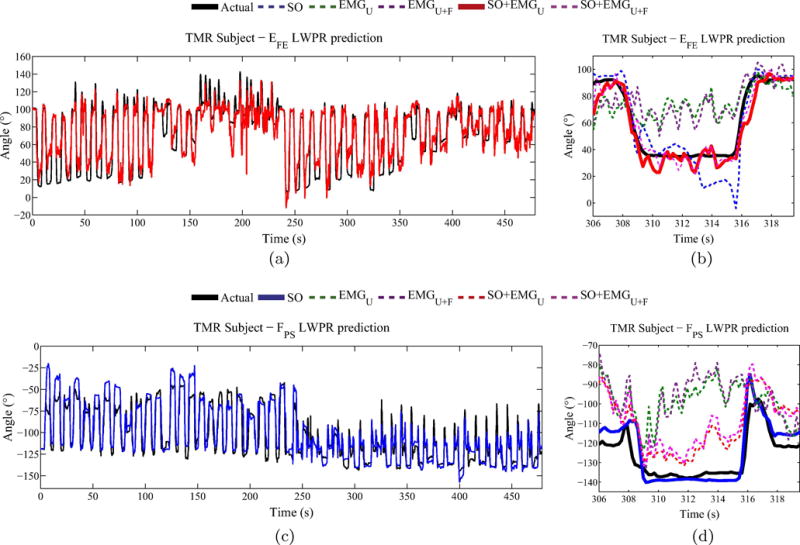
TMR subject joint angle prediction. Joint angle LWPR estimation for a TMR subject for (a) E_FE, with a single reach shown in (b), and (c) F_PS, with a single reach shown in (d). The best performing input is plotted with a solid line (shoulder orientation combined with upper arm EMG for E_FE and shoulder orientation for F_PS).

ANOVAs were used to statistically evaluate the performance of each set of input features. For control subjects, a total of four three-way ANOVAs with repeated measures were performed, comparing RMSE and R² values for both estimated joint angles. Within-subject factors were input feature set (SO, EMG_U, EMG_U+F, SO+EMG_U, SO+EMG_U+F), estimator (LWPR, TDANN), and laterality (unilateral, bilateral). For TMR subjects, a total of four two-way ANOVAs with repeated measures were performed, again comparing RMSE and R² values for both estimated joint angles. The same within-subject factors as with the control subjects were analyzed, except for laterality due to amputation. Greenhouse-Geisser corrections were applied as necessary and the significance level was 0.05. Post-hoc analysis was performed using paired t-tests with Bonferroni corrections.

3.1. Control: Elbow Flexion/Extension

For E_FE in control subjects, we a found significant main effect of input feature set for both RMSE (F(4, 28) = 7.48, p ≪ 0.001) and R² (F (4, 28) = 6.28, p = 0.001). When comparing input feature sets, pairwise t-tests with a Bonferroni correction applied to the confidence intervals showed that SO+EMG_U performed significantly better than SO (p < 0.05) in RMSE and R², and performed better than EMG_U (p < 0.05) in RMSE. SO+EMG_U+F performed better than EMG_U (p < 0.05) in RMSE and R². A significant main effect of the estimator was also found, with LWPR outperforming the TDANN in both RMSE (F(1, 7) = 62.44, p ≪ 0.001) and R² (F(1, 7) = 85.75, p ≪ 0.001).

In addition, there was a significant interaction between the estimator and the input feature set (F(4, 28) = 2.98, p < 0.05) for both RMSE and R². As the number of input features increased, LWPR increasingly outperformed the TDANN. Finally, there was also a significant interaction between laterality, estimator, and input feature set (F(4, 28) = 3.32, p < 0.05) for R². For a given estimator and input feature set, unilateral reaches performed better than bilateral reaches.

3.2. Control: Forearm Pronation/Supination

For F_PS in control subjects, there was a significant main effect of the input feature set for both RMSE (F(1.52, 10.63) = 6.94, p < 0.05) and R² (F(1.52, 10.64) = 7.57, p < 0.05). Pairwise tests showed that SO+EMG_U+F performed significantly better than EMG_U in both RMSE and R² (p < 0.005) and EMG_U+F in R² (p = 0.05). SO+EMG_U performed significantly better than EMG_U (p < 0.05) in both RMSE and R², and EMG_U+F performed significantly better than EMG_U (p = 0.01) in R². As before, there was a significant main effect of the estimator in RMSE (F(1, 7) = 50.51, p ≪0.001) and R² (F(1, 7) = 131.55, p ≪ 0.001) and a significant interaction between the estimator and input feature set in RMSE (F(4, 28) = 4.82, p < 0.005) and R² (F(4, 28) = 4.52, p < 0.01). Again, LWPR outperformed the TDANN, especially as the number of input features increased. While unilateral reaches typically gave better performance than the bilateral reaches, statistical significance was not achieved.

3.3. TMR Results

For E_FE in TMR subjects, there was a significant main effect of the input feature set for both RMSE (F(4, 8) = 4.44, p < 0.05) and R² (F(4, 8) = 17.49, p = 0.001). Pairwise tests showed that SO+EMG_U performed significantly better than EMG_U+F (p < 0.05) and SO+EMG_U+F performed significantly better than EMG_U (p < 0.05), with respect to R². A significant main effect for the estimator was found (F(1, 2) = 19.51, p < 0.05), with LWPR outperforming the TDANN in RMSE. No significant interaction was found between input feature set and estimator.

For F_PS in TMR subjects, there was also a significant main effect of the input feature set for both RMSE (F (4, 8) = 57.10, p ≪ 0.001) and R² (F (4, 8) = 36.13, p ≪ 0.001). SO alone performed significantly better than EMG_U (p < 0.05) for RMSE, and SO+EMG_U+F performed significantly better than EMG_U (p < 0.005) for RMSE and EMG_U+F for R² (p < 0.05). While LWPR outperformed the TDANN in most cases, there was no significant main effect of the estimator or interaction between the estimator and the input feature set.

4. Discussion

4.1. Recommendations for Control of Elbow Flexion/Extension

In designing controllers that predict elbow flexion/extension for people with transhumeral amputations, we make the following recommendations for choosing inputs:

• Use a combination of shoulder orientation and upper arm EMG for the best performance.

  The results in control subjects (Results – Control: Elbow Flexion/Extension section, Tables 2a & 3a) and the TMR subjects (Results – TMR Results section, Table 4a) point to this set of inputs producing the lowest RMSE and highest R² values. These results also provide evidence to support a previous result suggested in [10]. The addition of forearm EMG did not provide any statistically significant difference in performance—in fact, performance slightly decreased in most cases.

• If only shoulder angle or upper arm EMG can be chosen, choosing either one will give similar results.

  The results in control subjects (Results – Control: Elbow Flexion/Extension section, Tables 2a & 3a) and the TMR subjects (Results – TMR Results section, Table 4a) show the similarity in RMSE and R² values between these inputs and there was no statistically significant difference.

The addition of forearm EMG did not aid significantly in improving estimation, most likely because the EMG signals acquired from the forearm region are largely irrelevant in the E_FE movement. While brachioradialis, a known elbow flexor, may have shown up in the EMG, its contribution was likely greatly overshadowed by the biceps brachii EMG signals. Furthermore, the brachioradialis muscle was not specifically targeted for EMG recording, since forearm electrodes were arranged to mimic TMR sites, and not target specific muscles. As a result, the addition of forearm EMG channels may have reduced the accuracy of the estimators by not allowing them to achieve more optimal weights for more relevant input features. An advantage of omitting forearm EMG as an input is that the recommended input set of shoulder orientation and upper-arm EMG can be chosen for most people with transhumeral amputations, even if they lack targeted reinnervation.

4.2. Recommendations for Control of Forearm Pronation/Supination

In designing controllers that predict forearm pronation/supination for people with transhumeral amputations, we conclude the following for choosing inputs:

• We cannot make a clear recommendation due to conflicting results between control subjects and TMR subjects. However, the results in TMR subjects point to using shoulder orientation for best performance.

  In TMR subjects (Results – TMR Results section, Table 4b), shoulder orientation produces the lowest RMSE and highest R² values. In contrast, the results in control subjects (Results -Control: Forearm Pronation/Supination, Tables 2b & 3b) point to shoulder orientation in combination with upper arm EMG and forearm EMG producing the best performance. Consequently, the results in control subjects do not corroborate the findings for TMR subjects and merit further study, discussed below.

For the control subjects, placing extra EMG channels around the forearm helped to improve estimator performance. We expect to see this improvement since the muscles that control F_PS are located where the forearm electrodes were placed. Even in the absence of forearm EMG, however, the combination of shoulder orientation and upper arm EMG performed significantly better than each of those inputs individually. In both unilateral and bilateral reaches, SO+EMG_U was able to achieve R² values greater than 0.7, indicating a strong fit. Based on these results, we would have recommended that all available inputs (EMG and shoulder orientation) be used when designing controllers that predict pronation/supination for people with transhumeral amputations both with and without reinnervation.

However, for all three TMR subjects, both estimators performed best in predicting F_PS when using only shoulder orientation as the input. In fact, in all three subjects, the addition of EMG to shoulder orientation decreased performance, as can be seen in Fig. 3d. There are three potential reasons why these results may conflict with those of control subjects. First, since the anatomy of the subjects’ TMR sites are very different from an unimpaired forearm, it is likely that EMG from reinnervated nerves that would correspond to controlling F_PS may not be as strong as that from forearm muscles. Second, EMG signals corresponding to F_PS over TMR sites may not be as clear when performing simultaneous movements with other degrees-of-freedom when compared to sequential, single degree-of-freedom movements [22]. Third, since the subjects have been trained to control their prostheses by using sequential, single degree-of-freedom movements, they may have lost the ability to coordinate F_PS movements with other joints. This loss of coordination would affect the quality of the EMG signals from reinnervated sites when performing simultaneous multiple degree-of-freedom movements. Extensive training with simultaneous movements prior to performing the experiments may help mitigate these differences from control subjects, which would improve the subject’s musculature and coordination when performing these reaches, thereby improving the EMG signal quality.

The conflicting results emphasize the need to perform studies that include subjects both with and without amputation, given their differences in anatomy and limb control strategies.

4.3. Methodological Differences from Prior Studies

There were two key differences between our study and those of Pulliam et al. [6] and Kaliki et al. [9]. The first difference involves the use of mirrored bilateral reaches in addition to unilateral reaches. The second difference was the use of LWPR in addition to the TDANN for methods of prediction. Both of these differences were important in determining the recommendations given in Sections 4.1 and 4.2.

In order to find the best performing set of inputs among EMG and shoulder orientation for prediction, multiple methods of prediction should be tested. The studies of Pulliam et al. [6] and Kaliki et al. [9] predicted distal arm joint angles only using a neural network. However, to find the best performing set of inputs, we included LWPR for prediction. In our study, not only did LWPR generally outperform the TDANN in prediction of the joint angles, but the statistically significant differences between input sets we reported were only apparent in LWPR. Across all of the experiments, 15 of the 18 sets of inputs that achieved R² values greater than 0.7 occurred when using LWPR as the predictor. As a result, had we only used the TDANN for prediction, we would have drawn incorrect conclusions with respect to the best performing inputs.

In order to evaluate the performance of predictors on subjects with an amputation, mirrored bilateral reaches must be used. The studies of Pulliam et al. [6] and Kaliki et al. [9] predicted distal arm joint angles using only unilateral reaches on unimpaired subjects—sensors used in prediction were placed on the same arm as the predicted joint angles. However, due to amputation, mirrored bilateral reaches are necessary for training a person with an amputation, measuring distal arm joint angles on the unimpaired arm. Consequently, our study also looked at the performance of mirrored bilateral reaches in control subjects. While the estimation for unilateral reaches statistically significantly outperformed those of the mirrored bilateral reaches, the estimators still performed strongly in the bilateral case, since the best results in the mirrored bilateral experiments with control subjects still achieved R² values greater than 0.7. In addition, for the TMR subjects, who also performed bilateral mirrored reaches, the best LWPR estimation performs better than all the average RMSE and R² values with the control subjects.

4.4. Expectations for Closed-Loop Control

The relationship between offline performance metrics and online, real-time performance for myoelectric control systems is an emerging area of research and there are currently conflicting results in the literature. Jiang et al. [12] showed that differences in offline performance, measured through R², do not correlate—or at best correlate only weakly—to changes in online performance [12]. However, a study by Ameri et al. [4] showed consistent differences in performance in both offline joint angle estimates evaluated using R² and online performance metrics when comparing two types of multiple degree-of-freedom prosthetic control paradigms. Given the nebulous relationship between offline and online performance, it is possible that R² may not necessarily be the best predictor of online performance. Consequently, our results warrant further study and validation with online performance.

One way to implement a controller based on the techniques used in this paper is as follows. First, sufficient simultaneous kinematic and EMG training data would need to be collected with the patient, which can be done similarly to our training process. An inertial measurement unit mounted in the socket could replace the motion capture system to retrieve joint angles. A movement onset classifier (for example, using Linear Discriminant Analysis on the kinematic and EMG measurements) could be used to detect the onset of a movement. Upon classification of movement, an independent joint controller would move the prosthesis to the correct position and orientation based on the measured joint angles and EMG. The movement onset classifier would also help to smooth out noisy predictions during periods of no movement produced by our estimator, which can be seen in Figs. 3a–3b.

5. Conclusions

In this paper we have shown that by combining the inputs of shoulder orientation and EMG we can achieve better results in predicting the angle of elbow flexion/extension and forearm pronation/supination in reaching movements. We showed that when estimating elbow flexion/extension, the best results will be achieved when combining shoulder orientation with upper arm EMG. This result was further validated in three subjects with transhumeral amputations and targeted muscle reinnervation. In control subjects we showed that a combination of shoulder orientation, upper arm EMG, and forearm EMG representing reinnervation sites performs the best in estimating forearm pronation/supination. These results did not match the best performing input set for the reinnervated subjects (shoulder orientation). We suspect this mismatch is due to differences in musculature and the need for more training with simultaneous movements, though further study is necessary.

Anonymized raw data files containing EMG and motion capture data during arm movements from subjects, as well as the code to analyze the data, can be found at http://bretl.csl.illinois.edu/prosthetics

Table 1.

List of notation.

Abbreviation	Meaning
EMG	Electromyography
TMR	Targeted Motor Reinnervation
EFE	Elbow Flexion/Extension
FPS	Forearm Pronation/Supination
TDANN	Time-Delayed Adaptive Neural Network
LWPR	Locally-Weighted Projection Regression
RMSE	Root Mean Square Error
R2	Coefficient of Determination
SO	Shoulder Orientation
EMGU	Upper Arm EMG
EMGU+F	Upper Arm EMG + Forearm/Reinnervated EMG
SO+EMGU	Shoulder Orientation + Upper Arm EMG
SO+EMGU+F	Shoulder Orientation + Upper Arm EMG + Forearm/Reinnervated EMG