Frequency-Swept Integrated Solid Effect

Abstract

The efficiency of continuous wave dynamic nuclear polarization (DNP) experiments decreases at the high magnetic fields used in contemporary high-resolution NMR applications. To recover the expected signal enhancements from DNP, we explored time domain experiments such as NOVEL which matches the electron Rabi and nuclear Larmor frequencies to mediate polarization transfer. However, satisfying this matching condition at high frequencies is technically demanding. As an alternative we report here frequency-swept integrated solid effect (FS-ISE) experiments that utilize low power sweeps of the exciting microwave frequencies to constructively integrate the negative and positive polarizations of the solid effect, thereby producing a polarization efficiency comparable to (±10% difference) NOVEL. Finally, the microwave frequency modulation results in field profiles that exhibit new features that resemble a “stretched” solid effect.

Introduction

The history of the development of both nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR) techniques provides clear examples of the evolution from continuous wave (CW) to pulsed methods that enable researchers to achieve a variety of new experimental goals. For instance, Fourier transform methods revolutionized the sensitivity of NMR and multidimensional experiments dramatically increased the resolution. Similarly, pulsed EPR methods have enabled a variety of new structural studies and dramatically increased resolution allowing observation of new couplings and multiple paramagnetic species. As a hybrid of the two techniques, it would not be surprising if DNP evolved along a similar path. Specifically, after more than half a century since its birth¹ and following two decades of development of high frequency DNP instrumentation for CW experiments^2–8, DNP is transitioning from CW to pulsed techniques. The initial efforts to develop time domain DNP resulted in a handful of experiments^9–14 demonstrating time domain polarization transfer methods and applications preparing polarized targets for neutron diffraction experiments. In the case of the former, at low field (0.35 T) and room temperature^15,16, polarization was transferred from the photo-excited triplet state of pentacene to the protons of the host crystal of naphthalene. Since the lifetime of the triplet state is short, the time domain DNP mechanisms were preferred over CW DNP.

The motivation for developing pulsed DNP in NMR applications is somewhat different. In this case, the polarization enhancements available from CW DNP mechanisms (the solid effect and cross effect) scale at least as ${\omega }_0^{-1}$, and therefore decrease dramatically in high field experiments^17–23. This decrease motivates the quest for DNP mechanisms that are independent of B₀, and pulsed DNP is an untapped resource with high potential. However, time domain experiments using high frequency microwaves are technically challenging due to the limited availability of high power, pulse microwave amplifiers and microwave switches operating in the 150–600 GHz regime. Nevertheless, recent advances in this area^24,25 stimulated us to initiate investigations of different pulse schemes for DNP. In particular, we have demonstrated that high DNP efficiencies are possible using the NOVEL pulse sequence, which is a lab frame-rotating frame analogy of cross polarization²⁶. Furthermore, we showed that by adiabatically ramping the amplitude of the microwave locking pulse (ramped-NOVEL)²⁷ it is possible to improve the efficiency of constant amplitude NOVEL by a factor of 1.6.

Here, we present a study of pulsed DNP that utilizes the frequency swept integrated solid effect (FS-ISE), which is closely related to NOVEL. Originally, the ISE was performed by sweeping the Zeeman field B₀, with both the amplitude and frequency of the microwaves held constant¹⁰. For triplet-DNP, the ISE performs optimally at the NOVEL condition since it facilitates fast polarization transfers²⁸. However, since our goal is to use this pulse sequence to enhance signal intensities in high-resolution magic angle spinning (MAS) NMR experiments, which require time stable, homogeneous B₀ fields, it is technically clear that sweeping the B₀ field is not an option. Results reported here demonstrate that the ISE can be implemented efficiently by sweeping the microwave frequency rather than the B₀, an approach that takes advantage of the state-of-the-art fast arbitrary waveform generator (AWG) to modulate the frequency of the microwave pulses. We found that for free radical polarizing agents, the FS-ISE yields enhancements comparable to NOVEL. Furthermore, for radicals, FS-ISE can be performed with Rabi frequencies that are an order of magnitude lower than for the NOVEL condition. In this case, the polarization transfer is slower, but achieves a similar efficiency because the lifetime of the radical is not an issue as in triplet-DNP. Thus, the FS-ISE can be performed with the microwave field strengths used in current MAS DNP spectrometers and therefore could be much more widely applicable than NOVEL or its ramped version.

Results and Discussion

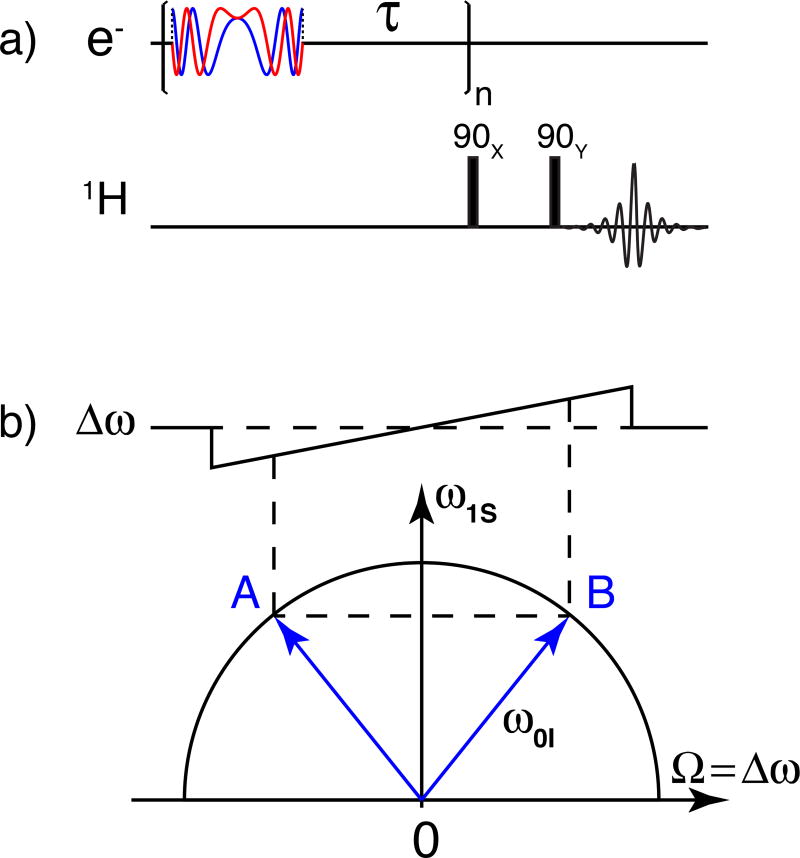
The pulse sequence for the frequency-swept ISE is illustrated in Figure 1a. The waveforms (real and imaginary parts) of the chirp pulses were calculated based on the following equation.

$$s(t)=\text{exp}\{i\underset{0}{\overset{t}{\int }}\mathit{\text{dt}}\text{'}[(\frac{t\text{'}}{{\tau }_p}-\frac{1}{2})\mathrm{\Delta }\omega \left]\right\}$$

where τ_p is the pulse length and Δω/2π is the width of the frequency sweep. The frequency modulation is performed with single sideband mixing of the carrier frequency with the desired waveform from the AWG. This scheme is achieved by essentially operating a quadrature phase detector backwards, taking the real and imaginary channels as the input instead of output. FS-ISE involves three events including the inversion of electron spin at the center of the sweep (point O) sandwiched by double quantum (DQ) and zero quantum (ZQ) transitions at points A and B, respectively (Fig. 1b)²⁸. Note that the enhancements at A and B would cancel if it were not for the fact that the electron spin is inverted at O. The fact that those enhancements interfere constructively gives rise to the name “integrated solid effect” to distinguish it from the unresolved solid effect in which the DQ and ZQ enhancements partially overlap and cancel.

Figure 1.

(a) Pulse sequence for the frequency-swept integrated solid effect. ¹H signals are detected with a solid echo. (b) During the sweep, the spin system undergoes three adiabatic events including DQ and ZQ at A and B, respectively, as well as electron spin inversion at O. The semicircle represents the relationship ${\omega }_{0I}^2={\mathrm{\Omega }}^2+{\omega }_{1S}^2$, which is satisfied at A and B where Ω is the microwave frequency offset. The inversion leads to the constructive addition of DNP enhancement at A and B, thus the name integrated solid effect.

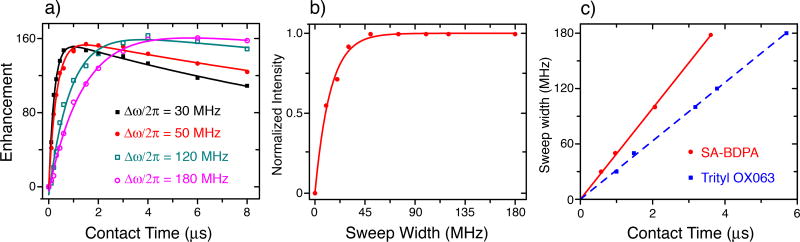
Figure 2 shows the DNP enhancements as a function of the sweep width Δω / 2π and the length of the contact time τ_p. The Zeeman field value, B_0, was set on resonance with the EPR line and the microwave field strength was adjusted to match the NOVEL condition ω_1S / 2π = ω_0I / 2π∪15 MHz. At each Δω/2π ranging from 5 MHz to 180 MHz, we obtained an optimum contact time (Figure 2a). The optimum enhancement with respect to the sweep width is given in Figure 2b, suggesting that a sweep width of 50 MHz is sufficient. Furthermore, we extracted the optimum sweep rate from Figure 2a and compared the results from two different radicals including trityl-OX063 and sulfonated-BDPA (SA-BDPA)²⁹ (Figure 2c). We found that SA-BDPA was capable of a faster sweep rate when compared to trityl-OX063 (50 MHz/µs vs. 32 MHz/µs).

Figure 2.

(a) DNP enhancement as a function of the contact time and the sweep width on a sample of 40 mM trityl-OX063 in glycerol-d₈/D₂O/H₂O (60/30/10 volume ratio) at 80 K and ~0.35 T with microwave irradiation being on resonant. The microwave Rabi frequency was set to match the NOVEL condition corresponding to ω_1S / 2π = 15 MHz. At each sweep width, there exists an optimum contact time. The corresponding maximum enhancement is normalized and plotted in (b) suggesting that a sweep width of ~50 MHz is sufficient. Similar results were obtained for sulfonated-BDPA (SA-BDPA)²⁹ (Fig. 4). The correlation between the sweep width and the optimum contact time in (c) indicates a faster optimum sweep rate for SA-BDPA (50 MHz/µs) compared to trityl-OX063 (32 MHz/µs) due to stronger coupling in SA-BDPA.

The optimum sweep rate found in FS-ISE is governed by the adiabatic nature of the pulse sequence when operating at the NOVEL condition²⁸. All three aforementioned events at A, B, and O are adiabatic processes resulting from the interplay between the sweep rate and the e⁻-¹H pseudo secular hyperfine coupling (for A and B) or between that rate and the microwave field strength (for O). In general, the stronger hyperfine coupling and microwave field strength enable a faster sweep rate²⁸. This explains the more rapid sweep rate in SA-BDPA compared to trityl-OX063. In SA-BDPA, the free electron has strong proton hyperfine couplings of up to 5.3 MHz^29–32, whereas in trityl-OX063 the coupling is mainly from the electron to the protons of the solvent, which is less than 1 MHz^33,34.

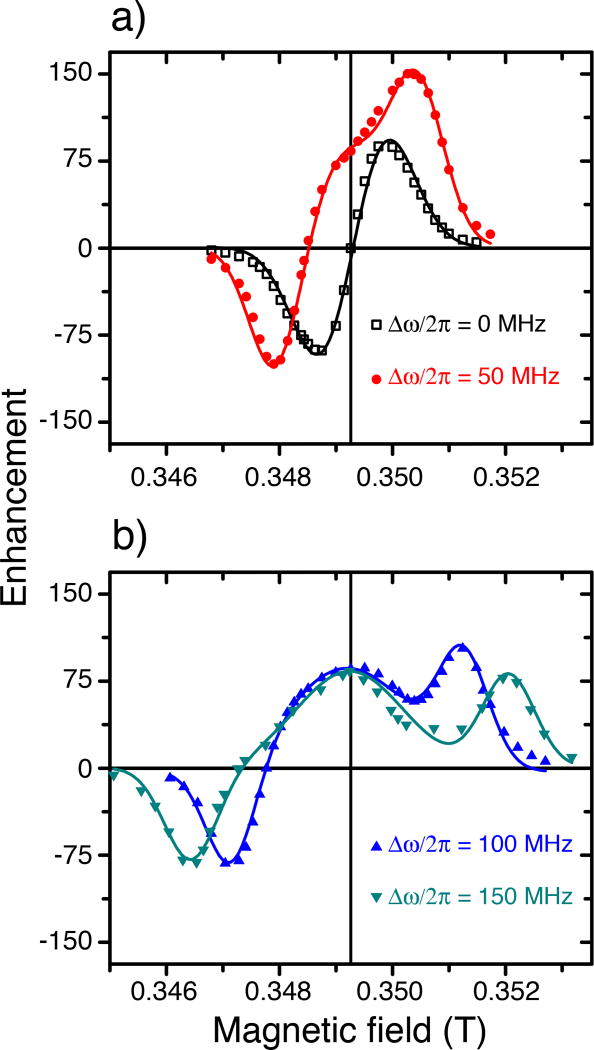
The DNP Zeeman field profiles of the ISE sequence are shown in Figure 3, where again the sequence is operating at the NOVEL condition. The contact time of 3 µs was used throughout, as it was near optimal regardless of Δω / 2π (Figure 2a). The magnetic field B₀ was incremented and the RF tuning/matching was adjusted at each of the data points. At Δω / 2π = 0 (constant frequency) the DNP field profile resembles that of unresolved solid effect with no enhancement at the center. This is partially due to line broadening of the EPR spectrum by the strong hyperfine coupling in SA-BDPA as well as the e⁻-e⁻ interaction at high concentration. However, the primary reason is that at the NOVEL condition the microwave field can no longer be treated as a small perturbation as in the CW solid effect. Thus, even a sample with a low concentration of trityl-OX063 (5 mM) with a very narrow EPR linewidth exhibits an unresolved solid effect field profile at Δω / 2π = 0 and ω_1S / 2π = ω_0I / 2π (data not shown).

Figure 3.

(a) DNP field profiles obtained with constant microwave frequency (black) and with microwave chirp pulses of different sweep width including 50 MHz (red), and (b) 100 MHz (blue) and 150 MHz (green). With the microwave frequency kept constant, the DNP Zeeman field profile is characteristic of unresolved solid effect or differential solid effect without an enhancement at the center (black). The enhancement at this position is non-zero when chirp pulses were used which is indicative of FS-ISE. Furthermore, the normal solid effect peaks were displaced linearly with increasing the sweep width. The data were obtained at 80 K on a sample of 40 mM SA-BDPA in glycerol-d₈/D₂O/H₂O (60/30/10 volume ratio).

At Δω / 2π > 0, the enhancement at the center (on resonance with the EPR line) becomes nonzero which is characteristic of the FS-ISE sequence. The efficiency of the ISE then decreases going away from the center of the EPR line. In fact, the FS-ISE field profile is expected to follow the EPR lineshape¹⁰. In addition, we observed positive and negative peak enhancements, which resemble those expected from the SE but these are displaced from the position of the original solid effect peaks. The displacement is found to be half of Δω / 2π, similar to the observation by Hovav et al. in frequency-modulated CW DNP³⁵. Therefore, the full field profile of the frequency-swept ISE is a convolution of the intrinsic FS-ISE and the “displaced” or “stretched” SE field profiles. This is a new feature of the FS-ISE that was not observed experimentally in earlier papers.^10,16,28,35

It is worth noting that the “stretched” SE shows not only resemblances but also differences in comparison to the previous study on frequency-modulated CW DNP. The underlying reason is that both our study and the work by Hovav et al.³⁵ utilized frequency modulation but with fundamentally different focuses (ISE vs. SE) and experimental settings (strong power pulse vs. low power CW). In particular, Hovav et al. showed that, under the optimal condition, frequency modulation improved the DNP enhancement by a factor of 2–3. This required modulation amplitudes smaller than the ¹H Larmor frequency and repetition rates faster than the spin-lattice relaxation rate of electron (1/T_1e). In comparison, we also found that the “stretched” SE can be very efficient (Fig. 3a). However, FS-ISE requires sweeping through both DQ and ZQ transitions, thus necessitating modulation amplitudes larger than twice the ¹H Larmor frequency. Furthermore, when operating at the NOVEL condition, FS-ISE leads to a fast polarization transfer, thus the repetition rate is slower than 1/T_1e to allow electron polarization to recover upon being depleted. Nevertheless, further investigation is required to determine if the “stretched” SE remains efficient at high fields and under MAS conditions.

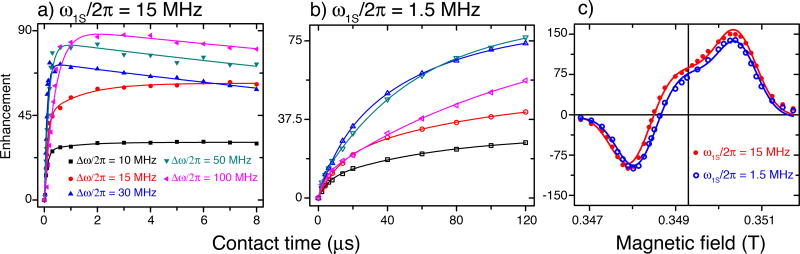
In Figure 4, we present a comparison of the FS-ISE with ω_1S ≪ ω_0I that demonstrates the feasibility of using this pulse sequence far below the NOVEL condition. In particular, we set ω_1S / 2π =1.5 MHz instead of 15 MHz which corresponds to ~1% of the microwave power. Figure 4a and 4b show that FS-ISE operates differently under the two conditions. In comparison, the pulse length in Figure 4b is about 2 orders of magnitude longer. Nevertheless, the DNP field profiles are very similar (Fig. 4c) and the enhancements at the center and at the stretched solid effect are almost identical. Note that the adiabaticity of the inversion of electron spin is proportional to ${\omega }_{1S}^2/{\dot{\omega }}_{\mu w}$ or P_μw/ω̇_μw, in which P_μw and ω̇_μw is the microwave power and sweep rate, respectively²⁸. Thus, at 1% power, the sweep rate needs to be 100 times slower or the pulse length needs to be 100 times longer.

Figure 4.

Comparison of ISE at the NOVEL condition and far below the NOVEL condition. DNP enhancements were measured at different contact times and sweep widths at microwave field strength of 15 MHz (a) and 1.5 MHz (b) in the SA-BDPA sample at 80 K. In (a) the behavior is similar to what is observed with trityl-OX063 (Fig. 2a), whereas, the enhancement in (b) monotonically increases. The pulse length was limited to 120 µs due to the memory of the AWG. In (c) are the DNP field profiles obtained with 15 MHz (red, solid circle) and 1.5 MHz (blue, open circle). The contact time was 2 µs and 120 µs, respectively. In both cases, the sweep width was 50 MHz as suggested by the data in (a) and (b). The two field profiles are similar.

In contemporary MAS DNP spectrometers, even though the microwave power available is ~10 W, the field strength is ≤1 MHz due to the absence of a microwave resonant structure^36,37. Thus, ω_1S is 2–3 orders of magnitude below the NOVEL condition. In order to satisfy the NOVEL matching condition, one would need to not only increase the microwave power, but also and more importantly to increase the Q factor by using a microwave cavity. Roughly speaking, a combination of 10²–10³ W of power and a Q factor of ~10²–10³ is needed to match the NOVEL condition at high field (> 5 T), making NOVEL a technically demanding sequence. Furthermore, the high Q factor would significantly restrict the filling factor, reducing the absolute sensitivity of the experiment. The fact that ISE can operate far below the NOVEL condition alleviates the field strength requirement as well as the restriction in the filling factor.

Note that even though our data show a highly efficient FS-ISE at ω_1S / 2π =1.5 MHz, it does not mean that the sequence can be straightforwardly applied to contemporary DNP/NMR spectrometers operating in the range of 400–800 MHz. The reason is that the transition moment of the ZQ and DQ scales with $B_0^{-1}$. In going to high fields one would need to maintain the ratio ω_1S / ω_0I which equals to 10% in our case. Such a ratio would still translate into strong microwave fields (tens of MHz). Moreover, the sweep width scales roughly with B₀ and thus so does the optimum pulse length. The pulse length might get very long even for slow relaxing radicals such as SA-BDPA. Thus, it is very likely that for FS-ISE to work at high fields ω_1S / 2π will need to account for a significant fraction of ω_0I / 2π. Nevertheless, the flexibility to operate below the NOVEL condition makes FS-ISE a very promising approach for high field pulsed DNP.

In comparison, we found that ISE and NOVEL give similar enhancements (±10% difference). This was not the case for triplet-DNP where ISE showed superior performance. This is probably because of the broad EPR line of the triplet state. The ISE makes use of all the spin packets by sweeping either the B₀ or microwave frequency, whereas the efficiency of NOVEL might be compromised if the excitation bandwidth is small compared to the EPR linewidth. Furthermore, NOVEL requires homogenous field strength for optimum efficiency whereas ISE appears to be more robust.

Conclusions

In summary, we have presented experimental data that indicates that FS-ISE is a new strategy for time domain DNP. In contrast to the original implementation of the ISE that employs sweeps of B₀, our strategy is suitable for high-resolution NMR applications. The frequency modulation is conveniently achieved with high precision by using an arbitrary waveform generator. FS-ISE can be performed under various microwave power settings. When operated at the NOVEL matching condition, ISE exhibits fast polarization transfer. At lower microwave field strength similar to that being used in MAS DNP spectrometers, the buildup time for the polarization is increased when utilizing ISE, but it achieves the same efficiency. Our findings expand the repertoire of pulse sequences for DNP and emphasize the advantages of using an AWG to manipulate microwave pulses.

Experimental Section

Samples used in our study include glycerol-d₈/D₂O/H₂O (60/30/10 volume ratio) glassy matrix doped with 40 mM of SA-BDPA or 40 mM of trityl-OX063. Experiments were performed at 80 K on a X-band EPR spectrometer equipped with a MD-4 ENDOR resonator as described previously.²⁷ We emphasize on the use of an arbitrary waveform generator (AWG) to modulate the microwave frequency. The AWG functionality is available from Bruker BioSpin as an upgrade to the existing spectrometer. The waveform of the chirp pulses with linear frequency sweep comes as part of a standard library included in the Xepr software, making it convenient to program the ISE sequence. The program takes the center frequency, the sweep width and the pulse length as inputs, which can be varied independently.

The chirp pulse was applied repeatedly with suitable repetition rate for the nuclear polarization to build up. The recovery delay τ (Fig. 1a), essentially the inverse of the repetition rate, was 8 ms and 2 ms for a sample containing SA-BDPA and trityl-OX063, respectively. The ¹H NMR signals were read out by a solid echo sequence using a Spincore NMR spectrometer. The data processing was done with Matlab. The enhancement is calculated from NMR signals obtained with and without microwave irradiation. The DNP-enhanced signals were measured at 3 T_B whereas the off signals were measured at 3 T₁ to ensure the enhancement is not biased due to the fact that T₁ is much longer than T_B.