A Combined PLS and Negative Binomial Regression Model for Inferring Association Networks from Next-generation Sequencing Count Data

Abstract

A major challenge of genomics data is to detect interactions displaying functional associations from large-scale observations. In this study, a new cPLS-algorithm combining partial least squares approach with negative binomial regression is suggested to reconstruct a genomic association network for high-dimensional next-generation sequencing count data. The suggested approach is applicable to the raw counts data, without requiring any further pre-processing steps. In the settings investigated, the cPLS-algorithm outperformed the two widely used comparative methods, graphical lasso and weighted correlation network analysis. In addition, cPLS is able to estimate the full network for thousands of genes without major computational load. Finally, we demonstrate that cPLS is capable of finding biologically meaningful associations by analysing an example data set from a previously published study to examine the molecular anatomy of the craniofacial development.

I. Introduction

A major challenge of genomics and other high-throughput omics-data is to detect interactions from large-scale observations. By identifying co-varying components and significant relationships, it is possible to display conditional dependencies among the considered particles and discover the underlying network structure representing functional associations. The networks can be used, for example, to discriminate between different biological phenotypes or manipulate the process for therapeutic goals. Computational approaches, such as the ones presented and compared in this work [1], [2] provide a screening tool to discover associations between genes, proteins and metabolic components through high-throughput data on a large scale.

At the core of the network reconstruction lies a connectivity score that represents the strength of association or interaction between two components. The connectivity score can be defined in various ways, ranging from a simple Pearson correlation coefficient to a model based approach, where higher order and non-linear relationships can also be explored. The use and the interpretation of the correlation networks for continuous omics -data has been well investigated before [3]–[6]. However, expressions of thousands of genes, for example, are often measured from relatively few samples. In small sample sizes, the sample correlation coefficient is a fairly unstable and inaccurate estimate of the true correlation [7].

More sophisticated methods and algorithms have been developed and used for inferring latent network structures especially from microarray gene expression data. One group of such methods uses sparsity to select the edges (associations) between the nodes (components) of the network [2], [8]–[10]. Bayesian Network Inference with Java Objects (BANJO) [11], Algorithm for the Reconstruction of Accurate Cellular Networks (ARACNe) [12], weighted correlation network analysis (WGCNA) [1], [13] and a partial least squares (PLS) regression approach [14], [15] have also been applied to genomic network construction.

In recent years, next-generation sequencing (NGS) technologies have revolutionised the accessibility of the genome and transcriptome data at a base pair level [16], [17]. Compared to traditional microarrays, NGS delivers gene expression profiling data much cheaper and faster [18]. Gene expression is characterised by measuring the mRNA levels present in cells of interest. This information can then be used to determine how the transcription process is affected, for example, in the presence of certain drug treatment or whether there are differences between healthy and diseased states. The advancements of NGS enable researchers, for example, to characterise mutations in the entire cancer genome, gain a deeper understanding of cancer biology, and thus improve diagnosis and potentially design personalised therapies [19]. Importantly, the type of data NGS produces differs from the first generation sequencing technologies. Instead of replicating DNA with the polymerase chain reaction and then producing long reads of nucleic acid sequences, NGS provides a large amount (millions) of shorter reads. These short reads are then aligned to reference sequences to determine their origin in the reference genome. The data consists of positive integers: how many short reads were aligned to each gene (site) in the reference genome. Larger counts represent more active genes, that is, genes passing their information to be used in the synthesis of functional gene products, often proteins.

Whereas the log ratio expression values from microarray data are typically assumed to be normally distributed, the same assumptions can not be made for NGS count data. Thus, new approaches for analysing NGS data are needed. Existing methods for identifying co-expression gene networks from RNA-sequencing data rely mostly on the sample correlation matrix [20], [21]. Besides correlation, Allen and Liu present a log-linear graphical model for inferring genetic networks from high-throughput sequencing data [22] assuming that the data consists of conditionally independent Poisson random variables.

Assuming that the read counts (or more specifically, the expected number of read counts within a given region of the transcriptome from a given experiment) follow a negative binomial distribution has been shown to satisfactorily capture both biological and technical variability [23]–[25]. The choice of the negative binomial distribution can be justified by the following. The process, where one takes an RNA transcriptome and chooses a location at random to produce a read, is a Poisson process. The reads exist within some continuous space and the counts of those reads within intervals of space (such as a selected depth of the sequence) are Poisson distributed. However, the inability of Poisson distribution to model unequal mean and variance for the read counts makes it a poor model for explaining the variability between biological replicates. The dispersion parameter of the negative binomial distribution allows us to model this variation. When there is no biological variation between the replicates, the negative binomial distribution reduces to Poisson. Thus, in some NGS applications, technical variation can be treated as Poisson, on top of which the biological variation is represented by the overdispersion parameter of the negative binomial distribution.

In this paper, we propose a generalisation of the earlier works presented by [14], [15]. First, we use a PLS approach to compress the variability in the data into a small number of covariates by finding linear combinations of the original variables, and then we fit a regression model with these new covariates as predictors to estimate direct and indirect associations from the count data under different experimental settings. We assume that the NGS data follows a negative binomial distribution and thus, the estimation problem is solved in the generalised linear model framework using a negative binomial regression model. The rest of the paper is organised as follows. In Materials and Methods section, we present the methods and algorithms we use to recover the between compound associations and also give a short description of the comparison methods. We also guide the readers through the simulations studies conducted in order to asses and measure the performance of the different network construction methods. Next, we show the Results of the simulation studies and finally conclude with Discussion.

II. Materials and Methods

A. Association score based on partial least squares regression

The core of the network analysis is a connectivity score, s_jk, j = 1, ⋯, p, k = 1, ⋯, p, between the genes x_j and x_k, which represents the strength of the association or interaction between the two components. NGS data are often characterised by a large number of variables p measured from a relatively small number of samples, n. Dimension reduction methods, such as PLS, can deal with these sort of “large p, small n” -problems. PLS components are latent uncorrelated variables given by the linear combinations of the original predictors, see [26]–[28] for details. The components are computed such that they maximise the covariance between two sets of variables. These components condense information and extract the most important features of the original data and can further be used as predictors in the chosen traditional analysis methods.

PLS regression has previously been used with continuous microarray data in order to detect associations between gene expressions leading to an association network [14], [15], [29]. As proposed by Pihur, Datta, and Datta [15], the association scores are achieved by fitting p PLS regression models such that each gene at a time is predicted with the remaining p − 1 genes. In the context of the RNA-sequencing count data, we adopt a similar approach. First, we compute a selected number of PLS components v (we use three components throughout the analyses) from the count data that is centered to mean zero and scaled to variance one as usual. Second, we fit a generalised linear model where the PLS components predict the observed counts. The score measuring the association between the pair of genes x_j and x_k is finally computed as a sum of the products of the PLS and regression coefficients estimated in steps one and two, over the number of PLS components v. As the coefficients may be different depending on whether the gene is acting as an independent or dependent variable, the final score is symmetrised by taking the average of the two cases.

Here, the role of the PLS step is merely to identify meaningful covariates to be used for the construction of the association network and the subsequent negative binomial modelling step ensures that the data structure is correctly accounted. The coefficients for the PLS components are the key components in quantifying the strength of the association. A step by step description of the algorithm, referred to as count data PLS (cPLS), is given below. The algorithm is implemented in R-function that is available upon request.

B. Description of the cPLS -algorithm

• S1Let the RNA sequence data of interest consist of p genes x₁, ⋯, x_p. Set one gene x_j at a time as a response variable and rest of the genes x₁, ⋯, x_j−1, x_j+1, ⋯, x_p, as explanatory variables. Scale the explanatory variables to mean zero and unit variance.
• S2
  As proposed by [15], compute v PLS components by fitting p PLS models such that each gene at a time is predicted with the remaining p − 1 genes. The resulting orthogonal latent factors $t_j^{(\ell )}$ are linear combinations of genes x₁, ⋯, x_j−1, x_j+1, ⋯, x_p, and are sequentially constructed: for ℓ = 1, $X^{(\ell )}=X_{-j}^{(1)}$ is set as a design matrix with p − 1 columns without the gene j. Then, we can compute the PLS coefficients as

  $$c_j^{(\ell )}=\frac{X^{{(\ell )}^T}{x}_j}{{\Vert X^{{(\ell )}^T}{x}_j\Vert }_2}$$
  and form the first PLS component as

  $$t_j^{(\ell )}=\sum _{(k\ne j)}^p{c}_{jk}^{(\ell )}{X}_k^{(\ell )}.$$
  For the subsequent components with ℓ ≥ 2, X^(ℓ) is defined as a deflated matrix

  $$X^{(\ell )}=X^{(\ell -1)}-t_j^{(\ell -1)}{[t_j^{{(\ell -1)}^T}{t}_j^{(\ell -1)}]}^{-1}{t}_j^{{(\ell -1)}^T}{X}^{(\ell -1)},$$

  but the coefficients and components are computed as for the first PLS component.

• S3
  Fit a negative binomial model with

  $$logE(x_j)={(t_j^{\ell })}^T\beta +logN,$$

  where gene x_j (on the original count scale) is a response variable, $t_j^{\ell }$ are the v PLS components, N is an offset variable including the total number of mapped read counts in each sample, expected value of gene j is μ, and the variance is defined via var(x_j) = μ + μ^(2/θ), where θ is a parameter to be estimated. The total read count is included as an offset term for the following reason. If we observe that in comparison to gene j, gene k has, for example, twice as many reads aligned to it, it can mean two things: 1) gene j is expressed with twice as many reads compared to gene k, or 2) both genes are expressed with the same number of transcripts but gene j is twice as long as gene k and produces twice as many fragments (randomly fragmented small pieces of RNA), i.e., the sequencing depth of gene j is twice that of gene k. To account for the different sequencing depths, the logarithm of the total read counts (sums of read counts of all genes for each sample) is included in the model.

• S4
  For each gene pair j and k, compute the association score

  $${\widehat{s}}_{jk}=\sum _{\ell =1}^v{\widehat{\beta }}_{j\ell }{\widehat{c}}_{jk}^{(\ell )},$$

  where v is the number of the PLS components, β̂_jℓ is the regression coefficient from the negative binomial model relating to the gene j with PLS component ℓ as a dependent variable, and ${\widehat{c}}_{jk}^{(\ell )}$ is the PLS coefficient of the PLS component ℓ when gene j is a response variable and gene k one of the explanatory variables.

• S5Save the score ŝ_jk in the association score matrix S₀ and return to step 1 with gene x_j+1 as the response variable.
• S6
  When Steps 1–5 are repeated for all p genes and the upper and lower triangles of the matrix S₀ are filled, set the diagonal of S₀ to ones. Finally, symmetrize $S=0.5·(S_0+S_0^T)$. Thus, the final association score between genes j and k is an averaged form

  $${\widehat{s}}_{jk}=\frac{{\sum }_{\ell =1}^v{\widehat{\beta }}_{j\ell }{\widehat{c}}_{jk}^{(\ell )}+{\sum }_{\ell =1}^v{\widehat{\beta }}_{k\ell }{\widehat{c}}_{kj}^{(\ell )}}{2}.$$
• S7For convenience, we transform the association scores to have values between [−1, 1]. Note however, that positive scores do not necessarily imply that two genes are positively correlated and vice versa.

C. Inferring the edges of the network

After computing all the pairwise connectivity scores, we need to to determine which of these are statistically significant in order to be able to build the network. Formally, we need to test multiple hypotheses

$$\begin{array}{l}{H}_0:s_{jk}=0,H_1:s_{jk}\ne 0,\\ j=1,\cdots ,p,k=1,\dots ,p,j\ne k\end{array}$$

where s_jk are the population association scores. To assess the significance, we make use of an empirical Bayes approach and then compute local false discovery rate (FDR) as proposed by Efron [30]. Following Efron’s formulation, it is assumed that an association score ŝ_jk comes from a mixture distribution

$$f(s)=p_0{f}_0(s)+p_1{f}_1(s),$$

where p₀ and p₁ are the mixing proportions, f₀(s) is the density corresponding to the “no association present” -scores (null distribution), and f₁(s) is the density corresponding to the “association present” -scores. The ratio f₀(ŝ_jk)/f(ŝ_jk) represents an upper bound on the posterior probability of ŝ_jk coming from the distribution f₀(s) (no association between genes j and k). In practice, the mixture density f(s) can be empirically estimated by fitting a smooth density curve to the histogram of observed ŝ_jk. As for f₀(s), one can parametrically estimate the distribution by assuming normal distribution with the estimate of the expected value ave(ŝ_jk) and sample variance var(ŝ_jk). Thus, by evaluating the value of the ratio for each ŝ_jk, we get a likelihood for ŝ_jk coming from the null distribution, and by comparing it to the selected value q (the maximum false discovery rate that we are ready to accept), the network structure can be inferred. If ŝ_jk < q, an edge between genes j and k is added to the network.

For the empirical local false discovery rate to perform satisfactorily, it is assumed that the mixing proportion p₀ is close to one (majority of the scores represent no association present). Also, the distribution of the observed scores should be approximately normal, which holds true for the PLS-based scores based on the central limit theorem while the sample size is relatively large.

D. Comparison methods

We compare our cPLS algorithm with two widely used network inferring methods, weighted correlation network analysis (WGCNA) and graphical lasso (glasso).

WGCNA [1] uses a sample correlation matrix to measure the between-gene pairwise associations. However, instead of hard thresholding (selecting a single threshold correlation value, such as 0.5), the edges of the network are inferred with so called soft thresholding. The observed correlations are transformed to association scores as ŝ_jk = |cor(x_j, x_k)|^β, where β is selected according to the scale free topology criterion. In a scale free topology, few genes are highly connected to their surroundings, while most of the genes have low connectivity. Scale free topology structure and the optimal value for β can be assessed by a linear fit, see [1] for details. As β increases, smaller correlations, corresponding to “no interaction present” -cases, approach zero. Often a choice of β = 6 is large enough so that the resulting network represents approximate scale free topology [13]. This choice was also used in our simulation studies described in Section 3. Finally, the inclusion or rejection of the edges in each network requires then setting a threshold parameter, which we chose to be zero. If a pairwise weighted correlation was, rounded to two decimals, equal to zero, the edge in question was not included in the network.

Glasso is an algorithm that estimates a graph from a given data using the sparsity pattern of an inverse covariance matrix [2], [8]: if two random variables are conditionally independent (conditional on all other variables present), the corresponding element of the inverse covariance matrix is zero. Thus, the non-zero elements of a sparse inverse covariance matrix are interpreted as pairwise partial correlations, in the presence of all other variables. In general, a challenging problem in sparse estimation of the graphical models is the selection of the regularisation parameter. We make use of the highly efficient rotation information selection criterion (ric) [31] that avoids possibly time consuming cross-validations or subsamplings. After selecting the optimal value for the regularisation parameter, the edges corresponding to the nonzero elements of the estimated inverse covariance matrix, are selected in the network.

E. Normalising and transforming the data

In the extensive literature of differential expression methods for RNA-sequencing data, some sort of data pre-processing, often referred to as normalisation, is required [32], [33]. Normalising data aims at ensuring that the gene expression levels are comparable within and across samples. Different sequencing depths, represented by varying library sizes, are one of the most apparent factors causing the read counts of the samples being measured on different scales, and thus incomparable. Another issue is encountered, when a small number of genes are highly expressed only in a subset of samples. This can cause the remaining genes to be under-represented when a substantial proportion of the library size is consumed by the highly expressed genes.

In the context of NGS data, WGCNA has previously been used after normalising the data. Iancu et al. [20] combine WGCNA with total count and upper quartile normalisation [24], [33] to examine the coexpression networks structures from RNA-sequencing data. Similarly, Kogelman et al. [21] first removed the between-sample bias by removing the effect of the different total read counts [23] and then performing variance-stabilising normalisation [34]. Both normalisations result in data that can be analysed as continuous. To account for the between-sample biases when building the networks with WGCNA and glasso, we decided to apply a trimmed mean of M-values (TMM) normalisation [24]. In addition, the differing library sizes are accounted for by mapping the read counts to counts per million (CPM) scale. In cPLS, models are adjusted for differing library sizes by including an offset term, as described in cPLS algorithm on Section 2.2.

More importantly, for the analyses that employ the sample correlation matrix, normalisation does not remove the between-gene correlations introduced by the wide range of read counts. Highly expressed outliers can dominate the between-gene correlations, leading to a positive correlation, even if the genes were not associated. The cPLS-algorithm models the dispersion correctly by fitting a negative binomial model. However, for WGCNA and glasso, the data should be either transformed or instead of correlation, some more robust measure of association should be used. For glasso, we solved the issue by log(x + 1)-transforming the expression data. This transformation makes the distribution more symmetric. For WGCNA, we use an alternative approach and replace the Pearson’s correlation with Spearman’s rank correlation, which is more robust to outliers and thus suitable for right skewed distributions.

F. Generating multivariate count data

Here we describe the simulation studies performed in order to examine how well we can recover the underlying association network structures using the proposed cPLS algorithm.

When measuring the performance of the association network construction algorithms, it is necessary to have a record of the “true” underlying network structure. This can be implemented by generating data with a specific covariance structure from a multivariate distribution of choice or associating selected genes via latent variables. Methods to generate counts from a multivariate Poisson distribution exist [35], but the RNA sequencing data is better described by negative binomial distribution. Works on the multivariate negative binomial data are fewer [36]. We developed three alternative approaches utilising Gamma-Poisson mixture distribution, multinomial distribution, and NGS-simulators for generating count data resembling, as closely as possible, real life NGS data. These approaches are described below.

1) Generating count data based on the overdispersed Poisson distribution: In the first approach we construct the association network through the underlying latent variable structure

• S1From multivariate normal distribution, generate a chosen number of latent variables u for n samples. We chose to generate 10 latent variables u ~ N₁₀(0, I₁₀) for n observations.
• S2For each new gene j, sample a value N_u ~ Bin(10, 0.05) to define the number of latent variables to which the gene is connected. Then sample N_u observations, without replacement, from 1, 2, …, 10 to indicate the components of u the gene is associated with. In this setting, genes that share at least one common latent variable are considered to be connected. The more latent variables the genes share, the stronger the connection.
• S3For each sample i, generate ε_i ~ Gamma(10, 0.1), where 10 is the shape parameter and 0.1 is the scale parameter. This choice causes overdispersion by keeping the expected value of the generated counts the same, but by increasing their variation.
• S4For each new gene j, generate a length-10 vector β_j of regression coefficients such that the i^th component in β_j is 1, if u_i was sampled in step 2, and the 0, otherwise.
• S5For each new gene j, sample a realistic average read count μ_j using a source RNA sequencing data. We computed average read counts for the 20531 samples in kidney renal clear cell carcinoma RNA-sequencing data [37] and randomply selected one of those with read count larger than 10, without replacement for each gene j.
• S6
  Generate a new vector of read counts x_j such that for gene j of the sample i

  $$x_{ij}~\text{Poisson}({\epsilon }_i{\mu }_j{e}^{u^{\prime }{\beta }_j}).$$

  Here, the overdispersion parameter ε represents the between sample variation, μ_j is the average read count sampled in Step 5, and the linear predictor u′β_j constructs the between gene association.

2) Generating count data based on multinomial distribution

The second approach is based on an underlying multivariate normal distribution.

• S1
  For each sample i, generate latent expression levels u = (u₁,…, u_p), u ~ N_p(0, σ), where

  $$\mathrm{\sum }=\left(\begin{array}{llllllll}1\hfill & \rho \hfill & \rho \hfill & \cdots \hfill & \rho \hfill & 0\hfill & \cdots \hfill & 0\hfill \\ \rho \hfill & 1\hfill & \rho \hfill & \cdots \hfill & \rho \hfill & 0\hfill & \cdots \hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & \ddots \hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ \rho \hfill & \rho \hfill & \cdots \hfill & 1\hfill & \rho \hfill & 0\hfill & \cdots \hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & \cdots \hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill & \ddots \hfill & \ddots \hfill & ⋮\hfill \\ 0\hfill & 0\hfill & 0\hfill & \cdots \hfill & 0\hfill & \cdots \hfill & 0\hfill & 1\hfill \end{array}\right).$$

  Regardless of the total number of genes p, the off-diagonal elements of σ, the correlations between the m first genes are ρ. We chose a ρ = 0.9 indicating strong associations between the respective genes while the off-diagonal elements of zero indicate no association at all. Thus, the m first genes are the “important” genes whose connectivities we expect to be present at the resulting network. The mean structure of the true expression levels can be chosen to represent the design under the study, such as differential expression levels between two groups of samples.

• S2Let λ_j = exp(u_j), for each j = 1, …, p.
• S3Choose a realistic total read count C. We sampled without replacement total read counts from a kidney renal clear cell carcinoma RNA-sequencing data [37].
• S4
  For each sample i, generate a p-vector of read counts from a multinomial distribution

  $$\text{Multinomial}(C,{\lambda }_1/{\lambda }_{\text{Tot}},\cdots ,{\lambda }_p/{\lambda }_{\text{Tot}}),$$

  where ${\lambda }_{\text{Tot}}={\sum }_{j=1}^p{\lambda }_j$.

The number of important genes m was selected to be 3 for p = 100 and 10 for p = 1000, resulting in total of 9 and 45 important pairwise associations, respectively.

3) Generating count data using NGS-simulators

As the application of the NGS method has become a common approach in delivering genome information, the demand for realistic NGS-like data to test the performance of the new analysis methods has increased. One recently published solution contributing to this demand is an NGS-simulator called SimSeq [38]. SimSeq produces realistic NGS-like data without making distributional assumptions by resampling counts from a large source RNA-sequence dataset. Thus, the distributional properties of the source dataset are transferred to the matrix of the simulated read counts. NGS data is typically collected under an experimental design, where one is interested in comparing the expression levels of genes between two groups of samples exposed to different conditions. Accordingly, given a real life RNA-sequencing data with samples in two treatment groups, SimSeq generates a new set of read counts for known m differentially expressed genes and p − m equally expressed genes.

In the third simulation approach, we generate count data using SimSeq-simulator and kidney renal clear cell carcinoma data [37] with 20, 531 genes and 144 paired samples (72 unique individuals) each having a tumor and a non-tumor replicate. To avoid simulated samples consisting only of zero read counts, we filter the Kidney data and include only the genes having more than one hundred non-zero read counts. This resulted in 16, 416 genes measured from 144 samples. If larger sample size is needed, the source data set could be replicated to increase the sample size. For paired data, SimSeq requires a minimum number of 2n samples in each treatment group.

As the true correlation structure of the kidney data is not known (and evaluating the performance of different network reconstruction methods requires that it is), we impose a known correlation structure on the source data by adding sampled read counts to the observed read counts. This is based on the fact that cov(x_j + z, x_k + z) = cov(x_j, x_k) + cov(x_j, z) + cov(z, x_k) + cov(z, z), where z is random number that is sampled from the empirical distribution of all observed read counts. The algorithm creating the wanted structure is described in detail below.

• S1From the source dataset, select randomly (without replacement) m genes to be differentially expressed and p − m genes to be equally expressed.
• S2Assume that the non-differentially expressed genes are not connected. Consider the differentially expressed genes and divide them up into g different groups.
• S3Consider the first m/g differentially expressed genes of the first sample. Draw a random sample (read count) from an empirical distribution of the read counts of all genes included in the source dataset. Add this value to the observed read counts of the first group of differentially expressed genes. Finally divide the resulting sum by two in order to maintain the original magnitude of the read counts, and round the result to nearest integer. Repeat for each sample i.
• S4Consider the next set of m/g differentially expressed genes. Add random effects to these genes as described in Step 3, going through all n samples. Repeat until the read counts of all g groups of differentially expressed genes are treated. Now, within each sub group, the m/g differentially expressed genes are all connected with each other. Thus, the source dataset includes now g · 0.5 · (m/g) · (m/g −1) associations.
• S5Use SimSeq to generate a selected number of datasets of size n, see [38] for details.

G. Measures of performance

To assess the performance of the cPLS-algorithm, we computed the following quantities for each simulation case:

• Sensitivity: true positives / (true positives + false negatives), i.e., the proportion of the true “important” connectivities that the algorithm was able to recover (amongst all important connectivities)

• Specificity: true negatives / (false positives + true negatives), i.e., the proportion of the true weak “unimportant” connectivities that the algorithm was able to recover (amongst all unimportant connectivities)

• F1-score [39]: a harmonic mean of sensitivity and specificity

• True discovery rate: true positives / (true positives + false positives), i.e., proportion of the true important connectivities amongst all connectivities that the algorithm declared to be important.

• True non-discovery rate: true negatives / (true negatives + false negatives), i.e., proportion of the true unimportant connectivities amongst all connectivities that the algorithm declared to be unimportant.

The sensitivity, specificity, true discovery rate and true non-discovery rate are averaged over all simulation rounds. High (close to one) values for each of these measures indicate good performance of the network construction method in question. For the cPLS-algorithm, the measures of performance are computed for the networks constructed by setting the threshold value for the local FDR to 0.10. This means, that we included the interactions for which the FDR, the likelihood of ŝ_jk being absent, was ≤ 0.10. The total number of true associations was a) 80/12204 b) 3/45 c) 50/525 for a) overdispersed Poisson, b) multinomial and c) SimSeq models with p = 100/1000 genes, respectively.

III. Results

The results of the simulation studies for three comparative methods, are presented in Tables I and II. The sensitivities, specificities and the F1-scores averaged over 1000 simulation rounds are given in Table I while the true discovery and non-discovery rates averaged over 1000 simulation rounds are included in Table II. Next, we review the main results.

TABLE I.

The sensitivities, specificities and F1-scores for cPLS (with false discovery rate set to 0.10) and its comparative methods, glasso and WGCNA.

Simulation model	n	p	Sensitivity			Specificity			F1-score
			cPLS	glasso	WGCNA	cPLS	glasso	WGCNA	cPLS	glasso	WGCNA
Overdispersed Poisson	20	100	0.722	0.000	0.978	0.998	1.000	0.717	0.838	0.000	0.827
	20	1000	0.690	0.000	0.971	1.000	1.000	0.687	0.817	0.000	0.805
	100	100	0.588	0.000	1.000	1.000	1.000	0.773	0.741	0.000	0.872
	100	1000	0.687	0.000	0.998	1.000	1.000	0.927	0.814	0.000	0.961
Multinomial	20	100	0.142	0.000	1.000	1.000	1.000	0.773	0.249	0.000	0.872
	20	1000	0.092	0.000	1.000	1.000	1.000	0.774	0.168	0.000	0.873
	100	100	0.979	0.000	1.000	1.000	1.000	0.995	0.989	0.000	0.997
	100	1000	0.929	0.000	1.000	1.000	1.000	0.995	0.963	0.000	0.997
SimSeq	20	100	0.785	0.000	0.926	0.997	1.000	0.624	0.878	0.000	0.747
	20	1000	0.900	0.000	0.954	0.992	1.000	0.544	0.944	0.000	0.693
	100	100	0.826	0.000	0.921	0.996	1.000	0.783	0.903	0.000	0.846
	100	1000	0.982	0.000	0.956	0.995	1.000	0.652	0.988	0.000	0.775

TABLE II.

The true discovery and true non-discovery rates for cPLS (with false discovery rate set to 0.10) and its comparative methods glasso and WGCNA.

Simulation model	n	p	True discovery rate			True non-discovery rate
			cPLS	glasso	WGCNA	cPLS	glasso	WGCNA
Overdispersed Poisson	20	100	0.879	0.000	0.054	0.995	0.984	0.999
	20	1000	0.979	0.000	0.074	0.992	0.976	0.999
	100	100	0.997	0.000	0.144	0.987	0.969	1.000
	100	1000	0.993	0.000	0.323	0.992	0.975	1.000
Multinomial	20	100	0.126	0.000	0.003	0.999	0.999	1.000
	20	1000	0.076	0.000	0.000	1.000	1.000	1.000
	100	100	0.906	0.000	0.115	1.000	0.999	1.000
	100	1000	0.930	0.000	0.019	1.000	0.975	1.000
SimSeq	20	100	0.718	0.000	0.025	0.998	0.990	0.999
	20	1000	0.112	0.000	0.002	1.000	0.999	1.000
	100	100	0.660	0.000	0.042	0.998	0.990	0.999
	100	1000	0.164	0.000	0.003	1.000	0.999	1.000

Based on the F1-scores in Table I, from the three comparative methods, the cPLS -algorithm and WGCNA shared the first place in best performance, both being ranked number one in six different simulation settings. WGCNA outperformed cPLS when data was generated multinomial simulation model, whereas cPLS performed better with SimSeq-data. In all three simulation models, when p was held fixed, the performance of the WGCNA improved as the sample size n increased. As for cPLS, the same phenomenon was seen in multinomial and SimSeq models. In most cases, when the sample size n was held fixed but the dimension of the data, p, was increased, the F1-scores declined or stayed at the same level. Exceptions for this were cPLS and WGCNA in overdispersed Poisson model when n = 100, and cPLS in SimSeq model with both sample sizes. Thus, the true associations were more difficult to identify in higher dimensions, but increasing the sample size improved the performance. Overall, cPLS dealt best with the increasing number of genes.

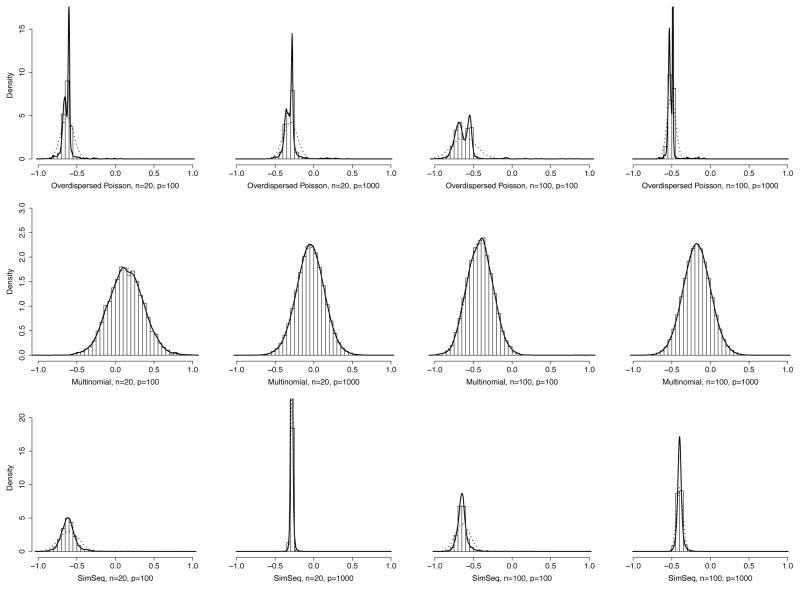
As seen in Table II, the cPLS-algorithm also maintained high true discovery rates, excluding few exceptions in multinomial and SimSeq settings, but was clearly superior to the reference methods even then. In multinomial setting, true associations were harder to detect with smaller sample sizes and cPLS suffered from over selection, but still performed better than glasso or WGCNA. In Fig. 1, it can be seen, that for data generated by multinomial simulation model, the distribution of the computed association scores is sleek, with not many larger association scores standing out.

Fig. 1.

Distributions of the cPLS-association scores in all simulation settings presented in Table 1. The plots include histograms of the association scores, fitted densities (solid black line) and the respective normal distribution curves (black dotted lines). These fitted densities and normal distributions match the ones used in computing the local FDR:s.

Increasing the sample size to n = 100 improved the performance significantly, leading to both the sensitivities and the true discovery rates rise over 0.90. In contrast, in SimSeq setting, several false positives appeared when the dimension was elevated to p = 1000. In this setting, the number of false positive associations is not necessarily the number of associations which the network construction algorithms failed to reject. In addition to the correlation structure built by adding the random effects, the source data may include strong associations that occur naturally between the genes and reflect in the computed association scores. Fig. 1, shows that the distributions of the association scores for SimSeq-model with p = 1000 are extremely peaked, making it difficult for local FDR to identify the true associations.

In the overdispersed Poisson setting with lower sample sizes, cPLS performed slightly better than WGCNA. However, when sample size rose from n = 20 to n = 100, WGCNA did better job in discovering the true associations. This might be due to the fact that the overdispersed Poisson model stands out with the largest number of true associations, which may not match with cPLS assuming only a small number of the associations being significant.

Comparing the F1-scores alone does not give a full picture of the performance. When taking a look at the true discovery rates in Table II, it can be seen that the true discovery rates of the WGCNA method remained low. This was due to the large amount of false positivities. The true non-discovery rates are, perhaps, misleadingly high, due to fact that overall only few associations were left out of the networks and in most cases these were correctly identified as non-significant associations. Thus the number of false negative associations stays low. In all settings, the weighted correlations computed with WGCNA were rounded to two decimal places and the threshold for rejecting an edges of the network was set to zero. This selection might not have been reasonable in all settings, as, for example, this leads to including an edge having a weight 0.01. This suggested by the resulting low specificities and true discovery rates seen in Tables I and II. To investigate the effect of the threshold parameter selection, we repeated the WGCNA analysis with varying threshold parameters, as seen in Table III. As expected, the true discovery rates increase as the threshold parameter increases, but at the same time, the sensitivities decrease. There does not seem to be one optimal threshold parameter value that would lead to a balanced state between sensitivities and true discovery rates. In addition, setting a nonzero threshold requires again an additional user-selected threshold parameter value and does not differ much from selecting the edges based on whether the unweighted pairwise Spearman’s correlation coefficient is above, say, 0.5.

TABLE III.

The specificities and true discovery rates for WGCNA with varying thresholds for including edges in a final network. The results are shown for n = 20, p = 100 case with all simulation models and averaged over 1000 simulation rounds.

Simulation model	Threshold	Sensitivity	Specificity	True discovery rate	True non-discovery rate
Overdispersed poisson	0.00	0.978	0.717	0.054	0.999
	0.10	0.593	0.996	0.740	0.993
	0.20	0.563	0.999	0.929	0.993
	0.30	0.527	1.000	0.979	0.992
	0.40	0.490	1.000	0.993	0.992
	0.50	0.473	1.000	0.998	0.991
Multinomial	0.00	1.000	0.773	0.003	1.000
	0.10	0.962	0.999	0.347	1.000
	0.20	0.865	1.000	0.802	1.000
	0.30	0.718	1.000	0.879	1.000
	0.40	0.521	1.000	0.786	1.000
	0.50	0.314	1.000	0.575	1.000
SimSeq	0.00	0.929	0.624	0.025	0.999
	0.10	0.746	0.968	0.201	0.997
	0.20	0.657	0.987	0.347	0.996
	0.30	0.565	0.994	0.491	0.996
	0.40	0.478	0.997	0.618	0.995
	0.50	0.384	0.999	0.739	0.994

As seen in Table I, glasso, with the ric selection criteria for the optimal regularisation parameter, tends to under select edges in all simulation settings and thus the sensitivities remained zeros. All in all, glasso included very few associations in any of the networks. The specificities were all rounded to ones, as most of the associations were not significant and by detecting no significant associations, these non-significant associations were identified correctly. The observed under selection property might be a result of the true associations blending among the false correlations arising from the highly expressed outliers. From the methods compared, glasso can be especially sensitive to this phenomenon, where the majority of the estimated associations seem equally strong, and thus, all of them are shrunk towards zero.

However, it is known that in some settings, ric suffers from under selections leading to high number of false negative discoveries [40]. This being the case, [40] recommends applying stability approach to regularisation selection (stars). The idea behind stability approach is to use the least amount of regularisation that simultaneously makes the inverse covariance matrix sparse and replicable under random sampling. As a drawback, especially in larger dimensions, stars is not very efficient. For comparison, we repeated the glasso analyses for the first 200 simulation rounds by applying the stars selection criteria. The results averaged over 200 rounds are presented in Table IV. It seems, that in lower dimensions, stars performed better than ric. Nevertheless, the true discovery rates still remained low.

TABLE IV.

The measure of performance for glasso with stability approach to regularization selection (stars) averaged over 200 simulation rounds.

Simulation model	Sensitivity	Specificity	F1-score	True discovery rate	True non-discovery rate
Overdispersed poisson	0.469	0.969	0.632	0.209	0.991
	0.000	1.000	0.000	0.000	0.976
	0.527	0.945	0.677	0.237	0.984
	0.000	1.000	0.000	0.000	0.975
Multinomial	0.885	0.983	0.931	0.037	1.000
	0.000	1.000	0.000	0.000	1.000
	1.000	0.988	0.944	0.048	1.000
	0.793	0.970	0.873	0.003	1.000
SimSeq	0.501	0.953	0.657	0.099	0.995
	0.000	1.000	0.000	0.000	0.999
	0.597	0.915	0.723	0.067	0.996
	0.000	1.000	0.000	0.000	0.999

In a similar setting, [41] explored the consistency of ℓ₁-based methods (as glasso) for sparse latent variable -like models and showed that the methods failed dramatically for models with nearly linear dependencies between the variables. They also showed, that assumption needed for consistency on models derived from real life RNA-sequencing data never hold even for modest sized networks. This supports our findings and thus we suggest that glasso should be used with caution as in these sort of applications it easily becomes unreliable in practice.

IV. Practical application example

In this section, we construct genetic association networks for real life RNA-sequencing data that are collected to examine the molecular anatomy of the craniofacial (facial bone structure) development [42]. Facial malformations due to the failure of midline fusion of the two plates of the skull forming the hard palate, cleft lip/palate, are among the most common birth defects [43]. The condition can be treated with surgical interventions during the first months of life. However, the effects on speech, swallowing, hearing, and appearance can cause long-lasting disadvantages for health and social integration [44].

Apart from some syndromic cases, the genetic and environmental factors contributing to the cleft lip and cleft palate formation remain largely unknown. Much of the current knowledge on the development of head organogenesis is derived from the animal models with targeted mutations. Mus musculus, the house mouse, provides a useful model for global expression studies using RNA-sequencing for identifying gene expression patterns driving the murine palate development. The condition-related genes and loci discovered in mouse model can be further explored in humans. The mouse models also provide valuable information on gene-gene and gene-environment interactions.

The study providing the data [42] focused on E14.5 palate, soon after medial fusion of the two palatal shelves. The palate was partitioned into multiple slots: both the bony anterior and the muscular posterior compartments were divided into oral and nasal, as well as the medial and lateral domains. Here, we reconstruct a genomic co-expression network for one specific anatomical region, analysing data that consists of three replicates related to the anterior domain of the lateral palate compartment (ADLPC). In addition, we examine how the main findings change in the replicates collected from an other anatomical region, the posterior domain of the lateral palate compartment (PDLPC). The data are available through the FaceBase Consortium [45], www.facebase.org.

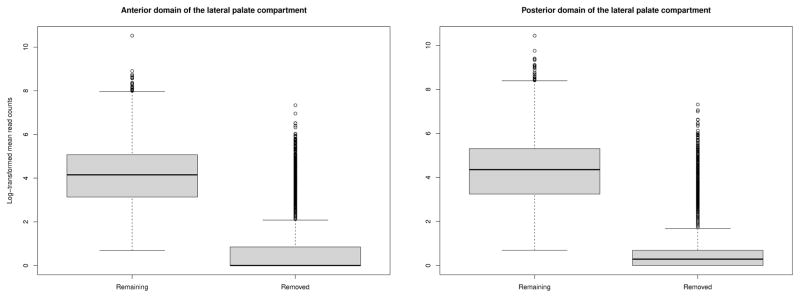
Both data represent an example of p ≫ n -data with 21, 761 genes measured on three replicates. In order to increase the statistical power and to reduce the false discovery rate, part of the genes were filtered out prior the analyses according to the following criteria. First, genes with “N/A” gene names were removed, resulting in 17, 757 genes in the ADLPC data and 20, 025 genes on the PDLPC data. As the goal of the network analysis is to examine how genes vary together, the genes with least variation, i.e., genes with two or three ties were removed. From ADLPC data, this step filtered out 5, 973 genes and from PDLPC data 6262 genes. Lastly, we filtered out sex related genes, such as the ones located in Y-chromosome, or the ones located in X-chromosome and relating to X-inactivation. The sex related genes can give artefact difference calls, as the sexes of the embryos used for RNA-sequencing analysis are not determined. Thus, if some samples are from females and some from males, the variation or differences relating to sex cannot be separated from other, potentially more interesting biological variation. The distributions of the remaining and removed genes for both data sets are given in Fig. 2, showing that the genes removed were likely to have very low read counts compared to the remaining genes. The subsequent analyses were performed on the remaining 11, 788 genes on ADLPC data and 13, 757 on PDLPC data.

Fig. 2.

Distrubutions of the log-transformed mean read counts from the genes that were removed in comparison to those remaining, measured from anterior and posterior domains of the lateral palate compartment. The removed genes had either two or three ties across all three replicates or were related to sex determination.

In these data, the number of PLS-components to be used in cPLS is limited by the number of replicates. In the negative binomial model fitting step, with three replicates, already two PLS-components would lead in a saturated model as one parameter would be used for each PLS-component and one for the intercept. Thus, the analyses are run with one PLS-component. The construction of the whole association network was completed in 5.6 minutes with 2.4 GHz Intel Core i5 processor and 16 GB 1600 MHz DDR3 memory.

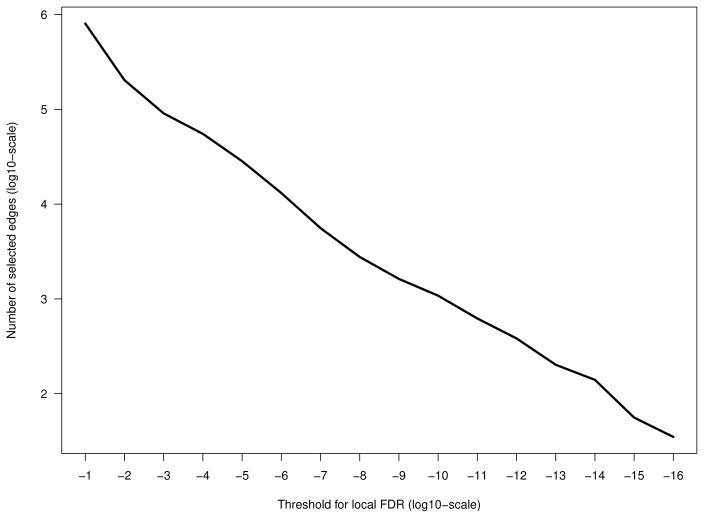
After constructing the full matrix of the association scores, the local FDR is used to determine which edges were included in the final ADLPC network. Fig. 3 shows the relation of the local FDR threshold parameter value and the number of the interactions. With 69, 472, 578 potential undirected pairwise interactions, the threshold parameter needs to be tightened to a very small value in order to result in an interpretable network. We chose to set the threshold to 10⁻¹⁵, which resulted in including the edges having an association score above −0.799 or below 0.799. Thus, the final network consists of 47 genes and 56 interactions between them. This association network is visualised in Fig. 4, using the Cytoscape software, freely downloadable at www.cytoscape.org [46].

Fig. 3.

Number of selected edges in a network with varying threshold parameters for the local FDR. Both axes are on log10-scale.

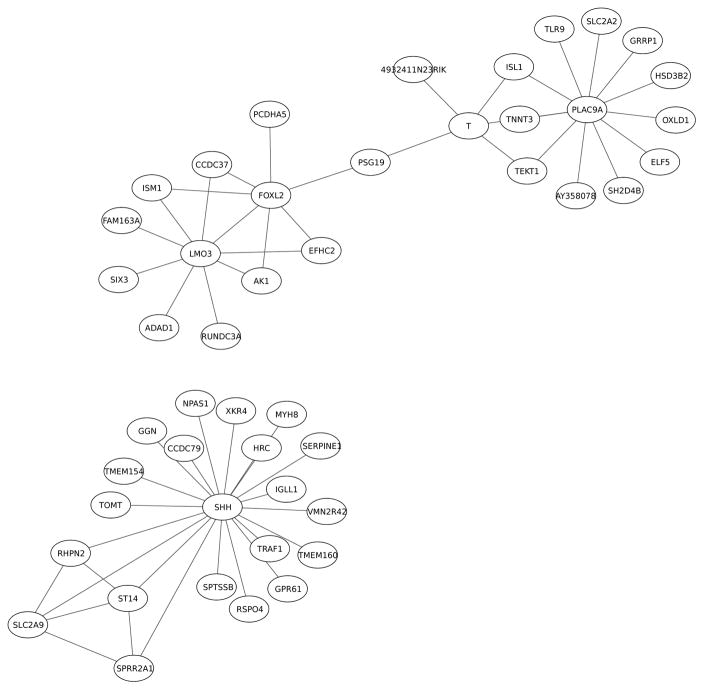
Fig. 4.

Gene-gene -association network of the anterior domain of the lateral palate compartment of E14.5 palette. The network includes 47 genes (nodes) and 56 interactions (edges) between them.

The single gene with highest connectivity in the ADLPC network is SHH (sonic hedgehog). SHH is a known key player in craniofacial development, with mutations giving a wide eye separation (highly expressed SHH) or cyclops only one eye (no SHH) [47], [48]. An other hub gene, oncogenic LMO3 is involved in signaling, and is known to interact with tumor suppressor gene p53 and HEN2 [49]. Gene FOXL2 has recently been related to cartilage, skeletal development and insulin-like growth factor 1 -dependent growth [50]. Also, some transcription factors can be seen in central locations.

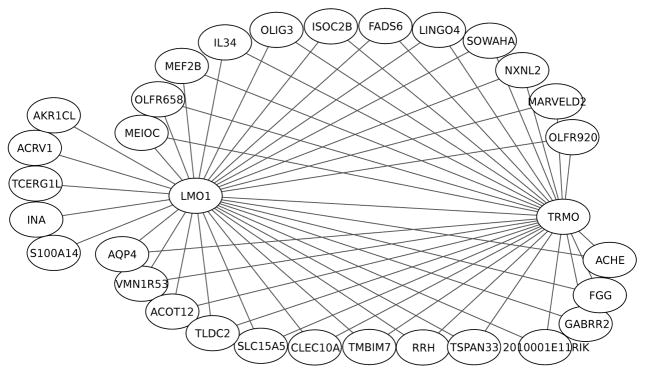
Next, two comparative analyses are performed on PDLPC data. First, to see how the strongest associations are distributed in PDLPC data, we again construct the full matrix of the association scores using cPLS and plot the network consisting of the same number of associations as was selected for ADLPC data. The network is visualised in Fig. 5. This network is dominated by two genes, LMO1 and TRMO. LMO1 belongs, similarly to LMO3 appearing in ADLPC network, to the family of LIM protein coding genes, and is predominantly expressed in the brain. TRMO, in turn, is located close to cleft lip/palate related gene FOXE1 both in human and mouse genome. Previous studies have discovered that the region surrounding FOXE1 has shown association in the development of cleft lip and palate [51].

Fig. 5.

Network including 56 strongest associations under posterior domain of the lateral palate compartment. The selected associations connect 32 unique genes.

Second, to see what happened to the connectivity of all the important genes discovered in ADLPC data (hubs), we select ten strongest associations relating to these genes and plot their network, shown in Fig. 6. Here, SHH and PLAC9A are connected directly and via TCFL5, whereas in ADLPC network they were located in separate modules. Similarly to ADLPC network, genes LMO3 and FOXL2 are located in the same module, but this time indirectly through nine different genes. The interesting association between TRMO and LMI protein coding family member LMO3 reappears also in this network. These findings serve as hypotheses for additional experiments to validate any of the interactions but the literature search conducted suggests that cPLS was able to find biologically meaningful associations.

Fig. 6.

Connectivities of the hub genes SHH, LMO3, FOXL2, and PLAC9A under posterior domain of the lateral palate compartment. Ten highest interactions relating to each of the hub gene are included in this network.

To highlight the efficacy of the cPLS-method, we also conducted WGCNA and glasso analyses on ADLPC data. Importantly, The authors of R-package WGCNA do not recommend using their method for data sets consisting of fewer than 15 samples (WGCNA package FAQ). They state that in a typical high-throughput setting with large number of variables, correlations on fewer than 15 samples tend to be too noisy for the network to be biologically meaningful. However, we computed the Spearman’s correlation matrix, where the read counts are replaced with their ranks. In this case, it results in a data set consisting of three numbers: 1, 2, and 3, which leads to a correlation matrix consisting of four distinct values: −1, 1, −0.5, and 0.5. When the matrix is raised to the power of six (β = 6) the final adjacency matrix consists of two distinct values: 1.00000 and 0.015625. If we then assume that the off-diagonal elements having value 1.00 are the “significant” associations, we end up having a network with 23, 404, 938 associations. Thus, we conclude that in this application, using WGCNA is not reasonable.

Next, we attempted to fit glasso for log(x + 1)-transformed read counts data. Despite using the Meinhausen-Bühlmann-approximation and ric-criteria for optimal tuning parameter value selection, after 72 hours, the glasso had not yet found a solution to a problem. The sheer dimension of the problem is of course huge, but we also speculate, that as shown by [41], the conditions required by glasso are not met, and thus finding an optimal solution is challenging and the resulting inferred edges of the network would be more or less random.

V. Conclusion

In this paper, we introduced a new algorithm to construct an association network for high-dimensional count data and demonstrated its capability to find biologically meaningful associations both in simulations and in the real life RNA-sequencing data. The suggested approach is applicable to the raw counts data, without pre-processing. The parameters for the associations are estimated using PLS regression model based approach. We have adopted our PLS term construction from our previous work [15] for microarray data where this particular formulation seemed to work better than some other variants compared. In any event, certainly additional variants of PLS or other algorithms for latent factor models can always be attempted. However, a full scale implementation of such models including selections of tuning parameters etc. will be time consuming and may be suitable for a future paper.

In the first step of the algorithm, we compress the covariation of the count data into a small number of PLS-components and in the second step, these components are used as predictors in a negative binomial model. Despite the fact that PLS requires the count data to be centered and scaled, it captures well the main features of the gene expression data and thus provides a small number of reasonable covariates bringing the inference problem to a much lower dimension. The actual inference problem is then solved with correct model specification assuming the count data to be following a negative binomial distribution. In the settings investigated, the cPLS-algorithm outperformed the two comparative methods, glasso and WGCNA.

The cPLS-algorithm is designed especially to be used for inferring latent networks from RNA-sequencing data, but another good application of this would be for example in correlation network type applications where the counts are from an operational taxonomic unit (OTU) table. Negative binomial regression model could be easily replaced, for example, with Poisson regression. Also, the networks could be adjusted for other covariates as well, by including these additional variables in the negative binomial model step along the PLS components. In the Practical application example, the comparisons between networks related to two different anatomical regions were descriptive and a solid statistical framework for differential network analysis of networks reconstructed from NGS data will be left for future work.

In general, separating the true associations from the noise is a difficult task [52]. This is emphasised especially with RNA-sequencing data, where the variance of the observed expression levels often outweighs their mean. These highly expressed outliers cause pairwise correlations, especially Pearson’s correlations, to be larger than they are in reality. Thus, correlation based network construction methods often suffer from high number of false positives. To prevent this, some measures should be taken, for example, in a form of transforming the data prior analysis or using more robust tools to measure the associations. In our simulation studies, we noticed that the non-normal data fully disabled glasso. Even normalising and log-transforming the data did not respond to the assumption of multivariate normal expression distributions. Thus it seems that there is no quick and easy solution to apply glasso in the context of NGS data, without adjusting the method to meet the distributional assumptions of the data. For more information on generalised graphical models, see [53], [54] and the citations within.

The cPLS and WGCNA were able to estimate the full network for thousands of genes without major computational load. In cPLS, computing the PLS components or fitting a negative binomial model are relatively light procedures (estimating the parameters of the negative binomial model takes longer from these two steps). However, repeating the two steps p times may require some time. For WGCNA, the Spearman’s rank correlation matrix does not require intensive computations. In contrast, estimating the (sparse) inverse covariance matrix of the multivariate Gaussian distribution with glasso is computationally demanding, especially in high dimensions. However, utilising an approximation suggested by Meinahausen and Bühlmann [8], where the estimation of a full inverse covariance matrix is replaced by fitting a lasso model to each variable using the other as predictors, speeded up the computations remarkably.

In addition, all three compared methods, cPLS, WGCNA, and glasso have tuning steps, that is, they include parameters whose values are to be selected in some way either to increase network sparsity (WGCNA and glasso) or to decide how much of the original variation will be captured by components that present the data in a lower dimension (number of PLS terms in cPLS). For WGCNA and cPLS, we used a fixed tuning parameter value, adapted from previous work or literature. For glasso, we compared two different criteria for optimal tuning parameter value selection. Between the two methods, ric performed the selection swiftly, whereas stars took longer. In high dimensions ric and stars gave identical results, but in lower dimension, ric repeatedly under selected edges, whereas stars, in most cases, resulted in better sensitivities and specificities, as seen in Table IV.

Biographies

Maiju Pesonen received her M. Sc. degree in statistics in 2010 from the University of Turku and Ph. D. degree in statistics in 2016 from the University of Turku, Finland. Currently, she does postdoctoral research at the Aalto University, in the Finnish Centre of Excellence in Computational Inference (COIN), Finland. Her research interests include association networks, missing or censored data problems, evolution, and population genetics.

Jaakko Nevalainen received his M. Sc. degree in mathematical statistics in 1998 from the University of Jyväskylä and his Ph. D. degree in statistics in 2007 from the University of Tampere, Finland. His theoretical research has mainly been on the framework of analyzing clustered, multivariate data by nonparametric means and with possibly informative cluster size. In addition, he has been involved in collaborative research in several large longitudinal studies on e.g. diabetes, prostate cancer and nutrition, as well as in research making use of new technologies like multicellular imaging and mass spectrometry. Currently, he is a professor of biostatistics at the University of Tampere, Finland.

S. Steven Potter received his PhD from the University of North Carolina in 1976 and did postdoctoral research at Harvard Medical School. He studies developmental genetics, and has participated in the FACEBASE, GUDMAP and LungMAP consortia. His first paper, published in Nature, showed that mitochondrial DNA is maternally inherited. He studies the gene expression programs that drive development. He has published over 125 papers with a total of over 13,000 citations according to Google Scholar. Currently he is a professor in the Division of Developmental Biology at Cincinnati Children’s Medical Center.

Somnath Datta received his M. Stat. degree in mathematical statistics and probability in 1985 from the Indian Statistical Institute, Calcutta, and the PhD degree in statistics and probability in 1988 from Michigan State University, USA. He has published over 130 research articles in various areas of statistics, biostatistics and bioinformatics and collaborated with statisticians, scientists, and engineers from various universities. His research has been funded by CDC, NSA, NSF, and NIH. Currently he is a full professor at the University of Florida, hired in 2015 under the preeminence initiative. He is an elected member of the International Statistical Institute, and elected fellows of the American Statistical Association and the Institute of mathematical Statistics. He is the current president elect of International Indian Statistical Association.

Susmita Datta received her M. S. degree in applied statistics in 1990 and PhD degree in statistics in 1995 from the University of Georgia, Athens, Georgia, USA. She has published almost 100 research articles in various areas of statistics, biostatistics, population biology, bioinformatics and proteomics. She has collaborated with biostatisticians, chemists, geneticists and other scientists from various universities. Her research has been funded by mainly NSF and NIH. Currently, she is a full professor in the Department of Biostatistics at the University of Florida. She was hired in 2015 under the preeminence initiative. She is an elected member of the International Statistical Institute, and elected fellows of the American Statistical Association and the American Association for the Advancement of Science.