Inferring neuronal network functional connectivity with directed information

This study brings together the techniques of voltage-sensitive dye recording and information theory to infer the functional connectome of the feeding central pattern generating network of Aplysia. In contrast to current statistical approaches, the inference method developed in this study is data driven and validated by conductance-based model circuits, can distinguish excitatory and inhibitory connections, is robust against synaptic plasticity, and is capable of detecting network structures that mediate motor patterns.

Abstract

A major challenge in neuroscience is to develop effective tools that infer the circuit connectivity from large-scale recordings of neuronal activity patterns. In this study, context tree maximizing (CTM) was used to estimate directed information (DI), which measures causal influences among neural spike trains in order to infer putative synaptic connections. In contrast to existing methods, the method presented here is data driven and can readily identify both linear and nonlinear relations between neurons. This CTM-DI method reliably identified circuit structures underlying simulations of realistic conductance-based networks. It also inferred circuit properties from voltage-sensitive dye recordings of the buccal ganglion of Aplysia. This method can be applied to other large-scale recordings as well. It offers a systematic tool to map network connectivity and to track changes in network structure such as synaptic strengths as well as the degrees of connectivity of individual neurons, which in turn could provide insights into how modifications produced by learning are distributed in a neural network.

NEW & NOTEWORTHY This study brings together the techniques of voltage-sensitive dye recording and information theory to infer the functional connectome of the feeding central pattern generating network of Aplysia. In contrast to current statistical approaches, the inference method developed in this study is data driven and validated by conductance-based model circuits, can distinguish excitatory and inhibitory connections, is robust against synaptic plasticity, and is capable of detecting network structures that mediate motor patterns.

understanding how the organization of neurons into neural circuits enables the different functions of the brain is one of the core goals of neuroscience and is a prerequisite for studying how the structures of these networks are modified by learning. Major advances have been made in the methods and techniques for simultaneously recording activity in large numbers of neurons (Alivisatos et al. 2012; Peterka et al. 2011; Stevenson and Kording 2011). With the ability to collect a large volume of data, the next step is to reverse-engineer the neural signals and to delineate the underlying circuits that have generated the activity. Integrating the techniques of large-scale recordings with analytical tools would contribute tremendously to delineating and deciphering functional connectomes. Functional connectivity provides greater insights than anatomical connectivity because it captures the active functional structure of the circuit, the strengths of different neural pathways, and the relevance of various neurons in the network. The main focus of this study was to develop and test a tool that can be used to reliably detect functionally relevant connections using a scalar metric based on the information provided in the neuronal recordings alone.

Several statistical or information theoretic tools have been used to infer the directed functional connectivity of a neural circuit (see Brown et al. 2004). In general, two different types of signals are analyzed by dedicated methods: methods that focus on inferring connectivities using local field potentials (LFPs) (Cadotte et al. 2008; Dhamala et al. 2008; Malladi et al. 2015, 2016) and methods that focus on spiking activities from neuronal-level recordings (Cai et al. 2016b; Gerhard et al. 2013; Kim et al. 2011; Nowak and Bullier 2000; Perkel et al. 1967; Quinn et al. 2011; Truccolo et al. 2005). There are also methods that can be applied to both signal types by analyzing the interactions among predefined states of the recordings (Friedman et al. 2016; Gat et al. 1997). Among methods that analyze spiking signals, one of the most commonly used tools is the cross-correlation histogram (cross-correlogram), which deploys spike-triggered histograms to find the causal relationship between two neurons (Nowak and Bullier 2000; Perkel et al. 1967). Truccolo et al. (2005) and Kim et al. (2011) employ a point process-generalized linear model (GLM) framework together with Granger causality (GC), whereas Quinn et al. (2011) and So et al. (2012) calculate directed information (DI) based on the same framework to detect pairwise causal influences; similarly, Gerhard et al. (2013) use the coupling strengths obtained from the spline coefficients fitted with the GLM to reconstruct functional connectivity.

Among all the above-mentioned techniques, DI has many advantages. Cross-correlation and cross-correlogram are defined on two processes and cannot reliably distinguish monosynaptic and polysynaptic connections or common-input structures. GC assumes that the past samples in the recording have a linear influence on the future sample and that noise in the signal is modeled as Gaussian (Barnett and Seth 2014). In contrast, DI is model free, because its calculation is based simply on entropy (Massey 1990). The burden of reducing the estimation error of DI is hence shifted to the estimation of entropy for neural recordings. To fully exploit the advantages of DI, an accurate and data-driven entropy estimator should be used in conjunction with DI.

Neural spike trains are commonly used to represent spiking signals and are generated by segmenting the continuous time spiking data using a predetermined unit time called bin width into discrete time binary sequences, where a 1 bit indicates a spike and a 0 indicates no activity. Generally, the statistical properties of neural spike trains are estimated through a parametric approach, the GLM (Kim et al. 2011; Quinn et al. 2011; So et al. 2012; Truccolo et al. 2005). GLM assumes that the likelihood of a future spike is modeled as the exponent of the linear combination of past activity of the spike trains. Because spiking activity may not always fit the GLM assumption, a data-driven approach to extract statistical properties without assuming a linear relationship among spikes in one or more neural recordings is more desirable. Context tree weighting (CTW), a universal entropy estimators developed for data compression (Jiao et al. 2013), is a tool that does not assume a linear relationship among data in neural spike trains and thus may serve as a good technique to infer functional connectomes. Yet the depth of the tree used to determine the length of the memory needs to be set externally, usually arbitrarily or by past experience. Also, CTW assumes that all firing patterns are equally likely, and this method of assigning all patterns equal weight is very data intensive and does not provide insight into the data structure. In this study, we implemented a different method that utilizes the context tree framework—context tree maximizing (CTM), which, in addition to being data driven, also automatically finds the appropriate tree depth as well as the best tree structure that fits the data in the a posteriori sense and prevents overfitting (Csiszár and Talata 2006; Volf and Willems 1995), in which case the model tends to fit the noise other than the underlying patterns and relationships of the signals. Because it is data driven, CTM is not constrained by model types and is able to detect both linear and nonlinear relationships between spike train sequences.

In this report, we begin by reviewing the theoretical basis for DI for discrete time series. We then estimate DI for spike train data using CTM and construct a synaptic profile from the tree model that allows us to view the synaptic influence with different kinetics and time courses and differentiate excitatory and inhibitory connections. Next, we use a heuristic to determine direct vs. indirect connections. To demonstrate the robustness of our approach, we test it using a sparse Poisson spiking model and several small realistic conductance-based neuronal circuits. The performance is further tested with a larger network that resembles the central pattern generator (CPG) network of the Aplysia feeding circuit. Finally, we apply the technique to actual data obtained from voltage-sensitive dye (VSD) recordings of a buccal ganglion from Aplysia and identify some promising putative connections.

Our method of constructing connectivity diagrams from large-scale recordings is an automated, comprehensive framework for inferring neuronal network structures. It is robust against synaptic plasticity such as facilitation and depression. It is able to exclude indirect connections, differentiate excitatory from inhibitory synapses, and infer the time course of the synaptic responses. This method is generally applicable to analysis of neural network structures and could be used to track functional changes due to change of behavioral states, neuromodulation, or learning. Preliminary results of this work were reported in abstract form (Cai et al. 2015, 2016a) as well as in a conference paper (Cai et al. 2016b).

Throughout this report, $X_a^b$ for b > a is a shorthand for the vector [X_aX_a+1 . . . X_b-1X_b], whereas X^b is simply the string of random variables $X_1^b$ from the beginning up to index b. An uppercase letter denotes a random variable, whereas a lowercase denotes one realization of that random variable. We denote a string $s=x_{b-k}^b$, and then $s\prime =x_{b-k^{\prime }}^b$ where k′ ≤ k is a suffix of s, denoted by $s\text{⩾\hspace{0.17em}}s\prime$; yet if k′ < k, s′ is called a proper suffix of s, denoted by $s\succ s\prime$.

METHODS

Directed Information

DI will be used to quantify information flow from one neuron to another. It is an entropy-based measure that bears much resemblance to mutual information and can be applied to both discrete and analog random processes. We focus on the first case, because we segmented spikes in time using fixed bin widths into neural spike trains and the random process used to represent these discretized neuronal activities is then a discrete time and binary alphabet random process.

DI was originally formulated by H. Marko and formally defined by J. Massey (Massey 1990). It measures the amount of single-directional information flow from random sequence X to sequence Y. It is defined as

$$I\left(X^n\to Y^n\right)=H\left(Y^n\right)-H\left(Y^n\parallel X^n\right)$$ (1)

where

$$H\left(Y^n\right)={\displaystyle \sum _{i=1}^{n}H}\left(Y_i\parallel Y^{i-1}\right)$$ (2)

is the chain rule of entropy quantifying the entropy of Y itself and

$$H\left(Y^n\parallel X^n\right)={\displaystyle \sum _{i=1}^{n}H}\left(Y_i|Y^{i-1},X^i\right)$$ (3)

is the causally conditioned entropy. Causally conditioned entropy is the entropy of Y conditioned on the causal part of X in addition to the history of itself. In the formulation of mutual information, the conditional entropy term in Eq. 3 is $H\left(Y_i|Y^i{}^{-\text{1}},X^n\right)$ instead. DI quantifies the reduction in entropy given the causal part of X in addition to the history of Y.

In practice, the DI rate, which is defined as $\overline{I}(X\to Y)={\text{lim}}_n{}_{\to \infty }\frac{1}{n}I(X\to Y)$, is most commonly used because it is bounded by the largest entropy a random variable can achieve, which in binary spike trains is 1. With a slight abuse of terminology, we refer to the DI rate simply as DI for the remainder of this report. Both the entropy rate for Y alone as well as the causally conditioned entropy rate can be estimated by using entropy estimators that directly provide the $H\left(Y_i|Y^i{}^{-\text{1}},X^i\right)$ terms. Such an approach is demonstrated by estimators 1 and 3 in Jiao et al. (2013), where the asymptotic equipartition property is evoked and entropy rate or divergence rate is estimated directly. It is also possible to estimate the entropy rates by using plug-in estimators that approximate the probability distribution $P\left(Y_i|Y^i{}^{-\text{1}},X^i\right)$, with which entropy rates can later be calculated, such as in estimators 2 and 4 in Jiao et al. (2013). In this study, we focused on estimator 1, for its faster convergence rate based on our simulations. We used a context tree-based algorithm to estimate causally conditioned entropy. Causally conditioned entropy rate obtained via the asymptotic equipartition property is shown to converge in the almost sure sense (Venkataramanan and Pradhan 2007) as well as in the L₁ sense (Jiao et al. 2013). Almost sure sense convergence is when the probability of the estimate and the true distribution being the same goes to 1. L₁ convergence is that the expected value of the absolute error goes to 0.

In actual implementations, convergence is data dependent. For neurons with tonic firing activity, the convergence is faster. The fluctuation of the DI value is <0.1% with a spike train whose length is in the order of 10³ data points. In this favorable case, if the bin width is 10 ms, typically <1 min of data is needed. For neurons with phasic activity, the DI rate curve stabilizes slower. Based on simulations, roughly 2 min of data is needed depending on the diversity of the spiking patterns, which differs from neuron to neuron.

Context Tree Estimation

To calculate DI, the conditional entropy terms in Eq. 1 need to be estimated. Multiple entropy or plug-in probability estimators are available, which aim to detect patterns in data sequences and to minimize entropy in the area of data compression. Examples include Lempel-Ziv (Ziv and Lempel 1978), Burrows-Wheeler transform (Burrows and Wheeler 1994), and prediction by partial matching (Cleary and Witten 1984). However, context tree-based algorithms show a faster convergence (Gao et al. 2008). In this section, we provide a brief description of how a tree model generates a sequence. If we know that tree model entirely, the likelihood of the observed sequence as well as its conditional probability can be calculated. Yet if the model is unknown, it is necessary to first use the sequence to estimate a tree model that most likely (in the a posteriori sense) has generated the given sequence, and with this estimated model we can then obtain the probability measure we need to calculate DI.

Tree structure.

Tree structures are commonly used to model finite-alphabet, finite memory, stationary and ergodic sources that have generated the observed sequences. We denote a unique tree structure by T. Assume that a fictive tree model T has depth D. Its symbols are drawn from a finite alphabet $A=\{0,\dots ,\left|A\right|-\text{1}\}$, and the cardinality (also known as the size) of the alphabet is |A|. For a complete tree model, it then has D levels, and on each level every node splits up into |A| branches, and therefore there are |A|^D leaf nodes (see Fig. 1A for a simple example). Note that this complete tree corresponds to a Markov chain model of order D. Each leaf defines the complete path from the root to a leaf, with the segments closer to the root being more recent and the ones closer to the leaves older. It represents a context that is unique and is independent of all others. A context is denoted by s and represents the history of spike activity with a duration of depth D times bin width. The tree T is formed by all its contexts. Associated with each leaf there is a parameter vector θ_s, an |A|-dimensional simplex [θ_s(0),…, θ_s(|A| − 1)], with each entry dictating the probability of the next symbol being a, where a ∈ A. Let yⁿ be a sequence generated by this tree T. If all the digits y_i in yⁿ that follow the same context s are grouped into a new sequence y_s, then the subsequent $y_s=\left\{y_i|y_i\in y^n,y_{i-D}^{i-1}=s\right\}$ emitted by the same leaf is modeled as an independently identically distributed (i.i.d.) process. Furthermore, y_s′ is independent of y_s if s′ ≠ s, for s, s′ ∈ T. Because each leaf is modeled as an i.i.d. source, the probability of an outcome yⁿ using the known tree model T is

$$P_{\mathcal{T}}(y^n)={\displaystyle \prod _{s\in \mathcal{T}}P(y_s)}$$ (4)

$$={\displaystyle \prod _{s\in \mathcal{T}}{\displaystyle \prod _{a=0}^{\left|A\right|-1}P{(a|s)}^{c_s(n,a)}}}$$ (5)

where c_s(n, a), a ∈ A, is the count of all occurrences of symbol a that directly follow the context s.

Fig. 1.

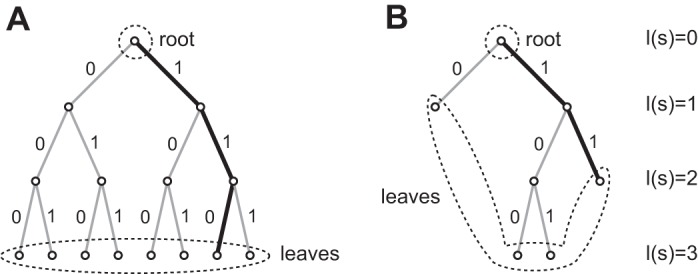
A binary context tree structure with maximum depth 3. A: a complete tree with leaves associated with all possible 2³ = 8 contexts. All contexts are equally long with 3 digits. The highlighted path refers to (Y_n-3 = 0, Y_n-2 = 1, Y_n-1 = 1), which also shows that the branch segment closer to the root corresponds to a newer sample (y_n-1) and the segment closer to the leaf corresponds to an older one (y_n-3). B: a trimmed tree with only 4 contexts. Note that any trimmed branch cannot be a suffix of another branch. In this case, both context …011 and context …111 are mapped to the same branch—the highlighted branch …11.

However, a tree structure does not have to be complete, and this is one advantage over the Markov chain model. If the lengths of the branches are allowed to vary, letting some longer contexts be merged into one shorter context, the number of contexts can be markedly reduced (Fig. 1B) and therefore the model’s complexity is also substantially reduced. The tree model can be simplified as long as the tree is irreducible, which means that no branch can be a suffix of another. The entire class of irreducible tree models is denoted by $\mathcal{I}$. This requirement is automatically guaranteed by the tree structure itself.

In many scientific applications such as neural spike trains, the real model that has generated the observation is never known. An intermediate step is to assume that we know the tree structure T but do not know the leaf parameters. In this scenario, the leaves could be used to partition the observation yⁿ into individual y_s. Because the subsequence y_s corresponds to each context s is i.i.d., an appropriate estimator for a memoryless source can be used to find its parameters.

Estimation of leaf parameters.

In this work, leaf parameter estimation was accomplished through the Krichevskii-Trofimov (KT) estimator (Krichevsky and Trofimov 1981). KT estimator is a Bayesian estimator, and it also has the capability to be implemented sequentially for potential real-time applications. Suppose a sequence Xⁿ is i.i.d and each variable X_i can only take on values from a finite-sized alphabet A; therefore, xⁿ is generated by a multinomial with parameter [θ(0),…, θ(|A| − 1)]. Denote a symbol in the alphabet by a, for a ∈ {0,1,…, |A| − 1}. Let the count of each symbol a observed before index n be c(n, a), but for simplicity we denote it as c(a). The KT estimator produces an estimate of the probability of an entire realization xⁿ of a stationary memoryless string using Bayesian statistics (See appendix a for details). Let us denote the estimate of such an i.i.d. sequence by P̂(xⁿ). It can be computed sequentially as

$$\widehat{P}(X_n=a,x^{n-1})=\frac{c(a)+\gamma }{c(0)+c(1)+.\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}+c(\left|A\right|-1)+\gamma \left|A\right|}\widehat{P}\left(x^{n-1}\right)=\frac{c(a)+\gamma }{(n-1)+\gamma \left|A\right|}\widehat{P}\left(x^{n-1}\right)$$ (6)

starting with P̂(ϕ) = 1, which means an empty string starts with probability 1 (see appendix a). Here γ is the “add-something” parameter of the sequential estimator (Krichevskii 1997). Most often $\text{γ}=\frac{1}{2}$, such that the error of the estimated log likelihood is uniformly bounded (Krichevsky and Trofimov 1981).

In the framework of context tree estimation, for a Markov chain process Yⁿ with order D, we simply have for each context s

$$\widehat{P}(Y_n=a|Y_{n-D}^{n-1}=s)=\widehat{P}(a\left|s\right)=\frac{c_s(a)+\frac{1}{2}}{(n_s-1)+\frac{\left|A\right|}{2}}$$ (7)

which is the conditional probability needed for Eq. 5.

Maximum a posteriori tree model with penalties.

After estimating the leaf parameters θ_s of a tree structure, we next searched the entire set of all irreducible tree models I for the tree structure that described the observed data best in the a posteriori sense. Because KT estimator is used to produce an estimate P̂(a|s), maximizing P̂_T(yⁿ) in Eq. 5 among all assumed model Ts yields the maximum a posteriori estimator, which is equivalent to minimizing the negative log likelihood −logP̂_T(yⁿ). Negative log likelihood of a sequence is the number of bits needed to encode that sequence in the field of compression. Intuitively, the lower the number, the better fit the model has. However, in an effort to control complexity and prevent overfitting, we want to penalize models with higher orders and find a model with limited tree depth D₀, D₀ ≤ D. We can introduce a minimum description length criterion that takes into account the cost of the model: the number of bits needed to describe the tree model itself including both the parameters as well as the tree structure. Define the cost of the model to be

$${\Gamma }_T=\left(|T\hspace{0.17em}|+\left|u:u\prec s\right|\right)\cdot \log \left|A\right|$$ (8)

where |T| is the number of contexts (i.e., the number of leaves); $\left|u\hspace{0.17em}:\hspace{0.17em}u\prec s\right|$ is the total number of inner nodes. A tree with the same number of leaves but a higher order requires more bits to detail all the layers of the longer branches. This condition often arises in compression where an optimal trade-off between the code length of the sequence and the cost of the model is desired (Volf and Willems 1995). With this penalty term, we construct our objective function as a trade-off between the model complexity and finding a tree model that maximizes the a posteriori probability:

$$\widehat{T}\hspace{0.17em}(y^n)=\underset{T\in I}{\mathrm{arg\; min}}\{-\log \hspace{0.17em}{\widehat{P}}_T(y^n)+{\text{Γ}}_T\}$$ (9)

minimized among set $I$. This objective function can be solved recursively, and the penalty term can be readily broken down and incorporated into the recursive optimization process (Volf and Willems 1995). We define the maximized probability ${\widehat{P}}_s^{\ast }$ at node s as

$$\begin{array}{l}{\widehat{P}}_s^{*}(y^n)=\{\begin{array}{cc}\max \{\frac{1}{\left|A\right|}{\widehat{P}}_s(y^n),\frac{1}{\left|A\right|}{\prod }_{a=0}^{\left|A\right|-1}{\widehat{P}}_{s_a}^{\ast }(y^n)\},& \text{\hspace{0.17em}0}\le l\text{(}s\text{)}\hspace{0.17em}<\hspace{0.17em}D\\ \frac{1}{\left|A\right|}{\widehat{P}}_s(y^n),& l\text{(}s)\text{\hspace{0.17em}=}\hspace{0.17em}D\end{array}\\ \end{array}$$ (10)

Here s_a is a child node of s, which represents a string with symbol a appended to the end of the string represented by s. P̂* at the root level is the maximized probability for this sequence. The recursive process defined by Eq. 10 is equivalent to solving the optimization problem Eq. 9, which is expanded in details in appendix b. We can interpret the recursive maximizing process this way: if ${\widehat{P}}_s(y^n)\ge {\displaystyle {\prod }_{i=0}^{\left|A\right|-1}{\widehat{P}}_{s_a}^{*}(y^n)}$, branches below s are trimmed as in Fig. 1B. Assume that the depth D of the model we start with is deeper than that of the actual source. It is worth noting, however, that the magnitude of D is limited by the amount of data points and is actually conveniently bounded by a function of the length of the data n, which is D(n) = o(log n) (Csiszár and Talata 2006).

This method is the so-called context tree maximizing (CTM) algorithm (Willems et al. 2000). Although CTM is not a consistent estimator in general, it has a very low computational complexity as well as a low memory requirement, and by penalizing complex models, it mitigates the problem of overfitting.

Probability Estimation for Multiple Neurons

Because neural spike trains are discrete time binary sequences where |A| = 2, a binary context tree is used to estimate the probabilities of individual neurons. However, to calculate the causally conditioned entropy term in DI, the individual term P(y_i|yⁱ⁻¹, xⁱ) is needed to calculate H(Y_i|Yⁱ⁻¹,X_i) for Eq. 3. The most common way to estimate joint probability is to augment X with Y. Let Z = X + 2Y and conduct the context tree estimation algorithm on Z, whose alphabet size is then 4. Context tree estimation is executed on this new sequence Z to find P̂(z_i|zⁱ⁻¹). In fact, P̂(z_i|zⁱ⁻¹) = P̂(x_i,y_i|xⁱ⁻¹,yⁱ⁻¹). To obtain the P̂(y_i|xⁱ⁻¹,yⁱ⁻¹) term needed for DI, we simply take the marginal about X. This way, we can calculate the DI, which indicates the strength of the influence, from one neuron to another.

Reconstructing the Synaptic Profile

In addition to estimating the strength of information flow through a synaptic connection quantified by DI, it is also essential to distinguish excitation from inhibition as well as to infer the synaptic profile. We define synaptic profile as the time course of the synaptic action. It is a set of parameters that depict the relative impact of spikes with respect to time lags in neuron X on the likelihood of observing a spike in neuron Y. We specifically examined whether a 1 bit (spike) in X leads to a higher probability of Y having a 1 (excitation) or lower probability of a 1 bit (inhibition) compared with the average firing rate of Y. This problem of extracting the synaptic parameters only pertains to binary neural spike trains.

From the tree structure estimated using the joint sequence Z = X + 2Y discussed in Probability Estimation for Multiple Neurons, we can obtain how likely Y will be a 1 seeing certain contexts, which is defined by $P(Y_n=1|X_{n-D_0}^{n-1},Y_{n-D_0}^{n-1})$, where D₀ is the depth of the longest branch of the truncated tree. To describe the influence from the context digit i, we need to find P(Y_n = 1|X_n−i = 1) for each i ∈ {0,…, D₀}. P(Y_n = 1|X_n−i = 1) can be obtained by taking the marginal of the target context index i:

$$\widehat{P}(Y_n=1|X_{n-i})={\displaystyle \sum _{\begin{array}{c}\forall y_{n-k},k\in \{1,\dots D_0\}\\ \forall x_{n-k},k\ne i\end{array}}\widehat{P}(Y_n=1|X_{n-D_0}^{n-1},Y_{n-D_0}^{n-1})\times \widehat{P}(X_{n-D_0}^{n-1}\backslash X_{n-i},Y_{n-D_0}^{n-1}\left|X_{n-i}\right)}$$ (11)

where

$$\widehat{P}(X_{n-D_0}^{n-1}\backslash X_{n-i},Y_{n-D_0}^{n-1}|X_{n-i})=\frac{\{\text{count of context }{X}_{n-D_0}^{n-1},Y_{n-D_0}^{n-1}\}}{\text{{count of context }{X}_{n-i}\}}$$ (12)

Theorem 1.

Two binary sequences Xⁿ and Yⁿ are both Markov chains, of order D_X and D_Y, respectively. Then, for i ≤ max{D_X, D_Y},

$$\underset{n\to \infty }{\lim }\widehat{P}\left(Y_n\right|X_{n-i})-P(Y_n\left|X_{n-i}\right)=0$$ (13)

The proof of theorem 1 can be found in appendix c.

Then, simply subtracting away the average firing rate of neuron Y would produce the synaptic profile:

$$W(i)=\widehat{P}(Y_n=1|X_{n-i}=1)-\widehat{P}(Y_n=1)$$ (14)

The value and shape of W(i) not only convey the sign of the synaptic action, with positive values signaling synaptic excitation and negative values synaptic inhibition, they also depict the time course of the effect of a presynaptic spike in X on the firing probability of Y, which can help classify synapses as fast vs. slow. In Fig. 2, the synaptic profile differentiates a fast excitatory synapse from a much slower inhibitory synapse, providing information on the time course of the synaptic influence. Also note that the synaptic profile defined here is closely related to the cross-correlogram. The conditional probability term P̂(Y_n = 1|X_n−i = 1) is equivalent to the right side of the cross-correlogram normalized by the spike count of the presynaptic neuron X. Conversely, if the average firing rate of the postsynaptic neuron Y is subtracted away from the right side of the normalized cross-correlogram, we obtain W(i) defined in Eq. 14. The values from these two metrics could differ because of different estimation approaches.

Fig. 2.

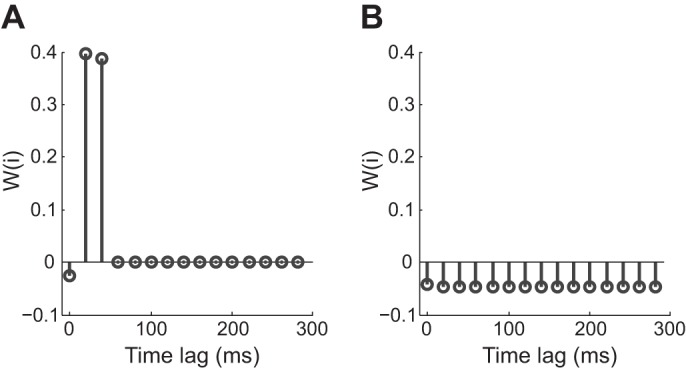
Synaptic profiles illustrating the time course of the synaptic action and distinguishing excitatory vs. inhibitory synaptic actions. A: profile of synapse AB from the network illustrated in Fig. 6A. The bin width used in this example was 10 ms. The influence from A to B is fast and strong. The values are positive, which indicates that the synapse is excitatory. B: profile of synapse BD from Fig. 6A. The influence from B to D is negative, suggesting an inhibitory connection. It is weak yet has a longer duration compared with AB.

Eliminating Indirect Connections

A positive DI value between two neurons does not guarantee an actual direct link between these two neurons. In fact, the information can flow through an indirect route. Quinn et al. (2011) describes two fundamental structures where indirect connections could be incorrectly identified as direct connections: the cascade structure and the proxy structure (Fig. 3). In the proxy configuration, the path of information flow is from X via Z to Y, but a false connection from X to Y could be detected. In the cascade configuration, neuron Z drives neuron X and neuron Y through two different paths, but a false connection could be detected between X and Y. To address this issue, Quinn et al. (2011) employ Kramer's concept of causally conditioned directed information (CCDI) (Kramer 1998), which is defined as

$$I(X^n\to Y^n\parallel Z^n)\triangleq H(Y^n\parallel Z^n)-H(Y^n\parallel X^n,Z^n)$$ (15)

The interpretation of this measure is very intuitive. If a connection between X and Y is suggested by DI and yet Z is the agent that actually directly influences Y, then the entropy estimate of Y knowing Z alone can account for the external information Y receives, and knowing X additionally would not yield any more information and, therefore, would not reduce the entropy further. On the other hand, if I(Xⁿ →Yⁿ‖Zⁿ) > 0, the connection between X and Y is direct and should be kept in the graph. Any context tree estimation method can easily estimate the H(Yⁿ‖Xⁿ,Zⁿ) term by joining the bits of the spike trains from X, Y, and Z to form an alphabet of size 8, an example of which is W = X + 2Y + 4Z.

Fig. 3.

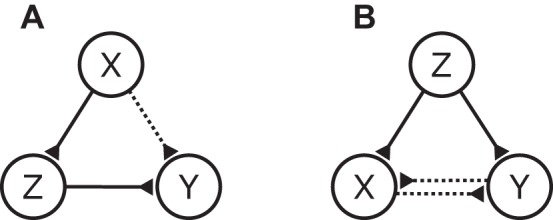
Two fundamental types of indirect connections. A: proxy configuration. The path of information flow is from X to Z to Y, yet a false connection from X to Y can be detected. B: cascade configuration. Neuron Z is driving neurons X and Y through 2 different paths, and a false connection can be detected between X and Y.

Strictly speaking, to identify whether a connection is direct, it is necessary to calculate CCDI simultaneously conditioned on all other neurons, which on one hand creates a forbiddingly large number of states and on the other demands a large amount of data to estimate those states. However, a heuristic is employed here analyzing small triangular structures. Evoking data processing inequality (DPI) for DI (see theorem 2), it is sufficient to perform CCDI analysis on all groups of three neurons that form the structures identified in Fig. 3 to eliminate all single-path indirect connections.

Definition 1.

Random sequences Uⁿ, Vⁿ, and Wⁿ form a directed causal chain if I(Uⁿ → Vⁿ) > 0, I(Vⁿ⁻¹ → Uⁿ) = 0, I(Vⁿ → Wⁿ) > 0, I(Wⁿ⁻¹ → Uⁿ) = 0, and I(Uⁿ → Wⁿ‖Vⁿ) = 0. With a slight abuse of notation, we denote this causal chain as Uⁿ → Vⁿ → Wⁿ. Using the notation of Markov chains, this relationship is expressed as Uⁱ → V_i, Vⁱ → W_i for i = 1, 2, …, n.

Theorem 2 (DPI for DI).

If Uⁿ → Vⁿ → Wⁿ causally, then I(Vⁿ → Wⁿ) ≥ I(Uⁿ → Wⁿ) and I(Uⁿ → Vⁿ) ≥ I(Uⁿ → Wⁿ).

The proof of theorem 2 can be found in appendix d.

We define a “1-relay” link as an indirect link with one intermediate relay neuron, a “2-relay” link as an indirect connection with two intermediate neurons, and so on. A “1-relay” link conveys more information than a “2-relay” link in signal transmission with noise, according to DPI. Therefore, by calculating CCDI on all groups of three and deleting links with 0 CCDI values, we can eliminate all single-path indirect connections. The limitation of this heuristic is that if multipath indirect connections arise, the indirect link might not be eliminated, and conditioning on more neurons is required.

Calculating Final DI Values

For every circuit analyzed, continuous time spiking signals were converted into discrete time spike trains using bin widths ranging from 2 ms to 30 ms with an increment of 1 ms. The DI algorithm was executed on all these spike trains. This range of bin widths was chosen in order to survey a sufficient amount of history to capture causal influences. From this, we plotted the values of DI vs. bin widths, where true connections had DI curves that plateaued after an initial rise (see Fig. 6C). If the DI curve for a connection had at least four consecutive values larger than a 0.01 threshold, all nonzero entries were averaged to produce the final DI value. In cases where four consecutive values > 0.01 did not occur, DI was set to 0.

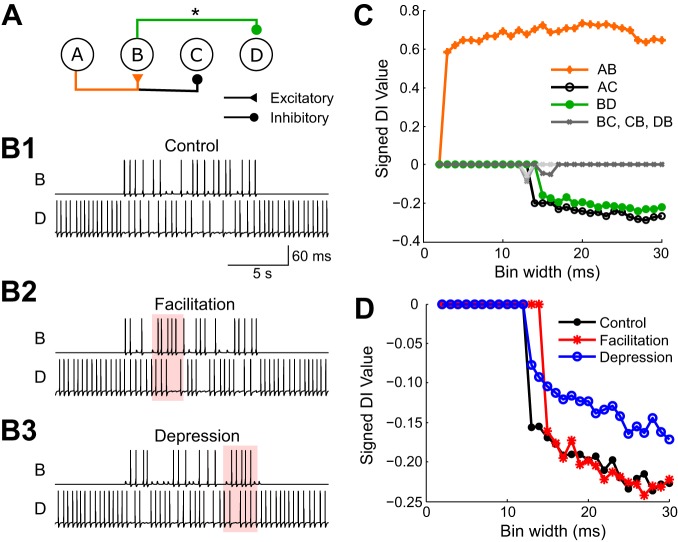
Fig. 6.

DI tested on a network with synaptic plasticity. A: a neural circuit in which neuron A excites neuron B and inhibits neuron C. Neuron B inhibits neuron D. Facilitation or depression was added to synapse BD (marked with an asterisk). B: sample traces generated by the circuit in three conditions: control (B1), facilitated (B2), and depressed (B3). The area of interest where the effects of plasticity can be observed is marked in pink. In B2 the strength of the synapse increases where spikes come in quick succession, whereas in B3 the strength of the synapse decreases where spikes closely follow each other. C: signed DI values plotted against bin widths for condition B2 with facilitation. D: signed DI values for synapse BD against different bin widths for all 3 different conditions.

The threshold of 0.01 was chosen based on a few preliminary receiver operating characteristic analyses generated from simulated neuronal spike trains. Typical excitatory and inhibitory synapses were simulated with the sparse Poisson spiking model detailed in Sparse Poisson spiking model. This value consistently yielded satisfactory results on realistic conductance-based network models and was therefore retained.

Implementation of Directed Information

The entire connectivity analysis was implemented in MATLAB. The software package includes a wrapper function that executes pairwise DI analysis, identifies triangular structures where indirect connections occur, and carries out causally conditioned DI on these structures to eliminate indirect connections. The package also includes a subfunction that conducts CTM estimation of sequences of any arbitrary alphabet size and can also generate the synaptic profile if needed. The implementation of the CTM-DI algorithm does not require specialized toolboxes from MathWorks and can be executed on open-source software such as Octave. This package can be found in our online depository (http://www.ece.rice.edu/neuroengineering/) with examples and instructions.

VSD Recording Technique

Aplysia californica (20–45 g) were obtained from the University of Miami National Institutes of Health National Resource for Aplysia. Animals were anesthetized by injection of isotonic MgCl₂ (0.5 ml/g). The buccal ganglia were isolated and pinned down to a Sylgard-lined imaging chamber containing artificial seawater (ASW) with a high concentration of divalent ions [in mM: 330 NaCl, 10 KCl, 90 MgCl₂(6H₂O), 20 MgSO₄, 30 CaCl₂(2H₂O), 10 HEPES] with a pH adjusted to 7.5. The ganglion was stained with the VSD, RH-155 (0.25 mg/ml; AnaSpec), for 7 min and imaged for 120 s in normal ASW [in mM: 450 NaCl, 10 KCl, 30 MgCl₂(6H₂O), 20 MgSO₄, 10 CaCl₂(2H₂O), 10 HEPES] with a pH adjusted to 7.5 and containing 10× dilution of RH-155 similar to Hill et al. (2015). The bath solution was maintained at 23°C room temperature. An Olympus BX50WI upright microscope was equipped with a ×20  0.95 NA water immersion objective. Light from a 150-W halogen bulb was passed through a 710/40 band-pass filter (BrightLine), and a 0.8 NA Olympus condenser, through the ganglia and projected to a 128 × 128 CMOS camera (Redshirt Imaging) recording at 2.5 kHz. The neurons were recorded for 2 min, which was preceded by a 15-s nerve stimulation (10 Hz, 100 V, 0.5 ms) and application of 40 μM l-DOPA (Tocris) to facilitate the induction of buccal motor programs (Kabotyanski et al. 2000). Twenty-eight cells were marked, and signals from pixels overlaying each cell were averaged to obtain the recording of a given neuron (see Fig. 8A). Each VSD signal was band pass filtered in MATLAB (Butterworth, Fpass1 = 15 Hz, Fstop1 = 0.1 Hz, Fpass2 = 1 kHz, Apass = 0.1, Astop1 = 60, Astop2 = 60). Spikes were detected in the VSD signal with a slope threshold method. If the peak of a signal differed by 2.5 times the standard deviation from the baseline measured 4 ms before and differed by 3 times the standard deviation from the postspike period measured 4.8 ms afterward, then a spike was said to occur. The spike times were then converted to binary spike trains (see Fig. 8B).

Fig. 8.

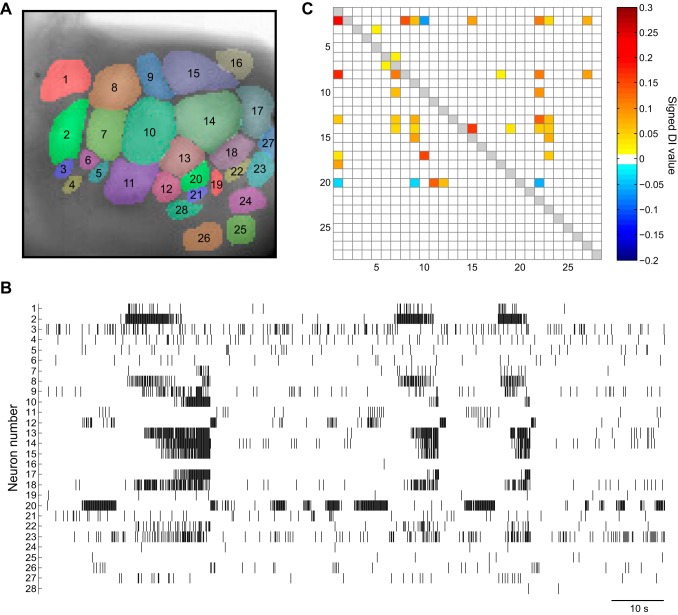
Analyzing VSD recording data with DI. A: VSD imaging surface of the caudal surface of the left buccal hemiganglion and kernel markup of the recording surface. B: raster plot of a 2-min VSD recording from the ganglion. C: adjacency matrix of the network obtained from DI analysis. Many putative connections were detected.

RESULTS

Validating the Connectivity Metric

Sparse Poisson spiking model.

As a first step to validate the method, a simple model of two neurons was used to examine the effect of various conditions and parameters on DI. This model is a variation of the sparse Poisson spiking model (Cutts and Eglen 2014). When the firing pattern of a neuron is sparse, a homogeneous Poisson process with a fixed rate can be used to model its spiking activity.

Neuron X was designed to be the “master neuron.” Spiking activity in X was generated by a Poisson model with a total length of T seconds and a rate of λ_X. For a fixed bin width Δ, the digitized sequence had n = T/Δ samples and on average k = λ_XT spikes. λ_X was chosen such that k ≪ n and that signal X was sparse. Spikes in neuron Y were generated directly based on the spikes in X, and therefore this synapse was excitatory. d represented the delay between a spike in X and a spike in Y and P(Y_i = 1|x_i−d = 1) the probability of one spike in X eliciting one spike in Y, which quantified the strength of the synapse. Some “jitter” was also introduced in Y’s spikes, and this temporal variation was defined by a Gaussian random variable w ~ N(0, σ²). Some baseline level activity was added to Y, which was defined by a Poisson process with rate λ_Y in addition to the spikes induced by X. MATLAB implementation of this model can also be found in our online repository.

In actual experiments, normalized DI Ĩ(X → Y) = Ī(X → Y)/H̄(Y) is preferred because it bounds the DI value between 0 and 1 as well as normalizing the information Y receives with respect to the level of information in itself. Normalized DI was used in the following results.

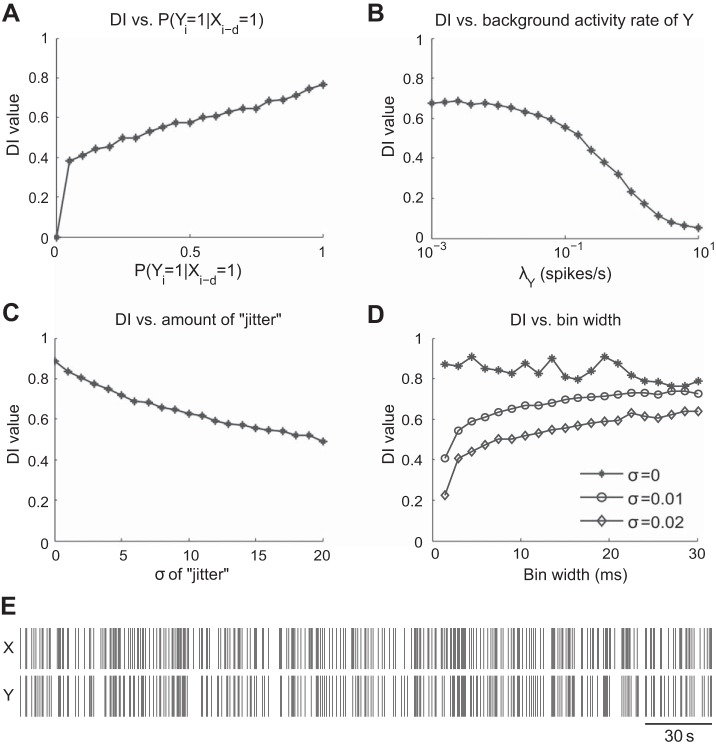
In the first example, we examined the effect of synaptic strength on Ĩ(X → Y) values. In this case, T = 600 s, Δ = 0.01 s, λ_X = 0.01, d = 0.05 s, and $\sigma =\frac{1}{\sqrt{2}}\Delta =0.00\text{7}$. Background activity of Y was suppressed by setting λ_Y ≈ 0. P(Y_i = 1|x_i-d = 1) was varied from 0 to 1 with an increment of 0.05. As expected, DI value increased with increased synaptic strength as the baseline activity level in the postsynaptic neuron was kept constant (Fig. 4A). Also note that normalized DI was plotted and the jump at 0 was caused by thresholding.

Fig. 4.

Trends of normalized DI tested under the sparse Poisson spiking model. Parameters such as synaptic strength, background activity rate of the postsynaptic neuron, amount of “jitter” for postsynaptic spikes, and bin width were examined. A: relationship between DI and varying levels of synaptic strength. Synaptic strength was varied by changing the probability of a postsynaptic spike being elicited after a presynaptic spike. As predicted, DI value increases with a stronger synapse when the baseline activity level in Y is kept constant. B: relationship between baseline activity level λ_Y of Y and DI. The value of DI decreases as the baseline activity in Y increases. C: relationship between the variance of the time course of the synaptic action and DI. The value of DI is inversely related to the variance of the time course. D: relationship between bin width and DI for different levels of “jitter.” A large drop in DI can be observed for σ ≥ 0.01 for small bin widths (≤3 ms). However, relatively small changes in DI can be seen for bin widths ≥ 10 ms. At σ = 0, DI remains high regardless of the size of the bin width. E: sample spike trains generated by the Poisson spiking model. λ_Y = 0.1 and other parameters are the same as the model in B.

In the second example, we examined the effect of background activity level in Y on Ĩ(X → Y) values. λ_Y was varied from 0.001 to 10 while the synaptic strength P(Y_i = 1|x_i-d = 1) was held constant at 0.8. Although the synaptic strength was kept constant, DI value decreased as the baseline activity level of Y increased (Fig. 4B), illustrating that DI is not solely determined by synaptic strength. Indeed, DI quantifies the amount of information flow from one neuron to another. DI quantifies how much the information present in neuron Y can be accounted for by the information in X. Therefore, if X accounts for only a small portion of the spikes in Y, then DI would be relatively small.

In the third example, we examined the effect of the variation in the time course of the synaptic response on normalized directed information. Let P(Y_i = 1|x_i-d = 1) = 0.8, and λ_Y ≈ 0. σ was increased from 0 to 0.02. It makes intuitive sense that more variance in the distance between a pre- and a postsynaptic spike made the pattern more unpredictable, and hence the lower the DI value (Fig. 4C).

In the final example, we examined the effect of varying bin width on Ĩ(X → Y) in the presence of noise. Bin widths between 1.5 ms and 30 ms were examined. When the synaptic delay had 0 variance, different bin widths should not have any influence on the normalized DI values, because each time a presynaptic spike occurred CTM was sure to find a postsynaptic spike exactly d/Δ bins away. We demonstrated this by setting P(Y_i = 1|x_i-d = 1) = 0.8 and σ = 0 (Fig. 4D). Note that the fluctuation in DI was caused by the artifact of binning an already discretized signal. Then, we set σ = 0.01 and 0.02. In the presence of synaptic time course variation, however, as we used smaller bin width Δ, normalized DI became smaller as well. Essentially, (d + w)/Δ landed in more different patterns as Δ decreased. This result illustrates that a small bin width is not always desirable in order to detect a slow connection, whose slower dynamics entails a greater range of variation in the time course of its synaptic response.

Simulated neural networks.

Next, we used the realistic networks generated in the neurosimulator SNNAP (Simulator for Neural Networks and Action Potentials) to further validate CTM-DI. SNNAP has the ability to simulate each neuron with a set of Hodgkin-Huxley-type conductance-based equations and different types of chemical and electrical synapses with or without plasticity (Av-Ron et al. 2006, 2008; Baxter and Byrne 2007; Ziv et al. 1994). This toolbox also has the ability to introduce random noise into various components of the mathematical formulation such as the membrane leakage current and the synaptic current. SNNAP has been used to model the CPG in the buccal ganglion of Aplysia (Cataldo et al. 2006; Susswein et al. 2002), and therefore it is a useful tool to check the performance of our method. It is also worth noting that, unlike the previous example, which is based on a linear spiking model, SNNAP can simulate realistic neural connections and their activity. The Java-based SNNAP software, as well as all the networks used in this section, can be found in the online repository.

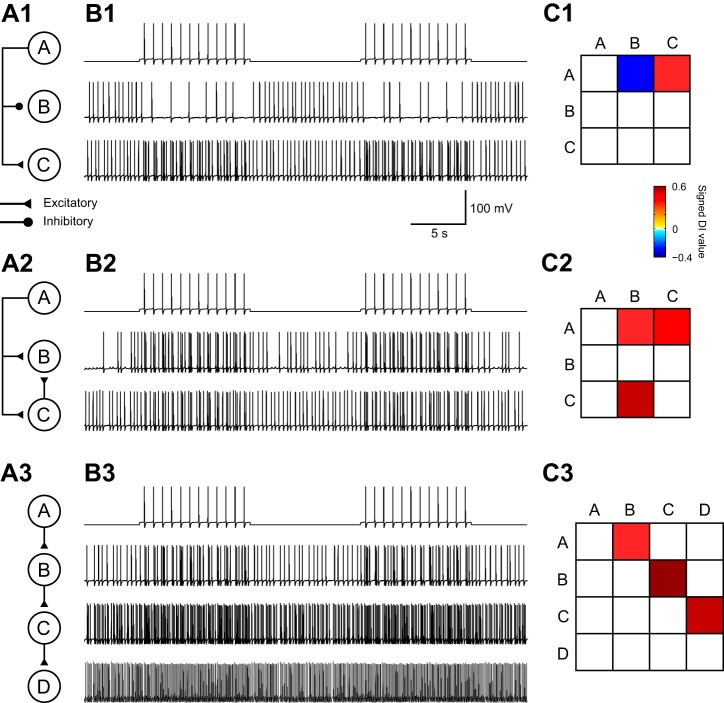
We began by testing our method using three simple circuits without synaptic plasticity. For all three circuits, simulations were 200 s in duration and neuron A was activated by a depolarizing current (0.57 nA, 10 s) added at an interstimulus interval of 10 s. The connectivity matrix detected by DI was represented as a heat map. In this heat map, rows represent presynaptic cells and columns represent postsynaptic cells. Therefore, each entry of the matrix represents a connection from the cell of the corresponding row to the cell of the corresponding column. Warmer colors indicate excitatory connections, whereas cooler ones indicate inhibitory connections (Fig. 5C). In the network of Fig. 5A1, DI correctly distinguished the excitatory connection from the inhibitory connection. The network of Fig. 5A2 contained a convergence of a direct and an indirect path, and the method was able to identify the correct connections without incorrectly eliminating the disynaptic connection. In the network of Fig. 5A3, the four neurons formed a feedforward chain. The method successfully predicted the appropriate connections and eliminated all indirect connections that could possibly arise from the long chain.

Fig. 5.

DI correctly inferred the connectivity in 3 simple networks. A1: neuron A inhibits neuron B and excites neuron C. A2: a network with convergence of a direct connection and a disynaptic connection, where neuron A excites neurons B and C and neuron C excites B. A3: a chain of feedforward excitation from neuron A to neuron D. B: simulated membrane potential for each neuron within the corresponding network in A. Each trace corresponds to the adjacent neuron in A. C: DI values inferred from the spike activity. A row is a presynaptic neuron, whereas a column is a postsynaptic neuron. Warm colors represent excitatory connections, whereas cool colors represent inhibitory connections. Note that DI values are always positive. Signs determined with the method introduced in Reconstructing the Synaptic Profile are attached to the DI values for ease of visualization.

As a comparison, we applied the cross-correlogram method on these three examples. The bin width of each network was chosen to be the same as that used in the CTM-DI method, and the total number of bins the cross-correlogram has was 2D + 1, where D was the maximum depth we used to initialize the tree. A χ²-test with a significance level of 0.01 was used to detect significant relations. The strengths of the connections were determined by Equation 6 in Shao and Tsau (1996), and the directions of the connections were determined by the locations of the peaks or troughs. The cross-correlogram performed comparably on networks A1 and A2. However, on network A3, the cross-correlogram failed to eliminate the indirect connections AC and BD.

We next tested the effect of synaptic plasticity on DI. Three different conditions were simulated in which the plasticity was manipulated for synapse B to D: no plasticity, with facilitation, and with depression. No other synaptic connections within this network had plasticity. Sample signal traces from the simulations are shown in Fig. 6B. Estimates of DI were made on spike trains with different time resolutions (Fig. 6C). This example shows that the method is able to correctly infer the network even in the presence of synaptic plasticity (Fig. 6D). Note that introducing depression reduced the DI value but did not eliminate it entirely in this connection.

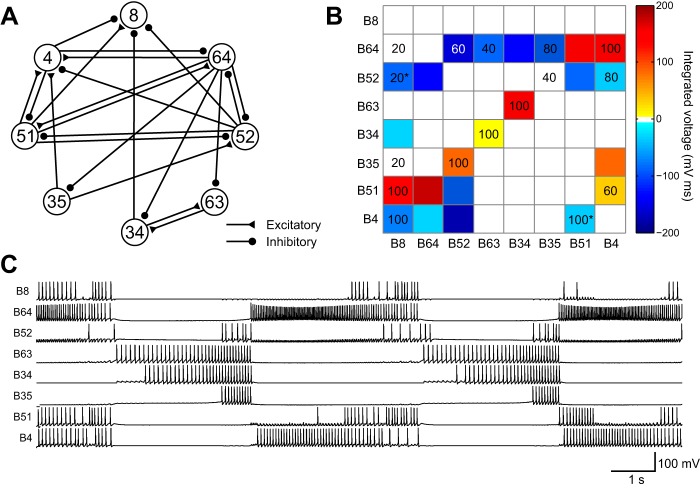
We next tested the algorithm on a model of components of a CPG circuit of Aplysia (Cataldo et al. 2006), which simulates some of the neuronal activity underlying feeding behavior. The model was slightly modified to simulate ingestion buccal motor patterns. The model included eight known neurons: B4, B8, B34, B35, B51, B52, B63, and B64 (Fig. 7). This network contains excitatory and inhibitory synaptic connections, many of which exhibit facilitation or depression. Finally, some of these neurons contain regenerative properties that elicit recurrent spike activity that outlasts the excitatory input. All of these features are present in the actual feeding CPG of Aplysia, and therefore this model provides a comprehensive test for DI. White Gaussian noise was introduced into the membrane leakage currents for all cells and the synaptic currents for all synapses. Five trials of simulations, each 2 min long, were generated. In this network, 2 min of simulated data was sufficient for the algorithm to converge. The algorithm correctly identified on average 9.2 (5.6 + 3.6) key connections (Fig. 7B and Table 1), and, together with true negatives, DI correctly located or rejected 41.4 of all 56 possible connections (diagonals excluded). The number of false positives was on average less than one synapse per trial. The number of false negatives, however, was on average 12.4 (3.4 + 9) synapses per trial. However, it is worth noting that seven of the undetected synapses were weak connections: B64-B34, B52-B64, B52-B51, B34-B8, B25-B4, B51-B52, and B4-B52. When these connections were trimmed from the simulator, the quality of the feeding pattern was not affected. This possible simplification illustrates the importance of a functional connectome, which identifies active information pathways that are in a subset of the anatomical connectome. Three essential connections, B64-B51, B51-B64, and B4-B64, went undetected throughout all five trials. The electrical coupling between B64 and B51 might have been overlooked by DI because the connection did not produce any clear spike-to-spike relationship, which is a limitation of this method. The inhibitory synapse B4-B64 was not detected by DI presumably because the B4-B64 synaptic connection did not have adequate strength to overcome the strong regenerative properties of B64. There were on average 1.4 incorrect signs, all of which were inhibitory synapses inferred to be excitatory. The B4-B51 synaptic connection was a biphasic synapse with an early excitatory and a later inhibitory component. The excitatory component seemed to override the inhibitory component, leading DI to infer an excitatory rather than inhibitory connection.

Fig. 7.

Testing a conductance-based model of the central pattern generator (CPG) in the buccal ganglion of Aplysia. A: connections of the CPG model. B: the same model network represented in a matrix format. Values represented as colors in the matrix were obtained from integrated voltages of the postsynaptic potentials from the simulation. Numbers inside the matrix indicate % of time a given synapse was detected by DI. A number on a colored background is a true positive. A number on a white background is a false positive. A number marked by an asterisk indicates an incorrect sign, which occurred at B52-B8 and B4-B51. Zero values were not included. C: simulated spiking activity of the CPG.

Table 1.

DI performance on simulated CPG network

	True (+)		True (−)	Incorrect Sign		False (+)		False (−)
Trial	E-E	I-I	N-N	E-I	I-E	E-N	I-N	N-E	N-I
1	6	4	32	1	0	0	1	3	9
2	5	4	31	1	0	2	0	4	9
3	5	5	32	1	0	1	0	4	8
4	6	2	33	2	0	0	0	3	10
5	6	3	33	2	0	0	0	3	9
Mean	5.6	3.6	32.2	1.4	0	0.6	0.2	3.4	9
SD	0.2	0.5	0.4	0.2	0	0.4	0.2	0.2	0.3

Letters with dashes indicate the DI detection − actual. For example, E-E denotes that DI inferred an excitatory (E) connection and this connection was indeed modeled as excitatory. I-N denotes that DI inferred an inhibitory (I) connection between two neurons but no (N) connection was actually modeled between these neurons.

Mapping Connectivity of Recorded Neurons

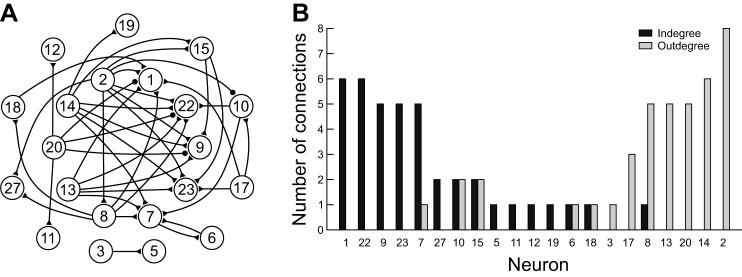
After DI was tested on the simulated CPG network, DI was applied to VSD recordings (Fig. 8). Neurons with <10 spikes were excluded from the analysis. Bin widths ranging from 2 ms to 30 ms were used to generate spike trains, on which DI was applied. The DI algorithm detected many putative connections, their signs (i.e., excitatory or inhibitory), and their relative strengths of influence (Fig. 8C). Some of the detected connections were consistent with visual inspection, such as 2-1, 14-15, and 17-10, in which activity of one neuron seemed to follow the activity of the other. The algorithm also revealed some connections that would otherwise be difficult to observe, such as 2-10, 3-5, and 8-27.

We next examined a general architectural feature of the inferred network from the VSD recordings by determining whether the recorded neurons could be categorized as either sources or sinks. We compared the indegree and outdegree for each neuron (Fig. 9B). In graph theory, indegree is the number of incoming connections to a node, and outdegree is the number of outgoing connections from a node (Chartrand and Zhang 2012). Nodes with positive indegrees and 0 outdegrees are sinks, whereas those with positive outdegrees and 0 indegrees are sources. Neurons either primarily sent outgoing (e.g., 2, 8, 13, 14, 17, and 20) connections or primarily received (e.g., 1, 7, 9, 22, and 23) connections, which suggests that information generally flows unidirectionally in the network and that these sources and sinks are specialized neurons and may be premotor and motor neurons, respectively. This pattern of connectivity of neurons will aid in identifying cells in the buccal ganglion network. For example, neuron 20 makes many outgoing connections and is located in a region of the ganglia where many pattern initiator neurons are found.

Fig. 9.

Patterns of connectivity of the preparation in Fig. 8. A: inferred connectivity diagram. B: indegrees and outdegrees of neurons. Neurons without any connections are not shown. This graph shows neurons that primarily receive connections (left) and those that send out connections (right).

DISCUSSION

Our method of exploiting the CTM entropy estimator together with DI can infer functional connectivity in small realistic simulated neural networks. The CTM-based estimator has the advantage of low computational complexity and fast convergence, being nonparametric, as well as being able to mitigate overfitting. We have shown that our implementation of CTM can identify direct connections, eliminate indirect connections, reliably distinguish excitatory from inhibitory synaptic actions, and quantify the amount of information flow from one neuron to another (Fig. 5). Furthermore, this inference technique based on DI is robust against signal nonlinearities, which linear methods such as GC or estimates based on the generalized linear model might not be able to capture. For example, it is able to detect connections with facilitation or depression (Fig. 6), which are common throughout invertebrate and vertebrate nervous systems.

A sound CTM-DI theoretical framework requires the observed sequences to be stationary. We believe this assumption is valid, because in the VSD recordings the buccal motor patterns are similar from one to the next and so the underlying system appears to be stationary during the limited frame of the analysis. The context tree method analyzes different contexts, which are patterns, independently. Therefore, it is able to analyze not only tonic activity but also phasic activity. The result of the CTM-DI algorithm is the average strength taking into account all the different spiking patterns in the recording window.

The CTM-DI based method has its own limitations. A challenge for the DI-CTM approach is a combination of weak connections and sparse activity. Many networks use spatial summation of multiple weak connections (Adesnik et al. 2012); therefore, weak connections may be a fundamental component of a network. Detecting weak connections is one of the general disadvantages of using discrete time spike trains that other analyses using point process-GLM-based GC and DI encounter as well. Bin widths that are used to segment a spiking signal into a binary spike train are small compared with the interevent intervals of spikes. As a result, 0s predominate the sequence. Maximum entropy is achieved when 0s and 1s are equally likely. With predominantly 0s, the entropy of the sequence is already low, and then any further drop in entropy due to conditioning on another sequence will be negligible. This problem could potentially be mitigated by dynamically setting a baseline firing rate. Another limitation of our method, as well as other methods analyzing binary spike trains, is the difficulty in detecting inhibitory synapses, especially when the postsynaptic cell is already inactive or is completely suppressed. Such synapses, however, could have a significant influence on the network despite not being detected by DI. Strong inhibition and weak excitation are challenging for statistical methods because they are based on spike trains that do not reflect information on subthreshold excitatory or inhibitory postsynaptic potentials, which are all mapped to the value 0. Further developments of the DI method might include a combination of spike train analysis and analysis of the analog signals. Presynaptic inhibition is another challenge for pairwise causality analysis, which requires conditioning on more than one neuron.

Despite some limitations, the CTM-DI-based method has practical advantages. It naturally turns its focus onto active neurons that are generating information and playing an important role in the network. It captures the salient, active communication pathways of a neural network. The method produced promising results on the realistic Aplysia buccal CPG network. DI correctly identified many connections in the CPG model circuit with a relatively small false positive rate. We applied the technique to the VSD recordings of the Aplysia buccal ganglion and discovered some interesting putative functional connectome structures. In a single recording this method identified 40 putative synaptic connections, a feat that would be virtually impossible with pairwise intracellular electrodes. The DI analysis suggested that neurons tended to be either sources or sinks and rarely have an equal number of indegree and outdegree connections. This finding indicates that the flow of information in the feeding network tends to be unidirectional. However, additional experiments are needed to confirm this observation. It will be interesting to apply the technique to ganglia before and after different forms of learning such as operant and classical conditioning (Brembs 2003; Lechner et al. 2000; Lorenzetti et al. 2006; Nargeot et al. 1999). DI has the potential to identify distributed sites of plasticity and the ways in which the circuit is reconfigured by learning. The results of this study indicate that this method is highly versatile and correctly infers the connectivity of networks containing many different features in complex circuits. This versatility indicates that this technique can also be applied to more complex systems such as the vertebrate central nervous system.

GRANTS

This work was supported by Grant 362804 from The University of Texas System Neuroscience and Neurotechnology Research Institute.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials, in specific MATLAB files and SNNAP model files, related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is: http://www.ece.rice.edu/neuroengineering/. These materials are not a part of this manuscript, and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

Z.C., C.L.N., D.A.B., J.H.B., and B.A. conceived and designed research; Z.C. and C.L.N. analyzed data; Z.C., C.L.N., D.A.B., J.H.B., and B.A. interpreted results of experiments; Z.C. and C.L.N. prepared figures; Z.C. drafted manuscript; Z.C., C.L.N., D.A.B., J.H.B., and B.A. edited and revised manuscript; Z.C., C.L.N., D.A.B., J.H.B., and B.A. approved final version of manuscript; C.L.N. performed experiments.

APPENDIX A: SEQUENTIAL KT ESTIMATOR

Likelihood function P(yⁿ|θ) is modeled as a sequence of multivariate Bernoulli variables with parameters θ = (θ₀, …, θ_|A|-1), where θ_i > 0 and ${{\displaystyle \sum }}_{i=0}^{M-1}{\theta }_i=\text{1}$. In a realization yⁿ, the count for symbol a_i ∈ A is denoted by c_i for simplicity in notation and ${{\displaystyle \sum }}_{i=0}^{\left|A\right|-1}=n$. The probability of this specific string yⁿ being generated is

$$P\left(y^n\right|\mathbf{\theta })={\displaystyle \prod _{i=0}^{\left|A\right|-1}{({\theta }_i)}^{c_i}}$$ (16)

A Dirichlet (γ, . . ., γ) distribution is the prior, denoted by P(θ|γ) where γ is the hyperparameter:

$$P=(\mathbf{\theta }|\gamma )=\frac{\text{Γ}(\gamma \left|A\right|)}{\text{Γ}{(\gamma )}^{\left|A\right|}}{\displaystyle \prod _{i=0}^{\left|A\right|-1}{\theta }_i^{\gamma -1}}$$ (17)

where Γ(·) is the gamma function. Let us denote the estimated probability generated specifically by the KT estimator by P̂. Then the probability of the sequence is

$$\begin{array}{c}\widehat{P}\left(y^n\right)=P\left(y^n\right|\gamma )={\displaystyle \underset{\theta }{\int }P}(\mathbf{\theta }|\gamma )P(y^n|\mathbf{\theta })d\mathbf{\theta }\\ =\frac{\text{Γ}(\gamma \left|A\right|)}{\text{Γ}{(\gamma )}^{\left|A\right|}}\end{array}$$ (18)

$${\displaystyle {\int }_0^1{\displaystyle {\int }_0^{1-{\theta }_0}\dots }{\displaystyle {\int }_0^{1-{\theta }_0\dots -{\theta }_{\left|A\right|-2}}}}{\displaystyle \prod _{i=0}^{\left|A\right|-2}{\theta }_i^{c_i+\gamma -1}}\times {\left(1-{\theta }_0\dots -{\theta }_{\left|A\right|-2}\right)}^{c_{\left|A\right|-1}+}{}^{\gamma -1}d{\theta }_{\left|A\right|-2}\dots d{\theta }_0$$ (19)

$$=\frac{\text{Γ}\left(\gamma \left|A\right|\right){\displaystyle {\prod }_{i=0}^{\left|A\right|-1}\text{Γ}\left(c_i+\gamma \right)}}{\text{Γ}{\left(\gamma \right)}^{\left|A\right|}\text{Γ}\left(n+\gamma \left|A\right|\right)}$$ (20)

We express θ_|A|−1 = 1 − θ₀… −θ_|A|−2. θ here is a |A|-dimensional simplex. The integral in Eq. 19 is the multivariate beta integral. When γ = 1/2, this estimated probability evaluates to

$$\widehat{P}(y^n)=\frac{\text{Γ}\left(\frac{\left|A\right|}{2}\right){\displaystyle {\prod }_{i=0}^{\left|A\right|-1}\text{Γ}\left(c_i+\frac{1}{2}\right)}}{{\pi }^{\frac{\left|A\right|}{2}}\text{Γ}\left(n+\frac{\left|A\right|}{2}\right)}$$ (21)

Using the properties of the gamma function Γ(x) = (x − 1)Γ(x − 1) as well as $\text{Γ}\left(\frac{1}{2}\right)=\sqrt{\pi }$, it is easily shown that

$$\widehat{P}(y^n)=\frac{\text{Γ}\left(\frac{\left|A\right|}{2}\right){\displaystyle {\prod }_{i=0}^{\left|A\right|-1}\left(c_i-1+\frac{1}{2}\right)\left(c_i-2+\frac{1}{2}\right)\cdots \left(\frac{1}{2}\right)\text{Γ}\left(\frac{1}{2}\right)}}{{\pi }^{\frac{\left|A\right|}{2}}\left(n-1+\frac{\left|A\right|}{2}\right)\left(n-2+\frac{\left|A\right|}{2}\right)\cdots \left(\frac{\left|A\right|}{2}\right)\text{Γ}\left(\frac{\left|A\right|}{2}\right)}$$ (22)

which is exactly Eq. 6. Equation 21 also shows that P̂(ϕ) = 1 (in this case n and c_i are 0).

APPENDIX B: INCORPORATING PENALTIES INTO RECURSIVE MODEL FINDING

For the objective function defined by Eq. 9 in terms of code length with total number of nodes as a trade-off

$$\widehat{T}\left(y^n\right)=\arg \hspace{0.17em}\underset{\mathcal{T}\in I}{\min }-\log {\hspace{0.17em}\widehat{P}}_{\mathcal{T}}\left(y^n\right)+(\left|\mathcal{S}\right|+\left|u:u\prec s\right|)\log \left|A\right|$$ (23)

Take exp{−(·)} on both sides and we have

$$\exp \{-\widehat{\mathcal{T}}(y^n\left)\right\}={\widehat{P}}_{\mathcal{T}}\left(y^n\right)\exp \{-\left|\mathcal{S}\right|\log \left|A\right|-\left|u:u\prec s\right|\log \left|A\right|\}$$ (24)

$$={\left(\frac{1}{\left|A\right|}\right)}^{\left|u:u\prec s\right|}\cdot {\displaystyle \prod _{s\in \left|S\right|}\widehat{P}(y^n|s)}{\displaystyle \prod _{s\in \left|S\right|}{\left|A\right|}^{-\left|\mathcal{S}\right|}}$$ (25)

$$={\left(\frac{1}{\left|A\right|}\right)}^{\left|u:u\prec s\right|}\cdot {\displaystyle \prod _{s\in \left|S\right|}\frac{1}{\left|A\right|}\widehat{P}(y^n|s)}$$ (26)

Therefore, it is clearly shown that a penalty factor of $\frac{1}{\left|A\right|}$ is applied to the estimate of each leaf. The term ${(\frac{1}{\left|A\right|})}^{\left|u:u\prec s\right|}$ corresponds to the penalty generated by all the inner nodes. While this term cannot be factored into individual contexts, it can be understood this way: if instead of the parent node the child nodes are kept as contexts, the parent node still needs to be kept and hence 1 more node in addition to the child nodes is added to the structure. Therefore, a factor of $\frac{1}{\left|A\right|}$ is added to the product term in Eq. 10.

APPENDIX C: PROPERTY OF THE PROFILE ESTIMATOR

Proof of Theorem 1

Let Z be a new random variable with an alphabet of size 4 obtained by Z = 2X + Y, then $P(Z_n|Z^n{}^{-\text{1}})=P\left(Z_n|Z_{n-D_0}^{n-1}\right)$, where D₀ = max{D_X, D_Y}. Let P(Z_n|Zⁿ⁻¹) denote the true conditional probability of Z. Denote the KT estimate of the conditional probability by P̂_KT(Z_n|Zⁿ⁻¹) and the maximum likelihood (ML) estimate by P̂_ML(Z_n|Zⁿ⁻¹). We know that ∀k ∈ {1,…, D₀}

$$\widehat{P}(Y_n=1|X_{n-i})={\displaystyle \sum _{\begin{array}{c}\forall x_{n-k},k\ne i\\ \forall y_{n-k}\end{array}}{\widehat{P}}_{\text{KT}}\underset{A}{\underbrace{(Y_n=1|X_{n-D_0}^{n-1},Y_{n-D_0}^{n-1})}}\times \widehat{P}\underset{B}{\underbrace{(X_{n-D_0}^{n-1}\backslash X_{n-i},Y_{n-D_0}^{n-1}|X_{n-i})}}}$$ (27)

First note that ${\widehat{P}}_{\text{KT}}(Y_n=1|X_{n-D_0}^{n-1},Y_{n-D_0}^{n-1})$ is obtained by taking the marginal of ${\widehat{P}}_{\text{KT}}(Z_n|Z_{n-D_0}^{n-1})$, where for each a ∈ Z

$${\widehat{P}}_{\text{KT}}(Z_n=a|Z_{n-D_0}^{n-1})-{\widehat{P}}_{\text{ML}}(Z_n=a|Z_{n-D_0}^{n-1})$$ (28)

$$=\frac{c\left(a\right)+\frac{1}{2}}{n+\frac{\left|A\right|}{2}}-\frac{c(a)}{n}$$ (29)

$$=\frac{\frac{1}{2}(n-c(a)\cdot \left|A\right|)}{n^2+\frac{\left|A\right|}{2}n}$$ (30)

As n → ∞, Eq. 30 → 0. Since the maximum likelihood estimate (MLE) is asymptotically consistent, we have

$${\widehat{P}}_{\text{KT}}(Z_n=a|Z_{n-D_0}^{n-1})-P(Z_n=a|Z_{n-D_0}^{n-1})={ϵ}_1\stackrel{n\to \infty }{\to }0$$ (31)

The second term for Eq. 11 is calculated by

$$\widehat{P}(X_{n-D_0}^{n-1}\backslash X_{n-i},Y_{n-D_0}^{n-1}|X_{n-i})=\frac{c(X_{n-D_0}^{n-1},Y_{n-D_0}^{n-1})}{c(X_{n-i})}$$ (32)

where c(·) is the count function. If Zⁿ is Markovian, Zⁿ⁻¹ ∩ {X_n-i = 1} is also Markovian. We then can use the typicality theorem for stationary, irreducible Markov chains (Csiszár 2002). For a fixed-order D₀, the empirical frequency of a length D₀ string tends to its true probability:

$$\left|\frac{\widehat{P}(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})}{P(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})}\right|<C\sqrt{\frac{\log \hspace{0.17em}\log \hspace{0.17em}n}{n}}$$ (33)

$$1-C\sqrt{\frac{\log \hspace{0.17em}\log \hspace{0.17em}n}{n}}<\frac{\widehat{P}(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})}{P(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})}<1+C\sqrt{\frac{\log \hspace{0.17em}\log \hspace{0.17em}n}{n}}$$ (34)

$$\left|\widehat{P}(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})-P(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})\right|<C\cdot P(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})\sqrt{\frac{\log \hspace{0.17em}\log \hspace{0.17em}n}{n}}$$ (35)

Since $P(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})$ is bounded by 1,

$$\left|\widehat{P}(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})-P(Z_{n-D_0}^{n-1}\backslash X_{n-i}|X_{n-i})\right|={ϵ}_2\stackrel{n\to \infty }{\to }0$$ (36)

Putting everything together, we have

$$\widehat{P}(Y_n=1|X_{n-i})={\displaystyle \sum _{\begin{array}{c}\forall x_{n-k},k\ne i\\ \forall y_{n-k}\end{array}}{\widehat{P}}_{\mathrm{K}\mathrm{T}}(A)\times \widehat{P}(B)}$$ (37)

$$={\displaystyle \sum _{\begin{array}{c}\forall x_{n-k},k\ne i\\ \forall y_{n-k}\end{array}}[P(A)+{ϵ}_1][P(B)+{ϵ}_2]}$$ (38)

$$={\displaystyle \sum _{\begin{array}{c}\forall x_{n-k},k\ne i\\ \forall y_{n-k}\end{array}}[P(A)P(B)+{ϵ}_{1}P(B)+{ϵ}_{2}P(A)+{ϵ}_1{ϵ}_2]}$$ (39)

$$=P(Y_n=1|X_{n-i})+{\displaystyle \sum _{\begin{array}{c}\forall x_{n-k},k\ne i\\ \forall y_{n-k}\end{array}}[{ϵ}_{1}P(B)+{ϵ}_{2}P(A)+{ϵ}_1{ϵ}_2]}$$ (40)

and then

$$\widehat{P}(Y_n=1|X_{n-i})-P(Y_n=1|X_{n-i})={\displaystyle \sum _{\begin{array}{c}\forall x_{n-k},k\ne i\\ \forall y_{n-k}\end{array}}[}{ϵ}_{1}P(B)+{ϵ}_{2}P(A)+{ϵ}_1{ϵ}_2]$$ (41)

$$\le 2^{(2D_0-1)}({ϵ}_1+{ϵ}_2+{ϵ}_1{ϵ}_2)$$ (42)

In most neural science applications, D₀ is finite and does not grow with n; therefore $2^{(2D_0-1)}<\infty$. Because ϵ₁P(B), ϵ₂P(A), and ϵ₁ϵ₂ tend to 0 as n → ∞, the statement is proved.

APPENDIX D: ELIMINATING INDIRECT CONNECTIONS

Proof of Theorem 2

The first inequality can be easily shown, because we have Wⁿ as a common receptor.

$$I(U^n\to W^n)=H(W^n)-H(W^n\parallel U^n)$$ (43)

$$=H(W^n)-{\displaystyle \sum _{i=1}^{n}H}(W_i|W^{i-1},U^i)$$ (44)

$$=H(W^n)-\left[{\displaystyle \sum _{i=1}^{n}H}(W_i|W^{i-1},U^i,V^i)+{\displaystyle \sum _{i=1}^{n}I}(W_i;V^i|W^{i-1},U^i)\right]$$ (45)

$$=H(W^n)-H(W^n\parallel U^n,V^n)-{\displaystyle \sum _{i=1}^{n}I}(W_i;V^i|W^{i-1},U^i)$$ (46)

We can expand I(Vⁿ → Wⁿ) similarly:

$$I(V^n\to W^n)=H(W^n)-H(W^n\parallel U^n,V^n)-{\displaystyle \sum _{i=1}^{n}I}(W_i;U^i|W^{i-1},V^i)$$ (47)

Then

$$I(V^n\to W^n)–I(U^n\to W^n)={\displaystyle \sum _{i=1}^n}\left[I(W_i;V^i|W^{i-1},U^i)-\underset{=0}{\underbrace{I(U^i;W_i|W^{i-1},V^i)}}\right]$$ (48)

$$={\displaystyle \sum _{i=1}^{n}I(W_i;V^i|W^{i-1},U^i)}$$ (49)

$$\ge 0$$ (50)

The term I(W_i; Uⁱ|Wⁱ⁻¹, Vⁱ) = 0 because I(Uⁿ → Uⁿ||Vⁿ) = 0.

To show the second inequality, we express DI as a cumulative sum of mutual information:

$$I(U^n\to V^n)={\displaystyle \sum _{i=1}^{n}I(U^i;V_i|V^{i-1})}$$ (51)

$$=\underset{A}{\underbrace{{\displaystyle \sum _{i=1}^{n}I(U^i;V^i)}}}-\underset{B}{\underbrace{{\displaystyle \sum _{i=1}^{n}I(U^i;V^{i-1})}}}$$ (52)

and

$$I(U^n\to W^n)=\underset{C}{\underbrace{{\displaystyle \sum _{i=1}^{n}I(U^i;W^i)}}}-\underset{D}{\underbrace{{\displaystyle \sum _{i=1}^{n}I(U^i;W^{i-1})}}}$$ (53)

$$A={\displaystyle \sum _{i=1}^{n}I(U^i;V^i)}={\displaystyle \sum _{i=1}^{n}I(U^i;W^i,V^i)}-{\displaystyle \sum _{i=1}^{n}I(U^i;W^i|V^i)}$$ (54)

$$={\displaystyle \sum _{i=1}^{n}I(U^i;W^i,V^i)}-{\displaystyle \sum _{i=1}^n\left[H(U^i|V^i)-H(U^i|V^i,W^i)\right]}$$ (55)

$$={\displaystyle \sum _{i=1}^{n}I(U^i;W^i,V^i)}-{\displaystyle \sum _{i=1}^n\left[H(U^i|V^i)-H(U^i|V^i)\right]}$$ (56)

$$={\displaystyle \sum _{i=1}^{n}I(U^i;W^i,V^i)}$$ (57)

Because Vⁱ contains all the information in Wⁱ, H(Uⁱ|Vⁱ, Wⁱ) = H(Uⁱ|Vⁱ). On the other hand,

$$C={\displaystyle \sum _{i=1}^{n}I(U^i;W^i)={\displaystyle \sum _{i=1}^{n}I(U^i;V^i,W^i)-{\displaystyle \sum _{i=1}^{n}I(U^i;V^i|W^i)}}}$$ (58)

Therefore,

$$A-C={\displaystyle \sum _{i=1}^{n}I(U^i;V^i)-{\displaystyle \sum _{i=1}^{n}I(U^i;W^i)}}$$ (59)

$$={\displaystyle \sum _{i=1}^{n}I(U^i;V^i|W^i)}$$ (60)

Now, we look at the remaining terms:

$$B={\displaystyle \sum _{i=1}^{n}I(U^i;V^{i-1})={\displaystyle \sum _{i=1}^{n}I(U^{i-1},U_i;V^{i-1})}}$$ (61)

$$=\underset{=0}{\underbrace{{\displaystyle \sum _{i=1}^n}I(V^{i-1};U_i|U^{i-1})}}+{\displaystyle \sum _{i=1}^{n}I(V^{i-1};U^{i-1})}={\displaystyle \sum _{i=1}^{n}I(U^{i-1},V^{i-1})}$$ (62)

The reverse DI ${\displaystyle {\sum }_{i=1}^{n}I\left(V^i{}^{-\text{1}};U_i|U^i{}^{-\text{1}}\right)}=I(V^n{}^{-\text{1}}\to U^n)=0$ per problem statement. Similarly,

$$D={\displaystyle \sum _{i=1}^{n}I(U^i;W^{i-1})={\displaystyle \sum _{i=1}^{n}I(U^{i-1},W^{i-1})}}$$ (63)

From Eq. 60 we know that

$$B-D={\displaystyle \sum _{i=1}^{n}I(U^{i-1};V^{i-1})-{\displaystyle \sum _{i=1}^{n}I(U^{i-1},W^{i-1})}}$$ (64)

$$={\displaystyle \sum _{i=1}^{n}I(U^{i-1};V^{i-1}|W^{i-1})}$$ (65)

Then,

$$I(V^n\to W^n)-I(U^n\to W^n)$$ (66)

$$=A-C-(B-D)$$ (67)

$$={\displaystyle \sum _{i=1}^{n}I(U^i;V^i|W^i)-{\displaystyle \sum _{i=1}^{n}I}(U^{i-1};V^{i-1}|W^{i-1})}$$ (68)

$$={\displaystyle \sum _{i=1}^n\left[I(U^i;V^i,W^i)-I(U^i;W^i)-I(U^{i-1};V^{i-1},W^{i-1})+I(U^{i-1};W^{i-1})\right]}$$ (69)

$$={\displaystyle \sum _{i=1}^n[I(U^i;V_i,W_i|V^{i-1},W^{i-1})+I(U^i;V^{i-1},W^{i-1})-I(U^i;W_i|W^{i-1})}-I(U^i;W^{i-1})-I(U^{i-1};V^{i-1},W^{i-1})+I(U^{i-1};W^{i-1})]$$ (70)

$$={\displaystyle \sum _{i=1}^{n}I(U^i;V_i,W_i|V^{i-1},W^{i-1})-{\displaystyle \sum _{i=1}^{n}I(U^i;W_i|W^{i-1})}}$$ (71)

$$=I(U^n\to V^n,W^n)-I(U^n\to W^n)$$ (72)

$$\ge 0$$ (73)

Equation 71 follows from Eq. 70 because of Eq. 62. Therefore, I(Vⁿ → Wⁿ) ≥ I(Uⁿ → Wⁿ) and I(Uⁿ → Vⁿ) ≥ I(Uⁿ → Wⁿ).