Bayesian inference can account for the interaction between sensory data and past experience in many behaviors. Here, we show, using smooth pursuit eye movements, that the priors based on past experience can be adapted over a very short time frame. We also show that a single model based on direction-specific adaptation of the strength of visual-motor transmission can explain the implementation and adaptation of priors for both target direction and target speed.
Keywords: gain control, smooth pursuit eye movements, monkeys, extrastriate area MT, frontal eye fields, sensory-motor adaptation
Abstract
Bayesian inference provides a cogent account of how the brain combines sensory information with “priors” based on past experience to guide many behaviors, including smooth pursuit eye movements. We now demonstrate very rapid adaptation of the pursuit system’s priors for target direction and speed. We go on to leverage that adaptation to outline possible neural mechanisms that could cause pursuit to show features consistent with Bayesian inference. Adaptation of the prior causes changes in the eye speed and direction at the initiation of pursuit. The adaptation appears after a single trial and accumulates over repeated exposure to a given history of target speeds and directions. The influence of the priors depends on the reliability of visual motion signals: priors are more effective against the visual motion signals provided by low-contrast vs. high-contrast targets. Adaptation of the direction prior generalizes to eye speed and vice versa, suggesting that both priors could be controlled by a single neural mechanism. We conclude that the pursuit system can learn the statistics of visual motion rapidly and use those statistics to guide future behavior. Furthermore, a model that adjusts the gain of visual-motor transmission predicts the effects of recent experience on pursuit direction and speed, as well as the specifics of the generalization between the priors for speed and direction. We suggest that Bayesian inference in pursuit behavior is implemented by distinctly non-Bayesian internal mechanisms that use the smooth eye movement region of the frontal eye fields to control of the gain of visual-motor transmission.
NEW & NOTEWORTHY Bayesian inference can account for the interaction between sensory data and past experience in many behaviors. Here, we show, using smooth pursuit eye movements, that the priors based on past experience can be adapted over a very short time frame. We also show that a single model based on direction-specific adaptation of the strength of visual-motor transmission can explain the implementation and adaptation of priors for both target direction and target speed.
we live in and interact with a world that changes continuously. To make matters worse, the sensory information we receive about our environment is not always reliable. The brain has strategies to overcome the challenges in guiding behavior that are created by the combination of a mutable world and unreliable sensory knowledge. One strategy is to create predictions based on experience and weigh those predictions against sensory evidence. The predictions would be most useful if they were adaptable, sometimes over very short time-scales, to the dynamic world.
Bayesian inference is a formal system that unifies and explains quantitatively the interplay between past experience and current sensory information in guiding behavior. In Bayesian inference, sensory information provides a likelihood function that defines the probability of the given sensory signals given the actual stimulus. Past experience creates a “prior” that defines the probability of each stimulus. Behavior arises from a posterior that defines the probability of each stimulus given the likelihood and the prior (Knill and Saunders 2003; Kording 2014; Körding and Wolpert 2006). Bayesian inference has been invoked to describe features of multiple complex behavioral phenomena, including estimation of target motion for the initiation of smooth pursuit eye movements (Yang et al. 2012); estimation of the parameters of arm movements (Körding et al. 2004; Körding and Wolpert 2004; Verstynen and Sabes 2011); aspects of visual perception (Knill 2007; Weiss et al. 2002); and cue combination in multisensory integration (Alais and Burr 2004; Battaglia et al. 2003; Fetsch et al. 2011). In many ways, it is unsurprising that behavior conforms to the principles of Bayesian inference. In our opinion, the more important question is how the brain implements the features of behavior that we can understand in the framework of Bayesian inference.
We are using smooth pursuit eye movements as a test bed for understanding how the brain combines sensory evidence and past experience, first, through carefully contrived behavioral measurements and, second, by computational modeling of potential neural circuit mechanisms. Early work revealed an effect of experience and expectation on the initiation of anticipatory smooth pursuit eye movement (Kowler and Steinman 1979a, 1979b; Kowler et al. 1984), without testing whether those effects could be understood in terms of Bayesian inference. Recently, our laboratory showed that an interaction of priors with sensory evidence can account for the visual motion-driven initiation of smooth pursuit eye movements, and that the pursuit system uses two independent priors for direction and speed estimation (Yang et al. 2012). A prior for target direction develops with several days of experience pursuing a narrow range of directions, and the prior competes with the strength of sensory information. A prior for low-target speeds seems to be aligned with the low-speed prior used to explain the relationship between stimulus contrast and speed perception (Weiss et al. 2002).
In the present paper, we analyze pursuit behavior in sufficient depth to predict a neural circuit mechanism that could lead to behavior consistent with Bayesian inference. We do so with experiments designed to reveal the intrinsic properties of the pursuit system’s priors, going well beyond simple demonstrations of their existence. First, we show that the priors for target direction and speed adapt very rapidly. For both direction and speed, eye movements are biased toward the parameters of target motion on the previous trial and the size of the bias increases with consecutive exposures to a given target motion. Second, we use a mechanistic computational analysis to understand the two priors and how the generalization between them can be understood in terms of a single mechanism. That mechanism is based on the previously demonstrated mechanism of rapid modulation of the gain of visual-motor transmission. The role of the smooth eye movement region of the frontal eye fields (FEFSEM) in control of the gain of visual-motor transmission (Tanaka and Lisberger 2001, 2002a) implicates this area in the implementation of a behavior with features that would result from Bayesian inference.
MATERIALS AND METHODS
We conducted experiments on three male rhesus monkeys that weighed between 10 and 14 kg. Before the start of experiments, monkeys were implanted surgically with 1) hardware on the skull to restrain head movement, and 2) a scleral search coil (Fuchs and Robinson 1966) to track eye movements (Ramachandran and Lisberger 2005). Surgeries were carried out under aseptic conditions using isoflurane general anesthesia and were followed by administration of analgesics to minimize postsurgical pain. Following complete recovery from surgery, monkeys were trained to fixate and smoothly track moving visual targets. The horizontal and vertical components of eye position were monitored through analog signals produced by the scleral search coil system. Signals proportional to eye velocity were obtained by passing the eye position voltages through an analog circuit that differentiated signals at frequencies below 25 Hz and rejected signals at higher frequencies (−20 dB/decade). These analog signals were sampled at 1 kHz and stored for data analysis. All procedures had been approval in advance by Duke’s Institutional Animal Care and Use Committee and were in agreement with the National Institutes of Health’s Guide for the Care and Use of Laboratory Animals.
Visual Stimuli and Behavioral Paradigm
Visual targets were displayed on a 24-in. CRT monitor with a refresh rate of 80 Hz. The monitor was placed 40 cm from the monkeys’ eyes and created a field of view spanning 62° (horizontal) by 42° (vertical). The targets were similar to those used in Yang et al. (2012). There were four different targets: a sine wave grating at 6 or 100% contrast and a patch of dots at 12 or 100% contrast (Fig. 1, top left). The sine-wave grating had a spatial frequency of 0.5 cycles/° and was vignetted by a two-dimensional Gaussian function with a standard deviation of 1°. The patch stimulus consisted of 72 dots inside a circular aperture that was 4° in diameter. One-half of the dots in the patch stimulus were bright, and one-half were dark, to render the average luminance the same as the background. Contrast was determined as the difference in luminance between the bright and dark dots divided by the sum of the luminance of the bright and dark dots, expressed as a percentage. To vary the reliability of the sensory stimulus, many of our experiments compared pursuit responses to high-contrast patches and low-contrast gratings, to maximize the difference in responses elicited by the two targets for a given target speed (Yang et al. 2012). To verify that the stimulus form itself was not an important independent variable, we also ran control experiments that varied only contrast and held stimulus form (patch or grating) constant.
Fig. 1.
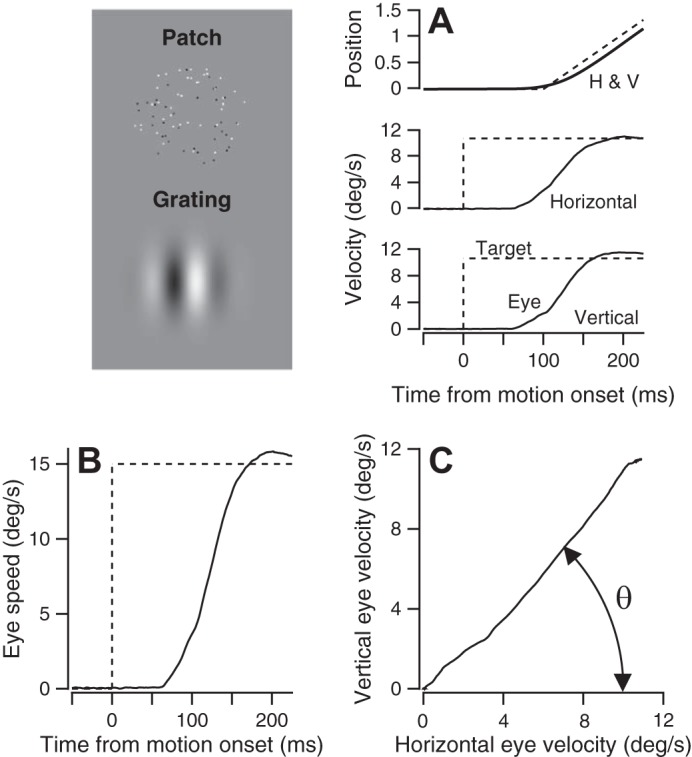
Methods for evoking, recording, and analyzing smooth pursuit eye movements. Top left: the two different stimuli we used are shown: patches of 100% correlated random dots and Gaussian vignetted sine wave gratings. Both are shown at 100% contrast. A: horizontal and vertical components of eye/target position and velocity are shown as a function of time. Dashed and solid curves show target and eye movement, respectively. Note that the target position trace starts to ramp 100 ms after the onset of local stimulus motion within a stationary aperture. B: eye speed averaged across multiple responses to a given stimulus as a function of time. C: eye velocity vector averaged across multiple responses to a given stimulus, obtained by plotting horizontal vs. vertical eye velocity for the first 100 ms of the averaged response. Theta (θ) defines the direction of the eye movement, computed by minimizing the vertical component of the vector.
Experiments comprised a sequence of behavioral trials, each of which began with the monkey fixating a central spot on the screen. In trials that required pursuit of a moving stimulus, the fixation spot disappeared after a fixation time of 800–1,600 ms, and a visual stimulus appeared and began moving in a specific direction at a specific speed. To reduce the chances of an early catch-up saccade, stimulus movement began with 100 ms of local pattern motion: the grating stimulus drifted or the dots of the patch stimulus moved at 100% coherence with the chosen direction and speed within a stationary virtual aperture. After 100 ms, the pattern and the aperture moved en bloc with the parameters of the previous local motion. Monkeys’ were rewarded with juice for successfully tracking the position of the center of the aperture within an invisible 4 × 4° window. In one experiment that presented passive visual motion without pursuit, the fixation point remained on throughout the trial, the period of local stimulus motion endured 100 ms, the en bloc motion of stimulus and aperture was omitted, and the monkeys were rewarded for maintaining fixation throughout the trial. The sequences of trials in each experiment are outlined at the top of each section in the results.
Data Analysis
Analysis in all experiments was performed on trial-averaged data for each condition. Saccades were detected automatically from eye-speed traces using a combination of acceleration and velocity thresholds. Traces were inspected by eye to ensure proper detection of saccades. We treated data points during saccades as missing data. Our results were remarkably similar, and our conclusions were unaffected if we simply excluded the 30–36% of trials that had a micro- or macrosaccade in the interval from 0 to 200 ms after the onset of target motion.
The time of initiation of smooth pursuit eye movement was determined by visual inspection of trial-averaged traces for each target form, contrast, direction, and speed, separated according to the history of previous stimuli. All further analysis was performed on the average horizontal and vertical eye velocity (Fig. 1A) in the first 100 ms following smooth pursuit onset (the open-loop period after Lisberger and Westbrook 1985), to avoid any effects of visual feedback. Eye direction was determined by a simple iterative approach. In effect, we quantified the eye velocity vector by plotting vertical vs. horizontal eye velocity for each millisecond during the first 100 ms of pursuit (Figure 1C) and then rotated the eye velocity vector to minimize the vertical component of the resultant eye movement in the first 100 ms of smooth pursuit. We rotated the eye velocity vector using a rotation matrix:
| (1) |
where θ is the angle of rotation; H and V are the horizontal and vertical components of eye velocity, respectively; and Hrot and Vrot are the horizontal and vertical components of eye velocity rotated by θ, respectively. Eye speed was obtained by squaring and adding the average horizontal and vertical velocity components from the original measurements and taking the square root (Fig. 1B). To obtain the numbers reported in the paper, we then averaged eye speed across the interval from 50 to 100 ms after the onset of pursuit.
Bayesian Model of Speed Prior Adaptation
To model the adaptation of the speed prior, we used an approach similar to that used in Yang et al. (2012). We started with Bayes’ equation:
| (2) |
where is the true speed of the target, is the sensory signal for the speed of the target, represents the likelihood of target speed given sensory information, represents the speed prior, and represents the posterior that results from combining the likelihood and prior. The likelihood and prior were both modeled as Gaussians giving the maximum a posteriori estimate:
| (3) |
where is the variance of the likelihood distribution, is the variance of the prior distribution, and μprior is the mean of the prior distribution. The mean and variance for estimates of target speed are then computed as:
| (4) |
| (5) |
We used a least squares procedure to find the parameters for Eqs. 4 and 5 that gave the best fit for four different distributions in our data: fast and slow priors, high- and low-contrast targets. The fits had six adjustable parameters: the mean of the fast prior, the mean of the slow prior, the variance of the fast prior, the variance of the slow prior, the variance of the high-contrast likelihood, and the variance of the low-contrast likelihood. The means of both likelihood distributions were 10°/s. Based on the theory proposed by Ma et al. (2006), we assume that the likelihood function for pursuit is, or is derived from, the population response in area MT (middle temporal). Preliminary data from our laboratory on the responses of MT neurons confirm the assumption that the center of the population response does not depend on the contrast or stimulus form of the targets we used for our behavioral experiments (J. Yang and S. Lisberger, unpublished data).
We obtained data for the fitting procedure by combining across responses to each given target motion across multiple experiments for each monkey. For each daily experiment, we first z-scored individual trials according to:
| (6) |
where μexp and σexp are the mean and standard deviation of eye speed for a given experiment, and is the average eye speed during a single trial across the interval from 75 to 100 ms after pursuit initiation. We used this later interval here to move the estimates of target speed closer to the actual target speeds. We then combined the z-scored data across all experiments into a single distribution and converted each data point back to eye speed according to the equation:
| (7) |
where z is the z-score, σall is the standard deviation obtained by averaging all experimental standard deviations, and μall is the mean of eye speed across all experiments. This method of z-scoring was chosen to avoid increasing artificially the variance of the combined distributions due to (albeit small) day-to-day differences in eye speed for a given target motion.
Visual-Motor Gain Multiplication Model of Direction and Speed Prior Adaptation
We took two different approaches to modeling the mechanism of adaptation of direction and speed priors, based on the assumption that the adaptation occurs in sensory vs. motor coordinates. The sensory and motor coordinate frame models make different predictions that are discriminated by our data. Note that the models described in this section explicitly are not Bayesian models, but rather are more mechanistic models that attempt to understand how Bayesian inference might emerge from neural circuits and known neural circuit functions. While we propose that visual-motor gain is a vehicle for instantiating priors, the gain parameters in these models and the plots of gain in our figures explicitly are not prior probability distributions.
Sensory coordinate system model.
We modeled adaptation of the direction or speed prior as an enhancement of the gain of visual-motor transmission that is selective for the direction of the previous target motion. We began by assuming a Gaussian distribution, G (mean, standard deviation), of directions for the sensory likelihood. We centered the Gaussian at 0° and assigned it standard deviations given by σlow contrast for the low-contrast target and σhigh contrast for the high-contrast target:
| (8) |
For the direction prior experiment, we modeled the single trial enhancement of visual-motor gain as a Gaussian that was centered on the direction of the prior-adapting trial (θ) and with amplitude Ampdirection and standard deviation σdirection. We offset the Gaussian vertically by +1, to enhance gain along a specific direction without affecting gain in other directions:
| (9) |
For the speed context experiment, we modeled context-dependent changes in visual-motor gain as a Gaussian that was centered on the direction of the prior and probe trials, defined as 0, with standard deviation σspeed.
| (10) |
The posterior distributions that were used to predict eye direction and speed were obtained by multiplying the sensory likelihoods obtained for Eq. 8 with the gain enhancement Gaussians obtained for Eqs. 9 and 10.
| (11) |
We decoded the estimate of target direction from the multiplied distribution via vector averaging. To fit the model to our direction prior data, we used a least squares approach to determine the values of σlow contrast, σhigh contrast, Ampdirection, and σdirection that best reproduced the effect sizes in our data. We fitted the model simultaneously for the prior directions of 15, 45, and 90° for the high- and low-contrast stimuli and found a single set of parameters that reproduces the entire data set.
To fit the model to our speed prior data, we used the same likelihood obtained for Eq. 8 in the direction prior model. We then used a least squares approach to determine the values of Ampspeed and σspeed that best reproduced the effect sizes in our data. We fitted this model simultaneously for the slow, control, and fast contexts. We allowed Ampspeed to have different values for the three different speed contexts. Relative eye speeds were estimated based on the differences between the amplitudes of the posteriors obtained for different contexts.
Motor coordinate system model.
We modeled the single-trial adaptation of the direction prior as an enhancement of the gain of motor output along the horizontal and vertical axes that define approximately the motor coordinate system in the floccular complex of the cerebellum (Krauzlis and Lisberger 1996). To keep the model tractable, we consider only quadrant I, from rightward to upward directions. Probe trials provided rightward motion, and so we represented the sensory likelihood as a Gaussian centered at 0° for cardinal direction probes and 45° for oblique direction probes, both with standard deviations of 45°. We modeled the prior probability for the single trial effects as a “motor-enhancement” Gaussian centered at 90° with amplitude Ampmotor and standard deviation σmotor. As before, we assumed that the amplitude of this motor enhancement would be scaled according to the relative activation in the mean direction of the Gaussian on the prior-adapting trial:
| (12) |
Therefore, the effect of the prior would be largest when the prior-adapting trial presented purely vertical target motion. The effect of the prior-adapting trial’s direction on the response to the probe trial was modeled as a multiplication between the sensory likelihood and motor-enhancement Gaussians. Again, we decoded the direction of the posterior using vector averaging. We used a least squares procedure to find the values of Ampmotor and σmotor that gave the best fit to the effect size in our data when target motion in the prior-adapting trial was rotated 45° relative to that in probe trial. We then used these values to predict the effect sizes for the conditions where the prior and probe directions differed by 15 and 90°. We performed the fitting procedure for the cases where 1) the probe direction was 0° and the prior direction was 45° (cardinal direction probe), or 2) the probe direction was 45° and the prior direction was 90° (oblique direction probe).
RESULTS
Two features of target motion determine pursuit behavior: speed and direction. A previous publication from our laboratory (Yang et al. 2012) showed that the pursuit system uses a competition between past experience and sensory evidence to estimate each of these features of target motion. We now show that the priors for target speed and direction are subject to adaptation on short time scales. Then we exploit the adaptation to explain how the pursuit circuit might implement a comparison of sensory evidence and prior experience. The results outlines our experiments, results, and associated models sequentially, first for the speed prior and then for the direction prior. At the end of the results, we present computational modeling that 1) outlines a possible neural mechanism of adaptation of priors, and 2) constrains the neural site and mechanisms of the priors and their adaptation within the known framework of the pursuit circuit.
Experiment 1: Single-Trial Adaptation of a Prior for Target Speed
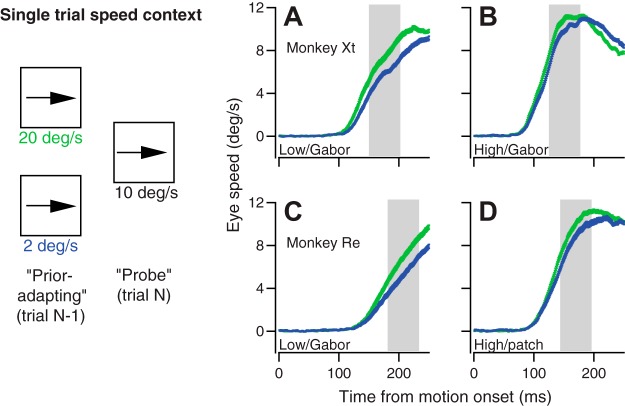
Our first behavioral experiment used strategically contrived pairs of trials to study single-trial adaptation of the prior for target speed. In each pair of trials, the first (“prior-adapting”) trial presented target motion chosen randomly to be either 20 or 2°/s, and the second (“probe”) trial always presented target motion at 10°/s (Fig. 1, left). Targets were a 100% contrast patch of dots and 6% Gabor in the experiments conducted on monkey Re. Recognizing the potential confound of mixing target forms, we used a 100% contrast patch of dots, 100% contrast Gabor, 12% contrast patch of dots, and 6% Gabor in monkey Xt.
Eye speed in the probe trials was biased according to the target speed in the prior-adapting trial, as illustrated in the trial-averaged eye speed traces in Fig. 2, A–D. Here, we compare the responses to the 10°/s probe target motions and show that the eye moved faster on probe trials that were preceded by a 20 vs. a 2°/s prior-adapting trial (Fig. 2, A–D). Furthermore, eye speed was modulated more by the prior-adapting trial for the low-contrast (A, C) vs. high-contrast (B, D) probe target. This was true for both the comparison of responses to targets of matched-form (A, B) and of mixed-form (C, D). To quantify the effects of the target speed in the prior-adapting trial on eye speed in the probe trials, we averaged eye speed across the interval from 50 to 100 ms after the onset of pursuit, in the second half of the open-loop interval, for responses to target motion at 10°/s. Following the precedent of Osborne et al. (2005), we take the eye velocity at this time as the pursuit system’s estimate of target speed.
Fig. 2.
Single-trial speed prior paradigm and examples of the trial-over-trial effect of the speed of the previous target motion on the initiation of pursuit. Left: diagram shows pairs of consecutive trials used to adapt and probe priors for target speed. The experimental design provided a sequence of prior-adapting and probe trials where the probe speed always was 10°/s. A–D: each graph shows trial-averaged eye speed traces in response to the 10°/s probe trials. Green and blue traces show probe trials that were preceded by prior-adapting trials that presented target motion at 20 vs. 2°/s. Error bands represent SE. The gray shaded regions represent the time points where eye speed was averaged for further analysis, from 50 to 100 ms after the initiation of pursuit. In A and B, the stimuli were a low- and high-contrast grating, respectively, for monkey Xt. In C and D, the stimuli were a low-contrast Gabor and high-contrast patch of dots, respectively, for monkey Re.
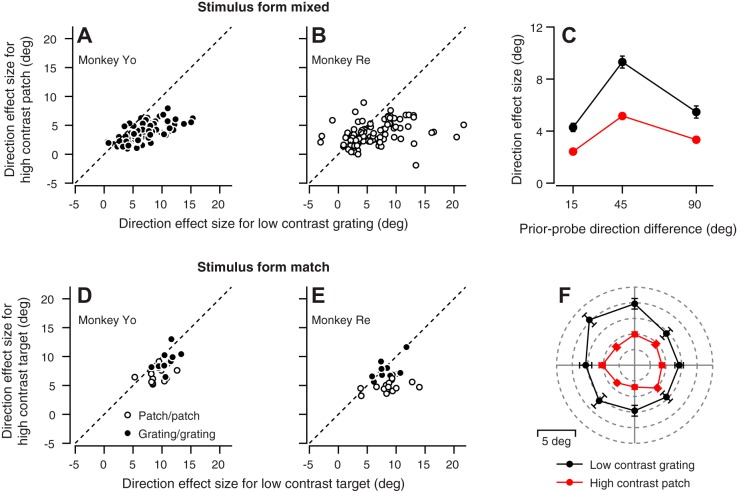
The initiation of pursuit consistently was modulated more by the prior-adapting trial for low-contrast vs. high-contrast probes. We summarize the effect of the prior-adapting trial across our experiments by calculating the “speed effect size,” defined as the relative change in eye speed when the prior-adapting trial was 20 vs. 2°/s (Fig. 3). The data in Fig. 3, A and B, fall below the unity line, indicating a larger speed effect size for the low-contrast stimuli compared with the high-contrast stimuli (monkey Xt: low-contrast mean = 0.20, high-contrast mean = 0.12, P = 1.6 × 10−5, paired t-test, n = 16 experiments; monkey Re: low-contrast mean = 0.18, high-contrast mean = 0.11, P = 0.0012, paired t-test, n = 16 experiments). Importantly, the response to the low-contrast target was affected more by the speed of the prior-adapting trial under conditions, regardless of whether target-forms were mixed (Fig. 3B, statistics for monkey Re given above) or matched (Fig. 3A, grating/grating: low-contrast mean = 0.24, high-contrast mean = 0.13, P = 9.7 × 10−4, paired t-test, n = 8 experiments; patch/patch: low-contrast mean = 0.17, high-contrast mean = 0.11, P = 0.0036, paired t-test, n = 8 experiments).
Fig. 3.
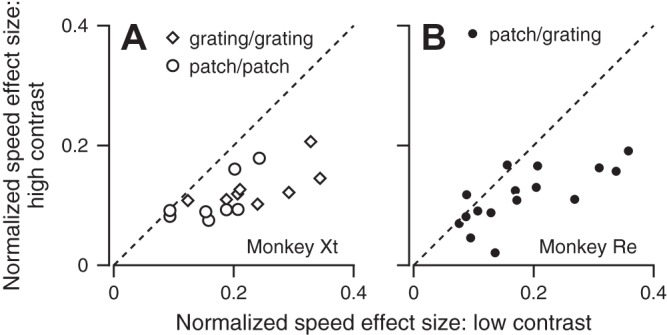
Effect of stimulus contrast on the size of the single-trial effect of the previous target motion’s speed. In both graphs, each symbol plots the mean size of the effect of the prior-adapting trial on the speed of the response to a high- vs. low-contrast stimulus. Different symbols show data for different experiments. In A, the high- and low-contrast targets were matched in form, and different symbols show responses for the two different stimulus forms. In B, the high- and low-contrast targets were a patch of dots and grating, respectively.
Finally, we asked whether the pursuit (rather than the stimulus) on the prior-adapting trial has any effect on the pursuit in the probe trial, when the target speeds are held constant on the prior and probe trials. We performed a median split of probe trials into two groups according to the gain of pursuit on the prior-adapting trial and looked for, but did not find, differences in the gain of pursuit on the probe trials in the two groups. Importantly, we used only pairs of trials with the same target speeds and contrasts so that we were looking for effects of eye velocity in the prior-adapting trial independent of any effects of stimulus. This negative finding does not mean that the pursuit on the prior trial is not the mechanistic cause of the adaptation of the prior, but rather that we cannot see any effect of pursuit that is independent of the parameters of target motion.
Experiment 2: Rapid Adaptation of a Prior for Target Speed
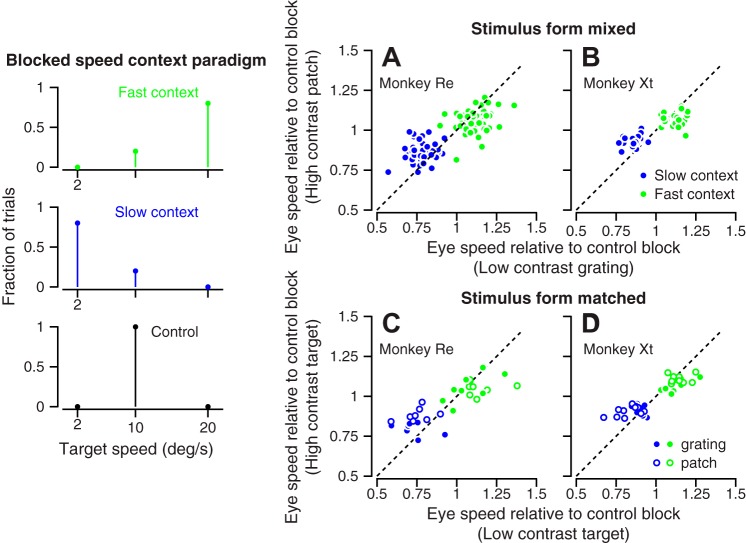
Our second behavioral experiment used blocks of 50 trials with different blends of target speed to study longer-term adaptation of the priors for target speed. The left panel of Fig. 4 outlines the experimental design. During “fast context” blocks, 80% of the trials delivered target motion at 20°/s, and 20% of the trials delivered target motion at 10°/s. During “slow context” blocks, 80% of the trials consisted of target motion at 2°/s, and 20% of the trials consisted of target motion at 10°/s. A third block of 20 trials served as a control with 100% of the targets moving at 10°/s. Thus, target motion at 10°/s served as a probe that presented the same stimulus across contexts, allowing analysis of the effect of context independent of the effect of stimulus speed. For the data presented in this section, the direction of target motion remained fixed within each experiment; we relax that constraint later in the paper. In each daily experiment, we collected approximately five repetitions each of the fast and slow contexts, each followed by a control block.
Fig. 4.
Longer-term effect of speed context on target speed estimation. Left: the diagram illustrates the blend of target speeds used in the fast-context, slow-context, and control blocks. In A–D, each graph summarizes data across many experiments. Green and blue symbols show data obtained during the fast- and slow-speed contexts, respectively. Each symbol plots eye speed in response to 10°/s target motion for the high-contrast target vs. that for the low-contrast target. Values were normalized to eye speed for the same target motion during the control blocks. In A and B, the visual stimuli were of mixed forms: a high-contrast patch of dots and a low-contrast grating. In C and D, the visual stimuli were matched in form. A and C: monkey Re. B and D: monkey Xt.
Compared with the single-trial adaptation of the prior, longer blocks of fast or slow prior-adapting target motions produced larger effects on the responses to a probe target motion at 10°/s. Again, we quantified the effects of context on pursuit by averaging eye speed across the interval from 50 to 100 ms after the onset of pursuit, in the second half of the open-loop interval, for responses to target motion at 10°/s. We then normalized these measurements relative to eye speed for the same target motion in the control blocks. In all four graphs of Fig. 4, the data for the fast context (green symbols) plot at normalized eye speeds greater than one, and below the unity line indicating larger normalized eye speeds for low-vs. high-contrast targets. The data for the slow context (blue symbols) plot at normalized eye speeds less than one, and above the unity line, indicating smaller normalized eye speeds for low- vs. high-contrast targets.
Context had a stronger effect for the low-contrast vs. the high-contrast targets in both monkeys (Fig. 4, A–D). The results did not depend on whether the high- and low-contrast targets presented matched stimulus forms (Fig. 4, C and D) or mixed stimulus forms (Fig. 4, A and B). In the fast speed context, the difference in normalized eye speed between the high- and low-contrast targets averaged 0.052 and 0.046, respectively, and was statistically significant when stimulus forms differed (P = 0.0026 and n = 21 in monkey Xt; P = 1.6 × 10−4 and n = 54 experiments in monkey Re, paired t-test). The difference averaged 0.043 and 0.056 and also was statistically significant when stimulus forms were matched (P = 0.0023 and n = 20 in monkey Xt; P = 0.046 and n = 16 experiments in monkey Re, paired t-test). In the slow speed context, the mean difference in normalized eye speed between the high- and low-contrast targets averaged −0.069 and −0.082, respectively (P = 4.5 × 10−6, n = 21 and P = 1.3 × 10−9, n = 54, paired t-tests), in monkeys Xt and Re, respectively, when stimulus forms differed, and −0.052 and −0.101, respectively (P = 0.0027, n = 20 and P = 0.0014, n = 16, paired t-tests), in monkeys Xt and Re, respectively, when the targets comprised the same stimulus form. The speed effect sizes for the high-speed and low-speed contexts in Fig. 4 are approximately twice the size of the single-trial effects shown in Figs. 2 and 3.
Our premise, discussed later in the paper, is that reduction of stimulus contrast renders the representation of motion in the brain “weaker” or “less reliable” and, if Bayesian inference is operating, should allow priors to have a stronger influence on the motor behavior. Thus we take the data shown so far as qualitative evidence that pursuit behavior can be described as Bayesian inference with a speed prior that is subject to adaptation on a short time scale.
Model 1: Bayesian Inference Can Account for the Effect of Speed Context on Estimates of Target Speed
To test how our data could be explained by Bayesian inference, and to understand how the speed contexts were affecting speed priors, we fitted a Bayesian model (equations in materials and methods) to the distributions of the estimates of target speed in our data. Our fitting procedure allowed different values for the mean and variance of the speed prior between the fast and slow context blocks. It allowed different values for the variance and amplitude of the likelihood distribution between the low- and high-contrast targets, but required the mean of the likelihood distributions to be the same for the two speed contexts (10°/s).
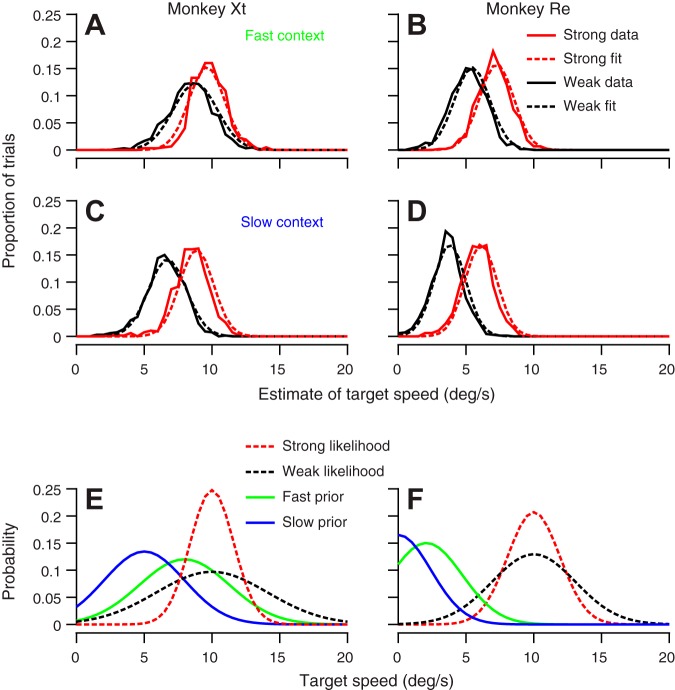
The optimized model predicted distributions of estimated target speed that fitted our data well (Fig. 5, A–D, dashed vs. continuous lines; for each of the eight fits, the mean root squared error was between 0.0075 and 0.017). For both monkeys, the speed prior that reproduced the data shifted toward higher speeds and broadened in the fast context compared with the slow context (Fig. 5, E and F). Furthermore, the likelihood inferred for the high-contrast target has a smaller variance and larger amplitude than that for the low-contrast target (Fig. 5, E and F), consistent with the idea that lower contrast targets provide less reliable sensory information. In truth, it is not surprising that the model in Fig. 5 fits our data well. We present the model to show 1) that our data are compatible with Bayesian inference, and 2) that specific adaptations of the prior distributions can account for our data. Also, we note that estimates of target speed seldom reached the actual target speed of 10°/s, even for the high-contrast target (red curves in Fig. 5, A–D). We attribute this short-fall to the fact that we measured eye velocity 75–100 ms after the onset of pursuit for Fig. 5. This choice ensures that we were studying the open-loop visual-motor response, untainted by feedback, but may quantify eye speed before the full expression of pursuit’s estimates of target speed. Measurements at later times would have yielded more veridical estimates of target speed, but might have been contaminated by visual feedback.
Fig. 5.
Bayesian model for the effects of context on speed estimation. A–D: solid and dashed traces show probability distribution of eye speeds from the data and inferred posterior distributions from the optimized Bayesian model, respectively. Red and black traces show results for the high- and low-contrast targets, respectively. A and B: results for the fast context. C and D: results for the slow context. Results are shown for monkeys Xt (A and C) and Re (B and D). E and F: red and black dashed traces show the inferred likelihood distributions for the high- and low-contrast targets, respectively. Green and blue traces show the inferred prior distributions in the fast and slow contexts, respectively. Results are shown for monkeys Xt (E) and Re (F).
We think of population responses in area MT as potential correlates of the likelihood distributions for Bayesian inference. The model’s predictions about the likelihood distributions are compatible with existing data showing that the population response in area MT has lower amplitudes at lower contrasts (Krekelberg et al. 2006; J. Yang and S. Lisberger, unpublished observations). Our modeling did not take into account the fact that the center of the MT population responses shifts subtly toward higher preferred speeds as contrast is lowered. We note that the shift toward higher preferred speeds is in the wrong direction to account for the lower estimates of target speed by pursuit for low-contrast targets. Thus the actual priors might be centered at lower speeds than reflected in our estimates.
Experiment 3: Single-Trial Adaptation of a Prior for Target Direction
In our third experiment, we studied rapid adaptation of priors for target direction by presenting target motions in strategically contrived, linked pairs of trials (Fig. 6, left). In each pair of trials, the first (“prior-adapting”) trial consisted of target motion at 15°/s in a direction randomly chosen from ±15, ±45, and ±90° relative to a probe direction that was fixed throughout the experiment. The second (“probe”) trial always delivered target motion at 15°/s in the central, probe direction. Probe directions were different on different days; for presentation, we have rotated the directions so that the probe direction was always defined as 0°.
Fig. 6.
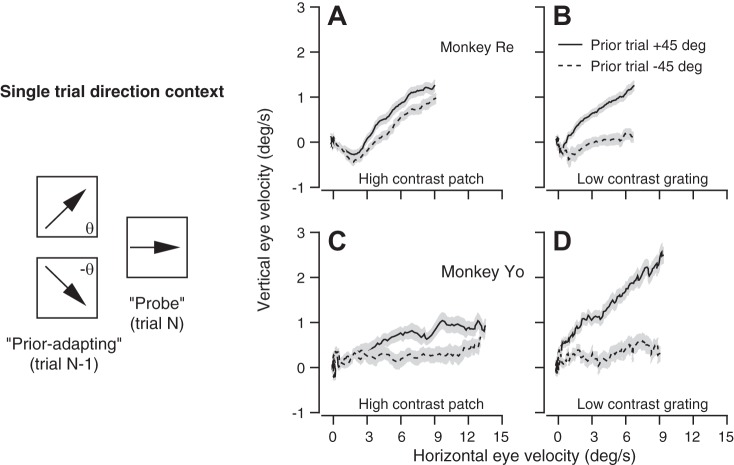
Single-trial direction prior paradigm and examples from one experiment of trial-over-trial effects on the direction of pursuit. Left: diagram shows how pairs of consecutive trials were used to adapt and probe trial-over-trial changes in priors for target direction. A–D: each graph contains average eye velocity vectors for target motion in direction 135° during probe trials. Solid and dashed traces show data when the target motion in the prior-adapting trial was rotated +45° (counterclockwise) or −45° (clockwise), respectively, relative to the direction of the probe target motion. Traces start at target motion onset and progress out to 100 ms after smooth pursuit eye movement initiation. Error bands represent the SE of the vertical component of eye velocity. In A and C, the visual stimulus was a high-contrast patch of dots. In B and D, the visual stimulus was a low-contrast grating. Graphs are from monkeys Re (A and B) and Yo (C and D).
The trajectory of eye velocity at the initiation of pursuit on a probe trial is biased toward the direction of target motion on the prior-adapting trial. Trial-averaged eye velocity vectors from two example experiments (Fig. 6, A–D) show that the effect was present in both monkeys and is considerably stronger for the low-contrast target (B, D) vs. the high-contrast target (A, C). The eye velocity vectors are biased counterclockwise (solid curves) or clockwise (dashed curves) when the prior-adapting trial was 45° counterclockwise or clockwise from the probe direction. The target motion in the prior-adapting trial must cause the rotation of the eye velocity vector in the probe trial, because each graph compares average responses to the same stimulus form moving in the same direction at the same speed. Each vector in Fig. 6 contains data from target motion onset to 100 ms after smooth pursuit initiation. Thus the end of each trace represents the approximate end of the open-loop period of smooth pursuit. Each vector has been rotated so that zero is the direction of the probe target motion on the second trial of each pair. The tendency for all vectors to point up and right reflects inherent anisotropies that favor horizontal eye motion and will rotate all vectors in a counterclockwise direction for the 135° (up and left) probe direction shown here. The important observation is the difference between the curves in each graph.
Eye movements were more susceptible to the bias in eye direction created by the prior-adapting trial when probed with the low- vs. the high-contrast target. We defined “direction effect size” for each combination of prior and probe directions as the difference in the directions of the eye movement on the probe trial when the direction of target motion in the prior-adapting trial was +θ vs. –θ from the probe direction. In Fig. 7, A and B, the data for most of the experiments plot below the unity line, indicating that the effect size is larger for the low-contrast target compared with the high-contrast target (P = 1.4 × 10−22 and 1.4 × 10−8 for monkeys Yo and Re, respectively, paired t-test, n = 99 data points from 33 experiments in each monkey).
Fig. 7.
Effect of stimulus contrast on the size of the single-trial directional effect. In A, B, D, and E, symbols plot the mean size of the effect of the prior-adapting trial on the direction of the response to a high-contrast vs. a low-contrast probe target across many experiments. A and B: each symbol shows data for a different combination of prior-adapting and probe directions. Each experiment provided 3 symbols, for prior-adapting targets in directions of ±15, ±45, and ±90° relative to the probe direction. The high-contrast target is a patch of dots, and the low-contrast target is a grating. D and E: Prior-adapting targets had directions of ±45° relative to the probe direction. The high- and low-contrast targets were matched in form. C: symbols show direction effect size for different prior-probe direction differences. F: polar plot shows the mean direction effect size for different probe directions. Each symbol represents the end of a vector where the length of the vector indicates the effect size and the angle of the vector shows the direction of the probe target motion. In C and F, red and black symbols show effects for high- and low-contrast probe targets, respectively. Data were combined across monkeys Yo and Re. Error bars represent SE.
The size of the effect of the direction of the prior target motion was consistently larger for low- vs. high-contrast probe targets for all directions of probe target motion (Fig. 7F). The effect of contrast also was consistent across the full range of differences in the direction of the prior and probe target motions (Fig. 7C). However, the size of the direction effect was larger for prior-probe direction differences of ±45 vs. ±15 or ±90° (Fig. 7C). We will use this effect later in the paper to define the coordinate frame of adaptation of the direction prior.
We obtained the data in Figs. 6 and 7, A and B, using a low-contrast moving grating and a high-contrast moving patch of dots as stimuli. Figure 7, D and E, shows results from experiments in both monkeys under conditions that varied contrast but not stimulus form. As before, the points plot below the unity line, indicating that the effect of the prior-adapting trial depends on the contrast of the probe target, even when stimulus form is held constant (monkey Yo patch/patch: low-contrast mean = 9.01, high-contrast mean = 6.64, P = 0.0012, paired t-test, n = 12 experiments; monkey Yo grating/grating: low-contrast mean = 10.69, high-contrast mean = 9.10, P = 0.0031, n = 12 experiments; monkey Re patch/patch: low-contrast mean = 8.60, high-contrast mean = 4.66, P = 5.4 × 10−5, n = 14; monkey Re grating/grating: low-contrast mean = 8.43, high-contrast mean = 7.42, P = 0.043, paired t-test, n = 14). We note that the difference between the direction effect sizes for high- and low-contrast probe targets was greater for patch than for grating targets, although we do not know whether this difference would hold up to further testing.
Experiment 4: Stimulus Features that Create Stronger Priors
In our fourth experiment, we altered the properties of the stimuli in the prior-adapting trial to determine the stimulus features that were effective at adapting priors. We used the trial-over-trial direction adaptation paradigm from experiment 3. The probe trial always was the same and presented target motion in a given direction at 15°/s. The prior-adapting trial presented motion at ±45° relative to the probe direction. We modulated the stimuli used in the prior-adapting trials by changing four metrics in four different sessions: 1) the contrast of the visual stimulus during the prior-adapting trial; 2) passive visual motion stimulation vs. active pursuit during the prior-adapting trial; 3) number of repetitions of the prior-adapting trial before each probe trial; and 4) intertrial interval between the prior-adapting and probe trial.
Recency, repetition, active responses, and higher contrast in the prior-adapting trial all created stronger effects on the initiation of pursuit in the probe trial.
-
1.
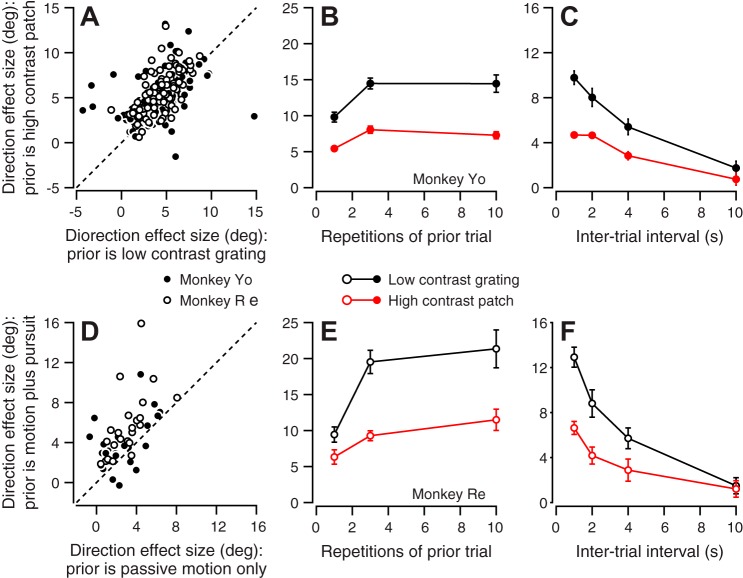
The effectiveness of the adapting stimulus depends on the contrast of the visual motion stimulus during the prior-adapting trial. Plotting the results for each experiment as a separate symbol (Fig. 8A) reveals larger effects when the prior-adapting trial presented a high-contrast patch of dots vs. a low-contrast grating; many of the points lie above the unity line. The mean difference in direction effect size was 0.95 and 1.37° for monkey Re and monkey Xt, respectively (P = 0.0017 and 2.3 × 10−11, paired t-test, n = 99 data points from 33 experiments in each monkey).
-
2.
Passive visual motion on the prior-adapting trial is sufficient to bias the direction of pursuit on the probe trial, but the size of the direction effect is greater if the monkey actually pursues the target on the prior-adapting trial. The multiple data points in Fig. 8D represent direction effect sizes for different combinations of prior-adapting and probe directions on multiple experimental days. Most points plot above the line of slope 1, indicating that the direction effect was larger when the monkey pursued the target in the prior-adapting trial vs. when the prior-adapting trial delivered 100 ms of passive visual stimulation. The difference averaged 1.9° and was statistically significant in both monkeys (P = 9.0 × 10−5 and 0.016, paired t-test, n = 24 data points from 8 experiments each in monkeys Re and Yo). Still, passive visual stimulation on the prior-adapting trial did create a significant directional bias on the probe trial, with a mean direction effect size of 3.02 and 2.56° in the two monkeys (P = 2.0 × 10−8 and 3.2 × 10−6, Student’s t-test, n = 24 data points from 8 experiments each in monkeys Re and Yo).
-
3.
The number of repetitions of the prior-adapting trial affects the size of the effect on the direction of pursuit in the probe trial (Fig. 8, B and E). Compared with repeating the prior-adapting trial only once, repeating the prior-adapting trial 3 or 10 times significantly increased the subsequent directional bias in both monkeys (n = 14 and 8 experiments in monkeys Yo and Re, respectively) and for probe trials that presented motion of high-contrast (red symbols, P = 3.8 × 10−4 and 0.0027, paired t-test) or low-contrast (black symbols, P = 0.0037 and 9.4 × 10−5, paired t-test) targets. The direction adaptation reached an asymptote quickly: there was no difference in direction effect size between 3 and 10 repetitions.
-
4.
The duration of the intertrial interval, measured from the end of one trial to the start of the next, affects the size of the effect of prior-adapting target motion on the direction of pursuit in the probe trial (Fig. 8, C and F). The direction effect size decreased gradually as the intertrial interval increased from 1.5 to 10 s, again in both monkeys and for both target contrasts (n = 8 experiments each in monkeys Yo and Re).
Fig. 8.
Effect of the qualities of the stimulus in prior-adapting trials on the size of the directional effect. A: symbols plot the mean direction effect size when the prior-adapting trial was a low-contrast grating vs. a high-contrast patch. Each symbol shows data for a different combination of prior-adapting and probe directions: each experiment provided 3 symbols. Open and solid symbols show data from monkeys Re and Yo, respectively. B and E: symbols show the mean direction effect size for different number of prior-adapting trial repetitions. C and F: symbols show the mean direction effect size as a function of the duration of the intertrial interval between the prior-adapting and probe trials. B and C contain data from monkey Yo. E and F contain data from monkey Re. Red and black symbols show effects for high- and low-contrast targets, respectively. Error bars represent SE. D: symbols plot the mean direction effect when the prior-adapting trial consisted of active pursuit vs. 100 ms of passive visual motion. Open and solid symbols show data from monkeys Re and Yo, respectively.
Experiment 5: Generalization between Adaptation of Speed and Direction Priors
Our ultimate goal is to understand how brain circuits could implement a behavior with features that are compatible with Bayesian inference. Twenty years ago, we identified a component of pursuit that allows context to modulate the strength, or “gain,” of visual-motor transmission (Schwartz and Lisberger 1994; Tanaka and Lisberger 2001). A previous paper from our laboratory (Yang et al. 2012) suggested that priors operate through this gain-control mechanism. More recently, our laboratory found that gain control occurs in a retinal, rather than a motor, frame of reference (Lee et al. 2013). The existence and properties of gain control in the pursuit system, and its possible causal role in the competition between sensory evidence and prior experience (Yang et al. 2012), motivate our next steps in experimental and computational analysis.
We performed data analyses and computational modeling to determine whether changes in gain control could be the mechanism of short-term adaptation of priors, and by association also the mechanism of priors more generally. In particular we ask the following: 1) is the generalization between the adaptation of speed and direction priors consistent with a model where the two priors share a common mechanism?; 2) can we understand the adaptation of priors for target direction and speed in terms of a change in the gain of visual-motor transmission?; 3) do priors, like gain control (Lee et al. 2013), operate in a coordinate frame that is closer to the sensory coordinates of the retina rather than the motor coordinates defined in the cerebellar and brainstem pathways for pursuit?
Experiment 5a: Effect of directional prior adaptation on eye speed.
In these experiments, the prior-adapting trial consisted of target motion at 15°/s in a direction randomly chosen from ±15 and ±90° relative to a probe direction, and the probe trial always delivered target motion at 15°/s in the central, probe direction (in fact, we have simply reanalyzed data from experiment 1). We averaged eye speed in the probe trials across the interval from 50 to 100 ms after the initiation of pursuit for prior-adapting trials with target motions at ±15 and ±90° relative to the probe direction. We quantified the effect of direction prior adaptation on eye speed as the difference between the probe eye speeds for prior-adapting target motion at ±15 and ±90°. Our logic was that close-together, prior-adapting and probe directions should show larger effects on eye speed compared with orthogonal prior-adapting and probe directions.
The effect of direction-prior adaptation on eye speed almost always was positive (Fig. 9, A and B) for both monkeys and for both the high-contrast (red) and low-contrast (black) targets. The mean value was 0.28 and 0.50°/s in monkeys Re and Yo, respectively (P = 4.6 × 10−16 and 2.2 × 10−18, paired t-test, n = 33 experiments in each monkey). In Fig. 9, A and B, the effect of target contrast on eye speed also appears in the shift along the x-axis between the black and red symbols. We conclude that adaptation of the direction prior generalizes to target speed estimation. We realize it is intuitively obvious that direction adaptation should generalize to eye speed: below, we will show that the quantitative extent of generalization is an emergent prediction of a model where a single neural mechanism implements both direction and speed priors and their adaptation.
Fig. 9.
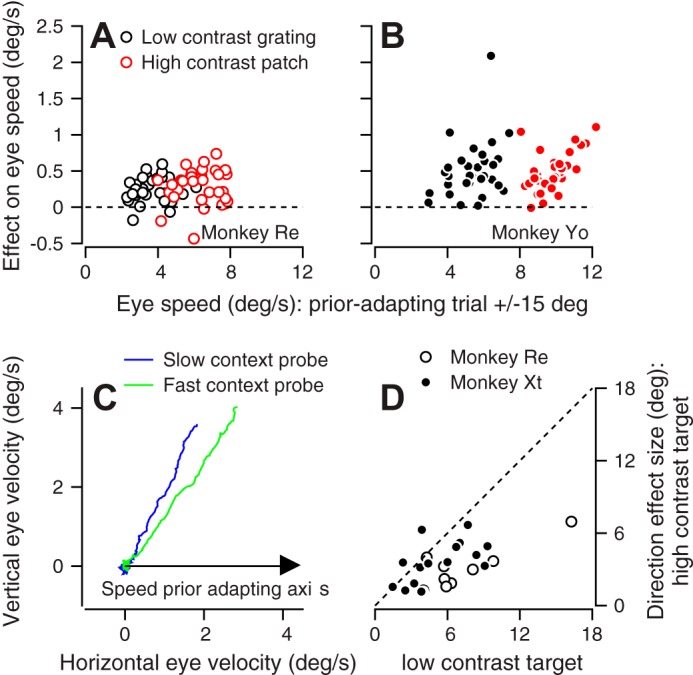
Interaction between direction and speed priors. A and B: symbols plot the difference between the eye speeds in the probe trial when the direction of the prior-adapting trial was ±15° vs. ±90° from the direction of the probe trial. Red and black symbols show average responses for multiple experiments in probe trials with high- and low-contrast targets, respectively. A: monkey Re. B: monkey Yo. C: blue and green traces plot the trial-averaged eye velocity vectors during the slow and fast context, respectively, for probe target motion in the 45° direction during a speed context experiment run at 0°. D: symbols show the effect of speed context on eye direction for the +45° probe trials. Each symbol plots eye direction during the slow-speed context minus eye direction during the fast-speed context; responses for high- vs. low-contrast targets appear on the y- vs. x-axis.
Experiment 5b: Effect of speed prior adaptation on eye direction.
In these experiments, we presented blocks of target motions that created a fast or slow speed context in one direction (as in experiment 2), and probed the effects of speed context on the direction of pursuit with infrequent probe target motions rotated 45° counterclockwise. In Fig. 9C, for example, we presented blocks of either the fast-context or slow-context with rightward motion, and we delivered probe targets that moved 45° counterclockwise at 10°/s.
Eye velocity vectors averaged across trials (Fig. 9C) reveal that eye direction in the probe trials was biased more toward the direction used to adapt the speed prior during the fast context (green) compared with the slow context (blue). To summarize the data across all experiments, we defined direction effect size as the difference in eye direction in the probe trials between the fast and slow contexts. The positive values in Fig. 9D indicate that the eye direction was more biased toward the direction of the prior-adapting target motion during the fast context compared with the slow context in every experiment. The symbols plot below the unity line, indicating that eye direction was influenced more by speed context for the low-contrast compared with the high-contrast probe target. The mean direction effect sizes were 7.35 and 5.22° for the low-contrast target in monkeys Re and Xt and 3.09 and 3.51° for the high-contrast target degree in monkeys Re and Xt, respectively. We conclude that adaptation of the speed prior directly affects target direction estimation. Again, this is an effect that would be expected intuitively, and most important is the quantitative agreement with emergent predictions of the model developed next.
Model 2: Modulation of the Gain of Visual-Motor Transmission Can Account for Direction and Speed Priors, and Generalization between Them
To determine how plausible neural mechanisms might create behaviors with the features expected of Bayesian inference, we studied a model that includes modulation of the gain of visual-motor transmission, based on the mechanisms present in the pursuit system (Lee et al. 2013; Schwartz and Lisberger 1994). Our goal was to show how a biologically-based model could implement adaptation of direction and speed priors and their effects on the initiation of pursuit, and to determine whether the effects occur in retinal or motor coordinate frames. The main feature of our model was multiplication of a sensory evidence function derived from a visual-motion population response (Fig. 10A) by a function that implements direction-selective modulation of the gain of visual-motor transmission (Fig. 10, B and D) to obtain a distribution of possible target motions (Fig. 10, C and E) from which the eye speed and direction are determined. Thus our model follows the evidence for direction-selective control of the strength of visual-motor transmission in pursuit (Lee et al. 2013; Schwartz and Lisberger 1994), and the curves in Fig. 10, B and D, are exactly direction-selective control of gain. Even though some of its elements are distributions related to the components of Bayesian inference, note that model 2 has distinctly non-Bayesian internal components and is meant to emulate behavior consistent with Bayesian inference without being strictly Bayesian.
Fig. 10.
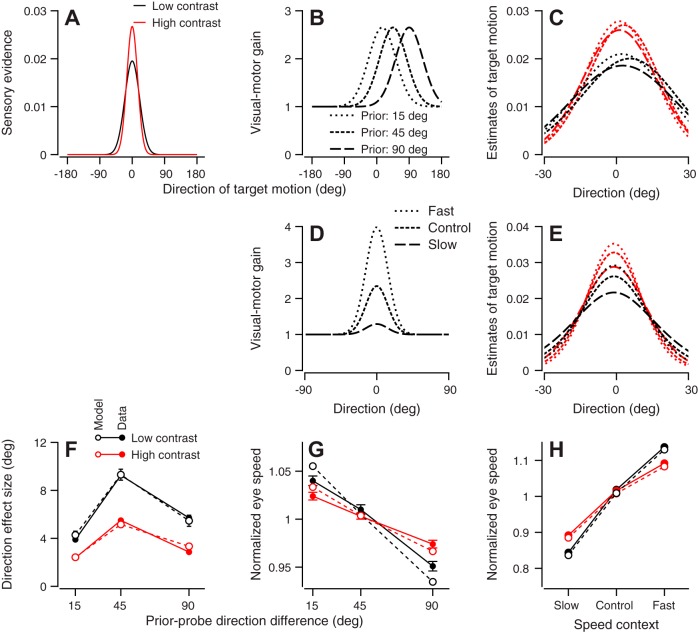
Visual-motor gain as a mechanism for adaptation of priors. A: traces show the sensory evidence functions predicted by the model for the low- and high-contrast targets. B: curves show the inferred effect of a prior-adapting target motion on visual-motor gain for different probe target directions. Dashed lines of increasing length show the gains for conditions where the prior-probe direction difference was 15, 45, and 90°, respectively. C: traces show the distributions of possible target motions. Dashed lines of increasing length show the inferred functions for conditions where the prior-probe target direction difference was 15, 45, and 90°, respectively. D: dashed lines of increasing length show the inferred visual-motor gain for the fast, control, and slow contexts, respectively. E: dashed lines of increasing length show the inferred distributions of possible target motions for the fast, control, and slow contexts, respectively. F: open and solid symbols show model predictions and actual data, respectively, for direction effect size for different prior-probe direction differences. G: open and solid symbols show model predictions and actual data, respectively, for normalized eye speed for different prior-probe direction differences. H: open and solid symbols show model predictions and actual data, respectively, for normalized eye speed during the slow, control, and fast contexts. Data from monkeys Re and Yo have been combined in F and G. Data from monkeys Re and Xt have been combined in H. In all panels, red and black traces and symbols show results for high- and low-contrast targets, respectively.
Optimization of the model produced almost perfect matches to the data (Fig. 10, F and H). Figure 10, A–C, shows the functions used in the model after it had been optimized for single-trial adaptation of the direction prior (experiment 1) by adjusting the amplitudes and standard deviations of the Gaussians for the sensory evidence and the gain control (Fig. 10, A and B). On the basis of Fig. 7F, we performed the optimization under the constraint that the amplitude of the gain control had to be the same for each direction of prior-adapting target motion. This model captures quite nicely the effects of prior-probe direction difference and stimulus contrast on the shift in eye direction (Fig. 10F). These effects can be seen as small shifts in the direction represented by the peaks of the superimposed distributions of possible target motions in Fig. 10C: as the prior-probe direction difference shifts from 15 to 45 to 90°, the peaks of the dotted, short-dashed, and long-dashed curves shift first to the right and then partway back to the left. The optimized sensory evidence functions in the model (Fig. 10A) are consistent with the idea that decreases in stimulus contrast reduce the amplitude of the likelihood function provided by the sensory representation of visual motion.
To reproduce the effects of adaptation of speed priors, we allowed the model to optimize the visual-motor gain functions to fit the data for the blocked speed context, rather than the smaller single-trial effects, but we reused the sensory evidence functions from the optimized direction prior model. Thus the visual-motor gain functions (Fig. 10D) used to reproduce the effect of speed context were larger in amplitude but similar in shape to those used to model the single-trial direction data. The effects of multiplying the sensory evidence function by the gain function can be seen in the distributions of possible target motions (Fig. 10E), and the latters’ amplitudes were used to estimate the relative eye speed across different conditions: for the fast-, control, and slow-contexts, there is a progressive decline in the amplitude of the functions shown by the dotted, short-dashed, and long-dashed curves, respectively.
Analysis of generalization between direction and speed in our model suggests that a single mechanism, namely direction-specific control of the gain of visual-motor transmission, can account for both the direction and speed priors. We performed this analysis of the model the same way we had performed the analysis of the data: by 1) evaluating the effect on eye speed for the model that had been fitted to the experiments on direction prior adaptation; and 2) evaluating the effect on eye direction for the model that had been fitted to the experiments on speed prior adaptation. It was not possible to simply fit a single model to all of the data because none of our experiments used a single adapting situation to systematically control the speed and direction priors by the same amount at the same time.
When we optimized the model to predict single-trial adaptation of the direction prior (experiment 3), the normalized eye speed predicted by the model agreed well with the eye speed measured in experiment 5a (Fig. 10G, compare open and solid symbols). The values plotted for the model in Fig. 10G were taken from the amplitudes of the relevant distributions of possible target motions in Fig. 10C: as the direction of the target motion in the prior-adapting trial shifted from 15 to 45 to 90°, the amplitude of the dotted, short-dashed, and long-dashed curves, respectively, decreased. Thus the predicted eye speed decreased as the prior-probe direction difference increased. This is an emergent property of a model whose parameters we optimized to fit the relationship between the size of the effect on eye direction (not speed) and probe-prior direction difference (Fig. 10F).
When we optimized the model to predict the effect of the two speed contexts on eye speed, it predicted an effect on eye direction that agrees with the data (experiment 5b, Fig. 9, C and D). In the experiments, we tested the response to targets that moved in directions of 45° relative to the prior-adapting trials in the speed contexts. We modeled a probe trial that was rotated 45° by shifting the sensory evidence functions of Fig. 10A so that they were centered at 45°. We then multiplied the shifted sensory evidence by the slow- and fast-context visual-motor gains of Fig. 10D. We estimated the model’s prediction of eye direction as the vector average of the resulting distributions of possible target motions. Subtracting the predicted eye directions for the slow- and fast-context resulted in a predicted direction effect size of 6.47 and 3.17° for the low- and high-contrast targets, respectively. These values are in close agreement with the average direction effect sizes in Fig. 9D of 5.99 and 3.36° for low- and high-contrast targets, respectively. Again, this is an emergent property of a model that had been optimized to reproduce the effects of the two speed contexts on eye speed. The optimized model was able to predict successfully an interaction between speed priors and eye direction that was not used to optimize it.
Failure of gain modulation in motor coordinates.
The model we tested in Fig. 10 assumes that the directional prior is implemented in retinal coordinates, based on the direction of the target motion in the prior-adapting trial(s). We can see intuitively that the predictions of the “retinal” model depend on the prior-probe direction difference, and not on the absolute direction of either target motion. For example, it predicts that the expression of the direction prior should be the same whether the probe target motion is along a cardinal or oblique axis. In contrast, we had the intuition that implementation of a prior through modulation of the gain of visual-motor transmission in the horizontal-vertical coordinate frame of the motor system would make predictions that depended on whether the probe target motion was along a cardinal or oblique axis. Therefore, we analyzed our data separately according to the axis of the probe motion, and we also tested the predictions of a computational model that implements priors in motor coordinates.
In our data, the effects of adapting the prior for target direction did not depend on whether the probe direction was along a cardinal axis or an oblique axis. The effect of prior direction on the direction of the response to a probe target motion was the same whether we pooled all pairs of trials or separated them into groups where the direction of the probe trials was along a cardinal or an oblique axis (Fig. 11G).
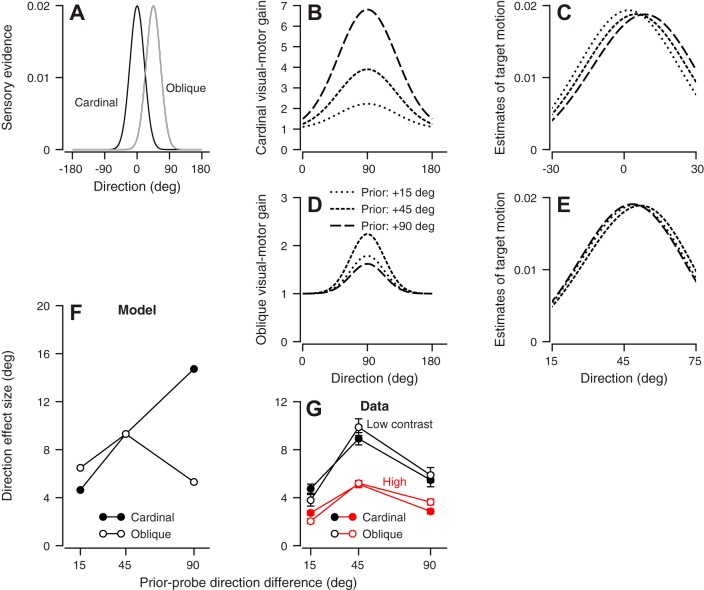
Fig. 11.
Motor coordinate model of prior adaptation for direction estimation. A: black and gray traces show the sensory evidence functions used in the motor model for cardinal and oblique probe directions, respectively. B and D: dashed lines of increasing length show the inferred priors for the motor model when the prior-probe direction difference was 15, 45, and 90°, respectively, for cardinal (B) and oblique (D) probe directions. C and E: traces show the distributions of possible target motions. Dashed lines of increasing length show the inferred functions for conditions where the prior-probe target direction difference was 15, 45, and 90°, respectively, for cardinal (C) and oblique (E) probe directions. F: model’s prediction of effect size as a function of prior-probe target direction difference. G: mean effect size in our data. Red and black symbols show results from high- and low-contrast targets, respectively. In F and G, solid and open symbols show the predictions and data for cardinal and oblique probe directions, respectively.
The data in Fig. 11G contradict the predictions of a model with gain control organized in the horizontal and vertical directions that constitute the coordinate system for motor control of pursuit in the cerebellum (Krauzlis and Lisberger 1996). Here, the sensory evidence functions (Fig. 11A) shift as a function of the direction of the probe stimulus, but the visual-motor gain functions (Fig. 11, B and D) remain fixed at 90°. The amplitudes of the gain functions depend on the size of the projection of the prior direction onto the fixed motor axis.
Figure 11 shows two scenarios where the probe target moves at 0 or 45°. Then, different values of prior-probe direction difference (15, 45, 90°) will activate the motor system in different ways for cardinal vs. oblique probe directions. For the 0° probe direction (cardinal), a 90° prior-adapting target motion yields the largest amplitude gain function (Fig. 11B). The peaks of the resulting distributions of possible target motions (Fig. 11C) shift to the right as the prior-probe difference increases from 15 to 45 to 90° (dotted, short-dashed, and long-dashed traces, respectively). Therefore, a prior-probe direction difference of 90° has the largest effect on the eye direction in the probe trial (Fig. 11F, solid symbols). For the 45° probe direction (oblique), the peak of the resulting distribution of possible target motions (Fig. 11E) shifts to the right as the prior-probe difference increases from 15 to 45° (dotted and short-dashed traces, respectively), but back to the left when the prior-probe difference is 90° (long-dashed traces). Now, a 90° prior-adapting direction again will yield the largest amplitude gain function, but the prior-probe difference is 45° (Fig. 11F, open symbols). Thus priors in motor coordinates predict, incorrectly, that the relationship between direction effect size and the prior-probe difference should depend on whether the probe direction is along a cardinal or oblique axis. We reject the motor coordinate model.
The models in Figs. 10 and 11 make several assumptions that allow them to fit the data. First, they instantiate the prior through a previously described mechanism that controls the gain of visual-motor transmission for pursuit (Schwartz and Lisberger 1994; Tanaka and Lisberger 2001, 2002a). The effect of context on the gain control is modeled as a direction selective increase in gain above a baseline of 1, where a horizontal line at 1 would create the prior-less performance of pursuit. Second, they represent sensory evidence as distributions, motivated by the concept of probabilistic population codes (Ma et al. 2006). It is clear how sensory evidence is represented in the population response in area MT (Krekelberg et al. 2006; Priebe and Lisberger 2004), but it remains unclear how or if those population responses would be converted to a neural construct that would be recognized as a likelihood function. Thus the internal representation of the sensory evidence may end up being quite different from the construct in our model. Finally, the models assume that direction is read out as the peak of the distributions of possible target motions and speed as the amplitude. Given that the distributions of possible target motions may not even exist in the brain, this is a computational mechanism that will need to be understood in terms of neural responses and circuits. Thus one could characterize our model as “opportunistic” and as a hybrid between neural and statistical concepts. We agree, but we think that the model still has the strength of reproducing the details of our data set based on well-defined assumptions, and of showing that our data can be accounted for by a direction-selective adjustment of the gain of visual-motor transmission.
DISCUSSION
Our paper elaborates the evidence that Bayesian inference describes some properties of smooth pursuit eye movements and provides two important advances in understanding that framework. First, we show that priors for target speed and direction in the smooth pursuit eye movement system are adaptable over very short timescales. Second, we provide computational evidence that priors for speed and direction are implemented using a single mechanism, and that the mechanism is closely related to the previously demonstrated modulation of the gain of visual-motor transmission for pursuit (Lee et al. 2013; Schwartz and Lisberger 1994; Tanaka and Lisberger 2001).
Bayesian Inference in the Smooth Pursuit Eye Movement System
On the basis of the criteria set out by Ma (2012), we think that pursuit behavior operates in a way that is consistent with Bayesian inference. However, we cannot say (and do not care) whether pursuit is Bayes optimal, and, according to Ma (2012), optimality is not a criterion for Bayesian inference. Our use of the terminology of Bayesian inference derives from the parallels between our data on pursuit and features of other behaviors that have been categorized by their investigators as Bayesian (Alais and Burr 2004; Battaglia et al. 2003; Fetsch et al. 2011; Knill 2007; Knill and Saunders 2003; Kording 2014; Körding et al. 2004; Körding and Wolpert 2004, 2006; Verstynen and Sabes 2011; Weiss et al. 2002). Our goal is to understand how neural circuits implement the competition between sensory evidence and past experience that is a hallmark of the Bayesian framework. The advantages and accessibility of the circuit for pursuit eye movements make us think we have an excellent chance of understanding how it creates behaviors consistent with Bayesian inference, perhaps while using internal principles that have little in common with Bayesian inference (Bowers and Davis 2012). If we can succeed, then it may be possible to generalize to the neural mechanisms of other behaviors with similar properties.
Bayesian inference provides a formal system for understanding the interaction between experience (priors) and sensory information (likelihoods). The previous paper from our laboratory (Yang et al. 2012) and our present results imply that pursuit estimates the speed and direction of target motion by comparing priors based on previous target motions with the sensory data from the target motion itself. We suggest that the speed and direction contexts in our experimental design alter the initiation of pursuit on probe trials because the contexts alter the prior. As one would expect for Bayesian or probabilistic inference, the efficacy of the priors depends on the contrast of the probe target, which defines the reliability of the sensory data. Priors have larger effects on the ensuing behavior when a low-contrast moving target creates weak and unreliable visual motion signals compared with when a high-contrast moving target creates strong, reliable visual motion signals.
Our unpublished data (J. Yang and S. G. Lisberger), as well as Krekelberg et al. (2006), show that the population response in area MT is smaller in amplitude and noisier for the motion of low-contrast targets, consistent with our view that low-contrast targets provide a less reliable likelihood function. Still, there has been some disagreement about whether weaker pursuit initiation for low-contrast targets is the result of a competition between sensory evidence and priors, or if the decoder that converts the population response in MT to estimates of target speed is sensitive to the amplitude as well as the preferred speed at the peak of the population response. Our data resolve this disagreement. They show that priors are adaptable and can alter systematically the response to a given motion of a given stimulus form and contrast. Thus the estimate of target speed (or direction) depends on the history of target motions, even though the population response in MT is statistically the same. Of course, if one includes adaptation of the prior as part of the decoder, then our framework is the same as the one proposed by Krekelberg et al. (2006).
In the present paper, we show that priors for target direction and speed are adaptable on the scale of single trials. Thus the pursuit system is continuously attempting to learn and predict upcoming target motions. Our conclusion is supported most strongly by the fact that we are able to influence directional and speed priors with two-trial blocks. That priors can be adapted over such short timescales demonstrates that sensory-motor systems are learning continuously the statistics of the environment to update priors. The ability of priors to adapt so quickly is especially important, given our constantly changing environment and the potential unreliability of sensory information.
There are strong similarities between the fast-adapting priors we have demonstrated in our paper and the longer-term priors demonstrated by Yang et al. (2012). First, the expressions of the fast-adapting and long-term priors for target speed and direction all depend on the strength of visual motion. Second, implementation of fast-adapting and long-term priors can be simulated by a mechanism that invokes modulation of the gain of visual-motor transmission. Taken together, these similarities suggest a tight linkage between fast-adapting and long-term priors. One intriguing possibility is that the fast-adapting priors contribute to the formation of the long-term priors. At the extreme, they may be the same phenomenon.
Two facts argue that adaptation of priors is the result of a sensory-motor system reacting to its recent history of inputs, rather than the product of a high-level cognitive phenomenon. First, single-trial adaptation of the direction and speed prior is maladaptive because the probe direction and speed are perfectly predictable: a cognitive phenomenon would not adapt. Second, the effects of the speed context generalize to all target motions in a high-speed or low-speed block, and they come and go gradually: a cognitive phenomenon might be specific to a narrow range of stimuli and would come and go abruptly. Thus we think we are exploring an automatic property of the brain that may generalize to all sensory-motor systems, as well as to perception and more complicated processes such as choice.
Implementation of Priors through Modulation of the Gain of Visual-Motor Transmission
Control of the gain of visual-motor transmission by the FEFSEM is one of the main components of the smooth pursuit system. Measurements of motor performance imply that the gain of visual-motor transmission is low during fixation and high during pursuit. For example, brief visual motion perturbations during fixation induce a relatively small behavioral response, while identical visual motion perturbations during active pursuit induce larger eye velocity responses (Schwartz and Lisberger 1994). Additional evidence suggests that gain control is continuous, an extension of the switch suggested by Luebke and Robinson (1988). The role of the FEFSEM has been demonstrated by microstimulation experiments. Subthreshold microstimulation of FEFSEM enhances the eye movement response to a target perturbation delivered during fixation, as if the perturbation had been presented during active pursuit (Tanaka and Lisberger 2001), and also enhances the eye velocity at the initiation of pursuit for a given target motion (Tanaka and Lisberger 2002a). The supplementary eye fields also may participate in pursuit gain control (Missal and Heinen 2001).
We suggest that priors for target speed and direction are implemented through a single mechanism based on direction-selective modulation of the gain of visual-motor transmission. Prior publications also pointed to a tight linkage between priors and control of the gain of visual-motor transmission for pursuit. Tabata et al. (2006) revealed that behavioral responses to target perturbations during fixation could be modulated by past experience. They suggested that these perturbations were modulated via the adjustment of visual-motor gain. Yang et al. (2012) used a neural-network model of FEFSEM and area MT to show that priors in the pursuit system could be implemented as a form of gain control. They suggested that priors were created by structured changes in the recurrent connectivity within the FEFSEM. Our analysis in the present paper shows that adjustment of the gain of visual-motor can account for the effects of both the speed and direction contexts we used to adapt the direction and speed priors, as well as the generalization between direction and speed. Finally, our data imply that the brain implements priors in a retinal coordinate frame, consistent with the retinal coordinate frame of gain control (Lee et al. 2013).
Parallels between the properties of the FEFSEM and the computational mechanisms we used to model our data imply that the FEFSEM is a promising neural locus for priors. The direction tuning of FEFSEM neurons is in retinal coordinates (Tanaka and Lisberger 2002b), in agreement with the coordinate system of both gain control and priors. The demonstration that the output of FEFSEM controls the gain of visual-motor transmission agrees with our computational demonstrations that a neural circuit that implements gain control can lead to behaviors that are consistent with Bayesian inference. That said, our model based on gain control is distinctly not a Bayesian model, and likewise the neural circuit implementation also may not be at all Bayesian.
Previous studies have established similar models to explain pursuit behavior during target-blanking of translating bars (Bogadhi et al. 2013) and anticipatory pursuit (Orban de Xivry et al. 2013). A common feature of all three models (theirs and ours) is the existence of two components driving pursuit behavior: a sensory component driven by visual motion and an extrasensory component driven by experience-based expectation. The primary difference between our model and the other two is the way that the two components are combined. The other models combine the two components via a weighted sum, in which the weights are determined by the reliability. In our model, the expectation component influences behavior by selectively enhancing the gain of visual-motor transmission for a portion of the sensory representation. The strength in our model is that it takes advantage of a feature of the pursuit system that already has been established at both the behavioral and neural level: visual-motor gain control. At the behavioral level, the gain of eye speed responses to visual-motion perturbations depends on context. At the neural level, microstimulation of FEFSEM increases the gain of behavioral responses to visual-motion perturbations. Therefore, our model provides a neurophysiological road map for investigating how the neural pursuit system actually combines expectation and sensory information.
Generalizability to Other Sensory-Motor Systems
The behavioral findings of our paper generalize to other sensory-motor systems, suggesting that they represent a fundamental feature of brain function. In saccadic eye movements, the direction of an eye movement made during a memory-guided saccade task is biased toward the direction of a saccade on a previous trial (Papadimitriou et al. 2015). This is consistent with our finding that single trials affect target direction estimation. Important similarities include 1) the maximum effect for the pursuit system is at ±45°, within the maximum range for the saccade system (41–78°); and 2) the decrement of effect size with increasing intertrial interval. Unfortunately, Papadimitriou et al. (2015) did not probe directly whether the reliability of sensory information on the probe trials altered the effect of the prior-adapting trial. In the arm movement system, priors for target position are capable of adapting over relatively short time scales. Verstynen and Sabes (2011) showed that priors for reach direction develop within blocks of ~100 trials, according to the statistics of targets that are encountered in each block, and that reach direction on any given trial is affected by the direction required on the previous trial. Thus the timescales for reach and pursuit prior adaptation are quite similar.
The smooth pursuit eye movement system seems ideal for our ultimate goal of understanding how neural circuits lead to behaviors that have features of Bayesian inference. First, adaptation of speed and direction priors shares features with other sensory-motor systems. Second, we are able to control precisely the formation and expression of priors in the pursuit system over very short timescales. Third, the skeleton of the smooth pursuit neural circuitry is well known and easily accessible, and the present paper connects existing neural data to Bayesian inference. Future neural recordings should reveal how behavior compatible with Bayesian inference could arise from the action of neural circuits.
GRANTS
National Institutes of Health (NIH) Grant R01-EY-003878, internal funds from Duke University, and a gift from the Howard Hughes Medical Institute supported the research. T. R. Darlington received support from the Wakeman Endowment Fund, the Duke University Medical Scientist Training Program (T32 GM-007171), and from NIH award F30-EY-027684.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
T.R.D. and S.G.L. conceived and designed research; T.R.D. and S.T. performed experiments; T.R.D. and S.T. analyzed data; T.R.D. and S.G.L. interpreted results of experiments; T.R.D. prepared figures; T.R.D. drafted manuscript; T.R.D. and S.G.L. edited and revised manuscript; T.R.D. S.T., and S.G.L. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Steven Happel for technical assistance, and Jeff Beck for numerous helpful discussions.
REFERENCES
- Alais D, Burr D. The ventriloquist effect results from near-optimal bimodal integration. Curr Biol 14: 257–262, 2004. doi: 10.1016/j.cub.2004.01.029. [DOI] [PubMed] [Google Scholar]
- Battaglia PW, Jacobs RA, Aslin RN. Bayesian integration of visual and auditory signals for spatial localization. J Opt Soc Am A Opt Image Sci Vis 20: 1391–1397, 2003. doi: 10.1364/JOSAA.20.001391. [DOI] [PubMed] [Google Scholar]
- Bogadhi AR, Montagnini A, Masson GS. Dynamic interaction between retinal and extraretinal signals in motion integration for smooth pursuit. J Vis 13: 5, 2013. doi: 10.1167/13.13.5. [DOI] [PubMed] [Google Scholar]
- Bowers JS, Davis CJ. Bayesian just-so stories in psychology and neuroscience. Psychol Bull 138: 389–414, 2012. doi: 10.1037/a0026450. [DOI] [PubMed] [Google Scholar]
- Fetsch CR, Pouget A, DeAngelis GC, Angelaki DE. Neural correlates of reliability-based cue weighting during multisensory integration. Nat Neurosci 15: 146–154, 2011. doi: 10.1038/nn.2983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs AF, Robinson DA. A method for measuring horizontal and vertical eye movement chronically in the monkey. J Appl Physiol 21: 1068–1070, 1966. [DOI] [PubMed] [Google Scholar]
- Knill DC. Robust cue integration: a Bayesian model and evidence from cue-conflict studies with stereoscopic and figure cues to slant. J Vis 7: 1–24, 2007. doi: 10.1167/7.7.5. [DOI] [PubMed] [Google Scholar]
- Knill DC, Saunders JA. Do humans optimally integrate stereo and texture information for judgments of surface slant? Vision Res 43: 2539–2558, 2003. doi: 10.1016/S0042-6989(03)00458-9. [DOI] [PubMed] [Google Scholar]
- Kording KP. Bayesian statistics: relevant for the brain? Curr Opin Neurobiol 25: 130–133, 2014. doi: 10.1016/j.conb.2014.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Körding KP, Ku SP, Wolpert DM. Bayesian integration in force estimation. J Neurophysiol 92: 3161–3165, 2004. doi: 10.1152/jn.00275.2004. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature 427: 244–247, 2004. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian decision theory in sensorimotor control. Trends Cogn Sci 10: 319–326, 2006. doi: 10.1016/j.tics.2006.05.003. [DOI] [PubMed] [Google Scholar]
- Kowler E, Martins AJ, Pavel M. The effect of expectations on slow oculomotor control. IV. Anticipatory smooth eye movements depend on prior target motions. Vision Res 24: 197–210, 1984. doi: 10.1016/0042-6989(84)90122-6. [DOI] [PubMed] [Google Scholar]
- Kowler E, Steinman RM. The effect of expectations on slow oculomotor control. I. Periodic target steps. Vision Res 19: 619–632, 1979a. doi: 10.1016/0042-6989(79)90238-4. [DOI] [PubMed] [Google Scholar]
- Kowler E, Steinman RM. The effect of expectations on slow oculomotor control. II. Single target displacements. Vision Res 19: 633–646, 1979b. doi: 10.1016/0042-6989(79)90239-6. [DOI] [PubMed] [Google Scholar]
- Krauzlis RJ, Lisberger SG. Directional organization of eye movement and visual signals in the floccular lobe of the monkey cerebellum. Exp Brain Res 109: 289–302, 1996. doi: 10.1007/BF00231788. [DOI] [PubMed] [Google Scholar]
- Krekelberg B, van Wezel RJA, Albright TD. Interactions between speed and contrast tuning in the middle temporal area: implications for the neural code for speed. J Neurosci 26: 8988–8998, 2006. doi: 10.1523/JNEUROSCI.1983-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Yang J, Lisberger SG. Control of the gain of visual-motor transmission occurs in visual coordinates for smooth pursuit eye movements. J Neurosci 33: 9420–9430, 2013. doi: 10.1523/JNEUROSCI.4846-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisberger SG, Westbrook LE. Properties of visual inputs that initiate horizontal smooth pursuit eye movements in monkeys. J Neurosci 5: 1662–1673, 1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luebke AE, Robinson DA. Transition dynamics between pursuit and fixation suggest different systems. Vision Res 28: 941–946, 1988. doi: 10.1016/0042-6989(88)90103-4. [DOI] [PubMed] [Google Scholar]
- Ma WJ. Organizing probabilistic models of perception. Trends Cogn Sci 16: 511–518, 2012. doi: 10.1016/j.tics.2012.08.010. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nat Neurosci 9: 1432–1438, 2006. doi: 10.1038/nn1790. [DOI] [PubMed] [Google Scholar]
- Missal M, Heinen SJ. Facilitation of smooth pursuit initiation by electrical stimulation in the supplementary eye fields. J Neurophysiol 86: 2413–2425, 2001. [DOI] [PubMed] [Google Scholar]
- Orban de Xivry J-J, Coppe S, Blohm G, Lefèvre P. Kalman filtering naturally accounts for visually guided and predictive smooth pursuit dynamics. J Neurosci 33: 17301–17313, 2013. doi: 10.1523/JNEUROSCI.2321-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osborne LC, Lisberger SG, Bialek W. A sensory source for motor variation. Nature 437: 412–416, 2005. doi: 10.1038/nature03961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papadimitriou C, Ferdoash A, Snyder LH. Ghosts in the machine: memory interference from the previous trial. J Neurophysiol 113: 567–577, 2015. doi: 10.1152/jn.00402.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG. Estimating target speed from the population response in visual area MT. J Neurosci 24: 1907–1916, 2004. doi: 10.1523/JNEUROSCI.4233-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran R, Lisberger SG. Normal performance and expression of learning in the vestibulo-ocular reflex (VOR) at high frequencies. J Neurophysiol 93: 2028–2038, 2005. doi: 10.1152/jn.00832.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz JD, Lisberger SG. Initial tracking conditions modulate the gain of visuo-motor transmission for smooth pursuit eye movements in monkeys. Vis Neurosci 11: 411–424, 1994. doi: 10.1017/S0952523800002352. [DOI] [PubMed] [Google Scholar]
- Tabata H, Miura K, Taki M, Matsuura K, Kawano K. Preparatory gain modulation of visuomotor transmission for smooth pursuit eye movements in monkeys. J Neurophysiol 96: 3051–3063, 2006. doi: 10.1152/jn.00412.2006. [DOI] [PubMed] [Google Scholar]
- Tanaka M, Lisberger SG. Regulation of the gain of visually guided smooth-pursuit eye movements by frontal cortex. Nature 409: 191–194, 2001. doi: 10.1038/35051582. [DOI] [PubMed] [Google Scholar]
- Tanaka M, Lisberger SG. Enhancement of multiple components of pursuit eye movement by microstimulation in the arcuate frontal pursuit area in monkeys. J Neurophysiol 87: 802–818, 2002a. doi: 10.1152/jn.00409.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka M, Lisberger SG. Role of arcuate frontal cortex of monkeys in smooth pursuit eye movements. I. Basic response properties to retinal image motion and position. J Neurophysiol 87: 2684–2699, 2002b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verstynen T, Sabes PN. How each movement changes the next: an experimental and theoretical study of fast adaptive priors in reaching. J Neurosci 31: 10050–10059, 2011. doi: 10.1523/JNEUROSCI.6525-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat Neurosci 5: 598–604, 2002. doi: 10.1038/nn0602-858. [DOI] [PubMed] [Google Scholar]
- Yang J, Lee J, Lisberger SG. The interaction of bayesian priors and sensory data and its neural circuit implementation in visually guided movement. J Neurosci 32: 17632–17645, 2012. doi: 10.1523/JNEUROSCI.1163-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]