Automatic and intentional influences on saccade landing

When making an eye movement to a target location, the presence of a nearby distractor can cause the saccade to unintentionally terminate at the distractor itself or the average position in between stimuli. With probabilistic mixture models, we quantified how both unavoidable capture and goal-directed targeting were influenced by changing the task and the target-distractor separation. Using this novel technique, we could extract the time course over which automatic and intentional processes compete for control of saccades.

Abstract

Saccadic eye movements enable us to rapidly direct our high-resolution fovea onto relevant parts of the visual world. However, while we can intentionally select a location as a saccade target, the wider visual scene also influences our executed movements. In the presence of multiple objects, eye movements may be “captured” to the location of a distractor object, or be biased toward the intermediate position between objects (the “global effect”). Here we examined how the relative strengths of the global effect and visual object capture changed with saccade latency, the separation between visual items and stimulus contrast. Importantly, while many previous studies have omitted giving observers explicit instructions, we instructed participants to either saccade to a specified target object or to the midpoint between two stimuli. This allowed us to examine how their explicit movement goal influenced the likelihood that their saccades terminated at either the target, distractor, or intermediate locations. Using a probabilistic mixture model, we found evidence that both visual object capture and the global effect co-occurred at short latencies and declined as latency increased. As object separation increased, capture came to dominate the landing positions of fast saccades, with reduced global effect. Using the mixture model fits, we dissociated the proportion of unavoidably captured saccades to each location from those intentionally directed to the task goal. From this we could extract the time course of competition between automatic capture and intentional targeting. We show that task instructions substantially altered the distribution of saccade landing points, even at the shortest latencies.

NEW & NOTEWORTHY When making an eye movement to a target location, the presence of a nearby distractor can cause the saccade to unintentionally terminate at the distractor itself or the average position in between stimuli. With probabilistic mixture models, we quantified how both unavoidable capture and goal-directed targeting were influenced by changing the task and the target-distractor separation. Using this novel technique, we could extract the time course over which automatic and intentional processes compete for control of saccades.

saccades are rapid, ballistic eye movements that facilitate our ability to process information from our surroundings. By shifting the target of our gaze to a new location, saccades allow us to direct our high-resolution fovea to locations of interest for fine-grained visual processing. Many of these eye movements are automatic and reactionary, with our gaze shifting rapidly toward a flashing light or an abruptly moving stimulus. These unconscious responses make ecological sense, as they help ensure that both our fovea and our attention can be directed to potential threats as quickly as possible. As such, it is perhaps unsurprising that the likely targets for saccadic eye movements can be quite well predicted by the low-level properties of the visual scene (Itti and Koch 2001; Serences and Yantis 2006; Theeuwes 1994). However, at other times individuals view a scene with specific aims or goals in mind. Rather than passively responding to visual saliency, here they actively investigate their visual environment and intentionally direct their eye movements toward the task goal (if it is known) or toward the regions within the scene thought most likely to contain the task-relevant information (Bacon and Egeth 1994; Folk et al. 1992, 1994; Folk and Remington 1998; Serences and Yantis 2006).

For example, when searching for a friend on a crowded street, an individual should direct their eye movements toward the last location they saw their friend, rather than toward the most salient features in the scene, to improve the chances of finding them quickly. To achieve this intentional targeting, the visual system exerts top-down control over the programming of the eye movement (Serences and Yantis 2006; van Zoest et al. 2004; Yantis 1993). This task-related signal is thought to inhibit the automatic capture toward salient stimuli and boosts neural activity corresponding to specific task-relevant locations, assisting in the attentional selection of these regions. Here we explore the interactions between automatic and intentional targeting and examine how the competition between these processes changes, depending on both the proximity of objects in the visual world and the delay (and hence available processing time) before initiating the eye movement. To achieve this, we manipulated the spatial separation between visual objects and investigated how varying the goal location with different task instructions influenced the distribution of saccade landing positions in response to the sudden appearance of two objects.

In sparse visual scenes, the sudden appearance of a visual stimulus triggers a fast, accurate saccade toward its location (Franconeri et al. 2004; Jonides and Yantis 1988; Yantis 1993). This eye movement is typically considered to be automatic, occurring without the observer’s explicit intention to move their eyes, and requires intentional suppression if the individual is to either maintain their fixation or to instead initiate a saccade to another location (Theeuwes et al. 1998). Indeed, even when individuals are specifically attempting an alternative eye movement, the sudden appearance of a distractor stimulus will often instead capture their gaze to its location (Boot et al. 2005; Godijn and Theeuwes 2002; Irwin et al. 2000; Ludwig et al. 2008; Ludwig and Gilchrist 2003; Theeuwes et al. 1998, 1999; Wu and Remington 2003). While the strength of this oculomotor capture can be modulated (e.g., with task instructions; Wu and Remington 2003), even with strong manipulations it is difficult to fully eliminate the capture toward abrupt onsets. These results point to a fundamental role of low-level stimulus salience in causing stimulus capture and suggest that neither top-down control nor changes to the low-level properties of the stimuli can entirely extinguish the stimulus-driven selection of a distractor as a potential saccade target.

While the appearance of a single stimulus might lead to oculomotor capture, when multiple stimuli appear simultaneously in close proximity, the landing position of the resulting saccade is often biased toward an intermediate location between the stimuli. This spatial bias is known as “the global effect” (Coren and Hoenig 1972; Findlay 1982). Interestingly, the global effect has been found to occur even when the visual stimuli are sufficiently differentiated so that the target and distractor are unambiguous (Coren and Hoenig 1972; Findlay 1982; Jacobs 1987; Ottes et al. 1985; Van der Stigchel and Nijboer 2013; Walker et al. 1997). This suggests that the effect does not arise due to decision confusion in identifying the target stimulus. Indeed, the prevalence of the global effect does not vary as a function of target and distractor discriminability (Jacobs 1987). Furthermore, even in tasks in which both stimuli are potential targets [i.e., the participant must simply saccade to either (STE) stimulus], the global effect is still observed. However, manipulations of low-level properties of the stimuli, which do not change the discriminability of the target per se, such as manipulating their relative salience (Deubel et al. 1984; Findlay 1982; Findlay et al. 1993), can substantially modulate the proportion of global effect saccades observed. These findings suggest that the global effect arises from similarity in the visual properties of the stimuli, causing competition in automatic target selection processes. These effects have been modeled in terms of activity in the superior colliculus (SC; Meeter et al. 2010; Trappenberg et al. 2001; Viswanathan and Barton 2013).

The delay before participants initiate their eye movement is also important. Indeed, the strongest biases in landing position toward the average location have consistently been found for shorter saccade latencies, while longer delays lead to increasingly accurate eye movements (Chou et al. 1999; Coëffé and O’Regan 1987; Edelman and Keller 1998; Eggert et al. 2002; Findlay 1982; Godijn and Theeuwes 2002; Heeman et al. 2014; Jacobs 1987; McSorley and Findlay 2003; Ottes et al. 1985; Van der Stigchel and Nijboer 2011, 2013; Vitu et al. 2006). For example, Ottes and colleagues (1985) demonstrated that, while the most rapid subset of saccades exhibited a substantial global effect, those in which the saccade was executed longer than 300 ms after the appearance of the stimuli were completely accurate. This time course, in which only those saccades initiated rapidly after stimulus appearance will reliably generate an averaging saccade, has been consistently observed across different studies (Eggert et al. 2002; McSorley and Findlay 2003) and has been attributed to the top-down effects of goal-related selection influencing target selection (van Zoest et al. 2004). This suggests that the global effect is a latency-sensitive process originating from the automatic, exogenous processing of abruptly appearing visible stimuli.

The relative separation between visual stimuli is another critical factor in the generation of averaging saccades. For stimuli appearing outside of the immediate 1.5° of visual angle surrounding the current fixation (the “foveal dead zone”; Vitu 2008), the boundary between predominantly averaging saccades and predominantly individualized saccades has been consistently reported at target-distractor separations of 20–30° in angular distance (Ottes et al. 1984; Van der Stigchel and Nijboer 2011, 2013; Vitu 2008; Walker et al. 1997). For example, Ottes and colleagues (1984) showed a distinct averaging effect when two targets were separated by 30°, but bimodal responses when they were separated by 90°. Similarly, the work of Walker and colleagues (1997) suggested that only distractors occurring within a strict ±20° angular window surrounding the target altered saccade amplitude. However, some more recent studies have shown evidence of averaging saccades occurring at larger separations (Arai et al. 2004; Van der Stigchel et al. 2009, 2012; Van der Stigchel and Nijboer 2011). This raises the possibility that, rather than a strictly defined window, the transition between accurate and averaging saccades might be more gradual.

In one of the most detailed studies of the spatial range of the global effect, Van der Stigchel and Nijboer (2013) examined a variety of different target and distractor separations (between 12.5° and 55°). Rather than relying on the mean saccade landing position, which can often conflate saccades erroneously directed to the distractor object with those targeting the global location, they instead quantified the strength of the global effect by comparing unimodal and bimodal fits to the data. They found that only separations smaller than 45° were better fit by a unimodal distribution, and, although they did observe some averaging saccades beyond this range, they concluded that the global effect does not occur beyond 55° separation. However, their analyses did not allow for the possibility that the observed saccade landing distribution incorporated a mixture of stimulus capture (to either the target or distractor location) and averaging saccades. Additionally, when two stimuli appear simultaneously, the average latency of saccades increases as the separation between the stimuli increases. This effect is known as the remote distractor effect (RDE; Walker et al. 1997) and, since for the same spatial separation the strength of the global effect decreases as saccade latency increases, by analyzing their data irrespective of saccade latency the true prevalence of the global effect at larger separations may have been obscured.

The behavioral and neural evidence, both from human (Chou et al. 1999) and animal studies (Dorris et al. 2007; Edelman and Keller 1998; Glimcher and Sparks 1993; van Opstal and van Gisbergen 1990) has broadly supported the idea that the global effect occurs because potential saccade targets are encoded as vectors within a neural population code (Tipper et al. 1997). In this framework, competition between the vector representing the target and that of the distractor drives both the delays in saccade initiation and saccade averaging (Meeter et al. 2010; Rizzolatti et al. 1987; Sheliga et al. 1995; Trappenberg et al. 2001). The slowing of saccadic reaction times due to the presence of a distractor (RDE) arises from the visible stimuli mutually inhibiting each other, slowing the overall rate at which activity accumulates toward the threshold of movement initiation. When these stimuli are sufficiently close, instead of inhibiting one another, they are instead treated as a single activation. While this release from inhibition allows saccades to be initiated more rapidly, it also results in a bias of the executed saccades toward the average (global effect) location. These populations have been postulated to reside within the SC (Glimcher and Sparks 1993), an area where signals from multiple brain regions including the parietal eye fields, frontal eye fields, and sensory areas are integrated (Moschovakis et al. 1996; Proudlock and Gottlob 2007).

However, the existence of the long-distance lateral inhibitory connections required by neural models of SC is debated (Arai et al. 2004; Isa and Hall 2009; Lee and Hall 2006; Marino et al. 2015). This has led researchers to question whether saccadic behavior truly results from simple population codes in SC, or if it is better explained by interactions between low-level oculomotor processes and decision-making processes emerging from other areas (Christie et al. 2015). Although electrical stimulation of the SC has been shown to elicit saccades to the corresponding spatial location, stimulation of multiple locations simultaneously results in averaging saccades to the intermediate location (Glimcher and Sparks 1993). Interestingly, as noted by Christie and colleagues (2015), this averaging in response to stimulation occurred for separations that far exceeded the spatial window in which behavioral averaging is typically observed. Coupled with their own findings, in which they examined the influence of spatially specific priming on saccadic reaction times, this led them to suggest that the transition from averaging saccades to stimulus-specific saccades may not occur in SC. Instead they propose that the average location is always the dominant activity on the saccade map, and the tendency to saccade accurately at larger separations occurs due to the influence of “high-level decision making processes” (see p. 1548 in Christie et al. 2015) as participants attempt to fulfil their assigned task (i.e., selecting a specific target for their eye movement).

Alternatively, while their priming paradigm may have functioned as a good probe for the effects of stimulus activity in SC, the presence of the priming stimuli may have led to inhibition of these locations as potential motor goals. Using an anti-saccade task, Viswanathan and Barton (2013) have previously demonstrated that global effects were elicited by distractors that were positioned close to the task goal, and not by the stimulus location per se. Based on this, they suggested that the global effect occurs because of interactions between competing movement goals without necessarily influencing stimulus localization. When comparing saccades of similar latency, they found that anti-saccades elicited a stronger global effect, with this difference consistent with the idea that the lower activity at the saccade goal during anti-saccades (Everling et al. 1999) results in a greater relative influence of the distractor. As, in such a task, the intermediate position between physical stimuli is located far from the intermediate position between the inferred goal location and the distractor, these results suggest that this activity must incorporate top-down knowledge of the task. Applied to the results of Christie and colleagues (2015), the inhibition of the prime locations as potential goal locations (to prevent automatic saccades until the appearance of the go stimulus) could have resulted in the broad, separation-invariant reduction in saccadic reaction times that they observed.

The influence of saccade latency on the frequency of averaging saccades is typically thought to represent an increased role of top-down selection of the task-goal as the delay before movement initiation increases (van Zoest et al. 2004, 2012). Thus, while low-latency saccades are thought to reveal competition occurring between ascending sensory information, those initiated later are dominated by the influence of intentional, top-down selection of the goal location. This makes task instructions critical, as they directly affect the intentional selection of the movement goal. Indeed, previous studies have demonstrated that simply emphasizing to participants the requirement to make a highly accurate eye movement reduces the likelihood of making saccades to the global effect location (Coren and Hoenig 1972; Findlay 1982; Findlay and Kapoula 1992). Both paradigms in which participants must saccade to a target stimulus (STT) in the presence of a clearly differentiated distractor stimulus, and those in which participants are shown two potential targets stimuli and are instructed to saccade to either (STE), have been found to result in a considerable global effect (Van der Stigchel and Nijboer 2011), although the task-related processes that would occur in such a task would arguably differ substantially.

Despite this important role of task instructions, a frequently used alternative paradigm, ostensibly to eliminate the influence of top-down selection, is to present two identical stimuli and to give the participants ambiguous instructions as to what is the task goal (i.e., “participants were instructed to move their eyes as fast as possible to the stimuli presented”; see p. 31 in Heeman et al. 2014). In this task, which we will term saccade to ambiguous (STA), the task instructions are deliberately vague as to what is the explicit task goal. Typically, these studies report a stronger global effect and argue that, in the absence of top-down control, saccades predominantly land at the midpoint of the stimuli, as this is the “default” behavior (e.g., Silvis and Van der Stigchel 2014). However, the absence of explicit instructions about the task goal does not prevent participants from inferring what they think is required of them, and, when unsure where to look, executing an eye movement to the midpoint (bringing both stimuli closer to the fovea) is indeed a valid strategy. To dissociate the task goal from eye movements to either location, we developed a novel task in which participants are required either to deliberately saccade to a target stimulus or to the intermediate location in between stimuli. By comparing the tasks, we could then assess how intentional selection alters the distribution of saccade landing positions.

We aimed to investigate how the spatial separation between two targets influences both the speed at which saccades are initiated, and the tendency to execute saccades to the average location. We examined saccades toward a target stimulus in the presence of a distractor separated by up to 75°. We quantified the frequency of executing an averaging global effect saccade under these different conditions by fitting the data with probabilistic mixture models and, through examination of several different variations of the models, determining which components were necessary to fit the observed saccade landing distributions for each of our different conditions. This approach enabled us to make very sensitive estimates of the proportion of saccades captured toward either the target, distractor, or intermediate location. Additionally, we sought to explicitly examine the influence of task instructions by varying whether participants were instructed to saccade to the target location or to the intermediate location between the two stimuli. This additional manipulation revealed the interactions across time between automatic stimulus capture, the global effect, and intentional top-down selection.

EXPERIMENT 1

In the first experiment, we investigated how different target-distractor separations influence the prevalence of the global effect, and how this relationship changes with the latency of the saccade. Additionally, in separate blocks, we varied the instructions to participants, asking them to execute a saccade either to the target object (defined by color) or to the intermediate position between the two objects. This manipulation enabled us to examine the proportion of saccades unavoidably directed toward the target, distractor, or intermediate location, regardless of which was the task-goal location. By contrasting the landing distributions for the same separation across the two tasks, we additionally quantified the role of top-down processes in determining saccade targets.

Methods

Participants.

Eight naive individuals (20–29 yr old; 2 male) took part in the experiment. All participants had normal or corrected-to-normal visual acuity. Informed consent was obtained before the study in accordance with the guidelines of the Helsinki Declaration, and the protocol was approved by the Cambridge Psychology Research Ethics Committee.

Apparatus.

Participants were seated comfortably, with their head stabilized by a chin rest, within a black felt-clad housing that extended from the monitor to behind the participant’s head. This eliminated peripheral distractions and ensured that only the testing monitor was visible to them. Participants viewed the experiment on a 21-in. linearized CRT monitor operating at 85 Hz and viewed at 60 cm. Eye movements were monitored by measuring each participant’s right eye using an infrared video-based eye tracker (Eyelink 1000 Desktop System; SR Research), operating at 1,000 Hz.

Stimuli and procedure.

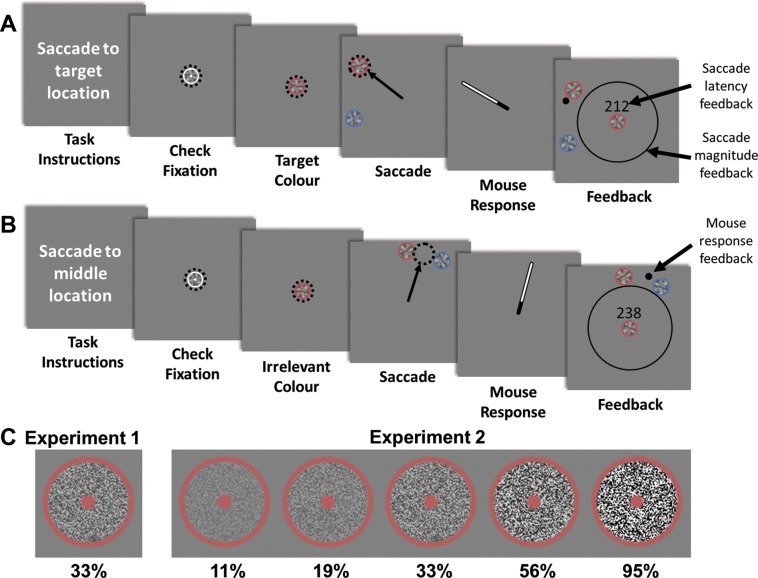
The experiment consisted of two separate tasks which differed only in the instructions given to the participants (Fig. 1). In the two task conditions, the instructions were to either “move your eyes as fast as possible to the object that matches the same color as the fixation object” (STT), or “move your eyes as fast as possible to the point in between the two objects” (saccade to middle; STM). The stimuli and experimental procedure remained identical between the two tasks, with the participant simply instructed to ignore the colors of the fixation and stimuli during the STM task. The order of tasks was counterbalanced across participants, and the experiment was organized so that participants completed all of the blocks of one task before beginning the second task. All of the blocks for each task were completed within a single day, with a separation of at least 1 day before participants began the blocks of the other task.

Fig. 1.

Procedure for the two different tasks. The procedure for the saccade to target (STT; A) and saccade to middle (STM; B) tasks are shown. Participants were required to maintain fixation until the disappearance of the fixation stimulus, at which stage they executed an eye movement as rapidly as possible to the task goal location. Immediately afterwards, they were required to indicate the goal location with the computer mouse. They were then given feedback regarding the magnitude (but not the angle) of their saccade (to discourage participants undershooting the goal location) and the latency of their saccade (with participants instructed to aim for 200 ms or faster) and were shown the location of their perceptual response in relation to the target and distractor. C: a close-up view of the stimuli, with the different contrast modifications used in experiment 2.

Each trial began with the appearance of a white-colored stimulus in the center of the display (Fig. 1). After 200 ms of steady fixation, the experimental trial began, and the color of the stimulus changed to the target color. After 1,500–2,000 ms, two peripheral stimuli appeared at 8° in the periphery, and the fixation stimulus disappeared. This disappearance was the cue for the participants to move their gaze as rapidly as possible to the goal location. The separation between target and distractor was either 15, 30, 45, 60, or 75° for both tasks, with an additional single target (no distractor) condition in the STT task. The angle at which the stimuli appeared was randomized, and, in conditions in which there was a target stimulus, the distractor could appear either clockwise or counterclockwise from the target stimulus. The online onset of the saccade was determined using both a spatial (>1.5° from display center) and a velocity (>30°/s) criterion, while the online offset was determined when velocity dropped <30°/s. On detection of the saccade onset, the stimuli were extinguished, and, once the saccade offset was detected, a response bar extending from the fixation to 10° in the periphery appeared. The angle of the bar was initially random, but participants could manipulate its position via the mouse cursor to indicate the location of the task goal. This meant that, after making their eye movement (and regardless of the accuracy of their eye movement), participants were required to give an additional perceptual response about the location of the task goal. This allowed us to examine whether perceptual localization of the goal location also varied when eye movements were directed toward nongoal locations.

Following this response, participants were given feedback about the accuracy of their perceptual response and the appropriateness of their saccade. Importantly, no feedback was given regarding the accuracy of the eye movement relative to the goal. Instead, the feedback informed them about the magnitude of their saccade, to prevent excessive undershooting (as the error in saccade angle scales with eccentricity), as well as the duration of the delay from when the stimuli appeared to when they initiated their saccade. Participants were instructed to attempt to initiate their eye movement within 200 ms of the fixation disappearing and to monitor the feedback about their saccade eccentricity to ensure they moved fully toward their intended location on each trial (and did not make progressively shorter saccades as they fatigued). This feedback, about both their saccade eccentricity and latency, encouraged participants to continue to make both accurate and rapid eye movements throughout the entire experiment. Additionally, the location of their perceptual response, as well as the presented location of the target and distractor, was shown. After a short delay, a white fixation object reappeared at the screen center, and the next trial was initiated once participants had maintained their fixation at that location for more than 500 ms.

The colors of target and distractor objects were drawn without replacement from four different color values. These were defined in LCH (lightness chroma hue) color space with a luminance of 50, chromaticity of 50, and hue varying to generate red (25), blue (280), green (170), and yellow (100) colors. Stimuli themselves consisted of posterized white noise (split into 3 tones) with a medium contrast level (RMS: 33%) surrounded by a colored outer ring with a central colored dot (Fig. 1A). The stimuli were designed so the overall saliency of each stimulus could be varied by manipulating the contrast of the internal noise patch, while the color identity of the stimulus (defined by the ring and central dot) would remain discriminable.

Each session started with a custom 13-point calibration procedure consisting of concentric circles. At the start of each trial, there was a strict fixation check to ensure that eye position was still being accurately recorded. If this initial fixation check failed, the experimenter could initiate either a drift correction or recalibration procedure. Trials were randomized such that, for each separation tested, there was an equal distribution of all possible color pairs in each block. Trials were automatically repeated within each block if the participant broke fixation (any deviation from a 1.5° window around the fixation dot or movements exceeding 30°/s) before it was time to make the response saccade, initiated their saccade too fast (i.e., before the fixation disappeared) or too slow (i.e., more than 400 ms after fixation disappeared), made a saccade less than one-half the distance between the fixation object and the stimuli (i.e., <4°), or if they blinked during the trial at any time before they had completed their response saccade. These criteria, and the automatic repetition of failed trials, ensured that there would be an approximately equal number of valid trials in all conditions available for analysis.

Each task was tested separately, on different days, during a 90-min session in which 10 blocks were completed for each task. Each block lasted approximately 8 min, and participants were encouraged to take a small pause between blocks. At the beginning of each block, participants were verbally reminded of the experimental task to ensure that they were always aware of their movement goal location.

Data preprocessing.

In addition to errors detected online, we performed a more precise offline analysis to ensure the inclusion criteria were met. In the offline analyses, saccades were detected based on their velocity distribution (Engbert and Mergenthaler 2006) using a moving average over 20 subsequent eye position samples. Saccade onset was detected when the velocity exceeded the median of the moving average by 3 SDs for at least 20 ms. This enabled us to compute more accurate offline times of saccade onset, offset, and landing and to exclude any additional trials that, despite passing the online analysis, did not meet inclusion criteria when the eye movement was analyzed in more detail. After this additional offline filtering, we were left with an average of 565 trials (94%) in the STM task and 683 trials (95%) in the STT task (which included the no distractor condition). This meant that, for both tasks, each of the different target-distractor separation conditions had ~113 trials available for analysis per participant.

Modeling: target, distractor, and intermediate locations.

To separate the proportion of saccades that were directed toward the target, intermediate, or distractor locations, we fit the data with a probabilistic mixture model, using a maximum likelihood procedure (fmincon function of the statistics toolbox in MATLAB; The MathWorks, Natick, MA). Throughout the paper, the goal location will refer to the intended saccade goal. In the STT task, in which there was a clear distinction between the target and distractor stimulus, the target stimulus was also the goal location, whereas, in the STM task, both stimuli together indicated the goal without being located at the goal location themselves. Nonetheless, to provide consistency of analysis between the two conditions, we maintained the assignment of target and distractor categories in the STM task, and used these categories for modeling and statistical comparison purposes.

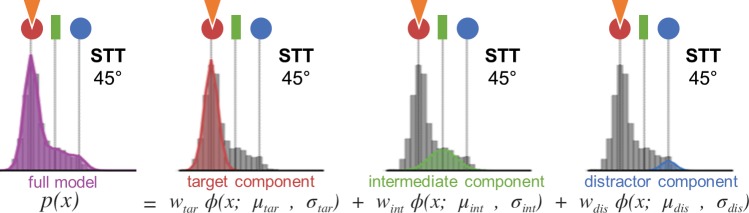
The full model (illustrated in Fig. 2) consisted of a mixture of Gaussian components centered on the target, distractor, and intermediate locations, described as follows:

$$p(x)=w_{\text{tar}}\varphi (x;{\mu }_{\text{tar}},{\sigma }_{\text{tar}})+w_{\text{int}}\varphi (x;{\mu }_{\text{int}},{\sigma }_{\text{int}})+w_{\text{dis}}\varphi (x;{\mu }_{\text{dis}},{\sigma }_{\text{dis}})$$ (1)

where x is the saccade end point angle from the origin, w is weight, and ϕ (x; μ, σ) is the normal probability density function with mean μ and standard deviation σ. Here the distribution of saccade landing positions can be described as the probabilistic mixture of saccades targeting either the target (tar), distractor (dis), or intermediate (int) location. The target and distractor components (µ_tar and µ_dis) were centered on the actual locations at which the stimuli occurred, whereas the intermediate component (µ_int) was centered on the midpoint between them,

Fig. 2.

Probabilistic mixture model. The data show a histogram of saccade landing end-point distributions for fictitious data on the STT task with a target and distractor separation of 45°. The target, distractor, and intermediate locations are shown by red, blue, and green symbols, respectively, while the task goal (here “saccade to target”) is indicated by the orange triangle. The general formula for the full model is shown with a diagram of the corresponding Gaussian distribution shown above each component. The sum of the Gaussians is shown in purple. Each component consists of a weight, determining its relative strength in the mixture, a fixed parameter for the Gaussian’s center (target, intermediate, or distractor), and a parameter for the width of the distribution. We additionally examined simpler variations of the model in which we selectively eliminated different components to test their necessity for accurately describing the data.

$${\text{μ}}_{\text{int}}=\frac{{\text{μ}}_{\text{dis}}+{\text{μ}}_{\text{tar}}}{2}$$ (2)

Rather than fitting σ_tar, σ_dis, and σ_int as free parameters, we fit just two parameters, α and β. The width of target and distractor components were set equal to each other and to the α parameter,

$${\text{σ}}_{\text{tar}}={\text{σ}}_{\text{dis}}=\text{α}$$ (3)

whereas the width of the intermediate component was defined in terms of β, a ratio of the target-distractor separation, such that as the distance between the stimuli increased the width of the intermediate component also increased,

$${\text{σ}}_{\text{int}}=\text{β}\left|{\text{μ}}_{\text{dis}}-{\text{μ}}_{\text{tar}}\right|$$ (4)

Prior exploratory analyses supported this relationship. The parameters α and β were shared across all target-distractor separations and both tasks. The resulting parameter estimates provided a close match to those found when each target-distractor separation and task was independently fit.

To determine the necessity of each of the components (e.g., whether the data could be explained just as well at some separations without the global effect), we derived two simpler variants of the model, which consisted of either a single component centered on the intermediate location (global effect only; Eq. 5), or two components centered on the target and distractor (stimulus capture only; Eq. 6).

$$p(x)=w_{\text{int}}\varphi (x;{\text{μ}}_{\text{int}}{,\text{\hspace{0.17em}σ}}_{\text{int}})$$ (5)

$$p(x)=w_{\text{tar}}\varphi (x;{\text{μ}}_{\text{tar}}{,\text{\hspace{0.17em}σ}}_{\text{tar}})+w_{\text{dis}}\varphi (x;{\text{μ}}_{\text{dis}}{,\text{\hspace{0.17em}σ}}_{\text{dis}})$$ (6)

We fit each of these different models to the participants’ data and computed the AICc (Akaike Information Criterion with correction for finite data). The AICc is a means for evaluating the appropriateness of different models (which may differ in their number of free parameters) for a given data set. Importantly, this method is based on the likelihood of the fits and encompasses a penalty based on their number of free parameters, meaning that, for a more complicated model to be more likely (i.e., to have a lower AICc), it must explain more of the variance to make up for its additional parameters. To determine whether the full model was necessary, we expressed these scores as ΔAICc relative to the full model. This allows the differences between the full model and the alternative, simpler models to be clearly expressed. If an alternative model could describe the data better than the full model, then it would have a ΔAICc score below 0. Thus the ΔAICc allows us to examine the quality of models with different numbers of parameters to determine which is the best descriptor of the data. To quantify changes in the weights for the target, distractor, and intermediate components across time, or across different angular separations, we examined the average slope across subjects of a regression line fit through the weights. This average slope was then tested against zero to determine whether there was a significant trend across time. Additionally, to aid comparisons, we defined “short-latency-saccades” as those occurring less than 200 ms after stimulus onset.

Modeling: stimulus capture, global effect, and task goal.

To decompose the data into automatic and intentional components, we compared the weights obtained from the full model across the two tasks. For clarity, these new combined weights will be referenced with a capital “W,” while the weights found within tasks will remain a lowercase “w” with the additional superscript indicating from which task they originate.

We first computed the influence of the task goal by taking the mean of the difference between the target weights in STT and STM task and the intermediate weights in the STM and STT task (Eq. 7). This determines the mean change in the probability of landing at a given location when it is vs. is not the task goal,

$$W_{\text{goal}}=\frac{(w_{\text{tar}}^{\text{STT}}-w_{\text{tar}}^{\text{STM}})+(w_{\text{int}}^{\text{STM}}-w_{\text{int}}^{\text{STT}})}{2}$$ (7)

We then computed the mean weight of unavoidable capture toward the global effect location across both tasks by averaging the intermediate component weight in the STT task with the intermediate component weight in the STM task, less the newly derived weight of the task goal,

$$W_{\text{global}}=\frac{w_{\text{int}}^{\text{STT}}+(w_{\text{int}}^{\text{STM}}-W_{\text{goal}})}{2}$$ (8)

The mean weight of unavoidable capture toward the distractor location was simply the average of the distractor component in both tasks,

$$W_{\text{dis}}=\frac{w_{\text{dis}}^{\text{STT}}+w_{\text{dis}}^{\text{STM}}}{2}$$ (9)

The average weight of the capture toward the target location was the average of the target weight in the STT task, minus the newly derived weight of the task goal, and the weight of the target in the STM task,

$$W_{\text{tar}}=\frac{(w_{\text{tar}}^{\text{STT}}-W_{\text{goal}})+w_{\text{tar}}^{\text{STM}}}{2}$$ (10)

Together, the newly derived mean weights for target and distractor then sum to give the weight of capture toward stimulus locations,

$$W_{\text{stim}}=W_{\text{dis}}+W_{\text{tar}}$$ (11)

The weights defined in this way sum to 1,

$$W_{\text{stim}}+W_{\text{global}}+W_{\text{goal}}=1$$ (12)

Changes in the weights across time were quantified by finding the average slope across subjects of a line fit through the weights across time. This average slope was then tested against zero to determine whether there was a significant trend across time.

Results and Discussion

Saccade latency.

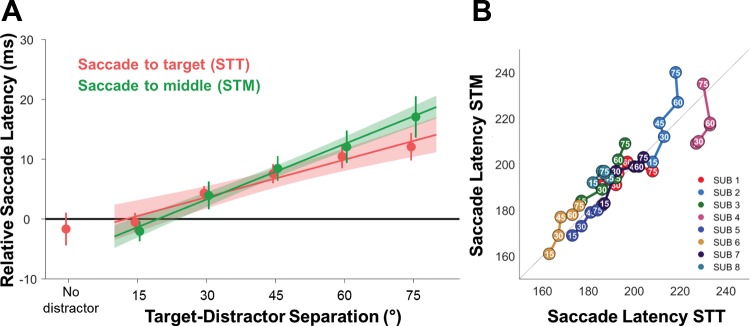
The different saccadic latencies for the two tasks and different angles of separation are shown in Fig. 3A, with red indicating the STT task, and green the STM task. The saccade latency for each participant was normalized to their median saccade latency at 15° target-distractor separation across both tasks. We normalized to the smallest separation, as opposed to the no distractor condition, to examine whether the saccade latency with two targets separated by 15° was different than the saccade latency with a single stimulus (Fig. 3).

Fig. 3.

Saccade latency for the different tasks and target-distractor separations. A: the changes in saccade latency between the two tasks as the target-distractor separation increased. Here saccade latency was expressed as the relative difference between the median saccade latency at a 15° separation across both tasks per subject, with the data showing the mean differences with SE. The shaded region indicates the 95% confidence intervals for a linear fit. B: the median saccade latency for each of the subjects (SUB 1−8) on both tasks. Here a strong correlation between the times in both tasks is evident, demonstrating that the time to initiate their saccade is closely related in both tasks. Additionally, the trend for larger separations to have slower saccade latency is evident within individual subjects’ data, with the distance from the origin increasing as target-distractor separation increases.

To examine whether the addition of a second stimulus influenced the saccade latency, we compared the 15° target-distractor separation condition for both tasks with the no distractor condition. We found that there was no difference in the saccade latency for either the STT [P = 0.60; t(7) = 0.54] or the STM [P = 0.93; t(7) = 0.09] tasks, suggesting that a 15° separation between the target and distractor was insufficient to induce a RDE. Furthermore, this also demonstrated that the mere presence of an additional stimulus did not alter median saccade latency. Additionally, we found no difference at 15° target-distractor separation between the two tasks [P = 0.65; t(7) = 0.47]. However, as target-distractor separation increased, there was a significant linear trend with larger separations, resulting in a longer delay on average before saccade initiation for both tasks [slope: STT, 0.21 ± 0.10; P < 0.001; t(7) = 5.89; STM, 0.31 ± 0.18; P < 0.002; t(7) = 4.96] as shown in Fig. 3A. This trend was not accompanied by changes in the intercept of the linear fit [STT = −2.65 ± 4.84; P = 0.17; t(7) = 1.55; STM = −6.03 ± 7.65; P = 0.61; t(7) = 2.23].

There were no significant differences between either the slope [Fig. 3B; P = 0.21; t(7) = 1.38] or the intercept [−3.38 ± 12.17; P = 0.46; t(7) = 0.78] of the linear regression parameters across the different tasks. This suggests that the size of the RDE depended on the separation between the two stimuli, regardless of the participants’ task and status of the additional stimulus as a distractor. Finally, there was a significant mean correlation between participants’ latency on the STT task and their latency on the STM task [r = 0.76 ± 0.23; P < 0.001; t(7) = 9.23] with on average 58% of the variance in saccade latency shared between the two tasks (Fig. 3B).

Mouse responses.

For all of the different target-distractor separations, the mouse responses were exceptionally accurate for both tasks. Indeed, 94.5 ± 9.7% of mouse responses were directed toward the task goal (i.e., within ±25% of the separation, corresponding to 0 ± 15° for a 60° separation in the STT task). In contrast, only 55.9 ± 19.2% of saccades were on average directed toward the task goal, by this same criterion. Even though more rapidly initiated saccades resulted in participants seeing the stimuli for less time before the eye movement, there were no notable correlations between accuracy in the perceptual task and saccade latency (P > 0.05). This suggests that even the most rapidly initiated saccades allowed for sufficient visual processing for participants to correctly locate the goal location.

Saccadic landing positions.

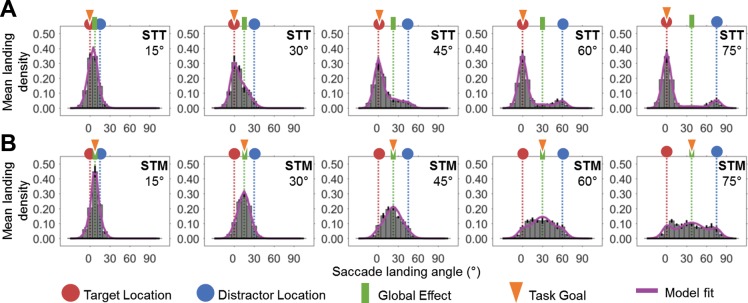
We quantified the accuracy of saccadic eye movements by examining the distribution of saccade landing positions relative to the target (red), distractor (blue), intermediate (green), and goal location (orange) for each target-distractor separation (Fig. 4). The histograms were constructed by sorting the data into 7.5° wide bins, which ensured that, even at the smallest tested separation, there was one bin in between the target and distractor. Clear differences can be seen between the saccadic landing position for the two tasks at all of the different target-distractor separations examined. Specifically, in the STT task (where the goal location was the target stimulus), there were substantially more saccades directed toward the stimulus assigned as the target than in the STM task (where the task goal was the intermediate location). Thus participants successfully adjusted their eye movements, depending on the task requirements. As the close distances between the stimuli make it difficult to discern by inspection the differences between averaging saccades and saccades directed toward either the target or distractor stimulus, we fit the distributions with a probabilistic mixture model to allow us to estimate the probability of targeting each of these different locations.

Fig. 4.

Histograms of landing position for different target-distractor separations. Distributions of the average landing position across participants for the STT (A) and STM (B) task are shown. Note that the goal location in the STT task was the target location (red), while the goal location for the STM task was the intermediate location (green). From the histograms above, it can clearly be seen that the simple change of task goal resulted in substantially different distributions for all of the different target-distractor separations, with the effects most noticeable at larger separations. The purple line indicates the average full model fit to the collapsed data for each subject.

Model fitting.

We fit both the full model and simpler alternatives (global effect only; stimulus capture only) to each participant’s data. To determine which model provided the best fit, we then contrasted the AICc of each of these models with that of the full model. This allowed us to determine which components were necessary to capture the saccade landing distribution. Overall, the full model provided the best description of the data when comparing across all target-distractor separations and both tasks (ΔAICc ± SE relative to full model; stimulus capture only = 905 ± 117; global effect only = 813 ± 162). Indeed, even when looking at the sum of AICc across separations within each task separately, the full model was still the better description for both the STT (stimulus capture only = 285 ± 51; global effect only = 709 ± 149; Fig. 5A) and STM (stimulus capture only = 621 ± 72; global effect only = 104 ± 16; Fig. 5C) task. In general, as target-distractor separation increased, both alternative models became increasingly poor fits to the data. However, our results indicate that both stimulus capture and global effect components were critical, even for the smallest target-distractor separations.

Fig. 5.

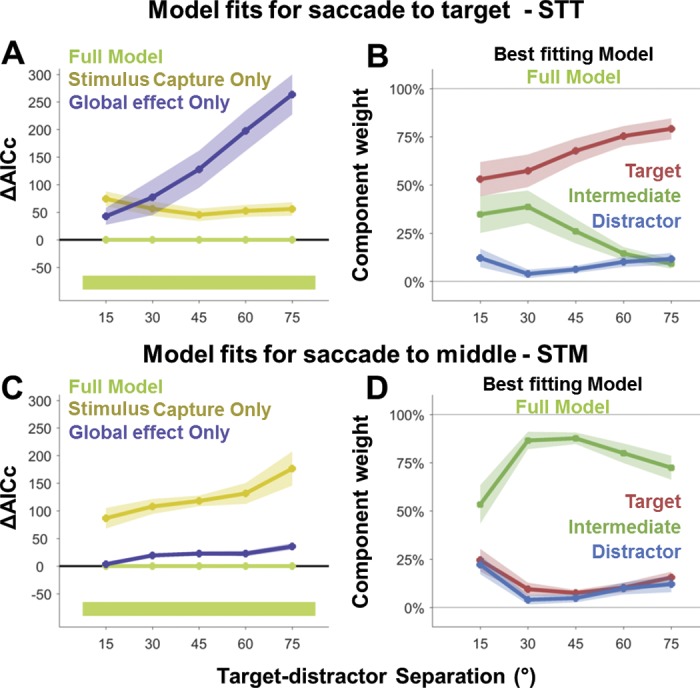
The AICc of the different model fits and the weights of the best model for different target-distractor separations in the STT and STM tasks. For both the STT (A) and STM (C) task, the full model, which included a target, distractor, and intermediate component, was always the best fit to the data (with the lowest change in AICc for each separation indicated by the thick bar beneath). The weights for the best fitting full model for both STT (B) and STM (D) are also shown.

The weights of each of the components provided an estimate of the proportion of saccades directed toward that location. The average fits to each of the different target-distractor separations are overlaid in purple in Fig. 4 for both tasks. The associated weights for the target, distractor, and intermediate components at the different target-distractor separations for the full model are shown in Fig. 5, B and D for the STT and STM task, respectively. Here we found that the highest weighted component was the one situated at the task goal location for both the STT (goal = 66.5 ± 11.2%; other = 33.5 ± 11.2%) and STM (goal = 76.0 ± 14.0%; other = 24.0 ± 14.0%) tasks. In the STT task, when averaging across separations, most saccades were directed toward the target location (67 ± 11%). Only a small proportion of saccades was captured toward the distractor location (9 ± 4%), with the remainder targeting the intermediate location (25 ± 13%).

Supporting previous findings, we found that the likelihood of executing a saccade toward the global effect location in the STT task decreased as the separation between the target and distractor stimulus increased [slope = −0.50 ± 0.46%/°; P = 0.017; t(7) = 3.12], while the weight for the target component increased [slope = 0.47 ± 0.4%/°; P = 0.013; t(7) = 3.29]. Across different target-distractor separations, the distractor weight remained unchanged [slope = 0.03 ± 0.10%/°; P = 0.356; t(7) = 0.99]. Importantly, despite the reduction in the weight of the intermediate component as separation increased, even at 75° separation there was evidence for the global effect [9.1 ± 2.5%; P = 0.008; t(7) = 3.65]. This suggests that, even at this large separation, a significant proportion of saccades was still captured to the global effect location.

In the STM task, we found that most saccades were accurately directed toward the intermediate location (76 ± 14%), with only a small component weight associated with the stimulus locations (12 ± 7% average at each location). This demonstrates that participants could alter targeting of their eye movements in response to the task requirements and had no difficulty in deliberately targeting the empty space between the two stimuli.

While the intermediate [STT vs. STM; P < 0.001; t(7) = 8.48] and target [STT vs. STM; P < 0.001; t(7) = 9.05] components differed substantially between the two tasks, the distractor component (which was never the goal location) remained consistent [STT vs. STM; P = 0.56; t(7) = 0.61]. This suggests that, while task instructions influenced the probability of saccades landing at the task location, the proportion of saccades that were unavoidably captured by the distractor location did not differ between the two tasks.

Model fitting across time.

As the prevalence of the global effect is known to decrease as saccade latency increases, and saccade latency itself is known to increase as target-distractor separation increases, it was important to also analyze the results as a function of saccade latency. We binned the data into 30-ms overlapping bins (with each bin separated by 10 ms) and fit each of our model variants independently to each time bin. This allowed us to examine how both the weights and the widths of the components within the mixture model changed as saccade latency increased (Fig. 6). At the individual level, we eliminated time bins that contained less than 15 trials, while at the group level we eliminated the bins in which less than 50% of participants had sufficient trials to be included.

Fig. 6.

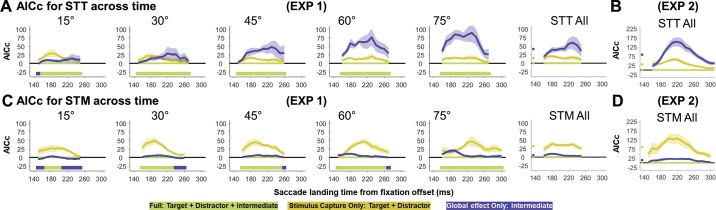
The change in AICc across target-distractor separations, task, and experiments as a function of saccade latency. The average AICc for the different models across participants for experiment 1 (EXP 1; A and C) and experiment 2 (EXP 2; B and D) as a function of saccade latency for the STT and STM task is shown. While the green line indicates the full model, the yellow and purple lines indicate the ΔAICc of stimulus-capture-only and global-effect-only models relative to the full model, respectively. In experiment 1, the full model almost always fits the data better than either of the alternative simpler models. Indeed, as the panel collapsed across separations shows, when considering all target-distractor separations, the full model was always the best model (with the small square indicating the average ΔAICc collapsed across separations and saccade latency). This pattern is true also for the data of experiment 2. Here the data collapsed across contrast is presented, and, while the plots are substantially smoother due to the increased number of trials, they match very closely with the data found in experiment 1.

The changes in AICc scores for the different models as a function of saccade latency are shown in Fig. 6, with the best fitting model at each time bin denoted by the solid bar under the curve. Here we again found that, across both tasks and for all target-distractor separations, the full model was on average the best fitting model (ΔAIC relative to full model; stimulus capture only = 24.7 ± 3.8; global effect only = 24.4 ± 5.7). Even when looking at the average change in AICc for either the STT (stimulus capture only = 15.7 ± 3.4; global effect only = 41.7 ± 12.4) or the STM (stimulus capture only = 32.6 ± 5.4; global effect only = 5.6 ± 2.5) task separately, the full model fit the data significantly better than the alternatives. Although for some specific time bins there are exceptions where the global-effect-only models provided a marginally better fit, these predominantly occurred only for very long latency saccades in the STM condition [i.e., when almost all saccades were correctly targeting the intermediate (goal) location]. Overall, it is clear that distinct target, distractor, and averaging components were necessary to accurately account for how saccade landing positions change with saccade latency.

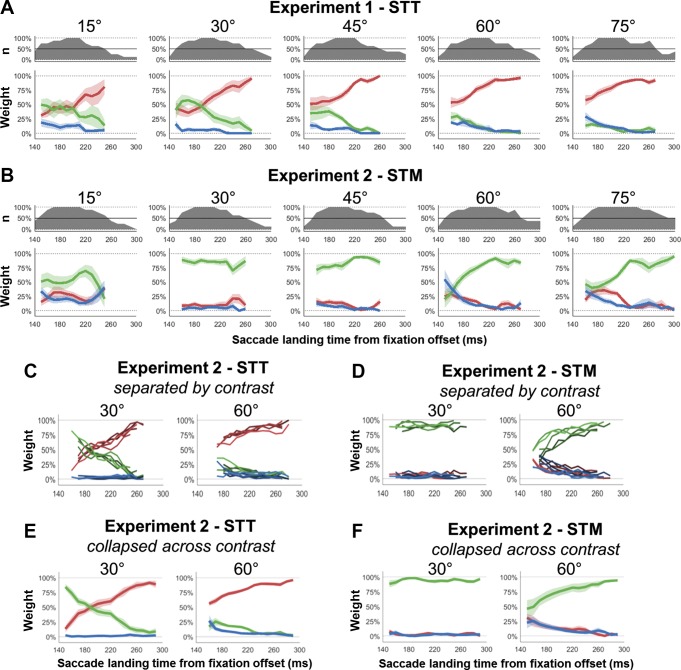
The changes in the weights for the model found to provide the best fit, the full model, are shown in Fig. 7 for the different target-distractor separations in the STT (A) and STM (B) tasks. The probability of making an eye movement that terminated at the goal location (red lines in A, green lines in B) approached 100% as saccade latency increased. While for each target-distractor separation there was substantial capture toward the goal locations for short-latency saccades (STT: 55.2 ± 9.4%; STM: 60.1 ± 17.5%) for all separations [first 30 ms of data, see Methods; STT, all separations; all P < 0.0019; all t(7) > 4.82; STM, all separations; all P < 0.0019; all t(7) > 4.85], as saccade latency increased, the proportion of saccades directed toward the goal location significantly increased for all separations for both the STT task [slope = 0.38 ± 0.19%; P < 0.0008; t(7) = 5.64] and the STM task [slope = 0.23 ± 0.11%; P < 0.0005; t(7) = 5.36].

Fig. 7.

Histograms of landing position for different target-distractor separations. The mean weights for the target (red), distractor (blue), and intermediate (green) model components across participants are shown for each of the different target-distractor separations (columns) and for both STT (A) and STM (B) tasks. As the latency distributions for individuals varied significantly, above each set of weights is the proportion of participants with sufficient data for inclusion in the average at that time point. Averages of <50% of the participants are not shown. The weights for each of the different contrasts examined in experiment 2 are shown in C and D for STT and STM, whereas the weights collapsed across contrast are shown in E and F, respectively. Importantly, although 8 new participants were examined, the data for experiment 2 closely match the equivalent separations in experiment 1.

Had there been no influence of task on the most rapidly executed saccades, then we would have expected identical weights at low latencies between the two tasks for the same target-distractor separation. Instead we found significant differences between the tasks for short-latency saccades for the target [STT vs. STM; P < 0.001; t(7) = 5.71] and intermediate weights [STT vs. STM; P < 0.002; t(7) = 4.96]. In contrast, the weight of the distractor component did not significantly vary for any of the separations [STT vs. STM; P = 0.537; t(7) = 0.65]. These average differences held also for each individual separation, apart from the 15° target-distractor separation in which neither target [STT vs. STM; P = 0.080; t(7) = 2.04], intermediate [STT vs. STM; P = 0.339; t(7) = 1.03], nor distractor [STT vs. STM; P = 0.059; t(7) = 2.25] weights varied. This is probably because, at the smallest separation, the components were difficult to separate, given the limited trials available once binned across time. Nevertheless, these results show that even the most rapidly executed saccades displayed a systematic bias in their landing position toward the task goal.

Dissociating automatic capture from intentional task-related targeting.

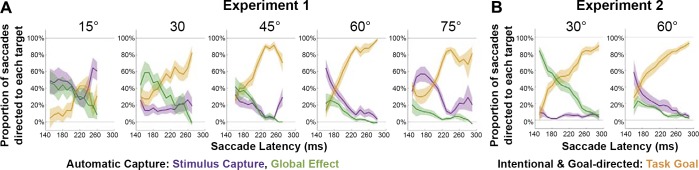
By comparing each of the different weights across the two tasks, we can differentiate between changes in the probability of executing an automatic saccade toward a stimulus or the intermediate location (automatic capture) and the influence of the task (intentional and goal directed). We performed this operation at each time bin for each of the target-distractor separations examined. This allowed us to derive the time course of interactions between compulsory capture and intentional goal-related activity. The results are shown in Fig. 8, where the proportion of saccades which are intentionally directed toward the task goal (orange) are estimated independently of those that are unavoidably captured toward either of the stimulus locations (purple; stimulus capture) or the average location (green; global effect).

Fig. 8.

Automatic and intentional capture effects in time for different target-distractor separations. By comparing the STT and STM task for each of the different target-distractor separations, we could generate estimates for the proportion of saccades unavoidably captured toward either the location of stimuli or the global effect location and those that were intentionally directed toward the task goal for both experiment 1 (A) and experiment 2 (B). This reveals how the proportion of saccades dedicated to different locations changes with the delay before movement onset.

We found that, apart from the smallest 15° target-distractor separation, in which weights were less clearly differentiated, the task goal had an influence on the probability of targeting different locations even for short-latency saccades [goal weight 30–75° separation: 36.0 ± 4.0%; all P < 0.0034; all t(7) > 4.33]. Additionally, for all separations, the influence of the task was found to significantly increase for saccades initiated later in time [slope = 0.54 ± 0.14%; P < 0.0001; t(7) = 10.68]. As the task influence increased, the relative proportion of saccades automatically captured toward either of the stimulus locations [slope = −0.25 ± 0.12%; P < 0.0006; t(7) = 5.86] or toward the average location [slope = −0.29 ± 0.12%; P < 0.0003; t(7) = 6.66] decreased. This supports the idea that longer delays before executing saccades result in increased top-down influence on the targeting of the saccade. Furthermore, the initial capture toward the global location for rapidly executed saccades decreased as target-distractor separation increased [slope per degree of separation = −0.55 ± 0.44%; P < 0.010; t(7) = 3.48]. Again, this was even more apparent if the smallest 15° target-distractor separation was excluded [slope = −0.80 ± 0.49%; P = 0.002; t(7) = 4.67].

Nonetheless, for all target-distractor separations, there was a significant global effect component for short-latency saccades [mean global = 30.5 ± 14.4%; all P < 0.020; t(7) > 2.98]. Similarly, we observed a significant proportion of unavoidable capture toward the stimulus locations at all separations [mean stimulus = 38.9 ± 17.0%; all P < 0.004; t(7) > 4.12], with the proportion increasing as the separations increased beyond 30° [slope = 0.91 ± 0.29%; P < 0.0001; t(7) = 8.82]. Despite these changes, the initial strength of the task-related goal component did not appear to change as the separation increased above 30° [slope = −0.10 ± 0.56%; P = 0.613; t(7) = 0.53]. These results suggest that the strength of capture toward either the stimulus or average location is dependent on the separation, while the initial strength of the goal is relatively invariant to the spatial separation of the stimuli.

EXPERIMENT 2

In the second experiment, we investigated the influence of stimulus salience on the interactions between unavoidable capture (to either the stimuli or the global effect location) and intentional goal-directed targeting. We manipulated stimulus saliency by varying the contrast of the noise patch contained within the two stimuli. While we hypothesized that the saliency of the stimuli should influence the speed of saccade initiation, with faster saccades executed toward stimuli with a higher contrast, it was not clear whether higher contrast would affect the proportion of capture toward the stimuli and the global effect location equally. For example, higher contrast may disproportionately increase the likelihood of capture toward the stimulus locations, as their signal strength becomes stronger relative to the background, but this change may occur without increasing the strength of the averaging location.

Methods

Participants.

An additional eight naive individuals (19–28 yr old; 1 male) took part in experiment 2. All participants had normal or corrected-to-normal visual acuity, and none of them had participated in the previous experiment. Informed consent was obtained before the study in accordance with the guidelines of the Helsinki Declaration, and the protocol was approved by the Cambridge Psychology Research Ethics Committee.

Stimuli and procedure.

The experiment proceeded identically to experiment 1, except for the following modifications. We varied the contrast of the stimuli within five levels (11, 19, 33, 56, and 95% Michelson contrast). As our posterized noise consisted of three distinct tones (a light, mid-, and dark tone), we changed the contrast by varying the range between the light and dark tone located within each stimulus (while the midtone remained the same gray as the background). As in the first experiment, we tested both the STT and the STM task; however, we did not include the single target condition within the STT task as in experiment 1. Instead of examining a large range of target-distractor separations, we examined only separations of 30° and 60°. Finally, in experiment 2, the irrelevant color cue at fixation in the STM task was changed to a completely different color that did not match either stimulus. While this means the two tasks were not completely identical (as in experiment 1), it was done to preclude the possibility of the color at fixation biasing participants toward the matching color target stimulus during the STM task and to enable us to rule out any role of the fixation color on our results.

Data preprocessing.

Eye movement data were additionally analyzed offline as in experiment 1. Excluding the trials already detected by online analysis, after offline filtering, we were left with an average of 672 trials (96%) in the STM task and 665 trials (95%) in the STT task. This meant that each condition for each participant had ~67 trials available for analysis (and 335 when collapsed across contrast).

Results

Saccade latency.

The differences in saccade latency (relative to the median latency at 33% contrast across both tasks) are shown in Fig. 9A. As can be seen for both 30° and 60° separations, there was a substantial decrease in saccade latency as the contrast increased, occurring in both tasks. The rate of change in relative saccadic latency as a function of the log contrast was significantly different from zero for both the STT [30°: P = 0.031; t(7) = 2.69; 60°: P = 0.007; t(7) = 3.80] and STM [30°: P < 0.001; t(7) = 8.25; 60°: P = 0.003; t(7) = 4.53] tasks. While the decrease in latency as contrast increased differed significantly between tasks at 30° [STT vs. STM; P = 0.042; t(7) = 2.49], there was no difference in the slope at 60° [STT vs. STM; P = 0.267; t(7) = 1.21]. When combining data across contrasts, there was a significant difference between 30° and 60° target-distractor separations for both the STT [P < 0.001; t(7) = 6.67] and STM [P < 0.001; t(7) = 6.32] task. However, there were no differences between the two tasks in the median saccade latency for either 30° [P < 0.216; t(7) = 1.36] or 60° [P < 0.207; t(7) = 1.39] separations. Additionally, there were no differences in the average median reaction time between subjects in either the 30° or 60° separations of experiment 1 and the same separations with equivalent contrast in experiment 2 [i.e., experiment 1 (30°) vs. experiment 2 (30°; 0.33% contrast)] for either the STT [30°: P = 0.143; t(7) = 1.65; 60°: P = 0.135; t(7) = 1.69] or STM [30°: P = 0.367; t(7) = 0.96; 60°: P = 0.415; t(7) = 0.87] task.

Fig. 9.

Saccade latency for 30° and 60° stimulus separation and the influence of stimulus contrast. A: the relative differences in saccade latency as stimulus contrast increased for both the STT (red) and STM (green) task for either 30° (left) or 60° (right) separation between stimuli. As contrast increased, there was a reduction in the latency of saccades in both tasks, with the reduction occurring slightly more rapidly in the STM task when stimuli were 30° separated. B: each participant’s saccade latency for each contrast level (1 = lowest, 5 = highest) on both the STT and STM task are plotted. Almost all participants show a steady decrease in saccade latency as contrast increases, while the overall latencies for 30° are visibly faster than for 60° (as was found in experiment 1).

Mouse responses.

As in experiment 1, in both tasks the mouse responses were highly accurate across the different target-distractor separations. We found that 94.5 ± 9.7% (mean ± SE) of the mouse responses were directed toward the task goal (i.e., within ±25% of the separation), compared with only 55.9 ± 19.2% of the saccades. We again found no significant correlation between accuracy in the perceptual task and saccade latency (P > 0.05).

Model fitting across time.

We fit the time course of the data with all three variations of the model both separated and collapsed by stimulus contrast for the STT (Fig. 7C) and STM (Fig. 7D) task. Across the different stimulus contrasts, we observed little consistent differences in the weights. To test whether the time courses of the weights differed as contrast changed, we fit the changes in the target, distractor, and intermediate weights as saccade latency increased for each participant. We could then examine for each participant whether there was a linear trend in either the slope or intercept of the time course changes as the contrast changed. We found that, for the 30° target-distractor separation, there were no consistent changes in the slope of the weights as contrast changed for either the STT [all P > 0.123, all t(7) < 1.75] or STM [all P > 0.193, all t(7) < 1.44] task. For the 60° target-distractor separation, there were no changes for the STT task [all P > 0.193; all t(7) < 1.44], while in the STM task there was a significant decrease in the intermediate weight as contrast increased [mean ± SD; −0.06 ± 0.06%; P = 0.021; t(7) = 2.98] and no change for the target [0.00 ± 0.09%; P = 0.901; t(7) = 0.13] or distractor [0.06 ± 0.09%; P = 0.114; t(7) = 1.81] weights. Thus, across the different separations and model components, there were no consistent changes in the time course as the contrast of the stimuli changed. Instead, the main effect of decreasing stimulus contrast appeared to be a modulation in the time of saccade onset without substantial influences on the underlying dynamics. This meant that, although low-contrast trials had a smaller proportion of rapid onset saccades than high-contrast trials, for a given saccade latency individuals had largely similar weights for each of the different model components. Due to this lack of differences in the weights across time, we collapsed the different contrast data together for the remainder of the analysis, benefiting from both the overall increase in the number of trials and from the fact that contrast differences resulted in saccade onset being spread across a greater range of latencies (which increased the overlap in saccade initiation between participants).

The full model provided the best description of the data across the different target-distractor separations for both the STT (ΔAIC relative to full model; stimulus capture only = 33.6 ± 12.0; global effect only = 88.9 ± 27.1) and STM task (stimulus capture only = 97.3 ± 49.9; global effect only = 15.9 ± 8.2), as indicated by the small squares at the start of each figure (see Fig. 6, B and D). Thus, as in experiment 1, the full model (with components situated on the target, intermediate, and distractor location) was required to best describe the data. Importantly, the weights for each separation, combined across contrast, closely corresponded with the weights found in experiment 1 for equivalent target-distractor separations. Thus we replicated the weights found in response to rapid-onset saccades as well as the time course in the second experiment with an additional eight naive participants.

We again decomposed the weights into automatic and intentional capture effects. As shown in Fig. 8B, even for target-distractor separations of 60°, there was evidence for the presence of the global effect in short-latency saccades [19.2 ± 3.9%; P = 0.002; t(7) = 4.98], although it was notably stronger when the separation was only 30° [59.0 ± 6.5%; P < 0.001; t(7) = 9.13]. Additionally, the probability of eye movements being automatically captured toward either the global effect location or the location of either of the visible stimuli traded off as the separation between the stimuli changed, i.e., closer stimuli generated substantially more averaging [30 vs. 60°; 59.0 ± 6.5 vs. 19.2 ± 3.9%; P = 0.001; t(7) = 5.35] and fewer stimulus-directed saccades [30 vs. 60°; 3.9 ± 2.0 vs. 33.6 ± 8.8%; P = 0.006; t(7) = 3.92] than further separated stimuli, regardless of task. However, the time course of the goal-directed activity was found to be almost identical across the two conditions [30 vs. 60°; 37.1 ± 7.7 vs. 47.3 ± 7.8%; P = 0.173; t(7) = 1.52], suggesting that the influence of top-down selection emerges with a similar time course, regardless of the separation between the stimuli. Finally, as in experiment 1, the proportion of saccades directed toward the goal increased as saccade latency increased [slope = 0.19 ± 0.07%; P < 0.0001; t(7) = 7.62], while the proportion captured to either the stimulus [slope = −0.05 ± 0.06%; P = 0.050; t(7) = 2.36] or global effect location [slope = −0.14%± 0.06%; P = 0.0002; t(7) = 6.98] decreased.

DISCUSSION

We investigated the influence of spatial separation and behavioral goals on the automatic and intentional control of saccadic eye movements. Specifically, we examined how increasing the distance between two simultaneously appearing stimuli altered both the speed and accuracy with which saccades were made toward a goal location. By explicitly asking participants to move their eyes either toward a specific stimulus or toward the midpoint between two stimuli, we characterized how deliberate goal-related selection interacts with automatic stimulus-driven capture. We found that, regardless of task instructions, the distribution of saccade landing positions was best described as a probabilistic mixture of saccades directed to the target, distractor, and intermediate location. This meant that, even when individuals intended to move their eyes to a certain goal location, their saccades were often automatically redirected toward another location.

We found that increasing stimulus separation had opposite effects on the proportion of saccades captured toward visible stimuli (stimulus capture) and those captured toward the intermediate location in between stimuli (the global effect). This meant that, as separation increased, the proportion of saccades captured to the global effect location decreased, while the proportion captured to the visible stimulus locations increased. However, rather than finding an explicit spatial window in which averaging saccades occurred, our results suggested that the likelihood of observing an averaging saccade continuously decreased as target-distractor separation increased. Yet, even with target-distractor separations as large as 75°, we observed a substantial proportion of global effect saccades at short latencies. Thus it appears the global effect was present well beyond the proposed 20° spatial window (Van der Stigchel and Nijboer 2013; Walker et al. 1997).

There are several reasons why, in contrast to previous studies, we may have been able to observe the presence of the global effect at such large stimulus separations. First, we gave explicit and clear instructions in both of our tasks so that participants knew precisely what was the goal location for their saccades. A less explicit definition of the task goal, either through ambiguous instructions (STA) or having participants make a choice between either stimulus (STE), leaves ambiguity as to the goal location (e.g., De Vries et al. 2016; Silvis and Van der Stigchel 2014; Van der Stigchel et al. 2012) and makes the discrimination of automatically directed saccades from intentional movements difficult.

Second, our probabilistic mixture model analysis allowed us to disambiguate global effect, stimulus capture, and intentional task-related saccades. Rather than having a single average landing position measure (e.g., Choi et al. 2016; Van der Stigchel and de Vries 2015; Walker et al. 1997), which is insensitive to the differences between these components, this approach allowed us to detect averaging saccades even when they were not the most frequent response. It also ensured erroneous saccades to the distractor location were not counted toward the global effect. This is frequently evident in studies using median saccade landing position, where an equal distribution of responses to the target and distractor (with only a tiny fraction of saccades to the intermediate location) can, nevertheless, result in a median saccade landing position in between the two distributions. Thus, despite its ubiquitous use in studies of the global effect, the median or mean saccade landing position is a poor metric for quantifying the proportion of averaging saccades. While examinations of distributions (i.e., comparing unimodal and bimodal fits) are an improvement (Van der Stigchel et al. 2012; Van der Stigchel and Nijboer 2013), decomposing the distributions into their constituent parts creates a much more accurate estimate of saccade targeting behavior (De Vries et al. 2016).

Third, by explicitly asking participants to target the intermediate location (STM), we could dissociate automatic capture from task-related selection. This provided a sensitive measure able to capture targeting of the global effect location at large separations. Despite some previous findings of global effect at large spatial separations, there has seemingly been a reluctance to interpret the global effect as occurring over a greater range. One reason for this may be the difficulty it poses to neural models, as a larger spatial region of spatial interaction would call for even more long-range lateral interactions, something that is already questioned in current models (Christie et al. 2015; Lee and Hall 2006; Marino et al., 2012). For instance, although Van der Stigchel and colleagues (2011) observed a global effect even for far distractors, they interpreted this as distinct from the “traditional” global effect as it occurred for greater separations and was seemingly automatic. Interestingly, they argued that it was the lack of top-down selection in their first experiment that led to this nontraditional automatic global effect, while the presence of top-down selection in their second experiment was what allowed no averaging to be observed. In contrast, we argue that the global effect is a purely bottom-up effect.

We found clear evidence for saccades directed to both the intermediate location and the stimulus location at all spatial separations tested. Importantly, this was true even when the task goal aligned with the intermediate location, a condition in which additional processes related to goal selection presumably should only reinforce the intermediate location. Furthermore, the proportion of saccades directed toward the stimuli increased, and those to the global effect location declined as stimulus separation increased. This contrasts with Christie et al. (2015), who found that center-of-gravity effects did not change with stimulus separation. Unfortunately, because the priming paradigm of Christie and colleagues (2015) does not permit any meaningful analysis of the saccade landing positions, and the combined analyses of both two- and four-stimulus arrays (and hence the center-of-gravity instead of the intermediate position) makes determining what is the equivalent “global effect location” unclear (i.e., is there an intermediate location between each stimulus or simply a single center-of-gravity activation?), direct comparison with their results is difficult. Nevertheless, while we would also suggest that regions outside of the SC involved in processing of the task likely play a critical role in the predominance of the global effect, we would suggest that spatial separation directly affects the likelihood of automatic, stimulus-driven saccades being directed toward either physical stimulus locations or toward the global effect location.

Consistent with Viswanathan and Barton (2013), we propose that motor representations for the individual stimuli compete with that of the intermediate position, with the weightings determined by the target-distractor separation. With increased delay before movement onset, top-down, task-related processes continually influence this competition and increasingly bias selection toward the task-relevant location. Thus the most rapid saccades reveal intermediate stages of this competition, where processes have reached threshold before explicit knowledge of the task has had sufficient time to influence activity. Similarly, although averaging saccades were observed for separations in excess of 35°, in their detailed analyses of the spatial interactions governing the global effect using an STT paradigm, Van der Stigchel and Nijboer (2013) argued that “a genuine global effect is observed when the endpoint distribution is unimodal with the peak between the two stimuli.” While with this definition they conclude that the global effect is only present less than 35°, they also acknowledge that there is a linear trend in the probability of observing averaging saccades. Based on the present findings, we argue that automatic stimulus-driven capture, to either the stimulus locations themselves or to the average position between them, is present whenever multiple stimuli occur. The distance between the stimuli determines whether, for short-latency saccades, this automatic capture is toward the stimuli themselves or toward the average location. However, this transition is continuous without a defined spatial window. While the specific requirements of the task, as well as the salience of the stimuli and the difficulty in discriminating them, all influence the proportion of observed averaging saccades between different experimental paradigms, when these variables are appropriately controlled, automatic capture, both toward the stimuli and to the global effect location, can be observed for all separations.

The Role of Task Instructions on the Global Effect

In examining the global effect, researchers typically have asked participants to saccade to either of two stimuli (STE; i.e., two target paradigms; De Vries et al. 2016), to saccade to a specific stimulus (STT; i.e., target and distractor paradigms; Walker et al. 1997), or have shown two stimuli and given ambiguous (or nonexistent) instructions about the task goal (STA; i.e., ambiguous instruction paradigms; Silvis and Van der Stigchel 2014). However, each of these methods has certain limitations in interpreting the influence of task on performance. With two target paradigms (STE), it is unclear which of the stimulus locations the subject classified as his or her intended goal. This means that a researcher cannot discern the difference between saccades that were intentionally directed toward a specific goal location and those that were automatically captured toward one of the stimulus locations. The participants may have intentionally selected one of the object’s locations as their intended movement goal, but nevertheless found that their gaze was captured toward the other location.

In experiments with both a target and a distractor stimulus (STT), the proportion of saccades to the distractor can be analyzed to estimate the frequency of unintentional capture toward the distractor location. However, as the goal location and the target location are always identical, the frequency of unavoidable capture toward the target location (which inadvertently happens to be correct) cannot be discerned. Our results suggest that the proportion of unavoidable capture toward the distractor stimulus provides a good approximation for the proportion fortuitously captured toward the target location, which in these cases is also the goal location. This is a clear problem with the most common metric used, median landing position, as, unless the data are mirrored around the intermediate location, the proportion of saccades landing at the distractor could substantially shift the median toward the middle of the distribution.

In paradigms with ambiguous instructions (STA), these problems are compounded, as different participants, or even the same participant on different trials, may have different inferences as to their required task. In such a situation, when two identical stimuli appear, moving one’s eyes to the midpoint (which shifts the fovea closer to both stimuli) is objectively just as valid a strategy as selecting either one of the stimuli. By not giving instructions, it has been argued that top-down influences on saccade targeting are avoided. For example, Silvis and Van der Stigchel (2014) explain that, “A unique feature of this paradigm is that participants are generally not instructed to aim for a specific target and are simply told to move their eyes as quickly as possible toward the information that appears on the screen” (p. 358). The use of instructions is argued to be unnecessary, as the averaging behavior seen is believed to be the “default” behavior. However, other studies have shown that increasing the predictability of stimulus locations (Aitsebaomo and Bedell 2000; Coëffé and O’Regan 1987; He and Kowler 1989) or increasing the accuracy demands of the task (Findlay and Blythe 2009; Findlay and Kapoula 1992) both result in a substantially weaker global effect. This suggests that intentional modulation from the task can indeed influence averaging behavior.

A recent study by Heeman and colleagues (2014) explicitly investigated the use of ambiguous instructions by testing a “no instruction” condition (STA), in which participants were simply told to move their eyes “as fast as possible to the stimuli presented” (p. 31), as well as a condition with explicit instructions to saccade to a specific target (STT). They found more accurate saccades when explicit instructions were given, even for the most rapidly executed saccades. By providing evidence that even saccades with low latency are biased, this suggests that the perceived task or attentional set of the observer cannot be ignored (Folk et al. 1992, 1994; Folk and Remington 1998). Thus the data from tasks utilizing ambiguous instructions likely represent the influence of ambiguous top-down information (which within individual participants may represent different, explicit strategies), as opposed to being absent of top-down information.

Time Course of Intentional Control

In the present study, we developed a modified version of the global effect paradigm that enabled us to separate the influences of incidental capture and intentional, goal-directed targeting. We achieved this by manipulating the task instructions so that, in the different tasks, the movement goal was dissociated from the location of the target stimulus or global effect location. By contrasting the two identical paradigms, varying only in task goal, we could compare the component weights for each participant and dissociate the influence of automatic capture toward visible stimuli from the slower, intentional effects arising from the top-down selection of the task goal. Not only was this the first demonstration of a task explicitly requiring the participant to saccade to the midpoint between two stimuli, but we were also able, from behavioral data alone, to derive the time course over which goal-related planning influences saccade targeting.

We found that the influence of task increased with saccade latency until saccades initiated as late as 300 ms almost all landed accurately at the task goal. However, we also found that there was a nonnegligible influence of task on even the fastest initiated saccades. These findings conflict with the conclusions of Heeman et al. (2014). These authors argued that, although activity in the SC represents a combination of both automatic (bottom-up) and intentional (top-down) processes (Bompas and Sumner 2011; Meeter et al. 2010; Trappenberg et al. 2001), the intentional influences take longer to process when coding saccade targets, leaving the fastest initiated saccades almost entirely exogenously driven. Instead we find a considerable influence of task even for the most rapid saccades.

Rather than representing a dynamic response to the stimuli on the current trial, some of this early influence of task may instead represent an anticipatory response to the overarching task demands. For example, when participants are in a block in which they must explicitly saccade to the stimulus that matches the color at fixation, they may prime the relevant feature detectors in anticipation of the stimulus appearing (Folk et al. 1992, 1994; Wu et al. 2014). Conversely, when explicitly required to move their eyes to the global effect location, participants may be able to preemptively boost attention to lower spatial frequencies that are more likely to encompass both stimuli (Ludwig et al. 2007). As such, while our results certainly provide evidence that the task influences even rapid eye movements, this influence may be more akin to preattention filters (Folk et al. 1992) than active selection based solely on visual processing of the stimuli.

Nevertheless, these findings give strong support to the idea that the general increase in saccade accuracy for longer latency saccades is due to task-related, top-down feedback. Furthermore, they support the suggestion that this time course is related to the time it takes for task-related signals from higher visual areas (i.e., frontoparietal regions), responsible for selection and decision making, to be propagated back to early visual areas where they can boost the processing of the selected visual stimuli and facilitate targeting the correct location for the upcoming eye movement (reverse hierarchy theory; Hochstein and Ahissar 2002). Indeed, the time course observed in the current experiment corresponds well with a range of different studies investigating visual search, spatial cueing, and eye movements that have suggested attentional selection takes ~150–200 ms to reach primary visual cortex (Buffalo et al. 2010; Mehta et al. 2000). Here the demands of the task are critical in determining the delay, as the longer times required to reach decision thresholds for more difficult tasks can substantially alter the speed at which intentional selection influences task performance.

This matches well with previous results showing that, while changing the discriminability of the target does not eliminate the biases observed for rapidly executed saccades, it does influence the overall saccade landing distribution, presumably by influencing the time it takes for intentional selection to influence behavior. For more difficult discriminations, intentional selection would be delayed, meaning that, while early saccades would still be predominantly influenced by low-level stimulus properties, the improvement from selection would develop more gradually. Interestingly, we observed that the intentional goal-directed influence on saccade targeting appeared to follow the same time course, regardless of separation. As such, the time course of attentional selection appeared to be unchanged by stimulus separation, which itself does not affect stimulus discriminability. Similarly, while our contrast manipulation altered the saliency of the noise patch within stimuli, it affected both stimuli equally and did not alter the visibility of the colored ring (which was the feature critical in discriminating between target and distractor). Thus, also in experiment 2, the time course of intentional selection remained largely similar across contrast conditions.

Manipulation of Contrast

In experiment 2, we manipulated the contrast of both of the stimuli to see whether this manipulation altered the strength of stimulus capture and/or the global effect. While the overall contrast influenced median saccade latency, with higher contrast stimuli producing more rapid eye movements, we were not able to discern a differential effect on the probability of making an averaging saccade. However, the results of experiment 2 not only replicated the findings of experiment 1 with an additional eight naive subjects, but allowed us, by collapsing across contrast levels, to generate a substantially smoother and more robust time course, due to the greater number of trials. Indeed, the close correspondence between results from the two experiments suggests our findings are robust and generalizable to the wider population.

Although our contrast manipulation did not differentiate between stimulus capture and the global effect, future experiments could extend our findings by manipulating the contrast of the two stimuli independently and using our method to quantify how stimulus competition affects the likelihood of capture to stimulus or global effect locations. Varying the contrast may bias averaging saccades toward the higher contrast stimuli, resulting in saccades directed not to the intermediate position but somewhere in between there and the stimulus. Alternatively, the global effect location may be unaffected by the contrast of individual stimuli and instead reflect the center of mass of the two stimuli or the bisected distance between the two, independent of the visibility of each stimulus. It would also be interesting to compare with perceptual judgments of the midpoint between the stimuli, to see if they remain accurate under these circumstances, or if the differences in contrast between the stimuli bias the perceptual midpoint location toward the more salient stimulus.

In the first experiment, the two tasks were kept as close to identical as possible, with the only difference between the tasks being the verbal instructions. While this ensured that we could ascribe differences in our results to the task itself, it meant that in the STM task participants were also required to ignore the color of the fixation. In experiment 2, the fixation color was changed to a nonmatching color during the STM task. Despite this change, we replicated the results of experiment 1, suggesting that this color cue played no role in our results. Nevertheless, there was a very slight tendency for the weight of the target stimulus to be slightly larger than the distractor stimulus during the STM task in experiment 1 (when instead they should be identical, as seen in experiment 2). Future studies could investigate whether task-irrelevant color cueing of one of the stimuli is able to influence the targeting of automatic, stimulus-driven eye movements and, perhaps more importantly, whether it can also influence the position of the global effect location.

Perceptual Judgments

We had participants perceptually localize the goal location after each saccade by indicating its location with the computer mouse. This was an important control to ensure that participants could accurately localize the stimuli on every trial. It also allowed us to examine whether the cases in which participants made non-goal-directed eye movements were associated with changes in the accuracy of perceptual localization. We found no such change in the mouse response accuracy, regardless of the accuracy of eye movements.

These results support the work of Eggert and colleagues (2002), who found a global effect in a saccade target task, but failed to find a similar effect for perceptual localization judgments. However, it is important to note that visual information available before the saccade may have benefited from continued processing even after saccade initiation. Thus, although there was sufficient information to accurately localize the goal location by the time of the mouse response, this information may not yet have been available for motor planning at the time of saccade initiation.

Despite the inaccuracies in saccade end points, evidence from studying attentional shifts (Deubel and Schneider 1996) has shown that participant’s attention is located at the intended target location, irrespective of where the eyes land. This implies that, even when sudden onsets or averaging causes the executed saccade to be inaccurate, the target selection remains precise (Van der Stigchel and de Vries 2015). Given the proposed tight coupling between attention and action (Hoffman and Subramaniam 1995; Shepherd et al. 1986; Van der Stigchel and Theeuwes 2005), this suggests that, while many factors may contribute to the accuracy of the enacted motor command, target selection is likely to remain tightly focused on the actual saccade target. Previous work showing that the global effect represents averaging between the saccade goal and distractors (and not between stimuli per se) provides further evidence as to why the perceptual localization of the target stimulus might be unaffected (Viswanathan and Barton 2013). Our results, in which the intermediate location was equally well localized in the STM task, regardless of saccade landing position, further suggest that the spatial interactions responsible for the errant eye movements in global effect tasks are independent from perceived location.

Conclusions

We developed a novel paradigm in which task instructions were manipulated to investigate how intentional target selection interacts with the spatial separation between stimuli. To quantify these effects, we implemented a probabilistic mixture model that could produce estimates of the proportion of saccades directed to different locations and how this varied with changes in saccade latency. By contrasting our model fits across tasks, we could extract the proportion of saccades that were automatically directed toward the location of visible stimuli or the global effect location and distinguish these from the proportion that was intentionally targeted to the goal location. We found evidence that both visual object capture and the global effect co-occurred at short latencies for all separations, but their influence declined as latency increased and eye movements came under increasing top-down control. Furthermore, we found that, as the separation between the stimuli increased, capture came to dominate the landing positions of fast saccades, with reduced global effect. Yet even at the largest separations, we found evidence for the global effect in rapidly initiated saccades. Using the mixture model fits, we could recreate the time course over which the competition between automatic capture and intentional targeting played out. These results demonstrate a powerful method for extracting the time course of target selection from eye movement data and have importance for our understanding of saccade target selection.

GRANTS

This work was supported by the Wellcome Trust.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

D.A.-M. and P.M.B. conceived and designed research; D.A.-M. performed experiments; D.A.-M. analyzed data; D.A.-M. and P.M.B. interpreted results of experiments; D.A.-M. prepared figures; D.A.-M. drafted manuscript; D.A.-M. and P.M.B. edited and revised manuscript; D.A.-M. and P.M.B. approved final version of manuscript.