The 4-2-1 family structure in China: a survival analysis based on life tables

Abstract

Concern about ensuring old-age support in 4-2-1 families—consisting of four older people (paternal and maternal grandparents), two parents, and only one child—has risen with the increase in the number of families with only one child. In this article, using life table data and probability theory, we examine survival probabilities and coexistence durations for China’s 4-2-1 family structure, as well as urban and rural differences and conduct a sensitivity analysis. We find that once the grandparents have all entered the “old-age” phase (over 60 years old), the probability that all four will survive is only 0.61. The four grandparents are likely to coexist for 16 years after the birth of their grandchild, then one will die and the remaining three will probably spend another 8 years together; finally, after another dies, the surviving two will coexist for another 5 years. There is no significant difference between urban and rural families in terms of the duration of their coexistence. As the ages at which the parents had their child rise, the durations become shorter. The pressure of old-age support in such families is not as severe as expected.

Introduction

The 4-2-1 family structure refers to families in which three generations coexist in a variety of family forms. The structure emphasizes a social living community, including four older people (paternal and maternal grandparents), two parents, and one child, based on relationships of marriage, kinship, and adoption. This family structure falls under the generalized concept of a family household, rather than being restricted to the real coexistence of family members within a household (Song 2000). Consequently, the so-called 4-2-1 family structure is formed as long as direct kinship exists, without there being any need for all the family members to actually live together (Guo et al. 2002). The formation of the 4-2-1 family structure has three requirements: first, three generations coexist with paternal and maternal grandparents and parents all living; second, the marriage relation is between only children, i.e., both the father and the mother are the only children in their families; and finally, the child is the only one in the family (Song 2000).

In addition to the above mentioned strict definition of the 4-2-1 family structure, some researchers have defined the community as consisting of the only child couple, grandparents from both sides and the child as a generalized 4-2-1 family structure, but in which other structures are included, such as the 4-0-1 family and the 3-1-1 family, up to a total of 24 distinct family structures (Qi and Guo 2007). The 4-2-1 family structure discussed in this article, unless specifically stated otherwise, is that corresponding to the strict definition.

Due to the traditional Chinese concept of “more children, more happiness”, the 4-2-1 family structure rarely appeared before the one-child family planning policy was strictly implemented in China, so it did not receive much attention. With the overall implementation of the family planning policy and the appearance of low fertility levels, the total amount of only children increased quickly. At the end of 2007, the quantity of only children younger than 30 was more than 150 million (Yang and Wang 2007). With more and more only children reaching marriageable age, the probability of marital unions between only children has increased greatly, and in big cities the probability might be as high as 70% (Liu and Liu 1996). By 2015, there will be 1.58 million 4-2-1 families in China with the total reaching 1.85 million in 2035. If we calculate the amount in terms of the more general definition, in 2015 there will be 2.91 million such families and 13.47 million in 2035 (Qi and Guo 2007).

The 4-2-1 family structure has had a great impact on many issues, such as population reproduction, sex ratio at birth, population aging, and old-age support. The issue which has received the most attention is the enormous impact exerts on family support, which refers to the financial support, instrumental support, and emotional support which children (especially the adult son and his family) offer to their elderly parents, and a series of social services such as those providing medical expenses, care of sick parents, and funeral services (Wang 2003). In rural China, the majority of older adults who had lived as peasants or worked in certain informal sectors when they were young and continued to work when older until becoming unable to do so, had scant access to social security (Randel et al. 1999). Recently China has begun the establishment of social security retirement system in rural areas. However, in the foreseeable future, such a system will not cover all of the rural population, and the pension that these rural residents receive will be far from sufficient to support them in their old age. Even in the cities, the old-age social security system fails to cover all the older people; furthermore, the nursing institutions for the older adults are not perfect. As a result, almost all the elderly have to live by relying upon the help and care that their children or relatives provide (Ikels 1997). Because family support is the main method of supporting the older adults, many people are afraid that the 4-2-1 family structure will burden the family support system; more specifically, the parents, i.e., the middle generation, will have to support two pairs of grandparents and the only child. Even worse, when both parents get old, the only child, i.e., the third generation, will eventually have to support two parents and all four grandparents, six persons in all (Tu 1995; Song 2000).

These concerns are based on an imprecise understanding of the question, due to the fact that people have taken it for granted that four or six older people will coexist for a long time after they pass into old age. As far as the pressure to support older adults is concerned, the first issue that needs to be considered is at what point the grandparents will pass into old age after the formation of the 4-2-1 family. Even if a 4-2-1 family is formed which has both paternal and maternal grandparents, while all four are young enough to work, the support pressure will not be intense or may not even exist during this period. On the contrary, younger grandparents tend to offer their son or daughter financial support or take care of the grandchild (Silverstein et al. 2007). Second, even though all four grandparents may grow old, as their ages increase they will pass away. Consequently, the probability of coexistence will decrease with increased age, and the 4-2-1 family will turn into a 3-2-1, 2-2-1, or even 1-2-1 family structure, so a couple will not have to support four older people at the same time. Finally, the percentage of older people aged from 60 to 64 who cannot take care of themselves is only 3.2%, and for older people in the 60–69 age range, the percentage is only 5.1%, so the problem of daily nursing care for older people under 70 is not that prominent (Du and Wu 2006). However, by merely overemphasizing the four older people or even the six older people in the 4-2-1 structure, we may exaggerate the family support problem to some extent.

Until now, the quantitative study of potential old-age support pressure for the 4-2-1 family has been an underdeveloped subject. Even less is understood about the evolution of the 4-2-1 family structure after its formation: how many grandparents will coexist for how long? One study has projected the number of 4-2-1 families (Qi and Guo 2007), but, to our knowledge, no study has examined the possibilities of the existence of 4-2-1 families and shared years of the family while 4, 3, 2, or 1 grandparents are alive. With a view to clearing up misapprehensions about support in the 4-2-1 family, this study, based on the hypothesis that the parents and the child are all living, has taken data from life tables and probability theory to analyze the survival probability and survival time of the 4-2-1 family after its formation. In order to assess the influence that change in family structure has had on the pressure of supporting older family members, this study has also analyzed the duration of the 4-2-1, 3-2-1, 2-2-1, and 1-2-1 family and the ages of the grandparents in each family structure. Due to the significant urban–rural divide in China, we also analyze the urban–rural difference in the above mentioned indicators. Furthermore, as some parameters are so important in calculating these indicators, we also carry out a sensitivity analysis with age variations for the mother and father.

Methods and data

Methods

Due to the fact that the focus of the study is the survival situation of grandparents and the pressure experienced by the family regarding their support, survival analysis, and probability theory have been adopted to investigate the survival probability of grandparents while the child and parents are all living.

The probability analysis of the coexistence of three generations

In survival probability analysis, the population of x years old in the life tables is l _x, the population aged x + n is l _x+n, and the probability of survival from x to x + n is _n P _x, so,

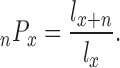1

In the 4-2-1 family structure, the birth of the child makes the structure come into effect. Henceforth, we will use the age of the child as a standard and define the initial age of the child as 0, and the age difference between the child and the father is f, while the difference between the child and the mother is m; the age difference between the child and the paternal grandfather, paternal grandmother, maternal grandfather, and maternal grandmother are, respectively, labeled ff, fm, mf, and mm. We use events to define individual survival. See Table 1.

Table 1.

Key to event labels

A 1	The child survival event
A 2	The father survival event
A 3	The mother survival event
A 4	The paternal grandfather survival event
A 5	The paternal grandmother survival event
A 6	The maternal grandfather survival event
A 7	The maternal grandmother survival event
B	All four grandparents coexistence event
C	At least three grandparents survival event
D	At least two grandparents survival event
E	At least one grandparent survival event
F	The four grandparents coexistence event when the child and the parents are alive
G	At least three among the four survival event when the child and the parents are alive
H	At least two among the four survival event when the child and the parents are alive
I	At least one among the four survival event when the child and the parents are alive

If we suppose that the loss of a spouse or child has no influence on expected lifespan and death probability, the above mentioned events are independent. We infer from Formula 1 that the probability that the father can live from f to f + n can be expressed as 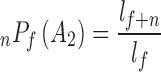. For the sake of convenience, we will use P as the short form of _n P _x, correspondingly, 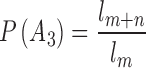, , , , 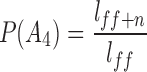, 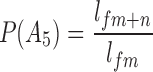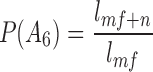and 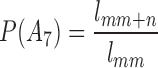. One point that needs to be mentioned is that all the formulas refer to male life tables and female life tables, respectively, based on the sex associated with the event objectives. After the individual survival probability has been calculated, we can use it as a basis to obtain the survival probability of different numbers of people among the grandparents.

The survival probability of all four:

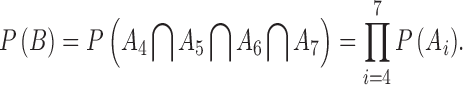2

The survival probability of at least three among the four:

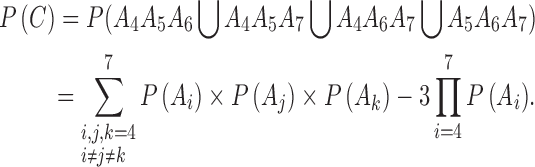3

The survival probability of at least two among the four:

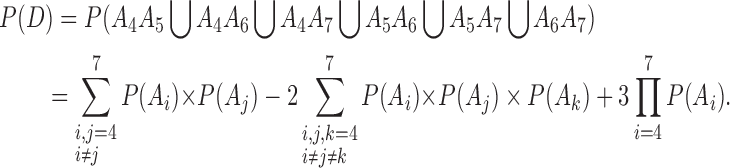4

The survival probability of at least one among the four:

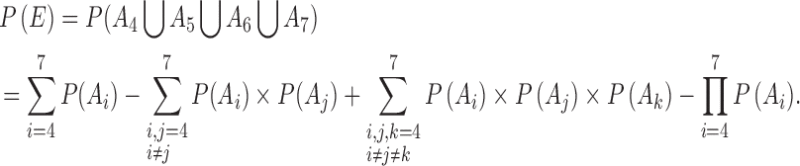5

Accordingly, on the condition that the child and parents are living, the probability formula of the coexistence of the three generations in the 4-2-1 family structure can be rewritten as follows:

While the child and parents are all living, the survival probability of the four grandparents is:

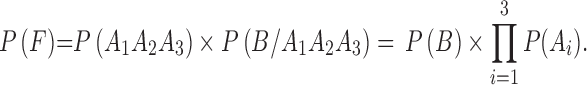6

While the child and parents are all living, the survival probability of at least three among the four is:

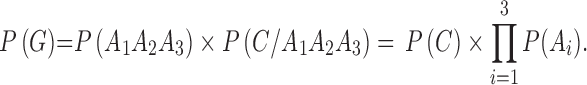7

While the child and parents are all living, the survival probability of at least two among the four is:

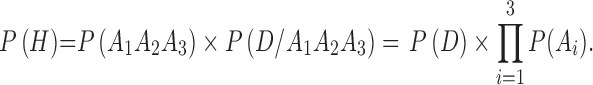8

While three generations coexist, the survival probability of at least one among the four is:

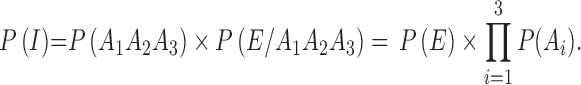9

Analysis of the number of years the three generations will coexist

In addition to the coexistence probability, we are also concerned with the number of years the grandparents will coexist, which is crucial to the study of the pressure of supporting older family members. Formulas 6–9 can help us obtain a series of survival probabilities which produces a survival probability curve which can correspond to a life table with an initial number of persons of 1; we can then use each curve to calculate the number of years that three generations coexist in the 4-2-1 family. In each formula, P _x+1 represents the coexistence probability when the child is x + 1 years old, and P _x is the coexistence probability when the child is X years old; L _x stands for the duration of three generations’ coexistence when the child is from 0 to N years old, so according to the life table calculation method, based on the age of the child, in each year from 0 to N, the duration of the coexistence is:

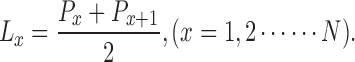10

Because the maximum age of the life tables we have adopted is 90, when the child is N + 1 years old, the paternal grandfather is already 90, the maximum age in the tables. As in the method for calculating the number of person-years lived for the final open-ended group in life tables, when we calculate the duration of coexistence when the child is N + 1 years old, we can refer to the following formula:

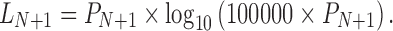11

By adding up the survival years of the grandparents at the child’s different ages, we can obtain the number of years the three generations will coexist after the birth of the child.

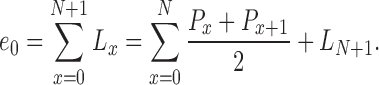12

Data

The formation of the 4-2-1 family is influenced by many factors, such as, expected life span at birth, age differences between the male and the female, and childbearing age, etc. (Song 2000). We can see from the “Methodology” section that the data is mainly from the life tables plus some age data. The life tables are based on the 2000 population census, generally speaking, which was a successful census, but nevertheless suffered from a serious problem—the rate of missing reports is 1.81% (Population Census Office of the State Council 2002). Although this rate is acceptable according to international standards, it is much higher than the 0.06% of missing reports in the 1990 population census (Lavely 2001; Walfish 2001). In the population census in 2000, population death indicates that people died between November 1st, 1999 and October 31st, 2000. The data on the death rate is also questionable because the missing death reports make the reported death rate lower than it ought to be (Li and Sun 2003). This study has used the life table developed by Li et al. (2005) in which the missing reports of population and death are adjusted for. Since the 4-2-1 family structure appears both in urban and rural areas, the life tables used in this study are the male and female life tables for the urban population, the total population and the rural population. For the specific data itself, see Li et al. (2005).

As for average childbearing age, different data sources provide different results. Childbearing is usually influenced by the marriage age. According to previous childbearing studies, the beginning of the childbearing age is 1 year later than the age at first marriage (Guo 2004). Guo (2004) analyzed the year 2000 population census data and found that in 1990, for a male, the average first marriage age was 23.8, and for a female it was 22.0; in 2000, for a male, the average had reached 25.6 and for a female 23.6. However, in accordance with the standardized average first marriage age table obtained using the data from the family planning and reproductive health survey of 2001, after the standardization of the age structure to the 1990 structure, the average first marriage age of childbearing-aged women increased from 21.8 in 1990 to 22.4 in 1995, and 22.6 in 2000; i.e., the age increased by 0.8 years in 10 years (Pan 2003). In contrast, other data showed that in 1980 the first child bearing age was 24.4, which decreased to 23.4 in 1990 and then maintained a steady state (Liang 2004).

The average childbearing age is thus still controversial. Moreover, there can be widely varying age differences between the father and the child, between the mother and the child, as well as between the grandparents and their grandchild. This study restricts the data as shown in Table 1. For the whole country, when the child is born, the father is 25, the mother is 23, the paternal grandfather is 49, the paternal grandmother is 47, the maternal grandfather is 47, and the maternal grandmother is 45. Ages for urban families are higher than those of the total population, and ages for rural families are the lowest, as can be seen in Table 2.

Table 2.

Ages for old generations when the child is born

Age	Urban	National	Rural
Father	26	25	24
Mother	24	23	22
Paternal grandfather	51	49	47
Paternal grandmother	49	47	45
Maternal grandfather	49	47	45
Maternal grandmother	47	45	43

Results

In accordance with the methods and data described above, this study has obtained the following results. We will first discuss the survival probability and duration of coexistence of three generations for the total population.

Survival probability

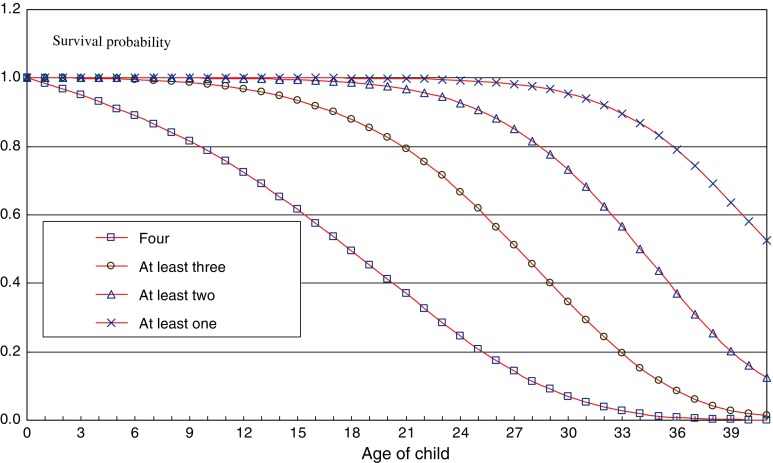
The survival probabilities for the total population are exhibited in Fig. 1. The horizontal axis represents the age of the child and the vertical axis, the survival probability.

Fig. 1.

Age-specific survival probability curves concerning the coexistence of three generations in the 4-2-1 family structure

Survival probability when all four grandparents are living

We can see from Fig. 1 that after the baby is born (0 years old), the survival probability of the grandparents goes into almost a linear decline. When the child is 15, the grandparents officially cross the threshold into old age, at 60 years old; however, the co-survival probability of the four is as low as 0.61. When the child is 20, the coexistence probability of the four is only 0.41; in addition, their ages are under 70, which belongs to younger old age. When the child’s age is from 20 to 29, the four older adults enter into the middle old-age period, while the coexistence probability decreases dramatically from 0.41 to 0.09. After the child reaches age 30, the four grandparents cross into the oldest old-age period, and the coexistence probability becomes very low.

Survival probability of at least three among the four

The survival of at least three grandparents includes two possible scenarios: three older people are living or all four are living. In this situation, the probability is higher than that of having all four co-survive. While the child passes from age 20 to 29, the survival probability of at least three grandparents decreases from 0.82 to 0.40, respectively; from 30 to 35, the probability falls from 0.34 to 0.11; by the time the child is aged over 35, all the four older people will have entered into the oldest age bracket, and the survival probability of at least three drops to below 0.10.

Survival probability of at least two among the four

Compared with the survival probability of at least three grandparents, the survival probability of at least two is higher. When the child is 34, the probability is 0.50, and while the child is between the ages of 35 and 41, during which all the grandparents are in the oldest period of old age, the probability decreases steadily to 0.13.

Survival probability of at least one among the four

Before the child’s 25th birthday, the survival probability of at least one grandparent is above 0.99, and between the ages of 25 and 30, the probability decreases to 0.95; this means that the probability that all four grandparents will have died before the child reaches his or her thirties is under 0.05. Between the ages of 31 and 41, the survival probability decreases from 0.95 to 0.52.

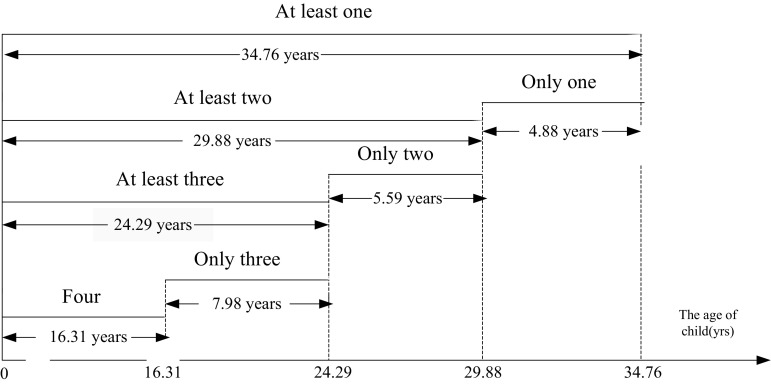
A duration analysis of the coexistence of three generations

While the child and his or her parents are living, the years of coexistence of all three generations in the 4-2-1 family is shown in Fig. 2. The years of coexistence during which all four older people are living is 16.31 years. During this period, when the age of the child is from 0 to 10, all four grandparents are under 60, while when the child is aged from 11 to 16, they pass into old age, but still remain in a younger old-age period, during which they are under 65.

Fig. 2.

Survival years of grandparents in the 4-2-1 family structure, conditional on the survival of two parents and one child

When the child reaches 16, one of the grandparents will pass away, leaving a family structure of 3-2-1. For 8 years, when the child is aged from 16 to 24, there will only exists three older people, whose ages are between 61 and 73, during which period the majority can take care of themselves, and what they need is mainly financial and emotional support. However, for older persons in rural areas, their daily care needs might be more considerable.

When the child is 24, two of the grandparents will have died, while another two remain living, which makes for a 2-2-1 family structure with a 5-year duration, after which there will be only one older person still existing in the family. When the child is aged between 30 and 35, only one of the grandparents will still be living.

Urban and rural difference

China’s dualistic urban and rural system has produced a large gap in socio-economic development between the cities and the countryside. Here we are not going to present the survival probability figures due to the difficulty in recognizing the urban and rural difference, as the lines are too close. See Table 3 for the difference in coexistence durations.

Table 3.

Urban–rural difference in survival years

Survival years	Urban	Rural
Four	17.00	16.55
Only three	8.20	7.96
Only two	5.90	5.41
Only one	4.91	4.68

As can be seen from Table 3, while the child and the parents are living, the years of coexistence during which all four older people are still alive in urban areas is 17.00 years, while those for rural 4-2-1 families amount to 16.55 years. The four urban durations are longer than their corresponding rural ones, but generally speaking the difference is not very significant.

When the child is born, the ages of the urban paternal grandfather, paternal grandmother, maternal grandfather, and maternal grandmother are 51.0, 49.0, 49.0, and 47.0 years old, respectively, and those of their rural counterparts are 47.0, 45.0, 45.0, and 43.0, with a gap of 4 years when the child is born. So even if there are no obvious differences in those durations, there are differences in the grandparents’ ages when the structure changes from one mode to another.

The urban population enjoys higher life expectancy, which indicates better access to medical care than their rural counterparts. And, given higher educational attainment and better work opportunities, the urban population usually marries at a later age. The age gap between urban and rural fathers is 2 years, the same as the gap between urban and rural mothers. In addition, different life expectancies for urban and rural populations mean different mortality patterns and levels. All these age differences and life expectancies affect the results obtained.

Sensitivity analysis of the effect of ages on coexistence durations

Since some key parameters like ages are so important in the final results, we will now introduce a sensitivity analysis to examine how age variations can affect survival probability and coexistence durations. Here we will simply present the results of coexistence durations. As there are too many age variations, we will merely modify the age gap between the father and the child from 25 to 31 and keep the other age gaps fixed. The results are shown in Table 4.

Table 4.

Sensitivity analysis on coexistence durations (years)

Father’s age when child born	Four	Only three	Only two	Only one
25	16.31	7.98	5.59	4.88
27	14.97	7.72	5.53	4.87
29	13.68	7.43	5.46	4.86
31	12.44	7.12	5.37	4.83

As can be seen from Table 4, as the father’s age when his child is born rises from 25 to 31, and the mother’s age changes from 23 to 29, with the spousal age gap being fixed, the most significant resulting change affects the duration of the four grandparents’ coexistence, which decreases from 16.31 to 12.44 years, but no obvious changes occur to other durations.

Discussion

Chinese culture is rooted in filial piety, which is also the basis of Chinese society (Xie 2000). The sense of filial piety is central to generate the public opinion supervision system of the traditional intergenerational support model; in addition, public opinion and laws have enforced the centrality of family support for their elders (Hong and Liu 2000). Conventionally, the security of older people depends on the family, and corresponding social norms and policies have come into being. Furthermore, in rural China, the concept of “raising children for old age” has become rooted in people’s minds, so much so that the idea of saving money for one’s own old age is seldom considered (Chu 2001). In rural China, the support of older people depends on their families; hence, family support provided by adult children has been the dominant form of ensuring the security of older people in rural areas (Xu and Yuan 1997).

With the steady development of the economy, the Chinese government will gradually acquire the capacity to take over the duty of caring for older people which has traditionally been assumed by families (Burgess 2002). However, for the foreseeable future, China will not be able to establish a reliable, high-quality old-age social security system covering both rural and urban areas. China will take steps to establish a social security system for the elderly; nevertheless, for a long period in the future, family support will remain the main form of care in rural areas (Chen 2000; Chu 2001). Given this situation, an increase in the numbers of one-child families in China causes people great anxiety regarding the old-age support issue in 4-2-1 families. This study, to the best our knowledge, to explore survival probabilities and durations of coexistence for the 4-2-1 family structure by means of the application of life table data and probability theory, has reached the following conclusions.

First of all, the coexistence probability of the four grandparents decreases rapidly, being only 0.61 when they are all elderly (i.e., 60 or older). After the child is born, the four coexist for 16 years, and then one of them dies, which turns the 4-2-1 family model into a 3-2-1 structure. We can infer from the intergenerational age difference that during the 16 years when the four grandparents are alive, their individual ages are no higher than 65, so they possess the capacity to work for most of that time. Even after turning 60, the percentage of older people aged from 60 to 64 who cannot take care of themselves is only 3.2% (Du and Wu 2006), and so they are still able to work and live independently. During this period, for families living near one another, say in a city or in a village, grandparents can provide financial support and look after the child. Even if they live apart, urban grandparents can also provide financial support for couples, and rural grandparents can take care of a grandchild left behind, as more and more rural couples migrate to cities to seek opportunities and jobs. To sum up, we can say that the probability of having to support four older people simultaneously is very slim; on the contrary, it is the grandparents who will provide financial support and take care of the child during the first 16 years.

Second, during the 8 years when the child is 16–24 years old, there are only three grandparents living, and the parents will still be under 50; as a result the problem of the coexistence of four or even six elderly people in a family does not exist. During this period, the grandparents still belong to the “young” old-age bracket, and the percentage of older people aged from 65 to 69 who cannot look after themselves is as low as 5.1% (Du and Wu 2006), so care of the elderly in daily life is not the dominant problem. When the child reaches 24 years of age, the oldest grandparent in the family is 73 and the youngest 69. At this point, the elders cross into the “middle” old-age bracket (70–79). Here, while the percentage of families who have to take care of an ailing member increases, relatively speaking it is still low. During this period, financial support is the dominant issue in rural areas, as the child has to support elderly grandparents who have already lost their capacity to work.

Third, when the child is aged over 24, even though all the older people are in the “middle” old-age bracket, the family structure becomes 2-2-1 or even 1-2-1 because there are only two grandparents or even one grandparent surviving. As a result, the problem of support is not that serious.

Fourth, there is no significant difference in the length of coexistence between urban and rural families. When the 4-2-1 structure shifts from one mode to another, urban and rural grandparents have different ages due to the age gap between urban and rural grandparents existing when the child is born.

Finally, key age parameters exert an influence on coexistence durations. If the ages of the parents at the time their child is born go up, the four durations decrease, and the most significant drop occurs for the durations of four grandparents coexisting.

The emergence of the 4-2-1 family is a result of the one-child policy, and the marriage of two only children is the factor leading directly to the emergence of the 4-2-1 family, a prominent feature of which is the separation of two nuclear families and the building of a new family rather than a simple combination of two nuclear families (Liang 2004). In traditional Chinese culture, on the condition that three generations are alive, there are two kinds of families which may be formed around such a kinship structure. In one, the one-child couple and their child make up a nuclear family while two pairs of older couples make up two independent empty nest families; in the other, one of the older couples, the only child couple and the child build a nuclear family together while the other older couple makes up an empty nest family. The central problem that the 4-2-1 family will bring is a special contradictory relationship between three generations, or between two or three families and the emergence of a large number of “DINK” (Double Income, No Kids) families. But as China’s population rapidly ages and the proportion of the elderly rapidly increases up to 25% in 2050 according to an UN projection, the 4-2-1 family structure, intertwined with rapid aging, may go beyond the individual family and burden the social security system, if this elderly population is covered in such a system.

There exist some limitations to this study. The assumptions made regarding the age differences have an impact on the results. And the assumption that all survival events are independent is quite draconian, as longevity is hereditary and some events, such as death of the spouse, exert a corresponding effect on physical and psychiatric illnesses and will also affect survival. Another factor which affects the numerical results lies in the life tables. With the increase in life expectancy, it would be better to use a higher maximum age, for example 100 years. But, due to data limitations, we are unable to obtain life tables with higher maximum ages—the maximum age in the life table we have used in the study is 90. Moreover, the results we obtain will be affected by the mortality pattern in the life tables. This study, which examines survival probabilities and coexistence durations for China’s 4-2-1 family structure, as well as urban and rural differences and sensitivity analysis, is an investigation based on certain hypotheses with the help of life tables and probability theory, but it will be necessary to use empirical data to test the results.