Cellular trade-offs and optimal resource allocation during cyanobacterial diurnal growth

Significance

Cyanobacteria are important players in Earth’s biogeochemical cycles and a promising resource for the synthesis of renewable raw materials. Of particular interest are the cellular organization that enables fast growth and the corresponding intracellular limits on growth rates. Here, we develop a constraint-based computational model of phototrophic growth to investigate the optimal allocation of cellular resources in a diurnal light environment. The model-derived optimal metabolite partitioning during diurnal growth is in qualitative agreement with recent experimental data. Our results suggest that phototrophic metabolism at fast growth rates is highly optimized and strongly dependent on the timing characteristics of enzyme synthesis. Furthermore, we demonstrate that the experimentally observed pattern of glycogen accumulation is in agreement with predictions based on optimal resource allocation.

Abstract

Cyanobacteria are an integral part of Earth’s biogeochemical cycles and a promising resource for the synthesis of renewable bioproducts from atmospheric CO₂. Growth and metabolism of cyanobacteria are inherently tied to the diurnal rhythm of light availability. As yet, however, insight into the stoichiometric and energetic constraints of cyanobacterial diurnal growth is limited. Here, we develop a computational framework to investigate the optimal allocation of cellular resources during diurnal phototrophic growth using a genome-scale metabolic reconstruction of the cyanobacterium Synechococcus elongatus PCC 7942. We formulate phototrophic growth as an autocatalytic process and solve the resulting time-dependent resource allocation problem using constraint-based analysis. Based on a narrow and well-defined set of parameters, our approach results in an ab initio prediction of growth properties over a full diurnal cycle. The computational model allows us to study the optimality of metabolite partitioning during diurnal growth. The cyclic pattern of glycogen accumulation, an emergent property of the model, has timing characteristics that are in qualitative agreement with experimental findings. The approach presented here provides insight into the time-dependent resource allocation problem of phototrophic diurnal growth and may serve as a general framework to assess the optimality of metabolic strategies that evolved in phototrophic organisms under diurnal conditions.

Cyanobacterial photoautotrophic growth requires a highly coordinated distribution of cellular resources to different intracellular processes, including the de novo synthesis of proteins, ribosomes, lipids, and other cellular components. For unicellular organisms, the optimal allocation of limiting resources is a key determinant of evolutionary fitness. Owing to the importance of cellular resource allocation for understanding evolutionary trade-offs in bacterial metabolism, the cellular “protein economy” and its implications for bacterial growth laws have been studied extensively, albeit almost exclusively for heterotrophic organisms under stationary environmental conditions (1–7). For photoautotrophic organisms, including cyanobacteria, growth-dependent resource allocation is further subject to diurnal light–dark (LD) cycles that partition cellular metabolism into distinct phases. Recent experimental results have demonstrated the relevance of time-specific synthesis for cellular survival and growth (8–10). Nonetheless, the implications and consequences of a diurnal environment for the cellular resource allocation problem are insufficiently understood, and computational approaches hitherto developed for heterotrophic growth are not straightforwardly applicable to diurnal phototrophic growth (11).

Here, we propose a computational framework to quantitatively assess the optimality of diurnal resource allocation for phototrophic growth. We are primarily interested in the stoichiometric and energetic constraints that shape the cellular protein economy, that is, the relationship between the maximal growth rate and the relative partitioning of metabolic, photosynthetic, and ribosomal proteins during a full diurnal cycle. Going beyond established constraint-based analysis (12–15), we aim to obtain an ab initio prediction of emergent properties that arise from a narrow and well-defined set of parameters and assumptions about cyanobacterial growth, and to contrast these emergent properties with known and experimentally observed cellular behavior. To this end, we assemble and numerically evaluate an autocatalytic genome-scale model of cyanobacterial growth, based on a high-quality metabolic reconstruction of the cyanobacterium Synechococcus elongatus PCC 7942. Our model significantly improves upon previous computational analyses of diurnal phototrophic growth (14, 16–18) and takes recent developments in constraint-based analysis into account (19–22). Our approach is closely related to resource balance analysis (23, 24) and dynamic enzyme-cost flux balance analysis (25), as well as integrated metabolism and gene expression (ME) models (21, 26), but explicitly accounts for the properties of diurnal phototrophic growth.

Using S. elongatus PCC 7942 as a model system, our starting point is the fact that almost all cellular processes depend upon the presence of catalytic compounds, typically enzymes and other cellular macromolecules. The respective reaction rates are limited by the abundances of these catalytic compounds at any point in time. Therefore, a self-consistent description of cyanobacterial growth must take the synthesis of catalytic macromolecules into account. De novo synthesis of cellular macromolecules increases the capacity of the respective reactions but happens at the expense of available resources in terms of carbon precursors and energy—the timing and amount of macromolecular synthesis can therefore be described as a cellular resource allocation problem: What is the amount and temporal order of intracellular synthesis reactions that gives rise to maximal growth of a cyanobacterial cell in a diurnal environment? To study the respective stoichiometric and energetic constraints, we only require knowledge about the stoichiometry of the reaction network, as provided by a metabolic network reconstruction, as well as knowledge about the stoichiometric composition and catalytic efficiency of the macromolecules, quantities for which reasonable estimates exist. In the following, we therefore seek to assess the emergent properties of phototrophic diurnal growth, based only on best a priori estimates of model parameters. Our key results include (i) a computational framework that predicts the dynamics of intracellular synthesis reactions of a cyanobacterium under diurnal light conditions, (ii) model-derived emergent dynamics that are in qualitative agreement with experimental observations about metabolite partitioning during diurnal growth, (iii) an estimate of the maximal rate of cyanobacterial phototrophic growth that is close to observed experimental values, indicating a highly optimized metabolism, and (iv) a predicted optimal timing of diurnal glycogen accumulation that matches recent experimental observations and suggests a physiological role for circadian rhythms to coordinate metabolism.

Model Construction

A Computational Model of Cyanobacterial Growth.

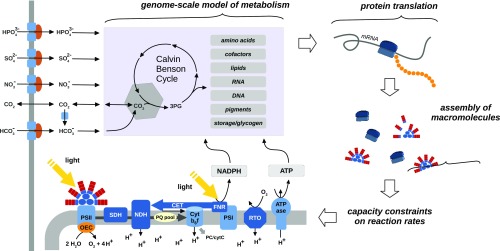
We assembled a constraint-based model of a self-replicating cyanobacterial cell based on a genome-scale metabolic reconstruction of the cyanobacterium S. elongatus PCC 7942. The genome-scale reconstruction provides a manually curated stoichiometric description of all metabolic reactions relevant to cellular growth: Photons are absorbed by light-harvesting antennae, the phycobilisomes, attached primarily to photosystem II (PSII). The energy derived from absorbed photons drives water splitting at the oxygen-evolving complex (OEC) and, via the photosynthetic electron transport chain (ETC), results in the regeneration of cellular ATP and NADPH. The ETC consists of a set of large protein complexes, PSII, the cytochrome b₆f complex (Cytb₆f), photosystem I (PSI), and ATP synthase (ATPase), embedded within the thylakoid membrane. The uptake of nutrients, in particular inorganic carbon, is described by simple uptake reactions and only constrained by the abundance of the respective transporters. Carbon cycling is not considered explicitly; the respective energy expenditure is considered as part of general maintenance. Inorganic carbon is assimilated via the Calvin–Benson cycle. The product of the ribulose-1,5-bisphosphate carboxylase/oxygenase (RuBisCO), 3-phosphoglycerate, serves as a substrate for the biosynthesis of cellular components, such as DNA, RNA, lipids, pigments, glycogen, and amino acids. The amino acids synthesized by the metabolic network serve as building blocks for structural, metabolic, photosynthetic, and ribosomal proteins. Key aspects of the model are depicted in Fig. 1. For a brief synopsis of the model and its parameters see Materials and Methods. The model encompasses a total of $465$ macromolecules and 1,112 reactions, including $645$ metabolic and exchange reactions and $616$ metabolic genes, as well as $467$ reactions describing the synthesis of macromolecules.

Fig. 1.

An autocatalytic computational growth model of S. elongatus PCC 7942. Energy and reducing agents are derived from the photosynthetic light reactions and drive the fixation of inorganic carbon via the Calvin–Benson cycle, as well as the subsequent synthesis of cellular macromolecules. The synthesis of precursors required for the assembly of macromolecules is described using a genome-scale stoichiometric reconstruction. The capacity of each metabolic reaction depends on the availability of the respective catalyzing enzymes. Enzymes are translated using their constituent amino acids; amino acids are themselves the products of metabolism. The abundances of all macromolecules relevant to cellular growth (metabolic enzymes, transporters, photosynthetic and respiratory protein complexes, phycobilisomes, and ribosomes) are time-dependent quantities that are governed by the respective differential mass balance equations. The time-dependent synthesis of cellular macromolecules constitutes a global resource allocation problem: We seek to identify the timing and amount of intracellular synthesis reactions such that the limiting resources are allocated to give rise to maximal growth over a full diurnal cycle. CET, cyclic electron transport; Cyt, cytochrome; FNR: ferredoxin–NADP⁺ reductase; NDH, NADPH dehydrogenase; OEC, oxygen-evolving complex; PQ, plastoquinone; RTO, respiratory terminal oxidase; SDH, succinate dehydrogenase.

Phototrophic Growth Is Autocatalytic.

To implement the stoichiometric and energetic dependencies of phototrophic growth, the rate of each reaction within the model is constrained by the abundances of the respective catalyzing macromolecules and their respective catalytic efficiencies. In particular, at any point in time, each metabolic reaction is constrained by the abundances of its catalyzing enzymes (or enzyme complexes) and their respective catalytic turnover numbers $k_{\mathrm{cat}}$. The latter values are sourced globally from databases (27, 28), as detailed in Materials and Methods. Protein synthesis is limited by the abundance of ribosomes and modeled according to general principles of peptide elongation, taking into account energy expenditure (one ATP and two GTPs per amino acid) and consumption of amino acids. Light absorption at PSII is constrained by the reported effective cross-section of phycobilisomes and depends on (variable) phycobilisome rod length (SI Appendix, Fig. S1). Detachment of phycobilisomes from PSII reduces energy transfer to the OEC. For simplicity, light absorption at PSI is assumed to take place in the absence of phycobilisomes, using an effective cross-section per PSI complex, and energy spillover from PSII is not considered (see SI Appendix for further discussion). For the photosynthetic and respiratory ETCs, maximal catalytic rates per protein complex are sourced from the literature and listed in Materials and Methods. We note that the constraint-based computational model only incorporates upper bounds for the maximal rates of the respective reactions and processes. The actual rates may be lower due to (unknown) fractional saturation.

Describing Dynamic Resource Allocation.

During a full LD cycle, the capacity constraints induced by the abundances of catalyzing macromolecules on reaction rates must be fulfilled at each point in time. Catalyzing macromolecules, however, can be synthesized de novo, depending on the availability of cellular resources (in terms of energy and carbon precursors), and may increase over time, and thereby increase the capacity of the respective reactions. In the following, we denote the abundances of macromolecules (metabolic enzymes, transporters, photosynthetic and respiratory protein complexes, phycobilisomes, and ribosomes) at time $t$ by the vector $M(t)$. The elements of $M(t)$ are time-dependent quantities that are governed by the respective differential mass balance equations. That is, any change in abundance is determined by the difference between synthesis and degradation reactions. We note that, in addition to the abundances of catalyzing macromolecules, $M(t)$ also contains the abundance of a set of noncatalytic macromolecules. Noncatalytic macromolecules, such as DNA and nonmetabolic proteins, do not constrain the capacity of any reaction within the model. Nonetheless, their synthesis is included as part of the energy expenditure related to cellular growth and is enforced as an additional constraint. See Materials and Methods for details. We are primarily interested in diurnal dynamics, and hence a timescale of several hours. Following the arguments of Rügen et al. (18) and Waldherr et al. (25), we therefore assume that internal metabolites are in quasi-steady state. The resulting computational model then consists of the stoichiometric network reconstruction, the synthesis reactions for cellular macromolecules, and the abundance constraints for noncatalytic macromolecules, as well as the capacity constraints induced by the elements of $M(t)$.

Implementing the Constraint-Based Model.

Using the computational model, we seek to identify solutions such that the timing and amount of synthesis reactions give rise to the highest possible growth rate over a full diurnal cycle. To this end, the model is supplemented with periodic boundary conditions for the macromolecules of the form

$$M(t_0+24\mathrm{h})=\mu \cdot M(t_0),$$ [1]

where $t_0$ is the initial time and $\mu$ is the multiplication factor corresponding to growth. The periodic boundary condition in Eq. 1 represents balanced growth in a periodic environment: We assume stationary diurnal experimental conditions, such that the average measured cellular composition per unit biomass after a full diurnal period is invariant. Eq. 1, in conjunction with the computational model and the objective to maximize growth in the form of the multiplication factor $\mu ⟶\max$, defines a self-consistent resource allocation problem for diurnal phototrophic growth of the cyanobacterium S. elongatus PCC 7942. To implement the problem, time is discretized using a Gauss implicit method (midpoint rule). After discretization of time, the problem is transformed into a sequence of linear optimization problems and solved to global optimality using a binary search. See Materials and Methods and SI Appendix for details about the computational methods.

We emphasize that we impose no further ad hoc constraints on the timing and amount of synthesis reactions. Likewise, our computational framework does not presuppose any knowledge of cellular regulatory mechanisms. Rather, and characteristic for constraint-based optimization, the solution is solely obtained based on the assumption that metabolism and macromolecular synthesis are organized such that the timing and amount of cellular synthesis reactions maximize growth in the form of the multiplication factor $\mu ⟶\max$. We note that the elements of $M$ at time $t_0$ are themselves an outcome of the resource allocation problem and not specified externally (except for noncatalytic macromolecules). In addition to the stoichiometric information required to construct the computational model, the only kinetic parameters are the catalytic efficiencies of enzymes, enzyme complexes, and other catalytic macromolecules. We argue that reasonable approximations of these quantities exist for almost all cellular macromolecules. Using this narrow and well-defined set of assumptions and parameters, we seek to derive the emergent properties of diurnal phototrophic growth. For details of the implementation and a discussion of the limits of applicability see Materials and Methods and SI Appendix.

Results

Growth Under Constant Light.

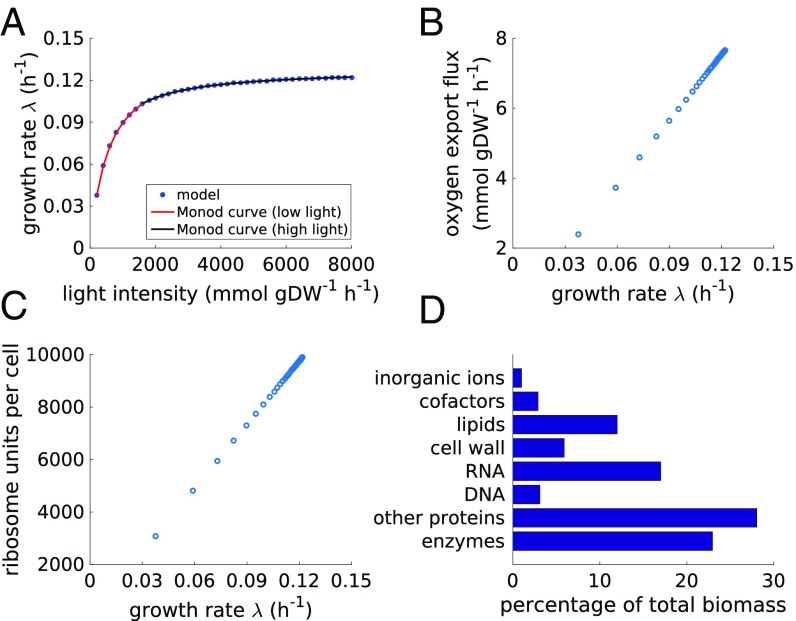
Before evaluating diurnal dynamics, we investigate light-limited growth under constant light. Our aim is to compare the results to conventional flux balance analysis (FBA) and thereby to verify the consistency of the model. Solving the global resource allocation problem, we obtain the multiplication factor $\mu$ and the growth rate $\lambda =\log (\mu )/24\mathrm{h}$ as a function of the light intensity, as well as the cellular composition for different growth rates. Key results are shown in Fig. 2. To compare model properties with previous results obtained using conventional FBA, we use a reference light intensity $I=150\hspace{0.17em}\mathrm{\mu }\mathrm{mol}$ of photons ${\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2}$ resulting in the absorption of $15.9\hspace{0.17em}\text{mmol}$ of photons per gram dry weight (gDW) per hour, a growth rate of $\lambda =0.03\hspace{0.17em}{\mathrm{h}}^{-1}$ (multiplication factor $\mu \approx 2$), and an oxygen evolution rate of $1.92\hspace{0.17em}\mathrm{mmol}\cdot {\mathrm{gDW}}^{-1}\cdot {\mathrm{h}}^{-1}$. These values are in quantitative agreement with values previously estimated using FBA (13, 14). In particular, performing a conventional FBA on the metabolic reconstruction of S. elongatus PCC 7942 using a static biomass objective function (BOF) and a light uptake of $15.8\hspace{0.17em}\mathrm{mmol}$ of absorbed photons ${\mathrm{gDW}}^{-1}\cdot {\mathrm{h}}^{-1}$ results in an oxygen evolution rate of $1.92\hspace{0.17em}\mathrm{mmol}\cdot {\mathrm{gDW}}^{-1}\cdot {\mathrm{h}}^{-1}$ and a growth rate of $\lambda =0.03\hspace{0.17em}{\mathrm{h}}^{-1}$. We note that quantitative agreement between results obtained from the global resource allocation problem and conventional FBA cannot be expected a priori, as the former are also based on capacity constraints induced by kinetic parameters (the catalytic efficiencies) whose values are globally sourced from databases (Model Construction). In contrast to the static preassigned BOF used in FBA, the cellular composition of the autocatalytic model is an emergent result of the global resource allocation problem (Fig. 2D). The allocated abundance of catalytic macromolecules is in quantitative agreement with previously reported BOFs (13, 14).

Fig. 2.

Model properties obtained for balanced growth under constant light. (A) The maximal growth rate $\lambda$ as a function of light intensity. The growth rate $\lambda$ is consistent with a Monod growth law (see also SI Appendix, Fig. S2). (B) Oxygen evolution as a function of the growth rate $\lambda$. (C) Ribosome content per cell as a function of the growth rate $\lambda$, assuming a cell dry mass of $1.5\mathrm{pg}$. (D) The cellular composition for a light intensity of $150\mu \mathrm{mol}$ of photons ${\mathrm{m}}^{-2}\cdot {\mathrm{s}}^{-1}$.

Adaptations to Different Light Intensities.

When solving the computational model for different (but constant) light intensities, the growth rate, as well as the oxygen evolution rate, increases with increasing light intensity (Fig. 2A and B). We note that the ratio between light intensity and absorbed photons depends on the assumed maximal effective cross-section of PSII, reported to be ${\sigma }_{\mathrm{PSII}}\approx 1\hspace{0.17em}{\mathrm{nm}}^2$ (29). The results shown in Fig. 2A indicate that the reported value significantly underestimates the actual effective cross-section (with no further impact on model results; see also SI Appendix). Similar to results obtained for models of heterotrophic growth (1, 2, 7), the relative amount of ribosomes linearly increases with increasing growth rate (Fig. 2C). We observe that growth as a function of light saturates at a growth rate of ${\lambda }_{\max }=0.1281\hspace{0.17em}{\mathrm{h}}^{-1}$ (multiplication factor $\mu \approx 18$, doubling time $T_D\approx 5.4\hspace{0.17em}\mathrm{h}$), estimated using a Monod growth equation (Fig. 2A). The maximal doubling time obtained from the autocatalytic model is therefore slightly lower but still within the range of the fastest published doubling time of S. elongatus PCC 7942, reported as $T_D=4.9\hspace{0.17em}\mathrm{h}\pm 0.7\hspace{0.17em}\mathrm{h}$ ($\lambda \approx 0.14\hspace{0.17em}{\mathrm{h}}^{-1}$) by Yu et al. (30).

Sensitivity Analysis.

Because the computational model primarily provides an upper bound for the maximal specific growth rate, we performed a sensitivity analysis of growth rate as a function of estimated parameters, in particular with respect to the catalytic efficiencies $k_{\mathrm{cat}}$. Although the sensitivity with respect to the catalytic efficiencies of individual enzymes is low (SI Appendix, Figs. S3–S5), a major determinant of maximal growth rate is the assumed ratio of noncatalytic proteins (SI Appendix, Figs. S6–S7). These proteins fulfill no immediate catalytic role within our model, and their synthesis is enforced with a fixed quota relative to catalytic proteins (Materials and Methods). Based on recent proteomics data for slow-growing cells of S. elongatus PCC 7942 (31), the relative quota of noncatalytic proteins was determined to be $55$% of total protein mass. No experimental estimates exist for fast-growing cells. If the true ratio for fast-growing cells is assumed to be $\sim 20$%, the resulting growth rate is ${\lambda }_{\max }\approx 0.20\hspace{0.17em}{\mathrm{h}}^{-1}$, corresponding to a doubling time of $T_{\mathrm{D}}=3.5\hspace{0.17em}\mathrm{h}$, and slightly exceeding the reported maximal growth rate of S. elongatus PCC 7942.

A Day in the Life of S. elongatus PCC 7942.

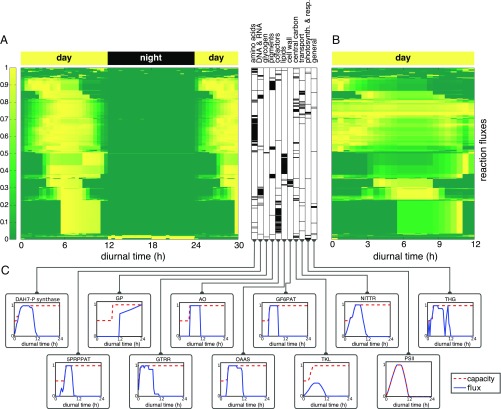
Going beyond constant light conditions, our main interest is a solution of the global resource allocation problem for diurnal light. The light intensity is modeled as a sinusoidal half-wave with a peak value of $600\mathrm{\mu }\mathrm{mol}$ of photons ${\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2}$, except as otherwise noted. The computational objective is to maximize growth in the form of the multiplication factor $\mu \to \max$ in Eq. 1, as detailed in Model Construction. We seek to identify a time-dependent flux pattern (or patterns) that maximizes the overall growth of the cell during a diurnal cycle. Growth rates and overall cellular composition (shown in SI Appendix, Fig. S8) depend on the peak light intensity; the results (SI Appendix, Figs. S9 and S10) are qualitatively similar to the case of constant light already depicted in Fig. 2. The numerical results are robust with respect to (small) changes in parameters. Fig. 3 shows the resulting metabolic flux pattern for a reference day as a function of diurnal time (Fig. 3A), and the relative flux values normalized to the RuBisCO carbon fixation flux (Fig. 3B), as well as selected examples of fluxes corresponding to different functional categories (Fig. 3C).

Fig. 3.

A solution of the time-dependent resource allocation problem over a full diurnal cycle. (A) Metabolic fluxes as a function of diurnal time. All fluxes are normalized to the unit interval. To indicate the periodicity of the solution, the beginning of the subsequent light period is also shown (hours 24 to 30). The global cellular resource allocation problem gives rise to a highly coordinated metabolic activity over a diurnal period. Metabolism is organized into distinct temporal phases, ranging from synthesis of amino acids and pigments, to synthesis of lipids, DNA/RNA, and peptidoglycan, to synthesis of cofactors. The functional category of each flux is indicated by a black bar in the table adjacent to the plot. (B) Excerpt of the light period. The flux values are normalized to the carbon fixation flux (RuBisCO) and scaled to the unit interval. Ordering is identical A. Normalization to RuBisCO flux emphasizes relative carbon partitioning rather than the dependence of metabolic fluxes on total light input. (C) Selected metabolic fluxes and their corresponding enzymatic capacity bounds. Dashed red lines indicate the respective enzymatic capacities (proportional to enzyme amount). Photosynthesis and reactions of central metabolism closely follow light availability, as exemplified by the reactions of the Calvin–Benson cycle (e.g., transketolase TKL) and the ETC (e.g., PSII). Metabolic activity during the early light period is dominated by amino acid synthesis. Shown is DA7-P for the synthesis of aromatic amino acids, the associated nitrate uptake (NITTR), and synthesis of pigments (e.g., GTRR toward chlorophyll). At later times, metabolic activity shifts to DNA and RNA synthesis (e.g., purine synthesis by 5PRPPAT) and lipid synthesis (e.g., OAAS), followed by the synthesis of peptidoglycan (e.g., GF6PAT) and cofactors (such as L-Asp-O toward nicotinamide adenine dinucleotide). During the night, glycogen is used via the glycogen phosphorylase (GP). We note that synthesis of enzymes can significantly precede reaction flux (see subplot for GP). Abbreviations are as follows: DAH7-P synthase, 3-deoxy-D-arabino-heptulosonate 7-phosphate synthetase; GP, glycogen phosphorylase; AO, aspartate oxidase; GF6PAT, glucosamine-fructose-6-phosphate aminotransferase; NITTR, nitrate transporter; THG, transhydrogenase; 5PRPPAT, 5′-phosphoribosylpyrophosphate amidotransferase; GTRR, glutamyl-tRNA reductase; OAAS, 3-oxoacyl-ACP synthase; and TKL, transketolase.

The solution of the global cellular resource allocation problem exhibits a highly coordinated metabolic activity over a diurnal period: Oxygenic photosynthesis is active during the light period. Inorganic carbon is imported and assimilated via the Calvin–Benson cycle (anabolism); respiratory components (catabolism) are active during the dark period. We highlight two results from the computational model. First, we observe that growth is dynamic. The instantaneous growth rate follows a specific pattern over the light period. The growth rate is low in the early morning, increases over the course of the light period, and decreases again toward dusk (SI Appendix, Fig. S11). Such a dynamic growth rate over a diurnal cycle was recently reported for the cyanobacterium Synechocystis sp. PCC 6803 (32), and is also observed when the sinusoidal light input is replaced by a square-wave LD cycle that is typically used in experiments (SI Appendix, Fig. S11). Second, we observe that growth is exclusive to the light period. During the night phase, glycogen is mobilized and used for cellular maintenance, serving as a substrate for cellular respiration via the oxidative pentose phosphate pathway (OPPP) and ultimately cytochrome C oxidase. Although this observation is unsurprising given the known data on S. elongatus 7942 and other (nonnitrogen fixing) cyanobacteria, we emphasize that cessation of metabolic activity during darkness is not self-evident but is already the result of a cellular trade-off: Limited metabolic activity at night implies that available enzymatic and ribosomal capacity is not used during the night, resulting in idle enzymatic capacity. To avoid or reduce the timespan of such idle capacity would require the synthesis of additional storage compounds before the dark period. Increased storage synthesis, however, entails additional enzymatic costs for the synthesis and utilization of glycogen. To demonstrate this trade-off, we conducted an in silico experiment using an artificially reduced cost for the enzymatic capacity required for glycogen synthesis and utilization. The synthesis costs of the respective enzymes were neglected. In this case, cellular synthesis also prevails during the night phase, driven by an increased amount of stored glycogen at dusk (SI Appendix, Fig. S12). The in silico simulation experiment, however, also reveals that the amount of necessary additional storage capacity is significant: The high storage requirements explain why such behavior is not observed for the original parameters.

Metabolite Partitioning During Diurnal Growth.

The results obtained from the global resource allocation problem can be compared with known experimental observations about metabolite partitioning during diurnal growth. Although no ¹³C flux measurements over a full diurnal cycle have been conducted yet, several studies have investigated the transcriptome, proteome, and physiology of S. elongatus PCC 7942 and other cyanobacteria over a full 24-h diurnal cycle (9, 31, 33, 34). Published transcriptome studies of cyanobacteria typically show global rhythms in gene expression, including a significant reduction of the transcriptional output during the dark period (33, 35, 36). Although environmental LD cycles are sufficient to drive transcriptional and metabolic rhythms, metabolic rhythms are also influenced by the cyanobacterial circadian clock and persist in (previously entrained) cultures under constant light (9, 37, 38). Several transcriptomic studies described a broad temporal order of diurnal growth, typically distinguishing between genes peaking at dawn versus genes peaking at dusk (9, 35). The former set includes genes associated with the Calvin–Benson cycle, as well as genes associated with amino acid synthesis; the latter set includes genes associated with glycogen mobilization and OPPP (9). The observed temporal order is consistent across different cyanobacterial strains: For the cyanobacterium Synechocystis sp. PCC 6803, Saha et al. (34) report an upregulation of PSI and PSII transcripts, genes for amino acid metabolism, and genes from the Calvin–Benson cycle at the beginning of the light period, whereas essential genes for glycogen catabolism showed upregulation in the dark period. Behrenfeld et al. (39) report that metabolism is dominated by amino acid synthesis between sunrise and noon in a synchronized culture of Prochlorococcus (strain PCC 9511).

The computational results of the global resource allocation problem, shown in Fig. 3, closely replicate this temporal order: Metabolism at dawn is dominated by amino acid synthesis and synthesis of pigments. Photosynthetic activity and reactions of central metabolism closely follow light availability. Later within the light period, metabolic activity shifts to DNA and RNA synthesis, lipid synthesis, and the synthesis of peptidoglycan and cofactors. We note that synthesis of enzymes can precede reaction flux, for example, for the glycogen phosphorylase (plot GP in Fig. 3C). Overall, the differences in activity between light and dark metabolism, as well as the initiation of amino acid metabolism at dawn, and storage metabolism (see The Dynamics of Glycogen Accumulation), are in qualitative agreement with reported metabolite partitioning during diurnal growth. Nonetheless, we must note that several caveats limit a direct comparison of individual reaction rates to currently available data. Current transcriptomics data are predominantly measured under constant light conditions using previously entrained (synchronized) cultures. Such measurements are motivated by the aim to discern the effects of the circadian clock versus light-driven regulation and conceal actual resource allocation. Furthermore, gene expression is not necessarily indicative of metabolic flux. Measurements also typically involve slow-growing cultures, with reduced requirements for de novo protein synthesis. Correspondingly, proteomics measurements typically exhibit strongly reduced diurnal variability (31, 40) compared with transcriptomics data. The qualitative agreement of results obtained from the computational model with transcriptomics data may therefore provide further incentives for experimental studies to focus on de novo protein synthesis in fast growing cultures, and thereby to enable a quantitative comparison of the timing of protein synthesis with predictions obtained from models of cellular resource allocation.

The Dynamics of Glycogen Accumulation.

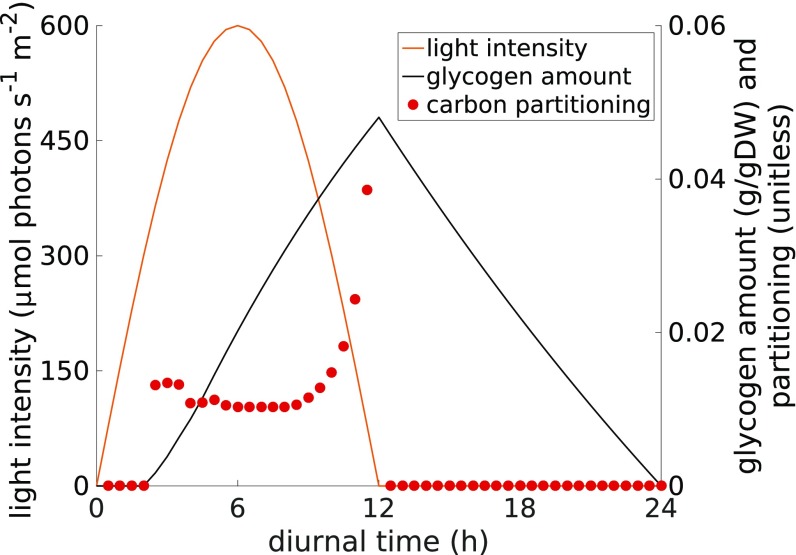
Glycogen is the main storage compound in cyanobacteria. Cells accumulate glycogen during the light phase and mobilize it as a source of carbon and energy during the night. It was recently shown that the timing of glycogen accumulation is under the tight control of the cyanobacterial circadian clock, and disruption of the clock results in altered glycogen dynamics (9). We therefore investigate the dynamics of glycogen accumulation in the context of the global resource allocation problem. We note that our simulation does not impose any ad hoc constraints on the kinetics and timing of glycogen synthesis. Rather, accumulation of glycogen is a systemic property that emerges as a consequence of optimal resource allocation. Fig. 4 shows the time course of glycogen accumulation obtained from the global resource allocation problem over a diurnal period, as well as the predicted carbon partitioning ratio during the light period. After a brief lag phase at dawn, stored glycogen increases linearly within the light period and peaks at dusk. The constant rate of glycogen accumulation through the light period is in excellent agreement with recent data from S. elongatus PCC 7942 (9) and Synechocystis sp. PCC 6803 (34). To verify the robustness of our approach, and because most experimental studies use a square-wave light intensity rather than a sinusoidal function, we also investigate glycogen accumulation using a square-wave light function, resulting in a similar functional form (SI Appendix, Fig. S13). We emphasize that the linear slope is not self-evident but emerges as a trade-off between at least two conflicting objectives: (i) minimizing carbon withdrawal during the early growth period when assimilated carbon could rather be used to increase enzymatic and ribosomal capacity versus (ii) minimizing enzymatic capacity for storage (glycogen) synthesis. The former objective favors withdrawal of carbon late during the light period, whereas the latter objective favors constant withdrawal throughout the light period using a glycogen synthesis pathway with low capacity. To the best of our knowledge, the initial lag phase has not yet been noted experimentally, but might provide a stimulus for further experimental evaluation.

Fig. 4.

Timing and dynamics of glycogen accumulation over a full diurnal cycle. After a brief lag phase, cells accumulate glycogen during the light period and mobilize it as a source of carbon and energy during the night. The model makes no assumptions about the specific timing and amount of glycogen accumulation. Rather, glycogen accumulation emerges as a trade-off between conflicting objectives. Shown are absolute amounts of stored glycogen per gram dry weight, as well as the carbon partitioning. Carbon partitioning is defined as the ratio, on a per carbon basis, between the flux toward glycogen synthesis and the carbon assimilation (RuBisCO) flux.

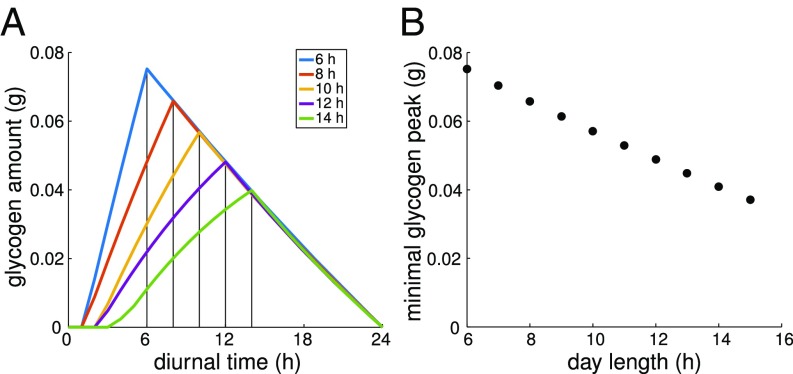
Glycogen Accumulation for Variable Day Lengths.

To highlight glycogen accumulation as a systemic property, we also investigate the minimal amount of accumulated glycogen for different photoperiods. Fig. 5A shows the resulting time courses for different lengths of day versus night periods. Fig. 5B shows the minimal amount of glycogen required at the end of the light period. The overall form of glycogen accumulation remains largely identical. We note, however, that the amount of glycogen required at dusk exhibits a certain plasticity. First, if the night period is doubled, slightly less than twice the glycogen is required to sustain night metabolism. Second, although the minimal amount of glycogen required at dusk exhibits a lower bound, cells can accumulate more glycogen with no discernible effects on overall growth yield. In this case, certain synthesis tasks, in particular, lipid synthesis, can be relegated to the end of the night period, thereby requiring less enzyme capacity during the day at the expense of an increased glycogen storage at dusk (SI Appendix,Figs. S14–S16).

Fig. 5.

(A) Time courses of glycogen accumulation for different lengths of the light period (day length). (B) Minimal glycogen requirements for different day lengths. Peak glycogen content is always observed at dusk. Although the minimal amount of glycogen required at dusk exhibits a lower bound, cells can accumulate more glycogen with no discernible effects on overall growth yield. Higher glycogen at dusk implies increased metabolic activity shortly before dawn at the expense of slightly reduced synthesis reactions during the light period.

Discussion

Phototrophic growth under diurnal conditions requires a precise coordination of metabolic processes, and the resulting constraints and trade-offs are challenging to describe using constraint-based analysis and conventional FBA (20). Here, we have developed a genome-scale model that allowed us to investigate the stoichiometric and energetic constraints of diurnal phototrophic growth in the context of a global resource allocation problem. Building upon previous works (1, 6, 15, 18, 23, 25, 26), our approach is based on the fact that growth is inherently autocatalytic: The cellular machinery to sustain metabolism is itself a product of metabolism. Our foci have therefore been the net stoichiometric and energetic implications of diurnal growth on the de novo synthesis of proteins and other cellular macromolecules. Our aim was an ab initio prediction of optimal diurnal resource allocation: How are metabolism and the synthesis reactions of cellular macromolecules organized over a full diurnal cycle? What is the optimal timing of glycogen accumulation during the light phase? From the perspective of cellular resource allocation, these questions can be asked without detailed knowledge about regulatory mechanisms and their corresponding kinetic parameters. Rather, similar to conventional FBA (26), predictions are obtained based on the assumption that the synthesis reactions of metabolism are organized such that their timing and magnitude result in maximal growth over a full diurnal cycle, motivated by the fact that a similar optimization might have taken place during evolution (11).

The results obtained from the computational model allowed us to pinpoint several energetic trade-offs and constraints related to diurnal growth. Overall, the model-derived time courses are in qualitative agreement with previous experimental observations about flux partitioning in S. elongatus PCC 7942 and other cyanobacteria: Growth is dynamic and takes place during the light phase. Carbon fixation and the reactions of central metabolism largely follow light availability. The synthesis reactions for amino acids and pigments dominate metabolism during the early light period, whereas other synthesis reactions peak at later time points. In the absence of light, almost all metabolic activity ceases, and cellular metabolism is dominated by respiratory activity.

Although well known experimentally, we emphasize that, in the computational model, the cessation of metabolic activity during darkness is a consequence of a trade-off between the cost of unused enzymatic capacity during darkness and the cost of additional storage that would be required for synthesis reactions to take place in the absence of light. In this respect, the function of the storage compound glycogen is analogous to a cellular battery or capacitor: We expect that, if glycogen synthesis and utilization did not entail additional enzymatic (and other) costs, synthesis reactions would continue during the night. Within our computational framework we tested this hypothesis using an in silico experiment with modified enzyme synthesis costs.

For our reference parameters, the predicted timing characteristics of glycogen accumulation did match recent experimental observations (9, 34). The emergent dynamics of glycogen accumulation also points to a role of the circadian oscillator to modulate metabolite partitioning during growth. It has been shown recently that the circadian oscillator controls the timing of glycogen accumulation such that accumulation occurs at a constant rate through the light period and that a disrupted circadian clock results in an increased glycogen accumulation early in the day (9). The disrupted pattern of glycogen accumulation is, indeed, significantly different from the optimal profile predicted here. A manifest hypothesis is therefore that cyanobacterial growth is organized according to a temporal program that evolved to maximize growth in a periodic environment, and that the circadian clock is a regulatory circuit that modulates the transcriptional program of the cell to approach this metabolic optimum. Misalignments between metabolism, clock, and environmental cycles will therefore result in impaired growth, as has recently been observed (10).

From a more general perspective, we consider our approach to be a suitable framework to study metabolic optimality in time-dependent and fluctuating environments. In this respect, cyanobacterial phototrophic growth is an ideal test case because the regular and periodic environmental changes allow us to formulate the global resource allocation problem in a well-defined way. As yet, similar efforts to investigate proteome allocation have primarily focused on heterotrophic organisms in time-independent environments (21, 24, 41). These recent analyses reveal several interesting differences with respect to our results. In particular, the model-derived (maximal) growth rates for Escherichia coli corresponding to an optimally allocated proteome were consistently higher than the experimentally measured rates. In the model, the latter could be supported with $95\%$ less proteome under certain conditions (21). This finding was attributed to cellular “bet hedging” in (generalist) wild-type E. coli against unknown environmental challenges. Furthermore, significant protein production without detectable growth benefit was observed experimentally (21, 41). In contrast, the model-derived maximal growth rates reported here were within the range of the (maximal) growth rates observed for S. elongatus PCC 7942 [even though actual growth rates observed in a laboratory are typically significantly slower (42)]. Because the resource allocation problem only provides upper bounds for the growth rate, based on the assumption of an optimally allocated metabolism, and does not incorporate several detrimental factors, such as light damage and possible photoinhibition, the close correspondence between observed and model-derived values suggests that cyanobacterial metabolism operates close to optimality, at least in experiments designed for rapid growth.

We emphasize that the model-derived maximal growth rates should be interpreted as an order-of-magnitude approximation, not as precise estimates. For example, a major unknown factor is the relative amount of noncatalytic proteins, reported to be up to 55% of total protein for slow-growing cells (31). We hypothesize that, for fast-growing cells, this percentage is considerably lower. The impact of noncatalytic proteins as (condition-specific) niche-adaptive proteins on the maximal growth rate was already discussed by Burnap (6). The question to what extent slow-growing cyanobacteria perform cellular bet hedging similar to E. coli and how the allocation of proteome to non-growth-related processes correlates with resistance to adverse environmental and (sudden) stress conditions remains a timely question for further research, with implications for biotechnological strain design.

In future iterations, we anticipate that our computational model can be significantly improved upon and is applicable beyond the questions considered here. We envision a stoichiometric whole-cell model, with a focus on energetic constraints, that allows us to assess the optimality of metabolic strategies in diverse environments. Of particular interest are the energetic implications of carbon cycling (43), light damage and its repair, and the coupling of metabolic processes to the cell cycle, as well as the temporal segregation of incompatible metabolic processes, such as nitrogen fixation in certain cyanobacteria (44). We conjecture that global resource allocation models, together with the methodology described here, will allow us to assess the condition-dependent cost and benefit of individual genes (45) in the context of a growing cell, and thereby facilitate the study of metabolic adaptations and metabolic diversity of cyanobacteria (46) with the ultimate aim of understanding the limits of phototrophic growth in complex environments.

Materials and Methods

Constraint-Based Analysis and Metabolic Optimality.

Constraint-based methods, such as FBA, are highly successful computational tools for understanding the organization of microbial metabolism (11, 13, 14, 26). Their predictive power is based on the fact that fluxes through enzymatic reactions are not independent but are subject to mass balance constraints. Specific predictions are obtained by assuming the metabolic fluxes are organized such that they fulfill certain evolutionary optimality principles. The most common optimality principle is to maximize a BOF. That is, FBA seeks to identify a (steady-state) flux solution that maximizes the growth yield of a cell by maximizing the synthesis flux toward a set of predefined biomass components given by the BOF. Predictions are therefore not obtained based on knowledge about cellular regulation but based on how metabolism ought to adapt if the assumed evolutionary optimality principle holds. See Westermark et al. (11) for a recent review. Along similar lines, our approach seeks to maximize the growth yield of a cell over a full diurnal cycle by maximizing the multiplication factor $\mu \to$ max in Eq. 1. In contrast to conventional FBA, and following recent developments in constraint-based analysis (18, 23–26), the capacity constraints of individual reactions are explicitly part of the model.

Metabolic Network Model.

All simulations are based on a genome-scale conditional FBA (cFBA) model (18). The model is derived from a genome-scale metabolic reconstruction of the cyanobacterium S. elongatus PCC 7942. The reconstruction covers $616$ genes and consists of $662$ metabolic reactions and $539$ metabolites. The reconstruction process was analogous to previous reconstructions (12, 14, 15). The original metabolic network reconstruction is provided together with the simulation data in an online repository (see SI Appendix for details).

Model Components and Their Role.

The computational model consists of three types of components: steady-state metabolites, noncatalytic components, and components with catalytic function. The noncatalytic components are denoted as “quota” components and fulfill no explicit catalytic function within our model but are required for the functioning of the cell. Their synthesis is enforced (using a fixed quota) and contributes to the overall energy and carbon expenditure of growth. We note that, different from ME models (26), we do not aim for a mechanistic representation of processes such as transcription, translation, or assembly of macromolecules. Rather, we focus on overall energetic and stoichiometric constraints on diurnal time scales of several hours. Faster processes are not considered.

Components with Catalytic Activity.

Enzymes, ribosomes, and several other macromolecules constitute components with catalytic function. For each of these components, a synthesis reaction is implemented. Macromolecules (e.g., photosystems) assemble once all constituent compounds (amino acids or protein subunits) are available. All components are synthesized using their molecular stoichiometry, as derived from the amino acid sequence. Special attention is paid to the stoichiometries of the photosynthesis and respiration complexes, such as the photosystems or the ATPase. The respective stoichiometries are listed in SI Appendix, Tables S1–S8. The amounts of all components with catalytic activity are time-dependent quantities, and, at each point in time, their amount provides an upper bound to the rates of the reactions they catalyze. We impose no further constraints on the timing of synthesis and abundance of catalytic macromolecules.

Capacity Constraints Imposed by Catalytic Macromolecules.

Assuming that a component (e.g., an enzyme) $e$ catalyzes a reaction $r$, the model implements the capacity constraint

$$v_r(t)\le M_e(t)\cdot k_{ca{t}_e}^r\mathit{\text{,}}\forall t\ge 0\mathit{\text{,}}$$ [2]

where $v_r(t)$ denotes the flux through reaction $r$ at time $t$, $M_e(t)$ denotes the concentration of enzyme $e$ at time $t$, and $k_{ca{t}_e}^r$ is the turnover number of the enzyme $e$ for reaction $r$. The capacity constraint provides an upper bound for the flux through a reaction; the actual flux may be lower due to incomplete saturation or cyclic flux (47). Although an approximation, the upper bound in Eq. 2 is supported by a recent large-scale evaluation of absolute metabolite concentrations in E. coli (48). The study showed that the large majority of metabolite concentrations exceed the corresponding $K_{\mathrm{M}}$ values, often more than tenfold (with the notable exception of central metabolism), indicating a trend toward saturation of most enzyme active sites (48). In case several reactions are catalyzed by the same component or enzyme, the sum of their fluxes, weighted by the turnover rates, is bound by the enzyme amount. The capacity constraint holds analogously for all macromolecules, including the components of the ETC and ribosomes.

Noncatalytic Quota Components.

Main noncatalytic molecules, denoted as quota components, are vitamins, several cofactors, lipids, cell wall, inorganic ions, DNA, and RNA, as well as nonmetabolic proteins. These components have to be produced at the same rate as catalytic proteins and macromolecules, although they do not reinforce the autocatalytic cycle. We enforce the synthesis of noncatalytic quota components by imposing an initial amount proportional to their fraction of the whole cell weight, and we require balanced growth (Eq. 1). Noncatalytic (quota) proteins compete with catalytic proteins for ribosomal capacity.

Steady-State Components.

Turnover of metabolic reactions is considerably faster than the de novo synthesis of proteins. Following earlier work (18, 25), we therefore assume that internal metabolites are at quasi-steady state. The concentrations of internal (nonexchange) metabolites are not explicitly represented in Eq. 1, and the metabolic network is assumed to be balanced at all time points. Similar to conventional FBA, we neglect dilution by growth of internal metabolites.

Turnover Rates.

The turnover rates used in the capacity constraint Eq. 2 are sourced from the Braunschweig Enzyme Database (BRENDA) (27). We computationally retrieved all wild-type values from all organisms for each enzyme and assigned the median of the corresponding retrieved values as the turnover number of the respective enzyme. For enzymes with no turnover numbers available, we followed ref. 49 and assigned the median of all retrieved turnover numbers. Turnover numbers for the seven macromolecules of ETC were sourced from the primary literature and are listed in Table 1. The ribosomal capacity is assumed to be $15$ amino acids per second (55).

Table 1.

Parameters for the cFBA model

Compound	Catalytic efficiency	Ref.
PSI	500 s−1	50
PSII	1,000 s−1	50
NDH-1	130 s−1	51
Cytb6f	200 s−1	50
Cyt c oxidase	670 s−1	52
SDH	1,300 s−1	53
ATPase	1,000 s−1	54
Ribosome	15 amino acids/s	55
Enzymes	Various	27, 28

Solving the global resource allocation problem requires knowledge of the catalytic turnover numbers of macromolecules. All values are sourced from the primary literature. Cyt, cytochrome; Cytb6f, cytochrome b6f complex.

Maintenance Requirements.

In addition to the processes explicitly included within the model, cells have an additional energy expenditure, usually denoted as “maintenance” in FBA models. Along similar lines, our model includes a basal maintenance constraint that hydrolyzes ATP with a rate of 0.13 $\mathrm{mmol}\cdot {\mathrm{gDW}}^{-1}\cdot {\mathrm{h}}^{-1}$.

Optimization Objective and Solving Routine.

The objective of the resource allocation problem is to maximize the multiplication factor $\mu \to$ max in Eq. 1. The dynamic variables are discretized in time using the implicit midpoint rule numerical scheme. Discretization yields a set of linear constraints that, together with the steady-state, capacity, production, and balanced growth constraints, form a quadratically constrained program (linear for any given $\mu$).

To obtain the optimal resource allocation that maximizes $\mu$, a binary search over the growth rate $\mu$ is performed, and, in each step, a new linear program is solved, as described in ref. 18. Biologically speaking, if the cell can grow at rate ${\mu }_1$ and at a rate ${\mu }_2\ge {\mu }_1$, then it should also be able to grow at any growth rate ${\mu }_c$, with ${\mu }_1\le {\mu }_c\le {\mu }_2$. Thus, a binary search is an appropriate algorithm.

From a numerical perspective, the linear programs solved within the binary search are ill-conditioned. Even when the constraint matrices are suitably scaled, standard commercial solvers cannot be used due to lack of numerical precision. Instead, SoPlex (56–58), a more stable open-source solver that can perform iterative refinement of the solution, has been used. Further details of the implementation are provided in SI Appendix.