DIELECTROPHORESIS ASSISTED LOADING AND UNLOADING OF MICRO-WELLS FOR IMPEDANCE SPECTROSCOPY

Abstract

Dielectric spectroscopy (DS) is a non-invasive, label-free, fast, and promising technique for measuring dielectric properties of biological cells in real time. We demonstrate a microchip that consists of electro-activated micro-well arrays for positive dielectrophoresis (pDEP) assisted cell capture, DS measurements, and negative dielectrophoresis (nDEP) driven cell unloading; thus, providing a high throughput cell analysis platform. To the best of our knowledge, this is the first microfluidic chip that combines electro-activated micro-wells and DS to analyze biological cells. Device performance is tested using Saccharomyces Cerevisiae (yeast) cells. DEP response of yeast cells is determined by measuring their Clausius-Mossotti (CM) factor using biophysical models in parallel plate micro-electrode geometry. This information is used to determine the excitation frequency to load and unload wells. Effect of yeast cells on the measured impedance spectrum was examined both experimentally and numerically. Good match between the numerical and experimental results establishes the potential use of the micro-chip device for extracting sub-cellular properties of biological cells in a rapid and non-expensive manner.

1. Introduction

Dielectric spectroscopy (DS) is a non-invasive, label-free, fast, and promising technique for measuring type, size, and dielectric properties of biological cells in real time [1–6]. This technique involves application of a small test voltage and measurement of AC current in a wide range of frequencies; providing an impedance spectrum [7, 8]. Biophysical models, such as the single shell model, can be used to analyze the measured impedance spectrum. The analysis can yield sub-cellular electrical properties, enabling characterization of biological cells [9]. It has been shown that membrane capacitance and cytoplasm conductivity becomes dominant on impedance at frequencies around 1 MHz and 10 MHz, respectively [10]. Ability to perform DS measurements on a micro-chip enables real-time determination of cell responses to external stimuli such as variations in pH [11], osmolality [12], and even drug uptake [13].

Single cell dielectric spectroscopy can provide information from cells without considering cell-cell interactions. However, biological cells do interact with neighboring cells in their medium. As an example, a single yeast cell is affected by the presence of the other cells in wort (the liquid extracted from the mashing process) in a fermentation process. In this interaction, for instance, release of growth factors, change in the local pH, concentration of the waste products, and the local temperature are affected. As a result, measuring a small population of biological cells can mimic the cell behavior in real-world applications more effectively, provide a statistically significant result, and lead to better understanding of physical and chemical responses of cells [14]. In order to have a reliable set of cell dielectric parameters from an impedance measurement, volume fraction of cells should be around 10%. Considering this volume fraction range, the number of 5 μm radius cells in 1 ml of cell suspension is around 200 million. Culturing this many cells is impractical, especially for primary cells. Therefore, there is a need for miniaturizing dielectric spectroscopy device dimensions to reduce the required number of cells [15]. Microfluidic platforms operating with nano and microliters of samples are ideal candidates for miniaturized dielectric spectroscopy. However, such devices need to decrease the sample volume while maintaining the cell volume fraction above a desired threshold value.

In order to collect cells and particles in a confined geometry, several cell-handling methods, including optical tweezers [16–19], chemical patterning [20, 21], nano-electrode arrays [22–24], micro-well arrays [25–31], and combination of the aforementioned methods [32], have been developed. Especially, micro-well arrays enable large scale arraying and high throughput measurements [33, 34]. Many researchers used gravitational force to load cells inside the micro-wells [35, 36]. As an illustration, Yuan et al. collected a mixture of human glioma and murine fibroblast cells in 150,000 cylindrical micro-wells, and reported that more than 50% of the micro-wells were filled with the cells [37]. The main problem in gravity based micro-well array loading is its low cell trapping efficiency and long trapping time. In order to overcome this problem, additional cell capture mechanisms are required. A large number of methods have been developed to capture cells more effectively including magnetic [38], optical [16], hydrodynamic [39], acoustic [40], and electrical forces [41]. Using electrical forces to capture cells has been utilized frequently due to its simplicity, high selectivity, contact free approach, and its potential to be integrated into microfluidic systems. Combination of micro-well arrays with dielectrophoretic force, which is the motion of polarizable particles in a non-uniform electric field, enabled researchers to capture biological cells in confined well geometries more effectively in shorter periods of time. Electro-activated micro-wells have been used for several applications such as cell sorting and cell manipulation [40–44]. Kim et al. proposed a microfluidic device made up of electro-active micro-wells to capture cells using positive dielectrophoresis (DEP) and then lyse them using electroporation [42]. In another study, Cordovez et al. showed that electro-active micro-wells can serve to capture, store, and even repel different diameter (6 to 20 μm) polystyrene particles [43]. Yoshimura et al. reported a microfluidic device consisting of 10,000 micro-wells in order to produce “cell couplets” [44]. After capturing, cells could be analyzed to determine their properties. Morimoto et al. used immunofluorescent labeling on cells and isolated them in micro-wells, where molecular analyses of cells were performed [45]. Kobayashi et al. used three different kinds of biochemical assays (immunostaining, viability/apoptosis, and FISH) for cancer cell discrimination after capturing cells by electro-activated micro-wells [46]. Most of published articles relied on injection of expensive biochemical reagents, microscopy, and molecular analysis methods to find cell types and their properties. As a non-invasive, inexpensive, and label-free technique, dielectric spectroscopy could be used to analyze the cells after capturing them in the micro-wells.

In this study, we demonstrate the efficiency of a new microfluidic device for capturing and then measuring the dielectric response of biological cells. The yeast cells are introduced with a low volume fraction (1%) and cell enrichment and unloading inside the micro-wells are established using positive DEP and negative DEP, respectively; facilitating high throughput cell processing. Captured cells are analyzed using the dielectric spectroscopy method, which enables real-time measurements of sub-cellular dielectric properties of the biological cells.

2. MATERIALS AND METHODS

Photolithography supplies (photoresists, developers, and remover) were purchased from Microchem Corp. (Westborough, MA, USA). All other chemicals used were of analytical grade and obtained from Sigma-Aldrich (St Louis, MO, USA). All solutions were prepared with 18 MΩ·cm ultrapure water obtained from Millipore Alpha-Q water system (Bedford, MA, USA). A Leo-Zeiss 1450VPSE variable pressure electron microscope equipped with an EDAX Genesis 4000 XMS System was used for SEM characterization. SEM images were taken at 3000× magnification factor and 5 kV resolution. Yeast cells (Saccharomyces cerevisiae) were grown in a shaking incubator at 30°C and under constant shaking speed at 250 rpm. The growth medium (YEPD Broth) consisted of 20 g/l peptone, 10 g/l yeast extract, 20 g/l dextrose dissolved in deionized water. The cells were collected at the stationary growth phase after one day of culture in shaking incubator, and they were harvested by centrifugation for 2 min at 3000 rpm, and suspended in measurement buffers. The harvested cells were spherical and 6.0 ± 0.4 μm in diameter. The volume fraction of yeast cells was measured using hematocrit tubes. An aliquot of yeast cell suspension was introduced into a hematocrit tube, and the tube was centrifuged at 2000 rpm for 2 minutes. The volume fraction was found comparing the volume of the cell pellet to the tube volume.

LCB (Low Conductivity Buffer) is an isotonic buffer consisting of 229 mM sucrose, 16 mM glucose, 1 μM CaCl₂, and 5 mM Na₂HPO₄ in double distilled water (pH 7.4). The conductivity of LCB was adjusted by adding PBS (Phosphate Buffer Saline) and the conductivity was measured using a conductivity meter (Con11, Oakton).

2.1. Photolithography

The microfluidic chips used for experiments are fabricated using standard photolithography techniques. Figure 1 shows the fabrication procedure. First, the glass substrates are cleaned for 10 minutes using ultrasonic cleaning in 1 M KOH solution, acetone, and isopropyl alcohol (IPA), respectively; followed by rinsing with type-1 deionized (DI) water, and drying with Nitrogen. The slides are then placed on a hot plate that was kept at 140°C for 15 minutes to be completely dried. The positive photoresist (S1813) is spin coated on the slides using a two-step process with the following rotation speeds: (1,000 rpm for 10 s and 4,000 rpm for 30 s with 300 rpm/s acceleration/deceleration). Coated slides are soft baked on a hot plate at 115°C for 1 minute, and then, they are exposed to 110 mJ/cm² UV light through a transparency mask using a Karl SUSS MJB3 mask aligner. The UV exposed area is dissolved in MF-26A developer solution by immersing the slides inside the solution for 10 s. The developed slides are cleaned using DI water and dried by gentle flow of Nitrogen. Afterwards, the slides are placed inside a sputter coater (EMS300TD, Emitech). The sputter coater is adjusted to coat slides with 3 nm Chromium layer and 22 nm gold layer. The slides are then immersed in PG remover solution at 80°C to remove the unexposed photoresist and metal layers on top of it. In the next step, negative photoresist (SU8-3025) is spin coated under the same conditions as those used for the positive photoresist. The photoresist is then soft baked on hot plate at 95°C for 12 minutes and is exposed to 400 mJ/cm² UV light. Immediately after exposure, the slides are post exposure baked on hot plate at 95°C for 3 minutes and 40 seconds. Finally, the slides are immersed in SU8 developer to remove the unexposed areas.

Figure 1.

Microfabrication process of DEP chip using two-step photolithography process. a) Electrode fabrication, b) micro-wells and micro-channel fabrication, and c) electrode alignment and device assembly.

2.2. Device assembly

The channels for fluid flow are fabricated using 70 μm thickness double sided tapes (DST) cut by a craft cutter machine (Silver Bullet). Finally, the slide containing the micro-wells and the electrode is aligned with the top electrode using the mask aligner. The assembled device is compressed using binder clips and placed in a convection oven at 75°C for 15 minutes to enhance adherence of the double sided tape to glass slides and to ensure that the device is well-sealed. Figure 2a shows the assembled microfluidic device composed of micro-wells and the microchannel sandwiched between an electrode pair. Figure 2b illustrates the orientation of micro-wells on the gold electrode. There are 441 micro-wells in a 21×21 array, where each column is placed with an offset relative to the neighboring column to increase the chance of trapping the cells in a flow through system. This configuration also maximizes the volume fraction of cells in the device. Figure 2c is the SEM image of one of the micro-wells. It can be seen that the wells are fully developed in the SU-8 developing process. Smooth well-corners reduce extremely high electric fields at the edges, and decrease the probability of cell attachment on well-corners due to pDEP. The inlet and outlet ports of the microchannel are drilled using a diamond drill bit before joining the two parts. Two pieces of PDMS are used to ensure leak free fluidic port connections. Strong irreversible binding between PDMS and glass is obtained using oxygen plasma cleaner. Copper tapes are used for electrical connections and the connection between the copper tape and gold electrode is achieved using silver epoxy (MG chemicals). Figure 2d illustrates the working principle of the microfluidic device. Firstly, biological cells are captured inside the micro-wells using pDEP forces and then microfluidic device is connected to a high precision impedance analyzer (HP Agilent 4194A) and the impedance spectra are measured. Finally, cells are extracted from the wells using nDEP forces, and they are directed towards the outlet using fluid flow generated by a syringe pump (NE-4000).

Figure 2.

a) Assembled microfluidic chip, b) a microscopy picture of gold electrode and micro-wells, c) SEM image of one micro-well, d) the working principle of microfluidic device, and e) the computational domain consisting of medium solution, SU-8, and spherical yeast cells. The yeast cells are modeled consisting of an inner cytoplasm covered by a membrane modelled as an interface.

2.3. Experimental setup

Thickness of the electrodes is about 25 nm, which maintains their transparent nature and allows observation of biological cells between the electrode pairs under a microscope. Most previous studies used ITO as transparent electrodes. However, resistivity of ITO (3.0–160×10⁻⁴ Ω.cm [47]) is higher than gold (2.04×10⁻⁵ Ω.cm [48]). Transparency of thin gold electrodes combined with its low resistivity, bio-compatibility [49], and chemical inertness led us to select gold as the electrode material. In order to image the biological cells, microfluidic device is placed on an inverted microscope stage (Olympus IX81). The inlet port is connected to a syringe pump to feed the microfluidic device with 1% yeast cell suspension (88×10⁶ cells/ml) at 1ml/hr flow rate, and outlet port is connected to a drain. Electrical ports are connected to a function generator (Tektronix AFG3102) which is programmed to apply AC signals with a desired amplitude and frequency for DEP assisted loading and unloading of the micro-wells. After capturing the cells, the electrical ports are connected to high and low terminals of a high precision impedance analyzer (HP Agilent 4194A) through a test fixture (HP 16047A). Impedance measurements are performed in 1 kHz–40 MHz frequency range, and the measured data is recorded using MATLAB R2014b software.

2.4. Numerical modeling

The computational domain consists of spherical cells located at the bottom of a 30×30×30 μm well. The well itself is placed in a microchannel with 70 μm depth. Schematic of the simulation domain is shown in Figure 2e. Bottom part of the domain (the well-surroundings) is made up of negative photoresist SU-8. Top and inside of the well (except cells) is filled with a solution. The cells are modeled as spherical membranes encapsulating the cytoplasm. The material electrical properties used in numerical simulations are as follows. SU-8 photoresist has a relative permittivity of 3.2 and negligible electrical conductivity [50]. The medium is low conductivity buffer (LCB) which has a relative permittivity of 80 and electrical conductivity of 0.05 S/m. Dielectric properties of Saccharomyces Cerevisiae (yeast) cells are measured in a microfluidic device consisting of parallel plate electrodes in a micro-channel, and the subcellular electrical properties are calculated using the methodology given in Sabuncu et al. and presented in the supplementary information [9]. Yeast cells’ inner cytoplasm and outer layer are found to have relative permittivities of 60 and 12.6 and electrical conductivities of 0.3376 and 6.27×10⁻⁵ S/m, respectively. These results are in good agreement with previously published results [51].

The electric field is modeled using combination of Gauss’ and charge conservation equations in the frequency domain: ∇.(σE + jωD) = 0, where σ is the electrical conductivity, E is the electric field, and D is the electric displacement field. The electric field and electric displacement field can be written as E = −∇φ and D = ε_rε₀E, where φ, ε_r, and ε₀ represent electric potential, relative permittivity, and vacuum permittivity, respectively.

Electrodes are located at the bottom and top surfaces of the domain. Boundary conditions on the electrodes are 1 V and 0 V for the bottom and top surfaces, respectively. All side surfaces are considered periodic due to the large number of wells, separated 15 μm from each other. The contact impedance boundary condition is used to represent the cell membrane, which approximates a thin layer of material that impedes the flow of current normal to the boundary, but does not introduce any additional conduction path tangential to the boundary. COMSOL Multiphysics software is used for discretization of the geometry and numerical solution of aforementioned equations in the frequency domain. Grid refinement studies are performed to ensure convergence of the numerical solution. More information on the grid refinement study is presented in the supplementary information (Figure S1).

2.5. DEP Theory and Dielectric Spectroscopy

DEP is the motion of polarizable particles suspended in an ionic solution and subjected to a spatially non-uniform external electric field. Time averaged dielectrophoretic force generated by constant phase electric field is given by 〈 F⃑_DEP 〉 = 2πr³ε₀ε_rRe[K(ω)]∇E² where r is the radius of particle, ε₀ is permittivity of vacuum, ε_r is relative permittivity of the medium, ∇E² is the gradient of square of the electric field, and Re[K(ω)] is the real part of the CM factor, which is written as $K(\omega )=\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{{\epsilon }_p^{\ast }+2{\epsilon }_m^{\ast }}$, where *, p, and m denotes complex value, particle, and medium, respectively. The complex permittivity is calculated as ${\epsilon }^{\ast }=\epsilon -\frac{j\sigma }{\omega }$, where ε is the permittivity, σ is the conductivity, $j=\sqrt{-1}$ and ω is the angular frequency. Sign of Re[K(ω)] distinguishes positive and negative DEP responses. Particles more polarizable than the medium are pulled towards higher electric fields and exhibit pDEP response, while particles less polarizable than the medium are repelled towards lower electric fields and exhibit nDEP.

Dielectric spectroscopy is a well-known non-invasive technique to measure electrical properties of cell suspensions. In this method, a small AC voltage is applied to a cell suspension and the response current is measured. The impedance is then calculated by dividing voltage by current. This process is repeated in a desired frequency range, and analyzing impedance spectrum enables determination of the dielectric properties of individual components of the suspension. Since the applied voltage for the dielectric spectroscopy measurements is small (200 mV) and the measurement process is fast (<5 s), the spectroscopy signal neither will have a considerable effect on the cell packing inside the wells, nor the cells will change their properties during the measurement. Sabuncu et al. [9] developed a microfluidic device in order to analyze impedance spectrum of cell suspensions. In this method, the effect of electrode polarization is extracted by fitting the impedance spectrum into a combination of constant phase element and the Cole-Cole model [52]. Fitting the corrected dielectric spectrum using the Maxwell-Wagner mixture model [52] allows determination of the CM factor. Moreover, modeling biological cells using single-shell and double-shell models allows extraction of the dielectric properties of sub-cellular components [9].

3. RESULTS AND DISCUSSION

The electric field lines will be concentrated within the micro-wells, exhibiting high electric fields inside the micro-wells and lower electric fields outside of the micro-wells due to the electrodes’ orientation. The numerically calculated electric fields are given in the supplementary information (Figure S2). These electric field gradients enable DEP-based cell manipulation. For example, cells can be loaded into the micro-wells using pDEP and they can be unloaded using nDEP. In order to determine the frequencies for loading and unloading the micro-wells, the real part of CM factor is calculated using a device with parallel plate electrodes and the procedure explained by Sabuncu et al. [9]. The details of the CM factor measurement is presented in the supplementary information. Figure 3a shows the time averaged real part of CM factor for yeast cells suspended in LCB (0.05 S/m) in 1 kHz–40 MHz frequency range at different time periods. The time averaged data was obtained using repeated measurements at every two minutes in 10 minute periods. This figure illustrates time dependent behavior of yeast cells that could result from the ion exchange between the cell cytoplasm and LCB medium. Results show negligible changes in the crossover frequency within 10 minutes, while the DEP experiments are conducted within a couple of minutes following the introduction of cells to the device. Using CM spectrum of cells at 0–10 minutes, pDEP and nDEP responses are expected at f = 5 MHz and f = 10 kHz frequencies, respectively. These frequencies were tested experimentally using the micro-well setup. In the experiments, the flow was initiated at 1 ml/hr flow rate, and simultaneously, the electrodes were energized at 2 V_pp AC voltage to manipulate the cells. Figures 3b and 3c verify DEP response of yeast cells suspended in 0.05 S/m LCB, at 5 MHz and 10 kHz, respectively. These figures clearly show that at 5 MHz, cells are captured inside the micro-wells by gravitational and pDEP forces, while at 10 kHz, nDEP pushes the yeast cells outside the wells, against gravity. Finally, the cells are washed away and the microchip is free of the cells as shown in Figure 3d. Strong nDEP forces overwhelming the gravitational force are crucial for unloading the device. Simple force equilibrium relations for a single yeast cell, estimates that it takes more than 1 minute for cells to occupy the wells under gravitational and buoyancy forces. Furthermore, not all the cells will settle down inside the micro-wells by these forces. The video in the electronic supplementary information shows the cells are captured by pDEP, they remained packed during DS measurements and finally applying nDEP will unload the wells and the cells are washed away. Experimental impedance results (Figure S3) show that on the impedance spectra, there is a considerable effect of cells being concentrated inside the micro-wells than just having randomly dispersed cells between the electrodes. Moreover, pDEP force is applied for 5 seconds at four different initial yeast concentrations (0.5, 1.5, 2.5, and 3.5%) in 0.05 S/m LCB solution to show the effect of degree of loading in the micro-wells. The impedance magnitude data is shown in Figure S4. Experimental results show that the results for 0.5, 1.5, and 2.5% are different but after 2.5%, the impedance magnitude data reaches a steady state, which suggests that micro-wells are fully loaded. Furthermore, the electrodes are energized for different periods of time, and the analysis shows that after 10 s, the impedance spectrum does not change, which means that the micro-wells are completely full. As a result, it is concluded that the loading efficiency of the DEP device is 60–70 cells per well in 10 s using a 1% volume fraction yeast cell suspension at 2 V_pp and 5 MHz excitation.

Figure 3.

a) Real part of CM factor for yeast cells suspended at 0.05 S/m LCB solution as a function of frequency for 0–10, 10–20, and 20–30 minutes time periods after being placed in the LCB solution from growth media. The procedure for extracting CM factor is the same as in [9]. Response of yeast cells to 2V_pp AC electric field at b) f = 5 MHz, and c) f = 10 kHz, d) clean array after the yeast cells are washed away.

Yeast growth medium has a conductivity of around 0.20 S/m, whereas mammalian cells cultures have a conductivity on the order of 1 S/m. At high conductivities (~1 S/m), pDEP is non-existent for mammalian cells [53]. Moreover, for high conductivity buffers, electrode polarization effect dominates the system and DS is not accurate. However, for yeast cells, pDEP still is strong enough to capture cells in their growth medium, and the experiments conducted at 0.20 S/m medium conductivity, which is close to the yeast growth medium, demonstrates that the device is capable of manipulating yeast cells in their growth medium. In order to find out how the presence of yeast cells will change the impedance spectrum of the device, yeast cells are suspended in 0.01, 0.05, and 0.20 S/m LCB solutions, and the suspension is fed to the microfluidic device using a syringe pump. The yeast cells are captured inside the wells by applying AC signal with 2 V_pp amplitude and 5 MHz frequency for 10 seconds, and the impedance spectrum of cells is measured in 1 kHz – 40 MHz frequency range. Each experiment is repeated three times and the averaged values are shown in Figure 4. Figures S5a and S5b show the normalized standard deviation of the impedance magnitude and the phase angle. The normalized standard deviation in all cases is less than 1% in a significant range of the frequency spectrum. Figure 4a shows the impedance magnitude and phase angle variation as a function of frequency for both 0.05 S/m LCB and yeast cells suspended in 0.05 S/m LCB. The figure illustrates that introducing the cells will increase the impedance value at low frequencies, where the cell membrane effectively insulates the cytoplasm, and the current can only flow around the cells. As a result, presence of cells adds extra resistance to the current flow and increases impedance. As the frequency increases, the cell membrane becomes more permeable to AC electric field, and current flow through the cell starts to depend on the ratio of the complex conductivity of the cytoplasm to that of the bulk solution. Finally, the interfacial polarization happens, and the AC current across cell membrane increases. Since the cytoplasm conductivity is higher than the medium conductivity, the presence of cells decreases the impedance at higher frequencies. Based on phase angle graphs, presence of cells increases the absolute value of phase angle at lower frequencies because cell membrane acts as an insulator and the system is more capacitive. However, at higher frequencies, the cell membrane becomes permeable to electric currents and the system is less capacitive which means decrease in absolute value of phase angle. Figures 4b and 4c illustrate the impedance magnitude and phase angle variation as a function of frequency for yeast cells suspended in 0.01, 0.05, and 0.20 S/m LCB solution. Figures 4b and 4c show that increasing conductivity decreases impedance and phase angle value and the system becomes less resistive.

Figure 4.

a) Experimentally measured impedance spectrum of microchip device for pure LCB and yeast suspended in 0.05 S/m LCB. Lines show the results for pure LCB while symbols show yeast suspended LCB, b) experimentally measured impedance value and c) phase angle for yeast cells suspended in 0.01, 0.05, and 0.20 S/m LCB.

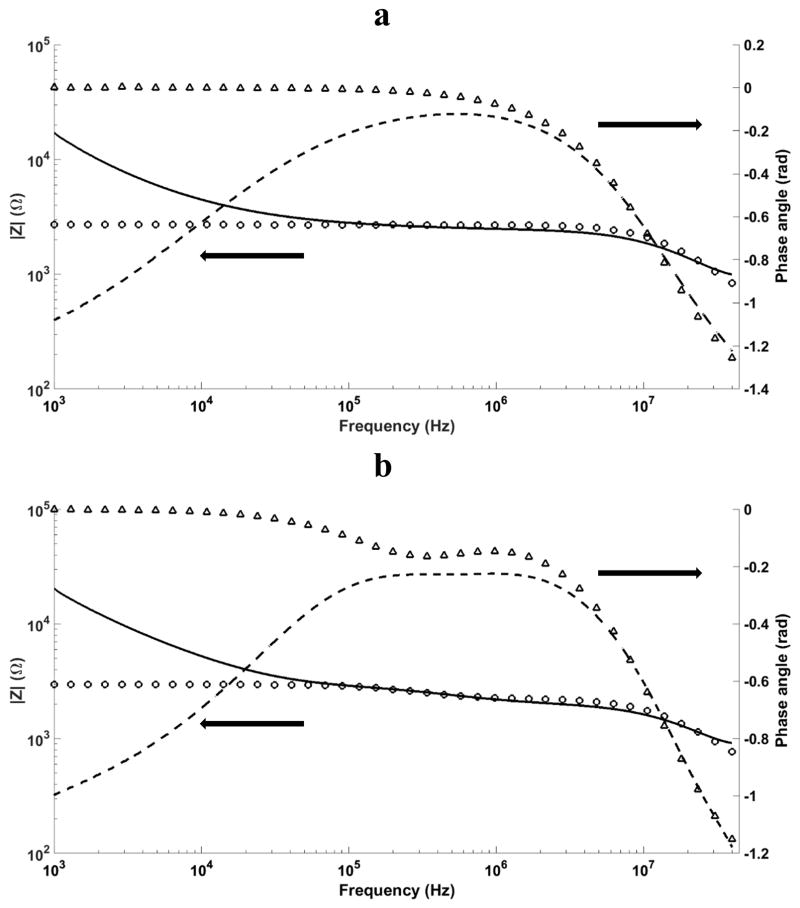
Simulations are performed in 1 kHz–40 MHz frequency range and the impedance spectra are calculated. It should be noted that the real device consists of 441 identical wells that can be considered as parallel elements. As a result, the computational impedance is divided by 441 to be comparable with experimental results. Figures 5a and 5b depict the experimental and numerical impedance spectra for both LCB and yeast suspended in LCB at 0.05 S/m conductivity. Comparisons between numerical and experimental results show good qualitative agreements with less than 10% error in between 100 kHz – 20 MHz range, where the interfacial dispersion occurs. Discrepancy in the lower frequency region is mainly due to the electrode polarization (EP) effects in experiments, which dominates the system and not considered in the simulations. EP happens due to charge accumulation at electrode/electrolyte interface causing large potential drop and formation of a large impedance at the interface [49]. The discrepancy in the higher frequency region mainly arises from the experimental inductance effects at frequencies above 20 MHz. Another important point here is the presence of two distinct impedance changes observed in figure 5b. The first impedance change (~ 10⁵ – 10⁶ Hz) is due to the cell membrane polarization at moderate frequencies and the second one (~4×10⁶ – 4×10⁷ Hz) is related to medium-SU8 interfacial dispersion.

Figure 5.

Comparison between numerical and experimental Impedance data (magnitude and phase angle) for a) pure LCB solution (0.05 S/m), and b) yeast cells suspended in LCB. Solid and dashed lines represent experimental impedance magnitude and phase angle results, while circles and triangles show numerical impedance magnitude and phase angle values.

4. CONCLUDING REMARKS

In this study, we fabricated and tested a fully integrated microfluidic device consisting of electro-activated micro-well arrays for capturing biological cells and measuring the impedance spectrum of trapped cell suspension. The transparent nature of 25 nm thick gold electrodes enables monitoring biological cells using an optical microscope. DEP response of yeast cells were predicted by calculating the real part of CM factor using a previously established method. Rapid loading and unloading of yeast cells were observed using positive and negative DEP. The effect of cells on impedance spectrum was experimentally studied. Moreover, numerical impedance results have shown good agreements with the experimental data. Consistency between numerical and experimental data show the capability of the microfluidic device in measuring the dielectric spectrum of biological cells and its potential to extract sub-cellular properties of biological cells. This device can potentially be used for any biological cell provided that the pDEP and nDEP response frequencies of that particular cell are known.

Since the cells are stably trapped inside the micro-wells, external stimuli could be altered at will and the cell responses can be measured in real time. Furthermore, cell unloading capability of the device enables measurements of different cells of interest for multiple times. Future work will focus on developing analytical and numerical methods to relate the sub-cellular dielectric properties with impedance spectrum, and how the changes in external stimuli affect sub-cellular properties. This requires development of a reliable equivalent circuit model for the device. In addition, decreasing electrode polarization effects will increase device sensitivity in the low-frequency region, which can be achieved by using fractal electrodes, as previously shown by our group for a simple parallel and planar electrode devices [49, 54].