Noninvasive Estimation of Epicardial Dominant High-Frequency Regions During Atrial Fibrillation

Abstract

Introduction

Ablation of high dominant frequency (DF) sources in patients with atrial fibrillation (AF) is an effective treatment option for paroxysmal AF. The aim of this study was to evaluate the accuracy of noninvasive estimation of DF and electrical patterns determination by solving the inverse problem of the electrocardiography.

Methods

Four representative AF patients with left-to-right and right-to-left atrial DF patterns were included in the study. For each patient, intracardiac electrograms from both atria were recorded simultaneously together with 67-lead body surface recordings. In addition to clinical recordings, realistic mathematical models of atria and torso anatomy with different DF patterns of AF were used. For both mathematical models and clinical recordings, inverse-computed electrograms were compared to intracardiac electrograms in terms of voltage, phase, and frequency spectrum relative errors.

Results

Comparison between intracardiac and inverse computed electrograms for AF patients showed 8.8 ± 4.4% errors for DF, 32 ± 4% for voltage, and 65 ± 4% for phase determination. These results were corroborated by mathematical simulations showing that the inverse problem solution was able to reconstruct the frequency spectrum and the DF maps with relative errors of 5.5 ± 4.1%, whereas the reconstruction of the electrograms or the instantaneous phase presented larger relative errors (i.e., 38 ± 15% and 48 ± 14 % respectively, P < 0.01).

Conclusions

Noninvasive reconstruction of atrial frequency maps can be achieved by solving the inverse problem of electrocardiography with a higher accuracy than temporal distribution patterns.

Introduction

The use of advanced signal analysis methods has shown that AF is maintained by high-frequency sources located at the junction of the atria with the left pulmonary veins (PV) or at others sites of the atria, both in animal models and in humans.^1–7

Several clinical studies have shown that, instead of empirically targeting the PVs,⁸ AF may be eliminated by directly ablating AF-driving sources or “rotors,” that maintain the fibrillation with a hierarchical pattern from dominant frequency (DF) regions.^9–11 Thus, non-invasive identification of high-frequency sources location prior to the ablation procedure could be used to select patients and to guide the ablation procedure.

Previous studies on the inverse problem solution during AF have shown paradoxically simple activation patterns^12,13 that do not correspond with the complex propagation patterns recorded either in animal models^1,2,14 or epicardially in patients^4,15 and have not been validated with simultaneously recorded potentials. For these reasons, the acceptance of the inverse-problem solution as a guidance for AF ablation is still controversial. We have recently described the limitations encountered during the estimation of detailed voltage and phase propagation patterns during AF from noninvasive recordings.¹⁶ In contrast, activation frequencies computed using spectral analysis has shown to be preserved on the torso surface.¹⁷ The aim of the present study is to evaluate the performance of the inverse problem solution in detecting and characterizing intracardiac DF distributions during AF. To this purpose, we (1) determined the feasibility and accuracy of computing dominant frequency (DF) maps from noninvasive recordings in AF patients in which surface and endocardial potentials were simultaneously acquired; and (2) assessed the accuracy of the inverse problem solution in the voltage, phase, and frequency domains by using realistic AF mathematical models to guide interpretation of the recorded body surface potentials in patients.

Methods

Simultaneous Body Surface and Intracardiac Recordings in AF Patients

Four patients admitted for ablation of drug-refractory paroxysmal AF (males, 46.5 ± 6.4 years old) were studied. The ablation protocol as previously described was approved by the Institutional Ethics Committee of our institution and both patients gave informed consent.¹⁷ Three patients arrived in sinus rhythm and AF was induced using electrical burst pacing.¹⁸

In order to reconstruct the electrical activity on the heart surface by solving the inverse problem of the electrocardiography, body surface potential mapping (BSPM) technique was used whereby multichannel electrocardiograms (ECGs) were recorded with a custom-made vest of 67 chest ECG leads.¹⁷ The geometry of the atria and torso of each patient was obtained by segmentation of computed axial tomography (CAT) images. Specifically, images with a spatial resolution of 0.5 mm were acquired prior to the ablation procedure and segmented by using 3D Slicer.¹⁹

Body surface recordings were obtained simultaneously with intracardiac EGMs. In two patients, intracardiac EGMs were obtained from the following catheters: (1) a standard tetrapolar catheter in the right atrial appendage (RAA); (2) a roving Navistar catheter (3.5-mm tip, 2–5–2 interelectrode distance; Thermo-Cool, Biosense-Webster, Diamond Bar, CA, USA) used to obtain a DF map of both atria by sequentially obtaining EGMs at different atrial sites (>200 points) for at least 5 seconds; and (3) a decapolar circular mapping Lasso catheter (Biosense-Webster) placed either at the left superior pulmonary vein (LSPV) or right superior pulmonary vein (RSPV). Biatrial intracardiac signals were sequentially acquired at a sampling rate of 977 Hz and dominant frequency (DF) analysis was performed in real time using a CARTO navigation system with embebbed spectral capabilities (CARTO XP, version 7.7; Biosense-Webster). After mapping both atria and once the highest DF site was identified, the ablation catheter was placed at that site (i.e., LSPV for patient 1 and RAA for patient 2) and a central venous bolus of adenosine (12–18 mg) was administered to produce significant transient atrioventricular block avoiding ventricular activity.^16,17

In two additional patients, body surface recordings were obtained simultaneously with a 64-pole basket catheter (Constellation, Boston Scientific, Natick, MA, USA) located sequentially on the right and left atria. Additionally, a standard tetrapolar catheter was placed in the coronary sinus (CS) and a 20-pole catheter in the opposite atrium to the basket catheter. With the basket catheter located inside each atrium, a central bolus of adenosine (12–18 mg) was administered.

Computational Models of the Atria and Torso

To further support with more complete mapping data our observations in patients in which we have a limited number of simultaneous recordings, we made use of mathematical models in which the electrical activity is known for the entire atrial surface. Realistic mathematical models of the two atria and torso with different AF impulse propagation patterns were used to evaluate the performance of the inverse problem solution by comparing the generated EGMs to those computed by solving the inverse problem of the electrocardiography.

The electric potentials on the epicardium were calculated from a realistic computerized model of the atria. The active tissue of the atria consisted of 577,264 nodes that represent a realistic human morphology.²⁰ The action potential of each node was simulated by using a modified version of Courtemanche’s mathematical transmembrane kinetics²¹ with an I_K,Ach formulation.^6,16

Atrial fibrillation in the in-silico realistic model was induced by an S1–S2 stimulation protocol. Mathematical computations were performed using an adaptive time-step solver on a Graphical Processing Unit (NVIDIA Tesla C2075 6G).²² Transmembrane potentials were computed for a simulation time of 4 seconds after stabilization of the model and were resampled to 1 kHz.

Simulated electrograms (EGMs) were computed by using transmembrane potentials according to Equation (1) at 1 mm distance from the epicardial surface:²¹

$$\text{EGM}={\displaystyle \sum _{\overrightarrow{\mathrm{r}}}\left(\frac{\overrightarrow{\mathrm{r}}}{{\mathrm{r}}^3}\right)}\cdot \overrightarrow{\nabla }{\mathrm{V}}_{\mathrm{m}}$$ (1)

where $\overrightarrow{\mathrm{r}}$ is the distance vector between the measuring point and a point in the tissue domain, $\overrightarrow{\nabla }$ denotes the gradient operator, and V_m is the transmembrane potential.

The computed potentials on the epicardium U_A were used to compute the body surface potentials U_T by applying the forward problem of the electrocardiography by using the boundary element method, as described in Equation (2):

$${\mathrm{U}}_{\mathrm{T}}={\text{MU}}_{\mathrm{A}}$$ (2)

where M is the field transfer matrix between the atrial surface A and the torso surface T. Those surfaces were discretized by plane triangles and the registration of the three vertices of each triangle. The transfer matrix was calculated by using the boundary element method as described in Equation (3):²³

$$\mathrm{M}={\left[{\mathrm{D}}_{\text{TT}}-{\mathrm{G}}_{\text{TA}}{\mathrm{G}}_{\text{AA}}^{-1}{\mathrm{D}}_{\text{AT}}\right]}^{-1}\cdot \left[{\mathrm{G}}_{\text{TA}}{\mathrm{G}}_{\text{AA}}^{-1}{\mathrm{D}}_{\text{AA}}-{\mathrm{D}}_{\text{TA}}\right]$$ (3)

where D_XY is the coefficient matrix that represents the contribution of the potential of a bounding surface Y to a surface X and G_XY is the coefficient matrix representing the contribution of the voltage gradient of a bounding surface Y to a surface X. Assuming that Y is a surface with N_Y nodes and X is a surface with N_X nodes.

Simulated ECGs were used to estimate the inverse computed epicardial electrograms (icEGM) by solving the inverse problem of electrocardiography as described below. In order to evaluate the performance of the inverse problem under a realistic noisy situation, icEGM were calculated before and after the addition of white noise in the computed ECG signals (i.e., signal to noise ratio of 10 dB).

Noninvasive Characterization of Epicardial AF Activity

We estimated icEGM from both patient recordings and body surface voltages computed in the mathematical models, by solving the inverse problem of the electrocardiography. The inverse problem was solved by computing the inverse of the field transfer matrix atrial-torso matrix:

$${\mathrm{U}}_{\mathrm{A}}={\mathrm{M}}^{-1}{\mathrm{U}}_{\mathrm{T}}.$$ (4)

Since M is ill-conditioned and possible potential sources may exist outside of atrial surface U_A, its inverse matrix cannot be computed in terms of classical linear algebra. We solved the system by using zero-order Tikhonov’s method in which the potentials on the surface of the atria U_A were estimated from the potentials on the torso according to Equation 5:^23,24,26

$${\mathrm{U}}_{\mathrm{A}}\left(\mathrm{\lambda }\right)={\left({\mathrm{M}}^{\mathrm{t}}\mathrm{M}+\mathrm{\lambda }{\mathrm{I}}^{\mathrm{t}}\mathrm{I}\right)}^{-1}{\mathrm{M}}^{\mathrm{t}}{\mathrm{U}}_{\mathrm{T}}$$ (5)

where M is the field transfer matrix between the atria and the torso and can be calculated according to the Equation (4), I is the identity matrix and λ is the regularization parameter. In order to estimate the optimal regularization parameter λ, an automatized version of the graphical method of the L-curve was used.²⁵

The accuracy of the icEGM was compared for the (1) voltage, (2) phase, and (3) frequency domains. Specifically: (1) instantaneous phase was computed by applying the Hilbert’s transform;¹⁶ (2) power spectral density and DF were computed by using Welch’s periodogram with a Hamming window of 2 seconds, 50% overlap, and a resolution of 0.25 Hz; and (3) voltage was obtained from preprocessed bipolar intracardiac recordings.²⁷

The accuracy of reconstructed EGMs was quantified by measuring the relative error between normalized voltage, phase, and spectrum of recorded or modeled EGMs and icEGM. In AF patients, icEGMs were compared with the simultaneously recorded endocardial EGM in three simultaneously recorded catheters; RAA, LSPV, and RSPV. In mathematical models, electrograms from 5,988 points of the realistic atria were compared. Statistical significance (P < 0.05) was assessed using the t-test mean difference between the relative errors for the three domains (i.e., voltage, phase, and frequency) at each node in the atrial model. The relative error for each node in the voltage and phase domain was computed as the mean relative error over the 5-second signal. For the frequency domain, the relative error for each node was computed as the mean relative error in each frequency in the range from 3 to 20 Hz.

Results

Noninvasive Identification of Atrial DFs During AF

Performance of the inverse problem for the voltage, phase, and frequency domains was assessed by comparing simultaneous intracardiac electrograms with the estimation of the inverse problem solution in AF patients with different distribution patterns of activation frequency. In addition, inverse computed DF maps were compared with DF maps obtained either previously (first 2 patients) or simultaneously (last 2 patients) to the body surface recordings.

In Figure 1A,C, intracardiac EGMs of patient 1 with a left-to-right dominant frequency pattern with increasing activation rates from the RA, to RSPV and LSPV at 5.75 Hz, 6.75 Hz, and 7 Hz, respectively, are shown. Comparing the intracardiac EGMs (i.e., blue) with the icEGMs (i.e., red), there was a significant error for both the voltage and the phase, whereas the morphology of the power spectrum and the measured DF values were similar. In fact, similar DF values were found on the RA, the LSPV, and the RSPV after solving the inverse problem to those obtained in the simultaneous EGMs. CARTO DF maps and inverse-computed DF maps also showed a good correspondence since the same hierarchical activation rate pattern (i.e., right to left frequency gradient) can be inferred from both maps. The actual activation frequencies, however, cannot be directly compared since they were not acquired simultaneously and the displayed surface maps correspond to the time of the adenosine infusion and adenosine is known to accelerate atrial frequencies, especially at the driving sites.⁶

Figure 1.

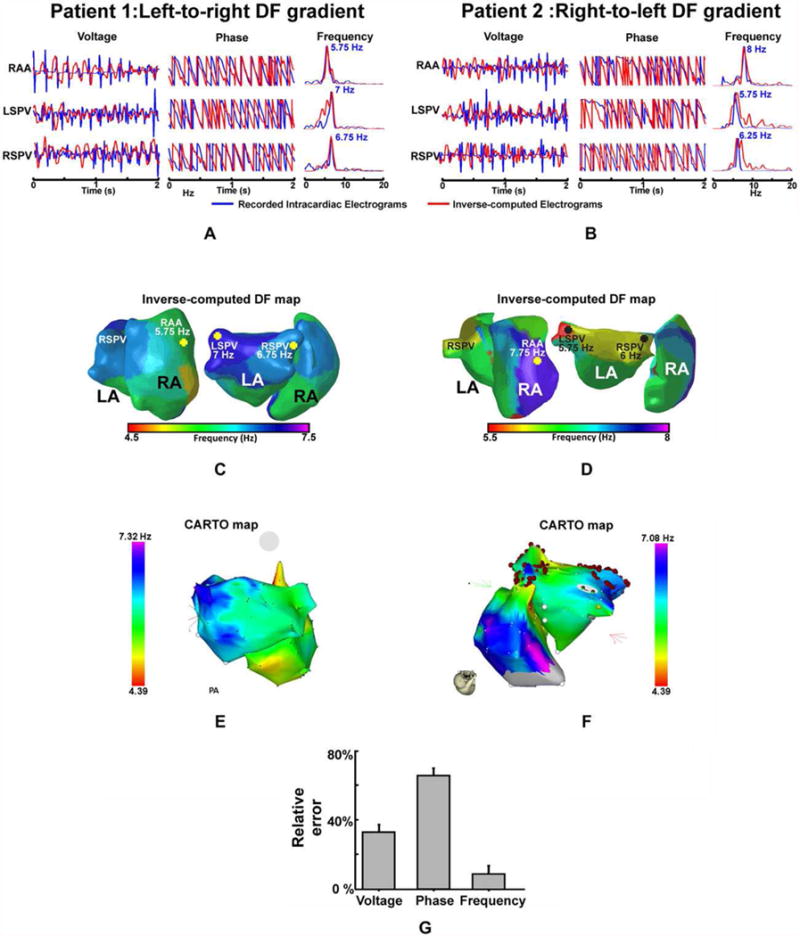
Validation of the inverse problem during human AF for the voltage, phase, and frequency domains. A and B: Intracardiac (blue) and inverse-computed (red) EGMs at the right atrial appendage (RAA), right superior pulmonary vein (RSPV), and left superior pulmonary vein (LSPV) and their corresponding instantaneous phase and spectra for patient 1 (A), with a left-to-right DF gradient, and for patient 2 (B), with a right-to-left gradient. C and D: Inverse-computed DF maps, posterior (right) and right lateral (left) biatrial views of patients 1 and 2, respectively. E and F: CARTO maps of patients 1 and 2. G: Numerical analysis of the relative error in the voltage, phase, and frequency reconstruction in patients for the three selected recorded and inverse-computed EGMs for each patient. For a high quality, full color version of this figure, please see Journal of Cardiovascular Electrophysiology’s website: www.wileyonlinelibrary.com/journal/jce

Patient 2 (Fig. 1B,D) presented a right-to-left dominant frequency pattern that was still present after isolation of PVs, with activation frequencies progressively decreasing from the RA, to RSPV and LSPV at 8 Hz, 6.25 Hz, and 5.75 Hz, respectively. Frequencies estimated from the icEGMs presented a similar activation pattern and frequency values as those measured invasively, whereas the reconstruction of the EGMs or the instantaneous phases presented a lower similitude. As shown in Figure 1F, these results were consistent with the CARTO maps, demonstrating a high similarity to the reconstructed DF maps, which also presented similar high dominant frequency distributions in the RA and LSPV and a right-to-left frequency gradient. Systematic comparison between intracardiac and icEGMs for the two AF patients corroborated those results with significantly lower relative error for frequency spectrum estimation than for the voltage or the instantaneous phase (i.e., 8.8 ± 4.4% vs. 32 ± 4% and 65 ± 4%, respectively, P < 0.01), as depicted in Figure 1G. Additionally, the inverse problem allowed the reconstruction of the entire atrial DF maps for the same time interval as shown in Figure 1C,D. Global DF map determination enabled the location of the highest DF site in the LSPV for patient 1 and in the RAA for patient 2, which is consistent with the DFs measured in the intracardiac recordings.

In two additional patients (patients 3 and 4), DF maps were further validated by comparing inverse-computed EGMs with simultaneously recorded signals obtained at 71.8 ± 8.9 sites per atrium (total of 287 sites). Results of the comparison of inverse-computed and recorded EGMs are presented in Figure 2. Overall, DF maps allowed the clear identification of the highest DF sites (in the right atrium of both patients) and the direction of the DF gradient, although the DF match varies in different atrial locations. Again, accuracy in the frequency domain, with a 12.8 ± 3.2% error was higher than in the voltage and phase domains, with relative errors equal to 35.8 ± 6.6% and 65.4 ± 4.1%, respectively.

Figure 2.

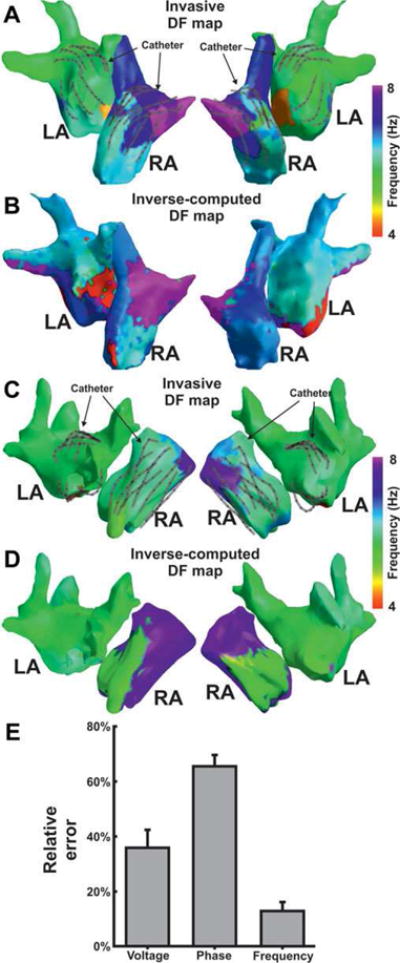
Validation of inverse computed DF maps. Inverse computed (A,C) and simultaneously recorded DF maps (B,D) for patients 3 and 4 in which a multipolar catheter was sequentially placed in the right and left atria. E: Numerical analysis of the relative error in the voltage, phase, and frequency reconstruction in both patients for a total of 287 EGMs recorded in both atria of the two patients (71.8 ± 8.9 simultaneously recorded sites). For a high quality, full color version of this figure, please see Journal of Cardiovascular Electrophysiology’s website: www.wileyonlinelibrary.com/journal/jce

Accuracy of the Inverse Problem Resolution

In Figure 3, a mathematical model with a left-to-right DF gradient is shown. In this case, the DF gradient is governed by a rotor located at the left atrium as visible from the voltage and phase maps (Fig. 3A). Under an ideal situation, in which the representation of the cardiac activity in the torso and the subsequent inverse problem resolution are performed without the addition of noise, inverse-computed voltages and phases represent a smoothened version of original epicardial potentials. However, while some activation wavefronts are properly estimated, other activation wavefronts are missed (icEGMs in Fig. 3B). On the other hand, dominant frequencies are accurately estimated by solving the inverse problem in most parts of the atria except for certain sites near the interatrial septum.

Figure 3.

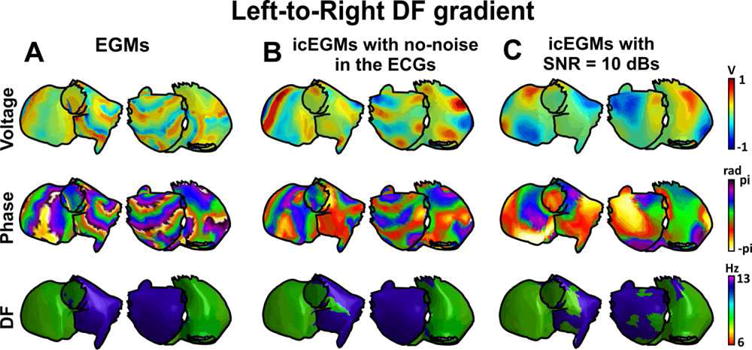
Inverse-computed voltage, phase, and dominant frequency (DF) maps for simulated AF with a left-to-right DF gradient. A: Voltage, phase, and DF maps for generated epicardial electrograms (EGM). B: Voltage, phase, and DF maps for inverse computed electrograms (icEGM) without added noise. C: Voltage, phase, and DF maps for icEGM with added noise on surface potentials at 10 dB SNR. For a high quality, full color version of this figure, please see Journal of Cardiovascular Electrophysiology’s website: www.wileyonlinelibrary.com/journal/jce

Epicardial potentials reconstructed after addition of noise at 10 dB SNR present an increased smoothening of both voltage distribution and phase to an extent at which activation wavefronts do not match after forward and inverse problem resolution (Fig. 3C). Dominant frequency estimation was again performed accurately for most of the atrial surface.

Figure 4 shows a mathematical model with a dominant rotor located at the right atrium giving rise to a right-to-left DF gradient. As in the previous example, the resolution of the inverse problem produced a simplified version of the activation pattern of the potential and phase maps, especially under a realistic scenario with a signal to noise ratio of 10 dB. Nevertheless, the addition of the noise did not modify the DF map.

Figure 4.

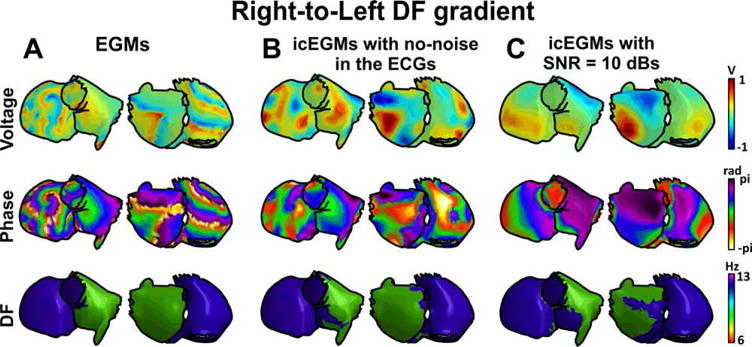
Inverse-computed voltage, phase, and dominant frequency (DF) maps for simulated AF with a right-to-left DF gradient. A: Voltage, phase, and DF maps for generated epicardial electrograms (EGM). B: Voltage, phase, and DF maps for inverse computed electrograms (icEGM) without added noise. C: Voltage, phase, and DF maps for icEGM with added noise on surface potentials at 10 dB SNR. For a high quality, full color version of this figure, please see Journal of Cardiovascular Electrophysiology’s website: www.wileyonlinelibrary.com/journal/jce

The accuracy of the icEGM to represent the voltage, phase, and frequency domains of original EGMs was systematically analyzed with and without the addition of white noise (Fig. 5). As shown in Figure 5A, error obtained for the DF distribution error was lower than the error obtained for the voltage and phase domains, both in the absence and presence of noise (i.e., P < 0.01). Notice that the addition of noise produced increased relative errors for the three domains. Nevertheless, the error increase was significantly smaller in the frequency domain than in the other two domains (i.e., P < 0.01), confirming our hypothesis that the frequency domain was the most robust parameter against noise.

Figure 5.

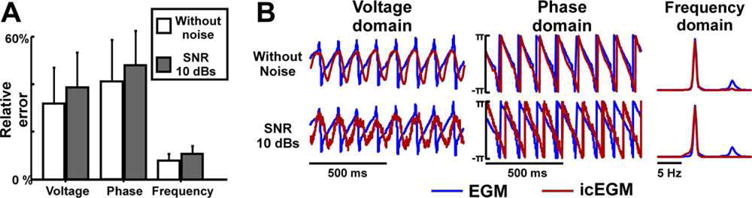
Comparison between simulated and inverse-computed EGMs. A: Relative error between inverse computed electrograms (icEGM) and original electrograms (EGM) with and without the addition of white noise to the surface electrocardiograms (i.e., signal to noise ratio [SNR] of 10 dB). B: Comparison between the original EGMs and icEGMs at a selected atrial site. For a high quality, full color version of this figure, please see Journal of Cardiovascular Electrophysiology’s website: www.wileyonlinelibrary.com/journal/jce

The effect of noise in the performance of the inverse problem resolution can also be observed in Figure 5B, where a representative example of EGM from the model in Figure 3 is shown. In the absence of added noise, reconstructed EGMs matched modeled EGMs, although sharp voltage transitions were smoothened. However, after the addition of noise to surface potentials, a more pronounced filtering effect of higher order spectral components was observed, resulting in spatial smoothening and a poorer estimation of voltages and phases. This effect might be due to the need to select a higher regularization parameter with added noise. Notice that smoothening produced a non-linear modification of the instantaneous phases for each instant, which may explain the poor spatiotemporal reconstruction of the AF propagation patterns shown in Figure 3. In the spectral domain, the dominant peak was well preserved with a reduced power of higher order spectral components confirming that, although the inverse problem may have limitations to reconstruct AF propagation patterns, it allows an accurate reconstruction of DF maps.

Discussion

The main finding of the present study is that noninvasive estimation of activation frequencies in the atria by solving the inverse problem of the electrocardiography is feasible and can be used to accurately compute activation frequency maps during AF. Here we show that inverse quantification of atrial DF is more accurate than estimation of voltage distributions or their instantaneous phase.

Noninvasive Estimation of Atrial Activation Patterns

The inverse problem of the electrocardiography was first applied for solving the electrical activity in the atria for the determination of earliest activation sites during atrial ectopies or pacing.^13,28,29 Solution of the inverse problem during non-fibrillatory rhythms has already been proven to be accurate by comparing inverse-computed and intracardially recorded isochronal maps. However, inverse-computed isopotential maps during AF show somewhat surprisingly simple patterns that have not been validated with simultaneous intracardiac data.^12,13 According to our results, voltage maps may not be inverse-reconstructed accurately because there is a trade-off between the smoothening introduced by large regularization parameters and an over-reconstruction of noise in the computed electrograms due to small regularization parameters and, consequently, the optimal regularization parameters tended to underestimate the complexity of AF patterns. As we have previously shown,¹⁶ the simplified potentials that reach the torso surface may still contain the most relevant features of rotational drivers of AF, which may explain the reported success of the inverse-guided ablation of rotors.¹² However, these results still need to be independently reproduced with simultaneous intracardiac mapping by other laboratories.

Noninvasive Estimation of Atrial Dominant Frequencies

There are experimental and clinical data supporting the notion that in many cases AF is maintained by a region with the highest activation rate.^9,11,30 In accordance with such notion, ablation of the highest DF in the atria has been shown to be an effective therapy for terminating the arrhythmia.⁹ We have recently demonstrated in a randomized clinical trial that in patients with paroxysmal AF, ablation of high-frequency sites only is non-inferior and safer than empirical circumferential ablation of all PVs. Interestingly, this result was obtained isolating only a mean of 2.22 ± 1.1 PVs.¹⁰

Atrial DFs have been estimated from surface recordings for decades³¹ and have shown good correlation with global intracardiac atrial DFs.^32,33 In a more recent study, we have shown that extensive recordings of surface potentials by BSPM allow detecting the highest DFs and not only the global activation rate of the overall atrial tissue.¹⁷ However, surface frequency maps only provide a rough estimation of the location of the atrial highest DF site.

Here we have shown that solution of the inverse problem of the electrocardiography allows locating this highest DF site in a patient-specific model of the atria, an observation that has been validated using simultaneously recorded intracardiac electrograms. Our simulation study further suggests that inverse estimation of the atrial activation frequency of atrial electrograms during AF based on the DF calculation is more accurate than the estimation of temporal-based features such as isopotential or phase maps, especially under a realistic noise scenario. The smoothing effect of the torso at non-negligible distances from the atria results in the summation of nearby potentials.¹⁶ That smoothing effect is required during classic inverse problem solution using quadratic regularization parameters in the presence of noise, but it introduces phase distortions that preclude an accurate reconstruction of spatiotemporal variations of non-stochastic phenomena like AF. Nevertheless, the present study demonstrates that the inverse problem can be used to accurately reconstruct the DF map and consequently detect the region of the atria that hierarchically maintains AF.

Limitations of the Study

In this study we have validated the estimation of inverse-computed atrial DF maps with a limited sample of patients. However, these patients represent variable locations of the highest DF site location (i.e., right vs. left) and may be representative of a broader range of atrial DF patterns. In some of these patients we did not have simultaneous information of the entire atrial surface, and in order to overcome this limitation we used mathematical models in which the activity in the entire atria is known to support our observations regarding the superiority of DF estimation over time-based metrics. Although the mathematical models employed may be over-simplistic, they were complex enough to demonstrate our hypothesis: that the main spectral components (namely, the DFs) are better preserved in the inverse solution than the morphology of the EGMs or their phases. A more complex mathematical model is likely to increase errors in the inverse solution and is therefore expected to make the DF robustness relative to the EGM morphology even more significant.

Finally, analyzed ECG segments correspond to an intravenous adenosine injection that does not only produce a transient atrioventricular block but also accentuates the highest frequencies, without affecting the atrial frequency gradient or the location of the highest DF site.^6,34 For this reason, the estimated frequencies may be higher than those that would be recorded under basal conditions.

Conclusion and Clinical Implications

Atrial high-frequency sources can be identified noninvasively by solving the inverse problem of electrocardiography with a higher accuracy than the morphology of potentials or their phase. Noninvasive computation of DF maps prior to and during an ablation procedure may help in patient selection and personalized procedure planning.