Quantifying the mechanisms for segmental duplications in mammalian genomes by statistical analysis and modeling

Abstract

A large number of the segmental duplications in mammalian genomes have been cataloged by genome-wide sequence analyses. The molecular mechanisms involved in these duplications mostly remain a matter of speculation. To uncover, test, and further quantify the hypotheses on the mechanisms for the recent duplications in the mammalian genomes, we have performed a series of statistical analyses on the sequences flanking the duplicated segments and proposed a dynamic model for the duplication process. The model, when applied to the human duplication data, indicates that ≈30% of the recent human segmental duplications were caused by a recombination-like mechanism, among which 12% were mediated by the most recently active repeat, Alu. But a significant proportion of the duplications are caused by some mechanism independent of the repeat distribution. A less sure but similar picture is found in the rodent genomes. A further analysis on the physical features of the flanking sequences suggests that one of the uncharacterized duplication mechanisms shared by the mammalian genomes is surprisingly well correlated with the physical instability in the DNA sequences.

The mammalian genomes are filled with duplicated sequences of different sizes. In the last few years, researchers have found that ≈3.5–5% of the human genome (1, 2), ≈1.2–2% of the mouse genome (3, 4), and 3% of the rat genome (5) contain recent segmental duplications (genomic sequence blocks whose identity level is >90% and length is >1 kb). Nonetheless, a clear delineation of mechanisms responsible for those recent duplications in the mammalian genomes remains elusive: Unequal crossovers usually cause tandem duplications; long interspersed transposable element 1 (L1) retrotransposon machinery can only cause interspersed duplications of <1 kb (6). Recently, a detailed analysis on the duplication breakpoints in a specific genomic region showed that some segmental duplications may have been caused by Alu-mediated recombination events (7). Later, Bailey et al. (8) reported that a significant portion of the interspersed segmental duplications terminated within an Alu repeat. These results led to the suggestion that the primate-specific burst of Alu retrotransposition activity is the primary cause of the recent boom of segmental duplications in the human genome (8). However, given the highly dynamic nature of the Alu repeats in the recent past (9), estimation of its contribution to the segmental duplication process could be biased if its evolutionary dynamics are not taken into consideration.

To quantitatively assess the relative contribution of Alu recombination mechanism to the process of segmental duplication without bias, we developed a dynamic mathematical model that formulates the evolution of the repeat distribution in the duplication flanking regions (see Fig. 1 for the definition of flanking regions) as a Markov process with the time measured by the divergence level in the duplicated sequences since duplication. The results from the model suggest that, although the duplication flanking regions may have been involved in Alu recombination significantly more often than pairs of randomly selected genomic regions, Alu recombination contributes to only ≈10–12% of the segmental duplications in the human genome.

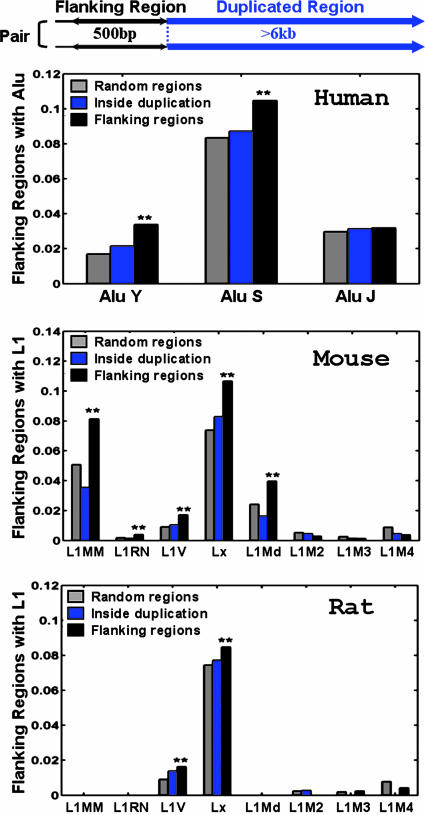
Fig. 1.

The appearance frequencies of various subfamilies of repeats detected in the duplication flanking regions in the human (hg16 shown here), mouse, and rat genomes. The relationship between the flanking regions and the duplicated regions is shown in a pair of segmental duplications above the top histogram. In this report, the length of the flanking regions is 500 bp, and the duplicated regions are >6 kb. The fractions of the flanking sequences containing different subfamily repeats are compared with the two control sets: sequences randomly selected from the whole genome and sequences randomly selected from inside the duplication regions. The names of the different subfamilies of Alu and L1 are listed on the x axis, roughly ordered according to their ages (from younger to older). Two-sample t tests are used to determine the statistical significance of the repeat overrepresentation in the flanking regions compared with the two controls, respectively. **, The frequency in the flanking regions is significantly higher than that in the controls, with P < 0.05. The statistics are based on the following sample sizes. Human random regions, 20,918; human inside the duplication regions, 13,321; human flanking sequences, 9,788; mouse random regions, 15,824; mouse inside the duplication regions, 6,766; mouse flanking sequences, 3,288; rat random regions, 6,274; rat inside the duplication regions, 3,631; rat flanking sequences, 1,652.

The largest fraction of duplications is thus not accounted for by recombination between interspersed repeats according to our computation. We therefore attempted to uncover evidence for a repeat-independent mechanism and discovered that the regions flanking duplications are enriched for sequences with low helix stability and high DNA flexibility. These physicochemical properties also characterize sequences known to be “fragile” sites (10, 11) for genetic rearrangement. Thus, segmental duplications may share a mechanism linked to genetic instability.

Methods

Sequence Preparation. We used four different segmental duplication mapping data sets from three different mammalian genomes in our study: the July 2003 Human genome assembly (hg16) (http://projects.tcag.ca/humandup) (2), the April 2003 Human genome assembly (hg15) (http://genome.ucsc.edu) (1), the February 2003 Mouse genome assembly (mm3) (4), and the June 2003 Rat genome assembly (rn3) (5). To avoid redundancy and ambiguity, we only selected the duplication pairs that (i) were only duplicated once, (ii) could not be included in any other duplications, (iii) were interchromosomal or at least 9 kb apart, and (iv) were >6 kb in length. The filtered duplication pairs for genome assemblies hg16, hg15, mm3, and rn3 are available as Data Sets 1, 2, 3, and 4 (respectively), which are published as supporting information on the PNAS web site. Two control sequence sets were created for each data set: One contained sequences randomly chosen from the corresponding genome assembly (http://genome.ucsc.edu), and the other contained sequences randomly selected from inside the duplicated regions.

Repeat Analysis. The repeats were identified according to the genome annotation database (http://genome.ucsc.edu). In this study, we considered a repeat as present in that flanking sequence if it was longer than a 100-bp threshold. For a pair of flanking regions to be identified as having a common repeat in a specific region (labeled as +/+), the repeat sequences had to be on the same side of the duplicated segments, face the same direction, and share at least 100 bp of high homology. For the Alu family, sequences from any subfamilies shared high homology (12, 13). For the L1 family, however, only sequences from the same subfamily were treated as highly homologous (14). In our model, the frequency of +/+ flanking region pairs in each age group was further normalized by subtracting the average frequency of repeats inside the duplicated segments, assuming that the repeats inside the duplicated region resulted from some repeat-independent mechanism and were uniformly distributed.

Model Parameters. All but two of the model parameters could be derived from the existing literature. They are enumerated in Table 4 in Supporting Appendix, which is published as supporting information on the PNAS web site. We chose a flanking region size that is large enough to minimize the effect of mapping and annotation errors (by allowing some gaps and shifts; see Figs. 5–7, which are published as supporting information on the PNAS web site) and yet sufficiently restrictive to distinguish the signals from the genomic background noise. To establish the most appropriate size of the flanking regions to be used in the study, we applied the model to the data sets generated from several different flanking region lengths (200, 500, 1,000, and 2,000 bp). The estimation of repeat recombination, measured by the h₁ value (see Model for definition), reaches its highest in the 500- and 1,000-bp data sets, thereby suggesting these two sizes to be optimal choices. The data presented in this report used a flanking region length of 500 bp.

Model Evaluation. We used a cross-validation method to test the performance of the model and the confidence intervals of the estimated parameters. The complete data set was randomly partitioned into two equally sized groups: an in-sample set to estimate the parameters and an out-of-sample set to cross-validate and measure the significance of the estimated parameters. The goodness of fit was tested in the out-of-sample data by using the parameters estimated from the in-sample data (for details, see Supporting Appendix). In Results, we report the mean values and standard deviations of the parameters estimated in 50 independent trials.

Stability and Flexibility Computation. The helix stability of the DNA duplex was estimated by the average strand dissociation Gibbs free energy (ΔG) in overlapping 50-bp windows, computed by the nearest neighbor model experimentally verified by Breslauer et al. (15). The DNA flexibility was estimated by the average twist angle in overlapping 50-bp windows computed by the method in ref. 16.

Results

Sequence Analyses: Repeat Distribution. We began by analyzing the repeat composition in the flanking regions of the mapped segmental duplications in the two assemblies of human genome (hg15 and hg16), as well as the two rodent genomes (mm3 and rn3) (see Methods). Consistent with the previous report on the human segmental duplications (8), we detected a significant overrepresentation of the repeats from the younger Alu subfamilies (AluY and AluS) in the flanking regions compared with random regions in both human genome assemblies (Fig. 1), but no significant overrepresentation of long interspersed transposable elements was detected. In the mouse and rat genomes, although no overrepresentation of the short interspersed transposable elements (B1, B2, ID, and B4) was found (Fig. 8, which is published as supporting information on the PNAS web site), we detected a significant overrepresentation of the repeats from the younger L1 subfamilies in the flanking sequences compared to random regions (Fig. 1). Therefore, the human genome and rodent genomes are enriched with the most recently active family of interspersed repeats in the duplication flanking regions [Alu in the human genome (17) and L1 in the rodent genomes (18, 19)]. The generality of the observation suggests that the recombination mediated by high-homology repeats may be a ubiquitous mechanism driving segmental duplications in all of the mammalian genomes.

However, to test the above hypothesis, one needs to consider the highly active history of the overrepresented repeats in the duplication flanking regions and the reliability of the genome assembly and duplication mapping data. Therefore, we conducted a detailed analysis on the hypothesis through a mathematical model that incorporates the evolutionary dynamic of the active repeats and minimizes the effect of assembly or mapping errors.

Model. The repeats that caused duplications by recombination should reside on the same side of the duplicated segment, face the same direction, and share enough homologous sequences. Therefore, intuitively, we could directly estimate the contribution of repeat recombination to duplication by measuring the excessive level of such repeat configurations in the flanking regions of the newly duplicated segments before any erosion on the sequence occurs through mutation events. However, the newly duplicated segments are almost identical and are, therefore, most prone to genome assembly errors, making the estimations unreliable. In contrast, if we used the “older” duplications, which are less prone to assembly errors; we could potentially overestimate or underestimate the contribution of the repeats. For instance, the actively amplifying transposable repeats can be inserted into the flanking regions after duplication and can form a configuration that falsely suggests a recombination event, resulting in overestimation of the hypothesis. Conversely, the repeats in the flanking regions can also lose their initial configuration after the recombination incident because of point mutations and deletions after duplication, consequently leading to underestimation of the hypothesis.

To resolve the above dilemma, we incorporated the evolutionary dynamics of the repeats and the duplicated segments in our model. Over time, all of the repeats in the flanking regions, regardless of whether they have caused the duplication by recombination, are subject to changes in their configurations. Assuming that the mechanisms of segmental duplication and their relative contribution have been well conserved over time, the current repeat configuration in the flanking regions of duplications of different ages may be viewed as sampled from its stationary distribution. If the evolutionary rates of the repeats and the duplicated segments are known, the relative contribution of repeat recombination to segmental duplications can be estimated from the stationary distribution.

To explain the model, we begin by introducing some notations. In our model, each pair of the duplication flanking regions is assigned to a state specified by the configuration of the interspersed repeats in the flanking regions and the age of the duplication event. There are three possible repeat configurations in a pair of flanking regions (defined in Fig. 1): The flanking regions share a common repeat when they contain a repeat from the same family in the same direction and with sufficient length of homology (+/+) (see Methods); or, one of them has a repeat and the other has no repeat or a repeat of different direction (+/–); or, neither of them contains repeats (–/–). The ages of the duplication events are estimated by the sequence divergence level between the duplicated segments and are grouped into bins with divergence interval ε. A flanking region pair is assigned to the age group k if the corresponding duplicated segments have a divergence level of d, where 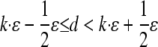. The divergence interval is chosen to be ε = 1% based on the sample size needed in each age group to draw statistical conclusions without being too affected by corrupting noise (see Table 5 in Supporting Appendix for details). This partition results in eight age groups after the duplications with extremely low divergence levels (d < 0.5%) are omitted because of their proneness to assembly errors. In the following text, we use the vector 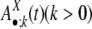to represent the frequencies of flanking region pairs in the kth age group with different configurations of the repeats from family at evolution time 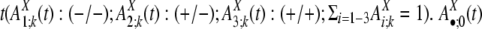represents the configurations of repeat X in the flanking regions of the new duplications at evolution time t. Let h₁ = 1 – h₀ represent the fraction of the duplications caused by the repeat recombination mechanism, and, among those, let 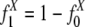represent the fraction mediated by repeat family X. (The product 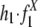represents the relative contribution of the repeat family X to the duplications through the recombination-like mechanism.) 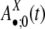can be expressed by using h₁, 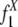, and X repeat distribution in randomly paired sequences from the genome (R_X) (for details, see Supporting Appendix). Our model tests the following hypotheses: null hypothesis, recombination between repeats from family X does not contribute to segmental duplications, i.e., 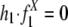; alternative hypothesis, recombination between repeats does contribute to segmental duplications, i.e., .

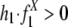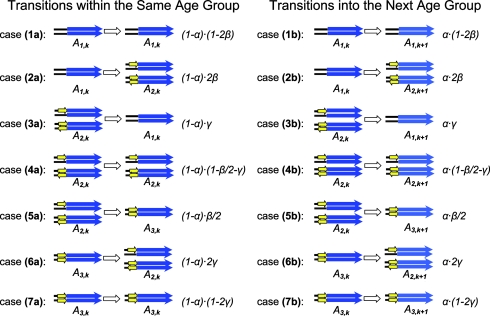
The model describes the dynamically changing state distribution of the flanking regions as a Markov process over evolutionary time under the effect of accumulating mutations and repeat amplifications. Table 1 lists in details all of the possible transitions between states in a small time interval (Δt) and the corresponding transition probabilities expressed in the evolutionary rates of the repeats and duplicated segments. A schematic representation of the model integrating the details in a small example is displayed in Fig. 2.

Table 1.

All possible transitions between different states of the duplication flanking regions in a short evolution period Δt

The state of the flanking region pair is defined by the configuration of the repeats (yellow arrows) in the flanking regions and the age group (k) of the duplicated segments (blue arrows) and is schematically displayed. Shown are all the possible transitions within the same age group (k), with the corresponding transition probabilities, and all the possible transitions into the next (older) age group (k to k + 1), with the corresponding transition probabilities. The transition probabilities are expressed by the evolution rates of the repeats and duplicated segments. α, the rate of duplicated segments evolving into an older age group in Δt; β, the insertion rate of the repeat in the flanking regions by mechanisms, such as retrotransposition, in Δt; γ, the decay rate of the repeats in the flanking regions due to mutations in Δt. (See Supporting Appendix for details.)

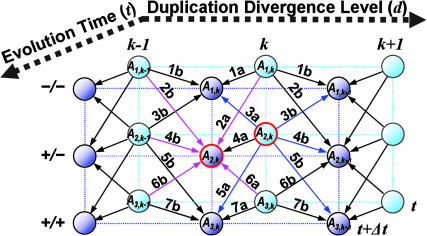
Fig. 2.

A schematic display of our mathematical model formulating the changes in the distribution of flanking region pairs over different states as a Markov process over evolution time. At a particular evolution time, t, the flanking region pairs are distributed over different states (circles), defined by the configuration of the repeats in the flanking region (–/–, +/–, or +/+) and the age group of the duplicated segments (k). During evolution, in each time interval Δt, the flanking region pairs may change their state through many possible transitions (arrows). The change in the distribution of the flanking region pairs in a particular state at time t +Δt from time t depends on how much has entered into this state from other states and how much has exited out of this state in interval Δt since time t. The in-flow and out-flow are the sum of the corresponding transition probabilities (1a-7a and 1b-7b), whose details can be found in Table 1. Take A_2,k (circled red) for example; at evolution time t, the flanking region pairs in state A_2,k can change into other states (blue arrows) in time interval Δt. At the same time, the flanking region pairs in other states can change into state A_2,k (maroon arrows). The difference between A_2,k(t) and A_2,k(t + Δt) can be calculated by taking the difference between the sum of the out-flows (blue arrows) and in-flows (maroon arrows). Given enough evolution time, the process will reach the stationary state, in which the distribution over different states does not change with time any more, because each state has identical in-flow and out-flow. In the A_2,k example above, the sum of the blue arrows is equal to the sum of the maroon arrows in the stationary state.

The model rests on two assumptions: First, the evolutionary dynamic rates and the mechanisms of segmental duplication as well as their relative contribution have been well conserved over a long period of evolutionary time. Second, the state distribution evolution in the flanking regions has reached its stationary state; i.e., despite the uninterrupted dynamic changes in the state of each individual flanking region pairs, the distribution over different states among all of the flanking region pairs stays unchanged. Formally, there exists a sufficiently large T, such that for any time t or s with t, 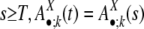, where k ≥ 0. For a detailed example of stationary states, see Fig. 2. Under those assumptions, we can evaluate the two free parameters of the model (h₁ and 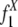) based on the observed data if the evolutionary rates are known (see Supporting Appendix for details).

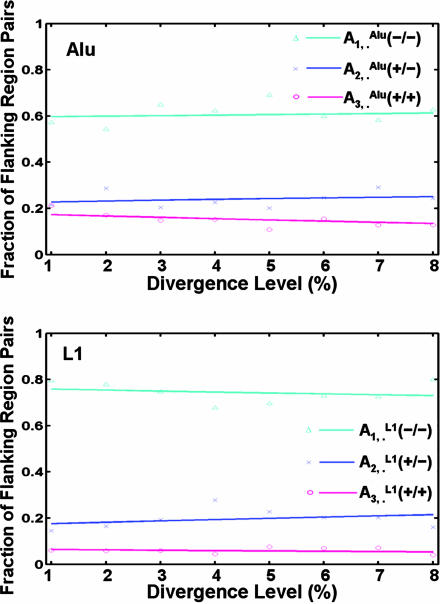
We applied the model to the duplication flanking regions in the human genome on the distribution of their states specified by repeats from the Alu (X = Alu) and L1 (X = L1) families, respectively, whose evolutionary rates have been well characterized (see Table 4) (9). Two different data sets (hg15 and hg16) (1, 2) were used. The free parameters in the model and their corresponding standard deviations were determined by cross-validation (see Methods). For both data sets (Fig. 3 and Fig. 9, which is published as supporting information on the PNAS web site), the model with the estimated parameters fit exceedingly well with the state distribution of the flanking regions specified by Alu repeats (P > 1–10^–4 in the goodness-of-fit test; see Supporting Appendix), whereas the null model (with 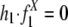; see Supporting Appendix) could not explain the observed Alu distribution adequately (P = 0.04). As expected, the null model explained the L1 distribution in the flanking regions quite well (P = 0.86), although the model with the estimated parameters did slightly better (P > 1–10^–4). See Table 2 for a list of the relative contributions of Alu and L1 by recombination to the recent segmental duplications in the human genome as estimated by the model.

Fig. 3.

The fitting of the model to the distribution of the Alu and L1 repeats in the duplication flanking regions in the human genome (hg16 shown here). The fractions of flanking region pairs with different repeat distribution patterns are computed in each group of different sequence divergence levels (d). We estimated the parameters and fitted our model to the distribution of Alu and L1 in the flanking region sequence pairs, respectively. The various symbols represent the real data, and the smooth lines are the theoretical trajectories of the model for the optimal choices of the parameters h₁ and f₁. The total number of flanking regions pairs is 4,894.

Table 2. The contribution of repeat recombination, estimated by the model from the data sets in different regions.

Data set	Flanking, %	Permuted, %	Inside, %	Outside, %
Alu(hg15)	12.1 ± 1.4	0.5 ± 2.3	91.8 ± 2.2	3.8 ± 0.8
Alu(hg16)	12.9 ± 1.0	0.2 ± 1.3	92.5 ± 1.3	3.7 ± 0.7
L1(hg15)	3.1 ± 1.0	0.4 ± 1.5	92.1 ± 1.8	2.7 ± 1.0
L1(hg16)	6.9 ± 1.1	0.8 ± 2.0	92.7 ± 1.4	2.7 ± 1.0

Shown are data from the original data set from the duplication flanking regions, the permuted data set from the flanking regions, the data set from the regions inside the duplication, and the data set from the regions outside the duplication, far away (>3,000 bp) from the breakpoint. All the data are shown as mean ± SD (for more detailed results, see Supporting Appendix).

To further measure the significance of the contribution to the duplication process by the recombination in these two repeat families, we compared the estimated contribution (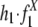) from the original data set to three control data sets: The permuted data set is created by randomly switching the partners in the flanking region pairs while preserving the total repeat frequencies. The outside and inside data sets are obtained from positions farther outside or inside the duplicated regions, respectively. The results are listed in Table 2. As anticipated by the model, the estimated contributions in the permuted and outside data, where random distribution is expected, are very close to 0; whereas in the inside data, where no random distribution is expected, the estimations are very close to 1 (Table 2). The contribution of Alu recombination to the duplication () estimated from flanking data is ≈12%, which is significantly higher than the estimation from the permute and outside data sets. However, the contribution of L1 recombination estimated from the flanking data set is much lower and does not differ significantly from either the permute or outside data set.

The hg15 and hg16 data sets were independently mapped by different research groups using different strategies (1, 2), and it has been shown that the earlier map (hg15) contains more artifacts caused by assembly errors than the later one (2). Despite such differences, the model still gives consistent results between the two assemblies. It is also reassuring to find that, for both repeat families, the model estimated that the fraction of the duplications caused by the recombination-like mechanism (h₁) is ≈30% (for details, see Supporting Appendix), although their contributions to the duplication mechanisms are quite different. The consistency in the parameter values suggests the robustness of our model against errors in assembly, mapping, and annotation. This robustness is mostly due to the parsimony of the model and the way in which the model accounts for a reasonable amount of errors and efficiently removes the corrupting noise.

For the mouse and rat genomes, a good estimation of the evolutionary dynamic parameters of the interspersed repeats is still lacking. Furthermore, the available duplication mappings in the rodent genomes are likely to be less accurate because of the unfinished status of the genome assemblies (3, 5). Those factors prevented us from applying the model accurately to the rodent data sets as we did for the Alu and L1 repeats in the human genome. However, if one approximates the mutation rates in the rodent genomes by doubling the corresponding rates in the human genome and the rodent L1 insertion rate by tripling the human L1 insertion rate, then it is possible to reach a fairly good fitting for the L1 distribution in the mouse and rat data sets (Fig. 9). The contribution of the L1 repeats to the recent segmental duplications through the recombination-like mechanism is then estimated at ≈10% in the rodent genomes.

In conclusion, in all of the mammalian genomes examined, our model estimates that ≈10–12% of the recent segmental duplications were caused by the recombination between the most active interspersed repeat elements in the genome (Alu in human and L1 in rodents). The results from the model further suggest that the segmental duplications are likely to be caused by multiple mechanisms, and a large fraction (≈70%) of the duplications are caused by some unknown mechanism independent of the interspersed repeat distributions, which is consistent with the conclusions of ref. 20.

Further Sequence Analysis: Physical Properties. In the process of searching for repeat-independent mechanisms, we discovered an enrichment of DNA sequences that are physically unstable around the duplication boundaries. The physical properties of the DNA duplex plays an important role as the initial step in many molecular processes, as shown in transcription (21), replication (22), and the large genome rearrangement events that originated from the chromosomal fragile sites (10, 11). Therefore, it is possible that similar properties can initiate or facilitate the segmental duplication process in the mammalian genomes.

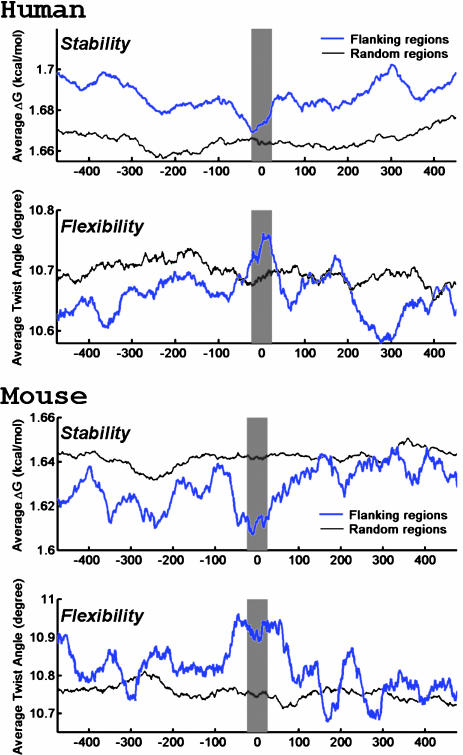
To explore possible repeat-independent explanations and to avoid the bias introduced by the AT-rich regions in Alu and L1 repeats, we analyzed the flanking sequences that do not contain any repeats for their helix stability (15) and DNA flexibility (16) (see Methods for details). These two features are suggested to be the specific characteristics of the fragile sites in the genome where genetic rearrangements frequently occur (10, 11). In the mouse and human data sets, there is a slight decrease of the average helix stability and an increase of the average DNA flexibility at the duplication junction compared with the other regions either inside or outside the duplicated segments (Fig. 4). To test the significance of these observations, we counted the number of duplication junctions (–250 to +250 bp flanking the boundary) that contain sequence sites with both exceptionally low helix stability and exceptionally high flexibility. The criteria for recognizing such a site is that the average ΔG in its centering 50-bp window is <1.3 kcal·mol^–1·bp^–1 (the bottom 0.5% of random genomic sequences) and that the average twist angle is >14° per bp (the top 0.5% of random genomic sequences) (10, 11). We found enrichment of such potential fragile sites in the repeatless duplication flanking regions from all of the three mammalian genomes compared with the randomly selected genomic regions (Table 3). The enrichment of these characteristic sites is statistically significant in all of the data sets, except in the rat genome, where it is just on the verge of being significant. Interestingly, the significance level increases with the degree of finishing of the genome assemblies, suggesting that the lack of significance in the rat genome could be explained by the incompleteness of the current assembly.

Fig. 4.

The helix stability and DNA flexibility in the repeatless duplication flanking sequences in the human (hg16 shown here) and mouse genomes. The average helix stability and the average DNA flexibility in the flanking regions around the duplication junction (blue line) and the repeatless random genomic regions (gray line) are estimated by the average ΔG and the average helix twist angle in overlapping 50-bp windows, respectively. The shaded regions indicate the duplication junction where there is a slight decrease in the helix stability and a slight increase in the DNA flexibility. The mapped duplication boundary is at 0 bp, the negative base pair positions are coordinates outside the duplicated region, and the positive base pair positions are coordinates inside the duplicated region.

Table 3. The enrichment of the fragile sites in the repeatless duplication flanking sequences in different mammalian genomes.

Genome	Flanking, % (n)	Random, % (n)	Fold	P value
Human (hg16)	4.82 (2,052)	1.99 (2,964)	2.42	<10-7
Human (hg15)	3.81 (2,863)	2.41 (5,280)	1.58	<10-5
Mouse (mm3)	3.68 (815)	2.51 (2,632)	1.47	<0.05
Rat (rn3)	4.21 (570)	2.76 (1,123)	1.53	0.07

Listed are the percentages of the flanking and random regions containing fragile sites and the total number of sequences examined. Also shown are the folds of enrichment. The significance of the enrichment (P values) was computed by using two-sample t tests for binomial proportions.

The overrepresentation of sequences with physical features similar to the fragile sites in the duplication flanking regions suggests that segmental duplications may share a mechanism linked to genetic instability. Although these results represent evidence for the hypothesis that some repeat-independent mechanism is involved in the recent mammalian segmental duplications, the hypothesis needs to be explored further.

Discussion

From previous studies (2) and our detailed analysis on gaps and shifts in the duplication flanking regions (see Figs. 5–7), we conclude that the current map of segmental duplications is still tainted with errors from assembly, mapping, and annotation. In the presence of these errors, an analysis on sequences strictly at the mapped duplication boundaries will underestimate or even diminish the signals left by the repeat recombination. Using a flanking region size that allows some gaps and shifts helps us to minimize the effect of these errors on our analysis. In addition, by incorporating our knowledge of the related evolutionary processes in the dynamic model, it was possible to decrease the effect of random noise. Therefore, despite the nature of the data, our method was found to be quite robust. Of course, the accuracy of the results will increase with the finishing stages of the genome assembly and the improvement on the mapping and annotation schemes.

Interspersed segmental duplications are significantly more abundant in the human genome than in the rodent genomes (3–5). It was suggested that the difference is due to the recent burst of primate Alu retrotransposition activity (8). However, the rough estimations from our model suggest that the relative contribution from the most active repeats through the recombination-like mechanism remains more or less constant in the human and rodent genomes. Therefore, the answer to why the genomes have different amounts of segmental duplications is to be sought elsewhere [for example, the difference in the tolerance for large duplications, the difference in effective population sizes, or the finishing stage of the genome assembly (23)].

Segmental duplications have been shown to be associated with the genome rearrangement events during species evolution (24, 25) and the copy number fluctuations (26–29) and other rearrangements (30) in genomic sequences during cancer development. Therefore, some of the mechanisms used by segmental duplications, such as recombination mediated by interspersed repeats (31, 32), may be shared by other genomic rearrangement events. Suggested by the fragile sites we found in the duplication flanking sequences and their association with the breakpoints of the syntenic blocks (24, 25), perhaps another common mechanism could be correlated to the specific physical properties in the DNA sequences. In fact, it has been suggested that segmental duplications in yeast are caused by breakage-induced-replications induced by replication fork stalling at the AT-rich replication termination sites (33). These topics of future research may rely on mathematical models akin to the ones proposed here.