Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Aug 8.
Published in final edited form as: Nat Methods. 2016 Mar 28;13(5):443–445. doi: 10.1038/nmeth.3809

Sparse PCA Corrects for Cell-Type Heterogeneity in Epigenome-Wide Association Studies

Elior Rahmani 1, Noah Zaitlen 2, Yael Baran 1, Celeste Eng 2, Donglei Hu 2, Joshua Galanter 2,3, Sam Oh 2, Esteban G Burchard 2,3, Eleazar Eskin 4,5, James Zou 6, Eran Halperin 1,7,8
PMCID: PMC5548182  NIHMSID: NIHMS889019  PMID: 27018579

Abstract

In epigenome-wide association studies (EWAS), different methylation profiles of distinct cell-types may lead to false discoveries. We introduce ReFACTor, a method based on principal component analysis (PCA) for the correction of cell-type heterogeneity in EWAS. ReFACTor does not require knowledge of the cell counts, and it obtains improved estimates of the cell-type composition, resulting in improved power and control for false positives in EWAS. Corresponding software is available from http://www.cs.tau.ac.il/~heran/cozygene/software.shtml

Main Text

Recent work applying EWAS suggests an important role for DNA methylation as a mechanism involved with disease. In a standard EWAS of primary tissue such as whole-blood, methylation data represent the epigenetic states of a heterogeneous mixture of cell-types. Since the epigenome is highly variable across different cell-types, correlations between the phenotype of interest and the cell-type composition lead to a large number of false discoveries1,2.

The standard statistical analysis applied in EWAS uses a univariate test for correlation between the phenotype and each of the probed CpG sites. Thus, false discoveries due to cell-type heterogeneity can be addressed by adding the cell proportions as covariates. However, cell-type compositions are typically not measured and therefore a computational method has been proposed for the estimation of cell-type composition using a reference dataset which includes methylation measurements for sorted cells3. Unfortunately, reference data of whole-genome methylation levels from sorted cells are available for a small subset of different blood cells, and are not available for other tissues. Furthermore, the existing datasets are small3,4, and the individuals in the reference data are not matched for methylation altering factors such as age and sex, which may lead to inaccuracies in the cell-type estimates. Due to the above limitations, reference-free methods, which do not rely on external reference data have been proposed2,5.

We show that none of the current methods adequately controls for false positives and we present a new method, Reference-Free Adjustment for Cell-Type composition (ReFACTor), to address the shortcomings of current methods. ReFACTor is based on a variant of PCA, and it does not require a reference dataset, thus it can be applied to any tissue. PCA is a natural candidate for correction of cell-type heterogeneity, since the first several principal components (PCs) are correlated with cell-type composition6. However, only a small number of sites are significantly different between cell-types (known as differentially methylated regions, or DMRs), therefore using all the sites in PCA potentially reduces the correlation. Motivated by this observation, ReFACTor performs PCA on a subset of the sites that are differentially methylated across the different cell-types rather than a PCA on the entire set of CpG methylation sites. Specifically, ReFACTor selects the sites that can be reconstructed with low error using a low rank approximation of the original methylation matrix. Thus, in contrast to other methods in which unsupervised site selection is performed (e.g., FaST-LMM-EWASher2), ReFACTor does not use the phenotype in the selection process, making it useful as part of a quality control step in EWAS.

We evaluated the ability of ReFACTor to capture cell-type composition by simulations and real data. We first simulated mixture of cell-types and measured the correlation of the PCs of ReFACTor (ReFACTor components) with the cell proportions. We observe that the correlation between each of the cell-types and the linear predictor of the cell-type using the first several ReFACTor components is substantially improved compared to the first several PCs of a standard PCA. These results were robust to the simulation parameters (see Online Methods and Supplementary Fig. 1–3).

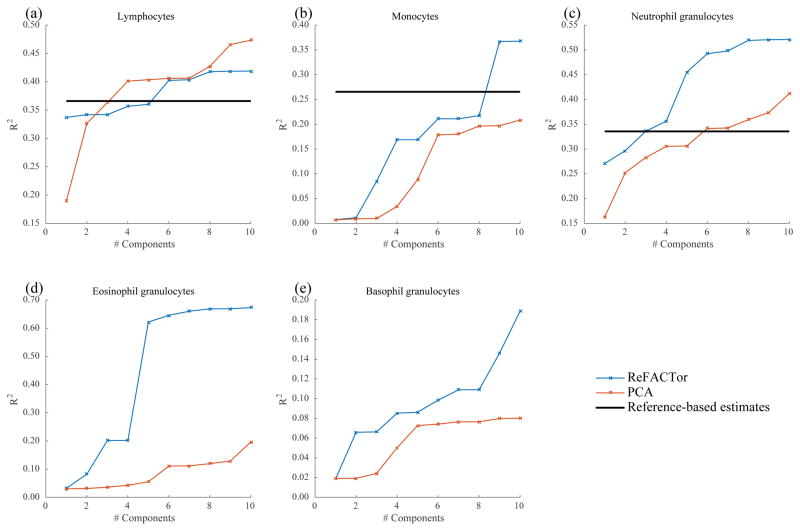
Next, we measured the performance of ReFACTor on real data from the GALA II dataset7 (n=489). The GALA II cohort contains whole-blood methylation data as well as cell count measurements for 78 of the samples, allowing us to evaluate the correlation between the measured cell-type proportions and the inferred ReFACTor components. We compared the results of ReFACTor to PCA, and to the available reference-based method3 (Fig. 1). Overall, ReFACTor’s correlation with the cell-type proportions is higher than PCA’s, and it outperforms the reference-based method with six components, the number of cell-types it estimates, even though the reference-based method leverages external data not available to ReFACTor. Although cell counts can potentially be used to adjust for tissue heterogeneity in EWAS, we observe that false discoveries can arise in the common case where cell counts are measured or estimated only for a small number of preselected cell-types (see Supplementary Note). False discoveries particularly arise in the absence of cell counts for cell-types that are correlated with the phenotype. In contrast, we find that ReFACTor’s PCs provide a good correction in such settings (Supplementary Tables 1–2 and Supplementary Fig. 4–5).

Figure 1.

Figure 1

Open in a new tab

The fraction of variance explained in each of the cell-types for which cell counts were available in the GALA II dataset (78 samples). The ReFACTor components are in blue, the PCs of standard PCA are in red, and the available estimates of the reference-based method are in black. (a) Correlation with lymphocytes cell count as a function of the number of components used in the linear predictor (squared linear correlation). (b) Correlation with monocytes cell count. (c) Correlation with neutrophil granulocytes cell count. (d) Correlation with eosinophil granulocytes cell count. (e) Correlation with basophil granulocytes cell count.

We further evaluated the control for false positives of ReFACTor using simulations. For each simulated dataset we generated a phenotype using a linear model of the cell-type proportions and a randomly chosen causal methylation site (Online Methods). We compared five approaches for EWAS analysis: uncorrected linear regression, linear regression with PCA, linear regression using ReFACTor components, FaST-LMM-EWASher2, and RefFreeEWAS5. We found that none of the methods adequately controls for false positives, however, ReFACTor obtains a significantly reduced level of false discoveries (Supplementary Fig. 6).

We compared the fraction of simulated datasets in which the truly associated methylation site obtained the best p-value (the detection power). We observe that the detection power was significantly higher using ReFACTor compared to other methods (Supplementary Fig. 7). We further considered the scenario in which the methylation differences in the causal site between the various levels of the phenotype are cell-specific, and where multiple sites are causal (Online Methods). In both scenarios ReFACTor outperforms all other methods (Supplementary Fig. 8–9).

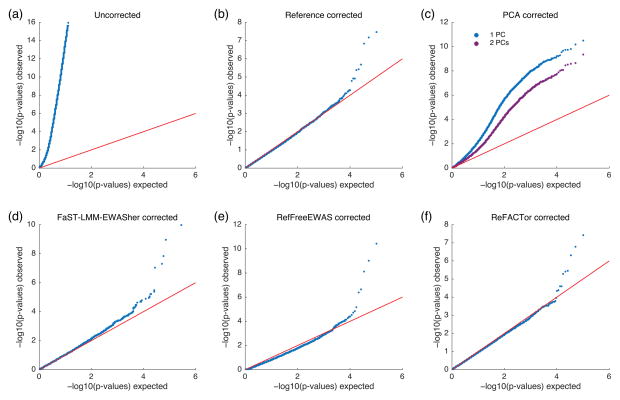
The correlation between the cell-type composition and ReFACTor’s PCs potentially allows for an improved correction of EWAS. We performed an EWAS using whole-blood methylation data from a recent study with rheumatoid arthritis (RA)8. Since the cell composition in blood of RA patients typically differs from the general population9, there is a risk for false discoveries that stem from unaccounted cell-type heterogeneity. We performed different approaches for correction of false discoveries (Fig. 2). As a baseline, we performed a logistic regression without adjusting the data for cell composition, resulting in a severe inflation of the test statistic, consistent with the results reported in previous studies2,5,8. We then adjusted the data using the estimates of the cell-type proportions obtained by the reference based method3. This correction removed the inflation by eliminating the cell composition confounder. We then proceeded with unsupervised methods for cell-type correction, namely using the first several PCs of a standard PCA, FaST-LMM-EWASher2 and RefFreeEWAS5. None of these unsupervised approaches were able to reconstruct the results obtained using the reference-based approach. In contrast, adjusting the data with only one ReFACTor component eliminated the inflation and revealed the three significant associations that were found by the reference-based approach (Supplementary Table 3).

Figure 2.

Figure 2

Open in a new tab

Results of the RA methylation analysis, presented by quantile-quantile plots of the –log10 p-values for the association tests. Significant deviation from the red line indicates an inflation arising from a confounder in the data. (a) No correction. (b) Correction using the reference-based estimates of the cell-type proportions. (c) Correction using the first couple of PCs of a standard PCA. (d) Correction using RefFreeEWAS. (e) Correction using FaST-LMM-EWASher. (f) Correction using the first ReFACTor component.

In conclusion, we observe that both ReFACTor and the reference based method resulted in a small number of significant sites in comparison to the uncorrected analysis. Theoretically, both of these methods might have over-corrected true signals. In order to exclude this possibility, we repeated the analysis where the set of sites chosen for the PCA step of ReFACTor were selected by considering only the controls and discarding the cases. This procedure also resulted with the same three associated sites (Supplementary Fig. 10). Since the PCA was performed on a small number of sites selected using a group of healthy samples, an over-correction is not likely in this case.

Similar to PCA, ReFACTor allows the flexibility to efficiently perform any desired downstream analysis once regressing out the ReFACTor components, such as association test for a large number of phenotypes, or logistic regression for dichotomous phenotypes. For example, this allows running permutation tests efficiently since the permutation needs to be performed on the residuals of the methylation data after regressing out the ReFACTor components. We note that in principle modifications of other existing methods2,5 could lead to similar utility in those methods.

The underlying assumption of ReFACTor is that the confounders are affected by a sparse set of methylation sites. Future work may further improve the performance of ReFACTor by using other feature-selection algorithms, as well as by optimizing the selection of the dimension parameters used in the algorithm.

Although our experiments focused on cell-type composition, we believe that ReFACTor is likely to perform well on other unknown confounders in EWAS. Other known confounders such as sex and age are also affected by a sparse set of CpGs10,11. However, as in any other unsupervised method, it is important to consider the possibility that an unknown confounder was not captured by the method due to deviations from the assumptions. Moreover, since ReFACTor corrects principal components of a set of DMRs, if by chance many of these DMRs are causal, ReFACTor will result in over-correction and loss of power. Our suggested approach in which the DMRs are chosen based on the controls alone should alleviate this potential risk.

Online Methods

The ReFACTor Algorithm

We assume that methylation levels have been measured at m methylation sites across n individuals. Let Oi be an m×1 vector of observed beta normalized methylation levels in an individual i, and let Ri be a k×1 vector corresponding to the individual’s specific cell-type composition. That is, Rhi is the fraction of cell-type h in individual i. Furthermore, let M be an m×k matrix corresponding to the mean value of each site for each cell-type, i.e., Mjh is the mean methylation value of cell-type h at CpG site j. The following generative model motivates the approach taken in ReFACTor. We assume the methylation level at site j cell-type h to be normally distributed with mean Mjh, and that the methylation measurement error is also normally distributed with mean 0. Thus, the model we assume can now be summarized as

Oi=MRi+εi,

where εi is normally distributed. Effects known to be correlated with methylation (e.g., age10, sex11, smoking12 and DNA sequence variation13,14) can be added to the model as fixed linear effects and can be regressed out.

In theory the variance of εji should depend on both i and j, or more precisely on j and on ∑hRhi2. However, we found that empirically reconstructing R is more robust when we make the relaxing assumption that εji~N(0,σj2). If we relax the non-negativity assumption of the entries of M and R, we obtain a formulation that is equivalent to factor analysis, and when σj is equal for all j the formulation is equivalent to PCA. We make the additional assumption that only a small subset of the sites are highly affected by R. Put differently, most rows of M are constant or near-constant, and only t rows of M are highly informative with respect to R, corresponding to the DMRs. This assumption is based on previous studies that considered only a small subset of sites for capturing the tissue composition1,3,6.

The ReFACTor algorithm gets as an input an observed m×n methylation matrix O, after centering and standardization of each site, the number of assumed cell-types k in the data, and the number of DMRs t, and its goal is to find R̂ that is correlated with the real cell-type proportions R. The algorithm proceeds as follows.

  1. Find a matrix V of dimensions m×k, consisting of the top k left-singular vectors of O (i.e., the top k eigenvectors of OtO).

  2. Compute Õ=VVtO, which is the k-rank approximation to O.

  3. For each site j, let d(j) be the distance between the jth row of O and the jth row of Õ.

  4. Construct O′ from O by taking a subset of the t rows with the lowest distances.

  5. Run PCA on O′, and return R̂, an estimate of R given by the solution (the scores of the first k principal components).

Intuitively, d(j) is low when the k-rank approximation of O approximates the jth row of O well. Therefore, sites with a low value of d(j) are more likely to be DMRs, assuming the first k PCs correspond to cell-type composition. Sites with high distances are more likely to be uncorrelated with the cell-type composition, and therefore removing them from the analysis results in a better correlation with the true cell-type composition. We note that the suggested approach captures the cell-type composition better than both common methods used in deconvolution of RNA expression data and an alternative approach in which we select the top t most variable sites (Supplementary Fig. 11 and 12).

The algorithm will scale to any sample size achievable by a PCA implementation, as the running time is dominated by the calculation of the k top left-singular vectors of O. The runtime of singular value decomposition is quadratic in the number of samples, however more efficient methods such as the power method or sampling techniques15,16 may result in considerably reduced runtime. Empirically, under a standard implementation of PCA, ReFACTor required no more than several minutes of execution time on all the datasets described here.

In principle, in the above procedure, one would want to use factor analysis instead of PCA, i.e., assume that different sites have different values of σj. Factor analysis is performed in iterations, where in each iteration the values of each site are scaled. The first iteration of factor analysis is equivalent to PCA after standardization of each of the sites, which is the step taken in ReFACTor. Empirically, applying more iterations of the factor analysis did not improve the performance, and the value of σj was close to the value inferred in the first iteration (data not shown).

The ReFACTor components can be added as covariates to an EWAS. In case of an inflated test-statistic due to cell-type composition, ReFACTor components can be added one by one until the desired decrease in inflation is achieved, similar to the approach suggested by Zou et al.2.

Parameters selection

Throughout the analysis we applied ReFACTor on the data with the top t=500 most informative methylation sites, consistent with a line of previous work that used subsets of 500–600 informative sites for capturing the cell-type composition1,3,6. We set k=6 to align with the number of cell-types estimated in whole blood by the reference-based approach, and throughout the paper, unless mentioned otherwise, we used the first six ReFACTor components in the analysis of real data and the first five components in the analysis of simulated data (simulated with k=5). The performance of ReFACTor was robust to a wide range of choices of t and to the choice of k (Supplementary Fig. 13–16).

Datasets and quality control

In order to evaluate the performance of ReFACTor, we used whole-genome methylation data from the GALA II dataset7, a pediatric Latino populations study. The study protocol was approved by the UCSF Human Research Protection Program and IRB approved informed consent was obtained from all participants prior to any study procedure. Blood samples were collected from 573 participants and assayed on an Illumina 450K DNA methylation chip. Additional blood samples were collected for 95 of the samples four months later, for obtaining cell counts. A complete blood count with automated white blood cell differential was performed by automated flow cytometry at CLIA certified laboratories (UCSF Medical Center, San Francisco, CA and Quest Diagnostics, Madison, NJ). Note that the results showing the correlation of ReFACTor to the cell counts (Fig. 1) demonstrate that methylation levels can predict cell-type composition in the future, which is most likely due to the fact that cell-type composition is stable over time. Out of the total 573 samples, 525 samples were available at the time of analysis (a subset of the individuals for which genotypes were collected as well as part of the GALA II study). Samples with inconsistencies in the available identifiers conversion file (between genotypes and methylation data) were dropped. In addition, samples that demonstrated extreme values in the first two principal components on the methylation levels were removed (more than 2 standard deviations). A total of 489 samples remained for the analysis (245 males and 244 females), and for 78 of them cell count measurements were available for five different cell-types: lymphocytes, monocytes, and three granulocytes subtypes - neutrophils, eosinophils, and basophils. Probes from sex chromosomes were discarded, as well as consistently methylated probes and consistently unmethylated probes (mean value higher than 0.8 or lower than 0.2, respectively), as was previously suggested for EWAS8, resulting in 102,503 probes that were included in the analysis. The data were SWAN17 normalized and corrected for batch using COMBAT18. For the analysis, we estimated cell proportion levels of CD8T, CD4T, NK cells, B cells, monocytes and granulocyte cells, using an existing reference-based approach3. In order to compare between the cell proportion estimates and the available cell counts, we collapsed the four estimates of lymphocyte cell-types (CD8T, CD4T, NK cells and B cells) into a single combined lymphocytes levels. For both the COMBAT normalization and the estimation of cell proportions we used the minfi package19. The GALA II methylation data is now publicly available in the Gene Expression Omnibus (GEO) database (accession number GSE77716).

We also measured the performance of ReFACTor on a dataset that was first studied in a recent association study of DNA methylation with rheumatoid arthritis (RA), including 354 cases and 332 controls8 (193 males and 493 females). Blood samples were collected from the participants and assayed on an Illumina 450K DNA methylation chip. The data are publicly available and were downloaded from the GEO database (accession number GSE42861). We repeated the quality control procedure for the data applied in a recently published work2 on the same data - filtered out consistently methylated probes and consistently unmethylated probes (mean value higher than 0.8 or lower than 0.2, respectively), as previously suggested8, resulting in 103,638 probes that were included in the analysis. The probe values were corrected for age, sex, smoking and batch using linear regression. For these data, we estimated cell proportion levels of T cells, NK cells, B cells, monocytes and granulocyte cells, similarly as was done for the GALA II dataset.

ReFACTor’s site selection

Informally, the sites selected by ReFACTor are chosen so that they are well approximated by Õ, the low rank approximation of the original methylation matrix O. Put differently, in Õ the jth row corresponds to an approximation of the jth methylation site (the jth row of O). Since the low rank approximation uses the eigenvectors of OtO, similarly to PCA, it maximizes the variance of the resulting low dimensional space defined by the k top eigenvectors. Thus, methylation sites that are highly variable across different cell-types (or generally across different values of a the main confounders) are expected to contribute substantially to the low rank approximation, and they will therefore be well approximated by the ReFACTor procedure. For a comparison between the feature selection and algorithmic details underlying ReFACTor and those of other methods see Supplementary Table 4.

Indeed, we found 90 methylation sites in the intersection of the 500 sites determined as the most informative by ReFACTor on the GALA II data, and the list of top DMRs previously reported in leukocyte cells1 based on sorted leukocytes4 (p-value<10−50, hypergeometric test). We also found 100 methylation sites in the intersection between the 500 sites determined as the most informative by ReFACTor on the RA data, and the list of DMRs previously reported in leukocyte cells1 based on sorted leukocytes4 (p-value<10−50, hypergeometric test). Remarkably, we found most of the sites selected by ReFACTor for the RA data to be the same sites selected for the GALA II data (270 sites in the intersection; p-value<10−50, hypergeometric test).

Data simulation

The methylation data were generated using a generative model in which a fraction p of the sites are DMRs; for each DMR we assume a normal distribution per cell-type (with a potentially unique mean for each cell-type). In non-DMR sites the mean methylation values of all cell-types are equal. Each site was assumed to have a unique variance. The parameters of the model were set according to a methylation reference of sorted white blood cells (assayed on an Illumina 450K platform)4. The reference data are publicly available and were downloaded from the GEO database (accession number GSE35069). Since the reference includes only six individuals, we assume that the mean values of the cell-types in DMRs are generated from a normal distribution with a standard deviation τ (shared across all DMRs). Thus, τ controls the level of cell composition information in DMRs. DNA methylation data were generated from a normal distribution (conditional on the range [0,1]) for five cell-types per individual i and per site j, and cell-type proportions were generated from a Dirichlet distribution. Finally, observed DNA methylation levels were composed for each individual by its simulated methylation levels and cell proportions. A random normal noise was added to every site to simulate technical noise (σ=0.01).

DNA methylation levels were simulated for the same set of 103,638 sites used in the RA analysis, and the Dirichlet parameters were estimated from the cell-type proportion estimates of the same data. Every simulated dataset included 500 individuals. We estimated τ from the reference of sorted cells using maximum likelihood and found that τ=0.07 fits the data best. The parameters of the normal distributions for generating the methylation levels were estimated from the reference as well. The proportion of DMRs was set to be p=0.07, following a previous report, in which the authors used the same reference of sorted cells in order to detect DMRs1. Applying a Bonferroni correction for multiple hypotheses correction results in about 15% of the sites crossing the significance threshold.

We simulated three scenarios in order to evaluate the detection power of the methods. First, we generated continuous phenotypes using a linear model of the cell composition, a causal methylation effect and a randomly distributed noise. The causal methylation site was randomly chosen, as well as one of the cell-types which was used in the linear model. The effect size of the cell-type was sampled from a standard normal distribution. We used several different levels for the effect size of the causal site. In the second set of simulations the phenotypes were simulated by a linear model of the cell composition, the methylation levels of a randomly chosen site in a randomly chosen cell type (as opposed to total methylation level at the causal site), and random noise. Finally, in a third set of simulations we simulated ten causal sites; we simulated the phenotype as a linear function of a randomly chosen cell-type, and then we randomly picked 10 sites and added to their methylation levels a linear dependency in the phenotype, with varying effect sizes. In these simulations methylation levels were simulated only for the 10,686 sites from chromosome 1 that were available in the RA data. The restriction to a small number of sites was done to reduce runtime - a few of the methods we assessed are computationally intensive and running hundreds of simulations becomes computationally prohibitive.

Estimating white blood cell proportions

Estimates were obtained using the default sites implemented in the minfi package19, defined and assembled for the 450K array1 based on the approach described by Houseman et al.3 and 450K reference data4.

FaST-LMM-EWASher and RefFreeEWAS

We executed FaST-LMM-EWASher2 and Ref-FreeEWAS5 using the default parameters. For the latter, we used 250 bootstraps in each execution and applied the methodology proposed by the author for determining the dimension parameter d (determined d=46 for the GALA II dataset and d=43 for the RA dataset).

Code availability

Python and R software associated with our method is available online (http://www.cs.tau.ac.il/~heran/cozygene/software.shtml), accompanied by a complete set of documentation and instructions. Additional tools for guiding the parameters selection for the ReFACTor algorithm are provided as well.

Supplementary Material

Supplementary

Acknowledgments

The authors acknowledge the families and patients for their participation and thank the numerous health care providers and community clinics for their support and participation in GALA II. In particular, the authors thank study coordinator S. Salazar; the recruiters who obtained the data: D. Alva, G. Ayala-Rodriguez, L. Caine, E. Castellanos, J. Colon, D. DeJesus, B. Lopez, B. Lopez, L. Martos, V. Medina, J. Olivo, M. Peralta, E. Pomares, J. Quraishi, J. Rodriguez, S. Saeedi, D. Soto, A. Taveras. E.H. is a faculty fellow of the Edmond J. Safra Center for Bioinformatics at Tel Aviv University. E.R. and Y.B. received fellowships from the Edmond J. Safra Center for Bioinformatics at Tel-Aviv University. E.H. and E.R. were supported in part by the Israel Science Foundation (Grant 1425/13), Y.B. and E.H. by the United States-Israel Binational Science Foundation (Grant 2012304). Y.B., E.H., and E.R. were partially supported by the German-Israeli Foundation (Grant 1094-33.2/2010), and by the National Science Foundation (Grant III- 1217615). E.R. was supported by Len Blavatnik and the Blavatnik Family Foundation. Y.B. has received a scholarship by the Dan David Prize. E.E. is supported by National Science Foundation grants 1065276, 1302448, 1320589 and 1331176, and National Institutes of Health grants R01-GM083198, R01-ES021801, R01-MH101782, R01-ES022282 and U54EB020403. This research was supported in part by the Sandler Foundation and the American Asthma Foundation, the National Institutes of Health (R01 ES015794, R01 HL088133, M01 RR000083, R01 HL078885, R01 HL104608, P60 MD006902, U19 AI077439, M01 RR00188); N.Z. was supported in part by an NIH career development award from the NHLBI (K25HL121295). J.G. was supported in part by NIH Training Grant T32 (GM007546) and career development awards from the NHLBI K23 (K23HL111636) and NCATS KL2 (KL2TR000143) as well as the Hewett Fellowship; This publication was supported by various institutes within the National Institutes of Health. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

Footnotes

Accession codes

The GALA II methylation data is now publicly available in the Gene Expression Omnibus (GEO) database (accession number GSE77716). The RA data are publicly available and were downloaded from the GEO database (accession number GSE42861). Methylation levels of sorted white blood cells for the simulations were downloaded from the GEO database (accession number GSE35069).

Author Contributions

E.R. and E.H. designed research, performed research, contributed analytic tools, analyzed data and wrote the paper. N.Z. and E.E helped with experiments design, data interpretation and in drafting the paper. Y.B. and J.Z. contributed expertise. C.E., D.H., J.S., S.O. and E.B. generated and contributed the data. D.H. also performed quality control analysis.

Competing financial interests

The authors declare no competing financial interests.

References

  • 1.Jaffe AE, Irizarry RA. Accounting for cellular heterogeneity is critical in epigenome-wide association studies. Genome Biol. 2014;15:R31. doi: 10.1186/gb-2014-15-2-r31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Zou J, Lippert C, Heckerman D, Aryee M, Listgarten J. Epigenome-wide association studies without the need for cell-type composition. Nat Methods. 2014;11:309–311. doi: 10.1038/nmeth.2815. [DOI] [PubMed] [Google Scholar]
  • 3.Houseman EA, et al. DNA methylation arrays as surrogate measures of cell mixture distribution. BMC Bioinformatics. 2012 doi: 10.1186/1471-2105-13-86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Reinius LE, et al. DNAifferential DNA methylation in purified human blood cells: implications for cell lineage and studies on disease susceptibility. PLoS One. 2012;7:e41361. doi: 10.1371/journal.pone.0041361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Houseman EA, Molitor J, Marsit CJ. Reference-free cell mixture adjustments in analysis of DNA methylation data. Bioinformatics. 2014;30:1431–1439. doi: 10.1093/bioinformatics/btu029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Koestler DC, et al. Blood-based profiles of DNA methylation predict the underlying distribution of cell types: a validation analysis. Epigenetics. 2013;8:816–826. doi: 10.4161/epi.25430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Pino-Yanes M, et al. Genetic ancestry influences asthma susceptibility and lung function among Latinos. J Allergy Clin Immunol. 2015;135:228–235. doi: 10.1016/j.jaci.2014.07.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Liu Y, et al. Epigenome-wide association data implicate DNA methylation as an intermediary of genetic risk in rheumatoid arthritis. Nat Biotechnol. 2013;31:142–147. doi: 10.1038/nbt.2487. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Goronzy JJ, et al. Dominant clonotypes in the repertoire of peripheral CD4+ T cells in rheumatoid arthritis. J Clin Invest. 1994;94:2068. doi: 10.1172/JCI117561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Horvath S. DNA methylation age of human tissues and cell types. Genome Biol. 2013;14:R115. doi: 10.1186/gb-2013-14-10-r115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Singmann P, et al. Characterization of whole-genome autosomal differences of DNA methylation between men and women. Epigenetics Chromatin. 2015;8:1–13. doi: 10.1186/s13072-015-0035-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Zeilinger S, et al. Tobacco smoking leads to extensive genome-wide changes in DNA methylation. PLoS One. 2013;8:e63812. doi: 10.1371/journal.pone.0063812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Shoemaker R, Deng J, Wang W, Zhang K. Allele-specific methylation is prevalent and is contributed by CpG-SNPs in the human genome. Genome Res. 2010;20:883–889. doi: 10.1101/gr.104695.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Wagner JR, et al. The relationship between DNA methylation, genetic and expression inter-individual variation in untransformed human fibroblasts. Genome Biol. 2014;15:R37. doi: 10.1186/gb-2014-15-2-r37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Halko N, Martinsson PG, Tropp JA. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 2011;53:217–288. [Google Scholar]
  • 16.Abraham G, Inouye M. Fast principal component analysis of large-scale genome-wide data. PLoS One. 2014;9:e93766. doi: 10.1371/journal.pone.0093766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Maksimovic J, Gordon L, Oshlack A, et al. SWAN: Subset-quantile within array normalization for illumina infinium HumanMethylation450 BeadChips. Genome Biol. 2012;13:R44. doi: 10.1186/gb-2012-13-6-r44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Johnson WE, Li C, Rabinovic A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics. 2007;8:118–127. doi: 10.1093/biostatistics/kxj037. [DOI] [PubMed] [Google Scholar]
  • 19.Aryee MJ, et al. Minfi: a flexible and comprehensive Bioconductor package for the analysis of Infinium DNA methylation microarrays. Bioinformatics. 2014;30:1363–1369. doi: 10.1093/bioinformatics/btu049. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary
NIHMS889019-supplement-Supplementary.pdf (837.4KB, pdf)

RESOURCES