Weak selection revealed by the whole-genome comparison of the X chromosome and autosomes of human and chimpanzee

Abstract

The effect of weak selection driving genome evolution has attracted much attention in the last decade, but the task of measuring the strength of such selection is particularly difficult. A useful approach is to contrast the evolution of X-linked and autosomal genes in two closely related species in a whole-genome analysis. If the fitness effect of mutations is recessive, X-linked genes should evolve more rapidly than autosomal genes when the mutations are advantageous, and they should evolve more slowly than autosomal genes when the mutations are deleterious. We found synonymous substitutions on the X chromosome of human and chimpanzee to be less frequent than those on the autosomes. When calibrated against substitutions in the intergenic regions and pseudogenes to filter out the differences in the mutation rate and ancestral population size between X chromosomes and autosomes, X-linked synonymous substitutions are still 10% less frequent. At least 90% of the synonymous substitutions in human and chimpanzee are estimated to be deleterious, but the fitness effect is weaker than the effect of genetic drift. However, X-linked nonsynonymous substitutions are ≈30% more frequent than autosomal ones, suggesting the fixation of advantageous mutations that are recessive.

It is a central tenet of the neutral theory of molecular evolution that the fixation of neutral variations is prevalent, or even predominant, at the molecular level (1–3). The detection of natural selection, both positive and negative, has thus been the focus of many recent analyses of genomic sequences (4–7). However, there have been fewer attempts at measuring the strength of selection (5, 8–10). Ohta (2, 3, 11, 12) may have been the first to stress the importance of weak selection in molecular evolution. With genomic data, we may now be able to answer the question: “How much of the molecular divergence between species is affected by weak selection, the strength of which does not overwhelm genetic drift?”

In some cases, positive selection has been shown to be more extensive than predicted by the neutral theory (6, 7, 13), but the analyses may not always inform about the strength of selection (see refs. 14 and 15). In principle, the strength of selection can be estimated from the polymorphism data because the changes in the level and pattern of polymorphism are determined by recombination and selection (5, 16). However, this signature is short lived (17). Similarly, the strength of negative selection within populations has been estimated (5), but how much it contributes to the divergence between species is not clear. Negative selection, if sufficiently weak, does allow divergence to proceed. Some (but probably not all) synonymous substitutions in Drosophila are likely such cases (8). Ironically, in species with a small effective population size, such as humans, in which divergence under negative selection is even more plausible, the low codon usage bias makes the measurement of selection on synonymous changes impractical.

An alternative approach to measuring the extent and strength of selection, both positive and negative, is to contrast the evolution of X-linked and autosomal genes (18, 19). If the fitness effect of a mutation is (partially) recessive, then this effect can be more readily manifested on the X chromosome than on the autosomes (20). When the recessive mutations are still rare, they will nonetheless be expressed in the hemizygous males of the XY system. On the other hand, autosomal mutations have to become sufficiently frequent to form homozygotes to be influenced by natural selection under random mating. Therefore, if recessive mutations are common, X-linked genes will evolve more rapidly when advantageous and more slowly when deleterious. The X-linked vs. autosomal approach has its limitations, because there are other factors influencing the relative rates of evolution in the X chromosome and autosomes (21–23). To correct for these factors, DNA sequences from much of the genomes of two closely related species would be needed. Human and chimpanzee are two species providing sufficient genomic data.

Materials and Methods

DNA Sequences. The human–chimpanzee “reciprocal best” alignments (made by using the July 2003 human assembly and the Nov 13, 2003, Arachne 4X draft chimpanzee assembly from the Broad Institute, Cambridge, MA) were downloaded from http://genome.ucsc.edu/goldenPath/hg16/vsPt0/axtBest. The quality scores of chimpanzee sequences were downloaded from http://hgdownload.cse.ucsc.edu/goldenPath/panTro1/bigZips. The bases in the chimpanzee genome sequence with quality values <20 were masked according to the position coordinate. The repetitive sequences in human–chimpanzee alignments were masked according to the annotations.

Intergenic sequences. We selected only aligned fragments that are longer than 1 kb and 50 kb away from any annotated human gene (ensembl 22) as intergenic regions. The cutoff in divergence is 5%, although the level is <2% for the majority of sequences used. In total, 71,667 autosomal and 6,115 X-linked fragments were used in this study.

Processed pseudogene sequences. Processed pseudogenes result from new retrotransposition. The sequences of 7,868 processed pseudogenes in the human genome were downloaded from www.pseudogene.org. These sequences were mapped to the corresponding human–chimpanzee alignments by using the fasta34 program (24) and our own scripts. The mapped pseudogene alignments were then translated into protein sequences for further confirmation. In total, 277 X-linked and 4,735 autosomal pseudogene alignments were used. The divergence cutoff in human and chimpanzee is the same as for intergenic regions. (We also used another pseudogene data set from www.bork.embl-heidelberg.de/Docu/Human_Pseudogenes; the results are highly consistent and are presented in Table 4, which is published as supporting information on the PNAS web site).

Coding sequences. Ensemble human gene coding sequences (version 22, www.ensembl.org) were used to blast against the human sequences in the human–chimpanzee alignments. We used only the best hits, with similarity of 100% and alignable length ≥ 90 bp for further analysis. We extracted the coding sequences from the human–chimpanzee alignments by using the sim4 program (25) and our own scripts. The extracted human and chimpanzee coding sequences were then translated into protein sequences for confirmation (by using the human ensembl coding sequences as references). We discarded any alignment with stop codons or indels that can cause a frameshift in either species. For genes with alternative splicing, the transcripts with the least human–chimpanzee divergence were adopted. In the end, 12,779 autosomal and 529 X-linked genes were selected for analysis.

Analyses. The K_a (the number of nonsynonymous substitutions per nonsynonymous site) and K_s (the number of synonymous substitutions per synonymous site) values for coding sequences were computed by the method of Li (26). The divergence for intergenic sequences (K_i) and for pseudogenes (K_ψ) was computed by the two-parameter method of Kimura (27).

The substitution rate and pattern at the C_pG sites are very different from the rest of the sequences, because C changes to T at a very high rate (28). If that had occurred, we would have observed CG↔ TG changes or CG↔ CA changes (CA being the reverse complement of TG). Therefore, we masked the C_pG sites by removing all of the CG dinucleotides in the human–chimpanzee alignments.

The number of 4-fold degenerate sites in coding sequences and the transversion substitutions at these sites (reported in Table 2) were counted by the divergence analyses implemented in the gcg 10.2 package.

Table 2. The numbers of transversional substitutions at 4-fold degenerate sites and intergenic sites in human and chimpanzee.

	TV4-f × 100		TVi × 100		Ratio TV4-f/TVi
Site	Unmasked	Masked	Unmasked	Masked	Unmasked	Masked
X	0.236 ± 0.023 (48,265)	0.139 ± 0.018 (38,842)	0.411 ± 0.003 (24,886,727)	0.343 ± 0.003 (13,159,821)	0.574 (P < 0.0001)	0.405 (P < 0.0001)
A	0.325 ± 0.005 (1,530,548)	0.198 ± 0.005 (1,180,609)	0.474 ± 0.001 (739,637,558)	0.391 ± 0.001 (389,317,592)	0.686 (P < 0.0001)	0.506 (P < 0.0001)
X/A	0.726 (P = 0.0007)	0.702 (P = 0.0012)	0.867 (P < 0.0001)	0.877 (P < 0.0001)	0.837 (P = 0.033)	0.800 (P = 0.029

Repetitive sequences and C_pG sites are shown. The number of sites appears in parentheses. P is the probability that the X/A ratio is ≥1. X, X chromosomes; A, autosomes.

Bootstrap. The bootstrap method (29) was used to infer 95% confidence interval estimations. In each replicate, the X-linked and/or autosomal genes (with the same sample size as the original data set) were randomly sampled with replacement from the original data set. The statistic values (mean K_a, K_s, K_ψ, or K_i) and the ratios [K_s/K_ψ, K_s/K_i, TV_4-f/TV_i (where TV is the transversional substitution rate), K_a/K_s, K_a/K_ψ, and K_a/K_i and those ratios for X-linked/automsomal genes (X/A)] were calculated based on the sampled data set(s). For each ratio estimation, the bootstrap method was replicated 10,000 times, and the 95% confidence intervals for that quantity were estimated (or the probability that the ratios were ≥ or ≤1; see Tables 1, 2, 3 for details).

Table 1. The numbers of substitutions at synonymous sites, at intergenic sites, and in pseudogenes in human and chimpanzee.

	Ks × 100		Ki × 100		Kψ × 100		Ks/Ki [Ks/Kψ]
Site	Unmasked	Masked	Unmasked	Masked	Unmasked	Masked	Unmasked	Masked
X	0.805 ± 0.033*	0.466 ± 0.027*	1.141 ± 0.006†	0.852 ± 0.005†	1.118 ± 0.044‡	0.799 ± 0.039‡	0.706 (0.635, 0.777) [0.720 (0.636, 0.810)]	0.547 (0.474, 0.623) [0.583 (0.496, 0.677)]
A	1.115 ± 0.009§	0.652 ± 0.007§	1.409 ± 0.002¶	1.026 ± 0.001¶	1.405 ± 0.011∥	0.958 ± 0.010∥	0.791 (0.778, 0.804) [0.793 (0.774, 0.810)]	0.635 (0.619, 0.649) [0.681 (0.658, 0.698)]
X/A	0.722 (0.650, 0.797)	0.714 (0.632, 0.798)	0.810 (0.802, 0.818)	0.830 (0.822, 0.840)	0.796 (0.740, 0.851)	0.834 (0.769, 0.903)	0.893 (P = 0.011) [0.907 (P = 0.059)]	0.861 (P = 0.010) [0.856 (P = 0.026)]

Repetitive sequences and C_pG sites are shown. The 95% confidence intervals of the ratios are given in parentheses. The boldface X/A values are used in estimations. P is the probability that the X/A ratio is ≥1. X, X chromosomes; A, autosomes.

^*No. of genes = 529.

^†No. of fragments = 6,115.

^‡No. of pseudogenes = 277.

^§No. of genes = 12,779.

^¶No. of fragments = 71,667.

^∥No. of pseudogenes = 4,735.

Table 3.

The numbers of nonsynonymous substitutions, K_a, and the ratios to K_s, K_ψ, or K_i from Table 1

	No. of genes	Ka × 100	Ka/Ks	Ka/Kψ	Ka/Ki
Repetitive sequences and CpG sites unmasked
X	529	0.514 ± 0.035	0.638 (0.539, 0.752)	0.459 (0.394, 0.532)	0.450 (0.393, 0.512)
A	12,779	0.498 ± 0.006	0.447 (0.434, 0.460)	0.354 (0.344, 0.365)	0.353 (0.345, 0.362)
X/A		1.032 (0.898, 1.176)	1.427 (P < 0.0001)	1.297 (P = 0.00041)	1.275 (P = 0.0006)
Repetitive sequences and CpG sites masked
X	529	0.362 ± 0.027	0.778 (0.637, 0.947)	0.453 (0.382, 0.535)	0.425 (0.365, 0.491)
A	12,779	0.322 ± 0.005	0.493 (0.476, 0.512)	0.336 (0.324, 0.347)	0.314 (0.305, 0.323)
X/A		1.124 (0.988, 1.265)	1.578 (P < 0.0001)	1.348 (P = 0.0004)	1.354 (P < 0.0001)

The 95% confidence intervals of the ratios or the probability that the ratio is ≤ 1 is given in parentheses. X, X chromosomes; A, autosomes.

Results

Lower K_s for X-Linked Genes than for Autosomal Genes. For coding sequence comparisons, we used 529 X-linked and 12,779 autosomal genes from the human–chimpanzee reciprocal best alignments (see Materials and Methods). In Table 1, the number of synonymous substitutions per 100 sites (K_s × 100) between human and chimpanzee is shown to be 0.805 ± 0.033 for X-linked genes, ≈30% lower than the corresponding number for the autosomes (1.115 ± 0.009). Given the large sample sizes used, the difference is highly significant (P < 0.0001, Kolmogorov–Smirnov test).

Calibration for X-Linked–Autosomal Differences in Mutation Rate, Ancestral Polymorphism, and GC Content. There are two known sources that could contribute to a smaller K_s on the X chromosome than on the autosomes: (i) a lower mutation rate and (ii) a smaller effective population size for X-linked genes, as described below. Because of the reduced mutation rate in females relative to that in males (21, 22), X-linked genes should have fewer mutations over time than autosomal ones. (Note that X-linked genes are transmitted through males only one-third of the time, whereas autosomes spend equal time in both sexes.) This phenomenon is often referred to as “male-driven evolution” (21, 22). Mutation rates for X-linked genes may also be lower than those for autosomal ones because of other mechanisms (30, 31). The second source is the difference in the effective population size between the X chromosome and autosomes. Total genic divergence is the sum of the level of ancestral polymorphism at the time of speciation and the amount of divergence since then (23). The contribution of the former is a function of the effective population size, which is generally smaller for X-linked genes than for autosomes (32).

To correct for the different mutation rates and levels of ancestral polymorphism between X-linked and autosomal genes, we calculated the per site divergence in intergenic regions (K_i) and in pseudogenes (K_ψ). Table 1 shows that, for both K_i and K_ψ, the reduction in sequence divergence for X-linked vs. autosomal genes is ≈20%, in contrast with the nearly 30% difference in K_s for coding sequences (the difference is significant; see the X/A ratio in Table 1). Apparently, synonymous changes in coding regions are subjected to additional forces, including natural selection. For the rest of this report, we shall use the ratios between K_s and K_i, rather than the ratios between K_s and K_ψ, as examples. Although the results are usually comparable, the sample sizes from the intergenic regions are much larger and, furthermore, the designation of pseudogenes may not always be accurate.

Another potential source of errors that needs to be addressed is the elevated mutation rate at the C_pG sites in the mammalian genome (28). The proportions of C_pG sites in the coding regions of X chromosomes and autosomes are 2.90% and 3.32%, respectively. The conclusions from the analyses with C_pG sites removed remain unchanged throughout this report (see all tables). Because we are contrasting the selective pressure on the X chromosome vs. autosomes, all types of mutations at C_pG sites or elsewhere are included in the analyses. The removal of C_pG sites was done mainly to show the absence of bias. Furthermore, the differences in the overall GC content between functional and nonfunctional DNA sequences are quite comparable on the X chromosome and on the autosomes (see Table 5, which is published as supporting information on the PNAS web site). Hence, the observed reduction in K_s for X-linked genes is not attributable to a possible GC content effect.

In Table 2, we carried out an additional analysis. The objective was to probe the possibility raised in the codon bias literature (28) that selection on transversions is different from synonymous changes in general. The ratio TV_4-f/TV_i shown in Table 2 is close to the K_s/K_i or K_s/K_ψ ratio of Table 1. For the X chromosomes, the TV_4-f/TV_i ratio is 0.574; the other two ratios are 0.706 and 0.720, respectively (Table 1). For autosomes, the TV_4-f/TV_ψ ratio is 0.686, vs. 0.793 and 0.791 for the other two ratios, respectively. Note that in all cases, the X/A ratio is significantly smaller than 1 (Tables 1 and 2). It is clear that the transversion pattern parallels the synonymous ones with respect to the difference between X chromosomes and autosomes.

Weak Selection Against Synonymous Substitutions. The salient results so far are (i) K_s is lower than either K_ψ or K_i for autosomal sequences and (ii) there is a further reduction in K_s, relative to the other two measures, for X-linked sequences (Table 1). Thus, X-linked genes are more highly constrained than autosomal genes. Constraint refers to the proportion of mutations (a) that do not become fixed relative to the neutral ones because of the action of natural selection. Selective constraint usually denotes the relative proportion of a: (1–a) for deleterious vs. neutral mutations. In this standard interpretation, only neutral mutations, accounting for 1–a of the total, become fixed. This interpretation, however, could not explain the larger constraint on the X chromosomes than on the autosomes. To do so, we have to assume the fixation of very slightly deleterious mutations, as explained below.

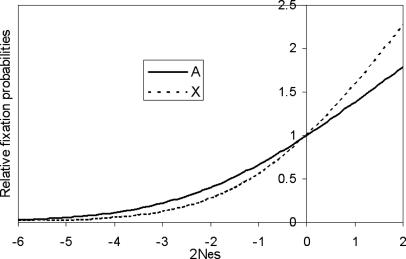
If a recessive mutation is advantageous, it is more likely to be fixed when it is on the X chromosome than on the autosomes. The trend would be reversed for deleterious mutations (20). However, for deleterious mutations, the difference in the probabilities of fixation is noticeable only when 0 > 2N_es > –5 (see Fig. 1), where N_e is the effective population size and s is the coefficient of selection against the homozygotes or the hemizygous males. The selective coefficient against the heterozygotes is assumed to be hs, where h is the dominance coefficient, generally between 0 and 1.

Fig. 1.

The fixation probabilities for X-linked and autosomal mutations under selection, relative to the neutral ones. The fixation probabilities are functions of effective population size (N_e), selective coefficient (s), dominance coefficient (h), and the effective male-to-female ratio (m). (See Supporting Methods.) Data shown are for cases of N_e = 10,000, h = 0.1, and m = 0.33.

The fixation probabilities for new mutations on the X chromosomes and on the autosomes are given in refs. 33, 20, and 34. These probabilities, relative to the neutral ones, are shown in Fig. 1 and explained more fully in Supporting Methods, which is published as supporting information on the PNAS web site. The probability is a function of N_es, h, and the effective male-to-female ratio (m). Fig. 1 is for cases of h = 0.1 and m = 0.33. At 2N_es ≈ –0.6, the synonymous substitution rate relative to the neutral rate is 0.716 and 0.790 for X-linked and autosomal genes, respectively, which appears to be a reasonably good fit to the observed numbers of 0.706 and 0.791 (Table 1). In Fig. 3, which is published as supporting information on the PNAS web site, we show that, over a wide range of values of h and m, the value of 2N_es has to be restricted between –0.3 and –1 to account for the observed K_s values. In other words, the primary determinant of K_s is 2N_es; the other parameters have a relatively minor effect.

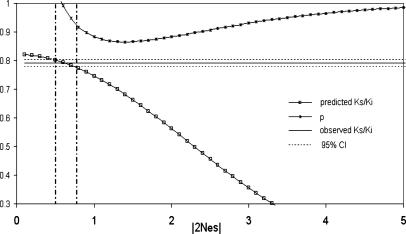
The above fitting ignores the possibility that a portion of synonymous changes might be advantageous. In what follows, we assume a portion of synonymous substitutions, p, to be deleterious with selection intensity s. The rest, 1–p, are assumed to be advantageous to the same degree, as in ref. 35. (Because we are dealing with very weak selection, with s < 1/2N_e, we do not define a separate neutral class with s = 0.) For any 2N_es value, there is a unique p value that would make the expected X/A ratio of Fig. 1 equal in fixation probability to an observed value. The observed X/A ratio of 0.90 (Table 1, the last two rows) was chosen to find the p value. The results are given in Fig. 2 and explained in the legends. In Fig. 2, we conclude that P > 0.90 and 0.5 < 2N_es < 0.8. Although Fig. 2 uses the same parameter values for h and m as Fig. 1, the tight clustering of curves in Fig. 3 suggests the robustness of the conclusion of large p and small 2N_es values. Numerical evaluations corroborate the suggestion, and Table 6, which is published as supporting information on the PNAS web site, provides the point estimates of p and 2N_es over a wide range of parameter values. In conclusion, the bulk of synonymous substitutions in human and chimpanzee are deleterious, but the selection intensity is extremely small, weaker than the effect of genetic drift.

Fig. 2.

Estimation of p (the proportion of synonymous substitutions under negative selection) and 2N_es when the X/A ratio is 0.9 (see the last two rows of Table 1). For all values of 2N_es, p is always >0.85. The K_s/K_i value is also a function of 2N_es; the case for h = 0.1, m = 0.33, and N_e = 10,000 is shown in the lower curve. The observed autosomal K_s/K_i at 0.791 further constrains 2N_es to <1 and p to >0.9. K_i is assumed to be the neutral rate.

Our estimation of p should not have been affected by any possible difference in recombination rate between X chromosomes and autosomes. Because the X chromosome does not recombine in males, it is expected to experience less recombination than the autosomes. According to the general Hill–Robertson effect (36), negative selection against X-linked mutations should be less effective, and their K_s should be somewhat higher than the autosomal values. The observation is in the opposite direction.

Positive Selection Driving Nonsynonymous Substitutions. In contrast with synonymous substitutions, the rate of nonsynonymous substitutions is higher on the X chromosome than on the autosomes when calibrated against K_s, K_ψ, or K_i. In Table 3, the ratios of K_a/K_s, K_a/K_ψ, and K_a/K_i are given for X-linked and autosomal genes. Although K_a/K_s is often used to indicate the rate of nonsynonymous substitutions relative to the neutral rate, K_s is, in fact, not a neutral rate between human and chimpanzee. K_a/K_ψ and K_a/K_i are clearly better indicators of the selective constraints on nonsynonymous substitutions. The X/A ratios are 1.297 and 1.275, respectively, for K_a/K_i and K_a/K_ψ (both significantly >1; see Table 3). The results suggest that recessive advantageous mutations do leave a footprint in the genomes of human and chimpanzee, in the form of a higher average K_a for X-linked genes.

Discussion

The contrast in the evolutionary rates in the coding regions of X-linked and autosomal genes suggests that both positive and negative selection operate extensively on the genomes of human and chimpanzee. For recessive deleterious mutations, the intensity of selection is very weak on the homozygotes and even weaker on the heterozygotes. The conclusion that >90% of synonymous substitutions in human and chimpanzee are deleterious raises challenging issues that are addressed below.

The Flux Model for Synonymous Substitutions. What is the nature of negative selection against synonymous changes? In the “flux” model of synonymous changes (35), the change from a preferred codon to an unpreferred one is governed by negative selection with intensity –s. In the other direction, it is positive selection with intensity s. Although a gene with 100% preferred codons is assumed to be the fittest, the actual codon usage is kept at a mutation-selection equilibrium that is below the optimum. If a population is in equilibrium, the numbers of advantageous and deleterious substitutions should be equal. Sometimes, the equilibrium is shifted downward because of, say, a reduction in effective population size, and there would be a larger flux of deleterious substitutions from preferred to unpreferred codons than advantageous mutations going in the other direction. However, to account for the observation of >90% deleterious substitutions, codon usage would have to be experiencing a very drastic shift from a strongly biased pattern to a neutral one. Because mammals generally have only weak or no codon usage bias (28), the flux model cannot account for the observation.

A Model of Compensatory Mutations. We believe our observation of pervasive weak selection against synonymous changes between human and chimpanzee demands a new model for synonymous substitutions. The large number of deleterious synonymous changes must be compensated by a smaller number of advantageous mutations, each, on average, having a larger effect on fitness. The idea of compensatory mutations was proposed by Ohta (11, 37). We are hopeful that such models will be developed and tested. Here, we wish to suggest a possible outline of such a model. A fundamental assumption of the flux model is that genes with 100% preferred codons are the fittest. This assumption has not been tested empirically; in fact, contrary evidence exists (8, 38). Nor is the assumption biologically justified. It seems more plausible that the preferred and unpreferred codons need to be in certain ordered sequences for optimal translation, and there may be more than one such optimal configuration. When an optimal configuration is attained, most synonymous changes would thus lead away from the fitness peak, and selection would be weakly negative. However, an occasional synonymous change may singly restore the configuration to another optimal frame. Such a substitution may offer a relatively large compensation in fitness.

A Concluding Note. Molecular evolution under the influence of weak selection is an idea that was championed by Ohta (2, 3, 11, 12) three decades ago. This study and many recent ones appear to uphold the idea (14, 39). It is particularly intriguing that the divergence between human and chimpanzee, dramatic as it is in phenotype, may have been driven by such weak selection.