Neuroimaging paradigms for tonotopic mapping (I): The influence of sound stimulus type

Abstract

Although a consensus is emerging in the literature regarding the tonotopic organisation of auditory cortex in humans, previous studies employed a vast array of different neuroimaging protocols. In the present functional magnetic resonance imaging (fMRI) study, we made a systematic comparison between stimulus protocols involving jittered tone sequences with either a narrowband, broadband, or sweep character in order to evaluate their suitability for the purpose of tonotopic mapping. Data-driven analysis techniques were used to identify cortical maps related to sound-evoked activation and tonotopic frequency tuning. Principal component analysis (PCA) was used to extract the dominant response patterns in each of the three protocols separately, and generalised canonical correlation analysis (CCA) to assess the commonalities between protocols. Generally speaking, all three types of stimuli evoked similarly distributed response patterns and resulted in qualitatively similar tonotopic maps. However, quantitatively, we found that broadband stimuli are most efficient at evoking responses in auditory cortex, whereas narrowband and sweep stimuli offer the best sensitivity to differences in frequency tuning. Based on these results, we make several recommendations regarding optimal stimulus protocols, and conclude that an experimental design based on narrowband stimuli provides the best sensitivity to frequency-dependent responses to determine tonotopic maps. We forward that the resulting protocol is suitable to act as a localiser of tonotopic cortical fields in individuals, or to make quantitative comparisons between maps in dedicated tonotopic mapping studies.

Introduction

Much has been learned about sound processing in the brain from the way the central auditory system is organised. For instance, the hierarchical organisation of the various auditory nuclei form progressive stages of sound processing with an increasingly complex encoding of sound attributes (Eggermont, 2001; Rees and Palmer, 2010). Within individual nuclei, the most prominent organisational feature undoubtedly relates to frequency tuning, which occurs throughout the classical auditory pathway up to the level of the auditory cortex. Neurons are laid out to form a systematic spatial progression of the sound frequency to which they are optimally sensitive (Clopton et al., 1974). This tonotopic/cochleotopic place-frequency code emerges in the inner ear's organ of Corti and is comparable to the retinotopic and somatotopic epithelial representations in the visual and sensorimotor systems, respectively (Sanchez-Panchuelo et al., 2010; Wandell and Winawer, 2011).

The brain's tonotopic organisation is not just of interest for our understanding of sound frequency processing. It also allows multiple adjacent functional subdivisions to be distinguished based on their separate tonotopic progressions. Reversals in tonotopic gradients indicate boundaries between neighbouring subnuclei or fields. This is particularly relevant when studying the auditory cortex in the temporal lobe, which is assumed to consist of several regions with distinct cytoarchitecture, connectivity, and function (Upadhyay et al., 2007; Woods et al., 2010). Whereas tonotopy-based parcellation schemes have become reasonably established for various mammalian species, the organisation of human auditory cortex remains debated and is largely based on extrapolation from other primates (Baumann et al., 2013).

However, in the last decade, non-invasive neuroimaging techniques have shed much light on the cortical tonotopic organisation in humans. Functional magnetic resonance imaging (fMRI) in particular has succeeded in painting an increasingly detailed picture regarding how sound frequency tuning varies across the cortical surface. Although early reports were somewhat contradictory (Formisano et al., 2003; Schönwiesner et al., 2002; Talavage et al., 2004), and some debate still remains on how tonotopic progressions relate to the layout of functional fields (reviewed by Saenz and Langers, 2014), the data from numerous studies have led authors to converge to a view that at least two abutting fields form a core auditory region. These comprise the human homologues of a primary field hA1 and a rostral field hR that together fold across the transverse superior temporal gyrus known as Heschl's gyrus (HG) (Humphries et al., 2010). These fields feature diagonally oriented, V-shaped tonotopic best-frequency progressions, with low frequencies being represented laterally on the crest of HG and high frequencies occurring on its medial banks (Langers and van Dijk, 2012). Additional belt fields likely exist in surrounding regions posteriorly on the planum temporale, laterally towards the superior temporal sulcus, or anteriorly near the planum polare, but these findings are more ambiguous and remain to be resolved (Striem-Amit et al., 2011; Talavage et al., 2004).

Numerous human tonotopy studies have so far reported remarkably consistent and similarly detailed results at least regarding the tonotopic organisation on HG, even if these were not always identically interpreted. Yet, different researchers employed highly diverging methodologies. Table 1 lists a representative number of studies and compares several key aspects of their designs. So far, a robust systematic comparison of these various approaches has not been conducted. As research interests shift from the qualitative outlining of tonotopic patterns to a more precise quantification of frequency representations, the choice of an optimal protocol will become increasingly important. A relevant question at this stage is which of the various employed methods are best for particular purposes and in particular contexts. The present study was carried out with this goal in mind. In this report, the influence of the type of sound stimulus will be investigated; in an accompanying paper, we compare a number of different acquisition protocols (Langers, 2014).

Table 1.

This table lists, for a representative set of fMRI studies of tonotopy in humans, the included number of subjects (N), the functional scan-time per session (t), the type, frequency range (f) and approximate intensity (I) of the presented stimuli, the nature of any task that subjects performed, the employed field strength (B₀), and the scanning method (based on the interval of scanner silence between image acquisitions: continuous = negligible intervals; clustered = short intervals; sparse = long intervals).

Study	N [‒]	t [min]	Stimulus	f [Hz]	I [dB]	Task	B0 [T]	Scanning
Talavage et al. (2000)	6	17	Bandpass	20–8.0 k	40	Detection	1.5	Continuous
Schönwiesner et al. (2002)	13	40	FM tones	250–8.0 k	?	Detection	3.0	Clustered
Formisano et al. (2003)	6	96	Tones	300–3.0 k	70	?	7.0	Sparse
Talavage et al. (2004)	7	97	Sweeps	125–8.0 k	40	Detection	1.5	Continuous
Seifritz et al. (2006)	6	24	Tones	125–8.0 k	90	?	1.5	Continuous
Langers et al. (2007)	10	32	Tones in noise	125–8.0 k	60	Detection	1.5	Sparse
Upadhyay et al. (2007)	8	20	Tones	300–3.0 k	70	?	3.0	Sparse
Riecke et al. (2007)	11	41	Tones in noise	500–3.2 k	70	Continuity	3.0	Clustered
Woods et al. (2010)	9	54	Tones in noise	225–3.6 k	80	One-back	1.5	Various
Hertz and Amedi (2010)	15	12	Sweeps	250–4.0 k	90	Fixation	3.0	Continuous
Humphries et al. (2010)	8	63	Complex tones	200–6.4 k	80	Passive listening	3.0	Sparse
Da Costa et al. (2011)	10	16	Sweeps	88–8.0 k	70	?	7.0	Continuous
Striem-Amit et al. (2011)	10	8	Sweeps	250–4.0 k	90	Passive listening	3.0	Continuous
Langers and van Dijk (2012)	20	24	Tones	250–8.0 k	40	Visual/emotional	3.0	Sparse
Moerel et al. (2012)	5	75	Natural sounds	180–6.9 k	?	One-back	3.0	Clustered
Dick et al. (2012)	9	68	Bandpass sweep	150–9.6 k	?	Detection	1.5	Continuous
Barton et al. (2012)	4	35	Narrowband	400–6.4 k	?	?	3.0	Sparse
Herdener et al. (2013)	6	22	Sweeps	500–8.0 k	70	Passive listening	3.0	Continuous
De Martino et al. (2013)	9	48	Various	180–7.0 k	60	One-back	7.0	Clustered
Norman-Haignere et al. (2013)	12	22	Tones	200–6.4 k	70	One-back	3.0	Clustered
Schönwiesner et al. (2014)	7	49	Tones in noise	200–8.0 k	75	Passive listening	3.0	Sparse

The majority of previous studies used either blocks of tonal stimuli (De Martino et al., 2013; Formisano et al., 2003; Langers and van Dijk, 2012; Norman-Haignere et al., 2013; Schönwiesner et al., 2014; Seifritz et al., 2006; Upadhyay et al., 2007), broadband natural sounds (De Martino et al., 2013; Moerel et al., 2012), or continuous or stepwise dynamic sweeps of tones or other narrowband content (Da Costa et al., 2011; Dick et al., 2012; Herdener et al., 2013; Hertz and Amedi, 2010; Striem-Amit et al., 2011; Talavage et al., 2004). We therefore included in our study three different stimulus types that we consider representative of these practices. These involved narrowband or broadband frequency distributions, or sweep content. In order for the stimuli to remain maximally comparable across the different types of runs, we chose to base all three stimulus types on jittered tone sequences. It is therefore likely that largely the same neural circuitry is recruited for the processing of all of our stimuli. Another reason to opt for stimuli that are instantaneously tonal in nature was to remain faithful to the traditional electrophysiological definition of tonotopy that involves a systematic spatial progression in characteristic frequency, which is defined based on tone stimuli (Rose et al., 1959). Of course, our particular choice of stimuli implies that our findings do not necessarily generalise to all other types of stimuli that have been employed by others. Given the already diverse literature, this seems an inevitable limitation. Nonetheless, we consider that our stimuli capture a design parameter that is crucial for neuroimaging studies on tonotopy.

One difficulty that arises when comparing different stimulus paradigms is that they all tend to require tailored analysis methods. For example, blocks of tone stimuli can be analysed using a traditional block- or event-related regression model. A measure of frequency tuning can subsequently be extracted by appropriately combining the frequency-specific regression coefficients (Humphries et al., 2010). In contrast, sweep sequences are most conveniently analysed using Fourier methods. The phase of the extracted frequency component corresponding with the periodicity of the sweep presentations represents a correlate of frequency tuning (Talavage et al., 2004). Finally, broadband sounds tend to be analysed by means of generative models that allow optimal tuning characteristics to be determined by fitting predicted model outputs to the observed responses (Moerel et al., 2013). To complicate matters, all of these methods involve non-linear computations. As a result, it is difficult to establish a single approach that allows the results from different paradigms to be compared directly.

One could apply different analysis methods to the various paradigms, but this would confound the interpretation of the results in the sense that it would be impossible to determine whether a particular paradigm performed better because the stimuli were inherently more suitable, or because the analysis method was more sensitive. Moreover, given the lack of a gold standard regarding the tonotopic organisation of human auditory cortex, it would be impossible to infer which method is best if outcome differences between methods were found. This would make it difficult to determine which paradigm is most effective.

To circumvent these issues, we opted for a data-driven approach to determine how much information is available in the data to be utilised for the assessment of frequency tuning. Because this approach does not rely on a parametric model relating to the observable response shapes, it allows us to apply the same analysis methodology to the data obtained with all three stimulus types. Multi-linear regression was used to determine the responses to different conditions within each protocol, followed by a principal component analysis (PCA) and a generalised canonical correlation analysis (CCA) to summarise the variances within and between the datasets, respectively. We propose that quantification of the amount of power in the time series data that is sensitive to frequency-tuning is an informative metric, which is relevant to any future studies, including those utilising tailored analysis methods.

Methods

Seven healthy volunteers (gender: 3♂, 4♀; age [years]: 33.6 ± 5.5, range 26–42) were included in this fMRI study on the basis of written informed consent and in approved accordance with the requirements of the Medical School Research Ethics Committee at the University of Nottingham. Subjects reported no history of neurological or hearing impairments.

Imaging session

Subjects were positioned supinely in the bore of a 3.0-T MR system (Philips Achieva, Best, the Netherlands) that was equipped with a 32-channel receive head coil. The scanner coolant pump was turned off during all measurements and subjects wore foam ear plugs and MR-compatible electrostatic headphones (NordicNeuroLab AudioSystem, Bergen, Norway) to diminish ambient noise levels.

At the beginning of the session, after the acquisition of an anatomical reference scan, subjects performed an automated audiometric test in situ whilst no scanning took place. Subjects were presented with a series of pure-tone stimuli in the left or right ear at particular adaptively chosen frequency and intensity combinations, and were instructed to press a button whenever they perceived a tone. The derived threshold curves were used to calibrate the stimulus delivery in subsequent functional runs, as described below. For the remainder of the session, subjects passively watched a silent video showing a nature documentary.

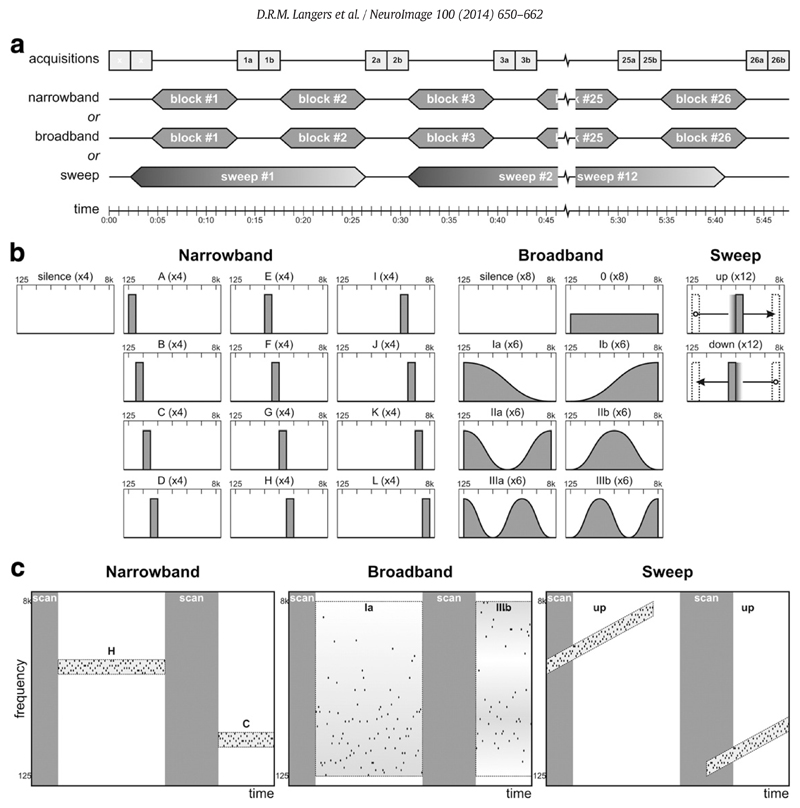
The functional imaging session comprised six 6-minute runs, each consisting of a dynamic series of high-resolution T₂*-sensitive 2-D gradient-echo echo-planar imaging (EPI) acquisitions (alternatingly 2.2 or 11.0-s repetition time; 40-ms echo time; 90° flip angle; 128 × 126 × 25 matrix; 192 × 168 × 37.5-mm³ field of view; 1.5 × 1.5 × 1.5-mm³ reconstructed voxel size; 0-mm slice gap; EPI-factor 53). A sparse scanning method was used in which pairs of two contiguous 2.2-s volume acquisitions were separated by 8.8 s of scanner inactivity (Edmister et al., 1999; Hall et al., 1999), yielding a 13.2-s acquisition period (see Fig. 1a). The acquisition volume was positioned in an oblique axial orientation, tilted forward parallel to the Sylvian fissure and approximately centred on the superior temporal gyri. Regional saturation slabs were added to null signal from the eyes. Additional preparation scans were acquired to achieve stable image contrast and to trigger the start of stimulus delivery, but these were not included in the analysis.

Fig. 1.

Experimental design. (a) The fMRI protocol consisted of 26 pairs of 2.2-s functional acquisitions separated by 8.8-s periods of scanner inactivity in each of the six runs per subject. In the narrowband and broadband runs, randomised stimuli were presented in blocks during the scan-to-scan intervals; in the sweep runs, 24.2-s upward or downward tone sweeps were repeated twelve times. (b) All stimuli consisted of sequences of jittered tones with frequencies between 125 Hz and 8 kHz presented at a rate of 10 Hz and loudness of 60 phon. For the narrowband sequences, twelve different stimulus conditions each comprised tones selected from a ½-octave frequency interval. For the broadband sequences, tones were selected from the entire 6-octave interval according to one of seven different probability distributions. For the sweep sequences, a ½-octave wide frequency window was swept up or down at a fixed rate on a logarithmic frequency scale. The narrowband and broadband runs additionally included silent baseline conditions; the sweep sequences were all separated by 4.4 s of silence. (c) Spectrotemporal illustration of a short excerpt of each of the stimulus protocols. Jittered sequences of pure tones (black dots) were presented, whilst scanning (grey bars) was performed in sparse fashion.

During the functional scanning, sound stimuli were delivered that consisted of sequences of pure tones presented at a rate of 10 per second. Each tone lasted 75 ms, with 5-ms cosine ramps. In order to achieve constant loudness, each tone was played diotically at a level above the individual threshold that corresponded with the intensity level difference between 0 and 60 phon at the presented frequency according to the ISO-226 standard (Suzuki et al., 2003). To reduce startle due to sequence on- and offsets, levels were faded in and out during the first and last 1.1 s of the sequence.

Tone frequencies were randomly selected according to three different criteria, labelled narrowband, broadband, and sweep (see Fig. 1b,c).

• For the narrowband sequences, tones were randomly selected from one of twelve ½-octave wide intervals spanning frequencies of 125–177, 177–250, …, or 5657–8000 Hz. Sequences were 8.8 s long and coincided with the periods of scanner inactivity. The resulting 13 conditions (12 types of jittered tone blocks, plus a silent baseline condition) were randomised and each presented four times per subject.

• For the broadband sequences, tones were randomly selected from a 6-octave wide interval spanning frequencies of 125–8000 Hz according to one of seven sinusoidal probability distributions. Similar to the narrowband sequences, sequences were 8.8 s long and coincided with the periods of scanner inactivity. The resulting 8 conditions (7 types of jittered tone blocks, plus a silent baseline condition) were randomised and each presented six or eight times per subject.

• For the sweep sequences, tones were randomly selected from a ½-octave wide interval that was gradually swept either upward or downward between low-frequency (125–177 Hz) and high-frequency (5657–8000 Hz) extremes at a rate of 1 octave per 4.4 s. The resulting sequences were 24.2 s long and padded with 2.2 s of silence on both ends. Twelve upward sweeps were presented in one run, and twelve downward sweeps in another. Given the periodicities of the acquisition protocol (6 × 2.2 = 13.2 s) and the stimulus protocol (13 × 2.2 = 28.6 s), the responses to the sweep sequences were sampled at 13 different phases.

Two functional runs were performed per stimulus type in an order that was counterbalanced across subjects.

Data analysis

Data were preprocessed using the SPM12 software package (Wellcome Department of Imaging Neuroscience, http://www.fil.ion.ucl.ac.uk/spm/) (Friston et al., 2007). Functional imaging volumes were corrected for motion effects using rigid body transformations and co-registered to the subject's anatomical image. Voxel signals were converted to fMRI units of percentage signal change using the LogTransform toolbox (http://www.fil.ion.ucl.ac.uk/spm/ext/#LogTransform), and images were moderately smoothed by convolution with a 5-mm full-width at half-maximum (FWHM) Gaussian kernel. The two images of each acquired pair were averaged to form a single image volume. The anatomical images were segmented and all images were normalised and resampled at 1-mm resolution inside a bounding box of x = − 75… + 75, y = − 60… + 40, z = − 20… + 30 in Montreal Neurological Institute (MNI) stereotaxic space. Cortical surface meshes were generated from the anatomical images using the standard processing pipeline of the FreeSurfer v5.1.0 software package (Martinos Center for Biomedical Imaging, http://surfer.nmr.mgh.harvard.edu/) (Dale et al., 1999).

Linear regression models were formulated for each of the three stimulus protocols. Models included a constant baseline term, plus n_k stimulus regressors consisting of a vector of zeros and ones (where n_narrowband = 12, n_broadband = 7, and n_sweep = 12). In the narrowband and broadband models, these regressors encoded the stimulus condition that was presented preceding each acquired image pair, except for the silent condition that served as baseline. In the sweep model, the regressors encoded the distinct phases of the sweep at an instant 4.4 s before the middle of each acquired image pair to account for the hemodynamic response delay. The image pair that followed the silent gap between sweeps (with assigned phase equal to 0°) served as baseline. The phases for the downward sweeps were conjugated (i.e. reversed) compared to the upward sweeps to account for the opposite direction; thus, low and high phases always corresponded with low and high sound frequencies, respectively.

Individual subject models as well as fixed-effects group models were evaluated. To determine brain regions with significant sound-evoked activity, omnibus F-tests were carried out on the n_k stimulus-related regression coefficients, averaged across runs. To define a region of interest (ROI), the group-level results were thresholded at a confidence level p < 0.001 and a cluster size k_E > 1.0 cm³. The activation clusters according to the narrowband, broadband, and sweep models were merged to obtain a single ROI comprising 39,072 voxels in bilateral auditory cortex (see Results). The activation levels of all ROI voxels in response to the various conditions were aggregated into 39,072 × n_k data matrices Y_k. These matrices were subsequently analysed separately by means of PCA to summarise the variances within datasets, as well as analysed together by means of generalised CCA to summarise the covariances between datasets (Hwang et al., 2013; Izenman, 2008; Lattin et al., 2002). In all analyses, second-order moments relative to the baseline signal were used instead of variances relative to the mean; in other words, data were not centred.

PCA (Hotelling, 1933a, 1933b) produced an ordered set of principal components (indexed i = 1…n_k) for each dataset. Each component was described by a 39,072-element map x_i,k characterising the component's strength across voxels, and an n_k-element response profile v_i,k characterising the component's strength across conditions. The scaling of x_i,k and v_i,k was fixed by constraining the response profiles to have unit root-mean-square amplitude, thus allowing the maps to be interpreted in units of percentage signal change. Principal component maps are orthogonal, as are the corresponding response profiles $(\text{i}.\text{e}.{\mathbf{\text{x}}}_{i,k}^{\text{T}}{\mathbf{\text{x}}}_{j,k}={\mathbf{\text{v}}}_{i,k}^{\text{T}}{\mathbf{\text{v}}}_{j,k}=0\text{iff}i\ne j).$ The products ${\mathbf{\text{x}}}_{i,k}{\mathbf{\text{v}}}_{i,k}^{\text{T}}$ cumulate to form optimal approximations of the original dataset Y_k in least-squares sense.

Generalised CCA (Kettenring, 1971) produced an ordered set of canonical variates (indexed i = 1…min{n_k}) for each dataset. Each variate consisted of a 39,072-element map z_i,k that described the strength of the variate across voxels. It was derived from the original dataset Y_k by means of canonical coefficients c_i,k according to z_i,k = Y_kc_i,k (in fMRI, c_i,k can be identified with a contrast vector). The scaling of the z_i,k and c_i,k was fixed by constraining the maps to have unit root-mean-square amplitude. Canonical variates are constructed such that the average pairwise correlation across corresponding variates of the three datasets is maximal (equivalent to optimising ${\displaystyle {\sum }_{k,l}{\mathbf{\text{z}}}_{i,k}^{\text{T}}{\mathbf{\text{z}}}_{i,l}}$), whilst variates are constrained to remain orthogonal within each dataset individually at the same time $\left(\text{i}.\text{e}.{\mathbf{\text{z}}}_{i,k}^{\text{T}}{\mathbf{\text{z}}}_{j,k}=0\text{iff}i\ne j\right).$

Results

Significance maps

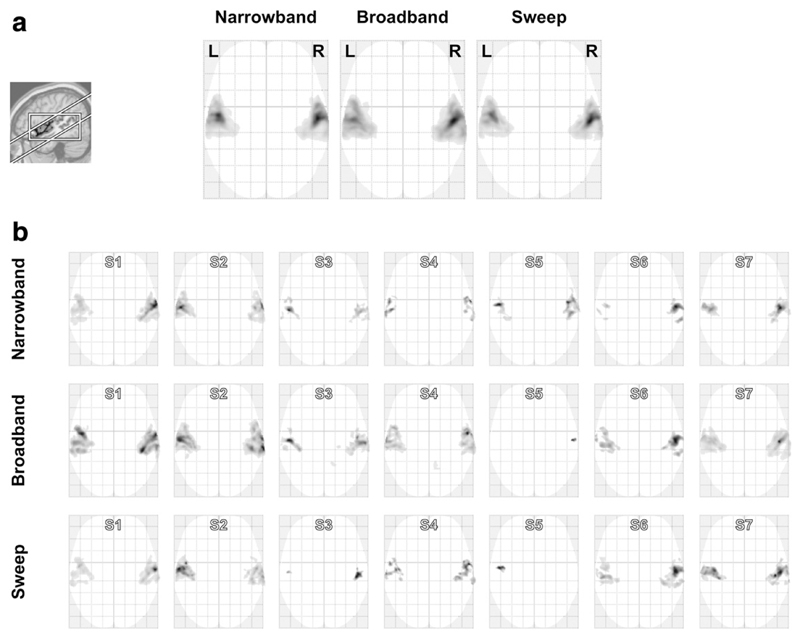
Fig. 2a shows the group-level significance maps for each of the three stimulus protocols, thresholded at a voxelwise significance level p < 0.001 and cluster size k_E > 1.0 cm³; uncorrected statistics were used because these maps were used to define ROIs, not to rigorously prove the existence of sound-evoked activation. The broadband sequences evoked the most extensive activation (38.8 cm³), followed by the narrowband sequences (30.0 cm³) and the sweep sequences (26.1 cm³). A single ROI was defined consisting of the set-wise union of these narrowband, broadband, and sweep activation clusters (39.1 cm³).

Fig. 2.

Activation to narrowband, broadband, and sweep sequences according to (a) a fixed-effects group model, and (b) models for all seven subjects (S1–S7) individually, thresholded and overlaid on a glass brain using a maximum-intensity projection. The inset shows the approximate orientation of the imaging volume and the employed analysis' bounding box.

Fig. 2b compares the subject-level activations for the narrowband, broadband, and sweep protocols. For these individual maps, the cluster extent threshold was lowered to k_E > 0.1 cm³. Activation remained mostly confined to the temporal lobe, but extents and significance levels varied widely across subjects and stimuli: for some combinations, bilateral cortex was extensively and strongly activated, whereas in others only a small unilateral focus barely exceeding the visualisation threshold was observed. In some subjects, the narrowband sequences resulted in the most significant activation, although in a majority the broadband sequences evoked the most extensive responses; the sweep sequences did not outperform the other two stimuli, but in many subjects still resulted in comparable activation.

Principal component analysis

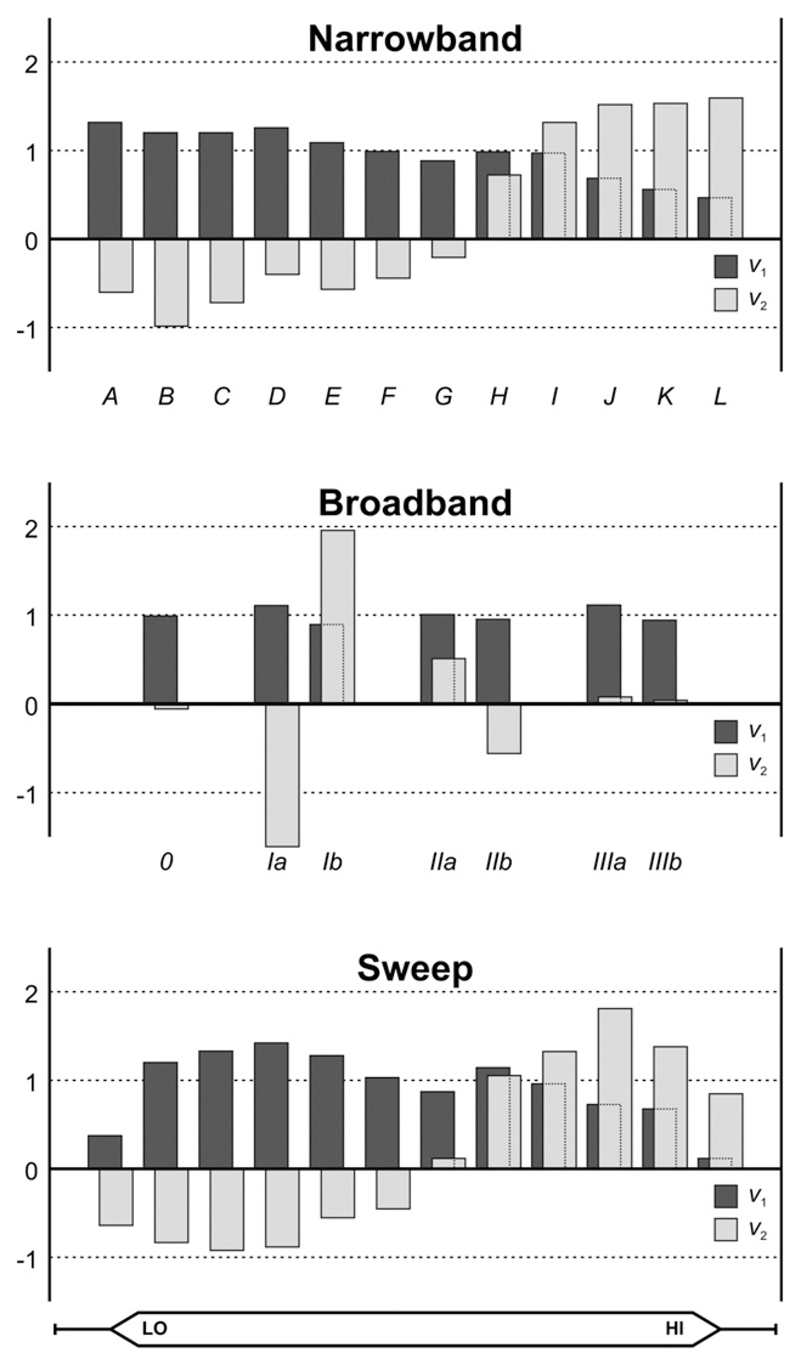
Fig. 3 shows the group-level response profiles for the 1st and 2nd principal components as a function of the n_k conditions illustrated in Fig. 1b (k = narrowband/broadband/sweep). For all three stimulus protocols, the 1st component's profile, v₁, depended only weakly on the condition. For the narrowband sequences, a moderate decline in activation was observed as the stimulus frequency increased. For the broadband sequences, a close to uniform response profile was obtained, although the response to the low-frequency-dominated stimulus Ia was stronger than that to the high-frequency-dominated stimulus Ib, consistent with the decline in the narrowband profile. Finally, for the sweep sequences, in addition to a downward trend towards the higher frequencies, a weaker response was observed at phases corresponding with the low- and high-frequency endpoints of the sweep. This is attributable to a sluggish growth of the measurable hemodynamic response for the lowest frequencies at the onset of the upward sweeps or, similarly, for the highest frequencies at the onset of the downward sweeps. Overall, the 1st components' profiles always represented uniformly positive sound-evoked activation as compared to silence, with slightly more signal power occurring for low sound frequencies as compared to high ones. The latter is partly due to stronger evoked responses in voxels tuned to low-frequencies and partly due to a larger prevalence of such low-frequency voxels (as shown below).

Fig. 3.

Barplots show the normalised frequency profiles of the first two principal components (v₁ and v₂, in dark and light grey, respectively) that were extracted from the narrowband, broadband, and sweep data separately. For all three types of stimuli, the first component encoded a near-uniform response to all sound frequencies (interpretable as activation) and the second component encoded additional positive response contributions to high sound frequencies and negative response contributions to low sound frequencies (interpretable as tonotopic frequency tuning). The labels beneath the bars correspond with the stimulus conditions illustrated in Fig. 1b.

The 2nd component's profile, v₂, showed a much stronger dependence upon the stimulus condition. For the narrowband sequences, the profile showed an almost monotonic transition from negative values for low frequencies to positive values for high frequencies. The zero-crossing occurred slightly above the middle of the employed frequency range. For the broadband sequences, negligible response contributions were observed for the stimuli 0, IIIa, and IIIb. Most notably, the profile was negative for the low-frequency-dominated stimulus Ia and positive for the high-frequency-dominated stimulus Ib. This trend agrees with the narrowband profile. Moreover, weaker positive and negative contributions to the extremal-frequency-dominated stimulus IIa and the mid-frequency-dominated stimulus IIb match the weakly negative contribution in the narrowband profile at the middle frequencies, just before its zero-crossing. Finally, for the sweep sequences, the 2nd component's response profile was again similar to that for the narrowband sequences, except that its magnitude was smaller for the most extreme frequencies due to delayed response build-up at the sweep onset. Overall, the 2nd components' profiles always represented a differential response to the low and high frequencies, with a gradual transition occurring for intermediate frequencies.

In summary, the 1st component always encoded general sound-evoked “activation”, whereas the 2nd component always encoded differential tuning to low and high frequencies due to “tonotopy”. Keeping in mind these interpretations, we now turn to the corresponding component maps, visualised as volumetric projections (averaged across the z-direction) and cortical surface cross-sections (displayed on semi-inflated temporal lobes) in Fig. 4.

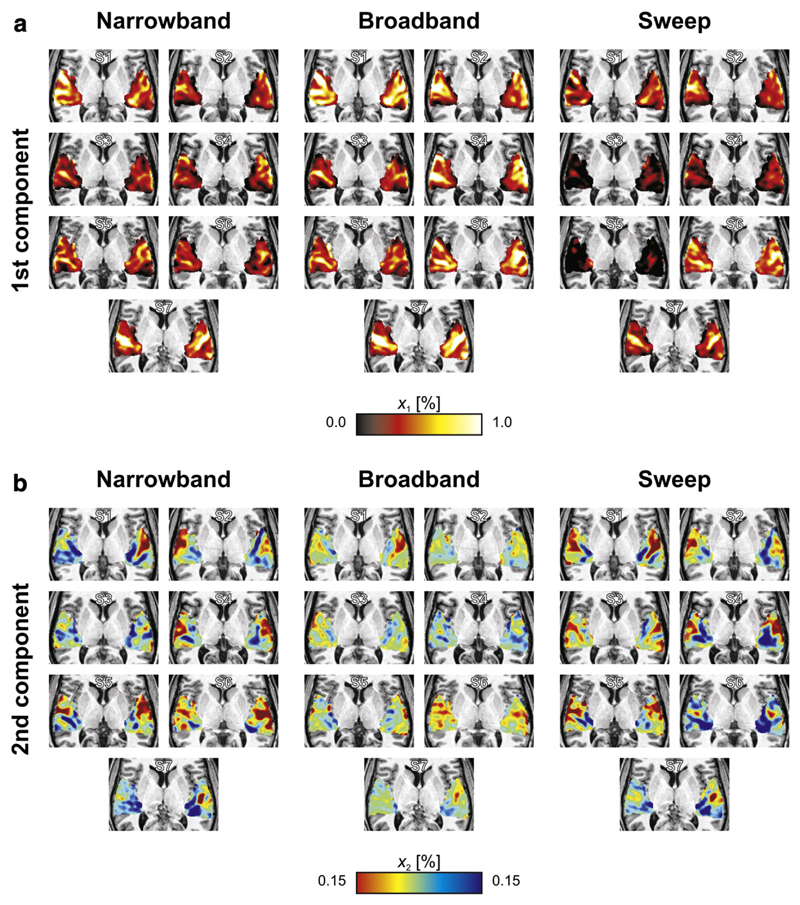
Fig. 4.

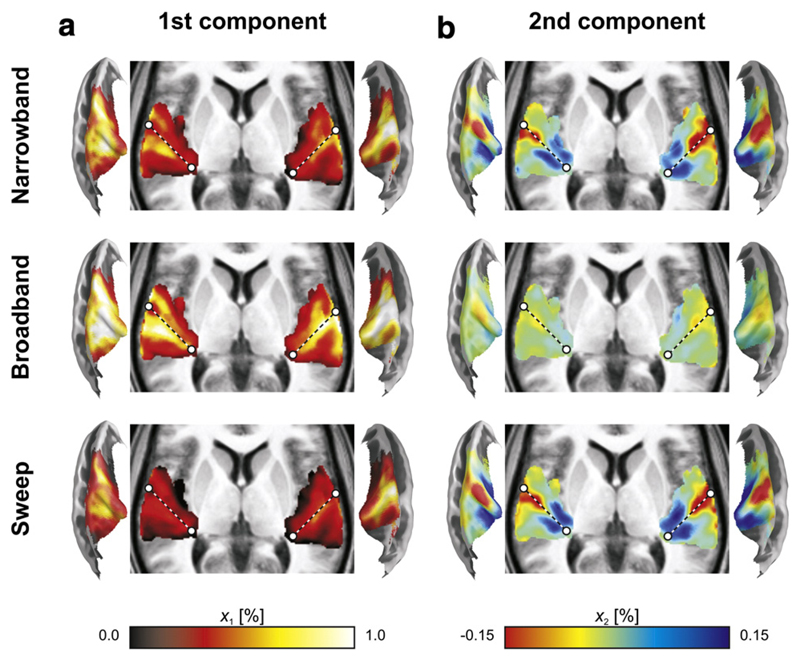
Volumetric projections across the z-direction (with dashed lines approximately outlining the axis of Heschl's gyrus) and semi-inflated cortical surface cross-sections display the maps x_i,k of the first two principal components that were extracted from the narrowband, broadband, and sweep data separately. (a) Activation maps, from the 1st component, consisted of response maxima on the caudal and rostral banks of Heschl's Gyrus (HG). Broadband sequences evoked the strongest activation, followed by the narrowband sequences, and lastly the sweep sequences. (b) Tonotopic maps, from the 2nd component, consisted of a low-frequency endpoint on lateral HG and two high-frequency endpoints on medial HG. Although qualitative patterns were similar, broadband sequences revealed the weakest map, whilst the narrowband and sweep sequences evoked more pronounced differences in frequency tuning.

The activation patterns in the 1st components were qualitatively similar for all three stimulus protocols. A primary activation maximum was observed on the caudal bank of HG (the central axis of which is sketched by a dotted line to facilitate comparisons), whilst a secondary peak was found laterally on its rostral bank. Quantitatively, the activation was strongest for the broadband sequences, intermediate for the narrowband sequences, and weakest for the sweep sequences.

The tonotopic patterns in the 2nd components also showed a high degree of similarity between the various protocols. A pronounced negative extremum was observed on the lateral crest of HG. Two positive extrema occurred around the medial end of HG, one caudally and one rostrally. Quantitatively, the narrowband and sweep sequences resulted in virtually identical maps; the broadband sequences, however, evoked considerably lower signal amplitudes.

The overall magnitudes of the various components are quantified in Table 2. The components' signal powers were based on the eigenvalues of the moment matrix (i.e., the uncentred covariances) of the beta-maps in the columns of the data matrices Y_k. Relatedly, the power fraction equals the power of each component divided by the total signal power across components, whilst the root-mean-square (RMS) amplitude equals the square root of the signal power. The values in Table 2 confirm the earlier observations regarding the magnitudes of the activation maps in the 1st component: broadband > narrowband > sweep, and the tonotopic maps in the 2nd component: sweep ≈ narrowband > broadband.

Table 2.

The table lists the total signal power of the data contained in the matrix Y; i.e. the activation level (expressed as a percentage signal change) squared, averaged across all ROI voxels and all stimulus contrasts. It also specifies how this total power is decomposed into additive contributions from the various principal components. The listed power fractions equal the corresponding signal powers expressed as a proportion of the total power; the root-mean-square (RMS) activation amplitudes equal the square root of the corresponding signal powers.

		Narrowband	Broadband	Sweep
Signal power [(%)2]	1st component	0.2048	0.4009	0.1028
	2nd component	0.0052	0.0008	0.0062
	Other components (mean)	0.0003	0.0003	0.0003
	ToTal	0.2130	0.4031	0.1125
Power fraction [‒]	1st component	0.962	0.995	0.914
	2nd component	0.024	0.002	0.055
	Other components (mean)	0.001	0.001	0.003
	ToTal	1.000	1. 000	1.000
RMS-amplitude [%]	1st component	0.45	0.63	0.32
	2nd component	0.07	0.03	0.08
	Other components (mean)	0.02	0.02	0.02
	ToTal	0.46	0.63	0.34

Fig. 5 summarises the maps of these first two components in individual subjects. (Note that PCA was not performed separately for all individual subjects. Instead, the group-level response profiles of Fig. 3 were employed to decompose the individual data. This ensures that component maps retain exactly the same interpretation across subjects, and avoids some of the detrimental effects of the poorer signal-to-noise in an individual's data.) Typically, the activation maps showed a number of elongated activation maxima running more or less parallel to HG. The tonotopic maps showed high-frequency representations medially and low-frequency representations laterally, often involving multiple apparent extrema. Comparing the maps, various individual features could be reproducibly observed across the three stimulus types, indicating that much of the apparent structure in these maps is not just due to chance, but reflects underlying neurophysiology.

Fig. 5.

Volumetric projections across the z-direction of the individual maps corresponding with the frequency profiles of the principal components shown in Fig. 3. Despite inter-individual variability, results remained interpretable as activation maps and tonotopic maps in all subjects (S1–S7). Apart from differences in the overall magnitudes of the maps, outcomes within subjects were quite consistent across the three stimulus conditions.

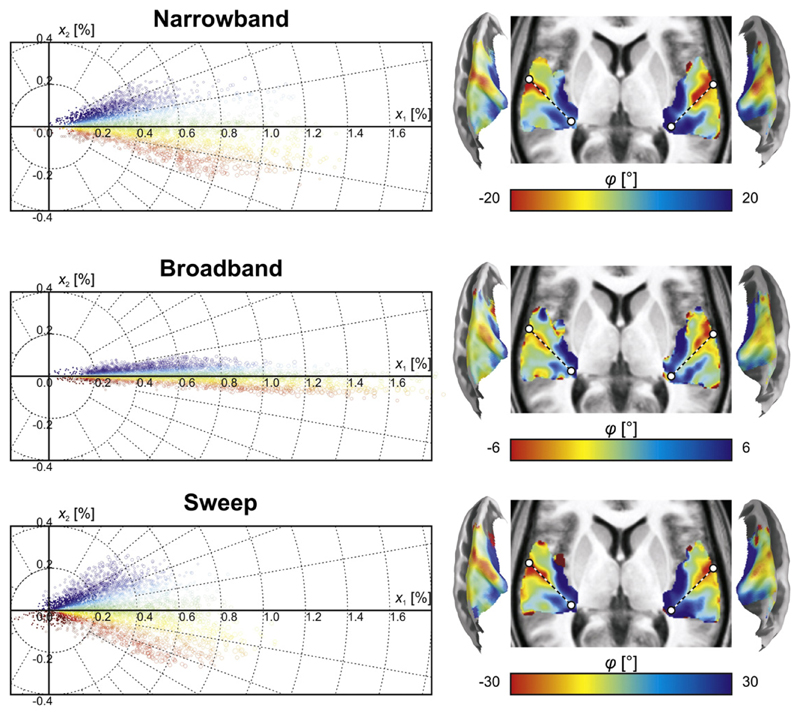
In Fig. 6, the group-averaged voxel amplitudes in the 1st and 2nd component maps are plotted against each other. Each voxel contributes one data point to the scatter plot. Because the ratio of the two amplitudes most accurately reflects the shape of the response profile of an individual voxel irrespective of its general excitability (Langers and van Dijk, 2012), voxels were colour-coded according to the polar angle in this plot. The patterns were all centred around 0°, but the range of polar angles differed between stimulus protocols. Compared to the narrowband sequences, the broadband sequences provided more signal power associated with general activation (1st component), but much less signal power associated with frequency tuning (2nd component). In contrast, the sweep sequences provided similar power relating to tuning, but less power related to activation in general. The corresponding spatial maps were all qualitatively similar; the most notable differences occurred at the edges of the activation cluster where activation levels were low and the signal-to-noise was thus poorest.

Fig. 6.

The magnitudes of the 1st and 2nd components (x₁ and x₂) are plotted against each other for the data based on narrowband, broadband, and sweep sequences; each point corresponds to one voxel. The scatter in the horizontal direction reflects differences in activation level, whilst that in the vertical direction reflects differences in frequency tuning. The angles in the polar scatter plots were colour-coded to result in a better correlate of frequency tuning. The resulting tonotopic maps were similar across all three types of stimuli and primarily differed at the edges of the activation cluster where signal to noise was poorest. The dashed line approximately outlines the axis of Heschl's gyrus, which forms the border between putative core fields hA1 and hR.

Generalised canonical correlation analysis

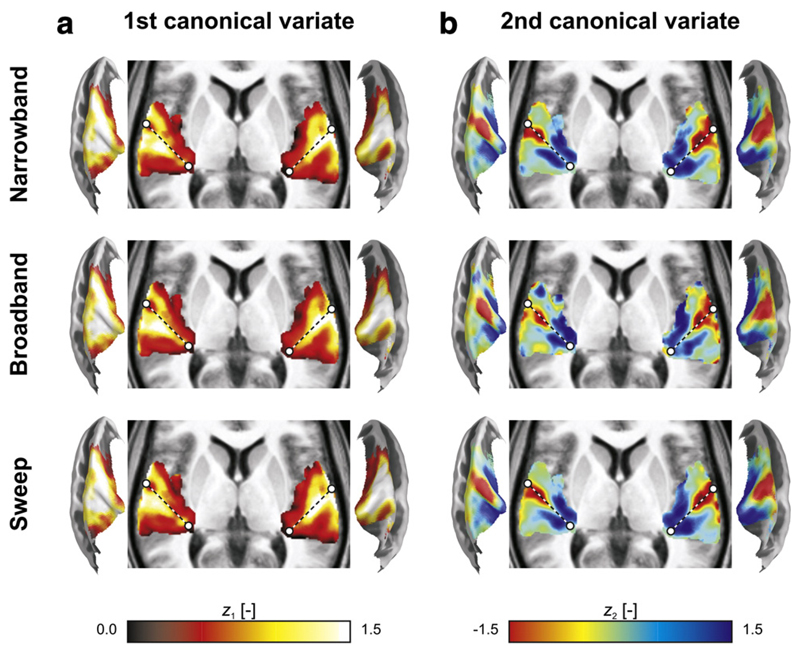
The results of the generalised CCA are displayed in Fig. 7. The 1st and 2nd canonical variates had spatial distributions that closely resembled those of the 1st and 2nd principal component maps, respectively (compare Fig. 7 to Fig. 4). A notable difference concerned the scale: the canonical variates all had similar overall magnitudes. This is merely due to the constraints, which allow principal component maps to be expressed as percentage signal change (akin to original fMRI units), whereas canonical variates have unit RMS amplitude (akin to normalised z-scores).

Fig. 7.

Volumetric projections across the z-direction (with dashed lines approximately outlining the axis of Heschl's gyrus) and semi-inflated cortical surface cross-sections display the maps z_i,k of the first two canonical variates that were extracted from the narrowband, broadband, and sweep data simultaneously. (a) Activation maps, from the 1st canonical variate, and (b) tonotopic maps, from the 2nd canonical variate, were very similar to the principal component maps (see Fig. 4) except for scaling factors, and their interpretation was identical.

Nevertheless, subtle differences are apparent. The pairwise correlations between the 1st canonical variates (reflecting activation) amounted to R_{narrowband,broadband} = 0.991, R_{narrowband,sweep} = 0.990, and R_{broadband,sweep} = 0.985. The correlations between the 2nd canonical variates (reflecting tonotopy) amounted to R_{narrowband,sweep} = 0.944, R_{broadband,sweep} = 0.871, and R_{narrowband,broadband} = 0.865. Thus, all correlations were very high, especially for the 1st canonical variates. For the 2nd canonical variates, both correlations involving the broadband sequences tended to be weaker than the correlation involving the narrowband and sweep sequences only, suggesting that the broadband tonotopic map was an “odd one out”.

Discussion

Activation and tonotopy

All analyses that we employed identified two primary signal contributions. The interpretation of these components proved highly consistent across the three stimulus types (narrowband vs. broadband vs. sweep) as well as across the two analysis methods (PCA vs. CCA). The current results also agree very well with the outcomes of one other study that previously employed PCA to analyse tonotopic maps in a larger cohort of 40 participants (Langers et al., 2012). Although a possible critique of data-driven analyses is that they are always prone to extract apparent patterns from data due to their model-free nature, the detailed agreement of our observations across several independent datasets forms strong evidence that the extracted features are reproducible neurophysiologically meaningful indicators and did not arise merely due to chance.

The strongest signal contribution that we observed represented a near-uniform activation to all sound stimuli relative to the silent baseline periods. Sensitivity to sound-evoked activation is a desirable property of an experimental protocol because it allows the identification of sound-responsive brain regions in individual subjects. Thus the experiment may act as a functional localiser of auditory cortex. For this reason, a silent condition is usually included in auditory neuroimaging studies. However, for the purpose of tonotopic mapping, this is not strictly required. For instance, one could directly compare the fMRI signal to low and high sound stimuli alone in a predefined mask of the auditory cortex. Yet, the omission of a silent reference condition has several disadvantages. First, it does not allow sound-responsive regions to be identified in individuals. Although at the group level sound-evoked responses tend to form smooth clusters that consistently cover an extensive part of the superior temporal plane, in individual subjects activation tends to be structured into multiple elongated clusters (Brechmann et al., 2002) of which the number, size, shape, orientation, and location may vary across individuals to a certain degree. This is exemplified by the individual results in the present study (see Fig. 5). Because the assessment of frequency tuning will be least reliable in voxels with the weakest responses, knowledge of sound-evoked activation and the related significance levels is informative when interpreting tonotopic maps, especially at the subject level. Second, the overall activation level confounds the best frequency measure if the baseline is unknown. For instance, if the response to high frequencies is found to be marginally stronger than that to low frequencies, this could indicate that the particular voxel responds to all sounds equally with only a weak preference for higher frequencies. However, it could also mean that the voxel is sharply tuned to only the highest frequencies, but simply has a small excitability. These two scenarios indicate entirely different tuning properties, but are impossible to distinguish when a baseline measure is absent. This is also the reason why, in Fig. 6, the ratio of signal contributions was colour-coded as the most accurate correlate of frequency tuning, rather than the 2nd component itself. Therefore, even if quantification of sound-evoked activation levels in general is not a primary goal in a tonotopic mapping study, then the ability to determine activation maps is still highly desirable.

The second signal contribution was found to involve positive signals related to high-frequency sound stimuli and negative signals related to low-frequency sound stimuli. Superimposed upon the first component, this signifies high-frequency preferences for voxels with positive coefficients in the 2nd component's map, and low-frequency preferences for negative voxels. (Note that the sign of the profile or map of a component individually is undetermined in PCA, although their product is meaningful; that is, the profile and map may simultaneously be flipped without changing the interpretation of the component.) Low-frequency voxels were found on the distal crest of HG, whilst high-frequency voxels were found on its caudal and rostral medial banks. This pattern is highly consistent with the majority of the current literature, and the most popular interpretation is that two separate tonotopic progressions are laid out in a V-shape contained in two regions (Langers, 2014). Together, these form a core area that stretches transversely across HG (Saenz and Langers, 2014). They most likely form the human homologues of primary auditory field hA1 (on caudal HG) and rostral field hR (on rostral HG) corticals, which constitute core auditory cortex in primates (Baumann et al., 2013; Hackett et al., 2001).

Another putative tonotopic core field RT anterior to R has been proposed in some primate studies (Kaas and Hackett, 2000). We did not observe such an additional progression, nor could we confirm additional separate tonotopic progressions in the more lateral belt areas of the superior temporal gyrus and sulcus (Striem-Amit et al., 2011). This could be due to the fact that we used tone sequences, which may be less effective in exciting non-primary processing areas. Moreover, tonotopic progressions in some belt areas have been suggested to connect seamlessly to those in core fields, rendering them difficult to discriminate based on functional criteria alone (Kusmierek and Rauschecker, 2009). Finally, we note that besides the nowadays commonly reported primary progressions in putative hA1 and hR, the existence of other tonotopically organised areas has so far not been disambiguated in humans.

PCA: covariances within datasets

Since the profiles of the principal components were constrained to unit RMS amplitude, the amplitudes contained in the corresponding maps provide a measure of the amount of signal power that is associated with the component, relative to the silent baseline. The maps in Fig. 4, the scatterplots in Fig. 6, and the summary statistics in Table 2 therefore provide a measure of how much signal variability is available to identify activation (in the 1st principal component) and tonotopy (in the 2nd principal component), irrespective of the particular analysis method that is used to assign an activation level or best frequency. Assuming identical contributions across the three stimulus paradigms from e.g. random thermal noise and uncontrolled physiological fluctuations, these amplitudes are indicative of the achievable signal to noise ratio and sensitivity of the experiment. The table also lists how much power was contained on average in the remaining discarded components; because these were much weaker, more difficult to interpret, and less reproducible across the three different datasets, they are not described in detail and will not be further discussed.

Regarding the 1st component, which reflected generic sound-evoked activation, our PCA results showed good agreement with the trends in the extent of activation clusters that were detected using the group-level regression model (Fig. 2). The broadband tone sequences proved to be the most effective stimuli. Relatively speaking, this component alone explained more than 99% of the total signal power contained in the regression coefficients (i.e. the various “beta maps”). In absolute terms, the signal power was twice as large as that evoked by the second-most effective type of stimulus (narrowband tone sequences). This is perhaps not surprising. Due to their nature, these broadband sequences are able to excite a large population of neurons with a diverse range of characteristic frequencies, whereas the narrowband sequences each target a much smaller sub-population of neurons tuned only to a particular frequency region. However, it should be realised that although the excitation was spread across many neurons, most neurons are expected to respond to only a subset of tones in the sequence. In contrast, for narrowband sequences, if a neuron responds to one tone, it would be expected also to respond well to all other tones in the sequence given their spectral proximity. If responses added linearly, one would expect response levels to be the same given that the total number of tones was close to identical and their overall statistical distribution across an entire run was always uniform. It is apparent from our results therefore that non-linear mechanisms play a role. Such mechanisms are numerous. At the neural level, response adaptation and habituation occur in the form of repetition suppression, rendering a repeated similar stimulus less effective in evoking responses than a sequence of very different stimuli (Grill-Spector et al., 2006; Krekelberg et al., 2006; Lanting et al., 2013). Also, it may be argued that broadband sequences are less predictable, possibly leading to differences in top-down attentional modulation (Costa-Faidella et al., 2011). Furthermore, at a metabolic and hemodynamic level, response saturation occurs due to ceiling effects in the transfer of metabolites and the dilation of blood vessels (Binder et al., 1994). Such non-linearities are more prone to dominate if all neural activity is concentrated in particular regions rather than spread across the cortical surface. This would explain why the broadband sequences proved most effective. Authors that employed naturalistic stimuli have further argued that such stimuli are more effective because of their richness, associative meaning, and ecological validity (Moerel et al., 2012). Although this explanation may well apply to those experiments, it does not extend to our jittered tone stimuli.

Our finding that sweeps are the least effective stimuli is perhaps less intuitive. Although still more than 90% of the total power was explained by the first component alone, the sweeps evoked activation that was approximately twofold smaller in an absolute sense than that due to the narrowband sequences. Since the sweeps consisted of ½-octave intervals that slowly shifted in the frequency domain, they were very similar to the narrowband sequences on short time scales. As far as the sweep had an effect at longer time scales, it should be expected to widen the range of stimulation frequencies, and thus prove a more effective stimulus for the same reasons as argued above in relation to the broadband sequences. In our opinion, the most plausible explanation for the low effectiveness of the sweep sequences is that the duration of the silent period between sweeps may have been too short to allow the hemodynamic response to return fully to baseline. The timing of our protocol was based on other studies in the literature. In particular, Da Costa et al. (2011) reported reliable tonotopic maps based on a relatively modest amount (16 min) of data acquired per subject using a 7-T scanner. They alternated 28-s stepwise sweeps with 4-s periods of silence, as compared to 24.2-s sweeps and 4.4-s periods of silence in our 3-T study. A trade-off should be made between maintaining the silent period long enough to allow the hemodynamic response to recover, whilst keeping it short enough to allow a sufficient number of sweeps to be presented in given time. The best sensitivity to activation is expected to be obtained if the silent interval is increased to approach the hemodynamic impulse response duration (Birn et al., 2002; Liu et al., 2001), that is on the order of 10 s (Backes and van Dijk, 2002; Hall et al., 2000). Since this would decrease the duty cycle of the sweep presentations, the sensitivity to tonotopic differences in tuning would then moderately decrease (for fixed total measurement time).

Regarding the 2nd component, the stimuli ranked oppositely so that the broadband sequences performed worst. Although the extracted component could still be clearly seen to reflect tonotopically organised tuning differences, only a fraction of a percent of the observed signal power could be attributed to the 2nd component for broadband stimulation. In absolute terms, this component was at least six times weaker than the corresponding component for the two other types of stimuli. The reason behind this relatively poor sensitivity can be easily understood. The various broadband sequences covered the same frequency range and their spectral distributions showed substantial overlap. The component profile in Fig. 3 revealed that essentially all discrimination between low- and high-frequency tuned voxels was based on responses to the stimuli labelled Ia and Ib, which comprised highly skewed distributions favouring either the low- or high frequencies (see Fig. 1). Since these two (out of seven) stimuli were only presented in 12 (out of 44) trials per subject, it is not surprising that the signal power attributable to this component was limited. If only these two stimuli had been included in addition to the silent baseline periods, instead of the full set of stimuli that we employed, then the increase in signal power of this component can be expected to amount to a factor of three, approximately (based on the proportion of trials that involved the respective stimulus conditions). This would still make the broadband sequences substantially less sensitive to tonotopic differences than the other stimuli, but the difference in terms of detectable signal power would be reduced to a factor of two.

With regard to the sensitivity to frequency tuning, the sweep sequences outperformed the narrowband sequences, although only by a narrow margin. Whereas 5.5% of the total signal power was attributable to this component for sweep sequences, and only 2.4% for narrowband sequences, this difference was partly driven by differences in the strength of the first component. In absolute terms, the power differed by only a factor of 1.2. It is not entirely clear what mechanisms may explain this difference. Perhaps neural adaptation effects are less prominent due to the more dynamic nature of the sweeps. Alternatively, contrasts in response amplitudes may appear enlarged as a result of deactivation occurring in response to neighbouring frequencies due to inhibitory sidebands.

Summarising our PCA results, we find that broadband sound stimuli were most efficient in evoking responses but least efficient in differentiating between differently tuned brain areas. Conversely, sweep sequences provided the best sensitivity to differences in frequency tuning, but resulted in weak evoked responses overall. The narrowband sequences offered the best compromise between both criteria: they provided a sensitivity to tonotopy that was comparable to the sweep sequences, but a substantially larger sound-evoked response magnitude. It should be pointed out that the design of the sweep experiment may likely be improved by increasing the duration of the silent periods between sweeps: this should improve sensitivity to activation at the cost of a modest reduction in sensitivity to frequency tuning, thus likely rendering the performance of this type of stimulus very comparable to that of the narrowband sequences in this experiment. Moreover, the broadband design could be made more efficient by omitting the higher-order stimuli (IIa, IIb, IIIa, and IIIb), thereby making it more competitive with regard to tonotopic mapping, although still more sensitive to activation but less sensitive to tonotopy than the other two stimulus types.

CCA: covariances between datasets

The PCA analysis that was used here has the advantage that it is well suited to collapse the high-dimensional data corresponding with the various stimuli into a manageable number of informative lower-dimensional components. However, a disadvantage is that the interpretation of the components is not necessarily the same across the datasets. PCA is performed on one dataset at a time, and the outcomes for each dataset are in no way influenced by the other datasets. As a result, one might for instance argue that perhaps the broadband sequences proved less sensitive to tonotopic differences because some of the signal power related to frequency tuning ended up spreading over the remaining components (i.e. the third and higher components). Essentially, despite the fact that the component maps had a highly similar appearance and the profiles had a highly similar interpretation, there is no guarantee that they can be directly compared in a fair fashion.

In an attempt to overcome and address this issue, we performed a complementary analysis based on generalised CCA. This method attempts to find linear combinations (of maps, in our case) in all three datasets simultaneously, in such a way that the average correlation between pairs of maps of distinct datasets is maximal. In the context of fMRI, CCA has been used to identify brain networks with similar activation across groups, subjects, tasks, or voxels (Friman et al., 2001; Sui et al., 2010; Varoquaux et al., 2010). We used this method to extract maximally similar activation patterns that occurred across sets of stimulus conditions. Loosely speaking, CCA attempts to find maps that can be constructed from each of the datasets individually, but nevertheless have a maximally identical interpretation across datasets. This property is complementary to that of PCA.

The maps that resulted from this analysis proved virtually indistinguishable from the PCA maps, except for obvious scaling differences that are intrinsic to the methods. In particular, their interpretation remained the same: the 1st canonical variate summarised sound-evoked activation irrespective of frequency, whilst the 2nd canonical variate revealed the tonotopic organisation due to differences in frequency tuning. Nevertheless, upon closer examination the tonotopic map derived from the broadband sequences proved to differ more from the maps generated from the other two stimulus types, compared with the divergence between the other two maps. Although all similarities were high, this appears to be consistent with the previous conclusion that broadband sequences offer particular sensitivity towards activation, whereas narrowband and sweep sequences are more advantageous to extract tonotopy.

The fact that both the PCA and CCA analyses resulted in such comparable outcomes suggests that the obtained results were simultaneously maximally representative of the individual datasets and maximally similar across the types of stimuli. We argue that this shows that the employed data-driven approach proved sensitive to activation and tonotopy in all datasets, despite the fact that no a priori model, set up to extract precisely these features, was employed. At the same time, we were able to show that the balance between sensitivity to activation and tonotopy was different for the three stimulus types.

Design recommendations

Finally, how should the presented findings be interpreted in relation to which type of stimulus is most suitable for tonotopic mapping? The answer to this question depends upon the particular goals of an individual study.

If a functional localiser is needed that identifies regions of (auditory) cortex in individuals that are sensitive to sound, but that also provides a qualitative tuning map (e.g. to identify the gradient reversal that marks the boundary between the putative areas hA1 and hR), then a paradigm with broadband sequences appears suitable. We advise that three conditions should be included in such a paradigm: a silent baseline, plus a low- and a high-frequency dominated broadband stimulus similar to our stimuli Ia and Ib. Given that, in the current study, only ~ 12 min of data were acquired per stimulus type, it should be possible to implement such a paradigm in the context of a more broadly scoped auditory neuroimaging session.

If, however, tonotopic maps are the primary outcome of interest, for example when studying plastic tonotopic reorganisation in relation to auditory disorders, then narrowband or sweep sequences would seem more appropriate. They allow most signal power to be extracted that is related to frequency tuning in individual voxels, and thus provide more information for the optimal assessment of tonotopic patterns. As explained in our accompanying paper that focusses on imaging paradigms (Langers, 2014), sweep sequences have the potential disadvantage that frequency-dependent tuning and time-dependent hemodynamics are confounded. For that reason, we suggest that a design based on blocks of tone sequences rather than sweeps should be used. Depending on the available time and required frequency resolution, an appropriate number of conditions may be chosen.

Note that data-driven analysis was employed in this report in order to allow objective comparison of the three stimulus types. For an experimental design that is based on one of these types of stimuli only, model-driven approaches are preferable to enable confirmatory hypothesis testing.