Abstract
Non-negative matrix factorization (NMF) by the multiplicative updates algorithm is a powerful machine learning method for decomposing a high-dimensional nonnegative matrix V into two nonnegative matrices, W and H where V ~ WH. It has been successfully applied in the analysis and interpretation of large-scale data arising in neuroscience, computational biology and natural language processing, among other areas. A distinctive feature of NMF is its nonnegativity constraints that allow only additive linear combinations of the data, thus enabling it to learn parts that have distinct physical representations in reality. In this paper, we describe an information-theoretic approach to NMF for signal-dependent noise based on the generalized inverse Gaussian model. Specifically, we propose three novel algorithms in this setting, each based on multiplicative updates and prove monotonicity of updates using the EM algorithm. In addition, we develop algorithm-specific measures to evaluate their goodness-of-fit on data. Our methods are demonstrated using experimental data from electromyography studies as well as simulated data in the extraction of muscle synergies, and compared with existing algorithms for signal-dependent noise.
Keywords: nonnegative matrix factorization, generalized inverse Gaussian, Kullback-Leibler divergence, dual, J-divergence, EM algorithm, signal-dependent noise, empirical entropy, empirical likelihood, high-dimensional data, electromyography, muscle synergy, explained variation, Akaike Information Criterion
1 Introduction
Nonnegative matrix factorization (NMF) was introduced as an unsupervised, parts-based learning paradigm, in which a high-dimensional nonnegative matrix V is decomposed into two matrices, W and H, each with nonnegative entries, V ~ WH by a multiplicative updates algorithm (Lee & Seung, 1999;2001). In the past decade, NMF has been increasingly applied in a variety of areas involving large-scale data. These include, but not limited to, neuroscience, computational biology, natural language processing, information retrieval, biomedical signal processing and image analysis. For a review of its applications, the interested reader is referred to Devarajan (2008) and references therein.
Lee & Seung (2001) outlined algorithms for NMF based on the Gaussian and Poisson likelihoods between two nonnegative matrices. Ever since their seminal work, numerous variants, extensions and generalizations of the original NMF algorithm have been proposed in the literature. For example, Hoyer (2004), Shahnaz et al. (2006), Pascual-Montano et al. (2006) and Berry et al. (2007) extended NMF to include sparseness constraints. Wang et al. (2006) introduced LS-NMF that incorporated variability in the data. Cheung & Tresch (2005) and Devarajan & Cheung (2012) extended the NMF algorithm to include members of the exponential family of distributions while Devarajan et al. (2005, 2006, 2008, 2011) formulated a generalized approach to NMF based on the Poisson likelihood that included various well-known distance metrics as special cases. Dhillon & Sra (2006) and Kompass (2007) have also proposed generalized divergence measures for NMF. Cichocki et al. (2006, 2008, 2009, 2011) extensively developed a series of generalized algorithms for NMF based on α- and β-divergences while Fèvotte et al. (2011) recently extended it by proposing some novel algorithms. The work of Cichocki et al. (2009) provides a detailed reference on this subject.
The main focus of this paper is on NMF algorithms for signal-dependent noise with particular emphasis on the generalized inverse Gaussian family of distributions. This family includes the well-known gamma model for signal-dependent noise as a special case. It also includes the inverse Gaussian model as a special case, among others. Each model incorporates signal-dependence in noise in structurally different ways based on the mean-variance relationship, as evidenced in the forthcoming sections. These models are embedded within the framework of the exponential family of models outlined in Cheung & Tresch (2005) and can be obtained as special cases of β-divergence proposed in Cichocki et al., (2006, 2009). In each case, the NMF algorithm is based on maximizing the likelihood or, equivalently, minimizing a cost function defined by the Kullback-Leibler divergence between the input matrix V and the reconstructed matrix WH.
We describe an approach to NMF for signal-dependent noise by extending the standard likelihood approach to include two well-known alternative cost functions from information theory for quantifying this divergence, namely, the dual Kullback-Leibler divergence and the J-divergence. Based on these measures, we propose three NMF algorithms applicable when the data exhibit signal-dependent noise. For each algorithm, we provide a rigorous proof of monotonicity of updates using the EM algorithm. We describe a principled method for selecting the appropriate rank of the factorization and develop algorithm-specific measures to quantify the variation explained by the chosen model. We demonstrate the applicability of our methods using experimental data from electromyography (EMG) studies as well as simulated data in extracting muscle synergies, and compare the performance of our proposed methods with existing algorithms for signal-dependent noise.
The remainder of the paper is organized as follows. Section 2 provides the necessary background required for the information-theoretic approach described in this paper. It is intended to serve as a brief tutorial on fundamental concepts, terminology, basic quantities of interest for our problem and their interpretations. Section 3 provides a detailed overview of existing NMF algorithms for signal-dependent noise and places them within the broader context of NMF algorithms based on generalized divergence measures. Furthermore, it describes our proposed NMF algorithms for signal-dependent noise and provides multiplicative update rules. Section 4 outlines methods for model selection and evaluation while section 5 presents an application of our methods to EMG data and a comparison to existing methods. Section 6 provides a summary and conclusions. Detailed proofs of monotonicity of updates for the proposed algorithms are relegated to the Appendix.
2 Background and Preliminaries
2.1 Directed Divergence and Divergence
Suppose we are interested in testing a set of hypotheses denoted by Hi, i = 0, 1, that a random variable X is from population i with probability measure μi Assume that μ0 and μ1 are absolutely continuous with respect to each other and that X takes values on the entire real line. Let P(Hi) denote the prior probabilities, f, g the density functions, and F, G the distribution functions corresponding to the hypothesis Hi, i = 0, 1, respectively. If P(Hi|x) denotes the conditional (or posterior) probability of Hi given X = x, then using Bayes’ theorem, we have,
and
Hence,
i.e., the logarithm of the likelihood ratio, defined as the negative difference between the logarithm of the odds in favor of H0 before and after the observation X = x, is the information in X = x for discrimination in favor of H0 against H1 (Kullback & Leibler, 1959).
Suppose that x is not given and there is not specific information on the whereabouts of x other than x ∈ S. The mean information per observation, averaged over all the values x of X, for discrimination in favor of H0 against H1 is thus
| (1) |
This quantity is known as Kullback-Leibler divergence between f and g, the negative log-likelihood or empirical entropy. Similarly, the measure I(g, f) is defined as the mean information per observation, averaged over all the values x of X, for discrimination in favor of H1 against H0 and is given by
| (2) |
This quantity is known as dual Kullback-Leibler divergence between f and g or the empirical likelihood. In light of the above definitions, I(f, g) and I(g, f) are also referred to as directed divergences. These quantities are nonnegative definite and are zero if and only if f(x) = g(x) almost everywhere (Kullback & Leibler, 1959; Owen, 2001).
Using directed divergences I(f, g) and I(g, f), one can define J-divergence J(f, g) as
| (3) |
which is a measure of the divergence or the difficulty of discriminating between the hypotheses H0 and H1. A key feature of J(f, g) is symmetry with respect to the measures μ0 and μ1. It has all the properties of a distance measure (metric) except the triangle inequality, is nonnegative definite and is zero if and only if f(x) = g(x) almost everywhere (Kullback & Leibler, 1959).
2.2 Motivating NMF for Signal-Dependent Noise
2.1 The Generalized Inverse Gaussian Distribution
A non-negative random variable X is said to be a member of the family of generalized inverse Gaussian (GIG) distributions if its probability density function is given by
| (4) |
where γ > 0, δ > 0, ξ ∈ R and Kξ is the modified Bessel function of the third kind with index ξ. In the limiting case δ → 0 when ξ > 0, f(x) reduces to a gamma distribution with density
| (5) |
where α = ξ > 0 and . The mean-variance relationship can be written as
| (6) |
and thus indicates a quadratic dependence of variance on the mean. When , f(x) reduces to an inverse Gaussian distribution with density
| (7) |
where λ = δ2 and . The mean-variance relationship can be written as
| (8) |
and thus indicates a cubic dependence of variance on the mean.
Other special cases of the GIG family of distributions include the inverse gamma and hyperbolic distributions (Eberlein & Hammerstein, 2004). In this paper, we focus on the gamma and inverse Gaussian distributions as data generating models for signal-dependent noise in the context of NMF.
2.2 Divergence Measures for Signal-Dependent Noise
The discrimination information functions defined above were introduced by Kullback & Leibler (1951) and serve as divergence measures for comparing two distributions or probability models. Using appropriate densities for f(x) and g(x) in equations (1)-(3) based on the Gaussian (normal), gamma or inverse Gaussian models, one can obtain various divergence measures for NMF based on the empirical entropy, empirical likelihood or a combination of these. Throughout the presentation, we shall use KL, KLd and J to denote Kullback-Leibler, dual Kullback-Leibler and J-divergence, respectively. In each case, the subscripts N, G and IG are used to refer to the Gaussian, gamma and inverse Gaussian models, respectively. The term KL divergence has been used in the literature to refer to that based on the Poisson model. However, it is important to note that the terms KL, dual KL and J-divergence used in this paper refer to generic divergence measures between any two densities f and g as defined in equations (1)-(3) and are not model-specific. Each divergence measure can be defined specifically for a particular choice of model as outlined below.
For two normal random variables with means μ1 and μ2 (and equal variance σ2) and corresponding probability density functions f(x) and g(x), it can be shown that
| (9) |
Using equation (5), it can be shown that for two gamma random variables with means μ1 and μ2 (and common shape parameter α) and corresponding probability density functions f(x) and g(x),
| (10) |
| (11) |
and
| (12) |
Similarly, using equation (7), it can be shown that for two inverse Gaussian random variables with means μ1 and μ2 (and common shape parameter λ) and corresponding probability density functions f(x) and g(x),
| (13) |
and
| (14) |
It will become clear in §3 that none of the parameter coefficients in the divergence equations (9)-(14) play any role in the derivation of the NMF algorithms. Hence, we assume that 2σ2 = α = λ/2 = 1 without loss of generality. It should be noted that this assumption is consistent with the basic formulation in NMF and that numerous other divergence measures available in the literature for NMF implicitly make such assumptions (Cichocki et al., 2006, 2008, 2009; Févotte et al., 2011; Kompass, 2007; Devarajan & Cheung, 2012).
We motivate non-negative matrix factorizations in the context of dimension reduction of high-dimensional electromyography (EMG) data. EMG data is typically presented as a matrix in which the rows correspond to different muscles, the columns to disjoint, sequentially sampled time intervals, and each entry to the EMG signal of a given muscle in a given time interval. In EMG studies, the number of muscles, p, is typically less than fifty, the number of time intervals, n, is typically in the tens of thousands, and the matrix of EMG signal intensities V is of size p×n so that each column of V represents an activation vector in the muscle space at one time instance. Our goal is to find a small number of muscle synergies, each defined as a non-negative, time-invariant activation balance profile in the p-dimensional muscle space. This is accomplished via a decomposition of the matrix V into two matrices with nonnegative entries, V ~ WH, where W has a size p × r, so that each column is a time-invariant muscle synergy in the p-dimensional muscle space and the matrix H has size r × n, so that each column contains the activation coefficients for the r synergies in W for one time instance. The number of synergies r is chosen so that (n + p)r < np. The entry hai of H is the coefficient of time interval i in synergy a and the entry wja of W is the expression level of synergy a in muscle j, where a = 1, 2, …, r.
The first step in obtaining an approximate factorization for V is to define cost functions that measure the divergence between the observed matrix V and the product of the factored matrices WH. We can express this in the form of a linear model as follows:
| (15) |
where ε represents noise. NMF algorithms for signal-dependent noise based on KL divergence (equations (10) and (13), respectively) for gamma and inverse Gaussian models exist in the literature (Cheung & Tresch, 2005; Cichocki et al, 2009; Fèvotte et al, 2011). In this paper, we propose three novel NMF algorithms for handling signal-dependent noise, specifically based on dual KL and J-divergence for gamma and inverse Gaussian models (equations (11), (12) and (14)). The appropriate cost function for each model is obtained by simply substituting μ1 and μ2 in equations (9)-(14) with V and WH, respectively.
2.3 Application of NMF to EMG Data
We present an application involving the analysis of EMG data, electrical signals recorded from muscles that reflect how they are activated by the nervous system for a particular posture or movement. It is well-known in the literature that EMG data exhibits signal-dependent noise (Harris & Wolpert, 1998; Cheung et al., 2005). One long standing question in neuroscience concerns how the motor system coordinates the activations of hundreds of skeletal muscles, representing hundreds of degrees of freedom to be controlled (Bernstein, 1967). They define an immense volume of possible motor commands that the central nervous system (CNS) must search through for the execution of even an apparently simple movement. It has been argued that the CNS simplifies the complexity of movement and postural control arising from high dimensionality by activating groups of muscles as individual units, known as muscle synergies (Tresch et al., 2002; Giszter et al., 2007; Bizzi et al., 2008; Ting et al., 2012). As modules of motor control, muscle synergies serve to reduce the search space of motor commands, reduce potential redundancy of motor commands for a given movement, and facilitate learning of new motor skills (Poggio and Bizzi, 2004). Numerous laboratories have utilized linear factorization algorithms to extract muscle synergies from multi-channel EMGs recorded from humans and animals (reviewed in Bizzi and Cheung, 2013). In particular, several studies have demonstrated that the muscle synergies returned by the Gaussian NMF could be neurophysiological entities utilized by the CNS for the production of natural motor behaviors (Saltiel et al., 2001; Tresch et al., 2006; Overduin et al., 2012).
It has been further posited that muscle synergies for locomotion are basic units of the so called central pattern generators (CPGs) whose organizations are independent of the pattern of sensory feedback. Cheung et al. (2005) sought to demonstrate this possibility by recording hind-limb EMGs from bullfrogs during jumping and swimming, before and after deafferentation, or the surgical procedure of eliminating sensory in-flow into the spinal cord by cutting the dorsal nerve roots. By applying a manipulated version of the Gaussian NMF to the data matrix that pooled the intact and deafferented EMGs together, they found 3 to 6, out of 4 to 6, muscle synergies were preserved after deafferentation. The preserved synergies were then interpreted as basic components of the CPGs. Here, we ask whether the NMF algorithms based on gamma or inverse Gaussian noise can better identify CPG components by discovering more muscle synergies shared between the pre- and post-deafferentation data sets than the traditional Gaussian NMF. We hypothesize that the NMF algorithms derived from signal-dependent noise outperform the Gaussian NMF in their ability to discover shared muscle synergies, because signal-dependent noise formulations should better model the noise properties of EMG signals than a Gaussian formulation (Harris and Wolpert, 1998).
The data analyzed here were previously described in Cheung et al. (2005). Briefly, EMGs during unrestrained jumping and swimming were collected from four adult bullfrogs (Rana catesbeiana), before and after a complete hind-limb deafferentation was achieved by severing dorsal roots 7 to 9. Intramuscular EMG electrodes were surgically implanted into the following muscles in the right hind-limb: rectus internus major (RI), adductor magnus (AD), semimembranosus (SM), semitendinosus (ST), iliopsoas (IP), vastus internus (VI), rectus femoris anticus (RA), gastrocnemius (GA), tibialis anticus (TA), peroneus (PE), biceps (BI), sartorius (SA), and vastus externus (VE). The collected EMG signals were amplified (gain of 10,000) and bandpass filtered (10-1000 Hz) through differential alternating-current amplifiers, then digitized at 1000 Hz. Using custom software written in Matlab (R2010b; Math-Works, Natick, MA), the EMG signals were further high-pass filtered with a window-based finite impulse response (FIR) filter (50th order; cutoff of 50 Hz) to remove any motion artifacts, then rectified, low-pass filtered (FIR; 50th order; 20 Hz), and finally integrated over 10-ms intervals. The pre-processed data of each muscle were then normalized to the maximum EMG value of that muscle attained in the entire experiment.
The EMG signal is a spatiotemporal summation of the motor action potentials traveling along the muscle fibers of the thousands of motor units in the recorded muscle. The high-frequency components of the EMG reflect, in addition to noise, the contribution of these action potentials. In motor neuroscience, it is customary to perform low-pass filtering on the recorded EMGs to obtain an envelope of muscle activation, which should reflect the higher-level control signals originating from the brain and spinal cord that specify the degree of muscle contraction for generating the desired force (with the force magnitude dictated by the muscle’s force-length and force-velocity relationships). Since we are interested in discovering structures at the level of control signals for muscular contraction (i.e., muscle synergies), and since signal-dependent noise is thought to occur at this control-signal level, it is appropriate to apply NMF to filtered EMG data. There is a sizable literature on using the Gaussian NMF algorithm for extracting muscle synergies from filtered EMG data (reviewed in Bizzi and Cheung, 2013). Moreover, filtering the EMGs before NMF extraction would allow an easier comparison of our results with those in the literature.
One approach to visualizing signal-dependence in this data is to plot the variability as a function of the mean for EMG signals from each muscle separately. Any observed trend in the mean-variance relationship would indicate some form of signal-dependence, the exact nature of the relationship being dependent on the data generating mechanism. For each muscle, the mean and variance of the EMG signal were computed for moving windows across time. Several window sizes ranging from 3-50 were explored and it was observed that mean-variance relationship was not sensitive to the choice of window size. Our choice of window size was based on a physiological justification. There has been an earlier result suggesting that bursts with 275 msec. duration could be a fundamental pulse unit in the frog spinal cord (Hart and Giszter, 2004). Since our integration time interval is 10ms, we used a window size of 28 so that each window corresponded to the duration of this fundamental drive.
Using equation (6), the mean-variance relationship for a gamma model can be rewritten in terms of the standard deviation σ(X) as
Taking the logarithm on both sides, we obtain
Fig. 1(A) shows a plot of the logarithm of the estimated standard deviation against the logarithm of the estimated mean for moving windows across time for the intact jump of one frog for the muscle TA. The black solid line represents a linear fit to this data. The proximity of the estimated slope of this line to unity provides strong evidence that a gamma model adequately represents the mean-variance relationship in this data. The logarithmic transformation provides variance stabilization and aids in interpreting the slope of the fit. Panels (A)-(D) in Fig. 1 display such plots for each of the four behaviors of selected muscles and frogs. At the top of each panel in this figure, the estimate of the slope and goodness-of-fit measures such as the root mean squared error (RSE) and adjusted R2 are listed along with frog behavior and name of muscle. This figure is representative of the mean-variance relationship typically observed in our frog EMG data. Supplemental Table 1 lists the estimates of slope and adjusted R2 (mean ± SD for N = 4 frogs) from the least squares fit for each behavior and muscle. It is evident from these results that the gamma model provides an overall good fit of the EMG data.
Figure 1.
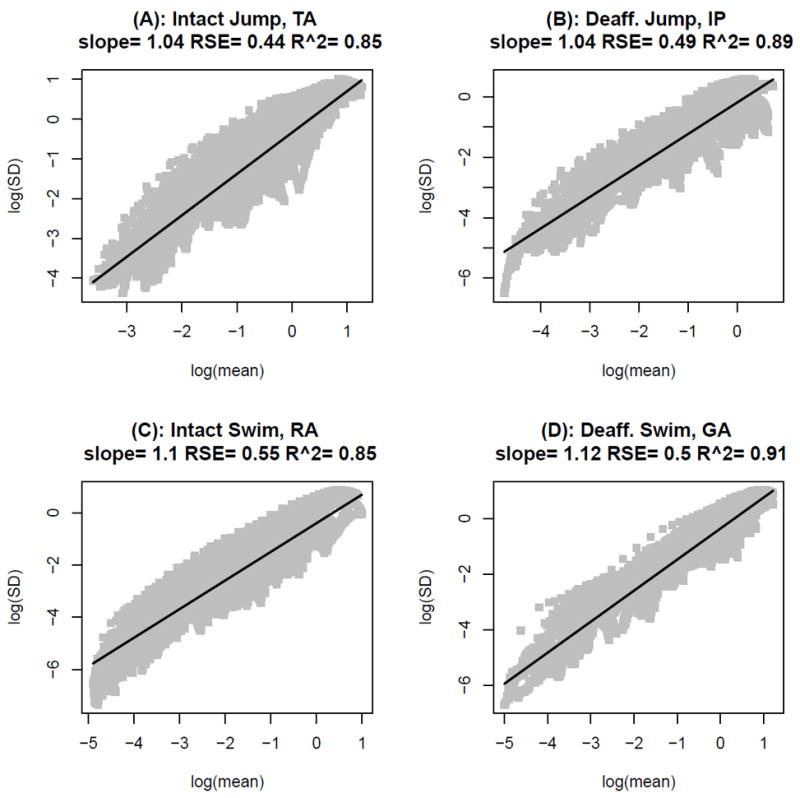
Illustration of the mean-variance relationship for the frog EMG data. Plot of the logarithm of the estimated standard deviation against the logarithm of the estimated mean for moving windows across time for each behavior of selected muscles and frogs. Each panel displays the mean-variance relationship for a particular behavior. A, Intact Jump B, Deafferented Jump C, Intact Swim D, Deafferented Swim. In each panel, the black solid line represents a linear fit to the data and estimates of the slope, root mean squared error (RSE) and adjusted R2 are listed at the top of each panel.
In the following section, we discuss NMF algorithms for signal-dependent noise. We begin with a survey of existing work in this area before proceeding to describe three novel algorithms for this problem. A detailed analysis of the data sets described here, including a comparison of existing approaches to our proposed methods, is presented in Section 5.
3 NMF Algorithms for Signal-dependent Noise
3.1 Existing Work
Cheung & Tresch (2005) proposed a heuristic NMF algorithm for the exponential family of distributions that embeds the Gaussian, Poisson, gamma and inverse Gaussian models. They provided generalized multiplicative update rules for W and H by modifying the step-size in the gradient based on the negative log-likelihood (or, equivalently, KL divergence). In independent work, Cichocki et al. (2006) also proposed a similar heuristic algorithm based on the generalized β-divergence and provided multiplicative update rules for W and H. β-divergence between the input matrix V and reconstructed matrix WH is given by
| (16) |
β-divergence includes the Gaussian (β = 2), Poisson (β → 1), gamma (β → 0) and inverse Gaussian (β = −1) models as special cases. It should be noted that this generalized divergence is related to the other divergence measures independently described in the literature (such as those in Kompass (2007), Cichocki et al. (2008) and Devarajan et al. (2005, 2011)) via transformations. For NMF algorithms based on gamma and inverse Gaussian models stemming from the work of Cheung & Tresch (2005) and Cichocki et al. (2006), monotonicity of updates cannot be established and they remain heuristic. Recently, however, Fèvotte et al. (2011) proposed a rigorous Majorization-Maximization (MM) algorithm based on β-divergence that enables monotonicity of updates for W and H to be theoretically established. Moreover, they provided generalized multiplicative update rules for W and H that were seen to be different from heuristic updates. We refer to these as the heuristic and MM algorithms for gamma and inverse Gaussian models. In each algorithm, it is straightforward to see that the divergence measure for gamma and inverse Gaussian models is that based on KL divergence. For the NMF problem V ~ WH, using equation (10) the kernel of KL divergence for the gamma model can be written as
| (17) |
This is commonly referred to as the Itakuro-Saito divergence (Cichocki et al., 2009; Fèvotte et al, 2011). Heuristic updates for W and H are given by
| (18) |
| (19) |
and MM updates are given by
| (20) |
| (21) |
Similarly, using equation (13) the kernel of KL divergence for the inverse Gaussian model can be written as
| (22) |
Heuristic updates for W and H are given by
| (23) |
| (24) |
and MM updates are given by
| (25) |
| (26) |
Using results from Cheung & Tresch (2005), Cichocki et al. (2006) and Fèvotte et al. (2011), it is straightforward to obtain the above update rules in each specific case. For consistency, we use the notation , , and to represent the heuristic and MM algorithms for gamma and inverse Gaussian models, respectively.
3.2 Proposed Algorithms
In this section, we propose two novel NMF algorithms based on dual KL divergence, one each for the gamma and inverse Gaussian models, and one algorithm based on J-divergence for the gamma model. We use the notation , and JG, respectively, to denote these three algorithms presented in Theorems 1-3. Closed form multiplicative update rules for W and H are provided for each while proofs of monotonicity of updates are detailed in the Appendix.
3.1 Gamma Model: Algorithm based on dual KL divergence
Using equation (11), the kernel of dual KL divergence for the gamma model can be written as
| (27) |
Theorem 1
The divergence in (27) is non-increasing under the multiplicative update rules for W and H given by (28) and (29). It is also invariant under these updates if and only if W and H are at a stationary point of the divergence.
Proof
See Appendix.
Update rules for H and W are
| (28) |
| (29) |
3.2 Gamma Model: Algorithm based on J Divergence
Using equation (12), the kernel of J divergence for the gamma model can be written as
| (30) |
Theorem 2
The divergence JG(V, WH) defined in (30) is non-increasing under the multiplicative update rules for W and H given by (31) and (32). It is also invariant under these updates if and only if W and H are at a stationary point of the divergence.
Proof
See Appendix.
Update rules for H and W are
| (31) |
| (32) |
3.3 Inverse Gaussian Model: Algorithm based on dual KL divergence
Using equation (14), the kernel of dual KL divergence for the inverse Gaussian model can be written as
| (33) |
Theorem 3
The divergence defined in (33) is non-increasing under the multiplicative update rules for W and H given by (34) and (35). It is also invariant under these updates if and only if W and H are at a stationary point of the divergence.
Proof
See Appendix.
Update rules for H and W are
| (34) |
| (35) |
Using equations (13) and (14), J-divergence for the inverse Gaussian model can be written in terms of V and WH. However, we note that closed form multiplicative updates cannot be obtained using the EM approach, and monotonicity of updates cannot be theoretically established.
Remark
The divergences (27), (30) and (33) and their corresponding update rules for W and H (equations (28,29), (31,32) and (34,35), respectively) contain Vij in the denominator of various terms. Theoretically, this should not cause any numerical issues (such as division by zero) since Vij > 0 for both gamma and inverse Gaussian models (i.e., zero is not in their domain). However, in a practical setting, due to data preprocessing a few zero entries may sometimes occur in the input matrix V. In such cases, it is reasonable to set the zero entries to the smallest non-zero entry in V.
4 Model Selection and Measuring Goodness-of-Fit
Starting with random initial values for W and H, the multiplicative update rules for any given NMF algorithm outlined in §3 ensure monotonicity of updates for that run; however, the algorithm may not necessarily converge to the same solution on each run. In general, NMF algorithms are prone to this problem of local minima. For a given NMF algorithm and a pre-specified rank r factorization, the corresponding divergence (or reconstruction error) computed at the final converged values of W and H for a set of random initial values can be used directly in model selection and to measure goodness-of-fit. One solution is to utilize the factorization from the run that results in the best reconstruction (quantified by minimum reconstruction error across multiple runs) for evaluation using different quantities. Below, we define two quantities of interest for this purpose based on algorithm-specific minimum reconstruction error E.
4.1 Proportion of Explained Variation
We propose several new measures to quantify the variation explained by the various algorithms for signal dependent noise discussed in this paper. For each pre-specified rank r the proportion of explained variation (or empirical uncertainty), R2, is dependent on the particular algorithm and model used in the factorization. For the Gaussian NMF algorithm, R2 is the well-known quantity given by
| (36) |
where RSS is the residual sum of squares, SST is the total sum of squares and is the minimum reconstruction error (E), calculated based on the kernel of the Gaussian likelihood Σi,j (Vij − (WH)ij)2. The Gaussian likelihood for NMF is obtained using (9) and was first proposed by Lee & Seung (2001).
For each algorithm, R2 is computed based on the corresponding minimum reconstruction error (E), as listed in Table 1. In the R2 column of this table, the numerator of each quantity within parentheses (other than the Gaussian) is the minimum reconstruction error (E) calculated using equations (17), (22), (27), (30) and (33), as appropriate. The quantity (WH)ij in each numerator is the (i, j)th entry of the reconstructed matrix WH (also obtained as for a given rank r). In the corresponding denominator of each quantity, each entry of the reconstructed matrix WH is replaced by the grand mean of all entries of the input matrix V, . The underlying principle in the calculation of R2 is that the algorithm-specific reconstruction error E quantifies the performance of the model as determined by the entries (WH)ij while in the absence of the model V ~ WH, the best approximation of (WH)ij is provided simply by the grand mean of all observations in the data. This is a direct extension of the definition of R2 in equation (36) for the Gaussian model to non-linear models such as the gamma and inverse Gaussian. The algorithm-specific R2 measures the proportionate reduction in uncertainty due to the inclusion of W and H and, therefore, can be interpreted in terms of information content of the data (see Cameron & Windmeijer, 1996; 1997 for more details).
Table 1.
Algorithm-specific Proportion of Explained Variation R2
| Algorithm | R2 | ||
|---|---|---|---|
| Gaussian |
|
||
| , |
|
||
|
|
|
||
| JG |
|
||
| , |
|
||
|
|
|
4.2 Akaike Information Criterion (AIC)
For a particular algorithm and a pre-specified rank r, AIC is given by
| (37) |
where E is the corresponding minimum reconstruction error, ψ = (p + n)r is the total number of parameters estimated in the model for a p×n input matrix V and , α and for the Gaussian, gamma and inverse Gaussian models, respectively. The model (rank r factorization) that results in the smallest AIC is chosen as the optimal model. The calculation of algorithm-specific E is detailed in §4.1 and the determination of τ is outlined in §5.
5 Implementation of Algorithms on EMG Data
In this section we present a detailed application of NMF algorithms based on signal-dependent noise in the analysis of the EMG data described in Section 2. Time-invariant muscle synergies were extracted from each of the intact and deafferented EMG data sets of each frog using each of the eight NMF algorithms described earlier, including one based on normally distributed noise (Gaussian), four based on gamma noise (including , , and JG), and three based on inverse Gaussian (IG) noise (including , and ). The NMF update rules were implemented using Matlab. It should be noted that none of the pre-processed data sets contained zero entries. For every extraction, the muscle synergies (W) and their associated time-varying activation coefficients (H) were initialized with random matrices whose components were uniformly distributed between 0 and 1. Convergence was defined as having 20 consecutive iterations with a change of R2 smaller than 10−8 (with R2 for each algorithm defined in Table 1), but if convergence was not reached within 500 iterations, the extraction was terminated. The number of muscle synergies r extracted from each data set was successively increased from 1 to 13; at each number, extraction was repeated 20 times, each time with different random initial matrices.
AIC was calculated as follows. Let c denote the parameter 2σ2, α or λ/2 depending on the model. In the specification of the divergence for each algorithm (§2.2.2, equations (9)-(14)), we assumed that c = 1 without loss of generality. In order to ensure that the EMG data fit this assumption, a global test of the null hypothesis H0 : c = 1 against the two-sided alternative HA : c ≠ 1 was performed for each model. The mean-variance relationship for the gamma and inverse Gaussian models can be written using equations (6) and (8), respectively, and is described in detail in §2.2.3. This relationship was used to obtain an estimate α or λ in these models. For the Gaussian model, σ2 was estimated using the approach described in Morup & Hansen (2009). In addition, these parameters were estimated using standard maximum likelihood methods. In each case, the estimate of c was approximately 1 and the 95% confidence interval for this estimate included 1 (p-values for these tests ranged from 0.15 to 0.77) thereby providing strong evidence in favor of the null hypothesis c = 1. (p = 0.29). For the Gaussian model, σ2 was estimated using the approach described in Morup & Hansen (2009). The 95% confidence interval for the estimate of σ2 is (0.50, 1.37) with a mean of 0.93 (p = 0.77). Based on this empirical evidence, c was taken to be 1 and the appropriate value of τ was used in equation (37) for each model. The best model order was selected by identifying the rank r giving the minimum AIC for each data set and algorithm. Supplemental Table 2 lists the dimensionality of the data set, i.e., number of columns n in equation (37), for each frog and behavior.
Since for this application we are primarily interested in the ability of each algorithm to identify features shared between the intact and deafferented EMG data sets (or features interpretable as units of CPGs), performance of each algorithm was assessed by the similarity between the intact and deafferented muscle synergies, quantified with two measures. The first measure used was the scalar product between best-matching pairs of intact and deafferented synergies, calculated after the synergies were normalized to unit vectors. The second measure used was the cosine of the principal angles between the subspaces spanned by the intact and deafferented synergy sets (Golub and Van Loan, 1983). Both measures were used in Cheung et al. (2005).
5.1 NMF Algorithms based on Signal-dependent Noise Outperformed Gaussian NMF
In analysis of motor patterns from natural behaviors, it has remained difficult to determine, a priori, the number of muscle synergies composing the data set. Most previous studies on muscle synergies have relied on ad hoc measures to determine this number either by locating the cusp of the R2 curve plotted against the rank r (e.g., d’Avella et al., 2003; Cheung et al., 2005; Tresch et al., 2006), or by finding the minimum number of synergies that produced an R2 greater than a certain arbitrary threshold (e.g., Cheung et al., 2012). Here, we explored using the AIC as a principled, objective measure of selecting the model order that best described the data without over-fitting (Akaike, 1987). For every algorithm and data set, we plotted the AIC against the number of synergies extracted r, and the preferred model order was indicated by the number at which the curve attained a minimum AIC (Fig. 2, *).
Figure 2.
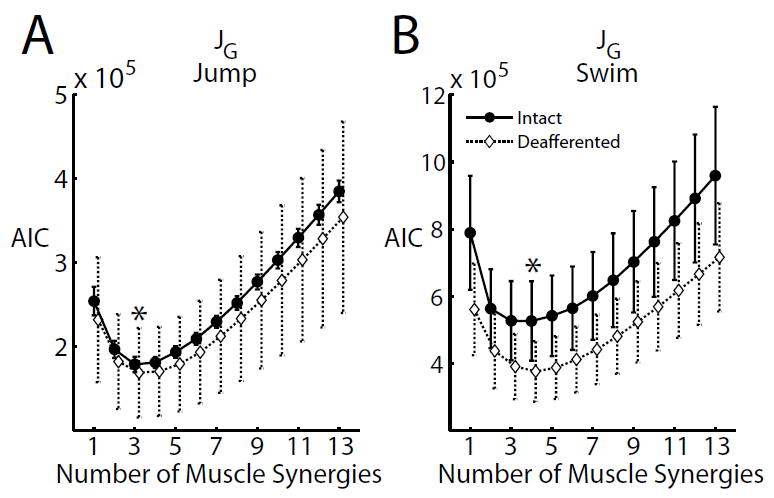
Selecting the number of muscle synergies for the JG algorithm using AIC. To determine the model order, the number of muscle synergies extracted was successively increased from 1 to 13; at each number of synergies, the AIC was calculated using equation (37). A, Plot of AIC against the number of muscle synergies extracted for both the intact (black solid) and deafferented (dotted) jump (4 frogs; mean ± SD). B, Plot of AIC for intact (solid black) and deafferented (dotted) swim. The model order with minimum AIC was found to be 3 for jump, and 4 for swim (*).
The model order selected using the AIC was in general consistent across animals for all four behaviors (intact jump, deafferented jump, intact swim, and deafferented swim) and all algorithms. For the Gaussian and all gamma-based algorithms, the selected model order in each behavior differed at most by only 1 across frogs; for the IG-based algorithms, the selected order differed across frogs by 2 to 3 in most instances, and by 4 only in one instance (Fig. 3). While IG algorithms ( , and ) consistently indicated a rank of 8 to 13 muscle synergies, Gaussian, , and suggested a rank of 1 to 2 synergies. The JG algorithm, on the other hand, indicated a rank of 3 synergies for intact and deafferented jump (Fig. 2A, Fig. 3), and 4 synergies for intact and deafferented swim (Fig. 2B, Fig. 3). A previous study (d’Avella et al., 2003) has argued, based on a detailed kinematic analysis, that there are at least 3 muscle synergies underlying frog hind-limb kicking, with 2 synergies controlling kick direction during limb extension, and 1 for executing limb flexion. It thus appears that the model orders selected for the JG algorithm are the most physiologically interpretable. We further verified that at these ranks, all signal-dependent noise algorithms returned synergies that explained the EMGs with an R2 of at least 85% (Table 2). In addition, all three proposed algorithms returned synergies that explained the EMGs with an R2 of at least 93%, a significantly higher fraction compared to that of existing signal-dependent noise algorithms for which R2 values ranged from 85% to 93%. In the ensuing analysis, we will measure the performances of all algorithms at the ranks determined from the results of the JG algorithm.
Figure 3.
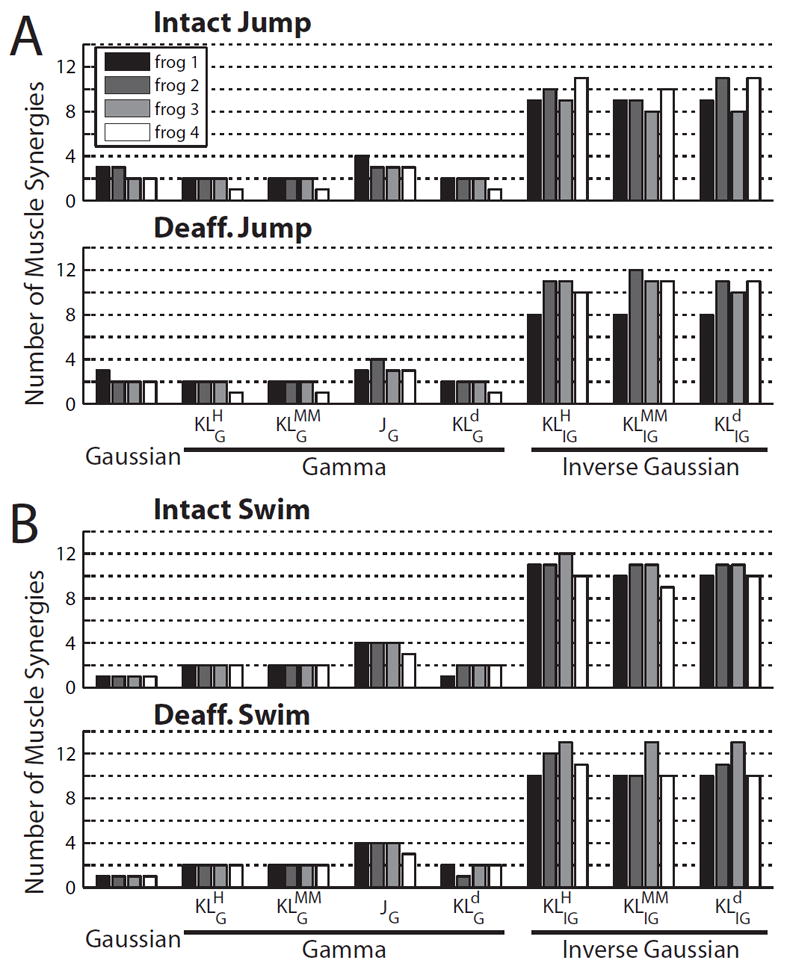
The number of muscle synergies selected for the different NMF algorithms. For each behavior (A, intact and deafferented jump; B, intact and deafferented swim) and each algorithm, the number of muscle synergies selected for each frog was determined by selecting the rank with minimum AIC. Note that the selected numbers for all behaviors and algorithms were quite consistent across animals.
Table 2.
The proportion of explained variation (R2) achieved by the NMF algorithms in four different frog behaviors at the rank determined by the JG algorithm
| Algorithm | Intact Jump r = 3 | Deaff. Jump r = 3 | Intact Swim r = 4 | Deaff. Swim r = 4 | |
|---|---|---|---|---|---|
|
| |||||
| Gaussian | 87.69 ± 1.21 | 87.38 ± 1.04 | 85.43 ± 1.83 | 87.89 ± 4.51 | |
|
|
91.97 ± 1.48 | 90.58 ± 1.17 | 87.17 ± 1.13 | 90.11 ± 2.47 | |
|
|
91.97 ± 1.48 | 90.58 ± 1.17 | 87.16 ± 1.13 | 90.11 ± 2.47 | |
|
|
98.93 ± 0.35 | 98.74 ± 0.11 | 96.46 ± 0.41 | 97.62 ± 0.77 | |
| JG | 97.85 ± 0.64 | 97.41 ± 0.29 | 93.56 ± 0.55 | 95.50 ± 1.38 | |
|
|
90.97 ± 2.06 | 88.72 ± 0.58 | 86.67 ± 0.87 | 89.49 ± 2.30 | |
|
|
90.89 ± 2.07 | 88.68 ± 0.52 | 86.50 ± 0.83 | 89.43 ± 2.25 | |
|
|
99.79 ± 0.11 | 99.77 ± 0.05 | 98.94 ± 0.30 | 99.37 ± 0.22 | |
Table 2 lists the proportion of explained variation (R2) achieved by the NMF algorithms in four different frog behaviors at the rank determined by the JG algorithm. The number of muscle synergies underlying intact and deafferented jump was assumed to be 3, and that underlying intact and deafferented swim, to be 4. These model orders were determined by selecting the ranks that resulted in the smallest AIC values when the JG algorithm was applied to the data sets. All R2 values shown are averages across frogs (N = 4; mean ± SD).
The seven NMF algorithms based on signal-dependent noise outperformed the Gaussian NMF in their ability to identify features shared between the intact and deafferented EMG data sets. This is indicated by the generally higher similarity between the intact and deafferented muscle synergy sets, measured by both the scalar product (Fig. 4A, 4C) and the cosine of principal angle (Fig. 4B, 4D), when the non-Gaussian NMFs were applied. In particular, for both similarity measures, performance of the JG algorithm exceeded that of the Gaussian algorithm in 3 of 4 frogs in the jump data sets (frogs 2, 3, 4; Fig. 4A, B), and also in 3 of 4 frogs in the swim data sets (frogs 1, 2, 3; Fig. 4C, D). Overall, the three best performing algorithms in terms of these measures were JG (mean scalar product = 0.8698; N = 4×2 = 8); (0.8695), and (0.8650). The worst performing algorithm was Gaussian (0.7648).
Figure 4.
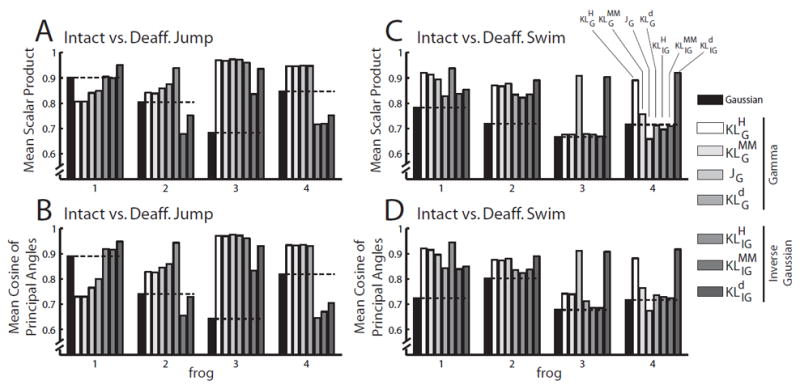
Signal-dependent noise NMFs outperformed the Gaussian NMF. In this application, we are primarily interested in each algorithm’s ability to identify structures shared between the intact and deafferented data sets; thus, our measures of algorithm performance are based on quantifying the similarity between the intact and deafferented muscle synergies. For both the scalar-product (A and C) and principal-angle (B and D) measures, overall the seven NMFs based on signal-dependent noise outperformed the Gaussian NMF in their ability to extract features shared between data sets. In each graph, the level of similarity achieved by the Gaussian algorithm (black) is marked by a horizontal black dotted line for ease of visual inspection.
Table 3 lists the proportion of explained variance (R2) achieved by the NMF algorithms at the ranks with minimum AIC. For every algorithm, the number of muscle synergies underlying each behavior of each frog was determined by selecting the rank that resulted in the smallest AIC values. All R2 values shown are averages across frogs (N = 4; mean ± SD).
Table 3.
The proportion of explained variation (R2) achieved by the NMF algorithms at the ranks with minimum AIC
| Algorithm | Behavior | Rank (N= 4; median ± SD) | R2 (N = 4; mean ± SD) | |
|---|---|---|---|---|
|
| ||||
| Gaussian | Intact Jump | 3 ± 0.58 | 85.16 ± 4.08 | |
| Deaff. Jump | 2 ± 0.50 | 82.91 ± 3.52 | ||
| Intact Swim | 1 ± 0.00 | 56.78 ± 4.89 | ||
| Deaff. Swim | 1 ± 0.00 | 56.58 ± 12.33 | ||
|
|
Intact Jump | 2 ± 0.50 | 86.66 ± 3.64 | |
| Deaff. Jump | 2 ± 0.50 | 85.22 ± 1.09 | ||
| Intact Swim | 2 ± 0.00 | 76.66 ± 3.68 | ||
| Deaff. Swim | 2 ± 0.00 | 80.00 ± 5.07 | ||
|
|
Intact Jump | 2 ± 0.50 | 86.66 ± 3.64 | |
| Deaff. Jump | 2 ± 0.50 | 85.22 ± 1.09 | ||
| Intact Swim | 2 ± 0.00 | 76.66 ± 3.69 | ||
| Deaff. Swim | 2 ± 0.00 | 80.00 ± 5.07 | ||
|
|
Intact Jump | 2 ± 0.50 | 98.21 ± 0.77 | |
| Deaff. Jump | 2 ± 0.50 | 98.05 ± 0.17 | ||
| Intact Swim | 2 ± 0.50 | 92.81 ± 2.80 | ||
| Deaff. Swim | 2 ± 0.50 | 94.78 ± 2.70 | ||
| JG | Intact Jump | 3 ± 0.50 | 98.05 ± 0.79 | |
| Deaff. Jump | 3 ± 0.50 | 97.61 ± 0.47 | ||
| Intact Swim | 4 ± 0.50 | 93.03 ± 1.28 | ||
| Deaff. Swim | 4 ± 0.50 | 95.18 ± 1.05 | ||
|
|
Intact Jump | 10 ± 0.96 | 99.07 ± 0.38 | |
| Deaff. Jump | 11 ± 1.41 | 98.84 ± 0.54 | ||
| Intact Swim | 11 ± 0.82 | 99.25 ± 0.34 | ||
| Deaff. Swim | 12 ± 1.29 | 99.61 ± 0.30 | ||
|
|
Intact Jump | 9 ± 0.82 | 98.41 ± 0.45 | |
| Deaff. Jump | 10 ± 1.73 | 98.67 ± 0.49 | ||
| Intact Swim | 11 ± 0.96 | 98.50 ± 0.46 | ||
| Deaff. Swim | 10 ± 1.50 | 98.95 ± 0.43 | ||
|
|
Intact Jump | 10 ± 1.50 | 99.98 ± 0.02 | |
| Deaff. Jump | 10 ± 1.41 | 99.98 ± 0.01 | ||
| Intact Swim | 11 ± 0.58 | 99.92 ± 0.03 | ||
| Deaff. Swim | 11 ± 1.41 | 99.97 ± 0.02 | ||
It is clear from the results shown in Tables 2 and 3 that all three proposed algorithms outperformed existing algorithms in terms of fraction of explained variation (R2), both at the ranks with minimum AIC and at the ranks determined by the JG algorithm. A closer look also revealed that the variability of this fraction (estimated by the standard deviation) was significantly lower for the proposed algorithms relative to existing methods, indicating a higher overall confidence level in the variation explained by these methods. The JG algorithm provided a much better balance between R2 and choice of rank based on minimum AIC compared to any other algorithm. The ranks chosen by the algorithm based on minimum AIC were similar to those of existing gamma based algorithms; however, this algorithm was able to explain a much higher fraction of variation in the data. The algorithm explained the maximum variation (highest overall R2) amongst all algorithms while the Gaussian algorithm provided the smallest R2 and rank. Furthermore, variability of R2 was also the highest for the Gaussian algorithm, suggesting an overall lower confidence level in the variation explained by this algorithm.
5.2 Muscle synergies extracted by the JG algorithm were physiologically interpretable
In this section we compare swim muscle synergies extracted using the standard Gaussian algorithm with those identified by the JG algorithm in one specific individual (frog 2), and illustrate how the latter set could be more physiologically interpretable. In the extraction results returned by the Gaussian formulation, a very high similarity between the pre- and post-deafferentation synergies was observed in 2 of the synergy pairs (scalar product > 0.90; Fig. 5A, synergies 1 to 2); a moderate similarity, in 1 synergy pair (scalar product = 0.90; Fig. 5A, synergy 3); and total dissimilarity, in the last pair (scalar product = 0.06; Fig. 5A, synergy 4). By contrast, the JG algorithm found 3 synergy pairs with high similarity (scalar product > 0.90; Fig. 5B, synergies 1 to 3); in the last pair, the similarity was modest (scalar product = 0.62; Fig. 5B, synergy 4), but the muscles active in both the intact and deafferented synergy vectors were the same (RI, AD, SM, and ST). Overall, the synergy extraction results from this frog demonstrate that the JG algorithm, derived from a signal-dependent noise assumption, is better able to discover structures preserved after deafferentation than the traditional Gaussian algorithm.
Figure 5.
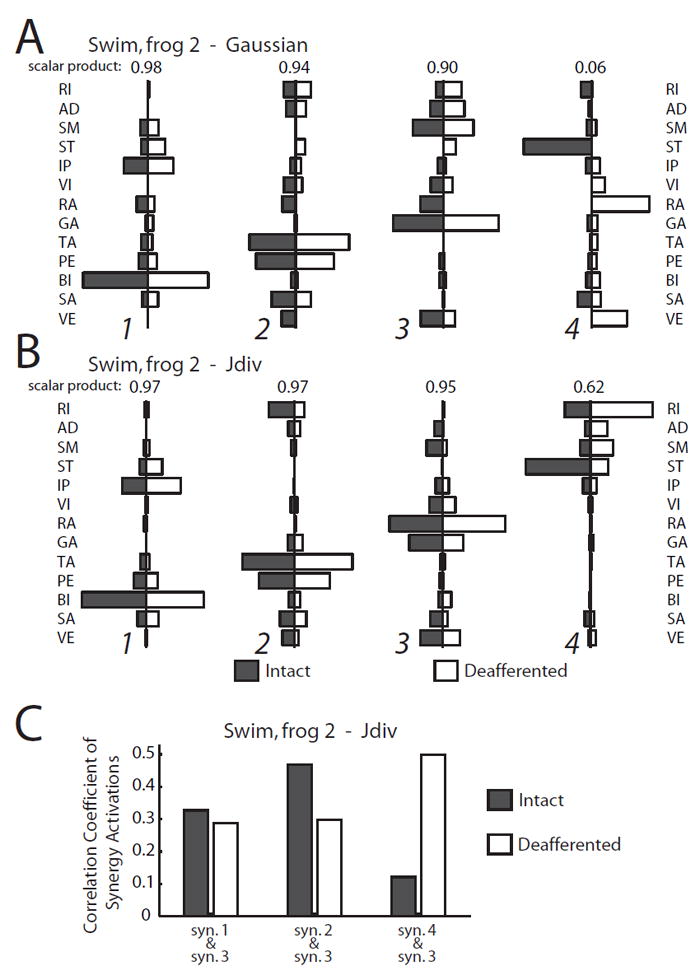
Muscle synergies extracted by the JG algorithm were physiologically interpretable. A, Intact (black) and deafferented (white) muscle synergies for swimming (frog 2) returned by the Gaussian algorithm. The scalar product similarity between each synergy pair is indicated above the pair. The intact and deafferented synergies for pair 4 were totally dissimilar. B, Intact (black) and deafferented (white) muscle synergies for swimming (frog 2) returned by the JG algorithm. Here, even in the least similar pair (pair 4, scalar product = 0.62), the sets of muscles found to be active in the intact and deafferented synergies were still identical. C, The correlation coefficient between the activation of muscle synergy 3 (the extension synergy) and those of muscle synergies 1, 2, and 4, respectively, before (black) and after (white) deafferentation. Note that the correlation between synergies 3 and 4 increased 5-fold after deafferentation. This suggests that sensory feedback is essential in triggering or maintaining the activation of synergy 4 during the flexion phase of the swim cycle.
The muscular compositions of the synergies returned by the JG algorithm could also be biomechanically interpreted. Synergy 3 (Fig. 5B), for instance, was composed of the hip extensor SM, knee extensors VI, RA, and VE, and the ankle extensor GA. Examination of the time-varying coefficients associated with this synergy revealed that it was active only during the extension phase of every swim cycle; thus, it is likely that muscle synergy 3 functions to propel the animal forward through extension of the hip, knee, and ankle joints. Synergy 1 (Fig. 5A, 5B), discovered by both the Gaussian and JG algorithms, consisted of the hip flexors IP and BI; synergy 2 (Fig. 5A, 5B), on the other hand, consisted primarily of the ankle flexors TA and PE, and the hip/knee flexor SA. It is no surprise that both of these synergies were indeed active during the flexion phase of every swim cycle.
The activation pattern of synergy 4 identified by JG (Fig. 5B) was more complex. During the intact state, it was primarily active during limb flexion; after deafferentation it was activated only during limb extension. Consistent with this switch of activation phase for this synergy after the loss of sensory feedback, the correlation coefficient between the activation coefficients of synergy 4 and those of the extension synergy 3 increased 5-fold after deafferentation (Fig. 5C). Since three muscles in this synergy -RI, SM, and ST - have both hip extension and knee flexion actions, it is possible that before deafferentation, this synergy executes knee flexion while after deafferentation, it aids limb extension. It thus appears that sensory feedback functions both to inhibit its activation during extension, and facilitates or triggers its activation during flexion. Such an inference about the contribution of afferents to the inhibition and activation of this muscle synergy would be difficult with the synergy sets obtained by the Gaussian NMF (Fig. 5A) given that the Gaussian algorithm failed to discover this synergy from the deafferented data set.
5.3 Comparison of results using algorithms derived from the same noise distribution
In the preceding sections, we compared the performance of various algorithms in extracting muscle synergies based on AIC, the fraction of explained variation (R2), their ability to identify features shared between the deafferented and intact EMG data (measured by the scalar dot product and cosine of the principal angle) and their physiological interpretability. In this section, we perform a comparison of muscle synergies extracted by different NMF algorithms from the same EMG data set in order to understand how the underlying noise assumption and cost function used in the NMF algorithm may impact the muscular compositions of the extracted synergies. Algorithms based on the same noise distribution but different cost functions tended to return similar muscle synergies. For instance, using and as reference algorithms, the scalar product values (mean ± SD; over 4 frogs) between the synergies returned by gamma based NMF algorithms and were (i) higher than those between the synergies returned by the Gaussian NMF algorithm and and (ii) higher than those between inverse Gaussian based NMF algorithms and (Fig. 6A). Similarly, the scalar product values (mean ± SD; over 4 frogs) between the synergies returned by inverse Gaussian based NMF algorithms and were (i) higher than those between the synergies returned by the Gaussian NMF algorithm and and (ii) higher than those between gamma based NMF algorithms and (Fig. 6B).
Figure 6.
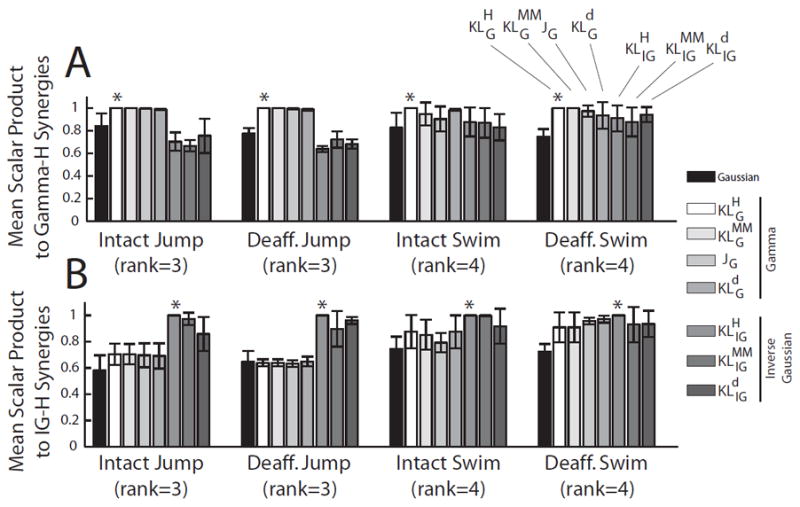
Comparison of results using NMF algorithms derived from the same noise distribution. We performed a comparison of the muscle synergies extracted by different NMF algorithms from the same EMG data set in order to understand the effects of the NMF-noise distribution and the cost function employed on the muscular compositions of the extracted muscle synergies. A, In each frog, the set of muscle synergies extracted by each algorithm was matched to the set returned by the gamma-based algorithm (*), and their similarity was quantified by the scalar product values averaged across the synergy set. Shown in the plot are values averaged across frogs (N = 4; mean ± SD). Values for the were 1.0 by definition. In this comparison, scalar product values from the gamma algorithms tended to be higher than those from the Gaussian or IG-based algorithms. This difference is especially obvious for the intact jump and deafferented jump data sets. B, Same as A, except that the comparison was performed by matching synergies of each algorithm to synergies returned by the IG-based algorithm (*). In this comparison, scalar product values from IG-based algorithms tended to be higher than those from the Gaussian or gamma-based algorithms. Again, this difference is especially obvious for the intact jump and deafferented jump data sets.
Our analysis shows that in our frog EMGs, algorithms derived from the same noise distributions tended to return similar muscle synergies. The noise distribution appears to play a critical role in determining the muscular compositions of the synergies extracted from the data. Similarly, the cost function (divergence measure) employed for formulating the update rules exerts its own influence on the extraction results. Indeed, the best rank (rank with minimal AIC) and R2 values from algorithms assuming the same noise distribution but employing different cost functions were still different (Table 3). This is because these algorithms derived from different cost functions returned different activation coefficients (H). As an illustrative example, we present in Fig. 7 the muscle synergies extracted by all eight algorithms from the deafferented jump EMGs of frog 2. In this case, the results produced by the four gamma-based NMF algorithms are nearly identical. However, it is important to note that the synergies extracted by the three IG-based NMF algorithms are quite different, exposing the activation of different muscles as determined by the choice of cost function.
Figure 7.

Both the noise distribution and the cost function employed for formulating the NMF update rules could influence the muscular compositions of the extracted muscle synergies. Here we show the muscle synergies extracted from one particular data set (frog 2, deafferented jump) by different NMF algorithms. The results returned by the four gamma-based algorithms were almost identical (as suggested by Fig. 6). However, the gamma-synergies were clearly different from the Gaussian and IG-based synergies. Also, the muscle synergies returned by the three IG-based synergies were also somewhat different from each other. Thus, both the noise distribution and the cost function used for deriving the NMF update rules could influence the structures of the basis vectors extracted.
6 Evaluating NMF Algorithms on Simulated Data Sets
In this section, we present a detailed application of the proposed NMF algorithms to the analysis of simulated data. We implemented the algorithms on simulated data sets generated by known muscle synergies (W) and time-varying activation coefficients (H), so that the performance of each NMF algorithm can be evaluated by comparing the extracted results with the original W and H.
In our simulations, we are interested in how well each algorithm performs as a function of noise distribution and noise level in the data. For every distribution and noise amplitude tested, 10 simulated data sets were generated. Each data set, consisting of 15 muscles and 5000 time points, was produced by linearly combining 5 muscle synergies. The components of both W and H were drawn from a uniform distribution defined over (0, 1). The simulated data were then corrupted by one of the three noise types - Gaussian, gamma, and inverse Gaussian - at different noise magnitudes quantified by the signal-to-noise ratio (SNR), defined as
where Vij is the original, uncorrupted data point, and Ṽij is the noise-corrupted data point. For Gaussian noise with mean μ and variance σ2, noise for each data point was generated by the Matlab function, normrnd, with μ = Vij and σ set to 0.04, 0.05, 0.07, 0.1, 0.2, 0.3, 0.5, 1.0, 1.5, and 2.0, respectively. These choices of σ produced data with an SNR ranging from 0.17 to 225. For gamma noise with mean (equation (5)), the Matlab function gamrnd was used, with and α set to 0.1, 0.5, 0.25, 1.0, 2.5, 5.0, 10, 50, 100, 250, and 500, respectively (SNR of 0.1 to 500). For inverse Gaussian noise with mean μ (equation (7)), noise for each data point was generated by combining the Matlab functions makedist and random, with μ = Vij and λ set to 0.1, 0.2, 0.5, 0.75, 1, 2, 5, 7, 10, 12, 14, 16, 18, 20, 30, 40, and 100, respectively (SNR of 0.14 to 139).
The eight NMF algorithms described in this paper (Gaussian, , , , JG, , , and ) were then applied to each of the simulated data sets for extracting 5 muscle synergies. In every extraction, the NMF update rules were implemented using Matlab (R2013b). The W and H matrices were initialized with random components drawn from a uniform distribution over (0, 1). Convergence was defined as having 20 consecutive iterations with a change of algorithm-specific R2 (Table 1) smaller than 10−8, but if convergence was not achieved within 500 iterations, the extraction was terminated. Extraction was repeated 20 times for each data set, each time with different initial random matrices. The extraction repetition with the smallest reconstruction error among the 20 repetitions was then selected for performance evaluation. The ability of each algorithm in identifying the muscle synergies was quantified by the scalar product between the original and extracted synergy vectors (after the synergies were normalized to unit vectors), averaged over the 5 synergies. For the activation coefficients, performance was assessed by the Pearson’s correlation coefficient (ρ) between the components in the original H and those in the extracted H, again averaged over the 5 synergies.
For Gaussian-noise data sets, the Gaussian algorithm outperformed , JG and all IG-based algorithms in the identification of both W and H (Fig. 8; *, p < 0.05; Student’s t-test). The superiority in performance of the Gaussian NMF over all other algorithms was especially obvious for the extraction of H (Fig. 8B). For the extraction of W, however, performances of Gaussian, , and were comparable (Fig. 8A).
Figure 8.
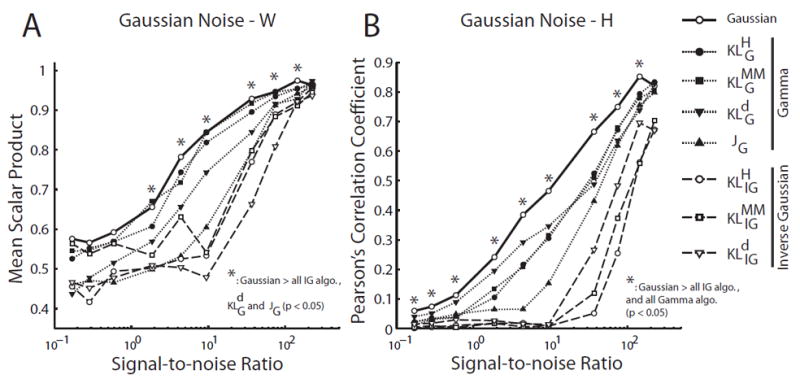
Gaussian NMF outperformed the signal-dependent noise NMFs in data sets corrupted by Gaussian noise. We evaluated the performance of each algorithm in simulated data sets (N = 10) generated by known W (15 × 5 matrix) and H (5 × 5000 matrix), but corrupted by random Gaussian noise at different signal-to-noise ratios (SNR). A, Performance of NMF algorithms in identifying the basis vectors (W). Performance of each algorithm in each data set was quantified by the scalar product between the extracted vectors and the original vectors, averaged across the 5 basis vectors in the W matrix. Shown in the plot are mean scalar product values, defined as above, averaged across 10 simulated data sets. The Gaussian NMF algorithm outperformed all IG-based NMF algorithms and 2 of the gamma-based NMF algorithms ( and JG) over a wide range of SNR (*; Student’s t-test; p < 0.05). B, Performance of NMF algorithms in identifying the coefficients (H). Performance of each algorithm in each data set was quantified by the Pearsons correlation coefficient (ρ) between the extracted coefficients and the original coefficients (over a total of 5 × 5000 = 25,000 values). Shown in the plot are ρ values averaged across the 10 simulated data sets. The Gaussian NMF algorithm outperformed all of the gamma- and IG-based NMF algorithms over almost all tested SNR (*; p < 0.05).
In data sets with simulated gamma noise, the gamma- and IG-based algorithms performed equally well, and better than Gaussian, in the identification of H over all tested noise magnitudes (Fig. 9B). For W identification, the gamma- and IG-based algorithms were similar in performance when the SNR was above ≈ 3 (Fig. 9A). The gamma algorithms outperformed all other algorithms when noise magnitude was very high, the (Fig. 9A; +, p < 0.05).
Figure 9.
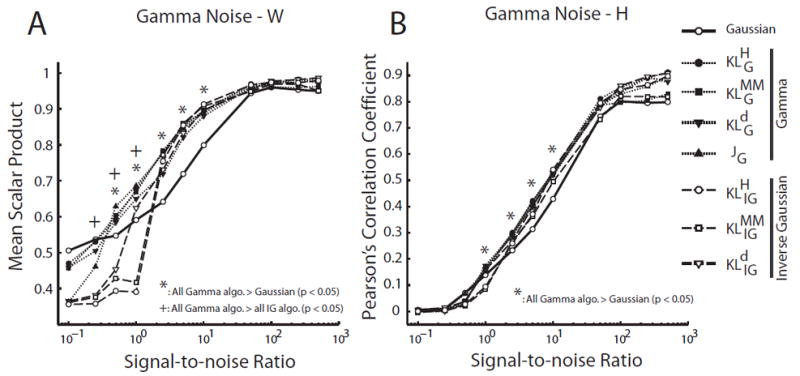
Gamma-based NMF algorithms outperformed the Gaussian NMF algorithm in data sets corrupted by gamma noise. We evaluated the performance of each algorithm in simulated data sets (N = 10) generated by known W (15 × 5 matrix) and H (5 × 5000 matrix), but corrupted by random gamma noise at different signal-to-noise ratios (SNR). A, Performance of NMF algorithms in identifying the basis vectors (W). Performance of each algorithm in each data set was quantified by the scalar product between the extracted vectors and the original vectors, averaged across the 5 basis vectors in the W matrix. Shown in the plot are mean scalar product values, defined as above, averaged across 10 simulated data sets. Gamma-based algorithms outperformed the Gaussian algorithm (but not the IG-based algorithms) at moderate noise magnitude (*; Student’s t-test; p < 0.05); but at high noise magnitudes, the gamma algorithms performed better than both Gaussian- and IG-NMF algorithms (+; p < 0.05). B, Performance of the NMF algorithms in identifying the coefficients (H). Performance of each algorithm in each data set was quantified by the Pearsons correlation coefficient (ρ) between the extracted coefficients and the original coefficients (over a total of 5 × 5000 = 25,000 values). Shown in the plot are ρ values averaged across the 10 simulated data sets. Gamma-based algorithms outperformed the Gaussian algorithm, but not the IG-based algorithms, at moderate noise levels (*; p < 0.05).
In data sets corrupted by inverse Gaussian noise, for W identification, not surprisingly the IG-based algorithms outperformed the gamma-based algorithms (Fig. 10A; *), which in turn outperformed the Gaussian (Fig. 10A; +, *). For H identification, while the performances of all signal-dependent noise NMFs were almost indistinguishable, they clearly did much better than the Gaussian (Fig. 10B, *).
Figure 10.
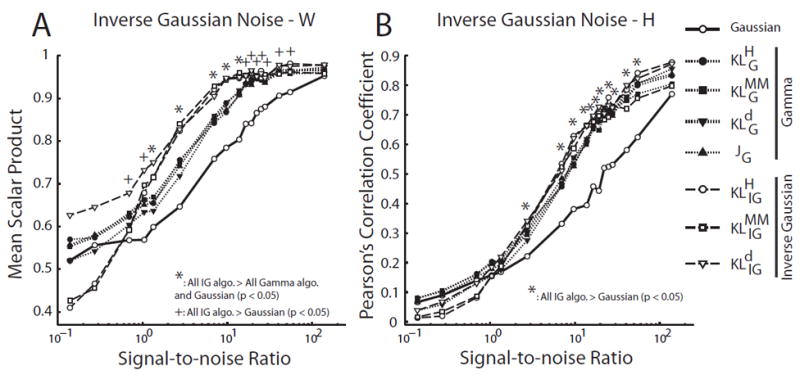
The inverse Gaussian NMF algorithms outperformed the Gaussian- and gamma-based NMF algorithms in data sets corrupted by inverse Gaussian noise. We evaluated the performance of each algorithm in simulated data sets (N = 10) generated by known W (15 × 5 matrix) and H (5 × 5000 matrix), but corrupted by random inverse Gaussian (IG) noise at different signal-to-noise ratios (SNR). A, Performance of NMF algorithms in identifying the basis vectors (W). Performance of each algorithm in each data set was quantified by the scalar product between the extracted vectors and the original vectors, averaged across the 5 basis vectors in the W matrix. Shown in the plot are mean scalar product values, defined as above, averaged across 10 simulated data sets. At moderate noise levels, IG-based algorithms clearly outperformed both the Gaussian and gamma algorithms (*; Student’s t-test; p < 0.05); at high and low noise levels, IG-based algorithms still performed better than the Gaussian (but not the gamma) algorithm (+; p < 0.05). B, Performance of the NMF algorithms in identifying the coefficients (H). Performance of each algorithm in each data set was quantified by the Pearsons correlation coefficient (ρ) between the extracted coefficients and the original coefficients (over a total of 5 × 5000 = 25,000 values). Shown in the plot are ρ values averaged across the 10 simulated data sets. IG-based algorithms outperformed the Gaussian NMF over a wide range of SNR (*; p < 0.05).
Overall, the simulation results highlight the need for using the NMF algorithm derived from a noise distribution that matches the noise type of the data for the most accurate identification of both W and H. However, under certain conditions, even when the noise assumed by the NMF algorithm and the data noise type do not completely agree, the extracted results may still contain substantial information about the underlying data structure. We have seen, for instance, that in data with gamma noise, IG-based NMF algorithms could identify muscle synergies as well as gamma-based NMF algorithms could. It should be noted that even when the identified W is reasonably close to the original generating bases, the H identified by the same algorithm may not be as accurate (and vice versa). For example, in data with Gaussian noise, at SNR ≈ 10 the gamma-based algorithm performed at the same level as the Gaussian algorithm for W identification, and returned muscle synergies that matched the originals with scalar product > 0.8 (Fig. 8A); however, for H the extraction results from were not only much worse than Gaussian, but also matched the original quite poorly (ρ ≈ 0.3) (Fig. 8B).
7 Some Recommendations
As argued by our extraction results from simulated data (Figs. 8, 9, 10), for a data set with known noise properties, using NMF algorithms derived from a noise distribution that matches that of the data should yield the most accurate estimations of both W and H. The noise distribution of the data can be determined using the exploratory approach outlined in §2.2.3 for the EMG data presented in this paper. However, if the noise characteristics of the data are not known or cannot be reasonably determined, it is preferable to first evaluate the algorithms on a data set with a clear prediction, based on the biology of the processes generating the data, of what the underlying W or H could be, and see which algorithm produces results that best match such predictions. The best-performing algorithm can then be used in other data sets of a similar nature for a further understanding of the biology. The noise distribution assumed by this best-performing algorithm would in turn allow an understanding of the noise structure of the data set. For the frog EMG data presented here, 2 of the 3 best-performing algorithms (i.e., algorithms that discovered the most number of synergies shared between the intact and deafferented data, or features interpretable as CPG components, while explaining most of the variation in the data) were derived from the gamma noise distribution. These are the JG and algorithms while is the third best-performing algorithm. Thus, it is evident that signal-dependent noise in the EMGs is closer to the gamma than to the inverse Gaussian distribution. This also agrees with the empirical observation and conclusion in §2.2.3 that the gamma model provides a good fit to the mean-SD relationship of the EMG data.
Although we focused primarily on NMF algorithms for handling EMG data with signal-dependent noise in this paper, other matrix factorization algorithms have been used for extracting muscle synergies in addition to NMF (Tresch et al., 2006). In a variety of applications, NMF has been shown to provide a parts-based, local representation of the data in contrast to the holistic representation provided by vector quantization and the distributed representation provided by principal component analysis (PCA) (Devarajan et al., 2008). PCA is based on the Gaussian model and requires non-overlapping, orthogonal components with mixed signs. On the other hand, independent component analysis (ICA) seeks a linear representation of non-Gaussian data such that the resulting components are statistically independent (Hyvärinen & Oja, 2000; Devarajan, 2011). The representation provided by ICA has been shown to capture the essential structure of the data in various applications involving blind source separation. Independence implies uncorrelatedness and in the case of the Gaussian distribution they are equivalent, implying independent principal components. Thus PCA and ICA require different but stronger assumptions, particularly with regards to application to EMG data. In general, PCA provides dimensionality reduction while ICA results in perceptually relevant components. NMF provides interpretable components, however it is limited by the non-negativity requirement on the input data and the resulting components. From an exploratory data analysis perspective, it is important to note that each of these methods comes with its owns merits and demerits and that the extent of its usefulness depends on the specific application at hand. When data occur naturally on the non-negative scale such as the EMG signals presented in this paper, it appears more intuitive and reasonable to apply a factorization that retains the non-negativity requirement on the resulting components (muscle synergies). These nonnegativity constraints are compatible with the intuitive notion of combining parts to form a whole. In NMF, these components are additive, linear combinations of the parts that are overlapping and non-orthogonal. The resulting “parts” extracted by NMF from the EMG data can naturally be interpreted as representations of motor primitives - or basic modules of motor control - whose existence has been demonstrated in physiological experiments (Bizzi and Cheung, 2013). Moreover, the extension of this approach to non-Gaussian models described in this paper is particularly relevant for applications involving signal dependent noise. Such modeling flexibility is not provided by other methods.
Summary and Conclusions
In this paper, we proposed a comprehensive extension of methods for handling data with signal-dependent noise in NMF. We outlined three novel algorithms based on dual KL and J-divergence for the gamma and inverse Gaussian models. A rigorous proof of monotonicity of updates has been provided for each algorithm. In addition, algorithm-specific measures for quantifying the variation explained by the chosen model have been proposed. Using EMG as well as simulated data, we demonstrated superior performance of these algorithms in delineating muscle synergies by systematically comparing them with existing approaches for signal-dependent noise. It is evident from the methods and results presented that there is a need for more general models for data in which the variance of the signal depends on its mean. It is not entirely surprising that, among all algorithms considered, those based on signal-dependent noise clearly outperformed the Gaussian model. However, among all algorithms considered based on signal-dependent noise, those based on dual KL and J-divergence showed the best overall performance, both in terms of selecting the appropriate model for a given data set and the fraction of variation in the data that was explained by the chosen model. For each data set considered, all three proposed algorithms explained the variation in the data better than existing methods. The variability in the explained variation was also observed to be the smallest for the proposed algorithms. In particular, muscle synergies extracted by J-divergence were the most physiologically interpretable and corroborated with previous findings. The proposed methods therefore provide useful alternatives to current approaches in handling signal-dependent noise and would augment the literature on this topic.
Supplementary Material
Acknowledgments
Research of KD was supported in part by NIH Grant P30 CA06927. V. C. K. C. was supported by NIH grants NS44393 and RC1-NS068103-01 to Emilio Bizzi. We thank Prof. Emilio Bizzi of MIT for his enthusiastic support of this study.
Appendix
We present detailed proofs of the Theorems stated in Section 3. In the proof of each Theorem, we will make use of an auxiliary function similar to the one used in the Expectation-Maximization (EM) algorithm (Dempster et al., 1977; Lee & Seung, 2001). Note that for h real, G(h, h′) is an auxiliary function for F(h) if G(h, h′) ≥ F(h) and G(h, h) = F(h) where G and F are scalar valued functions. Also, if G is an auxiliary function, then F is non-increasing under the update .
Proof of Theorem 1
The cost function (27) can be re-written as
| (38) |
Its auxiliary function is
| (39) |
where such that Σa γa = 1.
Note that −log(Σa WiaHaj) ≤ − Σaγa (log WiaHaj − log γa). Therefore, and G(Haj, Haj) = F(Haj). The minimizer of F (Haj) is obtained by solving . Using (39), we get
| (40) |
Solving the above equation results in the update rule for H given in (28). Similarly, we can re-write the cost function (27) in terms of Wia and obtain the update rule given in (29).
Proof of Theorem 2
The cost function (30) can be re-written as
| (41) |
Its auxiliary function is
| (42) |
where γa is as defined in the proof of Theorem 2.
Note that . Therefore, and G(Haj, Haj) = F(Haj). The minimizer of F (Haj) is obtained by solving . Using (42), we get
| (43) |
Solving the above equation results in the update rule for H givenin (31). Similarly, we can re-write the cost function (30) in terms of Wia and obtain the update rule given in (32).
Proof of Theorem 3
The cost function (33) can be re-written as
| (44) |
Its auxiliary function is
| (45) |
where γa is as defined in the proof of Theorem 2.
Note that . Therefore, and G(Haj, Haj) = F(Haj). The minimizer of F (Haj) is obtained by solving . Using (45), we get
| (46) |
Solving the above equation results in the update rule for H given in (34). Similarly, we can re-write the cost function (33) in terms of Wia and obtain the update rule given in (35).
References
- Akaike H. Factor analysis and AIC. Psychometrika. 1987;52(3):317–332. [Google Scholar]
- Bernstein N. The co-ordination and regulation of movements. Oxford: Pergamon; 1967. [Google Scholar]
- Berry MW, Browne M, Langville AN, Pauca VP, Plemmons RJ. Algorithms and applications for approximate nonnegative matrix factorization. Computational Statistics and Data Analysis. 2007;52:155–173. [Google Scholar]
- Bizzi E, Cheung VCK, d’Avella A, Saltiel P, Tresch M. Combining modules for movement. Brain Research Reviews. 2008;57:125–133. doi: 10.1016/j.brainresrev.2007.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bizzi E, Cheung VCK. The neural origin of muscle synergies. Frontiers in Computational Neuroscience. 2013;7:51. doi: 10.3389/fncom.2013.00051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cameron AC, Windmeijer FAG. R-Squared measures for count data regression models with applications to health care utilization. Journal of Business and Economic Statistics. 1996;14(2):209–220. [Google Scholar]
- Cameron AC, Windmeijer FAG. An R-squared measure of goodness of fit for some common nonlinear regression models. Journal of Econometrics. 1997;77(2):329–342. [Google Scholar]
- Cheung VCK, Tresch MC. Nonnegative matrix factorization algorithms modeling noise distributions within the exponential family. Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference; 2005. pp. 4990–4993. [DOI] [PubMed] [Google Scholar]
- Cheung VCK, d’Avella A, Tresch MC, Bizzi E. Central and sensory contributions to the activation and organization of muscle synergies during natural motor behaviors. Journal of Neuroscience. 2005;25(27):6419–6434. doi: 10.1523/JNEUROSCI.4904-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung VCK, Turolla A, Agostini M, Silvoni S, Bennis C, Kasi P, Paganoni S, Bonato P, Bizzi E. Muscle synergy patterns as physiological markers of motor cortical damage. Proceedings of the national Academy of the Sciences USA. 2012;109(36):14652–14656. doi: 10.1073/pnas.1212056109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cichocki A, Zdunek R, Amari S. Csiszar’s Divergences for Non-negative Matrix Factorization: Family of New Algorithms. Lecture Notes in Computer Science, Independent Component Analysis and Blind Signal Separation, Springer, LNCS-3889. 2006:32–39. [Google Scholar]
- Cichocki A, Lee H, Kim Y-D, Choi S. Non-negative matrix factorization with α-divergence. Pattern Recognition Letters. 2008;29(9):1433–1440. [Google Scholar]
- Cichocki A, Zdunek R, Phan AH, Amari S. Nonnegative matrix and tensor factorizations: applications to exploratory multi-way data analysis and blind source separation. John Wiley; 2009. [Google Scholar]
- Cichocki A, Cruces S, Amari S. Generalized Alpha-Beta divergences and their application to robust nonnegative matrix factorization. Entropy. 2011;13:134–170. [Google Scholar]
- d’Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nature Neuroscience. 2003;6(3):300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. 1977;39:1–38. [Google Scholar]
- Devarajan K, Ebrahimi N. Molecular pattern discovery using nonnegative matrix factorization based on Renyi‘s information measure. Proceedings of the XII SCMA International Conference; 2-4 December 2005; Auburn, Alabama. 2005. ( http://atlas-conferences.com/c/a/q/t/98.htm) [Google Scholar]
- Devarajan K. Proceedings of the Joint Statistical Meetings. Seattle, Washington: 2006. Nonnegative matrix factorization - A new paradigm for large-scale biological data analysis. CD-ROM. [Google Scholar]
- Devarajan K. Nonnegative matrix factorization - An analytical and interpretive tool in computational biology. PLoS Computational Biology. 2008;4(7):E1000029. doi: 10.1371/journal.pcbi.1000029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devarajan K, Ebrahimi N. Class discovery via nonnegative matrix factorization. American Journal of Management and Mathematical Sciences. 2008;28(3&4):457–467. [Google Scholar]
- Devarajan K, Wang G, Ebrahimi N. A unified approach to nonnegative matrix factorization and probabilistic latent semantic indexing, (July 2011) Cobra Preprint Series. 2011 doi: 10.1007/s10994-014-5470-z. Working Paper 80. http://biostats.bepress.com/COBRA/Art80. [DOI] [PMC free article] [PubMed]
- Devarajan K. Problem Solving Handbook in Computational Biology and Bioinformatics. Part 5. Springer; 2011. Matrix and Tensor Decompositions; pp. 291–318. [DOI] [Google Scholar]
- Devarajan K, Cheung VCK. Proceedings of the Joint Statistical Meetings. San Diego, California: 2012. On the relationship between non-negative matrix factorization and generalized linear modeling. [Google Scholar]
- Dhillon IS, Sra S. Advances in Neural Information Processing Systems. Vol. 19. MIT Press; 2005. Generalized nonnegative matrix approximations with Bregman divergences. [Google Scholar]
- Eberlein E, Hammerstein EA. Generalized hyperbolic and inverse Gaussian distributions: Limiting cases and approximation of processes. Progress in Probability. 2004;58:221–264. [Google Scholar]
- Févotte C, Idier J. Algorithms for nonnegative matrix factorization with the β-divergence. Neural Computation. 2011;23(9):2421–2456. [Google Scholar]
- Giszter S, Patil V, Hart C. Primitives, premotor drives, and pattern generation: a combined computational and neuroethological perspective. Progress in Brain Research. 2007;165:323–346. doi: 10.1016/S0079-6123(06)65020-6. [DOI] [PubMed] [Google Scholar]
- Golub GH, Van Loan CF. Matrix Computations. Baltimore, MD: Johns Hopkins University Press; 1983. [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Hart CB, Giszter SF. Modular premotor drives and unit bursts as primitives for frog motor behaviors. Journal of Neuroscience. 2004;24(22):5269–5282. doi: 10.1523/JNEUROSCI.5626-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyer PO. Nonnegative matrix factorization with sparseness constraints. Journal of Machine Learning Research. 2004;5:1457–1469. [Google Scholar]
- Hyvärinen A, Oja E. Independent component analysis: Algorithms and Applications. Neural Networks. 2000;13(4-5):411–430. doi: 10.1016/s0893-6080(00)00026-5. [DOI] [PubMed] [Google Scholar]
- Kompass R. A generalized divergence measure for nonnegative matrix factorization. Neural Computation. 2007;19:780–791. doi: 10.1162/neco.2007.19.3.780. [DOI] [PubMed] [Google Scholar]
- Kullback S. Information Theory and Statistics. New York: Wiley; 1959. [Google Scholar]
- Kullback S, Leibler RA. On information and sufficiency. The Annals of Mathematical Statistics. 1951;22:79–86. [Google Scholar]
- Lee DD, Seung SH. Learning the parts of objects by nonnegative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- Lee DD, Seung SH. Algorithms for nonnegative matrix factorization. Advances in Neural Information Processing Systems. 2001;13:556–562. [Google Scholar]
- Morup M, Hansen LK. Tuning pruning in sparse non-negative matrix factorization. 17th European Signal Processing Conference (EUSIPCO 2009); 2009. pp. 1923–27. [Google Scholar]
- Overduin SA, d’Avella A, Carmena JM, Bizzi E. Microstimulation activates a handful of muscle synergies. Neuron. 2012;76(6):1071–1077. doi: 10.1016/j.neuron.2012.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual-Montano A, Carazo JM, Kochi K, Lehmann D, Pascual-Marqui RD. Nonsmooth nonnegative matrix factorization (nsNMF) IEEE Transactions on Pattern Analysis and Machine Intelligence. 2006;28(3):403–415. doi: 10.1109/TPAMI.2006.60. [DOI] [PubMed] [Google Scholar]
- Poggio T, Bizzi E. Generalization in vision and motor control. Nature. 2004;431(7010):768–74. doi: 10.1038/nature03014. [DOI] [PubMed] [Google Scholar]
- Saltiel P, Wyler-Duda K, d’Avella A, Tresch MC, Bizzi E. Muscle synergies encoded within the spinal cord: evidence from focal intraspinal NMDA iontophoresis in the frog. Journal of Neurophysiology. 2001;85(2):605–619. doi: 10.1152/jn.2001.85.2.605. [DOI] [PubMed] [Google Scholar]
- Shahnaz F, Berry M, Pauca VP, Plemmons RJ. Document clustering using nonnegative matrix factorization. Information Processing and Management: An International Journal. 2006;42(2):373–386. [Google Scholar]
- Ting LH, Chvatal SA, Safavynia SA, McKay JL. Review and perspective: neuromechanical considerations for predicting muscle activation patterns for movement. International Journal of Numerical Methods in Biomedical Engineering. 2012;28(10):1003–1014. doi: 10.1002/cnm.2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tresch MC, Cheung VCK, d’Avella A. Matrix factorization algorithms for the identification of muscle synergies: evaluation on simulated and experimental data sets. Journal of Neurophysiology. 2006;95(4):2199–2212. doi: 10.1152/jn.00222.2005. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Saltiel P, d’Avella A, Bizzi E. Coordination and localization in spinal motor system. Brain Research Reviews. 2002;40:66–79. doi: 10.1016/s0165-0173(02)00189-3. [DOI] [PubMed] [Google Scholar]
- Wang G, Kossenkov AV, Ochs MF. LS-NMF: A modified nonnegative matrix factorization algorithm utilizing uncertainty estimates. BMC Bioinformatics. 2005;7:175. doi: 10.1186/1471-2105-7-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


