Abstract
Objectives
To establish an in vivo, normative patellofemoral cartilage contact mechanics database acquired during voluntary muscle control using a novel dynamic magnetic resonance (MR) imaging-based computational methodology and validate the contact mechanics sensitivity to the known sub-millimeter methodological inaccuracies.
Design
Dynamic cine phase-contrast and multi-plane cine images were acquired while female subjects (n=20, sample of convenience) performed an open kinetic chain (knee flexion-extension) exercise inside a 3-Tesla MR scanner. Static cartilage models were created from high resolution three-dimensional static MR data and accurately placed in their dynamic pose at each time frame based on the cine-PC data. Cartilage contact parameters were calculated based on the surface overlap. Statistical analysis was performed using paired t-test and a one-sample repeated measures ANOVA. The sensitivity of the contact parameters to the known errors in the patellofemoral kinematics was determined.
Results
Peak mean patellofemoral contact area was 228.7±173.6mm2 at 40° knee angle. During extension, contact centroid and peak strain locations tracked medially on the femoral and patellar cartilage and were not significantly different from each other. At 30°, 35°, and 40° of knee extension, contact area was significantly different. Contact area and centroid locations were insensitive to rotational and translational perturbations.
Conclusion
This study is a first step towards unfolding the biomechanical pathways to anterior patellofemoral pain and OA using dynamic, in vivo, and accurate methodologies. The database provides crucial data for future studies and for validation of, or as an input to, computational models.
INTRODUCTION
Patellofemoral (PF) osteoarthritis (OA) and its potential precursor, chronic idiopathic patellofemoral pain (PF pain), are common, costly, and debilitating conditions [1]. Previous literature has suggested that changes in intrinsic (e.g., muscles forces) or extrinsic (e.g., high impact loads) factors can create force imbalances at the joint level that alter cartilage contact mechanics, leading to PF pain and ultimately triggering cartilage degeneration [2, 3]. For example, high impact loading involving micro tears has long been regarded as a precursor to progressive chondropenia and ultimately to OA [4, 5]. In addition, repetitive mechanical loading of injured cartilage has been shown to result in degeneration [6]. Although the cartilage response to mechanical loading is well documented at the tissue and cellular levels in animal models [2, 7–10], it remains untested in vivo. Thus, despite a long history and variety of studies focusing on PF contact [11–19], to date the biomechanical pathway to PF OA remains elusive [20].
Our inability to define the precise in vivo mechanical pathogenesis of OA is partially due to the lack of in vivo, dynamic cartilage contact mechanics data. Previous studies [14, 16, 18, 21, 22], using a variety of methodological approaches (e.g., in vivo, cadaver-based, and computational modeling), have provided insights into PF contact mechanics. Yet, their methodological limitations and insufficient validation has restricted our ability to establish direct links between pathological joint kinematics, altered contact mechanics, and the onset of cartilage degeneration. The clinical utility of most previous in vivo PF contact mechanics studies is limited by the exclusion of functional movements and dynamic neuromuscular control patterns during which the PF pain is typically induced [23]. Suzuki and associates [21] did evaluate PF contact location during stair ascent in healthy volunteers. As this study did not quantify PF contact area and did not provide validation of the methods used, it is difficult to compare these results to the previous studies or apply these results clinically. Finite element and multi-body modeling methods [16, 24–26] tend to focus on evaluating PF contact stresses. Large inter-study variations have been reported, which are likely due to the different modeling methods and assumptions used across studies [25]. More importantly, these models are rarely validated and even the input parameters accuracy is often unknown [27]. Thus, the quality of the output variables is uncertain. In order to advance our understanding of the biomechanical pathway to PF OA, in vivo studies evaluating PF cartilage contact during a variety of dynamic functional tasks are needed. Furthermore, for these data to be clinically relevant and for clearer cross-study comparisons, the accuracy, validity, and/or reliability must be evaluated and reported.
The ultimate goal of this project is to quantify how alterations in joint kinematics and contact mechanics are correlated with OA and its progression. To achieve this goal, the current study had two primary objectives 1) to provide an in vivo normative database for dynamic PF cartilage contact mechanics acquired non-invasively in female subjects during a functional movement, and 2) to quantify the sensitivity of these parameters to the known sub-millimeter kinematic inaccuracies of the study methodology [28]. As the sensitivity may be subject-specific, this analysis was done over a large portion of the study cohort. Contact mechanics were broadly defined to encompass contact area and its centroid location, along with the peak strain location. The activity evaluated was open kinetic chain knee extension, as this has been shown to result in a mid-level of PF pain, similar to stair ascent/decent and jumping [23]. In order to compare the current data to previous in vivo studies, two questions were addressed using the normative database: 1) Are contact centroid and peak strain locations different? and 2) Do the contact mechanics change during knee extension?
MATERIALS AND METHODS
Twenty healthy female volunteers (26.8±8.1years, 162.3±10.8cm, 57.3±7.7kg) with no prior history of PF pain or OA participated in this IRB approved study. The subject pool was a sample of convenience, recruited from the local area. A single leg, selected at random, was examined for each subject. All the volunteers provided written informed consent prior to entering the study. Subjects with contraindications to magnetic resonance (MR) imaging or who had a history of lower body injury/trauma or knee joint pathology/pain were excluded.
2.1 MR data acquisition
All static and dynamic images were acquired using a 3T MR scanner (Achieva, Philips Medical Systems, Best, NL). For dynamic imaging, subjects laid supine with their knee and hip supported in slight flexion. Flexible transmit-receive coils were securely placed medial, lateral, and anterior to the knee. Dynamic cine-PC (CPC) MR images (FOV=200x200mm, pixel_size=0.78x0.78x8mm, TR=5.04msec, temporal resolution=60.5msec, 2NEX) were acquired while subjects performed a cyclic (30 cycles/min) open kinetic chain flexion-extension exercise to the beat of an auditory metronome [29]. In addition, multi-plane cine (MPC) data (FOV=200mmX200mm, pixel size=0.78x0.78x8mm, TR=3.2msec, temporal resolution=80.5 msec, 2NEX) were acquired during this exercise [28]. CPC imaging captured dynamic anatomical data in a single sagittal plane along with the corresponding three-dimensional (3D) pixel velocity, whereas MPC imaging captured purely anatomical images (5–7 sagittal planes) at each time frame. All dynamic data were represented using 24 time frames. Subsequently, the wedge was removed and the lower limb was placed in the anatomically neutral position. Then 3D, high-resolution, static, fat-sat, gradient recalled echo (FS-GRE), sagittal-plane MR images (field of view=140mmX140mm, 512x512pixels: interpolated in Fourier space from 216x240pixels, resolution=0.27mmx0.27x1mm, TR=10.6msec, TE=5.1msec) were acquired using an 8-channel knee coil.
In addition to the FS-GRE, a 3D GRE and a 3D proton density image set were acquired. These three static acquisitions were read by a radiologist in order to rule out the presence of any knee pathology (e.g., cartilage defects, torn ligaments, meniscal damage, trochlear dysplasia, tendinitis, patella alta/baja, etc).
2.2 MR data processing
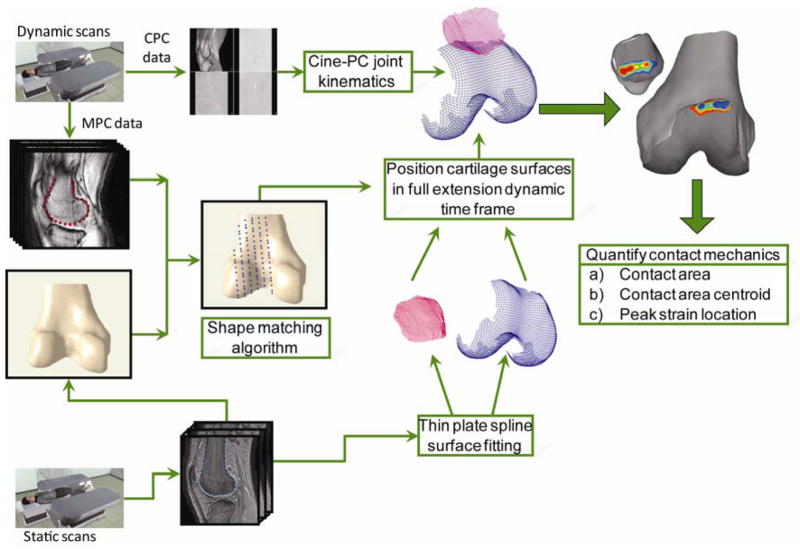
The contact mechanics were calculated by creating rigid models of the patellar and femoral bone and cartilage surfaces, defining the transformation from the static to full extension dynamic pose, and then applying the PF kinematics (derived from the CPC data) to the cartilage surfaces (Figure 1). To begin, the PF cortical surfaces were manually segmented from the FS-GRE images in MIPAV (NIH, Bethesda, MD). This generated a cloud of points representing the exterior cortical surface. These points were fitted with triangles in order to create a surface model, which was smoothed with a deviation limit of 0.2mm (Geomagic Inc, Research Triangle Park, NC). Similarly, sparse patellar and femoral point clouds were created by segmenting the dynamic MPC data at the full extension time frame (Figure 1). Next, by registering the sparse dynamic model to the high-resolution static model, it was possible to position the static model in its correct position and orientation for the full extension time frame. This registration process [28], using an iterative closest point algorithm (Geomagic Inc), created a transformation matrix that defined the optimal translation and rotation of the dynamic model that minimized the distance between the bone’s dynamic point cloud and its static 3D surface.
Figure 1.
Dynamic data were acquired while subjects performed open kinetic chain exercise inside the MR scanner. Cine-PC (CPC) data were used to generate patellofemoral joint kinematics, whereas multi-plane cine (MPC) data were used to generate sparse dynamic models for the same movement. Static bone models were generated using high resolution static scans. By registering the sparse dynamic models from the MPC data to the high resolution static bone models, the static bone models could be accurately positioned in their dynamic full extension pose (location and orientation). The transformation matrix generated by the registration was used to position the high resolution cartilage models (represented with thin plate splines) in the dynamic full extension time frame. These cartilage models were then placed into the correct pose for each time frame based on the CPC joint kinematics. Cartilage overlap was used to calculate contact mechanics parameters.
2.3 Cartilage Surface models
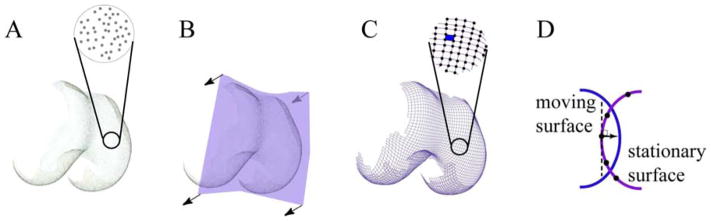
Point clouds representing the patellar and femoral cartilage surfaces were created similarly to the bone models (Figure 2). Even with relaxed musculature and a fully extended knee, minimal contact occurs between the cartilage surfaces [30]. Thus, the cartilage surfaces in the region of contact were manually approximated by maintaining the nominal curvature of the cartilage that was not in contact. The next step required converting the point cloud description of the surface into a mathematical expression so that the contact mechanics could be quantified. This was accomplished using a thin-plate spine (TPS) surface [31, 32] in MATLAB (Mathworks Inc., Natick, MA). Surface fitting errors were set to the static image pixel resolution. The TPS surfaces were then re-sampled with a rectangular grid of points (0.15–0.19mm apart) and trimmed to fit the cartilage morphology (Figure 2).
Figure 2. Calculating contact area.
A. By segmenting the outer cartilage surface, each body is represented by a cloud of points. As these points are randomly distributed, the surface is defined by the location of each point. B. The first step in determining the distance between this surface (femur) and the patella is to create a mathematical model of the femoral cartilage surface. This was accomplished using a mathematical thin plate spline (TPS) surface fitted over the point clouds. The process of fitting a TPS can be visualized as taking a flexible rectangular sheet (purple) and warping it until it fits to the outer surface of the cartilage. Once trimmed, the surface is now defined by a mathematical equation. C: The new surface generated by the TPS is re-sampled into a series of grid points (black dots) that are spaced in a rectangular grid, creating grid patches (blue filled space). D. In order to calculate the distance between surfaces, the distance from the stationary grid point to the moving surface was quantified. The normal (perpendicular) vector to the stationary surface at the grid point defined the direction of the distance vector between the stationary grid point and the moving surface.
2.4 Normative cartilage contact mechanics
The 3D PF kinematics [33] were derived by integrating the CPC data (accuracy=0.33mm [29]). All kinematics were defined relative to an anatomical coordinate system fixed in each bone [34, 35], such that medial, superior, and anterior defined the positive x-, y-, and z-directions. The) position and orientation of the cartilage surfaces throughout extension were quantified by first moving them to their correct position in the full extension time frame using the previously calculated transformation matrix. Then the CPC kinematic data were used to calculate the cartilage surface pose in all time frames (accuracy of <0.78mm and <1.73° [28].
The contact mechanics were defined relative to both the femoral and patellar cartilage surfaces. To calculate femoral contact mechanics, the patellar kinematics were defined relative to the femur. Thus, mathematically, the femur was the “stationary” and the patella was the “moving” body. For patellar contact mechanics, the opposite applied. The distance from each grid point on the stationary surface to the moving surface (Figure 2) was defined by determining the intersection of the stationary grid point‘s surface normal with the moving surface [31].This distance was termed as an overlap if it was below a subject-specific threshold value (0.59mm ± 0.52mm). The threshold value was constant for each subject and was determined based on previous research demonstrating that the PF contact area never reaches zero. Specifically, if with the initial threshold value of zero a subject demonstrated zero contact for any time frame, the threshold value was raised so that the analytical solution produced at least minimal contact for all time frames. The contact area for each surface was defined as the region of overlap (Figure 1). The size of the contact area was defined as the sum of all grid elements within the contact area. For rectangular and triangular areas the Bretschneider’s and Heron’s formulae were used, respectively [36].
The contact area centroid was determined as the weighted average of each grid patches’ location within the contact grid. The weighting was based on the patch area. Peak strain location was defined as the single stationary surface contact grid point corresponding to the maximum overlap value. To ensure that the peak strain represented the region of maximal strain, the locations of the first ten peak overlap points were identified for each time frame. It was then verified that these ten points created a contiguous region, inclusive of the peak strain. This verification confirmed that using a single point to represent the peak strain location was valid.
2.5 Statistical analysis
Since data were collected in evenly spaced temporal increments, each variable of interest was interpolated to single knee angle (-1° to 55°) increments for averaging and comparisons. All statistical analyses were run for knee angles from 40° to 10° at 5° increments, because variations in subject limb length prevented all subjects from reaching the full range. To determine whether the contact area changed during extension, paired t-tests were performed (SPSS, ver21.0, IBM, Armonk, NY). Comparing the differences between the contact centroid and the point of maximal strain locations required evaluation of 18 total observations associated with each individual (x, y and z values over six knee angles). Therefore, a repeated measures ANOVA was employed over the six angles, using dimension-wise difference. In the event of rejection of the null hypothesis, appropriate post-hoc analysis was performed. Prior to running the statistics, analyses were run to ensure that the assumptions of normality, homogeneity, and sphericity were met. Separate analyses were run for patellar and femoral surfaces. Statistical significance was set at p = 0.05.
2.6 Sensitivity analysis
A single parameter deterministic sensitivity analysis [37] was performed to quantify how potential inaccuracies in each kinematic parameter influence the contact mechanics. For 11 subjects (randomly selected from the study cohort) the patellar position and orientation was computationally perturbed (changed) from its original experimental values and then used to calculate the contact mechanics. Based on the accuracy of the study methodology [28], the perturbation was ±1mm and ±1°, in each of the coordinate system directions for four specific time frames (full extension, mid-flexion, full flexion, and mid-extension). This resulted in 48 perturbations over four time frames for each subject. The influence of each perturbation on contact area was analyzed by calculating the ratio of the change in contact area from its unperturbed position to the entire femoral cartilage area, inclusive of both condyles. Centroid and peak strain location sensitivities were analyzed by comparing the values of these locations pre- and post-perturbations. An error of less than 1mm resulting from any perturbation indicated that the process to calculate these locations diminished the kinematic inaccuracies and thus, was insensitive to the specific perturbation.
RESULTS
The patella shifted 3.0mm, 23.6mm, and 1.7mm (lateral, superior, and anterior) and rotated 2.89°, 18.36°, and 0.6° (medial tilt, extension and varus rotation) relative to the femur as the knee extended from 40° to 10°. This was similar to the PF kinematics of an independent control cohort [34].
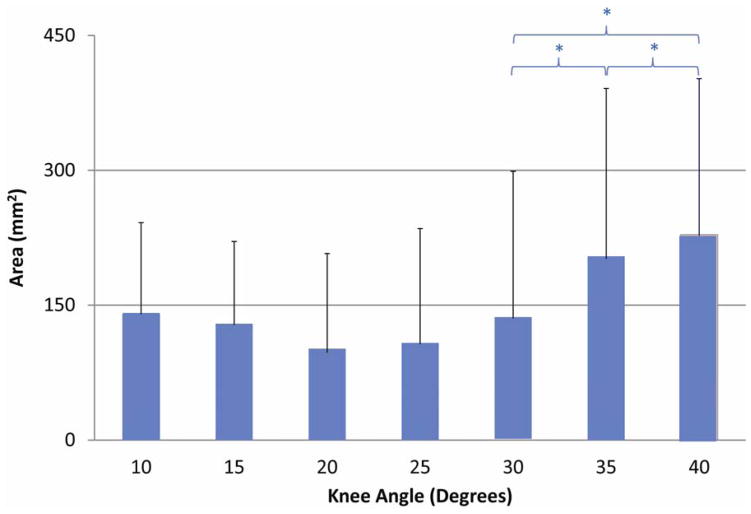
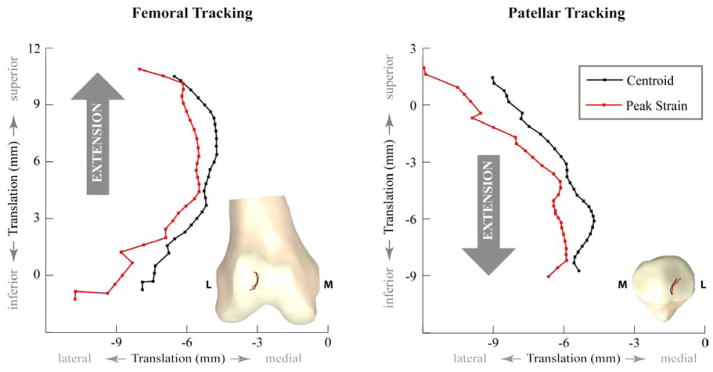
Peak PF contact area was 228.7±173.6mm2 at a 40° knee angle (Table 1). During extension, significant differences were found between 30°, 35° and 40° knee angles (Figure 3). Centroid and peak strain locations on the femoral and patellar cartilage tracked medially during extension (Figure 4) and were not significantly different from each other on either cartilage surface. For femoral contact, both medial (n=6) and lateral (n=14) centroid tracking patterns were observed. On the patellar cartilage three tracking patterns emerged; the centroid location followed a central (n=4), a medial (n=6), or a lateral (n=10) path.
Table 1.
Normative contact mechanics data arranged from maximum flexion → full extension. Contact area values are reported in mm2 with ±1SD. Contact centroid and peak strain locations on both patella and femur are reported in millimeters (±1SD) with medial, superior, and anterior directions as positive.
| Knee Angle | Contact Area (±SD) | Centroid on Femur | Centroid on Patella | Peak Strain on Femur | Peak Strain on Patella | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Medial | Superior | Anterior | Medial | Superior | Anterior | Medial | Superior | Anterior | Medial | Superior | Anterior | ||
| 40 | 228.7 (173.6) | −7.9 (6.1) | −0.8 (3.2) | 4.8 (2.4) | −9.0 (7.0) | 1.5 (3.0) | −3.6 (1.5) | −10.8 (9.5) | −1.3 (3.6) | 5.9 (2.4) | −12.0 (11.0) | 2.0 (3.1) | −3.4 (2.0) |
| 35 | 204.7 (187.8) | −6.8 (6.6) | 1.2 (3.5) | 5.5 (2.5) | −7.8 (7.1) | −0.4 (2.8) | −3.4 (1.5) | −8.3 (9.9) | 0.7 (4.0) | 6.4 (2.7) | −9.6 (10.8) | −0.4 (3.5) | −3.2 (2.3) |
| 30 | 137.4 (163.5) | −5.6 (6.9) | 3.0 (3.5) | 6.0 (2.3) | −6.4 (7.4) | −2.3 (2.9) | −3.1 (1.9) | −6.6 (9.7) | 2.9 (4.0) | 6.7 (2.5) | −7.7 (10.3) | −2.4 (3.4) | −3.1 (2.5) |
| 25 | 108.9 (130.1) | −5.2 (8.1) | 4.8 (3.5) | 6.3 (2.3) | −5.7 (8.2) | −4.1 (3.1) | −2.8 (2.0) | −5.5 (10.5) | 4.8 (4.2) | 6.8 (2.5) | −6.2 (11.0) | −4.4 (3.4) | −2.7 (2.8) |
| 20 | 100.8 (108.7) | −4.8 (7.5) | 6.8 (3.3) | 6.2 (2.0) | −4.8 (7.0) | −5.6 (2.8) | −2.7 (1.8) | −5.5 (10.1) | 6.7 (3.8) | 6.9 (2.2) | −6.4 (10.5) | −5.7 (3.5) | −2.5 (2.5) |
| 15 | 129.5 (94.3) | −5.0 (7.5) | 8.6 (3.4) | 6.1 (1.9) | −5.0 (6.2) | −7.1 (2.7) | −2.5 (1.6) | −6.2 (9.6) | 9.1 (3.6) | 6.7 (2.3) | −6.0 (9.3) | −7.2 (3.2) | −2.3 (2.3) |
| 10 | 125.1 (92.8) | −6.5 (5.8) | 10.5 (3.1) | 5.6 (2.3) | −5.4 (5.0) | −8.8 (2.6) | −2.1 (1.3) | −8.0 (8.6) | 10.9 (3.4) | 6.0 (2.5) | −6.7 (8.6) | −9.1 (2.7) | −2.0 (1.8) |
Figure 3.
Patellofemoral contact area during extension. Significant differences between knee angles are indicated with a * (p=0.05)
Figure 4.
Average values of contact centroid and peak strain locations on the femur and patella. Insets on each graph demonstrate the actual migration of contact centroid and peak strain locations on femoral and patellar cartilage. Since the view of the patella model is posterior to anterior for a right leg, right is lateral (L) on the model, but not on the graph. On average, both contact centroid and peak strain locations stayed on the lateral side of the PF joint.
The ten peak strain points were contiguous, with the exception of one time frame for five subjects. In these five (out of 480) time frames, the ten peak strain locations split between two different locations. This occurred due to the anatomical shape of the PF joint. Thus, the methodological approach of representing the peak strain location using a single point was deemed appropriate.
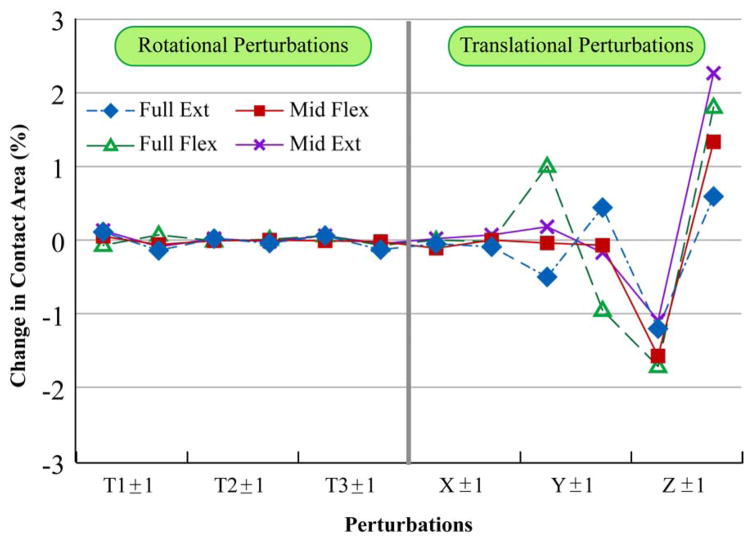
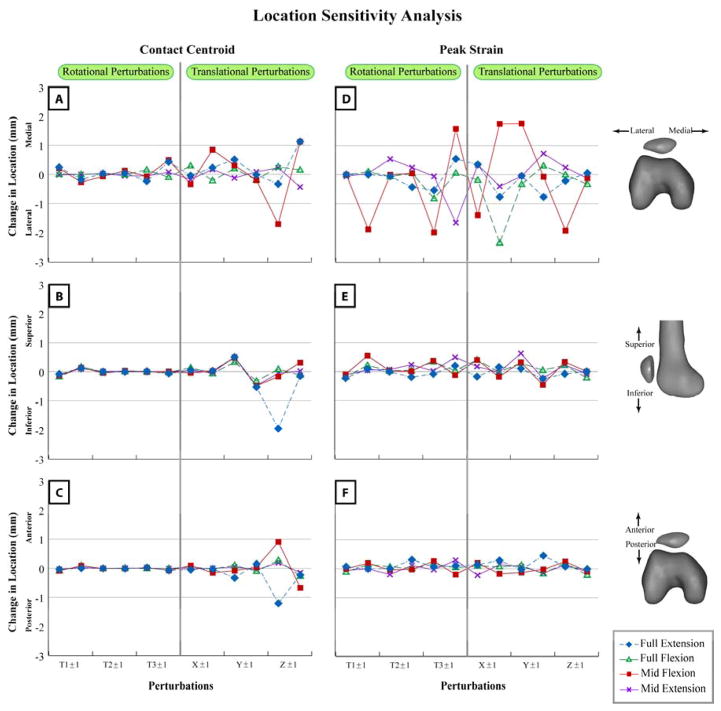
Contact area was insensitive to perturbations in both rotational, as well as translational degrees of freedom for all stages of the movement cycle (Figure 5). Contact area was most sensitive to translational perturbations in the anterior-posterior direction (~2% of femoral cartilage area). Similar to contact area, the centroid location (Figure 6) was insensitive to rotational perturbations and was only sensitive to anterior-posterior perturbations (<2mm). Only peak strain medial-lateral locations (Figure 6) were sensitive to kinematic perturbations. Full extension and mid-extension positions were the least sensitive to the perturbations.
Figure 5.
Mean contact area sensitivity reported as percent change with respect to femoral cartilage area. Full Ext = Full extension pose, Full Flex = Full flexion pose, Mid Flex = Mid-flexion pose, Mid Ext = Mid-extension pose. T1±1, T2±1, and T3±1: Perturbations in PF flexion-extension, medial-lateral tilt, and varus-valgus rotation. X±1, Y±1, and Z±1: Perturbations in PF medial-lateral, superior-inferior, and anterior-posterior displacement. The first data point in the graphical pair on the x-axis is the positive direction: flexion, medial tilt, varus rotation, and medial, superior, and anterior displacement. For example, X1±1 indicates the sensitivity of contact area to medial perturbation and then to lateral perturbation.
Figure 6.
Comparing sensitivity of contact centroid (A, B, C) and peak strain (D, E, F) locations. Mean change in location with respect to unperturbed location is plotted in the medial (A, D), superior (B, E), and anterior (C, F) directions. T1±1, T2±1, and T3±1: Perturbations in PF flexion-extension, medial-lateral tilt, and varus-valgus rotation. X±1, Y±1, and Z±1: Perturbations in PF medial-lateral, superior-inferior, and anterior-posterior displacement. The first data point in the graphical pair on the x-axis is the positive direction: flexion, medial tilt, varus rotation, and medial, superior, and anterior displacement. For example, X1±1 indicates the sensitivity of locations to medial perturbation and then to lateral perturbation.
DISCUSSION
Patellofemoral pain and PF OA are considered to occur primarily from alterations in the dynamic state of the PF joint. Thus, by providing a validated, dynamic, in vivo PF cartilage contact database, acquired during volitional activity in healthy female subjects, this study provides crucial data for future studies of PF pain and OA. In addition, these data can be used for validation of, or as input to, future computational models. It is a clear advancement over previous studies that have little to no validation and have typically been limited to static analyses, cadaver studies, animal-based methodologies, or generic computational models [14, 18, 21, 38–40].
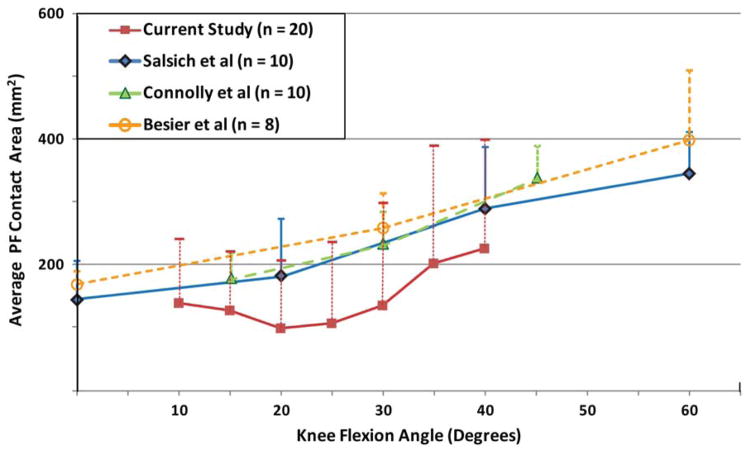
The average contact area (Figure 7) agreed with past static in vivo study results [14, 18, 41], but tended towards smaller values. Unfortunately, based on the variability across studies, it is difficult to extract a common baseline for comparison. Specifically, Besier and colleagues [41] reported that cartilage contact area increased with increased isometric quadriceps load, but Salsich and colleagues [18] reported no change with isometric quadriceps contractions. Further, out of these three previous studies, it would be expected that the female cohort (n=8) during the low-load trial [41] would have the lowest contact areas due to the fact that they had the smallest reported average weight and height, along with the lowest load on the patella, but this was not the case. The variability in contact area across subjects was clearly much higher in the current study, as compared to past static in vivo studies. Part of this variability is likely due to the larger variation in the subject height and weight. For example, the difference in variability for height and weight was 130% and 40% larger than in the Connolly et al study [14]. As no study to date has correlated contact mechanics to subject size parameters, future studies should evaluate these relationships in order to determine the most appropriate scaling/normalization factors for contact mechanics. In addition, the current variability may be attributable to the dynamic nature of the study. As PF contact is a dynamic phenomenon constituting multiple factors, the higher variability in the current study is likely an accurate depiction of the true variations across subjects due to multiple dynamic factors including PF kinematics, neuromuscular control patterns, and soft-tissue constraints.
Figure 7.
Contact area comparison between current study and previous in vivo static studies. In order to make a common baseline for comparison, only data pertaining to healthy female volunteers were considered. Furthermore, only contact area data that corresponded with active quadriceps contraction were considered. In cases where quantitative data were not available, it was approximated from graphical data.
Contact area has previously been shown to change between knee angles up to and through fullextension [14, 18, 41]. Yet, currently differences were only found in early extension. This discrepancy is likely due to the fact that PF static and dynamic poses are task specific phenomenon [30, 42, 43]. Specifically, this slight discrepancy in results likely arises from variation in neuromuscular control between the static and dynamic tasks. The previously employed static tasks were the same across knee angles (the knee was secured at the desired angle and an isometric quadriceps force was exerted with the leg stationary). Although quadriceps contraction represented a small percentage of either body weight or maximum voluntary co-contraction, it could not represent the physiological dynamic loading during a volitional task. Conversely, the current task changed as the leg extended. In early extension, the lower leg was accelerated from zero to maximum angular velocity against gravity then decelerated to a complete stop at terminal extension while still working against gravity. Thus, the neuromuscular control catered to changing dynamic demands. In addition, during a free kicking exercise, the required quadriceps load increases as the leg extends [44]. The quadriceps load in terminal extension pulls the patella proximal of the trochlear groove, decreasing the congruency with the femoral cartilage. This loss of congruency allowed the dynamic ligament and muscle forces to have a stronger influence [45], resulting in complex contact patterns.
The differences in contact centroid locations that have been reported for static in vivo [14] and dynamic functional activities [21] clearly illustrate the influence of neuromuscular control, anatomical shape parameters, and gravity on contact mechanics. The one previous dynamic PF contact study found that as the knee extended from 40° to 10° during stair ascent, the contact centroid tracked 13mm superiorly and 8mm inferiorly on the femoral and patellar surfaces, respectively [21]. This was different than the migration seen for the same knee angle range in the current study (11.2mm superiorly and 10.2mm inferiorly). The variances between these two dynamic tasks likely reflect the fact that during stair ascent the quadriceps load begins high and diminishes to near zero at full extension, whereas in free extension against gravity, the load increases as the knee extends [46]. This same rationale would explain the much larger lateral shift and medial tilt along with smaller anterior shift in the current versus the previous study [21]. Lastly, during static positioning with active quadriceps contraction [14] the patellar centroid migration was much reduced (6mm inferiorly over a 30° knee angle range), in comparison to the two dynamic activities. Thus, incorporating dynamic activities in future studies evaluating altered PF cartilage contact in patients with PF pain or OA is important for quantifying the influences of numerous dynamic factors that may be associated with contact mechanics.
Peak strain location, as reported in the current study, is a relatively new measure that has not been reported in previous studies. The peak strain is an indicator of peak stress pattern and thus, could ultimately indicate future mechanical failure of the cartilage. Although no differences were found between contact centroid and peak strain locations throughout the movement cycle, the results may differ in pathology. Thus, future work is needed to evaluate if such a difference can be found during a dynamic task and if the peak strain locations differ between these groups.
As there is no gold standard for evaluating cartilage contact properties in vivo, the sensitivity analysis provided a strong validation that small inaccuracies in kinematic parameters did not influence the contact mechanics calculations. This agreed with the sensitivity analysis conducted by Li and colleagues [39] on a wear predicting deformable contact model. The insensitivity of the contact mechanics to rotational inaccuracies (with the exception of the peak strain medial-lateral location at mid-flexion) clearly illustrates that these errors do not affect the calculation of contact mechanics. This is logical as the patella is quite small and even large rotations (about the patellar center) result in small translations of any point on the body. The locations of the contact centroid and peak strain were insensitive to translational perturbations, as the 1mm perturbations resulted in errors that were typically less than 25% of the perturbation. Again, the primary exception to this was the sensitivities found during mid-flexion. As both the centroid and the peak strain locations were insensitive to all perturbations at mid-extension, this time frame should be considered for future studies focusing on PF joint function, impairment, and pathology. Another interesting point is that the translational perturbations primarily caused errors in the contact centroid location in the same direction (e.g. inferior perturbations resulting in the contact centroid being shifted inferiorly). Thus, it would be expected that pathological changes in PF kinematics (e.g., excessive lateral shift or patella alta) would be mirrored by similar changes in the centroid location. Ultimately, the sensitivity analysis clearly demonstrated that extending the single point tracking methodology to determine cartilage mechanics is valid.
Caution must be used when applying this sensitivity analysis to other methodological approaches as sensitivity is highly dependent on the methodology used. For example, the accuracy of tracking PF kinematics by matching bi-plane radiography with CT models is excellent (0.35mm, [47]). Unfortunately, an MR model is required for analyzing contact mechanics and replacing the CT model with an MR model would greatly diminish the kinematic accuracy [39]. In addition, since the current techniques for quantifying contact kinematics are dependent on shape matching, this sensitivity analysis is specific to the PF joint and would need to be re-evaluated if the technique was to be applied to any other joint. Lastly, the moderately higher sensitivity in peak strains for three out of the 11 subjects was determined to be due to the PF bone shape in these subjects. Thus, future evaluation of the relationship between PF bone shape and contact mechanics is warranted.
This study was delimited to a female cohort, as knee OA is most prevalent in elderly women [48] and similarly, PF pain is most prevalent in young females [49]. However, both conditions do affect the male population, thus future studies focusing on males need to be devised. Although the open kinetic chain movement used in this study represents a task that induces PF pain to a similar level as jumping and stair ascent/descent [23], the closed bore environment of the MR scanner limits the variety of dynamic tasks that can be performed. Future improvements in MR technology will remove this limitation. This study focused on minimizing the required methodological assumptions by using direct deduction of experimental data. In doing so it was limited to evaluating a partial set of contact parameters. Assessment of parameters such as contact stress and strain is important. However, determining these parameters requires complex computational modeling approaches involving numerous assumptions (e.g. musculoskeletal tissue properties) and our future goals include implementation of this approach as well.
CONCLUSION
The biomechanical pathway to cartilage degeneration is still not fully understood and the factors associated with OA have not been fully evaluated in an in vivo setting. This database provides a necessary foundation for exploring how PF pain, knee OA, PF kinematics, and cartilage mechanics are interrelated. This is a first step towards unfolding the biomechanical pathways using dynamic, in vivo, and highly accurate analyses. Peak strains and peak contact pressures are regarded as parameters of interest and will be evaluated in future developments of this project. Neuromuscular control plays an important role in loading and unloading the PF joint as seen in the variation in contact mechanics between the current and previous studies. Thus, future studies focusing on the dynamic effect of active muscular contractions on contact mechanics are warranted.
Acknowledgments
FUNDING RESOURCES
This research was supported by the Intramural Research Program of the NIH Clinical Center.
The authors would like to thank Sara Sadeghi for her help in enrolling subjects; Emily Wible, Ali Siddiqui, and Vincent Ma for their help with data preparation; Aaron Heuser, PhD (Statistics and Epidemiology Section, Clinical Center, NIH) for his statistical expertise, and the Diagnostic Radiology Department at the National Institutes of Health for providing instrumentation and support for the MR imaging. This research was supported by the Intramural Research Program of the NIH Clinical Center
Footnotes
CONTRIBUTIONS
Both authors contributed to the conception and design of the study. Both authors equally contributed to the data collection, analysis and interpretation. Initial draft was provided by BSB and critically reviewed by FTS.
CONFLICTS OF INTERESTS
The authors have no conflicts of interests related to this study.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Utting MR, Davies G, Newman JH. Is anterior knee pain a predisposing factor to patellofemoral osteoarthritis? Knee. 2005;12:362–365. doi: 10.1016/j.knee.2004.12.006. [DOI] [PubMed] [Google Scholar]
- 2.Natoli RM, Athanasiou KA. Traumatic loading of articular cartilage: Mechanical and biological responses and post-injury treatment. Biorheology. 2009;46:451–485. doi: 10.3233/BIR-2009-0554. [DOI] [PubMed] [Google Scholar]
- 3.Powers CM, Bolgla LA, Callaghan MJ, Collins N, Sheehan FT. Patellofemoral pain: proximal, distal, and local factors, 2nd International Research Retreat. J Orthop Sports Phys Ther. 2012;42:A1–54. doi: 10.2519/jospt.2012.0301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Buckwalter JA, Mankin HJ, Grodzinsky AJ. Articular cartilage and osteoarthritis. Instr Course Lect. 2005;54:465–480. [PubMed] [Google Scholar]
- 5.Guilak F. Biomechanical factors in osteoarthritis. Best Pract Res Clin Rheumatol. 2011;25:815–823. doi: 10.1016/j.berh.2011.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mandelbaum B, Waddell D. Etiology and pathophysiology of osteoarthritis. Orthopedics. 2005;28:s207–214. doi: 10.3928/0147-7447-20050202-05. [DOI] [PubMed] [Google Scholar]
- 7.Ewers BJ, Dvoracek-Driksna D, Orth MW, Haut RC. The extent of matrix damage and chondrocyte death in mechanically traumatized articular cartilage explants depends on rate of loading. J Orthop Res. 2001;19:779–784. doi: 10.1016/S0736-0266(01)00006-7. [DOI] [PubMed] [Google Scholar]
- 8.Ramage L, Nuki G, Salter DM. Signalling cascades in mechanotransduction: cell-matrix interactions and mechanical loading. Scand J Med Sci Sports. 2009;19:457–469. doi: 10.1111/j.1600-0838.2009.00912.x. [DOI] [PubMed] [Google Scholar]
- 9.Milentijevic D, Helfet DL, Torzilli PA. Influence of stress magnitude on water loss and chondrocyte viability in impacted articular cartilage. J Biomech Eng. 2003;125:594–601. doi: 10.1115/1.1610021. [DOI] [PubMed] [Google Scholar]
- 10.Milentijevic D, Torzilli PA. Influence of stress rate on water loss, matrix deformation and chondrocyte viability in impacted articular cartilage. J Biomech. 2005;38:493–502. doi: 10.1016/j.jbiomech.2004.04.016. [DOI] [PubMed] [Google Scholar]
- 11.Steinkamp LA, Dillingham MF, Markel MD, Hill JA, Kaufman KR. Biomechanical considerations in patellofemoral joint rehabilitation. Am J Sports Med. 1993;21:438–444. doi: 10.1177/036354659302100319. [DOI] [PubMed] [Google Scholar]
- 12.Hungerford DS, Barry M. Biomechanics of the patellofemoral joint. Clin Orthop Relat Res. 1979:9–15. [PubMed] [Google Scholar]
- 13.Besier TF, Gold GE, Beaupre GS, Delp SL. A modeling framework to estimate patellofemoral joint cartilage stress in vivo. Med Sci Sports Exerc. 2005;37:1924–1930. doi: 10.1249/01.mss.0000176686.18683.64. [DOI] [PubMed] [Google Scholar]
- 14.Connolly KD, Ronsky JL, Westover LM, Kupper JC, Frayne R. Differences in patellofemoral contact mechanics associated with patellofemoral pain syndrome. J Biomech. 2009;42:2802–2807. doi: 10.1016/j.jbiomech.2009.07.028. [DOI] [PubMed] [Google Scholar]
- 15.Escamilla RF, Zheng N, Macleod TD, Edwards WB, Imamura R, Hreljac A, et al. Patellofemoral joint force and stress during the wall squat and one-leg squat. Med Sci Sports Exerc. 2009;41:879–888. doi: 10.1249/MSS.0b013e31818e7ead. [DOI] [PubMed] [Google Scholar]
- 16.Farrokhi S, Keyak JH, Powers CM. Individuals with patellofemoral pain exhibit greater patellofemoral joint stress: a finite element analysis study. Osteoarthritis Cartilage. 2011;19:287–294. doi: 10.1016/j.joca.2010.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goudakos IG, Konig C, Schottle PB, Taylor WR, Hoffmann JE, Popplau BM, et al. Regulation of the patellofemoral contact area: an essential mechanism in patellofemoral joint mechanics? J Biomech. 2010;43:3237–3239. doi: 10.1016/j.jbiomech.2010.07.029. [DOI] [PubMed] [Google Scholar]
- 18.Salsich GB, Ward SR, Terk MR, Powers CM. In vivo assessment of patellofemoral joint contact area in individuals who are pain free. Clin Orthop Relat Res. 2003:277–284. doi: 10.1097/01.blo.0000093024.56370.79. [DOI] [PubMed] [Google Scholar]
- 19.Goodfellow J, Hungerford DS, Zindel M. Patello-femoral joint mechanics and pathology. 1. Functional anatomy of the patello-femoral joint. J Bone Joint Surg Br. 1976;58:287–290. doi: 10.1302/0301-620X.58B3.956243. [DOI] [PubMed] [Google Scholar]
- 20.Wilson W, van Donkelaar CC, van Rietbergen R, Huiskes R. The role of computational models in the search for the mechanical behavior and damage mechanisms of articular cartilage. Med Eng Phys. 2005;27:810–826. doi: 10.1016/j.medengphy.2005.03.004. [DOI] [PubMed] [Google Scholar]
- 21.Suzuki T, Hosseini A, Li JS, Gill TJt, Li G. In vivo patellar tracking and patellofemoral cartilage contacts during dynamic stair ascending. J Biomech. 2012;45:2432–2437. doi: 10.1016/j.jbiomech.2012.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Goudakos IG, Konig C, Schottle PB, Taylor WR, Singh NB, Roberts I, et al. Stair climbing results in more challenging patellofemoral contact mechanics and kinematics than walking at early knee flexion under physiological-like quadriceps loading. J Biomech. 2009;42:2590–2596. doi: 10.1016/j.jbiomech.2009.07.007. [DOI] [PubMed] [Google Scholar]
- 23.Thomee R, Grimby G, Wright BD, Linacre JM. Rasch Analysis of Visual Analog Scale Measurements before and after Treatment of Patellofemoral Pain Syndrome in Women. Scandinavian Journal of Rehabilitation Medicine. 1995;27:145–151. [PubMed] [Google Scholar]
- 24.Guess TM, Liu H, Bhashyam S, Thiagarajan G. A multibody knee model with discrete cartilage prediction of tibio-femoral contact mechanics. Comput Methods Biomech Biomed Engin. 2011 doi: 10.1080/10255842.2011.617004. [DOI] [PubMed] [Google Scholar]
- 25.Fitzpatrick CK, Baldwin MA, Rullkoetter PJ. Computationally efficient finite element evaluation of natural patellofemoral mechanics. J Biomech Eng. 2010;132:121013. doi: 10.1115/1.4002854. [DOI] [PubMed] [Google Scholar]
- 26.Anderson AE, Ellis BJ, Maas SA, Peters CL, Weiss JA. Validation of finite element predictions of cartilage contact pressure in the human hip joint. J Biomech Eng. 2008;130:051008. doi: 10.1115/1.2953472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Trepczynski A, Kutzner I, Kornaropoulos E, Taylor WR, Duda GN, Bergmann G, et al. Patellofemoral joint contact forces during activities with high knee flexion. J Orthop Res. 2012;30:408–415. doi: 10.1002/jor.21540. [DOI] [PubMed] [Google Scholar]
- 28.Borotikar BS, Sipprell WH, 3rd, Wible EE, Sheehan FT. A methodology to accurately quantify patellofemoral cartilage contact kinematics by combining 3D image shape registration and cine-PC MRI velocity data. J Biomech. 2012;45:1117–1122. doi: 10.1016/j.jbiomech.2011.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Behnam AJ, Herzka DA, Sheehan FT. Assessing the accuracy and precision of musculoskeletal motion tracking using cine-PC MRI on a 3. 0T platform. J Biomech. 2011;44:193–197. doi: 10.1016/j.jbiomech.2010.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Powers CM, Ward SR, Fredericson M, Guillet M, Shellock FG. Patellofemoral kinematics during weight-bearing and non-weight-bearing knee extension in persons with lateral subluxation of the patella: a preliminary study. J Orthop Sports Phys Ther. 2003;33:677–685. doi: 10.2519/jospt.2003.33.11.677. [DOI] [PubMed] [Google Scholar]
- 31.Boyd SK, Ronsky JL, Lichti DD, Salkauskas K, Chapman MA. Joint surface modeling with thin-plate splines. J Biomech Eng. 1999;121:525–532. doi: 10.1115/1.2835083. [DOI] [PubMed] [Google Scholar]
- 32.Borotikar BS. Applied Biomedical Engineering, vol D Eng. Cleveland: Cleveland State University; 2009. Subject specific computational models of the knee to predict anterior cruciate ligament injuries. [Google Scholar]
- 33.Sheehan FT, Zajac FE, Drace JE. In vivo tracking of the human patella using cine phase contrast magnetic resonance imaging. J Biomech Eng. 1999;121:650–656. doi: 10.1115/1.2800868. [DOI] [PubMed] [Google Scholar]
- 34.Seisler AR, Sheehan FT. Normative three-dimensional patellofemoral and tibiofemoral kinematics: a dynamic, in vivo study. IEEE Trans Biomed Eng. 2007;54:1333–1341. doi: 10.1109/TBME.2007.890735. [DOI] [PubMed] [Google Scholar]
- 35.Sheehan FT, Mitiguy P. In regards to the “ISB recommendations for standardization in the reporting of kinematic data”. J Biomech. 1999;32:1135–1136. doi: 10.1016/s0021-9290(99)00077-9. [DOI] [PubMed] [Google Scholar]
- 36.Beyer WH. Standard Mathematical Tables and Formulae. CRC Press; 1991. [Google Scholar]
- 37.Doubilet P, Begg CB, Weinstein MC, Braun P, McNeil BJ. Probabilistic sensitivity analysis using Monte Carlo simulation. A practical approach. Med Decis Making. 1985;5:157–177. doi: 10.1177/0272989X8500500205. [DOI] [PubMed] [Google Scholar]
- 38.Ward SR, Terk MR, Powers CM. Patella alta: association with patellofemoral alignment and changes in contact area during weight-bearing. J Bone Joint Surg Am. 2007;89:1749–1755. doi: 10.2106/JBJS.F.00508. [DOI] [PubMed] [Google Scholar]
- 39.Li L, Patil S, Steklov N, Bae W, Temple-Wong M, D'Lima DD, et al. Computational wear simulation of patellofemoral articular cartilage during in vitro testing. J Biomech. 2011;44:1507–1513. doi: 10.1016/j.jbiomech.2011.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sawatsky A, Bourne D, Horisberger M, Jinha A, Herzog W. Changes in patellofemoral joint contact pressures caused by vastus medialis muscle weakness. Clin Biomech (Bristol, Avon) 2012;27:595–601. doi: 10.1016/j.clinbiomech.2011.12.011. [DOI] [PubMed] [Google Scholar]
- 41.Besier TF, Draper CE, Gold GE, Beaupre GS, Delp SL. Patellofemoral joint contact area increases with knee flexion and weight-bearing. J Orthop Res. 2005;23:345–350. doi: 10.1016/j.orthres.2004.08.003. [DOI] [PubMed] [Google Scholar]
- 42.Brossmann J, Muhle C, Schroder C, Melchert UH, Bull CC, Spielmann RP, et al. Patellar tracking patterns during active and passive knee extension: evaluation with motion-triggered cine MR imaging. Radiology. 1993;187:205–212. doi: 10.1148/radiology.187.1.8451415. [DOI] [PubMed] [Google Scholar]
- 43.Freedman BR, Sheehan FT. Predicting three-dimensional patellofemoral kinematics from static imaging-based alignment measures. J Orthop Res. 2013;31:441–447. doi: 10.1002/jor.22246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Powers CM. Rehabilitation of patellofemoral joint disorders: a critical review. J Orthop Sports Phys Ther. 1998;28:345–354. doi: 10.2519/jospt.1998.28.5.345. [DOI] [PubMed] [Google Scholar]
- 45.Harbaugh CM, Wilson NA, Sheehan FT. Correlating femoral shape with patellar kinematics in patients with patellofemoral pain. J Orthop Res. 2010;28:865–872. doi: 10.1002/jor.21101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Powers CM, Lilley JC, Lee TQ. The effects of axial and multi-plane loading of the extensor mechanism on the patellofemoral joint. Clin Biomech (Bristol, Avon) 1998;13:616–624. doi: 10.1016/s0268-0033(98)00013-8. [DOI] [PubMed] [Google Scholar]
- 47.Bey MJ, Kline SK, Tashman S, Zauel R. Accuracy of biplane x-ray imaging combined with model-based tracking for measuring in-vivo patellofemoral joint motion. J Orthop Surg Res. 2008;3:38. doi: 10.1186/1749-799X-3-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.McAlindon TE, Snow S, Cooper C, Dieppe PA. Radiographic patterns of osteoarthritis of the knee joint in the community: the importance of the patellofemoral joint. Ann Rheum Dis. 1992;51:844–849. doi: 10.1136/ard.51.7.844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Boling M, Padua D, Marshall S, Guskiewicz K, Pyne S, Beutler A. Gender differences in the incidence and prevalence of patellofemoral pain syndrome. Scand J Med Sci Sports. 2009;20:725–730. doi: 10.1111/j.1600-0838.2009.00996.x. [DOI] [PMC free article] [PubMed] [Google Scholar]