Automated modification and fusion of voxel models to construct body phantoms with heterogeneous breast tissue: Application to MRI simulations

Abstract

Background

Human voxel models incorporating detailed anatomical features are vital tools for the computational evaluation of electromagnetic (EM) fields within the body. Besides whole-body human voxel models, phantoms representing smaller heterogeneous anatomical features are often employed; for example, localized breast voxel models incorporating fatty and fibroglandular tissues have been developed for a variety of EM applications including mammography simulation and dosimetry, magnetic resonance imaging (MRI), and ultra-wideband microwave imaging. However, considering wavelength effects, electromagnetic modeling of the breast at sub-microwave frequencies necessitates detailed breast phantoms in conjunction with whole-body voxel models.

Methods

Heterogeneous breast phantoms are sized to fit within radiofrequency coil hardware, modified by voxel-wise extrusion, and fused to whole-body models using voxel-wise, tissue-dependent logical operators. To illustrate the utility of this method, finite-difference time-domain simulations are performed using a whole-body model integrated with a variety of available breast phantoms spanning the standard four tissue density classifications representing the majority of the population.

Results

The software library uses a combination of voxel operations to seamlessly size, modify, and fuse eleven breast phantoms to whole-body voxel models. The software is publicly available on GitHub and is linked to the file exchange at MATLAB^® Central. Simulations confirm the proportions of fatty and fibroglandular tissues in breast phantoms have significant yet predictable implications on projected power deposition in tissue.

Conclusions

Breast phantoms may be modified and fused to whole-body voxel models using the software presented in this work; user considerations for the open-source software and resultant phantoms are discussed. Furthermore, results indicate simulating breast models as predominantly fatty tissue can considerably underestimate the potential for tissue heating in women with substantial fibroglandular tissue.

1. Introduction

Human voxel models incorporating detailed anatomical features are vital tools for the computational evaluation of electromagnetic (EM) fields within the body.^[1] One example research domain in which simulation of human voxel models has become a basis for ensuring patient safety is magnetic resonance imaging (MRI) studies. The IEC and FDA guidelines on maximum power deposition, quantified by specific absorption rate (SAR, with units W kg⁻¹), provide the basis for setting safe MRI scanner parameters controlling input power to the radiofrequency (RF) coil.^{[2, 3]} To comply with these guidelines for human studies, it is common practice to characterize RF transmit coils and medical implants using full-wave electromagnetic modeling in order to establish the parameters that ensure safe power and SAR levels.^[4] Commonly, finite-difference time-domain (FDTD) based methods are utilized owing to the ease of incorporating SAR calculations with heterogeneous body models.^[5–7]

In addition to whole-body human voxel models, phantoms representing regional anatomical features are often employed for EM simulations. While isolated regional phantoms suffice for certain applications, more thorough results may be obtained in some circumstances by fusing these smaller phantoms with a whole-body model. For example, localized breast voxel models have been developed for a variety of EM techniques utilizing short (relative to the body) wavelengths, including radiation dosimetry and ultra-wideband microwave imaging;^[8–11] however, the frequencies currently associated with human MR scanners (i.e., 64–450 MHz) correspond to longer EM wavelengths with which the effects of the remainder of the body cannot be ignored. Thus, simulating RF field behavior during breast MRI scans would ideally incorporate a female whole-body voxel model into the FDTD mesh. Although several adult female body models are available to the research community, all are oriented in the standing or supine positions;^[12–16] unfortunately, these orientations limit the existing voxel models’ applicability for simulating the filling factor of breast RF coils designed for women in the prone position, as is typically performed with MRI to avoid respiratory artifacts.^{[17, 18]}

Furthermore, the accuracy of breast phantoms is confounded by the anatomical variability of fatty (lipid) and fibroglandular tissues and their distinct material properties that affect electromagnetic exposure.^[8] Rudimentary efforts to model a prone breast either replaced or supplemented the body model with geometric volumes representing homogeneous breast tissues,^{[19, 20]} while improved breast phantoms with heterogeneous fibroglandular and adipose tissue structures have been generated by using image data conversion^{[11, 21, 22]} or software algorithms.^[23–28] Recognizing the need for anatomically-correct heterogeneous breast phantoms in conjunction with whole body voxel models, van der Velden et al. fused a body model with 3D image data acquired from five healthy volunteers and ultimately noted that the observed disparity of simulated SAR distributions among these models was due to indeterminate variations in size and tissue makeup.^[29] Breast size and tissue density have great variability among the patient population; to classify the extent of breast tissue density across women, radiologists largely have embraced the four tissue composition categories prescribed by the American College of Radiology (ACR) in the Breast Imaging Reporting and Data System (BI-RADS^®).^[30] Using this method, breast density is defined as (a) almost entirely fat, (b) scattered fibroglandular tissue, (c) heterogeneous fibroglandular tissue, and (d) extreme fibroglandular tissue. An analysis of projected SAR encompassing these four classifications is used as a test bed in this study.

In order to address the need to augment existing whole-body voxel models to account for prone imaging and the necessity to use heterogeneous breast tissue models, this work details a software procedure to seamlessly modify and fuse heterogeneous breast phantoms to whole-body voxel models. First, the breast phantoms are resized and appropriately situated with respect to the whole-body voxel model, and subsequent voxel extrusion and subtraction operations effectively fuse the breast anterior to the pectoral muscles of the whole-body voxel models. To illustrate the utility of this method, we performed simulations of 7 tesla MRI radiofrequency excitation of a whole-body voxel model fused with nine high-resolution, anatomically-correct breast phantoms spanning the four BI-RADS tissue density classifications, thus demonstrating the importance of being able to modify the few existing whole body models for particular studies. Results confirm the proportions of lipid and fibroglandular tissues in breast phantoms have significant yet predictable implications on projected SAR. Finally, usage of the publicly-available software and resultant phantoms is discussed.

2. Methods

2.1 Voxel models and software

Of the presently reported adult non-pregnant female whole-body models, “Ella” from the Virtual Population is the highest-resolution and most comprehensive tissue model of the adult female body.^[12] Disadvantages from the standpoint of breast modeling include the facts that Ella 1) represents a woman in the supine position and 2) does not include any fibroglandular tissue in the breast region. For this work, we adapted nine heterogeneous 0.5-mm resolution pendant breast phantoms produced by the Hagness group at the University of Wisconsin–Madison (UW) for modeling microwave interactions between 0.5 and 20 GHz.^[11] These phantoms were labelled according to the subject’s radiologist-assigned BI-RADS classification, denoted BI-RADS-a, -b, -c, and -d.^[30] At least two phantoms were developed for each category, with the exception of a single phantom for BI-RADS-d. All nine breast models included tissues defined as fatty, fibroglandular, transitional, and skin. Within the fatty and fibroglandular classes, the preceding Wisconsin–Calgary study of microwave dielectric properties identified increasing incongruence of conductivity and permittivity values above 500 MHz and accordingly divided both tissue classes into three tiers, each defined by single-pole Cole-Cole and Debye relaxation models.^[31] As these discrepancies in dielectric properties have not been observed in the RF band, in this work the three tiers for each tissue type were merged into single definitions as fat or fibroglandular tissues. The fat, fibroglandular, and skin tissues were assigned dielectric properties using the four-pole Cole-Cole equations stipulated by the IT’IS Foundation’s tissue properties database.^[32] Voxels designated as transitional were assigned dielectric and physical properties averaging the values from breast fat and gland tissues. The resulting tissue dielectric properties at 7 T were σ = 0.033 S/m and ε_r = 5.5 for breast fat, σ = 0.85 S/m and ε_r = 62 for breast gland, σ = 0.44 S/m and ε_r = 34 for transitional tissue, and σ = 0.64 S/m and ε_r = 50 for skin. For comparison to the approach of utilizing homogeneous phantoms, a hemispherical cylinder was also generated to represent the breast in the two extreme cases; that is, this geometry included a 1.5-mm skin layer with the remainder uniformly assigned either fatty or fibroglandular tissue.

The volumetric tissue data from the nine image-derived phantoms^[33] were imported into MATLAB^® (MathWorks, Natick, MA, USA). Since these voxel models only included heterogeneous tissue from a single breast, with the thorax modeled as uniform two-dimensional slabs of skin, fat, and muscle, modifications were necessary to enable seamless integration with the Ella body model. The voxels from the thorax slabs were removed and each phantom was duplicated for bilateral breast simulation. The breast phantoms were then enlarged using a nearest-neighbor interpolation routine to achieve a maximum 13.3-cm diameter in order to equally fill the RF coil. These dimensions were selected as a worst case to position the breast tissue 10 mm from the nearest coil conductor, as is the case with the actual RF coil. The resulting size of each breast phantom may be adjusted by providing the software routine with input parameters defining the desired dimensions. The finest-resolution Ella v1.3 voxel model, with 0.5-mm isotropic resolution, was imported into MATLAB for joining to the 0.5-mm breast phantoms. In accord with recent studies of MRI data segmentation between the breast and the pectoral muscle, the anterior extent of Ella’s chest wall remained flat and aligned on the coronal plane.^{[34, 35]} To position the breast phantoms on the Ella model before the fusing operation detailed below, two voxels were manually selected for centering the posterior coronal layer of all left and right breast phantoms. These locations were determined by orienting the base of each breast phantom on the inmost posterior coronal plane in Ella’s anterior thorax that solely overlapped breast tissue, fat, and skin, i.e., without encroaching on the pectoral fascia or adjacent muscle tissue. As a result, the medial extent of each breast phantom’s base was situated underneath Ella’s skin layer, whereas the lateral extent of the base extended in free space above the anterior skin layer, as shown in Figure 1a. The locations for positioning the breast phantoms may be revised by providing the software function alternate coordinates with respect to the body phantom.

Figure 1.

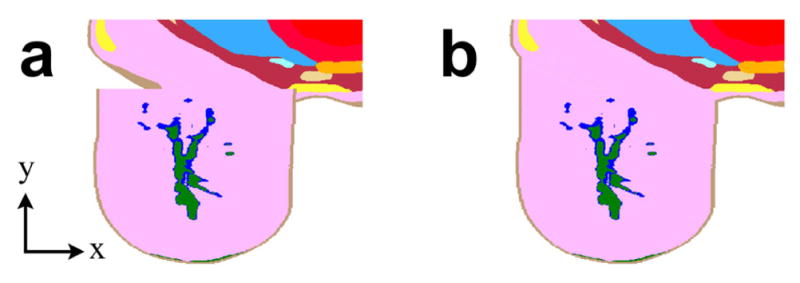
Renderings of breast phantom modification and fusion with whole-body voxel model

Two-dimensional axial mesh slices illustrate the (a) initial discontinuity and (b) subsequent joining of BI-RADS-a UW Phantom 1 and Ella, with skin tissue labelled brown, glandular tissue green, transitional tissue blue, and fatty tissues pink and yellow.

To automate integration of breast phantoms with a body model, we developed a software function to extrude and trim voxels from each breast phantom. First, voxels on the posterior coronal layer separated from Ella by free space were individually extruded toward the body model, penetrating the skin layer until encountering a voxel of adjacent tissue. By the same token, breast phantom voxels defined as skin that were situated inside the Ella phantom were removed from the phantom. Any remaining voxels from the heterogeneous breast phantoms that were co-located with the body model took meshing precedence in simulations, overwriting Ella voxels assigned skin, breast (fat), subcutaneous adipose tissue, and average infiltrated fat. These extrusion and trimming functions were applied independently for both the left and right breast positions. To illustrate this integration, the Ella voxel model fused with BI-RADS-b UW Phantom 2 is illustrated in Figure 1b.

2.2 Simulations

2.2.1 Mesh setup

All breast phantoms were exported in a file format to facilitate import into commercial FDTD software (XFdtd^® 7.4, Remcom, State College, PA, USA). A previously-described quadrature ¹H breast volume coil (as reported in Ref.^[19]) was positioned over each of the 11 right breast phantoms. As illustrated in Figure 2, the coil conductors were centered on the breast phantom and separated from the nearest skin voxel by 10 mm, as is the case in the actual coil former. The coil was driven by two sinusoidal feeds with appropriate 90° phase shifts to simulate quadrature operation. The frequency was set to 298 MHz to model operation at 7 T; the simulation frequency may be adjusted to model other field strengths, e.g., 128 MHz for 3 T. To account for the different impedances of the quadrature pair, current source feed amplitudes were adjusted to deliver equal input power to the two quadrature channels with less than 0.5% (−23 dB) variation. Cell gridding was adaptively set between 0.5 and 1.0 mm for the coil and breast phantom, and all curved conductor geometries utilized the software’s conformal meshing capabilities. The entire mesh was surrounded by a quarter-wavelength of free space padding cells and the boundary comprised seven perfectly matched layers. Simulations were run on a workstation with two linked NVIDIA GeForce GTX 780 GPU cards, each with 3 GB RAM and 2,304 cores, resulting in an average computational time of 73 minutes. Convergence was determined by transients dissipating to −50 dB deviation from the pure sinusoidal wave. Steady-state field data were calculated for all tissue voxels interior to the RF coil and globally on a central sagittal plane, and SAR data were calculated throughout the phantoms.

Figure 2.

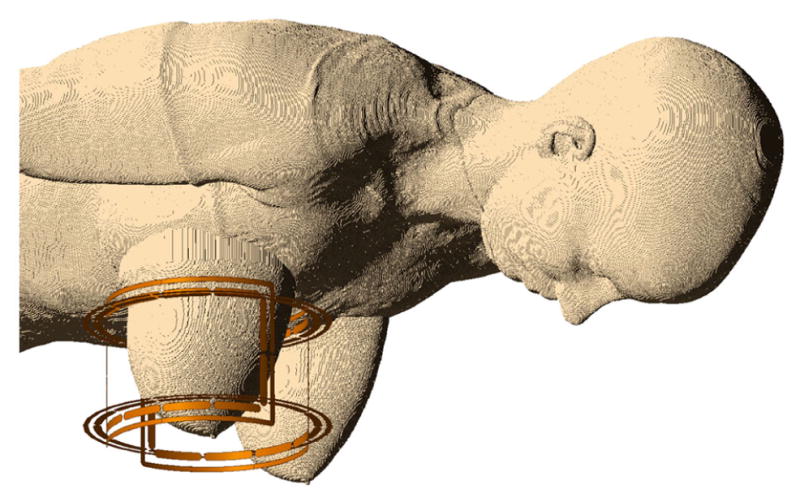
The Ella voxel model fused with BI-RADS-c UW Phantom 2, together surrounded by the quadrature volume breast coil

2.2.2 Analysis

Steady-state data output from FDTD simulations were imported into MATLAB for analysis. Mean transmit-field magnetic flux density (|B₁⁺|, with units T) was computed inside the volume RF coil; only tissue voxels were included and voxel size was taken into account during averaging. As MR scanners typically monitor SAR with respect to the transmit magnitude, all SAR results in this study were scaled to achieve an average |B₁⁺| of 1 μT at 100% duty cycle. Accordingly, the raw and 10-g spatial-average SAR for each case were gauged in watts per kilogram per squared microtesla (W/kg/μT²). To assess relative transmit coil power requirements as it relates to breast density, the net input (i.e., forward minus reflected) power required to achieve average |B₁⁺| of 1 μT was also noted.

3. Results

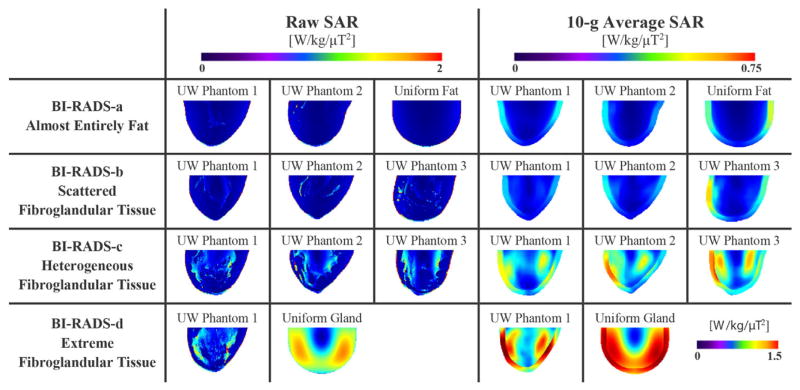
Figure 3 displays raw and 10-g average SAR plots on the central sagittal slice. As anticipated, the raw SAR plots reveal localized maxima in regions with higher conductivity and permittivity as compared to adipose tissue. Notably, all BI-RADS-c and -d phantoms resulted in maximum 10-g average SAR incorporating gland regions interior to the breast, whereas the maxima in all BI-RADS-a, -b, and uniform phantoms were in the skin layer on the breast surface. Furthermore, note the higher-density phantoms are more inclined to have internal SAR maxima as opposed to surface localization in the mostly-fatty cases.

Figure 3.

Raw and 10-g average SAR plots through the right breast’s central sagittal slice for the 11 phantom cases; extreme average SAR in the uniform glandular phantom required a separate scale bar for the single case

SAR data and coil efficiency for all cases are shown in Table 1. Compared to the mostly-fatty BI-RADS-a UW phantoms, the maximum local 10-g average SAR was threefold higher in the denser BI-RADS-d UW Phantom 1. Note the extreme case of a uniform cylinder of dense gland tissue resulted in almost fourfold the SAR of the otherwise worst-case BI-RADS-d UW Phantom 1. As expected with more substantial dielectric loads, coil transmit efficiency decreased with denser breast phantoms, as indicated by the increased power requirements to achieve an average |B₁⁺| of 1 μT throughout the breast.

Table 1.

Coil maximum 10-g average SAR and power efficiency data

Breast Phantom	Tissue Classification	Maximum 10-g Average SAR [W/kg/3T2]	Input Power [W] +
BI-RADS-a UW Phantom 1	almost entirely fat	0.30	0.63
BI-RADS-a UW Phantom 2	almost entirely fat	0.30	0.64
Uniform fat with skin layer	almost entirely fat	0.45	0.67
BI-RADS-b UW Phantom 1	scattered fibroglandular tissue	0.25	0.62
BI-RADS-b UW Phantom 2	scattered fibroglandular tissue	0.30	0.65
BI-RADS-b UW Phantom 3	scattered fibroglandular tissue	0.50	0.69
BI-RADS-c UW Phantom 1	heterogeneous fibroglandular tissue	0.61	0.72
BI-RADS-c UW Phantom 2	heterogeneous fibroglandular tissue	0.58	0.68
BI-RADS-c UW Phantom 3	heterogeneous fibroglandular tissue	0.69	0.72
BI-RADS-d UW Phantom 1	extreme fibroglandular tissue	0.89	0.75
Uniform gland with skin layer	extreme fibroglandular tissue	3.4	1.8

4. Discussion

The MATLAB functions developed for this study collectively facilitated 1) three-dimensional resizing, 2) placement with respect to the whole-body voxel model, and 3) voxel extrusion and subtraction to fuse all peripheral breast phantoms with the whole-body voxel model. In this study, the functions were performed on breast phantoms to illustrate the utility of fusing anatomical voxel models. The software may be applied to other regions, e.g., tumors, patient-specific features, or richly-detailed extremity phantoms. As an added benefit of this software method, the fusing operation does not modify the body model itself, nor require distribution with the body model. Therefore, any resulting secondary phantoms may be independently distributed under separate licensing terms. The software developed for this work is open-source, publicly-available in the GitHub repository, and linked to the file exchange at MATLAB Central.^[36] The bundled readme documentation details the function names and descriptions, input/output variables, and recommended execution sequence.

The simulation study findings demonstrated significant variation among breast phantoms with varying levels of fat and fibroglandular breast tissues. During RF transmission, breast tissues with higher electrical conductivity and permittivity values, i.e., skin and glands, intensify the electric field and consequently are subject to greater localized SAR. For instance, a dense heterogeneous (BI-RADS-d) breast model produced threefold higher maximum 10-g average SAR as compared to mostly fatty breasts (BI-RADS-a). The geometric phantoms representing homogeneous tissue illustrated the expected RF field interference patterns in a uniform, electrically large dielectric.^[37] The intensity of this effect was especially apparent with the homogeneous gland tissue phantom and its symmetric SAR distributions as shown in Figure 3; thus, the suitability of uniform phantoms for modeling in vivo breast scans is problematic. This study’s findings indicate simulating the breast as predominantly-fatty tissue can considerably underestimate the potential for tissue heating in women with extensive fibroglandular breast tissue. This line of reasoning suggests to conservatively characterize SAR for regulatory compliance, simulation analyses of breast coils should incorporate a heterogeneous breast model largely consisting of fibroglandular tissue.

To facilitate a straightforward comparison, this study assumed equivalent breast sizes and positioning within the RF coil structure. Future research may provide further insight into the effects on SAR with varying breast size and positioning. This study was also limited to a single validated coil design; simulations featuring other RF coils may be informative. Finally, this simulation study quantified SAR, which is currently the standard metric for safety regulatory compliance. Thermometry studies may further complement the simulated SAR data for predicting tissue temperature rise.

This work addressed two problems relevant to modeling the breast accurately—the need to augment existing body voxel models to account for prone imaging and to use heterogeneous breast tissue models. The software developed to fuse breast and body phantoms is publicly available and may be employed to join other anatomical features. The ensuing breast MRI simulation study presented herein incorporated several high-resolution, anatomically-correct breast phantoms. Simulation results indicate breasts with predominantly fibroglandular tissue are susceptible to significantly increased SAR as compared to breasts mostly composed of fat.