Moonshine: Diurnally varying hydration through natural distillation on the Moon, detected by the Lunar Exploration Neutron Detector (LEND)

Abstract

The Lunar Exploration Neutron Detector (LEND), on the polar-orbiting Lunar Reconnaissance Orbiter (LRO) spacecraft, has detected suppression in the Moon’s naturally-occurring epithermal neutron leakage flux that is consistent with the presence of diurnally varying quantities of hydrogen in the regolith near the equator. Peak hydrogen concentration (neutron flux suppression) is on the dayside of the dawn terminator and diminishes through the dawn-to-noon sector. The minimum concentration of hydrogen is in the late afternoon and dusk sector. The chemical form of hydrogen is not determinable from these measurements, but other remote sensing methods and anticipated elemental availability suggest water molecules or hydroxyl ions. Signal-to-noise ratio at maximum contrast is 5.6σ in each of two detector systems. Volatiles are deduced to collect in or on the cold nightside surface and distill out of the regolith after dawn as rotation exposes the surface to sunlight. Liberated volatiles migrate away from the warm subsolar region toward the nearby cold nightside surface beyond the terminator, resulting in maximum concentration at the dawn terminator. The peak concentration within the upper ~1 m of regolith is estimated to be 0.0125 ± 0.0022 weight-percent water-equivalent hydrogen (wt% WEH) at dawn, yielding an accumulation of 190 ± 30 ml recoverable water per square meter of regolith at each dawn. Volatile transport over the lunar surface in opposition to the Moon’s rotation exposes molecules to solar ultraviolet radiation. The short lifetime against photolysis and permanent loss of hydrogen from the Moon requires a resupply rate that greatly exceeds anticipated delivery of hydrogen by solar wind implantation or by meteoroid impacts, suggesting that the surface inventory must be continually resupplied by release from a deep volatile inventory in the Moon. The natural distillation of water from the regolith by sunlight and its capture on the cold night surface may provide energy-efficient access to volatiles for in situ resource utilization (ISRU) by direct capture before volatiles can enter the surface, eliminating the need to actively mine regolith for volatile resource recovery.

1. Introduction

The existence of mineral hydration at low latitudes on the lunar surface was announced in mutually corroborating reports from three spacecraft in September 2009 (Pieters et al., 2009; Sunshine et al., 2009; Clark, 2009). The detections used near-infrared spectroscopy of reflected sunlight, measured by the Moon Mineralogy Mapper (M³) on the Indian spacecraft Chandrayaan-1; the Visible and Infrared Mapping Spectrometer (VIMS) on Cassini from its 1999 flyby of the Earth–Moon system; and the High Resolution Instrument–Infrared (HRIIR) spectrometer on Deep Impact. Water concentration estimated from these observations ranges up to about 0.3 weight-percent (wt%). Fig. 1 displays an example of the 2.8 μm hydration feature in the Moon’s disc-integrated spectrum measured during the May 2008 transit of Earth by the Moon from Deep Impact (Livengood et al., 2011). Sunshine et al. (2009) used Deep Impact data from December 2007 and June 2009 lunar flybys to investigate the distribution of hydration and found the greatest hydration near the terminators and least near the subsolar point, implying a diurnal cycle of dehydration and rehydration. This deduction is supported by nadir-pointed ultraviolet spectroscopy with the Lyman-Alpha Mapping Project (LAMP) instrument on the Lunar Reconnaissance Orbiter (LRO), which shows a local minimum in hydration at noon, increasing approximately symmetrically toward either terminator (Hendrix et al., 2012). The presence of water in quantities that can be detected remotely is potentially valuable for in situ resource utilization (ISRU) in future space exploration, as well as for understanding surface processes on airless bodies throughout the Solar System and beyond.

Fig. 1.

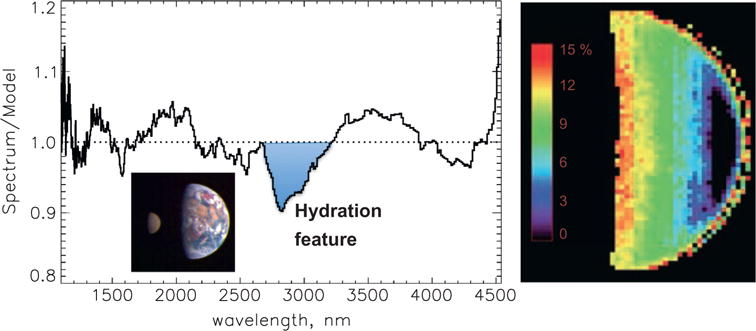
Spectroscopic detection of lunar mineral hydration. (Left) 2.8 μm feature in disc-integrated 1–5 μm spectrum divided by a model for reflectance plus thermal emission, from the pictured observation in a May 2008 transit of Earth by the Moon (Livengood et al., 2011). (Right) Map of lunar hydration feature band depth in June 2009, looking down on the north pole, showing strongest hydration at terminator; reprinted from Sunshine et al. (2009).

Independent measurements are essential to determine whether the enhanced hydration signature at the terminator is only an optical effect from grazing illumination, and whether the hydroxyl or water goes deeper than the illuminated surface. The Lunar Exploration Neutron Detector (LEND) on LRO can fulfill this role using a very different remote-sensing technique (Mitrofanov et al., 2010a; Vondrak et al., 2010), by measuring the flux of neutrons from the lunar surface. Neutron remote-sensing is insensitive to solar illumination and probes approximately a meter deep into the lunar surface, enabling LEND to test whether water/hydroxyl observed in hydration is more than a thin surface layer and to explore its concentration in the lunar surface at all times of the lunar day and night.

2. Observations and data reduction

LRO entered a circular polar orbit to map the Moon in September 2009 at an altitude of about 50 km, carrying LEND to determine the spatial distribution and quantity of hydrogen-bearing volatiles in the regolith. Possible water deposits within permanently shadowed regions (PSRs) near the Moon’s poles have been a target for exploration throughout the space age (e.g., Watson et al., 1961), and the polar regions are the primary target for LEND investigations (Sanin et al., 2012; Mitrofanov et al., 2010b). Investigating PSRs requires techniques to quantitatively detect hydrogen concentrations without direct sunlight. The natural emission of neutrons from the lunar surface probes anywhere, at any local time, within the upper ~1 m of the regolith, independent of the Sun. The lunar surface beneath the spacecraft rotates through the full range of longitude in half a month, and through the full range of local time in six months. More than two years of LEND data, from September 2009 through December 2011, provides enough data to enable LEND to address the variation of water at equatorial latitudes as a function of lunar local time. In December 2011, LRO moved to a more eccentric orbit that conserves fuel and favors the south pole but that is less conducive to measurements in the equatorial region. Data from the uncollimated epithermal neutron detector end in May 2011, when there was an instrument anomaly. The collimated detector has continued to collect data after the anomaly, with reduced sensitivity due to switching off two out of four detector elements.

LEND measures the leakage flux of neutrons that are produced by galactic cosmic-ray (GCR) impacts on lunar regolith materials. LEND integrates samples over intervals of 1 s, every ~1.6 km along-track (~0.05° latitude). The escaping neutron population is measured in thermal (E < 0.4 eV), low-energy epithermal (LEE, E = 0.4 eV–1 keV), and fast or high-energy epithermal (HEE, E > ~1 keV) neutron energy ranges, achieving energy discrimination due to screening by neutron-absorbing materials surrounding the detectors. Hydrogen strongly moderates the energy of neutrons in the epithermal range, suppressing epithermal neutron flux by degrading particle energy into the thermal range in correspondence to the abundance of hydrogen-bearing volatiles in the regolith (e.g., H, H₂, OH, H₂O). The Lunar Prospector Neutron Spectrometer (LPNS) used similar detectors to demonstrate in 1998 the ability to evaluate hydrogen in the polar regions at about 100 parts per million by weight (ppmw), or ~0.1 wt% water-equivalent hydrogen (WEH; Feldman et al., 1998, 1999). Early results from LEND located hydrogen in a PSR within Cabeus Crater near the south pole (Mitrofanov et al. (2010b), confirmed emphatically by the Lunar Crater Observation and Sensing Satellite (LCROSS) mission. The LCROSS mission launched with LRO and plunged the spent launch vehicle upper stage into the Cabeus PSR in October 2009 to eject a plume that included water, molecular hydrogen, and other volatiles that were observed by the LCROSS spacecraft and by instruments on LRO (Colaprete et al., 2010; Hurley et al., 2012).

LEND carries two detector systems sensitive to epithermal neutrons, the uncollimated Sensor for Epithermal Neutrons (SETN) and the Collimated Sensor for Epithermal Neutrons (CSETN), in which the detectors are housed inside a collimator structure that restricts the detector field of view on the lunar surface. Epithermal neutron detection rates measured by SETN and by CSETN are mapped in Fig. 2 with 2° sampling in latitude and longitude, composed from numerous 1-s integration intervals over the life of the mission. The SETN detector is mounted on the outside of the CSETN collimator housing at its nadir end (Mitrofanov et al., 2010a), which partially obstructs the horizon-to-horizon field of view on one side at high off-nadir angle. This obstruction is inconsequential to the effective field of view (FOV) of an uncollimated neutron detector like SETN, as can be demonstrated using results from the earlier LPNS instrument. LPNS mapped lunar neutron emission from an altitude of 30 km for 211 days (Maurice et al., 2004). Half the LPNS epithermal neutron signal was determined to originate within ~22 km of the subspacecraft point, an FOV of ~1.4° diameter in latitude and longitude at the equator. This FOV equates to a nadir-to-edge opening angle of ~36° at the spacecraft, much less than the nadir-to-horizon angle of 79° from 30 km altitude. The angular increase in path length through the regolith for escaping neutrons from buried sources results in anisotropic emission that is maximum at the local vertical from the surface and falls to zero at grazing angle on the horizon. The emission anisotropy results in a relatively narrow effective FOV that applies to LEND as well as it applied to the earlier LPNS instrument since it is due to the physics of the emission process, not the detection process. At the LRO mapping-orbit altitude of 51 km average, the comparable SETN field of view scales to ~2.4° in latitude–longitude extent at the equator. The effective opening angle of ~36° from nadir is much less than the nadir-to-horizon angle of 76.4°. As a result, the inner 50% of the SETN FOV is unobstructed and only a small part of the outer 50% can be obstructed, thus the FOV is not vignetted to a significant extent. The field of view of CSETN combines an uncollimated component with a collimated component that has a narrower field of view (Litvak et al., 2012a; Mitrofanov et al., 2010a). The uncollimated component comes from neutrons that penetrate the imperfectly opaque collimator wall with an FOV roughly comparable to SETN. This work uses all lunar-sourced neutrons (see below) that are detected in SETN and CSETN and thus makes no attempt to distinguish neutrons within collimation from neutrons out of collimation. The FOV of each detector system is much smaller than regions of interest for the present work, which span tens of degrees in latitude and longitude.

Fig. 2.

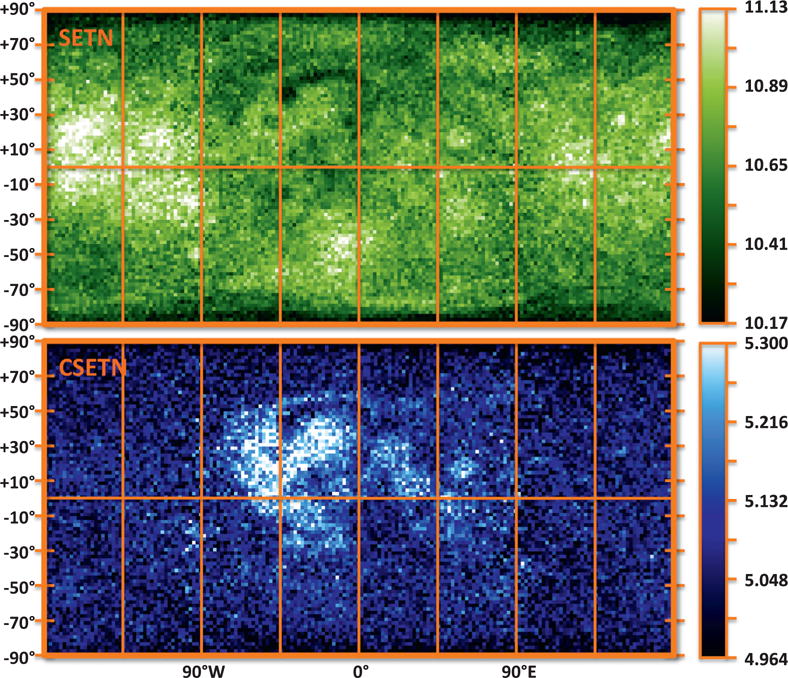
Maps of lunar epithermal neutron flux measured by LEND uncollimated detector SETN (upper) and collimated detector CSETN (lower), with corresponding color bars in units of neutron counts per second. Background pedestal signal has not been subtracted from the neutron count rates displayed here. Differing morphology is due to increased relative contribution in CSETN from higher-energy epithermal (HEE) neutrons that penetrate the collimator wall (Mitrofanov et al., 2011).

SETN and CSETN use identical ³He-filled gas proportional counter detectors, one in SETN and four in CSETN, although not all four CSETN detector elements were in operation at all times. Cadmium foil that encloses SETN absorbs most thermal-energy neutrons (E < 0.4 eV), permitting only neutrons of greater energy to reach the detector, while detection sensitivity diminishes with increasing energy to about 1/10th of maximum by about 1 keV and is negligible by ~100 keV (Litvak et al., 2012a), thus restricting sensitivity in SETN to the low-energy epithermal (LEE) range. The four CSETN detectors view the lunar surface through cadmium foil in otherwise open barrels of a collimator structure (Mitrofanov et al., 2010a). Neutrons that reach the CSETN detectors out of collimation are moderated in energy by passing through the polyethylene and boron-10 composition of the collimator wall. Even though the CSETN detectors have the same intrinsic sensitivity limits as the SETN detector, the energy spectrum sensed by CSETN includes a substantial fraction of high-energy epithermal (HEE) neutrons that originate from the lunar surface at energy greater than the ³He detector energy cut-off at ~1 keV before being moderated into the sensitivity range of the detector. As a result, the morphology of mapped lunar neutron emission measured by CSETN differs from SETN (Fig. 2) and resembles a map of high energy neutron emission (Litvak et al., 2012b; Eke et al., 2012). Not all four CSETN detectors were in operation at all times, and sensitivity is not perfectly uniform across all four detectors. Sensitivity differences between the detector elements are corrected by dividing each detector’s instantaneous signal by its time-average calibrated signal (minus estimated background) and multiplying by the time-average signal averaged over all four detector elements so that the detectors agree on a single time-average signal over the span of the data used here. The reported CSETN count rates in this work are scaled to be equivalent to four operational CSETN detectors to be consistent with pre-flight and early-mission work in which all four detector elements were in use.

Variations in the sensitivity of individual detectors and in the GCR flux that produces lunar neutrons and spacecraft-generated (background) neutrons are compensated in routine data reduction (Litvak et al., 2012a). The sensitivity of the proportional-counter detectors varies as a result of station-keeping maneuvers by the LRO spacecraft, conducted approximately every two weeks during the circular-orbit phase of the mission at times when the normal to the spacecraft orbit plane was approximately aligned with the Earth–Moon axis so that the spacecraft could communicate with the ground station at all orbital phases. Maneuvers thus took place when the spacecraft orbit was near longitudes ±90°. The LEND detectors are switched off for maneuvers to protect against electrical discharges in the high-voltage power supply caused by exhaust gases from the motor. The effect of these inactive periods can be perceived as a slight increase in noise on the mapped data at ±90° longitude in Fig. 2. These power-switching events vary in lunar local time since the orientation of the spacecraft orbit is fixed with respect to a sidereal reference frame and not the Moon’s synodic period. Three months after a station-keeping maneuver with the spacecraft orbiting in the dawn–dusk plane, a station-keeping event would occur with the spacecraft in the noon–midnight plane.

The LEND proportional counters exhibit charging behavior after switch-on, appearing as a gradual increase in sensitivity over a period of weeks that asymptotically approaches ~27% greater sensitivity than at switch-on in the example shown by Litvak et al. (2012a). This sensitivity variation is a shared property of all the LEND ³He detectors and appears consistent with surface charging on the insulated stand-off that supports the central electrode within the detector chamber, increasing the active length of the detector by roughly the same proportion in each detector. The variation in sensitivity is modeled as an exponential function, which describes the performance of resistive–capacitive circuits. Sensitivity in each individual LEND detector is calibrated independently using data acquired from a narrow region around each lunar pole, representing a repeatable measurement of neutron flux (Litvak et al., 2012a; Boynton et al., 2012). Calibrating by this standard also corrects for any long-term change in detector sensitivity, as well as secular variability in the lunar neutron leakage flux. Since lunar neutrons derive from galactic cosmic ray interactions with the lunar regolith, and background neutrons derive from GCR interactions with spacecraft materials, the total signal in the detector scales uniformly with changes in GCR flux. GCR flux, in turn, depends on heliospheric properties that change over the solar activity cycle. Since LRO took station during solar minimum and the mission has extended to the onset of solar maximum, calibration for changes in the GCR flux is a necessity.

Numerical modeling of the emergent LEE neutron flux from hydrogen-free (‘dry’) vs. hydrogenated (‘wet’) regolith shows that for modest concentrations, the quantity of hydrogen, [H], is linearly related to the inverse of the epithermal neutron detection rate as

$$[\mathrm{H}]=\Gamma (C_0/C_1-1),$$ (1)

where C₀ is the epithermal neutron detection rate from dry regolith, C₁ is the partially suppressed epithermal neutron detection rate from wet regolith, and Γ is a calibration constant with a value of ~2100 ppmw hydrogen, or ~1.91 wt% WEH, or ~3.61 wt% hydroxyl-equivalent hydrogen (HEH). Values for Γ come from fitting Monte Carlo model calculations such as those reported by Mitrofanov et al. (2010a,b) that assume hydrogen distributed uniformly with depth. Inverting expressions used by Feldman et al. (1998), based on similar modeling, retrieves Γ = 1.64 wt% WEH (~1800 ppmw H), suggesting 14% less hydrogenation for the same observed epithermal neutron contrast. The calibration factor is uncertain due to assuming composition of the regolith and the vertical distribution of hydrogen within the regolith column sensed by the detected neutron population. Lawrence et al. (2011) have shown that the vertical distribution of hydrogen can affect the energy spectrum of neutron flux suppression, particularly with hydrogen placed near the surface. The contribution of HEE neutrons to the population sensed by CSETN thus may require a calibration different from the LEE neutron calibration of SETN. We use the same standard calibration model for qualitative comparisons and consider effects from alternative distributions of hydrogen with depth. Regardless of the relevant calibration factor, suppressed neutron flux is an observable property that signals the presence of hydrogen in quantity proportional to the degree of suppression.

Applying the calibration expression in Eq. (1) requires subtracting spacecraft-sourced background signal from the total signal in each detector to reveal the lunar epithermal neutron component. Spacecraft-sourced neutrons account for ~8% of total signal in the SETN detector (Litvak et al., 2012a) with another ~3% of signal due to out-of-band contributions from lunar-sourced thermal neutrons. Thermal neutron flux is measured by another LEND detector and also is subtracted, leaving just the signal component due to lunar epithermal neutron flux. The spacecraft-sourced neutron background in the CSETN detector has been estimated by Litvak et al. (2012a) to be about 48% of the total signal, based on measurements during cruise to the Moon. An alternative estimate from fitting mapped data suggests a greater background value at 57 ± 5% of total signal (unpublished work by the present authors), within uncertainty of an estimate of 54% derived independently by Eke et al. (2012). The exact choice of background does not affect the sensitivity to contrast in comparing the signal from two regions, which depends only on the difference in signal, but the background choice affects the quantitative calibration, which depends on the ratio of the net signal in the two regions compared. For this work, we assume the 57% background value for CSETN. Alternatively, assuming the smallest of the available background estimates (48%) decreases the estimated hydrogen concentrations to 81% of values determined using the preferred background value, multiplying the uncertainties by a similar factor. If the CSETN background value were assumed to be 1-sigma greater than nominal (62% background), it would yield a retrieved hydrogen concentration 113% of the value from the nominal calibration. The uncertainty in the background for SETN is minor compared to the total signal in this detector, with comparable minor accuracy uncertainty in calibrated hydrogen concentration. The primary quantitative results for this work are drawn from the SETN detector, for which the uncertainty in background is of only minor consequence.

The profile of variations in epithermal neutron flux as a function of time of day near the equator is constructed by organizing measurements of neutron detection rate according to lunar local time. The local time of day is determined by the difference in subspacecraft longitude relative to subsolar longitude: 12:00 noon at zero difference; 06:00 at 90° difference (dawn), 18:00 at 90° difference (dusk), 00:00 at 180° difference (midnight). Each sample of neutron flux is distinguishable by four labels: subspacecraft lunar latitude and longitude, local time, and spacecraft event (clock) time. We combine neutron detections within 30° latitude north or south of the equator that fall within intervals of five minutes of local time (1.25° of lunar rotation), summed over all sampled longitudes measured in that local time interval and over the period of the data set, from mid-September 2009 through December 2011. The choice of ±30° latitude is somewhat arbitrary, based on balancing signal-to-noise, which favors selecting a wide interval, against restricting insolation of the surface to be most uniform, which favors selecting a narrow interval. We have tested both narrower (±20°) and broader intervals (±40°), with similar outcome. The local time interval is short enough that it samples diurnal variability at a fine scale, and long enough that there are no gaps in local time sampling. Shorter intervals are equally effective for the statistical methods used in this work, but would have resulted in more clutter within the graphics. Significantly longer intervals would be less well-suited to estimating uncertainties by population statistics due to an insufficient number of samples.

Measurements of epithermal neutron flux are accumulated by combining neutron detection samples, n_ijkl, that occur within the measurement interval τ_ijkl, where the discrete subscripts i, j, k, l, label sampled values of latitude (i), longitude (j), local time (k), and clock time (l). The length of the measurement interval τ_ijkl is 1 s or zero depending whether the particular detector is active, which is relevant to combining the four individual detectors within CSETN. The near-equatorial neutron detection count rate C_K in a specific local-time interval labeled by the index K is accumulated as the sum of neutron detections n_ijkl (after subtracting the estimated background from each sample), summed over samples that fall within the latitude range ±30°, summed over all sampled longitudes, within the 5-min range of local time centered on K, summed over all sampled events within the duration of the data set, divided by the corresponding sum over total sample measurement time:

$$C_K={\displaystyle \sum _{i_0}^{i_1}{\displaystyle \sum _j{\displaystyle \sum _{k_0}^{k_1}{\displaystyle \sum _l{n}_{\mathit{ijkl}}}}}}/{\displaystyle \sum _{i_0}^{i_1}{\displaystyle \sum _j{\displaystyle \sum _{k_0}^{k_1}{\displaystyle \sum _l{\tau }_{\mathit{ijkl}}}}}}.$$ (2)

The limits on the summations over latitude (i) and local time (k) indicate that these quantities are restricted to specific intervals, whereas the unrestricted summations over longitude (j) and clock time (l) indicate that they are drawn from all samples in the data set that meet the restrictions on latitude and local time.

The Earth–Moon system moves ~29° in orbital longitude every synodic month. As a result, a patch of the lunar surface appears beneath the spacecraft at 1.94 h earlier in local time in each lunation. The distinct pattern of neutron emission flux that is fixed to lunar geography (Fig. 2) results in a periodic variation in the diurnal neutron flux, with a period of 1.94 h of local time and 12.37 periods per lunar day (see Fig. 6). We use the mapped lunar neutron emission rate for each detector to compensate for the systematic variability of the neutron flux as a function of latitude and longitude, scaling down the detection rate in regions of high intensity and scaling it up in regions of low intensity. The detection count rate C_IJ at each latitude/longitude pixel position on the map is accumulated as a sum over all local times and all clock times that the spacecraft visited that location, divided by the total integration time of all samples at that location:

$$C_{IJ}={\displaystyle \sum _{i_0}^{i_1}{\displaystyle \sum _{j_0}^{j_1}{\displaystyle \sum _k{\displaystyle \sum _l{n}_{\mathit{ijkl}}}}}}/{\displaystyle \sum _{i_0}^{i_1}{\displaystyle \sum _{j_0}^{j_1}{\displaystyle \sum _k{\displaystyle \sum _l{\tau }_{\mathit{ijkl}}}}}}.$$ (3)

The limits on the summation over latitude (i) and longitude (j) indicate that these quantities are restricted to an interval centered on specific latitude/longitude coordinates labeled by the subscripts I and J, whereas the unrestricted summations over local time (k) and clock time (l) indicate that they are drawn from all samples in the data set at that position coordinate. A flat-fielding function F_IJ, normalized to average value unity, is constructed from the mapped count rates C_IJ by dividing by the average value of C_IJ. The individual count measurements n_ijkl that are used to compute the count rate C_K as a function of the local time K can then be divided by the flat-fielding function to counter the spatial dependence of the measured signal prior to combining the measurements:

$$C_K={\displaystyle \sum _{i_0}^{i_1}{\displaystyle \sum _j{\displaystyle \sum _{k_0}^{k_1}{\displaystyle \sum _l(n_{\mathit{ijkl}}/F_{IJ})}}}}/{\displaystyle \sum _{i_0}^{i_1}{\displaystyle \sum _j{\displaystyle \sum _{k_0}^{k_1}{\displaystyle \sum _l{\tau }_{\mathit{ijkl}}}}}},$$ (4)

where the value of the discretely-mapped flat-field function F_IJ is selected from the nearest neighbor to each latitude–longitude coordinate ij using the 2° per pixel map displayed in Fig. 2. If there were no variability in the neutron flux with lunar local time, then each measurement of neutron flux, n_ijkl, would be an individual instance of measuring the same underlying count rate C_IJ. Normalization by the flat-field function F_IJ in Eq. (4) would then result in each diurnally discrete sample of the count rate, C_K, being a reproduction of the global mean value of C_IJ plus stochastic noise.

Fig. 6.

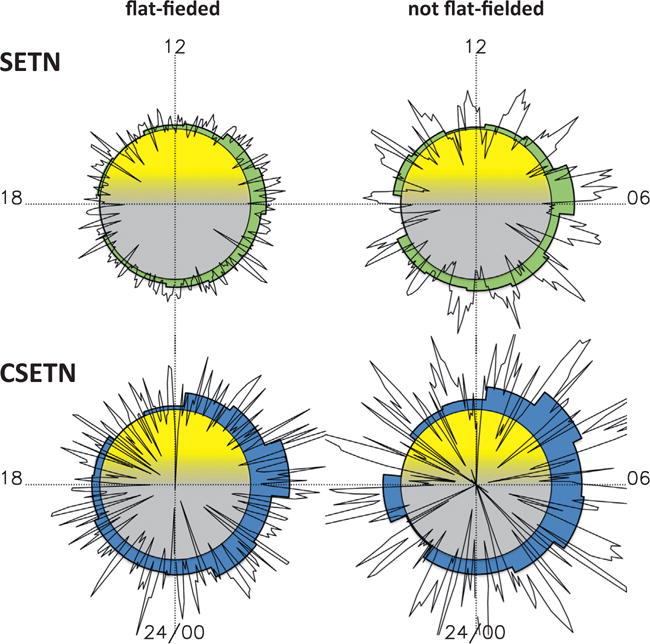
Effect of flat-fielding the neutron detection rates measured by LEND. (Left) Polar plot of hydrogen fraction in regolith, identical to Fig. 4, repeated here for comparison. (Right) Results from applying identical data-processing but without flat-fielding (Eq. (4)). The results show the same asymmetry toward more hydrogen at the dawn limb in both cases, but the non-flat-fielded data feature an additional periodic variation that is corrected by the flat-fielding operation.

The noise on the individual C_K values can be estimated using either Poisson statistics based on measured total neutron count in each measurement, or using population statistics derived from the actual distribution of C_K values within bins. Population statistics offers the benefit of sensitivity to undiagnosed contributions to noise – for example, the discrete character of the flat-fielding function means that each measurement n_ijkl is normalized by a value that does not perfectly represent the true underlying flux at that particular spatial coordinate. There may also be time-dependent variability in the individual measurements n_ijkl from which the maps are composed, such as defects in correcting variability in detector sensitivity or cosmic ray intensity, that map differently into the local-time binning of the data than the selenographic map. Population statistics enable capturing these effects as additional variability in the measured detection rate within broad bins of local time. Population statistics for the diurnally dependent count rate C_K are determined by binning together groups of measurements that are contiguous in local time to evaluate the mean and standard error of the mean, reported in the tables and displayed in Fig. 3 and following. Test calculations show that the uncertainty estimated as standard error of the mean is substantially greater than the uncertainty estimated from Poisson statistics by a factor of about 1.5 to two. The figures display C_K binned in intervals of five minutes of local time. The uncertainties estimated from this binning are confirmed by conducting the same calculations using finer binning, neglecting skipped values of local time at which there are no measurements. The uncertainties reported in the tables employ 1-min binning, essentially identical to uncertainties estimated from 5-min binning.

Fig. 3.

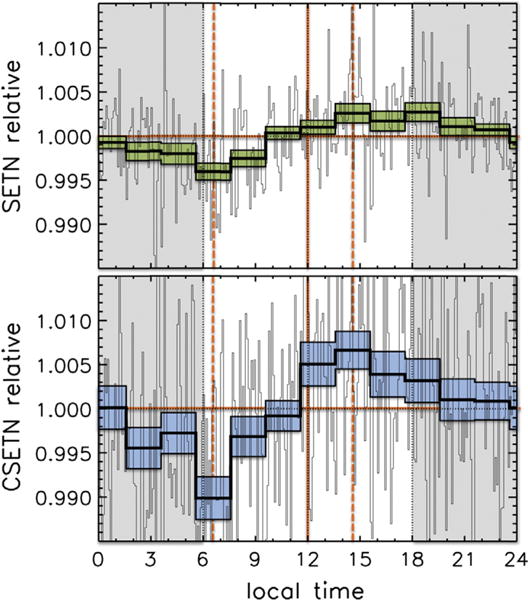
Equatorial neutron detection rate varies as a function of local time for SETN (upper) and CSETN (lower) epithermal neutron detectors, relative to the median. Gray regions at left and right indicate measurements during lunar night. The light-toned rapidly-varying histogram shows flux measured in intervals of 5 min of lunar local time. The bold histogram and shaded envelope show mean and standard error of the mean in two-hour intervals of lunar local time. Greatest flux suppression is near the dawn terminator, slightly biased toward the day side.

3. Results

Fig. 3 displays the flat-fielded neutron detection rates as a function of local time for each of the two LEND epithermal neutron detector systems, showing both the noisy distribution of five-minute sampled count rates as well as the mean and uncertainty of the detection rate in broad two-hour intervals. The center-time for the two-hour samples was selected by adjusting in increments of five minutes to maximize peak-to-peak contrast in the CSETN detector, applying the same sampling intervals to SETN. Maximum flux suppression is found in the CSETN bin centered at 06:35 local time and least flux suppression at 14:35, and similar maximum and minimum times for SETN. Tables 1 and 2 record the measured detection rates for lunar epithermal neutrons in the two-hour bins, the total integration time in each bin, and the estimated concentration by mass fraction of hydrogen or water estimated by applying Eq. (1) in each bin.

Table 1.

Uncollimated epithermal neutron detector (SETN) signal binned in local time.

Local time (24 h)	SETN (cps)	Integrated time (s)	[H] (ppmw)	WEH (wt%)
0:35	9.539 ± 0.007	1.23 × 106	6.7 ± 2.0	0.0060 ± 0.0018
2:35	9.530 ± 0.010	0.82 × 106	8.7 ± 2.6	0.0078 ± 0.0023
4:35	9.527 ± 0.011	0.99 × 106	9.4 ± 2.8	0.0084 ± 0.0025
6:35	9.507 ± 0.009	0.89 × 106	13.8 ± 2.4	0.0125 ± 0.0022	Apollo
8:35	9.522 ± 0.009	0.92 × 106	10.5 ± 2.4	0.0094 ± 0.0022	Apollo
10:35	9.550 ± 0.007	1.34 × 106	4.2 ± 2.0	0.0038 ± 0.0018
12:35	9.556 ± 0.007	1.19 × 106	2.9 ± 2.0	0.0026 ± 0.0018
14:35	9.571 ± 0.010	0.76 × 106	−0.4 ± 2.6	−0.0004 ± 0.0023
16:35	9.563 ± 0.011	0.92 × 106	1.3 ± 2.8	0.0012 ± 0.0025
18:35	9.572 ± 0.010	0.91 × 106	−0.7 ± 2.6	−0.0006 ± 0.0023
20:35	9.557 ± 0.010	0.99 × 106	2.7 ± 2.6	0.0024 ± 0.0023
22:35	9.553 ± 0.006	1.41 × 106	3.6 ± 1.9	0.0032 ± 0.0017
Mean	9.546 ± 0.002	12.37 × 106	5.2 ± 0.7	0.0046 ± 0.0006

Local time = midpoint of two-hour interval of local time on Moon.

“Apollo” indicates the local time intervals when Apollo astronauts were on the ground and collected samples.

Reference count rate = 9.569 ± 0.006 cps, uncertainty-weighted mean of maximum three two-hour intervals.

Table 2.

Collimated epithermal neutron detector (CSETN) signal binned in local time.

Local time (24 h)	CSETN (cps)	Integrated time (s)	[H] (ppmw)	WEH (wt%)
0:35	2.108 ± 0.005	4.55 × 106	11.1 ± 5.8	0.0100 ± 0.0052
2:35	2.098 ± 0.005	3.12 × 106	21.3 ± 5.8	0.0191 ± 0.0052
4:35	2.102 ± 0.005	3.26 × 106	17.2 ± 5.8	0.0155 ± 0.0052
6:35	2.086 ± 0.005	2.78 × 106	33.6 ± 5.9	0.0302 ± 0.0053	Apollo
8:35	2.101 ± 0.005	3.56 × 106	18.2 ± 5.8	0.0164 ± 0.0052	Apollo
10:35	2.106 ± 0.004	5.13 × 106	13.1 ± 4.9	0.0118 ± 0.0044
12:35	2.118 ± 0.005	4.45 × 106	1.0 ± 5.7	0.0009 ± 0.0052
14:35	2.121 ± 0.004	2.90 × 106	−2.0 ± 4.9	−0.0018 ± 0.0044
16:35	2.116 ± 0.006	3.00 × 106	3.0 ± 6.6	0.0027 ± 0.0060
18:35	2.114 ± 0.005	2.83 × 106	5.0 ± 5.7	0.0045 ± 0.0052
20:35	2.110 ± 0.005	4.06 × 106	9.1 ± 5.8	0.0082 ± 0.0052
22:35	2.109 ± 0.004	5.32 × 106	10.1 ± 4.9	0.0091 ± 0.0044
Mean	2.1078 ± 0.0014	44.97 × 106	11.3 ± 1.6	0.0102 ± 0.0014

Local time = midpoint of two-hour interval of local time on Moon.

“Apollo” indicates the local time intervals when Apollo astronauts were on the ground and collected samples.

Reference count rate = 2.119 ± 0.003 cps, uncertainty-weighted mean of maximum three two-hour intervals.

The maximum epithermal neutron flux measured by SETN covers a period of about six hours of local time, starting at 14:35 (bin center). The CSETN signal has a unique maximum, coinciding with the beginning of the plateau in SETN signal. The calibrated hydrogen/water concentration reported in the tables is computed using the average of the three maximum-signal bins in each detector as an approximation to the epithermal neutron flux from unsuppressed regolith, either hydrogen-free or at least hydrogen-minimum. Contrast between the most flux-suppressed interval at 06:35 and the maximum flux estimated in this way is 5.6 times uncertainty in both detector systems. Propagation of error in the tabulated hydrogen and hydration values computed using Eq. (1) incorporates the measurement uncertainty in each bin as well as the uncertainty in the dry-regolith reference flux. The observed distribution implies that the least-hydrogenated regolith appears in the mid- to late-afternoon while the most-hydrogenated regolith appears on the dayside of the dawn terminator. This distribution is partially consistent with observed mineral hydration (Hendrix et al., 2012; Sunshine et al., 2009), which showed peak hydration symmetrically near both dawn and dusk terminators and minimum hydration at noon. Minimal neutron suppression at the dusk terminator suggests that the total column of hydrogenated regolith at this local time is very small (Fig. 4), even though hydration in a thin surface layer may be comparable to the corresponding region near the dawn terminator.

Fig. 4.

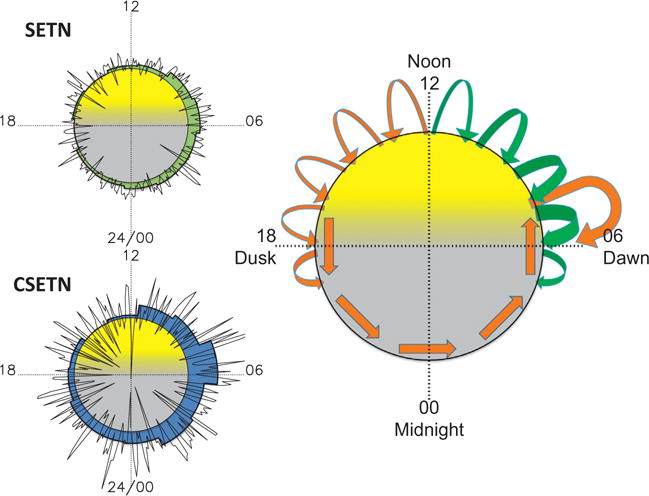
Hydrogen distribution with local time, and sketch of lateral transport processes; see tables for quantitative values. (Upper left) 5-min sampled hydrogen concentration as a function of local time, determined from SETN detector, two-hour binned estimates shown by green-shaded region. (Lower left) Similar display for CSETN detector, same scale, two-hour binned concentration shown by blue-shaded region, with distinct maximum in post-dawn bin. (Right) Schematic of volatile migration at equator by ballistic hopping (curved arrows) and transport in regolith by the Moon’s rotation (tangential arrows); source of volatiles is unspecified. Volatiles that initially migrate east (orange) condense or adsorb onto regolith overnight, then remobilize after dawn and migrate back to cold terminator (curved orange arrow). Volatiles that initially migrate west (green) are reinforced by previously-trapped volatiles that thermally desorb from the surface in the morning sector.

Horizontal diffusion driven by surface temperature gradients plausibly explains most of the features in the deduced distribution of hydrogen (Fig. 4). Volatile molecules should migrate symmetrically away from the temperature maximum at noon (Crider and Vondrak, 2002) due to surface thermal gradients that drive diffusion toward the cold surface beyond the terminator (Vasavada et al., 2012). Hydrogenated regolith that develops in the cold dusk sector rotates East through the night and across the dawn terminator into sunlight, where it encounters the volatiles that diffuse Westward across the warm sunlit surface toward the dawn terminator. The pileup of Eastward- and Westward-transported volatiles at dawn results in the greatest neutron flux suppression. As the surface rotates further East from dawn into sunlight, it warms and remobilizes volatiles that had been adsorbed on the regolith which diffuse away from the warm midday toward the dawn terminator, maintaining the highest concentration at dawn, similar to a model by Schorghofer (2014) for behavior of a persistent population of water. Hoffman and Hodges (1975), four decades ago, described a similar model for the transport and temporary sequestration of condensable lunar volatiles with a build-up to greater quantities at the dawn terminator.

The regolith achieves maximum desiccation in the afternoon, where the neutron leakage flux is greatest in both detector systems. The time elapsed for a patch of surface to rotate from maximum hydrogenation at dawn to maximum desiccation in the afternoon is about one-third of a lunar sol, or about ten terrestrial days. The mean speed of diffusion in the anti-sunward direction must be greater than 4.3 m/s, the equatorial tangential velocity due to rotation, in order for molecules desorbed in the morning sector to diffuse Westward fast enough to reach the terminator and pile up there. It is unlikely that horizontal transport of molecules is accomplished by diffusion through the regolith, since it takes days for molecules to fully desorb from the ~1 m maximum depth probed by neutron remote-sensing, while horizontal transport occurs at meters per second or faster. Molecules probably migrate over the surface by ballistic hops through free space (Crider and Vondrak, 2002). The actual depth of diffusion into and out of the regolith as well as the time required for the daily heat pulse to penetrate the highly insulating lunar surface to liberate volatiles (Vasavada et al., 2012) contribute to the observed phase lag that delays maximum dehydration until the afternoon.

The nightside temperature of the Moon (~100 K) is far below the freezing point of water and creates a cryopump, maintaining near-zero vapor pressure for water so that volatile molecules that fall to the surface adhere and the condensable component of the nightside atmosphere collapses. The atmosphere of thermally desorbed volatiles that develops over the daylit side of the terminator thus is positioned immediately adjacent to a vacuum with no intervening barrier. The atmosphere will flood into the nightside vacuum at speed comparable to the thermal speed of the molecules, which for hydroxyl and water is $\sqrt{2k_{B}T/m}\cong 430\mathrm{m}/\mathrm{s}$ at 200 K, a temperature appropriate for the near-terminator dayside (Vasavada et al., 2012). Conservation of mass requires that the slow-moving flux of volatiles adsorbed by the regolith and carried into daylight by the Moon’s rotation must equal the flux in the fast-moving population of thermally desorbed volatiles that travels in the opposite direction, toward the lunar nightside, in proportion to the ratio of the speeds. The fraction of volatiles above the surface at the terminator thus is about 4.3/430 = 1% of the total volatile burden at dawn, with 99% of volatiles temporarily sequestered beneath the surface. A detailed transport model will differ from these values in detail, but should be of roughly this magnitude.

The dawn-to-afternoon contrast of measured lunar neutron leakage flux differs between the SETN and CSETN detectors. Minimum-to-maximum contrast in CSETN is about 1.6%, compared to about 0.7% in SETN, both measured at about the same statistical significance. We consider four possible interpretations for the greater contrast measured in CSETN relative to SETN:

1. A random stochastic effect may be masking contrast that actually is the same.

2. The background count rate in one or both detector systems may be estimated incorrectly, leading to a falsely high or low contrast for the same difference in count rate.

3. Neutrons in the energy range detected by each of the detector systems may respond to a differing extent to the same hydrogen concentration, requiring different values of the calibration factor Γ in Eq. (1).

4. The physical distribution of materials in the actual regolith may differ from the modeled regolith (Mitrofanov et al., 2010a) in ways that significantly influence the response to hydrogen according to neutron energy.

The tables column in units of hydrogen concentration provides a convenient comparison for the statistical significance of the difference in contrast between the two detectors, since the unit conversion implemented in the tables is a shared multiplicative factor and the tabulated values already include propagation of error in computing the contrast. Each detector yields the maximum contrast just after dawn, relative to the mid-afternoon standard. The difference in contrast of each detector at dawn divided by the uncertainties combined in quadrature yields 3.1 σ discrepancy in the contrast measured by SETN and by CSETN. Expanding to an uncertainty-weighted average over the three bins centered on dawn again yields 3.1σ discrepancy; further expanding to average over the five bins centered on dawn increases the significance to 4.1σ discrepancy. Since the statistical significance of the measured discrepancy is preserved or increases when expanding the pool of measured values, we do not consider it to be significantly likely that the contrast discrepancy at dawn is a stochastic effect.

Background contributed by spacecraft-sourced neutrons is a small contribution to total count rate in the SETN detector, of order 8% (Litvak et al., 2012a), with another ~3% out-of-band signal from thermal neutron leakage. Doubling these estimated contributions to the total SETN count rate would increase the dawn contrast in SETN by a factor of only about 1.13, far short of resolving the factor of 1.6/0.7 = 2.3 discrepancy in contrast between SETN and CSETN. Background contributed by spacecraft-sourced neutrons is a large contribution to total count rate in the CSETN detector, of order 48–57% of total; either estimate is coarsely consistent with a background count rate similar to SETN in each of the individual CSETN detectors. A significant error in estimating the background detection rate in CSETN could possibly account for the discrepancy in the magnitude of the dawn contrast, although such an error would require that the CSETN detectors be subject to a significantly different background neutron detection rate than the SETN detector. Suppressing the dawn contrast derived from CSETN can be accomplished only by diluting the component of detected neutron flux identified as lunar, requiring that a reduced background be assumed for this detector system. Resolving a factor-of-two discrepancy in contrast would require assuming almost zero background in CSETN, which is not supported by background flux measured in cislunar space nor at the Moon. The discrepancy in contrast thus is not explainable as an artifact of inaccurate background estimation.

The calibration factor quoted for epithermal neutrons in presenting Eq. (1) is acknowledged to be probably incorrect to an indeterminate degree for the higher-energy HEE neutron population sensed by CSETN, since the calibration was derived from Monte Carlo calculations specifically for low-energy LEE neutrons detected by a ³He detector with no sensitivity to HEE neutrons. Since we observe that contrast is greater in CSETN data than in SETN data, the HEE neutron population must be more sensitive to changes in the presence of hydrogen in the regolith than the LEE population under the relevant circumstances. The linear correlation coefficient between the derived hydrogen quantities in the tables is high (0.92) and a linear fit between the SETN and CSETN estimated hydrogenation has a slope of 2 with a very small intercept, suggesting that CSETN is approximately twice as sensitive to hydrogen as SETN. Forcing the intercept to precisely zero yields a slope of 2.2, consistent with CSETN seeming to report more than twice the hydrogen content as SETN by applying Eq. (1) without adjusting the calibration factor, Γ. If the signal is in fact responding to the same small quantity of hydrogen within the regolith, that would imply that the calibration factor for CSETN should be reduced by a factor of approximately two. Any difference in the calibration factor, however, is a quantitative and not a qualitative effect. Since the calibration calculations were performed assuming LEE neutrons, we can safely quote results from the SETN detector as a best estimate for the concentration of hydrogen and water in the regolith.

Lawrence et al. (2011) investigated the effect on epithermal neutron flux suppression from changing the depth into the surface that is hydrogenated as well as the density of hydrogen in the regolith. The depth of hydrogenation has a very strong effect on the relative sensitivity of HEE and LEE neutron populations (Lawrence et al., 2011, their Fig. 2b and c), with magnitude comparable to the discrepancy in dawn-to-afternoon contrast in SETN and CSETN, for hydrogenation in a layer of 3–30 g/cm² thickness or 2–20 cm depth, assuming regolith density of order 1.5 g/cm³ (Vasavada et al., 2012). The effect is interpretable as the result of different source depths for HEE and LEE populations: neutrons that originate at shallow depths have greater mean energy (HEE) than neutrons that originate at greater depth (LEE), due to the greater number of energy-depleting scattering events experienced by neutrons that originate at depth. As a result, hydrogen isolated in the upper layer of regolith, above the nominal source depth for HEE neutrons, suppresses HEE neutron flux as much as if the same density of hydrogen were to extend more deeply (Fig. 5). LEE neutron flux is only partially suppressed when hydrogen is restricted to the upper layer and is more deeply suppressed by the same density of hydrogen if it extends all the way down to the nominal LEE neutron emission depth. If hydrogen were restricted to a layer below the nominal HEE emission depth, HEE neutrons would be relatively unsuppressed while LEE neutrons would be partially suppressed. If hydrogen were distributed evenly throughout the layer between surface and LEE emission depth, then both HEE and LEE neutrons would be suppressed proportional to the degree of hydrogenation. The difference in dawn-to-afternoon contrast between the SETN and CSETN diurnal profiles is consistent with diurnally variable hydrogenation in an upper layer that is present at dawn and reduced or absent by mid-afternoon. The depth of penetration in the shallow layer more completely fills the sensitive column for HEE neutrons than for LEE neutrons and can provoke a greater response in CSETN in straightforward fashion, consistent with the depth of the shallow upper layer that is hydrogenated.

Fig. 5.

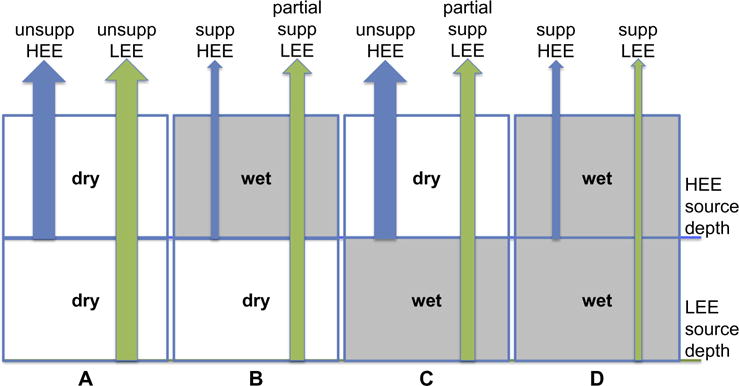
Conceptual model for effect of hydrogenation/hydration depth distribution on neutrons of differing energy. Upper layer lies between lunar surface and nominal depth of HEE neutron emission. Lower layer lies between HEE emission layer and nominal depth of LEE neutron emission. (A) “Dry” regolith in both layers: unsuppressed HEE and LEE neutron emission. (B) “Wet” regolith in upper layer, dry regolith in lower layer: suppressed HEE neutron flux, partially suppressed LEE neutron flux. (C) Dry regolith in upper layer, wet regolith in lower layer: unsuppressed HEE neutron flux, partially suppressed LEE neutron flux. (D) Wet regolith in upper layer, wet regolith in lower layer: suppressed HEE neutron flux, suppressed LEE neutron flux. Conceptual model based on calculations by Lawrence et al. (2011).

Sunshine et al. (2009) estimate ~0.1–0.3 wt% hydration at the lunar surface from reflectance spectroscopy, which enables an order-of-magnitude calculation for the relevant depth of hydration detected by LEND. The peak hydration at dawn sensed by SETN is 0.0125 ± 0.0022 wt%. Treating this is an average value for the ~100 cm column of regolith sensed by SETN, the fraction of the 100 cm SETN column that may be hydrated at 0.1–0.3 wt% is just 3–15 cm (range stretched by one sigma in either direction), nominally ~6 cm, well within the depth range that results in differential sensitivity in HEE and LEE neutrons according to Lawrence et al. (2011). The relevant depth of hydration thus is measurable in units of several centimeters, neither a microscopically thin skin layer nor multiple decimeters deep. Detailed Monte Carlo modeling will be needed to refine results further; this work is in progress, fleshing out the conceptual model of Fig. 5.

The presence of any hydration or hydrogen on the lunar surface at low latitude is surprising but has been confirmed by multiple missions using three remote-sensing methods: NIR reflectance spectroscopy; UV reflectance spectroscopy; and neutron flux suppression. The mineral hydration signature detected in reflected NIR light potentially could be formed by a surface monolayer that extends only microns to millimeters deep, whereas the neutron suppression requires a layer that penetrates several centimeters deep, at least. Neutron flux suppression thus requires orders of magnitude more diurnally mobile hydrogenated volatiles than the quantity of water or hydroxyl that minimally may suffice for the surface hydration. In addition, the discrepancy at the dusk terminator suggests that the processes that form detectable mineral hydration do not necessarily lead to emplacing sufficient hydrogen for measurable neutron flux suppression. Considering the very small magnitude of the neutron flux suppression at the equator, measurement artifacts or systematic effects on the neutron flux measurement must be considered.

There are four categories of phenomena that potentially could lead to a false neutron suppression signature:

1. Data reduction artifact.

2. Orbit asymmetry.

3. Uncorrected detector electronics sensitivity variation.

4. Insolation effect on detector electronics (e.g., heating).

There is no part of the data reduction pipeline between LEND and the PDS archive that explicitly responds to the value of lunar local time, but the methods that are unique to the present work conceivably might introduce a local time effect as an artifact. The accumulation of measured signal in bins of local time is a simple sum of measured counts and integration time (Eq. (2)). The division by a flat-fielding function (Eq. (4)) is less straightforward and offers a possible mechanism to originate an artifact. Fig. 6 compares the calibrated hydrogenation derived from each detector with and without flatfielding the data first. The contrast between low inferred hydrogenation in the afternoon/dusk and high hydrogenation near dawn appears with or without the flatfield correction, with a periodic variation that appears if the data are not flatfielded. Close inspection of the nonflatfielded results shows that the periodic component of the signal is out of phase between the detectors, consistent with the mapped neutron leakage flux (Fig. 2), in which HEE neutron emission measured by CSETN is brighter where LEE neutron emission measured by SETN is darker. The diurnal variability in the neutron flux clearly is not an artifact of the flat-fielding operation.

Routine station-keeping maneuvers stabilized the LRO orbit altitude and inclination during the time these data were collected. These maneuvers might have been phased inadvertently with local time such that the spacecraft may have been at somewhat higher or lower altitude near dawn, and the opposite near dusk. Changes in altitude change the partitioning between GCR-induced background and lunar neutron flux due to the changing solid angle subtended by the Moon. At low altitude, the Moon intercepts more of the sky from which the spacecraft otherwise is isotropically illuminated by cosmic rays, decreasing the spacecraft-sourced neutron flux. Detected lunar neutron flux increases at lower altitude due to the increasing solid angle of the Moon. Spacecraft-sourced neutrons in SETN are ~8% of total signal, and about 57% of total signal in CSETN. Lunar neutrons therefore account for 92% of signal in SETN (including 3% due to thermal neutrons) and about 43% of signal in CSETN. Any altitude-dependent effect due to cosmic-ray-induced background that is measurable in SETN thus could be expected to appear with about seven times the magnitude in CSETN (57/8), while any altitude-dependent effect due to lunar neutrons that is measurable in SETN would be half as significant in CSETN (43/92). Although CSETN exhibits greater minimum-to-maximum contrast than SETN, the difference is a factor of 2.3, not seven. Fig. 7 shows the five-minute binned neutron flux measurements compared to mean altitude in each five-minute bin of local time. The correlation coefficient for each detector’s measurements is near zero (|r| < 0.1), and they are of opposite sign. Thus, even if a correlation with altitude accounted for a small dawn-to-dusk asymmetry in one of the detectors, it would produce an asymmetry of opposite sign in the other detector. This is not observed, supporting the conclusion that variations in the spacecraft orbit did not create a dawn–dusk contrast artifact. The ascending and descending phases of the orbit are separated by twelve hours but the minimum and maximum bins in the neutron flux are not twelve hours apart (Fig. 4), further evidence that spacecraft orbit does not account for the observed signal modulation.

Fig. 7.

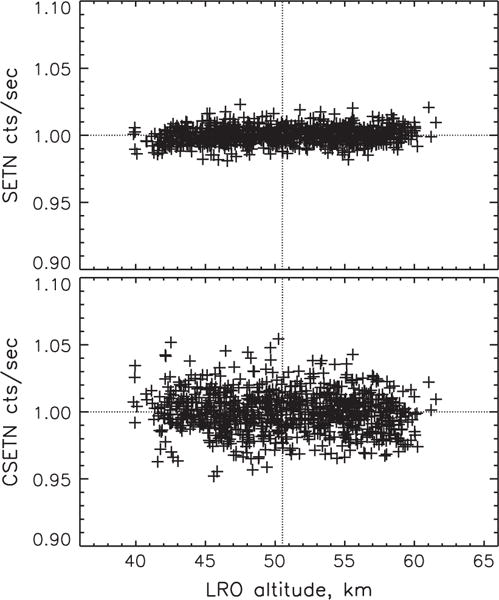
Relative signal in each of the LEND epithermal neutron detectors in comparison to average spacecraft altitude within bins of five minutes of local time. The near-zero correlation coefficient is of opposite sign for each detector.

LEND is switched off during station-keeping maneuvers to prevent damage to high-voltage electronics that may result from exposure to exhaust gases. This off–on power cycle resets the detectors to a low-sensitivity state from which they recover over about two weeks, calibrated to normalize performance to a fully charged detector. These power cycles occur when LRO orbits over a narrow range of longitude at arbitrary local time, but conceivably there could be a correlation between local time and uncorrected or over-corrected electronic effects. Fig. 8 investigates such effects as artificially suppressed sensitivity that recovers with time (Fig. 8A) or artificially enhanced sensitivity that decays with time (Fig. 8B) as the local time of the LRO orbit changes continuously toward earlier local time. It takes more than a day for the orbit to shift by one hour of local time, whereas the spacecraft orbit period is less than two hours. Electronic sensitivity effects thus must appear equally in measurements separated by twelve hours of local time since the time between ascending and descending phases of the orbit is very short compared to the time necessary to cover several hours of lunar local time. The observed maximum signal occurs in one well-defined sector of the lunar day, not two symmetric sectors, and the modulation of the signal is not rotationally symmetric about the Moon’s axis as it would be if an electronic effect were the source of a false signal.

Fig. 8.

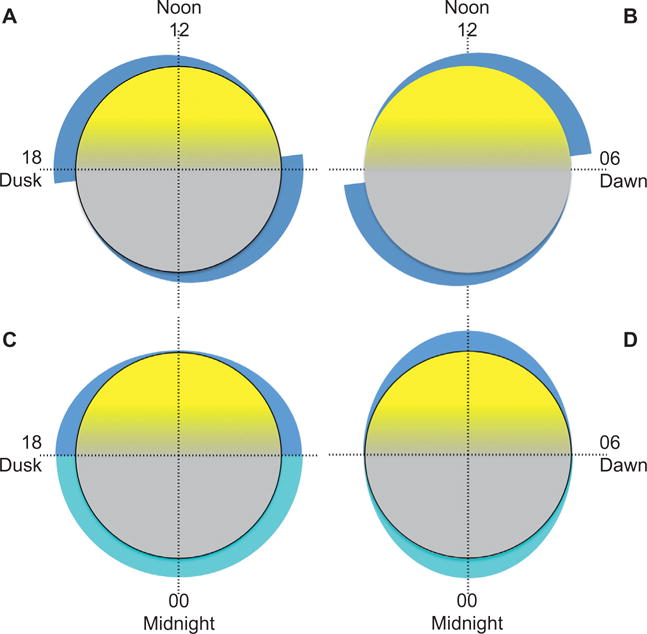
Putative artifact signal due to undiagnosed operational factors. (A) Suppressed neutron sensitivity near dawn, decaying with time, exaggerates hydrogen near dawn. Similar effect at ±12 h local time, due to short orbit period, exaggerates hydrogen in afternoon as well. (B) Enhanced neutron sensitivity in afternoon leads to nondetection of hydrogen in afternoon and pre-dawn and exaggerates hydrogen post-dawn and post-dusk. (C) Insolation effect on spacecraft (blue) that exaggerates detection of hydrogen post-dawn also exaggerates sensitivity pre-dusk. Lack of insolation on nightside leads to nondetection of hydrogen. Enhanced neutron sensitivity at noon would lead to similar pattern but with constant false hydrogen detection on nightside as well (turquoise). (D) Insolation that suppresses neutron flux when anti-lunar side of spacecraft is illuminated results in false detection of hydrogen at subsolar point.

Sunlight illuminating the spacecraft may affect instrument electronics in unanticipated ways (Fig. 8C and D). The standard LRO orientation points LEND and other instruments toward the nadir and presents the same side of the spacecraft to the Sun at all times. If insolation of the Sun-facing side of the spacecraft affects LEND electronics on the dawn side so as to suppress neutron sensitivity and create an exaggerated hydrogen signal at dawn, the same effect would create an exaggerated hydrogen signal at dusk (Fig. 8C, dark blue shading) and have no effect on the night side where the spacecraft is entirely in the dark, leaving a pattern with mirror symmetry through the noon–midnight plane and hydrogen detected at both terminators. If sunlight artificially enhances the apparent neutron sensitivity in proportion to insolation on the anti-lunar side of the spacecraft it would result in a minimum of retrieved hydrogen near noon, with the addition of a false hydrogen detection on the nightside where the spacecraft is not illuminated at all (Fig. 8C, blue plus turquoise shading). The pattern would still have mirror symmetry through the noon–midnight plane. Finally, if neutron sensitivity were suppressed proportional to insolation on the anti-lunar side of the spacecraft, it would result in an apparent maximum of hydrogenation at local noon and nowhere else (Fig. 8D, dark blue shading). If the effect of insolation on the anti-sunward side of the spacecraft persisted through the shadowed phase of the orbit, since the orbit period is so short, it would result in an apparent maximum of hydrogen at local midnight, too (Fig. 8D, turquoise shading). None of these distributions is observed, nor is any sum or multiple. No systematic effect on the LEND instrument or LRO spacecraft could create the pattern of epithermal neutron detection rates that is observed by the LEND detectors (Fig. 4).

Lunar surface temperature also slightly enhances or depletes the energy of leakage neutrons, possibly shifting a population of low energy epithermal (LEE) neutrons above or below the low-energy cutoff on the SETN and CSETN detectors imposed by the Cd foil, or slightly altering the interaction cross-section for neutrons on lunar materials (Little et al., 2003). The mapped variation in surface temperature at the equator (Vasavada et al., 2012) is almost perfectly symmetric on the dayside, with a slight decline over the course of the night from dusk to dawn (120 K down to 100 K) that is much smaller than the variation from terminator to noon on the dayside (100 K up to 380 K). An artifact in neutron detectability due to surface temperature would look somewhat like the systematic effect suggested for insolation on the spacecraft (Fig. 8C, blue plus turquoise), with a phase lag due to subsurface temperature at the point of last scattering for leakage neutrons which would rotate the pattern to put the minimum in apparent hydrogen concentration in the afternoon and the maximum well after dawn. This could superficially resemble the pattern of deduced hydrogen concentration, but fails to account for the fact of the gradual increase in neutron flux suppression over the lunar night as the temperature changes very mildly, followed by a gradual decrease in flux suppression over the lunar day, as the temperature changes far more dramatically. Most importantly, the temperature effect would occur most strongly in LEE neutrons of energy not too greatly different from thermal energy. LEE neutrons contribute a much smaller proportion of the neutron flux detected in CSETN than in SETN, yet the CSETN detectors respond with greater contrast from minimum to maximum flux than SETN. We thus conclude that no process other than an actual distribution of hydrogen on or in the lunar surface that is fixed with respect to local time can account for the observed diurnal variability of lunar epithermal neutron leakage flux.

4. Discussion

LEND data and optical detections of mineral hydration show that there is a quantity of hydrogen, at least some of it in the form of water, that is present at the lunar surface at low latitudes and that is mobile on a lunar diurnal time scale. The mean thermal speed of H atoms or H₂ in contact with the surface anywhere on the Moon is a large fraction of escape velocity, resulting in rapid losses unless the hydrogen is in a heavier molecule with much lower thermal speed, such as water, methane (CH₄), or ammonia (NH₃). The balance between source and loss processes required to maintain the present quantity of hydrogen-bearing volatiles constrains possible delivery mechanisms, some of which bear implications for the formation history of the Moon.

The Moon appeared thoroughly desiccated during the Apollo missions to the Moon. All Apollo landed operations were conducted between 06:20 and 09:30 local time, during the most hydrogen-rich part of the lunar day (Fig. 4), although ~99% of that hydrogen would have been beneath the surface. Water recently has been discovered trapped in agglutinates in Apollo regolith samples (Liu et al., 2012), even though it was overlooked at the time of the Apollo landings. The failure to discern water in the lunar surface at the time of the Apollo missions thus does not conclusively deny the presence of volatiles in small quantities, particularly given the difficulty of distinguishing water in Apollo samples from contamination by a substance that is so ubiquitous in the terrestrial environment. Even if a sample actually were pristine, it would be difficult to prove conclusively that any water it contains is not contamination acquired over four decades in storage.

The zonally averaged water-equivalent hydrogen concentration estimated from neutron flux suppression measured with SETN (Table 1) is 0.0046 wt% WEH averaged over ~1-m depth, which translates to 0.0069 g/cm² or 2.3 × 10²⁰ water molecules per square centimeter, assuming regolith density of order 1.5 g/cm³ (Vasavada et al., 2012). Methane-equivalent hydrogen would imply half this concentration of molecules, due to the greater quantity of hydrogen within the molecule. Since the rest of the discussion is primarily concerned with orders of magnitude, distinctions from water as the primary molecule are not significant. The quantity of molecules participating in diurnal variability is in addition to a possible immobile background concentration such as water trapped in agglutinates. Peak concentration in the dawn sector is about three times greater than the average. Mineral hydration detected by infrared spectroscopy sets a lower limit on the quantity of water that is diurnally variable. Sunshine et al. (2009) estimate hydration of order 0.1–0.3 wt% water or hydroxyl in the exposed surface, implying a diurnally variable population of order 0.1 wt%, zonally averaged. The minimum thickness of an optically detectable monolayer of hydrated material at the surface must be at least of order half a wavelength of the 2.8 μm band used to detect it in the near-IR. The total amount of water required to hydrate a monolayer of density 1.5 g/cm³ to this extent is 7 × 10¹⁵ mol/cm². The speed of desorbed volatiles diffusing across the terminator implies that only ~1% of total volatiles will be above the surface at the terminator, suggesting that the vertically integrated atmosphere at the terminator contains of order 1.6 × 10¹⁸ H₂O/cm² according to SETN, or a lower limit of 5 × 10¹³ H₂O/cm² according to NIR spectroscopy. This translates to a surface pressure on the order of ~10 nanobar or less. Gathered together in a single mass, the global quantity of mobile water implied by SETN is equivalent to a sphere ~1 km in diameter at 1000 kg/m³; with a comet-like density of 100 kg/m³ (~90% porosity), the sphere would be ~2.3 km in diameter. Condensed as a continuous liquid film over the entire Moon, the quantity of water measured by SETN would form a film 0.07 mm (70 μm) thick. The quantity of water required to hydrate a global micron-scale monolayer to the small extent observed optically would form a comet-density sphere of only ~0.07 km diameter, or a global film a tiny fraction of a micron thick. The six Apollo landing missions delivered exogenous volatiles from 1969 to 1972, but the maximum conceivable contribution is insignificant: treating the 15 metric ton mass of each fully-fueled lunar module as entirely converted to volatiles of 18 amu average mass (water) could account for an upper-limit global-average burden of no more than 8 × 10¹² mol/cm², three orders of magnitude less than the minimum quantity implied by hydration of a micron-scale monolayer.

Measurements of specific volatiles in the lunar atmosphere have been rare and not comprehensive. Apollo 17 deployed a mass spectrometer on the lunar surface that acquired in situ measurements of the lunar atmosphere at night and at sunrise only, over a period of ten months (Hoffman and Hodges, 1975). The Apollo 17 orbiter obtained ultraviolet spectroscopy of the atmosphere at pre-dawn and post-dusk (Feldman and Morrison, 1991), repeated forty years later with LAMP on LRO (Stern et al., 2013). The International Ultraviolet Explorer observatory accepted a proposal to search for emissions of OH resulting from cometesimal impacts on the Moon (Shemansky, 1990), but no results have appeared in the literature. Results from the Lunar Atmosphere and Dust Environment Explorer (LADEE) mission neutral mass spectrometer (Mahaffy et al., 2014) have not yet been formally released. LADEE passed through the lunar atmosphere at periselene over the dawn terminator at altitudes of 30–200 km through most of the mission, with a terminal phase at lower altitudes. The CHandra’s Altitudinal Composition Explorer (CHACE) instrument on the Moon Impact Probe of the Chandrayaan-1 mission detected mass numbers 18 and 44 (nominally, water and carbon dioxide) over a range of altitudes, peaking at ~0.4 nbar total pressure at ~70°S latitude and >15 km altitude; this result remains controversial (Sridharan et al. 2010).

The Apollo mass spectrometer results provide evidence for the existence at the Apollo 17 landing site of species with mass 16 amu (O or CH₄), 17 amu (NH₃ or OH), 18 amu (H₂O), 28 amu (N₂ or CO) 32 amu (O₂), and 44 amu (CO₂), as well as detecting ⁴He, ⁴⁰Ar, and ³⁶Ar (Hoffman and Hodges, 1975). Both CH₄ and NH₃ may contribute to epithermal neutron flux suppression with greater efficiency than water, due to the greater number of hydrogen atoms in each molecule. The stoichiometry of the hydrazine fuel and dinitrogen tetroxide (N₂O₄) oxidizer used in the lunar module rocket motors raises the possibility that the detected non-noble gas species could result from exhaust products, partial photolysis of leaked fuel, or reactions between leaked fuel and oxidizer from residual contents in the descent stage propellant tanks left on the surface. On the other hand, the detected species include only one possible nitrogen oxide (N₂O, 44 amu), whereas NO (30), NO₂ (46), or N₂O₄ (60 amu) also could be expected from unreacted oxidizer leaking from the tanks. Without the oxidizer, there would be no continuing source for hydrogen or carbon oxides that were detected at sunrise several months after the landing and exposure to solar ultraviolet radiation. Except for helium, the detected species behaved as if they were condensable at lunar nightside temperatures and displayed an increase above background as dawn approached at the Apollo 17 site, consistent with the mobilization of adsorbed/condensed gases from the illuminated regolith and diffusion of the liberated gas across the terminator to the instrument location. Saturation of the detector at each sunrise terminator crossing was interpreted as a combination of native atmosphere with outgassing from the instrument and surrounding site contamination as the surface and landed equipment warmed. The daytime atmospheric concentration was estimated to be of order 10⁷ mol/cm³. Assuming the detected atmosphere to be entirely water at typical morning temperature of ~300 K above adsorbed water not yet desorbed from the surface, the integrated atmospheric column constitutes about 10¹⁴ mol/cm², suggesting a total volatile abundance at the terminator of about 10¹⁴/0.01 = 10¹⁶ mol/cm², comparable to the lower limit estimate for spectroscopically detected mineral hydration (7 × 10¹⁵ mol/cm²) but four orders of magnitude short of the concentration implied by the neutron detection. No sensitive neutral gas detector was able to continue operations beyond the initial rise of the atmospheric density at dawn in order to measure peak concentration (Stern, 1999). The estimated daytime peak in atmospheric density at the surface thus has not been measured, by Apollo or any other mission. It may be that the native lunar atmosphere has been underestimated and contamination at the Apollo 17 landing site has been overestimated.

Molecular and atomic hydrogen are the only non-noble gas constituents of the lunar atmosphere whose concentration has previously been measured with much precision. Stern et al. (2013) have reported the near-surface number density of molecular hydrogen above the lunar night side near the terminators as (1.2 ± 0.4) × 10³ cm⁻³ at an assumed temperature of 120 K, consistent with lunar night and far above hydrogen condensation temperature, using the LAMP UV spectrometer on LRO. This abundance is four orders of magnitude less than the in situ Apollo estimate for daytime atmosphere and thus is only a trace of the lunar volatile inventory at low latitudes; the molecular hydrogen abundance, in turn, is about two orders of magnitude greater than the atomic hydrogen abundance (Feldman and Morrison, 1991). LAMP also has detected helium (Feldman et al., 2012) and set upper limits on the nightside density of several other atomic species in gas phase (Cook et al., 2013). Hendrix et al. (2012) have provided evidence from LAMP spectroscopy for diurnally variable mineral hydration in the exposed surface in daylight, but LAMP has no sensitivity to gaseous OH or H₂O, whose UV transitions are outside the bandpass of LAMP or the earlier Apollo 17 spectrometer (Feldman and Morrison, 1991; Budzien and Feldman, 1991). The scale height of molecular hydrogen computed for lunar gravity at 120 K is 308 km, resulting in an integrated column of about 4 × 10¹⁰ mol/cm², most of which is above the LRO spacecraft altitude and thus not directly observable.

Molecules that desorb from the surface are subject to photolysis by solar ultraviolet radiation, with lifetime of order 10⁵ s (Budzien and Feldman, 1991; Huebner and Carpenter, 1979; P.N. Romani, personal communication, 2014). The fate of the photolysis products is not clear, whether they are lost from the Moon or may re-encounter the surface to undergo recycling reactions. For the diurnally active volatile inventory to remain in equilibrium between supply and losses if there were no recycling, the rate of delivery of new molecules must be about equal to the measured abundance over lifetime, with the lifetime extended to ~10⁷ s to account for only about 1% of the inventory being above-ground in daylight at any moment. The diurnally active concentration of water-equivalent hydrogen estimated here from LEND measurements of neutron suppression implies a surface-average supply rate of water molecules to the lunar surface of ∂[H₂O]/∂t = 2.3 × 10²⁰/10⁷ ≈ 10¹³ mol/cm²/s. The lower limit set by optical measurements is ∂[H₂O]/∂t = 7 × 10¹⁵/10⁷ ≈ 10⁹ mol/cm²/s. The supply rate set by the Apollo estimate of surface atmospheric density for a mixture of molecules is ∂[mol]/∂t =10¹⁴/10⁵ ≈ 10⁹ mol/cm²/s, while the supply rate required by the empirically determined molecular hydrogen component of the atmosphere is ∂[H₂]/∂t = 4 × 10¹⁰/10⁵ = 4 × 10⁵ Mol/cm/s. Note that the lifetime is not extended for volatile quantities measured in gas phase above the lunar surface. The solar wind delivers a nearly constant supply of hydrogen that may implant in the lunar surface and react with oxygen from regolith materials to yield hydroxyl or water (Ichimura et al., 2012). Protons are delivered to the lunar surface by the solar wind at a rate of roughly 2 × 10⁸ p⁺/cm²/s, averaged over the whole surface (Crider and Vondrak, 2000). If every solar wind proton impacting on the lunar surface were incorporated into a hydrogen-bearing molecule (water, hydroxyl, hydrogen, etc.), then the available supply rate from the solar wind, 10⁸ mol/cm²/s, easily could account for the quantity of molecular hydrogen observed by LAMP and is within an order of magnitude of the Apollo 17 neutral atmosphere estimate and the lower limit on water concentration from spectroscopy. This is close enough that detailed modeling might resolve remaining discrepancies, but only if surface minerals were hydrated in only a micron-scale monolayer. A millimeter-thick monolayer would exceed resupply by the solar wind by three to four orders of magnitude. Solar wind implantation is five orders of magnitude too little to account for the diurnally active component of hydrogen detected by SETN, a major discrepancy unless molecular photolysis products can be retained and recycled with very high efficiency.

Surface-mediated chemical recycling reactions among hydrogen-bearing volatiles may extend the effective lifetime against permanent loss from the Moon’s environment. The hydrogen daughter from a water photolysis event that takes place during ballistic flight over the Moon’s morning sector is born at a speed less than a quarter the mean speed of an H atom ballistically launched from the surface at the same temperature, and thus has only a small probability of escape due to this velocity component. The momentum imparted to photolysis products by the solar UV photon that causes the photolysis is directed toward the Moon’s surface, delivering the products back to the surface where they may recombine. Ninety percent recycling efficiency would increase the effective lifetime against permanent loss by an order of magnitude, 99% would increase the lifetime by two orders of magnitude, and so on. Nearly complete recycling of photolysis products (99.999%) would be necessary for the solar wind to maintain equilibrium with the quantity of hydrogen detected by LEND at the Moon’s surface. Such high recycling efficiency may not be impossible, but it is not very plausible. The implied lifetime against permanent loss would be 10¹² s, about thirty-two thousand years. This is so long that sequestration by the polar cold traps should bleed away volatiles from the equatorial region unless there were an opposing process that liberates molecules from the cold traps to maintain equilibrium with the rate of delivery. Farrell et al. (2013) proposed that ejecta from meteoroid and micrometeoroid impacts at the poles as well as charged particle sputtering could transfer volatiles from the polar cold traps to lower latitudes. Highly efficient recycling of H₂O photolysis products combined with redistribution from the polar cold traps conceivably could maintain the detected hydrogen concentration at the equator with the solar wind as the source. Chemical recycling that is significantly less than 99.999% efficient would rule out the solar wind as the root source of hydrogen for currently mobile lunar volatiles, demanding a significantly greater influx of hydrogen than the solar wind, or requiring a decaying inventory from a past pulse of volatile input.

Meteoroid and micrometeoroid impacts could deliver hydrogen-bearing volatiles by direct impact, either as an occasional large pulse or a continual rain of minor impacts. Volatiles observed in the LCROSS ejecta plume included carbon monoxide, which is common in comets (Hurley et al., 2012; A’Hearn et al., 2012) and the Apollo mass spectrometer detected methane and ammonia in the predawn atmosphere, which also are common in comets. The short lifetime against photolysis implies rapid decay from an input pulse of volatiles unless there were recycling to extend the lifetime against loss. An unnoticed impact by a kilometer-scale body within the past five decades of optical observations and direct inspection of the Moon is unlikely, suggesting lifetimes must be extended to between fifty and a thousand years if an unobserved impact pulse were responsible for the modern volatile inventory. History holds no record of a sky-spanning comet that reached the Moon and disappeared, so only a volatile-rich dark body could account for the current volatile inventory with a single impact that might escape the notice of terrestrial observers. Such an impactor would have left a many-kilometer wide geologically new crater that would have been noticed by orbital reconnaissance. Multiple impacts by smaller volatile-rich bodies of ~100 m size strains credulity that all such impacts would occur on the Moon’s far side, where they cannot be observed, and none on Earth’s atmosphere, which would have been very obvious. At the small end of the impactor scale, the micrometeoroid flux can be estimated from measurements on Earth and other planets. Morgan and Shemansky (1991) estimate that micrometeoroids deliver 57.6 g/s to the Moon, or 1.5 × 10⁻¹⁶ g/cm²/s. Even if all of this material were H₂O, it would be only 5 × 10⁶ mol/cm²/s, two to three orders of magnitude too little to account for the minimal estimated atmosphere from Apollo 17. Orton et al. (2014) observe oxygen-bearing species in the stratosphere of Uranus that result from meteoroid impacts and infer a delivery rate of ~3.5 × 10⁵ mol/cm²/s. Making generous assumptions that the density of impactors scales as the inverse square of heliocentric distance, and ignoring lesser gravitational focusing compared to the mass of Uranus, this influx scales to only ~10⁸ mol/cm²/s, comparable to the solar wind delivery rate and equally inadequate.

Outgassing from the Moon itself could release a flux of indigenous volatiles retained from the Moon’s formation. With no recycling, the estimated supply rate of 10¹³ mol/cm²/s would have released approximately 2 × 10⁴⁷ water molecules from the Moon over 4.5 byr. A rough estimate of Earth’s current inventory of water can be computed by assuming an average ocean depth of 3 km to the abyssal plain, with ~3/4 coverage of Earth’s surface area, yielding about 10⁴⁶ water molecules in Earth’s current ocean inventory. This suggests an implausible twenty times the Earth’s current surface inventory of water has been lost by the Moon over its history. If recycling reactions were 99% efficient, the lifetime against permanent loss would increase to ~32 years and the implied loss of water would decrease to about one fifth of the modern ocean inventory, with continual delivery to the Moon’s surface of ~10¹¹ mol/cm²/s rising from below. This exceeds the solar wind supply rate by three orders of magnitude. The preferred formation scenario for the Moon is a giant impact on a proto-Earth, stripping material from the crust and upper mantle of either the proto-Earth or the impactor or both (reviewed by Asphaug, 2014). Observations of lunar mineralogy provide evidence for the existence of water in the Moon’s mantle (Klima et al., 2013) and some recently published models for the Moon’s formation support incorporating a high concentration of volatiles in the Moon’s bulk (Hauri et al., 2015).

Epithermal neutron suppression post-dusk is small (Figs. 3 and 4; tables), but appears to increase over the course of the lunar night as measured by both LEND epithermal neutron detector systems. Lunar nightside temperatures on the order of 100–120 K should immobilize migrating water molecules within a few hops across the surface from the terminator at either dusk or dawn (100s of km), but the nightside distribution of neutron flux suppression increases continuously from dusk to dawn over a range spanning thousands of kilometers. This feature is not an obvious consequence of any of the proposed mechanisms to deliver volatiles to the Moon’s surface. Water delivered to the surface from below by outgassing at the estimated rate of 10¹¹ mol/cm²/s would account for about 10¹⁷ mol/cm² over the course of the lunar night, three orders of magnitude less than the total concentration estimated from the LEND data and thus insufficient to account for building the hydrogen supply at the surface over the lunar night. The condensation temperature of methane is colder than the lunar nightside surface temperature, and methane scatters neutrons twice as effectively as water. If methane were a large fraction of the hydrogen-bearing volatiles at the lunar surface, it could diffuse westward at night in competition with lunar surface rotation eastward to yield the observed distribution. The solar wind could not supply methane, due to very little carbon at the lunar surface, but the other suggested mechanisms to supply volatiles could deliver methane along with water or other hydrogen-bearing volatile species.

5. Conclusions

The distribution in local time of epithermal neutron flux, measured by LEND on LRO at low latitude on the Moon, is consistent with a maximum of hydrogen-bearing volatiles just after lunar dawn but widely distributed at lesser concentration up to the afternoon and extending across much of the lunar night. The minimum of inferred hydrogen abundance is in the later afternoon and dusk. A distribution that is fixed near dawn despite lunar rotation requires that hydrogen-bearing volatiles must continually desorb from the surface and migrate across the nearest terminator from the warm sunlit surface to be readsorbed on the cold nightside surface. Conservation of volatile mass and momentum across the terminator requires that the relatively high translational speed of gas molecules migrating to the nightside be balanced by a much larger mass of adsorbed material moving with the regolith at the slow speed of lunar rotation toward the dayside, implying that only about 1% of the volatile inventory at the dawn terminator is in gas phase above the surface. Comparing the magnitude of response in the LEND uncollimated neutron detector SETN with the degree of mineral hydration by water or hydroxyl that has been observed spectroscopically is consistent with hydrogen located in a shallow layer of 3–15 cm depth, nominally about 6 cm. This depth is roughly consistent with the observed difference in response of two different epithermal neutron detectors in LEND.

The photolysis lifetime for the small fraction of volatiles that is above the surface and exposed to solar UV radiation at any given moment implies a delivery rate to the Moon’s surface of new hydrogen-bearing volatiles on the order of 10¹³ mol/cm²/s to maintain equilibrium if the hydrogen atom resulting from each water photolysis event were immediately lost from the Moon. This rate exceeds the upper limit on exogenous delivery mechanisms, by solar wind or micrometeoroids, by five orders of magnitude. Outgassing of indigenous volatiles from the Moon itself, at this rate, implies the loss from the Moon of 20 times Earth’s surface inventory of ocean water over the Moon’s history, which is not plausible. The only way to reconcile any potential volatile delivery mechanism with the quantity of mobile hydrogen-bearing volatiles inferred from neutron flux suppression is if photolysis products were chemically recycled with a minimum efficiency of 99%, yielding an effective lifetime against loss of at least 32 years, which would bring the total outgassing loss down to a fraction of Earth’s current surface inventory of water. Exogenous delivery mechanisms would require lifetime another three orders of magnitude greater in order to be effective sources for the inferred quantity of hydrogen and require additional assumptions to account for lunar volatiles not already all having been cold-trapped at the poles. Outgassing of primordial volatiles requires the least extreme assumption regarding extended lifetime against loss to space, and the existence of water dissolved in the Moon’s primordial mantle has been demonstrated by remote sensing of lunar minerals (Klima et al., 2013) and investigations of lunar samples (Hauri et al., 2015). The most congenial interpretation of the LEND measurements is that the Moon formed with a significant inventory of volatiles that continues to leak from the surface today.

Surface inventories of hydrogen-bearing volatiles near the equator may be of significant value for in situ resource utilization (ISRU), for astronaut life-support and to make fuel and oxidizer. Although polar inventories appear to be much greater (Colaprete et al., 2010), recovering resources from polar deposits requires expending energy to mine and to process cold regolith. LEND measurements imply hydrogen concentrations of ~0.1 wt% WEH in the polar regions that are relatively evenly distributed (Sanin et al., 2012). Recovering these volatiles would necessitate heating a large mass of regolith to smelt a modest mass of volatiles. Equatorial volatiles appear to be distilled from the surface in every lunation and recondensed near the dawn terminator by natural processes, with energy freely provided by sunlight. A cold surface such as a metal plate exposed to the tenuous atmosphere overnight and into the dawn could intercept those molecules that otherwise would be adsorbed within the regolith as part of the distillation/condensation cycle. The maximum concentration measured by LEND’s uncollimated detector SETN at dawn provides an estimate of the efficiency with which water could be collected over a patch of ground. At 0.0125 wt% WEH evaluated over a depth of 100 cm, the available water would be ~0.019 g/cm² or about 190 ml per square meter in each lunation. An alternative calibration by Feldman et al. (1998) suggests an amount of water ~14% less than this, ~160 ml/m². A 1-km square collecting region could capture 160–190 metric tons of water in each lunation. A simple heliostat sunshade could create an artificial permanently shadowed region on cryogenically cold plates throughout the lunar day so that volatile collection could continue at all times.

Diurnally active volatile inventories may exist on other airless rocky bodies. The body must have enough gravity that thermal speeds of volatile molecules are well below escape velocity and daytime temperatures near the terminator must be warm enough to remobilize most volatiles before local noon. Daytime temperature warm enough to mobilize volatiles restricts suitability to inside the orbit of Jupiter. Within the inner Solar System, suitable candidates include asteroids, Mars’ larger moon, Phobos, and the planet Mercury. Surface temperatures on main belt asteroids may not be sufficient to volatilize water and transport it by diffusion fast enough to keep up with short rotation periods on the order of a terrestrial day or less. Escape velocity for Phobos is much less than the Moon and thus direct escape to space by molecular species results in greater losses on the dayside. Surface gravity on Mercury is greater than on the Moon, and nightside temperatures are less due to its extremely slow rotation. Radiative equilibrium suggests that equatorial surface temperature on Mercury should equal the Moon’s mid-day temperature at ~40° longitude from the dawn terminator, within about 2.5 h of local time after dawn or ~19 Earth days. Since the maximum temperature on Mercury’s surface becomes quite high, surface volatiles at Mercury’s equator can be expected to completely desorb from the regolith well before noon and migrate across the terminator into night, yielding a pileup of localized volatiles in the dawn and pre-dawn sector. Photolysis lifetimes at Mercury are a factor of seven shorter than at Earth orbit due to greater insolation intensity, but the rotation rate is six times slower than the Moon, which decreases the fraction of volatiles in free space above the surface at any given location. The global average surface density of volatiles on Mercury relative to the Moon thus should scale in direct proportion with the volatile supply rate to the surface of Mercury relative to the Moon, wherever those volatiles might originate.

A definitive test for diurnally variable hydrogen abundance on the Moon is important scientifically, to understand the formation of the Moon, and for engineering and exploration purposes. Verifying the ability to snatch essential volatiles from free space at the Moon’s surface would make a dramatic change in the economics of lunar exploration that has lately put the Moon on the back burner of space exploration. A landed mission is essential to investigate the relevant materials and processes in situ, where contamination can be controlled and accounted for. Relevant instruments would include a neutron detector to evaluate buried hydrogen, comparable to orbital measurements, and a mass spectrometer to evaluate chemical composition of the atmosphere as well as samples drawn from depths down to at least ~15 cm. A simple flat horizontal plate at ambient temperature should suffice to condense volatiles during the lunar night and at dawn to enhance detectability. Atmospheric sensing must be capable of a wide dynamic range, from the nightside atmosphere of ~10³ mol/cm³ up to ~10¹² mol/cm³ in the lunar day. The instruments ought to operate throughout the lunar night to fully characterize the exchange of volatiles between the atmosphere and the surface, requiring either a nuclear power source or high capacity batteries to store power collected during the lunar day from photovoltaics.