Paying Medicare Advantage Plans: To Level or Tilt the Playing Field

Abstract

Medicare beneficiaries are eligible for health insurance through the public option of traditional Medicare (TM) or may join a private Medicare Advantage (MA) plan. Both are highly subsidized but in different ways. Medicare pays for most of costs directly in TM, and makes a subsidy payment to an MA plan based on a “benchmark” for each beneficiary choosing a private plan. The level of this benchmark is arguably the most important policy decision Medicare makes about the MA program. Presently, about 30% of beneficiaries are in MA, and Medicare subsidizes MA plans more on average than TM. Many analysts recommend equalizing Medicare’s subsidy across the options – referred to in policy circles as a “level playing field.” This paper studies the normative question of how to set the level of the benchmark, applying the versatile model of plan choice developed by Einav and Finkelstein (EF) to Medicare. The EF framework implies unequal subsidies to counteract risk selection across plan types. We also study other reasons to tilt the field: the relative efficiency of MA vs. TM, market power of MA plans, and institutional features of the way Medicare determines subsidies and premiums. After review of the empirical and policy literature, we conclude that in areas where the MA market is competitive, the benchmark should be set below average costs in TM, but in areas characterized by imperfect competition in MA, it should be raised in order to offset output (enrollment) restrictions by plans with market power. We also recommend specific modifications of Medicare rules to make demand for MA more price elastic.

1. Introduction

A Medicare beneficiary decides between health insurance from the public option of traditional Medicare (TM), or from a private plan offered through the Medicare Advantage (MA) program. Both options are highly subsidized but in different ways. Medicare pays most of the costs in TM directly, whereas if the beneficiary elects MA, Medicare makes a subsidy payment to the plan benchmarked against (though not necessarily equal to) beneficiary average TM costs in the same region. The benchmark affects the economic outcomes of the MA program: the supply of MA plans, the supplemental benefits these plans offer, any supplemental premium (positive or negative) charged to beneficiaries, beneficiary enrollment, and net Medicare costs. This paper addresses arguably the single most important decision Medicare makes about the MA program, setting the benchmark subsidy. We cast this decision, within the current policy vernacular, of whether to create a “level” or “tilted” playing field as between MA and TM.

The subsidy to MA plans has been controversial since the beginning of Medicare Part C more than 30 years ago. Originally, on the basis of anticipated efficiencies of managed care, Medicare paid private plans 95% of Medicare average costs. Less than 5% of beneficiaries were enrolled in private plans in the early 1990s, and those who did enroll tended to be healthier and less costly than average. In spite of some risk adjustment and the 95% rule, favorable risk selection into MA forced Medicare to pay more to private plans than it would have paid for the same beneficiaries in TM (McGuire, Newhouse and Sinaiko, 2011).

Part C, known as Medicare Advantage since the Medicare Prescription Drug, Improvement, and Modernization Act (MMA) of 2003, has changed substantially over the years. Now, payment rates are partly determined by bidding and quality scores, and average 102% of TM costs. Risk adjustment is improved. The share of enrollment in MA is presently at an historic high of 30% (MedPAC, 2016). Even with all these changes, the benchmark remains controversial, with most policy analysts recommending reducing it to 100% of TM costs so as to achieve “payment neutrality,” or “a level playing field.”¹ The argument for a level playing field goes like this: set the subsidy to MA equal to costs in TM and let beneficiaries choose between the programs based on the equilibrium MA plan premiums that emerge. If an MA plan is more efficient than TM, it can pass the saving along to beneficiaries in the form of lower premium/better benefits and attract enrollees.

While “payment neutrality” and “level playing field” sound appealing, the economics of health insurance markets imply that it is unlikely that a level playing field will be Medicare’s best rule for setting the level of the benchmark. In order to characterize the optimal level from the standpoint of efficiency, Section 3 of this paper applies the versatile model of health plan choice developed by Einav and Finkelstein (EF) and colleagues to the MA-TM setting. ² The EF model was designed to address risk selection in a dual-choice context of employer health insurance, and can be readily adapted to MA and TM. The well-known EF result is that the employer should set unequal subsidies to favor the more generous plan to counter the effect on premiums of risk selection into the more generous plan. A version of this result emerges here. If MA plans attract a favorable risk selection of beneficiaries (after risk adjustment), Medicare should set the subsidy to MA below that of TM – the first reason to tilt the playing field.

The EF model can incorporate other factors playing into choice of the benchmark, such as a second factor we study, the efficiency of MA plans in relation to TM. Efficient sorting requires that beneficiaries face an incremental premium for MA (in relation to what they pay in TM) equal to the incremental marginal cost of MA versus TM. The optimal benchmark is the subsidy that leads to that right incremental premium. With competition, equilibrium premiums in the MA sector will be forced to the average cost in MA of the enrollees net of the benchmark subsidy. If the benchmark payment is set at the average cost in TM (for payment neutrality), the equilibrium premium difference will be equal to the average cost difference between the two sectors, not the marginal cost difference required for efficiency. Thus, a marginal-average cost discrepancy is a second reason to consider a tilt.

A third reason to question a level playing field is a standard argument following from imperfect competition. MA plans have market power in some local markets. An MA plan with market power restricts output to raise its price (the premium). To attain the efficient division between the sectors in the presence of market power, Medicare should subsidize membership in MA by raising the benchmark payment.

Our paper addresses these issues empirically and analytically. Section 2 briefly summarizes some of the main features of the Medicare Advantage program, and also reviews the recent literature on the three empirical questions affecting choice of the optimal benchmark: selection net of risk adjustment, marginal cost savings of MA in relation to TM, and MA plan market power. Section 3 sets up the basic EF model, and then incorporates each of these features into the analysis.

We take an additional important step in the analysis of benchmark setting, situating, in Section 4, the basic EF model of MA-TM within Medicare’s payment rules to study how these also work to affect choice of the benchmark. For two distinct reasons, Medicare’s payment rules put a “kink” in demand for MA plans at the point where the premium beneficiaries pay for MA is exactly zero. The first reason for the kink comes from Medicare’s asymmetric treatment of plan bids above and below the benchmark. The second reason for the kink derives from the unequal salience of positive and negative premiums to beneficiaries. The economic effect of these rules is to make demand for MA less elastic, exacerbating the effects of imperfect competition. The kink drives the equilibrium premium to exactly zero, blocking premiums from going negatives as they may need to for efficiency. We substantiate the presence of a kink with empirical evidence on the distribution of MA premiums.

Section 5 draws the implications of our analyses. The policy short-hand phrases of “level playing field” and “payment neutrality” ignore features of the MA market that need to be taken into account in setting the right benchmark. When the MA market is reasonably competitive, the continued discrepancy between MA and TM of beneficiary expected cost conditional on risk adjustment score implies that the benchmark payment to MA plans should be below average cost in TM, by about 5–10%. Taking as the policy objective to maximize social surplus, in markets with imperfect competition, the benchmark should be higher, at or slightly above the TM average cost. If, however, plan profits are regarded as a cost (not a transfer), there is no cause to counter monopoly output restrictions with a subsidy.

Another set of conclusions has to do with related Medicare payment rules which we find to be counterproductive. Medicare hurts itself in markets with MA plan market power by attempting to share in savings. By making demand less elastic, the sharing rule forces Medicare to pay more in equilibrium for any given enrollment in MA. Premium regulations interfering with the salence of negative prices are also counterproductive. Reframing the way MA premiums are presented to beneficiaries could address this problem.

Our paper is related to several lines of research, most directly to the theoretical model introduced in Einav, Finkelstein and Cullen (2010) and extended in Einav and Finkelstein (2011) and other papers. The EF model develops an intuitive graphical framework for analyzing both theoretical and empirical issues regarding work on selection in insurance markets. Several recent papers in the economics literature estimate structural models of cost and demand to conduct welfare analysis in MA, including Cabral, Geruso and Mahoney (2014), Curto, Einav, Levin and Bhattacharya (2014), and Duggan, Starc and Vabson (2014). ³ Policy papers, such as Song, Cutler, and Chernew (2012), conduct targeted evaluations. We discuss the empirical findings of these and other papers bearing on the benchmark choice below in Section 2. The papers employing a structural model can estimate net benefits in dollar terms of counterfactual policy choices. We take a complementary approach to policy analysis here, focusing on “getting the price right,” an approach we believe to be in the spirit of the original EF model. Rather than attempting to estimate the demand and cost curves for both insurance sectors, we simply seek to identify the incremental marginal cost differences between the sectors, and, dependent on the MA sector market structure, identify the net subsidy (positive or negative) to MA so that right incremental marginal cost difference is transmitted to beneficiaries making the choice between MA and TM.

2. Institutional Background and Literature Review

2.1 Medicare Advantage

Since 1985, beneficiaries have had the option to choose health insurance through a private plan in Medicare Part C, currently known as Medicare Advantage (MA). MA plans must offer the same coverage as Traditional Medicare (TM), consisting of hospital care (Part A) and office-based care (Part B), and may offer greater coverage and/or offer additional benefits. Beneficiaries can buy subsidized drug coverage through independent Part D plans, or as part of their MA plan (MA-PD plans, the most common form). Beneficiaries in TM can also purchase private “Medigap” plans to cover the cost sharing in TM. In 2015, Medicare paid $170 billion to MA plans on behalf of 16.7 million beneficiaries, amounting to an historic high of 30 percent of beneficiaries (MedPAC, 2016).

Prior to the Balance Budget Act (BBA, 1997), plans were paid based on a county-level benchmark equal to average costs in TM; originally, 95 percent of a county’s average. In the BBA Congress set floors on these payments and raised benchmark levels to encourage MA plan entry. Payments were risk adjusted (for inpatient dx starting in 2000 and for outpatient and inpatient a transition starting in 2004). Since 2003, the MMA requires MA plans to make a bid meant to equal plan costs for basic Medicare benefits for an average Medicare beneficiary. If the bid exceeds the benchmark, the plan is paid the benchmark. If the bid is below the benchmark, the plan is paid the bid plus a “rebate” equal to a share of the benchmark less the bid. Prior to 2011, plans received 75% of the difference as a rebate. During 2006–2011, Medicare updated benchmarks by a combination of local and national growth rates, periodically “rebasing” the rates to local TM costs (if this rebasing increased the local benchmark payment). Since 2012, as specified in the Affordable Care Act (ACA, 2010), the rebate percentage ranges from 50–70% depending on plan quality scores. Plans must pass any rebate to beneficiaries in the form of lower premiums or better benefits. The asymmetry in treatment of bids above and below the benchmark kinks beneficiary demand at a zero premium. The importance of this kink for benchmark setting is explained in Section 4.

The ACA modified benchmark rules as well; MA is in transition (complete January 2017) to a system in which benchmark levels will be set at 95 to 115 percent of TM costs according to the TM cost quartile of the county. Counties in the highest cost quartile will have benchmarks equal to 95% of TM cost whereas the lowest cost counties will have benchmarks set at 115%. Plans may receive a 5 or 10% bonus based on quality scores. Four-fifths of counties have completed the transition from the old benchmark formula for 2016, and the rest will have made the transition by 2017 (MedPAC, 2016, 338). MedPAC (2016, 329) estimates that for 2015 the average payment (including about 4% for quality bonuses) was 102% of TM average costs. Bids average 94% of TM costs.

Medicare applies a risk adjustment formula to MA plan payment and regulates the frequency with which beneficiaries can move in and out of MA plans. Historically, risk adjustment of MA plan payments was primitive, and switching rules allowed beneficiaries to enroll/disenroll on a monthly basis. Early research on MA showed considerable favorable selection into MA plans even after the risk adjustment of plan payments (Newhouse and McGuire, 2014). Improvements in the risk adjustment formula and tightening of switching rules have reduced the degree of favorable selection into MA (Newhouse et al., 2015).

Beneficiaries pay a Part B premium to Medicare whether or not they choose an MA plan. The baseline monthly standard Part B in 2016 is $121.80 per month, but most beneficiaries continue to pay the 2015 premium of $104.90. ⁴ For most beneficiaries, the Part B premium could be automatically deducted from a social security check. The differential premium for MA is the premium chosen by the plan, which can be positive or negative. If a plan’s bid exceeds the benchmark, the plan must charge the difference to beneficiaries as a positive premium. If the bid is below the benchmark, the plan must pass the rebate through to beneficiaries in the form of lower premium or increased benefits. An MA plan including Part D benefits also gets a subsidy for the Part D coverage and may charge a positive or negative premium to beneficiaries for this part of coverage as well. To charge a negative premium, the plan “buys down” the automatic Part B premium, paying part of this premium on behalf of the beneficiary. Paying a positive premium requires beneficiaries to write a check, whereas negative premiums lead to a smaller automatic deposit from Social Security, creating a differential salience of positive and negative MA premiums. This is the second reason, elaborated on in Section 4, for the kink in demand at a zero MA premium.

2.2 Literature Review

We organize this review around the three empirical issues related to setting an optimal benchmark: selection net of risk adjustment, relative efficiency of the two plan types at the margin, and MA plan market power. Each factor plays a role in the EF model of MA-TM presented in Section 3.

Is There Favorable Selection into MA Net of Risk Adjustment?

There are two reasons why beneficiaries might be healthier/less costly in MA conditional on the risk score. The first is differences in coding practices. If the same person would be coded as sicker in MA than in TM, beneficiaries would be less costly, conditional on risk score in MA. MA plans, paid on the basis of diagnostic coding, have an incentive to encourage their providers to code more intensively than providers in TM, who are not paid according to reported diagnosis. MA plans may respond to these incentives by employing sophisticated health information systems that build in coding prompts to providers and staff. Some MA plans conduct “health risk assessments” to code otherwise overlooked diagnoses. Geruso and Layton (2015) find that MA plans code 6–16% higher for the same person as TM, and elevated coding is greatest in the vertically integrated MA plans like HMOs where a plan is in a better position to transmit incentives to providers. Other studies substantiate this finding (GAO, 2013; Kronick and Welch, 2014). MedPAC (2016) recommends downward adjustments in Medicare payments, fundamental revision of the coding formula (using two instead of one year of diagnostic data), and disregarding diagnoses from health risk assessments not supported by active treatment – all because of aggressive coding in MA. ⁵

The second reason is adverse selection. Measured risk scores capture only a portion of the variation in expected costs, and individuals with higher expected costs conditional on risk scores may prefer TM with its unlimited provider choice and no managed care techniques. Additionally, MA plans may purposively structure their product to deter higher cost beneficiaries conditional on risk score. A long line of research established favorable risk selection into MA. Prior to Medicare policy changes in the mid-2000s, the consensus in the health economics and policy literature was that MA plans benefited from favorable selection net of any risk adjustment transfers. ⁶ The Congressional Budget Office (1997), for example, concluded that selection more than undid Medicare’s practice at the time of paying on 95% of the risk-adjusted TM average, leading to a net average overpayment of 8% for every MA enrollee relative to their costs in TM. Morrisey et al (2013) repeated earlier methodology from the Physician Payment Review Commission (1996) to show that beneficiaries joining MA plans are less costly than those who do not, and those leaving MA plans are more expensive than those already in TM.

Recent research continues to find favorable selection into MA conditional on risk scores, but less than prior to improvements in risk adjustment and introduction of longer lock-in periods for plan enrollment. ⁷ McWilliams, Hsu and Newhouse (2012) compare selection in the early 2000s to years later in the decade and find declining selection as measured by self-assessed health status and utilization. Newhouse et al (2012) find mortality differences between MA and TM declined from 10% to 3% over the same period. Switchers into MA are 2.3% less expensive than stayers in TM (conditional on risk score) in Curto et al (2014). Newhouse et al (2015) in an analysis of MA switchers also finds recent declines in selection. ⁸ In their structural model of the MA sector, Curto et al use mortality to check for selection differences net of risk adjustment. ⁹ They find lower mortality in MA, conditional on risk score, though again, the mortality gap with TM is lower in the more recent periods. ¹⁰ By comparing costs conditional on risk score, Curto et al.’s estimate that MA plan enrollees are about 7 percent less costly than TM conditional on risk score captures both differences due to coding practices and differences due to selection.

In sum, evidence for differences in coding and for favorable selection into MA imply that net of risk adjustment, beneficiaries are 5–10% less costly in MA than in TM.

Are MA Plans Less Costly than TM for Similar Beneficiaries?

Quantity of health care, e.g., admissions, surgeries, and length of stay in hospitals, tend to be lower in MA than TM for otherwise similar beneficiaries. Quantity, not price, differences are relevant for social efficiency. ¹¹ Landon et al.s (2012) use national survey data to match beneficiaries in MA and TM by location and personal factors affecting use to compare procedure rates in MA and TM. Rates of ambulatory surgery and emergency department use were 20–30% lower in MA, with differences concentrated in “discretionary” procedures like hip replacements. In other work, Landon et al. (2015) compare resource use in episodes of care for diabetes and cardiovascular disease and found a 20% lower rate of service use in MA for both disease groups. Cost comparisons at the end of life also favor MA. (Stevenson et al., 2013)

Duggan et al (2015) follow Medicare beneficiaries in NYS who were involuntarily disenrolled from their MA plan following plan exit, finding that inpatient hospital utilization went up 60%, with rates of increase higher for elective procedures. With hospital costs about 40% of the total (and assuming no offsetting increase in outpatient costs), these estimates correspond to about a 20% lower cost for MA plans. Curto et al (2014) backed out MA costs implied by MA bidding patterns (and profit maximization with some market power) to conclude that MA plans provide TM benefits at 12% lower cost than TM.

There is no evidence that lower costs in MA come at the expense of lower quality, at least on average. Subjective quality ratings by beneficiaries are about the same in the two sectors and “objective” measures like rates of vaccination tend to favor MA (Newhouse and McGuire, 2014).

In sum, overall, research finds lower use for similar beneficiaries in MA without a quality reduction. There is no evidence of which we are aware that makes a distinction between savings for the marginal beneficiary (with respect to membership in MA) and the average beneficiary.

Do MA Plans Have Market Power?

Here we comment on the structure of the MA market. Review of pricing and the evidence on how changes in the benchmark payment is (or is not) passed through to beneficiaries is postponed until after Section 4 where we integrate our analyses with Medicare payment rules. Evidence on pricing and pass-through rates needs to be considered in light of Medicare regulations.

The supply side of many MA markets is highly concentrated. In 2015, the top four insurers enrolled 54 percent of beneficiaries (United Health, 20%; Humana, 19%; Aetna, 7%; Kaiser, 7%) (MedPAC, 2016). Proposed mergers (between Aetna and Humana and two other organizations outside the top four but in the top ten, Cigna and Anthem) would push concentration even higher. One insurer can offer multiple contracts in the same local market, for example, an HMO form and a PPO form, in order to compete in different market segments. Thus, while many markets have a large number of plan options, concentration at the insurer level is what matters for market power. Curto et al (2014) report that for 2006–2011, in the majority of counties, the three largest insurers had at least a 90% share of the MA market. In 2015, there was an average of just 3.2 insurers offering plans per county (MedPAC, 2016, 329). The average Herfindahl-Hirschman Index HHI index in counties during 2010–2012 was 4,464 in Pelech (2015). (An HHI above 2,500 indicates “high concentration.”) Product differentiation among plan types (e.g., with respect to network depth) enhances market power for a given number of insurers.

Interpretation of measures of MA market concentration needs to take account of the presence of the TM option. If shares of all beneficiaries in a county were used as a denominator, Herfindal-index type measures of concentration would fall sharply. However, as we discuss later, several papers find evidence that demand for an MA plan is inelastic (Curto et al (2014), Song, Landrum and Chernew (2012, 2013) and Cabral, Geruso and Mahoney (2014)). Curto et al. (2014) also estimated MA plans’ mark-ups and showed them to be on the order of 16% above variable costs, on average.

In sum, both structural and performance indicators (reviewed later) point to the existence of market power of MA plans in some markets.

3. Sorting Between MA and TM: Application of the Einav-Finkelstein Model

The EF model was created to analyze demand-driven risk selection between two plan options with fixed characteristics. In the two-option employer-based setting considered in EF (2011), sicker employees tend to have a higher demand for the more generous plan, leading to an adverse selection of the risks in the more generous plan at any premium difference between the plans. TM is “less generous” than MA in terms of demand-side cost sharing but “more generous” in terms of open networks and the absence of managed care. It is more accurate to think of these two options as simply different insurance products for which the degree of selection into MA is an empirical question. As in the EF employer-based setting, beneficiaries have heterogeneous costs and preferences and vary in their willingness to pay to remain in TM. Risk adjustment partially contends with cost heterogeneity and selection. To begin, we suppose there is one benchmark payment common to all beneficiaries (no risk adjustment).

In the standard EF model competition moves premiums to average costs in two plan options, whereas in Medicare, the TM premium is fixed and only the MA premium is determined in equilibrium. ¹² MA plans must provide at minimum the same benefits as in TM, but may add coverage, and may charge a positive or negative premium. In the EF framework, MA plan characteristics are fixed. The MA plan chooses only the level of the premium.

3.1 Demand and Cost

The lower part of Figure 1, a modification of the basic EF diagram, depicts demand for enrollment in MA, ${\mathrm{q}}_{\mathrm{MA}}$, as a function of the premium (p) for MA: ${\mathrm{q}}_{\mathrm{MA}}={\mathrm{Q}}_{\mathrm{MA}}(\mathrm{p}).$ As drawn, the demand curve for membership in MA indicates that while some beneficiaries would join an MA plan at a positive premium, others require the inducement of a negative premium to compensate for the more strict management of care and limited provider networks in MA. The inverse demand is $\mathrm{p}=\mathrm{P}({\mathrm{q}}_{\mathrm{MA}}).$ The length of the horizontal axis is $\overline{\mathrm{q}}$ representing all Medicare beneficiaries. Enrollment in TM, ${\mathrm{q}}_{\mathrm{TM}}=\overline{\mathrm{q}}-{\mathrm{q}}_{\mathrm{MA}}$, is read from right to left in Figure 1.

Figure 1.

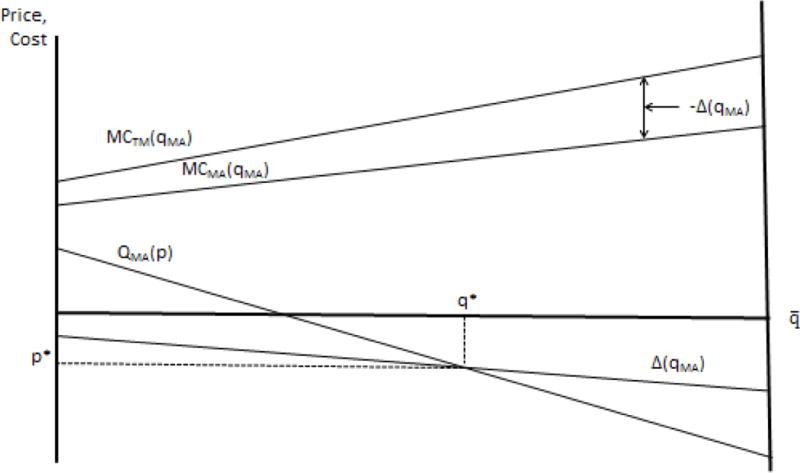
Demand, Cost and Efficient MA Enrollment

A key feature of EF-type models is that the demand curve orders beneficiaries according to their willingness to pay for MA membership. Cost curves for both MA and TM correspond to this ordering. Marginal cost curves are shown in the upper portion of Figure 1. The ${\mathrm{MC}}_{\mathrm{MA}}$ curve is the “marginal cost” of beneficiaries joining MA as the premium falls. ¹³ As drawn, an upward-sloping ${\mathrm{MC}}_{\mathrm{MA}}$ corresponds to favorable selection into MA. In other words, the first beneficiaries joining MA tend to be lower cost, so that marginal cost rises with level of enrollment. The marginal cost curve from the standpoint of TM, ${\mathrm{MC}}_{\mathrm{TM}}$, reflecting the same ordering of beneficiaries, is also shown in the Figure.

The relation of marginal cost curves for MA and TM in Figure 1 reflect any quantity and input price differences between the two sectors. Following our discussion in Section 2.2 we assume that costs are lower for the same beneficiary in MA than in TM. The difference between the marginal costs in the two sectors is $\mathrm{\Delta }({\mathrm{q}}_{\mathrm{MA}})={\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})-{\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}}),$“incremental marginal cost” in the EF terminology. As beneficiaries move from TM to MA, social cost savings are the difference in the costs between the two sectors. $\mathrm{\Delta }({\mathrm{q}}_{\mathrm{MA}})$ is negative throughout and shown in the lower portion of Figure 1. As drawn, savings by moving to MA are larger for more costly beneficiaries.

3.2 Efficient Enrollment and MA Premium

For efficiency, a beneficiary valuing MA over TM more than the incremental cost of MA should be in MA. Otherwise, the beneficiary belongs in TM. Efficient enrollment is where demand (or willingness to pay) equals incremental marginal cost, shown as ${\mathrm{q}}^{\mathrm{\ast }}$ in Figure 1. For beneficiaries to the left of ${\mathrm{q}}^{\mathrm{\ast }}$, the willingness to pay exceeds the incremental cost of being in MA. ${\mathrm{q}}^{\mathrm{\ast }}$ will be chosen by beneficiaries if the premium is equal to the incremental marginal cost. Thus, ${\mathrm{q}}^{\mathrm{\ast }}$ solves equation (1):

$$\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})=\mathrm{\Delta }({\mathrm{q}}_{\mathrm{MA}}).$$ (1)

We will refer to ${\mathrm{q}}^{\mathrm{\ast }}$ as the efficient enrollment in MA, efficient in a second-best sense of being subject to the ordering of beneficiaries joining MA dictated by the single-price p for MA. ¹⁴ We refer to ${\mathrm{p}}^{\mathrm{\ast }}\equiv \mathrm{P}({\mathrm{q}}^{\mathrm{\ast }})$ as the efficient premium.

3.3 Equilibrium Enrollment and MA Premium

Equilibrium enrollment depends on the Medicare benchmark, which we call R. For now we assume plans are simply paid the benchmark. We incorporate Medicare rules regarding bidding in Section 4 below. For a given R, the competitive (break-even) MA premium equates total revenue to MA plans (premium plus R) to average costs. Premium and costs are both functions of MA enrollment. The MA enrollment associated with competitive equilibrium, ${\mathrm{q}}^{\mathrm{e}}$, is given by the solution to (2):

$${\mathrm{AC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})-\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})=\mathrm{R}$$ (2)

Figure 2 adds the ${\mathrm{AC}}_{\mathrm{MA}}$ curve and an arbitrary R. Higher enrollment means a costlier population on average in MA. Figure 2 graphs ${\mathrm{AC}}_{\mathrm{MA}}$ – R and shows where the line describing the break-even premium intersects with demand, defining the market equilibrium. Depending on the level of R, equilibrium enrollment ${\mathrm{q}}^{\mathrm{e}}$ could be greater or less than ${\mathrm{q}}^{\mathrm{\ast }}$.

Figure 2.

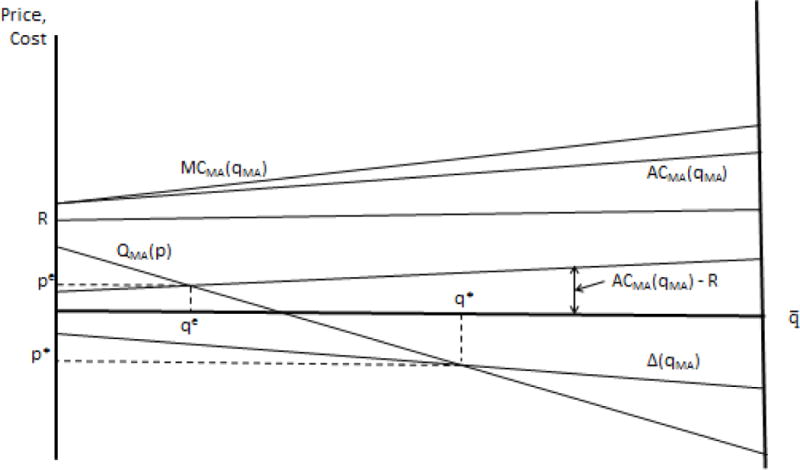
Equilibrium MA Enrollment

We can now apply the EF apparatus to characterize 1) the R that maximizes social efficiency with competitive supply, 2) the R corresponding to a “level playing field,” 3) the R that minimizes Medicare program costs, and 4) the R that counters market power of MA plans.

3.4 Efficient Benchmark

The efficient benchmark, R* satisfies the condition for efficiency (1), ${\mathrm{p}}^{\mathrm{\ast }}=\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\ast }})$ in competitive equilibrium (2). Combining these two expressions we have:

$${\mathrm{R}}^{\mathrm{\ast }}={\mathrm{AC}}_{\mathrm{MA}}({\mathrm{q}}^{\mathrm{\ast }})-\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\ast }})$$

R* is average cost in MA minus the incremental cost of MA versus TM at the efficient enrollment. At R*, the premium for MA will be equal to the incremental cost. Since the incremental cost is negative, the optimal MA premium will itself be negative.

Note that the optimal benchmark is not equal to any marginal or average cost in TM, which are themselves functions not values. In other words, there is no general definition of the optimal benchmark that can be stated in terms of TM costs alone. Note also that efficient enrollment in MA can be achieved by the right benchmark payment. Risk adjustment is not necessary to achieve optimal sorting, even in the presence of risk selection.

3.5 “Level Playing Field”

Although a level playing field is not in general the best policy, given the prominence of the term, we characterize a level playing field and compare it to optimality. The level playing field logic derives from principles of “managed competition” proposed by Enthoven (1993). If a beneficiary brings the same (risk-adjusted) payment from a regulator/sponsor to any plan, plans then compete on quality and supplemental premiums. ¹⁵ There are alternative definitions of a “level playing field” that could be considered. One is at the level of an individual. The playing field between MA and TM could be defined as level if Medicare pays the same for each beneficiary in MA as it pays in TM, as it would in a voucher-type subsidy for beneficiaries. Risk adjustment is obviously required if a level playing field is to work at the level of an individual beneficiary. An MA plan could be paid the predicted spending for a beneficiary had the beneficiary stayed in TM. This payment formula would not, however, lead to efficient sorting. Even if risk adjustment were perfect at predicting costs, the resulting equilibrium MA premium would be equal to the average saving in MA, not the saving for the marginal beneficiary, and efficient sorting would not be attained. And of course risk adjustment is not perfect, and leaves opportunities for selection and upcoding.

An alternative definition of level playing field, and one closer to our reading of the policy literature, is in terms of an average: the playing field between MA and TM can be said to be level if Medicare pays the MA plan the same (on average) per enrollee as it pays (on average) per beneficiary in TM. ¹⁶ In terms of cost and enrollment, the R associated with a level playing field according to this definition is ${\mathrm{R}}^{\mathrm{L}}$:

$${\mathrm{R}}^{\mathrm{L}}={\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})\equiv \frac{{{\displaystyle \int }}_{{\mathrm{q}}_{\mathrm{MA}}}^{\overline{\mathrm{q}}}{\mathrm{MC}}_{\mathrm{TM}}(\mathrm{q})\mathrm{dq}}{\overline{\mathrm{q}}-{\mathrm{q}}_{\mathrm{MA}}}$$

Note that ${\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})$ is not the average cost in TM of the beneficiaries $[0,{\mathrm{q}}_{\mathrm{MA}}]$ who choose MA. ${\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})$ is the average cost in TM of beneficiaries $[{\mathrm{q}}_{\mathrm{MA},}\overline{\mathrm{q}}]$, i.e., those who are in TM given enrollment ${\mathrm{q}}_{\mathrm{MA}}$ in MA. With favorable selection into MA, ${\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})>{\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})$.

${\mathrm{R}}^{\mathrm{L}}$ is a function of MA enrollment. And from (2), MA enrollment is a function of the level of the benchmark. This two-way relationship between the level-playing field benchmark and enrollment requires us to solve for the ${\mathrm{R}}^{\mathrm{L}}$ consistent with equilibrium. To do so, we plug the definition of ${\mathrm{R}}^{\mathrm{L}}$ into (2) to obtain the condition for level playing field equilibrium in terms of costs:

$${\mathrm{AC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})-\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})={\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})$$

which can also be written as:

$$\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})={\mathrm{AC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})-{\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})\equiv \mathrm{\Delta }\mathrm{AC}({\mathrm{q}}_{\mathrm{MA}})$$ (4)

Let ${\mathrm{q}}^{\mathrm{L}}$ be a solution to equation (4); then, ${\mathrm{p}}^{\mathrm{L}}\equiv \mathrm{P}({\mathrm{q}}^{\mathrm{L}})$ and ${\mathrm{R}}^{\mathrm{L}}\equiv \mathrm{R}({\mathrm{q}}^{\mathrm{L}}).{\mathrm{p}}^{\mathrm{L}}\mathrm{and}{\mathrm{q}}^{\mathrm{L}}$ are the premium and enrollment consistent with the level playing field benchmark.

The equilibrium condition (4) is satisfied at one value of ${\mathrm{R}}^{\mathrm{L}}$. Medicare could (and has in other contexts) ignore the equilibrium condition defining a level playing field and simply set a benchmark equal to average costs in TM as they happen to be at some point in time, but then, because enrollment depends on the benchmark, the resulting equilibrium will not in general satisfy the condition for a “level playing field.” ¹⁷

Figure 3 compares the level playing field to the efficient equilibrium. In an efficient equilibrium, the premium for MA is equal to the incremental marginal cost in MA. In a level playing field equilibrium, premium for MA is equal to the difference in average costs between MA and TM. The top portion of Figure 3 shows the relationship among the relevant marginal and average cost curves. With the increasing ${\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})$, ${\mathrm{AC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})<{\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}}).{\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})$ is also increasing, but since ${\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})$ is the average of beneficiaries to the right of ${\mathrm{q}}_{\mathrm{MA}}$ (not the left as the average for MA), ${\mathrm{AC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})>{\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}}).$ Thus, we know that for every value of ${\mathrm{q}}_{\mathrm{MA}}$, the difference in average costs between MA and TM is greater in absolute value than the difference in marginal costs. This is shown in Figure 3, along with the consequences for the relationship between ${\mathrm{R}}^{\mathrm{\ast }}$ and ${\mathrm{R}}^{\mathrm{L}}$. Since these cost differences are negative and $\mathrm{\Delta }\mathrm{AC}({\mathrm{q}}_{\mathrm{MA}})<\mathrm{\Delta }({\mathrm{q}}_{\mathrm{MA}}),{\mathrm{p}}^{\mathrm{\ast }}>{\mathrm{p}}^{\mathrm{L}}$ (i.e., is less negative, smaller in absolute value), and ${\mathrm{R}}^{\mathrm{\ast }}<{\mathrm{R}}^{\mathrm{L}}$.

Figure 3.

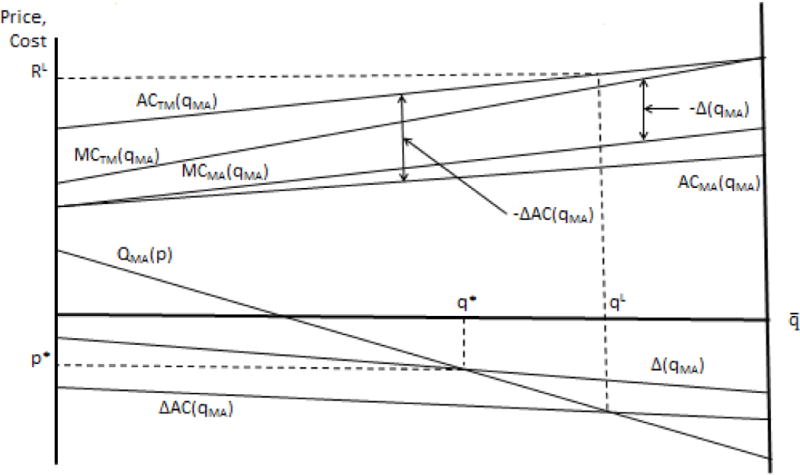
Level Playing Field and Efficient MA Enrollment

We can therefore state the following:

Observation 1

With favorable selection into MA, and increasing ${\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}}),$ a level-playing field policy is not efficient and leads to too many beneficiaries in MA.

Observation 1 is simply the main EF result about the need to subsidize membership in the more generous plan, translated into the MA-TM context.

Risk adjustment alters the properties of equilibrium, but will not in general lead to efficiency. Risk adjustment transfers funds to MA plan for beneficiaries likely to be high cost, and subtracts a payment for those likely to be low cost. But because the risk adjustment transfers are based on averages and not the marginal beneficiary, the transfers will not in general lead to the break-even premiums required for efficient sorting.

It may be useful to describe a special case in which the level playing field policy is optimal, i.e., leads to the optimal premium ${\mathrm{p}}^{\mathrm{\ast }}=\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\ast }})$ and optimal enrollment q*. Suppose MA saves the same cost for every beneficiary, ∆. And suppose there is either no favorable selection or any selection is exactly compensated by risk adjustment. Then the difference in average cost between MA and TM after risk adjustment will also be ∆. This is the premium that will emerge from competition, and is also the efficient premium (equal to the incremental marginal cost of MA).

3.6 Setting R to Minimize Medicare Program Cost

Medicare may seek to minimize Medicare payments rather than promote efficiency, leading to a different optimal rule for setting the level of the benchmark. Medicare faces a downward-sloping demand for MA plans, and can set R so as to take advantage of its “market power” in selling MA. Acting like a monopolist, Medicare restricts output by lowering R, causing higher premiums and lower MA enrollment. Note that Medicare’s market power is distinct from any market power of MA plans (which we consider next in Section 3.7).¹⁸

Medicare pays costs in TM directly and pays costs in MA less any premium collected from beneficiaries because of the zero-profit condition in competitive equilibrium. Let $\mathrm{B}({\mathrm{q}}_{\mathrm{MA}})$ denote Medicare’s total spending:

$$\mathrm{B}({\mathrm{q}}_{\mathrm{MA}})={{\displaystyle \int }}_0^{{\mathrm{q}}_{\mathrm{MA}}}{\mathrm{MC}}_{\mathrm{MA}}(\mathrm{q})\mathrm{dq}-\mathrm{P}({\mathrm{q}}_{\mathrm{MA}}){\mathrm{q}}_{\mathrm{MA}}+{{\displaystyle \int }}_{{\mathrm{q}}_{\mathrm{MA}}}^{\overline{\mathrm{q}}}{\mathrm{MC}}_{\mathrm{TM}}(\mathrm{q})\mathrm{dq}$$ (5)

Choosing ${\mathrm{q}}_{\mathrm{MA}}$ to minimize (5) yields (6), a marginal revenue equals marginal cost condition. Medicare’s “revenues” are what it collects in premiums, and its costs are the (negative) incremental cost of moving a beneficiary to MA:

$$\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{P}\text{'}({\mathrm{q}}_{\mathrm{MA}}){\mathrm{q}}_{\mathrm{MA}}\equiv {\mathrm{MR}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})={\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})-{\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}_{\mathrm{MA}})=\mathrm{\Delta }({\mathrm{q}}_{\mathrm{MA}})$$ (6)

The MR = MC condition is depicted in Figure 4 with a shifted perspective to highlight the region below the zero price point where the MR and MC curves will tend to intersect. Medicare-as-monopolist restricts output to equalize marginal revenue to marginal cost by lowering R. Let ${\mathrm{q}}^{\mathrm{m}}$ be the solution to (6), ${\mathrm{p}}^{\mathrm{m}}$ the premium at ${\mathrm{q}}^{\mathrm{m}}$, and ${\mathrm{R}}^{\mathrm{m}}$ the benchmark payment that leads to ${\mathrm{p}}^{\mathrm{m}}$. Then, ${\mathrm{q}}^{\mathrm{m}}<{\mathrm{q}}^{\mathrm{\ast }}$, ${\mathrm{p}}^{\mathrm{m}}>{\mathrm{p}}^{\mathrm{\ast }}$ and ${\mathrm{R}}^{\mathrm{m}}<{\mathrm{R}}^{\mathrm{\ast }}$. We can now state our second observation:

Figure 4.

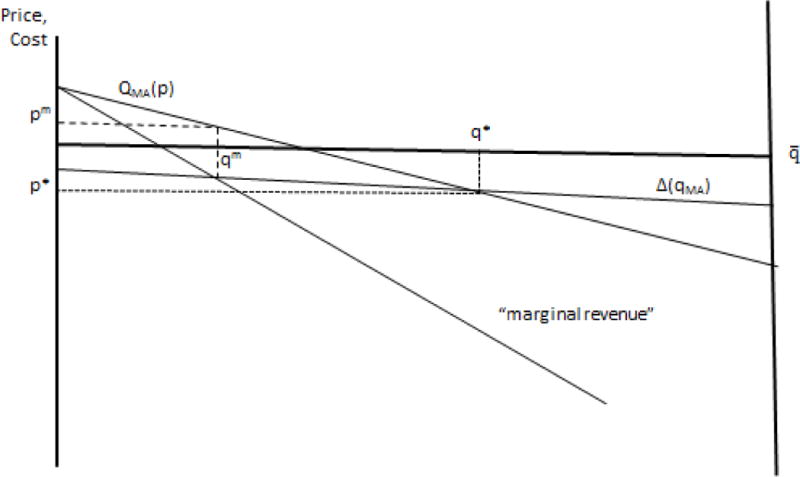
Medicare Budget Minimizing MA Enrollment

Observation 2

The benchmark subsidy that minimizes Medicare program costs induces too few enrollees to choose MA.

3.7 MA Plan Market Power

As discussed in Section 2.2, some markets for MA plans are imperfectly competitive. The MA plan with market power chooses the premium and enrollment to maximize profits. Given a benchmark payment R from Medicare, the plan will choose ${\mathrm{q}}_{\mathrm{MA}}$ to maximize:

$$\mathrm{\pi }({\mathrm{q}}_{\mathrm{MA}})={\mathrm{q}}_{\mathrm{MA}}({\mathrm{P}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{R})-{{\displaystyle \int }}_0^{{\mathrm{q}}_{\mathrm{MA}}}{\mathrm{MC}}_{\mathrm{MA}}(\mathrm{q})\mathrm{dq}$$

The solution to the monopolist’s profit-maximization problem which we call ${\mathrm{q}}^{\mathrm{\pi }}$ is given by:

$${\mathrm{P}}_{\mathrm{MA}}({\mathrm{q}}^{\mathrm{\pi }})+{\mathrm{q}}^{\mathrm{\pi }}{\mathrm{P}}_{\mathrm{MA}}^{\mathrm{\text{'}}}({\mathrm{q}}^{\mathrm{\pi }})={\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}^{\mathrm{\pi }})-\mathrm{R}$$ (7)

Marginal cost less the benchmark payment is effectively the marginal cost the plan must pay, and the profit maximizing plan equates this to marginal revenue by choosing ${\mathrm{p}}^{\mathrm{\pi }}\mathrm{and}{\mathrm{q}}^{\mathrm{\pi }}$ as shown in Figure 5. The MA plan with market power restricts output in relation to a competitive equilibrium for a given R: ${\mathrm{q}}^{\mathrm{\pi }}<{\mathrm{q}}^{\mathrm{e}}$.

Figure 5.

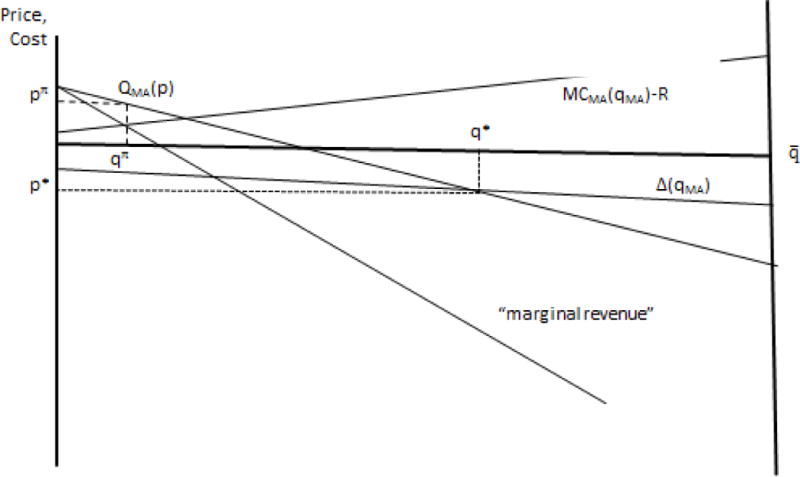
MA Plan with Market Power Maximizes Profits

Medicare can implement social efficiency by choosing a benchmark payment R to counteract the output restriction/price elevation effects of MA plan market power. The efficient premium and MA enrollment is attained when, as describe in section 3.2 above, ${\mathrm{p}}^{\mathrm{\ast }}\equiv \mathrm{ P}({\mathrm{q}}^{\mathrm{\ast }})=\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\ast }})$. Expression (7) for profit maximization can be written:

$${\mathrm{P}}_{\mathrm{MA}}({\mathrm{q}}^{\mathrm{\pi }})+{\mathrm{q}}^{\mathrm{\pi }}{\mathrm{P}}_{\mathrm{MA}}^{\mathrm{\text{'}}}({\mathrm{q}}^{\mathrm{\pi }})+\mathrm{R}={\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}^{\mathrm{\pi }})+\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\pi }})$$ (7′)

The condition for efficiency ${\mathrm{p}}^{\mathrm{\ast }}=\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\ast }})$ is satisfied at ${\mathrm{q}}^{\mathrm{\ast }}$ by an ${\mathrm{R}}^{\mathrm{\ast \ast }}$ which solves:¹⁹

$${\mathrm{R}}^{\mathrm{\ast \ast }}={\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}^{\mathrm{\ast }})-{\mathrm{q}}_{\mathrm{MA}}{\mathrm{P}}_{\mathrm{MA}}^{\mathrm{\text{'}}}({\mathrm{q}}^{\mathrm{\ast }})={\mathrm{MC}}_{\mathrm{TM}}({\mathrm{q}}^{\mathrm{\ast }})-\frac{\mathrm{\Delta }({\mathrm{q}}^{\mathrm{\ast }})}{\mathrm{\epsilon }({\mathrm{q}}^{\mathrm{\ast }})}$$ (8)

Where $\mathrm{\epsilon }({\mathrm{q}}^{\mathrm{\ast }})$ is the demand elasticity. It is easy to see that ${\mathrm{R}}^{\mathrm{\ast \ast }}>{\mathrm{R}}^{\mathrm{\ast }}$.

The optimal subsidy described above is derived under the assumption that Medicare’s objective is to maximize social surplus, weighing plan profits equally to beneficiary net welfare.²⁰ If, on the other hand, Medicare regards plan profits simply as a cost, there is no argument for elevating R** above R*. Intermediate cases, in which profits are valued but not as much as beneficiary welfare, would retain the feature that Medicare should increase the subsidy to MA plans to counteract output restrictions imposed by a firm with market power.

4. Rules for Bidding and Premium Setting: Putting a Kink in Demand for MA

This section incorporates some Medicare rules about MA plan bidding and premium setting. The rules for bidding and the rules about premium setting independently put a kink in the demand curve facing MA plans at p = 0. We explain the kink and its consequences for Medicare, staying within the EF framework of beneficiaries choosing between TM and MA plans with fixed characteristics. At the close of this section we assess the evidence supporting the presence of the kink.

4.1 Plan Bidding and Payment Rules

The 2003 MMA introduced bidding into MA plan payment rules. Each year, plans submit a bid. Bids are supposed to be based on costs and allowable profits but the research literature regards the plans as having sufficient flexibility within the current regulations to choose the bid based on profit maximization. ²¹ If the plan bids above the benchmark, Medicare pays the plan the benchmark. If the plan bids below the benchmark, Medicare pays the bid and in addition, pays a “rebate” equal to a share of the difference between the benchmark and the bid. Before 2012 plans’ share was 75% (Medicare retained 25% of the difference). The ACA reduced plans’ share and tied them to plans’ quality ratings. In 2014, plans’ rebates were 50%, 65% or 70%, with higher plan rebate shares rewarding plans with better quality scores.

Medicare rules connect the premium a plan charges to beneficiaries to the bid. If the bid exceeds the benchmark, the plan must charge the difference to beneficiaries in a premium (as was the case in Section 3). If the bid is below the benchmark, the plan must pass the rebate through to beneficiaries in the form of lower premium or increased benefits. Because plan characteristics are fixed in our model, the rebate must go to a lower premium. Note that Medicare’s sharing rules are asymmetric around the bid = benchmark (premium = 0) point. Let the plan’s bid be b and the share the plan keeps of the benchmark minus bid if the bid falls below the benchmark be s. Then, the premium a beneficiary pays is:

$$\mathrm{p}=\{\begin{array}{c}\mathrm{b}-\mathrm{R}\mathrm{if}\mathrm{b}\ge \mathrm{R}\\ \mathrm{s}(\mathrm{b}-\mathrm{R})\mathrm{if}\mathrm{b}<\mathrm{R}\end{array}$$ (9)

Medicare’s payment to the plan can be expressed as:

$$\{\begin{array}{c}\mathrm{R}\mathrm{if}\mathrm{b}\ge \mathrm{R}\\ \mathrm{b}+\mathrm{s}(\mathrm{R}-\mathrm{b})\mathrm{if}\mathrm{b}<\mathrm{R}\end{array}$$ (10)

Note that the plan’s revenue per enrollee, the sum of the premium and Medicare’s payment, is always just the bid.

Although the plan always receives exactly its bid, Medicare’s sharing rule for bids below the benchmark alters the relationship between enrollment and revenue for the plan in that range. Medicare retains a share of the “savings” if the bid is below the benchmark. To reduce the premium by $1 when the bid is above the benchmark, the plan must reduce the bid by $1. When the bid is below the benchmark, however, to reduce the premium by $1 the plan must reduce the bid by $\frac{\mathrm{\$}1}{\mathrm{s}}>\mathrm{\$}1$, putting a “kink” in the price the plan sees (the bid) as a function of enrollment. Figure 6 shows the original inverse demand, $\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})$, and the kink in the $\mathrm{b}({\mathrm{q}}_{\mathrm{MA}})$ relationship because of the shift in the sharing rule at the enrollent corresponding to p = 0. The figure is rescaled in relation to the previous ones to focus on the regions around the kink.

Figure 6.

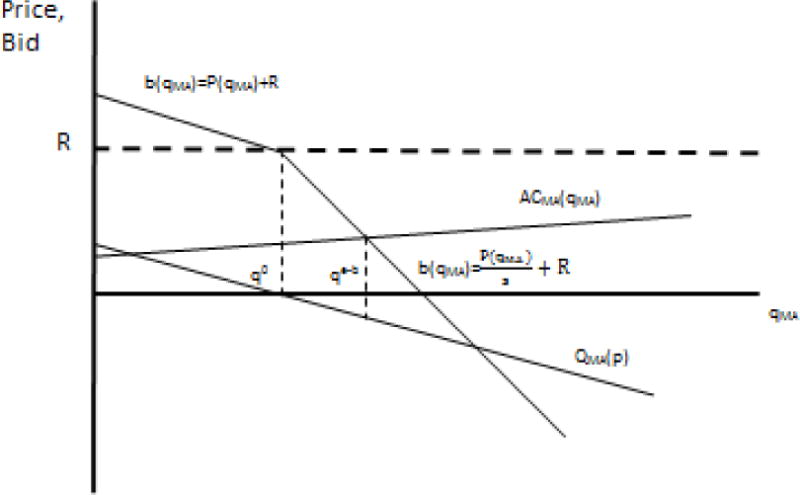
Medicare’s Asymmetric Sharing Rule: Competitive Equilibrium

Before introducing the second distinct reason for the kink, we explain how the kink affects outcomes for Medicare. The kink is innocuous when the MA market is competitive, but increases the monopoly mark up, costing Medicare, when the MA plan has market power.

4.2 Competitive Equilibrium with Bidding and Sharing

When competitive equilibrium results in a positive premium, the analysis in Section 3.3 applies with the modification that the sharing rule must be taken into account when the equilibrium premium to beneficiaries is negative. In a competitive equilibrium, average cost in MA must equal plans’ revenue. In the range of a negative premium the following two conditions must hold:

$${\mathrm{AC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})=\mathrm{b}({\mathrm{q}}_{\mathrm{MA}})=\frac{\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})}{\mathrm{s}}+\mathrm{R}$$ (11)

For a given R and s, call the enrollment that solves (11), ${\mathrm{q}}^{\mathrm{e}-\mathrm{b}}$, “competitive equilibrium with bidding.” ${\mathrm{q}}^{\mathrm{e}-\mathrm{b}}$ is shown in Figure 6.

For a given R, increasing the share, s, the plan keeps (and therefore must pass on in premiums), increases enrollment.²² However, the sharing rule is innocuous in the following sense:

Observation 3

With current rules in a competitive market, Medicare can attain any enrollment with various combinations of R and s, all with the same total cost to Medicare.

The result above follows immediately from zero profitability in competitive equilibrium. The premium associated with a ${\mathrm{q}}_{\mathrm{MA}}$ is given by beneficiary demand. One way or another Medicare must pay the difference between that premium and average cost. Mathematically, Medicare’s spending is $\mathrm{b}+\mathrm{s}(\mathrm{R}-\mathrm{b})=\mathrm{AC}({\mathrm{q}}_{\mathrm{MA}})-\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})$, which is constant given ${\mathrm{q}}_{\mathrm{MA}}$. Various combinations of R and s can cover $\mathrm{AC}({\mathrm{q}}_{\mathrm{MA}})-\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})$. The bid will change as R and s change, but Medicare payment and beneficiary premium will not change for a given ${\mathrm{q}}_{\mathrm{MA}}$.

4.3 The MA Plan with Market Power with Bidding and Sharing

The asymmetric sharing rule is not innocuous when the MA plan has market power. The MA plan with market power sets marginal cost equal to marginal revenue. We have previously defined marginal cost as ${\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})$. To find marginal revenue, begin with the relationship between enrollment and total revenue in the presence of Medicare’s asymmetric sharing rule. Let ${\mathrm{q}}^0$ be the number of enrollees joining MA when the premium is 0, i.e., $\mathrm{P}({\mathrm{q}}^0)=0$, then, for a given R and s, the plan’s total revenue as a function of the number of enrollees is given by:

$$\mathrm{TR}({\mathrm{q}}_{\mathrm{MA}}│\mathrm{R},\mathrm{s})=\{\begin{array}{c}{\mathrm{q}}_{\mathrm{MA}}(\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{R})\mathrm{if}{\mathrm{q}}_{\mathrm{MA}}\le {\mathrm{q}}^0\\ {\mathrm{q}}_{\mathrm{MA}}(\frac{\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})}{\mathrm{s}}+\mathrm{R})\mathrm{if}{\mathrm{q}}_{\mathrm{MA}}>{\mathrm{q}}^0\end{array}$$ (12)

From (12), the plan’s marginal revenue is:

$$\mathrm{MR}({\mathrm{q}}_{\mathrm{MA}}│\mathrm{R},\mathrm{s})=\{\begin{array}{c}{\mathrm{q}}_{\mathrm{MA}}{\mathrm{P}}^{\mathrm{\text{'}}}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{R}\mathrm{if}{\mathrm{q}}_{\mathrm{MA}}\le {\mathrm{q}}^0\\ \frac{{\mathrm{q}}_{\mathrm{MA}}{\mathrm{P}}^{\mathrm{\text{'}}}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})}{\mathrm{s}}+\mathrm{R}\mathrm{if}{\mathrm{q}}_{\mathrm{MA}}>{\mathrm{q}}^0\end{array}$$ (13)

When s < 1, the MR function in (13) is discontinuous at ${\mathrm{q}}^0$. The kinked demand curve implies a discontinuous MR curve.²³ Figure 7 depicts the discontinuous MR curve facing the MA firm with market power.

Figure 7.

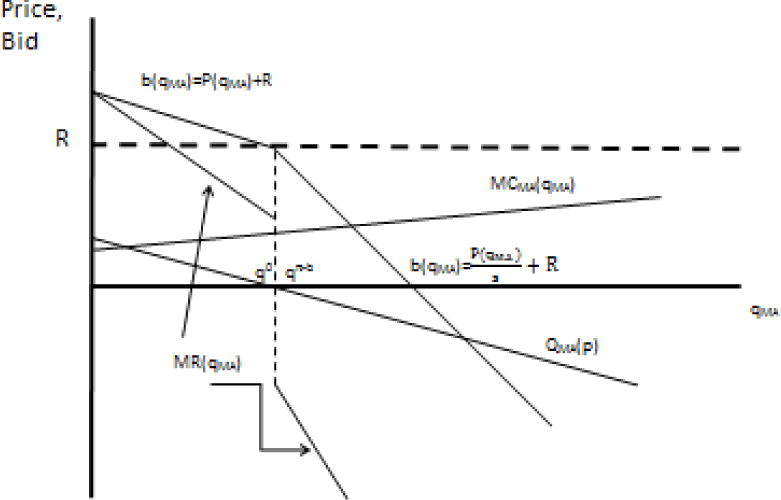
Medicare’s Asymmetric Sharing Rule: MA Plan with Market Power

There are three ranges of solutions for profit maximization. When MR = MC in the range ${\mathrm{q}}_{\mathrm{MA}}<{\mathrm{q}}^0$, s = 1, p > 0 and the analysis is the same as in Section 3.7 above. Figure 7 shows the second case in which the MC curve intersects MR at the point of discontinuity, ${\mathrm{q}}_{\mathrm{MA}}={\mathrm{q}}^0$ and p = 0. Obviously, many potential MC curves would lead to this same profit maximization equilibrium. Figure 7 shows the “profit-maximizing enrollment with bidding” as ${\mathrm{q}}^{\mathrm{\pi }-\mathrm{b}}$ in this case. When MR = MC in the range ${\mathrm{q}}_{\mathrm{MA}}>{\mathrm{q}}^0$, s < 1 and the following MR = MC condition applies:

$$\begin{array}{c}\mathrm{MR}({\mathrm{q}}_{\mathrm{MA}}│\mathrm{R},\mathrm{s})\equiv \frac{{\mathrm{q}}_{\mathrm{MA}}{\mathrm{P}}^{\mathrm{\text{'}}}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})}{\mathrm{s}}+\mathrm{R}={\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})\\ \frac{{\mathrm{q}}_{\mathrm{MA}}{\mathrm{P}}^{\mathrm{\text{'}}}({\mathrm{q}}_{\mathrm{MA}})+\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})}{\mathrm{s}}={\mathrm{MC}}_{\mathrm{MA}}({\mathrm{q}}_{\mathrm{MA}})-\mathrm{R}\end{array}$$ (14)

The effect of changes in R and s on profit maximization also depend on the range in which MR = MC. The analysis from section 3.7 applies when ${\mathrm{q}}^{\mathrm{\pi }-\mathrm{b}}<{\mathrm{q}}^0$. When ${\mathrm{q}}^{\mathrm{\pi }-\mathrm{b}}={\mathrm{q}}^0$ at the point of discontinuity, R and s could change, changing Medicare payments, but profit maximizing enrollment and premium would not change. Medicare could pay more or less to get to the same enrollment outcome ${\mathrm{q}}^0$.

In the range ${\mathrm{q}}^{\mathrm{\pi }-\mathrm{b}}>{\mathrm{q}}^0$, for a given benchmark R, increasing s, the share kept by the plan, increases enrollment, as shown by a comparative static analysis of (14).²⁴ In contrast to the competitive case, the various combinations of R and s that hit a given enrollment target are associated with different Medicare total payments. Consider enrollment $\widehat{\mathrm{q}}$. Medicare payments are total revenue from (12) less the premium collected from beneficiaries:

$$\mathrm{Medicare}\mathrm{Payments}=\widehat{\mathrm{q}}(\frac{\mathrm{P}(\widehat{\mathrm{q}})}{\mathrm{s}}+\mathrm{R}-\mathrm{P}(\widehat{\mathrm{q}}))$$

Condition (14) describes the combinations of R and s that lead to an enrollment being chosen. The R that leads to enrollment $\widehat{\mathrm{q}}$ given s is:

$$\mathrm{R}={\mathrm{MC}}_{\mathrm{MA}}(\widehat{\mathrm{q}})-\frac{{\widehat{\mathrm{q}}}^{\mathrm{P}\mathrm{\text{'}}}(\widehat{\mathrm{q}})+\mathrm{P}(\widehat{\mathrm{q}})}{\mathrm{s}}$$

Substituting for R yields Medicare payments as a function of s alone:

$$\mathrm{Medicare}\mathrm{Payments}=\widehat{\mathrm{q}}(\frac{\mathrm{P}(\widehat{\mathrm{q}})}{\mathrm{s}}+{\mathrm{MC}}_{\mathrm{MA}}(\widehat{\mathrm{q}})-\frac{\widehat{\mathrm{q}}{\mathrm{P}}^{\mathrm{\text{'}}}(\widehat{\mathrm{q}})+\mathrm{P}(\widehat{\mathrm{q}})}{\mathrm{s}}-\mathrm{P}(\widehat{\mathrm{q}}))={\mathrm{MC}}_{\mathrm{MA}}(\widehat{\mathrm{q}})-\mathrm{P}(\widehat{\mathrm{q}})-\frac{\widehat{\mathrm{q}}{\mathrm{P}}^{\mathrm{\text{'}}}(\widehat{\mathrm{q}})}{\mathrm{s}}$$

Because P’ <0, Medicare payments will fall as s goes up. Sharing s has an upper limit of 1 in which the plan keeps the full benchmark-bid gap. Medicare payments are minimized when s =1. Intuitively, because s < 1 makes the MR curve facing the MA plan steeper, the plan marks up marginal cost more as s falls.

Two important points emerge from the analysis in this section, summarized as follows:

Observation 4

The discontinuity in the MR schedule implies that profit-maximizing MA premiums will bunch at p = 0.

This bunching is an indication of the exercise of market power.

Observation 5

Medicare’s attempt to share in savings by setting s < 1 has the opposite effect: in the presence of an MA plan with market power Medicare must pay more to attain any given level of MA enrollment when s < 1, including the efficient level of enrollment.

Observation 5 is an implication of market power. Medicare enhances MA plan market power by setting s <1, and pays for it by needing to pay more in total to attain any level of MA enrollment.

4.4 Beneficiary Asymmetric Response to “Positive” and “Negative” MA Premiums

Medicare presents positive and negative premiums for MA plans to beneficiaries in different ways, leading to a second independent reason for an asymmetric demand response around p = 0.²⁵ The vast majority of MA plans include drug coverage so the incremental premium a beneficiary pays for joining an MA plan is the Part C premium, which can be zero or above, the Part D premium which can be zero or above, and any “buy down” of the Part B premium done by the plan. When a plan buys down, it pays part of the Part B premium to Medicare on behalf of the beneficiary. A plan “buying down” puts p < 0 in terms of our model.

When p > 0, beneficiaries see and pay the additional premium, by for example, writing a monthly check to the MA plan. But if a plan “buys down” the Part B premium (by paying part of the Part B premium to Medicare), most beneficiaries simply have less deducted from their social security check. Actively writing a check for a positive premium is less salient than passively having less automatically deducted from a social security check. In another context, Finkelstein (2009) finds that automatic deductions of toll charges on the highway allowed states – acting just like monopoly sellers – to raise toll rates because of the reduced salience of the automatic deductions.²⁶ Furthermore, research shows that zero is a special price. In binary choice situations, the higher-priced option is more disadvantaged at $1 versus $0 than at $11 versus $10.²⁷

Analysis of the kink in demand created by Medicare’s presentation of positive and negative premiums is similar to the analyses in Sections 4.2 and 4.3. The kink in this case is in the demand function itself, the ${\mathrm{Q}}_{\mathrm{MA}}(\mathrm{p})$ and the inverse demand $\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})$ Even when s =1 and there is no Medicare asymmetric sharing of benchmark less bid amounts, the bid function R + $\mathrm{P}({\mathrm{q}}_{\mathrm{MA}})$ would also be kinked at p =0, just as in the case of asymmetric sharing.

With competition, the kink by decreasing demand for any p < 0 affects market equilibrium. For a given R and cost structure that would lead to a negative equilibrium premium, enrollment is lower. In the case of an MA plan with market power, the effect of the kink is to exacerbate that market power by making demand less elastic in the range of negative premium. The asymmetry in demand response causes a discontinuity in the MR schedule as before, implying that, for a range of MC functions, profit maximization will be at p = 0.

In sum, the demand facing MA plans is kinked for two reasons at p = 0. When plans have market power, decreasing demand elasticity by kinking demand has adverse consequences for Medicare. There is one difference between the two alternative explanations for the kinked demand at p = 0 that is obscured by our use of the EF model. Within the EF framework, the plan characteristics are fixed and the only option an MA plan has to pass through a subsidy to consumers is by reducing the premium. In fact, MA plans can also improve coverage. Coverage improvements may not be subject to the unequal salience effect related to the second explanation for a kink. When plans can improve coverage, the inefficiency associated with the unequal salience can partially take the form of distorting the form of pass through to consumers against premium reductions which may remain “stuck” at a zero premium.

4.5 What is the Evidence for a Kink at p = 0?

The kinked demand and resulting discontinuous marginal revenue curve predicts a bunching up of equilibrium MA premiums at “zero” premium, i.e., no premium above or below the Part B premium. This is just what we see in Figure 8 for 2016, reproducing a pattern presented in Stockley et al (2014) for 2008. About 50% of beneficiaries are in plans with exactly a zero premium. The bunching in the Figure appears at the Part B premium of $104.60 per month.²⁸ There is nothing in the underlying fundamentals of benefits and costs that would imply so many plans price exactly at zero if pricing were competitively determined.

Figure 8.

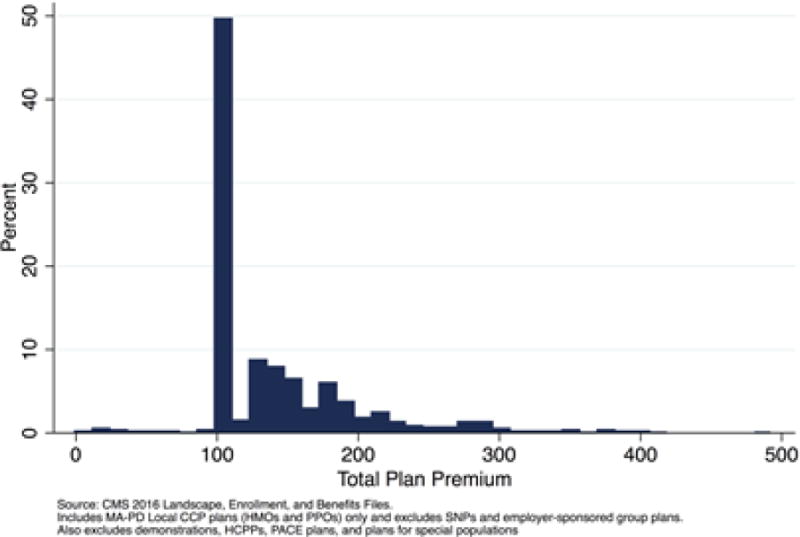
Enrollment Weighted Distribution of Total Plan Premiums in 2016

A second form of evidence comes from the papers studying the “pass-through” rate of the benchmark on to beneficiaries. With competition and a homogeneous beneficiary pool, a dollar increase in the subsidy Medicare pays (i.e., a dollar increase in the benchmark) will be passed forward dollar-for-dollar to consumers in the form of more coverage or lower premium.²⁹ The literature is consistent in finding a pass through of less than one, mostly around 50%, and in one paper, even less.

An apparent “pass-through rate” somewhat less than one is consistent with competition if the marginal enrollees brought to MA through a premium reduction are more costly than the average MA beneficiary, but this marginal/average effect is unlikely to move the pass through much away from 1.0 (Cabral, Geruso and Mahoney, 2014). A pass through of around 50% has been found in a number of studies using different empirical methods for identifying the effect of the benchmark (Song, Landrum and Chernew (2013), Cabral Geruso and Mahoney (2014) and Curto et al. (2014)). The lower pass-through rate is found by Duggan Starc and Vabson (2014) who exploit the approximately 10% higher benchmark payments to plans in counties with populations about 250K, finding no evidence of any effect on premiums, and a possibly small effect on coverage. Consistent with the interpretation that plans kept the higher payments as profits, they present suggestive evidence of higher advertising in the better-paid counties.

Most papers attribute the low pass through to MA plan market power. Duggan, Starc and Vabson (2014) argue that a pass through less than one is due to the relation between marginal revenue and demand. With linear demand, marginal revenue is steeper than demand, and if equilibrium is where payment equals marginal revenue, a given movement down the MR curve due to higher benchmark subsidy corresponds to less of a reduction in price to the consumer. However, this result is not general. If, for example, the price elasticity of demand is constant, the monopolist “marks up” costs at a constant rate greater than one, and a subsidy increase that decreases cost will be more than fully passed through to consumers.³⁰

Papers studying where pass through is high and low are informative about the role of market power and the presence of a kink contributing to the story. In Cabral et al (2014), while the average pass through is around 50%, is much higher, 74% in the most competitive MA markets, and much lower, only 13% in the least competitive markets. Stockley et al. (2014) found that the responsiveness of premiums and benefits to a change in R is greater when the plan is in the range of setting positive premium than when in the negative range, consistent with the kinked demand curve idea.

Pelech’s (2015) study of regulatory shocks to the market structure in MA on premiums and benefits is also consistent with a kinked demand.³¹ As plans gain market power, they ought to increase premium, decrease benefits, or both. In fact, there was little evidence for a premium increase overall, whereas benefits did decrease, consistent with plans being “stuck” at the kink of a zero premium. Furthermore, Pelech (2015) found benefits responded much more to a change in market structure for plans at zero premium than for plans charging a positive premium, as also would be predicted if premiums were stuck at zero.³²

In sum, data on the distribution of premiums in MA and studies of the pass through of the benchmark confirm that demand kinks at p =0, and MA plans have market power.

6. Discussion

Setting the level of the benchmark subsidy to Medicare Advantage plans is Medicare’s most important decision for managing MA. Much policy discussion centers around the idea of a “level playing field” as a basis for setting the benchmark. A level playing field is not a goal, per se, but a policy choice, and our paper shows that once the goal of an efficient MA program is laid out explicitly, the level playing field does not emerge as the policy answer except in a special and unrealistic case. The level playing field is associated with Enthoven-type logic but this logic does not go through with selection/upcoding, marginal/average discrepancies in MA efficiency, and MA plan market power. Furthermore, the level playing field logic neglects the fundamental point that average costs in TM are a function of enrollment, not a fixed value that can be identified and set as a subsidy.

We apply the versatile Einav-Finkelstein model to addressing the issue of how to set the level of subsidy. Not surprisingly, continued favorable selection into MA and substantial upcoding by MA plans implies that the benchmark should be set below average costs in TM. Considerations related to market structure, however, weigh in the other direction. Firms with market power restrict output. MA plans do so as well. The severe bunching of premiums at a “zero price” is an indication that market power is being exercised. Unless market power can be addressed by policy that changes market structure, the way to improve efficiency using the benchmark is to “subsidize monopoly” and set a higher benchmark where insurers have market power. This observation, together with the basic EF conclusion, implies that benchmarks should be set lower than TM average costs, except in markets with limited competition where they should be set at or above the TM average.

Irrespective of these perspectives on the level of the benchmark, Medicare should reconsider aspects of its payment rules that have anticompetitive effects and lead it and beneficiaries to pay too much for MA plans. The sharing rule, by seeming to “cut in” Medicare on savings has the opposite effect, as we prove in Section 4. When the MA plan has market power, Medicare must pay more to attain any given level of MA enrollment than it would without attempting to get a cut of the savings. By making beneficiary demand less elastic, Medicare raises the equilibrium price.

The other change in rules relates to balancing the salience of a positive and negative price for MA plans to beneficiaries, possible using ideas already proposed in Stockley et al (2014). The basic idea is to frame pricing so that beneficiaries “feel” the price for joining MA whether it is above or below the $121.80 price for Part B in TM. One simple way would be to, on the Plan Compare website, make clear that $121.80 is your price for TM and $105.00 is your price for MA Sunset Deluxe, and either of these prices will be deducted from your social security check. If another plan Sunset Deluxe Plus charges $130.00 per month, offer the option of also deducting that from the check. The current policy of making the positive price visible but the negative price obscure is a sure formula for kinking demand.

Although the EF model is well-suited to addressing the issue of the level of the benchmark, the assumption that plans are fixed, while fine for TM, misses any effect of MA plan payment methodology on the MA plan product itself. Inefficiencies of adverse selection take two main forms, inefficient plan choice and inefficient plan design, and our discussion here applying the EF model has been concerned with the first form of inefficiency only. While this is clearly a limitation, we believe it makes sense to address plan sorting with a good model relating the level of payment to equilibrium, whereas the issue of plan design is better addressed with approaches that are directed to the form of plan payment, such as papers that relate risk adjustment to incentives to provide services of different types.³³

Another element missing from our analysis is a consideration of “spillovers” from MA to TM and to the health sector generally. Baicker et al. (2013) find that lower-cost practice patterns in MA plans decrease costs in TM in the same locales. This is another argument against a level playing field, and in isolation would imply a higher subsidy to MA.

In closing, we note that TM itself is changing as the result of reforms initiated by the ACA, most notably by giving provider groups the option to form Accountable Care Organizations (ACOs) and be paid by a mix of prospective and fee-for-service payments. Beneficiaries who elect TM are attributed to ACOs by an algorithm run by Medicare based on where the beneficiary gets their primary care. ACOs have been reasonably well-accepted by provider organizations, but so far have had a measureable but small effect on patterns of care in TM (McWilliams et al., 2016). If ACOs have more of an impact, they will likely have an effect on beneficiary choice between TM and MA, and on the supply of health care inputs to the two sectors. Each of these forces could cause reconsideration of the appropriate level of subsidy to the MA program.