CNR improvement of MP2RAGE from slice encoding directional acceleration

Abstract

Purpose

While MP2RAGE shows the potential to generate B₁ insensitive T₁ contrast, the long TR of MP2RAGE (≥6 s at 7 T) is essential to provide the large dynamic range of apparent T₁ relaxation for dual inversion time acquisitions. We present a 2 direction (2D) accelerated MP2RAGE, which provides an increased flip angle while maintaining similar dynamic recovery as 1D accelerated MP2RAGE.

Method

Simulations were conducted to optimize 2D accelerated MP2RAGE parameters and healthy subjects were scanned with 1D and 2D accelerated MP2RAGE at 7 T. Images were compared visually and contrast to noise (CNR) between brain tissues was measured.

Result

Simulations showed that CNR is primarly determined by the TR, followed by the number of the first partition encoding steps in MP2RAGE. Keeping TR constant, a smaller number of partition encoding steps increases the achievable maximal CNR. In-vivo 2D MP2RAGE improves CNR between white and gray matters by 9% when compared to 1D accelerated MP2RAGE with identical voxel size.

Conclusion

We presented 2D accelated MP2RAGE at 7 T with the increased flip angle. We show that this leads to CNR improvement, and consequently a reduction of scan time to be compared to 1D accelerated MP2RAGE.

1. Introduction

Magnetization-prepared rapid gradient-echo (MPRAGE) [1] has been routinely used to provide 3D brain anatomical information based on T1 weighted tissue contrast. MPRAGE generates T₁ weighted contrast through inversion recovery (IR) preparation and segmented 3D gradient recalled echo (GRE) acquisition with appropriate time delay between the preparation and acquisition (TI). Typically, single k_z encoding is completed with linear view order along the k_z direction for each inversion preparation, which is repeated over different k_y values. TI, flip angle of excitation RF pulses (α) and the time gap between adjacent IR pulses (TR) are the key parameters to be optimized for maximum T1 contrast among white matter (WM), gray matter (GM) and cerebral spinal fluid (CSF) [2]. It is known that MPRAGE is sensitive to B1 inhomogeneity because the apparent relaxation during the readout $\left(1/{\mathrm{T}}_1^{\ast }=1/{\mathrm{T}}_1+ln\left(cos\alpha \right)/\tau \right)$, where τ is the time gap between adjacent RF pulses) spatially varies, depending on the actual flip angle. At ultra-high magnetic field (UHF; ≥7 T) which involves large B1 variation, the B1-induced intensity variation is undesirable for quantitative analysis, e.g. segmentation of brain tissue types.

Magnetization prepared 2 rapid acquisition gradient echoes (MP2RAGE) [3] can reduce image intensity inhomogeneity due to B₁ variation by acquiring two image volumes with different flip angles and inversion times [3,4]. Fig. 1. A shows the timing diagram of the MP2RAGE sequence. After the IR pulse, the first series of low flip angle (α₁) excited GRE acquisitions are collected to complete a single phase encoding (k_y) over the corresponding N_z partition encoding (k_z) steps, followed by the second series of GRE acquisitions with flip angle (α₂) for the same k-space coverage. The dual GRE acquisition per IR pulse is repeated N_y times to obtain two sets of 3D k-space data. The total scan time for an MP2RAGE is thus N_y times TR for full k-space sampling, and can be reduced by undersampling in the k_y dimension using parallel imaging reconstruction (i.e. k_y-direction acceleration) [3].

Fig. 1.

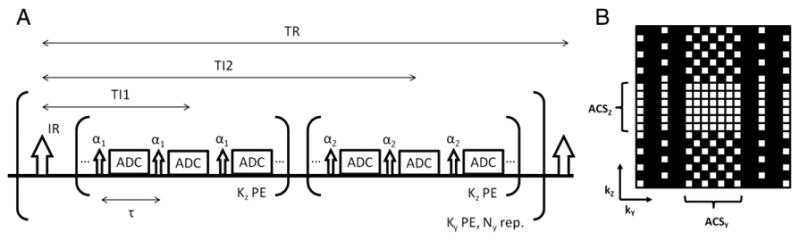
A sequence diagram of MP2RAGE (A) and the example of the proposed 2D accelerated acquisition paradigm with acceleration (acc.) in k_y (=3) and k_z (=2) directions (B). White dots indicate the sampled k-space locations.

Various methods have been proposed to reduce the scan time in MPRAGE-type acquisitions. One common technique is to skip and zero-fill parts of k-space, as in partial Fourier and elliptical sampling schemes. With recent hardware improvements, most importantly multi coil arrays, parallel imaging techniques are increasingly used, making use of the data redundancy when sampling the same object with multiple antennas [5–7]. The original 1D acceleration was extended to accelerate two dimensions [8–10]. Subsequently, the 2D undersampling patterns were optimized to maximize the distance of the point spread functions, known as Controlled Aliasing In Parallel Imaging (CAIPI) [11]. Recently, Brenner et al. proposed accelerated MPRAGE using CAIPI sampling pattern and elliptical acquisition window [12].

In this study, we hypothesize that the number of partition encoding steps acquired for each preparation, or N_z, significantly affects the MP2RAGE signal intensity due to its connection to the apparent T₁ relaxation during the GRE blocks. A simulation was conducted to test the effects of N_z on contrast to noise ratio (CNR) among different brain tissues. Healthy subjects were scanned using MP2RAGE with 1D (k_y direction only) and 2D (k_y and k_z direction) accelerations, and the reconstructed images are compared.

2. Material and methods

2.1. SNR and CNR calculation in MP2RAGE signal intensity

Marques and his colleagues defined the MP2RAGE signal using two different TIs and investigated the noise propagation in the previous study [3]. Here, the mathematical concept of SNR and CNR calculation in MP2RAGE is summarized.

When GRE_TI1 and GRE_TI2 are signal intensities at inversion times TI1 and TI2, then the MP2RAGE signal is described as

$$\mathit{\text{MP}}2\mathit{\text{RAGE}}={\mathit{\text{GRE}}}_{\mathit{\text{TI}}1}^{\ast }{\mathit{\text{GRE}}}_{\mathit{\text{TI}}2}/\left({\mathit{\text{GRE}}}_{\mathit{\text{TI}}1}^2+{\mathit{\text{GRE}}}_{\mathit{\text{TI}}2}^2\right)$$ (1)

where * is a complex conjugation operation, which makes the signal scaled between − 0.5 and 0.5.

Let x, A, and B represent random variables with variance of ${\sigma }_x^2$, ${\sigma }_A^2$ and ${\sigma }_B^2$, respectively.

If x is function of A and B, and if covariance between A and B is zero, then the general noise propagation equation of x can be expressed using the partial derivatives as,

$${\sigma }_x^2={\sigma }_A^2{\left(\partial x/\partial A\right)}^2+{\sigma }_B^2{\left(\partial x/\partial B\right)}^2$$ (2)

Replacing x in Eq. (2) with a MP2RAGE signal, given in Eq. (1), then subsequently, A and B will be replaced with GRE_TI1 and GRE_TI2. Assuming that σ_noise is the standard deviation in real numbers of GRE_TI1 and GRE_TI2, then the noise standard deviation in the MP2RAGE signal is simplified as

$${\sigma }_{\mathit{\text{MP}}2\mathit{\text{RAGE}}}={\sigma }_{\mathit{\text{noise}}}\sqrt{{\left({\mathit{\text{GRE}}}_{\mathit{\text{TI}}1}^2-{\mathit{\text{GRE}}}_{\mathit{\text{TI}}2}^2\right)}^2/{\left({\mathit{\text{GRE}}}_{\mathit{\text{TI}}1}^2+{\mathit{\text{GRE}}}_{\mathit{\text{TI}}2}^2\right)}^3}$$ (3)

CNR between tissues can be defined as the dynamic range of two different tissues divided by the sum of squares of noise on the MP2RAGE signal of each tissue. For example, CNR between WM and GM is;

$${\mathit{\text{CNR}}}_{\mathit{\text{WG}}}=\frac{{\mathit{\text{MP}}2\mathit{\text{RAGE}}}_{\mathit{\text{WM}}}-{\mathit{\text{MP}}2\mathit{\text{RAGE}}}_{\mathit{\text{GM}}}}{\sqrt{{\sigma }_{\mathit{\text{WM}},\mathit{\text{MP}}2\mathit{\text{RAGE}}}^2+{\sigma }_{\mathit{\text{GM}},\mathit{\text{MP}}2\mathit{\text{RAGE}}}^2}}.$$ (4)

CNR between GM and CSF can be described in the similar way. Note that the previous study [3] employed CNR efficiency, divided by square root of TR, but we used CNR between tissues, not including a time term because the direct comparison of MP2RAGE image at different TR's is also of interest in this study.

2.2. Simulation

A computable Bloch simulation of MP2RAGE signals of WM, GM, and CSF was conducted using sequence parameters modified based on ref. [2,3]. The initial longitudinal magnetization, M₀ was set to 100. The signal intensity was calculated with the longitudinal magnetization at each TI, multiplied by a sine term of the flip angle. The exponential T2 term and the different T2 of each tissue, respectively, were not considered. Flip angles were varied from 1° to 12°, and τ was set to 7 ms. N_z was varied from 80 to 180 in increments of 10. Assuming linear acquisition in the partition encoding step, TI₁/TI₂/TR was increased in 100 ms increments, up to a maximum TR = 7 s. T₁ of WM, GM and CSF at 7 T were assumed to be 1.05, 1.85, and 3.35 s, respectively [3]. σ_MP2RAGE in Eq. (3) was normalized by σ_noise and, CNR between WM and GM (CNR _WG) and between GM and CSF (CNR_GC) were calculated using Eq. (4). Also, MP2RAGE signals of each tissue were calculated with a B₁ inhomogeneity of ±40%, which was used in [3]. The optimized parameters for MP2RAGE were determined based on three criteria: 1) Screening the parameter sets that generate MP2RAGE signal variation of less than ±0.07 in WM, GM, and CSF with ±40% B₁ inhomogeneity, 2) MP2RAGE_WM > _GM > _CSF and 3) maximizing CNR_WG or CNR_GC, whichever is smaller.

2.3. Two dimension accelerated MP2RAGE

Fig. 1. A shows the MP2RAGE sequence diagram, as described in the introduction. TI₁ and TI₂ are defined as the time intervals between the IR pulse and the centers of the 1st and 2nd GRE acquisition, respectively. While the acceleration in k_y-direction reduces the scan time, reducing N_z (or k_z-direction acceleration) relaxes the saturation effect of the repetitive readout excitations, thereby leaving room for larger flip angles to obtain higher SNR with similar dynamic range of relaxation recovery as the original N_z. Since MP2RAGE needs to keep a constant TI₁ or TI₂ in each TR, the k_z-direction acceleration is not as flexible as in a GRE sequence without magnetization preparation. We modified a classical 2D CAIPI acquisition paradigm [11] for this study, as shown in Fig.1B. To maximize acceleration efficiency, all k-space except the reference acquisition in the center of k-space is usually undersampled with full acceleration in both k_y and k_z directions with CAIPI paradigm. However, the proposed acquisition is partially undersampled in the k_y and k_z projected space of reference acquisition. Fig. 1B shows the acquisition paradigm in the k_y - k_z space with white squares indicating the sampled k-space locations. In this case, the actual acceleration efficiency is reduced.

2.4. MR experiments

Three healthy subjects were scanned in 7 T scanner (Magnetom 7 T, Siemens, Erlangen) using a single transmit and 32 receive channel phased array head coil with IRB approval. Based on the simulation results, 7 scans were conducted using the optimized MR2RAGE parameters, including 4 scans with isotropic 1 mm voxel size and 3 scans with isotropic 0.75 mm voxel size. For convenience, we call the 1 mm protocols scans A to D, and the 0.75 mm protocols are called scans E to G.

Scans A to D (1mm³) were used to compare 2D accelerated MP2RAGE of varying TR (scans B to D) with 1D accelerated MP2RAGE with TR of 6 s (scan A). Scans E to G (0.75 mm) we used to see if CNR was improved in 2D accelerated MP2RAGE (F and G) with the 1D accelerated MP2RAGE with the same TR (scan E). The detailed parameters of scans A to G are described in Table 1. Z-direction partial Fourier (=6/8) is applied for the (0.75 mm)³ 1D accelerated scan (E) because the large number of N_z (> 200) accelerates the apparent T₁ relaxation recovery during the first acquisition, consequently cannot generate reasonable T1w images among brain tissues. Two 2D accelerated MP2RAGE scans with (0.75 mm)³ voxels were conducted with and without z-direction partial Fourier (6/8). These were scans F and G, respectively. In both phase encoding directions, 32 lines of reference (auto-calibration signal, ACS) were acquired.

Table 1. The optimized MP2RAGE parameters.

Voxel size (matrix)	Scan	Acc.	Partial Fourier	TR (s)	Nz	α1 (°)	α2 (°)	TI1 (s)	TI2 (s)	Scan time
1mm3 (192 × 192 × 176)	A	Ry =3	N/A	6.0	176	3	5	0.9	2.3	8:30
	B	Ry =3 Rz =2	N/A	5.0	104	5	6	1.0	2.2	7:05
	C	Ry =3 Rz =2	N/A	4.0	104	4	8	0.8	1.7	5:40
	D	Ry =3 Rz =2	N/A	3.0	104	4	8	0.6	1.4	4:15
(0.75 mm)3 (256 × 256 × 240)	E	Ry =3	6/8	6.0	180	3	5	0.9	2.3	10:36
	F	Ry =3 Rz =2	6/8	6.0	106	5	6	1.0	2.5	10:36
	G	Ry =3 Rz =3	N/A	6.0	101	6	8	1.0	2.4	10:36

2.5. Reconstruction

Two inversion images and the MP2RAGE signal intensity were reconstructed from raw data using custom MATLAB code. GRAPPA reconstruction was used for scans A and E [5]. Due to the irregular undersampling pattern in 2D accelerated MP2RAGE, shown in Fig.1B, an iterative Self-consistent Parallel Imaging Reconstruction from Arbitrary k-Space (SPIRiT) was used to reconstruct scans B, C, D, F and G [13]. Additionally, scans A and E (with classical 1D GRAPPA acceleration) were reconstructed using SPIRiT to test the effect of different image reconstruction algorithms. No filtering is applied during the image reconstruction. Zero filling is used for partial Fourier reconstruction in scans E and F.

2.6. In-vivo CNR calculation

In-vivo average CNR_WG values were calculated. First, a skull was sculped in INV2 images [14], and MP2RAGE signal was rescaled from 0 (−0.5) to 4055(+0.5). Then, using Freesurfer [15], WM and GM masks were generated and mean and standard deviation (std) values of WM and GM were calculated. CNR_WG was calculated using the equation,

$${\mathit{\text{CNR}}}_{\mathit{\text{WG}}}^{\mathit{\text{measured}}}=\frac{\mathit{\text{mean}}\left({\mathit{\text{MP}}2\mathit{\text{RAGE}}}_{\mathit{\text{WM}}}\right)-\mathit{\text{mean}}\left({\mathit{\text{MP}}2\mathit{\text{RAGE}}}_{\mathit{\text{GM}}}\right)}{\sqrt{\mathit{\text{std}}{\left({\mathit{\text{MP}}2\mathit{\text{RAGE}}}_{\mathit{\text{WM}}}\right)}^2+\mathit{\text{std}}{\left({\mathit{\text{MP}}2\mathit{\text{RAGE}}}_{\mathit{\text{GM}}}\right)}^2}}$$ (5)

Note that the measured CNR_WG values should be different to those in the simulation because M₀ and noise level in the simulation were simplified for the convenience. It is important that the CNR simulation assumes single representative T₁ values and consequently single MP2RAGE signal intensity in each tissues while in-vivo T₁ values of WM and GM vary with the relative large spectrum, as observed in a whole brain T₁ histogram of WM or GM [16]. In the various reasons other than T₁ variaion, which is addressed in Discusssion, standard deviation of MP2RAGE signal intensity in each tissue mask is expected larger than noise in images. Also, it should be noted that additional acceleration in 2D accelerated MP2RAGE induces SNR drop when compared with 1D accerelated MP2RAGE. The direct comparison between in-vivo CNR and the simulated CNR even with different acceleration should be interpreted carefully.

3. Results

3.1. Simulation result

The dependence of CNR_WG on N_z and TR is shown in Fig. 2. The achievable maximum tissue CNR_GC as well as CNR_WG increase as N_z decreases and TR increases (maximum CNR_GC is not shown here). In the simulation, maximum CNR_WG is improved by 56% with TR = 6 s when N_z is decreased from 180 to 100. Even TR = 4 s with N_z = 100 generates the similar range of maximum CNR as TR = 6 s with N_z = 180, as shown in Fig 2B. This achievable maximum CNR gain is induced by the increased optimal flip angle. Fig. 2.C presents the increasing tendency of the optimal flip angles when N_z is decreased in case of TR of 6 s. While alpah1 shows this consistent tendency, the decreasing tendency of alpha2 over Nz is not monotonic, which could be induced by the discrete MR parameters and multi-optimization selection criteria. Cases of other TRs show the similar trend (result not shown).

Fig. 2.

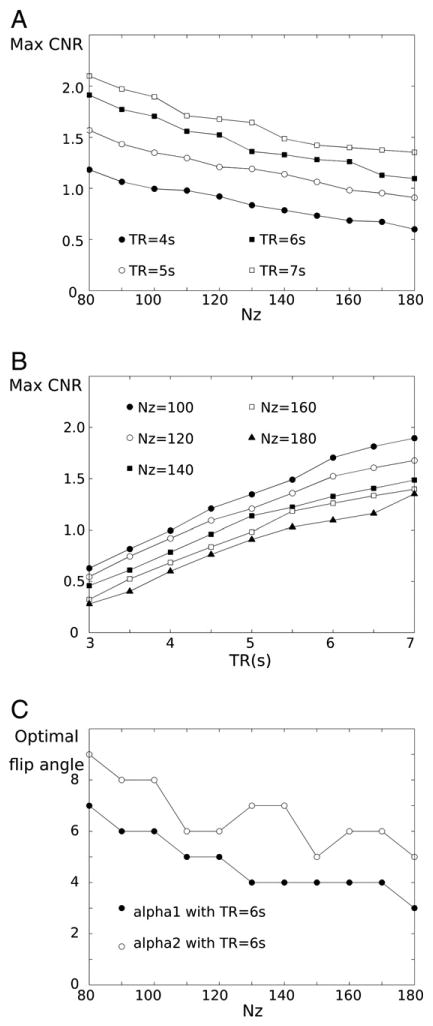
Simulation plots of achievable maximum CNR according to Nz (A) and TR (B), and optimal flip angle with TR of 6 s according to N_z (C). Note that an unit of CNR in A) and B) is arbitrary.

3.2. In-vivo result

Fig. 3 shows the representative MP2RAGE images and enlarged areas with different combinations of N_z, acceleration factors in k_y (R_y) and in k_z (R_z), and TR. In ^1mm3 scans, degradation in image quality is barely observed in MP2RAGE images with TR from 6 to 4 s (Fig.3A to C), but MP2RAGE with TR of 3 s (Fig.3D) shows increased noise in WM regions. Also, it can be observed that 2D accelerated MP2RAGE better suppresses noise compared to 1D accelerated MP2RAGE with the same TR (see the enlarged white matter region in Fig. 4F and G compared to 4E).

Fig. 3.

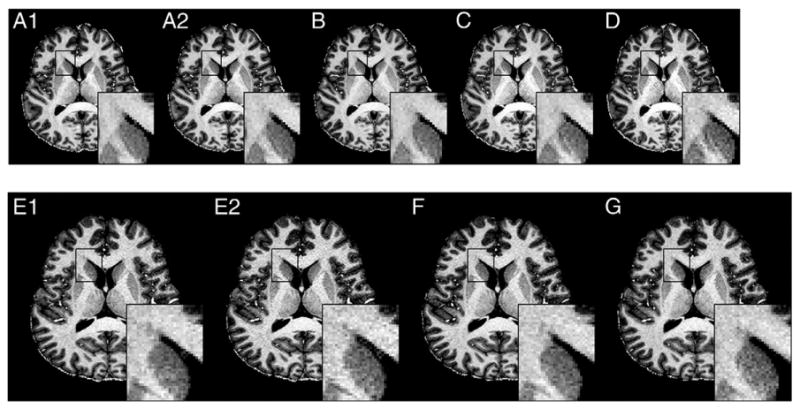
Example of whole brain MP2RAGE of isotropic 1 mm (A-D) and 0.75 mm (E-G) with different TR and acceleration (acc.) factor (R_y × R_z); A1 and A2) TR = 6 s, acc. = 3, scan time = 8:30, B) TR = 5 s, acc. = 3 × 2, scan time = 7:05,C) TR = 4 s, acc. = 3 × 2,scan time = 5:40, D) TR = 3 s, acc. = 3 × 2, scan time = 4:15, E1 and E2) TR = 6 s, acc. = 3, F) TR = 6 s, acc. = 3 × 2,and G) TR = 6 s, acc. = 3 × 3. The scan time of E1,2), F) and G scans is 10:26. A1 and E1 images were reconstructed using GRAPPA algorithm. A2 and E2 were reconstructed using SPIRiT.

Fig. 4. The comparison of in-vivo CNR measures in iso-1 mm scans(A-D) and iso-0.75 mm scans(E-G).

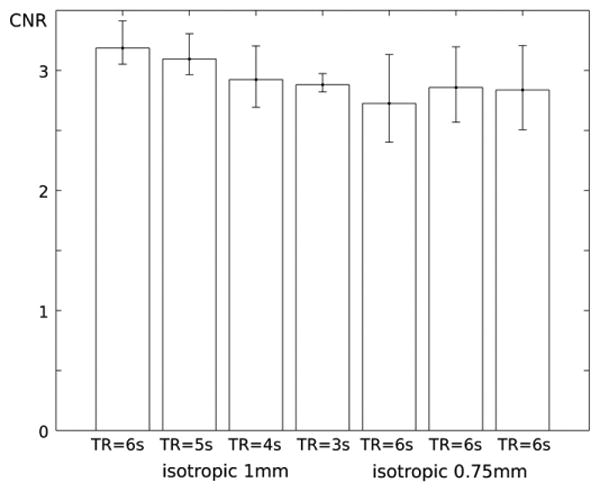
This qualitative difference can be confirmed by comparing average CNR_WG in each scan, and visualized in Fig 4. Average CNR_WG values were decreased by 2%, 7% and 8% as TR is decreased by 5, 4 and 3 s in scans B to D, compared to 1d accelerated SPIRiT reconstructed image. In (0.75 mm)³ protocols, average CNR_WG values were increased by 8 and 9% in 2D accelerated scans F and G when compared to 1D accelerated MP2RAGE using SPIRiT technique, or scan E2. Average CNR_WG values in MP2ARGE is 1% and 3% lower when using SPIRiT than using GRAPPA in ^1mm3 and (0.75 mm)³ protocols. Individual measures are described in supporting Table 1.

4. Discussion

Since apparent relaxation during the repetitive excitation (1/T₁* =1/T₁ + ln(cosα)/τ) is always shorter than the intrinsic T₁, a small N_z allows for a larger flip angle while yielding similar relaxation contrast to an MP2RAGE with large N_z, as shown in Fig 2. For this reason, the MP2RAGE with small N_z will result in improved SNR.

4.1. 2D accelerated MP2RAGE in 1 mm isotropic voxels

When considering the ratio of the presented 1D to 2D acceleration, or of the acquired readout lines, SNR penalty in 2D MP2RAGE is expected to be 23% compared to 1D acceleration. The simulation indicates the maximum CNR_WG with N_z of 100 with TR = 5 s is 23% higher than CNR with N_z 180 in case of TR = 6 s (1.34 vs 1.09). In-vivo CNR_WG in 2D accelerated MP2RAGE with TR of 5 s and N_z of 106 is 2% lower than in 1D accelerated MP2RAGE with TR of 6 s and Nz of 176. It could be explained that 23% of SNR penalty at TR of 5 s is canceled by the 23% of CNR gain due to the increased flip angle.

While the simulation predicts roughly 30% of CNR drop from TR of 5 s to 4 s and from 4 s to 3 s, in-vivo CNR_WG drop in 2D accelerated MP2RAGE was observed with 5% and 1% from TR of 5 s to 4 s and from 4 s to 3 s, respectively, as shown in Fig 4B to D. This discepancy could be explained by the variation of MP2RAGE signal intensity. The discrepancy between the expected CNR from the simulation and in-vivo CNR measrues is addressed in the following limition section.

Two dimentional accelerated MP2RAGE with TR of 5 s and 4 s is hardly noticeable visually, as demonstrated in Fig 3 (scans B and C). To that point, ^1mm3 2D accelerated MP2RAGE with TR of 4 s could be useful, with a total scan time under 6 mins.

4.2. 2D accelerated MP2RAGE in 0.75 mm isotropic voxels

The simulation indicates that the optimized MP2RAGE with N_z = 100 generates 56% higher CNR than with N_z = 180 while 23% and 33% of SNR penalties are expected with 3 × 2 and 3 × 3 acceleration. In in-vivo CNR_WG measures, 2D accelerated MP2RAGE with N_z = 106 (3 × 2 acceleration) and with N_z = 101 (3 × 3 acceleration) generated 9% and 8% higher CNR_WG than 1D accelerated MP2RAGE with N_z = 180. However, 9% and 8% of in-vivo CNR improvements with 2D acceleration are smaller than the expected 27% and 18%, when simply counting the expected gain and loss.

In iso 0.75 mm protocol, we have not tested the different TRs,e.g. TR of 4 or 5 s. However, it is expected that the 2D acceleration in MP2RAGE high resolution protocol provides the compatible CNR with less scan time than 1D accelerated MP2RAGE of TR of 6 s, as demostrated in the isotropic 1 mm protocol. In scan E, the in-vivo CNR_WG value was decreased by 3% in MP2RAGE image reconstructed using SPIRiT compared to MP2RAGE image reconstructed using GRAPPA. Optimized SPIRiT reconstruction parameters could generate the larger CNR values than those presented, e.g. iteration number.

4.3. 2D accelerated MP2RAGE acquisition paradigm

We used CAIPI-type of partially accelerated acquisition paradigm, visualized in Fig. 1B. Note that the partial acquisition in k-space leaving out the centre of k-space to acquire the reference lines was not accelerated in the most efficient way. When comparing the ratio of the full k-space to the partial acquisition, or the acceleration efficiency, ^1mm3 protocols of 2D accelerated MP2RAGE with acceleration (acc.) factor (R_y × R_z) of 3 × 2 (scans B through D) exhibit acc = 3.81 while the achievable maximum acceleration efficiency would be 5.21 if 32 lines of reference in the center of k-space are acquired. The acceleration efficiency in (0.75 mm)³ protocols of MP2RAGE with acc. = 3 × 2, and 3 × 3 were 4.08 and 5.68 while the achievable maximum acceleration efficiency would be 5.40 and 7.94 (F and G scans). The presented acquisition paradigm will be able to be optimized a using fully CAIPI-type sampling pattern [11] with elliptical k-space region while the center of the series of GRE readout is aligned at k_z = 0, as presented in Brenner and his colleagues' work [12]. That would further accelerate the scan time. Furthermore, the reconstruction algorithm should also be implemented directly on the scanner for an optimized workflow, while the SPIRiT reconstruction used in this study was iteratively solved in an off-line reconstruction. However, the maximized or increased acceleration is expected to be compensated by decreased SNR.

4.4. Limitation in the study

We optimized MP2RAGE parameter using the simulation, which was presented the reference [3], and calculated maximized CNR with the chosen parameterstion. We compared the achievable CNR from the simulation with in-vivo CNR values. While the comparison between A) and B) scans shows the good agreement with the simulation, in-vivo CNR drop from B) to D) scans is smaller than the expected from the simulation. Also, the expected CNR improvement in F) and G) scans is smaller than in-vivo, when considering SNR loss from the additioanl acceleration.

As addressed in Method section, we suspect the main source of this discrepancy might be MP2RAGE singal variation in tissues. The spatial variation of MP2RAGE signal intensity could stem from residual B₁ inhomogeneity, intrinsic T₁ differences across the brain, spatial coil sensitivity, and the spatial dependency of parallel imaging reconstruction efficiency or G-factor [17]. In addition, different proton density and T₂ values in tissues, which are not considered in the simulation, would generate the different level of noise over tisseus. For that reason, we expect the standard deviation of in-vivo MP2RAGE signal intensity in WM and GM ROIs in Eq. (1) are larger than the simulation.

Also, the simple noise assumption in the simulation, e.g. Gaussian distribution in the real comparment could not systhesize the complicate noise exposition in a real case. However, it is beyond the scope of the presented study.

5. Conclusion

We presented that a 2D accelerated MP2RAGE reduces the first PE steps or Nz, which allows increasing flip angle with the similar equilibrium magnetization during the inversion recovery. The increased flip angle in MP2RAGE would provide improved CNR with scan time or TR fixed, and reduce TR with relatively small CNR loss. The proposed 2D accelerated acquisition paradigm can also be useful in MPRAGE, especially at 3 T. Currently, 9 to 10° flip angles are typically used in MPRAGE at 3 T [18]. By decreasing N_z, a larger flip angle in 2D accelerated MPRAGE can be feasible to keep a similar dynamic range of recovery with the same TR in a conventional MPRAGE, but provide improved CNR. Then, high resolution (< 1mm³) 2D accelerated MPRAGE image could be feasible.