Temporal Variation in Single-Cell Power-Law Rheology Spans the Ensemble Variation of Cell Population

Abstract

Changes in the cytoskeletal organization within cells can be characterized by large spatial and temporal variations in rheological properties of the cell (e.g., the complex shear modulus G^∗). Although the ensemble variation in G^∗ of single cells has been elucidated, the detailed temporal variation of G^∗ remains unknown. In this study, we investigated how the rheological properties of individual fibroblast cells change under a spatially confined environment in which the cell translational motion is highly restricted and the whole cell shape remains unchanged. The temporal evolution of single-cell rheology was probed at the same measurement location within the cell, using atomic force microscopy-based oscillatory deformation. The measurements reveal that the temporal variation in the power-law rheology of cells is quantitatively consistent with the ensemble variation, indicating that the cell system satisfies an ergodic hypothesis in which the temporal statistics are identical to the ensemble statistics. The autocorrelation of G^∗ implies that the cell mechanical state evolves in the ensemble of possible states with a characteristic timescale.

Introduction

Adherent tissue cells exhibit a dynamic cytoskeleton (CSK), a heterogeneous structure that is organized as a complex network of three types of filaments, namely, actin filaments, microtubules, and intermediate filaments. It has been widely recognized that the network-forming actin filaments in living cells are dynamically remodeled (1, 2, 3, 4, 5) and highly adapted according to the surrounding environment (6, 7, 8) and external forces (9, 10). The complex shear modulus G^∗ of cells, which is composed of the storage modulus G′ and the loss modulus G″, has been measured using active rheological measurement techniques such as magnetic twisting cytometry (MTC). These rheological properties plausibly exhibit significant temporal variation in even a single cell monitored over time, due to the remodeling of the CSK network (11). Therefore, detailed knowledge of the temporal change in G^∗ is crucial to understand how the CSK components such as filamentous actin fluctuate to retain the ability to remodel and adjust flexibly according to external forces.

The number (ensemble) distribution of G^∗ has been extensively studied over the past two decades. Studies have revealed that the ensemble average of G^∗ follows single (11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25) or multiple (26, 27, 28, 29, 30) power-law behaviors over multiple decades of frequency centered around 10 Hz. A recent study (25) reported that the cell-to-cell (ensemble) variation of G^∗ also exhibits frequency- and chemical-dependent features that can be understood under the framework of the soft glassy rheology (SGR) model (12, 13, 14) of cell deformability. However, the temporal distribution of G^∗ of single cells is less well understood.

To elucidate the relationship between the temporal and the ensemble variations, we investigated the temporal variation in G^∗ of single cells cultured in a micropatterned substrate, in which cell migration is highly restricted and the cell shape remains unchanged (2, 31, 32, 33). Using atomic force microscopy (AFM) to probe these single cells placed at the same locations in the microfabricated substrate, we traced the time evolution of G^∗ for single cells as a function of frequency f. G^∗ exhibited a log-normal temporal distribution; notably, both the average and the variation within a single cell matched those of the ensemble of many cells. Moreover, we found that the inherent temporal variation of G′ was consistent with that of the ensemble of the cell population, suggesting that the rheological properties of cells under a spatially confined condition follow an ergodic condition in which the temporal statistics are identical to the ensemble statistics.

Materials and Methods

Substrate fabrication

A gold thin film with a chromium adhesion layer was micropatterned on a glass substrate. A square motif, with 30-μm side length and 50-μm spacing between neighboring sides, was produced by standard photolithography. In brief, a photoresist (OFPR-800 LB; Tokyo Ohka Kougyou, Tokyo, Japan) was coated onto the gold film, selectively illuminated via a chrome-plated quartz photomask under 436-nm ultraviolet light, and dissolved with a developer (NMD-3; Tokyo Ohka Kougyou). The gold and chromium films were etched away with a gold etchant (TFA; Transene, Danvers, MA) and a mixed solvent of diammonium cerium(IV) nitrate (Kanto Chemical, Tokyo, Japan) and perchloric acid (Kanto Chemical), respectively, in the square-shaped regions, which were identified under an optical microscope. Then, the substrate was immersed in 0.25 μg/mL hydroxy-EG6-undecanethiol (H355; Dojindo Laboratories, Kumamoto, Japan) in ethanol to form a self-assembled monolayer on the gold-patterned regions. Finally, fibronectin (BD Biosciences, San Jose, CA) as a 10 μg/mL solution was coated onto the square-shaped bare glass regions to promote cell adhesion in those locations.

Cell samples

Mouse fibroblast NIH3T3 cells (American Type Culture Collection, Manassas, VA) were cultured at 37°C and 5% CO₂ atmosphere for 1−2 d in Dulbecco’s modified Eagle’s medium (Sigma-Aldrich, St. Louis, MO) containing penicillin (100 units/mL), streptomycin (100 mg/mL) (Sigma-Aldrich), and 10% fetal bovine serum (HyClone, Logan, UT). The cells were suspended with trypsin (Sigma-Aldrich) and then deposited onto the micropatterned substrate. After incubation for 2 h in the same culture medium, the cell samples were gently washed to remove excess cells that did not adhere well on the square glass regions and then incubated for another 8 h. AFM experiments were conducted to quantify the rheological properties of highly spread cells in the square regions in CO₂-independent medium (Invitrogen, Carlsbad, CA) at room temperature.

AFM measurements of cell rheology

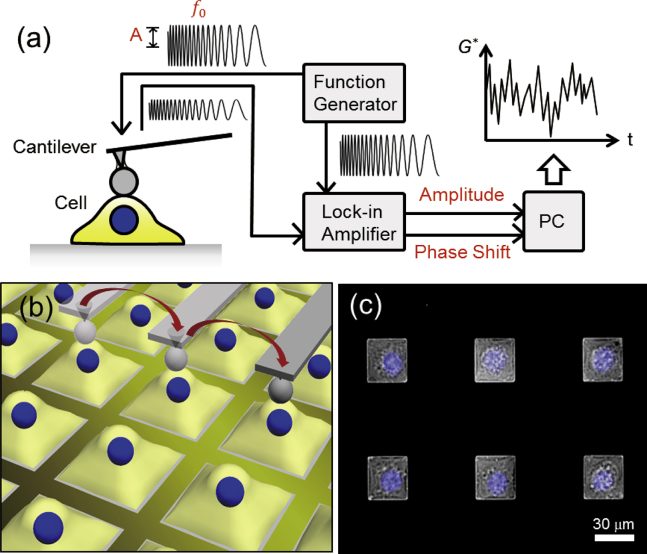
Details of the AFM system and its calibration have been described elsewhere (25, 34, 35). In brief, a commercial atomic force microscope (MFP-3D AFM; Asylum Research, Santa Barbara, CA) with a system for controlling microscope stage displacements at the millimeter scale (34) was used to examine the rheology of NIH3T3 cells. A colloidal probe cantilever, comprising a silica sphere with a radius R of ∼2.5 μm (Funakoshi, Tokyo, Japan) attached to the free end of the AFM cantilever (BL-AC40TS-C2, BioLever Mini; Olympus, Tokyo, Japan), was used for the force modulation measurements (35, 36, 37). An initial force of 650 pN was applied to a single cell at the center of a square adhesive region, and the modulation frequency was changed in a stepwise manner as f = 3, 5, 10, 25, 50, 100, 150, and 180 Hz, during which the amplitude at the free end of the AFM cantilever far from the cell surface was set at 10 nm. The indentation depth, which depends on the local stiffness of the cell at the measurement location, averaged ∼1.5 μm in this study. The amplitude and phase shift of the cantilever displacement with respect to the reference signal were detected with a lock-in amplifier (7260; Seiko EG&G, Tokyo, Japan) (Fig. 1).

Figure 1.

Schematics of the AFM force modulation of G^∗ of a single cell fluctuating in time (a) and the time-lapse measurement of single cells placed in square-shaped regions without cell-cell contact (b). The force modulation was examined at the center of the square region with a time interval of 80 s. The untreated cells were measured at the center of the square regions, and the same single cells were measured at the same locations after cytoD treatment. (c) Given here is an overlay of the phase contrast image of NIH3T3 cells cultured on the micropatterned substrate and the fluorescence image of the cell nuclei. To see this figure in color, go online.

For temporal experiments, after cells had been measured successively for 80 min with an interval time of 80 s, the cell sample was incubated for 20 min in 1 μM cytochalasin-D (cytoD), which inhibits actin filament polymerization, and the same cells were then measured again via oscillatory deformation. A challenge associated with single-cell temporal measurements is to maintain the cell shape during successive AFM indentations after the actin filaments are partially depolymerized because the cell adhesion is highly perturbed by depolymerizing the actin filaments. In this study, conducted at room temperature, we were able to measure several cells (n = 8 cells) in different dishes without observing any substantial change in cell shape over the relatively long measurement time.

To estimate the number distribution of G^∗, at least 50 single cells per condition were measured at the center of the square adhesive regions. In this study, we obtained the number distributions of cells in different dishes (n = 6 dishes) to estimate the ensemble variation associated with single cell rheology.

We used the Hertzian contact model, approximately expressed as follows (21, 38, 39, 40):

$$F^{\ast }=\frac{4R^{1/2}}{3\left(1-{\nu }^2\right)}\left(E_0{\delta }_0^{3/2}+\frac{3}{2}{E}_1^{\ast }{\delta }_0^{1/2}{\delta }_1^{\ast }\right),$$ (1)

where F^∗ (which is a complex function, as indicated by the asterisk) is the loading force with a small amplitude indentation oscillation; and δ₁^∗, around an operating indentation, δ₀, and E₀, is the Young’s modulus at zero frequency obtained from the approach force curve. During the indentation, cells undergo stress relaxation. In this study, the operating indentation (of ∼1.5 μm) could be considered constant because the change in deflection (<10 nm) was much smaller. We assumed the Poisson’s ratio of the cell v to be 0.5. The frequency-dependent Young’s modulus E₁^∗ is given by 2(1 + v)G^∗ (41). Eliminating the hydrodynamic drag force F_d^∗, given by F_d^∗/δ₁^∗ = ib(0)f, where b(h) is a viscous drag factor that depends on the separation distance h between the cell surface and the probe (42), we can obtain the G^∗ of cells as

$$G^{\ast }=G^{\mathit{\prime }}+i{G}^{\mathit{″}}=\frac{1-\nu }{4{\left(R{\delta }_0\right)}^{1/2}}\left[\frac{F_1^{\ast }}{{\delta }_1^{\ast }}-ib\left(0\right)f\right],$$ (2)

where G′ and G″ represent the storage and loss moduli of the cell, respectively, i is the imaginary unit, and $F_1^{\ast }=2{\left(R{\delta }_0\right)}^{1/2}{E}_1^{\ast }{\delta }_1^{\ast }/\left(1-{\nu }^2\right)$ The value of b(0) was determined by extrapolating values of b(h) measured at various separation distances at f = 100 Hz.

Data analysis

We analyzed G′ and G″ as a function of f using the software Igor Pro (WaveMetrics, Lake Oswego, OR) with a built-in global fitting procedure.

The standard deviation σ_X of a quantity X with a normal distribution is expressed by

$${\sigma }_X={\left[\frac{1}{n}\sum _{i=1}^n{\left(X_i-\langle X\rangle \right)}^2\right]}^{1/2},$$ (3)

where n is the number of data points, corresponding here to the number of measured cells for what we refer to as the “ensemble experiment” or the number of measured points for a single cell over the duration of what we refer to as the “temporal experiment”. Here X_i denotes the individual ith data, and 〈X〉 is the arithmetic mean of X. We define ${\sigma }_X^E$ and ${\sigma }_X^T$ as the ensemble (cell-to-cell) and the temporal variation of X, respectively. $\overline{Z}$ denotes the geometric mean of quantity Z with a log-normal distribution. Student’s t-test was used to test for statistically significant differences in the frequency-dependent component between the ensemble and temporal variations of G′.

Soft glassy rheology of cell deformability

The temporal behavior of the averaged G^∗ and its variation is less well understood, but it has been recognized in ensemble experiments of cell populations (13, 14, 15, 43) that G′ and G″ as a function of f follow the power-law structural damping model with additional Newtonian viscosity, which is expressed by

$$G^{\ast }=g\left(\alpha \right)\left(1+i\eta \right){\left(\frac{f}{f_0}\right)}^{\alpha }+i\mu f,$$ (4)

where α is the power-law exponent; and g(α) is Γ(1−α) cos(πα/2), where Γ denotes the gamma function. G₀ is a scale factor of the modulus at a scale factor of frequency f₀, which is generally arbitrarily set to be 1 Hz. The hysteresivity η(α) is equivalent to tan(πα/2), and μ is the Newtonian viscous damping coefficient.

According to the SGR model (44, 45), the mechanical state of cells on average evolves within an energy landscape with a high number of local minima. The typical depth of these minima is much larger than the thermal noise, and thus the temporal evolution in this energy landscape proceeds as a result of activation energy, such as a loading force in the case of active microrheological measurements (2, 14, 15, 46). As the frequency for the loading force is increased, G′ increases in a power-law manner, where the power-law exponent (sometimes referred to as the “fluidity”) corresponds to a degree to which the mechanical state of the cell undergoes hopping among the local minima. At the higher frequency limit of f = Φ₀, the modulus G′ = g₀ is conserved across changes in intracellular structure; it is considered that the cell mechanical state is no longer able to escape from the trapped local minima (13, 14, 15). Thus, the ensemble-averaged storage modulus $\overline{G^{\mathit{\prime }}}$ of each single cell is expressed as (25)

$$\overline{G^{\mathit{\prime }}}={\overline{g}}_0{\left(\frac{f}{{\overline{\Phi }}_0}\right)}^{\alpha },$$ (5)

where the point $\left({\overline{g}}_0,{\overline{\Phi }}_0\right)$ can be estimated by extrapolating the $\overline{G^{\mathit{\prime }}}$ versus f curves measured under control (untreated) and CSK-modified conditions (14, 15). The SD of G′,${\sigma }_{\text{log}{G}^{\mathit{\prime }}}$, is approximately expressed as (25)

$${\sigma }_{\text{log}{G}^{\mathit{\prime }}}={\sigma }_{\text{log}{g}_0}+\left(\text{log}{\overline{\Phi }}_0-\text{log}f\right){\sigma }_{\alpha },$$ (6)

where ${\sigma }_{\text{log}{g}_0}$ is the SD of the storage modulus at $f={\overline{\Phi }}_0$. The first term is independent of f, and the second term is the frequency-dependent component ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}$. Similarly, ${\sigma }_{\text{log}{G}^{\mathit{\prime }}}$ can be expressed as a function of $\text{log}{G}^{\mathit{\prime }}$ (25):

$${\sigma }_{\text{log}{G}^{\mathit{\prime }}}={\sigma }_{\text{log}{g}_0}+\frac{{\sigma }_{\alpha }}{\langle \alpha \rangle }\left(\text{log}{\overline{g}}_0-\text{log}\overline{G^{\mathit{\prime }}}\right).$$ (7)

An approximate expression of ${\sigma }_{\text{log}{G}^{\mathit{″}}}$ has been derived previously (see Eq. S19 in (25)).

Results

Temporal distribution of G^∗ of single cells

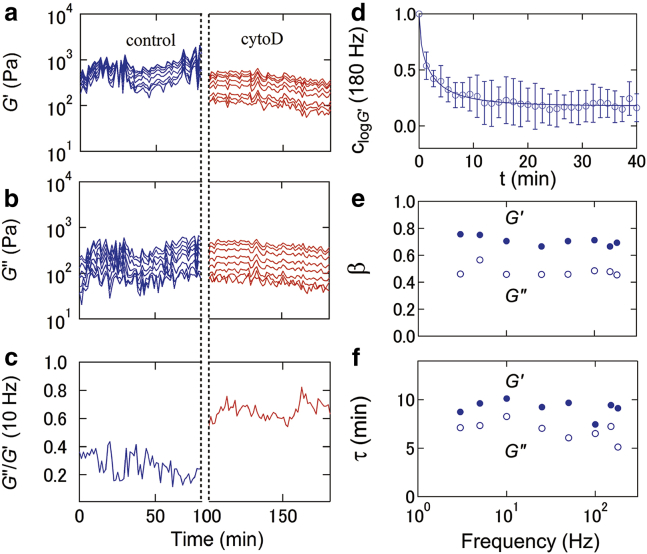
Fig. 2, a and b, shows a typical time course of G′ and G″ of a single cell, respectively, at different frequencies measured at the center of the square regions containing single adhered cells. Note that G′ and G″ markedly fluctuate with time under the control condition, as also observed by MTC (11), whereas the variation of the fluctuation amplitude in the time course of G′ and G″ is reduced markedly after treatment with cytoD. This result indicates that the fluctuation of G^∗ is intimately associated with the organization of actin filaments.

Figure 2.

Time course of G′ (a) and G″ (b) of NIH3T3 cells cultured in the square regions at different frequencies during the untreated condition (0–80 min) and the cytoD-treated condition (100–180 min) in which the cell was incubated for a period of 80–100 min after addition of cytoD at 80 min. The measurement frequency corresponds to 180, 150, 100, 50, 25, 10, 5, and 3 Hz from the upper to lower data plots. (c) Given here is the time course of G″/G′ at a frequency of 10 Hz. (d) Given here is the autocorrelation function of log G′, c_{log G′}(t) (n = 8), at f = 180 Hz for the untreated cells. The solid line represents the fitted result from the stretched exponential function, Eq. 8. The relaxation time τ (e) and stretching exponent β (f) of c_{log G∗}(t) for untreated cells is given as a function of frequency. To see this figure in color, go online.

The fluctuation profiles of both G′ and G″ at different frequencies were highly synchronized, indicating that these shear moduli follow a frequency-dependent function in time. Moreover, the ratio of G″ to G′ (G″/G′) of cells at 10 Hz converged at ∼0.3 in the control condition and increased markedly to ∼0.7 in the cytoD-treated condition (Fig. 2 c), revealing structural damping behavior depending on the CSK organization that can be modulated by actin polymerization (14, 15, 21, 47).

To understand how G^∗ evolves in the mechanically possible states, we investigated the autocorrelation of log G^∗ for untreated cells. A typical autocorrelation of log G′, $c_{\text{log}{G}^{\mathit{\prime }}}=\langle \text{log}{G}^{\mathit{\prime }}\left(0\right)\text{log}{G}^{\mathit{\prime }}\left(t\right)\rangle /\langle {\left(\text{log}{G}^{\mathit{\prime }}\right)}^2\rangle$ at f = 180 Hz, is shown in Fig. 2 d. The observed autocorrelation relaxed to a constant value in both G′ and G″; such behavior could not be fitted to a single exponential function but was consistent with a stretched exponential function:

$$c_{\text{log}{G}^{\ast }}\left(t\right)-c_{\text{log}{G}^{\ast }}\left(\infty \right)=\left(1-c_{\text{log}{G}^{\ast }}\left(\infty \right)\right)\text{e}\text{x}\text{p}\left\{-{\left(t/\tau \right)}^{\beta }\right\},$$ (8)

which is empirically employed to describe relaxation curves with multiple decay modes; τ and β are the relaxation time and the KWW stretched exponential power of the autocorrelation function of G^∗, respectively. We found that in both G′ and G″, τ was 5–10 min (Fig. 2 e); β was in the range of 0.4–0.8 (Fig. 2 f), indicating that the autocorrelation exhibits a multiple decay; and that these characteristics were not a function of frequency over the range of 3–180 Hz for these AFM experimental conditions.

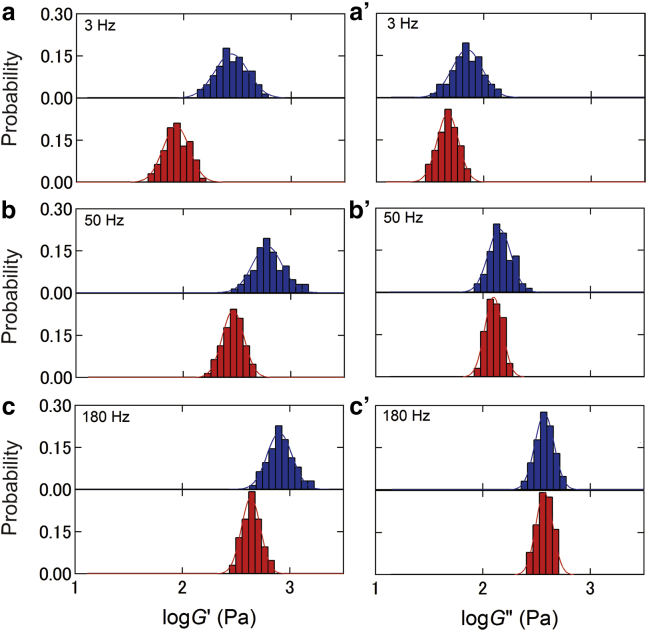
Fig. 3 shows the temporal distribution of G′ and G″, at different oscillation frequencies, which are estimated from Fig. 2, a and b, respectively. This log-normal distribution narrowed with increasing frequency f. Treatment with cytoD caused a decrease in both the average value and the width of this distribution.

Figure 3.

Temporal distributions of G′ (left) and G″ (right) moduli of a single NIH3T3 cell measured at the cell center under untreated (blue) and cytoD-treated (red) conditions at different frequencies: (a) 3, (b) 50, and (c) 180 Hz. The solid lines represent the fitted results of untreated and treated cells using a log-normal distribution function. To see this figure in color, go online.

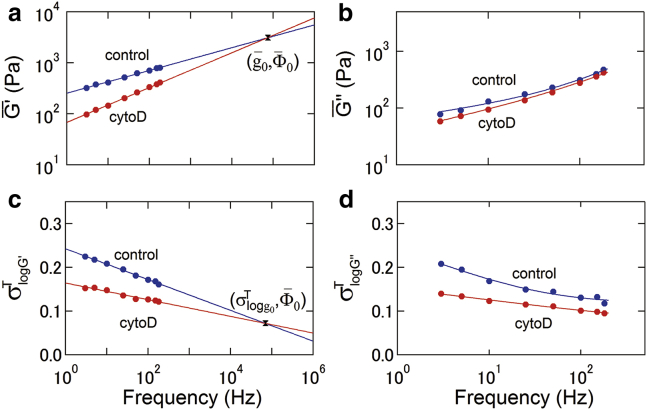
To clarify more quantitatively the temporal distribution of G^∗ shown in Fig. 3, we plotted the temporal average $\overline{G^{\ast }}$ and the SD of G^∗ distribution, ${\sigma }_{\text{log}{G}^{\ast }}^T$, versus frequency f (Fig. 4). Note that ${\overline{G}}^{\ast }$ (Fig. 4, a and b) and ${\sigma }_{\text{log}{G}^{\mathit{\prime }}}^T$ (Fig. 4 c) are well fitted to Eqs. 4 and 6, respectively. Moreover, there exists a characteristic frequency $f={\overline{\Phi }}_0$ at which the extrapolated lines of $\overline{G^{\mathit{\prime }}}$ and ${\sigma }_{\text{log}{G}^{\mathit{\prime }}}^T$ for the treated and untreated cells intersect with ${\overline{G}}^{\mathit{\prime }}={\overline{g}}_0$ and ${\sigma }_{\text{log}{G}^{\mathit{\prime }}}^T={\sigma }_{\text{log}{g}_0}^T$, respectively. These results indicate that the temporal average G′ value of cells follows a single power law based on the SGR model of cell deformability in the measured frequency range, as observed in the ensemble experiments (25). As shown in Fig. 4, b and d, the temporal average and the variation for G″ also follow the power-law rheology model, although there is no detectable difference in the temporal average between untreated and cytoD-treated cells.

Figure 4.

Frequency dependencies of $\overline{G^{\ast }}$($\overline{G^{\mathit{\prime }}}$ (a) and $\overline{G^{\mathit{″}}}$ (b)) of untreated (blue) and cytoD-treated (red) cells. Solid lines in (a) and (b) represent the fitted results from Eq. 4. The point where the curves of $\overline{G^{\mathit{\prime }}}$ intersect is defined as $\overline{G^{\mathit{\prime }}}={\overline{g}}_0$ at $f={\overline{\Phi }}_0$. Given here are frequency dependencies of σ_{log G′} (c) and σ_{log G″} (d) of untreated (blue) and treated (red) cells. Solid lines in (c) represent the fitted results from Eq. 6. The point where the curves of σ_{log G′} intersect is defined as (${\overline{\Phi }}_0$, ${\sigma }_{\text{log}{g}_0}$). Solid lines in (d) represent the fitted results from Eq. S19 in Cai et al. (25). To see this figure in color, go online.

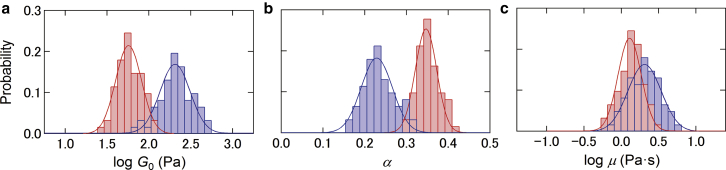
Fig. 5 shows the temporal distribution of the parameters of the power-law rheology of untreated and cytoD-treated cells, estimated from Eq. 4. The values G₀ and μ display a log-normal distribution, whereas the power-law exponent α exhibits a Gaussian distribution. These results are also consistent with those observed in the ensemble distributions (25).

Figure 5.

Temporal distribution of log G₀ (a), α (b), and log μ (c) of untreated (blue) and cytoD-treated (red) cells measured at the center location of the square region. The solid lines represent the fitted results of untreated and treated cells using a log-normal distribution function (a and c) and a normal distribution function (b). To see this figure in color, go online.

Inherent temporal variation of G′ of single cells

In a previous report on ensemble experiments of many cells within a population, the magnitude of ${\sigma }_{\text{log}{G}^{\prime }}^E$ measured by AFM oscillatory deformation varied significantly among cell sample dishes (i.e., among different cell populations of ostensibly the same cell type and culture conditions). However, the frequency-dependent component of ${\sigma }_{\text{log}{G}^{\prime }}^E$, ${\tilde{\sigma }}_{\text{log}{G}^{\prime }}^E$, which is defined as ${\sigma }_{\text{log}{G}^{\prime }}^E-{\sigma }_{\text{log}{g}_0}^E$, remained invariant among the cell samples (25). Those results suggested that ${\sigma }_{\text{log}{g}_0}^E$ includes experimental variation, such as instrumental noise and day-to-day influences under in vitro culture, in addition to the purely elastic component in terms of the SGR model of cell deformability. Therefore, ${\tilde{\sigma }}_{\text{log}{G}^{\prime }}^E$ corresponds to the frequency dependence of inherent cell-to-cell variation.

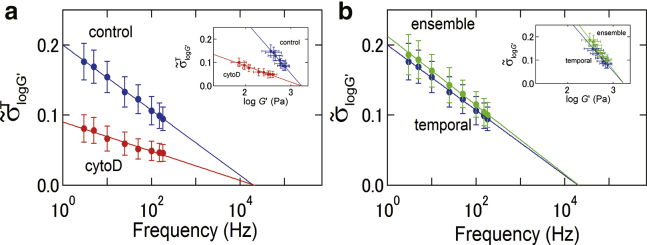
We measured the temporal change in G^∗ for cells (n = 8 cells) in different dishes. For each of the cells, we plotted ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ as a function of f, as shown in Fig. 4, and estimated ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$. Fig. 6 a shows the averaged frequency-dependent component of temporal variation ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ (n = 8 cells) as a function of log f. The magnitude of ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ was reduced as the actin filaments were depolymerized with cytoD. Moreover, we observed that the plot of ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ versus log G′ was well fitted to Eq. 7 (inset of Fig. 6 a). As parameterized by Eq. 3, the magnitude of the variation of a parameter depends on its absolute value. We observed that ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ of the treated cells was smaller than that of the untreated cells when both ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ values were evaluated at the same $\overline{G^{\ast }}$ value but at different frequencies (inset of Fig. 6 a). This result indicates that the observed difference between cytoD-treated and control cells in terms of ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ can be attributed to the altered presentation of the actin filaments. Therefore, we conclude that a strong coupling exists between the temporal variation and the cytoskeletal actin organization of cells.

Figure 6.

(a) Plots of ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$, which represents ${\sigma }_{\text{log}{G}^{\mathit{\prime }}}^T-{\sigma }_{\text{log}{g}_0}^T$ as a function of log f in untreated (blue) and cytoD-treated (red) conditions. The inset shows ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ versus $\text{log}\overline{G^{\prime }}$. Solid lines represent the fitted results from Eq. 6 in (a) and Eq. 7 in the inset. (b) Given here is a comparison of inherent frequency-dependent variations ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}$ for temporal (blue) and ensemble (green) experiments. The inset shows both ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}$ values as a function of $\text{log}\overline{G^{\prime }}$. Solid lines represent the fitted results from Eq. 6 in (a) and Eq. 7 in the inset. The number of these experimental data was n = 8 cells for the temporal variation and n = 6 dishes for the ensemble variation. To see this figure in color, go online.

Comparison between temporal and ensemble variations

Fig. 6 b shows the ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}$ values estimated from the ensemble and temporal variations of G′ for cell samples prepared under the same conditions (see Materials and Methods). For the ensemble experiments, ${\tilde{\sigma }}_{\text{log}{G}^{\prime }}^E$ was estimated by applying Eq. 6 to at least 50 cells in each dish (n = 6 dishes), and the averaged ${\tilde{\sigma }}_{\text{log}{G}^{\prime }}^E$ is plotted in Fig. 6 b. We find ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ to be in good agreement with ${\tilde{\sigma }}_{\text{log}{G}^{\prime }}^E$. We find no significant difference (p > 0.384) between the magnitudes of ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}^T$ and ${\tilde{\sigma }}_{\text{log}{G}^{\prime }}^E$ over the measured frequencies. This result indicates that, in this simple cell system, the variation of a single cell originating from the temporal remodeling of the CSK is comparable to the individual differences between cells, confirming that the single cell behaves in an ergodic way.

Discussion

Relationship between temporal and ensemble variations

The temporal variations of G^∗ observed in cells that have the potential to remodel the CSK and migrate along a 2D surface can be classified into two types: fluctuations due to the translational movement of the whole cell; and intrinsic, subcellular fluctuations. We measured the fluctuation of G^∗ of single cells placed in a spatially confined region. For the frequency-dependent SD of G′, ${\tilde{\sigma }}_{\text{log}{G}^{\mathit{\prime }}}$, the temporal variation was consistent with the ensemble variation (Fig. 6 b), where the changes in cell shape and lateral translations of the cell were restricted in micropatterned regions and measurement positions were controlled precisely via AFM. This observation strongly suggests that the intracellular dynamics correlated with these cells’ rheological properties satisfy an approximately ergodic hypothesis. That is, a single cell can sample the range of complex shear modulus over time that would also be measured for a population or ensemble of such cells at a single instant in time.

However, it was also observed that for the SD of the measured raw data of G′, σ_logG′, the ensemble variation was larger than the temporal variation (data not shown). This result is consistent with that of a previous investigation of single cells using MTC (11). The observed difference of σ_logG′ between the ensemble and temporal experiments came from the result that ${\sigma }_{\text{log}{g}_0}^E$ (0.132 ± 0.013) was larger than ${\sigma }_{\text{log}{g}_0}^T$(0.098 ± 0.011). In the ensemble experiment, the measurement location within cells is not identical because the location is the center of the square-shaped regions, not the center of cells that may fluctuate slightly. Furthermore, the intracellular architecture of a cell, including the CSK and other subcellular organelles (e.g., the cell nucleus) can vary among single cells in a given cell type and population, for many reasons; causes include variation in the cell cycle and responses to biochemical gradients. Such experimental errors and additional variations of intracellular structures may be minimized in the temporal experiments, as the cell lateral movement is minimized and the CSK and cell nucleus position does not fluctuate largely within these phenotype-committed cells that are adhered within a spatially confined condition.

Perturbation of CSK structures by the AFM external forces

The topographical shape of each single cell remained essentially unchanged after the incubation time of 10 h. Nevertheless, we observed a decorrelation of G′ at a characteristic time τ of ∼10 min. As explained below, such relatively fast dynamics of cell rheology may be stimulated by the deformation timescales imposed by the AFM. During the indentation at oscillating amplitude about a fixed mean depth into the cell, stress relaxation can occur whereby the CSK relaxes from the initial state to a metastable mechanical state (35, 48, 49, 50, 51, 52). After removing the indentation, the cell returns to its original macroscopic shape; in that time, however, the CSK may have reorganized to another conformation that differs from the initial state and cannot be restored solely via thermal agitation. As such, the AFM-induced indentation can change the local CSK organization irreversibly (in experimentally accessible timescales).

It has been reported that external forces often cause the reinforcement and fluidization of cells (4, 5, 9, 10, 13, 53). However, in this study, we observed no apparent increase or decrease in the stiffness of a given cell, even after repeated indentation. Furthermore, the cells exhibited no mechanical aging or rejuvenation. These results indicate that the applied force in these experiments constitutes a small perturbation that does not cause the structural reinforcement or fluidization of cells.

Possibility of mechanical diagnostics of single cells

The mechanical properties of cells are considered useful indicators for distinguishing between normal and abnormal cells. Previous studies have noted wide variation in the ensemble distribution of cell mechanical parameters within a population, characterized either by the Young’s modulus E measured by the AFM force-distance curve technique (54, 55, 56) or metrics of whole-cell deformability measured by optical (57) and hydrodynamic (58) techniques. Some studies have further noted a statistically significant difference in the average or mean mechanical property (e.g., the geometric mean of E) between normal cell populations and cancerous cell populations. However, in certain types of cell populations and sufficiently wide distributions, it is challenging to use such information to determine whether an individual cell is from the diseased population (e.g., a cancerous cell) because of significant overlap in the ensemble distributions of the measured property and the associated pervasiveness of false positives and false negatives at the single-cell level (54, 57). The reliability of classification can be improved by obtaining additional mechanical, physical, or chemical information for analysis with decision-making techniques. Our results imply that repeated measurements can also provide such complementary data. As shown in Fig. 6 b, the ensemble variation of G′ is identical to the temporal variation of G′ in the case of cells cultured in a spatially confined region. Therefore, the temporal distribution of single cells provides useful information about the single-cell state and how narrow one can expect this variation to be at the cell population level. Perhaps the most important implication of ergodic behavior is that repeated mechanical measurements can be expected to replicate the dispersion of an originating cell population in such a way that could allow mechanophenotyping from a small number of samples. Such capability is expected to be useful in the context of diagnostic techniques that rely on very few initial cells, e.g., the output of another cell sorting or separation apparatus.

Conclusions

We investigated the fluctuation of G^∗ of single cells placed in a spatially confined region. The results showed that the frequency-dependent G^∗, measured via AFM oscillatory deformation, exhibits single-exponent power-law rheology based on the SGR model of cell deformability. Furthermore, we found that this cell rheological property exhibits a type of ergodic behavior, in that the temporal variation in G′ for a single and spatially confined cell is comparable to the ensemble variation in that property for the cell population. These results suggest that the applied force of AFM oscillatory loading allows cells to access multiple CSK reconfigurations permitted in the ensemble statistics. This approach also provides access to the minimum variation in rheological properties expected at the population level, through analysis of single spatially confined cells over extended duration, as required for consideration of mechanophenotyping of individual cells.

Author Contributions

P.G.C., R.T., J.M.M., K.J.V.V., and T.O. conceived and designed the experiments. K.K.-S., A.S., and K.S. contributed to the microfabrication of the substrates. P.G.C. and R.T. performed the experiments and analyzed the data. P.G.C., R.T., J.M.M., K.J.V.V., and T.O. wrote the paper.

Editor: Jeffrey Fredberg.