Mechanism for Triggered Waves in Atrial Myocytes

Abstract

Excitation-contraction coupling in atrial cells is mediated by calcium (Ca) signaling between L-type Ca channels and Ryanodine receptors that occurs mainly at the cell boundary. This unique architecture dictates essential aspects of Ca signaling under both normal and diseased conditions. In this study we apply laser scanning confocal microscopy, along with an experimentally based computational model, to understand the Ca cycling dynamics of an atrial cell subjected to rapid pacing. Our main finding is that when an atrial cell is paced under Ca overload conditions, Ca waves can then nucleate on the cell boundary and propagate to the cell interior. These propagating Ca waves are referred to as “triggered waves” because they are initiated by L-type Ca channel openings during the action potential. These excitations are distinct from spontaneous Ca waves originating from random fluctuations of Ryanodine receptor channels, and which occur after much longer waiting times. Furthermore, we argue that the onset of these triggered waves is a highly nonlinear function of the sarcoplasmic reticulum Ca load. This strong nonlinearity leads to aperiodic response of Ca at rapid pacing rates that is caused by the complex interplay between paced Ca release and triggered waves. We argue further that this feature of atrial cells leads to dynamic instabilities that may underlie atrial arrhythmias. These studies will serve as a starting point to explore the nonlinear dynamics of atrial cells and will yield insights into the trigger and maintenance of atrial fibrillation.

Introduction

Excitation-contraction (EC) coupling is mediated by Calcium (Ca) signaling where membrane-bound voltage-sensitive channels induce the release of intracellular Ca, which leads to cell contraction (1, 2). The signaling between these channels occurs within thousands of dyadic junctions in the cell where a few L-type Ca channels (LCCs) are in close proximity to a cluster of Ryanodine receptors (RyRs), which control the flow of Ca sequestered within the sarcoplasmic reticulum (SR). Given the local nature of Ca signaling, the spatial distribution of dyadic junctions will determine the time course of Ca release in the cell. In cardiac cells, this distribution is dictated by the t-tubule system, which consists of tubular invaginations of the cell membrane that distribute membrane channels into the cell interior, insuring a uniform spread of excitation throughout the cell. However, the extent to which t-tubules penetrate the cell can vary substantially between cell types (3, 4). In ventricular cells, t-tubules extend deep into the cell along Z planes so that Ca signaling effectively occurs within the full 3D volume of the cell. This arrangement allows for a rapid and synchronized Ca release leading to a fast coordinated contraction. However, in atrial cells the extent of t-tubule penetration can vary substantially between cells and also between species (3). In a wide range of species (rat, guinea pig, cat, pig, human) atrial cell t-tubules are substantially less developed than in ventricular cells (4, 5). In these cells the bulk of Ca signaling occurs on the cell boundary and penetrates to the interior via diffusion (6, 7, 8). However, these studies also find substantial cell-to-cell variability so that the presence of t-tubules in a population of cells can range between sparse and virtually absent. On the other hand, studies in the atria of large mammals (sheep, cow, horse) reveal that these cells display a moderately developed t-tubular structure with some penetration into the cell interior (4, 9). In this case, Ca release occurred more similarly to ventricular cells, although large spatial gradients from the boundary to the interior were observed. In a recent study, Arora et al. (10) analyzed the distribution of t-tubule density in intact dog atrial cells. They found that the t-tubule distribution in these cells was mostly sparse, and substantially less developed than in ventricular cells. Also, they observed extensive cell-to-cell and regional variations in t-tubule density. In particular, they showed that almost 25% (12.5%) of atrial myocytes in the right (left) atrium did not display any t-tubule structure at all. These results indicate that the distribution of t-tubules in atrial cells can vary substantially between cells.

Ca release at an RyR cluster is typically initiated by a rise in Ca concentration due to a nearby LCC channel opening. However, under certain conditions, such as an elevated SR load, RyR clusters can fire in response to an increase in Ca concentration due to diffusion from a neighboring spark (6, 11). In this case, Ca release can occur in a domino-like fashion leading to a wave front of Ca release in the cell. These excitations are referred to as “spontaneous Ca waves” because they are usually triggered by local fluctuations in Ca release among RyR clusters (12, 13). These spontaneous Ca waves are believed to be highly arrhythmogenic because they can induce membrane depolarization due to inward NaCa exchange current (14, 15, 16). In atrial cells it is believed that spontaneous Ca release induces ectopic activity, which is responsible for initiation and maintenance of atrial fibrillation (AF) (17, 18, 19). Also, Ca cycling instabilities can induce dynamical heterogeneities in atrial tissue that may serve as a substrate for AF. Thus, the effect of Ca on AF is multifactorial, and likely to contribute as both the trigger and substrate for AF maintenance. However, up to now, the spatiotemporal dynamics of subcellular Ca in paced atrial cells has still not been fully understood. In particular, it is not known what kind of pacing-induced instabilities can occur in these cells.

In an elegant study, Thul et al. (6) constructed a simplified reaction diffusion model of Ca dynamics in atrial myocytes. This model accounted for the unique architecture of the atrial cell and predicted rich spatiotemporal dynamics. In particular, they identified the presence of ping waves in which Ca release at the cell boundary propagates to the cell interior via rotating waves along Z planes (6, 20). They argued further that the interplay between boundary-induced waves and normal Ca release would destabilize Ca cycling and could therefore be proarrhythmic (21). These studies are important because, to our knowledge, they are the first to suggest that the spatial geometry of Ca release sites can be crucial to instabilities that may lead to cardiac arrhythmias.

In this article, we explore this direction further by applying a physiologically detailed computational model of Ca cycling (22) in atrial myocytes. This model accounts for experimentally based Markovian dynamics of RyR and LCC channels, along with Ca fluxes due to a range of Ca cycling proteins. Our main finding is that under rapid pacing with an action potential (AP) clamp, atrial myocytes exhibit Ca waves that are nucleated at the cell boundary and proceed to spread throughout the cell interior. These Ca waves are referred to as “triggered waves” because they are only nucleated during the AP when a critical number of Ca sparks are ignited by LCC channel openings at the cell boundary. This feature of triggered waves makes them fundamentally different from spontaneous Ca waves, which are triggered by stochastic fluctuations of RyR that are independent of LCC channel openings. Consequently, the latency to triggered waves is substantially shorter than for spontaneous waves, which only occur after a long pause. Hence, triggered waves can be highly arrhythmogenic because they occur with short latency and can induce triggered activity during the AP. We analyze triggered waves in detail and show that their onset displays a sharp sigmoid dependence on the SR load. Furthermore, we show that this nonlinearity explains our observation of aperiodic Ca cycling in response to a periodic AP waveform. By visualizing subcellular Ca during pacing we show that this Ca cycling abnormality is caused by the complex interaction between paced Ca release at the cell boundary and triggered excitations that can propagate into the bulk of the cell. We argue that this nonlinear instability is unique to atrial cells, and can serve as a potential mechanism for the induction and maintenance of AF.

Methods

Computational cell model

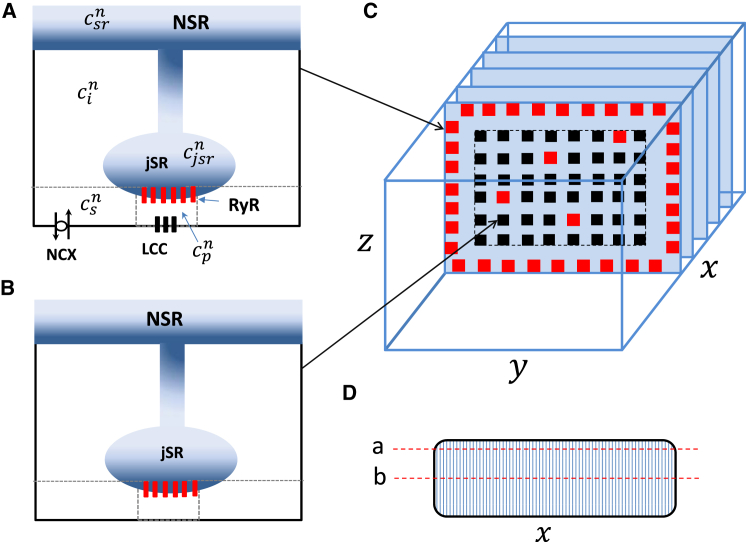
Spatially distributed cell model. To model the spatiotemporal distribution of Ca in atrial myocytes, we have implemented an established mathematical model due to Restrepo et al. (22) and Restrepo and Karma (23) (i.e., the Restrepo model). In this model, the cell interior is divided into an array of compartments that represent distinct intracellular spaces. The Ca concentration within these compartments is treated as spatially uniform, and neighboring compartments are diffusively coupled. To model the atrial cell architecture, we first distinguish compartments that are close to the cell membrane, where LCC and RyR channels occupy the same dyadic junction, and compartments away from the cell membrane that do not sense Ca entry due to LCCs. For convenience, we will refer to compartments near the membrane as junctional Ca release units (CRUs), and all other compartments as nonjunctional CRUs. To model each compartment, we denote the Ca concentration in compartment α as $c_{\alpha }^n$, where the superscript n indicates the location of that compartment in a 3D grid representation of the cell interior. In this study we will label our units according to the scheme n = (n_x,n_y,n_z), where n_x denotes the longitudinal direction, n_y is the width of the cell, and n_z is the height.

In Fig. 1, A and B, we show an illustration of the various compartments that comprise a junctional (nonjunctional) CRU near the cell membrane. The intracellular compartments described in the model are: 1) the proximal space with concentration $c_p^n$ and volume v_p. This compartment represents the volume of the cell that is in the immediate vicinity of the local RyR cluster. For junctional CRUs, this space includes 1–5 LCC channels along with a cluster of 100 RyR channels, whereas for nonjunctional CRUs, there are no LCC channels in the compartment. For junctional CRUs we will follow the Restrepo model, and take v_p to be the volume between the JSR and the cell membrane, which is roughly a pillbox of height 10 nm and diameter 100 nm. For nonjunctional CRUs, we note that recent experiments in atrial myocytes indicate the presence of large axial tubule structures that are closely associated with RyR clusters, and which likely restrict the local diffusion of Ca (24). However, the precise spatial arrangement of these structures at the scale of the RyR cluster are still not completely known. Thus, in this study we will first consider the case where the proximal space volume v_p of nonjunctional sites is the same as that of junctional sites. After this analysis, we will then analyze how our main results change when the volume v_p of nonjunctional sites is increased. 2) The submembrane space, with concentration $c_s^n$ and volume v_s, which represents a volume of space in the vicinity of the proximal space, but smaller than the local bulk myoplasm. For junctional CRUs, we follow the Restrepo model and take v_s to be 5% of the cytosolic volume within a CRU. This volume includes sodium-calcium exchange channels (NCX) that are regulated by Ca concentrations that vary much more quickly than the average Ca concentration in the myoplasm. For nonjunctional CRUs we will again consider a range of volumes v_s, and assess the response of the system to changes in this parameter. 3) The bulk myoplasm, with concentration $c_i^n$ and volume v_i, characterizes the volume of space into which Ca diffuses before being pumped back into the SR via the sarcoplasmic-endoplasmic reticulum calcium ATPase (SERCA) transporter. 4) The junctional SR, with concentration $c_{\text{jsr}}^n$, is a section of the SR network in which the RyR channels are embedded. 5) The network SR (NSR), with concentration $c_{\text{nsr}}^n$, represents the bulk SR network that is spatially distributed in the cell. To mimic the heterogeneity that is expected in a cardiac cell, we have also included spatial variation in the density of ion channels and transporters. In particular, if a CRU is designated as a junctional CRU, then the probability that we insert NCX and LCC channels will be taken to be 60%.

Figure 1.

Schematic illustration of the spatial architecture of Ca signaling in a cardiac atrial cell. Ca signaling and release occurs within dyadic junctions distributed in the 3D volume of the cell. Dyadic junctions close to the cell membrane (A) possess LCC and NCX channels, whereas interior junctions (B) do not have these channels. Here, the superscript n denotes the nth dyadic junction in a 3D grid representing the cell. (C) Shown here is the spatial architecture of the cell interior showing Z planes. All compartments in the other boundary are treated as junctional CRUs (red squares). To model different levels of t-tubule density, we let a fraction p of internal sites have properties of junctional CRUs, whereas the remainder are nonjunctional. (D) Given here is an illustration of line-scan (a), which is located at (n_x,10,18), and line-scan (b), which is located at (n_x,10,10). Here, n_x is the coordinate along the long axis of the cell. To see this figure in color, go online.

Our cardiac cell model consists of 60 planes representing Z planes, where each plane contains an array of 20 × 20 regularly spaced compartments (Fig. 1 C). All sites at the boundary of the cell are designated as junctional CRUs. To model different degrees of t-tubule invagination we set a fraction p of internal CRUs to be junctional CRUs, so that Ca signaling between LCC and RyR channels can then occur deep in the cell interior. We will first consider p = 0, which corresponds to the case where Ca signaling occurs only at the cell periphery. We will then relax this assumption and explore how EC coupling is modified by allowing junctional CRUs to penetrate the cell. Ca diffusion between sites is modeled by allowing a diffusive flux between nearest-neighbor compartments of the submembrane, the bulk myoplasm, and the network SR. This diffusive flux between nearest-neighbors i and j has the form $J_d^{ij}=\Delta c_{ij}/{\tau }_{ij}$, where Δc_ij is the concentration difference between the compartments, and τ_ij is the diffusion time constant. Because ultrastructural studies of atrial cells show that the distance between junctional and nonjunctional CRUs is larger than the distance between nonjunctional CRUs, we set the diffusion time between sites on the cell periphery and internal sites to be twice that between internal sites. To set the diffusive timescale between CRUs, we rely on our experimental studies, which show that subcellular Ca waves can travel at a wide range of velocities. At 5 Hz pacing, we find that wave velocities measured in different atrial cells can vary substantially in the range 50–200 μm/s. In this study, we have adjusted the subcellular diffusion timescales so that longitudinal planar waves propagate at velocities 100–200 μm/s at SR loads in the range 1250–1400 μm/s. The diffusive timescales for each set of model parameters are given in the Supporting Materials and Methods.

Visualization of subcellular Ca. To visualize subcellular Ca and compare with our experimental measurements, we have simulated line scans at various positions in the cell. Fig. 1 D shows an illustration of the cell cross section and indicates two longitudinal line scan positions indicated by line (a) placed near the cell boundary at position (n_x,10,18) and line (b) placed at the center of the cell with coordinates (n_x,10,10), where n_x denotes the coordinate along the longitudinal axis. To compare simulation results with those obtained experimentally and because line scans measure the average fluorescence in the vicinity of the scan position, we simulate an experimental line scan by averaging the dyadic junction Ca concentration over a 3 × 3 cross-section of the cell at a fixed Z plane. To compute this average, we first fix the position along the Z plane (n^y,n^z), and then compute the average,

$$c_{av}\left(n_x\right)=\frac{1}{9}\sum _{\begin{array}{c}{i}_y=-\mathrm{1,0,1}\\ i_z=-\mathrm{1,0,1}\end{array}}{c}_p\left(n_x,n_y+i_y,n_z+i_z\right).$$ (1)

We then plot c_av as a function of n_x to give an estimate of the local average fluorescence around the line-scan position. In this study, we pick a line scan close to the boundary so that n_y = 17 and n_z = 10.

Pacing protocol. In this study, we consider the dynamics of Ca cycling when the cell is paced with an AP clamp. Our AP clamp is taken to have the functional form (25) given by

$$V\left(t\right)=\{\begin{array}{ll}{V}_{\text{min}}+\left(V_{\text{max}}-V_{\text{min}}\right)\sqrt{1-{\left(\left(t-mCL\right)/xCL\right)}^2}\hfill & mCL\le t\le mCL+xCL\hfill \\ V_{\text{min}}\hfill & mCL+xCL<t<\left(m+1\right)CL\hfill \end{array},$$ (2)

which mimics an AP between a maximum voltage of V_max = 0 mV and membrane resting potential of V_min = −85 mV. Here, the variable CL denotes the pacing period, m is an integer denoting the mth paced beat, and x = APD/CL. Following previous studies (25), we let this ratio vary with pacing rate according to the functional form x = a/(a + CL), where a = 2/3.

Confocal Ca imaging in dog atrial cells

Anesthesia was induced in dogs with Propofol (0.05–0.2 mg/kg) then maintained with isoflurane (3–5%). Pacemaker leads were placed through the carotid into the right ventricular free wall and the animal was allowed to recover. After 1 week, the pacemaker was activated at a rate of 240 beats per min. Symptoms of heart failure development were monitored 2–3 times weekly including capillary refilling time, appetite, body weight, and ascites development. After 4–5 weeks, heart failure was confirmed by echocardiography when cardiac output fell below 25% and the dog was anesthetized again and the heart was removed by an intercostal incision. All procedures were approved by the Institutional Animal Care and Use Committee according to National Institutes of Health (NIH, Bethesda, MD) guidelines. Cell isolation was conducted using whole left atrial perfusion with a solution containing liberase (Sigma-Aldrich) enzyme (× mg/mL) for ∼45 min. Dog atrial myocytes were used for up to 30 h after isolation. Ca-fluorescence (via rhod-2, fluo-2, or Cal-520) measured using confocal microscopy was used to record intracellular Ca cycling in single myocytes superfused with modified Tyrode’s solution (at 36°C).

Results

Experimental observations of Ca waves under rapid pacing

Ca cycling in normal atrial cells

To explore the spatiotemporal dynamics of subcellular Ca cycling, we applied longitudinal line-scan imaging in isolated dog atrial cells. To investigate the response of atrial cells, we apply a pacing protocol that is specified by a pair of numbers (CL, n) where $CL$ is the pacing interval applied in milliseconds, and n is the number of beats applied at that interval. The rapid pacing protocol used in this study is specified by the sequence,

$$\left(1000,6\right)\to \left(500,15\right)\to \left(300,32\right)\to \left(200,35\right)\to 4\text{s}\text{pause}\to \left(1000,4\right).$$

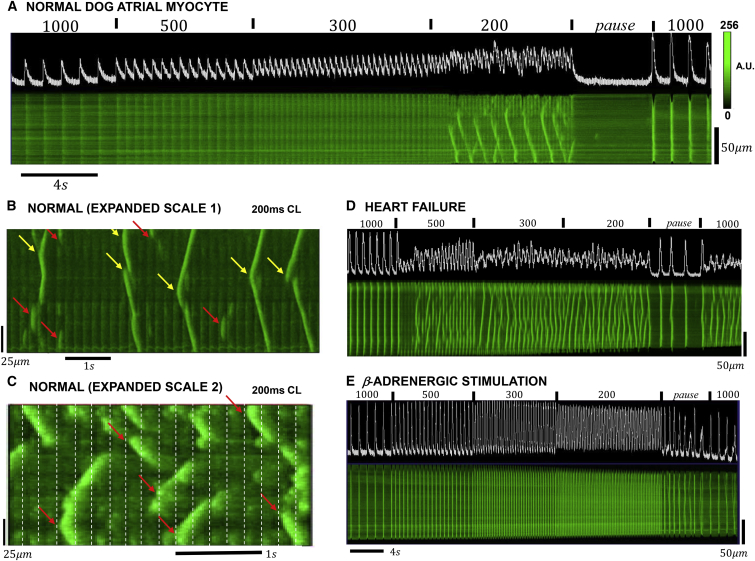
Fig. 2 A shows an example of the Ca transient and longitudinal line-scan images of a normal atrial cell driven by our rapid pacing protocol. At pacing CLs of 1000, 500, and 300 ms, we find that Ca release is periodic and spatially synchronized with the stimulus. However, at a pacing interval of 200 ms, we observe propagating Ca waves that occur during pacing. These waves appear as characteristic V-shaped fluorescence events that occur every 4–6 paced beats. Once formed, these waves are not interrupted by the Ca transients that are synchronized with the pacing stimulus. We also note that during the 4 s pause after rapid pacing no Ca waves are observed. Fig. 2, B and C, shows line-scan images of two different cells during rapid pacing at CL = 200 ms. Here, the timescale is expanded to more clearly see the relationship between paced release and Ca waves. Fig. 2 B shows several distinct characteristics of Ca wave propagation. In one case (yellow arrows), waves appeared substantially brighter than the stimulated release, and in all cases propagated from the source to either the cell boundary or until collision with another wave. The second type of propagation event (red arrows) are represented by smaller waves that propagate ∼10–30 μm. These waves appear to be initiated a short time after a pacing stimulus, and then cease to propagate on the next pacing stimulus. The timing of both types of Ca waves appears random with intervals between wave sources ranging from 2 to 10 beats. Wave sources also appear to be randomly located in the cell although the last two wave sources seem to originate in the same location (right most two arrows). Fig. 2 C shows a different sample where we observe a broader distribution of wave propagation distances. As in the previous example, waves appeared as bright events on a background Ca release that is synchronized with the pacing stimulus. Here, we note that some wave sources (red arrows) are closely aligned with the pacing stimulus times (vertical dashed lines). To estimate the onset of Ca waves in a population of cells, we recorded the CL when Ca waves are detected during the pacing protocol. In 179 myocytes measured in four normal dog atria the onset of Ca waves occurred at an average CL of 354 ± 8 ms. Detailed summary data of Ca wave activity in this population of cells will be published in a forthcoming publication.

Figure 2.

(A) Mean fluorescence intensity (top trace) and line-scan image of subcellular Ca in atrial cells driven by the rapid pacing protocol. In this case, the line-scan position is chosen be in the longitudinal direction and as close to the cell center as possible. (B) Given here is an expanded image of Ca waves during rapid pacing. Ca transient, and a line-scan image of an atrial cell, were paced at 200 ms. The yellow arrows indicate wave sources that initiate bright waves that spread to the cell boundary, or collide with another wave. The red arrows indicate small wavelets that spread on the order of 10–20 μm. (C) Given here is a higher magnification of a line-scan image in a different cell sample. In some instances (red arrow), Ca wave sources are synchronized with the stimulation line. (D) Given here is a line-scan image of Ca in a dog HF cell paced with the rapid pacing protocol. (E) Shown here is a line-scan image of Ca under β-adrenergic stimulation. To see this figure in color, go online.

Ca waves in rapidly paced HF cells

In this study, we have also performed line-scan imaging of subcellular Ca in atrial myocytes from failing heart. Fig. 2 D shows the Ca transient and the line-scan image of a paced HF cell. Ca wave activity is substantially increased and release is dominated by a combination of stimulus-induced release along with Ca wave propagation. At a pacing rate of CL = 500 ms or less, we note that Ca wave activity is substantial and is aperiodic from beat-to-beat. Inspection of the Ca transient reveals an aperiodic response that is not synchronized with the pacing stimulus. Finally, we note that during the 4 s pause a higher incidence of spontaneous Ca waves occur in the cell. In this case, we observe three events in which subcellular Ca is released in a synchronized fashion across the cell. This data is representative of a population of 73 cells from four HF dog atria. The average onset of Ca waves in this population of cells is CL = 467 ± 21 ms.

β-adrenergic stimulation

We have also explored the effect of β-adrenergic stimulation on Ca during the rapid pacing protocol. To accomplish this, we tested the effect of isoproterenol (0.01 μM) on the development of Ca wave activity. Fig. 2 E shows that isoproterenol effectively abolishes all aberrant Ca waves and that Ca release is spatially synchronized and in-phase with the stimulus. We also note that Ca release and cell contraction are larger than in control, and that Ca waves occur readily during the 4 s pause. In this example, we observe eight distinct Ca waves where the Ca transient rose to levels comparable to a paced beat.

Numerical modeling of EC coupling in atrial cells

SR load dependence of EC coupling in atrial cells

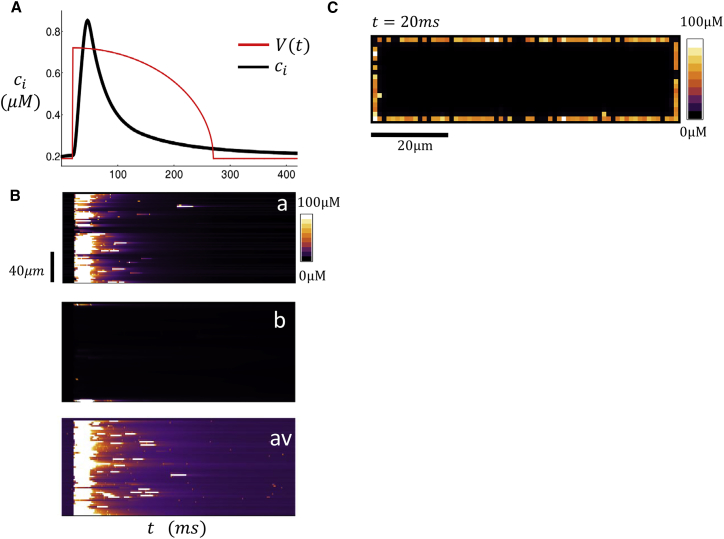
To explain the features observed in the experiments, we have applied our spatially distributed computational model. As a starting point, we first investigate the spatial distribution of Ca release in response to an AP clamp. In these simulations, we will consider the case in which all junctional CRUs are located at the cell boundary, where we set p = 0. In Fig. 3 A, we plot the Ca transient, defined as the whole cell average $c_i=\left(1/N\right){\sum }_{k=1}^N{c}_i^k$, along with a trace of the AP clamp driving our computational cell model of 60 × 20 × 20 CRUs. In this case, we have picked an AP clamp that corresponds to CL = 400 ms. When we fix the initial SR load (both NSR and JSR) to be c_sr = 1100 μM, we observe a typical Ca transient that rises rapidly (∼10–20 ms) after the AP upstroke and relaxes to its diastolic value as the SR is replenished on a slower timescale (∼109–200 ms). Fig. 3 B shows simulated line scans of the dyadic junction Ca concentration at positions (a) and (b) in the cell along with the spatial average line-scan (av) given by Eq. 1. Under these conditions of SR loading, we find that Ca is released only on the cell periphery. Hence, the line scan close to the cell boundary shows Ca sparks that are spatially synchronized due to the AP upstroke whereas the internal line scan reveals that there is no Ca release in the cell interior. Also, we note that our spatially averaged line scan receives contributions from both junctional and nonjunctional CRUs, and so appears synchronized with the boundary line scan because there is no contribution to the average from internal sites. Fig. 3 C shows a 2D image of a cross section of the cell. As expected, at t = 20 ms, when the Ca transient is close to its peak, Ca sparks are observed only at the periphery of the cell.

Figure 3.

(A) Ca transient and AP clamp during pacing for one beat with an initial SR load of 1100 μM. (B) Shown here is a computational line scan of the dyadic junction concentration at locations (a) and (b) within the atrial cell. The bottom trace plots the line scan for the spatial average c_av. (C) Shown here is a computational 2D image of dyadic junction Ca concentration. The image shown is 20 ms after the AP upstroke. To see this figure in color, go online.

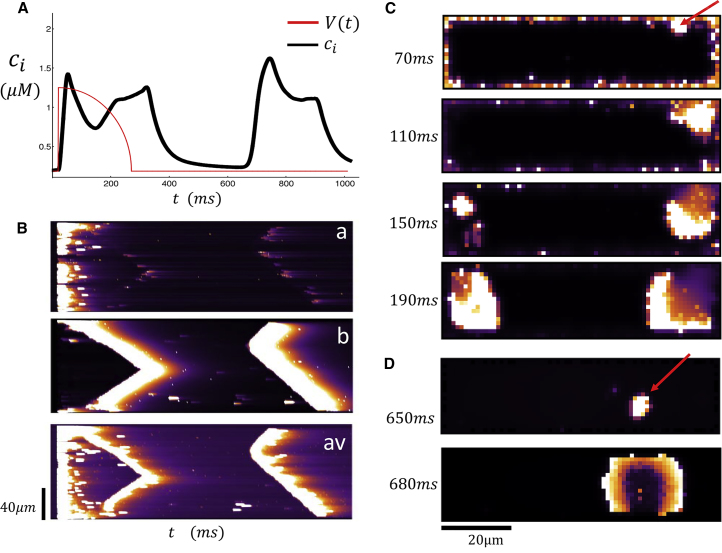
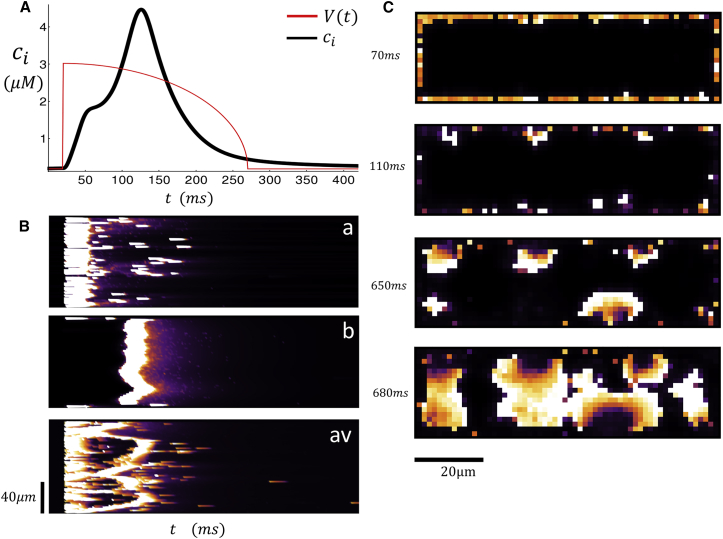
In Fig. 4, A–D, we repeat the same simulation for a larger initial SR load of c_sr = 1230 μM. In Fig. 4 A, we observe that the Ca transient rises rapidly and peaks within ∼10–20 ms after the AP upstroke. This peak is followed by a second increase, which starts at time t ∼ 180 ms and peaks at t ∼ 300 ms. After a longer waiting time of t ∼ 650 ms, we find that there is a third peak in the Ca transient when the membrane voltage is at the resting potential (V_m = −85 mV). Fig. 4 B shows line scans at various positions in the cell shown simultaneously with the Ca transient in Fig. 4 A. Along line-scan (a), we observe that the initial peak of the Ca transient is synchronized with a coordinated release of Ca at the cell membrane. However, along line-scan (b), we observe propagating Ca waves that originate from the cell boundary and end at the cell center. Thus, the early two peaks of the Ca transient correspond to a synchronized release at the cell boundary followed by a Ca wave that forms at the cell boundary and propagates to the cell interior. To compare with experimental line scans, we also show the spatial average c_av as a function of the longitudinal coordinate. Indeed, as in the experiments, we see that the fluorescence from the propagating wave is merged with the Ca released at the boundary. This observation demonstrates that propagating waves did not interfere with the stimulated release because they both occurred within different regions in the cell. Finally, we note that the late release at t ∼ 640 ms corresponds to a spontaneous Ca wave that originates from the cell interior. Again, this is most evident from line-scan (b), which shows that the Ca wave forms in the interior and gradually propagates outward.

Figure 4.

(A) Ca transient and AP clamp during pacing for one beat with an initial SR load of 1230 μM. (B) Shown here are simultaneous line scans at positions (a) and (b) and the spatial averaged line scan (av). (C) Shown here is a 2D image of a dyadic junction Ca concentration at the indicated times. The red arrow indicates the source of triggered Ca wave. (D) Shown here is a 2D image of a spontaneous Ca wave that originates in the cell interior. To see this figure in color, go online.

Our computational model indicates that there are two distinct mechanisms for Ca waves to form in an atrial cell. In the first case, waves are nucleated at the cell boundary at sites where LCC channels trigger local Ca release. These waves necessarily occur during the AP when LCC channels are open and we will refer to these wave events as “triggered Ca waves”. On the other hand, waves can also nucleate in the cell interior independently of LCC channel openings. These waves are the well-known “spontaneous Ca waves” that typically occur after a much longer latency. To visualize the spatiotemporal evolution of Ca during these release events, we also show snapshots of the 2D distribution of subcellular Ca. Fig. 4 C shows the distribution of Ca at a cross section passing through the center of the cell at times t = 70, 110, 150, and 190 ms. Here we see that a Ca wave is nucleated at the indicated position (red arrow) that occurs near the cell boundary and then proceeds to grow and spread throughout a large portion of the cell. In Fig. 4 D, we plot two snapshots at times t = 650 and 680 ms and find that a Ca wave is nucleated in the cell interior and proceeds to spread as an approximately spherical wave. A more detailed frame-by-frame analysis of the Ca dynamics confirms that this wave did not originate at the cell boundary.

In Fig. 5, we show the case where the SR load has been increased to c_sr = 1265 μM. In this case, we observe (Fig. 5 A) that the Ca transient rises within ∼20 ms, plateaus briefly, and then rises rapidly again at t ∼ 100 ms. To explain this time course in Fig. 5, B and C, we show simultaneous line scans along with 2D spatial images of subcellular Ca. Here, we observe that the initial rise in the Ca transient corresponds to Ca release at the cell boundary that is initiated by the rapid upstroke of the AP. This boundary release then proceeds to ignite multiple boundary waves, which proceed to propagate into the cell interior. Here we note that the line scan at position (b) displays a nearly simultaneous release of Ca because these propagating Ca waves activate internal release sites roughly simultaneously. As a result, the spatially averaged line-scan (av) indicates near-simultaneous release at the boundary along with a delayed Ca release into the cell interior. Indeed, the corresponding 2D images (Fig. 5 C) show multiple Ca waves originating at the cell boundary and propagating toward the cell interior. In this case, longitudinal waves are not observed because the activation of the internal cites occurs at multiple peripheral sites and propagates from the boundary inward.

Figure 5.

(A) Ca transient and AP clamp during pacing for one beat with an initial SR load of 1265 μM. (B) Shown here are simultaneous line scans at positions (a) and (b) and the spatial averaged line scan (av). (C) Given here is the 2D image of dyadic junction Ca concentration at the indicated times. To see this figure in color, go online.

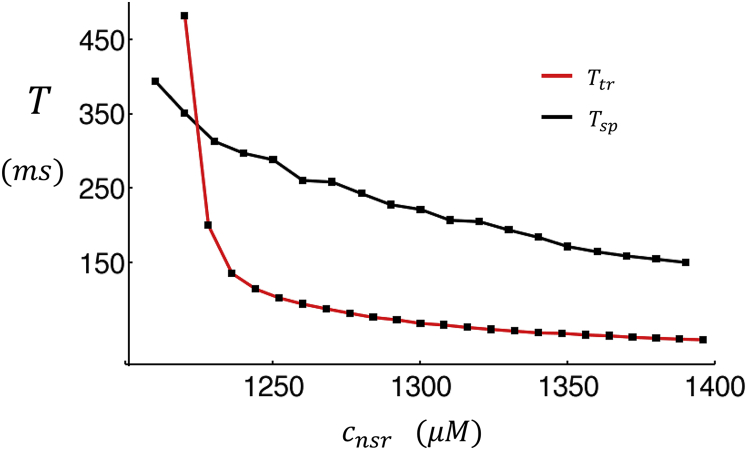
The essential finding from Figs. 4 and 5 is that triggered waves occur with shorter latency than spontaneous waves, and therefore should play an important role in the EC coupling of atrial cells. To summarize our main results, in Fig. 6 we have computed the mean waiting time for a Ca wave to excite a region in the cell interior. Here, we consider the average cytosolic Ca concentration c_i within a region of 10 × 10 × 10 CRUs in the cell interior. When a Ca wave crosses that region, the average concentration typically exceeds c_i ≈ 3.0 μM. Thus, we will take the mean waiting time to be the average time for the concentration to rise above a threshold c_i = 3.0 μM for the first time. We then average over 100 independent simulations to compute the mean waiting time to a Ca wave in the cell interior. In Fig. 6, we first consider the case where the cell is driven by an AP with CL = 400 ms, followed by a 2000 ms period where the voltage is kept at the resting potential of −85 mV. The waiting time for a Ca wave to ignite the cell interior is denoted as T_tr. We then repeat the same simulations but set the diffusion of Ca in the cytosol to be 0 at the cell boundary. In this case, only nonjunctional sites contribute to the nucleation of Ca waves because Ca diffusion from the boundary to the interior is eliminated. Under these conditions, all Ca waves are spontaneous, and their waiting time will be denoted as T_sp. Fig. 6 shows that for a broad range of SR loads, T_tr < T_sp. These results show directly that the frequency of Ca waves in the interior is dependent on Ca signaling at the cell boundary, i.e., that a large fraction of Ca waves is indeed triggered. For smaller SR loads, we find that the waiting time to a Ca wave is larger than the AP because the triggered excitations at the cell boundary do not lead to wave nucleation. In this case, we find that T_tr > T_sp because the initial AP leads to a partial draining of the NSR near the cell boundary, which further prolongs the waiting time to Ca waves. Thus, at low SR loads, Ca waves are mostly spontaneous because boundary excitations do not induce wave nucleation. However, the waiting time for these events are typically must longer than the AP, so that spontaneous activity at these range of SR loads is not typically observed when the cell is paced.

Figure 6.

Plot of the mean waiting time to a Ca wave that crosses a central region in the cell. The red line (T_tr) corresponds to the waiting time in the case where the cell is driven by an AP with triggered Ca release at the cell boundary. The black line (T_sp) corresponds to the waiting time to spontaneous Ca waves. In this case, the diffusion coefficient from junctional to nonjunctional sites is set to 0 so that triggered waves cannot occur. To see this figure in color, go online.

Model limitations and robustness

An important limitation of this study is that our spatially distributed Ca cycling model treats the intracellular space as a collection of compartments with spatially uniform Ca. This approximation substantially simplifies the structure of the intracellular space, which is composed of a complex array of physical structures. In particular, we mention the recent finding of Brandenburg et al. (24), who report that atrial myocytes have large tubular structures, oriented longitudinally, that are in close proximity to RyR clusters. These findings indicate that intracellular structures are complex and likely influence the extent of subcellular Ca diffusion. A second important limitation of our model is that the spatial distribution of Ca buffers in the cell interior is not known completely. This is particularly important because Ca buffers control the spatial spread of local Ca and likely play a crucial role in determining the onset of wave nucleation. Given the complexity and incomplete knowledge of subcellular diffusion barriers and buffers, we will assess the robustness of our main results to several key parameter changes. In particular, we will consider model parameters where: 1) the internal diffusion coefficient linking nearest-neighbor submembrane, cytosolic, and NSR sites is halved, so that Ca wave velocities are decreased by a factor of 2; 2) variations in the proximal space volume v_p, and the submembrane space volume v_s (in particular, we consider model parameters in which these volumes are increased by 50%); and 3) we also consider simulations in which the AP shape has a more triangular shape, which is closer to what is found in atrial myocytes. Simulation results exploring this range of parameters are described in the Supporting Materials and Methods, and indicate that our main findings are robust to these model and parameter changes.

Subcellular Ca dynamics during rapid pacing

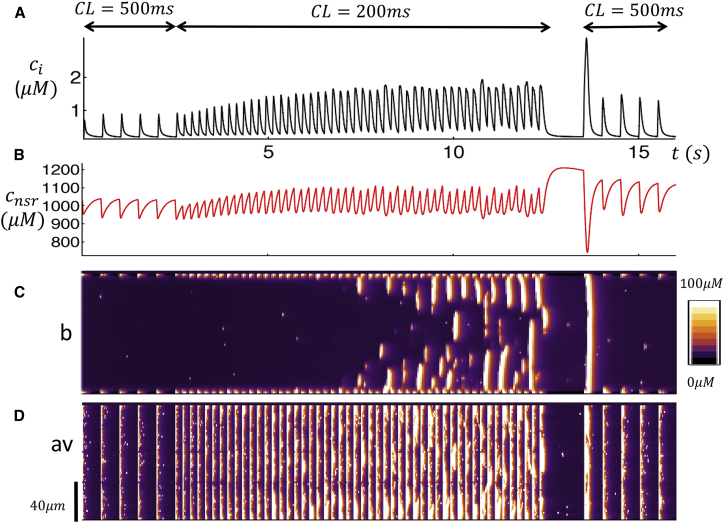
Here we apply our computational model to investigate the dynamics of Ca cycling during rapid pacing. To mimic the experimental setting, we pace the cell at CL = 500 ms for five beats, followed by pacing at 200 ms for 40 beats, followed by a 1 s pause and then a return to 500 ms for another five beats. In this way we evaluate the response of the cell to changes in pacing rate that are similar to the rapid pacing protocol used in the experiment. Fig. 7, A and B, shows the Ca transient and the NSR load during the pacing protocol. Fig. 7 C shows the line-scan image at position (b), and in Fig. 7 D we show the spatial average line-scan (av). Our simulation results reveal that during pacing at 500 ms Ca release occurs only on the cell boundary and that the response is periodic and in phase with the AP clamp. At a pacing rate of 200 ms, we find that the concentration of the NSR (c_nsr) increases gradually, and after ∼20 beats, triggered Ca waves begin to form. This is clearly shown by the line scan at position (b) (Fig. 7 C), which indicates that waves propagate into the cell interior with greater frequency as Ca accumulates in the NSR. Here, we point out that the spatially averaged line scan (Fig. 7 D) shows a combination of boundary Ca release and interior Ca release so that Ca waves and triggered Ca release are merged. Finally, we note that during the pause the NSR load builds as SERCA has an extended period of time to pump Ca back into the SR. However, no spontaneous Ca waves are observed during this period. Upon resumption of pacing at 500 ms, we find that the first beat was large as multiple Ca waves are ignited at the cell boundary. This is consistent with the experimental data shown in Fig. 2 A, where the subsequent beats after the pause are substantially larger than during the first period of 1000 ms pacing. In Fig. S3, we show the case where the cell is driven at a faster pacing rate (CL = 170 ms) for 40 beats. Here, we find again that Ca waves begin to occur with greater frequency as the SR load is increased. We note here that multiple Ca waves occur in the cell interior that appear to be insensitive to the pacing rate. This is similar to the experimental line scans shown in Fig. 2, B and C, in which multiple waves propagate across the pacing interval.

Figure 7.

Ca cycling during the rapid pacing protocol. (A) Given here is the Ca transient c_i when the cell is paced at CL = 500 ms (five beats), followed by rapid pacing at CL = 200 ms (50 beats), and then a 1 s pause followed by CL = 500 ms (five beats). (B) Given here is the NSR Ca concentration. (C) Shown here is a line-scan image at position (b). (D) Average line scan (c_av) is given. To see this figure in color, go online.

Role of t-tubule density

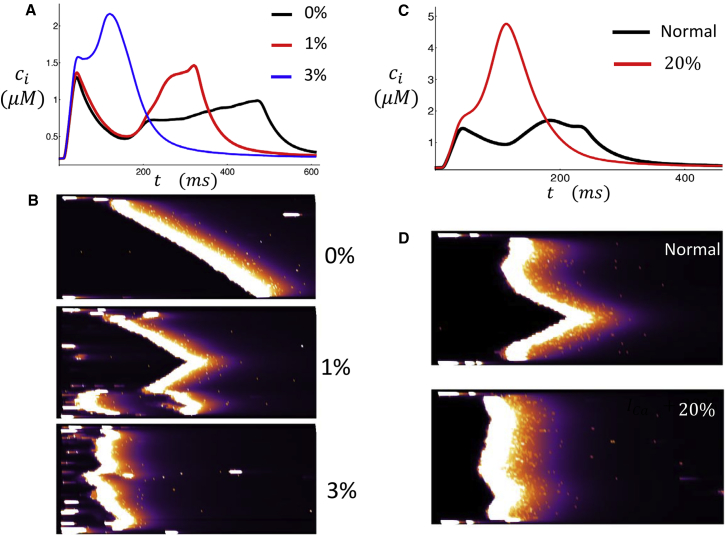
In this section we explore the relationship between EC coupling and the extent of t-tubule density in the cell interior. To model variation in t-tubule density, we let the cell interior have a fraction p of junctional CRUs. In Fig. 8 A, we plot the Ca transient in response to an AP clamp for p = 0%, 1%, 3% with initial NSR load c_nsr = 1230 μM. We observe that the time to the secondary peak after the AP upstroke is shortened substantially as p is increased. Fig. 8 B shows line scans through the center of the cell (position b) for the three different values of p. As p is increased, the number of wave sources in the cell also increases. Consequently, the latency to triggered waves is substantially reduced. In fact, for a density of membrane sites of just 3%, we find that the latency to triggered waves is so short that the secondary peak of the Ca transient merges with the stimulus-induced release. These results indicate that subcellular Ca release is highly sensitive to the degree of t-tubule penetration into the cell.

Figure 8.

(A) Ca transient during a single AP clamp for p = 0,1,3% junctional CRUs in the cell interior. The initial SR load is 1230 μM. (B) Given here are the corresponding line-scan images at position (b). (C) Shown here is a simulation of β-adrenergic stimulation. The black line is the normal Ca transient in response to an AP clamp. The red line corresponds to the case where I_Ca conductance is increased by 20%. (D) Given here are the corresponding line-scan images at location (b). To see this figure in color, go online.

β-adrenergic stimulation

To model the effect of β-adrenergic stimulation, we note that isoproterenol is known to increase Ca entry via LCCs. Thus, we will first consider the effect of increasing LCC conductance on the spatial distribution of subcellular Ca. Fig. 8 C shows the Ca transient in control and also where I_Ca is increased by 20%. In this case, the initial NSR load is taken to be c_nsr = 1230 μM, which is the same initial concentration used in Fig. 4. When the Ca current is increased, there is a much larger Ca transient and the characteristic double peak is absent. Fig. 8 D shows the corresponding simultaneous line-scan images at position (b). Here, we observe that increasing LCC current leads to a synchronized Ca release in the cell. The mechanism for this synchronization is that an increased LCC current promotes a larger number of trigger-wave sources. As a result, Ca activation of the cell interior occurs via multiple Ca waves, which activate the cell interior in a synchronized fashion. To further explore the role of β-adrenergic stimulation, we consider the effect of isoproterenol on the beat-to-beat response of a cell at steady-state pacing. In Fig. S4 we show the steady-state dynamics of a paced myocyte when I_Ca and SR SERCA conductance is increased substantially. Here, we find that these parameter changes leads to greater subcellular synchrony, which leads to a periodic beat-to-beat response. This result is consistent with our experimental findings (Fig. 2 E), which show that Ca cycling was effectively synchronized after the application of isoproterenol.

Nonlinear onset of triggered Ca waves

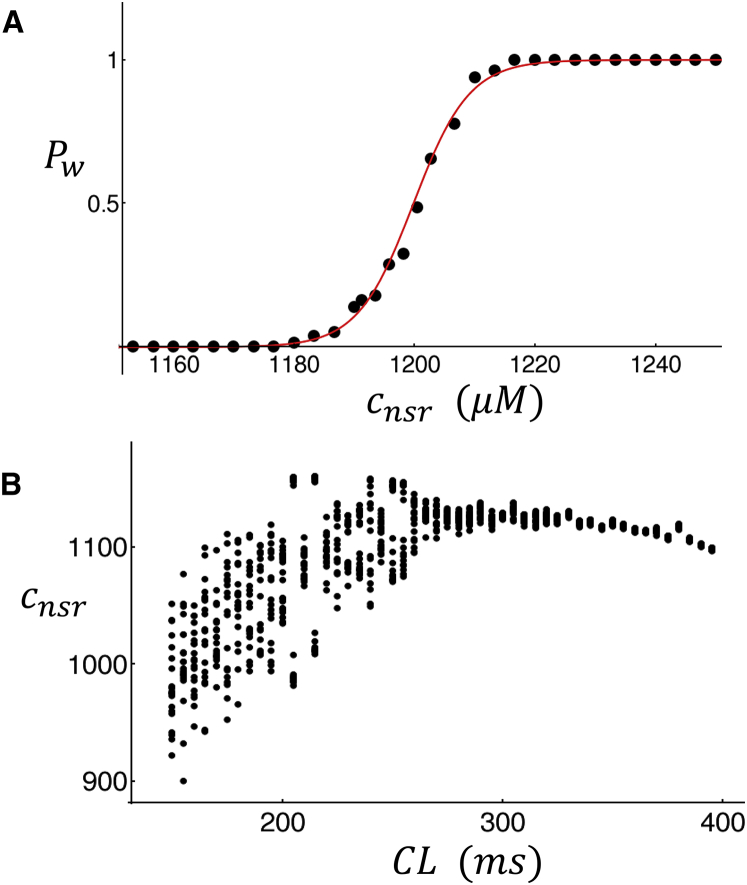
In this section we apply our computational cell model to determine the functional dependence of triggered waves on the SR Ca concentration. To accomplish this, we compute the probability, denoted as P_w, that a triggered wave occurs during a fixed time interval after an AP. To compute this probability, we fix the initial SR load and then pace the cell with an AP clamp with duration CL = 400 ms. We then compute the average diastolic Ca concentration in the cell interior defined as $c_i^{\text{int}}=\left(1/N_{\text{int}}\right){\sum }_{i=1}^{N_{\text{int}}}{c}_i$, where N_int is the number of interior CRUs. Our criterion for a triggered wave is that the internal concentration should exceed $c_i^{\text{int}}=3\mu \text{M}$. This criterion ensures that a substantial number of internal CRUs are triggered due to Ca wave activity. We then run 100 independent simulations and count the number of times that a triggered wave occurs in that time duration. In Fig. 9 A we plot P_w as a function of the initial NSR load showing a sharp sigmoid dependence. Here, we find that above a critical load c_nsr ∼ 1200 μM, the probability of triggered waves rises rapidly from P_w ∼ 0 to P_w ∼ 1 over a range of SR load of just ∼20–40 μM. This result shows that the probability that triggered waves occur is a sharp threshold function of the SR load.

Figure 9.

(A) The probability of occurrence of a triggered wave as a function of SR load during an CL of 400 ms. The probability is computed using 100 independent simulations. (B) Given here is the diastolic Ca concentration in the NSR. The cell is paced for 100 beats at the indicated CL, and the diastolic SR Ca concentration for the last 20 beats is plotted. To see this figure in color, go online.

Nonlinear dynamics of Ca cycling in atrial cells

Examination of the beat-to-beat dynamics of Ca cycling (Fig. 7; Fig. S3) reveals that the Ca transient exhibits aperiodic dynamics when triggered waves are formed. Here, we analyze the steady-state dynamics of a rapidly paced atrial cell to uncover the rate dependence of Ca release. To analyze the steady-state dynamics, we pace the atrial cell model to steady state and measure the diastolic SR load at each beat. This quantity is just the SR Ca concentration at the AP upstroke time t_i, denoted as $c_{\text{nsr}}^i=c_{\text{nsr}}\left(t_i\right)$. Fig. 9 B shows a plot of $c_{\text{nsr}}^i$ versus $CL$ for the last 20 beats of a total of 80 paced beats. For CL > 300 ms, the diastolic SR load does not vary substantially from beat to beat. However, if the CL is decreased further, then the $c_{\text{nsr}}^i$ varies substantially from beat to beat. This result demonstrates that the system response is aperiodic at rapid rates once triggered waves are initiated and interact with the normal Ca transients.

Discussion

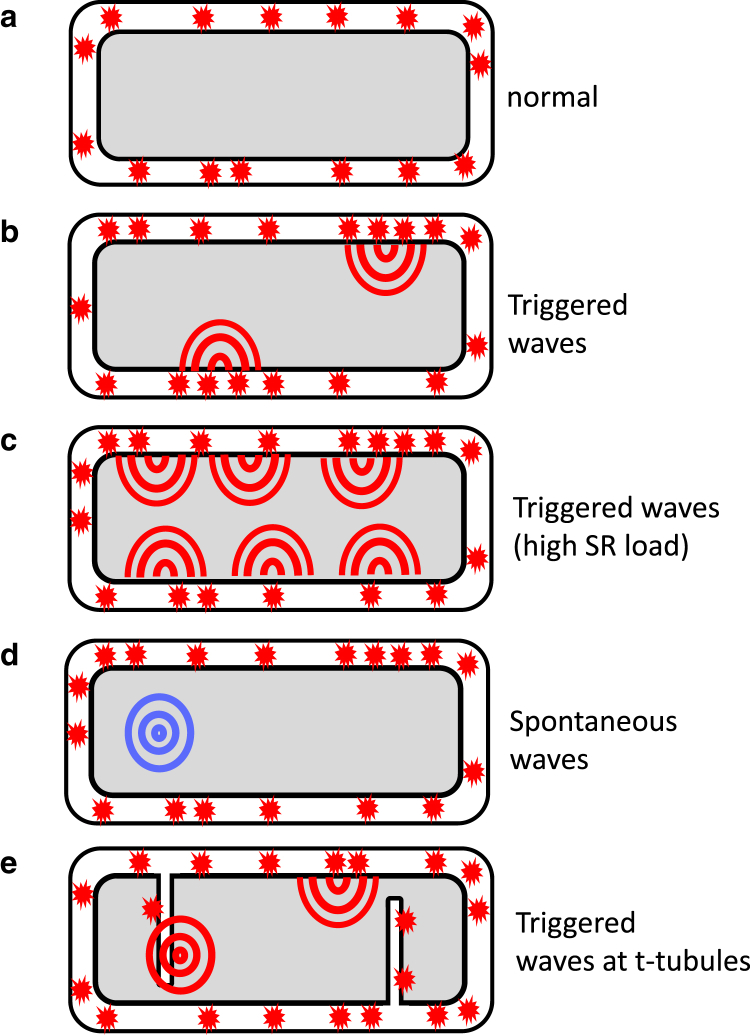
In this study, we have applied a physiologically based computational cell model that accounts for key features of atrial cell geometry. Using this model, we have explored the dynamics of subcellular Ca release in response to an AP clamp. Our simulation results reveal that, under moderate or low SR loads, Ca release occurs at the atrial cell boundary where LCCs trigger Ca release from nearby clusters of RyR. These numerical results are consistent with previous experimental and theoretical studies (7, 20) showing that Ca release is localized to the cell boundary and then diffuses gradually to the cell interior under normal conditions. However, in the case of increased SR loading, EC coupling in atrial cells displays much richer dynamics. The main finding is that when the SR load is increased, Ca release initiated by LCC openings at the cell boundary is sufficient to nucleate Ca waves that then propagate to the cell interior. These triggered waves are distinct from spontaneous Ca waves that can be nucleated in the cell interior and are independent of LCC openings. Fig. 10 illustrates the fundamental mechanism for triggered waves. The crucial insight is that the atrial cell geometry can be divided into junctional CRUs at the cell boundary and nonjunctional CRUs in the cell interior. Normal release at the boundary (Fig. 10 a) can then transition to triggered waves (Fig. 10 b), where Ca waves form at the interface between membrane and interior sites. This wave formation occurs at elevated SR loads when nonjunctional CRUs in the cell interior become more sensitized to Ca. Under these conditions, Ca diffusing from Ca sparks at junctional CRUs is sufficient to initiate a propagating Ca wave that emanates from the cell boundary. During rapid pacing, triggered waves disrupt the rhythmic response of the cell because they occur randomly and are not synchronized with the pacing interval. However, for larger SR loads, when the cell interior becomes highly sensitized to Ca, we find that triggered waves are nucleated at multiple sites on the cell boundary (Fig. 10 c). In this case, Ca release in the cell becomes synchronized with the AP, because triggered waves occur at each beat and activate the cell interior via centripetal waves. Spontaneous Ca waves (Fig. 10 d) can also occur in the interior due to RyR fluctuations, but the waiting time for these spontaneous waves is much longer because they form due to random RyR fluctuations, and are not activated by LCCs during the AP.

Figure 10.

Illustration of the distinct types of Ca release in an atrial cell. (a) Given here is the normal release due to Ca sparks at the cell boundary. (b) Here we show triggered waves that form at the boundary and propagate to the cell interior. (c) Shown here are multiple triggered waves occurring at the cell boundary leading to a synchronized Ca release. (d) Shown here are spontaneous Ca waves that form in the cell interior. (e) Given here are triggered waves occurring in the cell interior at t-tubules. To see this figure in color, go online.

Our basic mechanism for triggered waves is consistent with our experimental line-scan images. First, this mechanism explains the atrial cell response to rapid pacing shown in Fig. 2 A. Here, we note that it is well known that rapid pacing leads to elevated SR load due to the increased Ca entry into the cell (26). Thus, at low pacing rates, triggered waves are not observed because Ca release occurs mainly at the cell boundary and is synchronized with the pacing stimulus. However, as the SR Ca concentration rises at faster rates, the interior sites become more excitable and the formation of triggered waves becomes more likely. Once these waves occur, they propagate into the cell interior and the propagation dynamics is largely insensitive to the pacing stimulus, which only excites CRUs at the cell boundary. This result explains the experimental data showing that triggered waves, once formed, are not sensitive to the pacing stimulus (Fig. 2, A–C). This observation also indicates that the population of CRUs that fire during the AP upstroke must be distinct from those that are ignited by the propagating Ca waves. Indeed, this finding is consistent with the fact that the t-tubule structure in these cells is sparse, and that signaling between LCC and RyR occurs mostly at the cell boundary. A closer examination of Ca waves during rapid pacing (Fig. 2, B and C) indicates that the timing of wave initiation appears to be synchronized with the AP upstroke. This observation supports our claim that these waves are nucleated at the cell boundary due to LCC channel openings. However, we note that there are wave sources that do not appear to be induced by the AP. These events are likely due to waves that originate far from the line scan. In these cases, the wave front will reach the line scan after a delay and will not be synchronized with the AP. Finally, we also note that our experimental line scans show triggered waves as much brighter than the paced Ca release. This result is consistent with the fact that Ca release due to triggered waves is likely larger than release at the boundary because a larger number of sites can be recruited in the cell interior. The proposed mechanism also explains why Ca wave activity is substantially reduced during the pause after rapid pacing because triggered waves do not occur when LCCs are shut at the resting membrane potential. Thus, Ca wave activity can only be due to spontaneous Ca waves in the absence of active LCCs. However, because nucleation of spontaneous waves occurs with a much greater latency, the frequency of wave activity is substantially reduced during the pause.

In this study, we have explored the relationship between t-tubule density and subcellular Ca release. To investigate this relationship, we introduced a parameter p, which is the probability that an internal site possesses LCCs and NCX. Our numerical simulations reveal that variations in p can have a substantial effect on EC coupling in atrial cells. In effect, we find that, as the probability p is increased, the number of triggered waves increases substantially. In our simulations (Fig. 8 A), we find that just increasing the fraction of internal membrane sites to p = 3% ensures that Ca release is effectively synchronous throughout the cell because the number of nucleation sites is increased. In Fig. 10 d, we illustrate how t-tubule invaginations promote triggered-wave initiation. In this case, the 2 μm diffusion barrier at the cell boundary does not lead to a delay because triggered wave nucleation can occur at nonjunctional sites. Here, we will argue that the sensitivity of triggered waves to the probability p will have an important effect on the population dynamics of atrial myocytes. This is because recent experimental studies indicate that t-tubule density is highly variable in atrial cells (5, 10), and can range from sparse to virtually absent. Our results imply that EC coupling in a population of cells will also be highly heterogeneous because the population of cells with no t-tubules will release Ca only at the cell boundary, whereas the cells with sparse t-tubules should exhibit synchronous release due to multiple Ca waves. Therefore, the Ca transient should vary substantially in tissue due to the variability of t-tubule density. This result will also have implications on those HF cells that are known to have a less developed t-tubule system than normal. In these cells, HF remodeling is believed to disrupt the tight coupling between LCCs and RyRs, which leaves a larger population of RyR clusters that are “orphaned”. Our results imply that this progression will decrease the number of triggered waves in the cell interior. Therefore, the population of cells with a more substantial t-tubule system can potentially lose their synchronized Ca release because the number of triggered waves will be reduced. Interestingly, this progression can be arrhythmogenic because synchronized release in these cells will degenerate to an aperiodic response driven by the interplay between boundary Ca release and less frequent triggered waves. However, it is unclear if this effect will be relevant to the dog atria because t-tubules are sparse in these cells, and HF progression may not have a large effect on the spatial relationship between LCC and RyR channels.

In this study, we have also explored the effect of β-adrenergic stimulation on subcellular Ca release. Our main finding is that isoproterenol effectively synchronizes subcellular Ca release by promoting multiple triggered waves in the cell. To model β-adrenergic stimulation, we have increased both the LCC and SERCA conductance in the cell model. The effect of these changes is to increase the SR load due to the increased Ca entry and SERCA, and also to increase the signaling fidelity between LCC and RyR channels. These changes promote the nucleation of triggered Ca waves, so that multiple waves occur and lead to a synchronous Ca release in the cell. This case is similar to that shown in Fig. 5, where Ca is released rapidly due to multiple waves originating at the cell boundary. In this scenario, we find that Ca release is periodic during pacing because the same amount of Ca is effectively released at each beat. Here, the increased SERCA quickly replenishes the SR load over one beat, so that a full synchronized release can occur at the next beat. This result is consistent with our experimental line scans in Fig. 2 E, where we find that isoproterenol leads to a spatially uniform and periodic response. Furthermore, during the pause, multiple spontaneous Ca waves occurred, indicating that the SR load was indeed increased. This result is consistent with similar studies by Mackenzie et al. (7), who demonstrated that β-adrenergic stimulation facilitates coherent activation of the whole cell. Thus, isoproterenol synchronizes Ca release during pacing by promoting synchronized wave activation at multiple sites on the cell boundary.

Our experimental findings revealed that Ca transients exhibited aperiodic behavior during rapid pacing due to the complex interplay between paced Ca release and triggered waves. To explain this feature, we applied our computational model to compute the probability P_w that Ca waves occur during a CL. Our main result is that P_w exhibits a sharp sigmoid dependence on the SR load so that the probability that a triggered wave occurs increases substantially above a critical SR concentration. However, once Ca is released during a beat in which triggered waves occur, the SR load is depleted on the next beat and time is required to replenish the SR. Thus, a nonlinear dependence of the probability P_w on SR load naturally destabilizes the periodic pacing response that occurs in the absence of triggered waves. To quantify this result, we also computed the beat-to-beat diastolic SR load at steady state as a function of the pacing rate (Fig. 9 B). Indeed, we find that as the SR load builds, the system’s response becomes aperiodic as triggered waves begin to disrupt synchronized Ca release in the cell. In fact, previous studies have demonstrated that a nonlinear dependence of Ca release on SR load leads to dynamical instabilities such as alternans and even chaos (25, 27, 28, 29, 30). In particular, we note the classic work of Díaz et al. (31), who showed that when rat ventricular cells are paced periodically with small depolarizing pulses, Ca waves occur at alternate beats, causing an alternans response at the whole cell level. Furthermore, they showed that this wave propagation occurred only after the SR content exceeded a sharp threshold. In our study, we identify essentially the same mechanism where the atrial cell is driven by a small population of junctions rather than a reduced LCC current. Thus, the instability in ventricular myocytes caused by an abbreviated LCC current occurs naturally in atrial cells because the signaling between LCC and RyR is limited to a small population of junctions. Finally, we point out that in our system, triggered waves are stochastic in nature; therefore, deterministic approaches to understand the underlying instability will not directly apply.

In previous theoretical studies, Thul et al. (20, 21) pointed out that atrial cells, by virtue of their unique spatial architecture, are susceptible to dynamical instabilities caused by boundary induced wave propagation. Here, we have applied a physiologically based computational cell model to extend these findings to explain line-scan imaging data of rapidly paced atrial cells. Furthermore, we show that atrial cells are prone to instabilities that depend on the wave propagation nonlinearity described by the function P_w. This instability does not occur in ventricular cells in which the t-tubule system is well developed and Ca signaling occurs within the full 3D volume of the cell, leaving a limited number of available RyR clusters that can still support wave propagation. Thus, the fundamental feature of atrial cells that makes them prone to instabilities is the larger number of available nonjunctional CRUs that can be recruited in a nonlinear fashion at elevated SR loads. The implications of this finding for the genesis of atrial fibrillation deserves further exploration. Several experimental studies have shown that Ca cycling plays an important role in AF (17, 32). The results of our study suggest that triggered waves will play a crucial role in the underlying mechanisms. Indeed, the dynamical instability that we describe will lead to higher incidence of triggered activity that may be critical in the formation of ectopic excitations that drive atrial fibrillation. Moreover, triggered waves will also affect AP duration, possibly establishing regional repolarization gradients that can form a substrate for reentry. Finally, we also stress that the aperiodic dynamics of atrial cells under rapid pacing will induce dynamical heterogeneities that may be crucial to the maintenance of AF. Thus, our study uncovers, to our knowledge, new mechanisms that may be crucial to the initiation and maintenance of atrial fibrillation.

Author Contributions

Y.S., G.L.A., and J.A.W. designed research, performed research, contributed analytic tools, analyzed data, and wrote the paper.

Editor: Mark Cannell.