Comparison and validation of two computational models of Chagas disease: A thirty year perspective from Venezuela

Abstract

Background

Mathematical models can help aid public health responses to Chagas disease. Models are typically developed to fulfill a particular need, and comparing outputs from different models addressing the same question can help identify the strengths and weaknesses of the models in answering particular questions, such as those for achieving the 2020 goals for Chagas disease.

Methods

Using two separately developed models (PHICOR/CIDMA model and Princeton model), we simulated dynamics for domestic transmission of Trypanosoma cruzi (T. cruzi). We compared how well the models targeted the last 9 years and last 19 years of the 1968–1998 historical seroprevalence data from Venezuela.

Results

Both models were able to generate the T. cruzi seroprevalence for the next time period within reason to the historical data. The PHICOR/CIDMA model estimates of the total population seroprevalence more closely followed the trends seen in the historic data, while the Princeton model estimates of the age-specific seroprevalence more closely followed historic trends when simulating over 9 years. Additionally, results from both models overestimated T. cruzi seroprevalence among younger age groups, while underestimating the seroprevalence of T. cruzi in older age groups.

Conclusion

The PHICOR/CIDMA and Princeton models differ in level of detail and included features, yet both were able to generate the historical changes in T. cruzi seroprevalence in Venezuela over 9 and 19-year time periods. Our model comparison has demonstrated that different model structures can be useful in evaluating disease transmission dynamics and intervention strategies.

1. Introduction

Chagas disease, caused by the protozoan parasite Trypanosoma cruzi, is one of the world's most important neglected tropical diseases (NTDs). It infects approximately 6–7 million people worldwide (World Health Organization, 2016) and results in an estimated $627.46 million in healthcare costs and $7.19 billion in societal costs annually (Lee et al., 2013). Given its substantial burden Chagas is one of the ten NTDs targeted for control or elimination by 2020, with one of the London Declaration's stated goals for being 100% certified interruption of domestic transmission in Latin America (Tarleton et al., 2014). Historically, control of Chagas disease has focused on vector control. This can be achieved directly by vector reduction using insecticides or indirectly through housing modifications.

Mathematical models are simplifications of real life that are developed to address a particular need or question (Garnett et al., 2011). Model development must balance the actual complexity of biological systems with the simplifying assumptions that ensure computational tractability (Lee, 2008). Additionally, models are not a one size fits all. The applicability of different models to answer specific research and public health questions lies in appropriateness and flexibilities of specific methodologies employed. Thus, assessing and comparing mathematical models and determining if they capture relevant features of reality for a particular application is fundamental to optimal model design (St-Pierre, 2016). While model assessments and comparisons have been conducted in other fields/pathogens (notably human immunodeficiency virus (Hontelez et al., 2013; Eaton et al., 2012)), little has been done in the realm of NTDs (Hollingsworth et al., 2015).

In this study, we parameterize two differently structured, independently developed, Chagas disease transmission models to evaluate the same research question using the same input/baseline data. We compare model results, and discuss possible causes of differences. Comparing outputs from different models addressing the same question can help identify the strengths and weaknesses of the models to answer particular questions. For example, one model may be best at answering policy questions related to disease prevalence and control in humans, while another may be better suited to answer questions about ecology and vector control. Model comparison can also help us gain understanding on how data informs parameter estimation and impacts output. Understanding model strengths and weaknesses can aid various decision makers in knowing which model is best apt to answer questions and in interrupting model results, which can be helpful in achieving the 2020 goals.

2. Methods

We independently developed two T. cruzi transmission models (described below). The comparison consisted of simulating the transmission of T. cruzi in the domestic setting in the two models and comparing the resulting seroprevalence between the models and to the historical seroprevalence data. Table 1 shows key input parameter values and sources for both models, while Fig. 1 provides an outline of each model.

Table 1.

Model input parameters, values, and sources.

Parameter	PHICOR/CIDMA Model		Princeton Model		Source
	Symbol	Value	Symbol	Value
Probabilities (%)
Developing chronic Chagas	λH	25		–	(Bern, 2015)
disease given indeterminate phase
Chagas related mortality during acute stage	μHA	1		–	(Bern et al., 2017)
Chagas related mortality during chronic stage (20 years and older, annually)	μHC	7.84		–	(Rassi et al., 2007)
Transmission to dogs given bite of infected vector (% per bite)	ε	0.000008–0.0012a		–
Transmission to humans given bite of infected vector (% per bite)	εH	0.000001–0.000011a	hb	0.00058	(Nouvellet et al., 2013)
Transmission from acute stage to triatomine (% per bite)	Θa	0.4928–0.7392a	ha	0.61	(Pinto et al., 2008)
Transmission from indeterminate and chronic stage to triatomine (% per bite)	Θi	0.016–0.432a	hc	0.026	(Gurtler et al., 1996)
Transmission from dog to triatomine (% per bite)	Θd	0.19–0.56a		–
Triatomine feeding proportion for humans	pH	0–1a		–	(Pena-Garcia et al., 2014)
Rates
Triatomine contact rate (per bug per year)	β	41	β	41	(Arevalo et al., 2007)
Triatomine birth rate (per bug per year)		36	r	36	(Arevalo et al., 2007)
Triatomine death rate (per year)	dv	1.73	μ	1.73	(Arevalo et al., 2007)
Human birth rate	bH	3.2× death rate (United Nations, 2015)	w	2× death ratea
Human death rate (peryear)	dH	0.0149	d	0.0149	(The World Bank, 2016)
Additional Chagas related mortality rate during chronic stage (30 years and older)		–	Cm	0.00263386	Assumption
Dog birth rate	bD	Same as death rate		–
Dog death rate (per month)	dD	0.01667		–	Assumption
Numbers/Durations
Number of humans	NH	10,000	N	11,252 (Ache and Matos, 2001)
Number of dogs (per person)	ND	0.393		–	(Bonfante-Cabarcas et al., 2011; Rojas et al., 2008; Crisante et al., 2006; Berrizbeitia et al., 2013; Cardenas et al., 2006)
Triatomine carrying capacity (per person)		50		–	(Peterson et al., 2015)
Duration between the acute phase and the indeterminate phase (weeks)	πH	6	α	6	(Bern, 2015; Rassi et al., 2010)
Duration between the indeterminate phase and chronic phase (years)	λH	20		–	(Bern, 2015; Rassi et al., 2010)
T. cruzi incubation time in R. prolixus (weeks)		–	inc	1	(Dias Fde et al., 2015)

^aValue fitted during calibration process.

Fig. 1.

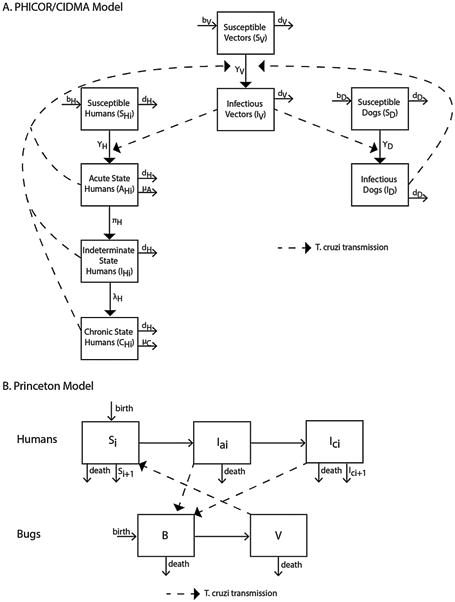
Model outline for a) the PHICOR/CIDMA model, and b) the Princeton model (i denotes different age groups in both models).

2.1. PHICOR/CIDMA model

This model was developed by a team at Johns Hopkins Bloomberg School of Public Health and the Center for Infectious Disease Modeling and Analysis (CIDMA) at Yale School of Public Health. It was originally developed to answer questions about vector control on T. cruzi transmission (i.e., measuring new acute Chagas cases) and the role of non-human hosts on a larger scale than previous models, and has three general age categories to explore potential target populations for interventions. Developed in Python (Python Software Foundation, Wilmington, DE), this compartmental simulation model represented vector and host populations involved in T. cruzi transmission and included triatomines, human hosts, and non-human hosts (i.e., dogs) and vector-borne transmission among these populations in the domestic habitat (Fig. 1). The model ran in monthly time steps (i.e., t = 1 month or 30 days), chosen due to the long disease course of Chagas, and simulated a 41-year period. During each time step, epidemiological and clinical rates defined transitions between model compartments, stratified by the different vector and host populations. Vectoral transmission in this model was governed by the force of infection.

Triatomine bugs could be susceptible (not infected with T. cruzi and able to become infected) or infectious (infected with T. cruzi and able to transmit to vertebrae hosts upon biting). Upon biting an infectious host (human and viable non-human), a susceptible bug had probabilities of becoming infected with T. cruzi, depending on the disease state of the host. The number of triatomine bugs (N_V = 475,972) in the model was determined from the carrying capacity, or the number of bugs sustainable in the habitat, which was assumed to be 50 bugs per person (consistent with previous work (Peterson et al., 2015)). The following formulas describe the susceptible and infectious states for triatomine bugs:

$$\frac{d{S}_V}{dt}=b_V-{\gamma }_V{S}_V-d_V{S}_V$$

$$\frac{d{I}_V}{dt}={\gamma }_V{S}_V-d_V{I}_V,$$

where b_v is the number of bug births, d_v is the triatomine death rate, and γ_V is the force of infection. The number of bug births is determined by the birth rate, carrying capacity, and total number of triatomines by the following formula:

$$b_V=\mathit{\text{birthrate}}\ast N_V\ast \frac{\mathit{\text{carrying capacity}}-N_V}{\mathit{\text{carrying capacity}}}.$$

The following formula determine the force of infection (ϒ_v):

$${\gamma }_V=\beta \left[\frac{p_D{\theta }_D{I}_D+p_H\left({\theta }_A{A}_H+{\theta }_I\left(I_H+{\theta }_C\right)\right)}{p_H{N}_H+p_D{N}_D}\right],$$

where β represents the triatomine biting rate, Θ is the probability of transmission (or infectivity), N_H, and N_D the number in the human and dog populations, respectively; p_H and p_D, and describe the vector feeding preferences for humans and dogs, respectively.

The human population (N_H) consisted of 10,000 persons at the start of the simulation and was comprised of three age groups, i: (0–19 years old, 20–39 years old, and 40 years and older following historical age-specific demographic data from the World Population Prospects (United Nations, 2015)). The human population is divided into four states: susceptible (S_H, not infected with T. cruzi and able to become infected), acute stage Chagas disease (A_H, infected with T. cruzi and able to transmit, exhibit mild and nonspecific symptoms, and person has microscopically detectable parasitemia), indeterminate stage Chagas disease (I_H, asymptomatically infected with T. cruzi and able to transmit), and symptomatic chronic stage Chagas disease (C_H, infected with T. cruzi, able to transmit, and show symptoms of chronic disease such as cardiomyopathy and/or megaviscera). Thus, a person in any of the three Chagas disease states are considered positive. Upon the bite of an infectious triatomine, a susceptible human had a probability of becoming infected with T. cruzi, based on the force of infection (γ_H), and once infectious, persons were remained infectious in absence of treatment (i.e., once seropositive, always seropositive, with no decay). Those in the acute and symptomatic chronic states of disease had probabilities of Chagas-related mortalities. These states and the transmission between them are described by the following four equations:

$$\frac{d{S}_{Hi}}{dt}=b_{Hi}-{\gamma }_H{S}_{Hi}-d_H{S}_{Hi}$$

$$\frac{d{A}_{Hi}}{dt}={\gamma }_H{S}_{Hi}-{\pi }_H{A}_{Hi}-\left(d_H+{\mu }_{HA}\right)A_{Hi}$$

$$\frac{d{I}_{Hi}}{dt}={\pi }_H{A}_{Hi}-{\lambda }_H{I}_{Hi}-d_H{I}_{Hi}$$

$$\frac{d{C}_{Hi}}{dt}={\lambda }_H{I}_{Hi}-\left(d_H+{\mu }_{HC}\right)C_{Hi}$$

where b_H is the number of people entering each age group (i.e., number of births or number of persons aging (United Nations, 2015)), d_H is the human death rate from all causes, μ_ha is the probability of Chagas related mortality in the acute phase of disease, and μ_HC is the probability of Chagas related mortality in the chronic phase. Two variables, π_h and λ_H, describe the rate of movement from the acute phase to the indeterminate phase and the indeterminate phase to the chronic phase, respectively.

The force of infection in humans from vectors, denoted ϒ_H, is defined by the following equation:

$${\gamma }_H=\frac{\varepsilon I_V}{N_H}\left(\beta \frac{p_H}{p_D+p_H}\right)$$

Dogs serve as reservoir hosts for T. cruzi and could be either susceptible (S_D) or infectious (I_D), with a susceptible dog becoming infected upon the bite of an infected vector based on the force of infection. Dogs could transmit T. cruzi to susceptible triatomines (i.e., triatomines could become infected upon biting an infected dog). The number of dogs in the model (N_D =3930) was determined from the literature based on the ratio of dogs to humans (Table 1). Equations dictating the movement of dogs between states and their force of infection are as follows:

$$\frac{d{S}_D}{dt}=b_D{N}_D-{\gamma }_D{S}_D-d_D{S}_D$$

$$\frac{d{I}_D}{dt}={\gamma }_D{S}_D-d_D{I}_D$$

$${\gamma }_D=\frac{\varepsilon I_{V1}}{N_D}\left(\beta \frac{p_D}{p_D+p_H}\right)$$

Here, b_D and d_D are birth and death rates of dogs, respectively. ε is the probability of T. cruzi transmission to dogs given the bite of an infected vector. As already described, β is the vector biting rate, and p_H and p_D, are vector preferences for humans and dogs, respectively.

Chagas prevention and control interventions are modeled as a reduction in contact between the triatomine and host populations, using the following formula to attenuate the force of infection:

$$\left(1-r_{ID}\right)\ast {\gamma }_V$$

where r_ID is the reduction in intradomiciliary transmission to domestic vectors due to control measures.

The PHICOR/CIMDA model was fitted to account for uncertainty in empirical data. Initial conditions assumed the values in Table 1, for fitted parameters, we started with the reported value and then allowed the calibration method to search in a range around these values. The model calibration used two methods: 1) a genetic algorithm that searched and identified combinations of parameter values within our search space, mean squared error measured goodness of fit of these sets compared to the published range and 2) a search for sets of parameter values that generated seroprevalence values within 0.5% of the published range to reflect the uncertainty around the reported seroprevalence and model's input parameter values. Table 1 lists the ranges for these parameters. Results are reported as the average across all the simulated years runs during a given timer period, with the range representing the minimum and maximum average over the time period across all simulation runs.

2.2. Princeton model

This model was developed in R (R Foundation for Statistical Computing, Vienna, Austria), by Dobson and Peterson at Princeton University (Fig. 1). It was originally developed to examine the dynamics of Chagas disease in an age-structured population, to look at how age-prevalence patterns of infection would change in response to different interventions. The model is an age-structured differential equation model that runs in 1 week time steps. Since the duration of the acute phase of Chagas disease is a matter of weeks, while the chronic phase is a matter of years, we selected one week time steps to capture the dynamics in both phases.

In this model, the human population (N) is divided into 6 ten-year age groups (i), each of which contains uninfected hosts, infected individuals in an acute phase, I_a, and a chronic phase, I_c. The uninfected human population in each age group i, is equal to N_i – (I_ai +I_ci). The population grows slowly with the birth rate, w, equal to two times the mortality rate, d. Individuals move from the acute phase into the chronic phase at rate α. All Chagas phases are considered positive. A maturation rate, m (=1/10), moves individuals into sequential age groups. Infected individuals in the chronic stage have an increased mortality rate, Cm. An age-dependent exposure term, Ba, accounts for the accumulation of T. cruzi infection in each age group. This determines the rates at which vectors are distributed across the host population and the rate at which humans of different ages acquire infection in the model.

The triatomine population is divided into uninfected bugs, B, exposed and incubating, X, and infected and infectious, V. The T. cruzi incubation period within the bugs is represented by inc. All bugs have a birthrate, r, and a death rate, μ. We assume a triatomine-human contact rate of β, with the transmission probability upon contact from humans to bugs being different between infection stages with h_a and h_c, representing the transmission probabilities from humans in the acute and chronic phases, respectively. The probability of transmission from bugs to humans is represented by h_b. Vector control interventions such as insecticide spraying or housing improvements are represented throughout the model by the terms HII and HDI. These terms represent the proportion of houses infested (HII) and the number of bugs per total houses examined (HDI; from the “House Infestation Index” and “House Density Index,” (Ache and Matos, 2001)). We use a density dependence parameter, del, which determines bug abundance relative to humans, and is calculated by:

$$\left(\frac{r-\mu }{100\mathit{\text{HDI}}}\right)\left(\frac{1}{1-\mathit{\text{HII}}}\right)$$

Vector control interventions are represented elsewhere in the model with two additional terms HII_R, and HDI_R, which represent the slopes of the regression of HII and HDI over time.

The full age-structured model can be described by the following set of equations:

Human hosts

$$\frac{d{S}_i}{dt}=m{S}_{i-1}-\beta h_{b}B{a}_i{S}_i\left(\frac{V}{N}\right)-S_i\left(d+m\right)$$

$$\frac{d{I}_{ai}}{dt}=\beta h_{b}B{a}_i{S}_i\left(\frac{V}{N}\right)-I_a\left(d+\alpha \right)$$

$$\frac{d{I}_{ci}}{dt}=\alpha I_{ai}+m{I}_{ci-1}-(d-m+Cm)I_{ci}$$

Triatomine dynamics

$$\frac{dB}{dt}=\frac{-B{\mathit{\text{HDI}}}_R}{(1-\mathit{\text{HII}})}$$

$$\frac{dX}{dt}=B\beta \left(\frac{h_a{\sum }_{i=1}^6{I}_{ai}+h_c{\sum }_{i=1}^6{I}_{ci}}{N(1-\mathit{\text{HII}})}\right)-X({\mu }_b+\mathit{\text{inc}})$$

$$\frac{dV}{dt}=X\mathit{\text{inc}}-{\mu }_{b}V$$

Intervention

$$\frac{dHT}{dt}=(-\mathit{\text{HII}})\left({\mathit{\text{HII}}}_R\right)$$

$$\frac{d\mathit{\text{del}}}{dt}=(-\mathit{\text{del}})\left({\mathit{\text{HDI}}}_R\right)$$

Initial conditions were set up for each ten year run using the observed age-prevalence relationships and estimates of average bug density and proportion of houses treated. Parameter variability is included in the model as an array of 100 random values within the 95% confidence intervals for each parameter generated with the function rtruncnorm from the package “truncnorm” (Trautmann et al., 2014). This package uses least squares to measure fit. For parameters obtained from experimental results, (i.e., triatomine mortality), the range of values observed in the given experiment were used. Values from this array were then selected for each parameter for each year of 100 runs of the model. Results are presented as the average and 95% confidence interval, with the confidence interval calculated from the mean and standard deviation of the simulation runs.

2.3. Differences between models

There are a few key differences between the PHICOR/CIDMA and Princeton models. They differ in the number of age groups included and how infection may vary by age (i.e., the Princeton model accounts for the rate at which humans of different ages acquire infection). While both models include a chronic state, only the PHICOR/CIDMA model differentiates between the indeterminate and determinate chronic Chagas disease states. Likewise, Chagas mortality representations differed. The host species in the models differ, which impacts transmission dynamics. Intervention representations also where accounted for differently in both models. The PHICOR/CIDMA model simulates a change in the force of infection, while the Princeton model simulates changes in bug abundance. These differences require data to calibrate.

2.4. Data sources

Both models utilized age-structured T. cruzi seroprevalence data from the national Chagas Disease Control Programme (CDCP) for Venezuela as reported in Ache and Matos (Ache and Matos, 2001). These data were originally collected by the Venezuelan Ministry of Health between 1958 and 1998 in regions of Venezuela considered to be at high-risk for Chagas disease. This historic data is reported in six 10-year age groups. The PHICOR/CIMDA model collapsed two sequential age groups so there where three groups total, while the Princeton model represent the same six groups. Due to Chagas' long disease course, the compartments of both models would tend to be at equilibrium in the absence of any intervention. Entomological interventions, including insecticide spraying and improvements of over 400,000 houses, were carried out during the same time. These interventions resulted in a drastic reduction in T. cruzi seroprevalence in Venezuela. However, control has slowed down since the turn of the century and there are reports of increases in T. cruzi prevalence in humans (Anez et al., 2004; Anez et al., 2011; Anez et al., 2016).

Each model accounted for the ongoing Chagas disease intervention and control programs in Venezuela over time differently. The PHICOR/CIDMA Model used data on the change in the force of infection (FOI) over time for the same Venezuelan dataset, as reported in Feliciangeli et. al (Feliciangeli et al., 2003), and determined the reduction in the FOI for each time interval. Yearly estimates were aggregated and used as proxies in place of specific historical interventions. The Princeton Model used both age-specific force of infection (calculated from the data for each successive ten year time interval) and changes in the house infestation indexes and house density indexes to estimate the change (i.e., slope calculated by regression in a linear model) in the number of bugs per house and in infested houses overtime (Fig. 2).

Fig. 2.

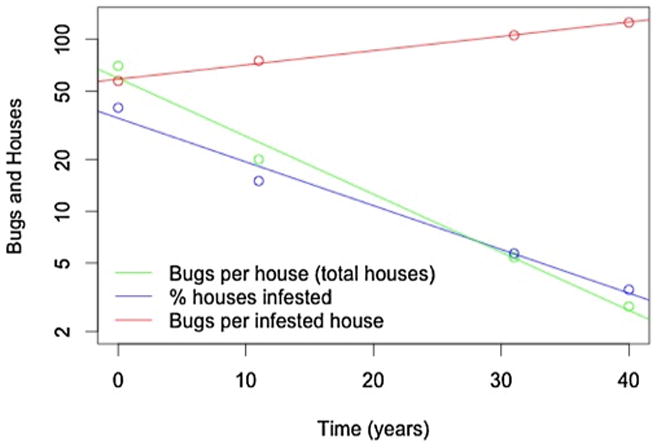
Entomological surveillance data for triatomine bugs and triatomine-infested houses from Ache 2001 for the time period of 1958–1998. The blue line indicates the percentage of houses infested with triatomine bugs; we assume the proportion of humans at risk of Chagas disease varies directly with this index. The green line is the average number of triatomine bugs per house, including those that are not infested. The red line is the average number of triatomine bugs per infested house, calculated from the two prior indices. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.5. Model comparison scenarios

We used the age-stratified seroprevalence data from Venezuela over the 41-year period of 1958–1998 (Ache and Matos, 2001) split into 4 time periods (historic data in Tables 2 and 3). In the first scenario, targeting the last time point, we independently calibrated our models to the first three time periods (first 32 years, 1958–1989) and compared observables for the last time period (last 9 years, 1990–1998). In the second scenario, targeting the last two time points, we calibrated our models to the first two time periods (first 21 years, 1958–1978) and compared observables for the last two time periods (last 19 years, 1980–1998). The PHICOR/CIDMA model allowed for the calibration of any number of time periods and simulation of the full 41 years of historical data, while the Princeton model used the seroprevalence of the time period prior to the simulated time period as a starting point to generate seroprevalences over the next 9 or 19 years. Observables of interest were age-stratified T. cruzi seroprevalence in humans and T. cruzi seroprevalence in triatomine bugs.

Table 2.

Average (range) simulated T. cruzi seroprevalence (%) for each time period using the PHICOR/CIDMA Model compared to historical Venezuelan data.

	Time Periods (Years)
	1958–1968	1969–1979	1980–1989	1990–1998
Historical Dataa
Ages 0–19 years	26.3 (18.3–29.8)	6.0 (3.4–11.0)	1.7 (0.9–2.6)	1.1 (0.42–2.0)
Ages 20–39 years	55.3 (46.6–64.7)	32.3 (26.9–36.5)	18.3 (11.5–27.6)	10.4 (5.5–16.8)
Ages 40 years and older	65.5 (62.2–68.5)	44.4 (38.2–52.7)	44.3 (36.2–48.9)	37.1 (27.2–43.9)
Targeting the Last Time Point
	Calibrated	Calibrated	Calibrated	Generated
Ages 0–19 years	25.4 (15.9–39.5)	10.8 (6.3–15.8)	4.2 (2.6–6.3)	1.7 (1.1–2.5)
Ages 20–39 years	55.5 (42.3–68.8)	32.2 (21.9–42.2)	15.8 (10.8–21.8)	7.8 (5.4–10.7)
Ages 40 years and older	63.4 (68.0–58.3)	51.9 (43.6–58.2)	36.7 (30.1–43.5)	25.0 (20.3–30.0)
Targeting the Last Two Time Points
	Calibrated	Calibrated	Generated	Generated
Ages 0–19 years	24.8 (14.8–39.5)	9.8 (5.5–14.7)	3.6 (2.1–5.5)	1.4 (0.9–2.1)
Ages 20–39 years	54.9 (41.3–68.8)	31.0 (20.6–41.1)	14.6 (9.8–20.4)	7.0 (4.8–9.8)
Ages 40 years and older	63.0 (57.4–68.0)	50.7 (42.2–57.3)	35.3 (28.7–42.1)	23.7 (19.2–28.6)

NOTE: average across all the simulated years and runs during each time period; range represents the minimum and maximum over the time period across all simulation runs.

^aAverage for age-groups combined from data reported in Ache and Matos (Ache and Matos, 2001); range represents the lower and upper bounds of the 95% confidence intervals reported for the individual age-groups.

Table 3.

Average (95% confidence interval) simulated T. cruzi seroprevalence (%) for each time period using the Princeton Model compared to historical Venezuelan data.

	Time Periods (Years)
	1980–1989	1990–1998
Historical Dataa
Ages 0–9 years	1.1 (0.9–1.2)	0.5 (0.42–0.56)
Ages 10–19 years	2.4 (2.2–2.6)	1.8 (1.6–2.0)
Ages 20–29 years	12.4 (11.5–12.8)	5.9 (5.5–6.3)
Ages 30–19 years	26.6 (25.5–27.6)	16.1 (15.4–16.8)
Ages 40–49 years	37.5 (36.2–38.8)	28.3 (27.2–29.4)
Ages 50 years and older	48.0 (47.0–48.9)	43.0 (42.1–43.9)
Targeting the Last Time Point
Ages 0–9 years	–	0.73 (0.71–0.75)
Ages 10–19 years	–	1.90 (1.88–1.93)
Ages 20–29 years	–	7.18 (6.99–7.37)
Ages 30–19 years	–	18.41 (18.02–18.81)
Ages 40–49 years	–	30.39 (30.01–30.78)
Ages 50 years and older	–	45.23 (45.07–45.39)
Targeting the Last Two Time Points
Ages 0–9 years	2.93 (2.88–2.98)	1.30 (1.27–1.33)
Ages 10–19 years	6.84 (6.72–6.96)	3.63 (3.58–3.69)
Ages 20–29 years	16.81 (16.37–17.25)	8.09 (7.98–8.20)
Ages 30–19 years	27.76 (27.30–28.21)	14.61 (14.39–14.82)
Ages 40–49 years	41.98 (41.56–42.40)	24.90 (24.53–25.27)
Ages 50 years and older	43.01 (42.95–43.07)	39.82 (39.64–40.01)

^aValues are average (95% confidence interval) as reported in Ache and Matos (Ache and Matos, 2001).

3. Results

3.1. PHICOR/CIDMA model

Table 2 shows the average simulated T. cruzi seroprevalence among humans for each age group for each time period and the range across the years for each time period. While the model generated seroprevalences were within the reported 95% confidence intervals of the observed prevalences, the average T. cruzi seroprevalence among 0–19 year olds was consistently higher than the historical data for the last three time periods (Table 2). Additionally, the modeled average seroprevalence for 1990–1998 among those 40 years and older is lower than the historical data (by a relative 36%, absolute difference of 13.4% when targeting the last two time points). These trends are most likely due to the lack of data to adequately represent the impact of Venezuela's historical Chagas interventions.

When calibrating to two time periods and targeting the last two, the PHICOR/CIDMA model generated consistent T. cruzi seroprevalence among the age groups. The resulting average seroprevalence between 1980 and 1989 was consistent between the calibrated scenario and the targeted scenario (absolute difference of 0.6% to 1.4% across the age groups). The generated seroprevalence for the last time period was consistent with the three calibration points, with an absolute difference of 0.3–1.3 across the age groups (Table 2).

Fig. 3 shows the simulated T. cruzi seroprevalence in humans compared to the historical data. The PHICOR/CIDMA model generated seroprevalences were statistically within the observed values for each of the scenarios for all time periods, except for 1969–1978. This may be due to the sharp decline in infestation following insecticide spraying interventions that may not be adequately captured by our modeled change in FOI. When targeting the last time period, the PHICOR/CIDMA model's generated seroprevalence was a relative 7.1% lower than the historical data (absolute difference of –0.65%); when targeting the last two time periods, the resulting seroprevalence was a relative 2.1% and 14.1% lower (absolute difference of −0.28% and −1.30%) than the obeserved historical data for 1980–1989 and 1990–1998, respectively. Fig. 2b shows the change in T. cruzi seroprevalence over the entire simulation for each of the three age groups; the circle represents the simulated average over the time period plotted at the middle of the time period (thus the monthly prevalence many exactly pass through the average) while the squares show the historical data. Compared to the observed prevalences, all model generated values were within an absolute difference of −13.4% (40 years and older for 1990–1998) to 1.9% (0–19 year olds for 1980–1989).

Fig. 3.

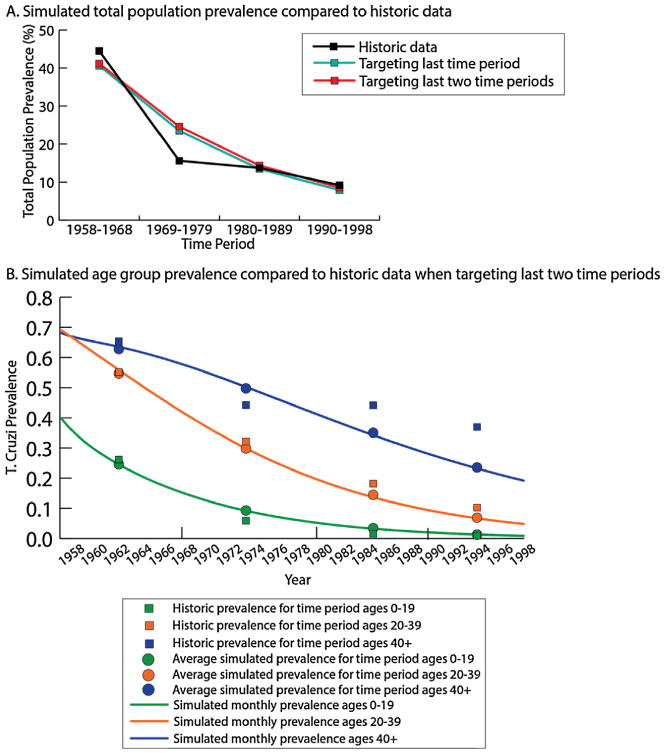
Simulated seroprevalence from the PHICOR/CIDMA model a) T. cruzi seroprevalence in the total population over the four time periods, and b) age-stratified seroprevalence over time with the average simulated seroprevalence compared to the historical seroprevalence when targeting the last two time periods.

3.2. Princeton model

This model produced seroprevalence curves that matched the directional trends for each age group reported in the historical data in both scenarios (Fig. 4, Table 3), with the seroprevalence values being closer to the observed values when targeting the last time point (i.e., 9 year simulation) than when targeting the last two time points (i.e., 19 year simulation values). When targeting the last time period (1990–1998), the absolute difference between the model generated and the observed seroprevalences ranged from 0.23% to 2.23% across age groups, with all model generated values higher than those in the data. The model generated seroprevalence values were closest to the historic values for two the youngest age classes, with an absolute difference of 0.23% and 0.10% for the 0–9 year and 10–19 year age groups, respectively. Compared to the historic data, the generated seroprevalences in the older age groups where higher, with the absolute difference being 2.31%, 2.09% and 2.23% for the 30–39 year, 40–49 year and 50+ year age groups, respectively. The model generated total population seroprevalence was 2.2% higher than the observed values (11.4% generated vs. 9.2% historical data).

Fig. 4.

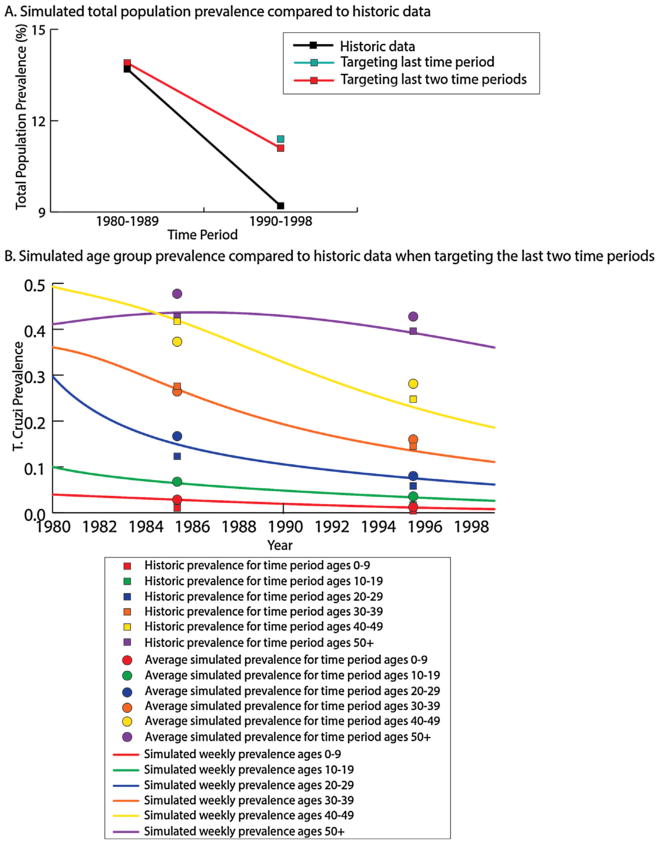
Simulated seroprevalence from the Princeton model for each age group a) T.cruzi seroprevalence in the total population over the four time periods, and b) age-stratified seroprevalence over time with the average simulated seroprevalence compared to the historical seroprevalence when targeting the last two time periods.

When targeting the last two time periods (1980–1998), the simulation values for each age class were similar to observed values for 1990–1998 than compared to the 1980–1989 period, but the overall seroprevalence values were more similar in the short term (for 1980–1989). Absolute differences between the model generated seroprevalences and the historical data ranged from −4.99% to 4.44% for 1990–98 and −3.40% to 2.19% for 1980–89, while the absolute difference for total population seroprevalence was 0.1% and 1.9% for 1980–1989 and 1990–1998, respectively. The average modeled seroprevalence in the youngest age group (0–9 years) where consistent with the historic data throughout the simulation (Fig. 3), with the difference between the model and the historical data being 1.83% and 0.8% for 1980–1989 and 1990–1998, respectively. The model underestimated the average seroprevalence in the oldest age group by an absolute difference of −4.99% for 1980–1989 and −3.18% for 1990–1998.

3.3. Comparison

Fig. 5 shows the model generated T. cruzi seroprevalence values from both models in addition to the historical Venezuelan data. Overall, the PHICOR/CIDMA model more closely estimated the total population seroprevalence for 1990–1998 in both simulations (Fig. 5a), while the Princeton model estimated age-specific seroprevalence that more closely aligned with the historic values reported when targeting the last time period. This is possibly due to the disproportional sampling of the historic data among the younger age groups (60% of total population sample are 0–19 years old). The PHICOR/CIMDA model generated seroprevalence for this younger age group are with (absolute difference 0.6%) compared to the observed value, thus the greater difference in the older age group (13.4% absolute difference compared to the observed data) is minimized. While the narrower age-groups of the Princeton model allowed it to generate age-specific seroprevalences closer to the historic data. In general, both models overestimated T. cruzi seroprevalence among younger age groups, while underestimating the T. cruzi seroprevalence in older age groups. Additionally, model generated values tended to be more similar to the reported historic data when calibrating to three time periods and estimating one. However, simulated seroprevalence for the last two time periods were still in line with the historical data.

Fig. 5.

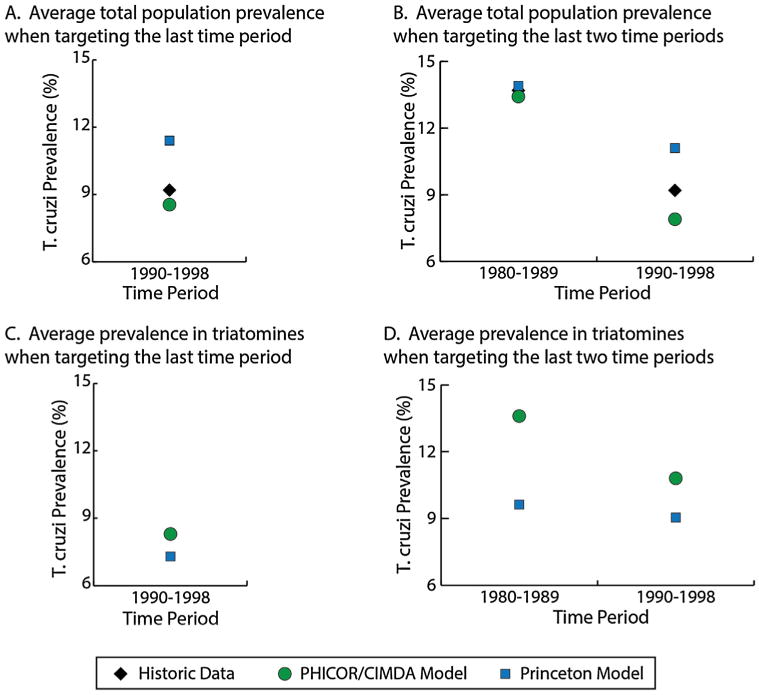
Comparison of models with historical data a) the average total population seroprevalence when targeting the last time period, b) the average total population seroprevalence when targeting the last two time periods, c) simulated T. cruzi seroprevalence among triatomines when targeting the last time period, and d) simulated T. cruzi seroprevalence among triatomines when targeting the last two time periods.

Compared to the historical data in Venezuela, the PHICOR/CIDMA model estimated a lower total population seroprevalence of T. cruzi (absolute −0.3% to −1.3% difference) whereas the Princeton model generated a higher total seroprevalence (absolute 0.1%–2.2% difference), as shown in Fig. 5a. When targeting only the last time period, the range of absolute difference across the age groups for the Princeton model was less than that of the PHICOR/CIDMA model (Princeton model: absolute 0.23%–2.23% difference, PHICOR/CIDMA model: absolute −12.1% to 0.6% difference). Compared to the historic data, when targeting the last two time periods, the PHICOR/CIDMA model generated T. cruzi seroprevalence was closer in the younger age groups, while the Princeton model generated seroprevalence was closer among older age groups. Between the models, the PHICOR/CIDMA model generated seroprevalence values for the combined age groups that fell between the averages produced by the Princeton model for all age groups except 40 years and older.

Even without data on the seroprevalence of T. cruzi in triatomine bugs, both models estimated similar T. cruzi seroprevalence values for the bugs across the two scenarios (Fig. 5c–d). The largest difference between models (13.6% vs. 9.6%) occurred for the 1980–1989 time period in the 19-year simulation (1980–1998).

4. Discussion

The ability of a model to generate historic data depends on the situation that is simulated (e.g., stable, rapid declines, or near elimination). Here, we modeled a scenario in which seroprevalence declined steadily for most of a 41 year period, in the presence of an intervention that waned toward the end of the time period. Our two independently developed models produced similar model genearated T. cruzi transmission in humans using different methodologies. Both models estimated the seroprevalence of T. cruzi in Venezuela over the evaluated time periods within an absolute difference ranging from −13.4% to 5.5% from the historical values across all age groups and scenarios.

Although they evaluate intervention effectiveness in different ways, both models overestimated the impact of the intervention on Chagas disease seroprevalence among older age groups (i.e., resulted in a lower estimated T. cruzi seroprevalence) and underestimated the impact among lower age groups (i.e., resulted in a higher estimated T. cruzi seroprevalence). These age groups are likely to be the most- and least-impacted by vector control interventions; the youngest age class theoretically contains the highest proportion of uninfected individuals, and thus would be the most affected, while the oldest age group would be the least affected by interventions, as this age group contains the lowest proportion of uninfected individuals and the most chronically infected individuals. As interventions such as those used for Chagas disease (e.g., housing improvements and indoor residual spraying) do not target a specific age group (vs. a vaccine for example), the impacts of interventions in many Chagas models tend to be consistent across all age groups or simulated for the entire population. Hence, it is not surprising that the two most extreme outcomes are the least precisely estimated. This illustrates the importance of accuracy when reporting information on interventions and their efficacies, as these can greatly impact model estimates that could inform policy decisions. It also emphasizes the challenge of fine-tuning models to reflect the differences in the impact of intervention in an age-dependent manner. This is critical for Chagas disease in particular, as the Pan American Health Organization uses T. cruzi seroprevalence of under 1% in children under five as a base indicator of success in vector control interventions (Salvatella et al., 2014).

While the historical data for Venezuela we used were the most comprehensive and long-term data on seroprevalence available, these data do have limitations for modeling purposes. First, data were accumulated over the time periods (condensed from monthly and annual information) and presented by Ache and Matos as averages (Ache and Matos, 2001). The starting and ending seroprevalence for each time period are not known, nor is the frequency of the data collection, which prevents us from knowing the true shape of the seroprevalence curves for each time period. Second, although it is well known that vector-borne T. cruzi infection in humans (i.e., Chagas disease) is consistently underreported by as much as 85% (Abad-Franch et al., 2014), it is likely that an increase in underreporting may have occurred in the last time period modeled (1990–1998), as only 15–18 municipalities per year were surveyed in that time period, down from 110 to 143 municipalities surveyed per year in the thirty years prior. Third, several details on Chagas disease interventions and their measureable impact on T. cruzi seroprevalence were not readily available or reported. For example, we do not know the number of houses that were treated, the total population size of the areas surveyed, intervention efficacy, or if all reported prevalence values were from individuals residing in the municipalities where entomological surveillance or interventions took place. More robust data to feed into and calibrate the models may lead to better estimates.

Historically, models for Chagas disease are underutilized compared to other infectious diseases, but hold promise (Nouvellet et al., 2015). A few modeling approaches (e.g., population dynamics, spatial models, force of infection, compartment models, etc.) have been used to represent Chagas disease and transmission in the past (Nouvellet et al., 2015). These models tend to be complex and evaluate biological or epidemiological systems. Our models were developed to answer more policy related questions and to focus more on relevant outcomes rather than to be complex and to evaluate, explore, and understand the dynamic relationships of T. cruzi transmission. It is important to highlight the benefit of including different features in Chagas disease transmission models. While the PHICOR/CIDMA and Princeton models differ in level of detail and included features (e.g., number of age groups included, separate indeterminate and determinate chronic Chagas disease states, other vertebrae host compartments, intervention representations, etc.), both were able to estimate the historical seroprevalence of T. cruzi in Venezuela with several similar trends in their results. This demonstrates that the level of detail necessary to include in models is dependent on the question being asked. For example, the current scenarios focused on targeting T. cruzi seroprevalence in the human population from nation-wide data accumulated over 10 year periods, thus the additional detail of an animal component may not be necessary. However, in the evaluation of T. cruzi transmission on a smaller scale (one house or one village) an intervention that would impact triatomine feeding sources or T. cruzi seroprevalence in animals, this component would be necessary to adequately answer the question at hand. These details can be important for answering different questions for achieving the 2020 goals for Chagas disease.

It should be noted that both models are simplifications and neither accounted for age-related general morality nor the potential for the clustering of exposure. However, the Venezuelan population age structure and life expectancy was relatively consistent over the modeled time period (United Nations, 2015; The World Bank, 2016), therefore both models made a simplifying assumption not to include age-related mortality. Neither model accounts for the potential clustering of exposure due to data limitations. Serological data will overlook heterogeneity of the population and the risk of Chagas disease will not be the same for each person. While the risk will not be identical, we modeled a limited area so there may not a be a substantial difference in terms of risk across the modeled population. Additionally, neither model took into account the accuracy of serological testing for Chagas disease and how it may change over time. However, given the point of this exercise was to estimate reported seroprevalence, this does not impact the current analysis.

5. Conclusions

While the PHICOR/CIDMA and Princeton models differ in level of detail and included features, both were able to target the historical seroprevalence of T. cruzi in Venezuela across a 41-year time period. Differing methods and level of detail between the models allow for different interventions and questions to be investigated, but both can be used to estimate T. cruzi seroprevalence and evaluate general intervention control approaches.