Abstract
Connectivity measures are (typically bivariate) statistical measures that may be used to estimate interactions between brain regions from electrophysiological data. We review both formal and informal descriptions of a range of such measures, suitable for the analysis of human brain electrophysiological data, principally electro- and magnetoencephalography. Methods are described in the space-time, space-frequency, and space-time-frequency domains. Signal processing and information theoretic measures are considered, and linear and nonlinear methods are distinguished. A novel set of cross-time-frequency measures is introduced, including a cross-time-frequency phase synchronization measure.
Keywords: Brain networks, EEG, MEG, ECoG, iEEG, Mutual information, Coherence, Connectivity, Causality
1. Introduction
Networks (Sporns, 2011) and rhythms (Buzsáki, 2006) are two conceptual paradigms, both alone and in combination, that have come to play a prominent role in the analysis, description, and understanding of human brain function. In this paper, we discuss a range of methods that have been developed and applied to human brain electrophysiological data. This includes especially extracranial electro- and magnetoencephalography (EEG and MEG, or jointly EMEG) as well as intracranial EEG (or iEEG, which encompasses electrocorticography, or ECoG) for the characterization of brain network connectivity at the millisecond time scale and centimeter length scale for EMEG and, potentially, the millimeter length scale for iEEG. We consider methods that can identify rhythmic interactions (in the space–frequency and space–time–frequency domains) as well as those useful for the characterization of non-rhythmic interactions (in the space–time domain).
Networks are described typically by a set of nodes and a set of edges. The edges, which connect the nodes in a pairwise fashion, define the network topology. If the nodes or edges can be embedded in a geometrical space, for example, the brain, then the network will have a geometrical structure as well. Typically, the network topology is described by a graph, and the connectivity is represented by an edge matrix. The analysis tools that we are interested in allow us to assign values to the elements of the edge matrix. These values may be real or complex numbers, or, to generalize the matrix concept somewhat, real-valued functions of time, depending on the connectivity measure.
Friston (1994) introduced the useful analytical categories of anatomical, functional, and effective connectivity into the brain functional imaging literature. Anatomical connections may be determined by a variety of invasive and non-invasive tract-tracing methods that, when successful, can provide a description of network geometry. These methods typically do not include EMEG, so we will not discuss anatomical connectivity further, except for a few brief observations. Anatomy may be an obviously useful starting point for subsequent physiological investigation. It may also serve as a measure of plausibility of results obtained from the analysis of physiological data. Anatomical connectivity may be represented by graphs that are either directed (if derived from a suitable invasive anatomical methods) or undirected (if derived from e.g., diffusion spectrum imaging). Anatomy cannot tell us how regions are coupled dynamically, except perhaps on very slow (e.g., neurodevelopmental) time scales.
Functional connectivity is based on the estimation of “temporal correlations between remote neurophysiological events” (Friston, 1994). Consequently, the resulting edge matrices are undirected (and therefore symmetric, unless time-lagged correlations are considered), but not necessarily binary. Correlation, coherence and related measures have been widely used in the electrophysiological literature to estimate functional connectivity in the space–frequency and space–time–frequency domains.
Effective (or more clearly, causal) connectivity is based on the estimation of “the influence one neural system exerts on another” (Friston, 1994). From a mathematical standpoint, the resulting edge matrices are directed and may be asymmetric, and non-binary. Estimation of causal connectivity therefore supports the inference of directional information flow. These include methods, such as multivariate autoregressive (MVAR) modeling and conditional mutual information measures.
Our focus is on estimating connectivity from EMEG and iEEG measures. This begs the question of how the nodes (i.e., brain regions) are defined between which the connectivity is measured. A complete discussion of this is beyond the scope of this paper. Nevertheless, it may be useful to address this issue, however briefly, at the outset.
One solution is to restrict our estimates to sensor locations, i.e., associate network nodes with sensors. While this can work relatively well for local field potentials recorded from iEEG, it raises some issues when using extracranial EMEG data. We would like to infer brain source locations and time series from the measured data and sensor locations, but here we run into the well-known non-uniqueness of the bioelectromagnetic inverse problem. Several methods that address this problem with respect to connectivity estimates are described later in this paper. For a more general discussion of the bioelectromagnetic inverse problem, see, e.g., Sarvas (1987), Mosher et al. (1999), Michel et al. (2004), and Greenblatt et al. (2005). An alternative that may permit us to remain in signal space (defined in Section 2), but remove some (but not all) of the inherent ambiguity relies on frequency domain measures using only the imaginary part of the spectral estimate (Nolte et al., 2004), as we describe later in this paper.
A number of approaches have been applied extensively to extracranial data to infer topographic patterns from extracranial data. These include principal components analysis (Dien and Frishkoff, 2005), with its nonlinear extensions such as varimax (Kaiser, 1958) and promax (Dien, 1998), blind source separation techniques (such as independent components analysis (Bell and Sejnowski, 1995; Hyvarinen and Oja, 2000) and SOBI (Belouchrani et al., 1997), and partial least squares (McIntosh et al., 1996). These methods support the estimation of signal space topography (i.e., the nodes of a graphical network), but do not by themselves provide a measure of connectivity between specific pairs of nodes, and therefore lie outside the scope of this paper.
Similar topographic techniques have also been applied to functional magnetic resonance data, leading, for example, to the identification of the nodes of default mode network (Raichle et al., 2001). A relatively recent review of functional connectivity measures applied to fMRI data may be found in (Li et al., 2000). The integration of simultaneously recorded fMRI and EEG data is an area of considerable current research interest, but will not be discussed here.
Our goal is to review many of the most widely used or most promising methods for the estimation of functional and effective connectivity from human brain electrophysiological data, unified from the perspective of considering the EMEG data as a multivariate random process. We seek to describe these methods both formally and informally. A secondary goal is to point to a small subset of the applications in which these methods have been applied successfully. We hope this approach will be helpful to scientific investigators who intend to apply connectivity measures to the experimental study of brain dynamics from EMEG data.
The structure of the paper is as follows. First we lay out briefly our elementary (and well-known) mathematical foundation, defining many of the variables that will be used later in the paper. Here, we distinguish between signal processing and information theoretic measures. Next, we describe connectivity measures in the space–time domain. Then we discuss space–frequency and space–time frequency measures that may be used to estimate connectivity for rhythmic interactions. In this section, we introduce some novel cross time–frequency measures. Finally, we consider some approaches that may be used to extend the array of measures from signal space to source space. Some of these connectivity estimation methods in signal space have been reviewed relatively recently by Kamiński and Liang (2005) and Pereda et al. (2005), although new results have been introduced since these reviews were published. Dauwels et al. (2010) have also summarized several of these methods, with specific application to the early diagnosis of Alzheimer's disease and mild cognitive impairment.
Before proceeding, we should note that the practical implementation of connectivity estimation from EMEG data consists of three related parts. First we need to define the measure(s) or algorithm(s) that we intend to apply to the data. This derives from an understanding of the experimental questions that are to be addressed. Second, once a method has been selected, it must, of course, be applied to the data, to obtain the preliminary estimates. These are preliminary until the application the third step, which is hypothesis testing. This paper is focused principally on the first, or measure-definition step. In some cases, such as the estimation of information theoretic measures, we spend some time on the estimation problem itself. In order to keep this paper to manageable proportions, however, we have little or no discussion of the hypothesis testing problem. The reader is directed to the cited references for specific methods for further details on this question. This does not mean, of course, that we think that hypothesis testing is not important, but rather that this essential step comes into play only after the methods have been defined, and the relevant measures have been estimated. For these reasons, we also omit discussion of the powerful technique of dynamic causal modeling (DCM) (Friston et al., 2003). DCM supports the selection of one of a set of connectivity models using Bayesian methods to select between candidate networks.
2. EMEG as a multivariate random process
EMEG data generally results from a discrete time sequence of voltage or magnetic field measurements made at a defined set of locations outside (EMEG), on, or sometimes in, the brain (iEEG). We identify each individual time series as a channel, which is associated with a physical measurement device, or sensor. For a single channel i, we represent the measurement at time t as vi(t) for M channels (or equivalently, M sensors). It will be convenient to represent the measurement across all channels at time t as an M × 1 column vector v(t). It is often therefore convenient to think of the multivariate measurement time series as a trajectory in an M-dimensional real linear vector space, the signal space V, v ∈ ℝM.
We consider the EMEG signal to be a random process, i.e., its state is indeterminate prior to observation. The individual measurements at channel i and time t are random variables. A specific sequence v(t) is a realization of the random process.
We adopt the model that our measurements are linear combinations of a finite set of underlying brain dynamical systems, each represented by a discrete current dipole time series (see e.g., Mosher et al., 1999). We assume that these dipole time series are themselves random processes whose trajectories cannot be determined from their initial conditions. The dipole time series trajectories may be represented in a finite dimensional linear vector space Q, the source space. The mapping Q → V is given by the so-called forward (or gain) matrix G, V = GQ. The EMEG connectivity problem then becomes one of estimating the interactions between these source dipole dynamical systems, or alternatively the measurements that are their mixed surrogates.
The random variables that we encounter in the EMEG connectivity problem are classified by convenience as observables (e.g., the signal space measurements), hidden variables (e.g., the dipole time series), or parameters (e.g., in describing interactions between time series using autoregressive models). Sometimes (as in the case of DCM), it may be useful to consider models themselves as random variables.
Associated with each random variable x is its probability density function (pdf) p(x). Unless otherwise noted, we do not assume a particular parametric form for the pdf's. We assume that our random variables of interest have an expected value and that this may be estimated as when the random variable is a function of discrete time (the ergodicity assumption).
Since our goal is to estimate coupling between pairs of nodes, where nodal activity is represented by a random process, it is not surprising that many of the measures depend on the estimation of random bivariates, 〈x, y〉. When these estimates are obtained directly from the (possibly filtered or transformed) data, we refer to them as signal processing measures, since they often derive from techniques used elsewhere in signal processing. Coherence is a widely used example of a signal processing method. Other methods are based on an estimation of a (typically joint) probability density function, e.g., p(x, y). The pdf estimate is then used to assess entropy or mutual information. We refer to these as information theoretic measures.
For the convenience of the reader, Table 1 groups together some of the symbols we use in this paper, along with their definitions.
Table 1.
Some of the more commonly used symbols in the paper are described here. In this paper, we use the typographic convention that scalars and functions are represented in lower case italics (e.g., v, f(v)), or upper case italics (e.g., M) when the scalar represents a range limit, vectors are shown in lower case bold italics (v), and matrices in upper case bold italics (V). Unless otherwise noted, we assume that vectors have column vector matrix representation.
| Symbol | Description |
|---|---|
| X, Y, V | Random processes (where we use V when we wish to emphasize the connection between the random process and the data time series) |
| x, y, v | Random variables |
| 〈x〉, 〈y〉, 〈v〉 | Expected values of random variables |
| N(μ, σ2) | Univariate normal distribution with mean μ and variance σ2 |
| N(μ, Σ) | Multivariate normal distribution with mean μ and covariance Σ |
| h(τ), α, A, (f) | Impulse response of LTI system, vector of AR model coefficients and its associated frequency-domain transfer function |
| Probability density function | |
| ℜ(), ℑ() | Real, imaginary parts of a complex number |
| ℝ, ℂ | Set of real numbers, set of complex numbers |
3. Space–time measures in signal space
3.1. Covariance, correlation, and lagged correlation
Conceptually, the simplest method for estimating functional connectivity from EMEG data would appear to be the use of the covariance measure. For two zero-mean random variables x and y, their covariance is given by cov(x, y) = 〈xy〉, cov(x, y) ∈ ℝ. The normalized covariance, or the Pearson correlation function, is given by ρ(x, y) = 〈xy〉/|〈x〉| · |〈y〉|, ρ ∈ (−1, 1), where |·| is the absolute value operator. There are problems with this straightforward approach, however. First, volume conduction due to overlapping sensor lead fields will generate spuriously high apparent correlations between sensor pairs. Second, instantaneous correlation is blind to directional information flow (which we discuss shortly in the context of Granger causality). These problems could be overcome to some extent through the use of lagged correlations ρ(x, y, τ) = 〈x(t)y(t − τ)〉/|〈x(t)〉| · |〈y(t)〉| for a suitable range of lags τ. As we describe below for quasi-causal information, the lagged correlation should also be corrected for zero-lag correlations that are propagated forward in time, but we omit the details here.
The time domain covariance/correlation approach has been used successfully with EMEG and iEEG (e.g., Gevins et al., 1987). Lagged covariance has been applied to EEG data (Urbano et al., 1998), and has also been applied to time series derived from near infrared functional brain imaging (Rykhlevskaia et al., 2006).
3.2. Granger causality
The principal interest in time series connectivity estimation lies in its potential for identifying and quantifying casual interactions between brain sources. Weiner (1956) proposed that a causal influence is detectable if statistical information about the first series improves prediction of the second series. An essentially similar and widely used operational definition of causality has been provided by Granger (1969), and has come to be known as ‘Granger causality’. A time series (random process) X is said to Granger-cause Y if X provides predictive information about (future) values of Y over and above what may be predicted from past values of Y (and, optionally, from past values of other observed time series Z1, Z2,…).
Although Granger causality is often identified with MVAR estimation (which we describe below), Granger causality refers to the general concept. The MVAR is only one tool to measure it. Other methods (such as conditional mutual information) may be used to infer Granger causality.
Taken together, methods such as MVAR modeling and mutual information estimation form the basis for causal connectivity estimation from physiological data.
3.3. Multivariate autoregressive (MVAR) model
Granger causality estimates between time series were first employed in econometrics using autoregressive (AR) models, and were later adapted for use with electrophysiological measurements. The econometric methods, in turn, were derived from signal processing applications, where a time series may be modeled as a linear combination of its past values plus and a random noise (or innovation) term. The AR coefficients are derived such that the corresponding linear combination of the past values of the signal provides for the best possible (in the least squares sense) linear prediction of the current value. In practice, the MVAR method reduces to a method for estimating these coefficients and using those to compute various interaction measures.
Since the MVAR method models time series as the output of a linear time-invariant (LTI) system, this clearly imposes a limitation when applied to an obviously nonlinear system like the brain. In addition, the linearity of the MVAR model also implies that the pdf of the output is Gaussian, as we show in Appendix A. Nevertheless, many nonlinear systems have linear or quasi-linear domains of applicability, and within this domain, MVAR models are able to capture significant properties of the system behavior. We return to this issue later in the context of information theoretic measures.
We begin by considering a univariate AR model. Given a scalar random process V such that the sequence {v(1), …, v(T)} is a realization of V, then
| (1) |
is an order K univariate autoregressive model of the process V, where is the delay embedding vector, a = {a(k)} are the AR filter parameters to be estimated, and εt ∼ N(0, σ2). The multivariate generalization of the AR model is straightforward. Given a vector random process V s.t. the sequence {v1, …, vT} is a realization of V. For N channels, let the single time slice vector be vt−1 = (v1(t − 1), …, vN(t − 1))T. Define the delay embedding vector . Then
| (2) |
is a multivariate autoregressive (MVAR) model of the random process V, where is a vector of concatenated channel readings, εt ∼ N(0, σ2I) Gaussian (white) noise and A = [A1, …, AK] is the matrix of filter parameters (to be estimated).
Since Eq. (2) models the dynamics of a random process we need to have a sufficiently long and stationary realization in order to make inference about the underlying matrix of the AR coefficients. The maximum likelihood estimate for A is given by
| (3) |
where .
Two practical approaches have been used in the literature for the estimation of autoregressive model parameters. A recursive filter parameter estimation technique (the LWR algorithm, Morf et al., 1978) may be combined with an information theoretic measure (Akaike, 1976). This approach is used typically (e.g., Ding et al., 2000) with electrophysiological data. Penny and Harrison (2006) describe an MVAR parameter estimation method based on Bayesian estimation of model order, and argue for advantages of the Bayesian approach. Regardless of approach one has to keep in mind that if the original data are passed through a temporal convolution filter (e.g., FIR or IIR), in most cases they will not follow an autoregressive model because of the moving average term introduced by such filtering (Kurgansky, 2010). Therefore, attempts of order estimation may fail as, for instance, the graph of Akaike criterion will not exhibit a local minimum corresponding to the process order. We also note that the MVAR coefficients depend on the physical units in which the data are recorded. To overcome this restriction, the coefficients may be transformed by use of the F-statistic (Seth, 2007).
The directed transfer function (DTF) method (Kamiński and Blinkowska, 1991; Kamiński et al., 2001) is the frequency domain representation of the MVAR model (Eq. (2)), and will be discussed in Section 4.9.
3.4. Applications of MVAR to EEG connectivity
MVAR estimation may be the first step for a variety of different connectivity measures, in both the time and frequency domains (Schlogl and Supp, 2006). As a result of well-developed and validated algorithms, the MVAR-based methods appear to be the most widely used techniques for EMEG causality estimation. A comprehensive review of these applications would far exceed the scope of this paper. We will simply point to several relatively recent examples where the MVAR approach has been applied with apparent success. Potential clinical applications include seizure focus and epileptogenic network identification (Ding et al., 2007), as well as early diagnosis of Alzheimer's disease (Dauwels et al., 2010). It has been applied both to continuous (Zhao et al., 2011) and event-related (Ding et al., 2000; Schlogl and Supp, 2006) data, in both signal and source space (Ding et al., 2007). The MVAR approach has also been used to study the coupling between EEG and EMG (electromyelographic) signals (Shibata et al., 2004).
Additional applications of the MVAR approach in the frequency domain, including use of the directed transfer function, may be found in Section 4.9.
3.5. Information theoretic approaches to causality estimation
Although MVAR approaches in the time and frequency domains have been widely used for causality estimation from EMEG signals, they are limited to modeling only the linear (i.e., Gaussian) component of the interactions. It is known, however, that significant physiological processes such as epilepsy (Pijn, 1990; Le Van Quyen et al., 1998, 1999) violate the Gaussianity assumption. In these cases, MVAR may either misallocate the nonlinearities, or ignore them entirely.
Information theoretic measures of connectivity may identify both linear and nonlinear components, and these may be separated, as we show below. Before describing some of the information theoretic measures that may be applied in the time domain, we first provide a brief background on the key concepts that underlie the specific information theoretic measures of interest. We then discuss methods for estimating nonlinear (non-Gaussian) interactions.
3.6. Entropy and information
First we will consider discrete random processes before generalizing to continuous random processes. Given random process X, with finite states xi ∈ A distributed as p(xi), the Shannon entropy (Shannon and Weaver, 1949) is defined as
| (4) |
−log p(xi) measures the uncertainty that the process X is in the state xi, so H(Xi) = 〈−log p(xi)〉. The Shannon entropy is interpreted conventionally as a measure of the number of bits (using the base 2 logarithm) required to specify the sequence Xi, i ∈ I.
When x is a continuous variable, the equivalent expression for Eq. (4) is given by the differential entropy
| (5) |
We note that, unlike the discrete entropy of Eq. (4), the differential entropy as defined by Eq. (5) depends on the physical units of x.
The Kullback–Liebler (K–L) divergence (Kullback and Liebler, 1951) is defined as
| (6) |
K–L divergence is an extension of the Shannon entropy that is critical for the development of mutual information. Intuitively, the K–L divergence measures the excess number of bits required to specify p(xi) with respect to a reference distribution q(xi) for Xi. In other words, Kp|q(Xi) is zero if p = q.
Then for two random processes X and Y, we can define the mutual information as
| (7) |
Intuitively, the mutual information M(Xi, Yj) is the K–L divergence which measures how the joint distribution differs from the independent distribution of x and y, i.e., the excess number of bits required by assuming distributions p and q are independent.
For continuous random variables x and y, the differential form of mutual information is given by
| (8) |
Two properties of mutual information are worth noting (writing M(Xi, Yj) as MI,J, etc.):
MI,J = HI + HJ−HI,J ≥ 0
MI,J provides no information regarding temporal ordering (i.e., it is symmetric under exchange of i and j).
3.7. Time-lagged mutual information
To overcome the symmetry inherent in Eq. (7), we can measure the mutual information between two time series, one of which has been shifted in time with respect to the other. Then the time-lagged mutual information is defined as
| (9) |
Eq. (9) measures the reduction in uncertainty in Xi given Yi−τ. By using a set of shifts, it is possible to build up a picture of the influence of one process on another as a function of lag between the two processes. Time-lagged MI thus has the essential asymmetric property that we are looking for. However, there may be practical problems when applying this measure to extracranial data, as we discuss next.
3.8. Lead fields, conditional mutual information, and quasi-causal information
When we make extracranial EMEG measurements, the overlapping sensor lead fields result in linear combinations of sources in the individual signal space measurements (Mosher et al., 1999). This implies high instantaneous correlation between signals that do not necessarily reflect the true instantaneous source correlations. In addition, since a source at time i − τ is typically correlated with itself at i, we would like a method that factors out the predictive self-information from the time-lagged mutual information, leaving the predictive time-lagged cross information. This is illustrated diagrammatically in Fig. 1.
Fig. 1.
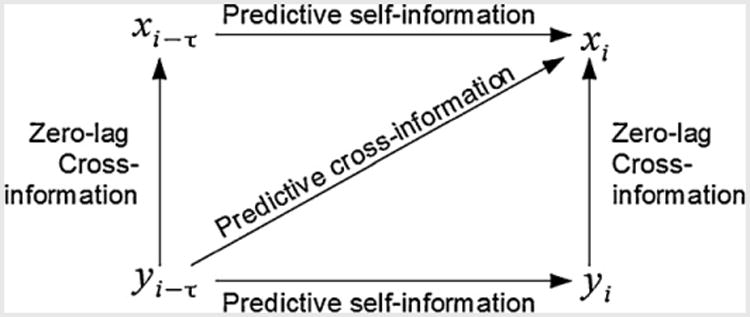
Zero-lag cross information (a function of overlapping lead fields) and predictive self-information should be factored out to obtain an improved estimate of the true predictive cross-information.
This problem has been addressed by Pflieger and Greenblatt (2005), using the quasi-causal information (QCI) method for estimating predictive cross information. QCI is an asymmetric measure which combines time-lagged mutual information (Eq. (9)) with conditional mutual information.
To understand QCI, we first need to define conditional mutual information. Given random processes X, Y, Z, with finite states xi ∈ A, yj ∈ A, zk ∈ A define the conditional mutual information as
| (10) |
M(Xi, Yj|Zk) measures the amount of information needed to distinguish the joint distribution of x and y, conditioned on z, from the conditionally independent distribution of x and y.
Now we combine time-lagged MI (Eq. (9)) with conditional MI (Eq. (10)) to obtain quasi-causal MI
| (11) |
We are not aware of any publications using QCI for the analysis of EMEG data, except for some preliminary reports (e.g., Pflieger and Assaf, 2004).
3.9. Transfer entropy
Transfer entropy was introduced by Schreiber (2000) and Kaiser and Schreiber (2002) to overcome the symmetry limitation of mutual information by using a Markov process to model the random processes X and Y.
First consider a Markov process of order k. The conditional probability to find X in state xt+1 given is , where is the delay embedding vector. Then the entropy rate is given by , i.e., hX measures the number of additional bits required to specify xt+1, given . If X is obtained from the discretization of a continuous ergodic dynamical system then the transfer entropy approaches the Kolmogorov–Sinai entropy (Schreiber, 2000).
Transfer entropy is a generalization of the entropy rate to two processes X and Y. The K–L divergence provides a measure of the influence of state Y on the transition probabilities of state X:
| (12) |
Transfer entropy measures the influence of process Y on the transition probabilities of process X. For continuous random variables x and y, Eq. (12) takes the form
| (13) |
Transfer entropy has been applied to TE estimates from ERP data in Martini et al. (2011).
3.10. Factoring linear and non-linear entropy with sphering
Given an N-dimensional multivariate continuous zero-mean Gaussian random variable with covariance Σ, x ∼ N(0, Σ), its density function g(x) is given by g(x) = (2π)N/2|Σ|1/2e−xTΣ−1x/z, where |Σ| is the determinant of the covariance matrix. We assume zero-mean with no loss of generality, since entropy does not depend on the mean.
Then by applying Eq. (5) to the normal distribution function g(x), the Gaussian differential entropy, Hg(x) is found to be (Shannon and Weaver, 1949; Ahmed and Gokhale, 1989)
| (14) |
If we ignore the first term in Eq. (14), which depends only on the dimension of the sample space, the Gaussian differential entropy depends on the covariance. In other words if we have estimated the covariance from the data, we can use this directly to estimate the entropy of a Gaussian process. Note that the Gaussian entropy depends in a linear manner on log|Σ|.
In addition, note that log|Σ| =0 for |Σ| = 1. This leads us to the useful result that by sphering the data, yielding a derived random variable x̃ = Σ−1/2 x, where x̃ ∼ N(0, I), we can estimate the linear (Gaussian) and nonlinear (non-Gaussian) entropies independently (Pflieger and Greenblatt, 2005). A similar approach is used for independent components analysis, whose algorithms depend on non-Gaussianity for component separation (Hyvarinen and Oja, 2000).
Sphering and pre-whitening both normalize the data by pre-multiplication by Σ−1/2. They differ, however, in the way the covariance is estimated. Typically, pre-whitening estimates the covariance from a data segment thought not to contain the signal(s) of interest. Sphering, on the other hand, may typically use the same data segment both to estimate the covariance, and then to normalize for subsequent analysis.
We note that unlike discrete entropy, differential entropy depends on the physical units (Shannon and Weaver, 1949), i.e., it is not invariant under diffeomorphism. Sphering rescales and normalizes the data by removing the Gaussian entropy. Thus, the remaining entropy is strictly nonlinear. However, it is not commensurate with the linear part (and thus cannot be added to form a total). However, strictly nonlinear entropies are commensurate with each other, due to the sphering normalization.
3.11. Correntropy-based Granger causality
Correntropy (Santamaria et al., 2006) is a recently developed second order statistic that is well-adapted by virtue of computational efficiency for estimation of non-Gaussian processes, including Granger causality (Park and Principe, 2008). For two discrete random processes X and Y, and lag τ, the cross correntropy (Santamaria et al., 2006; Liu et al., 2007) is defined as
| (15) |
where E(·)1 is the expectation operator, and G is the Gaussian kernel G(x, y) = 1/((2π)1/2σ)e−(x−y)2/2σ2 with kernel size σ (a free parameter). Since VXY(τ) is not zero-mean, we may define the centered correntropy (Park and Principe, 2008) as
| (16) |
A normalized version of UXY(τ), the correntropy coefficient (Xu et al., 2008), is given by
| (17) |
rCE ∈ [−1, 1] is a nonlinear extension of the correlation coefficient.
One motivation for interest in the correntropy function lies in the relative efficiency with the Gaussian kernels may be computed. However, to the best of knowledge, correntropy has not been extended to address the overlapping lead field problem, illustrated in Fig. 1, although this should be straightforward.
The motivation for the definition of correntropy flows from the theory of reproducing kernel Hilbert spaces (RKHS). However the details of the motivation go beyond the limited purpose of this paper. The interested reader is directed to Santamaria et al. (2006), Liu et al. (2007), and Park and Principe (2008). A relatively clear and accessible introduction to RKHS theory may be found in Daumé (2004). We also note the close relation between correntropy and Renyi entropy (Santamaria et al., 2006).
3.12. Estimation for information theoretic measure
Information theoretic measures based on continuous processes give rise to estimation problems different from those encountered with signal processing approaches, such as MVAR. This is due to the need to estimate the probability density function needed for computation of mutual information (MI) and transfer entropy (TE), and a similar problem arises with Gaussian kernel bandwidth using correntropy.
For MI and TE, two alternatives are available, coarse graining and binning (kernel estimation).
Coarse-graining converts a continuous process into discrete states (i.e., a discrete alphabet). For MI, coarse-graining converges to the continuous case monotonically from below, but this is not generally true for TE (Kaiser and Schreiber, 2002). Transformation invariance (under a diffeomorphism, e.g., change of physical units) holds for continuous densities but not for discrete probabilities (Kaiser and Schreiber, 2002). However, this should not be a problem for EMEG, where all time series have the same physical units. Coarse-graining has been applied to TE estimates from ERP data in Martini et al. (2011). Plausible results were obtained from group analysis (n = 12, 4 × 100 trials each) of the Simon task using scalp EEG data.
For continuous multivariate processes, density function estimation typically requires a non-parametric approach, since the form of the pdf is not known in advance. This suggests the use of kernel estimation methods (typically, but not necessarily using Gaussian kernels), e.g., Ivanov and Rozhkova (1981). The problem here is that one needs to estimate the minimum kernel bandwidth. This can introduce a serious problem, since different bandwidth choices yield different estimates, sometimes even reversing the direction of estimated information flow (Kaiser and Schreiber, 2002). Pflieger and Greenblatt (2005) have found empirically that a Gaussian kernel with standard deviation of 1 works well for sphered (i.e., normalized) data. As an additional difficulty, kernel estimation methods become more problematic as the number of dimensions increase, since the sampled data typically become increasingly sparse with increasing dimension.
Robust estimation of information theoretic parameters generally requires a relatively large number of data points (hundreds to thousands of time samples) recorded during the periods of relative stationarity. As a result, their application to real-time problems, such as those involved in the design of brain–computer interfaces, is probably of limited value (Quiroga et al., 2002; Gysels and Celka, 2004).
4. Space–frequency and space–time–frequency measures in signal space
Rhythmic brain activity often depends on transient oscillations (that is, intervals of rhythmic activity that persists for a relatively small number of cycles). These may be identified by using filters matched to the frequencies of interest. There are several widely used methods for studying oscillatory EMEG activity, the Fourier transform (and its closely related short time Fourier transform, or STFT), the wavelet transform, the Hilbert transform, and complex demodulation. Since the choice of transform method influences the connectivity measures that may be used, we will briefly discuss some properties of each of these methods before considering connectivity measures in the frequency and time frequency domains.
Frequency domain measures and time–frequency domain measures are essentially similar once the appropriate transforms from the time domain have been calculated. Therefore, we will consider these measures in the more general context of the space–time–frequency domain. However, we would like to point to the physiological plausibility of using time–frequency decomposition methods, based on the nature and inherent non-stationarity of the brain's oscillatory activity. When not described explicitly, the space–frequency measures may be obtained from the space–time–frequency measures by omitting the time variable from the expressions of interest.
After discussing briefly several commonly used transform methods, we consider those bivariate measures that are sensitive to linear coupling (coherence, phase variance, and amplitude correlation), including the linear component of a nonlinear interaction. Next, we describe frequency domain measures that can be computed from the MVAR coefficients. Then, we consider cross-time frequency measures. These are measures that are sensitive to interactions between the same frequency at different times, different frequencies at the same time, or different frequencies at the different times. Last, we look at methods that are sensitive to non-linear (specifically quadratic) coupling.
To some degree, the distinction between space–time and space–frequency measures is arbitrary. For example, if the original time series data are narrow-band filtered, the measures described for space–time connectivity in Section 3 may be used to make inferences regarding coupled oscillatory interactions. In addition, the Hilbert transform and complex demodulation (described below) are both well suited to inferring time-domain estimates of oscillatory activity. These estimates may then be analyzed using the methods described in Section 3. In spite of these ambiguities, however, in most cases the distinction between space–time and space–time–frequency measures is widely used and retains its value.
4.1. Fourier transform
The Fourier transform is a mapping from time domain to the frequency domain, given by , where x(t) is the time domain signal, X(ω) is its Fourier transform, and ω is the angular frequency. Although the properties of the Fourier transform are well known (e.g., Oppenheim and Schafer, 2010), we address two points of special relevance to connectivity estimation.
First, the Fourier transform is linear. This has an important implication for network identification. For linear time-invariant systems, such as those described by Eq. (1), there can be no cross-frequency interactions. For example, if there is 10 Hz activity in the input, then, in the ideal case, all of that will be mapped to 10 Hz activity in the output (although power and phase may vary). Cross-spectral interactions are therefore a signature of non-linear interactions.
Second, the practical application of Fourier transform methods entail using a discrete (rather than continuous) transform, combined with a windowing function to limit the transform to finite bounds and minimize the leakage of the high frequency components due to the finite bounds. Since the window width is typically fixed, the Fourier transform does not provide time domain resolution at a scale less than the window width. It is therefore of limited use for time–frequency analysis.
The short time Fourier transform (STFT) is probably the earliest method for time–frequency analysis, and is still used (e.g., de Lange et al., 2008). It is estimated by moving a sliding window through the data and computing the FT separately for each window. If a Gaussian window is used, the results are equivalent to convolution with a Gabor wavelet (Gabor, 1946). Unlike Morlet wavelet-based methods (described below), the Gabor wavelet does not entail an automatic window rescaling as a function of frequency of interest. Rescaling allows for a deterministic tradeoff between the time and frequency resolution.
4.2. Wavelet transform
A wavelet is a zero mean function that is localized in both time and frequency. A Morlet wavelet (Kronland-Martinet et al., 1987) is a complex valued wavelet that is Gaussian in both time and frequency.
| (18) |
By shifting and scaling the mother wavelet function, then convolving with a time series, it may be used as a matched filter to identify episodes of transient oscillatory dynamics in the time–frequency plane. The continuous wavelet transform of a discrete scalar time series x(t) with sample period δt is the convolution of x(t) with a scaled shifted and normalized wavelet ψ0. Then for time series x(t), the wavelet transform at time t and scale a, s(t, a) is given by
| (19) |
s(t, a) ∈ ℂ. To convert from scale to center frequency, use the relation fc = a/Tδt, a ≤ T/2 (note that T is a dimensionless index, while δt is a time interval with units e.g., seconds).
The wavelet transform may be applied to continuous EMEG data, but it is especially useful for the analysis of event-related data, where it may be used to extract phase-specific information relative to the event marker, as discussed below. Torrence and Campo (1998) provide a useful introduction to efficient methods for computing wavelet transforms. Wavelet transforms of event-related data as particularly useful, since they also permit the characterization of phase-locked and non-phase-locked components of the response (Tallon-Baudry et al., 1996).
4.3. Hilbert transform
The analytic signal was introduced into signal processing by Gabor (1946) as a method for estimating instantaneous frequency and phase from real-valued time series data (Cohen, 1995). Given a real-valued scalar time series x(t), its complex-valued analytic signal z(t) has a spectrum equal to that of x(t) for positive frequencies, and is zero for negative frequencies.
The analytic signal may be represented as z(t) = x(t) + ix̂(t), where x̂(t) is the Hilbert transform of (Zygmund, 1988).
Vector-valued time series generalize in a straightforward way from the scalar case.
The important point for our discussion that we can now represent the instantaneous phase as
| (20) |
The principal utility of the Hilbert transform approach to time–frequency analysis of electrophysiological data lies in its application to continuous (i.e., not event related) data, such as EEG ictal and peri-ictal time series. For event-related data, wavelet-based methods tend to be more suitable, although Hilbert transform methods may be used with comparable results (Le Van Quyen et al., 2001a; Bruns, 2004). In addition, the Hilbert transform may be used with broadband data, or, with appropriate pre-filtering, with narrow-band data. While broadband phase is well-defined mathematically, its physical interpretation raises some questions (Cohen, 1995). The choice between Hilbert transform and wavelet transform depends on computational convenience and applicability to the experimental data requirements, not mathematical fundamentals.
4.4. Complex demodulation
Complex demodulation is a method of harmonic analysis that permits estimation from a time series of the amplitude and phase at a selected frequency (Walter, 1968). As such, the results are essentially equivalent to bandpass filtering the time series, and then applying the Hilbert transform. However, since the method has been, and continues to be used for many years in EEG harmonic analysis (e.g., Hoechstetter et al., 2004), we describe it here briefly, following the approach of Draganova and Popiavanov (1999).
Assume a model for the time series as x(t) = A(t)cos(f0t + ϕ(t)) +x̄(t), i.e., the time series is a narrow band process and consists of a (possibly amplitude and phase modulated) cosine wave at frequency f0 and phase ϕ(t) as well as residual signal x̄(t). The problem is to estimate A(t) and ϕ(t).
Since eiθ = cos(θ) + i sin(θ), we can write x(t) = 1/2A(t)(ei(f0t+ϕ(t) + e−if0t+ϕ(t))) + x̄(t). Multiplying by e−if0t we obtain
| (21) |
Then applying a zero-phase-shift low pass filter f↓, we obtain the complex demodulation function for frequency f0 as
| (22) |
CDf0(t) ∈ ℂ. Then the time-varying amplitude of our hypothesized cosine function is A(t) = 2|CDf0(t)| and the time-varying phase is ϕ(t) = tan−1([ℑ(χ(t))]/[ℜ(χ(t))]) where χ(t) = CDf0(t)/|CDf0(t)|.
Now that we have considered the most widely used transform methods, we proceed to consideration of bivariate measures for connectivity estimation.
4.5. Coherence
Given two zero-mean time series x(t) and y(t) for channels X and Y respectively and their wavelet transforms sX(t, f) and sY(t, f) as defined in Eq. (19). Then we may define the cross spectrum as , where 〈·〉 is the expectation operator. Then the coherency is defined as the normalized cross spectrum
| (23) |
Note that CXY(t, f) ∈ ℂ, i.e., coherency is complex valued. Coherence is then defined as the real-valued bivariate measure of the correlation between complex valued signals, as defined in Eq. (24).
| (24) |
There is some inconsistency in the literature, since coherence is sometimes defined as the square of the number defined in Eq. (24).
For event-related data, the expectation may be estimated by averaging across trials.
Although coherence has been used widely in the experimental literature, it is important to note that there are some significant problems inherent in the interpretation of coherence estimates for connectivity analysis.
First, coherence confounds amplitude and phase correlations because it depends on complex-valued wavelet or Fourier coefficients. Changes in either phase or amplitude correlation may give rise to changes in coherence.
Second, volume conduction (e.g., when analyzing scalp-recorded EEG data) can give rise to spurious correlations that do not reflect real patterns of underlying connectivity. This is discussed below, where we describe the phase slope index. Coherence has been used widely for estimation of connectivity from EMEG (e.g., Payne and Kounios, 2009) and iEEG (Towle et al., 1999; Sehatpour et al., 2008) data. However, the disambiguation of amplitude and phase correlation is seldom considered in the experimental literature. This may be addressed by estimating separately the amplitude and phase contributions to the coherence, as described below.
4.6. Amplitude correlation
In order to determine the amplitude correlation between channels, we may use the cross-spectral amplitude correlation for channels X and Y, ACX,Y, defined in Eq. (25).
| (25) |
ACXY(t, f) ∈ [0, 1]. Sello and Bellazzini (2000) have introduced the cross-wavelet coherence function (CWCF), which measures a property essentially similar to the amplitude coherence, as defined in Eq. (26).
| (26) |
While Eqs. (27) and (28) measure essentially the same physical value, CWCF may have an advantage of numerical stability compared with AC, when one of the signals has a very small mean amplitude.
4.7. Phase synchronization
Once the time-dependent phase has been estimated on a channel-by-channel basis (e.g., by using the Hilbert transform or wavelet decomposition), phase synchronization between channel pairs may be measured using phase coherence (Hoke et al., 1989), or the phase-locking value (Lachaux et al., 1999), defined in (27).
| (27) |
PLV() ∈ [0, 1]. Theoretically, if two channels are completely synchronized, PLV = 1; if completely random, PLV = 0.
For continuous data, PLV is estimated over windows, typically from tens to hundreds of milliseconds in duration. For event-related data, PLV may be estimated sample point by sample point using wavelet transforms, averaged over a set of trials.
Kralemann et al. (2007, 2008, 2011) have shown that a coordinate transformation is required if Eq. (27) is to be used for the characterization of the dynamics of coupled nonlinear oscillators. While this is the case, however, Eq. (27) (which Kralemann et al. refer to as ‘protophase’) may still be used with relatively small error if the goal is simply to estimate connectivity between channels.
Since the PLV statistic was introduced to physiology in 1989 (Hoke et al., 1989), and following the influential 1999 paper of Varela et al. (1999), phase synchronization has become a significant tool for the study EMEG connectivity. This has been true especially in the study of epilepsy (e.g., Mormann et al., 2000; Le Van Quyen et al., 2001b; Nolte et al., 2008). Perhaps counter intuitively, it has been observed that seizure onset is preceded by a decrease in synchrony (Schindler et al., 2007). Ossadtchi et al. (2010) have combined PLV with a deterministic clustering algorithm, which has been successful in automatically identifying ictal networks from iEEG data.
Increased phase synchronization has also been observed during cognitive tasks (e.g., Lachaux et al., 2000; Bhattacharya et al., 2001; Bhattacharya and Petsche, 2002; Allefeld et al., 2005; Doesberg et al., 2008). Phase synchronization has also been studied as a measure for BCI design. For example, Gysels and Celka (2004) found that the sensitivity using phase synchrony alone was significant, but inadequate to serve as a classifier.
The wavelet local correlation coefficient (Buresti and Lombardi, 1999; Sello and Bellazzini, 2000), defined in Eq. (28) is an alternative measure of phase correlation. It has been used only to limited extent with EMEG data (Li et al., 2007).
| (28) |
4.8. Imaginary coherence and the phase slope index
The presence of volume conduction, with its consequent mixing of sources in the scalp-recoded EMEG, has long been recognized as a serious confound in the analysis of EMEG data. In the present context, this may cause significant problems for the interpretation of scalp coherence data (see Nolte (2007) for a good example, using simulated EEG data). Nolte et al. (2004; see also Ewald et al., 2012) have shown that, under a reasonable set of simplifying assumptions, the volume conduction effect may be factored out by considering only the imaginary part of the coherence. In Appendix A, we specify these assumptions, and provide a proof of this.
This result was then extended in Nolte et al. (2008) with the definition of the phase slope index, PSI. The method is based on the idea that interacting systems may be characterized by approximately fixed time delays, at least within a time window of interest. In the frequency domain, a fixed time delay corresponds to a linear shift in phase as a function of frequency. Using the imaginary component of the coherency to isolate interacting sources from volume conduction effects and using the definition of the (complex-valued) coherency (Eq. (23)) the phase slope index is defined as
| (29) |
Here we have limited our definition to the frequency domain. To the best of our knowledge, SI has not been implemented in the time frequency domain, which would require some methodological extensions.
For details that phase slope index is a weighted average measure of the change of phase as a function of frequency, see Nolte et al. (2008), in particular, their Eq. (5). The phase slope index has been applied to simulated and, to a limited extent, to experimental data, as described in Nolte et al. (2008). After normalizing with respect to the standard deviation, they show that the PSI has improved specificity (fewer false positives), when compared to MVAR measures using the same simulated datasets.
4.9. Directed transfer function (DTF)
The directed transfer function (DTF) method (Kamiński and Blinkowska, 1991) is the frequency domain representation of MVAR. Using the form found in the DTF literature (e.g., Kamiński et al., 2001), we rewrite Eq. (2) as
| (30) |
or
where A(k) is the filter parameter matrix for lag k, A(0) = −I, v(t − k) = (v1(i − k), …, vN(t − k))T for N channels, and εt ∼ N(0, σ2I). Then we can represent Eq. (30) in the frequency domain as
| (31) |
where . We define the transfer matrix T(f) from the relation
| (32) |
For a pair of channels i, j, the normalized directed transfer function from i → j at frequency f is defined as (Kamiński and Blinkowska, 1991). Thus measures the relative influence of channel j on channel i for frequency f, relative to the influence of all channels on channel i at that frequency, given the autoregressive model.
The full frequency directed transfer function (ffDTF), is similar to , except that it is normalized over all frequencies (Kamiński and Liang, 2005).
To estimate the DTF in practice, first the filter parameters are estimated in the time domain. Then, the discrete time Fourier transform may be used to estimate the transfer matrix.
Applications of DTF to EEG connectivity
DTF has been used relatively widely for effective connectivity estimation from EMEG data. We cite only a few examples here, including its application to sleep (Bertini et al., 2009), fMRI-EEG (Babiloni et al., 2005), and Alzheimer's disease (Dauwels et al., 2010). Based on simulation studies, Kus et al. (2004) conclude that simultaneous multichannel estimates are superior to pairwise estimates when using DTF and related measures. DTF has also been applied successfully in BCI applications (Shoker et al., 2006). A recent review of these and additional MVAR based frequency domain measures of connectivity may be found in Kurgansky (2010).
4.10. Cross time–frequency measures
Coherence and related measures look at interactions between differing spatial locations at the same time and frequency. These measures may be generalized in a straightforward way to consider time lags as well as interactions between differing frequency bands, as we discuss next.
Eq. (24) is defined for coherence between channel pairs at the same latency and center frequency. This implies that coherence cannot provide information on the direction of coupling (i.e., it may be used to infer functional but not effective connectivity). In this section, we define three bivariate cross-time–frequency measures, the cross time–frequency coherence, the cross time–frequency amplitude correlation, and the cross time–frequency phase locking value. To the best of our knowledge, these measures have not been described previously, and have not yet been applied to EMEG data.
We define the cross spectral coherence, cross time–frequency amplitude correlation, and cross time–frequency phase locking value as:
| (33) |
| (34) |
| (35) |
Since Eqs. (35)–(37) take time delays into account explicitly, they are suitable for estimating effective connectivity in the space–time–frequency domain.
If we are analyzing event-related data, e.g., with a Morlet wavelet transform, then each trial has a time marker. This permits the unambiguous definition of cross-spectral phase locking value, defined in Eq. (35).
To the best of our knowledge these measures have not been reported in the scientific literature. We are not aware of any applications of these cross time–frequency measures to electrophysiological data. However, a closely related cross-spectral amplitude correlation has been used by Schutter et al. (2006) to estimate interactions between canonical frequency bands (δ, θ, β) for a single electrode site (Fz). The bispectral bPLV (Darvas et al., 2009), described below, is a related cross frequency phase measure specific to non-linear interactions.
4.11. Modulation index
For some physiological applications, we would like to know if the amplitude at one frequency is coupled to the phase at another frequency. This is true of hippocampal theta/gamma coupling, for example (Lisman and Buzsáki, 2008). Canolty et al. (2006) have developed the modulation index to measure such coupling. Penny et al. (2008) describe a related method for estimating amplitude/phase coupling using a General Linear Modeling approach.
To compute the modulation index, first bandpass filter the time series data at each of the two center frequencies of interest, f1 and f2, then compute the analytic signal, via the Hilbert transform. Now construct the composite analytic signal as z(t) = Af2(t)eiϕf2(t) where Af2(t) is the amplitude of the f1 analytic signal, and ϕf2(t) is the phase of the f2 analytic signal. If the amplitude of f1 is statistically independent of the phase of f2, then the pdf of z(t) will be radially symmetric in the complex plane.
The modulation index has been used successfully by its developers to identify and characterize theta/gamma coupling in the human brain from iEEG data (Canolty et al., 2006).
4.12. Stochastic event synchrony
Stochastic event synchrony (SES) (Dauwels et al., 2008) is an algorithm that may be applied to wavelet transformed EMEG data to quantify the synchrony between channel pairs. As an algorithm, it is embodied by a set of rules for computing the similarity measure, rather than having a representation as a mathematical expression. Briefly, the algorithm reduces the time–frequency representation of the EMEG data to a set of parameterized half-ellipses (or “bumps”), and then measures the similarity between the bump patterns. For details on the algorithm, see (Dauwels et al., 2010), where the method has been applied to EEG data in a mild cognitive impairment study. Vialatte et al. (2009) applied the SES method to EEG data obtained from a steady state visual evoked potential paradigm.
4.13. Nonlinear measures in the space–frequency domain
Linear systems, such as those described by the MVAR model, input frequencies map to identical output frequencies with changes only in phase and amplitude; in other words, no new frequency oscillations may appear in the output that are not in the input. Nonlinear systems, however, may entail frequency shifts. This implies that methods sensitive to frequency shifts between input and output are therefore able to measures the corresponding non-linearities, both within and between channels. In particular, the bispectrum is a measure of quadratic nonlinearities in the frequency domain. For the quadratic case, input frequencies f1 and f2 result in an output at f1 + f2 (Nikias and Mendel, 1993). If the nonlinear system is analytic (i.e., has a Taylor series expansion), and if the expansion is not purely antisymmetric, then such a system will generally have a quadratic term that will generate frequency summed signals at the output.
For channels X, Y, and Z, define the wavelet bispectrum, BiSXYZ(t, f1, f2), as
| (36) |
where s{}(t, f) is defined in Eq. (19). Eq. (36) is a straightforward generalization from the frequency domain bispectrum definition given in Nikias and Mendel (1993).
Once the bispectrum has been defined, bicoherence and biphase-locking value may be defined. The wavelet bicoherence, bCohXYZ(t, f1, f2), is the expected value of the squared normalized wavelet bispectrum (van Milligen et al., 1996; Li et al., 2007) is given by
| (37) |
Darvas et al. (2009) have generalized PLV (Eq. (27)) to the bispectral case as
| (38) |
The bPLV measure has been applied successfully to iEEG data (Darvas et al., 2009), but successful applications to scalp EEG data have not yet been reported (Darvas, personal communication).
Tass et al. (1998) describe two methods for the identification of n:m phase locking from MEG data, where n and m are integers. These related approaches are based on estimation of Shannon entropy or conditional probability.
5. Source space extensions
The methods we have described may be applied to time series in general, although we have so far restricted their application to the measured EMEG data in signal space. To extend the analysis to source space, we need to apply inverse methods, collectively known as source estimation, that allow us to infer source time series from the signals. It is well-known that these methods are inherently ill-posed, but may nevertheless provide useful information.
In theory, there are two possible avenues to approach brain connectivity measures in source space. First, we might use a conventional inverse method to estimate source time series, and then apply a connectivity measure to the source space time series estimates. Second, in theory, we might modify existing methods to incorporate connectivity directly into the inverse estimate, but this second approach has not yet matured to point of successful application.
Conventional inverse methods are either overdetermined (dipole fitting) or underdetermined (e.g., minimum norm or beamformers). Both of these have been applied to the connectivity problem in source space in a limited number of studies.
Dipole coherence, described by Hoechstetter et al. (2004), is a straightforward application of the bivariate coherence measure to time series estimates obtained from a simple dipole model using complex demodulation. As such, it has the confounding of phase and amplitude correlation inherent in coherence estimates.
DICS (Gross et al., 2001) is a frequency or time–frequency (Greenblatt et al., 2010) domain beamformer that is well suited for source space coherence estimation. In this approach, the frequency-specific signal space covariance is used to construct a beamformer. The resulting source space estimates may then be combined pair-wise to obtain source space coherence estimates. Palva et al. (2010) have combined minimum norm estimation techniques applied to EMEG data with bivariate phase synchrony measures to map connectivity over the entire cortical surface. They were able to derive a number of network graph measures in differing canonical frequency bands using this approach.
6. Some practical guidelines
In this section, we address some possible obstacles that researchers may encounter in the interpretation of synchrony estimates from experimental data. While by no means comprehensive, we hope to describe some problematic issues of recognized significance, with the goals of adding to the readers' intuition, suggesting possible solutions, pointing the reader to relevant literature, and reflecting on the challenge of studying synchrony based on electrophysiological measurements. In particular, we address temporal filtering, temporal resolution, the EEG reference problem, and volume conduction.
6.1. Temporal filtering
Kurgansky (2010) and Barnett and Seth (2011) have recently addressed the problem of temporal filtering in the context of MVAR based estimation of Granger causality. Such temporal filtering may lead to a theoretically infinite AR model order of the filtered data. This problem arises because even if the original process is purely autoregressive and of finite order, any temporal filtering turns it into a moving average autoregressive (ARMA) process. In theory, an ARMA process can also be modeled by an AR process but with the infinite order. Therefore, practical order determination is problematic in this case. Because a higher order model will be needed after filtering, the accuracy of the underlying parameter estimates is affected adversely. Therefore it is preferable to temporally filter the data as little as possible. If it is necessary to remove low frequency trends, we recommend using a polynomial de-trend procedure. If filtering is unavoidable, the care must be taken (especially in case of IIR filters) to ensure that the poles of filter transfer function do not appear closer to the unit circle than those of the VAR model transfer function. This will ensure that the spectral radius of the filtered process is not increased.
We also note that in the case of AR-model-based Granger causality analysis, temporal filtering has sometimes been used in an attempt to emphasize certain band of interest. However, this is problematic, since it not only fails to emphasize the bands of interest, it may, in addition, introduce artifactual noise in the causality frequency profile in the interval corresponding to the filter stopband (Barnett and Seth, 2011).
Care must also be used when temporal filtering is used prior to phase synchrony estimation. Observed synchrony between brain assemblies is typically transient and often persists for 100–300 ms (Friston, 1997). Temporal filters with non-zero length impulse response may artifactually blend two adjacent time segments with distinct synchronization patterns, thereby adversely affecting the estimates of phase synchrony.
6.2. Temporal resolution of synchrony measures
It takes time to estimate the synchrony between two oscillations, and this obviously depends on the period of the oscillations of interest. The shorter the time interval (relative to the period of interest), the broader confidence intervals of the estimated synchrony indices are. For continuous (e.g., ictal or interictal) data, the recordings must be averaged over time. This requires confidence in the stationarity of the signal throughout the averaging interval. The problem is less severe when dealing with data recorded with an event related paradigm, where averaging over time may be replaced by averaging across trials, assuming stationarity over trials. Lachaux et al. (1999) describe a simulation example illustrating the relation between the imposed and estimated dynamics of phase synchrony measured by the phase-locking statistics which illustrates this problem. When feasible, the investigator should consider combining temporal and across-trial averaging to achieve a trade-off between the reliability of phase estimates and its temporal resolution.
6.3. EEG reference electrode
EEG recordings measure the potential difference at one or more scalp locations with respect to a reference location. The choice of reference should be very carefully considered when collecting the EEG data to be used for coupling estimates using coherence, phase-locking value or any measure of synchrony.
Fein et al. (1988) and Guevara et al. (2005) show that the use of common average in most cases will produce potentially misleading conclusions when estimating coherence and phase-locking values. One possible solution is to use differential montage. Differential (or bipolar) montages are obtained by subtraction of signals in neighboring sites to cancel the common reference signal. However, one has to keep in mind that such a differential montage is in fact a spatial filter that leaves in the data only the contributions of a small subset of superficial dipolar sources (Nunez, 1981) with specific orientations. Schiff (2005) proposes using a “double banana” montage to reduce the information removal effect of differential montages. If, however, it is necessary to use a common average montage, errors will be reduced by increasing the number of electrodes, and by extending the coverage to as much of the head as possible (Guevara et al., 2005).
Given an adequate spatial density of electrodes with known locations, the Laplacian operator with respect to the scalp surface (Nunez et al., 1997; Lachaux et al., 1999), or, equivalently, the scalp current density (SCD) transform (Pernier et al., 1988) are the (essentially equivalent) reference-free derivations of choice. They should be applied to the data prior to computing the synchrony measures. These methods compute an approximation to the second spatial derivative of scalp potential distribution. Thus, the result is proportional to the scalp current source/sink distribution. In general, deblurring methods, like the Laplacian and the SCD, have a diminished sensitivity to deeper sources, compared to average or physical references.
6.4. Volume conduction
The problem of volume conduction arises because source signals are mixed before detection by EMEG sensors (see Section 2, and e.g. Nunez, 1981; Lachaux et al., 1999). In addition to source estimation methods (described in Section 5) and imaginary coherence (described in Section 4.8), additional tools may reduce the effects of volume conduction on signal space connectivity measures. One good place to start is with a suitable choice of experimental design. If an event-related paradigm can be developed that has a contrast between conditions, it may be possible to show that there is a statistically significant change in connectivity as a function of the design contrast. While this does not reduce cross-talk per se, it does allow for functionally specific inferences. When analyzing EEG data, deblurring techniques, such as those described in Section 6.3, will tend to reduce cross-talk. Dipole simulations may also be used to obtain a measure of possible volume conduction effects. Lastly, MEG planar gradiometers have narrower lead fields than do EEG electrodes or MEG magnetometers or coaxial gradiometers, and may therefore be preferable for signal space estimates, when available (Winter et al., 2007). However, Palva et al. (2010) report significant differences between synchrony measures obtained from MEG signal space and source space estimates.
Volume conduction effects due to the addition of ‘brain noise’ (that is, signals from brain regions other than those of interest) may yield erroneous results at low signal/noise ratios. Haufe et al. (2011), using simulated data, have shown that several measures of causality connectivity may yield erroneous estimates of information flow, and that the phase slope index is relatively robust under these conditions.
7. Discussion
The principal goal of this paper has been to develop a comprehensive and unified description, both formal and informal, of methods that have shown promise for the characterization of brain connectivity from EMEG data. The motivation for this work is based on both a scientific and a technological foundation.
Starting from a neurobiological perspective, we hypothesize that transiently stable, macroscopic neural networks self-organize as the physical substrate for behavior (e.g., Mesulam, 1990; Friston, 1994; McIntosh et al., 1996; Sporns, 2011), and that this self-organization may be characterized in a statistically consistent fashion. Since it is likely that such transiently stable networks form the core of much, if not all, of the cognitive life of mammals, including humans, improved means of studying them and describing their properties in humans would represent a significant contribution to empirical and theoretical neuroscience. Furthermore, it seems likely that significant neurological disorders, most prominently epilepsy (e.g., Bartolome et al., 2000; Spencer, 2002; Chaovalitwongse et al., 2008; Ossadtchi et al., 2010) and Alzheimer's disease (Dauwels et al., 2010), as well as psychiatric disorders, such as schizophrenia (Clementz et al., 2004; Roach and Mathalon, 2008), affective disorders (Rockstroh et al., 2007) and autism spectrum disorder (Just et al., 2004; Koshino et al., 2005), may be due to disruptions of the normal ability to create and maintain such adaptive functional networks.
Although these views may be held widely in the neuroscience community, as yet there is relatively little direct experimental evidence to describe how specific networks organize during human behaviors. Existing brain imaging analysis methods using fMRI data typically view the brain as a single pattern of activity corresponding to a particular brain state. The ‘default network’ (Raichle et al., 2001) is one well-known example. What has been largely lacking, so far, is the ability to provide a dynamic picture of the interactions between brain regions, and their evolution over time, although the results we cite in this paper, as well as numerous other studies suggest that productive research is developing in this direction. Novel methods to integrate fMRI with simultaneously recorded EEG will certainly advance this frontier. Dynamic causal modeling, when applied to fMRI data, has been used to estimate a probabilistic deconvolution with the hemodynamic response function in order to indirectly assess the underlying electrical activity and use it for causal modeling (Marreiros et al., 2008).
From a technical perspective, we further hypothesize that these networks are accessible to study by combining electromagnetic recordings with structural and functional MRI. In fact, significant progress has been made in this area, as numerous citations in this paper bear witness. The use of these methods in the development of brain computer interfaces and neurofeedback seems particularly promising in the relatively near future. In our view, however, there are some obstacles that stand in way of more widespread application of these methods to experimental data.
Most importantly, we need to move these methods out of the hands of developers and other experts in signal processing, and into the hands of scientific investigators. A large variety of connectivity measures have been proposed and validated, typically by their developers. However, what seems to be lacking is a comprehensive connectivity toolkit, easily accessible to the cognitive and clinical electrophysiology communities, one that can be used by scientists who are not necessarily signal processing experts. To some extent this has been taking place, with the availability of various freeware (e.g., Fieldtrip, eConnectome, GCCA (Seth, 2010)) and commercial (e.g., ASA, BESA, EMSE) software packages. It seems, however, that these packages are still relatively immature in this regard, both in terms of their comprehensiveness, and also in terms of their ease of use. Comprehensiveness, in this case, means not only a suitable breadth of methods in both signal and source space, but also appropriate hypothesis testing and visualization features, as well as support for a variety of EMEG vendor formats.
It may seem to someone entering the field, that there is a bewildering array of connectivity measures, and there are no clear guidelines for their use. In fact, there appears to be some justification for this view. We lack a systematic comparison of measures and algorithms that would a permit an investigator who is not an expert in signal processing to choose the appropriate approach, given the scientific question to be answered. Dauwels et al. (2010) have addressed this issue in the study of mild cognitive impairment and Alzheimer's disease. However imperfectly, the current paper has attempted to be of some use in this context, as well.
Acknowledgments
This work was funded in part by U.S. National Institutes of Health grant R43 MH095439, M. E. Pflieger, P. I.
Appendix A
A.1. MVAR and Gaussianity
In this section, we show that the time series output of an MVAR model has a multivariate Gaussian probability density function.
We begin by restating Eq. (2), which defines the MVAR model.
| (A.1) |
where ε ∼ N(0, σ2I).
Now we introduce a new set of variables that facilitate the expression of a sequence vt+1, …, vt+M. For N channels, vt = (v1(t), v2(t), …, vN(t))T. We define the delay embedding vector for N channels and K delays as , .
Now define two new variables.
First, let , dim(A) = N × NK, dim(I) = N × N, and dim(Ã) = NK × NK.
Second, define , dim(Et+1) = NK × 1.
In words, Ã computes the new vt+1 and shifts the remaining vt, vt−1,… into the updated delay embedding vector . Because it is square, we can apply it sequentially, obtaining a valid product.
Using our new variables, we rewrite Eq. (A.1) as
This change of variables permits us to write . Continuing forward in time for P samples, we find that
Then assuming the determinant det(Ã) < 1, for large P, we find that
This tells us that if we wait a sufficiently long time, will depend only on the noise process E, and therefore v(t) will depend only on the noise process ε(t). If ε(t) is multivariate Gaussian, then sums of ε(t), and thus v(t), will be multivariate Gaussian as well. Furthermore, by the central limit theorem, if the ε(t) are independently distributed random processes, then in the limit, their sum will be Gaussian-distributed. This result may seem counter intuitive if one refers to an MVAR model that produces very narrow-band oscillations whose pdf is far from Gaussian (compare with Eq. (32), where T(f) would approach a delta function). We would like to note here that in this case, det(Ã) approaches unity and the model approaches the border of stability. However, in our experience working with the real data we have never encountered such narrow-band signals that are modeled with an MVAR model whose matrix would not meet the det(Ã) < 1 condition.
Thus we have shown that under a reasonable set of assumptions, the output of an MVAR process will have a multivariate Gaussian probability density function.
A.2. Imaginary coherence and volume conduction
In this section, we show that, given a set of assumptions, the imaginary part of the cross-spectrum (and therefore the imaginary part of the coherence) estimated from extracranial (EMEG) measurements, depends only on the correlation between underlying brain sources.
Assume the following statistical model:
Q = {Qk} is a set of K zero-mean, independent, complex-valued random processes with realizations qk(t), 0 ≤ k ≤ K. For a complex-valued number to have zero mean, we require that both the real and the imaginary parts have zero mean.
V = {vi, vj} are complex-valued random processes defined by vi(t) = Σk<Kgikqk(t) and vj(t) = Σk<Kgjkqk(t) where all of the lead field parameters gik and gjk are real-valued, i.e., there is no phase shift in going from q to v.
Physically, we interpret Q to be a set of dipole time series in the brain, V set set of (two scalp-measured EEG) time series, and each gik, gjk are the forward solutions from the kth dipole to the ith (resp.jth) sensor. The assumptions of linearity and zero-phase shift are made routinely when considering the EMEG forward problem. These derive from solving Maxwell's equations in the quasi-static case, which introduces errors of <1% for a frequency range below 1 kHz (Malmivuo and Plonsey, 1995).
Define the cross-spectrum for channels i and j as , where 〈·〉 represents the expectation operator, and * represents complex conjugation. If we write qk in terms of its real and imaginary parts as qk = ak + ibk, then 〈qk〉 = ∫ p(ak)ak dak + i ∫ p(bk)bk dbk where p(·k) is the probability density of ·k and the integration is assumed to span the entire range of values.
We want to show that, under the assumptions of the model, sij is real-valued.
In step 1, we show for complex-valued random variables x, y, where x is statistically independent of y (symbolically, x ⊥ y), this implies 〈xy*〉 = 〈x〉〈y*〉. Then, in step 2, we combine this result with the zero-mean, zero-phase-shift, linearity and independence assumptions of the model to obtain the desired result.
Step 1: Write 〈x〉 = ∫ p(ax)ax dax + i ∫ p(bx)bx dbx and 〈y*〉 = ∫ p(ay)ay day − i ∫ p(by)by dby.
Then
After multiplying the terms and writing the real and imaginary parts separately, we find that
Then since p(ax) ⊥ p(ay) ⇒ p(ax)p(ay) = (ax, ay), and similarly for the other variables, we get
or
| (A.2) |
Now consider 〈x, y*〉 = 〈[ax + ibx][ay − iby]〉. After cross multiplying and using the fact that the expectation of a sum is always equal to the sum of expectations, we obtain
| (A.3) |
Since Eq. (A.2) equals Eq. (A.3), we obtain
| (A.4) |
Note that 〈x〉 = 0 or 〈y*〉 = 0 implies 〈xy*〉 = 0.
Step 2: From the statistical model we have or
From the assumptions that the qk are zero-mean and qk ⊥ qk′, ∀k ≠ k′, combined with the result shown in Eq. (A.4), we find that
Thus, under the assumptions of the model, Sij is real-valued. As a corollary, we find that the imaginary part of Sij carries information about the correlation between sources. In other words, when the dipole time series are correlated, both real and imaginary parts of coherence change. For uncorrelated sources, however, the imaginary part of coherence is zero. Thus, we may use the imaginary part to estimate source space correlations. As with any correlation measure, imaginary coherence changes do not by themselves provide us with any direct information regarding causal interactions.
Footnotes
We use E() rather than 〈 〉 to avoid confusion with the Hilbert space inner product, which arises in the derivation of correntropy.
References
- Ahmed NA, Gokhale DV. Entropy expressions and their estimators for multivariate distributions. IEEE Trans Inform Theory. 1989;35:688–92. [Google Scholar]
- Akaike H. An information criterion. Math Sci. 1976;1:5–9. [Google Scholar]
- Allefeld C, Frisch S, Schlesewsky M. Detection of early cognitive processing by event-related phase synchronization analysis. Neuroreport. 2005;16:13–6. doi: 10.1097/00001756-200501190-00004. [DOI] [PubMed] [Google Scholar]
- Babiloni F, Cincotti F, Babiloni C, Carducci F, Mattia D, Astolfi L, et al. Estimation of the cortical functional connectivity with the multimodal integration of high-resolution EEG and fMRI data by directed transfer function. NeuroImage. 2005;24:118–31. doi: 10.1016/j.neuroimage.2004.09.036. [DOI] [PubMed] [Google Scholar]
- Barnett L, Seth AK. Behaviour of Granger causality under filtering: theoretical invariance and practical application. J Neurosci Methods. 2011;201:404–19. doi: 10.1016/j.jneumeth.2011.08.010. [DOI] [PubMed] [Google Scholar]
- Bartolome F, Wendling F, Régis J, Gavaret M, Guye M, Chauvel P. Pre-ictal synchronicity in limbic networks of mesial temporal lobe epilepsy. Epilepsy Res. 2000;61:89–104. doi: 10.1016/j.eplepsyres.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Bell A, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7:1129–59. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Belouchrani A, Abed-Meriam K, Cardoso JF. A blind source separation technique using second-order statistics. IEEE Trans Signal Proc. 1997;45:434–44. [Google Scholar]
- Bertini M, Ferrara M, De Gennaro L, Curcio G, Moroni F, Babiloni C, et al. Directional information flows between brain hemispheres across waking, non-REM and REM sleep states: an EEG study. Brain Res Bull. 2009;78:270–5. doi: 10.1016/j.brainresbull.2008.12.006. [DOI] [PubMed] [Google Scholar]
- Bhattacharya J, Petsche H, Feldmann U, Rescher B. EEG gamma-band phase synchronization between posteriorand frontal cortex during mental rotation in humans. Neurosci Lett. 2001;311:29–32. doi: 10.1016/s0304-3940(01)02133-4. [DOI] [PubMed] [Google Scholar]
- Bhattacharya J, Petsche H. Shadows of artistry: cortical synchrony during perception and imagery of visual art. Cognitive Brain Res. 2002;13:179–86. doi: 10.1016/s0926-6410(01)00110-0. [DOI] [PubMed] [Google Scholar]
- Bruns A. Fourier-, Hilbert-and wavelet-based signal analysis: are they really different approaches? J Neurosci Methods. 2004;137:321–32. doi: 10.1016/j.jneumeth.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Buresti G, Lombardi G. Application of continuous wavelet transforms to the analysis of experimental turbulent velocity signals. Proc 1st intl symp on turb shear flowphenom. 1999 [Google Scholar]
- Buzsáki G. Rhythms of the brain. New York: Oxford Univ. Press; 2006. [Google Scholar]
- Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, et al. High gamma power is phase-locked to theta oscillations in human neocortex. Science. 2006;313:1626–8. doi: 10.1126/science.1128115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaovalitwongse WA, Suharitdamrong W, Liu CC, Anderson ML. Brain network analysis of seizure evolution. Ann Zool Fenn. 2008;45:402–14. [Google Scholar]
- Clementz BA, Keil A, Kissler J. Aberrant brain dynamics in schizophrenia: delayed buildup and prolonged decay ofthe visual steady-state response. Cognitive Brain Res. 2004;18:121–9. doi: 10.1016/j.cogbrainres.2003.09.007. [DOI] [PubMed] [Google Scholar]
- Cohen L. Time-frequency analysis. Upper Saddle River, NJ: Prentice-Hall; 1995. pp. 39–41. [Google Scholar]
- Darvas F, Ojemann JG, Sorensen L. Biphase locking – a tool for probing non-linear interaction in the human brain. NeuroImage. 2009;46:123–32. doi: 10.1016/j.neuroimage.2009.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daumé H. From zero to reproducing Kernel Hilbert spaces in twelve pages or less. 2004 http://www.cs.utah.edu/∼hal/docs/daume04rkhs.pdf;
- Dauwels J, Vialatte F, Musha T, Cichocki A. A comparative study of synchrony measures for the early diagnosis of Alzheimer's disease based on EEG. NeuroImage. 2010;49:668–93. doi: 10.1016/j.neuroimage.2009.06.056. [DOI] [PubMed] [Google Scholar]
- Dauwels J, Vialatte F, Rutkowski T, Cichocki A. Measuring neural synchrony by message passing. Adv Neural Inform Process Syst. 2008;20:361–8. [Google Scholar]
- de Lange FP, Jensen O, Bauer M, Toni I. Interactions between posterior gamma and frontal alpha/beta oscillations during imagined actions. Front Hum Neurosci. 2008;2:1–12. doi: 10.3389/neuro.09.007.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dien J, Frishkoff GA. Principal components analysis of ERP data. In: Handy TC, editor. Event-related potential: a methods handbook. Cambridge, MA: MIT Press; 2005. pp. 189–208. [Google Scholar]
- Dien J. Addressing misallocation of variance in principal components analysis of event-related potentials. Brain Topogr. 1998;11:43–55. doi: 10.1023/a:1022218503558. [DOI] [PubMed] [Google Scholar]
- Ding L, Worell GA, Lagerlund TD, He B. Ictal source analysis: localization and imaging of causal interactions in humans. NeuroImage. 2007;34:575–86. doi: 10.1016/j.neuroimage.2006.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding M, Bressler SL, Yang W, Liang H. Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment. Biol Cybern. 2000;83:35–45. doi: 10.1007/s004229900137. [DOI] [PubMed] [Google Scholar]
- Doesberg SM, Roggeveen AB, Kitajo K, Ward LM. Large-scale gamma-band phase synchronization and selective attention. Cereb Cortex. 2008;18:386–96. doi: 10.1093/cercor/bhm073. [DOI] [PubMed] [Google Scholar]
- Draganova R, Popiavanov D. Assessment of EEG frequency dynamics using complex demodulation. Physiol Res. 1999;48:157–65. [PubMed] [Google Scholar]
- Ewald A, Marzetti L, Zappasodi F, Meinecke FC, Nolte G. Estimating true brain connectivity from EEG/MEG data invariant to linear and static transformations in sensor space. NeuroImage. 2012;60:476–88. doi: 10.1016/j.neuroimage.2011.11.084. [DOI] [PubMed] [Google Scholar]
- Fein G, Raz J, Brown FF, Merrin EL. Common reference coherence data are confounded by power and phase effects. Electroencephalogr Clin Neurophysiol. 1988;69:581–4. doi: 10.1016/0013-4694(88)90171-x. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Functional and effective connectivity in neuroimaging. Hum Brain Mapp. 1994;2:56–78. [Google Scholar]
- Friston KJ. Another neural code? NeuroImage. 1997;5:213–20. doi: 10.1006/nimg.1997.0260. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19:1273–302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Gabor D. Theory of communication. JIEE. 1946;93:429–57. [Google Scholar]
- Gevins AS, Morgan NH, Bressler SL, Cutillo BA, White RM, Illes J, et al. Human neu-roelectric patterns predict performance accuracy. Science. 1987;235:580–5. doi: 10.1126/science.3810158. [DOI] [PubMed] [Google Scholar]
- Granger CWJ. Investigating causal relations by econometric methods and cross-spectral methods. Econometrica. 1969;37:424–38. [Google Scholar]
- Greenblatt RE, Ossadtchi A, Pflieger ME. Local linear estimators for the bioelectro-magnetic inverse problem. IEEE Trans Signal Proc. 2005;53:3403–12. [Google Scholar]
- Greenblatt RE, Ossadtchi A, Kurelowech L, Lawson D, Criado J. Time-frequency source estimation from MEG data. Proc 17th Intl Cong Biomag. 2010:136–9. [Google Scholar]
- Gross J, Kujala J, Hämäläinen M, Timmermann L, Schnitzler A, Salmelin R. Dynamic imaging of coherent sources: studying neural interactions in the human brain. Proc Natl Acad Sci USA. 2001;98:694–9. doi: 10.1073/pnas.98.2.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guevara R, Velazquez JL, Nenadovic V, Wennberg R, Senjanovic G, Dominguez LG. Phase synchronization measurements using electroencephalographic recordings: what can we really say about neuronal synchrony? Neuroinformatics. 2005;3:301–14. doi: 10.1385/NI:3:4:301. [DOI] [PubMed] [Google Scholar]
- Gysels E, Celka P. Phase synchronization for the recognition of mental tasks in a brain-computer interface. IEEETrans Neural Syst Rehabil. 2004;12:406–15. doi: 10.1109/TNSRE.2004.838443. [DOI] [PubMed] [Google Scholar]
- Haufe S, Nikulin V, Nolte G. Identifying brain effective connectivity patterns from EEG: performance of Granger Causality, DTF PDC and PSI on simulated data. BMC Neurosci. 2011;12(Suppl 1):141. [Google Scholar]
- Hoechstetter K, Bornfleth H, Weckesser D, Ille N, Berg P, Scherg M. BESA source coherence: a new method to study cortical oscillatory coupling. Brain Topogr. 2004;16:233–8. doi: 10.1023/b:brat.0000032857.55223.5d. [DOI] [PubMed] [Google Scholar]
- Hoke M, Lehnertz K, Pantev C, Lükenhöner B. Spatiotemporal aspects of synergetic processes in the auditory cortex as revealed by the magnetoencephalogram. In: Basar E, Bullock TH, editors. Brain dynamics, progress and perspectives Springer series in brain dynamics. Germany: Springer-Verlag; 1989. pp. 516–21. [Google Scholar]
- Hyvarinen A, Oja E. Independent component analysis: algorithms and applications. Neural Netw. 2000;13:411–30. doi: 10.1016/s0893-6080(00)00026-5. [DOI] [PubMed] [Google Scholar]
- Ivanov AV, Rozhkova MN. Properties ofthe statistical estimate ofthe entropy of a random vector with a probability density. Probl Inform Transm. 1981;17:123–43. [Google Scholar]
- Just MA, Cherkassky VL, Keller TA, Minshew NJ. Cortical activation and synchronization during sentence comprehension in high-functioning autism: evidence of underconnectivity. Brain. 2004;127:1811–21. doi: 10.1093/brain/awh199. [DOI] [PubMed] [Google Scholar]
- Kaiser A, Schreiber T. Information transfer in continuous processes. Physica D. 2002;166:43–62. [Google Scholar]
- Kaiser HF. The varimax criterion for analytic rotation in factor analysis. Psychometrika. 1958;23:187–200. [Google Scholar]
- Kamińki M, Ding M, Truccolo WA, Bressler SL. Evaluating causal relations in neural systems: Granger causality, directed transfer function, and statistical assessment of significance. Biol Cybern. 2001;85:145–57. doi: 10.1007/s004220000235. [DOI] [PubMed] [Google Scholar]
- Kamiński M, Liang H. Causal influence: advances in neurosignal analysis. Crit Rev Biomed Eng. 2005;33:347–430. doi: 10.1615/critrevbiomedeng.v33.i4.20. [DOI] [PubMed] [Google Scholar]
- Kamiński MJ, Blinkowska KJ. A new method of the description ofthe information flow in the brain structures. Biol Cybern. 1991;65:203–10. doi: 10.1007/BF00198091. [DOI] [PubMed] [Google Scholar]
- Koshino H, Carpenter PA, Minshew NJ, Cherkassky VL, Keller TA, Just MA. Functional connectivity in an fMRI working memory task in high-functioning autism. NeuroImage. 2005;24:810–21. doi: 10.1016/j.neuroimage.2004.09.028. [DOI] [PubMed] [Google Scholar]
- Kralemann B, Cimponeriu L, Rosenblum M, Pikovsky A, Mrowka R. Phase dynamics of coupled oscillators reconstructed from data. Phys Rev E. 2008;77:066205. doi: 10.1103/PhysRevE.77.066205. [DOI] [PubMed] [Google Scholar]
- Kralemann B, Cimponeriu L, Rosenblum M, Pikovsky A, Mrowka R. Uncovering interaction of coupled oscillators from data. Phys Rev E. 2007;76 doi: 10.1103/PhysRevE.76.055201. 055201(R) [DOI] [PubMed] [Google Scholar]
- Kralemann B, Pikovsky A, Rosenblum M. Reconstructing phase dynamics of oscillator networks. 2011 doi: 10.1063/1.3597647. arX iv:1102.3064v1. [DOI] [PubMed] [Google Scholar]
- Kronland-Martinet R, Morlet J, Grossmann A. Analysis of sound patterns through wavelet transforms. Int J Pattern Recogn Artif Intell. 1987;1:273–302. [Google Scholar]
- Kullback S, Liebler RA. On information and sufficiency. Ann Math Stat. 1951;22:79–86. [Google Scholar]
- Kurgansky AB. Some questions in the study of cortico-cortical functional connections with the help of vector autoregressive models of multichannel EEG. J High Nerv Act. 2010;60:630–49. in Russian. [Google Scholar]
- Kus R, Kamiński M, Blinkowska KJ. Determination of EEG activity propagation: pair-wise versus multichannel estimate. IEEETrans BME. 2004;51:1501–10. doi: 10.1109/TBME.2004.827929. [DOI] [PubMed] [Google Scholar]
- Lachaux J, Rodriguez E, Le Van Quyen M, Lutz A, Martinerie J, Varela F. Studying single-trials of phase synchronous activity in the brain. Int J Bifurcat Chaos. 2000;10:229–39. [Google Scholar]
- Lachaux JP, Rodriguez E, Martinerie J, Varela FJ. Measuring phase synchrony in brain signals. Hum Brain Mapp. 1999;8:194–208. doi: 10.1002/(SICI)1097-0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Van Quyen M, Adam C, Baulac M, Martinerie J, Varela FJ. Nonlinear interdependencies of EEG signals in human intracranially recorded temporal lobe seizures. Brain Res. 1998;792:24–40. doi: 10.1016/s0006-8993(98)00102-4. [DOI] [PubMed] [Google Scholar]
- Le Van Quyen M, Foucher J, Lachaux JP, Rodriguez E, Lutz A, Martinerie J, et al. Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J Neurosci Methods. 2001a;111:83–98. doi: 10.1016/s0165-0270(01)00372-7. [DOI] [PubMed] [Google Scholar]
- Le Van Quyen M, Martinerie J, Adam C, Varela F. Nonlinear analyses of interictal EEG map the interdependencies in human focal epilepsy. Physica D. 1999;127:250–66. [Google Scholar]
- Le Van Quyen M, Martinerie J, Navarro V, Baulac M, Varela F. Characterizing neurodynamic changes before seizures. J Clin Neurophysiol. 2001b;18:191–208. doi: 10.1097/00004691-200105000-00001. [DOI] [PubMed] [Google Scholar]
- Li K, Guo L, Nie J, Li G, Liu T. Review of methods for functional brain connectivity detection using fMRI. Comput Med Imag Grap. 2000;33:131–9. doi: 10.1016/j.compmedimag.2008.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Yao X, Fox J, Jefferys JG. Interaction dynamics of neuronal oscillations analysed using wavelet transforms. J Neurosci Methods. 2007;160:178–85. doi: 10.1016/j.jneumeth.2006.08.006. [DOI] [PubMed] [Google Scholar]
- Lisman J, Buzsáki G. A neural coding scheme formed by the combined function of gamma and theta oscillations. Schizophrenia Bull. 2008;34:974–80. doi: 10.1093/schbul/sbn060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Pokharel PP, Principe JC. Correntropy: properties and applications in non-Gaussian signal processing. IEEE Trans Signal Process. 2007;55:5286–98. [Google Scholar]
- Malmivuo J, Plonsey R. Bioelectromagnetism: principles and applications of bioelectric and biomagnetic fields. New York: Oxford Univ. Press; 1995. [Google Scholar]
- Marreiros AC, Kiebel SJ, Friston KJ. Dynamic causal modelling for fMRI: a two-state model. NeuroImage. 2008;39:269–78. doi: 10.1016/j.neuroimage.2007.08.019. [DOI] [PubMed] [Google Scholar]
- Martini M, Kranz TA, Wagner T, Lehnertz K. Inferring directional interactions from transient signals with symbolic transfer entropy. Phys Rev E. 2011;83:011919. doi: 10.1103/PhysRevE.83.011919. [DOI] [PubMed] [Google Scholar]
- McIntosh AR, Bookstein FL, Haxby JV, Grady CL. Spatial pattern analysis of functional brain images using Partial Least Squares. NeuroImage. 1996;3:143–57. doi: 10.1006/nimg.1996.0016. [DOI] [PubMed] [Google Scholar]
- Mesulam MM. Large-scale neurocognitive networks and distributed processing for attention, language, and memory. Ann Neurol. 1990;28:597–613. doi: 10.1002/ana.410280502. [DOI] [PubMed] [Google Scholar]
- Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, Grave de Peralta R. EEG source imaging. Clin Neurophysiol. 2004;115:2195–200. doi: 10.1016/j.clinph.2004.06.001. [DOI] [PubMed] [Google Scholar]
- Morf M, Vieira A, Lee DTL, Kailath T. Recursive multichannel maximum entropy spectral estimation. IEEETrans Geosci Electron. 1978;16:85–95. [Google Scholar]
- Mormann F, Lehnertz K, David P, Elger CE. Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Phys D: Nonlinear Phenom. 2000;144:358–69. [Google Scholar]
- Mosher JC, Leahy RM, Lewis PS. EEG and MEG: forward solutions for inverse methods. IEEE Trans BME. 1999;46:245–59. doi: 10.1109/10.748978. [DOI] [PubMed] [Google Scholar]
- Nikias C, Mendel J. Signal processing with higher-order spectra. IEEE Signal Process Mag. 1993;10:10–37. [Google Scholar]
- Nolte G, Ziehe A, Nikulin V, Schlögl A, Krämer N, Brismar T, et al. Robustly estimating the flow direction of information in complex physical systems. Phys Rev Lett. 2008;100:234101. doi: 10.1103/PhysRevLett.100.234101. [DOI] [PubMed] [Google Scholar]
- Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M. Identifying true brain interaction from EEG data using the imaginary part of coherency. Clin Neurophysiol. 2004;115:2292–307. doi: 10.1016/j.clinph.2004.04.029. [DOI] [PubMed] [Google Scholar]
- Nolte G. Exploiting temporal delays in interpreting EEG/MEG data in terms of brain connectivity. 2007 http://videolectures.net/mda07_nolte_etd/;
- Nunez PL, Srinivasan R, Westdorp AF, Wijesinghe RS, Tucker DM, Silberstein RB, et al. EEG coherency. I: Statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales. Electroencephalogr Clin Neurophysiol. 1997;103:499–515. doi: 10.1016/s0013-4694(97)00066-7. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Electric fields of the brain: the neurophysics of EEG. New York, NY: Oxford University Press; 1981. [Google Scholar]
- Oppenheim AV, Schafer RW. Discrete-time signal processing. 3rd. Englewood Cliffs, NJ: Prentice-Hall; 2010. [Google Scholar]
- Ossadtchi A, Greenblatt RE, Towle VL, Kohrman MH, Kamada K. Inferring spatiotemporal network patterns from intracranial EEG data. J Clin Neurophysiol. 2010;121:823–35. doi: 10.1016/j.clinph.2009.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palva S, Monto S, Palva JM. Complex network measures of brain connectivity: uses and interpretations. NeuroImage. 2010;49:3257–68. [Google Scholar]
- Park I, Principe JC. Acoustics, speech and signal processing. Vol. 2008. ICASSP; 2008. Correntropy based Granger causality; pp. 3605–8. [Google Scholar]
- Payne L, Kounios J. Coherent oscillatory networks supporting short-term memory retention. Brain Res. 2009;1247:126–32. doi: 10.1016/j.brainres.2008.09.095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny W, Duzel E, Miller KJ, Ojemann JG. Testing for nested oscillation. J Neurosci Methods. 2008;174:50–61. doi: 10.1016/j.jneumeth.2008.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny W, Harrison L. Multivariate autoregressive models. In: Friston K, Ashburner J, Kiebel S, Nichols T, Penny W, editors. Statistical parametric mapping: the analysis of functional brain images. Chapter 40 London: Elsevier; 2006. [Google Scholar]
- Pereda E, Quiroga RQ, Bhattacharya J. Nonlinear multivariate analysis of neurophysiological signals. Prog Neurobiol. 2005;77:1–37. doi: 10.1016/j.pneurobio.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Pernier J, Perrin F, Bertrand O. Scalp current densities: concept and properties. Electroencephalogr Clin Neurophysiol. 1988;69:385–9. doi: 10.1016/0013-4694(88)90009-0. [DOI] [PubMed] [Google Scholar]
- Pflieger ME, Assaf BA. A noninvasive method for analysis of epileptogenic brain connectivity. Epilepsia. 2004;45(Suppl 7):70–1. [Google Scholar]
- Pflieger ME, Greenblatt RE. Using conditional mutual information to approximate causality for multivariate physiological time series. Int J Bioelectromagn. 2005;7:285–8. [Google Scholar]
- Pijn JPM. Quantitative evaluation of EEG signals in epilepsy: nonlinear associations, time delays and nonlinear dynamics. Amsterdam, NL: Rodopi; 1990. [Google Scholar]
- Quiroga R, Kraskov A, Kreuz T, Grassberger P. Performance of different synchronization measures in real data: a case study on electroencephalographic signals. Phys Rev E. 2002;65:041903. doi: 10.1103/PhysRevE.65.041903. [DOI] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98:676–82. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach BJ, Mathalon DH. Event-related EEG time–frequency analysis: an overview of measures and an analysis of early gamma band phase locking in schizophrenia. Schizophrenia Bull. 2008;34:907–26. doi: 10.1093/schbul/sbn093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockstroh BS, Wienbruch C, Ray WJ, Elbert T. Abnormal oscillatory brain dynamics in schizophrenia: a sign of deviant communication in neural network? BMC Psychiatry. 2007;7:44–53. doi: 10.1186/1471-244X-7-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rykhlevskaia E, Fabiani M, Gratton G. Lagged covariance structure models for studying functional connectivity in the brain. NeuroImage. 2006;30:1203–18. doi: 10.1016/j.neuroimage.2005.11.019. [DOI] [PubMed] [Google Scholar]
- Santamaria I, Pokharel PP, Principe JC. Generalized correlation function: definition, properties and application to blind equalization. IEEE Trans Signal Process. 2006;54:2187–97. [Google Scholar]
- Sarvas J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987;32:11–22. doi: 10.1088/0031-9155/32/1/004. [DOI] [PubMed] [Google Scholar]
- Schiff SJ. Dangerous phase. Neuroinformatics. 2005;3:315–8. doi: 10.1385/NI:03:04:315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindler K, Leung H, Elger C, Lehnertz K. Assessing seizure dynamics by analyzing the correlation structure of multichannel intracranial EEG. Brain. 2007;130:65–77. doi: 10.1093/brain/awl304. [DOI] [PubMed] [Google Scholar]
- Schlogl A, Supp G. Analyzing event-related EEG data with multivariate autoregressive parameters. Prog Brain Res. 2006;159:135–47. doi: 10.1016/S0079-6123(06)59009-0. [DOI] [PubMed] [Google Scholar]
- Schreiber T. Measuring information transfer. Phys Rev Lett. 2000;85:461–4. doi: 10.1103/PhysRevLett.85.461. [DOI] [PubMed] [Google Scholar]
- Schutter JLG, Leitner C, Kenemans JL, van Honk J. Electrophysiological correlates of cortico-subcortical interaction: a cross-frequency spectral EEG analysis. Clin Neurophysiol. 2006;117:381–7. doi: 10.1016/j.clinph.2005.09.021. [DOI] [PubMed] [Google Scholar]
- Sehatpour P, Molholm S, Schwartz TH, Mahoney JR, Mehta AD, Javitt DC, et al. A human intracranial study of long-range oscillatory coherence across a frontal–occipital–hippocampal brain network during visual object processing. Proc Natl Acad Sci USA. 2008;105:4399–404. doi: 10.1073/pnas.0708418105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sello S, Bellazzini J. Wavelet cross-correlation analysis of turbulent mixing from large-eddy-simulations. 2000 http://arxiv.org/abs/physics/0003029.
- Seth A. Granger causality. Scholarpedia. 2007;2:1667. [Google Scholar]
- Seth A. A MATLAB toolbox for Granger causal connectivity analysis. J Neurosci Methods. 2010;186:262–73. doi: 10.1016/j.jneumeth.2009.11.020. [DOI] [PubMed] [Google Scholar]
- Shannon CE, Weaver W. The mathematical theory of communication. Urbana, IL: University of Illinois Press; 1949. reprinted 1972. [Google Scholar]
- Shibata T, Suhara Y, Oga T, Ueki Y, Mima T, Ishii S. Application of multivariate autoregressive modeling for analyzing the interaction between EEG and EMG in humans. International Congress Series. 2004;1270:249–53. [Google Scholar]
- Shoker L, Sanei S, Sumich A. Distinguishing between left and right finger movement from EEG using SVM. Engineering in Medicine and Biology Society 2005 IEEE-EMBS 2005 27th Annual international conference. 2006:5420–3. doi: 10.1109/IEMBS.2005.1615708. [DOI] [PubMed] [Google Scholar]
- Spencer SS. Neural networks in human epilepsy: evidence of and implications for treatment. Epilepsia. 2002;43:219–27. doi: 10.1046/j.1528-1157.2002.26901.x. [DOI] [PubMed] [Google Scholar]
- Sporns O. Networks of the brain. Cambridge, MA: MIT Press; 2011. [Google Scholar]
- Tallon-Baudry C, Betrand O, Delpuech C, Pernier J. Stimulus specificity of phase-locked and non-phase-locked 40 Hz visual responses in human. J Neurosci. 1996;16:4240–9. doi: 10.1523/JNEUROSCI.16-13-04240.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tass P, Rosenblum MG, Weule J, Kirths J, Pikovsky A, Volkmann J, et al. Detection of n:m phase locking from noisy data: application to magnetoencephalography. Phys Rev Lett. 1998;81:3291–4. [Google Scholar]
- Torrence C, Campo GP. Practical guide to wavelet Aanalysis. BAMS. 1998;79:61–78. [Google Scholar]
- Towle VL, Carder RK, Khorasani L, Lindberg D. Electrocorticographic coherence patterns. J Clin Neurophysiol. 1999;16:528–47. doi: 10.1097/00004691-199911000-00005. [DOI] [PubMed] [Google Scholar]
- Urbano A, Babiloni C, Onorati P, Babiloni F. Dynamic functional coupling of high-resolution EEG potentials related to unilateral internally triggered one-digit movements. EEG Clin Neurophysiol. 1998;106:477–87. doi: 10.1016/s0013-4694(97)00150-8. [DOI] [PubMed] [Google Scholar]
- van Milligen BPh, Hidalgo C, Sanchez E. Nonlinear phenomena and intermittency in plasma turbulence. Phys Rev Lett. 1996;74:395–8. doi: 10.1103/PhysRevLett.74.395. [DOI] [PubMed] [Google Scholar]
- Varela F, Lachaux JP, Rodriguez E, Martinerie J. The Brainweb: phase synchronization and large-scale integration. Nat Rev Neurosci. 1999;2:229–39. doi: 10.1038/35067550. [DOI] [PubMed] [Google Scholar]
- Vialatte FB, Dauwels J, Maurice M, Yamaguchi Y, Cichocki A. On the synchrony of steady state visual evoked potentials and oscillatory burst events. Cognitive Neurodyn. 2009;3:251–61. doi: 10.1007/s11571-009-9082-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walter DO. The method of complex demodulation. Electroencephalogr Clin Neurophysiol. 1968;27(Suppl):53–7. [PubMed] [Google Scholar]
- Weiner N. The theory of prediction. In: Brackenbach E, editor. Modern mathematics for engineers. Chapter 8 New York: McGraw-Hill; 1956. [Google Scholar]
- Winter WR, Nunez PL, Ding J, Srinivasan R. Comparison of the effect of volume conduction on EEG coherence with the effect of field spread on MEG coherence. Stat Med. 2007;26:3946–57. doi: 10.1002/sim.2978. [DOI] [PubMed] [Google Scholar]
- Xu JW, Bakardian H, Cichocki A, Principe JC. A new nonlinear similarity measure for multichannel signals. Neural Netw. 2008;21:222–31. doi: 10.1016/j.neunet.2007.12.039. [DOI] [PubMed] [Google Scholar]
- Zhao C, Zheng C, Zhao M, Tu Y, Liu J. Multivariate autoregressive models and kernel learning algorithms for classifying driving mental fatigue based on electroencephalographic. Expert Syst Appl. 2011;38:1859–65. [Google Scholar]
- Zygmund A. Trigonometric series. 2nd. Cambridge, UK: Cambridge Univ. Press; 1988. [Google Scholar]


