Biphasic Finite Element Modeling Reconciles Mechanical Properties of Tissue-Engineered Cartilage Constructs Across Testing Platforms

Abstract

Cartilage tissue engineering is emerging as a promising treatment for osteoarthritis, and the field has progressed toward utilizing large animal models for proof of concept and preclinical studies. Mechanical testing of the regenerative tissue is an essential outcome for functional evaluation. However, testing modalities and constitutive frameworks used to evaluate in vitro grown samples differ substantially from those used to evaluate in vivo derived samples. To address this, we developed finite element (FE) models (using FEBio) of unconfined compression and indentation testing, modalities commonly used for such samples. We determined the model sensitivity to tissue radius and subchondral bone modulus, as well as its ability to estimate material parameters using the built-in parameter optimization tool in FEBio. We then sequentially tested agarose gels of 4%, 6%, 8%, and 10% weight/weight using a custom indentation platform, followed by unconfined compression. Similarly, we evaluated the ability of the model to generate material parameters for living constructs by evaluating engineered cartilage. Juvenile bovine mesenchymal stem cells were seeded (2 × 10⁷ cells/mL) in 1% weight/volume hyaluronic acid hydrogels and cultured in a chondrogenic medium for 3, 6, and 9 weeks. Samples were planed and tested sequentially in indentation and unconfined compression. The model successfully completed parameter optimization routines for each testing modality for both acellular and cell-based constructs. Traditional outcome measures and the FE-derived outcomes showed significant changes in material properties during the maturation of engineered cartilage tissue, capturing dynamic changes in functional tissue mechanics. These outcomes were significantly correlated with one another, establishing this FE modeling approach as a singular method for the evaluation of functional engineered and native tissue regeneration, both in vitro and in vivo.

Introduction

Articular cartilage is a hydrated, load bearing, and specialized tissue with unique biomechanical properties. Cartilage consists of a dense extracellular matrix of proteoglycans and collagen in a zonal structure. Disruption of this structure can lead to a degenerative catabolic cascade and loss of structural components, which ultimately reduces its mechanical function and precipitates cartilage erosion. Given the lack of intrinsic cartilage healing and limitations of current clinical treatments, tissue engineering has emerged as a viable strategy to restore tissue function. Combinations of various scaffolds and cell types have been used to generate engineered tissue analogues in vitro, which can match the mechanical properties and biochemical composition of the native tissue.¹

With the maturation of the field of cartilage tissue engineering, focus has now turned to evaluating potential therapies in large animal models^2–5 and human clinical trials.^6–8 As these translational studies move forward, it is essential to fully evaluate mechanical outcomes in addition to other functional attributes of the regenerate tissue.⁹ However, standard mechanical assessment methods for in vivo and in vitro studies generally do not use a common experimental framework, making comparisons across studies problematic. For example, most in vitro studies, evaluating both engineered and native tissue samples, employ samples that are formed (or sectioned) into predefined and regular geometries, making assessment relatively straightforward using well-defined testing approaches, such as unconfined and confined compression.^10,11 Conversely, native articular surfaces feature complex geometries and curvatures that change as a function of location. As such, indentation-type testing has been more commonly used to evaluate mechanics for in situ and in vivo samples.^10,12–16 An added benefit of indentation testing is that it generally preserves tissue structure, such that subsequent analysis of intact regenerate tissue by histology and other measures can be accomplished.

In addition to the type of sample, the type of analysis is also important. Articular cartilage exhibits both tension-compression nonlinearity as well as time-dependent viscoelastic (e.g., creep and stress relaxation) behaviors.^11,17,18 As such, it is important to measure both the equilibrium and time-dependent behavior of the tissue under loading and fit this behavior to relevant mechanical models to extract parameters that capture this time-dependent response, which are comparable across studies. Various constitutive models have been used to capture this behavior during confined, unconfined, and indentation testing, with cartilage modeled mathematically as a linear elastic,^11,12 linear biphasic,^10,13 and triphasic^19,20 material. A number of analytical solutions exist for these loading scenarios and, more recently, finite element (FE) methods have been developed to extend these analyses to samples of nonuniform geometries. These FE models have implemented constitutive frameworks, including cartilage as a poroelastic fiber-reinforced solid, consisting of a solid matrix phase with independent fiber reinforcement and a fluid phase.^15,21,22 Such models enable simulations of loading under complex geometries and boundary conditions, variations in constitutive model parameters, loading methods, and rates, for which closed form solutions are not possible.

Not only can FE models be used to predict mechanical response in unusual configurations, but also the same approach can be used to extract material properties through iterative optimization processes against experimental data. For instance, Athanasiou et al. modeled cartilage as a linear biphasic material and optimized the material constants to fit creep data from indentation tests.²³ DiSilvestro and Suh modeled bovine cartilage plugs as a biphasic poroviscoelastic material and curve fit six parameters to unconfined compression stress-relaxation data using a global optimization method.²⁴ Similarly, Olberding and Suh used indentation creep and stress-relaxation data to optimize the six material parameters for agarose gels.²⁵ Cao et al., performed microindentation on mouse cartilage and modeled it as an isotropic linear elastic biphasic material, using a differential evolution method to curve fit the three material parameters to a creep test.²⁶ Lei and Szeri developed a MATLAB and ABAQUS coupled method of optimizing biphasic poroelastic fiber-reinforced material constants from experimental data.²⁷ Keenan et al. developed a method to optimize biphasic material parameters, using the Cartilage Interpolant Response Surface, a look-up table over a small range of material parameters for creep indentation tests.²⁸ Finally, Seifzadeh et al. extended inverse FE analysis to 14 material parameters of a nonlinear fiber-reinforced biphasic poroviscoelastic constitutive model.²⁹ Recently, Chen et al., used FEBio to determine biphasic fiber-reinforced material parameters of cartilage under a creep load.³⁰

While the above technologies represent advanced approaches developed by leaders in the modeling field, few are readily accessible to the general research community, and this may underlie the paucity of mechanical data reported in large animal studies of cartilage repair. To address this, Weiss, Ateshian, and colleagues recently developed an NIH-sponsored freeware, FEBio, with a particular focus on use in soft tissue modeling.³¹ This shared resource contains an embedded recursive optimization algorithm that can be used as a low-cost method to solve inverse FE problems relevant to cartilage mechanics and engineered or regenerating cartilage tissues. Given that native tissue is quite complex and engineered and regenerate tissue are commonly evaluated using a variety of different testing modalities and constitutive frameworks, the objective of this study was to develop an FE analysis method to reconcile outputted parameters from the different testing modalities commonly employed in in vitro and large animal studies. To do so, we carried out paired analysis of biomaterials and in vitro-engineered cartilage using an indentation testing platform and conventional unconfined compression testing, and built FEBio models of both tests to reconcile mechanical parameters across testing platforms. Our findings provide a framework for comparison across testing methods and illustrate the applicability of the FEBio-based modeling approach to standardize reporting of mechanical outcomes for both in vitro and in vivo studies of cartilage regeneration.

Materials and Methods

Acellular hydrogels, native cartilage, and engineered mesenchymal stem cell-based cartilage specimens

Several different classes of materials were analyzed in this work, including acellular hydrogels, native articular cartilage, and engineered constructs at varying levels of maturation. Agarose hydrogels (Type VII Low Gelling Temperature; Sigma-Aldrich, St. Louis, MO) were used as homogenous starting materials for initial tests. Formulations included weight percentages of 4%, 6%, 8%, and 10% to span the wide range of equilibrium and dynamic mechanical properties found in native and engineered tissues.³² Gels were cast between plates separated by 2.25 mm spacers and individual cylindrical samples removed using a 4 mm diameter biopsy punch. In addition, osteochondral and chondral samples were harvested from the tibial plateau of juvenile cows (1–6 months; Research 87, Boylston, MA) using a reciprocating saw and a 4 mm biopsy punch, respectively. Porcine osteochondral segments were also harvested for mechanical testing from an unrelated in vivo study. These porcine osteochondral units (measuring ∼1 × 1 cm²) were isolated (by reciprocating saw) from the trochlear grooves of 18-month-old Yucatan minipigs, whose other hind limb was used in an unrelated study. Samples were acquired immediately after euthanasia. A total of six porcine samples were analyzed by indentation. As is detailed below for mechanical testing, osteochondral samples were potted in a mold using PMMA, which was subsequently filled with phosphate-buffered saline (PBS) containing protease inhibitors to maintain hydration during testing.

To explore the developing mechanics of engineered constructs, two studies were performed sequentially using mesenchymal stem cell (MSC)-based constructs. In each study, MSCs from a single bovine source were isolated and expanded through passage 2 (as in Ref.³³), trypsinized, and seeded at a density of 2 × 10⁷ cells/mL in 1% weight/volume methacrylated hyaluronic acid hydrogels.^34,35 Constructs of 4 mm in diameter were taken using a biopsy punch and cultured in a chemically defined chondrogenic medium³³ for 3, 6, and 9 weeks. At each time point, constructs were planed using a freezing-stage microtome, followed by mechanical testing (described in the next section “Mechanical testing by indentation and unconfined compression”) and determination of biochemical composition (Study 1, n = 4; Study 2, n = 6). Additional samples from each study were fixed in 4% paraformaldehyde, paraffin, processed, sectioned onto glass slides, and stained with Alcian blue (proteoglycans) or Picrosirius red (collagens). Further results and analysis refer to the combined data set from the two studies (n = 10), with results from each individual set shown in the Supplementary Figures S1–S3 (Supplementary Data are available online at www.liebertpub.com/tea).

Mechanical testing by indentation and unconfined compression

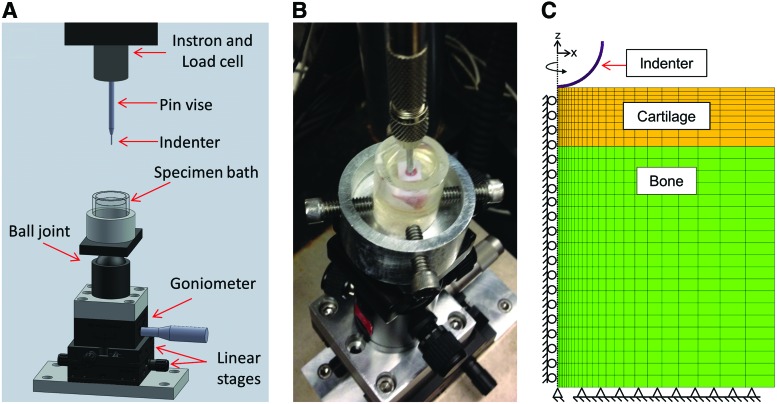
A custom indentation testing rig was fabricated (Fig. 1A) that permitted perpendicular alignment of the sample surfaces with the indenter. Displacement of the indenter was controlled using an Instron 5848 electromechanical testing system (Instron, Norwood, MA) (Fig. 1B). The indentation holding fixture consisted of a ball joint (Oben, New York, NY) and two linear stages (M-433; Newport, Irvine, CA) for gross adjustment and a goniometer (GON65-U; Newport) to allow fine control of the test specimen alignment. Samples lacking subchondral bone were placed at the bottom of a custom bath. Samples with subchondral bone were potted in poly(methyl methacrylate) (Ortho Jet; Lang Dental Manufacturing Company Incorporated, Wheeling, IL) and secured within the bath using set screws. Indentation was applied through an impermeable stainless steel 2 mm spherical indenter fixed in a pin vise (McMaster-Carr, Elmhurst, IL) in series with a 5 N load cell. Samples were immersed in a PBS bath that included protease inhibitors (Roche, Basel, Switzerland). For hydrogels and engineered constructs, the sample height was measured with digital calipers before testing. For osteochondral samples, cartilage thickness at the location of indentation was estimated by measuring the cartilage thickness at each exposed edge. Test locations were marked and samples were stained in Lugol's solution (5% I₂, 10% KI in water) overnight followed by μCT scanning (45 kV, 114 μA, vivaCT40; Scanco USA, Wayne, PA) postindentation to determine the actual cartilage thickness.

FIG. 1.

(A) Schematic of indentation testing setup. (B) Indentation test of a 4 mm diameter artificial chondral defect repaired with a hydrogel. (C) Front view of the 5° quasi-axisymmetric FEBio model of an indentation test. Color images available online at www.liebertpub.com/tea

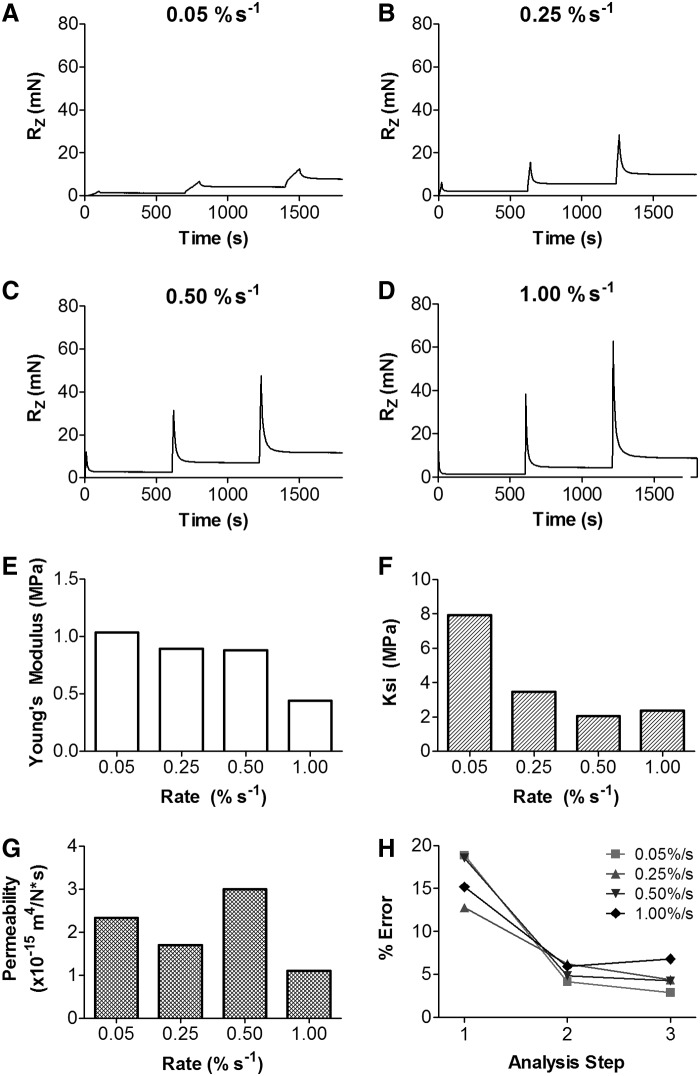
To determine the optimal indentation testing protocol, a series of tests were performed on juvenile bovine osteochondral samples. Three consecutive 5% strain stress-relaxation tests were performed with 2 mm spherical impermeable indenters at loading rates of 0.05%, 0.25%, 0.5%, and 1.0% strain/s with a 600 s relaxation period between each step. FE parameter optimization was performed (as described in the next section “Finite element model”). Young's modulus (E_Y), ksi (a term for fiber modulus), and permeability were output at each loading rate. In addition, parameter optimization was performed individually on each of the three consecutive stress-relaxation tests. Percent error was calculated by dividing the absolute difference between the loads from curve fit and experimental reaction curves by the experimental load.

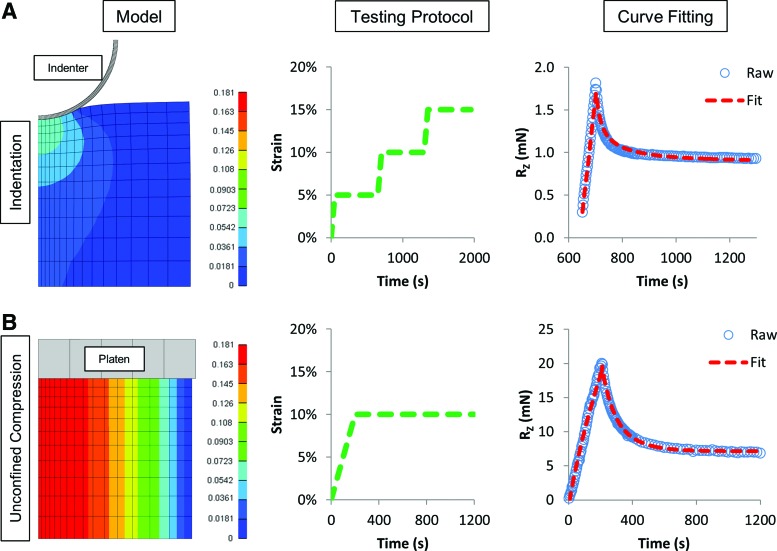
Based on the above, the final indentation protocol consisted of three consecutive stress-relaxation tests (compressive ramps spanning 0–5%, 5–10%, and 10–15% strain applied at a rate of 0.1%/s, with 600 s relaxation periods between each ramp, Fig. 2). Extension and load data were collected at a frequency of 10 Hz. Samples that were paired with unconfined compression tests were reequilibrated for 30 min in PBS with protease inhibitors before the next test.

FIG. 2.

(Left) FEBio model of (A) indentation and (B) unconfined compression tests showing peak fluid pressure distribution, (center) experimental testing protocols, and (right) representative curve fit of experimental data (second step shown for indentation test). Color images available online at www.liebertpub.com/tea

The unconfined compression testing protocol consisted of creep, stress-relaxation, and dynamic tests as previously described.³³ Briefly, a creep load of 0.02 N was applied at a velocity of 10 μm/s and held for 300 s. This was followed by a 10% compressive ramp at a rate of 0.05% strain/s followed by a 1000 s relaxation hold to equilibrium. Finally, a sinusoidal dynamic test was conducted at ±1% strain for 10 cycles at 1 Hz. Equilibrium modulus was calculated by dividing the equilibrium load at the end of the 1000 s hold by the measured cross-sectional area and applied strain. Dynamic modulus was calculated by performing a linear regression between stress and strain at 1 Hz and taking the slope of the resulting line.

Finite element model

Quasi-axisymmetric FE models of both the indentation and unconfined compression tests were created and solved in FEBio (version 1.8, www.febio.org).³¹ Samples for both tests were modeled as a 5° wedge of an idealized geometry (cylindrical disk). First, the wedge was modeled in SolidWorks (Dassault Systemes, Waltham, MA) and then imported into Trelis (version 15.1.3; Computation Simulation Software LLC, American Fork, UT) for mesh generation. Hexagonal elements were generated (n = 319–790) and imported to the FEBio suite to create the FE model. Axisymmetric boundary conditions were applied; displacement along the central axis was constrained to the z-direction, displacement across the front face of the wedge was barred in the y-direction, and displacement across the back face of the wedge was constrained by tension-compression contact with a coplanar rigid body (Fig. 1C).

All materials in the model were defined as poroelastic, consisting of an isotropic neo-Hookean solid phase with an isotropic fiber distribution; by definition, this fiber fraction only contributes in tension. The materials were modeled as having a constant (strain independent) permeability as an approximation of the average permeability across modeled strains.³⁶ Both the indenter and loading platen were modeled as impermeable rigid bodies. FEBio curve fitting was performed using the built-in Levenberg-Marquardt algorithm, a nonlinear least-squares minimization of the objective function (source code available at: http://febiodoc.sci.utah.edu/doxygen/). Experimental deformation data was loaded into the FEBio model to simulate the test. Next, a custom MATLAB program were used to implement the FEBio optimization algorithm, with measured load scaled 5/360 to account for the 5° wedge that was modeled. The optimization routine curve fit Young's modulus, ksi, and permeability between defined bounds. The upper and lower bounds were set plus and minus one order of magnitude from the initial guess and kept constant for each data set. Poisson's ratio was fixed at 0.4, and the solid volume fraction was set at 0.2. The unconfined stress-relaxation test was curve fit from the full data set; for indentation, the second step (5–10% strain) of stress-relaxation was curve fit (Fig. 2).

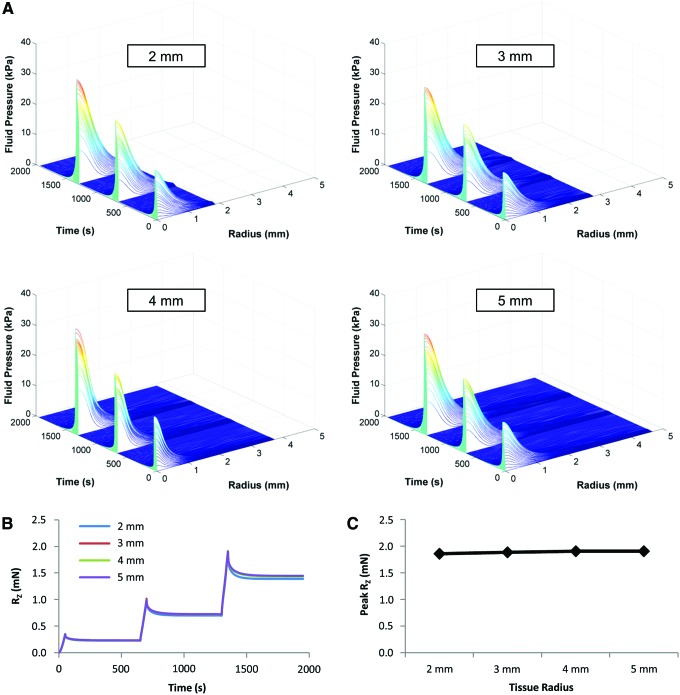
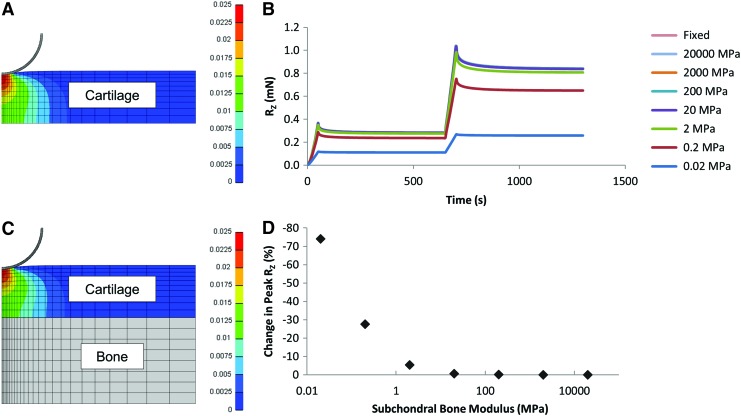
Sensitivity analyses were performed to determine the effect of tissue radius and subchondral bone modulus on the model outputs. Fluid pressure in the model was tracked as a dynamic outcome. In this study, the impact of relative tissue diameter was evaluated by fashioning models with sample radii of 2, 3, 4, and 5 mm, and visualizing the resulting fluid pressure profiles as a function of distance from the center of the tissue and time. To assess the role of the subchondral bone, a series of models were solved with the subchondral bone stiffness ranging from subphysiologic (20 kPa) to supraphysiologic (20 GPa). An infinitely stiff subchondral bone was simulated by creating a fixed displacement boundary condition.

Statistical analysis

FEBio optimization parameters were compared by two-way analysis of variance (ANOVA) with Bonferroni post hoc tests, with culture duration and loading method or gel type and loading method as independent variables. Equilibrium modulus, dynamic modulus, and the Hertz modulus were compared over time using one-way ANOVA with Bonferroni post hoc test. Linear regression was used to determine the relationship between each of the output parameters for the two different testing modalities and a Pearson correlation was performed to determine the statistical significance of the relationship between the two, p < 0.05 was considered significant. To test whether the linear regression outcomes were significantly different, a sum-of-squares F-test was used.

Results

Finite element model sensitivity

After developing an FE indentation model, we first varied several features of the model to help determine the best experimental framework to employ. Waterfall plots showed little difference in the fluid pressure profile (Fig. 3A) as a function of sample radius. The fluid pressure dissipated within 1.25 mm of the center of the tissue during the first stress-relaxation step, while the fluid pressure dissipated within 1.5 and 2 mm on the second and third steps, respectively. The normal reaction force (R_Z) also showed similar responses, with a slightly lower force response with the 2 mm radius tissue on the third step (Fig. 3B). The peak R_Z was stable across sample radii, with a slight decrease at 2 mm (Fig. 3C). None of the three parameters (fluid pressure, R_Z, and peak R_Z) differed at 3 mm or larger radius, indicating that it is not necessary to model any radius greater than 3 mm.

FIG. 3.

Sensitivity analysis for an FE model of indentation of a cartilage disk with height of 1 mm and radii of 2, 3, 4, or 5 mm using a spherical indenter with diameter of 2 mm at a rate of 0.1%/s. (A) Fluid pressure as a function of time and distance from the center as the radius of tissue increases from 2 to 5 mm. (B) Reaction force (R_Z) for 2 through 5 mm radius cartilage cylinders over three stress-relaxation steps. Note the near-identical force response at 2, 3, 4, and 5 mm radii. (C) Peak reaction force of the model as a function of sample radius. FE, finite element. Color images available online at www.liebertpub.com/tea

Assessing the role of subchondral bone, the normal reaction force (Fig. 4B) and percent change in peak reaction force relative to fixed displacement were examined. Results from this analysis showed that the fluid pressure distribution in the cartilage was similar with and without subchondral bone affixed (Fig. 4A, C). The normal reaction force increased as the bone modulus increased (Fig. 4B), with large differences in soft bone (<20 MPa) and much less pronounced changes with stiff bone (>20 MPa) (Fig. 4B). The peak R_Z decreased by 74% in the softest bone, but was less than 0.65% different for all bone moduli 20 MPa and above (Fig. 4D). These findings suggest that soft or remodeling subchondral bone would be expected to have the greatest effect on the FE model and interpretation of experimental data.

FIG. 4.

Peak fluid pressure distribution for (A) an osteochondral sample without bone and (B) an osteochondral sample with subchondral bone modeled. (C) Reaction force (R_Z) during two steps of stress relaxation indentation as a function subchondral bone moduli. (D) Change in peak reaction force for a range of subchondral bone moduli. Color images available online at www.liebertpub.com/tea

Indentation protocol

To determine appropriate methods for generating and fitting experimental data sets, load versus deformation data for a series of indentation stress relaxation tests of juvenile bovine osteochondral segments were acquired. The same sample was subjected to multiple indentation stress-relaxation tests (three ramps per test) at varying rates of applied strain (0.05%/s, 0.25%/s, 0.5%/s, and 1.0%/s) to determine the impact of indentation rate on the force–response curve and the optimized constitutive parameters derived from the test. Increasing the rate of indentation resulted in an increase in the linearity of the reaction force from 0.05%/s to 1.0%/s. In addition, the peak force at each step increased with increasing loading rate (Fig. 5A–D). FEBio optimization of these experimental data sets showed the curve-fit Young's modulus was stable as the rate increased until 1.00%/s, where there was a decrease (Fig. 5E). Ksi was stable from 0.25%/s to 1%/s, but fit to a higher value at the slowest rate, 0.05%/s (Fig. 5F). Permeability was the most variable parameter, with no clear dependence on the rate of indentation (Fig. 5G). Comparing between each of the three steps of stress-relaxation showed that fitting only to the first step resulted in a high error, while fitting to the second or third step resulted in the lowest amount of error (∼1/3 of the first step, Fig. 5E). Based on these data, we chose a final protocol using a loading rate of 0.1%/s and to fit data from the second (5–10% strain) step of the stress-relaxation indentation test.

FIG. 5.

Experimental reaction force (R_Z) from indentation testing of a 4 mm diameter chondral plug from the trochlear groove of a juvenile bovine knee. Indentation tests were performed at rates of (A) 0.05%/s, (B) 0.25%/s, (C) 0.50%/s, and (D) 1.00%/s on the same sample. Results from the FEBio parameter optimization at each loading rate showed that (E) the estimated Young's modulus was lower for fits to experimental data acquired at 1.00%/s, while (F) the value of ksi increased for fits to data acquired at 0.05%/s. The permeability (G) was the most variable parameter. (H) Calculation of % error showed that error was reduced when optimizations were performed on the second or third step of the indentation test.

In vivo tissue, acellular hydrogels, and in vitro growth of MSC-based constructs

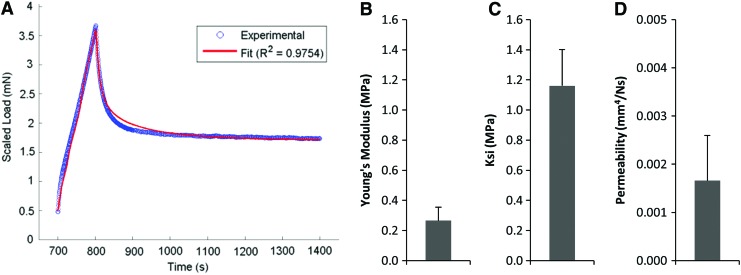
Having established a testing framework, we next tested native porcine osteochondral segments taken from an unrelated in vivo translational study. These control samples were taken from the trochlear grooves of unoperated limbs and were tested using indentation and modeled, and FEBio parameter optimization was successfully performed. We achieved good curve fits (Fig. 6A) and outcomes of Young's modulus (Fig. 6B), ksi (Fig. 6C), and permeability (Fig. 6D) that were consistent with literature values. Next, materials used for tissue engineering as well living tissue engineered constructs that were maturing with time in culture were assessed in both unconfined compression and paired indentation testing. Traditional outcomes were evaluated and FEBio constitutive model optimization yielded values for the Young's modulus (E_Y), ksi, and the permeability for each material group and time point, and for each testing modality. These were compared by Pearson correlation to determine if there was a relationship between parameters derived from the two distinct testing modalities.

FIG. 6.

(A) Example curve fit from native porcine samples and the (B) Young's modulus, (C) ksi, and (D) permeability of those samples (n = 6) outputted from the model. Color images available online at www.liebertpub.com/tea

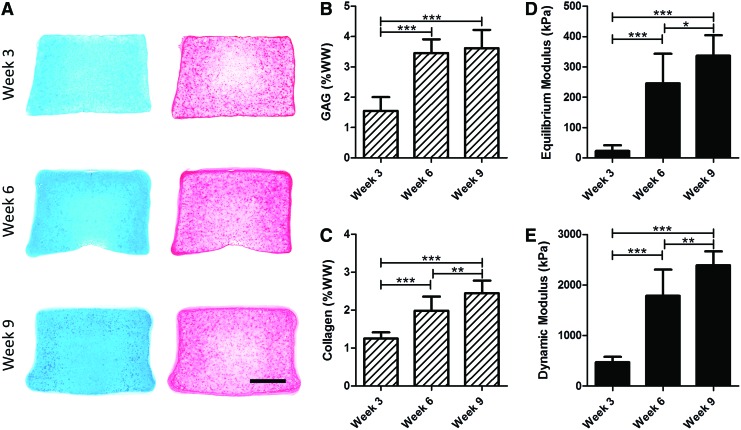
For traditional outcomes of the MSC-seeded constructs, histological analysis showed a time-dependent increase in proteoglycan and collagen deposition (Fig. 7A). Quantification showed significant increases in glycosaminoglycan (GAG) between weeks 3 and 6 and weeks 3 and 9 (p < 0.001, Fig. 7B) and collagen content at each time point (p < 0.01, Fig. 7B, C). Traditionally reported mechanical properties derived from unconfined compression, including the equilibrium (p < 0.05, Fig. 7D) and dynamic modulus (p < 0.01, Fig. 7E), also increased at each time point.

FIG. 7.

Maturation of engineered cartilage grown in vitro for up to 9 weeks. (A) Histological analysis (Alcian blue [left] and Picrosirius red [right]) as a function of time in culture (scale bar = 1 mm). (B) GAG and (C) collagen content as well as (D) equilibrium and dynamic modulus (E) derived from unconfined compression testing increased with duration of culture (*p < 0.05; **p < 0.01; ***p < 0.001; n = 10). Scatter plots showing the two individual studies are provided in Supplementary Figure S1. GAG, glycosaminoglycan. Color images available online at www.liebertpub.com/tea

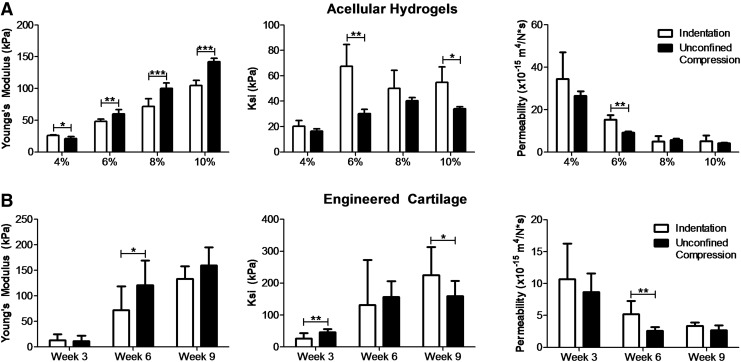
For acellular agarose hydrogels, results from FE parameter optimization showed an increasing Young's modulus (Fig. 8A, left) and decreasing permeability (Fig. 8A, right) with increasing gel concentration, as expected.^32,37 FEBio model parameter estimation of the MSC-seeded engineered cartilage constructs during maturation likewise showed an increase in Young's modulus and ksi (Fig. 8B left, 8B center) from week 3 to weeks 6 and 9 for both the indentation (p < 0.01) and unconfined compression models (p < 0.001), while the permeability decreased with time (Fig. 8B right, p < 0.001).

FIG. 8.

Mechanical properties as determined from FE parameter optimization of indentation testing (white bars) and unconfined compression (black bars). Young's modulus, ksi, and permeability were computed for paired testing of (A) acellular agarose hydrogels of 4%, 6%, 8%, and 10% weight/weight (n = 6) and (B) engineered cartilage constructs grown in vitro for 3, 6, and 9 weeks (n = 10). *p < 0.05; **p < 0.01; ***p < 0.001. Scatter plots for agarose hydrogels are shown in Supplementary Figure S2 and scatter plots showing the two individual engineered cartilage studies are shown in Supplementary Figure S3.

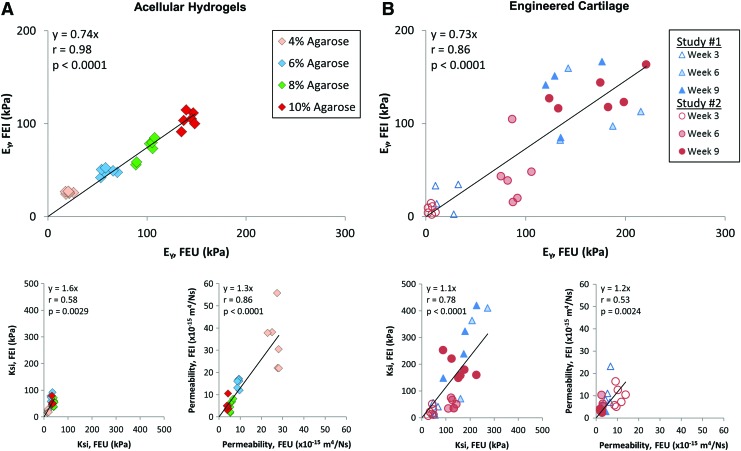
When comparing acellular agarose hydrogels across testing modalities (Fig. 9A), the Young's modulus had the highest correlation (slope = 0.74, r = 0.98, p < 0.0001). Ksi was more variable for these agarose hydrogels (slope = 1.6, r = 0.58, p = 0.0029), while permeability showed a lower correlation coefficient than for the Young's modulus (slope = 1.3, r = 0.86, p < 0.0001). Similarly, when comparing engineered cartilage across the two different testing modalities, the FEBio-extracted parameters showed the same trends in material properties (Fig. 9B). Specifically, there was a strong correlation between the Young's modulus extracted from each testing modalities (slope = 0.73, r = 0.86, p < 0.0001). The parameters ksi and permeability showed more variability, but both significantly correlated between testing modalities (ksi: slope = 1.1, r = 0.78, p < 0.0001; permeability: slope = 1.2, r = 0.53, p = 0.0024). Comparing the engineered cartilage linear regression slope to that of the agarose hydrogels showed that there was no significant difference in slope for any of the three outcome parameters (E_Y, p = 0.83; ksi, p = 0.31; permeability, p = 0.48).

FIG. 9.

FEBio optimization results from unconfined compression (FEU) versus results from indentation testing (FEI) on paired (A) acellular agarose hydrogels and (B) engineered cartilage constructs after varying periods of in vitro culture. Constitutive model parameters for Young's modulus (E_Y), ksi, and permeability significantly correlated between the two testing modalities, although greater variation was observed in the living engineered constructs. The regression lines between sample types were not significantly different. Color images available online at www.liebertpub.com/tea

Discussion

In this study, we developed FE models of indentation and extracted biphasic material properties through an inverse FE analysis approach using the freeware FEBio. In formulating this indentation testing and modeling methodology, we evaluated the model sensitivity to various boundary parameters, namely the radius of the tissue being tested and the underlying subchondral bone stiffness. Analysis of the impact of tissue radius suggested that, above a threshold of 3 mm, larger sample radius would not influence the overall results. This is consistent with previous reports, which showed that the change in tissue response is negligible when the tissue radius or height is four times greater than the radius of the indenter.¹⁵ This finding allows the localized determination of material properties and increased computational efficiency, since fewer elements are required in the model. Another key finding of the sensitivity analysis was with respect to the effect of subchondral bone modulus on the reaction force of an indented osteochondral sample. For soft or remodeling bone with a low Young's modulus (<20 MPa), the predicted reaction force decreased substantially. This finding suggests that, in such a context, testing would not provide an accurate representation of the cartilage surface layer, but rather would reflect the properties of both the cartilage and bone components together. Given that subchondral remodeling is a feature of many in vivo cartilage repair studies,² this finding suggests that it is important to consider the state of the subchondral bone in the assessment of cartilage repair.

After establishing a suitable indentation testing protocol, we successfully curve fit experimental data to our FE model. Using the FEBio parameter optimization algorithm, we determined the Young's modulus, ksi, and permeability for in vivo cartilage tissue (a complex inhomogeneous biological material), agarose hydrogels (a homogeneous acellular material), and in vitro matured engineered cartilage (an inhomogeneous biological material). Each of these materials has a different structure and therefore different mechanical response to indentation. Our model was able to capture the response of each of these three materials, which demonstrates the robustness and versatility of this approach. This tool allows for a large range of material to be analyzed using a singular framework, enabling comparisons to be made across material types.

In addition to indentation tests, we also modeled more traditional mechanical assays used in cartilage tissue engineering, namely the unconfined compression test, to reconcile commonly reported parameters in one constitutive framework. By paired analysis and modeling, we demonstrated the capacity of these FE models to accurately output constitutive parameters for both agarose hydrogels and engineered cartilage constructs grown in vitro. Although these mechanical testing methods have very different boundary conditions, we found a significant correlation between constitutive model outcome parameters derived from the different testing methods, across a range of material compositions and in vitro maturation states. Indeed, the model captured the stress-relaxation behavior of acellular and cellular materials well and resulted in good parameter optimization fits. We found that the Young's modulus had the strongest correlation between the two testing configurations. Interestingly, however, the slope of the correlation between these tests was not equal to one. This is likely due to the differences between testing methods and not error from the model. While unconfined compression engages the entire width of the sample, indentation is a localized test and engages a smaller part of the sample, where heterogeneities are known to arise, particularly at edges.³⁸

Our findings provide a framework for comparing data derived from in vitro testing in unconfined compression and in vivo testing by indentation. Unifying analyses of different mechanical tests allows for evaluation of tissue engineering strategies in all stages of development. Specifically, it enables comparisons of the noninvasive mechanical tests used in vivo to datasets collected previously, using other testing modalities. For example, if a construct is implanted in a cartilage defect and evaluated using indentation and the FE model, the outcomes can be directly compared to the in vitro maturation of a similar construct. In this way, one can place reparative outcomes in the context of both normal and engineered tissues to evaluate their function in vivo. This should accelerate the pace of discovery in the area of in vivo cartilage tissue engineering efforts and provides a framework for a more rigorous and standardized reporting of mechanical outcomes in these translational studies. In addition, these testing approaches may be incorporated into devices that operate in an arthroscopic manner, enabling more rigorous evaluation of repair progress during second-look arthroscopy procedures following cartilage repair.

Acknowledgments

This work was supported by the AO Collaborative Research Program Acute Cartilage Injury (ACI) Consortium. Additional funding was provided by the Penn Center for Musculoskeletal Disorders (P30 AR050950), the National Institutes of Health (R01 EB008722), and the Department of Veterans Affairs (I01 RX001213 and I01 RX000700).

Disclosure Statement

No competing financial interests exist.