First-pass myocardial perfusion MRI with reduced subendocardial dark-rim artifact using optimized Cartesian sampling

Abstract

PURPOSE

The presence of subendocardial dark-rim artifact (DRA) remains an ongoing challenge in first-pass perfusion (FPP) cardiac MRI. We propose a free-breathing FPP imaging scheme that is optimized to minimize the DRA and readily enables instantaneous image reconstruction.

MATERIALS AND METHODS

The proposed method suppresses Gibbs ringing effects — a major underlying factor for the DRA — by “shaping” the underlying point spread function through a two-step process: (i) an undersampled Cartesian sampling scheme that widens the k-space coverage compared to the conventional scheme; and (ii) a modified parallel-imaging scheme that incorporates optimized apodization (k-space data filtering) to suppress Gibbs-ringing effects. Healthy volunteer studies (n=10) were performed to compare the proposed method against the conventional Cartesian technique – both using a saturation-recovery gradient echo sequence at 3T. Furthermore, FPP imaging studies using the proposed method were performed in infarcted canines (n=3), and in two symptomatic patients with suspected coronary microvascular dysfunction for assessment of myocardial hypoperfusion.

RESULTS

Width of the DRA and the number of DRA-affected myocardial segments were significantly reduced in the proposed method compared to the conventional approach (width: 1.3 vs. 2.9 mm, p<0.001; number of segments: 2.6 vs. 8.7; p<0.0001). The number of slices with severe DRA was markedly lower for the proposed method (by 10 fold). The reader-assigned image quality scores were similar (p=0.2) although the quantified myocardial SNR was lower for the proposed method (p<0.05). Animal studies showed that the proposed method can detect subendocardial perfusion defects and patient results were consistent with the gold-standard invasive test.

CONCLUSION

The proposed Cartesian FPP imaging method significantly reduces the prevalence of severe DRAs compared to the conventional approach while maintaining similar spatial/temporal resolution and image quality.

INTRODUCTION

The effectiveness of first-pass perfusion (FPP) imaging using cardiac MRI has been broadly validated for detection of myocardial ischemia.(1–4) However, the presence of subendocardial dark-rim artifact (DRA) remains an ongoing challenge in FPP imaging, limiting the diagnostic performance of this technique in routine clinical practice.(5,6) Specifically, a major advantage of stress myocardial perfusion imaging using MRI over nuclear modalities is its ability to detect hypoperfusion at the subendocardial layer, considered to be the most ischemia-sensitive layer of the myocardium.(7) DRA is a major impediment in this regard since it may obscure true subendocardial defects and/or mimic such defects thereby causing inaccurate diagnosis. This is especially problematic in the case of patients with suspected coronary microvascular dysfunction (CMD) who do not have obstructive coronary disease (>50% epicardial stenosis) yet present with chest pain and are referred for ischemia evaluation using a stress/rest perfusion MRI exam. Furthermore, DRA can lead to errors in semi-quantitative and quantitative analysis, especially in subendocardial regions. Therefore, it is important to eliminate or significantly reduce DRA to increase the diagnostic reliability of FPP imaging.

During the past decade, major efforts have been made towards mitigating DRA. With Cartesian sampling, the so-called “k-t” accelerated methods (k-t BLAST/SENSE/PCA) utilize advanced model-based reconstruction to achieve high spatio-temporal accelerations thereby significantly improving in-plane spatial resolution to reduce DRA.(8–12) The underlying principle is that higher spatial resolution reduces the visual extent and severity of Gibbs ringing,(8) one of the major causes of DRA.(5,8,13) However, unlike conventional vendor-provided schemes that reconstruct each frame independently using parallel-imaging acceleration, “k-t” methods require temporal acceleration and specialized reconstruction software/hardware that are not available across different MRI scanner platforms. Furthermore, established k-t accelerated imaging methods require a breath-hold scan, which can be difficult to achieve especially during vasodilator stress studies.

More recently, non-Cartesian trajectories, specifically spiral and radial sampling, have also been applied to reduce DRA.(14–16) However, these trajectories are not available on most clinical scanners, especially when parallel imaging reconstruction is needed. Despite their promise, lack of integrated online/instantaneous image reconstruction and lack of robustness at 3T (challenge of maintaining k-space trajectory fidelity) have arguably limited the availability of non-Cartesian FPP techniques in routine clinical protocols.

In this work, we propose a modified Cartesian FPP imaging scheme that is capable of reducing the DRA compared to the conventional technique used in routine clinical practice. Compared with k-t-accelerated and/or non-Cartesian FPP imaging schemes, the distinguishing features of our proposed approach are: (a) the ease with which it can be implemented on any modern MRI scanner platform to achieve instantaneous/online image reconstruction, and (b) its inherent robustness to breathing motion.

MATERIALS AND METHODS

Overview of the Proposed Approach

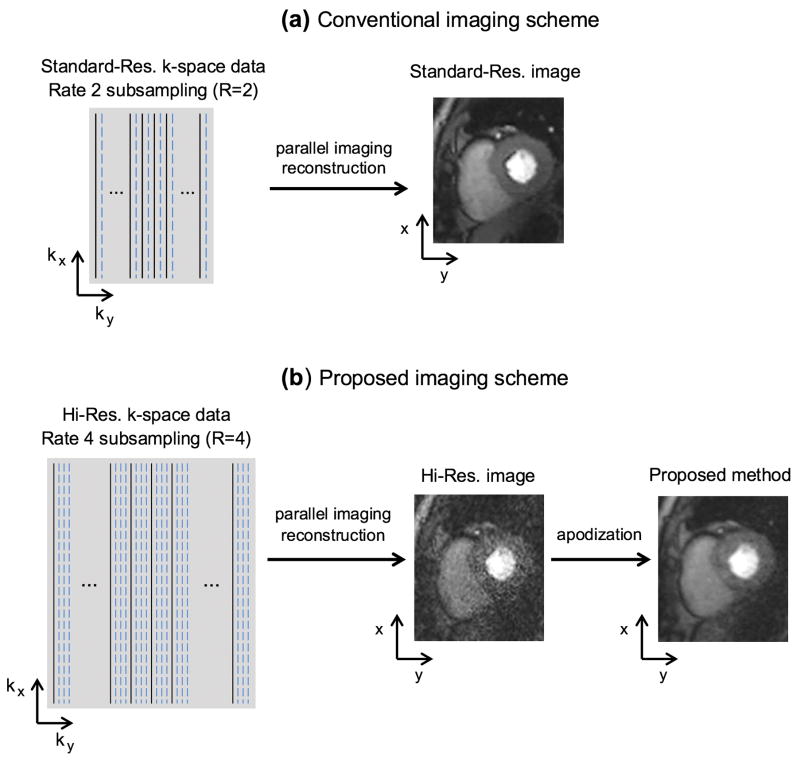
We propose a free-breathing Cartesian FPP imaging scheme that can reduce the DRA while providing similar image quality and equivalent resolution compared to the conventional free-breathing imaging scheme. Figure 1 provides a schematic overview of the conventional Cartesian imaging scheme for each FPP time frame and our proposed scheme, respectively. The conventional method in Fig. 1(a) acquires and reconstructs a standard-resolution (“standard-res”) FPP frame with the widely used 2-fold parallel-imaging rate (R=2 subsampling).

FIGURE 1. Acquisition and reconstruction schemes for the (a) conventional, and (b) proposed Cartesian FPP imaging methods.

(a): The conventional method uses typical k-space coverage (standard-res acquisition with PE resolution > 2.5 mm) and parallel-imaging rate (R=2). (b): For the proposed method, a widened k-space coverage is achieved (hi-res acquisition with PE resolution < 2 mm) using an unconventional parallel-imaging rate (R=4). The proposed method can cover ≈50% wider k-space coverage along the PE direction while having a similar temporal footprint for each FPP frame (thanks to the 2-fold higher subsampling rate). Following parallel-imaging reconstruction, an optimized apodization scheme (k-space data filtering) is applied to suppress Gibbs-ringing (major contributing factor for DRAs). The apodization step reduces the reconstructed resolution back to the standard resolution (similar resolution as the conventional method) but also increases the reconstructed SNR (compensating for the SNR loss caused by R=4 subsampling relative to R=2).

The proposed acquisition scheme (Fig. 1b) suppresses Gibbs ringing effects — a major underlying cause of the DRA (5,6) — through a two-step process: (i) acquisition of a high-resolution (“hi-res”) k-space data matrix, combined with (ii) apodized image reconstruction. Specifically, for each FPP time-frame, a k-space data matrix with markedly higher resolution is acquired covering a wider k-space area compared to the conventional method — in particular achieving ≈50% wider k-space coverage along the phase-encode (PE) direction. In order to maintain a similar acquisition window (“temporal footprint”) as the conventional method, an unconventionally high parallel-imaging rate (R=4 subsampling) is used. In the second step, following parallel imaging reconstruction, k-space data filtering — herein referred to as “apodization” — is applied to suppress the Gibbs ringing effects and compensate for the loss of signal-to-noise ratio (SNR) in the first step. The apodization scheme is optimized to maintain the same reconstructed resolution as the conventional approach. In essence, the proposed method aims to minimize the Gibbs ringing effects in Cartesian imaging by “shaping” the underlying point spread function (PSF). In the following, these steps will be described theoretically (based on PSF analysis), demonstrated using numerical simulations, and tested in FPP imaging studies.

Optimized Apodization Scheme

In this section, we will use the notion of PSF to describe the properties of a Cartesian imaging scheme in terms of Gibbs ringing, a major contributing factor to the DRA. Our modified Cartesian imaging scheme effectively shapes the underlying PSF by widening the k-space coverage (hi-res acquisition) combined with apodized reconstruction. PSF analysis is a classic tool to evaluate the resolution and artifact level of a data sampling scheme in linear imaging systems.(17) The PSF analysis for a self-calibrated parallel imaging setup (multi-channel acquisition) is similar to a simplified single-channel setup assuming that parallel imaging does not introduce aliasing image artifacts (distortions) in the reconstructed image, which is the case in most practical protocols using GRAPPA (18) or TGRAPPA.(19)

The analytical PSF expression for two-dimensional (2D) Cartesian sampling can be expressed as a 2D periodic “sinc” function, also known as the Dirichlet kernel (17), in the (x, y) image domain:

$$\mathit{PSF}(x,y)=\mathrm{\Delta }{k}_x\mathrm{\Delta }{k}_y\frac{sin(\mathrm{\pi }{\mathrm{N}}_{\text{RO}}\mathrm{\Delta }{k}_{x}x)}{sin(\pi \mathrm{\Delta }{k}_{x}x)}\frac{sin(\pi {\mathrm{N}}_{\text{PE}}\mathrm{\Delta }{k}_{y}y)}{sin(\pi \mathrm{\Delta }{k}_{y}y)}$$ [Eq. 1]

where N_RO and N_PE refer to the number of k-space samples along the readout and PE directions, denoted by k_x and k_y, respectively. The sampling step-sizes in k-space, denoted by Δk_x and Δk_y, are set to be the inverse of the field of view (FOV) size along the corresponding dimension to match the Nyquist sampling criterion.

Apodized image reconstruction, which is equivalent to a “data weighting” scheme in k-space, has been applied to non-Cartesian trajectories such as radial (16,20) and spiral (14,15) to suppress Gibbs ringing artifacts. In this work, a Gaussian kernel (21) is used as the apodization function:

$$A(k_x,k_y)=exp\left(-\pi \frac{{k_x}^2}{{({\mathrm{N}}_{\text{RO}}\mathrm{\Delta }{k}_x)}^2{{\mathrm{\Omega }}_x}^2}\right)exp\left(-\pi \frac{{k_y}^2}{{({\mathrm{N}}_{\text{PE}}\mathrm{\Delta }{k}_y)}^2{{\mathrm{\Omega }}_y}^2}\right)$$ [Eq. 2]

where the pre-defined apodization parameters Ω_x and Ω_y determine the “degree” of apodization along k_x and k_y dimensions, respectively.

The Gaussian apodizer has been shown to provide a near-optimal resolution trade-off (22,23) and is routinely used in nuclear imaging applications. A smaller apodization parameter (Ω_x or Ω_y) corresponds to a stronger apodization effect. In the proposed approach, the k-space data (following parallel imaging reconstruction) is multiplied (in k-space) by this apodization function before the inverse Fourier Transform (Fig. 1b). This operation is equivalent to applying a 2D Gaussian convolution filter in the image domain.

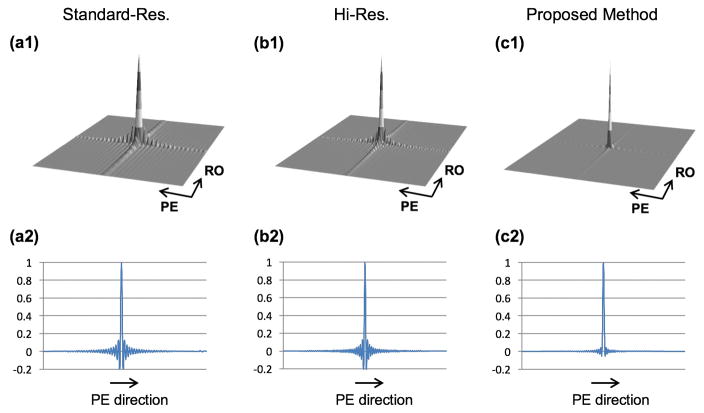
Figure 2 provides a straightforward demonstration of the effect of widening the k-space coverage (hi-res vs. standard-res acquisition) and apodization on the frequency and amplitude of Gibbs ringing oscillations in the PSF, which contribute to the DRA in the reconstructed images. The PSF and a one-dimensional (1D) cut along the PE direction for the following schemes are depicted: conventional (standard-res) in panel (a1–a2), hi-res acquisition with 50% higher resolution (wider coverage of k-space) along PE direction in panel (b1–b2), and the proposed approach (apodized reconstruction of hi-res acquisition) in panel (c1–c2). The plotted PSFs correspond to a k-space matrix size (readout × PE) of 192 × 128 for the standard-res scheme and a matrix size of 256 × 192 for the non-apodized hi-res and proposed schemes. For the PSF in panel (c), the Gaussian apodization function in Eq. 2 with the following parameters was used: Ω_x = 1.5 and Ω_y = 1.3. All PSFs were computed for a rectangular FOV size of 256 × 192 (arbitrary units) using an inverse discrete Fourier transform of the corresponding zero-padded k-space matrix as previously described.(16)

FIGURE 2. Comparison of point spread function (PSF) between conventional Cartesian imaging and the proposed approach.

The top row shows the PSFs and the bottom row is a 1D cut of the corresponding PSF along the phase-encode direction. (a1,a2): Conventional Cartesian imaging with standard-resolution acquisition. (b1,b2): Non-apodized Cartesian imaging with high-resolution acquisition. (c1,c2): Proposed Cartesian imaging approach with high-resolution acquisition (same as in Panel b) and apodized reconstruction (using the Gaussian apodizer in Eq. 2 with Ω_x = 1.5 and Ω_y = 1.3). It is seen that apodization clearly suppresses the side-lobe oscillations, which correspond to Gibbs ringing in the reconstructed images and potentially cause DRAs in FPP imaging. However, apodization also increases the main-lobe width, which corresponds to a uniform reduction in spatial resolution (linear effect) that can be easily and precisely measured by computing the FWHM of the corresponding PSF.

As seen in Fig. 2, increasing the prescribed resolution compresses the Gibbs ringing (higher frequency oscillations), hence reducing the spatial extent of the DRA that may result from these oscillations – although amplitude of the oscillations remains the same. In contrast, it is seen that apodization effectively suppresses the amplitude of the Gibbs oscillations in Fig. 2c (peak negative amplitude = −5.36%, which is 4 times lower than Fig. 2b), hence reducing both spatial extent and severity of the DRA that may result in a FPP imaging scenario.(5,16) It is well known that this gain comes at the price of increased width of the main lobe in apodized PSF, which corresponds to reduced spatial resolution.(24) Based on the classical definition of spatial resolution, effect of apodization on the reconstructed resolution can be quantified using the full-width at half-maximum (FWHM) of the underlying PSF.(17) For instance, in Fig. 2 the FWHM analysis (performed numerically, assuming millimeter units) implies that the resolution for the hi-res PSF in panel (b1–b2) is 1.0 × 1.0 mm² and is reduced to 1.3 × 1.5 mm² for the apodized PSF in panel (c1–c2), which is the same as the standard-res PSF.

Using the same approach, in general it can be shown that decreasing the Ω parameter for the Gaussian apodizer (Eq. 2) along each spatial dimension will increase the apodization effect (filtering strength in image domain), enhancing the level of Gibbs-ringing suppression and reducing the effective resolution along that dimension. The adopted apodization framework allows for retrospective adjustment/optimization of this ringing-suppression versus spatial resolution trade-off. In the proposed method, the choice of the apodization parameters (Ω_x, Ω_y) in Eq. 2 was optimized based on the desired in-plane resolution (pre-determined in the imaging protocol) as follows. The optimization problem is set up to find Ω_x and Ω_y so that the apodized resolution is closest to the desired resolution, that is:

$$\left({\mathrm{\Omega }}_x^{\ast },{\mathrm{\Omega }}_y^{\ast }\right)={\text{argmin}}_{\left({\mathrm{\Omega }}_x,{\mathrm{\Omega }}_y\right)}{\left|R_x\left({\mathrm{\Omega }}_x\right)-R_{x,0}\right|}^2+{\left|R_y\left({\mathrm{\Omega }}_y\right)-R_{y,0}\right|}^2$$ [Eq. 3]

where R_x (Ω_x) and R_y (Ω_y) denote the resolution (measured as FWHM of the corresponding PSF) along readout and PE direction after apodization using the function in Eq. 2, respectively, and R_x,0 and R_y,0 denote the desired resolution along each of the two directions. Since R_x (Ω_x) and R_y (Ω_y) are both monotonic functions, the bisection method (25) can be applied to efficiently solve this optimization problem, resulting in a fast algorithm for selection of the optimal apodization parameters.

Numerical Simulations

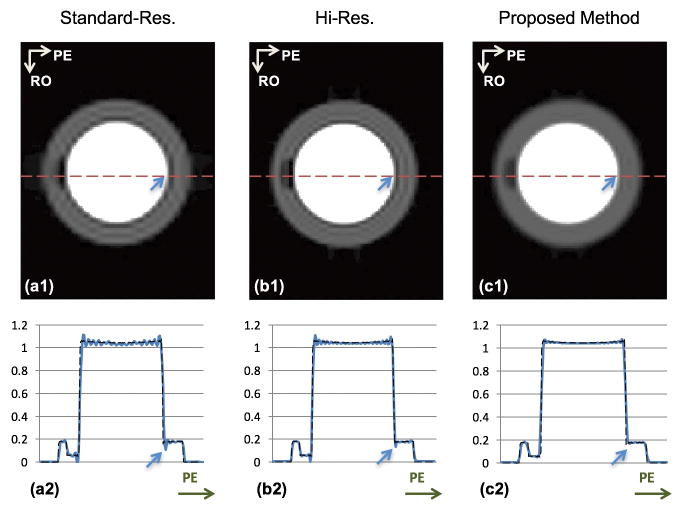
Numerical phantom simulations were conducted to test the effectiveness of the above-described method in reducing DRAs induced by Gibbs-ringing effects. To perform accurate numerical simulations, it is crucial to start from an analytical (continuous) expression of the k-space signal. This is because image discretization (pixel-wise representation) itself modifies the overall PSF, yielding an inaccurate analysis. Therefore, an analytical phantom resembling the FPP imaging scenario was derived. As described in Appendix A, based on a Fourier pair involving the Bessel function of the first kind,(26) the closed-form expression corresponding to the numerical phantom was derived: two overlapping circular disks and a low-intensity elliptical disk were used, resembling the left ventricle (LV) geometry and a perfusion defect, respectively.

Numerical simulations for the following three schemes were performed: the standard-res image (conventional method), non-apodized hi-res image, and the apodized hi-res image (proposed method). The simulations used the same acquisition/apodization parameters as the PSF analysis in Fig. 2 (specifically, 50% wider k-space coverage along PE for the hi-res acquisition). For each simulation scenario, the analytically-generated 2D k-space formula (Appendix A) was sampled on the corresponding discrete k-space Cartesian grid. Parallel imaging (GRAPPA) was incorporated in the simulation. Coil sensitivity maps for a 12-channel array were simulated based on a previously described method.(27) The parallel-imaging rate for the conventional and proposed methods was set to be R=2 and R=4, respectively. To better compare the Gibbs ringing effects (resulting from PSF oscillations), a 1D cut along the PE direction was also generated from a noise-free run of the numerical simulation.

Volunteer Studies

Myocardial perfusion imaging studies in healthy volunteers (n=10; 24±4 years old; 6 females) were performed on a 3T clinical scanner (Magnetom Verio; Siemens Healthcare, Erlangen, Germany). For the volunteer and patient imaging studies, local Institutional Review Board approval and written informed consent was obtained before each exam. A standard 12-channel cardiac-torso coil was used for data acquisition. For each volunteer, two free-breathing FPP scans were performed at rest (scan duration: 50 heartbeats). The first FPP scan was conducted according to our proposed modified Cartesian imaging method and the second FPP scan was acquired with the conventional scheme (time gap in between FPP scans: 12–15 minutes). Both scans used an ECG-gated FLASH pulse sequence with saturation-recovery magnetization preparation during first-pass of intravenous contrast media (0.05 mmol/kg dose of Gadoversetamide/Optimark) followed by a 20 mL saline flush (injection rate: 4 mL/s).

Table 1 summarizes the scan parameters for both the proposed and conventional FPP imaging methods. The conventional protocol was set based on the clinically used protocol at our institution, with the following parameters: in-plane resolution (readout × PE) = 2.2 × 2.7 mm²; FOV size (readout × PE) = 380 × 305 mm²; parallel-imaging rate R=2 using TGRAPPA (19); TR = 2.4 ms; matrix size = 176 × 112; number of acquired PE lines = 56 for each slice resulting in a temporal footprint (acquisition window per R-R interval) = 133 ms; saturation recovery time (TI) = 120 ms; flip angle = 12°; receiver bandwidth = 770 Hz/pixel; 3 contiguous slices acquired per each heart beat with 8 mm thickness, centered around the mid ventricle. For the proposed protocol, we aimed at empirically determining the acquisition parameters so that the acquired “hi-res” k-space data matrix (Fig. 1b) would provide at least 50% wider coverage along PE (on the basis of the above-described PSF analysis) and 25% wider coverage along readout – while maintaining a similar temporal footprint as the conventional method. Using the same FOV size as the conventional method, size of the hi-res k-space matrix was set to be 224 × 176 (achieving the desired widening of k-space coverage) and the parallel-imaging rate was chosen to be R=4. The trade-offs involved in using the alternative choice of R=3 and a more general description of optimizing the acquisition parameters are provide in Appendix B. As detailed in Table 1, these settings implied that the prescribed in-plane resolution was 1.7 × 1.7 mm² and the temporal footprint was 125 ms (using the same per-pixel receiver bandwidth as the conventional method). To determine the apodization parameters, we applied the optimization scheme described above with the objective function in Eq. [3] and a desired resolution of 2.2 × 2.7 mm², i.e., the same resolution as the conventional method following apodization. The resulting parameters were: Ω_x = 1.4 and Ω_y = 1.0.

TABLE 1. Scan parameters for the proposed and conventional first-pass perfusion imaging methods.

Both methods employed an ECG-gated FLASH pulse sequence with saturation-recovery magnetization preparation for data acquisition during a 50-heartbeat free-breathing scan.

	Proposed Method	Conventional Method
prescribed resolution (readout × PE)	1.7 mm × 1.7 mm	2.2 mm × 2.7 mm
reconstructed resolution	2.2 mm × 2.7 mm
parallel-imaging rate (TGRAPPA)	R = 4	R = 2
number of acquired phase-encode lines	44	56
temporal footprint (acquisition time) for each slice	125 ms	133 ms
TR (echo spacing)	2.8 ms	2.4 ms
k-space matrix size	224×176	176×112
FOV (readout × PE)	380 mm × 305 mm
TI (for SR pulse)	120 ms
flip angle	12°
receiver bandwidth per pixel	770 Hz/pixel
slice positions	3 contiguous short-axis slices acquired in each heart beat (8 mm thickness)

For both conventional and proposed methods, the image reconstruction scheme was performed independently for each time frame (one frame per R-R interval) using TGRAPPA (19) and there was no “sharing of k-space data” in between different frames. Therefore, respiratory motion (negligible during the ≈130 ms acquisition window for each frame) did not introduce noticeable artifacts in the reconstruction of each frame. For the proposed method, apodization was implemented within the standard image reconstruction platform provided by the vendor (“ICE environment”, Siemens Healthcare). Following the reconstruction, a vendor-provided retrospective nonrigid motion-correction scheme was applied to compensate for the breathing motion.(28) For both conventional and proposed methods, a mild temporal median filter (length: 3 frames) was then applied to the reconstructed FPP time-series to reduce noise. Images were all reconstructed “online” almost instantaneously following the FPP scan for both methods (display delay time: <50 seconds).

Image Analysis

Quantitative Analysis

For all studies, DICOM images were analyzed in Osirix (Pixmeo, Geneva, Switzerland), which is a freely available image analysis platform.(29) For each FPP study, the SNR was measured in the septal region using the difference method.(8,30,31) Quantitative assessment of DRA was performed by measuring its spatial width (as a surrogate measure of artifact severity) in the 8^th time frame following the initial wash-in of contrast in the LV cavity – corresponding to the early myocardial enhancement phase. Using the interpolated DICOMs, the DRA width (i.e., transmural extent of the artifact) was measured by finding the maximum length of signal dips along all polar direction (along rays starting from the LV cavity center and extending toward the endocardium) as described previously.(16) The number of segments affected by DRA (defined as having a DRA width of > 2 mm) was measured for each FPP study. To this end, the window level in the DICOM viewer was set as recommended in established guidelines (32) and the LV myocardium was segmented (total of 16 segments in the acquired 3 short-axis slices) according to the standard American Heart Association model.(33)

Qualitative Analysis

FPP images (12 frames starting from the LV cavity wash-in phase) for both imaging methods (conventional and proposed) were presented in random order to two expert readers blinded to the imaging method. The images were scored using a consensus-scoring scheme on a scale of 0–4 based on image quality (0: poor, 4: excellent). The DRA severity was graded segmentally on a 0–4 scale (0: no visible artifact, 4: severe artifact). Scores for image quality were averaged over all 3 imaged slices and, for each study, the maximum artifact scores over all 16 myocardial segments was assigned as the “DRA score.”

Statistical comparison of quantitative measures (SNR and DRA width) used the paired t-test, and statistical comparison of qualitative scores used the Mann-Whitney U test (34) (equivalent to Wilcoxon rank-sum test). Statistical analyses were performed in MATLAB (Mathworks, Natick, MA) and a two-tailed value of p<0.05 was considered to be statistically significant.

Animal Studies

To evaluate whether the proposed technique is able to detect subendocardial perfusion defects, rest myocardial perfusion MRI studies in dogs (n=3; 18–22 kg) were conducted and the detected perfusion defects were compared against late gadolinium enhancement (LGE) images (resolution: 1.6 × 1.6 × 6 mm³) as the reference. One animal was used as normal control and in the others myocardial infarction (MI) was created by ligating the left anterior descending artery for 3 hours followed by reperfusion. Of the two infarcted canines, one underwent the MRI study 7 days following reperfusion (acute infarct) and the other was studied 4 month post MI (chronic infarct). The study protocol was approved by the local Institutional Animal Care and Usage Committee. Imaging was performed using the same scanner platform and hardware settings as the volunteer studies. FPP scans (mid ventricular slice) were performed at rest using the proposed imaging method. The prescribed in-plane resolution was 1.5 × 1.5 mm² and the effective resolution was 2.2 × 2.2 mm² with the following apodization parameters: Ω_x = Ω_y = 1.3.

Patient Studies

Two symptomatic patients who were referred for adenosine stress/rest perfusion MRI exam for evaluation of myocardial ischemia were studied using the proposed FPP imaging method with the same settings/parameters as the volunteer studies. Both patients had no obstructive coronary disease (defined as >50% stenosis in any of the epicardial arteries) based on prior invasive coronary angiogram and were therefore suspected of having CMD.(37,38) Following the MRI exam (<8 days), both patients underwent an invasive coronary reactivity test, which is the clinical gold standard for detection of CMD.(39,40) The first patient (44 year old female) had a normal coronary reactivity test but the second patient (67 year old female with a history of type 2 diabetes) had an abnormal test. The stress scan was performed during free breathing after 3 minutes of intravenous adenosine infusion (rate: 140 mcg/kg/min; total duration: 4 minutes) and was followed by the rest scan after a 15 minute wait time (to allow for contrast washout). In case of a high heart rate during adenosine infusion (judged by the technologist), FPP acquisition was limited to 2 short-axis slices instead of 3.

RESULTS

Numerical Simulations

Figure 3 shows the results of numerical experiments. Images in the top row (Panels a1–c1) correspond to the standard-res, hi-res, and the proposed schemes, respectively. The bottom row shows a 1D cut along the PE direction for the corresponding 2D images. Note that the hi-res image and proposed image are from the same raw dataset but using different reconstruction. Comparing these two images illustrates the effects of apodization. As seen from the figure, the hi-res image still shows a thin but noticeable DRA. After apodization, the DRA is markedly reduced (consistent with the PSF analysis). As noted in the PSF analysis (Fig. 2), the simulation results corresponding to the conventional and proposed methods have the same resolution, i.e., 1.3 × 1.5 mm² (assuming mm units for the FOV dimensions). However, the severe DRA in the standard-res image is nearly eliminated in the proposed image. These numerical results suggest that, using our proposed sampling and reconstruction scheme, the DRA can be effectively reduced while providing similar resolution as the conventional approach.

FIGURE 3. Numerical simulation results.

The top row shows the reconstructed images corresponding to the standard-res, hi-res, and proposed schemes. The bottom row shows a 1D cut along the PE direction for the respective images, super-imposed on the “ground truth” signal intensity profile (arrows show corresponding pixel positions along PE). (a1,a2): Reconstruction of the analytical phantom with standard-res acquisition corresponding to the conventional method; (b1,b2): Non-apodized reconstruction with hi-res acquisition; (c1,c2): Apodized reconstruction of the hi-res acquisition (same k-space data as in Panels b1,b2) corresponding to the proposed method. Compared to the standard-res image in (a1,a2), the DRA (Gibbs ringing) is effectively eliminated in the apodized hi-res image in (c1,c2). The reconstructed resolution is the same between (a1) and (c1). Comparing (b1) versus (c1), the hi-res image still shows a thin but noticeable DRA. After apodization, Gibbs ringing is significantly suppressed (consistent with Fig. 2).

Volunteer Studies

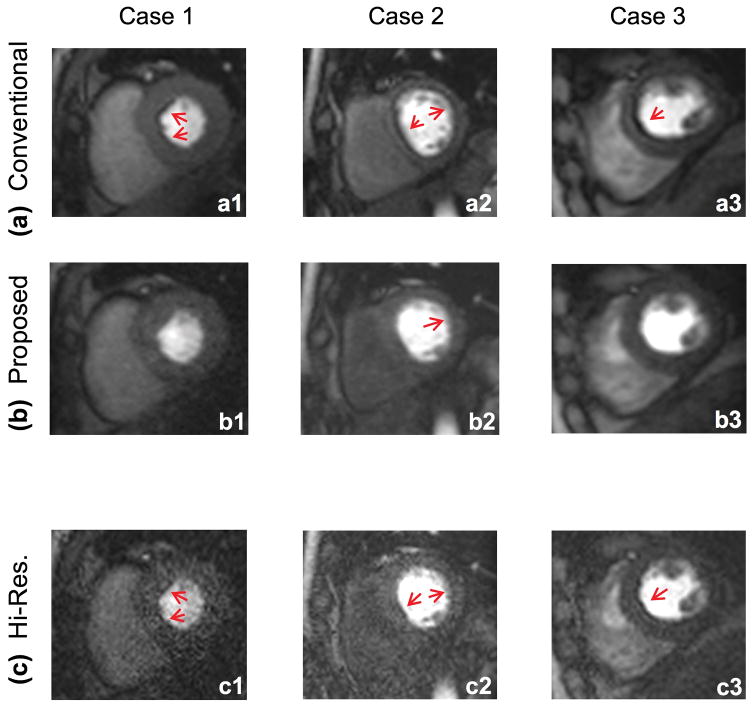
Representative FPP imaging results in three of the studied volunteers are shown in Fig. 4. All images were reconstructed “online” (generated within the scanner console) and nearly instantaneously (<50 seconds following the completion of the FPP scan). All of the presented images are in the same myocardial enhancement phase (8 frames after initial LV cavity enhancement). As can be seen from the figure, the number of segments affected by DRA and their severity is reduced in the proposed method (middle row) compared to the conventional method (top row). To demonstrate the benefits of (and the need for) apodization, we have also included the non-apodized hi-res images in the bottom row, which suffer from poor SNR and show some residual DRA (less severe compared to the conventional method).

FIGURE 4. Representative rest FPP images for three of the studied healthy volunteers.

All images correspond to the same myocardial enhancement phase (8 frames after initial wash-in of contrast agent in the LV cavity). Images in the top panel (a1–a3) correspond to the latest vendor-provided conventional FPP method with rate R=2 parallel imaging. The middle row (b1–b3) corresponds to the proposed imaging technique, i.e., optimally apodized reconstruction with hi-res acquisition using rate R=4 parallel imaging. There are significantly more segments affected by DRA in the top row (conventional method) compared to middle row (proposed method). Images in the bottom panel (c1–c3) correspond to the hi-res reconstruction (i.e., R=4 parallel imaging without apodization). As can be seen, these images suffer from low SNR and show thin yet detectable DRAs (red arrows). Image SNR is significantly improved after apodization and the DRA is reduced due to suppression of Gibbs ringing effects (consistent with Figs. 2 and 3).

Fig. 5 shows the representative FPP image series through the myocardial enhancement phase. These images correspond to case 3 in Fig. 4. The first frame corresponds to early myocardial enhancement phase (6 heartbeats after initial wash-in of contrast in the LV cavity. Each subsequent frame is showing every other heartbeat (i.e, skipping one R-R interval in between each frames). As seen in the figure, the DRA at the septal wall in the conventional image series is relatively severe and also persists through the myocardial enhancement phase hence closely mimicking the spatial/temporal behavior of a subendocardial perfusion defect. In contrast, the image series corresponding to the proposed method demonstrates a mild DRA (much lower artifact severity and width).

FIGURE 5. Representative FPP image time-series for one of the studied healthy volunteers.

(a): Conventional FPP imaging method; (b) Proposed method. These images correspond to case 3 in Fig. 4. The first frame corresponds to 6 heartbeats after initial wash-in of contrast in the LV cavity. Each subsequent frame is showing every other heartbeat (i.e., skipping one R-R in between each frame). The DRA at the septal wall in the conventional image series is relatively severe and persists through the myocardial enhancement phase. The image series corresponding to the proposed method shows a significant reduction in severity and width of the DRA.

Fig. 6 shows the histogram of the reader-assigned qualitative artifact scores (total of 30 scores for 30 slices in the n=10 perfusion studies). As seen in the figure, the number of myocardial slices with severe DRA (artifact scores = 3 or 4) is significantly lower for the proposed method (by 10 fold).

FIGURE 6. Histogram of DRA severity scores for each slice (total of 30 slices for the n=10 studies) for the conventional FPP imaging method (light gray) and the proposed method (dark gray).

The mean DRA score (averaged across n=10 studies) is lower for the proposed method (1.2 vs. 2.0 for the conventional and proposed methods, respectively; p<0.01). Most notably, the number of myocardial slices with severe DRA (artifact score = 3 or 4) is significantly lower for the proposed method compared to the conventional method (10 slices vs. 1 slice for the conventional and proposed methods, respectively).

Table 2 summarizes the result of quantitative and qualitative image evaluations comparing the proposed method versus the conventional method. The mean qualitative DRA score was lower for the proposed method (1.2±0.8 vs. 2.0±1.3; p<0.01). The maximal DRA width (averaged value across n=10 studies) was ≈1.3±0.9 mm for the images corresponding to the proposed method compared to ≈2.9±1.1 mm for the conventional method (p<0.001). Moreover, the prevalence of DRA-affected myocardial segments (among the 16 segments for each FPP scan) was significantly reduced for the proposed method compared to the conventional method (2.6±1.4 vs. 8.7±2.1; p<0.0001). The myocardial SNR at peak myocardial enhancement for the proposed method was significantly lower compared with the conventional method (12.9±7.5 for proposed vs. 18.8±5.9 for conventional, p<0.05). However, no significant differences in reader-assigned image quality scores were detected between the two methods (3.3±0.3 for conventional vs. 3.1±0.3 for proposed; p=0.2). It is worth mentioning that apodization significantly improved the SNR from 6.1±2.7 for the hi-res scheme to 12.9±7.5 for the proposed method (p<0.01).

TABLE 2.

Summary of mean qualitative/quantitative image quality and artifact scores in the volunteer myocardial perfusion imaging studies (n=10).

Parameter	Conventional method	Proposed method	P value
image quality score	3.3±0.3	3.1±0.3	0.2
qualitative artifact score	2.0±1.3	1.2±0.8	<0.01
DRA width [mm]	2.9±1.1	1.3±0.9	<0.001
# of DRA-affected segments	8.7±2.1	2.6±1.4	<0.0001
signal-to-noise ratio	18.8±5.9	12.9±7.5	<0.05

Animal Studies

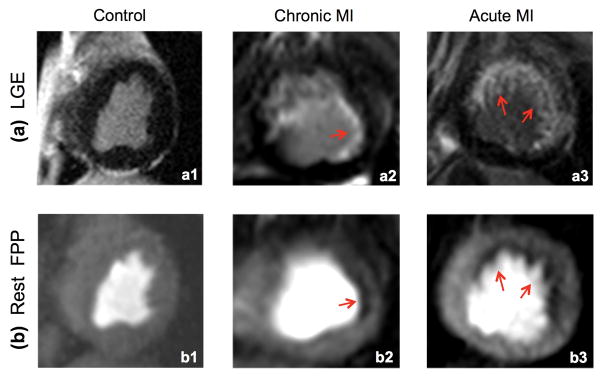
Figure 7 provides rest FPP results (proposed method) and corresponding LGE images for the canine studies. The control animal study (left column) displayed negative LGE and normal perfusion (no DRA). As observed in the LGE image for the chronic MI study, this animal had a small subendocardial infarct as visualized in panel (a2). A corresponding perfusion defect was clearly seen in the FPP image displayed in panel (b2), demonstrating the ability of the proposed method to resolve small defects. The width of this defect was ≈3 mm (note that the reconstructed resolution was 2.2 × 2.2 mm²). The acute MI study demonstrated a similar result (subendocardial perfusion defect consistent with LGE) with a larger defect region. Overall, among the 3 studies, only minimal DRA was observed in the acute MI study and the other two studies were virtually free of DRA. These results are consistent with the theoretical understanding (based on PSF analysis) that reduction of subendocardial DRA using the proposed method does not lead to elimination/masking of subendocardial perfusion defects in the reconstructed FPP images.

FIGURE 7. Results of the canine studies (n=3).

LGE images (top row) are used as the reference to evaluate whether the corresponding resting FPP images (bottom row) acquired using the proposed method can detect perfusion defects corresponding to the subendocardial infarcts. All perfusion images correspond to the peak myocardial enhancement phase. (a1,b1): Result of the control animal study with no perfusion defects, which is consistent with the negative LGE. (a2,b2): Result of the chronic MI study with a small subendocardial infarct (red arrow in a2). The perfusion defect (≈3 mm width) is clearly seen in (b2) demonstrating the ability of the proposed method to resolve small subendocardial defects. (a3,b3): Result of the acute MI study, which shows subendocardial perfusion defect in the all LGE-positive segments. Among the 3 studies, only minimal DRA is seen in (b3) and (b1, b2) are virtually free of DRA.

Patient Studies

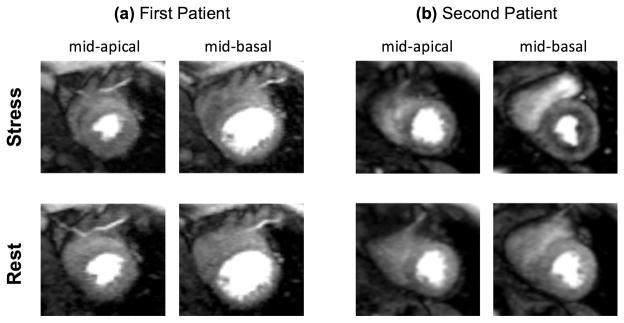
Both patients had normal rest perfusion studies without a noticeable dark rim artifact and normal LGE scans. Figure 8 shows the stress/rest perfusion results (peak myocardial enhancement phase) in two contiguous slices (mid-basal and mid-apical) for the studied patients. As described in the figure, the results for the patient with the positive invasive gold-standard test (abnormal coronary reactivity) in Fig. 8(b) show a stress-induced subendocardial hypoperfusion, which is consistent with the presence of CMD.(38)

FIGURE 8. Results of the stress/rest patient studies (n=2) using the proposed FPP imaging method.

Adenosine stress (top row) and rest (bottom row) perfusion results for the two studied patients: (a) case with normal invasive coronary reactivity test; (b) case with abnormal invasive coronary reactivity test. The stress/rest images correspond to the peak myocardial enhancement phase in two contiguous slices (left panel: mid-apical; right panels: mid-basal). Both patients had a normal rest perfusion study without a noticeable dark rim artifact and normal LGE scans. The result in (b) show a stress-induced subendocardial hypoperfusion — consistent with the presence of coronary microvascular dysfunction in this patient. The stress study in (b) was acquired with two slices (one slice dropped by the technologist) due to the high heart rate observed during adenosine infusion.

DISCUSSION

Current approaches for reduction of subendocardial dark-rim artifact (DRA) in FPP imaging involve either k-t accelerated high-resolution Cartesian imaging or non-Cartesian acquisition. In this work, we proposed an alternative approach based on modified Cartesian acquisition that enables free-breathing FPP imaging with near-instantaneous image reconstruction. Our results demonstrated that myocardial perfusion MRI using the proposed Cartesian sampling approach and optimized apodization scheme reduces the prevalence and severity of DRA compared to the state-of-the-art conventional method with similar resolution and image quality. The proposed image reconstruction scheme is integrated within the vendor-provided self-calibrating parallel imaging routine—which is available across nearly all clinical scanner platforms—thereby enabling instantaneous/online image reconstruction. The use of Cartesian sampling and “online” image reconstruction are desirable features that enable the developed method to be easily integrated into routine clinical workflow.

The proposed methodology involves widening the k-space coverage of Cartesian sampling by increasing the parallel-imaging rate beyond the conventional level. Combined with optimized apodization, this modified approach essentially “shapes” the underlying PSF (by attenuating its side lobes) to suppress Gibbs-ringing effects, which in turn minimizes ringing-induced DRAs. Besides suppressing Gibbs ringing, apodization improves the reconstructed SNR and can compensate for most of the SNR loss resulting from the unconventionally high parallel-imaging rate (R=4) used in the proposed method. We conducted numerical studies to demonstrate the effectiveness of optimized apodization and the methodological developments were then tested in healthy volunteer studies with comparison to the conventional method — demonstrating a significant reduction in DRAs, especially in reducing the prevalence of severe dark rims. Furthermore, preliminary stress/rest results in patients referred for ischemia evaluation demonstrated the potential of the developed method for detecting stress-induced subendocardial hypoperfusion in case of CMD.

In the absence of image artifacts, the size of the smallest detectable perfusion defect using a FPP imaging method depends on its effective resolution in the reconstructed frames. Unlike nonlinear reconstruction methods that may involve complicated resolution-lowering effects, the proposed method provides a straightforward measure of the reconstructed resolution. Specifically, since apodization is a linear process that can be accurately modeled using PSF analysis, the true spatial resolution of the reconstructed images can be precisely computed. The presented animal studies demonstrated that reduction of subendocardial DRA using the employed apodization scheme does not lead to elimination/masking of subendocardial defects in the FPP image series. In fact, resolution of the proposed method (ability to resolve perfusion defects) is predefined and fixed across all studies.

In addition to Gibbs ringing, another major contributing factor to the DRA in Cartesian imaging is known to be cardiac motion effects.(35) It should be noted that the scan parameters for the proposed method were designed so that its temporal footprint was similar to the conventional method. Therefore, it is expected that both methods had a similar level of motion-induced DRAs. Consequently, the relative difference seen between the two methods (in terms of reduced DRAs) is because of improvement in the underlying PSF (i.e., suppression of Gibbs ringing). Using the same logic, the residual DRAs for the proposed method are likely caused by cardiac motion effects, which were not suppressed by apodization.

For each volunteer study, we performed two contrast injections and the ordering of the injections (first the proposed method followed by the conventional method) was designed to deliberately disadvantage the proposed method. In fact, the FPP images acquired in the first injection have a higher blood pool-to-myocardium signal difference compared to the second injection, which implies that the first FPP scan is generally more prone to DRAs.

This choice of running the proposed method as the first FPP scan also contributed to its somewhat lower SNR compared to the conventional method (since the myocardial signal is higher for the second injection due to the residual contrast from the first injection). Nevertheless, although the quantitative myocardial SNR comparison showed a statistically significant loss (approximately 30%) for the proposed method compared to the conventional method, the reader-assigned image quality scores did not show a significant difference. This is consistent with a recent work (31) that compared high-resolution FPP imaging to standard resolution, demonstrating similar image quality scores despite a significant drop in SNR for high-resolution FPP imaging.

Although the presented results showed that the proposed Cartesian imaging method is a promising approach for reducing DRAs, its diagnostic benefits in detection of subendocardial ischemia remain to be evaluated. To this end, the presented stress/rest patient studies are a preliminary step towards assessing the performance of the developed approach versus the invasive gold standard in patients with suspected ischemic heart disease either due to underlying obstructive coronary artery disease or CMD (non-obstructive disease). It should be noted that, on the MRI platforms where the k-t accelerated methods (8) are available, the same principles proposed in this work can be synergistically used. Another study design limitation was the lack of direct comparison between the convectional and proposed methods in the patient studies. Such a direct comparison would require two separate administrations of the vasodilator stress drug in the same patient, which was not feasible in our approved clinical protocol. Furthermore, the impact of DRA reduction in improving the accuracy of quantitative myocardial blood flow assessment needs to be evaluated in future studies. Finally, the presented specifics of the methodology were optimized for the particular scanner hardware and field strength used at our laboratory. Therefore the described pulse sequence parameters need to be adapted to the utilized scanner hardware (depending on the field strength, coil array, etc.) to determine the parameters that optimize the trade-off between artifact suppression and image quality (as described in Appendix B).

In conclusion, we demonstrated the feasibility and effectiveness of a modified Cartesian acquisition scheme for free-breathing first-pass perfusion cardiac MRI designed to minimize the subendocardial dark-rim artifact compared to the conventional approach while maintaining similar spatial/temporal resolution and image quality. A key feature of the developed method is that it uses standard Cartesian parallel imaging and achieves near-instant “online” image reconstruction, potentially enhancing its accessibility in clinical settings compared to alternative (highly accelerated or non-Cartesian) schemes. Studies in healthy volunteers demonstrated that, compared to the conventional method, the prevalence of severe dark-rim artifacts were significantly reduced using the developed approach. Preliminary test results in infarcted canines and stress/rest studies in patients with suspected coronary microvascular dysfunction showed the ability of the developed method to detect subendocardial perfusion defects.

LIST OF ABBREVIATIONS

FPP

first-pass perfusion

DRA

dark-rim artifact

Standard-Res

standard resolution

Hi-Res

high resolution

PE

phase encoding

PSF

point spread function

SNR

signal to noise ratio

2D

two dimensional

1D

one dimensional

FOV

field of view

FWHM

full width at half maximum

LV

left ventricle

LGE

late gadolinium enhancement

MI

myocardial infarction

CMD

coronary microvascular dysfunction

Appendix A. Analytical Derivation of the Numerical Phantom

The numerical phantom used in Fig. 3 (see Methods) was formed using 3 components: two circular disks for the LV and one ellipsoid for the perfusion defect. Two concentric disks were used to mimic the LV: the larger and darker disk mimicking the myocardium while the smaller and brighter disk mimicking the blood pool. The 2D Fourier transform of a disk is the so-called jinc function, the 2D polar-coordinate analog of the sinc function. The jinc function can be expressed using J₁, the Bessel function of the first kind (26), as:

$$D(k_x,k_y)=\mathcal{F}[\mathit{circ}(r)]=2\pi r^2\frac{J_1(r\sqrt{{k_x}^2+{k_y}^2})}{r\sqrt{{k_x}^2+{k_y}^2}}$$

where r denotes the disk radius. Using classical properties of 2D Fourier transform (36), it can be shown that the Fourier transform of an elliptical disk with major radius a and minor radius b can be written as:

$$D(k_x,k_y)=\mathcal{F}[\mathit{ellip}(a,b)]=2\pi ab\frac{J_1(\sqrt{{(a{k}_x)}^2+{(b{k}_y)}^2})}{\sqrt{{(a{k}_x)}^2+{(b{k}_y)}^2}}$$

By super-position of the above-mentioned 3 components (blood pool, myocardium, and defect) with the required spatial shifts (linear phase modulation in k-space), the analytical phantom can be expressed in the 2D k-space as:

$$D(k_x,k_y)=({SI}_{in}-{SI}_{\mathit{out}})\mathcal{F}[\mathit{circ}(r_{in})]+{SI}_{\mathit{out}}\mathcal{F}[\mathit{circ}(r_{\mathit{out}})]+({SI}_{\mathit{deficit}}-{SI}_{\mathit{out}})exp\left(-i2\pi (k_x{x}_{\mathit{shift}}+k_y{y}_{\mathit{shift}})\right)\mathcal{F}[\mathit{ellip}(a,b)]$$

where the signal-intensity parameters (denoted by SI) were set so that the phantom has the following respective intensities for blood pool, myocardium, and defect regions: 1, 0.2, and 0.1.

Appendix B. Further Details on Protocol Optimization

Based on the described framework in Methods, there are two key constraints in choosing the protocol parameters for the proposed acquisition scheme: (a) matching the temporal acquisition window (footprint) to the conventional protocol (~130 ms); (b) matching reconstructed spatial resolution to conventional protocol (2.2 × 2.7 mm² in our study). The free parameters in the acquisition protocol that can be optimized include: parallel imaging undersampling factor denoted by R (limited to integers for simplicity), the prescribed resolution, and the apodization parameters (Ω_x and Ω_y). In the scanner hardware setup in the presented study (3T scanner with the standard 12-channel cardiac-torso coil array), the feasible range for R is R≤4, since R≥5 results in catastrophic noise amplification (g factor) that cannot be sufficiently recovered by apodized reconstruction. Also, R needs to be larger than the 2-fold undersampling factor used in the conventional protocol in order to accommodate the higher prescribed spatial resolution. This leaves us with two choices: R=3 or R=4. With R=3 and the other protocol parameters (TR and FOV size) fixed as in Table 1, to satisfy constraint (a) above, the prescribed in-plane resolution (assumed to be isotropic) should be 2.0 × 2.0 mm²; and to satisfy constraint (b), we need Ω_x = 2.4 and Ω_y = 1.2. With R=4, the same approach will yield the parameters used in our volunteer studies (see Methods).

The criteria for choosing between the two candidate imaging protocols, that is R=3 vs. R=4, includes: (i) the level of suppression of Gibbs-ringing effects, and (ii) the “apparent” SNR in the reconstructed images. For the first criterion, we used the normalized peak negative side-lobe amplitude to measure the level of Gibbs ringing oscillations in the corresponding PSF. The results for the phase-encode direction were: 21.71% (conventional method), 1.26% (R=3 protocol), 0.65% (R=4 protocol); and for the readout direction: 21.71% (conventional method), 14.31% (R=3 protocol), 3.84% (R=4 protocol). Therefore, the R=4 protocol provided a notably higher level of Gibbs ringing suppression compared to R=3 based on PSF analysis. For the second criterion, because of the complications in theoretical SNR quantification for TGRAPPA reconstruction, we used an empirical approach and performed a pilot study (2 volunteers, not shown) to confirm that R=4 imaging protocol can provide sufficient SNR.

It is important to note that in other hardware settings, e.g., on a 1.5T scanner platform, the SNR for R=4 will likely be insufficient (unless the latest generation of coil arrays are used) and therefore the R=3 protocol may be a better choice. To conclude, the choice of imaging parameters (the undersampling factor R, prescribed resolution, and apodization parameters) involves a trade-off between the level of suppression of Gibbs-ringing effects and the apparent SNR. To implement this framework in a given hardware setup: (step 1) a set of candidate protocols with different R factors (such as the two with R=3 vs. R=4 described above) should be determined on the basis of the constraints involving the desired spatial resolution and temporal acquisition window; (step 2) the optimal choice between the candidate protocols should be determined empirically to ensure sufficient SNR as described above. As a rule of thumb, on most scanner platforms available today, the protocol choice will be between R=3 and R=4, and could include R=5 for 3T scanners with the latest generation of ≥32 channel coil arrays.