Real-time inverse kinematics and inverse dynamics for lower limb applications using OpenSim

Abstract

Real-time estimation of joint angles and moments can be used for rapid evaluation in clinical, sport, and rehabilitation contexts. However, real-time calculation of kinematics and kinetics is currently based on approximate solutions or generic anatomical models. We present a real-time system based on OpenSim solving inverse kinematics and dynamics without simplifications at 2000 frame per seconds with less than 31.5ms of delay. We describe the software architecture, sensitivity analyses to minimise delays and errors, and compare offline and real-time results. This system has the potential to strongly impact current rehabilitation practices enabling the use of personalised musculoskeletal models in real-time.

Introduction

Real-time estimates of three-dimensional (3D) joint angles and moments have the potential to enable rapid patient evaluation, interactive patient treatment, and biofeedback for rehabilitation. A system is defined as real-time if it can provide information with a delay of less than 75 ms, after which the information loses its usefulness (Kannape and Blanke, 2013). Specifically, applications for real-time augmented sensory feedback have to reduce the perceived mismatch between the sensorimotor and augmented information.

Recently, researchers have used real-time computation of joint angles and moments as biofeedback variables for gait retraining (Barrios et al., 2010; Shull et al., 2011; Shull et al., 2013; van den Noort et al., 2015; Wheeler et al., 2011). Real-time biofeedback variables included knee adduction moment (Wheeler et al., 2011), hip internal rotation (Barrios et al., 2010), and trunk sway (Huffman et al., 2010). However, the computational complexity required to calculate these variables in real-time resulted in the adoption of simplified algorithms and models. For instance, real-time applications commonly use direct kinematics, i.e., estimation of joint angles assuming markers are rigidly attached to segments, instead of inverse kinematics that globally optimize models’ generalized coordinates to minimize marker tracking errors. While computationally inexpensive, the direct kinematics may produce less accurate joint angles estimates, introducing joint dislocations and/or changes in segment lengths (Lu and O’Connor, 1999). Computation of joint moments is also simplified at times. For instance, Wheeler et al. (2011) solved the knee adduction joint moment using the cross-product of position and ground reaction force vectors, which is a not always an acceptable simplification (Winter, 2005).

Van den Bogert et al. (2013) created a real-time system able to calculate joint angles, joint moment and muscle forces using inverse kinematics, inverse dynamics, and static optimisation respectively. Their system used an underlying musculoskeletal model, which defined bone lengths, joints, inertial parameters, and tendon attachments. However, the implemented musculoskeletal model is generic and cannot be personalised to reflect subject specific anatomy (van den Bogert et al., 2013). Importantly, the creation of subject specific musculoskeletal models is of major interest for future applications in rehabilitative medicine (Fregly et al., 2012). This interest is corroborated by recent studies on people walking with instrumented tibial implants where the use of a subject specific musculoskeletal model improved the accuracy of medial tibiofemoral contact force predictions (Gerus et al., 2013; Marra et al., 2015).

OpenSim (Delp et al., 2007) is a popular open-source software to analyse human motion based on the multibody dynamics engine Simbody (Sherman et al., 2011), which provides tools to solve inverse kinematics and inverse dynamics. Importantly, OpenSim is a generic simulation platform that can use musculoskeletal models from individualized bone geometries, joint parameters, and musculotendon paths built from medical images. These models can be generated using freely available tools such as NMSBuilder (Martelli et al., 2011; Valente et al., 2014). Finally, OpenSim can be used in conjunction with electromyogram-informed neuromusculoskeletal models (Pizzolato et al., 2015), which permit to estimate muscle forces and joint contact forces from subject specific muscle activation patterns. However, OpenSim is not enabled for real-time use, nor it can interface with any device or motion capture system. Commercial alternatives to OpenSim are available but they are also limited by different factors. Anybody (AnyBody Technology, Aalborg, Denmark) permits high levels of model personalisation, but currently does not operate in real-time. Visual 3D (C-Motion, Germantown, MD, USA) can be interfaced with different motion capture systems, including Qualisys (Gothenburg, Sweden) and Vicon (Oxford, UK), but only direct kinematics can currently be used in real-time to solve joint angles. Finally, Motek Medical (Amsterdam, Netherlands) implements the aforementioned methodology published by van den Bogert et al. (2013). Consequently, it is desirable to enable real-time use of the advanced features of OpenSim without simplifications or loss of accuracy.

The aim of this study was to (1) interface OpenSim with a Vicon motion capture system, (2) develop and freely release a software architecture to enable the use of OpenSim inverse kinematics and inverse dynamics in real-time, and (3) test the performance of the real-time system in terms of computational time, accuracy, and delay.

Methods

Real-time software implementation

We developed and freely released (Apache License, version 2) a software architecture in C++ that allows reading and processing motion capture data in real-time (Figure 1). This required the creation of a concurrent system where multiple threads process information on different processor cores. Each thread has a specific task in the processing pipeline and works asynchronously from other threads. Consequently, different steps of the processing pipeline operate in parallel. Threads access data via shared memory buffers. To preserve data integrity and avoid multiple threads to write on the same memory location at once, access to memory buffers is regulated following a publisher-subscriber software design pattern (Buschmann et al., 2007). OpenSim inverse kinematics and inverse dynamics algorithms were adapted to the software architecture and revised in order to read from memory buffers instead of accessing pre-recorded data saved into files. The software described and analysed in this paper, including the code necessary to enable the real-time use of OpenSim, is made available online (https://simtk.org/projects/rtosim and https://github.com/RealTimeBiomechanics/rtosim).

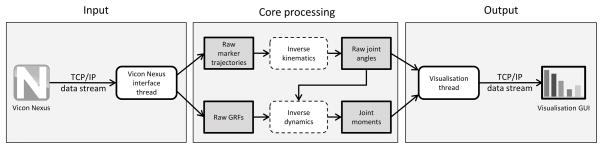
Figure 1.

Schematic representation of the real-time pipeline reading data from Vicon Nexus. White background corresponds to operation threads and grey background to buffers. ‘Inverse kinematics’ and ‘Inverse dynamics’ blocks are further expanded in Figures 2 and 3. The ‘Input block’ can be substituted to adapt the pipeline to a different motion capture system, independently from the ‘Core Processing’ block. In the same way, the ‘Output’ block, currently a visualization thread, can implement auditory or haptic feedback as well.

Vicon Nexus tracks, reconstructs, and automatically labels marker trajectories from Vicon cameras. It then synchronises marker trajectories with the ground reaction forces (GRFs) data measured from the available force plates and streams all data via TCP/IP. The Vicon Nexus interface thread (Figure 1) reads the data via the Vicon DataStream SDK and transform them into the OpenSim coordinate reference system. Marker trajectories are input for the inverse kinematics to calculate joint angles, which, together with GRFs, are used by the inverse dynamics analysis to compute joint moments. Finally, results are displayed in a Graphic User Interface (GUI), which is connected via TCP/IP to the Visualisation thread (Figure 1).

A generic OpenSim model represents the musculoskeletal system (bone, joints and muscles) that can be personalized to a specific individual by adjusting the models’ segments sizes to an individual’s anthropometry. Virtual markers are rigidly attached to different segments of the model. Inverse kinematics solves a weighted least square problem to minimises distance between virtual (x_i) and experimental (x̄_ι) markers positions in each recorded frame (Lu and O’Connor, 1999):

$$\underset{\mathit{q}}{min}({\sum }_i^N{w}_i{\Vert {\overline{\mathit{x}}}_{\iota }-{\mathit{x}}_i(\mathit{q})\Vert }^2)$$ (1)

Where q represents the vector of the model’s generalised coordinates and w_i the weight associated to the ith marker.

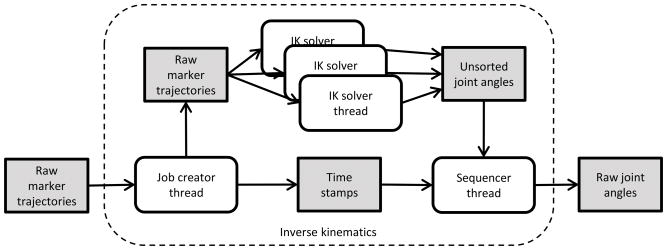
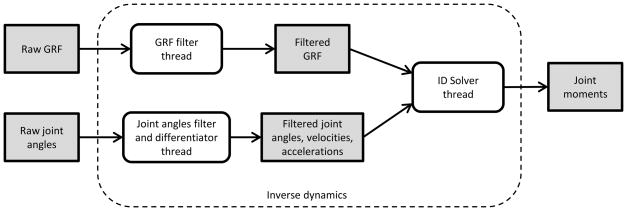
Real-time inverse kinematics must be able to process marker trajectories at least at the same frequency of the cameras. To this end, taking advantage of modern CPUs’ multicore architecture, we implemented a thread pool software pattern (Garg et al., 2002), where multiple inverse kinematics calculation threads concurrently solve a separate frame of marker data in a staggered fashion (Figure 2), independent of each other. They read the first available marker trajectories frame, compute the joint angles, and store them in a memory buffer. Then, a Sequencer thread time orders joint angle frames and stores them in the Raw joint angles memory buffer. A state-space filter implementation of a 2^nd order low pass Butterworth filter (van den Bogert et al., 2013) is used to filter both GRF and raw joint angles (Figure 3). The same filter also performs single and double differentiation of the filtered variable to calculate joint velocities and accelerations, which are subsequently required to solve the Inverse Dynamics Solver thread (Figure 3).

Figure 2.

Real-time implementation of inverse kinematics (IK). Each ‘IK solver thread’ reads and solves a different frame, which is read from the ’Raw marker trajectories’ buffer. Results are then stored in the ‘Unsorted joint angles’ buffer. The ‘Sequencer thread’ puts in the correct temporal order the ‘Unsorted joint angles’ using the time stamps stored in the ‘Times stamps’ buffer.

Figure 3.

Real-time implementation of inverse dynamics.

The inverse dynamics analysis implemented in the Inverse Dynamics Solver thread (Figure 3) solves the dynamic equation of motion:

$$M(\mathit{q})\ddot{\mathit{q}}+C(\mathit{q},\stackrel{.}{\mathit{q}})+G(\mathit{q})=\mathit{\tau }$$ (2)

Where q, q̇, q̈ are the position, velocity, and acceleration of the generalised coordinates. M, C, G are the mass, centrifugal and Coriolis, and gravitational forces matrices, respectively, whereas τ is the vector of unknown generalised forces. From now on, we will refer to generalised coordinates as joint angles, and to generalised forces as joint moments.

The real-time inverse kinematics and inverse dynamics are solved by calls to OpenSim’s respective APIs OpenSim::InverseKinematicsSolver and OpenSim::InverseDynamicsSolver and used within the IK Solver thread (Figure 2) and the ID Solver thread (Figure 3), respectively. Within the real-time code, the methods to read input data, such as marker trajectories and ground reaction forces, have also been modified to operate on single time frames available in the memory buffers. The reader is referred to full implementation details in the source code on GitHub (https://github.com/RealTimeBiomechanics/rtosim in directories lib/InverseKinematics/ and lib/InverseDynamics/).

Data collection

Motion data were recorded using a 12-cameras Vicon motion capture system (Oxford, UK) with an acquisition frequency of 200Hz. A split belt treadmill (Bertec Corporation, Columbus, OH, USA) was used to collect ground reaction force data at 1000Hz. The study was approved by Griffith University Human Research Ethics committee and one male subject (age: 29, weight: 73kg, height: 1.77m) gave his informed written consent to participate. The subject performed a static trial for calibration purposes, followed by treadmill familiarisation, and then walking (1m/s), fast walking (1.5m/s), and running (2.5m/s) for 60 seconds (12000 frames) each, corresponding to 53, 61, and 84 gait cycles respectively. 48 markers were used in the acquisition (see supplementary material). Collected data were used to create two different datasets: clean and raw. The clean dataset was created for the offline data processing and was prepared by manually cleaning, labelling, gap-filling, and saving the marker trajectories and GRF data in OpenSim file format (Mantoan et al., 2015). The raw dataset included only the raw binary data from the cameras and the treadmill (.x1d and .x2d Vicon file format). The raw dataset contained the data directly streamed from Vicon with marker errors and dropout and was used in conjunction with Vicon Virtual System software to recreate the same real-time conditions in the laboratory, including marker reconstruction and autolabelling steps. Both datasets were not filtered.

Data analysis

Three different analyses were performed in order to compare the differences between offline and real-time processed data. The first analysis was a speed test. We explored the effect of different OpenSim models, marker-sets, tasks, and number of threads on the real-time throughput, measured in frames per seconds (fps). Two different OpenSim models were scaled to the subject’s anthropometric dimensions. The first was the gait2392 model (Delp et al., 1990), a model provided with the OpenSim distribution. The second was a modification of the former model including constraints to enable the movement of patella and calculate compartmental knee contact forces (Lerner et al., 2015). The two models were chosen because of the different number of kinematic constraints included, in order to evaluate the effects of model complexity on the real-time performance. For both models we created three different virtual marker-sets, with 48, 32, and 14 markers respectively (see supplementary material). We performed the test using the clean dataset. A number of inverse kinematics solver threads (Figure 2), increasing from 1 to 20, calculated joint angles for each combination of models, marker-sets, and tasks. Only a single thread was used to solve the inverse dynamics (Figure 3). The mean throughput of the real-time pipeline was reported for each combination.

The second and third analyses used the scaled gait2392 model, the set of 32 markers. Joint angles and moments of hip flexion-extension, hip internal rotation, hip adduction-abduction, knee flexion-extension, and ankle plantar-dorsiflexion were calculated via the offline and the real-time pipelines. The offline pipeline used OpenSim inverse kinematics and inverse dynamics tools, and a 2^nd order Butterworth zero-lag filter at 6Hz to filter marker trajectories, joint angles, and GRFs (Winter et al., 1974) from the clean dataset. The real-time pipeline utilised the raw dataset.

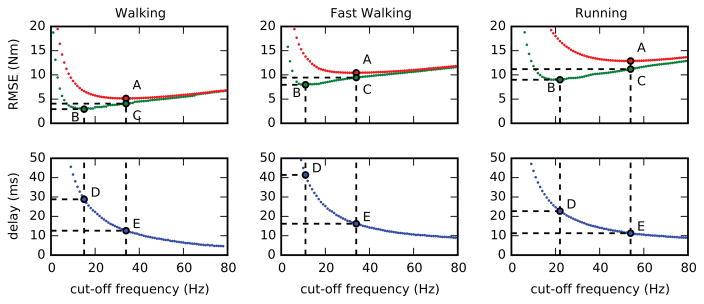
The second analysis determined the optimal cut-off frequency for the filter used in the real-time pipeline (Figure 1). The real-time data were processed using cut-off frequencies from 1 Hz to 80 Hz with a step of 1 Hz. The real-time’s single pass low pass filtering introduced time delays that were determined for each cut-off frequency using cross-correlation between the real-time and offline joint moments for each task. Joint moments were analysed since they reflect delays and errors in both joint angles and force plate data. To assess the similarity of joint moments calculated by the offline and real-time pipelines, the estimated time delays were used to create another data set of time-aligned-real-time joint moments, wherein the real-time joint moments were time-shifted according to the delay. Offline, real-time, and time-aligned-real-time joint moments were then divided in single gait cycles. Root mean square errors (RMSE) were calculated between offline and real-time joint moments to reflect the errors introduced by the time delay, as well as between the offline and time-aligned-real-time joint moments to reflect the error in time-varying joint moment magnitude. For each task, RMSE and time-aligned-RMSE were calculated for all joint moments and gait cycles and subsequently averaged to show differences in joint moments at each filtering frequency. This resulted in two curves, whose minima indicate the lower and upper boundaries for the selection of the real-time filter cut-off frequency.

The third analysis compared joint angles and moments calculated offline and in real-time, using the upper boundary filter cut-off frequency determined by the second analysis, which minimised both delay and RMSE. Initially, filtered joint angles and joint moments were calculated for all the gait cycles using both the offline and real-time pipelines. Mean and standard deviation were calculated across gait cycles for each filtered joint angle and joint moment to provide representative curves for each task. Real-time delay of filtered joint angles and joint moments relative to the offline processing were determined using the method described above. Delays determined from the cross-correlation analysis were used to create time-aligned-real-time filtered joint angles and joint moments, also as already outlined. Time-aligned-RMSE of filtered joint angles and joint moments were determined for each gait cycle, with mean and standard deviation subsequently calculated.

The real-time data processing was executed on a Dell Precision Workstation T7500, with 2 Intel® Xeon® Processors X5660 (12MB Cache, 2.80 GHz, 6 cores per processor), 8GB of RAM, and Linux (kernel 4.2.0–18). Inverse kinematics computations were performed with an accuracy of 1x10⁻⁵, the default value in OpenSim. OpenSim 3.3, Simbody 3.5.1, Vicon Nexus 2.2, Vicon Virtual System 1.3.2, and Vicon DataSetream SDK 1.5 were used. Overall computation time, including real-time marker reconstruction and labelling, streaming of data via TCP/IP, inverse kinematics, inverse dynamics, and filtering, was also measured via software using the POSIX timer functions.

Results

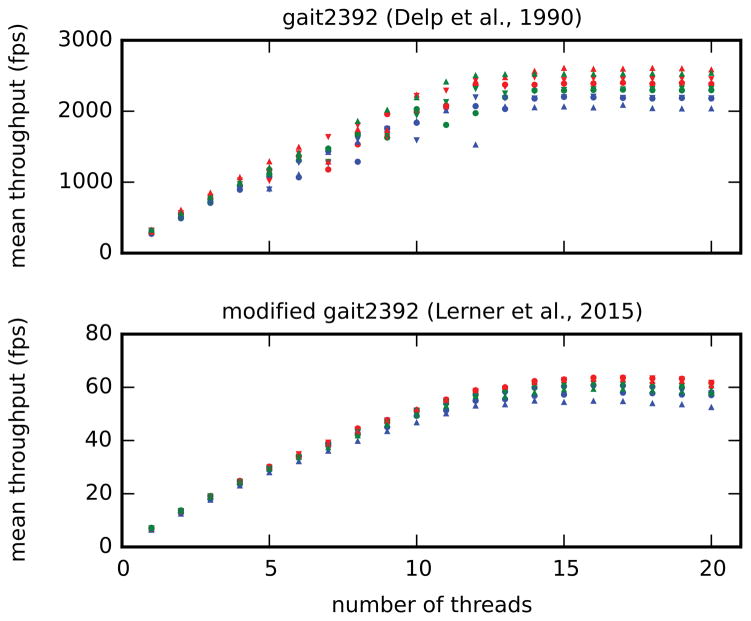
The first analysis (Figure 4) showed that the real-time throughput was marginally dependent on the task, but not on the marker-set. Use of multiple threads resulted in a linear increase of the mean throughput for up to 12 threads, which corresponded to number processor cores. Using the gait2392 model resulted in throughput from a minimum of 250 fps with a single thread to approximatly 2000 fps using 12 threads. Using the gait2392 modified by Lerner et al. (2015) resulted in mean throughput from 6 fps with a single thread to 50 fps with 12 threads.

Figure 4.

Mean throughput of the real-time system for increasing number of ‘IK solver threads’ (Figure C) and different combinations of trials, marker-set, and models. 12000 frames of walking (blue), fast walking (green), running (red), and three different marker-sets with 14 (▲), 32 (▼), and 48 (●) markers respectively were evaluated. Two different models (row 1: Delp et al., (1990) row 2: Lerner et al., (2015)) including different constraints were used.

The second analysis showed that real-time filter cut-off frequencies affected both RMSE’s and time delays between offline and real-time calculated joint moments (Figure 5). For walking the real-time filter cut-off frequency boundaries were 15 Hz and 34 Hz, corresponding to a time-aligned-RMSE of 2.92 Nm and 4.07 Nm (points B and C) with time delays of 28.8 ms and 12.6 ms respectively (points D and E). Fast walking resulted in similar cut-off frequency values, 11 Hz and 34 Hz, but time-aligned-RMSE of 7.96 Nm and 9.44 Nm, with 41.4 ms and 16.2 ms time delays. Finally, the cut-off frequency boundaries for running resulted in 22 Hz and 54 Hz, time-aligned-RMSE values of 8.99 Nm and 11.19 Nm, and 22.7 ms and 11.3 ms time delays.

Figure 5.

Mean RMSE (red), time-aligned-RMSE (green) and time delays (blue) between joint moments calculated offline (low pass filtered at 6 Hz) and in real-time as a function of the real-time cut-off frequency for 60 consecutive seconds of walking, fast walking, and running divided in single gait cycles. The points A and B represent the global minima of the two RMSE curves, D and E the respective time delays and C is the projection of the point A onto the time-aligned-RMSE curve. Time delays were calculated from cross-correlation analysis.

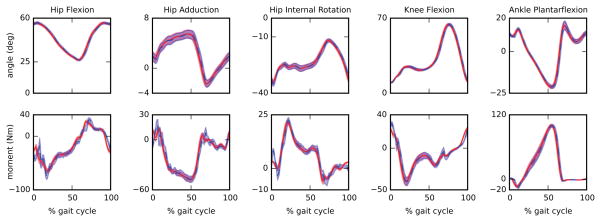
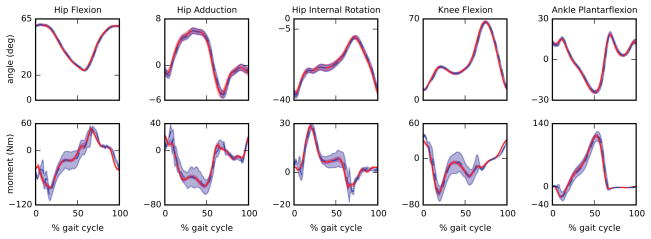
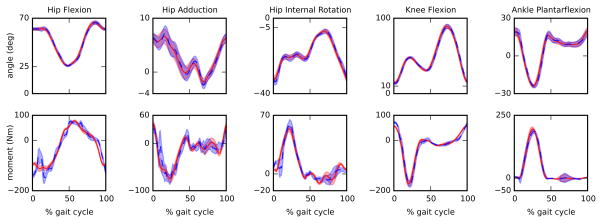
The third analysis showed that time delays ranged between 3.5 ms for hip flexion angle during walking and 20.5 ms for hip flexion moment during fast walking (Table 1). On average, joint angles time-aligned-RMSE varied from a minimum of 0.61 (0.37) deg for fast walking to a maximum of 1.04 (0.33) deg for running (Table 2). Joint moment time-aligned-RMSE varied from a minimum of 4.07 (2.19) Nm for walking to a maximum of 11.19 (6.16) Nm for running (Table 2). Figures 6, 7, and 8 show the average offline and real-time joint angles and moments for each task.

Table 1.

Time delays introduced by the real-time filtering. Filter cut-off frequency of 34 Hz was used for walking and fast walking tasks, and a cut-off frequency of 54 Hz was used for running. Average joint moments delays also reflect the results of analysis 2 (Figure 5). A cross-correlation analysis was used to compare offline and real-time data and calculate the delays.

Degree of Freedom	Walking		Fast Walking		Running
	Angles delay	Moments delay	Angles delay	Moments delay	Angles delay	Moments delay
	ms	ms	ms	ms	ms	ms
Hip Flexion	3.5	19.5	11.5	20.5	8.0	18.0
Hip Adduction	10.0	11.0	15.0	12.5	9.5	11.5
Hip Internal Rotation	7.5	9.0	14.0	15.5	11.0	10.5
Knee Flexion	9.0	13.0	14.5	18.0	9.5	10.5
Ankle	9.5	10.5	14.5	14.5	10.5	6.0
Average	7.9	12.6	13.9	16.2	9.7	11.3

Table 2.

Time-adjusted-RMSE of filtered joint angles and joint moments between offline and real-time data. For the real-time data, filter cut-off frequency of 34 Hz was used for walking and fast walking tasks, and a cut-off frequency of 54 Hz was used for running. For the offline data, filter cut-off frequency of 6 Hz was used. A total of 60 seconds per task were used in this analysis.

Degree of Freedom	Walking				Fast walking				Running
	joint Angle		Joint Moment		joint Angle		Joint Moment		joint Angle		Joint Moment
	RMSE		RMSE		RMSE		RMSE		RMSE		RMSE
	deg	SD	Nm	SD	deg	SD	Nm	SD	deg	SD	Nm	SD
Hip Flexion	0.91	0.02	7.36	0.54	0.39	0.01	14.22	2.00	0.81	0.05	21.91	2.13
Hip Adduction	0.16	0.01	5.74	0.51	0.21	0.02	10.25	1.01	0.53	0.04	13.67	1.49
Hip Internal Rotation	0.65	0.04	1.86	0.12	0.48	0.04	3.40	0.98	1.12	0.08	5.97	0.44
Knee Flexion	1.23	0.03	3.42	0.25	0.71	0.03	11.13	0.82	1.30	0.05	7.96	0.85
Ankle Plantarflexion	1.16	0.06	1.95	0.22	1.26	0.06	8.21	0.49	1.42	0.12	6.44	0.79
Average	0.82	0.39	4.07	2.19	0.61	0.37	9.44	3.77	1.04	0.33	11.19	6.16

Figure 6.

Comparison between filtered joint angles and joint moments computed offline (solid red) and in real-time (dashed blue) for gait cycles from 60 seconds of walking at 1 m/s (53 gait cycles). A cut-off frequency of 6 Hz and 34 Hz were used for the offline and real-time computation respectively. Shaded area represents 1SD.

Figure 7.

Comparison between filtered joint angles and joint moments computed offline (solid red) and in real-time (dashed blue) for gait cycles from 60 seconds of fast walking at 1.5 m/s (61 gait cycles). A cut-off frequency of 6 Hz and 34 Hz were used for the offline and real-time computation respectively. Shaded area represents 1SD.

Figure 8.

Comparison between filtered joint angles and joint moments computed offline (solid red) and in real-time (dashed blue) for gait cycles from 60 seconds of running 2.5 m/s (84 gait cycles). A cut-off frequency of 6 Hz and 54 Hz were used for the offline and real-time computation respectively. Shaded area represents 1SD.

Using the unconstrained gait2392 model, 32-markers marker-set, and 8 threads of inverse kinematics, the overall computation time to process a single data frame was less than 11 ms (Table 3). With the addition of the filtering time delay, the total delay was less than 31.5 ms.

Table 3.

Computation times to process a single data frame for each of the main steps in the real-time pipeline (Figures 1,2 and 3). For each of walking, fast walking, and running tasks, the computation times of 12000 frames were measured and then used to calculate mean and standard deviation (SD). Computation times associated with Vicon Nexus may vary depending on the version of Vicon Nexus. Also, given the multithreaded nature of the software, the GRF filtering can occur concurrently to the Inverse Kinematics, possibly reducing the total computation time. For this analysis the gait2392 OpenSim model, 32-markers marker-set, and 8 threads of inverse kinematics were used. Real-time filtering cutoff frequency were set to 34 Hz for walking and fast walking, and 54 Hz for running.

	Computation times	Walking		Fast walking		Running
		mean	SD	mean	SD	mean	SD
		ms	ms	ms	ms	ms	ms
Vicon Nexus	Marker reconstruction and labelling	3.078	0.333	3.226	0.355	3.483	0.487
	Data synchronisation	0.304	0.076	0.277	0.079	0.298	0.136
	Data transmission	0.183	0.051	0.162	0.030	0.167	0.054
Real-time OpenSim	Inverse kinematics	5.325	2.661	5.745	2.453	5.899	2.509
	Inverse Dynamics	0.347	0.051	0.345	0.058	0.356	0.085
	Joint angles filtering and differentiation	0.125	0.110	0.126	0.106	0.101	0.110
	GRF filtering	0.277	0.106	0.331	0.098	0.307	0.092
	Total	9.639	1.016	10.211	0.939	10.609	0.970

Discussion

We developed a software system that connects to a Vicon motion capture system and computes in real-time inverse kinematics and inverse dynamics using OpenSim without simplifications. We achieved a throughput up to 2000 fps for the gait2392 model, which is commonly used for gait analysis in OpenSim, and we described how to best select the cut-off frequency of the real-time filter to reduce the filter delay while minimising the error. Finally, when directly comparing results, offline and real-time pipelines showed close similarity between joint angles and moments.

Using more than 12 inverse kinematics threads did not result in any throughput improvement (Figure 4). This was due to hardware limitations and corresponded to all the 12 processing cores being used at 100% of their computational capacity. Nonetheless, the number of beneficial inverse kinematics threads is expected to increase when using a larger number of processing cores. Importantly, the single-threaded inverse dynamics solver did not present a computational bottleneck: the average computation time for the inverse dynamics varied from 0.347 ms for walking to 0.356 ms for running (Table 3), which corresponds to a theoretical throughput between 2800 and 2880 fps.

While joint moments and joint angles calculated in real-time and offline have limited differences (Table 2), these are still present even when they are time-aligned for maximum cross-correlation and when using the same cut-off frequency (Figure 5). Joint moments are calculated from filtered values of GRFs, centre of pressure, and joint angles. The filtering causes time delays that affect each of these signals’ frequency components differently, causing alteration in both time (Table 1) and magnitude (Table 2). These alterations of individual signals are combined in the inverse dynamics calculations, so resulting in larger distortions of the computed joint moments. This also explains the larger time delays observed for the joint moments when compared to the filtered joint angles (Table 1). Moreover, since the delay introduced by the real-time filtering is higher for frequency components closer to the cut-off frequency (Manal and Rose, 2007), the effects of the delay on the joint moment error is less evident when increasing the cut-off frequency (Figure 5). Conversely, higher cut-off frequencies result in noisy joint moments. A partial workaround would be applying forces and moments experienced by the force plates directly to the foot segment of the model, so avoiding the need to filter the centre of pressure, eliminating a possible source of error. However, this option was not available, since the raw data from the force plates were not accessible in real-time using the current version of Vicon DataStream SDK. Furthermore, mismatches in the filter cut-off frequencies used for kinematic and kinetic data introduce moments with artefacts (Kristianslund et al., 2012).

The use of constraints in the modified gait2392 (Lerner et al., 2015) model increased the solution times of approximately 40 times, resulting in a throughput of 50 fps when using 12 threads for inverse kinematics calculations (Figure 4). Constraints are used in multibody models to remove degrees of freedom and to define further relationships between coordinates. For example, Lerner et al. (2015) used weld constraints to create a closed-loop mechanism at the knee and enable the computation of the medial and lateral tibio-femoral contact forces. Also, the patella was constrained to move as a function of the knee flexion-extension angle using a coordinate coupler constraint. While the use of constraints is required to build a closed loop mechanism or implement a desired joint kinematics, it also increases the complexity of the model and the time required to solve the inverse kinematics problem (Sherman, 2014), discouraging their use in real-time applications. However, OpenSim provides an alternative approach to manage model constraints by solving a simplified model where constraint violations are permitted but with added penalisation in equation 2. This approach results in the same computational complexity of an unconstrained system, but the accuracy of the resulting kinematics must be evaluated for each model to ensure the correctness of the results.

When using a model without constraints, the system total delay was less than 31.5 ms (Tables 1 and 3), which is excellent for biofeedback applications. Delays are introduced at different stages of the process, and include marker reconstruction and labelling, filtering with phase delay, inverse kinematics and inverse dynamics processing, and data transmission. While data transmission delays cannot be optimised, both marker reconstruction and labelling depend on several factors related to the motion capture system and the data collection protocol, and their optimisation is mainly responsibility of the motion capture system manufacturers, Vicon in present case. However, care was taken to avoid marker occlusion during data collection, since they may slow the reconstruction and labelling process. Inverse kinematics and dynamics processing time depends on both the Simbody implementation of these tools and on the accuracy selected for the solver. Finally, the time delay introduced by the filter depends only on the cut-off frequency selection (Figure 5). The time delays could be accounted for by synchronising the feedback with the subsequent gait cycle, therefore allowing more time to compute the results. However, this approach would be an ad hoc solution suitable only for cyclical movements, such as walking, and cannot be applied in other contexts. Conversely, we presented a completely generic solution that can be used to the analysis of any task.

The experimental data used in this investigation was produced by Vicon cameras and a Bertec treadmill, but our system can be adapted to accept data from other devices or motion capture systems (e.g. Qualisys) provided they make available Application Program Interfaces to stream the data in real-time. Similarly, audio (Riskowski et al., 2009) or haptic feedback (Wheeler et al., 2011) can be used in place of the current visual feedback by substituting the Visualization thread in the real-time pipeline (Figure 1). Using a different treadmill, motion capture system, or filters, which directly affect the quality of the input data, could introduce additional source of variability and time delays in the results.

It could be argued that the analyses were performed by simulating real-time in the gait laboratory by replaying pre-recorded raw data files, which may not represent the real experimental conditions. However, Vicon Nexus was used in ‘live mode’ in conjunction with Vicon Virtual System, therefore reproducing the same behaviour whether the data were pre-recorded or produced by the treadmill and the cameras. Consequently, the operations for marker reconstruction and autolabelling were the same that would be performed during a real acquisition session in the gait laboratory. It is worth reporting that marker occlusions, marker mislabelling, or frame skipping were not observed when inspecting the raw dataset, so resulting in joint angles estimated via real-time pipeline that closely matched those obtained from the offline processing (Table 2). Nonetheless, issues in real-time recording or processing marker trajectories leading to larger errors cannot be excluded when using different motion capture systems, laboratory setups, and/or marker-sets. Conversely, sporadic spikes in the resulting joint moments were observed (Figures 6, 7, 8) and were mostly attributable to noise artefacts in computation of the centre of pressure, possibly caused by the treadmill’s belts.

Conclusion

Real-time estimation of joint angles and moments enables the use of methodologies to assess muscle function and evaluate joint contact forces for rapid clinical evaluation and biofeedback applications. For instance, static optimization has been used by van den Bogert et al. (2013) and electromyogram-informed models have already been applied in real-time for Achilles tendon rehabilitation after injury (Manal et al., 2012) and for monitoring in wearable robotics (Ceseracciu et al., 2015). However, those solutions were limited to a single generic model (van den Bogert et al., 2013), a individual joint (Manal et al., 2012), or used external devices to directly measure the joint angles (Ceseracciu et al., 2015). In this work we proposed a fully generic approach to calculate in real-time joint angles and moments that we plan to integrate with multiple degrees of freedom electromyogram-informed models (Pizzolato et al., 2015; Sartori et al., 2012). Our aim is developing a biofeedback system based on estimates of muscle and joint contact forces with the potential of strongly enhance current rehabilitation practices.