Constraint and Contingency Pervade the Emergence of Novel Phenotypes in Complex Metabolic Systems

Abstract

An evolutionary constraint is a bias or limitation in phenotypic variation that a biological system produces. We know examples of such constraints, but we have no systematic understanding about their extent and causes for any one biological system. We here study metabolisms, genomically encoded complex networks of enzyme-catalyzed biochemical reactions, and the constraints they experience in bringing forth novel phenotypes that allow survival on novel carbon sources. Our computational approach does not limit us to analyzing constrained variation in any one organism, but allows us to quantify constraints experienced by any metabolism. Specifically, we study metabolisms that are viable on one of 50 different carbon sources, and quantify how readily alterations of their chemical reactions create the ability to survive on a novel carbon source. We find that some metabolic phenotypes are much less likely to originate than others. For example, metabolisms viable on D-glucose are 1835 times more likely to give rise to metabolisms viable on D-fructose than on acetate. Likewise, we observe that some novel metabolic phenotypes are more contingent on parental phenotypes than others. Biochemical similarities among carbon sources can help explain the causes of these constraints. In addition, we study metabolisms that can be produced by recombination among 55 metabolisms of different bacterial strains or species, and show that their novel phenotypes are also contingent on and constrained by parental genotypes. To our knowledge, our analysis is the first to systematically quantify the incidence of constrained evolution in a broad class of biological system that is central to life and its evolution.

Introduction

Individual organisms or populations cannot produce every conceivable kind of phenotypic variation. In other words, phenotypic evolution is to some extent constrained. More precisely, an evolutionary constraint is a bias or limitation in the emergence of phenotypic variation in a given biological system (1). Examples of constraints on the organismal level include the absence of photosynthesis in higher animals, the absence of birds that can give birth to live young instead of to eggs, the general lack of teeth in the lower jaw of frogs, and the absence of palm trees in cold climates (1, 2). Other examples include constrained variation in segment number, orientation and identity in the fruit fly Drosophila melanogaster (3), and correlations among different characters, such as in allometric scaling (4). Molecular examples of phenotypic constraints include the absence of L-isomers in the 20 amino acids found in natural proteins (5), and a limited number of possible protein folds caused by the packing requirements of hydrophobic amino acids (6). It is useful to distinguish between absolute constraints, which occur when some phenotype cannot be produced, and relative constraints, when some phenotypes are more likely to arise than others.

A closely related concept is that of contingency. We speak of contingency when the origin of a novel phenotype depends on the history of a population, and specifically on preexisting genotypes or phenotypes (7, 8). For example, experimental evolution of Escherichia coli has shown that the emergence of citrate-utilization as a novel metabolic phenotype is contingent on the genetic history of a population (9). Analogously to constraints, one can distinguish between phenotypes that are absolutely or relatively contingent on evolutionary history. Although many anecdotal examples of constraints and contingent evolution exist, such examples do not allow one to quantify the potential for either phenomenon in any one class of biological system. We here undertake such a quantification using a computational approach applied to metabolic systems, which are ideal for this purpose for several reasons.

First, metabolic systems, and especially those of microbes, are an abundant source of new adaptations and innovations (i.e., qualitatively new adaptations). Especially important innovations are those that allow an organism to extract energy and chemical elements from new molecules, which can help it survive in new habitats. For instance, microorganisms have acquired the ability to utilize many nonnatural substances, such as polychlorinated biphenyls, chlorobenzenes, organic solvents, synthetic pesticides, and even antibiotics as food (10, 11, 12, 13, 14).

Second, experimentally validated computational methods such as flux balance analysis (FBA) provide efficient means to systematically predict metabolic phenotypes—the ability of an organism to survive on specific nutrients—from information about metabolic genotypes (15, 16). A metabolic genotype is the part of a genome encoding metabolic enzymes. However, computational analyses of metabolic systems often use a more abstract and compact representation of such a genotype, referring to it as the collection of chemical reactions that a metabolic reaction network is able to catalyze (17, 18, 19, 20, 21, 22, 23, 24, 25, 26).

Third, in metabolic systems, we are not restricted to studying the metabolism of any one organism, together with the constraints and contingencies it may be subject to. Instead, we can study the potential for contingency and constraint in entire classes of metabolic systems. To do so, we take advantage of Markov chain Monte Carlo (MCMC) algorithms (21, 23) (see Materials and Methods) that allow us to create large numbers of metabolisms. Each such metabolism is a complex network of chemical reactions with a given phenotype, but its complement of metabolic reactions is otherwise sampled at random from a universe of metabolic reactions that are known to exist among prokaryotes (see Materials and Methods). We refer to such metabolisms as “random viable metabolic networks”. The phenotypes we study are viability phenotypes, and specifically a metabolism’s ability to synthesize all essential biomass precursors in a minimal medium that harbors only a single carbon source. We consider 50 such carbon sources, i.e., 50 different metabolic phenotypes.

When analyzing phenotypic variability, it is important to consider the kinds of genotype changes that cause this variability. We focus on recombination-like processes as a means for genotypic change, and do so for two reasons. First, recombination is a ubiquitous force of genetic change, not only in eukaryotes but also in prokaryotes whose genomes are being continually reorganized through horizontal gene transfer. Second, in contrast to smaller-scale genetic change, such as point mutations, recombination causes larger-scale genetic change with greater potential to create novel phenotypes (27, 28, 29, 30, 31, 32). Thus, if we found that phenotypic evolution was constrained when recombination causes genotypic change, it would be even more constrained if point mutations caused such change.

In our simulations, we generated 1000 parental pairs of random viable metabolic networks for each of the 50 carbon utilization phenotypes. For each one of these 50,000 parental pairs, using a recombination-like process that mimics horizontal gene transfer in bacteria (see Materials and Methods), we generated 1000 offspring to obtain 50,000,000 recombinant metabolic networks. We focused on those recombinants that did not only retain viability on their parental carbon source, but also gained viability on at least one novel carbon source. For brevity, we will also refer to them as “innovative offspring”. We analyze their phenotypes and how they depend on parental phenotypes. In addition, we also study recombination among metabolic networks of 55 bacterial species or strains.

We find little evidence for absolute constraints and contingencies. That is, the metabolic phenotypes we consider can be brought forth through recombination among some parental metabolic networks. However, relatively constraints and contingencies are pervasive. Differences in the biochemical relatedness of carbon sources, and the ensuing correlations among different carbon usage phenotypes, can help explain some of these constraints and contingencies.

Materials and Methods

Genotype-phenotype representation in metabolic networks

The set of enzyme-catalyzed biochemical reactions that take place in an organism constitutes the organism’s metabolic reaction network, i.e., its metabolism. Each such metabolism contains a subset of the reaction universe of all biochemical reactions that are known to occur in some organism within the biosphere. We have manually curated a representation of the prokaryotic reaction universe, which comprises 5906 reactions known to occur in prokaryotes (see Supporting Materials and Methods for details). In this framework, we represent an organism’s metabolic genotype as a binary vector of length 5906, each entry of which corresponds to a given reaction in the universe, and is equal to 1 if the corresponding reaction is present in the network, and 0 otherwise. Hence, each genotype can be envisioned as a single member of a vast space of all possible metabolic networks, which contains 2⁵⁹⁰⁶ distinct genotypes. We determine the phenotype of a given metabolic genotype based on its ability to sustain life in one or more of 50 distinct minimal environments that differ only in the sole carbon source they contain (Supporting Materials and Methods). We consider a genotype viable on a given carbon source, if FBA (see Supporting Materials and Methods) predicts that it can produce all essential biomass precursors using this carbon source as its only carbon source (15). We used the biomass composition of the E. coli metabolic model iAF1260, because the sampling approach described in the next section starts from the E.coli metabolism (Supporting Materials and Methods). Our C++ implementation of FBA and the code necessary for the analyses in this article are available through this public github repository: https://github.com/rzgar/EMETNET.

Random sampling of parental metabolic network pairs from metabolic genotype space

We here employ a previously described in silico process that relies on MCMC random walks to generate randomly sampled viable metabolic networks, i.e., networks that are viable on a given carbon source, but that otherwise contain a random subset of reactions in the reaction universe (Supporting Materials and Methods) (21, 23). This procedure ensures uniform sampling from the set of all metabolic networks viable on a given carbon source. Our analyses required us to recombine pairs of parental metabolic networks (i.e., donor-recipient pairs) with particular features, such as a given genotypic distance (D), defined as the number of reactions differing between the parents. We used simultaneous genotype-converging MCMC random walks to generate pairs of metabolic networks with a given D (see Supporting Materials and Methods). We required parental metabolisms to be exclusively viable on a particular carbon source, i.e., to be inviable on all 49 other carbon sources we considered. In most of our analyses, we kept the number of reactions present in the metabolic networks constant and equal to that of E. coli with 2079 reactions.

Modeling a recombination-like process in metabolic networks

As in a previous contribution (32), we use a coarse-grained model of prokaryotic recombination that mimics the effects of horizontal gene transfer events between bacteria on metabolism (33, 34, 35, 36). This model is motivated by the importance of horizontal gene transfer as a means of genetic change. Through its high incidence, horizontal gene transfer can change the gene content of genomes on short evolutionary timescales (33, 37, 38). It can also occur between very distantly related organisms (39, 40). For several reasons, our recombination model also takes DNA deletions into consideration. The first is that during horizontal gene transfer, incorporating genes from a donor into a recipient genome relies on DNA rearrangements that can also delete resident genes (41). Second, the majority of newly acquired genes obtained via horizontal gene transfer reside in the genome only for short amounts of time (42). Third, the evolution of prokaryotic genomes is biased toward DNA deletions (43). Motivated by these observations, we here model prokaryotic recombination as a process where the transfer of biochemical reactions from a donor to a recipient is accompanied by concurrent deletion of reactions from the recipient metabolic network.

Specifically, to model recombination for each parental metabolic network pair, we generated 1000 recombinant offspring by 1) adding to the recipient metabolic network a given number n/2 of randomly chosen reactions that were present in the donor and absent from the recipient, followed by 2) deleting n/2 reactions randomly chosen from the recipient. Thus, the total number of reactions changed by a recombination event in the recipient is equal to n. In this contribution, we repeated most of our analyses by using three different values of n; namely n = 10, 20, and 30. Empirical observations also suggest that altering up to n = 60 reactions in a recombination event is biologically realistic, because horizontal gene transfer can affect long DNA regions (44). Importantly, the transferred material that is integrated into the host genome by recombination can constitute stretches of noncoding DNA, fragments of genes (45, 46), entire genes (47), multiple adjacent genes (48, 49), operons, transposable chromosomal elements, and plasmids, as well as other naturally occurring extrachromosomal elements (50). The length of contiguously transferred stretches may range from a few nucleotides (51) to >3 Mbp (44), i.e., some two-thirds of the length of the E. coli genome, which encodes >1300 reactions. In addition, some megabase-scale horizontally transferred DNA segments can become incorporated into a chromosome in the form of hundreds of smaller fragments (52). As we have discussed in a previous contribution ((32); Supporting Materials and Methods), the probability that a recombination event preserves viability exceeds 10⁻³ for values up to n = 60.

Modeling recombination in curated bacterial metabolic networks from the BiGG database

We used the R-package Sybil (53) to collect 55 well-annotated bacterial genome-scale metabolic networks available in the BiGG database (54). Each of these species or strains has its own biomass growth function, its own complement of reactions, and well-defined gene-reaction association rules that allowed us to model recombination on the level of genes instead of reactions. We used the genomic location of metabolic genes in these bacterial species or strains (55) to take gene linkage into account when modeling recombination.

To generate a recombinant metabolic network from a donor and a recipient organism, first a given stretch of DNA from the donor genome that contains a given number of metabolic genes is translated into reactions based on the gene-reaction association rules of the donor organism, and then the resulting reactions are added to the recipient metabolic network. Second, a given stretch of DNA from the recipient genome that contains a given number of metabolic genes is translated into reactions based on the gene-reaction association rules of the recipient organism, and then the resulting reactions are deleted from the recipient metabolic network.

In a recombination event between a pair of organisms, we set the number of genes in a given donor DNA stretch such that on average a given number of n = 5 reactions are added to the recipient metabolic network, and on average an equal number n = 5 of reactions are deleted from it. Because gene-reaction associations are not generally one-to-one and can be very complicated, and because most of the reactions that are encoded in a given stretch of DNA may already be present in the recipient metabolic network, the number of metabolic genes that needs to be added from donor to recipient genome, such that exactly n reactions are added to the recipient, will often be higher than n. In contrast, we found that the number of metabolic genes in a DNA stretch to be deleted from the recipient genome to eliminate n reactions from the recipient metabolic network is lower than n, because deletion of a single metabolic gene often causes elimination of multiple reactions.

More specifically, we modeled recombination among all distinct pairs of donor-recipient bacterial species or strains in our analysis (55 × 54 pairs). From each given pair we generated a recombinant offspring by adding a given (p) number of consecutive metabolic genes from the donor genome, followed by deleting a given (q) number of consecutive metabolic genes from the recipient genome. Importantly, we examined all possible combinations of (p) consecutive genes from the donor and (q) consecutive genes from the recipient. Thus, for a donor genome with $n$ metabolic genes, and a recipient genome with $m$ metabolic genes, we generated all (n – p + 1) × (m – q + 1) recombinant offspring, a number that exceeded 1,000,000 offspring for most pairs. Note that (p) and (q) are selected based on the gene-reaction association rules of the donor and recipient species or strains to ensure that any one recombination event adds on average five new reactions and deletes five reactions from the recipient metabolic network.

To study the effect of linkage on the emergence of novel phenotypes, we followed a second recombination procedure that neglects linkage between metabolic genes. That is, we added or deleted reactions randomly, just as we had done for randomly sampled metabolic networks, irrespective of the genomic position of the metabolic genes encoding these reactions. To do so, we examined all distinct donor-recipient pairs, and from each pair we generated the same number ((n – p + 1) × (m – q + 1)) of recombinant offspring as in the linkage-based approach, ensuring that on average five randomly chosen reactions are added from the donor and deleted from the recipient metabolic network.

To identify innovative offspring among all the generated recombinants, we used 30 carbon-containing metabolites on which none of the 55 bacterial species or strains are predicted to be viable (listed in Supporting Materials and Methods). To predict viability of a recombinant metabolic network using FBA, we used the objective function of the recipient, because recombinants are much more similar to the recipient than to the donor.

Results

All metabolic phenotypes can emerge through recombination

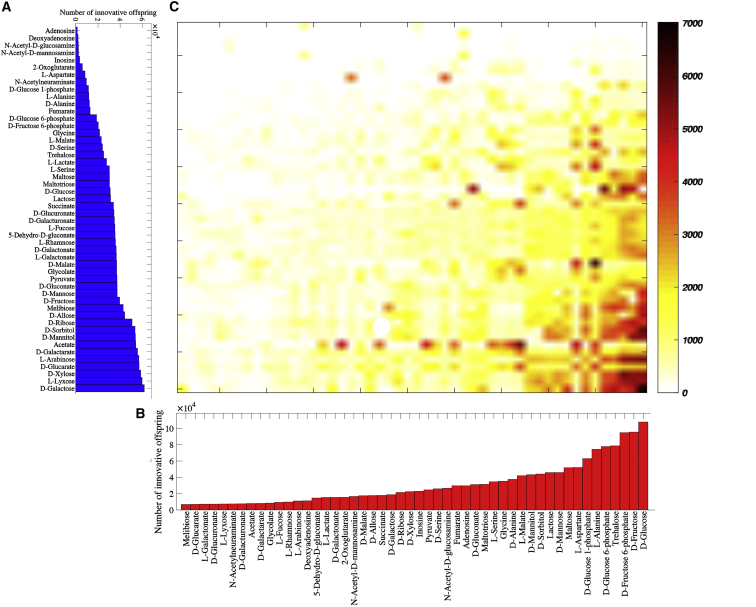
Our first analysis focused on the perhaps most fundamental question regarding absolute constraints: Do some parental phenotypes not give rise to any offspring with novel phenotypes? To find out, we quantified for each carbon source C_i and for each of the 1000 parental pairs viable on C_i, the number $N_{C_i\to }$ of offspring gaining viability on some new carbon source (C_j, j ≠ i, among their 10⁶ recombinant offspring, with n = 10 altered reactions relative to the parents). Fig. 1 a shows the distribution of this number, demonstrating that offspring with metabolic innovations can emerge from each of the 50 carbon usage phenotypes we analyzed. However, we also note that the number of offspring with a metabolic innovation varies greatly among different carbon usage phenotypes, ranging from 1433 for parents viable on adenosine to 61,835 for parents viable on D-galactose (per 1,000,000 offspring). We repeated this analysis by varying the number of reactions (n) altered during recombination, which shows that the relative abundance and the ranking of carbon sources in terms of the frequency of innovation stays almost the same for various n ((Figs. S1 and S2); n = 10 and 20, Spearman’s R = 0.9982; p < 10⁻⁶⁰; n = 10 and 30, Spearman’s R = 0.9750; p < 10⁻³³.) In sum, all parental phenotypes we consider can give rise to metabolic innovations.

Figure 1.

Recombination can create all 50 carbon-use phenotypes considered here. (A) The horizontal axis shows the number of innovative recombinant offspring (out of 1,000,000 offspring) resulting from recombination between parents viable exclusively on the carbon source specified on the vertical axis. (B) Shown here is the number of innovative recombinants (per 1,000,000 offspring) gaining viability on the novel carbon source specified on the horizontal axis. (C) Shown here is the number of innovative recombinant (per 1,000,000 offspring, coded according to the color legend) resulting from recombination between parents viable exclusively on the carbon source specified in (A), which have gained viability on the novel carbon source specified in (B). In these analyses, parental metabolic networks contain ||G|| = 2079 reactions, the same number as the E. coli metabolic network, and they differ in D = 100 reactions. Moreover, n = 10 reactions are swapped between parental metabolic networks during recombination.

Next, we asked whether different carbon usage phenotypes differ in their propensity to be found as novel offspring phenotypes, regardless of the parental phenotype. Fig. 1 b shows that this is indeed the case. But whereas all 50 carbon-usage phenotypes appear in the innovative offspring we analyzed, their prevalence $\left(N_{\to C_i}\right)$ varies by a factor 16 among carbon sources, ranging from 6783 innovative offspring gaining viability on melibiose to 107,784 gaining viability on D-glucose (among $50\times {10}^6$ recombinant offspring, and a total of 1,556,237 innovative offspring). This variability is similarly great with a number (n) of recombined reactions different from n = 10 (Figs. S1 and S2). We noted a negative correlation between $N_{C_i\to }$ and $N_{\to C_i}$ (Fig. S3), i.e., carbon-usage phenotypes that give rise to more innovative offspring are found less frequently as products of recombinational innovation.

Finally, Fig. 1 c shows the variability among different pairs of carbon sources in terms of their propensity for generating innovative offspring. In 2038 pairs (81.52% among the possible 2500 pairs of carbon sources (C_i, C_j), fewer than 1000 innovative recombinant (among 1,000,000 offspring) gain viability on C_j from recombination between parents viable on C_i, and only in 17 pairs (0.68%) do more than 5000 innovative offspring emerge. The largest number of innovative offspring (7071) emerges when parents viable exclusively on D-galactose give rise to offspring that gain viability on D-glucose.

To find out whether parental genotypic distance and the number of reactions in a metabolic network might affect our observations, we repeated our analyses with more divergent parents (D = 1000) and smaller metabolic networks (1800 and 1600 reactions, as opposed to the 2079 reactions identical to the number in E. coli, which we had used so far). Although recombination gives rise to fewer innovative offspring at higher D and for smaller networks (Fig. S4), the general patterns (Figs. S5, S6, and S7) remain similar to that of Fig. 1.

Also, we had so far recombined parents that were viable on the same carbon source. To find out whether this could affect our observations, we generated recombinational offspring where one parent is viable on glucose, and the other is viable on a different carbon source. We found that recombination again results in fewer innovative offspring (Fig. S8), but leaves the patterns observed in Fig. 1 intact (Figs. S9 and S10).

In sum, each of the 50 carbon usage phenotypes we consider can give rise to metabolic innovations. Conversely, recombinants can acquire viability on each of 50 carbon sources. Thus, at least from this analysis, there is no evidence for absolute constraints on carbon usage phenotypes. However, different carbon usage phenotypes differ greatly in their propensity to arise as metabolic innovations, providing a first line of evidence for relative constraints on metabolic innovation by parental phenotypes.

Novel metabolic phenotypes are relatively constrained by parental phenotypes

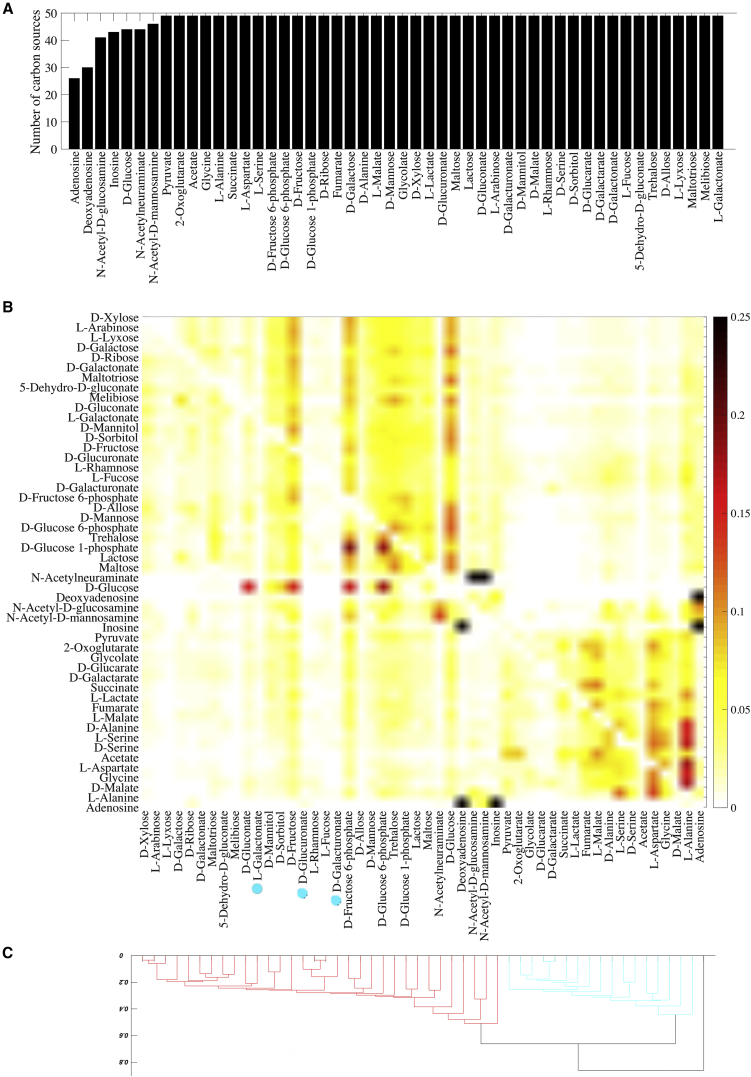
Our next analysis goes to the heart of the question we pose. For each of the 50 focal carbon sources C_i, we examined all innovative offspring originating from parents viable on C_i to find out whether gaining viability on each of the other 49 carbon sources (C_j, j ≠ i) is possible. For 43 of the 50 carbon sources C_i, this is the case (Fig. 2 a). That is, for such a parental carbon source C_i, at least one innovative offspring exists that gains viability on some new carbon source (C_j, j ≠ i). Even for the remaining seven carbon sources C_i, this holds for the majority of the carbon sources C_j. That is, starting from viability on five of the seven carbon sources C_i, recombination can produce viability on more than 40 of the 49 carbon sources C_j. The remaining carbon sources C_i are deoxyadenosine and adenosine, where recombination can produce metabolisms viable on 30 and 26 other carbon sources, respectively. Similar observations emerge when we repeat this analysis by increasing the number of reactions exchanged during recombination (Figs. S11 a and S12 a). In sum, for a majority (43 of 50) of parental phenotypes, there are no absolute constraints on metabolic innovation, i.e., all novel metabolic phenotypes considered here can arise through recombination.

Figure 2.

Emergence of innovative offspring can be constrained by parental phenotypes. (A) The horizontal axis shows the carbon source on which parental metabolisms are viable, and the vertical axis shows the number of novel carbon sources (among the remaining 49 carbon sources) on which at least one innovative offspring resulting from recombination between parental metabolic networks is viable. (B) Given here is the fraction of innovative recombinants (coded according to the color legend) resulting from recombination between parents viable exclusively on the carbon source specified on the vertical axis, which have gained viability on the novel carbon source specified on the horizontal axis. (C) Dendrogram of carbon sources clustered based on their innovation distance defined by the data in (B). We used the unweighted pair group method with arithmetic means for clustering carbon sources. Branches colored in red and cyan correspond to glycolytic and gluconeogenic carbon sources, respectively (except D-galacturonate, L-galactonate, and D-glucoronate (cyan circles), which are the gluconeogenic carbon sources). In these analyses, parental metabolic networks contain ||G|| = 2079 reactions, the same number as the E. coli metabolic network, and they differ in D = 100 reactions. Moreover, n = 10 reactions are swapped between parental metabolic networks during recombination.

Our next analysis (Fig. 2 b) provides evidence for abundant relative constraints, that is, some carbon-usage phenotypes C_j are more likely to emerge as metabolic innovations than others from parents viable on a given carbon source C_i. For example, 65.13% of the innovative offspring emerging from parents viable on glucose, gain viability on only four other carbon sources: 16.37% on D-fructose 6-phosphate, 17.72% on D-glucose 6-phosphate, 15.15% on D-fructose, and 15.89% on D-gluconate. The other 34.87% of metabolic innovations are distributed among 45 other carbon sources (on average each receiving 0.77% of the innovative offspring). As another example, for parents viable on D-serine, 46% of the innovative offspring gain viability on glycine (9.71%), L-aspartate (11.4%), L-alanine (16.73%) or D-alanine (8.16%) and the rest of 54% innovations is distributed among the other 45 carbon sources (each on average 1.2%).

We then clustered the 50 carbon sources based on their relative innovation distance in Fig. 2 b, where two carbon sources (C_i, C_j) are more distant if parents viable on C_i give rise to fewer offspring viable on C_j. Fig. 2 c shows that all glycolytic carbon sources (see Text S3) form one major branch of the resulting tree (colored red), and 17 of the 20 gluconeogenic carbon sources (exceptions: D-galacturonate, L-galactonate, and D-glucoronate) form another major branch (colored cyan). Hence, the propensity for innovation between carbon sources belonging to the same class is higher than those belonging to different classes. This observation hints at a cause of the relative constraints we observe, which we discuss in more detail in On the Underlying Causes of Constraints and Contingencies.

We observe qualitatively identical patterns when we repeat this analysis with altered numbers of reactions exchanged during recombination (Figs. S11 and S12), with altered genotypic distances among metabolic networks (Fig. S13), with smaller metabolic networks (Figs. S14 and S15), and with heterogeneous parental phenotypes (Figs. S16 and S17). However, in smaller metabolic networks, perhaps due to a substantially lower incidence of phenotypic innovation (Fig. S4), emergence of novel phenotypes is more constrained by parental phenotypes (Figs. S14 and S15). Moreover, for heterogeneous parental phenotypes where all the recipients are viable only on glucose and donors are viable on other carbon sources, carbon sources do not cluster according to innovation distance. The likely reason is that the recipient parental phenotype is constant in this analysis (Fig. S17).

In sum, different novel phenotypes are constrained in their evolution, because they originate with different probabilities from a given parental carbon-usage phenotype.

Emergence of innovative offspring is not absolutely, but only relatively, contingent on parental phenotypes

To complement our above analyses, we also studied whether some novel metabolic phenotypes are absolutely contingent on a specific parental phenotype. That is, can they only emerge from parents with this phenotype? To find out, we studied the parental phenotypes of all innovative offspring that have gained viability on a given carbon source C_j, and did so for all carbon sources C_j. Fig. S18 a shows that for all novel carbon-usage phenotypes C_j, innovative offspring can emerge from parents with at least 40 different phenotypes. Similar observations emerge when recombination alters a different number of reactions (Figs. S19 a and S20 a).

Although absolute contingency does therefore not exist in our study system, we observe relative contingency: different parental phenotypes C_i have a greater or lesser propensity to give rise to a given carbon-usage phenotype C_j (Fig. S18 b).

For example, 42.15% innovative offspring gaining viability on D-galactarate originate from parents viable only on four different carbon sources, namely D-malate (12.86%), D-galacturonate (11.99%), pyruvate (8.70%), and glycolate (8.61%). The other 57.85% originate from parents viable on the other 45 carbon sources (where each accounts for 1.28% of the innovative offspring on average). Another example regards viability on succinate, 20.8% of which originates from parents viable on acetate and the rest is distributed among other parental phenotypes (each contributing 1.65% on average).

And once again, classification of carbon sources based on their distance (Fig. S18 b) results in separation of glycolytic and gluconeogenic carbon sources (Fig. S18 c). We observe similar patterns when we repeat this analysis with a different number of reactions altered during recombination (Figs. S19 and S20), with higher genotypic distances among parental metabolisms (Fig. S21), with smaller metabolic networks (Figs. S22 and S23), and with heterogeneous parental phenotypes (Figs. S24 and S25). In smaller metabolic networks, perhaps due to the lower incidence of innovation (Fig. S8), relative contingency is most pronounced (Figs. S22 and S23).

In sum, although we do not observe absolute contingency, some parental phenotypes are much more likely than others to give rise to specific new metabolic phenotypes, which show relative contingency.

On the underlying causes of constraints and contingencies

As we observed in Figs. 2 c and S18 c, one specific measure of biochemical similarity among carbon sources can help explain the patterns of constraints and contingencies that we observed. That is, carbon sources can be broadly partitioned into glycolytic and gluconeogenic classes, where parents viable on a carbon source in one class are most likely to produce innovative offspring viable on a new carbon source in the same class. To provide complementary evidence that constraints increase with biochemical distance among carbon sources, we used two other biochemical similarity measures, and determined whether they are associated with the innovation distance between carbon sources.

The first defines the metabolic distance between a given pair of carbon sources (C_i, C_j) as the average shortest path between C_i and C_j in the substrate graph of 1000 metabolic networks viable on C_i (Supporting Materials and Methods). This network-based biochemical distance is significantly associated with the number of recombinants that are generated from parents viable on C_i, and that gain viability on carbon source C_j (Fig. S26, Pearson r = −0.2722, and p < 10⁻⁴¹). A second quantifier of distance relies on the superessentiality index, the proportion of random viable networks in which a given reaction is essential for viability on a given carbon source (Supporting Materials and Methods). Here also, innovation declines with increasing biochemical distance among carbon sources (Pearson r = –0.3935, and p < 10⁻⁸³, Fig. S27 a; Supporting Materials and Methods).

Another complementary analysis involving biochemical distance focuses on the individual reactions that can be transferred from donor to recipient, and that can lead to metabolic innovation. For this analysis, it is relevant that the majority of metabolic innovations is caused by the transfer of a single key reaction (32). We analyzed transferable reactions in greater depth, focusing on all 1000 parental donor metabolic networks viable on a given carbon source C_i, and on the (D/2 = 50) reactions that are present in the donor metabolic network, but are absent in the recipient, and so can potentially be transferred from the donor to the recipient. Specifically, we quantified the fraction of the 1000 parental donor metabolic networks viable on C_i in which at least one reaction among the (D/2 = 50) transferrable reactions can have C_j as a product or substrate, reasoning that such reactions may be especially prevalent among reactions causing viability on C_j. The number of innovative offspring that gain viability on C_j by recombining parents viable on C_i, increases significantly with the fraction of transferable reactions that involves C_j (Pearson r = 0.163, and p < 10⁻¹⁵; Fig. S27 b). It is not difficult to see that this association can also be a consequence of the relatedness of two carbon sources. The reason is that metabolic networks viable on a given carbon source C_i are likely to already have some reactions involving metabolically related carbon sources C_j. In this case, it is more likely that addition of a single novel reaction leads to the completion of a pathway in the recipient that is needed to metabolize C_j. We note that these correlation coefficients, albeit statistically significant, are low in magnitude, implying that these properties cannot fully explain the mechanism underlying phenotypic constraint. A more detailed analysis of each pathway connecting different carbon sources may be required to fully understand the causes of constraints and contingencies. We leave such an analysis for future work.

Emergence of innovative offspring is constrained by, and contingent on, parental genotypes of both donors and recipients

Our analyses thus far were focused on parental metabolic networks with given phenotypes, which allowed us to analyze constraints and contingencies emerging from such phenotypes. However, the emergence of novel phenotypes may also depend on parental genotypes, and we next analyzed such constraints. Random viable metabolisms are less than ideal for such an analysis for two reasons. First, they do not derive from any one organism with its specific gene-reaction association, and they do therefore not allow us to define genotypes on the level of genes. Second, our simple model of recombination for such metabolisms neglects the linkage of metabolic genes on chromosomes.

To overcome these limitations, we focused our next analysis on curated metabolic networks of 55 distinct bacterial strains or species. Their metabolic genes, reactions, gene-reaction association rules, metabolic gene locations, and biomass reactions are well studied and available from the BiGG database (54). We used 30 carbon sources on which none of the 55 metabolisms are viable to study the emergence of novel phenotypes (Supporting Materials and Methods). We examined all 2970 (= 55 × 54) distinct pairs of donor-recipient species or strains, and subjected them to recombination events that take into account metabolic gene linkage (see Modeling Recombination in Curated Bacterial Metabolic Networks from the BiGG Database). From each donor-recipient pair, we generated millions of recombinant offspring to identify innovative offspring, that is, offspring gaining viability on at least one of the 30 novel carbon sources.

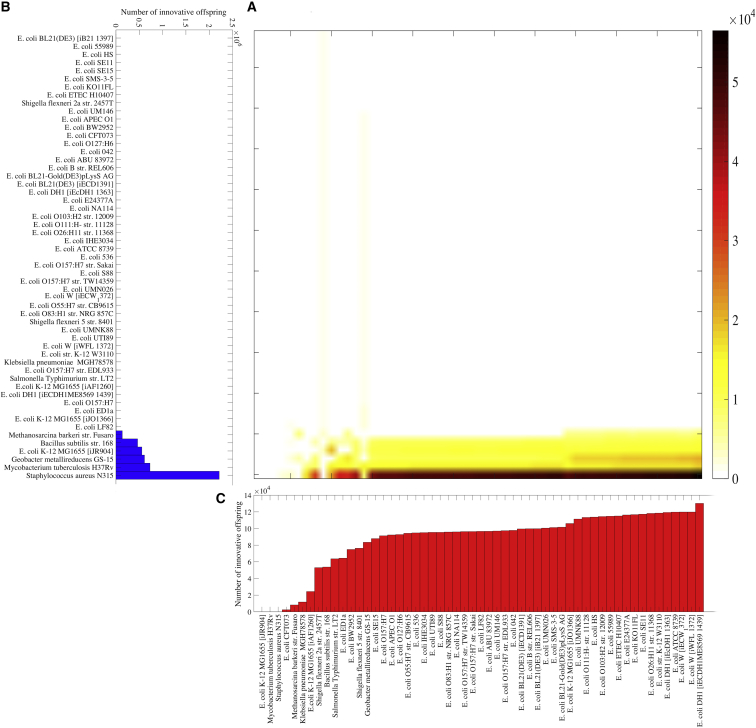
We observed that the emergence of novel phenotypes is strongly contingent on the recombining parental genotypes. Among the 2970 pairs of recombining parental genotypes, only 347 pairs (11.68%) brought forth at least one innovative offspring (Fig. 3 a). In addition, these 347 pairs vary greatly in the number of innovative offspring that they can generate. The highest number of innovative offspring (56,461, or 1.17% of recombination events) emerges when the donor is Staphylococcus aureus N315 and the recipient genotype is E. coli DH1, and the lowest number ((904), or 0.02% of recombination events) emerges when the donor is E. coli BL21 and the recipient genotype is Bacillus subtilis.

Figure 3.

Emergence of innovative offspring is contingent on and constrained by parental genotypes. (A) Shown here is the number of innovative recombinant offspring resulting from linkage-based recombination between bacterial DNA donors specified on the vertical axis of (B), and the corresponding recipients specified on the horizontal axis of (C) (number of recombinants encoded according to the color legend). (B) Shown here is the total number of innovative recombinant offspring involving the donor genotype specified on the vertical axis. (C) Shown here is the total number of innovative recombinant offspring involving the recipient genotype specified on the horizontal axis.

The emergence of innovative offspring was also strongly constrained by the donor genotype (Fig. 3 b). A quantity of 97.84% of all innovative offspring identified in this analysis was generated from only six donor genotypes. The other 49 donors together were responsible only for 2.16% of all innovative offspring. Recombination involving Staphylococcus aureus N315 donors caused an exceptionally large fraction of 45.97% of innovative offspring. Despite this strong relative constraint on donor genotypes, we did not observe any absolute constraints, because all 55 prokaryotic metabolisms generated at least one innovative offspring as donor genotypes—although the contributions of 49 metabolisms were so small that they are not visible in Fig. 3 b.

In contrast, the emergence of innovative offspring was not strongly constrained by the parental recipient genotype. That is, the majority of recipient metabolisms (48 out of 55) can generate approximately the same number of innovative offspring (Fig. 3 c). Only four of them generated considerably fewer innovative offspring, and three of them did not generate any innovative offspring as recipients (Fig. 3 c). Importantly, the potential of metabolic genotypes in generating innovative offspring when used as donors or recipients was highly asymmetric. For example, although Staphylococcus aureus and Mycobacterium tuberculosis accounted for most innovative offspring as donor genotypes, they did not generate any innovative offspring as recipient genotype. Similarly asymmetric biases emerged when we repeated the analysis with a recombination approach that does not take into account metabolic gene linkage, suggesting that such asymmetry is not caused by gene linkage but by the metabolic gene content of genomes (Fig. S28). In sum, the emergence of innovative offspring is strongly contingent on the genotypes of parental donor-recipient pairs, and especially on donor genotypes.

Discussion

In this study, we systematically analyzed the prevalence of constraint and contingency for emerging novel phenotypes in complex metabolic systems. We did so by computationally emulating recombination among thousands of parental metabolic network pairs with specific phenotypes, and created millions of recombinant metabolic networks.

Overall, we observed little evidence for absolute constraints in the origin of novel phenotypes, i.e., metabolic networks with most carbon-usage phenotypes can give rise to all 50 novel carbon-usage phenotypes we consider here. However, there is ample evidence for relative constraints, that is, some carbon-usage phenotypes are much more likely to arise relative to others from any one parental carbon-usage phenotype.

Similarly, we observed no absolute contingency in the origin of novel phenotypes, i.e., recombinant metabolic networks with a given novel carbon-usage phenotype can originate from all 50 parental phenotypes. In contrast, relative contingency is pervasive. That is, a given novel carbon-usage phenotype is much more likely to originate from some parental phenotypes than from others. Importantly, our observations remain qualitatively unchanged when we alter various properties of parental genotypes, such as their genotypic distance, which suggests that the different extents of constraints we observe may be an inherent property of metabolic systems.

We also analyzed the causes of constraints and contingencies, where several complementary analyses point to the importance of biochemical similarities among carbon source pairs (C_i, C_j), where parents are viable on C_i, and recombinant offspring gain viability on C_j. First, if parents are viable on a carbon source that belongs to one of two major biochemical classes (glycolytic or gluconeogenic), then recombinant offspring tend to gain viability on a carbon source within the same class (Fig. 2 c; Fig S18 c). Second, the smaller the number of reactions that separate C_i and C_j in a metabolic network, the greater the likelihood that offspring gain viability on C_j. Third, offspring gain viability on C_j most often if a reaction transferred between donor and recipient involves C_j. This, in turn, is most likely if the recipient already harbors some reactions necessary to metabolize C_j, and thus if catabolizing C_i and C_j involves similar reactions. Our analysis used carbon sources that are not very heterogenous. Many of them, for example, are sugars that play important roles in central carbon metabolism. This biochemical similarity among carbon sources reduces constraints, and it may be responsible for the paucity of evidence for absolute constraints.

One strength of our approach is that it can address contingency and constraint in an entire class of system, and not just a single organism. However, the approach also has several limitations.

First, any study relying on sampling is sensitive to sample size. For example, if we had analyzed only 100 parental metabolic networks and 100 recombinants per pair, we would not have observed any innovative offspring for most parental carbon usage phenotypes. Thus, we would have misleadingly concluded that absolute constraints are frequent in our study system. And even though we had generated a (computationally expensive) sample of 1,000,000 offspring for each parental phenotype, we did see a small number of carbon sources showing evidence for absolute constraints. Such apparent absolute constraints may disappear at even higher sample sizes (Fig. S29 a). In contrast, our assertion that relative constraints exist is less sensitive to sample sizes (Fig. S29 b). Our current analysis generated fewer than 1000 innovative metabolisms for most (C_i, C_j) pairs, and larger sample sizes may help us find out why some pairs (C_i, C_j) are more or less involved in metabolic innovation.

Second, our work is based on FBA (15, 16), which neglects the influence of gene and enzyme regulation. However, because regulatory changes toward optimal expression of enzymes readily occur, even on the short timescales of laboratory evolution, this limitation may not affect our main observations (Supporting Materials and Methods).

Third, a recent study showed that the genome-scale metabolic networks are likely to include thermodynamically impossible energy-generating cycles (EGCs), which are capable of charging energy metabolites without nutrient consumption (56). These EGCs can artificially inflate biomass flux and so may mislead evolutionary simulations. Most of our randomly sampled viable metabolisms indeed harbor EGCs (97.3% and 97.8% of sampled metabolisms viable on glucose and acetate, respectively; Supporting Materials and Methods). However, these EGCs do not strongly affect the emergence of novel phenotypes, nor do they substantially distort the patterns of relative constraint we observed (Figs. S30, S31, and S32; Supporting Materials and Methods).

Finally, in our simulations using random metabolic networks, following common practice in the field (17, 18, 19, 20, 21, 22, 23, 24, 25, 26), we define metabolic genotypes on the level of biochemical reactions rather than on that of genes or DNA. This representation neglects potentially important information, and especially the linkage of related metabolic genes on chromosomes, which may affect the outcome of recombination. To address this limitation, we also modeled recombination among metabolisms of 55 prokaryotic species or strains in a way that includes gene linkage information. This analysis also demonstrates strong constraints and contingencies in the emergence of novel metabolic phenotypes.

A previous experimental evolution study suggested a strong relative constraint in the emergence of a novel citrate utilization phenotype, which required thousands of generations of laboratory evolution subject to mutation and selection to emerge (9). Although our simulations are not strictly commensurate with any experimental study, for example, because we do not consider DNA changes explicitly, we speculate that such relative constraints would be less pronounced in any system where recombination is abundant, because recombination can cause larger-scale changes than mere point mutations that would alter individual reactions or transport processes (9). This was one motivation to choose recombination as an agent of genetic change in the first place, reasoning that any constraints visible in the presence of recombination might be even stronger in the presence of less dramatic genetic changes.

Metabolic systems are one of the three classes of biological systems in which phenotypic variation is crucial for evolutionary adaptation and innovation (57). The other two are macromolecules (protein and RNA) and regulatory systems. Predicting phenotypes in these systems is less straightforward than for metabolic systems (58, 59, 60). In proteins, for example, phenotypes form through a complex and incompletely understood 3D folding process (58), and in regulatory systems, gene expression phenotypes emerge from complex interactions among regulatory molecules (59, 60). Our understanding of inherent biases in phenotypic variability will not be complete until we understand contingencies and constraints in these classes of systems as well, which remains an important task for future work.

Author Contributions

S.-R.H. and A.W. designed research. S.-R.H. performed research. S.-R.H. and A.W. analyzed data and wrote the paper.

Editor: Reka Albert.

Supporting Citations

References (61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74) appear in the Supporting Material.