An Efficient Method for Estimating the Hydrodynamic Radius of Disordered Protein Conformations

Abstract

Intrinsically disordered proteins play important roles throughout biology, yet our understanding of the relationship between their sequences, structural properties, and functions remains incomplete. The dynamic nature of these proteins, however, makes them difficult to characterize structurally. Many disordered proteins can attain both compact and expanded conformations, and the level of expansion may be regulated and important for function. Experimentally, the level of compaction and shape is often determined either by small-angle x-ray scattering experiments or pulsed-field-gradient NMR diffusion measurements, which provide ensemble-averaged estimates of the radius of gyration and hydrodynamic radius, respectively. Often, these experiments are interpreted using molecular simulations or are used to validate them. We here provide, to our knowledge, a new and efficient method to calculate the hydrodynamic radius of a disordered protein chain from a model of its structural ensemble. In particular, starting from basic concepts in polymer physics, we derive a relationship between the radius of gyration of a structure and its hydrodynamic ratio, which in turn can be used, for example, to compare a simulated ensemble of conformations to NMR diffusion measurements. The relationship may also be valuable when using NMR diffusion measurements to restrain molecular simulations.

Introduction

Intrinsically disordered proteins (IDPs) and intrinsically disordered regions (IDRs) of proteins play important roles in central cellular processes such as cell-cycle regulation (1), transcription (2), membrane receptor signaling (3, 4), and nuclear transport (5). Thus, despite lacking a globular, folded structure—and often being substantially disordered under physiological conditions—they are able to perform specific and important biological functions (6).

Due to their high flexibility and fast dynamics, IDPs are difficult to characterize structurally, and are thus often described through integrative structural biology approaches (4, 7, 8). In addition to biophysical experiments, molecular simulation methods have emerged as central in our ability to describe disordered proteins and to interpret experimental data on these complex systems. In particular, much of our knowledge of the structural properties of IDPs and IDRs stems from combinations of molecular dynamics (MD) or Monte Carlo simulations and NMR spectroscopy (9, 10, 11, 12).

Recent years have witnessed dramatic advances in both the force fields and sampling methods used in MD simulations, and detailed comparisons, e.g., between simulations and NMR experiments, have shown continued accuracy in simulations of globular proteins, short, flexible peptides, and protein folding (13). In contrast, simulations of the unfolded state of folded proteins or IDPs (10, 14, 15, 16, 17, 18, 19) have suggested that many force fields result in overly compact structures. To help alleviate this problem and enable more accurate simulations of disordered proteins, several approaches for force field improvements have been suggested (15, 20, 21, 22, 23). Nevertheless, it still remains unclear which force fields perform best for a given system and molecular property (16).

Statistical coil models have also been used extensively to describe IDPs (24, 25, 26). Because of their computational efficiencies, these models are particularly attractive for sampling the many different kinds of structures IDPs may attain. Further, they have been shown to provide a relatively accurate description of the sequence-local structural properties as well as the overall expansion of the polypeptide chain (27).

The biological functions of disordered regions are intimately linked to their dynamical behavior, and the overall expansion of the polypeptide chain can be important for its ability to act as scaffolds and choreographers in, for instance, signaling. Specifically, different IDPs and IDRs have been found to have varying amounts and types of transient local structures, and they appear to be differentially compacted, likely reflecting the distribution of charges and/or hydrophobic amino acids along the chain (28).

Despite the increased focus on describing the global and local structural properties of IDPs and the molecular reasons for why individual disordered proteins have different levels of expansion, we still do not fully understand the relationship between protein sequence and structural properties. Similarly, the relationship between the local and global structural properties remains incompletely understood (29, 30, 31). Although computation has proven efficient in linking sequence with both local and global structure of IDPs, as well as their functions, the link between computation and experiment is far from trivial, and there is a continued need for validation of molecular simulations against experiments.

Whereas local structural properties can be experimentally assessed by a variety of NMR properties, including scalar and residual dipolar couplings and chemical shifts to provide residue-specific information (11), the overall expansion of the chain is accessible through other methods, including small-angle x-ray scattering (SAXS) (32, 33), pulsed-field gradient NMR diffusion measurements (PFG NMR) (34), size-exclusion chromatography (SEC) (35), or fluorescence correlation spectroscopy and dynamic light scattering (36). Although SAXS experiments probe the radius of gyration (R_g), PFG NMR, SEC, and fluorescence correlation spectroscopy depend on the hydrodynamic properties of the protein chain. In particular, PFG NMR generally reports on the translational diffusion coefficient (D_t) of a protein, although rotational motions may contribute under special conditions (37). D_t is in turn related to the hydrodynamic radius, R_h, through the Stokes-Einstein equation (38),

$$D_{\text{t}}=\frac{k_{\text{B}}T}{6\pi \eta R_{\text{h}}}.$$ (1)

Thus, by measuring D_t for a protein and a reference molecule with known R_h, PFG NMR provides a convenient and accurate method to measure R_h (34).

Although both R_g and R_h depend on the overall expansion of the polypeptide chain, they do so via different physical principles (Fig. 1), and they thus contain different information about proteins. Furthermore, because of the dynamic nature of IDPs, measured values of R_g and R_h are averages over a very large number of individual conformations that may differ substantially in size and shape. Because SAXS provides information about <R_g²> and PFG NMR provides information on <R_h⁻¹>, the two experiments effectively report on different statistical moments of the distribution of expanded conformations. This effect was elegantly exploited in a study that combined SAXS and NMR to investigate the unfolded state of an SH3 domain (39).

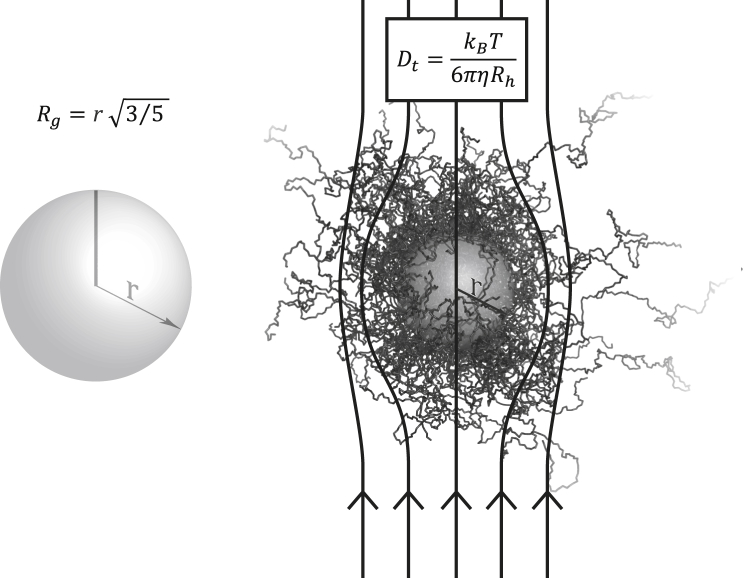
Figure 1.

Visual representation of the radius of gyration and hydrodynamic radius. (Left) The radius of gyration (R_g) of an object can be calculated as the root mean-square distance between each point in the object and its center of mass. Thus, for a protein, it directly reports on the typical distance between an atom and the center of mass of the protein. In the case of a solid sphere, $R_{\text{g}}=r\sqrt{3/5}$. (Right) The Stokes radius or hydrodynamic radius (R_h) of a solute is the corresponding radius of a hard sphere that diffuses at the same rate as that solute. D_t is the translational diffusion coefficient.

To utilize the information available in PFG NMR experiments to validate and determine computationally generated protein ensembles, it is desirable to have an effective and accurate method for calculating R_h from large conformational ensembles. Also, when experimental measurements are available for both R_g and R_h, it would be useful to have a method that relates the two at the molecular level. One method currently used to calculate hydrodynamic properties with substantial accuracy, including R_h and D_t, is provided by the HYDROPRO program (40, 41), which uses a surface-shell model and target-function minimization calculations. The surface-shell model is created by representing the molecule’s shape with a number of spheres. As the friction of the molecule only depends on the molecules in the solute-solution interface, the spheres inside the molecule are removed and the hydrodynamic properties are calculated based on the surface shell. The procedure is repeated for different levels of fine graining of the shell model and extrapolated to high resolution. The accuracy of these calculations, however, comes at a computational cost. Thus, for example, the calculation of R_h for a single conformation of a 200 aa residue protein on a single Intel i5 2.7GHz CPU core takes up to ∼30 min (depending on the accuracy required). This may complicate applications on ensembles that consist of many thousands of conformations, or when R_h needs to be calculated on the fly when used as a restraint in structure determination. We therefore sought to combine the accuracy of HYDROPRO and the ease of calculating the R_g by developing an efficient and sufficiently accurate method to relate R_g and R_h for unfolded and disordered protein ensembles.

We set out from earlier work (39) that had established an empirical relationship between R_g and R_h for selected proteins, but noted that the resulting parameters varied between the different proteins. We sought to expand that work by explicitly studying the chain-length dependency of the relationship between the ratio R_g/R_h and R_g. We thus generated coil models of different chain lengths and sequences, and used these to derive a relationship that can be used to estimate R_h from R_g (or vice versa) for proteins between 20 and 450 residues in length. The relationship is highly accurate, with a relative error of 3% in the estimated value of R_h, and it should be directly applicable to validation of structural ensembles of IDPs using experimental measurements of hydrodynamic properties.

Methods

We used Flexible-Meccano (24) with default settings to generate ensembles of three different types of polypeptide sequences with different chain lengths for each type (Table 1): 1) poly-valine, 2) polypeptides with a sequence composition similar to that of IDPs (Table S1) (42), and 3) a set of 12 IDPs whose R_h has previously been measured by PFG NMR experiments (Table S2) (43). For poly-valine and IDP-like polymers, we used chain lengths of N = 20, 30, 40, 80, 100, 200, 300, 400, and 450 residues, whereas the experimentally characterized IDPs were of lengths between 40 and 237 residues (43). The sequences of the random IDP-like polymers were generated to match the amino acid composition of the Disprot database (42) after removing engineered proteins, variants, fragments of <15 residues, and duplicate sequences.

Table 1.

Overview of Peptides Used in This Study

Ensemble	No. of Sequences	Sequence Length, N	Reference
Poly-valine	9	20,30,40,80,100,200,300,400,450	N/A
IDP-like	9	20,30,40,80,100,200,300,400,450	DisProt
IDP	12	40,61,92,95,104,110,112,140,189,198,234,237	(43)

See Supporting Material for additional details.

For each of the resulting 30 polypeptides, we generated 100 conformations using Flexible-Meccano. To examine whether our final model for calculating R_h is biased by the use of Flexible-Meccano to sample the structures, we also tested it using conformations sampled by all-atom MD simulations. In particular, we extracted ∼100 conformers from each of two previously published (20) very long simulations of HIV1-integrase and α-synuclein (12 and 20 μs, respectively) performed using the CHARMM22^∗ force field (44) in conjunction with the TIP4P-D water model (20).

We used HYDROPRO (40, 41) to calculate D_t for each of the structures. Before the HYDROPRO calculations, we added side chains to the Flexible-Meccano structures using PULCHRA with default settings (45). As the number of mini-spheres for calculating the surface-shell mode reached the upper limit allowed by HYDROPRO for peptides with chain length >300, we opted to calculate the hydrodynamic properties of these longer peptides using the coarser-grained “residue-based” model (HYDROPRO INDMODE 4 with default settings). For peptides with chain length ≤300, calculations were generally performed using the “all-atom” INDMODE 1 with default settings, but the values were also calculated using INDMODE 4 to examine the effect of this coarser model. In all cases, the resulting D_t values were converted to a R_h using the Stokes-Einstein relationship at 298 K and with η = 1 cP. For all conformations, we also calculated the R_g from the positions of the C_α atoms only, so that the relationship we have derived can be applied to backbone as well as all-atom models.

We also used the Kirkwood definition (46) to calculate R_h, using the pairwise distances, r_ij, between the C_α atoms only:

$$R_{\text{h}}^{-1}={\langle r_{ij}^{-1}\rangle }_{i\ne j}.$$ (2)

We calculated the asphericity (Δ) and prolateness (S) using

$$\Delta =\frac{3}{2}\frac{\text{tr}\left({\hat{Q}}^2\right)}{\text{tr}{\left(\hat{Q}\right)}^2}$$ (3)

and

$$S=27\frac{\text{det}\left(\hat{Q}\right)}{\text{tr}{\left(\hat{Q}\right)}^3},$$ (4)

where $\hat{Q}$ is a traceless matrix related to the gyration tensor, Q (47).

Results and Discussion

As the starting point for our approach, we followed previous work that developed an approximate relationship between R_g and R_h for specific proteins (9, 39). Theory suggests that in specific limiting cases, there is a simple relationship between R_g and R_h (48). For an idealized spherical molecule (representing either folded proteins or compact conformations of disordered proteins), for example, the ratio $R_{\text{g}}/R_{\text{h}}=\sqrt{3/5}\sim 0.78$. At the other end of the scale, renormalization group theory shows that for a disordered coil, the same ratio is between 1.2 and 1.6, depending on whether the chain is self-avoiding or not (49). Thus, the ratio $R_{\text{g}}/R_{\text{h}}$ depends on shape and compaction.

The fact that the $R_{\text{g}}/R_{\text{h}}$ ratio depends on the level of expansion is also reflected in the known, experimentally parameterized scaling laws for proteins that relate the chain length, N, to R_g and R_h. These generally take the form

$$R_{xs}=R_{0xs}{N}^{{\nu }_{xs}},$$ (5)

where x = {g, h} determines whether the relationship refers to R_g or R_h, and s = {folded, unfolded, IDP} refers to which of these states the scaling law is meant to describe. Empirically determined values for these parameters (Table 2) reveal that the scaling exponents $\left({\nu }_{xs}\right)$ are ∼0.33 for folded proteins and ∼0.6 for disordered proteins. The value for the compact state is thus as expected for structures where the volume scales linearly with the number of monomers. A scaling exponent of ∼0.6 for a disordered chain follows from both basic considerations of polymer chains (50) and more detailed renormalization group calculations (51).

Table 2.

Previously Determined Scaling Laws for Proteins

Rx	State	R0 (Å)	ν	Reference
Rg	folded	2.2	0.38	(56)
Rg	unfolded	1.9	0.60	(57)
Rh	folded	4.8	0.29	(34)
Rh	folded	4.9	0.28	(43)
Rh	unfolded	2.2	0.57	(34)
Rh	unfolded	2.3	0.55	(43)
Rh	IDP	2.5	0.51	(43)

In contrast to the similar scaling exponents, it is evident that the scaling factors, $R_{0xs}$, differ for R_g and R_h, and that they also depend on whether the protein is compact or expanded. Thus, as expected from theory, the scaling laws also show that the ratio R_g/R_h increases substantially in an expanded state compared to a compact state. Together, these results reiterate how R_g and R_h contain independent information that reports on the overall properties of the chain, so that their ratio depends on how expanded the chain is.

Based on the considerations outlined above, one might expect a phenomenological relationship that relates the ratio R_g/R_h to both the compaction of the chain, e.g., quantified via R_g as well as chain length, N. Such a relationship could be very useful to help interpret experimental measurements of R_g and R_h. At this point, it is, however, worth stressing that both the experimental and theoretical scaling laws generally refer to ensemble-averaged quantities. Thus, the parameters in Table 2 and the theoretical scaling exponents for disordered polymers refer to averages observed over an ensemble and are not expected to be directly applicable to individual conformations. Instead, we aim to fit them by calculating R_h from the R_g values of single structures.

To calculate R_h from R_g for individual conformations, Choy et al. (39) developed phenomenological relationships between the ratio R_g/R_h and the overall chain expansion, quantified as the R_g for single conformations. In particular, they created structural models of disordered conformations of several proteins, with various levels of expansion for each protein, and calculated R_g and R_h (using HYDROPRO) for each conformation. They found empirically that for each protein, the ratio R_g/R_h was well described as a linear function of R_g as

$$R_{\text{g}}/R_{\text{h}}=a{R}_{\text{g}}+b$$ (6)

(or, equivalently, R_h⁻¹ = a+bR_g⁻¹), and that the ratios for the smallest and largest R_g values converged to the values roughly expected for a spherical molecule and disordered state, respectively. Although a roughly linear relationship was observed for each protein, the values of a and b differed. Thus, for the shortest protein (crambin; 46 residues) they found a = 0.034 Å⁻¹ and b = 0.38, whereas for the longest (reduced lysozyme; 129 residues) they found a = 0.015 Å⁻¹ and b = 0.53.

These results suggested that there appears to be a general theory-based, but phenomenological, linear relationship between the ratio R_g/R_h and R_g, but that the details of this relationship depend on the length of the polypeptide chain. This dependency can be conceptually understood by the fact that the magnitude of R_g that is needed to be in the coil regime, and hence for the ratio R_g/R_h to increase, depends on the chain length.

We sought to extend this work to derive a relationship that can be used to estimate R_h from the calculated value of R_g for a given conformation for an unfolded protein of any length. This is important also because the length span of IDPs and IDRs is very wide (52). Using Flexible-Meccano (24), we generated conformational ensembles of three series of polypeptides (30 peptides in total) and with different chain lengths between 20 and 450 residues (Table 1; Tables S1 and S2), giving a total of 3000 individual structures. We chose this sampling method because it has previously been shown to provide accurate models of the local structure of unfolded proteins as well as a reasonably accurate description of the overall expansion of the chain (27). As we use the conformations simply to relate R_h to R_g, and not to model other properties of unfolded configurations, we expected the method to be sufficiently accurate, and validated this assumption using conformations obtained from state-of-the-art MD simulations (see below).

To account for potential sequence dependencies, we performed the Flexible-Meccano calculations on 1) poly-valine homopolymers, 2) sequences with an IDP-like amino acid composition, and 3) 12 authentic IDPs with measured R_h. In addition to the IDPs and IDP-like sequences, we chose to study poly-valine, since this amino acid is expected to sample expanded conformations similar to unfolded proteins and because it had previously been used as a homopolymeric model of protein conformations (53). Because the Flexible-Meccano model only has local structural propensities and excluded volume, and, e.g., no hydrophobic effect, we did not expect that the actual details of the sequence would have a big effect, nor did we observe such an effect (see below).

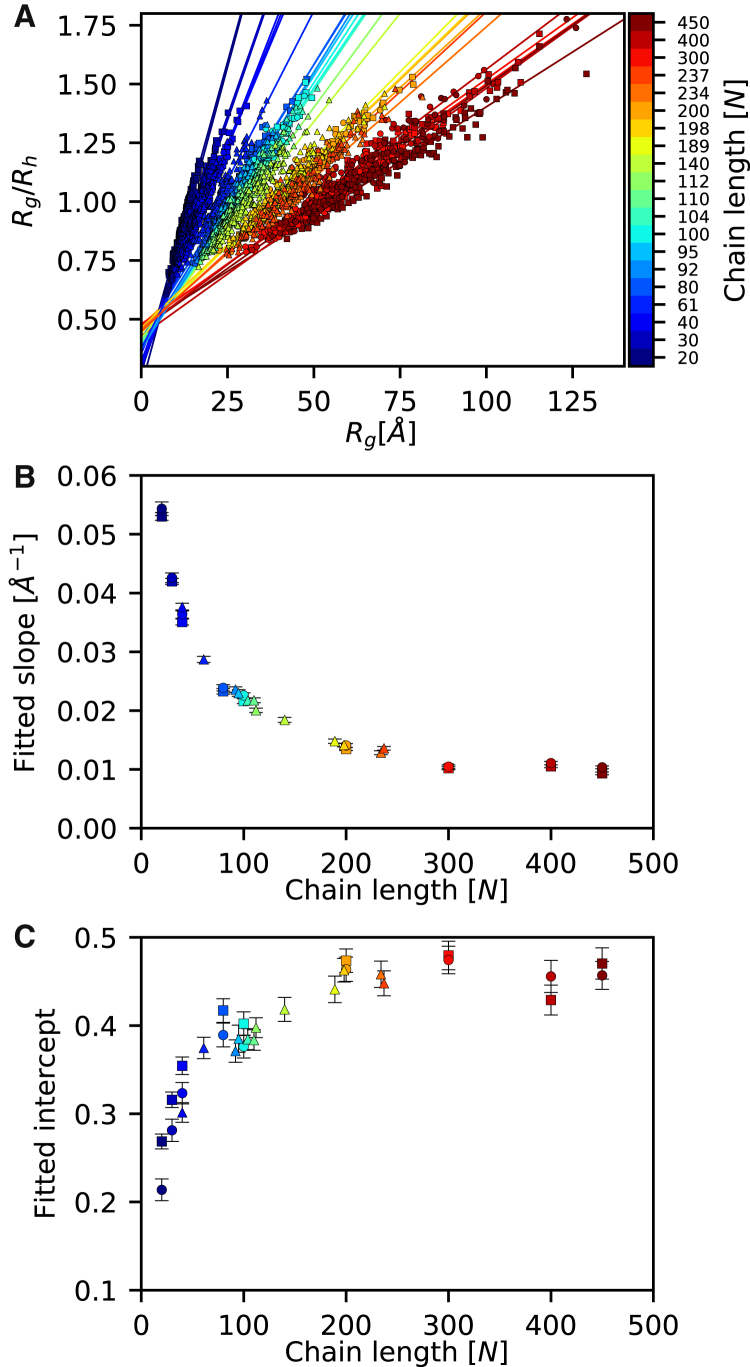
For each of the 100 conformations of the 30 peptides, we calculated R_h using HYDROPRO and R_g from the C_α atoms. We found that the R_g/R_h ratio for different individual peptide conformations spanned roughly the same range (0.8–1.6) as that suggested by theory for ensembles of compact globules and expanded chains, respectively (Fig. 2 A). As short polypeptides obviously are maximally expanded at a lower value of R_g compared to a long polypeptide, the slope depends on the chain length. This is clearly evident from a more detailed view of the ranges of R_g and R_h, and of the R_g/R_h ratio, that we sampled for each peptide (Figs. S1, S2, and S3), which also shows that the linear relationship holds for all three classes of peptides. For each peptide, we thus fitted the data separately to the linear relationship (Eq. 6), with the values of the two parameters, a_N and b_N, being different for each polypeptide and with the dependency of the chain length, N, explicitly stated (Fig. 2 A; Figs. S1, S2, and S3).

Figure 2.

An empirical relationship between R_g and R_h. For each of 30 polypeptides varying in length between 20 and 450 residues, we sampled 100 structures and calculated the hydrodynamic radius (R_h) and radius of gyration (R_g) for each structure. (A) In line with previous findings, we observed an approximately linear relationship between the ratio R_g/R_h and R_g, but with slope and intercept differing between polypeptides of different lengths (indicated by different colors). We fitted each dataset (indicated by the different shapes: squares for poly-valine; circles for IDP-like; and triangles for IDPs) to a straight line and observed that both the slope (B) and the intercept (C) systematically depended on the number of amino acid residues in the polypeptide. Error bars represent the error of fits. Note that the different sets of peptides appear to follow the same trends, suggesting that in this model it is the length of the peptide, not the composition, that is most relevant. The data for each peptide are shown separately in Figs. S1, S2, and S3. To see this figure in color, go online.

The best-fit values of a_N (Fig. 2 B) and b_N (Fig. 2 C) revealed the expected chain-length dependency of these two parameters. We also found that the values did not appear to depend on the sequence of the polypeptide, since peptides from the three different classes of the same length had comparable values of a_N and b_N (Fig. 2, B and C). We note here that this observation likely just reflects the choice of sampling model used (Flexible-Meccano), since it only takes sequence effects into account when modeling the local structural properties. Thus, in reality, one would expect that different peptides of the same length could have different compactions depending on their sequence composition (28). As the goal here, however, is to “translate” between R_g and R_h, we focus just on sampling different levels of compaction for proteins of different lengths.

Based on these data and the finding that the parameters a_N and b_N appeared to depend systematically on N, we aimed to derive a simple relationship to predict R_h from R_g and N. As a starting point for finding such a relationship, we used the theoretically and empirically justified scaling laws (Eq. 5; Table 2). By also assuming the empirically observed linear relationship (Fig. 2 A; Eq. 6) and making simplifying assumptions, we obtained the following expression (see also Supporting Material and Eq. S6), which we find describes the entire dataset with sufficiently high accuracy:

$$\frac{R_{\text{g}}}{R_{\text{h}}}\left(N,R_{\text{g}}\right)=\frac{{\alpha }_1\left(R_{\text{g}}-{\alpha }_2{N}^{0.33}\right)}{N^{0.60}-N^{0.33}}+{\alpha }_3.$$ (7)

We subsequently fitted the three parameters in Eq. 7 globally to the full set of R_g and R_h data for the 30 peptides. As R_h is averaged as <R_h⁻¹> we fitted (by the least-squares approach) a form of Eq. 7 expressing R_h⁻¹ as a function of R_g, N, and the three parameters and obtained the best-fit parameters α₁ = (0.216 ± 0.001) Å⁻¹, α₂ = (4.06 ± 0.02) Å, and α₃=(0.821 ± 0.002).

As a test of the robustness of the calculations and the dependency of the types of peptides we used in the fit, we also performed individual fits to the three peptide sets (poly-valine, IDPs, and IDP-like polymers). The results of the three fits were very similar, as evidenced, e.g., by the very similar models obtained for short, medium, and long chain lengths (Fig. S4). As a consistency check, we also compared the R_h values calculated using HYDROPRO with those calculated directly using the Kirkwood formula (Eq. 2) using the pairwise distances between the backbone C_α atoms (Fig. S5). As expected, the values derived by HYDROPRO, which take solvation effects into account, were ∼19% larger than those calculated directly from the atomic positions. Nevertheless, the two are surprisingly strongly correlated, suggesting that one may also estimate R_h using Eq. 2 (Fig. S5).

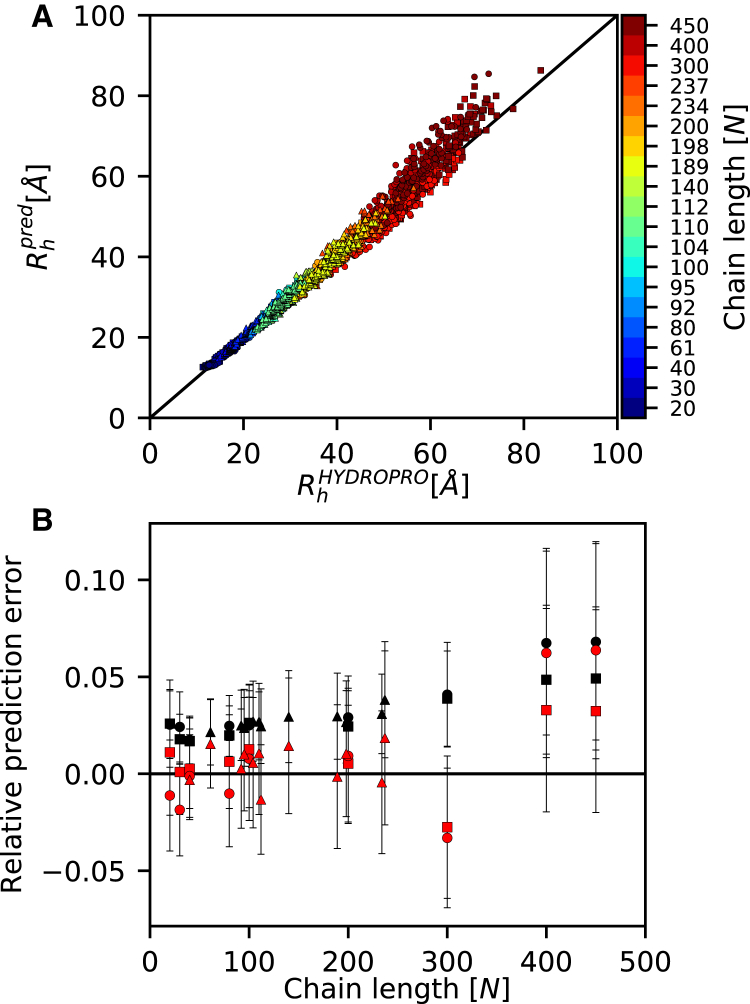
To visualize the quality of the global fit to Eq. 7, we used the equation to predict the entire set of R_h values from the C_α R_g data and chain lengths, and compared these values to those obtained directly using HYDROPRO. The results showed a very good relationship (Fig. 3 A), with a Pearson correlation coefficient of 0.99, an overall root mean-square deviation between the two values of 2 Å, and an average relative error in the predicted R_h of 3% and between 1.7 and 5.9% for the individual peptides. The average signed error is 0.4%, varying from −3.0 to 4.8% for the individual peptides, demonstrating that on average the equation provides an almost unbiased estimate of R_h.

Figure 3.

Quality of model for predicting the hydrodynamic radius. We assessed the quality of the global model (Eq. 7) by back-calculating R_h from R_g and N, and then compared the resulting values to those obtained by HYDROPRO. (A) The results show a strong correlation across the entire range of levels of compactions and chain lengths, with (B) a small increase in error (unsigned error in black) and a bias (signed error in red) toward overestimating R_h for the longest peptides (see also main text). Error bars represent the standard deviation. The differently shaped symbols represent the different datasets: squares for poly-valine, circles for IDP-like, and triangles for IDPs. To see this figure in color, go online.

We also analyzed to what extent the errors depended on the chain length. The results showed that the relative error was mostly constant for chain lengths between 20 and 300 residues (relative error 1–3%) (Fig. 3 B). For the two longest peptides (400 and 450 residues), for which the hydrodynamic properties were calculated using a coarser-grained model (see Methods), the errors were slightly larger (5–6%) with Eq. 7 generally overestimating R_h.

To test whether the differences in model used might be the cause of this observation, we also compared R_h calculated using the more detailed (atom-based) calculations with the coarser (residue-based) model for the peptides (N ≤ 300) where both calculations were possible (Fig. S6). The results suggest that the residue-based method underestimates R_h for the longest peptides, suggesting that the apparent overestimation from Eq. 7 compared to HYDROPRO for the longest peptides (Fig. 3) might in part be explained by the HYDROPRO values being underestimated in the residue-based model.

We also examined whether particular shapes of the conformers caused systematic effects on the error when using Eq. 7 to predict the R_h value. The asphericity (Δ) and prolateness (S) parameters have previously been used to describe the shapes of both folded and unfolded protein chains (54), and so we calculated these values for each of the conformations. In particular, we correlated the error of the predicted R_h values (Eq. 7 versus HYDROPRO) with the asphericity and prolateness (Fig. S7) and found a weak correlation between the error and these parameters.

All of the calculations described above are based on conformations of disordered protein structures that were generated by Flexible-Meccano. Because this model only takes steric repulsion and local structural preferences into account, we wanted to examine whether the observed relationship between R_g and R_h also holds for conformations generated by more realistic energy functions. Thus, we extracted ∼100 conformations from two previously published long MD simulations of the disordered apo N-terminal zinc-binding domain of HIV1 integrase and α-synuclein (20). These simulations were based on the CHARMM22^∗ force field in conjunction with the TIP4P-D water model, a combination that has been shown to provide a relatively realistic description of IDPs (20). We thus compared the R_h values calculated from Eq. 7 and HYDROPRO, and the results (Fig. S8) show that for these conformations also there is very good agreement between the two. Thus, the model that we obtained appears to be broadly applicable, and we conclude that overall, Eq. 7 provides a sufficiently accurate estimate of R_h, with an accuracy comparable to that inherent in using HYDROPRO (41).

Conclusions

IDPs are generally characterized by their lack of a well-defined secondary and tertiary structure and a broad distribution of conformations. Depending on the overall amino acid composition and sequence patterns, IDPs may also differ substantially in their compaction (28), which may, in turn, have important consequences for function and biophysical properties (55). Molecular simulations and modeling offer a unique opportunity to provide a link between sequence, structural properties, and function, but experimental validation is still required. Here, we provide a simple, general, fast, and accurate approach to calculate the R_h for large ensembles of disordered proteins from their R_g and chain length, N, and thereby enable comparison of computationally generated conformational ensembles against experimental values from, e.g., PFG NMR or SEC measurements. The model that we derived should also be useful when constraining, e.g., distributions of R_g using measurements of the average values of R_g and R_h (39). Future studies could also explore whether the relationship may be used for globular proteins with IDRs. The expression may also potentially be used in methods for restraining simulations using experimental data (12) and to exploit more generally the different averaging properties of SAXS, PFG NMR, and SEC experiments that depend on both the level of expansion and the shape of the disordered conformations.

Author Contributions

K.L.-L. conceived the idea; M.N. and E.P. performed the simulations and calculations; M.N. and K.L.-L. performed the fitting analyses; E.P., B.B.K., and K.L.-L., designed the research; M.N., B.B.K., E.P., and K.L.-L. analyzed the data and wrote the manuscript.

Editor: Rohit Pappu.