Dynamics of Tissue-Induced Alignment of Fibrous Extracellular Matrix

Abstract

Aligned fibers of extracellular matrix (ECM) affect the direction, efficiency, and persistence of migrating cells. To uncover the mechanisms by which multicellular tissues align their surrounding ECM before migration, we used an engineered three-dimensional culture model to investigate the dynamics of ECM alignment around tissues of defined geometry. Analysis of ECM alignment over time revealed that tissues rapidly reorganize their surrounding matrix, with a characteristic time that depends on the type of cell and the initial tissue geometry. We found that matrix metalloproteinase activity is not required for matrix alignment before cell migration. Instead, alignment is driven by Rho-mediated cytoskeletal contractility and accelerated by propagation of tension through intercellular adhesions. Our data suggest that multicellular tissues align their surrounding matrix by pulling collectively to exert strain, which is primarily a physical process. Consistently, the pattern of matrix alignment depends on tissue geometry and the resulting distribution of mechanical strain, with asymmetric tissues generating a higher degree of matrix alignment along their longest axes. The rapid ability of multicellular tissues to physically remodel their matrix enables their constituent cells to migrate efficiently along aligned fibers and to quickly change their direction according to other microenvironmental cues, which is important for both normal and disease processes.

Introduction

Within tissues, cells are surrounded by a fibrous network of extracellular matrix (ECM), an important structural component of the cellular microenvironment that also contains a variety of chemical and mechanical cues that influence cell fate. Cells can sense the mechanical rigidity of their surrounding ECM, and the topography of the polymer network dictates the number and spatial distribution of cell-matrix attachments (1, 2, 3). Individual ECM fibers can also serve as potential paths for cell migration, both in single- and multicellular contexts. For example, alignment of the ECM perpendicular to the boundary of a tumor is thought to precede invasion, with the aligned fibers providing tracks that guide migration of cancer cells, enhancing their migration efficiency and directional persistence (4, 5, 6). Oriented fibers can similarly facilitate metastatic intravasation (7). Moreover, we recently showed that the alignment of collagen fibers directly influences the direction and persistence of collective migration by non-metastatic cells (8). Cell-induced alignment of ECM fibers, therefore, appears to be an important component of the migration process, preceding cellular translocation. Although several studies have focused on the relationship between the structure of the ECM and the behavior of single cells of a particular type (5, 9, 10), little is known about the dynamics of multicellular-tissue-induced ECM alignment in three dimensions (3D), how the alignment process might vary across tissues comprised of different cell types, or what cellular processes drive the alignment of adjacent fibers in a multicellular context. Understanding the dynamic relationship between individual cells, their neighbors, and their surrounding ECM will provide insight into how these interactions might play a role in complex tissue microenvironments.

Here, we characterized and quantified the dynamics of tissue-induced alignment of the matrix surrounding 3D multicellular tissues. We used a microfabrication-based approach to vary the initial tissue geometry as well as the constituent cells. We investigated alignment dynamics at the level of both the individual fiber and the network, and we determined the relative roles of contractility and proteolysis in the alignment process. Generally, we found that tissues rapidly aligned their matrix within 24 h primarily by pulling on the adjacent matrix fibers, consistent with previous reports that collagen fibers can be aligned by mechanical strain alone, with the majority of fibers being aligned under 30% strain (5). Comparing different cell types and molecularly altering cell-cell force transmission revealed that strongly cohesive tissues aligned their surrounding matrix faster than weakly cohesive tissues. Altogether, our results provide, to our knowledge, novel insights into the complex relationship between multicellular tissues and their surrounding ECM, as well as how the level of coordination between constituent cells within a tissue contributes to these tissue-matrix interactions. Our findings suggest that matrix alignment occurs primarily due to a physical mechanism driven by tissue-induced strain, which is governed by cell-cell adhesion as well as tissue geometry. This appears to be a universal phenomenon that likely plays a role before collective migration in a variety of biological processes including development and cancer invasion.

Materials and Methods

Cell culture and reagents

Functionally normal EpH4 mouse mammary epithelial cells (11) were cultured in 1:1 Dulbecco’s modified Eagle’s medium (DMEM)/F12 medium supplemented with 2% fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA), 5 μg/mL insulin, and 50 μg/mL gentamicin (Sigma-Aldrich, St. Louis, Missouri). MDA-MB-231 human breast cancer cells (ATCC, Manassas, VA) and 4T1 murine mammary carcinoma cells (ATCC) were cultured in 1:1 DMEM/F12 supplemented with 10% fetal bovine serum and 50 μg/mL gentamicin. NIH3T3 mouse fibroblasts (ATCC) were cultured in 1:1 high glucose DMEM supplemented with 10% calf serum (Atlanta Biologicals) and 50 μg/mL gentamicin. Cells were maintained in a 37°C incubator under 5% CO₂. Intercellular force transmission was inhibited by transducing cells with an adenoviral vector containing a dominant-negative truncation mutant of E-cadherin lacking the N-terminal β-catenin binding domain (EΔ); the adenovirus containing green fluorescent protein (GFP) AdGFP was used as a control. Cells were transduced at a multiplicity of infection resulting in >99% transduction efficiency. Ectopic expression of E-cadherin was achieved using pcDNA3.1-E-cadherin-GFP (Addgene; 28009), with pcDNA3.1-yellow fluorescent protein (YFP) as a control, and MDA-MB-231 cells stably expressing these proteins were collected from pooled populations that were selected using G418 (1 mg/mL) for 3 weeks. The following reagents were used at the concentrations indicated: blebbistatin (12.5 μM; Sigma-Aldrich), Y27632 (20 μM; Tocris, Bristol, United Kingdom), lysophosphatidic acid (LPA) (10 μg/mL; Cayman Chemicals, Ann Arbor, Michigan), and GM6001 (40 μM; Calbiochem, San Diego, CA).

Microfabricated 3D tissues

3D multicellular tissues were constructed as described previously (12, 13, 14). Briefly, acid-extracted bovine type I collagen (Koken, Tokyo, Japan) was mixed at a final concentration of 4 mg/mL with growth factor-reduced Matrigel (BD Biosciences, San Jose, CA) in a 1:4 ratio and gelled at 37°C against a stamp of poly(dimethylsiloxane) (Sylgard 184, Ellsworth Adhesives, Germantown, WI) to generate micrometer-scale cavities of defined geometry. Cells were allowed to settle within the cavities, and then a second layer of the collagen and Matrigel mixture was placed on top of the gel. Tissues of circular cross section were comprised of ∼60–80 cells.

Confocal reflection microscopy

The fibrillar structure of collagen was visualized using a Nikon A1 laser-scanning confocal microscope in reflection mode. Cells were transduced with AdLifeAct-mRuby at a multiplicity of infection resulting in >99% transduction efficiency. Collagen matrices were illuminated with an Argon laser (488 nm) and imaged in reflection mode using a 40× oil-immersion objective. Image stacks (319 × 319 × 30 μm, spaced 2 μm in the z-direction) were acquired for each engineered tissue and the surrounding collagen fibers.

Quantifying fiber alignment and tissue-induced strain

Confocal stacks spanning 30 μm of the engineered tissues and their surrounding collagen fibers were projected onto a single image, creating a two-dimensional (2D) maximum-pixel-intensity z-projection to visualize the structure of the network around the tissues in the xy plane throughout the depth of the tissue. The projected images of the 3D engineered tissues were then linearized and segmented in ImageJ to quantify collagen alignment relative to the entire surface of the tissues up to a distance of 128 μm away. Collagen fiber angles were quantified using MATLAB by measuring the orientation of pixel intensity gradients of the confocal reflection images, as described previously (15). Fibers were considered to be aligned if they were oriented between 70° and 110° from the tissue surface; all other fiber angles were considered to be unaligned. At least 299 individual fiber angles were measured per time point per experimental replicate. Generally, the tissues exhibited a multiphasic decay behavior in the percentage of unaligned matrix fibers, eventually reaching a plateau value. The alignment half-life (t_1/2) was calculated by determining the midpoint in the time to reach the plateau value. A quantitative estimate of tissue-induced strain was calculated as a change in tissue diameter divided by the initial diameter. Three independent experimental replicates conducted on separate days were used for the fiber alignment and tissue-induced strain analyses. For each individual experimental replicate, at least five individual tissues per sample per time point were analyzed and pooled.

Real-time microscopy

Time-lapse movies of engineered tissues were collected between 0 and 8 h after seeding using a Nikon A1 laser-scanning confocal microscope in reflection mode fitted with a humidified environmental chamber held at 37°C and 5% CO₂.

Imaging and immunofluorescence analysis

Samples were fixed with 4% paraformaldehyde in phosphate-buffered saline and washed three times with phosphate-buffered saline. Nuclei were labeled using Hoechst 33342 and visualized under ultraviolet illumination. Fixed samples were blocked with 10% goat serum and 0.3% Triton X-100 and incubated overnight in primary antibody against β-catenin (Sigma-Aldrich) diluted 1:200 in blocking buffer. Blocked samples were washed with 0.3% Triton X-100 and incubated overnight with Alexa Fluor-conjugated secondary antibody (Invitrogen, Carlsbad, CA) diluted 1:1000 in blocking buffer, followed by additional washing. Samples were visualized using a spinning-disk confocal scanner (BD Biosciences) attached to a Nikon Ti-U microscope using a Plan Fluor 20× 0.45 NA objective.

Statistical analysis

Results were analyzed using GraphPad Prism (GraphPad Software, La Jolla, CA). To compare the number of fibers detected per subimage by our MATLAB analysis, we used a one-way analysis of variance (ANOVA). The Student’s t-test, or one-way ANOVA with Bonferroni’s post-test for multiple comparisons, was used to compare terminal values of both the percentage of unaligned fibers and tissue-induced strain where appropriate. Mean values represent at least three independent experiments and error bars represent the mean ± SE. For all statistical tests, p < 0.05 was considered to be statistically significant.

Results

Multicellular tissues exert strain that aligns surrounding matrix fibers

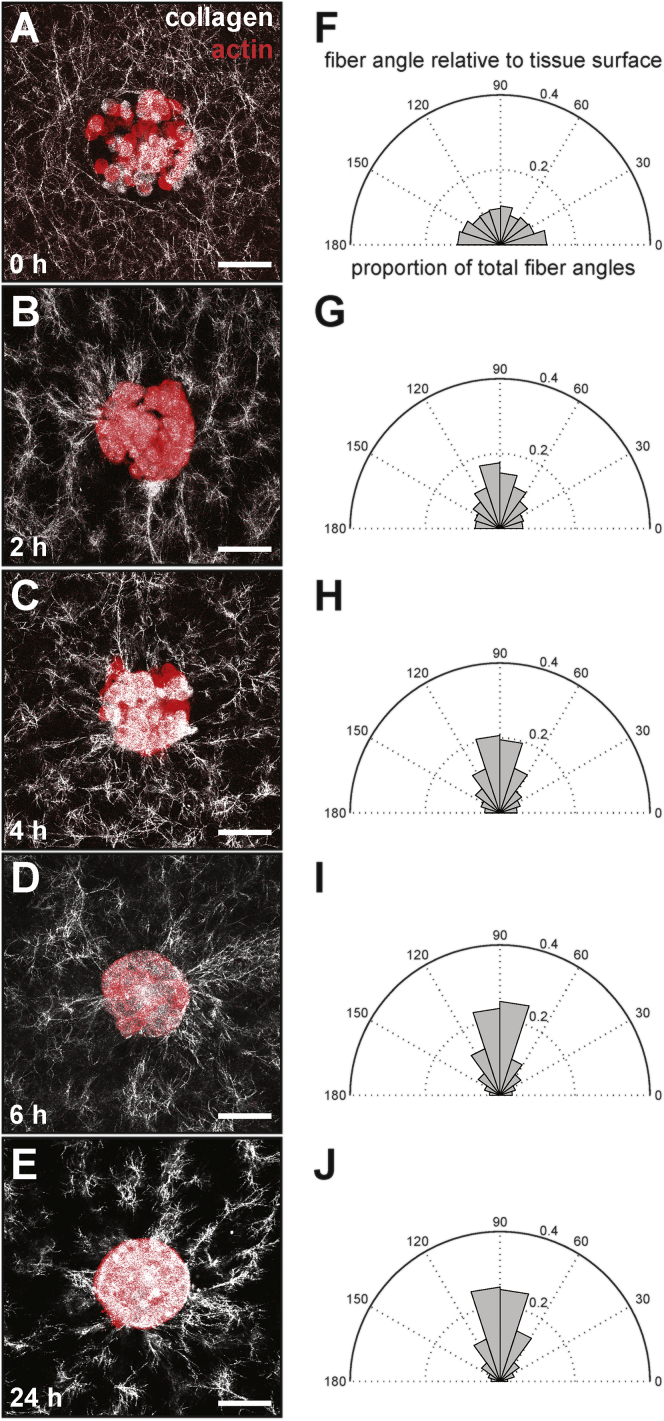
We took advantage of a microfabrication-based approach to generate hundreds of identically shaped 3D epithelial tissues embedded within an ECM gel and used this system to investigate the dynamics of the surrounding matrix alignment. In our previous work using confocal reflection microscopy (CRM) to image the structure of the collagen matrix, we had found that 100-μm-diameter circular tissues align the ECM radially around themselves within 24 h (8). To determine a more precise time frame for alignment, we visualized the matrix surrounding tissues of circular cross-sectional geometry at various time points between seeding (0 h) and 24 h and quantified the alignment of fibers adjacent to the tissues relative to the tissue surface (Fig. 1). We found that approximately half of the collagen fibers that were located within 100 μm of the tissues became aligned (i.e., oriented approximately perpendicular to the tissue surface) within 6 h. This alignment profile did not change significantly between 6 and 24 h, suggesting that the tissues rapidly aligned their surrounding matrix within a few hours after seeding. To further quantify changes in fiber alignment over time, we examined temporal variations in the percentage of unaligned collagen fibers located <100 μm from the surface of the tissues. This parameter exhibited an exponential-decay-like trend over time, reaching an asymptote of ∼50% unaligned fibers after 6 h (Fig. 2 A). Using these data, we computed a characteristic timescale for fiber alignment, which we called the alignment half-life (t_1/2). For mammary epithelial tissues of circular cross-sectional geometry, the alignment half-life was ∼3.1 ± 0.2 h, revealing that multicellular tissues can rapidly remodel their surrounding ECM.

Figure 1.

Engineered mammary epithelial tissues rapidly align adjacent collagen fibers. (A–E) Confocal images of circular EpH4 mammary epithelial tissues (red) and their surrounding collagen matrix (white) taken at (A) 0 h, (B) 2 h, (C) 4 h, (D) 6 h, and (E) 24 h after tissue seeding. (F–J) Corresponding fiber alignment relative to the tissue surface at (F) 0 h, (G) 2 h, (H) 4 h, (I) 6 h, and (J) 24 h after tissue seeding. The scale bar represents 50 μm. To see this figure in color, go online.

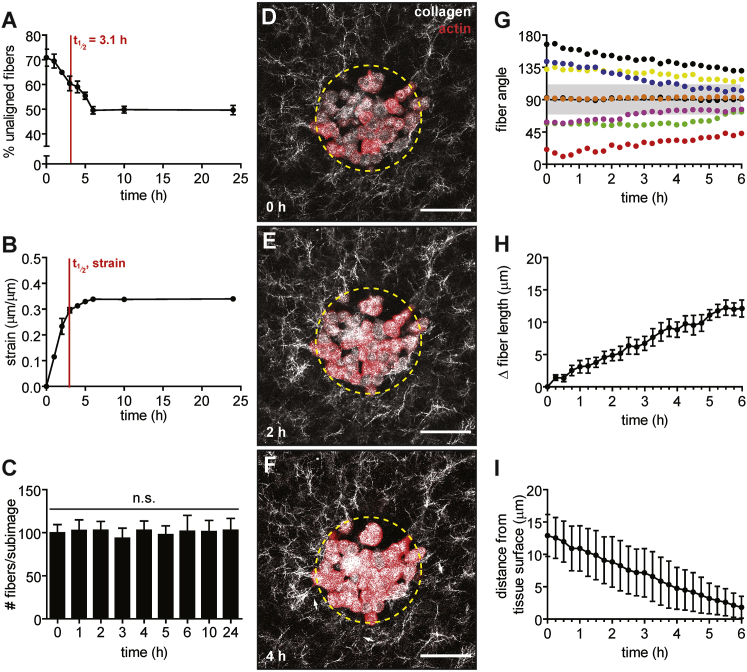
Figure 2.

Engineered mammary epithelial tissues contract inward, imposing a strain that correlates temporally with ECM alignment. (A) Percentage of unaligned fibers over time around EpH4 mammary epithelial tissues. The mean ± SE of three independent experimental replicates is shown. (B) Radial strain exerted by tissues over time. The mean ± SE of three independent experimental replicates is shown. (C) Number of fibers surrounding engineered tissues per subimage over time. The mean ± SE of three independent experimental replicates is shown. (D–F) Time-lapse confocal images of a representative circular epithelial tissue (red) and its surrounding collagen matrix (white) taken at (D) 0 h, (E) 2 h, and (F) 4 h after tissue seeding. The dashed yellow circle indicates the initial geometry and white arrows indicate collagen fibers aligned adjacent to the tissue surface. (G) Changes in fiber angle of eight individual fibers relative to the tissue surface from 0 to 6 h. Gray shaded region indicates fiber angles that are binned as aligned (i.e., oriented approximately perpendicular to the tissue surface). (H) Change in length over time of individual fibers adjacent to tissues. The mean ± SE of fibers from three independent experimental replicates is shown. (I) Change in the distance from individual fibers to the tissue surface over time. The mean ± SE of fibers from three independent experimental replicates is shown. The scale bar represents 50 μm. To see this figure in color, go online.

Immediately after seeding, the cells began to adhere to each other and to the surrounding matrix, and the tissue contracted inward (Fig. 2). By measuring the change in radius of the tissues, we approximated the strain exerted by the tissues on their adjacent matrix as a function of time (Fig. 2 B). We found that the radius of circular tissues shrank by ∼33.9 ± 0.3% within the first 6 h, suggesting that the tissue imposed a radial strain of ∼34% on the surrounding matrix. The strain did not increase between 6 h and 24 h. The trend of tissue-induced strain over time is concordant with the decay of unaligned fibers surrounding the tissues; both curves reached a plateau by ∼6 h. We also quantified the number of fibers surrounding the tissues, which did not change over time (Fig. 2 C), suggesting that collagen concentration remains approximately constant and that proteolysis and/or synthesis does not occur appreciably during the alignment process. To further visualize the dynamics of matrix alignment around individual tissues, we used time-lapse imaging. Consistent with our fixed time-point data, time-lapse analysis revealed that mammary epithelial tissues contracted within a few hours while simultaneously aligning the surrounding matrix (Fig. 2, D–F). These results suggest that fiber alignment around multicellular tissues is driven by tissue-induced strain on the matrix.

In addition to analyzing the overall changes in alignment of fibers over time, we also examined the behavior of individual collagen fibers during the first 6 h of tissue-induced alignment. We observed that individual fibers gradually became more perpendicularly oriented relative to the tissue surface, even if they were not fully aligned according to our metrics (i.e., oriented 70° to 110° from the tissue surface, Fig. 2 G). We also measured the change in length of individual fibers as well as their movements relative to the tissue surface. During the alignment process, individual fibers lengthened by 12.1 ± 1.3 μm within 6 h (Fig. 2 H). During the same period, the average distance of individual fibers from the tissue surface also decreased by 11.1 ± 3.2 μm (Fig. 2 I). Together, these results suggest that individual fibers within a network undergo lengthening and translational movements toward the tissue surface as they are aligned by the tissue, which may lay the foundation for creating fiber tracks along which cells from the tissue can migrate (8).

Proteolysis is not required for matrix alignment around multicellular tissues

Though our initial analysis did not indicate any change in the number of collagen fibers during matrix alignment (Fig. 2 C), previous studies have suggested that the matrix must be remodeled proteolytically by matrix metalloproteinases (MMPs) to facilitate cell migration. Therefore, we further investigated whether matrix alignment was influenced by MMP-dependent proteolysis before migration. To determine whether MMP activity is necessary for matrix alignment, we treated tissues with the broad-spectrum MMP inhibitor GM6001 and found that alignment half-life in these tissues (3.6 ± 0.3 h) was essentially the same as that of dimethylsulfoxide (DMSO)-treated controls (3.6 ± 0.5 h) (Fig. 3 A). The maximum strain in GM6001-treated samples was 33.5 ± 1.1%, which again was not significantly different from that of DMSO-treated controls (33.2 ± 0.5%) (Fig. 3 B). We could also find no qualitative differences in the structure of the fiber network surrounding GM6001- and DMSO-treated samples (Fig. 3 C). These results suggest that MMP activity is not required for alignment of the ECM surrounding mammary epithelial tissues. These results are consistent with the finding that single amoeboid tumor cells are able to deform matrix fibers and push themselves through the ECM in the absence of proteolysis (16). Others have shown, however, that MMP activity is required for efficient migration, particularly in regions of dense ECM where the small pore sizes prohibit cells from passing through the matrix (17). Tissue-mediated matrix alignment before cell migration, however, appears to be primarily a physical process.

Figure 3.

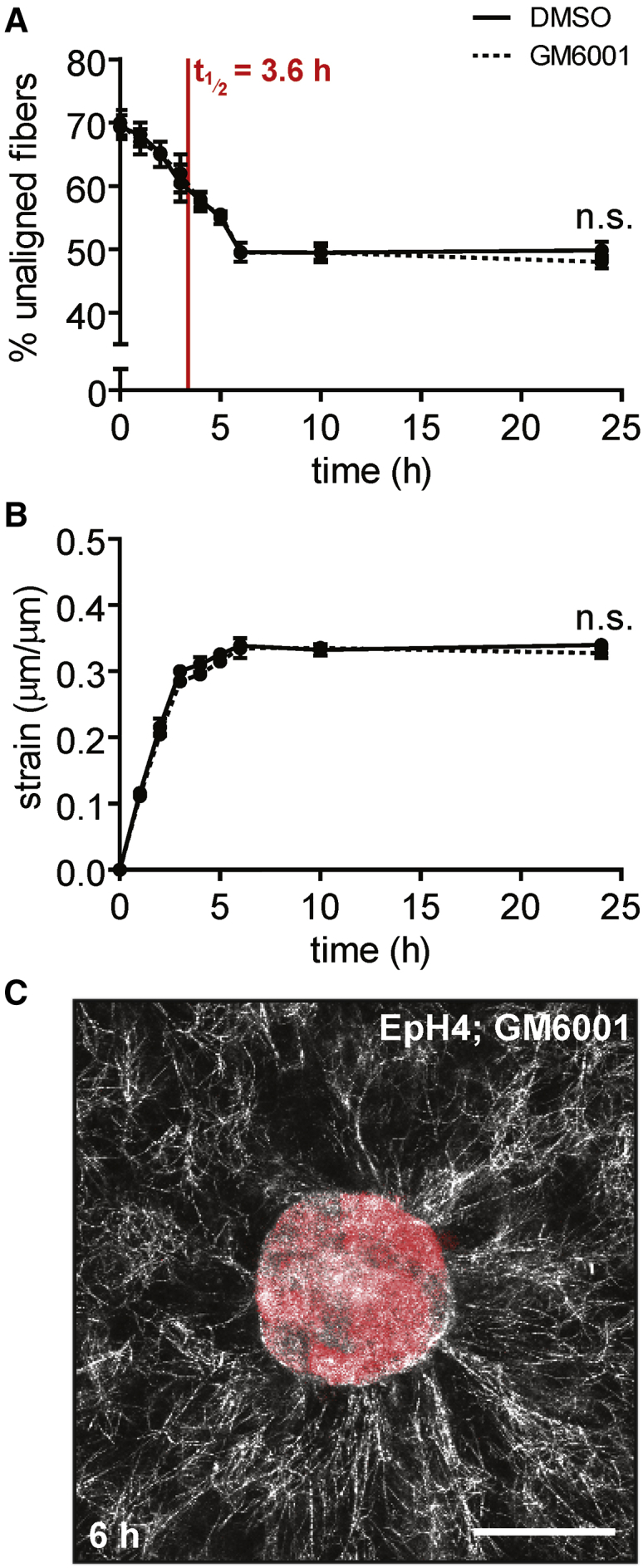
Inhibiting MMP activity does not affect the dynamics of matrix alignment around multicellular tissues. (A) Percentage of unaligned fibers over time for EpH4 mammary epithelial tissues treated with GM6001 (dotted line) or DMSO control (solid line). The mean ± SE of three independent experimental replicates is shown. (B) Radial strain over time exerted by EpH4 mammary epithelial tissues treated with GM6001 (dotted line) or DMSO control (solid line). The mean ± SE of three independent experimental replicates is shown. (C) Confocal image of a representative tissue treated with GM6001 at 6 h after seeding. The scale bar represents 50 μm. To see this figure in color, go online.

Cytoskeletal contractility drives matrix alignment around multicellular tissues

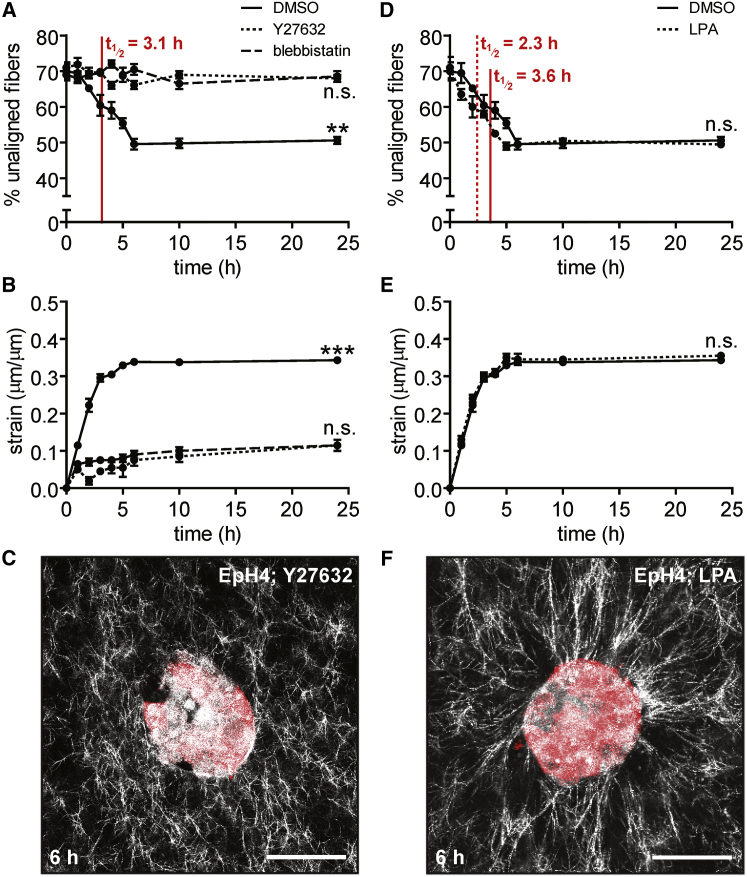
Given that we observed a decrease in tissue radius concurrent with matrix alignment, and that mechanical strain in the absence of biochemical factors and degradation is sufficient to align collagen fibers (5), we hypothesized that cytoskeletal contractility drives tissue-induced matrix alignment. We tested this hypothesis by pharmacologically manipulating cytoskeletal contractility. Upon treatment with the Rho kinase inhibitor, Y27632, the circular mammary epithelial tissues were unable to radially align their surrounding matrix, even after 24 h of culture (Fig. 4, A–C). Treatment with the myosin ATPase inhibitor blebbistatin had a similar effect. DMSO-treated control samples aligned the matrix on a timescale similar to that for untreated tissues (3.1 ± 0.3 h). In the presence of Y27632, tissues exerted less strain on the surrounding matrix over 6 h (7.5 ± 1.1%) than did DMSO-treated controls (33.5 ± 0.5%) (Fig. 4 B). Similarly, treatment with blebbistatin reduced the amount of tissue-induced strain (9.0 ± 0.7%). Conversely, increasing contractility by treating tissues with a Rho activator, LPA, decreased the alignment half-life (2.3 ± 0.1 h) compared to controls (3.6 ± 0.5 h) (Fig. 4 D). LPA-treated samples reached a maximum strain of 35.0 ± 0.7%, similar to DMSO-treated controls (33.8 ± 0.2%) except that LPA-treated samples reached the plateau within 5 h (Fig. 4 E). The fiber network surrounding LPA-treated samples was qualitatively similar to that of controls (Fig. 4 F). These data suggest that cytoskeletal contractility mediated by Rho/ROCK signaling is necessary for matrix alignment around mammary epithelial tissues. Varying cytoskeletal tension alters the dynamics of matrix alignment, with increasing contractility resulting in increased strain rate and a shorter time to alignment.

Figure 4.

Inhibiting contractility prevents fiber alignment and decreases tissue-induced strain, whereas enhancing contractility accelerates fiber alignment. (A) Percentage of unaligned fibers over time for EpH4 mammary epithelial tissues treated with Y27632 (dotted line), blebbistatin (dashed line), or DMSO control (solid line). The mean ± SE of three independent experimental replicates is shown. (B) Radial strain over time exerted by EpH4 mammary epithelial tissues treated with Y27632 (dotted line), blebbistatin (dashed line), or DMSO control (solid line). The mean ± SE of three independent experimental replicates is shown. (C) Confocal image of a representative EpH4 mammary epithelial tissue treated with Y27632 at 6 h after seeding. (D) Percentage of unaligned fibers over time for EpH4 mammary epithelial tissues treated with LPA (dotted line) or DMSO control (solid line). The mean ± SE of three independent experimental replicates is shown. (E) Radial strain over time exerted by EpH4 mammary epithelial tissues treated with LPA (dotted line) or DMSO control (solid line). The mean ± SE of three independent experimental replicates is shown. (F) Confocal image of a representative EpH4 mammary epithelial tissue treated with LPA at 6 h after seeding. ^∗∗p < 0.01, ^∗∗∗p < 0.001. The scale bar represents 50 μm. To see this figure in color, go online.

Tissue geometry affects the pattern of fiber alignment

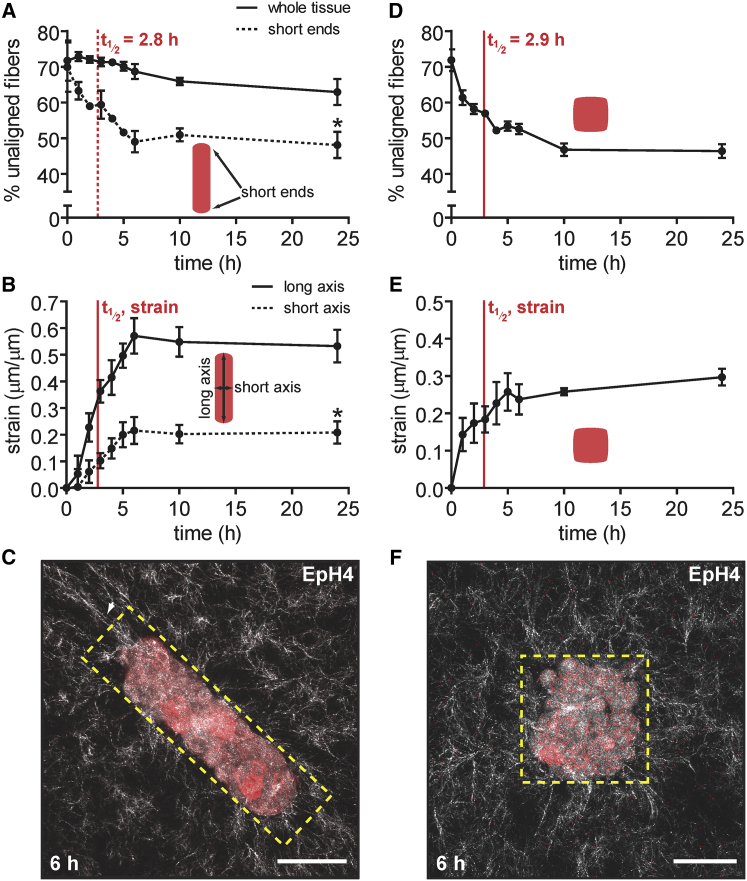
Tissue geometry determines the spatial distribution of mechanical stress experienced by cells within an epithelium (18), so we next asked whether the dynamics of matrix alignment similarly depended on the geometry of the multicellular tissues. In particular, we wanted to determine the effects of non-circular tissue geometry on the timescale for alignment. To that end, we created mammary epithelial tissues that were rectangular in cross-sectional geometry. As above, we visualized the matrix surrounding tissues at various time points and quantified fiber alignment. We found that these tissues also aligned their surrounding matrix, but primarily at the short ends of the tissues. Again, we found that ∼50% of the fibers surrounding these locations were aligned within 6 h, with an alignment half-life of 2.8 ± 0.2 h (Fig. 5 A). When alignment was measured around the tissue as a whole, however, we observed a much smaller proportion of aligned fibers, even after 24 h (Fig. 5 A). We also measured the changes in length and width of the tissue over time and calculated the tissue-induced strain along these axes as a ratio of tissue deformation along each axis to the corresponding radius of curvature. We found that strain along the short axis of the tissue was 20.8 ± 2.4%, whereas the strain along the long axis was higher (53.2 ± 3.5%) (Fig. 5 B), consistent with the fact that fibers align along the long axis at the short ends of the tissues. These results suggest that asymmetric tissue geometries result in asymmetric strain and asymmetric fiber alignment. In the case of rectangular tissues, we observed higher pericellular fiber alignment at locations that experience higher mechanical strain, that is, the short ends of the tissue (Fig. 5 C) from which cells migrate collectively (8).

Figure 5.

Tissue geometry affects the pattern of fiber alignment. (A) Percentage of unaligned fibers over time surrounding rectangular (200 × 50 × 50 μm) EpH4 mammary epithelial tissues (solid line) and at the short ends of the tissues (dotted line). The mean ± SE of three independent experimental replicates is shown. (B) Strain over time exerted by rectangular EpH4 mammary epithelial tissues along the long axis (solid line) and the short axis (dotted line) calculated as a ratio of tissue deformation along an axis to its corresponding radius of curvature. The mean ± SE of three independent experimental replicates is shown. (C) Confocal image of a representative rectangular tissue at 6 h after seeding. The dashed yellow rectangle indicates the initial geometry and the arrow indicates the alignment of collagen fibers at the short ends of the tissue. (D) Percentage of unaligned fibers over time surrounding square (100 × 100 × 50 μm) EpH4 mammary epithelial tissues. The mean ± SE of three independent experimental replicates is shown. (E) Strain over time exerted by square EpH4 mammary epithelial tissues. The mean ± SE of three independent experimental replicates is shown. (F) Confocal image of a representative square tissue at 6 h after seeding. Dashed yellow square indicates the initial geometry. ^∗p < 0.05. The scale bar represents 50 μm. To see this figure in color, go online.

We also created mammary epithelial tissues of square cross-sectional geometry. In contrast to rectangular tissues, we found that square tissues behaved similarly to tissues of circular cross section in that ∼50% of pericellular fibers were aligned within 6 h (Fig. 5 D). These tissues had an alignment half-life of 2.9 ± 0.2 h and imposed a strain of 29.7 ± 1.3% (Fig. 5, D and E). Although they were initially square in shape, the tissues became more rounded in morphology over time, particularly after 6 h. Consistent with this change in shape, the fibers adjacent to the corners of the tissues initially exhibited more prominent alignment (Fig. 5 F). Together, these results suggest that the initial geometry of a tissue determines subsequent patterns and dynamics of matrix alignment.

Tissue cohesion correlates with matrix alignment in tissues comprised of cancer cells

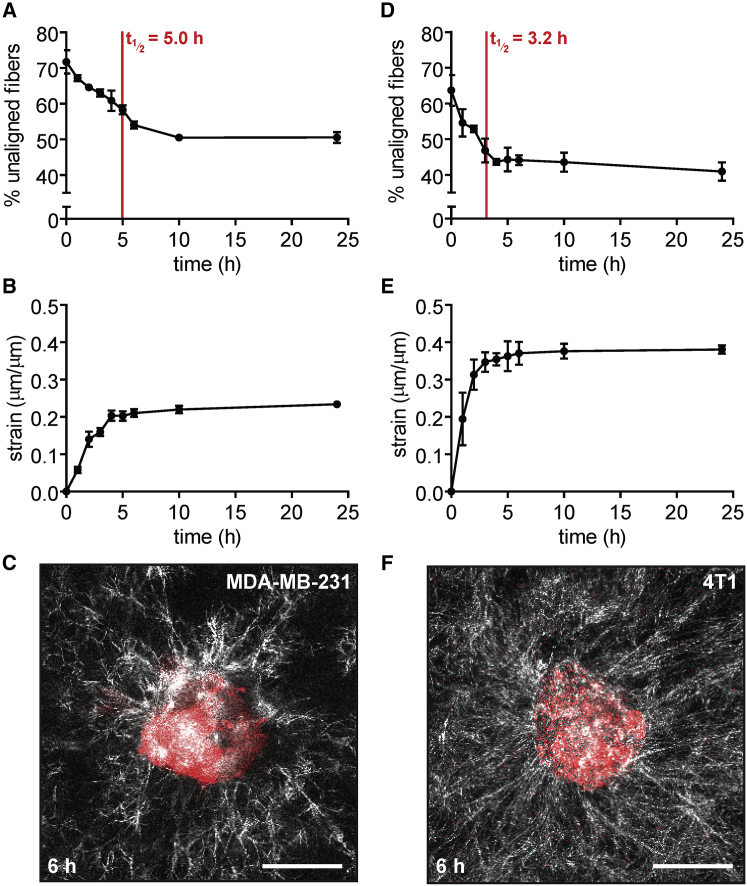
Cancer cells that have undergone epithelial-mesenchymal transition are more contractile than their more epithelial non-neoplastic counterparts (19). Since we observed that pharmacologically increasing contractility resulted in faster matrix alignment, we hypothesized that tissues comprised of highly contractile cancer cells would align their surrounding matrix faster than those of less contractile normal cells. To test this hypothesis, we created 100-μm-diameter circular tissues using MDA-MB-231 human breast carcinoma cells, which are mesenchymal in morphology and highly invasive in culture (20). These cells had previously been shown to radially align collagen matrix before invading when seeded as spheroids (6). Similar to tissues comprised of normal mammary epithelial cells, MDA-MB-231 breast cancer tissues aligned ∼50% of their surrounding ECM fibers within 24 h after seeding (Fig. 6 A). However, these tissues were slower to align their surrounding matrix, with an alignment half-life of 5.0 ± 0.5 h. In addition, breast cancer tissues imposed a lower radial strain (23.4 ± 0.3%) on the matrix over the course of 24 h (Fig. 6 B), which could contribute to the delayed time for matrix alignment. Fiber alignment in these tissues did not propagate beyond ∼50 μm (Fig. 6 C). MDA-MB-231 cells express low levels of the intercellular adhesion protein E-cadherin (21), and consistently, the tissues did not contract inward as uniformly as those comprised of normal epithelial cells. These results suggest that, whereas MDA-MB-231 cells are highly contractile individually, their multicellular tissues impose less strain on the ECM than non-malignant epithelial tissues.

Figure 6.

Breast cancer cells that express low levels of E-cadherin are slower to align their surrounding matrix than non-malignant mammary epithelial cells or breast cancer cells that express higher levels of E-cadherin. (A) Percentage of unaligned fibers over time for tissues comprised of MDA-MB-231 human breast cancer cells. The mean ± SE of three independent experimental replicates is shown. (B) Radial strain over time exerted by tissues comprised of MDA-MB-231 human breast cancer cells. The mean ± SE of three independent experimental replicates is shown. (C) Confocal image of a representative tissue comprised of MDA-MB-231 human breast cancer cells at 6 h after seeding. (D) Percentage of unaligned fibers over time for tissues comprised of 4T1 murine mammary carcinoma cells. The mean ± SE of three independent experimental replicates is shown. (E) Radial strain over time exerted by tissues comprised of 4T1 murine mammary carcinoma cells. The mean ± SE of three independent experimental replicates is shown. (F) Confocal image of a representative tissue comprised of 4T1 murine mammary carcinoma cells at 6 h after seeding. The scale bar represents 50 μm. To see this figure in color, go online.

To determine whether intercellular cohesion was important for alignment around tissues comprised of carcinoma cells, we also generated tissues of 4T1 murine mammary cancer cells, which have been found to express higher levels of E-cadherin (22). In these tissues, we observed nearly 60% fiber alignment within 6 h, with an alignment half-life of 3.2 ± 0.4 h (Fig. 6 D). Moreover, we also observed that these tissues imposed significantly higher strains on their surrounding matrix (38.0 ± 0.6%) than did those of MDA-MB-231 human breast cancer cells (Fig. 6 E). In these tissues, fiber alignment propagated farther into the matrix (Fig. 6 F). Together, these results suggest that tissue cohesion drives rapid matrix alignment around tissues comprised of cancer cells.

Fibroblast tissues exert large strains and rapidly align the matrix before migrating along aligned fibers

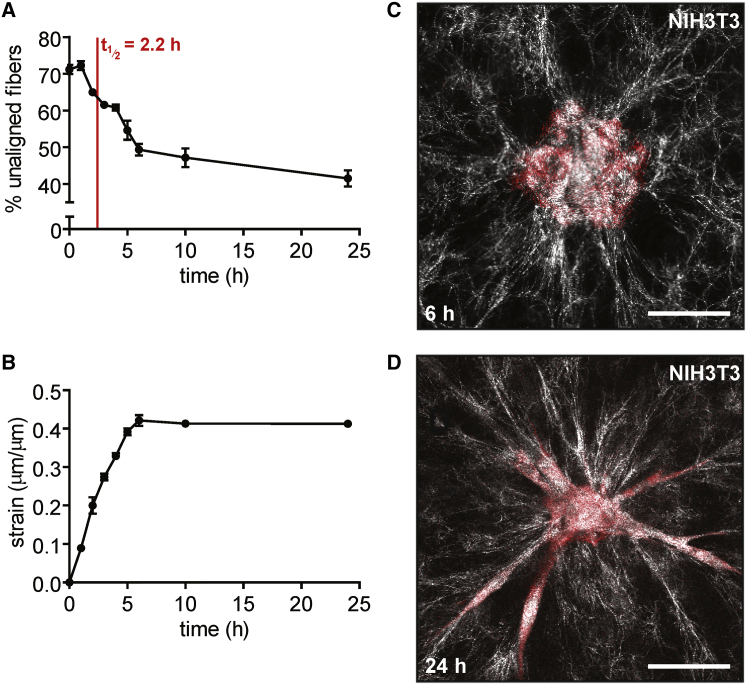
Fibroblasts are of mesenchymal origin and are generally more migratory than epithelial cells (23). Fibroblasts embedded in collagen or fibrin gels have been shown to rapidly exert mechanical strain on their surrounding ECM within 24 h, both as single cells and as multicellular aggregates (9, 24, 25), though the relationship between tissue geometry and the dynamics of matrix alignment has not been reported. Here, similar to normal mammary epithelial tissues, fibroblasts contracted inward after initial seeding and appeared to form intercellular adhesions during this process. However, the fibroblast tissues exerted a higher strain on the matrix (42.1 ± 0.8%), and correspondingly, the alignment half-life for these tissues was relatively short (2.2 ± 0.2 h) (Fig. 7, A and B). These results are consistent with studies using single primary human fibroblasts, which were shown to locally strain collagen gels and thereby reorganize and align the matrix within 5 h (10). Fibroblast tissues continued to align fibers between 6 and 10 h, reaching ∼60% alignment from 10 to 24 h (Fig. 7 C). Confocal imaging revealed that β-catenin localized to cell-cell junctions in the fibroblast tissues (Fig. S1), consistent with an apparent need for intercellular adhesions in rapid matrix alignment. We also noted that within 24 h, the fibroblasts began to migrate radially into the collagen matrix (Fig. 7 D). There did not appear to be any spatial preference in the direction of migration, as cells migrated outward from the entire circumference of the circular tissues, appearing to move in the direction of the nearest aligned collagen fibrils. Matrix alignment preceded migration and occurred on a much shorter timescale than for epithelial tissues.

Figure 7.

Fibroblast tissues exert large strains and rapidly align their surrounding matrix. (A) Percentage of unaligned fibers over time for tissues comprised of NIH3T3 fibroblasts. The mean ± SE of three independent experimental replicates is shown. (B) Radial strain over time exerted by tissues comprised of NIH3T3 fibroblasts. The mean ± SE of three independent experimental replicates is shown. (C) Confocal image of a representative fibroblast tissue at 6 h after seeding. (D) Confocal image of a representative fibroblast tissue at 24 h after seeding. The scale bar represents 50 μm. To see this figure in color, go online.

Intercellular adhesion facilitates rapid matrix alignment around multicellular tissues

Based on the differences between alignment induced by tissues comprised of the two different cancer cells, normal epithelial cells, and fibroblasts, we hypothesized that intercellular adhesion expedites matrix alignment by enabling the propagation of cytoskeletal contractility between neighboring cells. To test this hypothesis directly, we used an adenoviral approach to transduce normal epithelial tissues with a dominant-negative truncation mutant of E-cadherin that lacks the amino-terminal domain necessary for binding to β-catenin (EΔ), thus preventing connection to the actin cytoskeleton and transmission of force between adjacent cells (26). Expression of the EΔ mutant prevents β-catenin localization at cell-cell contacts (Fig. S2) (27). EΔ-expressing mammary epithelial tissues were unable to align more than ∼45% of fibers within 24 h, and had a much longer alignment half-life (5.5 ± 1.6 h) than GFP controls (3.0 ± 0.2 h), which behaved similarly to untransduced epithelial tissues (Fig. 8 A). Additionally, EΔ-expressing tissues exerted less strain on their surrounding matrix (28.0 ± 0.4%) than did control tissues (35.0 ± 0.4%) (Fig. 8 B). Moreover, fiber alignment around EΔ-expressing tissues did not propagate beyond ∼25 μm (Fig. 8 C). Together, these results suggest that the transmission of cytoskeletal contractility across multiple cells is important for generating strains on the matrix that are large enough to rapidly align fibers.

Figure 8.

Disrupting the intercellular transmission of force slows matrix alignment and decreases tissue-induced strain. (A) Percentage of unaligned fibers over time for EpH4 mouse mammary epithelial tissues transduced with EΔ, a mutant form of E-cadherin lacking the β-catenin-binding domain (dotted line), or GFP control (solid line). The mean ± SE of three independent experimental replicates is shown. (B) Radial strain over time exerted by EpH4 mammary epithelial tissues transduced with EΔ (dotted line) or GFP control (solid line). The mean ± SE of three independent experimental replicates is shown. (C) Confocal image of an EΔ-expressing EpH4 mammary epithelial tissue at 6 h after seeding. (D) Percentage of unaligned fibers over time for tissues comprised of MDA-MB-231 breast cancer cells expressing Ecad-GFP (dotted line) or YFP control (solid line). The mean ± SE of three independent experimental replicates is shown. (E) Radial strain over time exerted by tissues comprised of MDA-MB-231 breast cancer cells expressing Ecad-GFP (dotted line) or YFP control (solid line). The mean ± SE of three independent experimental replicates is shown. (F) Confocal image of an Ecad-GFP-expressing MDA-MB-231 tissue at 6 h after seeding. ^∗p < 0.05, ^∗∗∗p < 0.001. The scale bar represents 50 μm. To see this figure in color, go online.

To further investigate the role of intercellular cohesion and coordinated cytoskeletal contractility, we created a stable line of MDA-MB-231 human breast cancer cells that expressed elevated levels of an E-cadherin-GFP fusion protein (Ecad-GFP) (Fig. S3) (28). Since MDA-MB-231 tissues did not align the surrounding matrix as rapidly or exert as much strain as other cell types, we hypothesized that ectopically expressing E-cadherin in these tissues would result in a reduced alignment half-life and increased tissue-induced strain. We observed that Ecad-GFP-expressing MDA-MB-231 tissues aligned their surrounding matrix more rapidly (t_1/2 = 2.9 ± 0.6 h) and aligned a greater percentage (∼57%) of adjacent collagen fibers compared to YFP-expressing controls, which aligned ∼50% of their surrounding matrix with an alignment half-life of 3.8 ± 1.0 h (Fig. 8, D–F). Moreover, Ecad-GFP-expressing tissues exhibited higher levels of strain (38.2 ± 2.4%) than YFP-expressing controls (35.3 ± 0.7%) (Fig. 8 E). Overall, we noted a higher degree of variability in measurements of these tissues and, as a result, differences in terminal strain and matrix alignment at 24 h were not significant. Nonetheless, these results are consistent with our hypothesis that cytoskeletal contractility propagated across cells accelerates matrix alignment.

Discussion

Matrix alignment is associated with increased efficiency of cell migration (5). In the context of cancer invasion, collagen alignment has also been correlated with enhanced metastasis and poor prognosis (4, 29). Whereas the movement of cells along aligned matrix fibers has been frequently observed, the parameters that govern the initial alignment of the fibers remains poorly understood. Here, we used a 3D microfabricated tissue model to determine the dynamics by which multicellular tissues align their surrounding matrix before migration and the underlying mechanisms. This system enables a more precise quantification of changes in matrix alignment and tissue-induced strain on both short (∼1 h) and long (∼24 h) timescales. Moreover, using tissues of defined shape and cell density allows us to directly compare different cell types, treatment conditions, and tissue geometries. We found that tissues rapidly aligned their surrounding matrix by straining the network, with the majority of the fibers adjacent to the tissue surface oriented perpendicularly within 6 h. Cytoskeletal contractility was the driving force for matrix alignment, whereas MMP-dependent proteolysis was dispensable. We also found that the initial tissue geometry dictated subsequent patterns of matrix alignment.

Our data show that the timescale for matrix alignment is significantly faster than the timescale for migration. Here, we found that the matrix aligns within 6 h; previously, we observed collective migration from engineered mammary epithelial tissues to occur over 24–48 h (8). Alignment also preceded migration in fibroblast tissues. Our previous work suggests that tissue-induced matrix deformation and collective migration require comparable magnitudes of force, as the estimated range of traction stresses exerted by engineered tissues was similar for quiescent tissues deforming their surrounding fibrous matrix (4–120 Pa) and for tissues undergoing collective migration along aligned matrix fibers (0–120 Pa) (8, 18). However, in the case of collective migration, it appears that these forces must be exerted over longer periods of time and localized to the leading edge of migrating cohorts to result in cell translocation once fibers are aligned. Together, our data suggest that tissue-derived forces are first employed to align matrix fibers and subsequently to facilitate migration along them. These results are consistent with experimental and computational findings that single cells dispersed in a matrix initially align the fibers between them before beginning to migrate toward each other (30, 31). Given that matrix alignment precedes migration and provides directionality to cell movements, the ability of tissues to quickly align the matrix may be beneficial, enabling their constituent cells to make rapid changes in the direction of migration in accordance with changing microenvironmental cues. Tissue-induced fiber alignment may also serve as a form of cell-cell communication; it has been suggested that fiber alignment enables the transmission of stresses between cells that are spaced several cell diameters apart in a matrix, enabling communication via mechanotransduction (25).

The generation of mechanical force through cytoskeletal tension drives collective migration (8), so it is not surprising that cytoskeletal contractility also drives alignment of the ECM surrounding multicellular tissues. Consistent with our results, ROCK-mediated contractility has also been implicated in matrix contraction and fiber displacement (32, 33, 34, 35). That MMP activity has little to no effect on alignment indicates that tissue-induced matrix remodeling is primarily a mechanical process through which fibers in the ECM network are pulled into place by the cells within the tissue. Accordingly, others used finite element modeling to suggest that tension in the absence of degradation is sufficient to align collagen fibers (36). Furthermore, there are several experimental examples of reconstituted collagen fibers being aligned in the absence of cells via mechanical forces alone, such as through fluid flow or stretch (5, 37). The extent of alignment in these cases is determined by the amount of strain exerted on the collagen gels. For our data, plotting the change in the percentage of unaligned fibers as a function of strain (Fig. 9) reveals a clear relationship for all cell types, with increased tissue-induced strain correlating with increased fiber alignment (R² = 0.70). The dynamics and extent of matrix alignment around multicellular tissues thus appears to be determined primarily by the amount of strain that the cells within the tissues are collectively able to generate by pulling on their neighbors.

Figure 9.

Increased strain correlates with a decrease in the percentage of unaligned fibers across multiple cell types. Change in the percentage of unaligned fibers as a function of strain for tissues comprised of normal EpH4 mammary epithelial cells (circles), EΔ-expressing EpH4 cells (diamonds), MDA-MB-231 breast cancer cells (triangles), Ecad-GFP-expressing MDA-MB-231 cells (inverted triangles), 4T1 murine mammary carcinoma cells (hexagons), and NIH3T3 fibroblasts (squares). Line is linear regression of the combined data.

Paradoxically, contractility at the individual cell level does not necessarily correlate with increased matrix alignment at the tissue level, even though it has been suggested that the distance over which cell-matrix force transmission extends increases with increasing cellular contractility in fibrous matrices (36). We found that MDA-MB-231 breast cancer tissues aligned their surrounding matrix more slowly than normal mammary epithelial tissues. One possible explanation is that the collective contractility of the population of cells is important; increasing the contractility of an individual cell within a multicellular tissue does not necessarily translate to faster alignment around the tissue as a whole. Indeed, tissues comprised of 4T1 murine mammary carcinoma cells that express high levels of E-cadherin (22) were able to rapidly align the matrix. Moreover, our results using the EΔ mutant suggest that the intercellular transmission of cytoskeletal forces across cell-cell contacts may be critical to align the matrix around multicellular tissues. Intercellular connections enable forces to propagate across neighboring cells (38), resulting in greater tension applied at cell-matrix adhesions and consequently faster pericellular matrix alignment.

The correlation between fiber alignment and cell migration emphasizes the importance of determining the mechanisms by which tissues interact with their surrounding ECM, as the results have wide-ranging implications for both normal and pathological processes. Rho-mediated contractility in particular appears to be required for both alignment of the ECM and migration along matrix fibers for several different cell types (5, 39, 40), confirming the role of mechanotransduction and physical forces in a range of morphogenetic processes. Furthermore, it appears that coordinating intercellular adhesions enables the transmission of cell-derived forces over tissue-level length scales. When combined with cell-matrix adhesions, cell-derived forces can in turn yield larger ECM network deformations and faster migration speeds. Both of these interactions are important for large-scale tissue deformations in vivo, such as morphogenetic movements that occur during development (41). Our results also suggest that it may be beneficial for cancer cells to retain some level of epithelial characteristics and associated intercellular adhesions to propagate cytoskeletal tension and rapidly align the matrix before invading. Moreover, given that aligned collagen fibers appear to enhance metastatic potential (7), altering matrix alignment or the ability of tissues to align the matrix to slow or redirect invading cells are potential targets for cancer therapeutics. Further investigation of the physical interplay between cells and their ECM, especially through the use of tissue-equivalent culture models that better approximate the mechanical properties of living tissues (42), will continue to provide insight into how biomechanics contribute to cell migration during development and disease.

Author Contributions

A.S.P.-D., S.S., and C.M.N. designed the research; A.S.P.-D., B.A.N., and A.E.W. performed the experiments; A.S.P.-D. and B.A.N performed the data analysis; A.S.P.-D. prepared the figures; and the article was written by A.S.P.-D. and C.M.N.

Editor: Sean Sun.