Design of Elastic Networks with Evolutionary Optimized Long-Range Communication as Mechanical Models of Allosteric Proteins

Abstract

Allosteric effects often underlie the activity of proteins, and elucidating generic design aspects and functional principles unique to allosteric phenomena represent a major challenge. Here an approach consisting of the in silico design of synthetic structures, which, as the principal element of allostery, encode dynamical long-range coupling among two sites, is presented. The structures are represented by elastic networks, similar to coarse-grained models of real proteins. A strategy of evolutionary optimization was implemented to iteratively improve allosteric coupling. In the designed structures, allosteric interactions were analyzed in terms of strain propagation, and simple pathways that emerged during evolution were identified as signatures through which long-range communication was established. Moreover, robustness of allosteric performance with respect to mutations was demonstrated. As it turned out, the designed prototype structures reveal dynamical properties resembling those found in real allosteric proteins. Hence, they may serve as toy models of complex allosteric systems, such as proteins. Application of the developed modeling scheme to the allosteric transition in the myosin V molecular motor was also demonstrated.

Introduction

The functional activity of proteins and its precise regulation often relies on allosteric coupling between different functional regions within the macromolecular structure. According to the mechanical perspective, allosteric communication originates from structural changes mediated by a network of physically interacting residues (1). Much resembling the occurrence of a protein quake, local conformational motions initiated, e.g., upon ligand binding to one specific site, propagate themselves across the protein structure to spatially remote regions eventually generating a functional change in the conformation of another site.

Experiments have indeed evidenced the existence of communication networks in proteins, which are formed by only a set of amino acids and constitute allosteric pathways, physically linking remote binding sites (2, 3). Various computational strategies aimed at predicting such pathways have been developed, including structure-based network analysis (4, 5, 6), stochastic Markov modeling (7, 8), and sequence-based statistical methods (9, 10, 11, 12). Understanding of allosteric communication at the molecular level has also been widely addressed at atomistic resolution in molecular dynamics (MD) simulations (13, 14, 15, 16, 17, 18, 19).

To circumvent the heavy computational burden present in MD simulations, collective conformational motions and allosteric transitions in proteins have been, to a vast extent, investigated at the coarse-grained level using elastic-network models and the analysis of normal modes (20, 21, 22, 23, 24, 25, 26). Despite their approximate nature, such simplified descriptions have significantly contributed to understanding the mechanistic underpinnings of allostery in proteins (27, 28).

Although, in the majority of cases, the important question is considered to be how allostery works for a particular protein given its specific structure, there may also be more fundamental and general questions to be addressed, such as what generic design and functional principles are requisite to make allostery work, and which dynamical properties are unique to allostery. One possibility to approach such aspects would consist of a systematic screening of the biophysical properties among allosteric proteins with the available structural data, which has been sporadically attempted earlier (6, 29).

Here, in an attempt to address this subject, we present an alternative approach that is motivated by the idea to engineer, in silico, artificial spatial structures with dynamical properties resembling those found in real proteins. In previous works, such an approach was employed to design structures of elastic networks that can operate as a model molecular machine (30, 31, 32) or swimmer (33). Moreover, we recently used this machine to construct a model motor which, in its function, mimics the myosin protein motor (34).

In this article, we aim to establish a generalized structural model of an allosteric system. To this end, we design, using evolutionary optimization, elastic-network structures that, as the principal element of allostery, encode long-range coupling among two spatially remote local regions. We first explain how the strategy of iterative evolution was developed and then applied to stepwise improve starting from a random elastic network, the allosteric response in the emerging structures. In the designed structures, allosteric communication was then analyzed in terms of the propagation of strain, and its spatial distribution was used to identify pathways through which remote interactions are established. Moreover, the effect of mutations was demonstrated and the robustness of allosteric performance in the designed structures examined. Finally, application of the modeling scheme to allosteric communication in the myosin V molecular motor was demonstrated and commonalities with the designed model systems were exemplified.

Methods

Construction of random elastic network

The initial two-domain elastic network was constructed by first randomly folding two chains of linked beads, then bringing them into contact and finally determining the network connectivity. One chain consisted of 100 identical beads each and its folded form was constructed as follows. After fixing the position of the first bead, each next bead was placed at random around the position of the previous bead, with the following restrictions: 1) the distance to the preceding bead had to lie within the interval between l_min and l_max, 2) the new bead had to be separated from each previous bead by at least the distance l_min, and 3) the distance from the new bead to the geometric center of all previous beads should not exceed the threshold r_max. In the simulations, the prescribed values l_min = 4.0 Å, l_max = 5.0 Å, and r_max = 20.0 Å were used to generate a compactly folded backbone chain. After constructing two such chains, they were merged in such a way that they came into tight contact but still did not overlap. Positions of the 200 beads in the initial two-domain random structure are denoted by ${\overrightarrow{R}}_i^{\left(0\right)}$ and their spatial coordinates are provided as Supporting Materials and Methods. To complete the network construction, we have checked all distances $d_{ij}^{\left(0\right)}=\left|{\overrightarrow{R}}_i^{\left(0\right)}-{\overrightarrow{R}}_j^{\left(0\right)}\right|$ between beads i and j and introduced an elastic spring between those pairs of beads for which the distance $d_{ij}^{\left(0\right)}$ was below a prescribed interaction radius of r_int = 9 Å. With this choice, the initial two-domain elastic network had 1467 links. It should be noted that in this model, all length units are, in principle, arbitrary. When data from real protein structures is used, the distances between amino acids have the scale of Ångstroms. Hence, throughout the article, this notion is adopted.

Elastic conformational dynamics

The total elastic energy U of the network is the sum of contributions of all elastic links, i.e., $U=\left(1/2\right){\sum }_{i<j}^N\kappa {\text{Γ}}_{ij}{\left(d_{ij}-d_{ij}^{\left(0\right)}\right)}^2$. Here, N = 200 is the number of beads; κ is the spring stiffness constant (equal for all springs); $d_{ij}=\left|{\overrightarrow{R}}_i-{\overrightarrow{R}}_j\right|$ is the actual length of a spring connecting beads i and j in some deformed network conformation, with ${\overrightarrow{R}}_i$ being the actual position vector of bead i; and $d_{ij}^{\left(0\right)}$ is the corresponding natural spring length. Coefficients ${\text{Γ}}_{ij}$ have value 1 if beads i and j are connected by a spring (i.e., when $d_{ij}^{\left(0\right)}<r_{\text{int}}$), and equal 0, otherwise. The dynamics of the elastic network is governed by Newton’s equation of motion in the overdamped limit, where the velocity of each network bead is proportional to the forces applied to it. This limit is valid in the low Reynolds number regime of proteins at which inertial movements can be neglected. Hence, the equation for bead i was

$$\gamma \frac{d}{dt}{\overrightarrow{R}}_i=-\frac{\partial }{\partial {\overrightarrow{R}}_i}U+{\overrightarrow{f}}_i=-\kappa \sum _j^N{\text{Γ}}_{ij}\frac{d_{ij}-d_{ij}^{\left(0\right)}}{d_{ij}}\left({\overrightarrow{R}}_i-{\overrightarrow{R}}_j\right)+{\overrightarrow{f}}_i.$$ (1)

On the left-hand side, γ is the friction coefficient assumed to be equal for all beads. On the right side are the elastic forces exerted by network springs that are connected to bead i; they depend only on the change in the distance between two connected beads. Additionally, an external force ${\overrightarrow{f}}_i$ could be applied to bead i, which was used in probing allostery (see next section). Note that in the above equations the dependencies on γ and κ can be removed using the rescaled dimensionless time (κ/γ)t. To obtain the positions of network beads, and hence the conformation of the network at any time moment, the set of equations of motion was numerically integrated. In the simulations, a first-order scheme with a time step of 0.1 was employed. It should be noted that the same relaxational elastic-network model was previously applied in several studies of protein conformational dynamics (e.g., (30, 35, 36, 37)).

Pocket sites and probing of allostery

In the network model, the allosteric site and the regulates site were, for simplicity, each represented by two beads. Those beads have been selected in such a way that the two pockets were sufficiently remote from each other. At the same time, the two beads forming one pocket should be adjacent, but not directly connected by an elastic spring. In the constructed two-domain network, the allosteric pocket was defined by beads with indices 38 and 81, belonging to the first domain; and the regulated pocket was defined by beads with indices 149 and 189, belonging to the second domain.

To probe allosteric communication between the two pockets, a simple force-probe scheme was implemented. Conformational dynamics in the allosteric site was initiated through the application of additional forces, and the subsequent response generated in regulated site was probed by evaluating structural changes there. In the simulations, pair forces have been applied to the beads of the allosteric pocket. The forces were always acting along the direction given by the actual positions of the two pocket beads. Specifically, the force applied to pocket bead 38 was ${\overrightarrow{f}}_{38}=0.5\cdot \overrightarrow{u}$, with the unit vector $\overrightarrow{u}=\left({\overrightarrow{R}}_{81}-{\overrightarrow{R}}_{38}\right)/\left|{\overrightarrow{R}}_{81}-{\overrightarrow{R}}_{38}\right|$. The same force, but with the different sign, was acting on the second pocket bead, i.e., ${\overrightarrow{f}}_{81}=-0.5\cdot {\overrightarrow{f}}_{38}$. Such pair forces would induce only internal network deformations and result in a decrease in the distance between the two pocket beads, thus leading to closing of the allosteric pocket. Because this situation is apparently equivalent to assuming that an additional network bead became bound to the center of the two pocket beads, where it generated attractive forces between itself and each pocket bead, we can also say that the chosen force scheme mimicked binding of a fictitious ligand bead to the allosteric pocket. The action of the additional forces generated deformations of the network, which were first localized in the vicinity of the allosteric pocket, but which gradually spread over the entire network structure. The corresponding process of conformational relaxation was followed by integrating the equations of motion until a steady state of the elastic network (in which all motions were terminated) was reached (at final time T, see Supporting Materials and Methods). In the resulting conformation of the network, the effect of allosteric coupling was examined by evaluating the distance between the beads corresponding to the regulated site. This distance $d_{\mathrm{149,189}}\left(T\right)=\left|{\overrightarrow{R}}_{149}\left(T\right)-{\overrightarrow{R}}_{189}\left(T\right)\right|=:A$ is termed the “allosteric parameter”.

Evolutionary optimization

To design networks with perfected allosteric communication, a process of evolutionary optimization, consisting of mutations followed by selection, was applied iteratively, starting from the random network. In particular, the following sequence was carried out. First the allosteric response of the elastic network before the mutation was determined and the allosteric parameter A stored. Then a single structural mutation was performed by randomly selecting one network bead (except for one of the four pocket beads) and changing its equilibrium position. The new equilibrium position was chosen to be randomly oriented within a sphere of radius 2.0 Å around the old equilibrium position. To preserve the backbone chain of each domain, it was additionally required that, after the mutation, the distance between the mutated bead and its left and right neighbor in the chain would still lie within the interval between l_min and l_max. Furthermore, distances from the mutated bead to all other network beads should not be smaller than l_min. After the mutation, the network connectivity Γ_ij was updated by reexamining distances between all beads and the mutated bead; only those pairs that were separated by a distance less than r_int were linked by a spring. After a mutation, the elastic network may possess internal free rotations originating from loosely coupled network parts. They can lead to local movements free of energetic cost, which was to be prevented. Therefore, when the number of nonzero eigenvalues in the spectrum of the elastic network was smaller than 3N−6 (indicating the occurrence of internal rotation zero modes), the mutation was rejected. Once a mutation that fulfilled all criteria was found, probing of allostery in the new elastic network proceeded as described in the previous section, the allosteric parameter after the mutation A^mut was determined, and the mutation was evaluated by comparing the allosteric parameter before the mutation A with that after the mutation A^mut. Only mutations that were favorable, i.e., those that improved the allosteric response in the network, were selected. Two situations were distinguished. In the evolution process where symmetric coupling between the allosteric and regulated pocket was to be optimized, a mutation was accepted only if A^mut < A, and rejected otherwise. In the second independent evolutionary process corresponding to the asymmetric situation, the acceptance criteria for the mutations was A^mut > A. As a termination condition for the two evolution processes, we imposed (A – A^random) < −2.0 Å for the design of the network with symmetric coupling and (A – A^random) > 2.0 Å for the design of the network with asymmetric coupling. A^random denotes the allosteric parameter of the initial random network. During both design processes, the improvement of allosteric response in the evolving networks was recorded (see Fig. S1).

Strain propagation and pathways

In the initial random network, the two designed networks, and the selected mutant networks, the propagation of strain after ligand binding to the allosteric pocket was monitored. The strain of an elastic link connecting beads i and j was defined as $s_{ij}\left(t\right)=d_{ij}\left(t\right)-d_{ij}^{\left(0\right)}$. In the employed model, conformational changes corresponded to relaxation processes of the elastic network structure (see Eq. 1). Therefore, the energy injected locally at the allosteric site, as a consequence of ligand binding there, would not only be converted into deformations of elastic bead connections but would also dissipate. In particular, deformations of elastic springs become significantly damped the farther away they are located from the pocket. Because we still wanted to discuss the anisotropy of strain distribution in the network, a method in which the strain was normalized with respect to the distance from the allosteric site (in terms of the minimal path) was employed. Details are described in the Supporting Materials and Methods. For the visualization of strain, a link was colored blue (if s_ij > 0) or red (s_ij < 0) and the width corresponded to $\left|{\tilde{s}}_{ij}\right|$ (superscript $\sim$ refers to the normalized strain). To determine the communication chains shown in Fig. 5 the maximum absolute strain of each link during the simulation was stored and only those links whose normalized strain exceeded a prescribed threshold ${\tilde{s}}_t$ were considered (for details see Supporting Materials and Methods). For both designed networks, a threshold value of ${\tilde{s}}_t$ = 60% was imposed. To obtain the communication skeleton in the 52-196-197 double mutant of the designed network with symmetric cooperativity (shown in Fig. 6 B), a threshold of ${\tilde{s}}_t$ = 45% was used. For the 52-185 mutant of the designed network with asymmetric cooperativity (see Fig. 6 b), a threshold of ${\tilde{s}}_t$ = 25% was used.

Figure 5.

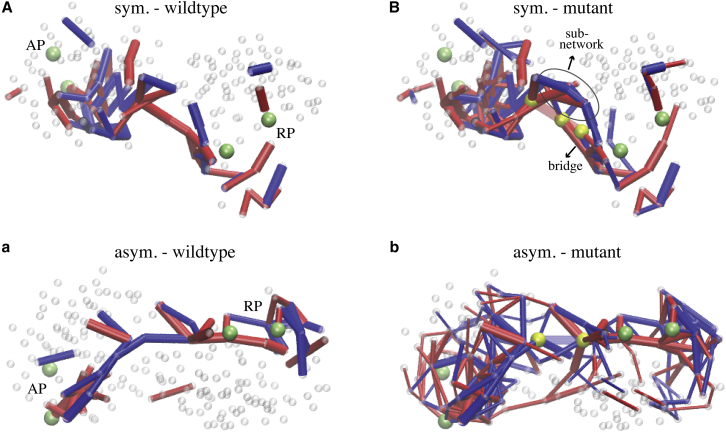
Communication chains in designed structures. (A and B) Elastic links, which are significantly involved in the transport of strain, are found to form simple connected chains that meander through the structure and connect the allosteric pocket in domain 1 (green beads, left side) with the regulated pocket in the remote second domain, domain 2 (green beads, right side). To see this figure in color, go online.

Figure 6.

Communication pathways in mutant structures. Communication chains in the designed wild-type network structures (A and a) are compared with the communication pattern obtained from strain propagation in a corresponding selected mutant structure (B and b). Communication chains in (A) and (a) are the same as shown in Fig. 5, but here another perspective is chosen for better comparison with the mutant structures. (B) Shown here are communication pathways in the 52-197-196 double mutant of the network with symmetric allosteric coupling. Beads with index 52, 197 and 196 are highlighted in yellow and the two bonds removed between them are shown as transparent. Links that, in this mutant, became important to redirect strain over the mutation site, are indicated by an ellipse. (b) Given here are communication pathways in the 52-185 mutant of the designed network with asymmetric allosteric coupling. Beads 52 and 185 are displayed in yellow and the deleted link between them is transparent. Allosteric communication in this mutant was maintained via a complex strain transportation network, and a simple chain, as found in the wild-type, was not available (compare a and b). To see this figure in color, go online.

Robustness

All mutations performed are listed in Table S1. For each mutant network, a robustness coefficient was computed as the ratio of the change in the pocket size of the regulated pocket in the considered mutant network and the pocket size change in the wild-type network, i.e., $\left({\tilde{d}}_{\mathrm{149,189}}^{\left(0\right)}-{\tilde{d}}_{149\text{,}189}^{\text{final}}\right)/\left(d_{\mathrm{149,189}}^{\left(0\right)}-d_{\mathrm{149,189}}^{\text{final}}\right)$. Here, the superscript “∼” denotes distances in the mutant network and superscript “final” denotes distances in the corresponding steady state of the elastic network after ligand binding to the allosteric site (i.e., at time T).

Application to allostery in the myosin V molecular motor

Details of the elastic network construction, modeling of ATP-binding, and quantification of allosteric coupling in the myosin V motor domain can be found in the Supporting Materials and Methods.

Results

Random elastic network and evolutionary optimization

Our structural model of an allosteric system was based on evolutionary optimization starting from a random elastic network. The initial random network was constructed as a two-domain structure. It was obtained by randomly folding two polymer chains independently, each consisting of 100 elastically linked identical beads and representing one domain, and then merging them such that they form a common domain interface. In the model, physical interactions between all beads (beyond those acting between neighboring beads in each chain) were introduced by connecting those two beads by an elastic link that had a separation smaller than a prescribed interaction radius. Thus the complete elastic network was obtained. Details of the construction are described in the Methods.

When elastic networks are constructed based on the structures of real proteins, the beads correspond to atoms or typically represent entire amino acid residues, and elastic links between them empirically mimic the effective interactions between them (38, 39).

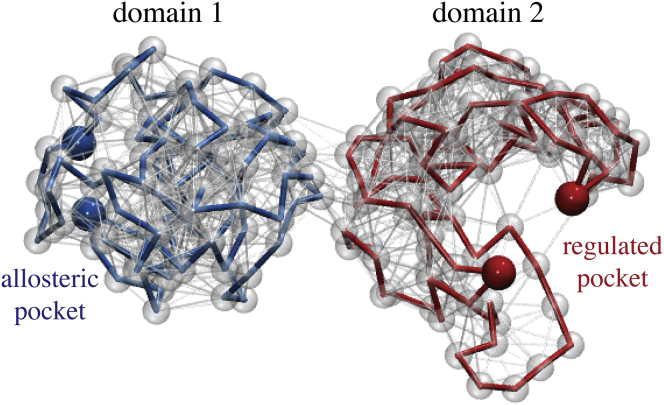
Here, we proceed with the constructed random network of two compactly folded coupled domains shown in Fig. 1. In each network domain a pocket site, for simplicity formed by two beads only, was chosen such that a sufficient separation of the two sites was ensured (see Methods). One site represented the allosteric pocket whereas the other mimicked the regulated pocket, respectively. As shown in Fig. 1, the pockets were located opposite to each other near the surface of the respective domain.

Figure 1.

Random elastic-network structure. Given here is the initial two-domain network consisting of 200 beads connected by elastic links. The randomly folded chains, each forming one domain, are shown as blue (respectively, red) traces of thick bonds. Other links are displayed as thin, in gray. In each domain the two beads representing the remotely placed pockets are highlighted as colored beads. To see this figure in color, go online.

With this setup, the ability of the elastic network to conduct allosteric communication between the pockets was examined using a simple force-probe scheme, in which conformational dynamics in the allosteric site was initiated through local binding of an additional ligand bead, and the subsequent response generated in the regulated site has been detected. In particular, attractive pair forces that were acting on the pocket beads of the allosteric site have been applied to mimic binding of the fictitious ligand bead to its center. The dynamics of protein elastic-networks consists of processes of overdamped relaxation motions (see Methods). Hence, as a result of such forces, all beads underwent coupled relaxation motions, bringing the elastic network from its original conformation (without the forces) to a deformed steady state of the network, with the ligand bead tightly bound to the allosteric site (i.e., with the forces applied for a long time). During this process, the additional forces tend to close this site, i.e., its two beads move toward each other, and first the elastic links localized in their vicinity became deformed. Eventually deformations propagated through the entire network structure until a final steady network conformation was reached. In the simulations, the conformational motions inside the network were followed by numerically integrating the equations of motion for all network beads (see Methods). The response generated inside the regulated pocket in the second domain was quantified in terms of distance changes between its two corresponding beads.

As we found, the random network structure did not reveal any allosteric coupling between the two sites. Whereas the allosteric site closed upon ligand binding, with the distance between pocket beads changing by ∼−4 Å, no response was detected at the regulated site, with a change of <10⁻⁴ Å (for the choice of lengths units, see Methods). Proceeding with this observation, an algorithm of evolutionary optimization aimed to design networks with pronounced allosteric communication, was established. The optimization process consisted of sequences of mutations followed by selection, which were applied iteratively starting from the initial random network. In each evolution step, the following sequence was carried out: 1) mutation: a single structural mutation was performed by randomly selecting one network bead (excluding one of the four pocket beads) and changing its equilibrium position, which corresponded to an alteration of elastic connections in the vicinity of the mutation spot; 2) probing of allostery: the force-probe scheme was applied in a simulation of the new mutant network structure and its conformation with the ligand bead bound to the allosteric site was obtained; and 3) selection: the allosteric response in the regulated pocket of the network before and after the mutation was compared and the mutation was scored favorable, and was accepted if the mutant network showed improved allosteric coupling between the two sites, otherwise it was rejected. The optimization procedure was iteratively applied and terminated, once a network structure with a prescribed level of sufficient allosteric coupling was obtained. Details of the implementation are described in the Methods.

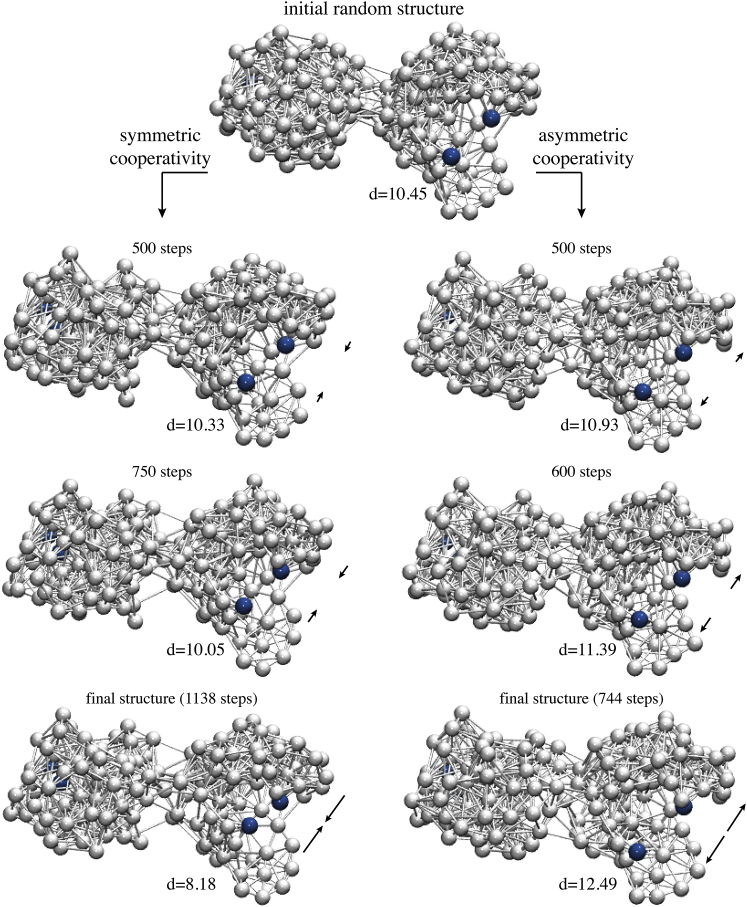
In this work two prototype examples of elastic network structures with allosteric coupling were designed and analyzed. In two independent simulations of evolutionary optimization, starting both times with the same initial random network, two different network structures with optimized allostery have been designed. The first one was designed under the side condition that allosteric coupling between the remote sites had symmetric cooperativity, i.e., binding of the ligand bead to the allosteric site and the concomitant closing of that pocket resulted in consequent closing of the regulated site. In the second case, the requirement was vice versa; allosteric communication was optimized under the premise that ligand-induced closing of the allosteric pocket triggered opening in the regulated site, i.e., asymmetric cooperative coupling was realized. In both cases, as a result of several hundreds of mutations that were needed during evolution to improve allosteric coupling, the networks underwent significant structural remodeling and concomitant rewiring of elastic interactions between their beads. In Fig. 2, snapshots of network architectures along the processes of evolution are displayed. For both designed networks, it could be observed that besides mutation-induced changes taking place inside the individual domains, their common interface became significantly remodeled. As evolution progressed, the allosteric response generated inside the regulated pocket upon ligand binding to the allosteric pocket was gradually enhanced during both design processes, as can be seen by comparing corresponding snapshots of network conformations in Fig. 2. In the next paragraphs the two prototype designed network structures are presented and their dynamical properties analyzed.

Figure 2.

Evolutionary optimization. Given here are snapshots of network conformations taken at different steps of accepted mutations along the processes of evolutionary optimization toward designing the two prototype allosteric networks. The initial random network structure is shown in the top row. Each depicted network conformation corresponds to the steady state with the allosteric pocket being closed after ligand binding and the allosteric response in the regulated pocket becoming progressively improved. In the design process of the network with symmetric cooperativity, the regulated pocket increasingly closed as evolution proceeds, whereas during the design of the network with asymmetric cooperativity, its ability to open emerged (indicated by black arrows). Pocket beads are highlighted in blue color and the size of the regulated pocket in Å is given for all snapshots. Mutation-induced structural changes and concomitant remodeling of elastic interactions can be seen by comparing snapshots. Final structures of designed networks are shown in the bottom row. To see this figure in color, go online.

Designed prototype networks

The designed networks are shown in Fig. 2 (bottom panel). Both networks retained the initial two-domain architecture after the evolution; however, their structures were clearly different from the initial random network. In both designed networks a pronounced domain interface with many interdomain links had emerged; such interface was rather sparse in the initial random network (see Fig. 2). Remodeling of that region under the process of evolution apparently points toward the importance of the pattern of elastic connections in the domain contact region for allosteric communication in our model systems. Those aspects will be further discussed in the next section.

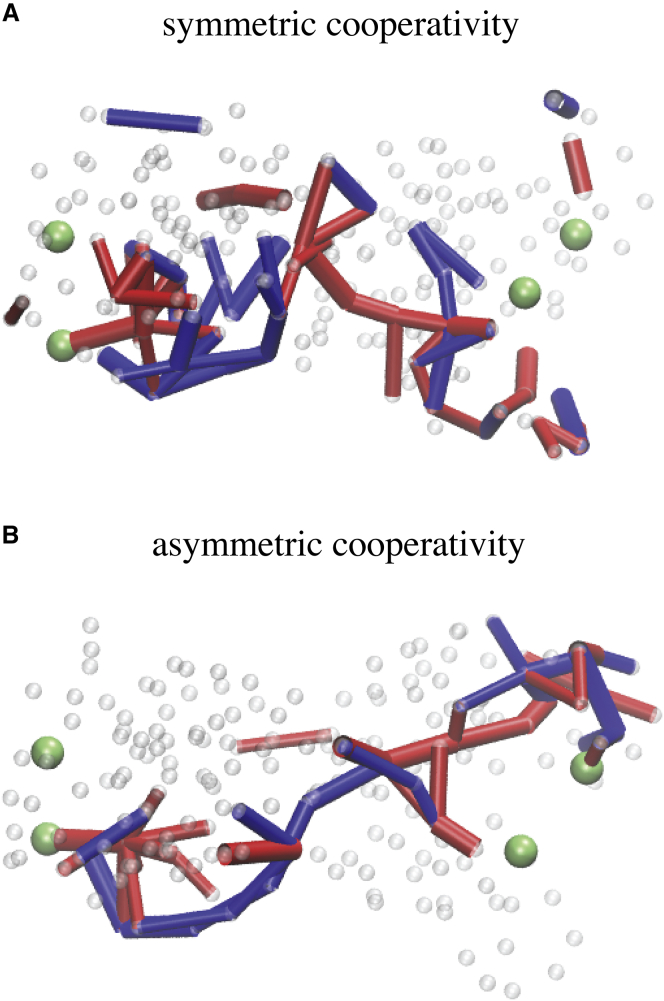
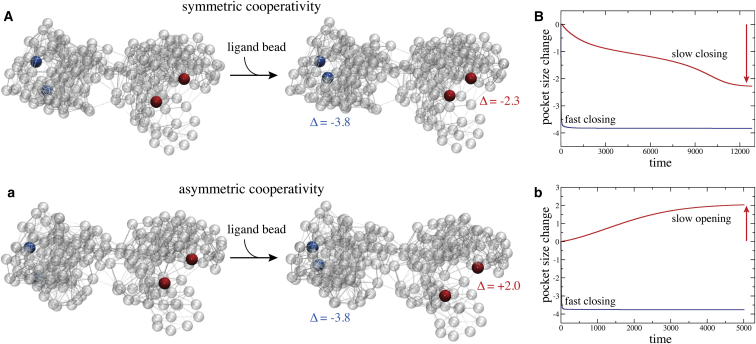
In Fig. 3, A and a, the two designed networks are shown, each in their equilibrium conformation and in the respective steady conformations, with the ligand bound to the allosteric pocket and the allosteric response having been triggered in the remote regulated sites. Traces showing changes in the size of both pockets upon binding of the ligand bead to the allosteric pockets are also provided (see Fig. 3, B and b). In both designed networks, the allosteric pocket closed rapidly when the ligand bead bound there, with the size changing by −3.8 Å in both cases. In striking contrast, motions inside the regulated pocket were much slower, when changes in its size only gradually set in and the pocket smoothly approached its closed conformation in the network with symmetric cooperativity (change by −2.3 Å), or open conformation in the network with asymmetric cooperativity, respectively (change by +2.0 Å). Movies visualizing conformational motions during the allosteric transition in the designed networks are provided as Movies S2 and S3.

Figure 3.

Allosteric coupling in designed network structures. (A and a) For both designed networks, the initial structure and the final structure with the ligand bound to the allosteric pocket are shown. Elastic connections between network beads are shown as thin transparent lines and pocket beads are colored blue (allosteric pocket) and red (regulated pocket), respectively. In both designed networks the initial and respective final structure is very similar (see text), but the large-amplitude motions of pocket beads evidencing intrastructure allosteric communication are apparent. In the network with symmetric cooperativity, ligand-induced closing of the allosteric pocket triggers allosteric closing of the regulated pocket, whereas, in the network with asymmetric cooperativity, the allosteric response consisted of opening of the regulated site. (B and b) Given here are traces showing changes in the size of both pockets upon binding of the ligand bead to the allosteric pockets (blue color for allosteric the pocket, red for the regulated pocket). To see this figure in color, go online.

Comparing the ligand-bound network conformation with the initial structure reveals that, in both designed networks, the conformational changes underlying allosteric dynamics did not involve any large-scale structural rearrangements but were rather governed by small-amplitude subtle motions. In fact, initial and ligand-bound structures compared by root mean squared deviations of only 0.6 Å in the symmetric case and 0.46 Å in the asymmetric case, respectively. Although local motions in the two pockets were indeed pronounced, the communication between them must therefore have resulted from cascades of small-amplitude displacements of network beads located in the regions connecting both pockets.

By the application of evolutionary optimization to the random network, we could successfully design special networks whose two-domain structure encodes enhanced allosteric interactions between two remote pockets. All three network structures are provided as Supporting Materials and Methods. Next, to unravel signatures that may underlie allosteric communication in the two prototype networks, we have analyzed the conformational dynamics in terms of mechanical strain propagating through the network structures.

Propagation of strain and communication pathways

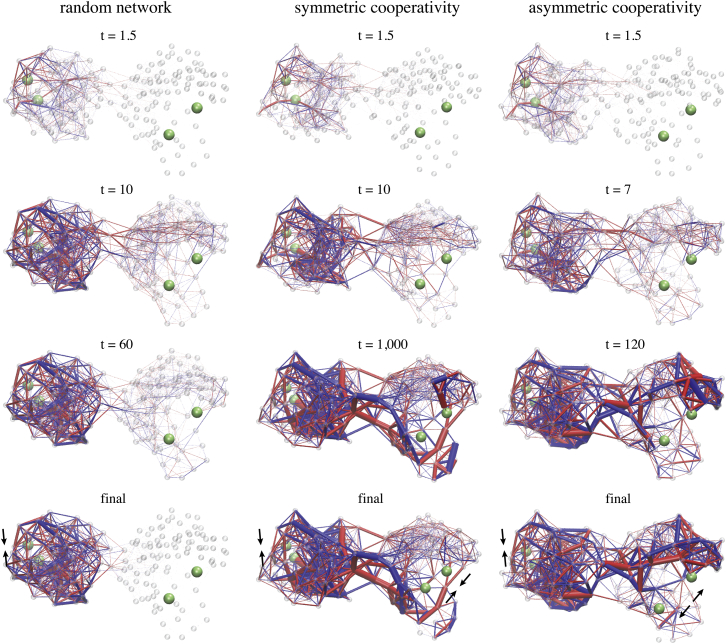
Apparently, allosteric interactions in our model systems result from conformational changes propagating from the allosteric site across the domain interface to the regulated site. Therefore, in both designed structures, the elastic strain inside the networks was computed during the entire simulation after ligand binding to the allosteric site until the steady state of the respective network was reached. The strain inside a network was determined in terms of the deformation of elastic links connecting the beads, i.e., deviations from their natural lengths in the initial ligand-free network. Details of the computation are found in the Methods and Supporting Materials and Methods. To conveniently visualize strain propagation, the network links are displayed bicolored, to distinguish stretching or compression, and their width is proportional to the magnitude of the respective deformation. To compare to the designed networks, the strain propagation was also followed in the initial random network, which was allosterically inactive. Snapshots of the strain distribution in all three networks taken at different time moments during the simulation are shown in Fig. 4. Movies visualizing conformational motions and the propagation of strain are provided as Movies S1, S2, and S3.

Figure 4.

Strain propagation. Propagation of strain subsequent to ligand-binding to the allosteric pocket is visualized in the random network and in the two designed structures. Snapshots taken at different time moments during each simulation are shown in similar perspectives. Network bonds are displayed bicolored, with blue indicating stretching of the bond and red denoting compression as compared to the corresponding natural bond length. The thickness encodes the absolute value of strain the link was subject to. To see this figure in color, go online.

In all three networks the strain was first localized in the vicinity of the allosteric pocket where the ligand was bound. After that, interactions between other beads also rapidly set in and the majority of links in domain 1 became deformed. In the random network, the distribution of strain in domain 1 was rather homogeneous; most links were stretched or compressed at similar levels and there was no distinctive feature present. In this network, no significant deformations of links located in the central domain interface region could be detected, and therefore spreading of strain into the second domain during the simulation was practically absent. The structure of this domain is apparently very stiff, preventing any internal conformational motions from occurring. Hence, the random elastic network cannot conduct allosteric communication. The situation in both designed networks was completely different. First, after ligand binding to the allosteric site, conformational motions spread across the domain interface and generated deformations in the second domain and in the vicinity of the regulated site. Second, not all elastic pair interactions in the designed structures were equally involved in the process of allosteric coupling. Instead, the temporal distribution of strain shows that communication between the remote pockets proceeded through specific subnetworks that were apparently critical for allostery in the designed structures. Those networks are formed by a subset of beads connected by springs that undergo major deformations and, hence, contribute essential pathways for the spreading of conformational motions from the allosteric site across the structure to the regulated site. In both designed network structures, such remarkably strained springs were found in domain 1 and, in contrast to the random network, in the central domain interface region and domain 2, where they form sparse clusters of important pair interactions between beads.

Regions in which the elastic links remained only marginally populated by strain were rather stiff as compared to the rest of the network. In that regard we observed that the structure of domain 2 in the designed networks is special. In the network with symmetric allosteric cooperativity, the two lobes in the tweezerlike domain structure, each harboring one of the pocket beads of the regulated site, were found to be quite flexible whereas the other parts in domain 2 were stiff (see Fig. 4). In the network with asymmetric allosteric coupling, the hinge region connecting both lobes appears to be very flexible instead (see Fig. 4). The specific pattern of flexibility in the designed networks has apparently emerged during the process of evolutionary optimization to make opening/closing motions of the regulated site possible, and hence enable the designed network architectures to conduct allosteric communication.

The analysis of strain propagation in the designed networks clearly reveals functionally important signatures underlying the investigated types of allosteric coupling. Nonetheless, the strain distribution was rather complex, and we therefore aimed to deduce simpler pathways that could characterize communication between the pockets, by focusing only on those network springs that carry major strain (see Methods). Results are shown in Fig. 5. In both networks, simple chains formed by significantly deformed adjacent network links were found to meander from the allosteric pocket in domain 1 via the domain interface to the regulated pocket in domain 2. Such chains are composed of a series of stretched springs in domain 1, that are potentially caused by the closing motion of the allosteric site. They are further connected to a linkage of compressed springs located in domain 2, and trigger the respective allosteric response there.

The identified communication chains are obviously critical for the transmission of conformational changes between the domains and therefore may represent a functional skeleton, critical for allosteric activity in the designed network architectures. Immediately, one may pose the question whether, and to what extent, allosteric coupling can be maintained if structural changes would be applied to such motifs.

Robustness of allosteric communication

With regard to the robustness of allosteric communication in the two designed networks, the intention was not to perform a systematic screening of the effect of structural perturbations. Instead, the aim was to present a demonstration. Therefore the analysis of robustness was limited to a few exemplary structural mutations: those applied to beads belonging to the identified communication pathways and on examining their influence on allosteric interactions. In a first set of simulations, mutations consisting of the deletion of only a single elastic link between two network beads were considered. In the realm of proteins, such type of perturbation would roughly correspond to the mutation of a single amino acid residue, resulting in specific local interactions disappearing. For each specific mutant network, a single simulation starting with ligand binding to the allosteric pocket was carried out and after completion, the response in the regulated pocket was quantified and the level of allosteric communication determined. The results are listed in Table S1. It is found that allostery in both designed networks is generally robust with respect to the removal of single interactions. To understand how long-range coupling between both pockets is maintained in the mutant networks, we have visualized the propagation of strain and determined communication pathways for some exemplary cases, similar to what has been performed for the designed wild-type networks (see previous section).

For the network with symmetric cooperativity, three cases were focused on in more detail, all of which maintained allosteric activity (see Table S1). They corresponded to a mutant with one major interaction at the central domain interface having been removed and another mutant with a link deleted in domain 2, closer to the regulated pocket. The computed communication chains in those two mutants are shown in Fig. S3. Movies of strain propagation in those two mutant networks are provided as Movies S4 and S5. To highlight robustness in the first designed network, a third example, consisting of a double mutant network in which both selected links were deleted, was also considered (see Movie S6). For all three mutant networks, we find that the strain propagation networks as well as the extracted communication chains are very similar to that of the wild-type networks, except in the vicinity of the respective mutation site (see Fig. 6, A and B; Fig. S3). There it is found that in the neighborhood of the deleted link, a few bead interactions that in the wild-type network have not played a major role in the transmission of strain, become important, forming a bridge through which strain was able to side-track the mutation site (see Figs. 6 B and S3). This result demonstrates that in the mutant structures, similar communication pathways are available which, together with the bridge motifs that compensate the mutation defect, are employed for the propagation of conformational changes and hence may provide the foundation for the robustness of allosteric coupling in this designed network.

For the designed network with asymmetric allosteric coupling, one mutant structure with a single deleted link located at the domain interface has been selected for illustration. Despite the mutation, it revealed full allosteric activity. Propagation of strain subsequent to ligand binding to the allosteric pocket is shown in Movie S7 and the extracted communication pathways are depicted in Fig. 6 b. It is found that the network of bead interactions through which communication between both pockets was transmitted is rather complex, with the strain populating large parts of the mutant structure. Hence, in contrast to the wild-type network, allosteric coupling in this mutant does not proceed via simple communication chains.

Although, generally, allosteric communication in both designed networks was found to be robust with respect to the deletion of a single bead interaction, there were still a few critical mutations that involved a drastic decrease in the coupling between both pockets. They can correspond to perturbations in the vicinity of either pocket, or are located at the domain interface (see Fig. S2, A and B). In the final step of investigations, the effect of stronger mutations was considered, where an entire bead was deleted in a simulation of each network. Those perturbations typically led to a remarkable drop or even complete knockout of allosteric communication (see Table S1).

Application to allostery in proteins

In this article, two prototype coarse-grained architectures of fictitious allosteric proteins have been successfully designed and investigated. In the final part of the article, it is demonstrated that the developed modeling approach, the analysis of strain propagation, and the methods to quantify and visualize communication pathways, can be applied in the structure-based investigation of real allosteric proteins. For the purpose of demonstration, the modeling scheme was applied to the popular myosin V (myoV) molecular motor, which steps along actin filaments operating as a processive cargo transporter (40). In molecular motors, the nucleotide pocket (where chemical events, consisting of ATP-binding and hydrolysis, take place) is typically spatially remote from the site where mechanical forces are exerted, e.g., on filaments, and allosteric regulation between them is essential for chemo-mechanical coupling and the motors’ functional activity.

Here, for the myoV motor domain (41), allosteric communication between the ATP-binding pocket and the actin-binding cleft was investigated. In the following, concepts and results are focused on whereas an in-detail description of the undertaken modeling can be found in the Supporting Materials and Methods. First, an elastic network of the nucleotide-free motor domain of myoV was constructed. Then, binding of an ATP molecule was emulated by applying precise forces only locally to the nucleotide-binding pocket, dynamically steering it to the experimentally known conformation that was complexed to an ATP analog (41). During this simulation, the entire conformational dynamics in myoV was monitored, and allosteric transduction of motions from the nucleotide-binding pocket to the actin cleft detected.

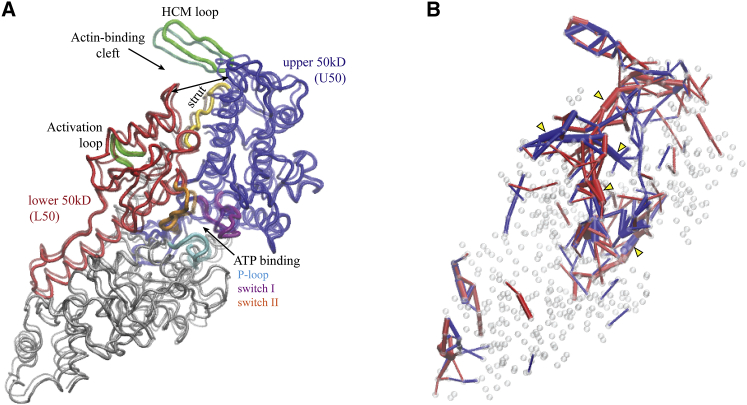
It is found that localized ATP-related dynamics, consisting of relative motions of the P-loop and switch I and II inside the nucleotide-binding pocket, was remarkably well reproduced. Initially, residues of the free pocket compared well with an RMSD of 2.4 Å to those corresponding to the ATP-bound conformation, although during the simulation, the RMSD dropped to zero (see Fig. S4), indicating that, locally, motions that corresponded to ATP-binding in myoV were perfectly reproduced. Furthermore, in response to ATP-binding to its pocket, it is found that conformational changes within the entire motor domain slowly set in and large-amplitude relative motions of the L50 and U50 were generated. As a result of these motions, the actin-binding cleft also underwent changes and significantly opened up (changes of 3.5 Å; see Fig. S4). In Movie S8, conformational motions during the allosteric transition in myoV are visualized, and in Fig. 7 A, the initial free conformation and that obtained after ATP-binding are superimposed, highlighting domain rearrangements and the coupled allosteric conformational changes between the nucleotide pocket and the actin site.

Figure 7.

Allosteric regulation in myosin V. In (A), the nucleotide-free structure of the myoV motor domain (shown as transparent) and the conformation obtained after modeling of ATP-binding (as solid) are superimposed. Significant opening of the actin-binding cleft resulting from allosteric interactions with the ATP-binding pocket was observed. Major domains are colored red and blue, and structural motifs involved in ATP-binding and interactions with actin are also highlighted. In (B), the identified communication pathways underlying allosteric regulation in myoV are shown. Coding of color and bond strength is similar to that used in the analysis of the designed networks (Figs. 4 and 5). Localization of elastic strain in the ATP and actin interaction motifs together with transport chains between them are clearly visible. Essential regions are marked by yellow arrows. To see this figure in color, go online.

Next, to elucidate mechanical aspects of allostery in myoV, strain propagation was analyzed, employing the same methods developed for the designed artificial protein networks. In Movie S9, propagation of strain subsequent to ATP-ligand binding is visualized, and snapshots taken at different time moments during the simulation are provided in Fig. S5. It was found that ATP-binding generated significant strain that was localized near the ATP motifs and further spread into the regions around the actin cleft. We observed that propagation of strain from the ATP-pocket to the actin site proceeded through well-defined subnetworks formed by spring connections that underwent significant deformations. The identified pathways and chains found to be essential for strain transport are shown in Fig. 7 B. Remarkably, regions in which strain was accumulated primarily coincided with the structural motifs of conserved residues that are critical for the mechanochemistry of the myoV motor. First, due to ATP-binding, considerable strain is localized to the P-loop, switch I, and switch II motifs, and in the regions bridging them, e.g., near the entrance to the ATP-pocket. Second, there are definite and pronounced transport pathways reaching from the switch I and switch II motifs into the L50 domain from where they meander further into the actin site (see Fig. 7 B). There, strain occupied critical motifs involved in interactions with actin filaments, e.g., the activation loop, the HCM loop, and the strut. The latter region provides the flexible linker between L50 and U50 domains and its strained state may explain opening of the actin cleft.

Exemplary mutations applied near the conserved motifs turned out to significantly reduce allosteric coupling in myoV (details are given in Supporting Materials and Methods).

Application of the modeling scheme, developed to design prototype structures with optimal allosteric coupling, was demonstrated here for the so-called “rigor state” (nucleotide-free, actin-bound) to “postrigor” state (ATP-bound, detached from actin) transition in the myosin V protein. This transition is well investigated experimentally, and based on previous computational studies (e.g., (37, 42)). In our simulations, the local conformational dynamics related to binding of an ATP ligand as well as the concomitant actin-site opening resulting from allosteric coupling was remarkably well reproduced, evidencing the applicability of the developed approach to the realm of protein allostery (see Discussion). Analysis of strain propagation revealed distinct functional signatures of intramolecular communication, and hence may provide interesting novel aspects for a mechanistic-level explanation of the allosteric regulation in myosin V.

Discussion

The phenomenon of allosteric coupling between different functional regions within a macromolecular structure is ubiquitously present in proteins and therefore raises important questions about the fundamental nature of the underlying mechanisms. In contrast to typically employed structure-based modeling of protein dynamics, a different methodology toward approaching such essential problems is presented in this article. Instead of considering real protein structures, artificial analog structures that encode pronounced long-range allosteric coupling between two spatially remote pockets were designed. The structures were represented by elastic networks, similar to the coarse-grained models widely used to describe conformational dynamics of real proteins.

A force-probe scheme consisting of ligand-binding to the allosteric pocket, following conformational motions spreading over the structure, and detecting the response generated in the regulated pocket, was implemented to evaluate the ability of the network to conduct allosteric communication. Initially starting with a random elastic network, which did not reveal any allostery, a scheme of evolutionary optimization was iteratively applied to design two prototype elastic-network structures with perfected allosteric coupling, one with symmetric and the second with asymmetric cooperativity.

In the designed networks, well-defined pathways and simple chains of important interactions, established by only a few network beads, were identified to constitute the signatures that underlie allosteric communication. Remote interactions were robust even if minor structural perturbations were applied. However, a single critical mutation could knock out completely allosteric communication in the designed networks.

Whereas the first descriptions of allosteric systems, namely the MWC and the KNF models (43, 44), were formulated more than 50 years ago in the absence of any structural data and were thus of a phenomenological nature, the development of very sophisticated experimental techniques and the vast amount of protein structures becoming available in the last decades have since allowed us to investigate allosteric communication in proteins on the molecular level and led to a decent understanding of the mechanism underlying allostery in several role model proteins. In the recent past, structure-based computational modeling, aiming to follow the conformational motions as the underpinning of allosteric effects in proteins, has gained a lot of attention. In particular, due to the timescale gap present in atomistic-level MD simulations, coarse-grained elastic network models that are limited to the mechanical aspect of protein operation became very popular to investigate slow allosteric transitions with timescales beyond the microsecond range. In those studies, the analysis of conformational changes is typically based on the computation of normal modes, and allosteric effects are discussed in terms of short- and long-ranged correlations of amino-acid residue displacements.

The aim in this study was to present a model that emphasizes the mechanical picture of allosteric systems. Therefore, the elastic network model was used. Here, however, the full elastic dynamics of the network was considered by always numerically integrating the nonlinear equations of motion and monitoring processes of conformational relaxation; no linearization was performed and the conformational dynamics beyond the limiting normal mode approximation could be followed. As a consequence, this model has the obvious advantage that it can resolve the temporal order of events that eventually establish allosteric communication in the network structures, starting from forces and strains that were first generated locally at the allosteric site as a consequence of ligand binding, followed by the subsequent propagation of conformational motions via the domain interface, to finally induce structural changes in the remote regulated pocket. This model, therefore, naturally includes causality as the guiding principle to manifest allosteric communication, and therefore is richer in its explanatory power compared to correlation-based analyses.

This model emphasizes the structural viewpoint of allostery (as described in (1)) in which allostery is regarded as a consequence of optimized communication between the remote functional sites, established through the propagation of strain along pathways that are formed by a set of interacting residues. The employed elastic network description clearly implies limitations. All network particles are of the same kind and physical interactions between them are incorporated into empirical effective potentials; thermal fluctuations were also neglected for simplicity. Despite such gross simplifications, the dynamical properties of the designed prototype allosteric structures reveal remarkable similarities with those found in real allosteric proteins: 1) specific parts of the structure are flexible, whereas other regions form stiff clusters; 2) the propagation of conformational changes that results in the long-range coupling of the remote sites proceeds through communication pathways involving only a few of the many intrastructural interactions; and 3) single critical mutations can knock out allosteric coupling.

Application of the modeling scheme to the rigor-to-postrigor transition in the myosin V molecular motor correctly reproduced the conformational dynamics corresponding to the ATP-binding related detachment from actin filaments via allosteric transduction. Despite the complexity of chemo-mechanical operation, simple communication pathways were identified that underlie allosteric coupling in this protein motor. Hence, the applicability of the developed approach to investigate protein allostery is demonstrated. Moreover, commonalities between the designed prototype networks and a real protein is exemplified. Although the artificial network structures have emerged as a result of simplified in silico evolution, they share functional properties with a protein structure that underwent real biological evolution to encode allosteric dynamics.

In summary, we may conclude that the designed elastic network structures can provide suitable physical models for the mechanics of complex allosteric biomolecules, such as proteins.

It should be remarked that the evolutionary pressure imposed in the design process consisted only in magnifying changes in the regulated pocket in response to ligand-induced changes in the allosteric pocket; no other requirements were imposed and the dynamical properties that actually improved allosteric communication in the evolving structures emerged autonomously. However, in future studies, design algorithms that involve coevolution can also be implemented and multiple optimization criteria can be imposed. Moreover, in future studies, the design and analysis of a larger number of allosteric elastic networks can be undertaken. That would allow us to compare properties such as communication pathways among them and possibly draw conclusions on the generality of such dynamical motifs.

Previously, the relaxational elastic-network approach employed in this study was already applied to model ATP-related dynamics in protein machines and to investigate allosteric coupling (35, 36, 45). Whereas in those studies allosteric coupling was only qualitatively discussed, the approach presented here may generally be applied in structure-based modeling and help in understanding important mechanistic aspects of protein allostery.

Added note

After finishing the article I became aware of two quite recently appeared works, in which the design of mechanical networks with allosteric coupling had also been undertaken (46, 47). There, however, different computational algorithms were used and optimization of allosteric coupling was performed within the linear response limitation; the underlying network architectures were also very different (e.g., 2D on-lattice models (46)). Both works principally demonstrate the applicability of design processes to obtain desired responses. The design process introduced in my article was developed completely independently and all results were presented already in January 2016 (see (48)). Besides other differences, its principal distinction is that during the design process, the allosteric response was optimized by always considering the full nonlinear elastic dynamics of the networks. The importance of nonlinearities for protein function involving allostery has previously been evidenced (e.g., in (49, 50)). The network architectures used in my study resemble more closely the 3D compact fold of real proteins; in fact, the designed networks can be regarded as coarse-grained representations of fictitious protein structures. Most importantly, this work goes beyond developing the design process. In fact, the main emphasis here was put on understanding mechanical properties underlying long-range communication in the designed networks; this was achieved by visualizing and analyzing propagation of strain, extracting communication pathways and chains that were critical for allosteric coupling, and investigating robustness of the designed functional properties.

Author Contributions

H.F. designed and performed research, analyzed data, and wrote the manuscript.

Editor: Monika Fuxreiter.

Supporting Material

Data S1. Text File Containing Spatial Coordinates of the Initial Random Network

First column: bead index (0–199); second, third, and fourth columns: x, y, and z coordinate of the bead position.

Data S2. Text File Containing Spatial Coordinates of the Designed Network with Symmetric Allosteric Coupling

First column: bead index (0–199); second, third, and fourth columns: x, y, and z coordinate of the bead position.

Data S3. Text File Containing Spatial Coordinates of the Designed Network with Asymmetric Allosteric Coupling

First column: bead index (0–199); second, third, and fourth columns: x, y, and z coordinate of the bead position.