A new concordance measure for risk prediction models in external validation settings

Abstract

Concordance measures are frequently used for assessing the discriminative ability of risk prediction models. The interpretation of estimated concordance at external validation is difficult if the case-mix differs from the model development setting. We aimed to develop a concordance measure that provides insight into the influence of case-mix heterogeneity and is robust to censoring of time-to-event data.

We first derived a model-based concordance measure (mbc) that allows for quantification of the influence of case-mix heterogeneity on discriminative ability of proportional hazards and logistic regression models. This mbc can also be calculated including a regression slope that calibrates the predictions at external validation (c-mbc), hence assessing the influence of overall regression coefficient validity on discriminative ability. We derived variance formulas for both mbc and c-mbc. We compared the mbc and the c-mbc with commonly used concordance measures in a simulation study and in two external validation settings.

The mbc was asymptotically equivalent to a previously proposed resampling-based case-mix corrected c-index. The c-mbc remained stable at the true value with increasing proportions of censoring, while Harrell’s c-index and to a lesser extent Uno’s concordance measure increased unfavorably. Variance estimates of mbc and c-mbc were well in agreement with the simulated empirical variances.

We conclude that the mbc is an attractive closed-form measure that allows for a straightforward quantification of the expected change in a model’s discriminative ability due to case-mix heterogeneity. The c-mbc also reflects regression coefficient validity, and is a censoring-robust alternative for the c-index when the proportional hazards assumption holds.

BACKGROUND

Assessing the performance of a clinical prediction model is of great practical importance to learn about the potential clinical value. An essential aspect of model performance is separating subjects with good outcome from subjects with poor outcome (discrimination) [1]. Concordance measures, also called concordance-statistics or c-statistics, are commonly used to assess the discriminative ability of risk prediction models. A c-statistic estimates for two randomly chosen subjects the probability that the model predicts a higher risk for the subject with poorer outcome (concordance probability) [2, 3]. The observed c-statistic of a risk prediction model in external validation data depends on the validity of the regression coefficients, but also on the heterogeneity of the case-mix [4–6]. Case-mix heterogeneity refers to the variation in subject characteristics and can readily be quantified by the standard deviation of the linear predictor [5].

Harrell’s concordance-index (c-index) is the most frequently used c-statistic for binary and for time-to-event outcomes, but is sensitive to censoring of time-to-event outcomes [7, 8]. An inverse probability weighting technique was proposed by Uno et al. to offset the dependence of the c-index on censoring [8]. For validation of proportional hazards regression models within model development data, Gönen and Heller proposed a censoring-robust concordance measure [7]. This model-based concordance measure, which was also suggested by Korn and Simon as a measure of explained variation [9], is a function of the regression coefficients and the covariate distribution and does not use observed event and censoring times. Consequently, in an external validation population it merely assesses the expected discriminative ability of the model, similar to a previously proposed case-mix corrected c-index [10]. This case-mix corrected c-index – based on resampling outcomes under the assumption of correct regression coefficients – was suggested to disentangle the effect of a different case-mix from incorrect regression coefficients on discrimination [4]. Such disentangling is relevant to the interpretation of a difference between the c-statistic at model development versus the observed c-statistic at external validation. We hereto calculate the difference between the c-statistic at model development and the case-mix corrected c-statistic at external validation to indicate the change in discriminative ability attributable to the difference in case-mix heterogeneity. Next, the difference between the observed c-statistic and the case-mix corrected c-statistic in external validation data expresses the change in discriminative ability due to the (in)correctness of the regression coefficients.

We aimed to develop a model-based concordance measure (mbc) to assess the discriminative ability of risk prediction models in external data. Since the most commonly used concordance measures all have their restrictions (Table 1), the new measure should be a valuable addition for: (1) assessment of the influence of case-mix heterogeneity on concordance of both logistic regression and proportional hazards regression models; and (2) censoring-robust measurement of a proportional hazards regression model’s concordance in external validation data. We studied the behavior of the newly developed concordance measure in external validation settings with simulation and two case studies.

Table 1. Use of mbc, c-mbc and commonly used concordance measures.

For proportional hazards regression models and logistic regression models, it is specified: how to measure concordance in an apparent validation setting (in patients whose data was used for model development); how to assess the influence of case-mix heterogeneity on concordance (Concordance assuming correct regression coefficients) in an external validation setting (in new patients); and how to measure concordance in an apparent validation setting.

	Apparent validation	External validation
	Concordance	Concordance assuming correct regression coefficients	Concordance
Proportional hazards regression models	c-index	case-mix corrected c-index	c-index
	Uno		Uno
	Gönen-Heller	Gönen-Heller
	mbc	mbc	c-mbc
Logistic regression models	c-index	case-mix corrected c-index	c-index
	mbc	mbc	c-mbc

THE MODEL-BASED CONCORDANCE

Notation

We will assess the discriminative ability of previously developed logistic regression models and proportional hazards regression models in new patient populations. Both regression models predict patient outcome Y based on a linear predictor $x^T\beta$, which is a linear combination of the patient’s baseline characteristics vector x and regression coefficient vector β. The random outcome variable $Y_i$ and its realization $y_i$ for patient i of n patients in the validation population takes values of 0 or 1 in case of a logistic regression model, and positive time-to-event values in case of a proportional hazards regression model. For a time-to-event realization of patient i we use the indicator ${\delta }_i$ to denote an observed event time $\left({\delta }_i=1\right)$ or a censored event time $\left({\delta }_i=0\right)$. When the $i^{th}$ row of a population’s design matrix X is the baseline characteristics vector $x_i$, the linear predictor $x_i^T\beta$ of patient i is the $i^{th}$ element of the vector Xβ. Note that an additional first element of $x_i$ is set to 1 for multiplication with a logistic regression model’s intercept. A linear predictor $x_i^T\beta$ of a logistic regression model is transformed by the logistic function to obtain prediction $p_i$. A linear predictor of a proportional hazards regression models is transformed into a prediction $p_i$ by the survival function $S\left(t|x_i^T\beta \right)=\mathit{exp}\left\{-{{\displaystyle \int }}_0^t{\lambda }_0\left(s\right)e^{x_i^T\beta }ds\right\}$, with ${\lambda }_0\left(t\right)$ the baseline hazard function of the proportional hazards regression model’s. Although the baseline hazard function is necessary to obtain absolute risk predictions, we will not need it in the remainder of this paper.

Derivation of the model-based concordance

The concordance probability is defined as the probability that a model predicts for two randomly chosen patients a higher risk for the patient with poorer outcome.

For a given patient population it is the probability that a randomly selected patient pair has concordant predictions and outcomes, divided by the probability that their outcomes are different (not “tied”). The probability that a randomly selected patient pair has concordant predictions and outcomes is [9]:

$$P\left(\text{concordant}\right)=\frac{1}{n\left(n-1\right)}{\displaystyle \sum }_i{\displaystyle \sum }_{j\ne i}\left[I(p_i<p_j)P(Y_i<Y_j)+I(p_i>p_j)P(Y_i>Y_j)\right]$$ (1)

Similarly, the probability that a randomly selected patient pair has unequal outcomes is:

$$P(\text{unequal Y})=\frac{1}{n(n-1)}{\displaystyle \sum }_i{\displaystyle \sum }_{j\ne i}\left[P(Y_i<Y_j)+P(Y_i>Y_j)\right]$$ (2)

Thus, the concordance probability CP in a patient population is obtained by dividing the probabilities of equation 1 and 2:

$$\mathit{CP}=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[I(p_i<p_j)P(Y_i<Y_j)+I(p_i>p_j)P(Y_i>Y_j)\right]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[P(Y_i<Y_j)+P(Y_i>Y_j)\right]}$$ (3)

With $P(Y_i<Y_j)=I(y_i<y_j)$ equation 3 returns Harrell’s c-index, but to obtain a model-based estimator we derive $P(Y_i<Y_j)$ from a regression model. For a logistic regression model the model-based probabilities $P(Y_i<Y_j)$ are:

$$P(Y_i<Y_j)=P\left(Y_i=0\right)P\left(Y_j=1\right)=\frac{1}{1+{\mathrm{e}}^{x_i^T\beta }}\frac{1}{1+{\mathrm{e}}^{-x_j^T\beta }}$$ (4)

Combining equations 3 and 4, and replacing $I(p_i<p_j)$ by $I\left(x_i^T\beta <x_j^T\beta \right)$ because the predictions are an increasing function of the linear predictor, results in the model-based concordance (mbc) for logistic regression models:

$$\mathit{mbc}\left(X\beta \right)=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[\frac{I\left(x_i^T\beta <x_j^T\beta \right)}{\left(1+{\mathrm{e}}^{x_i^T\beta }\right)\left(1+{\mathrm{e}}^{-x_j^T\beta }\right)}+\frac{I\left(x_i^T\beta >x_j^T\beta \right)}{\left(1+{\mathrm{e}}^{-x_i^T\beta }\right)\left(1+{\mathrm{e}}^{x_j^T\beta }\right)}\right]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[\frac{1}{\left(1+{\mathrm{e}}^{x_i^T\beta }\right)\left(1+{\mathrm{e}}^{-x_j^T\beta }\right)}+\frac{1}{\left(1+{\mathrm{e}}^{-x_i^T\beta }\right)\left(1+{\mathrm{e}}^{x_j^T\beta }\right)}\right]}$$ (5)

For a proportional hazards regression model the model-based probabilities $P(Y_i<Y_j)$ are [7]:

$$P(Y_i<Y_j)=-{{\displaystyle \int }}_0^{\infty }S\left(t|x_j^T\beta \right)dS\left(t|x_i^T\beta \right)=\frac{1}{1+{\mathrm{e}}^{{(x_j-x_i)}^T\beta }}$$ (6)

Combining equations 3 and 6, and replacing $I(p_i<p_j)$ by $I\left(x_i^T\beta >x_j^T\beta \right)$ because the time-to-event predictions are a decreasing function of the linear predictor, results in the model-based concordance (mbc) for proportional hazards regression models:

$$\mathit{mbc}\left(X\beta \right)=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[\frac{I\left(x_i^T\beta >x_j^T\beta \right)}{1+{\mathrm{e}}^{{(x_j-x_i)}^T\beta }}+\frac{I\left(x_i^T\beta <x_j^T\beta \right)}{1+{\mathrm{e}}^{{(x_i-x_j)}^T\beta }}\right]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[\frac{1}{1+{\mathrm{e}}^{{(x_j-x_i)}^T\beta }}+\frac{1}{1+{\mathrm{e}}^{{(x_i-x_j)}^T\beta }}\right]}$$ (7)

The denominator of equation 7 is equal to $n\left(n-1\right)$ since $\left[\frac{1}{1+{\mathrm{e}}^{{(x_j-x_i)}^T\beta }}+\frac{1}{1+{\mathrm{e}}^{{(x_i-x_j)}^T\beta }}\right]=1$.

Equation 3 assumes that model predictions $p_i$ and $p_j$ are different for every combination of i and j. Since model predictions may be equal for some combinations of i and j, e.g. when x is a binary marker, we can generalize equation 3, and similarly equations 5 and 7, by using $I(p_i\le p_j)$ instead of $I(p_i<p_j)$. Hence equation 3 can also be written in the familiar c-statistic format:

$$\mathit{CP}=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[I(p_i<p_j)P(Y_i<Y_j)+\frac{1}{2}I(p_i=p_j)P(Y_i<Y_j)\right]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}P(Y_i<Y_j)}$$ (3’)

In an apparent validation of a model with regression coefficient estimates $\widehat{\beta }$ the $\mathit{mbc}\left(X\widehat{\beta }\right)$ gives an estimate of the concordance probability. For proportional hazards regression models the $\mathit{mbc}\left(X\widehat{\beta }\right)$ is identical to the censoring-robust estimator proposed before by Gönen and Heller [7]. Gönen and Heller derived their model-based concordance measure from a reversed definition of the concordance probability, i.e. $\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[I(p_i\le p_j)P(Y_i<Y_j)+I(p_i\ge p_j)P(Y_i>Y_j)\right]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[I(p_i\le p_j)+I(p_i\ge p_j)\right]}$, conditioning on weakly ordered predictions. However, for fully continuous predictions and outcomes the two definitions of the concordance probability are equivalent since $p_1\le p_2$ implies $p_1<p_2$ and the summands in the de denominator, $\left[P(Y_i<Y_j)+P(Y_i>Y_j)\right]$ and $\left[I(p_i\le p_j)+I(p_i\ge p_j)\right]$, both equal 1 [11].

For proportional hazards regression models based on uncensored, continuous time-to-event outcomes, the $\mathit{mbc}\left(X\widehat{\beta }\right)$ is asymptotically equivalent to Harrell’s c-index when the proportional hazards assumption holds (Appendix 2). The same asymptotic equivalence holds for logistic regression models, with exact equality when the model contains only one categorical predictor (Appendix 2). In an external validation setting of a model with regression coefficients β the $\mathit{mbc}\left(X\beta \right)$ can be used as a benchmark value to assess the influence of case-mix heterogeneity on the concordance probability – comparable to the case-mix corrected c-index as proposed before [4] – since it assumes correct regression coefficients [10]. Appendix 1 contains the derivation of variance estimates of the mbc in model development and external validation settings.

Including the calibration slope in the mbc

In an external validation setting the $\mathit{mbc}\left(X\beta \right)$ does not use observed outcomes and is therefore not influenced by the validity of the regression coefficients in the validation data. Refitting the regression model to the validation data does not give insight into the discriminative ability of the previously developed model. To assess the influence of overall regression coefficient validity on concordance, we first estimate the calibration slope ${\gamma }_1$ in the validation data, i.e. the regression coefficient of a model that regresses the observed outcomes y on the linear predictors Xβ in the validation data [12]. If ${\widehat{\gamma }}_1=1$, the regression coefficients are on average correct in the validation data. In contrast, ${\widehat{\gamma }}_1<1$ indicates a weaker association between the linear predictor and the outcomes in the validation data. For logistic regression models, an intercept estimate ${\widehat{\gamma }}_0$ is required for estimation of the calibration slope ${\widehat{\gamma }}_1$. With $\widehat{\gamma }X\beta$ we will denote ${\widehat{\gamma }}_0+{\widehat{\gamma }}_{1}X\beta$ for logistic regression models and ${\widehat{\gamma }}_{1}X\beta$ for proportional hazards regression models. The $\mathit{mbc}\left(\widehat{\gamma }X\beta \right)$, which we label calibrated model-based concordance (c-mbc), assesses both the influence of case-mix heterogeneity and the overall validity of the regression coefficients β. Similar to the original Gönen and Heller estimator, the c-mbc does not directly depend on observed survival and censoring times. Instead, it is only based on the regression coefficients $\widehat{\gamma }$ and the distribution of the linear predictor Xβ. Since the effect of censoring on the bias of $\widehat{\gamma }$ is negligible, $\mathit{mbc}\left(\widehat{\gamma }X\beta \right)$ is expected to be insensitive to censoring as well. Table 1 gives an overview of the potential use of the mbc in relation to existing concordance measures.

CASE STUDIES

Unfavorable outcome after traumatic brain injury

To illustrate the use of the mbc and the c-mbc for logistic regression models, we revisit a case study on the prediction of 6-month outcome in patients with traumatic brain injury [4]. A model to predict unfavorable outcome (i.e., death, a vegetative state, or severe disability) was developed with data on 1,118 subjects (456 (41%) had an unfavorable outcome) from the International Tirilazad Trial [13]. The validity of the risk prediction model was studied in 1,041 subjects (395 (38%) had an unfavorable outcome) who were enrolled in the North American Tirilazad Trial [14]. The logistic regression model consisted of three predictors (age, motor score, and pupillary reactivity) for an unfavorable 6-month outcome [15].

The model showed reasonable discrimination in the development sample (c-index 0.749; mbc 0.749; Table 5). The larger variability of the linear predictor in the external validation sample than in the development sample (SD(Xβ) = 1.11 and SD(Xβ) = 1.03, respectively) substantially increased the expected discriminative ability (mbc = 0.767; 95% CI 0.759 – 0.775; Table 5). Including the validity of the regression coefficients (calibration slope 1.02) indicated a small additional increase in discriminative ability (c-index 0.779; c-mbc 0.774; Table 5).

Table 5. Case study of concordance measures (95% confidence interval) in logistic regression and Cox regression.

The logistic regression model for unfavorable outcome after traumatic brain injury was developed in the International Tirilazad Trial and validated in the North American Tirilazad Trial. The Cox regression model for survival after revascularization was developed in the SYNTAX trial and validated in the CREDO-KYOTO registry.

	Logistic regression		Cox regression
	Apparent validation	External validation	Apparent validation	External validation
SD(Xβ)	1.028	1.112	0.904	0.965
Calibration slope $\widehat{\gamma }$	1.000	1.023	1.000	0.785
Harrell’s c-index	0.749 (0.719 – 0.778)	0.779 (0.750 – 0.808)	0.744 (0.707 – 0.781)	0.725 (0.700 – 0.750)
Uno (τ = 4)			0.743 (0.705 – 0.782)	0.729 (0.687 – 0.771)
mbc = mbc(Xβ)	0.749 (0.721 – 0.778)	0.767 (0.759 – 0.775)†	0.707 (0.680 – 0.734)	0.719 (0.715 – 0.722)†
c-mbc = mbc( $\widehat{\gamma }$Xβ)		0.774 (0.746 – 0.803)		0.684 (0.667 – 0.700)

^†95% confidence interval based on the variance estimate of mbc(Xβ) under the assumption of true β

Survival after coronary revascularization

To illustrate the use of the mbc and the c-mbc for proportional hazards regression models, we apply them to a recent validation study of the SYNTAX Score II (SSII) [16]. The SSII has been developed by applying a Cox proportional hazards model to the data of the SYNTAX trial [17, 18]. The SSII uses 2 anatomical variables (anatomical Syntax Score and unprotected left main coronary artery disease) and 6 clinical variables (age, creatinine clearance, left ventricular ejection fraction, sex, chronic obstructive pulmonary disease, and peripheral vascular disease) to predict 4-year mortality after revascularization with CABG or PCI. For validation of SSII we use 3,986 patients of the Coronary REvascularization Demonstrating Outcome Study in Kyoto (CREDO-Kyoto) PCI/CABG registry cohort-2 [19].

There was a substantial difference in the development data between the mbc (0.707; Table 5) and both the c-index (0.744) and Uno’s concordance measure (0.743), probably due to a high proportion of censoring (90.1%). Under the assumption that the proportional hazards assumption holds until the follow-up is complete– the proportional hazards assumption of the Cox regression model was not rejected up till 4 years of follow-up (p=0.63) [20] – we may conclude from the simulations study that the mbc gives a better estimate of the concordance probability in this example. The larger variability of the linear predictor in the external validation sample than in the development sample (SD(Xβ) = 0.97 and SD(Xβ) = 0.90, respectively) increased the expected discriminative ability (mbc = 0.719; 95% CI 0.715 – 0.722; Table 5). However, including the validity of the regression coefficients in the external validation sample (calibration slope 0.785) indicated an overall decrease in discriminative ability (c-index = 0.725; Uno = 0.729; c-mbc = 0.684; Table 5). The difference between the c-mbc and both the c-index and Uno’s concordance measure was again considerable, likely due to a high proportion of censoring (89.7%). The proportional hazards assumption of the Cox regression model that was refitted to the external validation data was again not rejected (p=0.41).

SIMULATION STUDY

Methods

We simulated validation studies of a logistic regression model that aims to predict a binary endpoint and a proportional hazards regression model for a time-to-event endpoint. Both regression models were characterized by a linear predictor $x^T\beta$, with the baseline characteristic vector x consisting of a continuous predictor x1, e.g. age, and a binary predictor x2, e.g. sex. To mimic different external validation settings, we generated patient data (10.000 replications of 400 patients per setting) with different case-mix heterogeneity and different true regression coefficients (Table 2; Table 3). In a base case scenario (A), continuous predictors x1 were drawn from a standard normal distribution and binary predictors x2 were drawn from a Bernoulli distribution with success probability 0.2. Based on true predictor effects β₁ = β₂ = 1, we generated binary outcomes y from a Bernoulli distribution with success probabilities ${\left[1+\text{exp}\left\{-x^T\beta \right\}\right]}^{-1}$ (true intercept β₀ = −2) and time-to-event outcomes y from an exponential distribution with mean $\text{exp}\left\{-x^T\beta \right\}$.

Table 2. Simulation results for binary outcomes generated from a logistic regression model.

10,000 replications of 400 patients; casemix-corrected c-index based on 400 resampled outcomes per patient.

Simulation settings						Benchmark performance			Overall performance
	Case-mix		Coefficients			case-mix corrected c-index	mbc = mbc(Xβ)	SE[mbc]	Calibration slope $\widehat{\gamma }$	c-index	c-mbc = mbc( $\widehat{\gamma }$Xβ)	SE[c-mbc]
	Sd(x1)	p(x2)	β0	β1	β2
A	1	0.2	−2	1	1	0.760 (0.0077)	0.761 (0.0076)	0.0075	1.012 (0.154)	0.761 (0.030)	0.761 (0.030)	0.030
B	0.8	0.2	−2	1	1	0.728 (0.0073)	0.728 (0.0071)	0.0071	1.011 (0.175)	0.728 (0.033)	0.728 (0.032)	0.032
C	1.2	0.2	−2	1	1	0.790 (0.0077)	0.790 (0.0076)	0.0077	1.015 (0.141)	0.791 (0.028)	0.791 (0.028)	0.027
D	1	0.1	−2	1	1	0.755 (0.0077)	0.755 (0.0076)	0.0075	1.015 (0.162)	0.756 (0.032)	0.756 (0.031)	0.031
E	1	0.4	−2	1	1	0.765 (0.0075)	0.765 (0.0073)	0.0073	1.012 (0.147)	0.765 (0.029)	0.766 (0.028)	0.028
F	1	0.2	−2	0.8	1	0.760 (0.0077)	0.761 (0.0076)	0.0075	0.845 (0.146)	0.728 (0.033)	0.729 (0.032)	0.032
G	1	0.2	−2	1.2	1	0.760 (0.0076)	0.761 (0.0074)	0.0075	1.180 (0.162)	0.790 (0.028)	0.790 (0.027)	0.027
H	1	0.2	−2	1	0.5	0.760 (0.0076)	0.761 (0.0075)	0.0075	0.923 (0.152)	0.745 (0.032)	0.745 (0.032)	0.032
I	1	0.2	−2	1	2	0.760 (0.0076)	0.761 (0.0075)	0.0075	1.159 (0.160)	0.784 (0.028)	0.785 (0.027)	0.026
J	1	0.2	−3	1	1	0.760 (0.0078)	0.761 (0.0076)	0.0075	1.020 (0.203)	0.769 (0.042)	0.769 (0.041)	0.040
K	1	0.2	−1	1	1	0.760 (0.0076)	0.761 (0.0075)	0.0075	1.012 (0.133)	0.755 (0.025)	0.756 (0.025)	0.025

Table 3. Simulation results for time-to-event outcomes generated from a proportional hazards regression model.

10,000 replications of 400 patients; casemix-corrected c-index based on 25 resampled outcomes per patient.

Simulation settings						Benchmark performance			Overall performance
	Case-mix		Coefficients			case-mix corrected c-index	mbc = mbc(Xβ)	SE[mbc]	Calibration slope $\widehat{\gamma }$	c-index	c-mbc = mbc( $\widehat{\gamma }$Xβ)	SE[c-mbc]
	Sd(x1)	p(x2)	β0	β1	β2
A	1	0.2	−2	1	1	0.736 (0.0062)	0.736 (0.0057)	0.0056	1.003 (0.064)	0.736 (0.013)	0.737 (0.011)	0.011
B	0.8	0.2	−2	1	1	0.708 (0.0059)	0.708 (0.0055)	0.0054	1.004 (0.072)	0.708 (0.014)	0.709 (0.012)	0.012
C	1.2	0.2	−2	1	1	0.760 (0.0061)	0.761 (0.0056)	0.0057	1.003 (0.059)	0.761 (0.012)	0.761 (0.011)	0.011
D	1	0.1	−2	1	1	0.731 (0.0062)	0.731 (0.0057)	0.0056	1.004 (0.065)	0.732 (0.013)	0.732 (0.011)	0.011
E	1	0.4	−2	1	1	0.742 (0.0061)	0.742 (0.0056)	0.0056	1.003 (0.063)	0.742 (0.013)	0.742 (0.011)	0.011
F	1	0.2	−2	0.8	1	0.736 (0.0062)	0.736 (0.0057)	0.0056	0.826 (0.059)	0.707 (0.014)	0.707 (0.012)	0.012
G	1	0.2	−2	1.2	1	0.736 (0.0062)	0.736 (0.0056)	0.0056	1.168 (0.068)	0.760 (0.012)	0.760 (0.011)	0.011
H	1	0.2	−2	1	0.5	0.736 (0.0059)	0.736 (0.0056)	0.0056	0.901 (0.063)	0.723 (0.013)	0.720 (0.012)	0.011
I	1	0.2	−2	1	2	0.736 (0.0061)	0.736 (0.0056)	0.0056	1.057 (0.067)	0.748 (0.013)	0.745 (0.011)	0.011

To study the influence of case-mix heterogeneity on concordance measures we varied the standard deviation of the continuous predictor (0.8 and 1.2 in scenarios B and C respectively) and the success probability of the binary predictor (0.1 and 0.4 in scenarios D and E respectively). We studied the influence of overall regression coefficient validity by varying the true effects of the continuous predictor (0.8 and 1.2 in scenarios F and G respectively), the binary predictor (0.5 and 2 in scenarios H and I respectively), and the true intercept of the logistic regression model (−3 and −1 in scenarios J and K respectively).

Censoring times were generated from an exponential distribution with mean c for different choices of c to analyze the effect of different proportions of censoring. To illustrate the effect of a violation of the proportional hazards assumption, we alternatively generated time-to-event outcomes from an exponential distribution with mean $\text{exp}\left\{-x^t{\beta }_s\right\}$ and time-varying coefficients ${\beta }_s=\beta \text{exp}\left[-0.5s\right]$.

In each sample we calculated: the linear predictor Xβ with predictor effects β₁ = β₂ = 1 and intercept β₀ = −2 in case of binary outcomes; the calibration slope $\widehat{\gamma }$ as the regression coefficient of a model with the linear predictor $x^t\beta$ as the sole predictor; the $\mathit{mbc}\left(X\beta \right)$ and the $\mathit{mbc}\left(\widehat{\gamma }X\beta \right)$ with their variance estimates; Harrell’s c-index; the case-mix corrected c-index, i.e. the c-index based on either 25, 100 or 400 resampled outcomes for each linear predictor $x^t\beta$; and Uno’s concordance measure with the truncation time τ equal to the maximum follow-up time and to 80% of the maximum follow-up time in each replication. We used the rcorr.cens function in R package Hmisc and the Est.Cval function in R package survC1 for calculation of Harrell’s c-index and Uno’s concordance measure respectively [21–23].

Results

For binary outcomes and for uncensored time-to-event outcomes we found that the means of the mbc and the case-mix corrected c-index were very similar across the different validation settings (Table 2; Table 3). The empirical standard deviation of the case-mix corrected c-index was slightly higher as a result of resampling 400 binary outcomes and 25 time-to-event outcomes for each patient. However, the case-mix corrected c-index converged to the mbc with increasing numbers of resampled outcomes per patient (Figure 1).

Figure 1. mbc versus casemix-corrected c-index based on 25, 100 and 400 resampled outcomes per patients respectively.

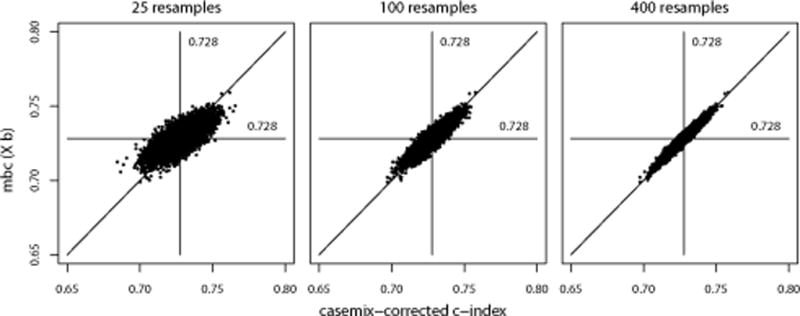
Setting B of the binary outcome simulation; 10,000 replications of 400 patients.

The means of the c-mbc and the c-index were very similar as well, although the empirical standard deviation was lower for the c-mbc in case of Cox regression (Table 2; Table 3). Standard deviation estimates of mbc and c-mbc were well in agreement with the simulated empirical variances (Table 2; Table 3). Across all validation settings, the c-mbc remained stable at the true value with increasing proportions of censoring of time-to-event outcomes, while the c-index and to a lesser extent Uno’s concordance measure increased unfavorably (Table 4; Supplementary figure 1). The empirical standard deviation of the c-mbc – again in good agreement with the standard deviation estimate – was structurally smaller than the standard deviation of the c-index and Uno’s measure. When outcomes were sampled from an exponential distribution with time-varying coefficients ( $\beta \left(s\right)=\beta \text{exp}\left[-0.5s\right]$), the proportional hazards assumption of the c-mbc was violated leading to an underestimation of the concordance probability, specifically in the absence of time-to-event outcomes (Supplementary table 1). As a result of the decrease of the true regression coefficients in time, all concordance measures increased with increasing proportions of censoring of time-to-event outcomes.

Table 4. Simulation results for time-to-event outcomes generated from a proportional hazards regression model with varying amounts of censoring.

10,000 replications of 400 patients.

Simulation settings							Concordance measures
	Case-mix		Coefficients			Cens %	c-index	Uno		c-mbc = mbc( $\widehat{\gamma }$Xβ)	SE[c-mbc]
	Sd(x1)	p(x2)	β0	β1	β2			τ = 0.8 max(FU)	τ = max(FU)
A	1	0.2	−2	1	1	0	0.736 (0.013)	0.736 (0.013)	0.736 (0.013)	0.737 (0.011)	0.011
						24	0.743 (0.015)	0.737 (0.014)	0.737 (0.014)	0.737 (0.012)	0.012
						50	0.751 (0.019)	0.738 (0.017)	0.738 (0.018)	0.737 (0.014)	0.014
						73	0.761 (0.025)	0.744 (0.031)	0.743 (0.034)	0.737 (0.017)	0.017
B	0.8	0.2	−2	1	1	0	0.708 (0.014)	0.708 (0.014)	0.708 (0.014)	0.709 (0.012)	0.012
						23	0.713 (0.016)	0.709 (0.014)	0.708 (0.014)	0.709 (0.013)	0.013
						50	0.720 (0.020)	0.710 (0.018)	0.709 (0.018)	0.709 (0.015)	0.015
						74	0.729 (0.027)	0.715 (0.033)	0.714 (0.036)	0.709 (0.019)	0.019
C	1.2	0.2	−2	1	1	0	0.761 (0.012)	0.761 (0.012)	0.761 (0.012)	0.761 (0.011)	0.011
						25	0.768 (0.014)	0.761 (0.013)	0.761 (0.013)	0.761 (0.011)	0.011
						50	0.778 (0.017)	0.763 (0.016)	0.763 (0.017)	0.761 (0.013)	0.013
						71	0.789 (0.023)	0.769 (0.029)	0.768 (0.032)	0.761 (0.015)	0.015
D	1	0.1	−2	1	1	0	0.732 (0.013)	0.732 (0.013)	0.732 (0.013)	0.732 (0.011)	0.011
						26	0.738 (0.015)	0.732 (0.014)	0.732 (0.014)	0.732 (0.012)	0.012
						52	0.746 (0.019)	0.733 (0.018)	0.733 (0.018)	0.732 (0.014)	0.014
						74	0.755 (0.026)	0.740 (0.033)	0.739 (0.036)	0.732 (0.017)	0.018
E	1	0.4	−2	1	1	0	0.742 (0.013)	0.742 (0.013)	0.742 (0.013)	0.742 (0.011)	0.011
						21	0.747 (0.014)	0.742 (0.013)	0.742 (0.013)	0.742 (0.012)	0.012
						46	0.755 (0.017)	0.743 (0.016)	0.743 (0.016)	0.742 (0.013)	0.013
						69	0.765 (0.023)	0.748 (0.027)	0.747 (0.029)	0.743 (0.016)	0.016
F	1	0.2	−2	0.8	1	0	0.707 (0.014)	0.707 (0.014)	0.707 (0.014)	0.707 (0.012)	0.012
						23	0.712 (0.016)	0.708 (0.014)	0.708 (0.014)	0.708 (0.013)	0.013
						50	0.719 (0.020)	0.709 (0.018)	0.708 (0.018)	0.709 (0.015)	0.015
						74	0.728 (0.027)	0.713 (0.033)	0.713 (0.036)	0.709 (0.019)	0.019
G	1	0.2	−2	1.2	1	0	0.760 (0.012)	0.760 (0.012)	0.760 (0.012)	0.760 (0.011)	0.011
						25	0.768 (0.014)	0.761 (0.013)	0.761 (0.013)	0.760 (0.011)	0.011
						50	0.777 (0.017)	0.763 (0.017)	0.762 (0.017)	0.760 (0.013)	0.013
						71	0.788 (0.023)	0.769 (0.030)	0.768 (0.032)	0.759 (0.015)	0.015
H	1	0.2	−2	1	0.5	0	0.724 (0.013)	0.724 (0.013)	0.724 (0.013)	0.721 (0.012)	0.011
						25	0.729 (0.015)	0.724 (0.014)	0.724 (0.014)	0.721 (0.013)	0.012
						52	0.737 (0.019)	0.725 (0.018)	0.725 (0.018)	0.721 (0.015)	0.014
						74	0.745 (0.026)	0.731 (0.033)	0.730 (0.037)	0.721 (0.018)	0.018
I	1	0.2	−2	1	2	0	0.747 (0.013)	0.747 (0.013)	0.747 (0.013)	0.744 (0.011)	0.011
						23	0.755 (0.014)	0.748 (0.013)	0.748 (0.013)	0.746 (0.012)	0.012
						47	0.767 (0.017)	0.749 (0.016)	0.749 (0.016)	0.749 (0.013)	0.013
						68	0.783 (0.022)	0.756 (0.028)	0.755 (0.030)	0.753 (0.015)	0.015

We further analyzed the relation between the c-index and the mbc, the calibration slope or the c-mbc with scatterplots of validation setting A (Figure 2). Variation in the mbc was small compared to the c-index, since case-mix heterogeneity (SD(Xβ)) was stable across the samples (left panel). With the limited number of 400 patients in each sample, the calibration slope – representing overall regression coefficient validity – varied substantially across the samples and was strongly related to the c-index (middle panel). Finally, the c-mbc – incorporating both case-mix heterogeneity and overall regression coefficient validity – correlated very well with the c-index (right panel).

Figure 2. Performance measures (y-axis) mbc, calibration slope and c-mbc versus the c-index (x-axis).

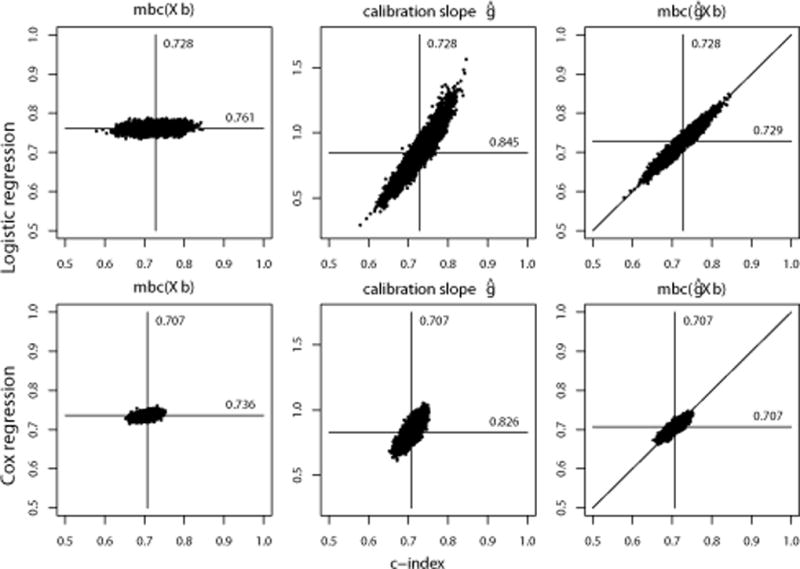
Setting A of the binary outcome simulation and the time-to-event outcome simulation; 10,000 replications of 400 patients.

When we changed case-mix heterogeneity (setting B-E), both the mean mbc and the mean c-mbc changed similarly, since the mbc’s assumption of correct regression coefficients held in these validation settings. As expected, when we changed the regression coefficients (settings F-I) the mbc remained the same while the c-mbc changed in accordance with the calibration slope. Changing the intercept of the logistic regression model (settings J-K) again affected only the c-mbc, but with a much smaller impact than a change in the regression coefficients of predictors.

DISCUSSION

We derived the mbc, which is a closed-form, censoring-robust alternative for the resampling-based case-mix corrected c-index. We showed that the mbc is asymptotically equivalent to a previously proposed, approximate case-mix corrected c-index. The c-mbc is comparable to Harrell’s c-index in independent data with binary and time-to-event outcomes and furthermore is robust to censoring of time-to-event outcomes, in contrast with the c-index and Uno’s concordance measure.

The mbc improves the understanding of a difference between the c-statistic at model development versus the observed c-statistic at external validation. The difference between the mbc at model development and the mbc at external validation indicates the change in discriminative ability attributable to the difference in case-mix heterogeneity. The difference between the c-mbc and the mbc in external validation data expresses the change in discriminative ability due to the (in)correctness of the regression coefficients. Thanks to their censoring-robustness, the mbc and the c-mbc facilitate measurements of concordance that are not biased by differences in censoring distributions between the development and the external validation setting.

The mbc and the c-mbc are model-based, i.e. they are based on the assumption that the true risks fit into the framework of a model. This assumption is necessary to evaluate the probability of the outcomes being ordered, conditional on the risk scores, i.e. $P_{ij}=P\left(Y_i<Y_j|x_i^T\beta ,x_j^T\beta \right)$. In this paper we used either a logistic regression model or a proportional hazards regression model to evaluate these probabilities. This may be a limitation compared to Harrell’s c-index and Uno’s concordance measure, since these pure rank-order statistics are applicable to any risk scoring system. However, since logistic regression and proportional hazards regression are commonly used to model binary outcomes and time-to-event outcomes respectively, the mbc and the c-mbc may often be valuable.

The c-mbc was shown to be very robust to censoring in the simulation study where the proportional hazards assumption held. When the proportional hazards assumption did not hold – as in our sensitivity analysis with time-dependent coefficients – the c-mbc gave different estimates than Harrell’s c-index and Uno’s concordance measure, even without censoring of time-to-event outcomes. In the presence of time-varying coefficients it may be better to assess discriminative ability in a limited follow-up period [8]. This was beyond the scope of our research, but we provided formulas for an mbc truncated at a fixed follow-up time in Appendix 3. When coefficients are time-dependent, the c-mbc could alternatively be based on more sophisticated conditional probabilities $P(Y_i<Y_j)$. Stare et al. proposed a measure for use with general dynamic event history regression models, including models with time-dependent coefficients, that reduces to the c-index for single-event survival data with neither censoring nor time dependency [24]. However, since all concordance measures for models with time-dependent coefficients will probably be sensitive to censoring, their use in practice needs additional study.

The c-mbc assumes a linear relationship (represented by the calibration slope ${\widehat{\gamma }}_1$) between linear predictors and either the log hazard for time-to-event outcomes or the log odds for binary outcomes. In the scenarios F, G, H and I of our simulation study this assumption was clearly violated, since the true effect of only one of two predictors was varied consecutively. Although the c-mbc was robust to violation of the linearity assumption in these scenarios – the mean c-mbc was very close to the mean c-index (Table 2; Table 3) – further research is necessary to understand the importance of this assumption. An alternative c-mbc that allows for potential non-linear relationships between linear predictors and outcomes could be considered.

We derived variance estimators for the mbc – under the assumption of correct regression coefficients – and the c-mbc – including regression coefficient uncertainty. Variance estimates were very well in line with the empirical variances of the simulation study. The empirical variances of the c-mbc were generally lower than those of the c-index and Uno’s concordance measure for proportional hazards regression models, especially in the presence of high proportions of censoring. The higher precision of the c-mbc is likely the result of its proportional hazards assumption.

In both case-studies the effect of more case-mix heterogeneity (larger standard deviation of the linear predictor) on discriminative ability was illustrated by an increase in the mbc in the validation data compared to the mbc in the development data. The influence on discriminative ability of a change in the strength of the association between predictions and outcomes (calibration slope above 1 in the logistic regression case study, calibration slope below 1 in the proportional hazards regression case study), was reflected in the difference between the c-mbc and the mbc in the validation data. The large difference of the c-mbc in comparison with the c-index and Uno’s concordance measure, emphasized the importance of using censoring-robust concordance measures when time-to-event outcomes are substantially censored.

In conclusion, the mbc is an attractive closed-form measure that allows for straightforward quantification of the expected change in a model’s discriminative ability due to case-mix heterogeneity in a validation setting. Moreover, the c-mbc also reflects the impact of regression coefficient validity on a model’s discriminative ability in external validation data, and is a censoring-robust alternative for the c-index when the proportional hazards assumption holds.

APPENDIX 1

Estimating the variance of the mbc

The $\mathit{mbc}\left(X\widehat{\beta }\right)$ estimates the concordance probability in an apparent validation setting. To obtain a variance estimate of $\mathit{mbc}\left(X\widehat{\beta }\right)$ we follow the derivation of the variance estimate of Gönen and Heller’s concordance probability estimator [7]. It starts with a local linear asymptotic approximation of $\mathit{mbc}(X\widehat{\beta })$ in the neighborhood of the point estimate ${\beta }_0=E\widehat{\beta }$:

$$\mathit{mbc}\left(X\widehat{\beta }\right)=\mathit{mbc}\left(X{\beta }_0\right)+{{\left[\frac{\partial E\left\{\mathit{mbc}\left(X\beta \right)\right\}}{\partial \beta }\right]}^T|}_{\beta ={\beta }_0}\left(\widehat{\beta }-{\beta }_0\right)+o_p\left(1\right)$$ (8)

With $\left({\beta }_0\right)={\left[\frac{\partial E\left\{\mathit{mbc}\left(X\beta \right)\right\}}{\partial \beta }\right]|}_{\beta ={\beta }_0}$, conditional on the covariates, the centered partial likelihood estimator $\left(\widehat{\beta }-{\beta }_0\right)$ is asymptotically independent of $\mathit{mbc}\left(X{\beta }_0\right)$. In addition, since $D\left({\beta }_0\right)$ converges to a constant, the asymptotic variance of $\mathit{mbc}(X\widehat{\beta })$ is approximately:

$$\text{var}\left\{\mathit{mbc}\left(X\widehat{\beta }\right)\right\}\approx \text{var}\left\{\mathit{mbc}\left(X{\beta }_0\right)\right\}+D{\left({\beta }_0\right)}^T\text{var}\left(\widehat{\beta }\right)D\left({\beta }_0\right)$$ (9)

The first part on the right hand side is the variance of the sample statistic $\mathit{mbc}\left(X{\beta }_0\right)$. It is easy to obtain since $\mathit{mbc}\left(X{\beta }_0\right)$ is the ratio of two U-statistics of degree 2:

$$\begin{array}{c}\mathit{mbc}(X{\beta }_0)=\frac{U_1}{U_2}\\ U_1=\frac{1}{n}{\displaystyle {\sum }_i{U}_1^{(i)},U_1^{(i)}=\frac{1}{n-1}}{\displaystyle {\sum }_{j\ne i}[I(p_i<p_j)P(Y_i<Y_j)+I(p_i>p_j)P(Y_i>Y_j)]}\\ U_2=\frac{1}{n}{\displaystyle {\sum }_i{U}_2^{(i)},U_2^{(i)}=\frac{1}{n-1}{\displaystyle {\sum }_{j\ne i}[P(Y_i<Y_j)+P(Y_i>Y_j)]}}\end{array}$$ (10)

From U-statistics theory we know that [25]:

$$\begin{array}{c}\frac{\sqrt{n}}{s}\left(\frac{U_1}{U_2}-\frac{{\theta }_1}{{\theta }_2}\right)\stackrel{d}{\to }N(0,1)\\ s^2=\frac{4\left[U_2^2{v}_{11}-2U_1{U}_2{v}_{12}+U_1^2{v}_{22}\right]}{U_2^4}\\ v_{11}=\frac{1}{n-1}{\displaystyle {\sum }_i{\left(U_1^{(i)}-U_1\right)}^2}\\ v_{12}=\frac{1}{n-1}{\displaystyle {\sum }_i\left(U_1^{(i)}-U_1\right)\left(U_2^{(i)}-U_2\right)}\\ v_{22}=\frac{1}{n-1}{\displaystyle {\sum }_i{\left(U_2^{(i)}-U_2\right)}^2}\end{array}$$ (11)

Hence

$$\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}\left\{\mathit{mbc}\left(X{\beta }_0\right)\right\}=\frac{s^2}{n}$$ (12)

Note that for proportional hazards regression $U_2\equiv 1$ and therefore the variance estimate reduces to $\frac{4v_{11}}{n}$.

The second part on the right hand side of equation 9 represents the variance of $\mathit{mbc}\left(X\widehat{\beta }\right)$ as a result of uncertainty in the regression coefficients. We can use the inverse of the likelihood information matrix to estimate $\text{var}\left(\widehat{\beta }\right)$. The function $D\left({\beta }_0\right)$ in equation 9 is estimated through numerical differentiation:

$${\widehat{D}}_i\left({\beta }_0\right)=\frac{\mathit{mbc}(X{\beta }_0+s_i{e}_i)-\mathit{mbc}\left(X{\beta }_0-s_i{e}_i\right)}{2s_i}$$ (13)

Where $s_i$ is the standard error of ${\widehat{\beta }}_i$ and $e_i$ is the i^th unit vector.

The variance of $\mathit{mbc}\left(X\widehat{\beta }\right)$ in an apparent validation setting was decomposed into a part due to sampling patients and a part due to regression coefficient uncertainty (equation 9). When $\mathit{mbc}\left(X\beta \right)$ is used in an external validation setting to assess the influence of case-mix heterogeneity on discriminative ability – assuming correct regression coefficients –, its variance is limited to the first part (equation 12). The c-mbc ( $\mathit{mbc}\left(\widehat{\gamma }X\beta \right)$) assesses both the influence of case-mix heterogeneity and the validity of the linear predictor Xβ in external data. The derivation of the variance estimate of $\mathit{mbc}\left(\widehat{\gamma }X\beta \right)$ is similar to equation 8–13. Replacing X by Xβ and β by γ in equation 8 results in:

$$\mathit{mbc}\left(\widehat{\gamma }X\beta \right)=\mathit{mbc}\left({\gamma }_{0}X\beta \right)+{{\left[\frac{\partial E\left\{\mathit{mbc}\left(\gamma X\beta \right)\right\}}{\partial \gamma }\right]}^T|}_{\gamma ={\gamma }_0}\left(\widehat{\gamma }-{\gamma }_0\right)+o_p\left(1\right)$$ (14)

Similar to equation 9, the asymptotic variance of $\mathit{mbc}(\widehat{\gamma }X\beta )$ is approximately:

$$\text{var}\left\{\mathit{mbc}\left(\widehat{\gamma }X\beta \right)\right\}\approx \text{var}\left\{\mathit{mbc}\left({\gamma }_{0}X\beta \right)\right\}+D{\left({\gamma }_0\right)}^T\text{var}\left(\widehat{\gamma }\right)D\left({\gamma }_0\right)$$ (15)

We can use equations 10–12 to estimate $\text{var}\left\{\mathit{mbc}\left({\gamma }_{0}X\beta \right)\right\}$, the inverse of the likelihood information matrix to estimate $\text{var}\left(\widehat{\gamma }\right)$ and numerical differentiation (equation 13) to estimate $D\left({\gamma }_0\right)$.

APPENDIX 2

Comparison of the mbc with Harrell’s c-index

We will show that within the development data, the mbc and the c-index are asymptotically equivalent for logistic regression models and – if the proportional hazards assumption holds – for proportional hazards regression models developed with continuous, uncensored time-to-event outcomes. We will start by showing that the mbc and the c-index are exactly equal at internal validation of a logistic regression model with one binary or categorical predictor.

Logistic regression

Harrell’s c-index – allowing for ties in predictions – is:

$$c_H\left(X\widehat{\beta },y\right)=\frac{{{\displaystyle \sum }}_{i,j:x_i^T\widehat{\beta }<x_j^T\widehat{\beta }}I\{y_i<y_j\}+\frac{1}{2}{{\displaystyle \sum }}_{i,j:x_i^T\widehat{\beta }=x_j^T\widehat{\beta }}I\{y_i<y_j\}}{{{\displaystyle \sum }}_{i,j}I\{y_i<y_j\}}$$ (16)

The mbc at internal validation can be written similarly as:

$$\mathit{mbc}\left(X\widehat{\beta }\right)=\frac{{{\displaystyle \sum }}_{i,j:x_i^T\widehat{\beta }<x_j^T\widehat{\beta }}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)+\frac{1}{2}{{\displaystyle \sum }}_{i,j:x_i^T\widehat{\beta }=x_j^T\widehat{\beta }}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)}{{{\displaystyle \sum }}_{i,j}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)}$$ (17)

The denominators of $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are equal when $\widehat{\beta }$ is estimated with logistic regression:

$$\begin{array}{c}{\displaystyle \sum _{i,j}P(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta })}={\displaystyle \sum _{i}P(Y_i=0|x_i^T\widehat{\beta })}{\displaystyle \sum _{j}P(Y_j=1|x_j^T\widehat{\beta })}=\\ ={\displaystyle \sum _{i}I\{y_i=0\}}{\displaystyle \sum _{j}I\{y_j=1\}}={\displaystyle \sum _{i,j}I\{y_i<y_j\}}\end{array}$$ (18)

With only one binary predictor x, the numerators are equal as well since:

$$\begin{array}{c}{\displaystyle \sum _{i,j:x_i^T\widehat{\beta }<x_j^T\widehat{\beta }}P(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta })}=\\ ={\displaystyle \sum _{i:x_i=0}P(Y_i=0|x_i^T\widehat{\beta })}{\displaystyle \sum _{j:x_j=1}P(Y_j=1|x_j^T\widehat{\beta })}=\\ ={\displaystyle \sum _{i:x_i=0}I\{y_i=0\}}{\displaystyle \sum _{j:x_j=1}I\{y_j=1\}}={\displaystyle \sum _{i,j:x_i^T\widehat{\beta }<x_j^T\widehat{\beta }}I\{y_i<y_j\}}\end{array}$$ (19)

And for ties:

$$\begin{array}{c}T={\displaystyle \sum _{i,j:x_i^T\widehat{\beta }<x_j^T\widehat{\beta }}P(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta })}=\\ {\displaystyle \sum _{i:x_i=0}P(Y_i=0|x_i^T\widehat{\beta })}{\displaystyle \sum _{j:x_j=0}P(Y_j=1|x_j^T\widehat{\beta })}+{\displaystyle \sum _{i:x_i=1}P(Y_i=0|x_i^T\widehat{\beta })}{\displaystyle \sum _{j:x_j=1}P(Y_j=1|x_i^T\widehat{\beta })}=\\ {\displaystyle \sum _{i:x_i=0}I\{y_i=0\}}{\displaystyle \sum _{j;x_j=0}I\{y_j=1\}+{\displaystyle \sum _{i:x_i=1}I\{y_i=0\}}}{\displaystyle \sum _{j:x_j=1}I\{y_i=1\}}=\\ ={\displaystyle \sum _{i,j:x_i^T\widehat{\beta }=x_j^T\widehat{\beta }}I\{y_i<y_j\}}\end{array}$$ (20)

Consequently, $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are exactly equal for a logistic regression model with one binary predictor. Following the same line of reasoning, it is easy to show that $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are equal for logistic regression models with one categorical predictor with any number of levels.

For logistic regression models in general, we stratify the subjects in risk groups $R_k$ of increasing linear predictor values. The mbc can be written as:

$$\mathit{mbc}\left(X\widehat{\beta }\right)=\frac{{{\displaystyle \sum }}_{\begin{array}{c}k,l:k<l\\ i\in R_k,j\in R_l\end{array}}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)+T\text{'}+\frac{1}{2}T}{{{\displaystyle \sum }}_{i,j}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)}$$ (21)

With $T\prime$ and T denoting the sum of conditional probabilities $P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)$ for respectively the subject pairs with different risk predictions but in the same risk group $\left(i\in R_k,j\in R_k:x_i^T\widehat{\beta }<x_j^T\widehat{\beta }\right)$ and the subject pairs with equal risk predictions $\left(x_i^T\widehat{\beta }=x_j^T\widehat{\beta }\right)$. The between-risk-group sums in $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are asymptotically equivalent since:

$$\begin{array}{c}{\displaystyle \sum _{i\in R_k,j\in R_l}P(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta })}=\\ {\displaystyle \sum _{i\in R_k}P(Y_i=0|x_i^T\widehat{\beta })}{\displaystyle \sum _{j\in R_l}P(Y_j=1|x_j^T\widehat{\beta })}~\\ {\displaystyle \sum _{i\in R_k}I\{y_i=0\}}{\displaystyle \sum _{j\in R_l}I\{y_j=1\}}={\displaystyle {\sum }_{i\in R_k,j\in R_l}I\{y_i<y_j\}}\end{array}$$ (22)

For subject pairs with different risk predictions but in the same risk group $\left(T\text{'}\right)$ and for subject pairs with equal risk predictions $\left(T\right)$, a similar equivalence between the $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ can be derived. In conclusion, the $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are asymptotically equivalent for logistic regression models.

Proportional hazards regression

Harrell’s c-index – without ties in predictions – is:

$$c_H\left(X\widehat{\beta },y\right)=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j\left\{I\left\{x_i^T\widehat{\beta }>x_j^T\widehat{\beta }\right\}I\{y_i<y_j\}{\delta }_i\right\}}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j\left\{I\{y_i<y_j\}{\delta }_i\right\}}$$ (23)

For uncensored time-to-event outcomes, it can be written as:

$$c_H\left(X\widehat{\beta },y\right)=\frac{{{\displaystyle \sum }}_{i,j:x_i^T\widehat{\beta }>x_j^T\widehat{\beta }}I\{y_i<y_j\}}{{{\displaystyle \sum }}_{i,j:i\ne j}I\{y_i<y_j\}}$$ (24)

The mbc at internal validation can be written similarly as:

$$\mathit{mbc}\left(X\widehat{\beta }\right)=\frac{{{\displaystyle \sum }}_{i,j:x_i^T\widehat{\beta }>x_j^T\widehat{\beta }}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)}{{{\displaystyle \sum }}_{i,j:i\ne j}P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)}$$ (25)

For continuous uncensored time-to-event outcomes, the denominators of $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are both $\frac{n\left(n-1\right)}{2}$ since $P\left(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)+P\left(Y_j<Y_i|x_i^T\widehat{\beta },x_j^T\widehat{\beta }\right)=1$.

Under the assumption of proportional hazards, the true conditional probability $P\left(Y_i<Y_j|x_i^T\beta ,x_j^T\beta \right)$ given one binary predictor with values $x_i=1$ and $x_j=0$ follows from equation 6:

$$P\left(Y_i<Y_j|x_i=1,x_j=0,\beta \right)=\frac{1}{1+\mathit{exp}\left\{\beta \right\}}$$ (26)

Since the observed frequency of $I\{y_i<y_j\}$ with $x_i=1$ and $x_j=0$ will converge to this true probability when the proportional hazards assumption holds, it follows that:

$$\begin{array}{c}{\displaystyle \sum _{i,j:x_i^T\widehat{\beta }>x_j^T\widehat{\beta }}P(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta })}={\displaystyle \sum _{\begin{array}{l}i:x_i=1\\ j:x_j=0\end{array}}P(Y_i<Y_j|x_i^T\widehat{\beta },x_j^T\widehat{\beta })}={\displaystyle \sum _{\begin{array}{l}i:x_i=1\\ j:x_j=0\end{array}}\frac{1}{1+exp\left\{\widehat{\beta }\right\}}}~\\ {\displaystyle \sum _{\begin{array}{l}i:x_i=1\\ j:x_j=0\end{array}}I\{y_i<y_j\}}={\displaystyle \sum _{i,j:x_i^T\widehat{\beta }>x_j^T\widehat{\beta }}I\{y_i<y_j\}}\end{array}$$ (27)

Applying the same stratification in risk groups $R_k$ of increasing linear predictor values as for logistic regression models, leads to the conclusion that $\mathit{mbc}\left(X\widehat{\beta }\right)$ and $c_H\left(X\widehat{\beta },y\right)$ are asymptotically equivalent for proportional hazards regression models, when the proportional hazards assumption holds.

APPENDIX 3

The truncated mbc

The truncated concordance probability $\mathit{CP}\left(\tau \right)$ in a patient population is:

$$\mathit{CP}\left(\tau \right)=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}[I(p_i<p_j)P(Y_i<Y_j,Y_i<\tau )+I(p_i>p_j)P\left(Y_i>Y_j,Y_j<\tau \right)]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[P\left(Y_i<Y_j,Y_i<\tau \right)+P\left(Y_i>Y_j,Y_j<\tau \right)\right]}$$ (28)

For the truncated model-based concordance $\mathit{mbc}\left(\tau ;X\beta \right)$ we again derive the probabilities $P\left(Y_i<Y_j,Y_i<\tau \right)$ from the proportional hazards regression model:

$$P\left(Y_i<Y_j,Y_i<\tau \right)=-{{\displaystyle \int }}_0^{\tau }S\left(t|x_j^T\beta \right)dS\left(t|x_i^T\beta \right)$$ (29)

Using integration by parts gives:

$$P\left(Y_i<Y_j,Y_i<\tau \right)=-{{\displaystyle \int }}_0^{\tau }\mathrm{d}\left[S\left(t|x_j^T\beta \right)S\left(t|x_i^T\beta \right)\right]+{{\displaystyle \int }}_0^{\tau }S\left(t|x_i^T\beta \right)\mathrm{d}S\left(t|x_j^T\beta \right)$$ (30)

The second integral on the right-hand-side of the equation can be written as:

$$\begin{array}{l}{\displaystyle {\int }_0^{\tau }S(t|x_i^T\beta )\mathrm{d}S(t|x_j^T\beta )}=-{\displaystyle {\int }_0^{\tau }S(t|x_i^T\beta )S(t|x_j^T\beta )}{\lambda }_0(t){\mathrm{e}}^{x_j^T\beta }\text{dt}\\ =-{\mathrm{e}}^{{(x_j-x_i)}^T\beta }{\displaystyle {\int }_0^{\tau }S(t|x_i^T\beta )S(t|x_j^T\beta ){\lambda }_0(t){\mathrm{e}}^{x_i^T\beta }\text{dt}}\\ ={\mathrm{e}}^{{(x_j-x_i)}^T\beta }{\displaystyle {\int }_0^{\tau }S(t|x_j^T\beta )}\mathrm{d}S(t|x_i^T\beta )\\ =-{\mathrm{e}}^{{(x_j-x_i)}^T\beta }P(Y_i<Y_j,Y_i<\tau )\end{array}$$ (31)

Substituting equation 31 into equation 30 results in:

$$P(Y_i<Y_j,Y_i<\tau )=\frac{1-S\left(\tau |x_i^T\beta \right)S\left(\tau |x_j^T\beta \right)}{1+{\mathrm{e}}^{{(x_j-x_i)}^T}\beta }$$ (32)

Since $S\left(\tau |x^T\beta \right)=S_0{\left(\tau \right)}^{{\mathrm{e}}^{x^T\beta }}$, equation 32 depends on the linear predictors $x_i^T\beta$ and $x_j^T\beta$, and on the baseline survival function $S_0\left(\tau \right)$ at time τ. The truncated model-based concordance results from equations 28 and 32:

$$\mathit{mbc}\left(\tau ;X\beta \right)=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[\left(1-S\left(\tau |x_i^T\beta \right)S\left(\tau |x_j^T\beta \right)\right)\left(\frac{I\left(x_i^T\beta >x_j^T\beta \right)}{1+{\mathrm{e}}^{{(x_j-x_i)}^T\beta }}+\frac{I\left(x_i^T\beta <x_j^T\beta \right)}{1+{\mathrm{e}}^{{(x_i-x_j)}^T\beta }}\right)\right]}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_{j\ne i}\left[\left(1-S\left(\tau |x_i^T\beta \right)S\left(\tau |x_j^T\beta \right)\right)\left(\frac{1}{1+{\mathrm{e}}^{{(x_j-x_i)}^T\beta }}+\frac{1}{1+{\mathrm{e}}^{{(x_i-x_j)}^T\beta }}\right)\right]}$$ (33)

In contrast with the original $\mathit{mbc}\left(X\beta \right)$ in equation 7, which is defined on the basis of complete follow-up, the truncated $\mathit{mbc}\left(\tau ;X\beta \right)$ weighs each patient pair by the probability that at least one of the patients encounters the event before follow-up time τ.