Flexible Force Field Parameterization through Fitting on the Ab Initio-Derived Elastic Tensor

Abstract

Constructing functional forms and their corresponding force field parameters for the metal–linker interface of metal–organic frameworks is challenging. We propose fitting these parameters on the elastic tensor, computed from ab initio density functional theory calculations. The advantage of this top-down approach is that it becomes evident if functional forms are missing when components of the elastic tensor are off. As a proof-of-concept, a new flexible force field for MIL-47(V) is derived. Negative thermal expansion is observed and framework flexibility has a negligible effect on adsorption and transport properties for small guest molecules. We believe that this force field parametrization approach can serve as a useful tool for developing accurate flexible force field models that capture the correct mechanical behavior of the full periodic structure.

1. Introduction

Metal–organic frameworks (MOFs)¹ are a new class of emerging materials with promising applications in gas storage,² adsorptive separation,^3,4 sensor devices,^5,6 and catalysis.⁷ These materials consist of metallic nodes and organic linkers that self-assemble into crystalline nanoporous materials. Some MOFs exhibit flexible behavior^8,9 upon external stimuli,¹⁰ which can heavily impact adsorption and diffusion properties. Large structural transformations¹¹ due to this flexibility include breathing,¹² gate-opening,^13,14 negative thermal expansion,¹⁵ and shear-driven structural destabilization.¹⁴ Most of these transformations are due to the unique connection in MOFs⁹ between the metal clusters and the organic linkers. Recent work of Ryder et al.^14,16 argues that low-frequency modes, in the THz regime, are responsible for large-scale flexibility and structural rearrangement. The large-scale flexibility in MOFs revolves around the behavior of metal clusters that can be thought of as “hinges” acting between rigid “struts”.^17,18 These hinges are shown schematically in Figure 1 for MIL-47(V), a three-dimensional, large-pore structure built up from infinite chains of corner-sharing V^IVO₆ octahedra linked by rigid terephthalate anions.¹⁹ MIL-47(V) is quite rigid at ambient conditions,¹⁹ but the same topology with a different metal (Al, Cr) leads to the MIL-53 structure that shows large-scale breathing.²⁰

Figure 1.

(a) Unit cell (1 × 2 × 2) of MIL-47(V) along the a direction. (b) The hinge is between the vanadium and the oxygens of the carboxylates.

To study framework flexibility and its related applications, classical force fields calculations are commonly used.²¹⁻²⁶ To account for the flexible behavior of the framework, functional forms of bonding, bending, and torsion potentials with the corresponding force field parameters have to be incorporated into the force field model. The construction and selection of such functional forms and parameters remains a major challenge in the development of accurate flexible force field models, which is evident from the scarce availability of flexible force fields in the literature.

The most widely used approach to obtain parameters for flexible force fields is the building block methodology. Here, nonperiodic ab initio calculations are performed on cluster models to extract force constants and references values.^{21−23,25,27} As the force field parameters are obtained independently, their collective behavior does not necessarily capture the overall mechanical motion of the unit cell because long-range interactions and long-range connectivity are not present in the cluster model. For example, inaccurate long-range interactions can lead to smaller bulk moduli as compared to ab initio calculations.²⁸ Bristow et al.²⁴ argued that a periodic structure should be used as a reference.

Alternatively, one could obtain parameters that reproduce the full vibrational spectrum, as was proposed by Gale et al.²⁸ The soft vibrational modes arise, in terms of force field potentials, from a combination of local (two-, three-, and four-body) bonding potentials and the long-range nonbonding potentials. Therefore, it is not straightforward to reproduce these lower-frequency modes, which was also found by Gale et al.²⁸ Moreover, a large number of fitting parameters makes this procedure tedious.

In this paper, we argue that reproducing the flexible behavior of the hinges in MOFs can be done by parametrizing the flexible force field on the elastic tensor. Gale et al.²⁹ used also the elastic tensor for the optimization of core–shell zeolite models. However, only a handful of parameters need to be optimized, and there is little ambiguity in the functional forms of the model. MOFs are chemically much more diverse than zeolites, and the challenging part for MOFs is modeling the connection of the linkers together via the hinges while making sure that the model reproduces the correct mechanical behavior.

The fourth-rank elastic tensor is related to the second-rank stress σ_αβ and strain ε_μν tensors in the elastic regime via Hooke’s law³⁰

1

where the Einstein summation notation is adapted and Greek indices denote Cartesian components. For the orthorhombic unit cell found in MIL-47(V), there are nine independent components of the elastic tensor when considering Voigt symmetry as shown in eq 2.

2

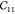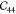The first three diagonal components of the elastic tensor , , and represent the stiffness along the principal crystal axes. The other diagonal components , , and 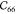are the shear coefficients that determine the resistance against angular deformation due to shear strain. The off-diagonal components , , and 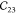are the tensile-coupling interactions between two principal axes.

In previous work by Dubbeldam et al.,¹⁵ a flexible force field for IRMOF-1 was parametrized on the experimental lattice parameter and excess CO₂ and methane adsorption isotherms. This IRMOF-1 force field also reproduced the experimental thermal expansion properties well. A later refinement was made³¹ to reproduce the ab initio elastic tensor with 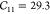GPa, GPa, and 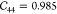GPa using the Dubbeldam force field vs the ab initio^32,33 values 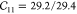GPa, GPa, and GPa.

In this work, we parametrize a new flexible force field for MIL-47(V) by fitting on the elastic tensor and use this example to discuss the benefits of the methodology. It is the hinges that largely determine the mechanical behavior, and we argue that modeling these correctly is vital. The chief advantage is that fitting on the elastic tensor allows the force field to reproduce soft, large-scale modes that are very difficult to optimize with other methodologies. Also, individual elastic constants contain directional information, and missing functional forms in the force fields can therefore be detected. Using our final model, we will also demonstrate that flexibility has negligible influence on the adsorption and diffusion properties of small adsorbates.

2. Computational Methodology

Generating force fields for classical simulations is an art.³⁴ It is impossible, with a finite amount of functional forms, to perfectly reproduce the ab initio energy landscape. Therefore, the most common route is to build up the force field from chemical entities like bonds, bends, and torsions and add physical behavior in layers on top of these.

For a small molecule, using harmonic functional forms for bonds, bends, and torsions can be sufficient to reproduce the molecular structure by tuning the equilibrium bond length, bend angles, and dihedral angles. The bond, bend, and torsion strengths could be obtained from ab initio calculations, such as density functional theory (DFT), by fitting them to the vibrational frequencies. Note, however, that the real vibrational spectrum is due not only to bonds, bends, and torsions but also to all of their cross-terms such as bond–bend, bond–torsion, bond–bend, bend–bend, and so forth. These couplings make the force field more accurate but also computationally more expensive. There is always this type of trade-off to be made.

Adding long-range interactions (van der Waals and electrostatics) on top of the intramolecular bonds, bends, and torsions leads to a complication: before, the reference distances and angles in the potentials were simply equal to the equilibrium distances and angles, but now, the reference distances and angles are different from the equilibrium distances because the equilibrium distances are affected by the long-range interactions.³⁵ In order to parametrize the intramolecular force field, all parameters need to be obtained at the same time. An equilibrium bond length can be the result of a very different reference length plus long-range interactions. Recently, methodology has been proposed to use genetic algorithms³⁶ to fit these types of force fields to DFT vibrational spectra.^27,37 Note that by doing so, effective parameters are obtained. That is, the method tries to best reproduce the vibrational frequencies for the given set of functional forms.

Figure 2 shows qualitatively the computed vibrational spectrum for IRMOF-1. The high frequencies are related to bond stretching, here the C–H stretch. As a function of decreasing frequency, the bond, bend, and torsion modes appear. Even if a force field is purely harmonic in its functional form, at finite temperature, the spectrum is anharmonic. The lowest frequencies are the large-scale atomic rearrangements.^14,16 These are heavily affected by long-range interactions (van der Waals and electrostatic), which are absent in force field approaches based on small clusters.

Figure 2.

Vibrational spectrum of IRMOF-1 at T = 298 K computed using the Fourier transform of the charge-weighted velocity autocorrelation function. Calculations are based on the Dubbeldam force field.³¹

If the linker molecules are based on generic force fields like DREIDING,³⁸ UFF,³⁹ CVFF,⁴⁰ or OPLS,^41,42, then there is only a (small) inherent error in the frequency spectrum of the linker. However, by fitting on elastic constants (which also inherently contain information on the frequency), this is decoupled from fitting the hinges. A reproduction of the elastic constants could mean that large-scale motion of the linker around the hinges is correctly modeled. This relies on the fact that linkers are rigid and hence the elastic properties of MOFs are dominated by the hinge–strut connection.

2.1. Fitting on Elastic Constants

The proposed fitting procedure in this work is shown in Figure 3. In this work, reference elastic constants are computed using ab initio calculations and also averaged with previous studies.

Figure 3.

Elastic tensor-based force field parametrization approach: functional forms and corresponding parameters are changed and/or added until the classical force field elastic tensor agrees with the ab initio-computed elastic tensor.

Next, the parameters of the hinges are initialized with reasonable values based on previous work,⁴³ other force fields, or chemical intuition. The structure is then minimized, and the elastic constants are examined. By comparing the obtained values to the ab initio values, a new set of force field parameters is chosen. By applying this process iteratively, the final parameter set is obtained.

2.2. Classical Force Field Calculations

All force field calculations were performed with the RASPA-2.0 code.^44,45 For MIL-47(V), initial functional forms and inorganic bonding parameters were chosen based on chemical intuition or from previous work.⁴³ The organic bonding parameters were taken from the OPLS-AA force field.⁴¹ Lennard-Jones parameters were taken from DREIDING,³⁸ and those not found in DREIDING were taken from UFF.³⁹ The force field-based minimization procedure is based on Baker’s minimization,⁴⁶ or mode-following technique,⁴⁷ that uses a generalized Hessian to obtain a true local minimum on the potential energy surface.³¹ The generalized Hessian, having dimensions (3N + 6) × (3N + 6), with N being the number of atoms, is given as

3

with the internal energy U, the force constant matrix 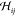, and the Born term being the second-order derivative of the internal energy with respect to the strains. The Born term accounts for distortions of the lattice, and and 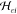are cross-terms.

The 0 K elastic tensor is defined as the derivative of the stress σ_αβ with respect to the strain ε_μν^30,48 at zero gradient and thus can be expressed in terms of the generalized Hessian⁴⁹

4

Greek indices are Cartesian components, and Latin indices refer to particle numbers. The relaxation term arises when more than one particle is present in the unit cell.⁴⁹ When the system is strained, the atoms need to relax relative to one another because before and after the strain is applied the system must be in a state of zero net force.

Note that the generalized 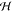Hessian encompasses the conventional Hessian 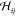and hence contains all information on the vibrational spectrum: elastic constants ⊃ frequencies. In addition, it contains information on the gradients and second derivatives of the internal energy with respect to the strain and the cross-terms of position gradients and strain gradients. Instead of fitting a large array of frequencies, the problem is reduced to fitting a smaller number of elastic constants. For a triclinic structure, such as CHA zeolite, there are 21 independent components, but for cubic structures, such as IRMOF-1, there are only 3. Table 1 shows the 0 K elastic constants computed using eq 4 for selected zeolites and IRMOFs. For IRMOF-1, the elastic constants are split into their two contributions: (1) the Born term and (2) the relaxation term. As can be seen from Table 1, the relaxation terms for IRMOF-1 are very large and is almost as large as the Born term, which explains the very small , , and 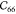shear values. Note that elastic constants as a function of linker length sharply drop (i.e., IRMOFs have the same topology, but the linker length is ordered as IRMOF-1 < IRMOF-10 < IRMOF-16).⁵⁰ MOFs are much softer and more flexible compared to zeolites, and nanoporous materials with larger pores are mechanically less stable than structures with small pores.

Table 1. Elastic Constants in GPa Calculated for Zeolites MFI and α-Quartz and IRMOF Series Calculated Using RASPA with the Born and Relaxation Contribution of the Elastic Constants of IRMOF-1 Given in the Last Two Rows.

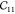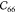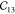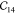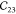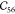MFI	97.71	88.99	79.36	28.65	26.27	23.09	12.09	26.49	–2.15	25.44	–7.93	–5.78	–0.78
α-quartz	94.55	94.55	116.04	49.97	49.97	38.06	18.43	19.67	–14.48	19.67	14.48		–14.48
IRMOF-16	12.11	12.11	12.11	0.1	0.1	0.1	3.38	3.38		3.38
IRMOF-10	15.97	15.97	15.97	0.15	0.15	0.15	3.93	3.93		3.93
IRMOF-1	29.3	29.3	29.3	0.985	0.985	0.985	11.91	11.91		11.91
-Born	71.87	71.87	71.87	27.81	27.81	27.81	20.91	20.91		20.91
-Relax	42.57	42.57	42.57	26.83	26.83	26.83	9.0	9.0		9.0

Due to this large relaxation, robust optimization algorithms are necessary. This avoids that the system might become stuck in a saddle point during relaxation. Baker’s minimization is a very robust algorithm for these types of computations.³¹

Elastic constants can also be obtained about the equilibrium relaxed structure by determining the variation of the total energy U with respect to the strain ε. The internal energy U(V,ε) of a crystal under strain ε can be Taylor expanded in powers of the strain tensor with respect to the initial internal energy of the unstrained crystal in the following way⁵¹

5

where the volume of the unstrained system is denoted V₀ and U(V₀,0) is the corresponding internal energy. Here, ξ_i takes the value 1 if the Voigt index is 1, 2, or 3, and otherwise, it takes the value 2.

This energy-strain methodology is the preferred method of some DFT codes^52,53 because the evaluation of all of the derivatives is computationally very expensive. Note that the total energy is minimized with respect to the atomic positions for each increment of strain ε. To evaluate the range of strains, we classically compute the energy-strain curves for IRMOF-1, as shown in Figure 4. Classically, we can compute the elastic constants up to machine precision using eq 4 and compare that to fitting on the energy-strain curves (also obtained classically using Baker’s minimization). The volume preserving strains can be used up to a strain of about 0.01, but the nonvolume preserving strains (for 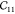) only work up to very small distortions. For 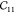, we find that the fitting procedure converges to the correct result for strains smaller than 0.01. However, the energy differences for such small elastic constants are tiny. Therefore, it is problematic to compute accurate minimized energies using DFT for these small strains, and so often a trade-off must be made. On the one hand, a small step needs to be made to be in the domain where the functional description is valid. On the other hand, for shallow energy landscapes, a larger step is necessary to have sufficiently high energy differences that would otherwise be lost in the numerical noise.

Figure 4.

Computing elastic constants from energy-strain curves: (a) symmetric strain 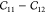(in orange) and asymmetric strain 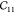(in green); (b) values as a function of the polynomial fit range (the converged value is obtained for strains smaller than 1% here; the line denotes the value obtained from eq 4). The inset shows the IRMOF-1 structure before and after applying the strain.

2.3. Ab Initio Density Functional Theory Calculations

It was recently shown by Tan et al.¹³ that good agreement of the elastic tensor can be obtained between ab initio DFT calculations and Brillouin scattering experiments. Furthermore, ab initio-calculated vibrational spectra are in good agreement with those obtained from inelastic neutron scattering and far-infrared synchrotron experiments.^14,16

Ab initio DFT calculations were performed to optimize the geometry and compute the elastic tensor⁵⁴ using the projector augmented wave (PAW) method as implemented in the VASP code.⁵⁵⁻⁵⁷ The valence electrons for the elements O and C include the 2s and the 2p electrons, and for V, they include the 4s and 3d electrons. The dispersion-corrected PBE exchange–correlation functional^58,59 with an energy cutoff of 600 eV was used. K-point sampling was set to 6 × 2 × 2 using the Monkhorst–Pack scheme,⁶⁰ and a Gaussian smearing of 0.05 eV was applied.

3. Results

MOFs can have shallow energy landscapes around the hinges. Therefore, we assess the effect of the step size δ and amount of displacements N used for the finite differences approach to compute the gradient of the forces.⁵⁴ As shown in Table 2, for δ = 0.02 Å, negative eigenvalues of the elastic tensor are obtained, violating the Born stability criteria^61,62 and hence suggesting a mechanically unstable unit cell.⁶³ A single imaginary frequency was observed for δ = 0.005 Å. Generally, it appears that smaller step sizes give larger elastic constants. As our ab initio reference, we averaged the elastic constants computed with δ = 0.015 Å, which is also the default value in VASP.

Table 2. Elastic Constants in Voigt Notation in GPa for MIL-47(V) with Various Step Sizes δ in Å and Displacements N^a.

N	δ		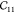								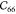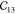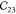λ1	λ6
2	0.005	45.11	85.16	34.58	46.26	7.24	10.80	24.14	16.00	49.11	4.59	125.52
	0.015	40.93	83.45	29.41	43.84	9.43	11.04	19.95	12.00	48.19	1.18	118.65
	0.020	39.90	80.61	27.33	43.45	7.05	7.22	19.00	10.49	47.04	–0.09	114.36
4	0.005	41.80	83.49	32.90	46.48	0.98	10.76	22.47	14.44	47.58	0.98	121.07
	0.015	38.13	82.86	29.70	43.72	9.89	11.42	18.74	11.43	48.10	1.32	117.32
	0.020	37.54	79.43	26.30	43.91	6.80	4.39	17.72	9.07	46.03	–0.31	111.36

^aThe smallest and largest eigenvalues are denoted λ₁ and λ₆, respectively, with negative eigenvalues denoted in bold.

The lattice parameters and elastic constants in Voigt notation from this work and from the literature^64,65 are presented in Table 3. Our force field is fitted on the average of the three ab initio-calculated elastic tensors, represented by the first three columns in Table 3.

Table 3. Elastic Constants of MIL-47(V) in Voigt Notation in GPa, Unit Cell Lengths in Å and Angles in Deg, and Volume V in Å^3a.

	Vanpoucke65	Ortiz64	PBE-D3b	FF43	FFb
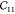	35.4	40.68	39.53	12.50	42.55
	67.6	62.60	83.16	37.90	70.54
	34.0	36.15	29.56	17.26	39.43
	44.2	50.83	43.78	52.73	45.02
	6.7	7.76	9.66	2.07	9.12
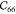	8.7	9.30	11.23	13.67	10.06
	15.2	12.58	19.35	–12.22	9.10
	10.2	9.28	11.72	–8.77	6.80
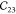	46.0	46.98	48.15	24.62	51.44
a	6.842	6.79	6.807	6.754	6.901
b	16.394	16.05	16.696	16.561	16.125
c	13.854	13.98	13.190	13.735	14.131
α	90.00	90.00	90.00	89.924	90.00
V	1554.1	1523.5	1499.1	1536.2	1572.6

^aConstants: Exp.:¹⁹a = 6.8179, b = 16.143, c = 13.939, α = 90.00, V = 1534.15 at T = 296 K.

^bThis work (FF = force field).

After manually exploring the initial force field parameter space, it becomes clear that no trial set with the existing functional forms is able to come close to reproducing all components of the ab initio elastic tensor. However, by inspecting which components of the tensor are off, we can elucidate which functional forms are missing. The elastic constants contain directional information, and bond interactions can affect only the elastic constants that are in the direction of the bond. Bends and torsions determine, when pressed in a certain direction, how much distortion happens in the perpendicular direction. Therefore, not only are the parameters optimized but also a force field with better functional forms can be obtained. This is an advantage over existing parametrization methods. We added one additional torsion potential (O2–V1–O1–V1), which was essential to reproducing the ab initio value (compare eq S2 with Table 3). The dominant changes by varying this torsion were found in , allowing us to tune this value of the elastic tensor independently. The final flexible force field is given in the Supporting Information.

The elastic constants of a previous flexible force field for MIL-47(V)⁴³ were assessed, and poor agreement was found compared to the ab initio values shown in Table 3. Note that we included a harmonic C–H vibration in the previous force field. Also, the Baker’s minimized structure indicates that the orthorhombic symmetry of the unit cell is broken. The distribution profile of the organic linkers’ torsion angles using our force field (Figure 5) is significantly more narrow, which is attributed to a 3.7 larger force constant for the O2–C3–C2–C1 torsion in this work. Setting this force constant to 600 K, as done in the previous force field,⁴³ results in a mechanically unstable unit cell (see eq S1).⁶³

Figure 5.

Distribution profile of the C1–C2–C3–O2 torsion angle, shown in the inset, at 300 K and 1 bar. Black and blue lines were computed with our force field and from Yot et al., respectively.

Using our flexible force field, negative thermal expansion can be predicted from molecular dynamics simulations in the NpT Parrinello–Rahman ensemble.⁶⁶ A volumetric expansion coefficient of α_V = −36.2 × 10^–6 K^–1 over a range of 0–800 K was obtained, as shown in Figure 6 and in agreement with previous work.⁶⁷

Figure 6.

Unit cell volume as a function of temperature of MIL-47(V), showing negative thermal expansion with a volumetric expansion coefficient of α_V = −36.2 × 10^–6 K^–1 over a range of 0–800 K. The red square at 0 K is the volume obtained from the Baker minimized structure. Results are from a molecular dynamics simulation in the NpT Parrinello–Rahman ensemble.⁶⁶

Single-component adsorption isotherms of CO₂, methane, and n-hexane were computed using Monte Carlo simulations with our flexible and a rigid force field. Simulations were conducted in the osmotic (μ₁N₂pT)⁶⁸ and grand-canonical (μVT)⁶⁹ ensembles, respectively. The force field parameters of the adsorbates were taken from the TraPPE force field.^70,71Figure 7 shows the adsorption isotherms, and no significant differences between the flexible and rigid material are observed.

Figure 7.

Single-component adsorption isotherms of CO₂, CH₄, and n-C₆ in MIL-47(V) at 303 K using flexible (open symbols) and rigid (closed symbols) force fields. Solid and dashed lines are Langmuir–Freundlich isotherms for rigid and flexible force fields, respectively.

Self-diffusivities of the aforementioned adsorbates were computed using the rigid and flexible force fields by performing molecular dynamics simulations in the NVT and NpT Parrinello–Rahman ensemble,⁷² respectively. The self-diffusion coefficient is obtained from the Einstein relation⁷³

6

with t being the time, N the number of particles, and r_i the center-of-mass. Figure 8 shows the self-diffusivities as a function of loading at various temperatures, and again, no significant differences are found.

Figure 8.

Self-diffusivity of CO₂, CH₄, and n-C₆ in MIL-47(V) as a function of loading at 300 and 600 K using flexible (open symbols) and rigid (closed symbols) force fields, respectively.

4. Discussion

The step size dependency of the gradient of the force, as reported in Table 2, shows an important point. For the same structure, a too small step size leads to negative eigenfrequencies, and a too large step size leads to negative eigenvalues of the elastic tensor. This behavior can be explained due to the shallow energy surface of the MOF. This suggests that numerical accuracy can affect whether a unit cell can be considered as mechanically stable and/or is not in a local minima on the potential energy surface. A recent study by Vanpoucke et al.⁶⁵ also illustrated difficulties when computing mechanical properties using plane-wave basis sets.

There is a still ongoing debate on the influence of flexibility for diffusion⁷⁴⁻⁷⁸ or adsorption.⁷⁷⁻⁷⁹ We argue that, when comparing the effect of framework flexibility, the rigid framework material should be obtained via a minimization procedure (such as Baker’s minimization in this study) using the flexible force field. Most authors use an ab initio-optimized structure as reference, but this is inconsistent because the material will move around the reference bonds, bends, and torsions that are imposed by the flexible force field and these values are not necessarily the same equilibrium values found from ab initio calculations or experiments.³⁵ A requirement is therefore that the flexible structure converges at low temperature to the rigid structure.⁷⁹ Stated oppositely, the rigid structure should be the 0 K optimized structure of the flexible model.

As can be seen from Figures 7 and 8, framework flexibility has negligible effects on the adsorption and transport properties of small adsorbates in MIL-47(V). This can be explained due to the fact that the adsorbates are considerably smaller than the channel size of MIL-47(V). We think that framework flexibility has considerable impact only when (i) adsorbates are confined^80,81 or (ii) phase transitions of the framework occur.¹²

Although Boyd et al.⁸² pointed out recently that generic flexible force fields, such as DREIDING,³⁸ UFF,³⁹ UFF4MOF,^83,84 BTW-FF,²⁴ and DWES¹⁵ produce bulk moduli within 5% of the DFT values, the elastic constants are much more sensitive.

Another advantage of this approach is that the construction of flexible force fields for functionalized MOFs should be straightforward. If the parent material reproduces the elastic constants well, than one can use functional forms and parameters from generic organic force fields to include the flexible modes of the substituted organic linkers.

5. Conclusions

In this work, we proposed fitting functional forms of bonding, bending, and torsion parameters of the hinges in MOFs on elastic constants. The elastic constants can be obtained from ab initio DFT calculations, but the step size of the numerical differentiation of the gradient of the force should be carefully chosen. Within this approach, missing functional forms of the force field can be detected based on when components of the elastic tensor are off.

To assess the effect of framework flexibility, the reference framework should be obtained utilizing a robust force field-based minimization procedure. As a proof of concept, it was shown for MIL-47(V) that framework flexibility has negligible influence on the adsorption and diffusion properties for small guest molecules. Negative thermal expansion was also predicted. This procedure should, in principle, also be suitable for a broader range of crystalline materials exhibiting flexibility.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b00310.

• Additional elastic constants and flexible force field parameters of MIL-47(V) (PDF)

This material is supported by The Netherlands Research Council for Chemical Sciences (NWO–CW), through a VIDI grant (D.D.), and through the Sandia National Laboratories Truman Fellowship Program, which is funded by the Laboratory Directed Research and Development (LDRD) Program (N.C.B.). Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525.

The authors declare no competing financial interest.