DYNAMIC REGISTRATION FOR GIGAPIXEL SERIAL WHOLE SLIDE IMAGES

Abstract

High-throughput serial histology imaging provides a new avenue for the routine study of micro-anatomical structures in a 3D space. However, the emergence of serial whole slide imaging poses a new registration challenge, as the gigapixel image size precludes the direct application of conventional registration techniques. In this paper, we develop a three-stage registration with multi-resolution mapping and propagation method to dynamically produce registered subvolumes from serial whole slide images. We validate our algorithm with gigapixel images of serial brain tumor sections and synthetic image volumes. The qualitative and quantitative assessment results demonstrate the efficacy of our approach and suggest its promise for 3D histology reconstruction analysis.

1. INTRODUCTION

The introduction of high-throughput scanning technology has allowed for routine digital 3D reconstruction of serial whole slide histology images [1]. However, registration of serial whole slide images is a challenge due to artifacts induced by sectioning, mounting, and imaging [2, 3, 4, 5]. Additionally, a single image may contain several gigabytes of data. The resulting 3D volumes can easily exceed modern computer memory limits, thus precluding the direct use of existing reconstruction methods [6, 7, 8, 9, 10, 11]. Although some registration methods have been developed for 2D gigapixel images [12, 13, 14, 15], there is no method that dynamically extends registration to serial gigapixel images aiming for 3D micro-anatomical structure reconstruction. To address this, we develop a new multi-resolution mapping and propagation method for serial image registration.

In practice, it is noticed that whole slide imaging stores more data than what is typically required for research or diagnosis. Furthermore, researchers and clinicians are often only interested in small subvolumes of data such as disease sites or histology hallmarks. Based on current methods, accessing such subvolumes requires the prior registration of the entire full-resolution whole slide image volume, leading to a high computational cost. To solve this problem, we develop a hierarchical image registration method that computes image deformation on-the-fly. In this way, we can minimize the computational burden and focus analysis on the tissue subvolumes of interest to domain experts. As most whole slide image files produced by digital scanners (e.g. Hamamatsu Nanozoomer 2.0-HT) contain a multi-resolution pyramid image representation, we also reduce computation by performing time consuming tasks, such as registration optimization, at a low resolution and mapping the resulting deformations to a high resolution for subvolume reconstruction.

2. METHODS

Our workflow for subvolume registration includes 1) low resolution pre-alignment, global and local registration, 2) multi-resolution transformation mapping, and 3) high resolution registration propagation (Figure 1).

Fig. 1.

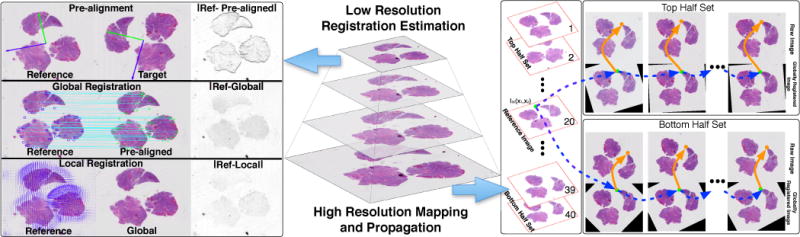
An overview of the proposed method for three-stage registration at low resolution (left panel) and high resolution mapping and propagation across serial images (right panel).

2.1. Low Resolution Whole Slide Registration

Serial tissue sections are typically mounted to glass slides at random locations and orientations. To facilitate full tissue registration, we first pre-align each tissue section to a reference section based on their contour principal axes [16]. Registration is computed between each sequential pair of images within the volume. Low resolution serial images are first converted to grayscale and recognized for tissue components with adaptive global thresholding. We denote the tissue contours as C = {x_i = (x_i1, x_i2)^T, ∀i}. With detected C, we next compute the centroid, μ ∈ ℝ², and construct the scatter matrix Σ = (Y − μ) (Y − μ)^T, where Y is a matrix with columns being {x_i, ∀i} and (Y − μ) is column-wise subtraction. After matrix diagonalization of Σ, we have two eigen values λ₁ and λ₂ (λ₁ ≥ λ₂) and two corresponding eigen vectors v₁ and v₂. This process is applied to both reference image and target image, with the resulting matrices composed with eigen vectors V_r = (v_r1 | v_r2) and V_t = (v_t1 | v_t2), respectively. We compute the rotation matrix candidates $R_{+}=V_r{V}_t^T$ and R₋ = −R₊. We take the rotation direction associated with the smaller difference between reference and pre-aligned images:

$$R^{\ast }=\underset{R\in \{R_{+},R_{-}\}}{\text{argmin}}||I_r-I_t(R{\mathbf{x}}_i-({\mu }_r-R{\mu }_t))|{|}_2,$$ (1)

where I_r and I_t are the reference and target image in grayscale, respectively. The resulting pre-aligned image can be obtained by $\widehat{I}=I_t(R^{\ast }({\mathbf{x}}_i-\mathrm{\Delta }\mu ))$, where Δμ = μ_r − R^*μ_t.

For global similarity transformation, we detect critical landmarks by Speeded Up Robust Feature (SURF) detector [17]. The detected tissue landmarks are then matched with local descriptors [18]. Since many cellular features are at least 5 μm in diameter, corresponding landmarks, such as nuclei, exist in adjacent 5 μm thick sections. These landmarks help mitigate the “banana” reconstruction problem [19].

The matched point pairs are used to estimate an optimal similarity transformation, T. Given two corresponding point sets $\mathcal{X}=\{{\mathbf{x}}_i:i=1,\dots ,N\}$ and $\mathcal{Y}=\{{\mathbf{y}}_i:i=1,\dots ,N\}$, we aim to minimize ${\displaystyle \sum _{i=1}^N\left|\right|T({\mathbf{x}}_i;s,\theta ,\mathbf{t})-{\mathbf{y}}_i|{|}^2}$ by optimizing the parameters {s, θ, t}, where s, θ, and t are the scale, rotation angle, and spatial translation vector, respectively. The optimal parameters for similarity transformation can be analytically solved [20].

Global registration is followed by a nonrigid registration to compensate for local tissue deformations by B-spline transformation. The optimal local deformations are found by simultaneously maximizing the normalized mutual information and minimizing transformation energy [21, 22].

2.2. Multi-Resolution Registration Mapping

The resulting global and local transformations estimated with whole slide images at low resolution can be mapped to high resolution image levels (Figure 2). We denote the pre-alignment, similarity, and nonrigid transformation at low image resolution as P, T, and D, respectively.

Fig. 2.

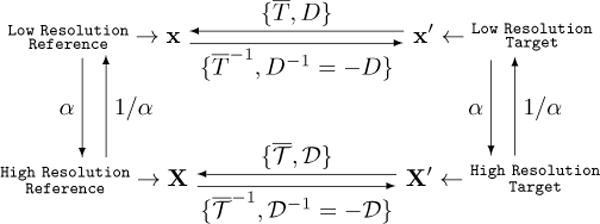
Diagram of mapping relationships between reference and target image at low and high resolution, respectively.

The pre-alignment and global registration can be simply denoted in a homogeneous coordinate system as follows:

where x = (x₁, x₂, 1)^T ; x and x′ are coordinates for reference and target image at low resolution; s is the similarity transformation scaling factor; R and $\widehat{R}$ are rotation matrices for the global and pre-alignment transformation, respectively; Δx = (Δx₁, Δx₂)^T is a spatial translation vector. We can combine transformation T with P and denote it as $\overline{T}$.

Let us denote the global and local transformation at a high image resolution as $\overline{\mathcal{T}}$ and $\mathcal{D}$, respectively. When mapping from low to high resolution, we can find $\overline{\mathcal{T}}$ by:

$$\left(\begin{array}{c}{X}_1/\alpha \\ X_2/\alpha \\ 1\end{array}\right)=\mathbf{x}=\overline{T}{\mathbf{x}}^{\prime }=\overline{T}\left(\begin{array}{c}{X}_1^{\prime }/\alpha \\ X_2^{\prime }/\alpha \\ 1\end{array}\right),\mathbf{X}=\overline{\mathcal{T}}{\mathbf{X}}^{\prime },$$

where X and X′ are coordinate for reference and target image at high resolution, α = 2^|ΔL| and ΔL is the resolution level difference between low and high resolution, given a standard 2× downsampling rate followed by most scanners. It is straightforward to have $\overline{\mathcal{T}}$ and ${\overline{\mathcal{T}}}^{-1}$ as:

$$\overline{\mathcal{T}}=\left(\begin{array}{cc}(sR\widehat{R})& \alpha \mathrm{\Delta }x\\ {\mathbf{0}}_{1\times 2}& 1\end{array}\right),{\overline{\mathcal{T}}}^{-1}=\left(\begin{array}{cc}{(sR\widehat{R})}^T& -\alpha {(sR\widehat{R})}^T\mathrm{\Delta }x\\ {\mathbf{0}}_{1\times 2}& 1\end{array}\right).$$ (2)

For local deformation, the transformation at high resolution level is:

$$\mathcal{D}(X_1,X_2)=\alpha D(X_1/\alpha ,X_2/\alpha )\approx \alpha \mathrm{\Phi }(D,(X_1/\alpha ,X_2/\alpha )),$$ (3)

where Φ(·) is a 2D interpolation function necessary for non-integer coordinates (X₁/α, X₂/α).

2.3. High Resolution Image Registration Propagation

We use the center image in the volume as the reference and map remaining images to the reference image with cascaded pair-wise transformations. In this way, all images are transformed to a common coordinate system for 3D histological structure reconstruction and spatial analysis.

To facilitate discussion, let us denote the i^th original image, globally registered image and locally registered image as I_i, ${\overline{I}}_i$, and ${\stackrel{\sim }{I}}_i$, respectively. Assuming there are N serial images in the imaging volume, we set image i^* as the reference image for the whole volume, where $i^{\ast }=\lfloor \frac{N}{2}\rfloor$ Correspondingly, the ${\overline{\mathcal{T}}}_i$ and ${\overline{\mathcal{T}}}_i^{-1}$ are global transformations from I_i to I_i+1, and from I_i+1 to I_i, respectively. ${\mathcal{D}}_i$ is the nonrigid deformation from ${\overline{I}}_i$ to ${\overline{I}}_j$, where j = i + 1 if i < i^* and j = i − 1 if i > i^*, respectively. Similarly, ${\mathcal{D}}_i^{-1}=-{\mathcal{D}}_i$ is the nonrigid deformation from ${\overline{I}}_j$ to ${\overline{I}}_i$. Note that ${\mathcal{D}}_{i^{\ast }}=\mathbf{0}$.

As the nonrigid registration at the low resolution is applied to the globally registered image sequence and only local alignment transformations for all adjacent image pairs are available, the way to find the aggregated transformation for a target image slide I_j, where |j − i^*| > 1, to the reference image $I_{i^{\ast }}$ at the high image resolution is not straightforward. We describe our method for mapping each pixel in the reference coordinate system to the corresponding location in a target image with the mapped local and global transformations from low to high image resolution as follows.

Step 1: As globally registered images ${\overline{I}}_i$ have the same dimensions as the reference image $I_{i^{\ast }}$ where i < i^*, we first map an arbitrary pixel $(X_1^{i^{\ast }},X_2^{i^{\ast }})\in \mathrm{\Omega }(I_{i^{\ast }})$ to globally registered image ${\overline{I}}_{i^{\ast }-1}$ space by nonrigid mapping ${\mathcal{D}}_{i^{\ast }-1}^{-1}=-{\mathcal{D}}_{i^{\ast }-1}$. The resulting point location after local deformation is $(X_1^{i^{\ast }-1},X_2^{i^{\ast }-1})=(X_1^{i^{\ast }},X_2^{i^{\ast }})-{\mathcal{D}}_{i^{\ast }-1}(X_1^{i^{\ast }},X_2^{i^{\ast }})$ (blue arrows in Figure 1).

Step 2: Next, $(X_1^{i^{\ast }-1},X_2^{i^{\ast }-1})\in \mathrm{\Omega }({\overline{I}}_{i^{\ast }-1})$ can be mapped to $\mathrm{\Omega }(I_{i^{\ast }-1})$ as: $(X_1^{\ast },X_2^{\ast })={\overline{\mathcal{T}}}_{i^{\ast }-1}(X_1^{i^{\ast }-1},X_2^{i^{\ast }-1})$ (orange arrows in Figure 1).

Step 3: Repeat Step 1 and 2 to propagate $\mathcal{D}$ and $\overline{\mathcal{T}}$ for aggregated transformation from $I_{i^{\ast }}$ to any arbitrary image in the volume. A similar procedure is applied to I_j, where j > i^*. The algorithmic description of this registration propagation is presented in Algorithm 1.

To support 3D reconstruction of micro-anatomical objects such as cells, we use OpenSlide [23] to dynamically extract a small region from each serial image to be registered with the multi-resolution registration mapping and propagation algorithm. By this approach, we effectively address the computer memory overflow problem due to the gigapixel image scale.

3. EXPERIMENTS AND RESULTS

We test our method for dynamic subvolume registration on a set of 40 serial hematoxylin and eosin stained tissue sections from a glioblastoma (GBM) biopsy. Each GBM serial section is cut to 5 μm thick and digitized at 0.2265 μm/pixel resolution, resulting in an overall image volume of 12.930 × 15.279 × 0.200mm³ (≈ 150 gigavoxels). From the entire image volume, we extract a registered 928 × 928 × 200μm³ (≈ 670 megavoxels) subvolume by performing whole slide pre-alignment, global and local registration at low resolution (L = 8) and mapping to a high resolution (L = 0).

Algorithm 1.

Registration Mapping and Propagation

Input: {Ii, i = 1, 2, …, N}: original serial images
Output: $\{{\stackrel{\sim }{I}}_i,i=1,2,\dots ,N\}$: registered serial images
Operator: ${\text{ℒ}}_{i:j}\triangleq {\text{ℒ}}_j(\cdots ({\text{ℒ}}_{i+\text{sign}(j-i)\times 2}({\text{ℒ}}_{i+\text{sign}(j-i)\times 1}({\text{ℒ}}_i(\cdot )))))$
1:	Compute reference image index $i^{\ast }\leftarrow \lfloor \frac{N}{2}\rfloor$
2:	Compute $\overline{\mathcal{T}},{\overline{\mathcal{T}}}^{-1}$, and $\mathcal{D}$ by Eqn (2) and (3), respectively
3:	for all i ∈ (i* − 1, i* − 2, …, 1) do
4:	for all $(x_1,x_2)\in \mathrm{\Omega }(I_{i\ast })$ do
5:	Set (X1, X2) ← (x1, x2)
6:	Set j ← i* − 1
7:	while j ≥ i do
8:	Local deformation: $(X_1,X_2)\leftarrow (X_1,X_2)-{\mathcal{D}}_j(X_1,X_2)$
9:	j ← j − 1
10:	${\stackrel{\sim }{I}}_i(x_1,x_2)\stackrel{\text{interpolate}}{\leftarrow }{I}_i\left({\overline{\mathcal{T}}}_{(i\ast -1):i}^{-1}(X_1,X_2)\right)$
11:	for all i ∈ (i* + 1, …, N) do
12:	for all (x1, x2) ∈ Ω (Ii*) do
13:	Set (X1, X2) ← (x1, x2)
14:	Set j ← i* + 1
15:	while j ≤ i do
16:	Local deformation: $(X_1,X_2)\leftarrow (X_1,X_2)-{\mathcal{D}}_j(X_1,X_2)$
17:	j ← j + 1
18:	${\stackrel{\sim }{I}}_i(x_1,x_2)\stackrel{\text{interpolate}}{\leftarrow }{I}_i\left({\overline{\mathcal{T}}}_{i\ast :(i-1)}^{-1}(X_1,X_2)\right)$

First, registration accuracy is examined visually for tissue edge discontinuity in distinct cross sections through the low resolution image volume in Figure 3. Each cross section plane is uniquely colored in the 3D view of the registered volume. Cross section locations are randomly selected and colored to match the y-z cross section views. Scaling in the z direction is increased to aid visual inspection of contour discontinuities. We observe the progressive improvement in registration for pre-alignment, similarity transformation, and nonrigid deformation. The subvolume montage view of a small tissue region of interest in Figure 4 shows a high correspondence across serial sections, suggesting the efficacy of our proposed method.

Fig. 3.

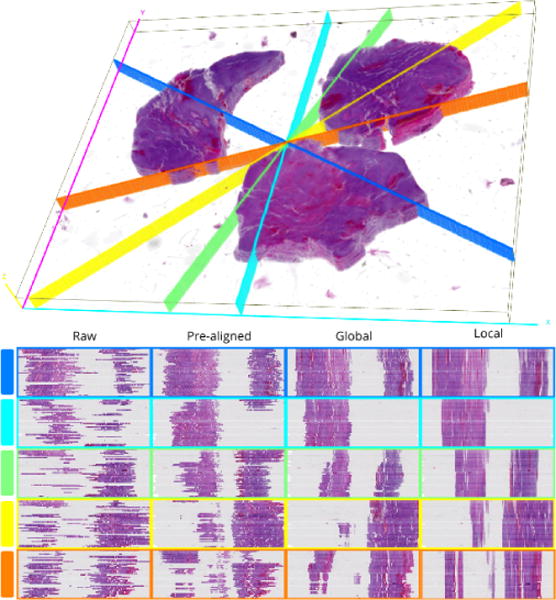
Qualitative evaluation of registration accuracy using random cross sections. Each row in the bottom panel displays the y-z cross sections at each registration stage for the corresponding cutting plane in the 3D rendered volume at the top.

Fig. 4.

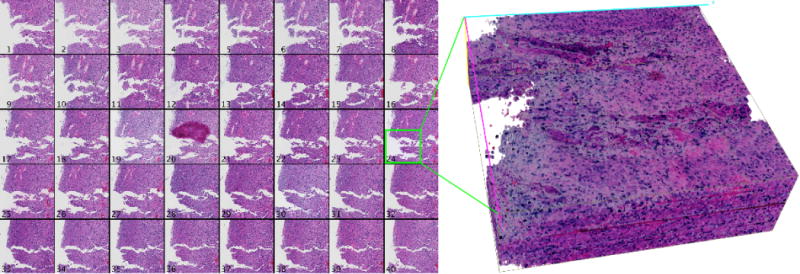
Results of high resolution mapping and propagation for a 4096 × 4096 pixel region of serial GBM sections. A montage of the registered region is presented on the left, and a 3D rendered volume corresponding to the green box is shown on the right.

Next, we quantitatively evaluate the proposed registration propagation and multi-resolution mapping method by computing the registration accuracy for ten synthetic image volumes. For each such synthetic ground truth volume, we replicate a single section from the GBM data set 50 times at levels 8, 7 and 6. We intentionally produce random global transformations and local deformations to the level 8 synthetic volumes to simulate distortions introduced by tissue processing. Global transformations are constructed using sheer, translation and rotation values drawn from $\mathcal{N}(0,0.001)$, $\mathcal{N}(0,p/3)$, where p is the smallest image dimension, and $\mathcal{U}(0,360)$, respectively. We extrapolate a 4 × 4 matrix, subject to $\mathcal{N}(0,4)$, to appropriate image dimensions for generating local deformations. The global and local deformations are scaled using Equation 2 and 3 to produce identical distortions for the level 7 and level 6 ground truth volumes.

Registration is performed for each distorted synthetic volume at level 8, and the average registration accuracy is computed for pre-alignment, global and local registration. The registration accuracy for each synthetic volume is measured by the background overlap between the synthetic ground truth and deformed volume [24]. The average registration accuracies at level 8 describe the distortion correction power at each sequential registration step. To explore the error in multi-resolution mapping, we scale the deformations at level 8 and apply them to level 7 and 6. The registration accuracy for each step at each level is presented in Table 1. We notice that sequential pre-alignment, global and local registration can correct most simulated distortions, and there is no substantial increase in error introduced by multi-resolution mapping from level 8 to level 6. The observed degradation from pre-aligned to global registration could result from the extra degree of freedom for scaling in the similarity transform estimation, given our synthetic data is not substantially scaled by simulated distortions. In the future, we plan to extend this work with iterative registration corrections across pyramidal resolution levels to further improve concordance across serial sections. Moreover, we intend to use human-annotated landmarks to extend our quantitative assessment.

Table 1.

Registration accuracy for each processing step at three different levels: Mean±Std (n = 50).

Level	Pre-aligned	Global	Local
L = 8	0.938 ± 0.005	0.903 ± 0.020	0.989 ± 0.001
L = 7	0.934 ± 0.005	0.900 ± 0.019	0.974 ± 0.001
L = 6	0.931 ± 0.005	0.897 ± 0.018	0.965 ± 0.001

4. CONCLUSION

We present a new method to dynamically register 3D subvolumes from serial gigapixel whole slide images. The optimal deformation at low resolution is first estimated with a multistage registration process through serial images. With the optimal transformations, we next create a mapping and propagation method that connects the reference coordinate at the low resolution level to a registered subvolume at the high resolution level. Both qualitative and quantitative evaluation results demonstrate the promise of our multi-stage and multi-resolution registration method for future 3D micro-anatomical structure reconstruction from serial whole slide histology images at gigapixel scale.