Asymmetric drop coalescence launches fungal ballistospores with directionality

Abstract

Thousands of fungal species use surface energy to power the launch of their ballistospores. The surface energy is released when a spherical Buller's drop at the spore's hilar appendix merges with a flattened drop on the adaxial side of the spore. The launching mechanism is primarily understood in terms of energetic models, and crucial features such as launching directionality are unexplained. Integrating experiments and simulations, we advance a mechanistic model based on the capillary–inertial coalescence between the Buller's drop and the adaxial drop, a pair that is asymmetric in size, shape and relative position. The asymmetric coalescence is surprisingly effective and robust, producing a launching momentum governed by the Buller's drop and a launching direction along the adaxial plane of the spore. These key functions of momentum generation and directional control are elucidated by numerical simulations, demonstrated on spore-mimicking particles, and corroborated by published ballistospore kinematics. Our work places the morphological and kinematic diversity of ballistospores into a general mechanical framework, and points to a generic catapulting mechanism of colloidal particles with implications for both biology and engineering.

1. Introduction

Spore morphologies and behaviours are essential descriptors of fungal species, and the mechanisms of spore discharge define two of the major phyla of fungi, Ascomycota and Basidiomycota [1–3]. Ascospores are launched by the turgor pressure built up within a liquid-filled tubular sac, termed the ascus, which shapes the direction of spore launch [1,4,5]. Basidiospores are launched by the surface tension (or surface energy) associated with liquid droplets accumulated on the spores [1,6,7]. However, the physical mechanism determining the launching directionality of basidiospores, referred to as ballistospores below [7], remains unknown.

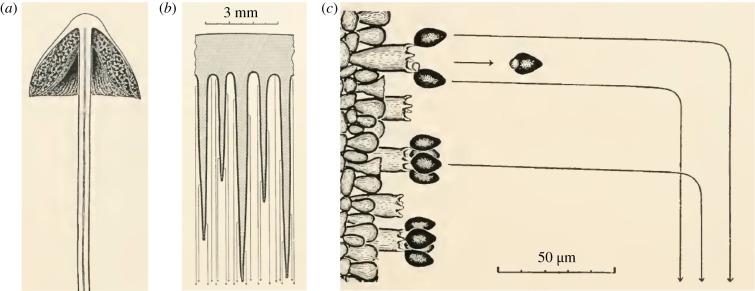
Basidiomycete ballistospore launching is frequently observed in gilled mushrooms (figure 1a) [1]. Spores develop on the tightly spaced gills and have a radius of gyration typically below 5 μm. A micrometric spore is first projected horizontally from a vertically oriented gill, and then driven by gravity to sediment in the interlamellar space (figure 1b), until the spore escapes the mushroom cap and is subsequently dispersed by air flows. Despite a large initial launching velocity (on the order of 1 m s⁻¹), the tiny spore can only travel a short distance (on the order of 100 μm) because of the viscous drag exerted by the surrounding air. Using mathematical models (vol. 1, ch. 17 [1]), Buller demonstrated that the launching trajectory can be divided into two phases (figure 1c). In the first phase, the spore follows the initial launching direction, but only for a short period (typically below 1 ms) because of the excessive air drag. In the second phase, the spore falls vertically at a small sedimentation velocity (typically below 1 mm s⁻¹), again due to air drag. Since the first phase is brief, gravity can only displace the spore vertically by an insignificant distance (less than a spore diameter). This insignificant gravitational effect in the first phase enabled Buller to accurately record, without high-speed imaging tools, the entire launching trajectory consisting of both phases (figure 1c). Within vertically oriented gills, the launching trajectories reported by Buller are predominantly in the horizontal direction. In figure 1c as well as figs 49 and 107 of volume 3 [1], initial spore movement is always orthogonal to the spore-bearing structure, and the maximum deviation from the horizontal direction is within ±15°.

Figure 1.

Ballistospore launching in a gilled mushroom. (a) Vertical section of a Panaeolus campanulatus sporocarp. (b) Magnified view depicting the vertically orientated gills (shaded area) on which spores are formed. The trajectories of the launched spores are indicated by arrowed light grey lines. (c) Further magnified view showing the trajectories of the spores discharged from the sterigmata on a single vertical gill. At the base of the launched spore is a liquid droplet resulting from the drop coalescence that powers the explosive launch. Images adapted from figs 84, 85 and 97 of volume 2 by Buller [1]. (Online version in colour.)

Why are the ballistospores launched orthogonally to the spore-bearing structure (the hymenium)? As Buller noted, these spores are sticky. If a spore attaches to any surrounding surface before reaching dispersive air flows, it will not disperse [1]. A likely explanation for directionality, albeit difficult to test as a hypothesis [8], stems from the advantage provided to a spore that clears the hymenium. An orthogonal arrangement maximizes horizontal travel distance in the first phase, creating a safety margin against small air currents and the random Brownian motion that might inadvertently carry the spores back to the initial supporting structure or to surrounding lamellar tissues. Of course, for a spore to successfully disperse, it cannot be launched so far that the spore sticks to the opposing gill. The same argument for directionality applies to species with either gilled or pored mushrooms. (Note that some ballistospores are launched directly into the open air, e.g. in yeasts and rusts, with typically larger spores. In those cases, an orthogonal launching direction maximizes the probability of escaping the viscous boundary layer formed around the hymenium [5,9].)

How do physical processes shape the orthogonal direction taken by a launching spore, the directionality consistently reported since 1909 [1]? Our paper attempts to address this unanswered question by advancing the mechanistic understanding of ballistospory beyond the energetic model. Note that the orthogonal direction is typically aligned with the spore's long axis, which in turn is strongly correlated with the longitudinal axis of the sterigma that initially supports the spore (figures 1c and 2a).

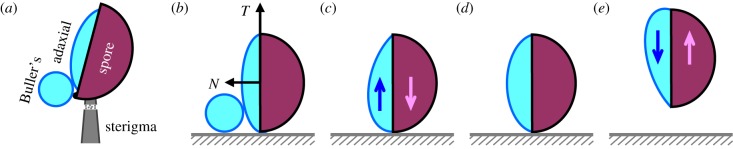
Figure 2.

Ballistospore launching upon drop coalescence. (a) Prior to the launching of a ballistospore, a spherical Buller's drop forms at the hilar appendix which is at the base of the spore, and a lens-shaped drop forms on the adaxial side. The spore is supported by a sterigma with an abscission zone indicated by the dotted area. (b–e) Conceptual model for ballistospore launching, where a spore-shaped particle is launched from a supporting substrate by the capillary–inertial process. The blue (dark) arrow denotes the force exerted on the merged drop by the particle, and the purple (light) arrow denotes the counter-force exerted on the particle. At the point of launching in (d), the net acceleration of the merged drop is zero and the compressive force between the particle and the substrate vanishes. Note that the sterigma is rotated 90° relative to figure 1.

1.1. Energetic model

Ballistospore discharge is powered by the surface energy released upon drop coalescence [1,7,10]. Although initial research has focused on the spherical drop (Buller's drop) at the hilar appendix of the spore [1,7], recent research using better imaging techniques suggests the typical involvement of a second drop [6,11–13], the lens-shaped adaxial drop that spreads longitudinally on the spore surface above the Buller's drop (figure 2a). A typical mature spore is shaped like a prolate ellipsoid, distorted asymmetrically with a flatter adaxial face and a more curved abaxial face along its long axis [2]. The long radius (semi-major axis) of a spore ranges approximately from 1.5 to 15 μm [2,9], while the radius of the full-grown Buller's drop ranges approximately from 0.3 to 10 μm [9]. The Buller's and adaxial drops are formed by the condensation of ambient water vapour, a process facilitated by hygroscopic substances secreted from the spore, e.g. mannitol, which is also known as manna sugar [14,15]. When the Buller's and adaxial drops grow large enough to touch each other, drop coalescence leads to spore launching.

The coalescence-induced launching process is primarily understood in terms of a lumped energetic model that links the kinetic energy of the merged drop to the surface energy released during drop coalescence [6,12,13,16]. Using Buller's drop radius (r_B) as the reference length scale, the released surface energy scales as σr²_B where σ is the liquid–air surface tension, and the kinetic energy scales as ρ_Lr³_Bu²_ci, where ρ_L is the liquid density and u_ci is a characteristic velocity. Equating these two energies, the capillary–inertial velocity is obtained as

1.1

The associated capillary–inertial time is

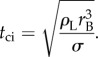1.2

For an aqueous Buller's drop with r_B ∼ 1 μm, u_ci ∼ 10 m s⁻¹ and t_ci ∼ 0.1 μs. Such a high-speed motion is difficult to resolve, especially given the microscopic length scale. As a result, mechanical analogies have been proposed to explain the launching mechanism, ranging from a two-part solid model launched with a stretched elastic band [10] to a ‘hinged’ human body jumping with its internal biochemical energy [12]. The essence of these analogies is a two-stage launching process [6,12]. In the first stage, the drop coalescence converts surface energy to kinetic energy, leading to liquid motion that scales with the capillary–inertial velocity. In the second stage, the momentum of the merged drop is partially transferred to the spore, resulting in the launch of the drop–spore complex that conserves the total momentum. The energetic model along with the two-stage momentum transfer is useful in understanding the self-propelled launching process [6,10,12], especially in explaining the launching speed of the ballistospore [12].

However, the energetic model has limitations. First, an energetic argument cannot explain the launching direction, which is crucial given that the spore must be launched away from supporting structures prior to dispersal in airflows [16–18]. Since the energetic model is insensitive to detailed configurations, prior work largely ignores the role played by the adaxial drop. (The adaxial plane is important in guiding the launching direction, as shown in this paper.) Second, the energetic model typically calculates the launching speed by assuming a perfect capillary–inertial energy conversion, an assumption that does not hold for a related phenomenon of coalescence-induced jumping drops. When pure liquid drops jump upon coalescence, the released surface energy is converted into translational kinetic energy with wide-ranging efficiencies, from 4% to 40% [19–21]. Third, the two-stage launching process outlined above is essentially a rigid-body model and cannot represent the true launching mechanism induced by liquid drop coalescence. In fact, a similar two-stage process has been used to explain the jumping of a nematode worm, a form of locomotion that is also powered by surface energy but hardly resembles the launching of a fungal spore [22,23].

To move beyond the energetic model, we will construct a model system (figure 2) that is conducive to experimental demonstration and numerical simulation. Our work reveals the different roles played by the Buller's drop and the adaxial drop, a pair that is asymmetric in size, shape and relative position: The spherical Buller's drop of smaller radius governs the launching momentum, while the flattened adaxial drop on the spore's adaxial plane governs the launching direction. We then validate these physical insights and discuss the biological implications for ballistospore launching.

2. Model system

We first construct a conceptual model of ballistospore launching. The model simplifies the mechanical role of the sterigma, but otherwise retains the essence of the Buller–adaxial drop coalescence. The conceptual model is experimentally implemented and numerically simulated. The results suggest the association of the point of launching with the instant of peak tangential momentum.

2.1. Conceptual model

Right before spore launch, the sterigma initially supporting the spore develops an abscission zone [24–26], facilitating sterigmal rupture to release the spore at the instant of launching [6,12] (figure 2a). The sterigmal walls dissolve around the abscission zone [26], forfeiting the main structural components that resist tensile loading. However, the sterigma still anchors the spore against bending and twisting, as indicated by the schematics in Miller & Miller [26]. The role of the sterigma in anchoring the spore is supported by published videos showing an apparently still spore prior to its launching [11,12]. Taken together, these observations suggest the sterigma's mechanical role as follows: the sterigma with an abscission zone can anchor the spore and withstand compressive force, but not any significant tensile force.

Given that the sterigma anchors the spore with a weakened tensile strength, how does the Buller–adaxial drop coalescence launch the spore with the precise directionality observed in figure 1? Since the launching direction is strongly correlated with the sterigma's axial direction, which in turn correlates with the tangential direction of the spore's adaxial plane [1,2], the coalescence process should impart a launching momentum to the spore that is predominantly in the tangential direction (essentially along the spore's long axis). The mechanism for imparting the tangential launching momentum is revealed by our model system (figure 2).

In figure 2b–e, the sterigma is replaced with a substrate, and a spore-like particle is launched from the substrate by a two-stage process. In the first stage, a round Buller's drop coalesces with a flattened adaxial drop at its bottom edge. The Buller's drop with a higher Laplace pressure drains towards the adaxial drop, and the merged drop first accelerates upwards as a result (figure 2c). The acceleration of the merged drop eventually turns into deceleration owing to the capillarity of the pinned drop. A zero acceleration corresponds to vanishing compressive force on the substrate and signifies the point of launching (figure 2d), marking the beginning of the second stage. Without any tensile force between the particle and the substrate, the particle is pulled upwards by the decelerating drop, and the drop–particle complex is launched into the air (figure 2e), along the tangential direction of the adaxial plane. (The tangential–normal TN coordinate system is attached to the spore, as in figure 2b.) The launching momentum is ultimately attributed to the impulse provided by the substrate, integrated over the first stage of drop acceleration represented by figure 2c. Although the adaxial drop is depicted as spanning the entire adaxial plane in figure 2b, partial coverage is also possible and the adaxial surface may be somewhat curved [2,6]. The same principle as depicted in figure 2 applies as long as the contact line is pinned at the near edge where Buller–adaxial drop coalescence initiates. The near-edge pinning is a reasonable assumption given the apparent wettability contrast leading to preferential growth on the adaxial (not abaxial) side of the spore.

Building upon existing two-stage models [6,12], our conceptual model accounts for the fluid dynamical process of the asymmetric drop coalescence. The essence of the asymmetric coalescence is captured: the globular Buller's drop has a smaller spherical radius and is placed off-centre to the flattened adaxial drop on the spore surface. Note that the schematics in figure 2b–d imply a fixed (non-rotating) spore, which preserves the sterigmal anchoring. The fixed spore is adopted in the numerical simulations below. For the experimental demonstration in figure 3, we mimic the sterigmal anchoring by placing the model spore at an orientation that minimizes prelaunching rotation.

Figure 3.

Experimental launching process of a spore-shaped particle. The polystyrene spherical cap is launched from a flat superhydrophobic substrate, following the coalescence of two inkjet-printed drops: the Buller's drop with a radius r_B = 104 μm and the adaxial drop with a base radius r_A = 200 μm. The two-stage launching process is demarcated by the point of launching at approximately 0.5 ms. After launching, the particle-drop complex continues to move along the spore's long axis; see also electronic supplementary material, movie S1 for later times.

2.2. Experimental demonstration

Our conceptual model is demonstrated in figure 3. The spore-shaped polystyrene particle is rendered hydrophilic with plasma oxidization, and placed on a superhydrophobic substrate [27] with the long axis pointing upwards. The adaxial drop is first deposited by cumulative inkjet printing on the flat face of the spore, and then the Buller's drop is accumulated on the superhydrophobic surface until coalescence occurs. Further experimental details can be found in electronic supplementary material, section S2. Compared to vapour condensation employed by real ballistospores [14], the inkjet accumulation alleviates the difficulty in capturing live launching processes involving two disparate time scales, the long period for drop accumulation and the short duration for drop coalescence.

The coalescence-induced launching process in figure 3 can be divided into two stages. In the first stage, the Buller's drop is absorbed into the adaxial drop and accelerated upwards. The accelerating drop exerts a compressive force on the particle against the substrate. The upwards acceleration of the drop turns zero (and then negative) at 0.5 ± 0.1 ms, which is the point of launching because no tensile force can be supported between the particle and the substrate. In the second stage that commences at the point of launching, the launched particle continues to move along the flat face (the long axis) of the spherical cap (see electronic supplementary material, movie S1).

A few aspects of the experimental implementation in figure 3 are worth noting. (i) The model particle is much larger than live spores and the characteristic capillary–inertial time in equation (1.2) is much longer, enabling temporal resolution of the launching process. For real ballistospores that are much smaller, high-speed imaging of microsecond resolution is not enough to capture the dynamic coalescence process [11,12]. Apart from the larger scale, the geometrical configuration resembles that in some real ballistospores (e.g. fig. 3D₄ in Webster et al. [6]). (ii) The cap-shaped particle is oriented with its long axis almost perpendicularly to the substrate, minimizing the rotation of the spore prior to launching (see electronic supplementary material, movie S1). Such an initial orientation is critical to the experiment, and the minimal rotation is consistent with the anchoring of a real ballistospore by the sterigma. (iii) A water–ethanol mixture is chosen as the working fluid to facilitate the experiments. The Buller's drop made of 70%vol water is still approximately spherical (superhydrophobic) on the substrate, and there is just enough adhesion to the substrate to prevent any bouncy motion during accumulative printing. In comparison, real Buller's and adaxial drops are aqueous solutions of sugars such as mannitol and hexoses [14,15]. These aspects of the drop–particle system are chosen to facilitate experimentation and are inconsequential to the capillary–inertial coalescence process leading to launching. The Ohnesorge number in figure 3 is approximately 0.04, which is in the capillary–inertial regime as discussed below.

2.3. Numerical simulation

The two-stage launching process inspires numerical simulations that focus on the first stage. The spore is immobile during the first stage, at the end of which the launching momentum is already determined. Therefore, the coalescence is simulated on the flat face of a fixed spore in this paper. Note that the fixed spore preserves the aforementioned sterigmal anchoring in all our simulations.

The interfacial flow is governed by the Navier–Stokes equations described in electronic supplementary material, section S3. The momentum equation for the merged liquid drop reads

2.1

where V is the velocity vector, t is the time, P is the pressure and μ_L is the liquid viscosity. As shown below, the asymmetric Buller–adaxial drop coalescence is governed by the Buller's drop radius, r_B, which is the smaller one of the drop pair. The properties of the Buller's drop are used to non-dimensionalize the momentum equation, e.g. length scales with r_B, stress scales with the capillary pressure σ/r_B, and the coalescence dynamics is governed by the capillary–inertial velocity u_ci and time t_ci. The resulting non-dimensional momentum equation is

2.2

where the dimensionless variables are represented with an asterisk, and the Ohnesorge number is defined as

2.3

When Oh ≪ 1, the system is in the capillary–inertial regime [20], in which the viscous term plays a secondary role and the actual Ohnesorge number has little bearing on the dynamics, as shown below. The nomenclature along with procedures for non-dimensionalization can be found in electronic supplementary material, section S1.

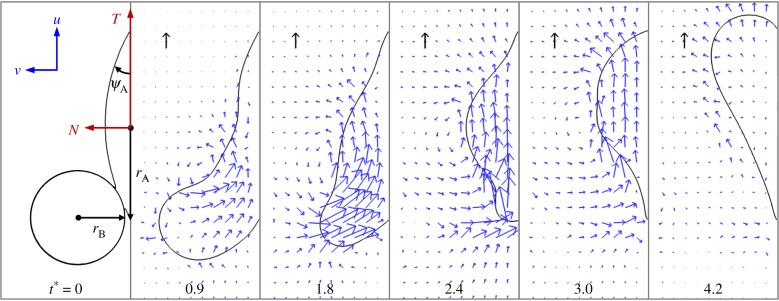
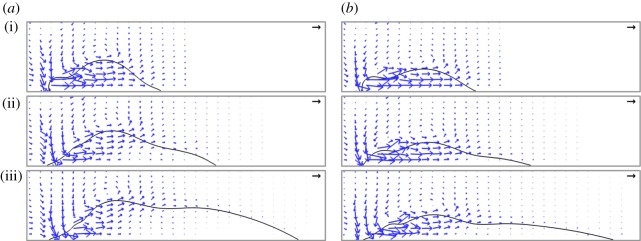
The coalescence process is simulated using the phase-field method [20,28,29] detailed in electronic supplementary material, section S3. The adaxial drop is attached to a flat substrate with a pinned contact line. The pinned area is effectively the wetted adaxial surface of the spore. The Buller's drop is situated tangent to the adaxial drop, with an off-centred configuration resembling the drop position in real ballistospores. The coalescence is initiated by the overlapping of diffuse interfaces in the phase-field implementation. In the three-dimensional (3D) simulations in figure 4 (see electronic supplementary material, movie S2), the relative position and size of the two coalescing drops approximate the experiment in figure 3. The corresponding velocity evolution is shown in figure 5a. Although the Buller's drop has an appreciable normal momentum at the beginning (t^* = 0.9), it is quickly redirected by capillarity to the tangential direction, parallel to the impermeable substrate (t^* = 1.8). When the tangential momentum reaches its peak value (t^* = 2.4), the normal component at that instant is an order of magnitude smaller than its tangential counterpart. Beyond this point, the merged drop swings upwards (t^* = 3.0), until the net tangential momentum reaches a nearly null value with a highly deformed drop (t^* = 4.2). Despite the fact that the spore is fixed in place in the simulations, the numerical results in figure 4 capture the essence of the coalescence process in figure 3, evident in the shape oscillation of the merged drop with respect to the spore.

Figure 4.

Numerical simulation of the coalescence process on a fixed substrate with Oh = 0.0126. The contact line of the adaxial drop is pinned, and the pinned area is effectively the wetted spore surface. The cap-shaped adaxial drop has a base radius r_A (not the spherical radius) given by r_A/r_B = 2. The cap angle of the initial adaxial drop is ψ_A = 30°. The unit velocity vectors (black arrows) represent u_ci and the dimensionless time is indicated by t^* = t/t_ci. See also electronic supplementary material, movie S2 for the entire process.

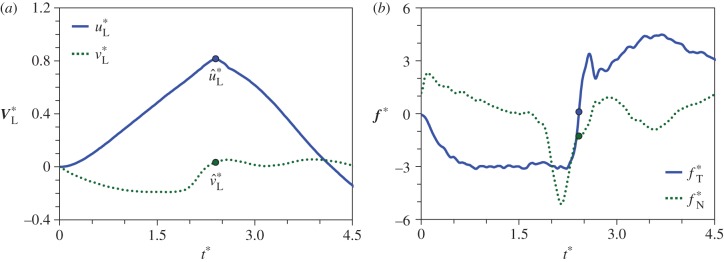
Figure 5.

Velocity and force evolution resulting from the coalescence process depicted in figure 4. (a) The average velocity of the merged drop, V^*_L = V_L/u_ci; and (b) the force exerted on the particle by the merged drop, f^* = f/(σr_B). The tangential and normal components are defined in the TN coordinate system in figure 4. At 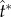(indicated by dots), the point when the tangential momentum peaks and the tangential force vanishes, the tangential velocity 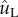is an order of magnitude larger than the normal velocity 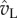. (Online version in colour.)

2.4. Launching condition

In our model, the point of launching coincides with the vanishment of tangential force on the particle (figure 2d). The force exerted on the particle by the merged drop is

2.4

where ℘ is the liquid momentum and V_L is the instantaneous velocity averaged over the entire liquid mass m_L. For the process in figure 4, when the tangential velocity u_L reaches the maximum at 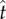(figure 5a), the corresponding tangential force f_T vanishes (figure 5b). At 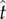, the tangential liquid velocity (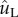) dominates the normal velocity (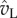). If the particle is mobile, it will be launched beyond 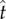, the point of peak tangential momentum.

The point of launching, 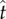, plays a central role in our model. Experimentally, the launching in figure 3 occurs at 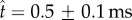or 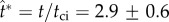, where t_ci = 0.17 ms is calculated using equation (1.2) based on r_B = 104 μm and the liquid properties in electronic supplementary material, section S2. Numerically, the point of peak tangential momentum occurs at 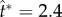in figure 5a. These results agree very well, especially considering the delay in launching caused by the finite adhesion between the coalescing water–ethanol drop and the superhydrophobic substrate. In both experiments and simulations, the merged drop approaches the shape of a spherical cap at the point of launching. Such a round shape is a signature of the pseudoequilibrium configuration [20] in the oscillation process with a zero net acceleration.

Our model adopts the vanishment of tangential force (f_T = 0) as the criterion for launching, and neglects the role of normal force f_N. During the coalescence process leading to launching, the normal force is small compared to the tangential force except for two periods in figure 5b. (i) In the beginning period of the coalescence (t^* = 0 to 0.4) when the normal momentum dominates. The presence of a significant normal force may explain the slight rotation of the spore at the beginning of the coalescence, most clearly seen in electronic supplementary material, movie S1. (ii) In the short period before the point of launching (t^* = 2.0 to 2.4) when the normal momentum quickly vanishes. By then, the tangential momentum is already close to the peak value and is the dominating component (figure 5a). Given the short durations of both periods with a significant f_N, the influence of the normal force on the launching process should be secondary.

2.5. Launching velocity

Figure 4 suggests that the Buller's drop plays an active role in the capillary–inertial coalescence process, and the adaxial drop acts more or less as a passive liquid reservoir. By the time the tangential momentum reaches its peak value in figure 4, the Buller's drop with a mass 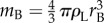has been drained into the adaxial drop at a velocity comparable to the capillary–inertial velocity u_ci, and the merged drop's motion is predominantly in the tangential direction because of capillary and solid confinements. Accordingly, the magnitude of liquid momentum is governed by the Buller's drop, while the direction approximately follows the adaxial plane. At the point of launching (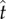), the liquid momentum follows:

2.5

and

2.6

where the hatted variables are evaluated at the point of peak tangential momentum (as in figure 5a), m_L = m_A + m_B is the combined mass of the adaxial drop (m_A) and the Buller's drop (m_B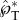), and and 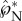are, respectively, the tangential and normal momentum non-dimensionalized by m_Bu_ci.

At the point of launching, the spore–liquid complex acquires the momentum of the merged drop and conserves it afterwards, giving rise to 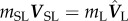, where m_SL = m_S + m_L is the combined spore–liquid mass and V_SL is the centre-of-mass launching velocity. Accordingly,

2.7

where 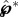is the non-dimensional liquid momentum at the point of launching, and m^* = m_B/m_SL is the ratio of the ‘active’ Buller's drop mass over the combined spore–liquid mass. Note that the ‘passive’ adaxial drop mass only appears in the denominator of this mass ratio through m_SL = m_S + m_A + m_B. With 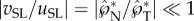, the launching velocity is dominated by the tangential component, u_SL, which can be reduced to

2.8

where the non-dimensional launching velocity (u^*_SL = u_SL/u_ci) is proportional to both the effectiveness of the coalescence-induced momentum generation (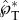) and the mass fraction of the active Buller's drop (m^*).

The capillary–inertial velocity (u_ci) scaling has long been recognized [6,9,10,12,13,16], along with the momentum conservation at the transition of the two-stage launching process [6,12]. Using these ideas, Noblin et al. [12] have calculated the magnitude of the launching velocity with the assumption of perfect capillary–inertial energy conversion. The energy conversion cannot be perfect for any real system because of the inevitable viscous dissipation [20]. Using the simulation in figure 4 as an example, the surface energy released by coalescence is ΔE = 0.77(4πσr²_B), assuming that the merged drop eventually takes the shape of a spherical cap of the same base radius as r_A. If the energetic calculation in the spirit of Noblin et al. is adopted, the useful part of the translational kinetic energy would be given by 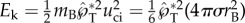, assuming that all the kinetic energy is carried by the Buller's drop as in [12] (in reality, the adaxial drop is also partially mobilized). For such an energetic model to yield the same launching momentum as the numerically simulated value, 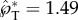(figure 8), an energy conversion efficiency of E_k/ΔE = 48% would need to be assumed. In addition to this quantitative limitation, the scalar energetic model is more fundamentally limited by its inability to predict the launching direction.

Figure 8.

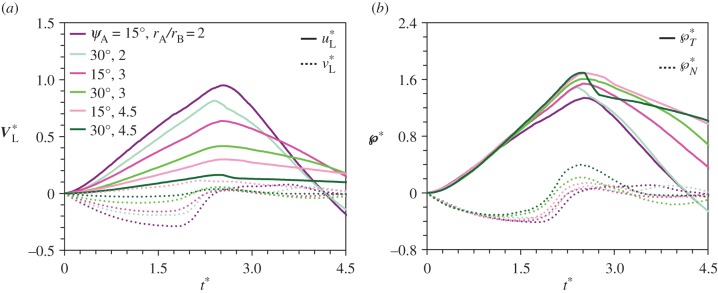
The momentum scaling of the merged drop. (a) The liquid velocity non-dimensionalized as V^*_L = V_L/u_ci. The scatter suggests that the mass-averaged velocity does not follow a naive capillary–inertial scaling. (b) The liquid momentum rescaled as ℘^* = m_LV_L/(m_Bu_ci) = (m_L/m_B)V^*_L. The collapse suggests that the momentum of the merged drop scales with m_Bu_ci. The parametric variations are the same as those in figure 7.

Given the limitations of the energetic model, we shall adopt the more appropriate capillary–inertial momentum scaling in equations (2.5) and (2.6). Our mechanistic model (along with numerical simulations) can accurately predict both the magnitude and direction of the launching velocity with equations (2.7) and (2.8). Indeed, our analysis of the launching velocity is confirmed by the trajectory of the launched particle in figure 3, which is approximately along the long axis of the initial particle, despite an appreciable self-rotation after launching (see electronic supplementary material, movie S1). Such a trajectory is consistent with the predominantly tangential liquid momentum at the point of launching (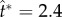 in figures 4 and 5a), which is retained by the launched particle–drop complex. Our mechanistic model is further tested below with numerical parametric variations and available experimental evidence, with a focus on the launching velocity prediction in equations (2.7) and (2.8) and the associated liquid momentum scaling in equations (2.5) and (2.6).

3. Liquid momentum scaling

The asymmetric coalescence of the Buller–adaxial drop pair is crucial to the liquid momentum scaling. For real ballistospores, the approximate range of the Buller's drop radius can be extracted from existing reports, but the parameters related to the adaxial drop are scarcely reported. Using numerical simulations, we now establish that equations (2.5) and (2.6) are applicable in the low-Ohnesorge-number regime, which is mainly governed by the radius of the aqueous Buller's drop. The capillary–inertial momentum scaling in this regime is insensitive to other parameters, as long as the drop pair is asymmetric in size, shape and relative position.

3.1. Capillary–inertial regime

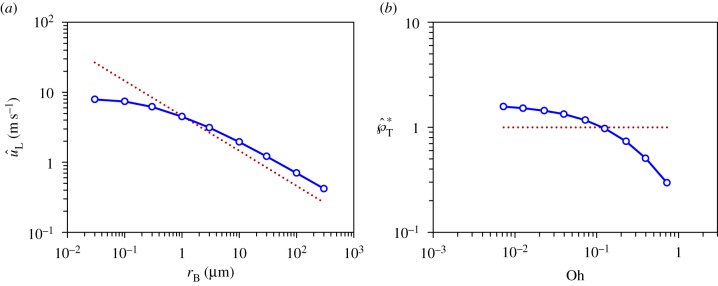
The Buller–adaxial drop coalescence results in the capillary–inertial momentum scaling in equations (2.5) and (2.6). These equations apply as long as the coalescence is in the capillary–inertial regime, signified by a small Ohnesorge number [20]. In figure 6, the Buller's drop radius varies from 0.03 to 300 μm in the 3D simulations, assuming negligible gravitational effects. The average velocity of the merged drop follows the capillary–inertial scaling 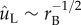at r_B ≥ 0.3 μm. Correspondingly, the non-dimensional tangential momentum 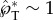at Oh ≤ 0.230, assuming properties of pure water at room temperature. At smaller drop radii, viscous effects become more prominent and the liquid motion no longer follows the capillary–inertial momentum scaling, although launching may still be possible at a reduced speed. The viscous ‘cutoff’ is set at r_B = 0.3 μm with 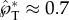, which is approximately half of the value at the small-Ohnesorge-number limit.

Figure 6.

The simulated velocity of the merged drop follows the capillary–inertial scaling (dotted line) in the small-Ohnesorge-number limit. (a) The maximum liquid velocity in the tangential direction 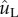as a function of the Buller's drop radius r_B; (b) The non-dimensional peak tangential momentum, 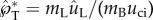, as a function of the Ohnesorge number, 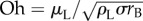. The conditions are the same as those in figure 4 except for the Ohnesorge number which varies with the Buller's drop radius. With pure water as the working fluid, the viscous ‘cutoff’ occurs around r_B = 0.3 μm (Oh = 0.230). At smaller radii, 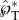is significantly less than unity. (Online version in colour.)

When Oh ≲ 0.2, the drop coalescence is in the capillary–inertial regime according to figure 6, and the specific Ohnesorge number is of little relevance to the scaling of the ensuing liquid momentum. For real ballistospores, the reported range of the Buller's drop radius (r_B) is between 0.3 and 10 μm [9], and the corresponding Ohnesorge number (Oh) is between 0.2 and 0.04 assuming the properties of pure water. Therefore, ballistospore launching is expected to follow the capillary–inertial momentum scaling.

3.2. Asymmetric drop arrangement

Based on published images [6,9,11–13], the drop coalescence is between two asymmetrically arranged drops, a spherical Buller's drop and a flattened adaxial drop that are off-centered to each other. As long as the asymmetric coalescence is in the capillary–inertial regime, the momentum scaling is insensitive to parameters associated with the adaxial drop, including the adaxial cap angle ψ_A, the radius ratio r_A/r_B, and the positioning angle β between the Buller's and adaxial drops. The asymmetric arrangement leads to the capillary–inertial momentum scaling with a dominant tangential component.

The shape and size of the adaxial drop are varied in figures 7 and 8 with different combinations of adaxial cap angle ψ_A and base radius r_A. Note that the conditions for the top case in figure 7a are identical to those in figure 4. For all cases in figure 7, the peak tangential momentum occurs around 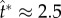, which is essentially the time required to drain the Buller's drop mass over a distance equal to its diameter (t ≈ 2r_B/u_ci = 2t_ci). This observation is consistent with the active role of the Buller's drop. Further, the fluid flow at 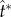is predominantly in the tangential direction. The passive role of the adaxial drop is apparent in the strong similarity in the velocity fields among different adaxial radii (r_A), especially at the near edge where the coalescence initiates. In figure 8a, the average liquid velocity V_L does not simply scale with u_ci. However, the liquid momentum (℘ = m_LV_L) does scale with m_Bu_ci in figure 8b, where the tangential and normal momentum under various conditions each collapse around a single curve. (The divergence after the peak tangential momentum is inconsequential since it is after the point of launching.) For all cases in figure 8b, 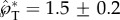while .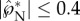

Figure 7.

The velocity fields at the point of peak tangential momentum (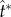): (a) ψ_A = 30°; (b) ψ_A = 15°. At each cap angle ψ_A, the radius ratio r_A/r_B = 2, 3, 4.5 from (i) to (iii), and the corresponding 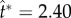, 2.50, 2.48 in (a) and 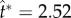, 2.52, 2.56 in (b). The conditions are otherwise identical to those in figure 4, although the orientation is rotated 90°. The unit vectors (black arrows) represent u_ci. See also electronic supplementary material, movies S2–S7. (Online version in colour.)

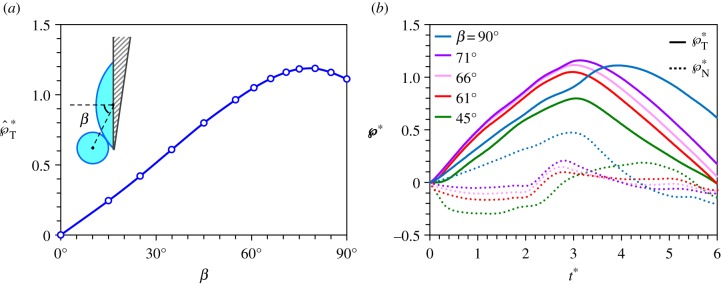
The role of the relative drop position is explored in figure 9 with two-dimensional (2D) simulations (detailed in electronic supplementary material, section S3), which are more versatile than their 3D counterparts in accommodating complex boundary conditions. The positioning angle β varies from 0°, where the symmetric coalescence leads to no net tangential momentum, to 90°, where the Buller's drop centre is on the adaxial plane and the asymmetric coalescence results in a large tangential momentum. As long as the Buller's drop is sufficiently off-centred (β≥ 45° when r_A/r_B = 2 and ψ_A = 30°), the normal momentum is redirected and turned into the tangential momentum, and the asymmetric coalescence ends up imparting a capillary–inertial velocity to the Buller's drop. The resulting peak tangential momentum is a weak function of the relative position with 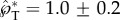(figure 9a), and this launching momentum is predominantly tangential with 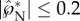(figure 9b).

Figure 9.

Variation of the positioning angle β defined in the inset, using 2D simulations with Oh = 0.0126, r_A/r_B = 2 and ψ_A = 30°. (a) The peak tangential momentum 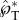as a function of β, indicating that 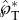is approximately unity for β≥45°. The slight reduction of the launching momentum when β is close to 90° is due to the placement of the Buller's drop past the adaxial plane, leading to a normal momentum initially pointing away from the substrate. (b) Evolution of the tangential and normal momentum for β≥45°, indicating the dominance of the tangential component. This is the only figure adopting 2D simulations in order to accommodate large β angles. The 2D results are slightly different in magnitude from their 3D counterparts. See also electronic supplementary material, movie S8 with β = 61°.

4. Ballistospore launching velocity

At the point of launching, the liquid momentum is transferred to the spore–liquid complex, giving rise to the launching velocity predicted by equations (2.7) and (2.8). We next validate our model with existing measurements on real ballistospores, and discuss the biological implications of the asymmetric drop coalescence.

4.1. Launching speed and direction

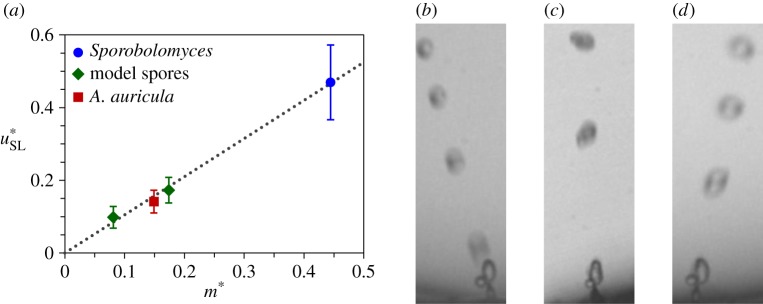
Our insights into the launching speed and direction are verified in figure 10 with experimental data on both live ballistospores and model particles. In terms of the launching speed, there are two data points in Noblin et al. [12] for which both the velocity and the masses can be accurately extracted. These data on Auricularia auricula and Sporobolomyces spores are plotted in figure 10a. The other two measurements in figure 10a are the tangential launching velocities of our model spores. All four data points fall closely onto the prediction of equation (2.8) with 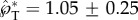. The agreement is remarkable considering that both live and model spores are plotted, and the Buller's drop radius varies by more than an order of magnitude between these two categories. The slight discrepancy in the numerical and experimental 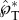may be due to the approximation of the adaxial drop as a perfect spherical cap, implying the unlikely shape of a circular adaxial plane on the spore. Interestingly, the 2D simulations in figure 9 give rise to a peak tangential momentum 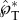that is closer to the experimental value.

Figure 10.

The speed and trajectory of launched ballistospores. (a) The launching velocity of live ballistospores is calculated from the velocities and Buller's drop radii reported in tables 1 and 2 of Noblin et al. [12], and that of spore-shaped particles is extracted from the launching trajectories in electronic supplementary material, movies S1 and S9 using procedures described in electronic supplementary material, section S2 and Liu et al. [30]. The linear fit according to equation (2.8) is 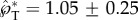, where the uncertainty indicates 95% CI of the fitting coefficient. The calculation of u^*_SL is based on the properties of pure water (fungal spores) or water–ethanol mixture (model spores), both at 20°C. (b–d) The launching trajectories of fungal spores, adapted from supplemental videos 14, 4 and 13 of Pringle et al. [11]. Each trajectory is rotated so that the long axis of the spore is approximately vertical. The trajectories in (b) and (d) represent the maximum deviation from the vertical (tangential) direction found in all videos in Pringle et al. [11], with deviations of 20° (b) and −15° (d). (Online version in colour.)

In terms of the launching trajectory, figure 10b–d are adapted from Pringle et al. [11], confirming that the launching of A. auricula spores is approximately along the long axis. Based on all the supplemental videos in Pringle et al. [11], the launching trajectory is within 20° of the tangential direction of the spore. The observed deviation can be partially attributed to the small normal component of the launching momentum. Numerical simulations in figure 8b suggest that 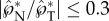, which corresponds to a deviation within 17°. In our experiments, the model spores are also launched approximately along the tangential direction, as long as the spore is carefully oriented to minimize its prelaunching rotation (electronic supplementary material, movies S1 and S9). Additional corroboration for the predominantly tangential launching direction can be found in the trajectories of Itersonilia perplexans spores in fig. 11 of Webster et al. [6], and in the trajectories of A. auricula spores in fig. 3 of Noblin et al. [12].

The numerical work in this paper mainly applies to elongated ballistospores, for which the adaxial surface can be approximated as a plane to first order. Although ballistospores typically adopt a somewhat elongated shape, rounded spores are occasionally encountered [1,2]. The tangential launching along the long axis appears to work well for the relatively elongated spores of I. perplexans and A. auricula, but less well for the more rounded spores of Sporobolomyces yeasts for which the long axis is ill-defined (e.g. fig. 4 of Noblin et al. [12]). Interestingly, the launching speed of the Sporobolomyces spore still follows the momentum scaling in equation (2.8).

4.2. Role of asymmetric coalescence

In the capillary–inertial regime, the asymmetric drop coalescence offers an intriguing division of roles in the generation of launching momentum: the Buller's drop in the form of a liquid globule ensures effective release of its surface energy to impart a substantial momentum, while the adaxial plane of the solid spore (covered with a flattened drop) orients the launching direction.

In terms of the effectiveness of momentum generation, the asymmetric coalescence not only releases a large fraction of the surface energy stored on the Buller's drop, but also converts a large portion of the released surface energy into translational kinetic energy. The effective conversion is evident in the dominance of translational over oscillatory motion at the point of launching (figure 4). Such a dominance gives rise to 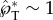, which is impressive considering that the capillary–inertial velocity is about the best attainable in self-propelled motion powered by surface energy. The effectiveness will be significantly reduced if the drop coalescence is symmetric instead, as shown in a related capillary–inertial colloidal catapult where the merged drop has a predominantly oscillatory motion [31].

In terms of the robustness of directional control, the predominantly tangential launching direction (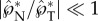) is insensitive to parametric variations, as long as the asymmetry in size, shape and position is preserved (e.g. with r_A/r_B ≳ 2, ψ_A ≲ 30° and β ≳ 45°). Such insensitivity is important given the natural variations in the drop/spore shape and the associated wettability across thousands of ballistospore species. Although the Buller's drop is well documented, the adaxial drop is insufficiently studied. With the model system represented by figure 3, we have experimentally observed the spore-shaped particle to launch with different adaxial cap angles ψ_A (see electronic supplementary material, movies S1 and S9). The observed insensitivity corroborates the conclusion that the adaxial drop plays a passive role in the asymmetric coalescence, but the adaxial plane guides the launching direction. Note that the asymmetry plays a critical role in the launching directionality, evident in figure 4 with the initially normal momentum turning into the eventually tangential one. Without the asymmetry, e.g. when the coalescence is between symmetric drops [31], it will not be possible to create a launching momentum that is tangential to the solid surface supporting the drops.

Our model simplifies the role of the sterigma and translates it into an anchoring support that cannot withstand any tensile force, thereby ignoring the finite rupture force between the mature spore and the sterigma. By implicitly accounting for the sterigmal anchoring with a fixed spore in our simulations, we have focused on the role of the asymmetric drop coalescence in producing tangential launching momentum. Further work is needed to differentiate the roles of the two solid components with strongly correlated directions—the spore with an adaxial plane and the sterigma with a longitudinal axis.

5. Concluding remarks

Integrating simulations and experiments, we have elucidated the capillary–inertial mechanism of ballistospore discharge arising from the asymmetric coalescence of a round Buller's drop and a lens-shaped adaxial drop. During coalescence, the Buller's drop drains towards the adaxial drop and is redirected by capillary and solid confinements, such that the merged liquid acquires a predominantly tangential momentum along the longitudinal axis of an elongated spore. The peak tangential momentum of the merged liquid is approximately given by the Buller's drop mass multiplied by the capillary–inertial velocity based on the Buller's drop radius. After the tangential momentum peaks, the decelerating liquid exerts a tensile force to pull the spore away from the sterigma. The launched spore–liquid complex retains the peak liquid momentum and follows a trajectory along the adaxial plane of the initial spore.

The ballistospore launching mechanism is analogous to a cannon. The rapid capillary–inertial coalescence process quickly releases the surface energy accumulated by the much slower condensation, providing the high power required to launch small projectiles [32]. The high quality of the ballistospore ‘cannon’ is reflected in the large tangential momentum (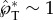) as well as the accurate directional control (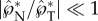). In equation (2.8), the speed of the ballistospore ‘projectile’ (u^*_SL) is largely determined by the relative quantity of ‘ammunition’ (m^*), which is proportional to the mass of the active Buller's drop. Consistent with the need to maximize m*, the spherical Buller's drop is much more prominent compared to the flattened adaxial drop, so much so that A. H. R. Buller focused exclusively on this globular drop, which was eventually named after him.

The asymmetric Buller–adaxial drop arrangement ensures that a ballistospore achieves effective momentum generation and robust directional control by a division of roles: the Buller's drop in the form of a liquid globule is used to maximize the release and conversion of surface energy, while the adaxial plane of the solid spore (covered with a flattened drop) is responsible for robustly orientating the launch. By distinguishing the two key functions of ballistospore launching, momentum generation and directional control, our mechanistic model offers a general mechanical framework to study the morphological and kinematic diversity of ballistospores. Beyond fungal biology, our work on the capillary–inertial catapulting mechanism has broader implications for both biology and engineering, such as ballistic launching systems for small projectiles [32–34] and self-cleaning systems for colloidal contaminants [31,35,36].

Data accessibility

Electronic supplementary material is available online.

Author's contributions

C.-H.C. conceived the project. F.L., R.L.C., J.J.F. and C.-H.C. designed the research. F.L. conducted simulations and R.L.C. performed experiments. All authors analysed data and wrote the paper. F.L. and R.L.C contributed equally to this work.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Science Foundation (CBET-1236373 and DMR-1121107) and the National Institute of Health (T32-GM008555). S.N.P was supported by the National Science Foundation (IOS-1439850). A.P. was supported by the Human Frontier Science Program. J.J.F. was supported by the Natural Sciences and Engineering Research Council of Canada.