Stiffness distribution in insect cuticle: a continuous or a discontinuous profile?

H Rajabi; M Jafarpour; A Darvizeh; J-H Dirks; S N Gorb

doi:10.1098/rsif.2017.0310

. 2017 Jul 19;14(132):20170310. doi: 10.1098/rsif.2017.0310

Stiffness distribution in insect cuticle: a continuous or a discontinuous profile?

H Rajabi ^1,^✉, M Jafarpour ², A Darvizeh ², J-H Dirks ³, S N Gorb ¹

PMCID: PMC5550976 PMID: 28724628

Abstract

Insect cuticle is a biological composite with a high degree of complexity in terms of both architecture and material composition. Given the complex morphology of many insect body parts, finite-element (FE) models play an important role in the analysis and interpretation of biomechanical measurements, taken by either macroscopic or nanoscopic techniques. Many previous studies show that the interpretation of nanoindentation measurements of this layered composite material is very challenging. To develop accurate FE models, it is of particular interest to understand more about the variations in the stiffness through the thickness of the cuticle. Considering the difficulties of making direct measurements, in this study, we use the FE method to analyse previously published data and address this issue numerically. For this purpose, sets of continuous or discontinuous stiffness profiles through the thickness of the cuticle were mathematically described. The obtained profiles were assigned to models developed based on the cuticle of three insect species with different geometries and layer configurations. The models were then used to simulate the mechanical behaviour of insect cuticles subjected to nanoindentation experiments. Our results show that FE models with discontinuous exponential stiffness gradients along their thickness were able to predict the stress and deformation states in insect cuticle very well. Our results further suggest that, for more accurate measurements and interpretation of nanoindentation test data, the ratio of the indentation depth to cuticle thickness should be limited to 7% rather than the traditional ‘10% rule’. The results of this study thus might be useful to provide a deeper insight into the biomechanical consequences of the distinct material distribution in insect cuticle and also to form a basis for more realistic modelling of this complex natural composite.

Keywords: insect cuticle, nanoindentation, material gradient, finite-element method, mechanical behaviour

1. Introduction

Insect cuticle is one of the most complex biological composites. It is known to have a spatial hierarchical architecture, which in the lowest level of hierarchy can be divided into several layers. A simplified insect cuticle traditionally consists of three layers [1]: (i) epicuticle, (ii) exocuticle, and (iii) endocuticle. Epicuticle is the outermost layer that is usually thin and has a cement-like chitin-lacking structure [2]. The other two layers, in contrast, have lamellar organizations and contain chitin [3]. Exocuticle is a stiff and highly sclerotized layer [4]. The sublayers in the exocuticle are dense and they usually form a three-dimensional (3D) helicoidal configuration [5]. Endocuticle, however, is less dense, softer, more hydrated and often resilin-bearing [6,7].

Depending on its concrete location on the insect body and its function, cuticle may have different chemical composition, thickness and layer configurations. The cuticle of the galeal wall of the moth Deilephila elpenor, for example, has an additional layer beside those mentioned before [8]. This layer, known as mesocuticle has a porous microstructure [9]. Such a layer can also be found in the cuticle of wing veins in Odonata [6]. However, the mesocuticle in the veins is unusually located between two exocuticle layers. In other arthropods, such as ticks, different layering of cuticle was previously reported. One good example is the cuticle of the mite Tydeus sp. (Tydeidae). The epicuticle in this species is exceptionally thick and does not fit the typical thickness profile of an insect cuticle [10].

Recently, the development and application of new microscopy techniques have helped to understand several aspects of insect cuticle histology and morphology. Confocal laser scanning microscopy (CLSM) allows the differentiation between the strongly, weakly and non-sclerotized chitinous materials [7,11,12]. Nano- and micromechanical testing methods allow researchers to measure material properties of micrometre-sized cuticle samples [1,13,14]. These studies indicate a large variation in the stiffness along the thickness of the cuticle. However, the quality and quantity of these variations are still largely unknown.

So far, two main hypotheses regarding the distribution of stiffness in insect cuticle can be found in the literature. According to the first one, the stiffness distribution through the thickness of the cuticle should be approximated as a gradient with a continuous increase from the softest (inside) to hardest (outside) layer [11,15]. The second hypothesis states that the stiffness is best represented using a discontinuous profile [16,17]. The discontinuity in this profile occurs at the interface of the layers. Which one is the correct model?

The limited thickness of cuticle samples and their fast desiccation rate make it still very difficult to verify the validity of either of the above two hypotheses by means of direct measurements. Hence, a possible way to answer this question is to numerically test both models and analyse the best fit. In this study, we developed sets of finite-element (FE) models based on the gula cuticle of the beetle, Pachnoda marginata, the elytra cuticle of the dung beetle, Copris ochus (Motschulsky), and the sternal cuticle of the locust, Locusta migratoria. The three mentioned cuticles generally show a typical pattern of epi-, exo- and endocuticle, except the last example which also includes a mesocuticle layer. These cuticles were selected based on their relatively well-studied microstructure and mechanical behaviour. We assigned several different stiffness profiles to these geometric models to simulate their mechanical behaviour subjected to nanoindentation. The aim was to find the vertical distribution of stiffness that results in the most accurate predictions of the mechanical behaviour compared to the available experimental data. The different layered structures and thickness ratios of individual layers in the selected species demonstrate the sensitivity of our models to variations in the geometric parameters and also enable us to test the general validity of the hypothesized stiffness profiles.

2. Material and methods

2.1. Stiffness profiles

To test the different stiffness gradient hypotheses, we developed an ABAQUS (v. 6.14) user-subroutine (USDFLD) with seven gradients of stiffness along the thickness direction of insect cuticle models. The tested stiffness gradients had either a continuous (C) or a discontinuous (DC) profile.

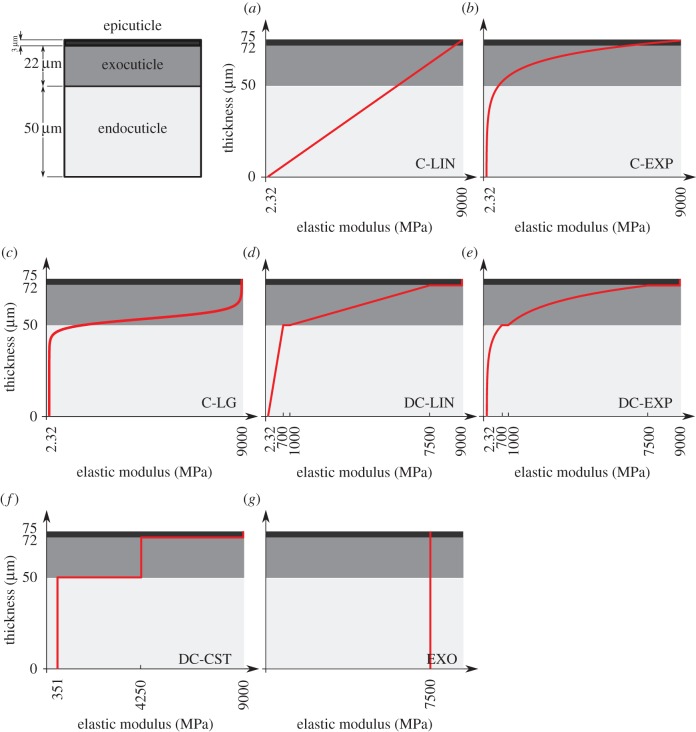
When considering a continuous stiffness profile, three functions were derived. The first one in this group represents a continuous linear stiffness profile increasing from a minimum elastic modulus at the innermost level (zero thickness) of the model to a maximum elastic modulus at its outermost level (figure 1a, C-LIN). The following function was employed to define the distribution of the elastic modulus along the thickness

2.1

where E(t) is the stiffness function and t is the thickness of the cuticle model. A and B are the rate of change of the elastic modulus along the thickness and the elastic modulus of the innermost level, respectively.

The second stiffness profile has a continuous exponential growth (figure 1b, C-EXP). The exponential function describing the variation of stiffness along the thickness in this profile is

2.2

Here, C and D are constants and can be determined by substituting the values of the maximum and minimum elastic moduli in the above equation.

A generalized continuous logistic function was used to define the variation of the stiffness in the third profile (figure 1c, C-LG). This function can be expressed in the following form [18]:

2.3

In the above equation, F and G are the lower and upper asymptotes, respectively. These two parameters can be determined using the minimum and maximum values of the elastic modulus, respectively; H and J characterize the magnitude of the elastic modulus in the inflection point and the position of this point along the thickness, respectively; I is the growth rate of the stiffness function; and K is the shape parameter.

Three other stiffness gradients were developed by considering discontinuous profiles with discontinuities at the interface of layers in the cuticle. The first and second profiles in this category have linear (figure 1d, DC-LIN) and exponential (figure 1e, DC-EXP) stiffness gradients through each of their single layers, respectively. Although the distribution of the stiffness in individual layers in any of these two profiles has the same functional form (linear/exponential), they have their own distinct functions with a set of certain parameters. In the third stiffness profile (figure 1f, DC-CST) belonging to this category, each layer has an elastic modulus, which remains constant across the thickness of that layer. The modulus assigned to each layer is different from those of other layers and its value depends on the material composition of the layer itself.

In addition to the stiffness gradients mentioned above, we developed another stiffness profile which is fully based on the material properties of the exocuticle (figure 1g, EXO). In this stiffness profile, the material properties, including the stiffness, were taken to be constant through the thickness. The stiffness was chosen to be equal to the elastic modulus of the exocuticle (§2.3).

2.2. Geometric models

The stiffness profiles developed in the previous section were assigned to FE models made based on the geometry of cuticles of three different species. The first geometric model is a model of the gula cuticle of the beetle P. marginata. The gula of P. marginata is formed by a typical cuticular structure consisting of three layers [1]: (i) an outermost cement-like epicuticle layer with a thickness of about 3 µm, (ii) a dense and relatively thick, 22 µm, exocuticle, and (iii) an innermost thicker, 50 µm, endocuticle layer. The same thickness as that of the gula cuticle, 75 µm, was assigned to the geometric model of this cuticular structure (see the sketch in the top-left corner of figure 1). The other dimensions of the model were also considered to be equal to 75 µm, forming a cube-shaped structure (figure 2a).

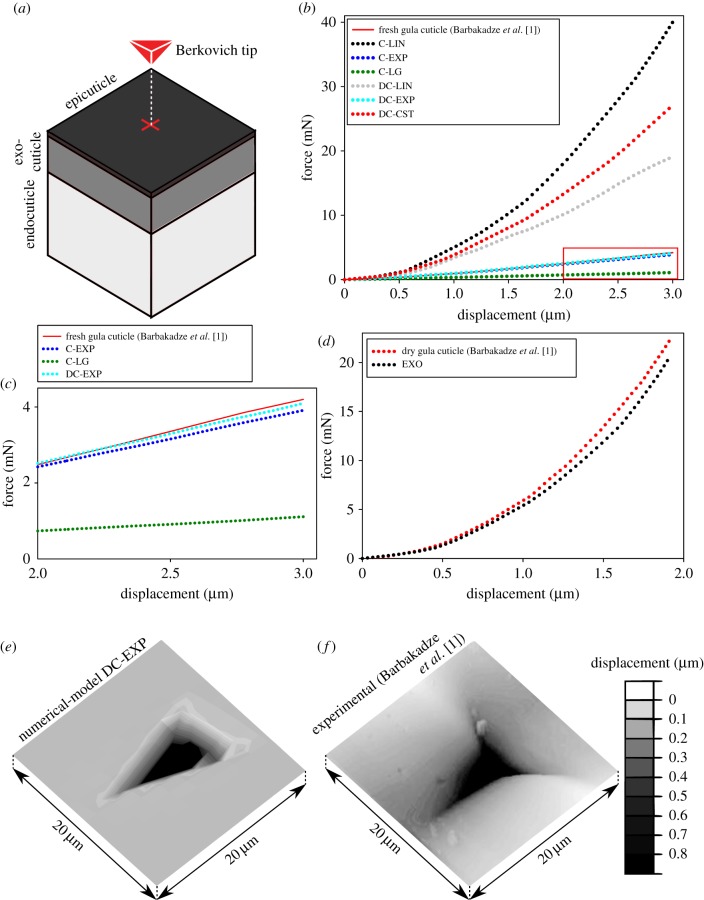
Figure 2. — Comparison of the results obtained from nanoindentation tests [1] and those from numerical simulations of the same experiment on the geometric model of the gula cuticle of the beetle *P. marginata*. (a) A schematic view of the FE model of the gula cuticle, the layers within the model, the Berkovich tip and the location of the applied force. (b) Comparison of force–displacement curves obtained from nanoindentation tests on the fresh gula cuticle (red line) and the models with a continuous linear (C-LIN), a continuous exponential (C-EXP), a continuous logistic (C-LG), a discontinuous linear (DC-LIN), a discontinuous exponential (DC-EXP) and a discontinuous constant (DC-CST) stiffness profile. (c) A magnified view of the force–displacement curves obtained from the experiment and numerical analysis of the models with C-EXP, DC-EXP and C-LG stiffness profiles. A very good agreement can be seen between the experimental data and those from the stiffness profile DC-EXP. (d) A good agreement is seen between the force–displacement curves obtained from nanoindentation tests on the desiccated gula cuticle [1] and the model made up of only exocuticle (EXO). (e,f) Plastic deformations of the gula cuticle model with the stiffness profile DC-EXP and the fresh cuticle sample. There is a good agreement between the deformed shapes and the maximum permanent deformations of the model and the gula cuticle subjected to the same imposed displacement.

When assigning a continuous stiffness profile to this model (figure 1a–c), the minimum and maximum values of the elastic modulus were chosen to be equal to the minimum value of that of the innermost layer (endocuticle) and the maximum value of that of the outermost layer (epicuticle), respectively. The logistic function (C-LG), compared to the linear (C-LIN) and exponential ones (C-EXP), has more parameters. Therefore, as an additional constraint, we set the position of the inflection point at the interface of the exocuticle and endocuticle layers. The magnitude of the elastic modulus at this point was assumed to be equal to the average of the maximum and minimum values of the elastic modulus of the endocuticle and exocuticle, respectively. We have chosen the growth rate and the shape parameter of the stiffness function in a way to reach the widest possible distribution of the elastic modulus across the thickness, while still satisfying the constraints mentioned before.

In the discontinuous stiffness profiles, when considering either a linear (figure 1d, DC-LIN) or an exponential (figure 1e, DC-EXP) gradient within each single layer, the parameters of the stiffness function were obtained using the maximum and minimum values of the elastic modulus of that layer. In DC-CST, which has a constant distribution of the elastic modulus within individual layers (figure 1f), the elastic moduli were taken as the average of the maximum and minimum values of the elastic modulus of those layers.

The stiffness gradients proposed in this study were also applied to two more cuticular structures with different layer configurations from that of the gula cuticle. One is the elytra cuticle of the dung beetle C. ochus (Motschulsky) [19]. With an average overall thickness of 65 µm, this cuticle consists of epi-, exo- and endocuticle layers, which can reach thicknesses up to 17.5 µm, 12.5 µm and 35.0 µm, respectively (see the sketch in the bottom-right corner of figure 3). It can be seen that, compared to the cuticle of the gula, the elytra cuticle has a relatively thick epicuticle whose thickness exceeds the thickness of the exocuticle.

Figure 3. — The experimental and numerical force–displacement curves of the elytra cuticle of the dung beetle *C. ochus* subjected to nanoindentation. The numerical results are given for different stiffness profiles. The best predictions were obtained from the analysis of the model with a discontinuous exponential stiffness profile (DC-EXP). The sketch in the bottom-right corner of the figure shows the comparative thickness of the layers and the location of the applied force.

Another geometric model was developed based on the sternal cuticle of the locust L. migratoria. According to the data reported by Klocke & Schmitz [13], in addition to the three common cuticular layers, there is a layer of mesocuticle in the cuticle of the sternal plate (figure 4f). The layers forming the sternal cuticle from the outermost to the innermost layer are (i) an epicuticle with a thickness of 1.0–1.5 µm, (ii) an exocuticle with a thickness of 3–5 µm, (iii) a mesocuticle with a thickness of 15–22 µm, and (iv) an endocuticle with a thickness of 15–22 µm. The stiffness gradients were assigned to the elytra and sternal cuticle models by the same method used for the gula cuticle.

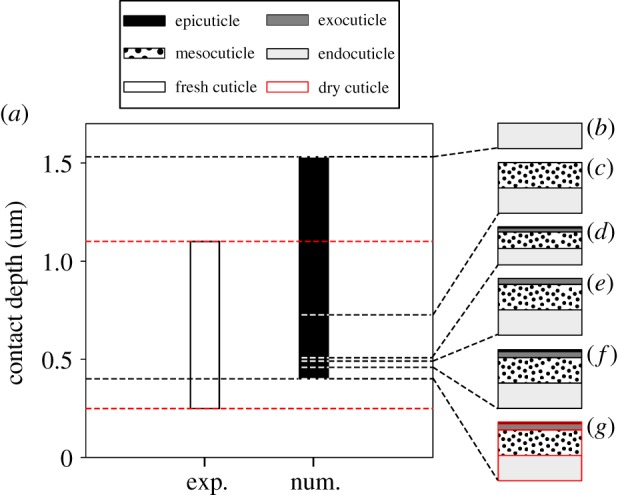
Figure 4. — (a) Comparison of the experimental and numerical results representing the indentation depths of the samples of the sternal cuticle of the locust *L. migratoria* under an indentation force of 1 mN. (b–g) Similar to the experiments [13], the developed models were considered to have different thicknesses, layer configurations and levels of desiccation. The sternal cuticle has four layers: epicuticle, exocuticle, mesocuticle and endocuticle. The total thickness of the layers in an intact sternal cuticle may vary between 34 µm (d) and 50.5 µm (f). The models in (b), (c) and (e) were developed by removal of some of the layers from the sternal cuticle. The model of the desiccated sternal cuticle is presented in (g). The numerical results are given for the model with a discontinuous exponential stiffness profile (DC-EXP). (Online version in colour.)

The developed geometric models were meshed using C3D20R elements, which are general-purpose quadratic twenty-node continuum elements. A second-order interpolation scheme resulted in an excellent performance of this type of elements. On the other hand, the use of reduced integration remarkably reduced the computational cost when these elements were employed.

2.3. Material properties

Most of our recent knowledge of the mechanical properties of insect cuticle is based on a limited number of experimental studies [20–23]. The currently available data indicate large variations in such properties. The variations in the reported data may come from several factors, including variations in humidity [11,21,22], measurement site [11] and even the used testing methods [24]. Here, we focus on the most recent data from the literature, in order to complete our models.

It is known that the development of highly localized normal and shear stresses, which is the case in our simulations, may result in the plastic deformation of insect cuticle [24,25]. Hence, here an elastic–perfectly plastic material model was used to simulate the mechanical behaviour of the cuticle under loading. To predict the onset of yielding, the von Mises criterion was employed. Based on this criterion, yielding occurs when the von Mises stress in an element of the model equals or exceeds the yield strength of the cuticle [26].

The results obtained from previous experimental studies indicate that the elastic modulus of the exocuticle may vary between 1.0 GPa and 7.5 GPa [1,21]. The variation in the reported data is much smaller for the epicuticle with an elastic modulus of about 9.0 GPa [1]. However, the variation of the elastic modulus is more pronounced for the endocuticle, ranging from 2.32 MPa to 700 MPa [13,21,27]. In contrast, there are comparatively few data in the literature regarding the material properties of the mesocuticle. The empirical data suggest the stiffness of the mesocuticle to be about 850 MPa [13]. This value corresponds to the elastic modulus of the mesocuticle of the rewetted sternal cuticle from the locust Locusta migratoria.

Based on the data from the measurements on fresh tibia of the locust Schistocerca gregaria, insect cuticle was assumed to have a yield strength of 72 MPa [22,28]. However, considering the effect of desiccation on the material properties of insect cuticle, the yield strength of the dried cuticle was chosen to be 85 MPa [28]. The Poisson's ratio of the cuticle was taken as 0.3 [29].

Table 1 lists the stiffness functions developed using the above-mentioned material properties.

Table 1.

Stiffness functions assigned to the geometric models developed based on the gula cuticle of the beetle P. marginata, the elytra cuticle of the dung beetle C. ochus (Motschulsky) and the sternal cuticle of the locust L. migratoria. The units of stiffness and thickness are MPa and µm, respectively.

		stiffness function
stiffness gradient	model description	gula cuticle	elytra cuticle	sternal cuticle^a
C-LIN	a continuous linear stiffness profile through the thickness of the model	E(t) = 119.97t + 2.32	E(t) = 138.43t + 2.32	—
C-EXP	a continuous exponential stiffness profile through the thickness of the model	E(t) = 2.32e^0.11t	E(t) = 2.32e^0.13t	—
C-LG	a continuous logistic stiffness profile through the thickness of the model	E(t) = 2.32 + ((8997.68)/(1 + 9.61e^−0.47t))	E(t) = 2.32 + ((8997.68)/(1 + 9.61e^−0.75t))	—
DC-LIN	a discontinuous stiffness profile with linear distributions of stiffness through the thickness of individual layers			—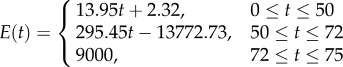
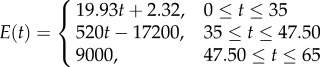DC-EXP	a discontinuous stiffness profile with exponential distributions of stiffness through the thickness of individual layers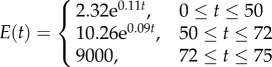
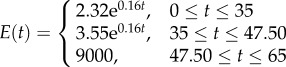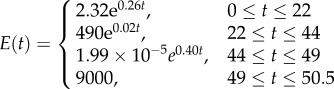DC-CST	a discontinuous stiffness profile with constant distributions of stiffness through the thickness of individual layers			—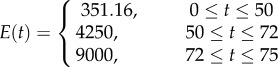
EXO	a constant stiffness profile the same as that of the exocuticle	E(t) = 7500	—	—

Open in a new tab

^aThe absence of information regarding the indentation depths of the test specimens made it impossible to provide a detailed comparison between the different stiffness profiles in the case of the sternal cuticle. Therefore, we present only the discontinuous exponential stiffness profile (DC-EXP) for this model. The stiffness function is given for the geometric model having a thickness of 50.5 µm.

2.4. Loading and boundary conditions

After assigning the appropriate material properties, an implicit analysis was carried out to simulate the nanoindentation tests conducted on the cuticle of the three mentioned insect species [1,13,19]. Similar to the experiments, simulations were performed by applying a concentrated force on the top surface of the models by means of a Berkovich indenter (figure 2a). For this purpose, the rigid indenter was placed at the centre of the model surface. Considering the fact that simulations were performed to replicate the experimental results, either a force or a displacement boundary condition was imposed on the indenter. The magnitude of the displacement/force applied to the models were also set to be equal to those applied to the cuticle samples in the experiments as follows: 3 µm displacement on the fresh gula cuticle [1], 1.9 µm displacement on the dried gula cuticle [1], 255 nm displacement on the elytra cuticle [19] and a force of 1 mN in the case of the sternal cuticle [13].

We used a surface to surface contact pair to constrain the penetration of the indenter into the models. On the other side, the displacements and rotations of the bottom surface of the models were fixed in all directions. A mesh convergence analysis was conducted, in each simulation, to find the suitable mesh size resulting in reasonably accurate results. All simulations were performed by consideration of geometric nonlinearity to capture the effect of potential large displacements during the indentation.

3. Results

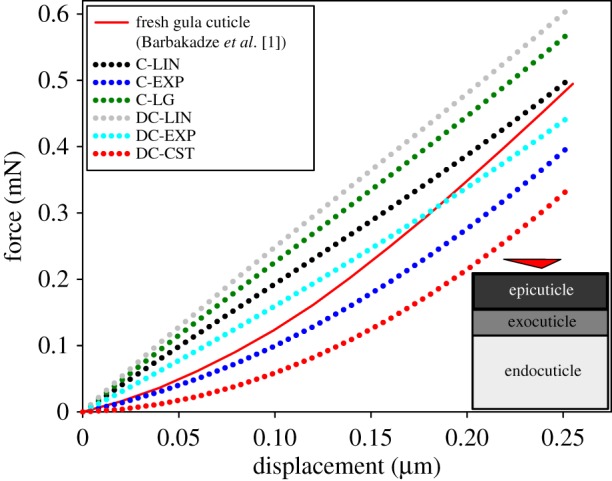
The results from the numerical simulation of the nanoindentation test on the geometric model of the gula cuticle of P. marginata with different stiffness profiles are shown in figure 2. As illustrated in figure 2b, the force–displacement curves of the continuous linear (C-LIN), continuous logistic (C-LG), discontinuous linear (DC-LIN) and discontinuous constant (DC-CST) stiffness profiles do not represent the results of the experiment on the fresh cuticle sample very well. In contrast, the results obtained from the exponential gradients of stiffness (C-EXP and DC-EXP) are found to closely match with the experimental data (figure 2c). When, for example, predicting the force required for a 3 µm displacement (as used in the experiments by [1]), the continuous stiffness profile (C-EXP) results in a mean absolute error of 87.2 µN. This error is lower for the discontinuous stiffness profile (DC-EXP), giving a mean absolute error of 39.9 µN. Figure 2c shows a detailed view of the force–displacement curves of these two stiffness profiles and that of the experiment. The mean and maximum absolute errors in the predicted force obtained from the analysis of all the developed stiffness profiles assigned to the geometric model of the gula cuticle are listed in table 2. It can be seen that the continuous linear profile (C-LIN) gives the worst prediction with a mean absolute error of 12.2 mN.

Table 2.

Mean and maximum absolute errors of the predicted force values measured for the different stiffness gradients assigned to the geometric models of the gula cuticle of the beetle P. marginata and the elytra cuticle of the dung beetle C. ochus.

	gula cuticle		elytra cuticle
stiffness gradient	mean absolute error (µN)	maximum absolute error (µN)	mean absolute error (µN)	maximum absolute error (µN)
C-LIN	12.2 × 10³	35.8 × 10³	43.3	70.2
C-EXP	87.2	29.1 × 10¹	40.6	89.1
C-LG	13.1 × 10²	30.9 × 10²	82.3	11.1 × 10¹
DC-LIN	58.5 × 10²	14.9 × 10³	10.6 × 10¹	14.0 × 10¹
DC-EXP	39.9	10.3 × 10¹	23.8	45.5
DC-CST	82.9 × 10²	22.9 × 10³	83.1	15.3 × 10¹

Open in a new tab

The force–displacement graph obtained from the model of the gula cuticle with a constant distribution of material properties (EXO) is presented in figure 2d. Interestingly, the mechanical response of this model to the nanoindentation is found to be in a good agreement with that of the desiccated cuticle. Both numerical and experimental curves in this figure have nearly the same shape and slope. The mean absolute error of the model in prediction of the force required for 1.9 µm is estimated to be less than 0.8 mN.

Figure 2e shows the permanent deformation of the gula model with the discontinuous exponential stiffness profile (DC-EXP) after removal of the load. Based on the numerical results, the maximum plastic deformation of the gula cuticle is 818 nm. This prediction is in very good agreement with the results from the experiments indicating a permanent deformation of about 847 nm under the same imposed displacement. A good accordance can also be observed between the shape of the deformed regions in the model and the test sample illustrated in figure 2e and f, respectively.

The force–displacement curves obtained from the FE simulation of the nanoindentation test on the geometric model of the elytra cuticle of the dung beetle C. ochus are given in figure 3 and compared with that of the experiment. The numerical curve is plotted for a displacement up to 255 nm, as used in the experiment [19]. As can be seen here, similar to the geometric model of the gula cuticle, the continuous and discontinuous exponential stiffness profiles (C-EXP and DC-EXP) are found to result in the best predictions of the mechanical behaviour of the elytra cuticle. In comparison to the continuous exponential stiffness profile (C-EXP), the model with the discontinuous exponential stiffness profile (DC-EXP) still leads to more accurate results (table 2). The mean absolute error of the numerically predicted force obtained from C-EXP and DC-EXP stiffness profiles are found to be 40.6 µN and 23.8 µN, respectively.

Figure 4 presents the indentation depths of several geometric models of the sternal cuticle of the locust L. migratoria under an indentation force of 1 mN and compares them with the data from the experimental study performed by Klocke & Schmitz [13]. The developed FE models have different thicknesses, layer configurations and levels of desiccation in accordance with those used in the experiments. Considering the absence of information on the indentation depths of the test specimens, we had no opportunity to examine the accuracy of all the stiffness profiles for the geometric models of the sternal cuticle. Therefore, the example of the sternal cuticle is used here, as an additional case study, only to examine the validity of the discontinuous exponential stiffness profile (DC-EXP). Klocke & Schmitz [13] have reported that, for tested cuticle samples with such different characteristics, the indentation depth ranged between 0.25 µm and 1.10 µm (no force–displacement curve was given by the authors). The numerical results, in contrast, lie between 0.41 µm and 1.53 µm.

The models shown in figure 4d and f were developed based on the characteristics of the fresh sternal cuticle. They contain all the layers of the cuticle; however, their respective thickness was considered to be equal to the minimum and the maximum values measured for the sternal cuticle (34.0 µm and 50.5 µm, respectively) [13]. The indentation depths of these two models are seen to be 0.46 µm (figure 4f) and 0.51 µm (figure 4d). The model presented in figure 4g is similar to that shown in figure 4f, but with the properties of the dried sternal cuticle. This model exhibited the smallest indentation depth in this series of simulations (0.41 µm).

In the next step, similar to the experimental study, the epi-, exo- and mesocuticle layers were removed from the top of the sternal model, one by one (figure 4e, c and b). Compared to the complete model (figure 4f), the removal of epi- (figure 4e), exo- (figure 4c) and mesocuticle (figure 4b) increases the measured indentation depth to 0.50 µm, 0.73 µm and 1.53 µm, respectively.

4. Discussion

Among the developed models in this study, those with continuous and discontinuous exponential distributions of stiffness (C-EXP and DC-EXP) through their thickness were found to represent the mechanical behaviour of insect cuticle with good agreement. Comparing these two stiffness profiles, the discontinuous stiffness profile (DC-EXP) showed a relatively better fit to the experimental data. This finding is of great importance because the discontinuous stiffness profile (DC-EXP) is likely to represent the natural material distribution within the histological layers of insect cuticle. Based on this profile, although the stiffness within each single layer in cuticle microstructure has an exponential gradient, there may be at least one discontinuity at the interface of each two layers. The validity of this stiffness profile can be verified by the data reported in several previous studies indicating a microscopically distinguishable border between the layers in insect cuticle [30,31]. Such a border can also be seen between the colours in CLSM images of cross sections of dragonfly wing veins, showing the layers with different levels of sclerotization [6].

The distribution of stiffness is hypothesized to strongly influence the functionality of insect cuticle. Referring to figure 1e, it can be seen that the mean value of the elastic modulus in the stiffness profile DC-EXP is somewhat shifted to the upper levels. This supports that the epi- and exocuticle in this profile are considerably stiffer than the endocuticle. In a previous study, we showed that the presence of a stiff cover can protect the insect exoskeleton against mechanical damage and wear [32,33]. Such stiff layers in the cuticle may also provide a better active controllability and stability during locomotion [34]. On the other hand, the presence of a soft core has been suggested to improve the dynamic behaviour of the cuticle by increasing its damping ratio and, therefore, avoiding unwanted oscillations [32]. The soft endocuticle may also prevent the transmission of mechanical stress to internal structures of the insect body, protecting inner organs from damage.

The proposed presence of material discontinuities at the interface of cuticle layers may be a strategy to prevent or reduce crack propagation. In a single layer structure (composed of only one material), a propagating crack encounters no potential barrier and would be able to traverse the whole thickness [35]. However, such material discontinuities may arrest the crack propagation and prevent the progress of the crack from one layer to another one. A similar mechanism has already been found in some multilayered biological composites, such as nacre [36]. The presence of material gradients within single layers, on the other hand, may serve as a mechanism that avoids sudden changes of the stiffness at the interfaces and, therefore, minimizes stress concentrations.

The observed nonlinearity in the force–displacement curves illustrated in figure 2 may arise from three sources: (i) the inhomogeneous stiffness distribution through the thickness of the models, (ii) the use of a geometric nonlinear analysis, and (iii) material plasticity. The former may lead to the displacement of the softest level in each model prior to the others. Subsequently, the other softer levels are displaced before the relatively stiffer ones. Such a consecutive displacement results in a continuous change in the slope of the force–displacement curve and, therefore, yields a nonlinear behaviour. The other two factors, in contrast, result in the nonlinear response of the models by including nonlinear terms in the compatibility and constitutive equations.

The robustness of our modelling approach was tested by performing a sensitivity analysis. Using this analysis, we evaluated the effects that resulted from variations in the dimension and material stiffness of the sternal cuticle (figure 4). Although the results showed the expected changes and, therefore, indicated the robustness of the model, a clear difference can be seen between the upper and lower limits obtained from experiments and numerical simulations. In other words, one can notice that the computational results are somewhat up-shifted, compared to the experimental data. This difference may arise from the fact that the experimental measurements were conducted on rewetted cuticle specimens rather than fresh ones. Depending on their water content after rehydration, the rewetted cuticle samples could be stiffer than those in the fresh state. Klocke & Schmitz [13] have also indicated that the values of the elastic modulus obtained in their study were considerably higher than those reported by other researchers [20,21], providing additional support for our hypothesis.

Previous studies showed that desiccation may remarkably influence the material properties of insect cuticle [21,22]. It has also been suggested that a dried endocuticle exhibits mechanical properties similar to those of the exocuticle [11,34]. These observations can be verified by our numerical results indicating that the gula cuticle model with constant material properties the same as those of the exocuticle (EXO) exhibited a displacement in agreement with that of the desiccated cuticle subjected to nanoindentation (figure 2d). Considering this and our previous study on the dynamic behaviour of insect cuticle [33], we may suggest that the stiffness profile EXO can be potentially employed to predict the mechanical behaviour of dried cuticle samples.

The results obtained from tensile tests on insect wings suggested that the mechanical behaviour of insect cuticle up to fracture can be approximated by a linear elastic material model [22]. Our previous numerical studies have also demonstrated the validity of such an assumption [32,33,37–40]. However, consideration of material plasticity is expected to have a crucial role in the realistic prediction of the stress state in insect cuticle subjected to the localized forces due to indentation [25]. This may consequently influence the displacement of the models. The good agreement observed between the experimental and numerical results in this study leads us to suggest that an elastic–perfectly plastic material model could be successfully employed to simulate the mechanical behaviour of insect cuticle subjected to localized stresses.

In this study, we used the von Mises stress criterion to predict the onset of yielding in our models. This criterion captures the overall shear stress in the material, which leads to the movement of dislocations and consequently causes yielding. Considering that yielding in insect cuticle may also occur by the same mechanism, the use of the von Mises criterion seems to be a reasonable choice.

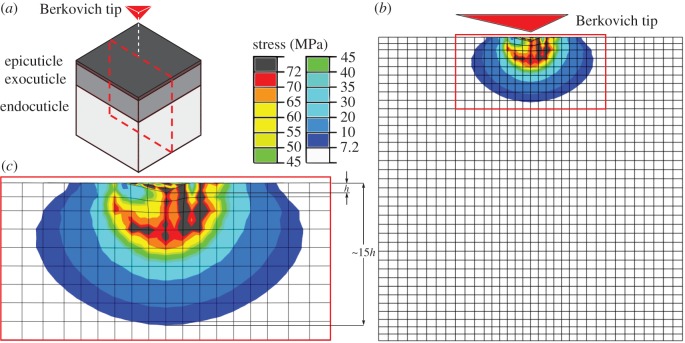
When performing an indentation test on a thin specimen mounted on a substrate, indentation measurements may be influenced by the mechanical properties of the substrate [41]. Previously, it has been suggested that, for a thin film, the influence of the substrate on the results obtained from an indentation test can be eliminated if the indentation depth does not exceed 30% of the film thickness [42]. Although later it was shown that the indentation depth at which the substrate has no significant influence on indentation measurements may vary with several parameters [43], its value is often recommended to be less than 10% of the thickness of the specimen [44]. Our computational analyses, however, suggest that the traditional ‘10% rule’ [41] may be only valid for homogeneous specimens. We have seen that, when performing an indentation test, the use of specimens with different stiffness gradients might change the stress field in the indentation zone. For example, looking at the shear stress beneath the indenter in the geometric model of the gula cuticle illustrated in figure 5 (and electronic supplementary material, video S1), one can notice a high stress concentration in this region. As can be seen here, in this model having an exponential stiffness gradient, in a depth of almost 15 times the indentation depth, the stress is one-tenth of the material yield strength. This level of shear stress is still high enough to cause the influence of the substrate on indentation results when the test specimen is not thicker than 15 times the indentation depth. This finding suggests a more conservative limit of almost 7% (one-to-fifteenth), rather than the 10% rule, which should be applied to the ratio of the indentation depth to the specimen thickness when indenting insect cuticle.

Figure 5. — (a) A scheme of the gula cuticle of the beetle *P. marginata*. (b) Distribution of the von Mises stress in a section of the gula cuticle with a discontinuous exponential stiffness gradient (DC-EXP). The stress is shown in the section shown by the dash line in (a). (c) A high stress concentration can be seen in the region beneath the indenter. In a depth of almost 15 times the indentation depth (h), the stress is still one-tenth of its maximum value.

5. Conclusion

This article presents the first numerical simulation of a nanoindentation test on insect cuticle. We use a combination of a continuous/discontinuous stiffness distribution, an elastic–perfectly plastic material model and a geometric nonlinear analysis to numerically simulate the mechanical behaviour of the cuticle from three insect species. The results from computational models with a discontinuous stiffness profile, but exponential stiffness gradients within individual layers were found to be in very good qualitative and quantitative agreement with the previous experimental data. The models with the mentioned stiffness profile were capable of predicting both stress distribution and deformation pattern (elastic and inelastic) of insect cuticle. Taking into account that direct experimental measurements on fresh cuticle samples of different organisms, not just insects, are still very challenging, the results of this study may provide a foundation for future numerical studies exploring the design principles underlying the functioning of the cuticle.

Acknowledgements

The authors would like to thank Prof. David Taylor (Trinity College Dublin) for his helpful comments during this study. We also appreciate the kind support of Mr Mohammad Rezasefat (Iran University of Science and Technology) in the beginning of this study.

Data accessibility

All supporting data are made available either in the article or the electronic supplementary material. The FE models can be made available on request: please contact HR at hrajabi@zoologie.uni-kiel.de; harajabi@hotmail.com.

Authors' contributions

H.R., J.-H.D. and S.N.G. designed the study. H.R., A.D., J.-H.D. and S.N.G. coordinated the study. H.R. and M.J. conducted the research and analysed the data. H.R. wrote the manuscript. H.R., M.J., J.-H.D. and S.N.G. reviewed the manuscript and contributed to its revision. All the authors discussed the results and gave their final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This study was financially supported by ‘Federal State Funding at Kiel University’ to H.R. The authors also acknowledge financial support by Land Schleswig-Holstein within the funding programme Open Access Publikationsfonds. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.

References

1.Barbakadze N, Enders S, Gorb S, Arzt E. 2006. Local mechanical properties of the head articulation cuticle in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae). J. Exp. Biol. 209, 722–730. ( 10.1242/jeb.02065) [DOI] [PubMed] [Google Scholar]
2.Neville AC. 1975. Biology of the arthropod cuticle. Berlin, Germany: Springer. [Google Scholar]
3.Weis-Fogh T. 1960. A rubber-like protein in insect cuticle. J. Exp. Biol. 37, 889–907. [Google Scholar]
4.Hopkins TL, Kramer KJ. 1992. Insect cuticle sclerotization. Annu. Rev. Entomol. 37, 273–302. ( 10.1146/annurev.en.37.010192.001421) [DOI] [Google Scholar]
5.Andersen SO. 1979. Biochemistry of insect cuticle. Annu. Rev. Entomol. 24, 29–59. ( 10.1146/annurev.en.24.010179.000333) [DOI] [Google Scholar]
6.Appel E, Heepe L, Lin CP, Gorb SN. 2015. Ultrastructure of dragonfly wing veins: composite structure of fibrous material supplemented by resilin. J. Anat. 227, 561–582. ( 10.1111/joa.12362) [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Michels J, Gorb SN. 2012. Detailed three-dimensional visualization of resilin in the exoskeleton of arthropods using confocal laser scanning microscopy. J. Microsc. 245, 1–16. ( 10.1111/j.1365-2818.2011.03523.x) [DOI] [PubMed] [Google Scholar]
8.Hepburn HR. 1985. Structure of the integument. In Comprehensive insect physiology, biochemistry and pharmacology, vol. 3 (eds Kerkut GA, Gilbert LI). New York, NY: Pergamon Press. [Google Scholar]
9.Schmitz A, Gebhardt M, Schmitz H. 2008. Microfluidic photomechanic infrared receptors in a pyrophilous flat bug. Naturwissenschaften 95, 455–460. ( 10.1007/s00114-008-0344-5) [DOI] [PubMed] [Google Scholar]
10.Brody AR. 1969. Comparative fine structure of acarine integument. J. N. Y. Entomol. Soc. 105–116. [Google Scholar]
11.Peisker H, Michels J, Gorb SN. 2013. Evidence for a material gradient in the adhesive tarsal setae of the ladybird beetle Coccinella septempunctata. Nat. Commun. 4, 1661 ( 10.1038/ncomms2576) [DOI] [PubMed] [Google Scholar]
12.Michels J, Appel E, Gorb SN. 2016. Functional diversity of resilin in Arthropoda. Beilstein J. Nanotechnol. 7, 1241–1259. ( 10.3762/bjnano.7.115) [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Klocke D, Schmitz H. 2011. Water as a major modulator of the mechanical properties of insect cuticle. Acta Biomater. 77, 2935–2942. ( 10.1016/j.actbio.2011.04.004) [DOI] [PubMed] [Google Scholar]
14.Sample CS, Xu AK, Swartz SM, Gibson LJ. 2015. Nanomechanical properties of wing membrane layers in the house cricket (Acheta domesticus Linnaeus). J. Insect Physiol. 74, 10–15. ( 10.1016/j.jinsphys.2015.01.013) [DOI] [PubMed] [Google Scholar]
15.Filippov AE, Matsumura Y, Kovalev AE, Gorb SN. 2016. Stiffness gradient of the beetle penis facilitates propulsion in the spiraled female spermathecal duct. Sci. Rep. 6, 27608 ( 10.1038/srep27608) [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Cloudsley-Thompson JL. 1950. The water relations and cuticle of Paradesmus gracilis (Diplopoda, Strongylosomidae). J. Cell Sci. 3, 453–464. [PubMed] [Google Scholar]
17.Riedel F, Vorkel D, Eaton S. 2011. Megalin-dependent yellow endocytosis restricts melanization in the Drosophila cuticle. Development 138, 149–158. ( 10.1242/dev.056309) [DOI] [PubMed] [Google Scholar]
18.Richards FJ. 1959. A flexible growth function for empirical use. J. Exp. Bot. 10, 290–301. ( 10.1093/jxb/10.2.290) [DOI] [Google Scholar]
19.Sun JY, Tong J, Zhou J. 2006. Application of nano-indenter for investigation of the properties of the elytra cuticle of the dung beetle (Copris ochus Motschulsky). IEE Proc. Nanobiotechnol. 153, 129–133. ( 10.1049/ip-nbt:20050050) [DOI] [PubMed] [Google Scholar]
20.Reynolds SE. 1975. The mechanical properties of the abdominal cuticle of Rhodnius larvae. J. Exp. Biol. 62, 69–80. [DOI] [PubMed] [Google Scholar]
21.Vincent JF, Wegst UG. 2004. Design and mechanical properties of insect cuticle. Arthropod Struct. Dev. 33, 187–199. ( 10.1016/j.asd.2004.05.006) [DOI] [PubMed] [Google Scholar]
22.Dirks JH, Taylor D. 2012. Fracture toughness of locust cuticle. J. Exp. Biol. 215, 1502–1508. ( 10.1242/jeb.068221) [DOI] [PubMed] [Google Scholar]
23.Dirks JH, Taylor D. 2012. Veins improve fracture toughness of insect wings. PLoS ONE 7, e43411 ( 10.1371/journal.pone.0043411) [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Parle E, Larmon H, Taylor D. 2016. Biomechanical factors in the adaptations of insect tibia cuticle. PloS ONE 11, e0159262 ( 10.1371/journal.pone.0159262) [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Ebenstein DM. 2011. Handbook of nanoindentation with biological applications. Singapore: Pan Stanford Publishing. [Google Scholar]
26.Budynas RG, Nisbett JK. 2015. Shigley's mechanical engineering design, 10th edn New York, NY: McGraw-Hill. [Google Scholar]
27.Ashby MF, Gibson LJ, Wegst U, Olive R. 1995. The mechanical properties of natural materials. I. Material property charts. Proc. R. Soc. Lond. A 450, 123–140. ( 10.1098/rspa.1995.0075) [DOI] [Google Scholar]
28.Parle E, Herbaj S, Sheils F, Larmon H, Taylor D. 2015. Buckling failures in insect exoskeletons. Bioinspir. Biomim. 11, 016003 ( 10.1088/1748-3190/11/1/016003) [DOI] [PubMed] [Google Scholar]
29.Combes SA, Daniel TL. 2003. Flexural stiffness in insect wings I. Scaling and the influence of wing venation. J. Exp. Biol. 206, 2979–2987. ( 10.1242/jeb.00523) [DOI] [PubMed] [Google Scholar]
30.Barth FG. 1973. Microfiber reinforcement of an arthropod cuticle. Z. Zellforsch. Mikrosk. Anat. 144, 409–433. ( 10.1007/BF00307585) [DOI] [PubMed] [Google Scholar]
31.Singh SS, Jansen MA, Franz NM, Chawla N. 2016. Microstructure and nanoindentation of the rostrum of Curculio longinasus Chittenden, 1927 (Coleoptera: Curculionidae). Mater. Charact. 118, 206–211. ( 10.1016/j.matchar.2016.05.022) [DOI] [Google Scholar]
32.Rajabi H, Shafiei A, Darvizeh A, Babaei H. 2016. Experimental and numerical investigations of crack propagation in dragonfly wing veins. Amirkabir J. Sci. Res. Mech. Eng. 48, 61–63. [Google Scholar]
33.Rajabi H, Shafiei A, Darvizeh A, Dirks JH, Appel E, Gorb SN. 2016. Effect of microstructure on the mechanical and damping behaviour of dragonfly wing veins. R. Soc. Open Sci. 3, 160006 ( 10.1098/rsos.160006) [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Dirks JH, Dürr V. 2011. Biomechanics of the stick insect antenna: damping properties and structural correlates of the cuticle. J. Mech. Behav. Biomed. Mater. 4, 2031–2042. ( 10.1016/j.jmbbm.2011.07.002) [DOI] [PubMed] [Google Scholar]
35.Anderson TL. 2005. Fracture mechanics: fundamentals and applications. Boston, MA: CRC press. [Google Scholar]
36.Barthelat F. 2010. Nacre from mollusk shells: a model for high-performance structural materials. Bioinspir. Biomim. 5, 035001 ( 10.1088/1748-3182/5/3/035001) [DOI] [PubMed] [Google Scholar]
37.Rajabi H, Ghoroubi N, Malaki M, Darvizeh A, Gorb SN. 2016. Basal complex and basal venation of Odonata wings: structural diversity and potential role in the wing deformation. PLoS ONE 11, e0160610 ( 10.1371/journal.pone.0160610) [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Rajabi H, Ghoroubi N, Darvizeh A, Appel E, Gorb SN. 2016. Effects of multiple vein microjoints on the mechanical behaviour of dragonfly wings: numerical modelling. R. Soc. Open Sci. 3, 150610 ( 10.1098/rsos.150610) [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Rajabi H, Darvizeh A, Shafiei A, Taylor D, Dirks JH. 2015. Numerical investigation of insect wing fracture behaviour. J. Biomech. 48, 89–94. ( 10.1016/j.jbiomech.2014.10.037) [DOI] [PubMed] [Google Scholar]
40.Rajabi H, Ghoroubi N, Darvizeh A, Dirks JH, Appel E, Gorb SN. 2015. A comparative study of the effects of vein-joints on the mechanical behaviour of insect wings. I. Single joints. Bioinspir. Biomim. 10, 056003 ( 10.1088/1748-3190/10/5/056003) [DOI] [PubMed] [Google Scholar]
41.Oliver WC, Pharr GM. 2004. Measurement of hardness and elastic modulus by instrumented indentation: advances in understanding and refinements to methodology. J. Mater. Res. 19, 3–20. ( 10.1557/jmr.2004.19.1.3) [DOI] [Google Scholar]
42.ASME. 1979. Standard test method for microhardness of materials ASME designation E384–73, 359–379.
43.Lebouvier D, Gilormini P, Felder E. 1989. A kinematic model for plastic indentation of a bilayer. Thin Solid Films 172, 227–239. ( 10.1016/0040-6090(89)90651-2) [DOI] [Google Scholar]
44.Fischer-Cripps AC. 2000. Factors affecting nanoindentation test data. In Introduction to contact mechanics, pp. 191–192. New York, NY: Springer. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

[RSIF20170310C1] 1.Barbakadze N, Enders S, Gorb S, Arzt E. 2006. Local mechanical properties of the head articulation cuticle in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae). J. Exp. Biol. 209, 722–730. ( 10.1242/jeb.02065) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C2] 2.Neville AC. 1975. Biology of the arthropod cuticle. Berlin, Germany: Springer. [Google Scholar]

[RSIF20170310C3] 3.Weis-Fogh T. 1960. A rubber-like protein in insect cuticle. J. Exp. Biol. 37, 889–907. [Google Scholar]

[RSIF20170310C4] 4.Hopkins TL, Kramer KJ. 1992. Insect cuticle sclerotization. Annu. Rev. Entomol. 37, 273–302. ( 10.1146/annurev.en.37.010192.001421) [DOI] [Google Scholar]

[RSIF20170310C5] 5.Andersen SO. 1979. Biochemistry of insect cuticle. Annu. Rev. Entomol. 24, 29–59. ( 10.1146/annurev.en.24.010179.000333) [DOI] [Google Scholar]

[RSIF20170310C6] 6.Appel E, Heepe L, Lin CP, Gorb SN. 2015. Ultrastructure of dragonfly wing veins: composite structure of fibrous material supplemented by resilin. J. Anat. 227, 561–582. ( 10.1111/joa.12362) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C7] 7.Michels J, Gorb SN. 2012. Detailed three-dimensional visualization of resilin in the exoskeleton of arthropods using confocal laser scanning microscopy. J. Microsc. 245, 1–16. ( 10.1111/j.1365-2818.2011.03523.x) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C8] 8.Hepburn HR. 1985. Structure of the integument. In Comprehensive insect physiology, biochemistry and pharmacology, vol. 3 (eds Kerkut GA, Gilbert LI). New York, NY: Pergamon Press. [Google Scholar]

[RSIF20170310C9] 9.Schmitz A, Gebhardt M, Schmitz H. 2008. Microfluidic photomechanic infrared receptors in a pyrophilous flat bug. Naturwissenschaften 95, 455–460. ( 10.1007/s00114-008-0344-5) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C10] 10.Brody AR. 1969. Comparative fine structure of acarine integument. J. N. Y. Entomol. Soc. 105–116. [Google Scholar]

[RSIF20170310C11] 11.Peisker H, Michels J, Gorb SN. 2013. Evidence for a material gradient in the adhesive tarsal setae of the ladybird beetle Coccinella septempunctata. Nat. Commun. 4, 1661 ( 10.1038/ncomms2576) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C12] 12.Michels J, Appel E, Gorb SN. 2016. Functional diversity of resilin in Arthropoda. Beilstein J. Nanotechnol. 7, 1241–1259. ( 10.3762/bjnano.7.115) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C13] 13.Klocke D, Schmitz H. 2011. Water as a major modulator of the mechanical properties of insect cuticle. Acta Biomater. 77, 2935–2942. ( 10.1016/j.actbio.2011.04.004) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C14] 14.Sample CS, Xu AK, Swartz SM, Gibson LJ. 2015. Nanomechanical properties of wing membrane layers in the house cricket (Acheta domesticus Linnaeus). J. Insect Physiol. 74, 10–15. ( 10.1016/j.jinsphys.2015.01.013) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C15] 15.Filippov AE, Matsumura Y, Kovalev AE, Gorb SN. 2016. Stiffness gradient of the beetle penis facilitates propulsion in the spiraled female spermathecal duct. Sci. Rep. 6, 27608 ( 10.1038/srep27608) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C16] 16.Cloudsley-Thompson JL. 1950. The water relations and cuticle of Paradesmus gracilis (Diplopoda, Strongylosomidae). J. Cell Sci. 3, 453–464. [PubMed] [Google Scholar]

[RSIF20170310C17] 17.Riedel F, Vorkel D, Eaton S. 2011. Megalin-dependent yellow endocytosis restricts melanization in the Drosophila cuticle. Development 138, 149–158. ( 10.1242/dev.056309) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C18] 18.Richards FJ. 1959. A flexible growth function for empirical use. J. Exp. Bot. 10, 290–301. ( 10.1093/jxb/10.2.290) [DOI] [Google Scholar]

[RSIF20170310C19] 19.Sun JY, Tong J, Zhou J. 2006. Application of nano-indenter for investigation of the properties of the elytra cuticle of the dung beetle (Copris ochus Motschulsky). IEE Proc. Nanobiotechnol. 153, 129–133. ( 10.1049/ip-nbt:20050050) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C20] 20.Reynolds SE. 1975. The mechanical properties of the abdominal cuticle of Rhodnius larvae. J. Exp. Biol. 62, 69–80. [DOI] [PubMed] [Google Scholar]

[RSIF20170310C21] 21.Vincent JF, Wegst UG. 2004. Design and mechanical properties of insect cuticle. Arthropod Struct. Dev. 33, 187–199. ( 10.1016/j.asd.2004.05.006) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C22] 22.Dirks JH, Taylor D. 2012. Fracture toughness of locust cuticle. J. Exp. Biol. 215, 1502–1508. ( 10.1242/jeb.068221) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C23] 23.Dirks JH, Taylor D. 2012. Veins improve fracture toughness of insect wings. PLoS ONE 7, e43411 ( 10.1371/journal.pone.0043411) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C24] 24.Parle E, Larmon H, Taylor D. 2016. Biomechanical factors in the adaptations of insect tibia cuticle. PloS ONE 11, e0159262 ( 10.1371/journal.pone.0159262) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C25] 25.Ebenstein DM. 2011. Handbook of nanoindentation with biological applications. Singapore: Pan Stanford Publishing. [Google Scholar]

[RSIF20170310C26] 26.Budynas RG, Nisbett JK. 2015. Shigley's mechanical engineering design, 10th edn New York, NY: McGraw-Hill. [Google Scholar]

[RSIF20170310C27] 27.Ashby MF, Gibson LJ, Wegst U, Olive R. 1995. The mechanical properties of natural materials. I. Material property charts. Proc. R. Soc. Lond. A 450, 123–140. ( 10.1098/rspa.1995.0075) [DOI] [Google Scholar]

[RSIF20170310C28] 28.Parle E, Herbaj S, Sheils F, Larmon H, Taylor D. 2015. Buckling failures in insect exoskeletons. Bioinspir. Biomim. 11, 016003 ( 10.1088/1748-3190/11/1/016003) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C29] 29.Combes SA, Daniel TL. 2003. Flexural stiffness in insect wings I. Scaling and the influence of wing venation. J. Exp. Biol. 206, 2979–2987. ( 10.1242/jeb.00523) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C30] 30.Barth FG. 1973. Microfiber reinforcement of an arthropod cuticle. Z. Zellforsch. Mikrosk. Anat. 144, 409–433. ( 10.1007/BF00307585) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C31] 31.Singh SS, Jansen MA, Franz NM, Chawla N. 2016. Microstructure and nanoindentation of the rostrum of Curculio longinasus Chittenden, 1927 (Coleoptera: Curculionidae). Mater. Charact. 118, 206–211. ( 10.1016/j.matchar.2016.05.022) [DOI] [Google Scholar]

[RSIF20170310C32] 32.Rajabi H, Shafiei A, Darvizeh A, Babaei H. 2016. Experimental and numerical investigations of crack propagation in dragonfly wing veins. Amirkabir J. Sci. Res. Mech. Eng. 48, 61–63. [Google Scholar]

[RSIF20170310C33] 33.Rajabi H, Shafiei A, Darvizeh A, Dirks JH, Appel E, Gorb SN. 2016. Effect of microstructure on the mechanical and damping behaviour of dragonfly wing veins. R. Soc. Open Sci. 3, 160006 ( 10.1098/rsos.160006) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C34] 34.Dirks JH, Dürr V. 2011. Biomechanics of the stick insect antenna: damping properties and structural correlates of the cuticle. J. Mech. Behav. Biomed. Mater. 4, 2031–2042. ( 10.1016/j.jmbbm.2011.07.002) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C35] 35.Anderson TL. 2005. Fracture mechanics: fundamentals and applications. Boston, MA: CRC press. [Google Scholar]

[RSIF20170310C36] 36.Barthelat F. 2010. Nacre from mollusk shells: a model for high-performance structural materials. Bioinspir. Biomim. 5, 035001 ( 10.1088/1748-3182/5/3/035001) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C37] 37.Rajabi H, Ghoroubi N, Malaki M, Darvizeh A, Gorb SN. 2016. Basal complex and basal venation of Odonata wings: structural diversity and potential role in the wing deformation. PLoS ONE 11, e0160610 ( 10.1371/journal.pone.0160610) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C38] 38.Rajabi H, Ghoroubi N, Darvizeh A, Appel E, Gorb SN. 2016. Effects of multiple vein microjoints on the mechanical behaviour of dragonfly wings: numerical modelling. R. Soc. Open Sci. 3, 150610 ( 10.1098/rsos.150610) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20170310C39] 39.Rajabi H, Darvizeh A, Shafiei A, Taylor D, Dirks JH. 2015. Numerical investigation of insect wing fracture behaviour. J. Biomech. 48, 89–94. ( 10.1016/j.jbiomech.2014.10.037) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C40] 40.Rajabi H, Ghoroubi N, Darvizeh A, Dirks JH, Appel E, Gorb SN. 2015. A comparative study of the effects of vein-joints on the mechanical behaviour of insect wings. I. Single joints. Bioinspir. Biomim. 10, 056003 ( 10.1088/1748-3190/10/5/056003) [DOI] [PubMed] [Google Scholar]

[RSIF20170310C41] 41.Oliver WC, Pharr GM. 2004. Measurement of hardness and elastic modulus by instrumented indentation: advances in understanding and refinements to methodology. J. Mater. Res. 19, 3–20. ( 10.1557/jmr.2004.19.1.3) [DOI] [Google Scholar]

[RSIF20170310C42] 42.ASME. 1979. Standard test method for microhardness of materials ASME designation E384–73, 359–379.

[RSIF20170310C43] 43.Lebouvier D, Gilormini P, Felder E. 1989. A kinematic model for plastic indentation of a bilayer. Thin Solid Films 172, 227–239. ( 10.1016/0040-6090(89)90651-2) [DOI] [Google Scholar]

[RSIF20170310C44] 44.Fischer-Cripps AC. 2000. Factors affecting nanoindentation test data. In Introduction to contact mechanics, pp. 191–192. New York, NY: Springer. [Google Scholar]

PERMALINK

Stiffness distribution in insect cuticle: a continuous or a discontinuous profile?

H Rajabi

M Jafarpour

A Darvizeh

J-H Dirks

S N Gorb

Abstract

1. Introduction