Jointly modeling the relationship between longitudinal and survival data subject to left truncation with applications to cystic fibrosis

Abstract

Numerous methods for joint analysis of longitudinal measures of a continuous outcome y and a time to event outcome T have recently been developed either to focus on the longitudinal data y while correcting for nonignorable dropout, to predict the survival outcome T using the longitudinal data y, or to examine the relationship between y and T. The motivating problem for our work is in joint modeling the serial measurements of pulmonary function (FEV1 % predicted) and survival in cystic fibrosis (CF) patients using registry data. Within the CF registry data, an additional complexity is that not all patients have been followed from birth; therefore, some patients have delayed entry into the study while others may have been missed completely, giving rise to a left truncated distribution. This paper shows in joint modeling situations where y and T are not independent, it is necessary to account for this left truncation in order to obtain valid parameter estimates related to both survival and the longitudinal marker. We assume a linear random effects model for FEV1 % predicted, where the random intercept and slope of FEV1 % predicted, along with a specified transformation of the age at death follow a trivariate normal distribution. We develop an EM algorithm for maximum likelihood estimation of parameters, which takes left truncation and right censoring of survival times into account. The methods are illustrated using simulation studies and using data from CF patients in a registry followed at Rainbow Babies and Children’s Hospital, Cleveland, OH.

1. INTRODUCTION

Longitudinal studies and clinical trials are often designed to study changes in a continuous marker, y, over time, estimate the time to a clinical event of interest, T, and/or to analyze the relationship between y and T. The continuous outcome variable, y, is measured repeatedly on each study participant and dropout due to the clinical event of interest causes values of the longitudinal measurement beyond that point to be unobserved or missing. When the probability of dropout is nonignorable, i.e. dependent on unobserved values of y or latent variables related to y, methods analyzing y alone are often biased whereas joint models, if properly specified, provide consistent estimates. Numerous approaches [1–13] have been developed for joint modeling of y and T in this situation and joint modeling continues as an active area of research.

The motivating problem for this work is joint modeling serial measurements of pulmonary function (FEV1 % predicted) and survival in cystic fibrosis (CF) patients using data from a CF registry at Rainbow Babies and Children’s Hospital (referred to as the Case Western Reserve University Cystic Fibrosis database or CWRU CF database) that has captured clinical visit data on all patients seen at the CF center since its inception in the 1950’s. Others [1, 14] have demonstrated a strong relationship between rate of pulmonary function decline and survival or age at death and thus joint modeling assuming a nonignorable relationship between pulmonary function and survival is preferable to methods ignoring information on death when estimating patterns of FEV1 decline in population cohorts. For CF patients, pulmonary function testing is routinely carried out at routine visits, beginning at age 6, the youngest age when this testing can be reliably measured. If a subject does not have pulmonary function measured at age 6, we assume that follow-up for that subject began at the age when their first measurement was obtained. For these subjects with delayed entry into the registry, their information on survival is left truncated in the sense that their follow-up began at the age of first pulmonary function testing rather than birth. To illustrate the degree of truncation in the registry, Figure 1 plots age of first visit with pulmonary function testing against calendar year of birth for the 1272 patients followed in the database. It can be seen that the earlier the patient was born, the more likely entry into the registry is to be delayed, as evidenced by an older age at first test. For example, patients born in the early 1940’s did not have their first pulmonary function test (PFT) recordings on average until age 20, whereas patients born in the 1990’s were recorded on average closer to the earliest possible age, age 6. Thus, the earlier the year of birth, the more severe the left truncation.

Figure 1.

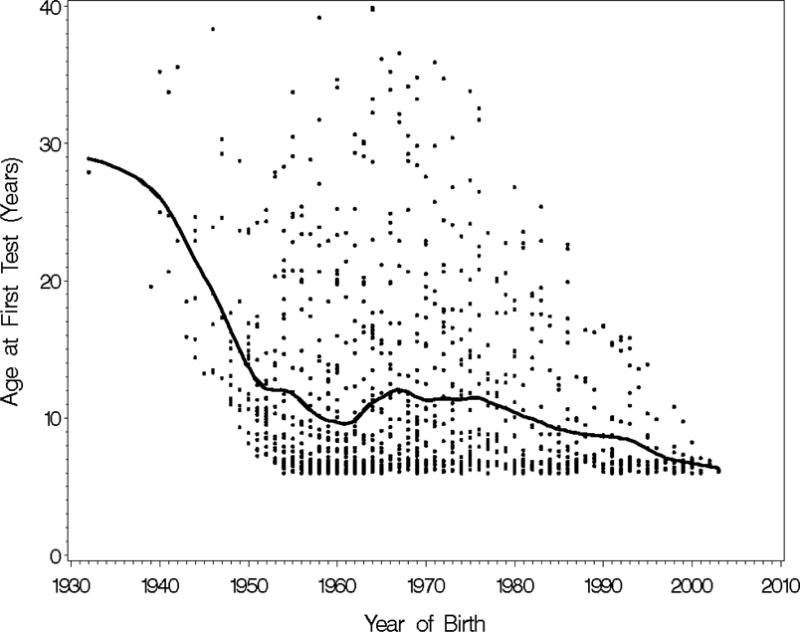
Plot of age of first test vs. year of birth. The black line is a spline curve.

Left truncated survival data occur when, as in the CF registry, follow-up does not begin at time or age 0 for some or all subjects in the sample. The need to account for left truncation in survival data to avoid bias in estimating the survival function or parameters related to survival is well-recognized [15]. However, while numerous joint modeling approaches have been developed assuming nonignorable relationships between y and T, [1–13], none of these methods deal with the additional bias caused by left truncation. We show in this paper that left truncation of survival or time to event must also be accounted for in joint modeling a longitudinal outcome and time to event in order to avoid bias both in the time to event estimates but also in parameters related to y. In particular, in CF registries, left truncation due to delayed entry can result in bias in estimates of rates of decline in pulmonary function as well as in survival estimates.

This paper presents an approach to jointly model longitudinal responses and time to event outcomes while correcting for left truncation and applies the methods to the CWRU CF database. In Section 2, we define the notation and describe the model. In Section 3, we derive an EM algorithm for computing maximum likelihood estimates that accommodates both nonignorable dropout and left truncation. These methods are applied to the CWRU CF database in Section 4. In Section 5, we present a simulation study based on the CWRU CF database, used to examine robustness of the model under various left truncation scenarios. The last section provides a discussion of the conclusions, strengths, and limitations of these methods.

2. MODEL AND NOTATION

Assume we have an observed sample of n subjects followed longitudinally in a registry, and interest is in describing patterns of change in a longitudinal measurement y over time as well as the time to a clinical event. For the CF registry y is FEV1% predicted and the clinical event is death. Assume here that the time scale is age, and let L_i denote the age when the ith subject began to be followed in the registry, where L_i > 0 indicates that follow-up began after birth and thus in the terminology of survival analysis, the subject’s survival data are left-truncated. Also define the left truncation indicator $I_i^{tr}$= 1 if L_i > 0 and $I_i^{tr}$= 0 otherwise. We observe either A_i = age at death, or C_i = age last known alive for the ith patient, along with the indicator δ_i = 1 if the patient died and δ_i = 0 otherwise. Our methods assume that survival ages A_i can be transformed to normality using some known function g(.), i.e. where $T_i^0$ = g(A_i), possibly conditional on covariates, is normally distributed. With the motivating example, the CWRU CF database, we consider a log transformation: g(A_i) = log(A_i) = $T_i^0$, assuming a lognormal distribution for A_i, but other transformations g(A_i) can be used. Similarly, defining C_i = g(C_i) and L_i = g(L_i) and letting T_i = min( $T_i^0$, C_i), the observed information on the transformed scale summarizing survival can be written as {L_i, T_i, δ_i, $I_i^{tr}$, i = 1,…,n). Note that when the log transformation $T_i^0$=log(A_i) is used, L_i = g(L_i) is defined to be −∞ when L_i =0. In addition, let $y_i={(y_{i1},\dots ,y_{i{n}_i})}^{\prime }$ denote the n_i × 1 vector of longitudinal measurements available for the ith subject in the observed sample, with corresponding n_i × 1 vector of measurements times (measured in age (years)), $t_i={(t_{i1},\dots ,t_{i{n}_i})}^{\prime }$.

The joint model we consider is formulated as a two-stage random effects model. The first stage describes the conditional distribution of the longitudinal measurements, y_i, given subject-specific regression random effects, b_i. This is written as:

$$y_i=Z_i{b}_i+e_i$$ (1)

where for i = 1, …, n, b_i is a q × 1 vector of subject-specific regression coefficients, $e_i={(e_{i1},\dots ,e_{i{n}_i})}^{\prime }$ is an n_i × 1 error vector distributed $N(0,{\sigma }_e^2{I}_i)$, and Z_i is an n_i × q known design matrix. When modeling the CF data, we initially assume y_i follows a linear trend with time; in this case, Z_i consists of a first column made up of all 1’s and the second column made up of the times (ages in years) of measurements for subject i, and b_i = (b_i0, b_i1) is the 2 × 1 vector of the unknown intercept and slope random effects.

The second stage of the model assumes that the (q + 1) × 1 random vector ${(b_i,T_i^0)}^{\prime }$ for each subject i = 1,.,n in the sample is a randomly selected observation from the possibly left truncated multivariate normal distribution $f_{bt}\left({(b,t)}^{\prime }|t>L_i;\alpha ,\mathrm{\Omega }\right)$, where the multivariate normal distribution $f_{bt}\left({(b,t)}^{\prime };\alpha ,\mathrm{\Omega }\right)$ is:

$$f_{bt}\left({(b,t)}^{\prime };\alpha ,\mathrm{\Omega }\right)~N\left(\left(\begin{array}{c}{W}_{1i}\\ W_{2i}\end{array}\right)\alpha ,\left(\begin{array}{cc}{\sum }_b& {\sigma }_{bt}\\ {\sigma }_{bt}^{\prime }& {\sigma }_t^2\end{array}\right)\right)=N(W_i\alpha ,\mathrm{\Omega }).$$ (2)

Here, α is a p × 1 vector of fixed effects parameters, and W_i1 (q × p) and W_i2 (1 × p) are known design matrices whose elements may depend on a subject-specific covariate vector w_i, and Σ_b, ${\sigma }_{bt}$, and ${\sigma }_t^2$ are variance and covariance parameters of the joint distribution. Note that when $I_i^{tr}$= 0, $f_{bt}\left({(b,t)}^{\prime }|t>L_i;\alpha ,\mathrm{\Omega }\right)$ is just the untruncated distribution in (2). The covariance parameter ${\sigma }_{bt}$between b_i and $T_i^0$, describes the association between the underlying random effects b_i and $T_i^0$. When ${\sigma }_{bt}$= 0, b_i and $T_i^0$are independent, implying also that y_i and $T_i^0$are independent, and joint modeling is not necessary. When $I_i^{tr}$=0 and δ_i = 0 (no truncation or censoring is present for subject i), or when ${\sigma }_{bt}$ = 0, together stages I and II imply the following marginal distribution of y_i: $y_i\sim \mathrm{N}(Z_i{W}_{1i}\alpha ,Z_i{\sum }_b{Z}_i^{\prime }+{\sigma }_e^2{I}_i)=\mathrm{N}(X_i\alpha ,{\sum }_i)$. Note that we assume throughout that the right censoring times C_i and left truncation times L_i are independent of each other and are non-informative in that, conditional on w_i, they are also independent of b_i, y_i, and $T_i^0$.

3. COMPUTATION OF MAXIMUM LIKELIHOOD ESTIMATES

In this section, we extend an EM algorithm for computation of maximum likelihood estimates of the parameters $(\alpha ,\mathrm{\Omega },{\sigma }_e^2)$ originally developed for the joint model of section 2 without left truncation [5], to incorporate left truncation of survival times. The extension of the EM algorithm to incorporate left truncation follows an approach proposed by Bee [16] for samples from a left-truncated normal distribution. This approach assumes that there are ‘latent’ observations that are unobserved due to the left truncation process, which become part of the hypothetical complete data specified in framing the EM algorithm. The procedure is outlined below; further details and theoretical justification of the approach are provided in Appendix B.

Because L_i and w_i may vary among subjects, we treat each subject as a separate stratum. To formulate the EM algorithm, we assume that for a subject with $I_i^{tr}$=1, the complete data consist of a random sample of m_i + 1 subjects from that stratum, where an unknown number m_i ≥ 0 of subjects had transformed times less than L_i and thus were not included in the observed sample, and the remaining subject with $T_i^0$> L_i is the one observed. If $I_i^{tr}=0$then m_i = 0 by definition. It is shown in Appendix B that the unobserved number of missing subjects, m_i, has a geometric distribution with mean E(m_i)= (1 − p_i)/p_i where $p_i=P(T_i^0>{\mathrm{L}}_{\mathrm{i}})=1-\mathrm{\Phi }[(L_i-W_{2i}\alpha )/{\sigma }_t]$. If m_i > 0, let ${(b_{ij}^{\ast },T_{ij}^{\ast })}^{\prime },j=1,\dots ,m_i$ denote the random vectors of random effects and survival times for the m_i unobserved subjects in stratum i. The EM formulation assumes that for each subject i, ${(b_i,T_i^0)}^{\prime }$ and ${(b_{ij}^{\ast },T_{ij}^{\ast })}^{\prime },j=1,\dots ,m_i$ constitute an independent random sample of size m_i + 1 from the multivariate normal distribution in equation (2).

Thus, to formulate the EM algorithm, the observed data consist of {y_i, T_i, δ_i, $I_i^{tr}$, and L_i, i = 1,…,n} and the complete data consist of b_i, e_i, T_i⁰, m_i, and if m_i > 0, $\{(b_{ij}^{\ast },T_{ij}^{\ast }),j=1,\dots ,m_i\}$, for i = 1, …, n. The observed data log-likelihood can be written as:

$${\text{LL}}_{\text{observed}}(\alpha ,\mathrm{\Omega },{\sigma }_e^2)={\displaystyle \sum _{i=1}^n\ln \{f(T_i,{\delta }_i,y_i}|L_i,I_i^{tr})\}={\displaystyle \sum _{i=1}^n\ln \{f(}{T}_i,{\delta }_i|y_i,L_i,I_i^{tr})\}+{\displaystyle \sum _{i=1}^n\ln \{f(y_i|L_i,I_i^{tr})\}}$$ (3)

A detailed expression for the observed data log-likelihood is shown in the Appendix (equation (A.1.1)). The complete data log-likelihood is simpler, and can be written as:

$${\text{LL}}_{\text{complete}}(\alpha ,\mathrm{\Omega },{\sigma }_e^2)={\displaystyle \sum _{i=1}^n\ln f_{bt}(b_i,T_i^0)}+{\displaystyle \sum _{i=1}^n\ln f_e}(e_i)+{\displaystyle \sum _{i=1}^n{I}_i^{tr}I(m_i>0){\displaystyle \sum _{j=1}^{m_i}\ln f_{bt}(b_{ij}^{\ast },T_{ij}^{\ast })}}$$ (4)

This can be shown to simplify to:

$${\text{LL}}_{\text{complete}}(\alpha ,\mathrm{\Omega },{\sigma }_e^2)=-\frac{1}{2}(n+{\displaystyle \sum _{i=1}^n{m}_i})\log |\mathrm{\Omega }|-\frac{1}{2}tr{\mathrm{\Omega }}^{-1}\left[\begin{array}{cc}{\displaystyle \sum _{i=1}^n{S}_{3i}}& {\displaystyle \sum _{i=1}^n{S}_{5i}}\\ {\displaystyle \sum _{i=1}^n{S}_{5i}^{\prime }}& {\displaystyle \sum _{i=1}^n{S}_{4i}}\end{array}\right]+{{\displaystyle \sum _{i=1}^n\left(\begin{array}{c}{S}_{1i}\\ S_{2i}\end{array}\right)}}^{\prime }{\mathrm{\Omega }}^{-1}{W}_i\alpha -\frac{1}{2}{\displaystyle \sum _{i=1}^n(1+m_i)}{\alpha }^{\prime }{W}_i^{\prime }{\mathrm{\Omega }}^{-1}{W}_i\alpha -\frac{{\displaystyle \sum n_i}}{2}\log ({\sigma }_e^2)-\frac{1}{2{\sigma }_e^2}tr{\displaystyle \sum _{i=1}^n{S}_{6i}}$$ (5)

where S_1i = $b_i+{\displaystyle \sum _{j=0}^{m_i}{b}_{ij}^{\ast }}$, S_2i = $T_i^0+{\displaystyle \sum _{j=0}^{m_i}{T}_{ij}^{\ast }}$, S_3i = $b_i{b}^{\prime }+{\displaystyle \sum _{j=0}^{m_i}{b}_{ij}^{\ast }{b}_{ij}^{\ast \prime }}$, S_4i = ${(T_i^0)}^2+{\displaystyle \sum _{j=0}^{m_i}{(T_{ij}^{\ast })}^2}$, S_5i = $T_i^0{b}_i+{\displaystyle \sum _{j=0}^{m_i}{T}_{ij}^{\ast }{b}_{ij}^{\ast }}$, and S_6i = $tr(e_i{e}_i^{\prime })={\displaystyle \sum _{k=1}^{n_i}{e}_{ik}^2}$, where by definition $T_{i0}^{\ast }=b_{i0}^{\ast }=0.$

The E-step of the EM algorithm calculates the expected values of the complete data log-likelihood (5) conditional on the observed data using current estimates of the parameters. The distribution of the complete data log-likelihood is multivariate normal and thus, is a member of the exponential family. Specifically only for exponential families, the t^th step of the E-step calculates the expected values of the sufficient statistics (i.e., ${\displaystyle \sum _{i=1}^n{S}_{1i}},$ ${\displaystyle \sum _{i=1}^n{S}_{2i}},$ ${\displaystyle \sum _{i=1}^n{S}_{3i}},$ ${\displaystyle \sum _{i=1}^n{S}_{4i}},$ ${\displaystyle \sum _{i=1}^n{S}_{5i}},$ $\text{and}{\displaystyle \sum _{i=1}^n{S}_{6i}}$ in equation (5)), conditional on the observed data and current estimates of the parameters. This is equivalent to finding the expected values, $S_{1i}^{(t)},S_{2i}^{(t)},S_{3i}^{(t)},S_{4i}^{(t)},S_{5i}^{(t)},\text{and}$ $S_{6i}^{(t)}$, where $S_{vi}^{(t)}=E(S_{vi}|y_i,L_i,T_i,{\delta }_i,I_i^{tr};{\alpha }^{(t)},{\mathrm{\Omega }}^{(t)},{\sigma }_e^{2(t)}),$ $\nu =1,\dots ,6,$(see Appendix A.2), conditional on the observed data for subject i, for each i = 1, …, n. As an example, the derivation of $S_{2i}^{(t)}$is shown in Appendix A.2. Expressions for all required expectations in the E-step are also given in Appendix A.2.

The M-step of the EM algorithm finds the values of the parameters α, Ω, and ${\sigma }_e^2$that maximize the complete data log-likelihood given the observed data. Given that the complete data log-likelihood from the E-step follows a distribution that is a member of the exponential family, the M-step computes the new updated parameter estimates in terms of the conditional expected sufficient statistics. Following Schluchter et al. [5], in the M-step, to update the fixed effects contained in α, we calculate the MLE of α assuming that the variance/covariance parameters in Ω are known and equal to Ω^(t). This is the generalized least squares estimate:

$${\alpha }^{(t+1)}={({\displaystyle \sum _{i=1}^n(1+{\widehat{m}}_i^{(t)})W_i^{\prime }}{({\mathrm{\Omega }}^{(t)})}^{-1}{W}_i)}^{-1}{\displaystyle \sum _{i=1}^n{W}_i^{\prime }}{({\mathrm{\Omega }}^{(t)})}^{-1}\left(\begin{array}{c}{S}_{1i}^{(t)}\\ S_{2i}^{(t)}\end{array}\right),$$

where ${\widehat{m}}_i^{(t)}$ is the current estimate of E(m_i). Similarly, assuming α is known and equal to α^(t), the MLE of the unstructured covariance matrix Ω can be calculated as:

$${\mathrm{\Omega }}^{(t+1)}=(n+{\displaystyle \sum _{i=1}^n{\widehat{m}}_i^{(t)})-1}\times \left\{{\displaystyle \sum _{i=1}^n\left(\begin{array}{cc}{S}_{3i}^{(t)}& S_{5i}^{(t)}\\ S_{5i}^{(t)}\prime & S_{4i}^{(t)}\end{array}\right)-{\displaystyle \sum _{i=1}^n{W}_i{\alpha }^{(t)}{\left(\begin{array}{c}{S}_{1i}^{(t)}\\ S_{2i}^{(t)}\end{array}\right)}^{\prime }-}{\displaystyle \sum _{i=1}^n\left(\begin{array}{c}{S}_{1i}^{(t)}\\ S_{2i}^{(t)}\end{array}\right)}{(W_i{\alpha }^{(t)})}^{\prime }+{\displaystyle \sum _{i=1}^n(1+{\widehat{m}}_i^{(t)})W_i{\alpha }^{(t)}{\alpha }^{(t)}\prime W_i^{\prime }}}\right\}.$$

As in Schluchter et al. [5], the M-step estimate of ${\sigma }_e^{2(\mathrm{t}+1)}$ is: ${\sigma }_e^{2(\mathrm{t}+1)}={\displaystyle \sum _{i=1}^n{S}_{6i}^{(t)}/{\displaystyle \sum _{i=1}^n{n}_i}}$.

Standard errors of parameter estimates are obtained via the bootstrap algorithm or numerically. For the latter, we use the SAS IML function NLPFDD, which is a nonlinear optimization method that approximates the derivatives of the observed data log-likelihood numerically using finite differences methods. The estimated Hessian matrix, $H(\widehat{\alpha },\widehat{\mathrm{\Omega }},{\widehat{\sigma }}_e^2)$, the matrix of second derivatives of the observed data log-likelihood, is evaluated at the maximum likelihood estimates, $\widehat{\alpha },\widehat{\mathrm{\Omega }},\text{and}{\widehat{\sigma }}_e^2,$obtained from the EM algorithm. The estimated covariance matrix of the maximum likelihood estimates is then calculated as $-H{(\widehat{\alpha },\widehat{\mathrm{\Omega }},{\widehat{\sigma }}_e^2)}^{-1}$.

4. EXAMPLE-CYSTIC FIBROSIS

As noted in Section 1, the motivating example comes from the Case Western Reserve University Cystic Fibrosis (CWRU CF) database. CF is a lethal, autosomal recessive disease and is most common among Caucasians [17]. We focus here on a measure of pulmonary function, forced expiratory volume in one second (FEV1), measured as a percentage predicted as compared to the average (non-CF) individual of predicted normal based on the patient’s age, gender, and height, referred to as FEV1 % predicted, [18–19]. Specifically, best yearly FEV1 % predicted is the longitudinal measurement for this study and is defined at the highest recording of FEV1 % predicted during a given calendar year for a given patient. Using only best yearly recordings is intended to minimize effects of suboptimal measurements of FEV1 % predicted that may be obtained during periods of acute illness in a given year. Although we could model survival from birth in the CWRU dataset, where all subjects are left truncated with follow-up beginning at age ≥6 years, we instead model survival and FEV1 decline conditional on survival to age 6, avoiding the need to model survival at ages <6 where we do not have information on survival. We therefore took the scale of A_i, C_i and L_i as age in years-6, where only those subjects with first pft at age >6 are considered left truncated ( $I_i^{tr}$=1).

We apply the proposed model to the 1272 patients of the CWRU CF database, divided into 6 birth cohorts, as follows: 1930–49, 1950–59, 1960–69, 1970–79, 1980–89, and 1990–2006. The first two decades when patients were born (1930–39 and 1940–49) and the last two decades when patients were born (1990–1999 and 2000–2006) were combined into respective cohorts (1930–49 cohort and 1990–2006 cohort) because of the small number of patients in the individual decade of birth cohorts. Since survival and degree of left truncation are of primary interest, the descriptive statistics for survival and age when first pulmonary function test (PFT) measurement was obtained for each birth cohort were assessed (Table 1). The difference between the age of first test and age 6 reflects the amount of left truncation within each cohort where the higher the age at first test, the more severe the left truncation. Mean ages at first test in Table 1 indicate the same trend shown in Figure 1, i.e. that earlier birth cohorts tend to have more severe left truncation. In the most recent birth cohort, 1990–2006, only 2 deaths were observed; therefore, survival estimates for this cohort are imprecise, and will not be analyzed separately in this study. The joint model described in Section 2 with correction for left truncation (referred to as JM-C) and the joint model of Schluchter et al. [1], which does not account for left truncation (referred to as JM-UN), were applied to the birth cohorts for comparison.

Table 1.

Survival statistics and age of first PFT by birth cohort.

Birth cohort	Number of subjects	Number of subjects who died	Average age at first test (± std. dev.)
1930–49	47	41	19.35 ± 7.43
1950–59	290	220	11.17 ± 6.19
1960–69	382	276	10.72 ± 7.18
1970–79	238	108	11.27 ± 6.55
1980–89	175	31	9.43 ± 4.72
1990–2006	140	2	7.75 ± 2.61
Total population	1272	678	10.74 ± 6.48

In nearly all birth cohorts, the JM-UN resulted in higher estimates of mean intercept (parameterized as FEV1 % predicted at age 6) and less negative estimates of the slope as compared to estimates from the JM-C model (Table 2 and Figure 2). The difference between the intercept and slope estimates from both models is greater in the earlier birth cohorts, when more patients are left truncated. The JM-UN also resulted in higher estimates of survival as compared to the JM-C, and the difference between the two models was greater in the earlier birth cohorts, where left truncation was more severe or pronounced (Figure 3 and Table 2).

Table 2.

Estimates of intercept (FEV1 % predicted at age 6), slope (% predicted per year), and E( $T_i^0$) (log(years survived from age 6)) from the lognormal joint model with correction for left truncation (JM-C) and the lognormal joint model without correction for left truncation (JM-UN), stratified by birth cohort.

Birth cohort	Intercept estimate (± SE)		Slope estimate (± SE)		E( $T_i^0$) estimate (± SE) (median age at death (yrs))◆
	JM-C	JM-UN	JM-C	JM-UN	JM-C	JM-UN
1930–49	80.63 ± 5.48	87.97 ± 4.26	−3.39 ± 0.46	−2.72 ± 0.22	2.80 ± 0.22 (22.44)	3.21 ± 0.08 (30.78)
1950–59	78.27 ± 1.68	80.04 ± 1.60	−3.04 ± 0.14	−2.76 ± 0.12	2.89 ± 0.06 (23.99)	3.04 ± 0.05 (26.91)
1960–69	81.68 ± 1.55	83.26 ± 1.47	−3.16 ± 0.13	−2.88 ± 0.12	2.80 ± 0.04 (22.44)	2.94 ± 0.04 (24.92)
1970–79	86.18 ± 1.89	88.52 ± 1.81	−2.93 ± 0.17	−2.66 ± 0.14	2.97 ± 0.07 (25.49)	3.13 ± 0.06 (28.87)
1980–89	100.66 ± 2.07	100.97 ± 2.06	−2.36 ± 0.15	−2.32 ± 0.15	3.44 ± 0.12 (37.19)	3.47 ± 0.12 (38.14)
1990–2006	101.19 ± 2.24	101.21 ± 2.23	−1.98 ± 0.23	−1.97 ± 0.23	–	–

^◆median age at death= exp(E( $T_i^0$))+6

Figure 2.

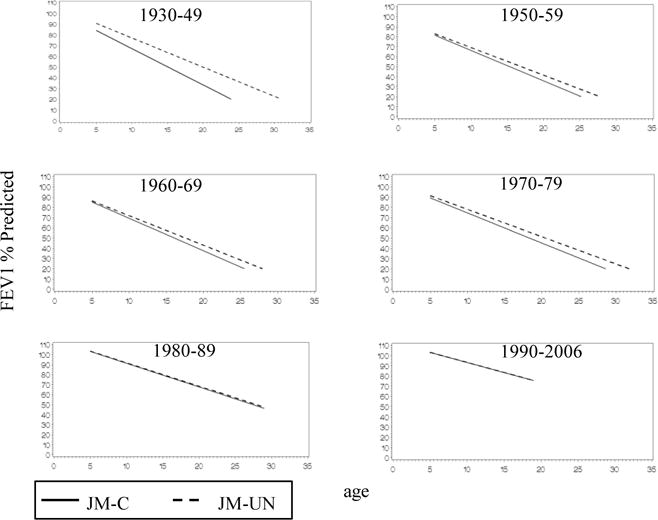
Estimates of the population mean regression of FEV1 % predicted vs. age by birth cohort from the lognormal joint model without correction for left truncation, JM-UN ( ) and from the lognormal joint model with correction for left truncation, JM-C ( ).

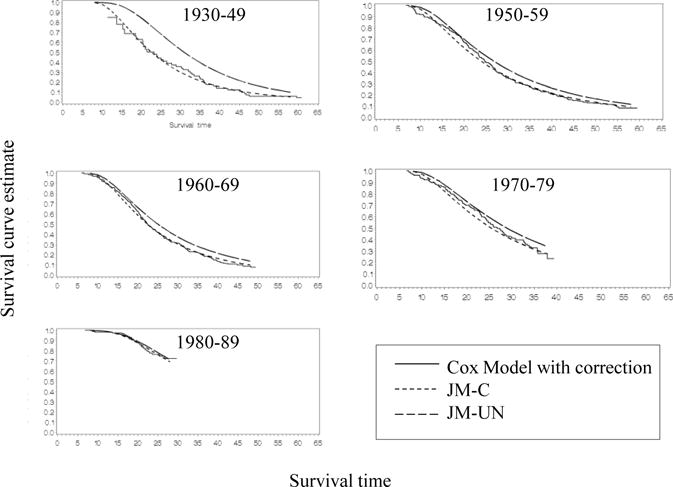
Figure 3.

Survival curve estimates by birth cohort from the lognormal joint model without correction for left truncation, JM-UN ( ), the lognormal joint model with correction for left truncation, JM-C ( ), and the Cox model with correction for left truncation ( ).

The estimates of survival from age 6, obtained from the lognormal joint models (with and without correction for left truncation), were compared to corresponding baseline survival curve estimates from Cox models (obtained with SAS Proc PHREG with and without correction for left truncation using the Entry= option) to assess the fit of the lognormal distribution for survival time. Since the survival curves estimated from the JM-C model agree closely with the corresponding survival curves estimated from the Cox model with correction for left truncation, the assumed lognormal distribution for survival appears to provide a reasonably good fit (Figure 3). The survival curve estimates from the JM-UN model also closely match the survival curve estimates from the Cox model without correction (not shown in Figure 3).

The estimates of intercept and slope of FEV1 % predicted and survival demonstrate the expected cohort effect, where earlier birth cohorts have lower intercepts, steeper slopes, and shorter survival times when compared to the later birth cohorts.

5. SIMULATION STUDIES

Simulation studies were carried out to assess performance of the JM-C model in comparison to the JM-UN model (not correcting for left truncation) under two scenarios. In the first scenario, data were generated from the joint lognormal model (equations 1 and 2), and the second scenario examined performance when the survival data were generated from a misspecified Weibull model. Simulations focused only on estimation of fixed effects terms in the vector α since these are usually of most interest. All simulations used 500 replications, with a sample size of 300 subjects (including unobserved left-truncated subjects).

In the first scenario, the means of the intercept $(b_{i0})$, slope $(b_{i1})$, and survival time $T_i^0$ depended on a continuous N(0,1) covariate $w_i$, as follows: $E(b_{i0}|w_i)={\alpha }_{b_0}+{\alpha }_{b_0|w}{w}_i$, $E(b_{i1}|w_i)={\alpha }_{b_1}+{\alpha }_{b_1|w}{w}_i$, and $E(T_i^0|w_i)={\alpha }_T+{\alpha }_{T|w}{w}_i$. True parameter values, obtained by fitting a no-covariate model to the CF data and by assuming a 10% increase in the means of $b_{i0}$, $b_{i1}$ and $T_i^0$ per one unit increase in $w_i$, were ${({\alpha }_{b_0},{\alpha }_{b_1},{\alpha }_T,{\alpha }_{b_0|w},{\alpha }_{b_1|w},{\alpha }_{T|w})}^{\prime }$ =(108.0, −1.65, 3.60, 10.8, 0.165, and 0.36)’, Σ_b = $\left(\begin{array}{cc}458.00& -18.40\\ -18.40& 2.05\end{array}\right)$, ${\sigma }_t^2=0.26$, ${\sigma }_e^2=105.00$, and ${\sigma }_{bt}=\left(\begin{array}{l}-3.23\\ 0.57\end{array}\right)$. For the second scenario, data were generated from a model where the marginal distribution of y_i was the same as in the first scenario and the conditional distribution of survival age A_i, given $b_{io}$, $b_{i1}$, and the N(0,1) covariate $w_i$, was Weibull rather than lognormal (for details, see Appendix C). As in scenario 1, this model implied that regressions of $b_{i0}$, $b_{i1}$, and $T_i^0$ on $w_i$ were linear where the regression parameters ${\alpha }_{b_0},{\alpha }_{b_1},{\alpha }_{b_0|w},{\alpha }_{b_1|w},\text{and}{\alpha }_{T|w}$were the same as in scenario 1. Estimates of ${\alpha }_T$from the models in scenario 2 were compared to log(33.7) = 3.517, where 33.7 is the median survival time when $w_i$= 0, and $b_{i0}$ and $b_{i1}$ were equal to their conditional means given $w_i$ (Appendix C). Under both scenarios, all survival times > 45 years were right censored. To simulate left truncation, with probability P, subject i was removed from the sample if A_i < L, where all combinations of the probability P =0.20, 0.50, and 0.80 and age at truncation L =10, 20, and 30 years were examined. All subjects, including those with first PFT at age 6, were considered left truncated when fitting the JM-C model.

When data were generated from the assumed lognormal model (scenario 1), the JM-C model performed well, with most parameters estimated with nonsignificant or <5% bias and 95% confidence interval coverages ranging from 92.0% to 96.8% (Table 3). In contrast, the JM-UN model produced negatively biased estimates of the regression coefficients ${\alpha }_{b_1|w}$and ${\alpha }_{T|w}$, and of ${\alpha }_{b_1}$in all cases. Except when left truncation was least severe (P=0.20, L=10), JM-UN estimates of ${\alpha }_{b_0}$were positively biased. As expected, the performance of the JM-UN model worsened as the degree of left truncation increased.

Table 3.

Comparison of % bias and confidence interval coverage (%CI) of parameter estimates from the joint model with correction for left truncation (JM-C) to estimates from the joint model without correction for left truncation (JM-UN). Data generated from lognormal model.

Left Truncation Age	Parameter	True value	Probability of left truncation
			0.2				0.5				0.8
			JM-C		JM-UN		JM-C		JM-UN		JM-C		JM-UN
			%Bias	%CI	%Bias	%CI	%Bias	%CI	%Bias	%CI	%Bias	%CI	%Bias	%CI
10	${\alpha }_{b_0}$	108.0	0.0	92.2	0	92.6	0.1	91.8	0.0	94.2	0.0	92.0	−0.2*	95.6
	${\alpha }_{b_1}$	−1.65	0.1	94.2	−0.6*	94.4	0.4	95.2	−0.9*	92.8	0.0	94.0	−2.0*	93.8
	${\alpha }_T$	3.6	0.0	94.8	0.0	94.6	0.0	96.8	0.1*	91.8	0.0	94.8	0.2*	94.4
	${\alpha }_{b_0|w}$	10.8	−0.2	94.4	0.6	94.4	−0.2	95.6	1.4*	95.6	0.4	95.4	1.2*	94.2
	${\alpha }_{b_1|w}$	0.165	2.5	94.0	−7.3*	94.8	2.0	95.6	−19.6*	92.2	−1.0	94.6	−22.2*	93.2
	${\alpha }_{T|w}$	0.36	0.7	94.4	−2.4*	93.0	0.3	94.8	−5.4*	89.2	0.4	95.2	−7.2*	86.8
20	${\alpha }_{b_0}$	108.0	−0.1	94.4	−0.2*	93.4	−0.2*	93.8	−0.8*	90.0	0.0	94.6	−0.9*	91.4
	${\alpha }_{b_1}$	−1.65	−0.2	96.4	−2.7*	91.0	−0.3	95.8	−8.2*	66.6	0.0	94.6	−12.8*	41.0
	${\alpha }_T$	3.6	0.0	96.2	0.5*	92.2	0.0	94.0	1.4*	65.0	0.0	95.4	2.3*	21.2
	${\alpha }_{b_0|w}$	10.8	0.7	94.2	1.6*	92.6	−0.8	95.0	3.4*	93.2	0.1	95.6	7.4*	92.2
	${\alpha }_{b_1|w}$	0.165	−0.2	95.4	−22.1*	94.0	3.8	94.8	−47.5*	87.0	3.8	94.6	−90.3*	65.2
	${\alpha }_{T|w}$	0.36	0.1	94.4	−5.6*	89.0	0.3	95.0	−−13.8*	65.2	1.4*	96.4	−26.7*	15.2
30	${\alpha }_{b_0}$	108.0	0.1	93.2	0.5*	94.6	0.0	94.2	−1.2*	88.0	0.0	94.4	−2.3*	79.2
	${\alpha }_{b_1}$	−1.65	−0.2	96.0	−5.2*	83.2	−0.3	95.8	−14.1*	31.2	−0.5	94.8	−27.0*	2.0
	${\alpha }_T$	3.6	0.1	96.2	1.1*	80.6	0.1	93.2	3.2*	11.4	0.2*	94.2	5.6*	0.0
	${\alpha }_{b_0|w}$	10.8	−0.7	94.0	0.9	95.6	−0.4	94.0	3.8*	93.8	−1.0	95.4	8.8*	92.2
	${\alpha }_{b_1|w}$	0.165	−0.9	94.4	−15.4*	93.8	−1.4	95.2	−50.2*	87.6	−2.4	94.8	−117.9*	56.0
	${\alpha }_{T|w}$	0.36	0.1	96.2	−2.7*	94.0	−0.2	95.4	−8.6*	82.4	−2.1	93.4	−29.0*	25.2

^*significant bias (p<0.05)

Under scenario 2, results (Table 4) showed that with the exception of estimation of ${\alpha }_T$, the corrected (JM-C) model’s parameter estimates had relatively small percent bias and coverage probabilities ranging from 91–96.4%. Although the JM-C estimates of ${\alpha }_T$had low bias, the confidence interval coverage probabilities were too low. Confidence intervals for ${\alpha }_T$from the JM-UN model also had poor coverage, and the JM-UN model’s estimates of ${\alpha }_{b_1|w}$and ${\alpha }_{T|w}$were negatively biased, with increasing bias and worsening confidence interval coverage as the degree of left truncation increased. The JM-UN estimator of ${\alpha }_{b_1}$was increasingly negatively biased as the degree of left truncation increased.

Table 4.

Comparison of % bias and confidence interval coverage (%CI) of parameter estimates from the joint model with correction for left truncation (JM-C) to estimates from the joint model without correction for left truncation (JM-UN). Data generated from Weibull model.

Left Truncation Age	Parameter	True value	Probability of left truncation
			0.2				0.5				0.8
			JM-C		JM-UN		JM-C		JM-UN		JM-C		JM-UN
			%Bias	%CI	%Bias	%CI	%Bias	%CI	%Bias	%CI	%Bias	%CI	%Bias	%CI
10	${\alpha }_{b_0}$	108	0.2*	92.6	0.2*	92.4	0.2*	93.2	0.2*	93.6	0.2*	92.2	0.2*	89.8
	${\alpha }_{b_1}$	−1.65	1.4*	94.6	0.2	95.8	1.1*	95.4	−0.1	94.8	1.2*	95.6	−0.8*	95.2
	${\alpha }_T$	3.517	−1.1*	75.4	−.9*	81.2	−1.0*	75.6	−0.8*	82.2	−1.0*	77.4	−0.7*	85.8
	${\alpha }_{b_0|w}$	10.8	0.0	94.8	0.3	94.8	0.1	96.0	0.6	95.4	0.8	96.0	0.9	97.0
	${\alpha }_{b_1|w}$	0.165	2.4	94.2	−12.7*	94.4	−2.1	96.0	−19.3*	92.6	−3.5	95.4	−26.1*	94.6
	${\alpha }_{T|w}$	0.36	0.5	94.4	−3.5*	90.6	0.4	95.6	−5.4*	87.8	−0.4*	95.6	−7.3*	84.8
20	${\alpha }_{b_0}$	108	0.2*	94.4	0.2*	93.0	0.2*	91.6	0.0	92.0	0.3*	90.0	−0.1	92.0
	${\alpha }_{b_1}$	−1.65	1.5*	94.6	−1.3*	95.2	1.6*	96.0	−6.8*	77.6	2.0*	91.0	−13.1*	45.0
	${\alpha }_T$	3.517	−1.1*	75.6	−0.5*	91.8	−1.0*	79.2	0.6*	89.0	−1.1*	85.6	1.8*	33.8
	${\alpha }_{b_0|w}$	10.8	0.3	93.0	−0.1	95.0	0.3	95.8	2.3*	94.6	−1.2	94.6	2.1*	94.6
	${\alpha }_{b_1|w}$	0.165	−0.2	94.4	−14.7*	96.0	1.3	95.2	−54.3*	82.2	10.0*	94.0	−94.2*	67.2
	${\alpha }_{T|w}$	0.36	0.4	94.2	−4.3*	91.4	1.6*	95.0	−12.8*	63.2	1.4*	94.8	−25.0*	15.4
30	${\alpha }_{b_0}$	108	0.1*	91.0	0.0	90.2	0.2*	92.6	−0.2*	92.4	0.2*	91.0	−0.5*	93.0
	${\alpha }_{b_1}$	−1.65	1.1*	95.2	−3.6*	88.8	1.6*	95.4	−11.8*	52.8	1.9*	93.0	−25.4*	4.4
	${\alpha }_T$	3.517	−1.1*	78.6	0.0	97.0	−1.1*	83.2	2.0*	46.2	−1.1*	89.4	4.8*	0.4
	${\alpha }_{b_0|w}$	10.8	0.7	94.6	1.2	93.2	1.4*	95.8	2.8*	92.8	−0.1	95.2	3.4*	94.4
	${\alpha }_{b_1|w}$	0.165	−3.6*	94.6	−13.0*	94.6	−7.8*	96.4	−41.9*	87.8	1.4	95.4	−112.0*	63.0
	${\alpha }_{T|w}$	0.36	0.1*	92.6	−0.7	93.0	0.6	96.0	−4.9*	91.8	2.0	94.4	−20.9*	46.6

^*significant bias (p<0.05)

6. DISCUSSION

In this paper, we present a method for dealing with bias caused by left truncation (delayed entry) in registry data, such as the CF data. Under the assumed model, correlation between y_i and $T_i^0$ is induced through nonzero correlations between random effects b_i and $T_i^0$ in a multivariate normal model. Previous studies [1,5] focused on the use of this joint model in the absence of delayed entry to examine the relationship between y and the time to event T and to deal with nonignorable dropout in y. This paper shows that more generally under this model, delayed entry of a subject i (i.e. where follow-up begins at age L_i) implies left truncation of that subject’s survival time, and correct inference requires that the left truncation be correctly specified in the log likelihood to be maximized (equation A.1.1).

We present a novel EM algorithm that includes as part of the “complete” data for subject i, the random effects and survival times from an unknown number of subjects, who were unobserved because their survival times were less than the left truncation time L_i of the observed subject. We note however that the EM formulation is just a device for finding parameter values that maximize the likelihood of the observed data. In principle, values of parameters that maximize this likelihood could be found by other more traditional maximization algorithms.

Simulation studies under data generated from the correctly specified lognormal model (scenario 1) showed that the JM-UN model resulted in biased estimates of most fixed effects parameters. In contrast, under this scenario, the JM-C performed well.

The analyses of the CWRU CF database were consistent with simulation findings. The JM-C model appeared to correct for biases in estimates of survival and FEV1 % predicted decline caused by left truncation and provided intuitively reasonable estimates. In contrast, the JM-UN model appeared to overestimate survival, and underestimate level and decline in FEV1 with bias that increased with the degree of left truncation.

In simulations where the survival model was misspecified (scenario 2), estimates of fixed effects parameters from both JM-UN and JM-C models had bias and/or incomplete confidence interval coverage, although estimates of parameters related to intercept and slope of y from the JM-C model had smaller bias as compared to the JM-UN model. These results emphasize the importance of assessing fit of the survival model; comparison of model estimates with Cox model estimates adjusting for left truncation as in Figure 3 is one possible approach. The methods proposed here should not be used when a large proportion of subjects have left-truncated survival times since in this case estimation of the left-hand tail of the survival distribution relies heavily on model assumptions. Finally, numerous authors who have studied and developed joint models like ours that rely on untestable assumptions (e.g., concerning specification of the relationship between y and $T^0$) have stressed the importance of carrying out sensitivity analyses under different models [5, 20–22].

Appendix A

A.1. The observed data log-likelihood

The observed data log-likelihood defined in equation (3) can be computed using the following formula:

$$\begin{array}{l}{\text{LL}}_{\text{observed}}(\alpha ,\mathrm{\Omega },{\sigma }_e^2)=-{\displaystyle \sum _{i=1}^n{\delta }_i\left\{\frac{1}{2}\ln (2\pi )+\frac{1}{2}\ln ({\sigma }_{t_i|y_i}^2)+\frac{1}{2}\left(\frac{{(T_i-{\mu }_{t_i|y_i})}^2}{{\sigma }_{t_i|y_i}^2}\right)+I_i^{tr}\ln \left[1-\mathrm{\Phi }\left(\frac{L_i-{\mu }_{t_i|y_i}}{{\sigma }_{t_i|y_i}}\right)\right]\right\}}+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}(1-{\delta }_i)\left\{\ln \left[1-\mathrm{\Phi }\left(\frac{T_i-{\mu }_{t_i|y_i}}{{\sigma }_{t_i|y_i}}\right)\right]-I_i^{tr}\ln \left[1-\mathrm{\Phi }\left(\frac{L_i-{\mu }_{t_i|y_i}}{{\sigma }_{t_i|y_i}}\right)\right]\right\}}\\ -\frac{1}{2}{\displaystyle \sum _{i=1}^n(1-I_i^{tr})\{n_i\ln (2\pi )+\ln |{\sum }_i|+(y_i-X_i\alpha )\prime {\sum }_i^{-1}(y-X_i\alpha )\}}+{\displaystyle \sum _{i=1}^n{I}_i^{tr}\{-\ln \left(1-\mathrm{\Phi }\left(\frac{L_i-{\mu }_t}{{\sigma }_t}\right)\right)-\frac{n_i}{2}\ln (2\pi )-\frac{1}{2}\ln (|v_{\mathit{yit}}|)-\frac{1}{2}\ln ({\sigma }_t^2)+\frac{1}{2V_i}(M_i^2+2V_i(A_i-0.5{\mu }_t^2/{\sigma }_t^2))}+\frac{1}{2}\ln (V_i)+\ln \left[1-\mathrm{\Phi }\left(\frac{L_i-M_i}{\sqrt{V_i}}\right)\right]\}\end{array}$$ (A.1.1)

where ${\mu }_{t|y}=E(T_i^0|y)=W_{2i}\alpha +{\sigma }_{bt}^{\prime }{Z}_i^{\prime }{\sum }_i^{-1}(y_i-X_i\alpha ),{\sigma }_{t|y}={\left[{\sigma }_t^2-{\sigma }_{bt}^{\prime }{Z}_i^{\prime }{\sum }_i^{-1}{Z}_i{\sigma }_{bt}\right]}^{1/2}$, ${\sum }_i=Z_i{\sum }_b{Z}_i^{\prime }+{\sigma }^2{I}_i$, $v_{\mathit{yit}}=\mathrm{var}(y_i|T_i^0)=Z_i\sum Z_i^{\prime }+{\sigma }_e^2{I}_i-Z_i{\sigma }_{bt}{\sigma }_{bt}^{\prime }{Z}_i^{\prime }/{\sigma }_t^2$, A_i = $-\frac{1}{2}(y_i^{\prime }{\mathrm{v}}_{\mathit{yit}}^{-1}{y}_i-2y_i^{\prime }{\mathrm{v}}_{\mathit{yit}}^{-1}{a}_{1i}+a_{1i}^{\prime }{\mathrm{v}}_{\mathit{yit}}^{-1}{a}_{1i})$, B_i = $y_i^{\prime }{\mathrm{v}}_{\mathit{yit}}^{-1}{a}_{2i}-a_{1i}^{\prime }{\mathrm{v}}_{\mathit{yit}}^{-1}{a}_{2i}$, $V_i=\frac{{\sigma }_t^2}{1+a_{2i}^{\prime }{\mathrm{v}}_{\mathit{yit}}^{-1}{a}_{2i}{\sigma }_t^2}$ (where $a_{1i}=Z_i{W}_{1i}\alpha -Z_i({\sigma }_{bt}/{\sigma }_t^2)W_{2i}\alpha$ and $a_{2i}=Z_i({\sigma }_{bt}/{\sigma }_t^2)$) and $M_i=V_i(B_i+{\mu }_t/{\sigma }_t^2)$. The first two summation terms of equation (A.1.1) represent the first term on the right hand side of equation (3), i.e. ${\displaystyle \sum _{i=1}^n\ln \{f(}{T}_i,{\delta }_i|y_i,L_i,I_i^{tr})\}$and the last two summation terms represent ${\displaystyle \sum _{i=1}^n\ln \{f(y_i|L_i,I_i^{tr})\}}$ = ${\displaystyle \sum _{i=1}^n(1-I_i^{tr})\ln \{f(y_i)\}}+{\displaystyle \sum _{i=1}^n{I}_i^{tr}\ln \{f(y_i|T_i^0>L_i)\}}$, where f(y_i) is the $N(X_i\alpha ,Z_i{\sum }_b{Z}_i^{\prime }+{\sigma }_e^2{I}_i)$density. The fourth summation term in (A.1.1) is derived by writing $f(y_i|T_i^0>L_i)=(1/P(T_i^0>L_i){\displaystyle {\int }_{L_i}^{\infty }f(y_i|T_i^0)f(}{T}_i^0)\partial T_i^0$, and completing the square for $T_i^0$inside the integral.

A.2. Computational details for the E-step of the EM algorithm

As noted in section 2, the E-step involves calculating the following for each subject i:

$$S_{vi}^{(t)}=E(S_{vi}|y_i,L_i,T_i,{\delta }_i,I_i^{tr};{\alpha }^{(t)},{\mathrm{\Omega }}^{(t)},{\sigma }_e^{2(t)}),v=1,\dots ,6,\text{and}{m}_i^{(t)}=E(m_i|L_i,I_i^{tr};{\alpha }^{(t)},{\mathrm{\Omega }}^{(t)},{\sigma }_e^{2(t)}).$$

For example, consider the calculation of $S_{2i}^{(t)}$. This is computed as follows:

$$S_{2i}^{(t)}=E(S_{2i}|y_i,L_i,T_i,{\delta }_i,I_i^{tr};{\alpha }^{(t)},{\mathrm{\Omega }}^{(t)},{\sigma }_e^{2(t)})=E(S_{2i}|\text{observed data})=E((T_i^0+{\displaystyle \sum _{j=0}^{m_i}{T}_{ij}^{\ast })}|y_i,L_i,T_i,{\delta }_i;{\alpha }^{(t)},{\mathrm{\Omega }}^{(t)},{\sigma }_e^{2(t)})=E(T_i^0|y_i,L_i,T_i,{\delta }_i)+E({\displaystyle \sum _{j=0}^{m_i}{T}_{ij}^{\ast }}|y_i,L_i,T_i,{\delta }_i).$$

We begin by considering separately the cases for δ_i =1 ( $T_i^0$is observed) and δ_i =0 ( $T_i^0$is right-censored).

When δ_i =1, $T_i^0$ is observed, so, $E(T_i^0|y_i,L_i,T_i,{\delta }_i=1)=T_i^0$. Given $T_{ij}^{\ast }$ are independent of (y_i, $T_i^0$, δ_i), but depend on L_i, $E(S_{2i}|\text{observed data})=T_i^0+E({\displaystyle \sum _{j=0}^{m_i}{T}_{ij}^{\ast }}|T_{ij}^{\ast }<L_i).$ Since the $T_{ij}^{\ast },$ j = 1,…, m_i, are identically distributed, this becomes

$$E(S_{2i}|\text{observed data})=T_i^0+E(m_i|L_i)E(T_{ij}^{\ast }|T_{ij}^{\ast }<L_i)=T_i^0+\left(\frac{1-p_i}{p_i}\right)M_{1i}^{\ast }$$

where $M_{1i}^{\ast }=E(T_{ij}^{\ast }|T_{ij}^{\ast }<L_i)$is given in equation (A.2.2).

When δ_i =0, $T_i^0$ is right censored, $T_i^0>C_i$, and $T_i^0$ is not dependent on L_i: $E(T_i^0|y_i,L_i,T_i,{\delta }_i=0)=E(T_i^0|T_i^0>C_i,y_i)$. As before, $T_{ij}^{\ast }$are identically distributed, independent of (y_i, $T_i^0$, δ_i), but depend on L_i; therefore,

$$E(S_{2i}|\text{observed data})=E(T_i^0|T_i^0>C_i,y_i)+\left(\frac{1-p_i}{p_i}\right)M_{1i}^{\ast }=M_{1i}+\left(\frac{1-p_i}{p_i}\right)M_{1i}^{\ast }$$

where $M_{1i}=E(T_i^0|T_i^0>C_i,y_i)$ is given in the Appendix (equation (A.2.1)).

Combining both cases when δ_i =1 and δ_i =0, $S_{2i}^{(t)}$ becomes:

$$S_{2i}^{(t)}=E(S_{2i}|\text{observed data})={\delta }_i{T}_i^0+(1-{\delta }_i)M_{1i}+\left(\frac{1-p_i}{p_i}\right)M_{1i}^{\ast }.$$

The other terms for the E-step, $S_{1i}^{(t)},S_{3i}^{(t)},S_{4i}^{(t)},S_{5i}^{(t)},\text{and}{S}_{6i}^{(t)}$, can be derived similarly.

The following additional quantities are needed for the E-step:

A.2.1. Conditional Moments of $T_i^0$ when right-censored and left-truncated

Conditional on y_i, $T_i^0$ is normal, with mean $u_i=W_{2i}\alpha +{\sigma }_{bt}^{\prime }{Z}_i^{\prime }{(Z_i{\sum }_b{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}(y_i-Z_i{W}_{1i}\alpha )$and variance $s_i^2={\sigma }_t^2-{\sigma }_{bt}^{\prime }{Z}_i^{\prime }{(Z_i{\sum }_b{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}{Z}_i{\sigma }_{bt}$. Using results in Johnson and Kotz [23] on the mean and variance of left- and right-truncated normal random variables, it can be shown that:

$$M_{1i}=E(T_i^0|T_i^0>C_i,y_i)=u_i+s_{i}H[(C_i-u_i)/s_i]$$ (A.2.1)

$$M_{2i}=E({(T_i^0)}^2|T_i^0>C_i,y_i)=s_i^2\{1+[(C_i-u_i)/s_i]H[(C_i-u_i)/s_i]-H{[(C_i-u_i)/s_i]}^2\}+{(M_{1i})}^2$$

And similarly, since $T_{ij}^{\ast }$ has mean $W_{2i}\alpha$ and variance ${\sigma }_t^2$it can be shown that:

$$M_{1i}^{\ast }=E(T_{ij}^{\ast }|T_{ij}^{\ast }<L_i)=W_{2i}\alpha -{\sigma }_t{H}^{\ast }[(L_i-W_{2i}\alpha )/{\sigma }_t]$$ (A.2.2)

$$M_{2i}^{\ast }=E({(T_{ij}^{\ast })}^2|T_{ij}^{\ast }<L_i)={\sigma }_t^2\left\{1-\left(\frac{L_i-W_{2i}\alpha }{{\sigma }_t}\right)H^{\ast }\left(\frac{L_i-W_{2i}\alpha }{{\sigma }_t}\right)-{\left[H^{\ast }\left(\frac{L_i-W_{2i}\alpha }{{\sigma }_t}\right)\right]}^2\right\}+{(M_{1i}^{\ast })}^2$$

where H(z)= ϕ(z)/(1−Φ (z)) and and H^*(z)= ϕ(z)/Φ(z), ϕ(z) is the standard normal probability density function, and $\mathrm{\Phi }(z)={\displaystyle {\int }_{-\infty }^z\varphi (x)\partial x}$is the standard normal cumulative distribution function.

A.2.2. Derived expectations for the E-Step

$$E(m_i|L_i)=(1-p_i)/p_i,p_i=P(T_i^0>L_i)=1-\mathrm{\Phi }\left(\frac{L_i-W_{2i}\alpha }{{\sigma }_t}\right).$$ (A.2.3)

$$\mathrm{E}(S_{1i}|\text{observed data})=((1-p_i)/p_i)\left(W_{1i}\alpha +({\sigma }_{bt}/{\sigma }_t^2)[M_{1i}^{\ast }-W_{2i}\alpha ]\right)+{\delta }_i\left(W_{1i}\alpha +({\sigma }_{bt}/{\sigma }_t^2)(T_i^0-W_{2i}\alpha )+{\sum }^{\ast }{Z}^{\prime }{(Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}[y_i-Z_i{W}_{1i}\alpha -Z_i({\sigma }_{bt}/{\sigma }_t^2)(T_i^0-W_{2i}\alpha )]\right)+(1-{\delta }_i)\left(W_{1i}\alpha +({\sigma }_{bt}/{\sigma }_t^2)(M_{1i}-W_{2i}\alpha )+{\sum }^{\ast }{Z}^{\prime }{(Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}[y_i-Z_i{W}_{1i}\alpha -Z_i({\sigma }_{bt}/{\sigma }_t^2)(M_{1i}-W_{2i}\alpha )]\right).$$

$$\mathrm{E}(S_{2i}|\text{observed data})={\delta }_i{T}_i^0+(1-{\delta }_i)M_{1i}+((1-p_i)/p_i)M_{1i}^{\ast }.$$

$$E\left(S_{3i}|\mathit{observed}\mathit{data}\right)={\delta }_i\{[I-{\sum }^{\ast }{Z}_i^{\prime }{(Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}{Z}_i]{\sum }^{\ast }+\left(D_i+E_i{T}_i^0\right){\left(D_i+E_i{T}_i^0\right)}^{\prime }\}+(1-{\delta }_i)\{[I-{\sum }^{\ast }{Z}_i^{\prime }{(Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}{Z}_i]{\sum }^{\ast }+D_i{D}_i^{\prime }+(D_i{E}_i^{\prime }+E_i{D}_i^{\prime })M_{1i}+E_i{E}_i^{\prime }{M}_{2i}\}+((1-p_i)/p_i)\left[{\sum }^{\ast }+K_i{K}_i^{\prime }+(K_i{J}^{\prime }+J{K}_i^{\prime })M_{1i}^{\ast }+J{J}^{\prime }{M}_{2i}^{\ast }\right]$$

where $D_i=W_{1i}\alpha -({\sigma }_{bt}/{\sigma }_t^2)W_{2i}\alpha +{\sum }^{\ast }{Z}^{\prime }{(Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}[y_i-Z_i{W}_{1i}\alpha +Z_i({\sigma }_{bt}/{\sigma }_t^2)W_{2i}\alpha ]$, $E_i=[I-{\sum }^{\ast }{Z}^{\prime }{(Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i)}^{-1}{Z}_i]({\sigma }_{bt}/{\sigma }_t^2)$, $K_i=W_{1i}\alpha -({\sigma }_{bt}/{\sigma }_t^2)W_{2i}\alpha$, and $J={\sigma }_{bt}/{\sigma }_t^2$.

$$\mathrm{E}(S_{4i}|\text{observed data})={\delta }_i{(T_i^0)}^2+(1-{\delta }_i)M_{2i}+((1-p_i)/p_i)M_{2i}^{\ast }.$$

$$E\left(S_{5i}|\mathit{observed}\mathrm{data}\right)={\delta }_i\left[T_i^0(D_i+E_i{T}_i^0)\right]+(1-{\delta }_i)\left[D_i{M}_{1i}+E_i{M}_{2i}\right]+\left(\frac{(1-p_i)}{p_i}\right)\left(K_i{M}_{1i}^{\ast }+J_i{M}_{2i}^{\ast }\right)$$

$$\mathrm{E}(S_{6i}|\text{observed data})={\delta }_{i}tr\{\mathrm{cov}(e_i|y_i,T_i^0)+(E(e_i|y_i,T_i^0))(E{(e_i|y_i,T_i^0))}^{\prime }\}+(1-{\delta }_i)tr\{\mathrm{cov}(e_i|y_i,T_i^0)+F_i{F}_i^{\prime }+(F_i{G}_i^{\prime }+G_i{F}_i^{\prime })M_{1i}+G_i{G}_i^{\prime }{M}_{2i}\}$$

where $F_i={\sigma }_e^2{I}_i{[Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i]}^{-1}(y_i-X_i\alpha +Z_i({\sigma }_{bt}/{\sigma }_t^2)W_{2i}\alpha ),$ $G_i=-{\sigma }_e^2{I}_i{[Z_i{\sum }^{\ast }{Z}_i^{\prime }+{\sigma }_e^2{I}_i]}^{-1}{Z}_i({\sigma }_{bt}/{\sigma }_t^2),$ and $\mathrm{cov}(e_i|y_i,T_i^0)={\sigma }_e^2[I_i-{\sigma }_e^2{({\sigma }_e^2{I}_i+Z_i{\sum }^{\ast }{Z}_i^{\prime })}^{-1}]$.

Appendix B

Details on Formulation of the EM algorithm

To formulate the EM algorithm, we modify and follow a general EM approach set forward by Bee [16] and McLachlan and Krishnan [24] for maximum likelihood estimation with grouped and truncated data. For the moment, we focus only on the complete data for a given subject i in terms of survival times and random effects. We consider two cases. If $I_i^{tr}=0$(no left truncation occurred with respect to subject i) the complete data for subject i consist of ( $T_i^0$, b_i) alone and implementation of the EM is straightforward. When $I_i^{tr}$= 0 the complete data log likelihood based on $(b_i,T_i^0)$ is just the logarithm of $f_{bt}\left({(b_i,T_i^0)}^{\prime };\alpha ,\mathrm{\Omega }\right)$ (2). However, if $I_i^{tr}=1$(left truncation due to delayed entry occurred) complete data for subject i are assumed to consist of data for the observed subject $(b_i,T_i^0)$where $T_i^0$>L_i, plus m_i ≥ 0 unobserved pairs $(b_{ij}^{\ast },T_{ij}^{\ast })$, j = 1,…,m_i where $T_{ij}^{\ast }$< L_i, and the $(b_{ij}^{\ast },T_{ij}^{\ast })$are undefined if m_i = 0. Note that m_i, which is unknown, is the number of unobserved “latent” subjects from the same stratum as subject i, (i.e., have the same values of L_i and w_i).

We focus on forming the complete data log likelihood corresponding to subject i when $I_i^{tr}=1$. Following McLachlan and Krishnan [24], the complete data model implies { $(b_i,T_i^0)$, $(b_{ij}^{\ast },T_{ij}^{\ast })$, j = 1,…,m_i } represent a random sample of size 1 + m_i from the untruncated multivariate normal density in equation 2. Thus the log likelihood for this “complete” data sample of 1 + m_i observations is:

$$\log f_{bt}({(b_i,T_i^0)}^{\prime };\alpha ,\mathrm{\Omega })+I(m_i>0){\displaystyle \sum _{j=1}^{m_i}\log f_{bt}(}{(b_{ij}^{\ast },T_{ij}^{\ast })}^{\prime };\alpha ,\mathrm{\Omega }).$$ (B.1)

The complete data log likelihood can also be specified in terms of the observed data $(b_i,T_i^0)$and the “missing” information: m_i and { $(b_{ij}^{\ast },T_{ij}^{\ast })$, j=1,…, m_i)}. The joint density can be factorized as the marginal density of m_i and the conditional density of $(b_i,T_i^0)$and { $(b_{ij}^{\ast },T_{ij}^{\ast })$, j = 1,…, m_i} given m_i. The conditional distributions of $(b_{ij}^{\ast },T_{ij}^{\ast })$, and of { $(b_{ij}^{\ast },T_{ij}^{\ast })$, j = 1,…, m_i} given m_i are respectively that of a sample of size one from a left truncated multivariate normal density, and a sample of size m_i from a right-truncated multivariate normal density. Leaving the density of m_i given $(b_{ij}^{\ast },T_{ij}^{\ast })$ unspecified for the moment and defining $p_i=P(T_i^0>L_i)$(equation A.2.3), with this factorization the complete data log likelihood can be written as:

$$\log f_m(m_i|T_i^0,b_i;\alpha ,\mathrm{\Omega })+\log \left\{\frac{f_{bt}({(b_i,T_i^0)}^{\prime };\alpha ,\mathrm{\Omega })}{p_i}\right\}+I(m_i>0){\displaystyle \sum _{j=1}^{m_i}\log \left\{\frac{f_{bt}({(b_{ij}^{\ast },T_{ij}^{\ast })}^{\prime };\alpha ,\mathrm{\Omega })}{1-p_i}\right\}}=\log f_{bt}({(b_i,T_i^0)}^{\prime };\alpha ,\mathrm{\Omega })+I(m_i>0){\displaystyle \sum _{j=1}^{m_i}{f}_{bt}({(b_{ij}^{\ast },T_{ij}^{\ast })}^{\prime };\alpha ,\mathrm{\Omega })}+\log f_m(m_i|T_i^0,b_i;\alpha ,\mathrm{\Omega })-\log p_i-m_i\log (1-p_i).$$ (B.2)

Since (B.1) and (B.2) are both expressions for the complete data log likelihood, they will be equal when except for an additive constant c not depending on (α, Ω),

$$\log f_m(m_i|T_i^0,b_i;\alpha ,\mathrm{\Omega })=\log p_i+m_i\log (1-p_i)$$

or

$$f_m(m_i|T_i^0,b_i;\alpha ,\mathrm{\Omega })=p_i{(1-p_i)}^{m_i}.$$ (B.3)

It can be seen that (B.3) defines a geometric distribution with probability p_i. As noted by McLaughlin and Krishnan [24], assuming the density (B.3) for m_i can be viewed as a device to produce the desired form (B.1) for the complete data log likelihood.

Intuitively we can think of the complete data as arising from a hypothetical sequential sampling scenario. All subjects sharing the same values of L_i and covariates w_i can be thought of as a stratum, where the target population consists of the union of all disjoint strata. Within a stratum (say the hth), all subjects have the same covariate vector w_i =w_h, design matrix W_i = W_h (equation 2) and truncation time L_h), and their distribution of survival time and random effects in equation (2) is N(W_hα, Ω). Subjects are randomly drawn from the target population until n untruncated observations are obtained Corresponding to each subject i in the sample, m_i is defined as the number of truncated (unobserved) subjects that were encountered from the same stratum up to the point where that subject was selected. If there are multiple left-truncated observations from the same stratum, then for each subject m_i is defined as the number of unobserved observations drawn from the stratum since the last untruncated observation was drawn from that stratum. Thus, for each observed subject in the sample, m_i is the number of failures (subjects unobserved because their transformed survival times are less than L_i) until the first success (subject with transformed survival time >L_i), where the probability of success is p_i. If for a given stratum, no subject with untruncated survival time is drawn, then no observations are observed at all from that stratum. This does not create bias under the assumed model. In the extreme case where all subjects share the same covariate values and left truncation time, if n is the observed sample size, then this model implies that the total number of unobserved subjects due to truncation, ${\displaystyle \sum _{i=1}^n{m}_i}$ is the sum of n independent geometric (p) random variables (where p₁= p₂=…= p_n= p), and thus has a negative binomial distribution, with parameters n and p.

To finish the formulation of the EM, we define additional “complete” data as e_i, i = 1,…,n, such that y_i = W_ib_i + e_i, i = 1,…,n. The e_i are assumed independent of (b_i, $T_i^0$, $b_{ij}^{\ast }$, $T_{ij}^{\ast }$and m_i) and their distribution depends only on ${\sigma }_e^2$, so including them with the complete data does not alter the interpretation above.

Because subjects are independent, and because e_i is independent of $(b_i,T_i^0)$for each subject i, the complete data log-likelihood for all subjects can then be written as in equation (3), i.e.

$${\displaystyle \sum _{i=1}^n\left\{\log f_{bt}({(b_i,T_i^0)}^{\prime };\alpha ,\mathrm{\Omega })+I_i^{tr}I(m_i>0){\displaystyle \sum _{j=1}^{m_i}\log f_{bt}(}{(b_{ij}^{\ast },T_{ij}^{\ast })}^{\prime };\alpha ,\mathrm{\Omega })\right\}}+{\displaystyle \sum _{i=1}^n\log f_e(e_i;{\sigma }_e^2}).$$

Appendix C

Weibull Model Used in Scenario 2 of Simulations

To generate data for scenario 2 of the simulations, random intercepts, slopes, and longitudinal response data y_i, i=1,…,n were generated using the same marginal mixed model and parameter settings used in scenario 1, implying ${\alpha }_{b_o}=108.0$, ${\alpha }_{b_0|w}=10.8$, ${\alpha }_{b_1}=-1.65$, and ${\alpha }_{b_1|w}=-0.165$. Conditional on b_i0, b_i1, and w_i,,the survival time A_i (years) was generated from a Weibull distribution with hazard function $\lambda (a|b_{i0},b_{i1},w_i)=\gamma {\lambda }_0{a}^{\gamma -1}\exp ({\eta }_0{u}_{i0}+{\eta }_1{u}_{i1}+{\eta }_2{w}_i)$where $u_{i0}=b_{i0}-E(b_{io}|w_i)$and $u_{i1}=b_{i1}-E(b_{i1}|w_i)$, with $(u_{i0},u_{i1})\perp w_i$ and where γ = 4.465, λ₀ = 1.05×10⁻⁷, γ₀ = −0.0113γ, η₁ = −0.3208γ, and η₂ = −0.36γ. Values of γ, λ₀, η₀ and η₁ were obtained by fitting a mixed model to the CF data to obtain empirical Bayes estimates of u_i0 and u_i1, and then fitting a Weibull regression model using Proc Lifereg in SAS, using these estimates as covariates. This model implies that the regression $T_i^0$on w_i alone is linear with slope ${\alpha }_{T|w}$=0.36, and the median survival when $u_{i0}$ $u_{i1}$ and w_i are zero is 33.7. Because in the lognormal models JM-C and JM-UN, ${\alpha }_T$is interpreted as the log of the median survival time when w_i =0, estimates of ${\alpha }_T$in the simulations were compared to log(33.7) = 3.517.